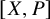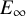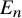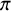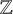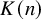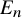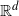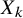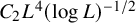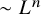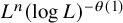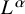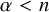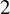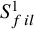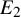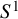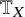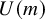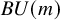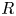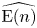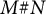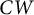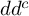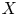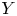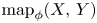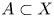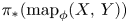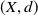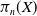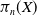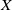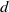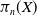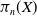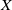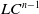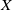113 results in 55Pxx
A study of the Ganea conjecture for topological complexity by using weak topological complexity
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 21 October 2024, pp. 1-21
-
- Article
-
- You have access
- HTML
- Export citation
The definable content of homological invariants II: Čech cohomology and homotopy classification
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 06 September 2024, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Hamiltonian ∐n BO(n)-action, stratified Morse theory and the J-homomorphism
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 2005-2099
- Print publication:
- September 2024
-
- Article
-
- You have access
- HTML
- Export citation
Deloopings of Hurwitz spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1651-1714
- Print publication:
- July 2024
-
- Article
-
- You have access
- HTML
- Export citation
Adams’ cobar construction as a monoidal
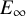 $E_{\infty }$-coalgebra model of the based loop space
$E_{\infty }$-coalgebra model of the based loop space
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 May 2024, e62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The homotopy decomposition of the suspension of a non-simply-connected five-manifold
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 17 April 2024, pp. 1-29
-
- Article
-
- You have access
- HTML
- Export citation
The Chromatic Fourier Transform
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 April 2024, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological reconstruction of compact supports of dependent stationary random variables
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-31
-
- Article
-
- You have access
- HTML
- Export citation
Degrees of maps and multiscale geometry
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 January 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cogroupoid structures on the circle and the Hodge degeneration
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 January 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chern classes in equivariant bordism
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The stable cohomology of self-equivalences of connected sums of products of spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Higher semiadditive algebraic K-theory and redshift
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 237-287
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moore’s conjecture for connected sums
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 04 December 2023, pp. 516-531
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A
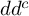 $dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM
$dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1651-1704
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spaces of functions and sections with paracompact domain
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 21 November 2023, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation
A natural pseudometric on homotopy groups of metric spaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 08 November 2023, pp. 162-174
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
On equivariant topological modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 06 November 2023, pp. 2638-2693
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Categories of graphs for operadic structures
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 155-212
- Print publication:
- January 2024
-
- Article
-
- You have access
- HTML
- Export citation
Reflexive homology
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 03 August 2023, pp. 1378-1405
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

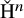 on the category of locally compact separable metric spaces each factor into (i) what we term their
on the category of locally compact separable metric spaces each factor into (i) what we term their 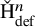 taking values in the category
taking values in the category 

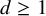
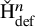 to show that a seminal problem in the development of algebraic topology – namely, Borsuk and Eilenberg’s 1936 problem of classifying, up to homotopy, the maps from a solenoid complement
to show that a seminal problem in the development of algebraic topology – namely, Borsuk and Eilenberg’s 1936 problem of classifying, up to homotopy, the maps from a solenoid complement 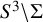
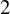
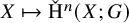 admit two main formulations: a more combinatorial one and a more homotopical formulation as the group
admit two main formulations: a more combinatorial one and a more homotopical formulation as the group 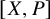
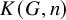
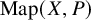
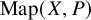
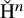 , embodies a substantial variety of classification problems arising throughout mathematics. We show, in particular, that if
, embodies a substantial variety of classification problems arising throughout mathematics. We show, in particular, that if