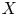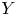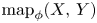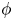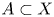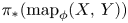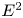1. Introduction
Let $\mathop {\rm map}\nolimits (X,\,Y)$![]() denote the space of continuous maps $X\to Y$
denote the space of continuous maps $X\to Y$![]() where $Y$
where $Y$![]() has the homotopy type of a nilpotent CW complex, and let $l\colon Y\to Y_{(P)}$
has the homotopy type of a nilpotent CW complex, and let $l\colon Y\to Y_{(P)}$![]() denote localization at the set of primes $P$
denote localization at the set of primes $P$![]() . The induced map
. The induced map
is known to be localization at $P$![]() on each path component under various assumptions on $X\!$
on each path component under various assumptions on $X\!$![]() . By the classical results of Hilton, Mislin, Roitberg and Steiner [Reference Hilton, Mislin, Roitberg and Steiner13, Theorems A and B], $X$
. By the classical results of Hilton, Mislin, Roitberg and Steiner [Reference Hilton, Mislin, Roitberg and Steiner13, Theorems A and B], $X$![]() can be a homologically finite CW complex. The more recent results of Klein, Schochet, and Smith [Reference Klein, Schochet and Smith16] (and [Reference Schochet and Smith26]) show that this also holds whenever $X$
can be a homologically finite CW complex. The more recent results of Klein, Schochet, and Smith [Reference Klein, Schochet and Smith16] (and [Reference Schochet and Smith26]) show that this also holds whenever $X$![]() is a compact metric space and one knows, a priori, that the function spaces involved are nilpotent. Similar results hold for spaces of sections (see Møller [Reference Møller24] for the case of a CW domain, and [Reference Klein, Schochet and Smith16] for the case of a compact metric domain). Here we address the question of nilpotency and localization for function and section spaces with more general paracompact domains by a unified approach; the case of a locally compact subspace of a Euclidean space has served as a particular motivation.
is a compact metric space and one knows, a priori, that the function spaces involved are nilpotent. Similar results hold for spaces of sections (see Møller [Reference Møller24] for the case of a CW domain, and [Reference Klein, Schochet and Smith16] for the case of a compact metric domain). Here we address the question of nilpotency and localization for function and section spaces with more general paracompact domains by a unified approach; the case of a locally compact subspace of a Euclidean space has served as a particular motivation.
To achieve our goal, we need a good grip on the homotopy groups of $\mathop {\rm map}\nolimits (X,\,Y)$![]() . Federer [Reference Federer10] constructed a spectral sequence of groups, arising from an exact couple, converging to $\pi _*(\mathop {\rm map}\nolimits (X,\,Y))$
. Federer [Reference Federer10] constructed a spectral sequence of groups, arising from an exact couple, converging to $\pi _*(\mathop {\rm map}\nolimits (X,\,Y))$![]() for a finite-dimensional CW complex $X$
for a finite-dimensional CW complex $X$![]() and a simple CW complex $Y$
and a simple CW complex $Y$![]() (see also [Reference Smith27] for a based rational version). Dyer [Reference Dyer8] generalized Federer's spectral sequence to the case of a paracompact Hausdorff space of finite covering dimension $X$
(see also [Reference Smith27] for a based rational version). Dyer [Reference Dyer8] generalized Federer's spectral sequence to the case of a paracompact Hausdorff space of finite covering dimension $X$![]() . The method was to represent $X$
. The method was to represent $X$![]() as an inverse limit of polyhedra and take the direct limit of Federer's exact couples. Analogous approaches were those of Dror Farjoun and Schochet [Reference Farjoun and Schochet7] and Klein, Schochet and Smith [Reference Klein, Schochet and Smith16].
as an inverse limit of polyhedra and take the direct limit of Federer's exact couples. Analogous approaches were those of Dror Farjoun and Schochet [Reference Farjoun and Schochet7] and Klein, Schochet and Smith [Reference Klein, Schochet and Smith16].
Here, we take the dual approach (as in [Reference Hilton, Mislin, Roitberg and Steiner13] and [Reference Møller24]), and express the nilpotent CW complex $Y\!$![]() as a weak limit of the refined Postnikov tower of principal fibrations $Y_q\to Y_{q-1}$
as a weak limit of the refined Postnikov tower of principal fibrations $Y_q\to Y_{q-1}$![]() . We note that, similarly as in the case of a CW complex $X$
. We note that, similarly as in the case of a CW complex $X$![]() , the associated tower of maps $\mathop {\rm map}\nolimits (X,\,Y_q)\to \mathop {\rm map}\nolimits (X,\,Y_{q-1})$
, the associated tower of maps $\mathop {\rm map}\nolimits (X,\,Y_q)\to \mathop {\rm map}\nolimits (X,\,Y_{q-1})$![]() is also one of principal fibrations under reasonable conditions. Of course, there is the spectral sequence of Bousfield and Kan [Reference Bousfield and Kan5] associated to any tower of fibrations, but that involves sets and groups acting on sets, and is not ready-made for localization. We observe that Federer's method admits an abstract generalization to any tower of principal fibrations and obtain a spectral sequence of groups (arising from an exact couple) and a slightly tweaked version thereof that contains sufficient information to detect localization of the limiting homotopy groups at the $E^2$
is also one of principal fibrations under reasonable conditions. Of course, there is the spectral sequence of Bousfield and Kan [Reference Bousfield and Kan5] associated to any tower of fibrations, but that involves sets and groups acting on sets, and is not ready-made for localization. We observe that Federer's method admits an abstract generalization to any tower of principal fibrations and obtain a spectral sequence of groups (arising from an exact couple) and a slightly tweaked version thereof that contains sufficient information to detect localization of the limiting homotopy groups at the $E^2$![]() -level. It seems that these observations are novel. To state our main result, we first let $\mathop {\rm map}\nolimits _\phi (X,\,Y)$
-level. It seems that these observations are novel. To state our main result, we first let $\mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() denote the subspace of $\mathop {\rm map}\nolimits (X,\,Y)$
denote the subspace of $\mathop {\rm map}\nolimits (X,\,Y)$![]() consisting of maps whose restriction to the closed subspace $A\subset X$
consisting of maps whose restriction to the closed subspace $A\subset X$![]() is a prescribed map $\phi \colon A\to Y$
is a prescribed map $\phi \colon A\to Y$![]() . Further let $X$
. Further let $X$![]() be a paracompact Hausdorff k-space; we will be using the shorthand $X\in {\rm PHK}$
be a paracompact Hausdorff k-space; we will be using the shorthand $X\in {\rm PHK}$![]() . (The obvious examples are metric spaces, compact Hausdorff spaces, and CW complexes.) Assume that $Y$
. (The obvious examples are metric spaces, compact Hausdorff spaces, and CW complexes.) Assume that $Y$![]() is a CW approximation to the inverse limit of successive principal fibrations with fibres $K(\pi ^q,\,n_q)$
is a CW approximation to the inverse limit of successive principal fibrations with fibres $K(\pi ^q,\,n_q)$![]() where $1=n_1\leqslant n_2\leqslant \dots$
where $1=n_1\leqslant n_2\leqslant \dots$![]() . Let $\check H^*(X,\,A;\pi )$
. Let $\check H^*(X,\,A;\pi )$![]() denote Čech cohomology with coefficients in the abelian group $\pi$
denote Čech cohomology with coefficients in the abelian group $\pi$![]() . Additionally, assume one of the following.
. Additionally, assume one of the following.
(i) $\phi =\mathop {\rm const}\nolimits _{y_0}$
 where $y_0$
where $y_0$ is nondegenerate; we use $\mathop {\rm map}\nolimits _{A\to y_0}(X,\,Y)$
is nondegenerate; we use $\mathop {\rm map}\nolimits _{A\to y_0}(X,\,Y)$ in this case.
in this case.(ii) $A\hookrightarrow X$
 is a closed Hurewicz cofibration (for example, $A$
is a closed Hurewicz cofibration (for example, $A$ may be empty).
may be empty).(iii) $(X,\,A)$
 is a proper pair (see definition 1.5) and $Y$
is a proper pair (see definition 1.5) and $Y$ is an ANR, i.e., an absolute neighbourhood retract for metric spaces.
is an ANR, i.e., an absolute neighbourhood retract for metric spaces.
Theorem 1.1 Take $f\in \mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() . There exists an upper half-plane homology type spectral sequence of groups where $E^2_{-p,q}$
. There exists an upper half-plane homology type spectral sequence of groups where $E^2_{-p,q}$![]() is isomorphic with $\check H^{n_q-q+p}(X,\,A;\pi ^q)$
is isomorphic with $\check H^{n_q-q+p}(X,\,A;\pi ^q)$![]() for $1\leqslant q\geqslant p\geqslant 0$
for $1\leqslant q\geqslant p\geqslant 0$![]() and trivial otherwise. The $n$
and trivial otherwise. The $n$![]() -th differential consists of morphisms $d^n_{-p,q}\colon E^n_{-p,q}\to E^n_{-p-n,q+n-1}$
-th differential consists of morphisms $d^n_{-p,q}\colon E^n_{-p,q}\to E^n_{-p-n,q+n-1}$![]() .
.
Assume also that $Y\!$![]() has only finitely many nontrivial homotopy groups or that $\mathop {\rm dim}\nolimits X\!$
has only finitely many nontrivial homotopy groups or that $\mathop {\rm dim}\nolimits X\!$![]() (respectively $\mathop {\rm dim}\nolimits (X,\,A)$
(respectively $\mathop {\rm dim}\nolimits (X,\,A)$![]() under (iii) above) is finite. Then $\mathop {\rm map}\nolimits _\phi (X,\,Y)$
under (iii) above) is finite. Then $\mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() is nilpotent and the spectral sequence converges to $\pi _k(\mathop {\rm map}\nolimits _\phi (X,\,Y),\,f)$
is nilpotent and the spectral sequence converges to $\pi _k(\mathop {\rm map}\nolimits _\phi (X,\,Y),\,f)$![]() for $k\geqslant 1$
for $k\geqslant 1$![]() .
.
The spectral sequence is natural with respect to maps of pairs $(X,\,A)\to (X',\,A')$![]() over $Y$
over $Y$![]() and with respect to maps $Y\to Y'$
and with respect to maps $Y\to Y'$![]() induced by maps of classifying spaces $K(\pi ^q_{Y},\,n_q+1)\to K(\pi ^q_{Y'},\,n_q+1)$
induced by maps of classifying spaces $K(\pi ^q_{Y},\,n_q+1)\to K(\pi ^q_{Y'},\,n_q+1)$![]() . Let $E^n_{-p,q}\to E'^n_{-p,q}$
. Let $E^n_{-p,q}\to E'^n_{-p,q}$![]() be the associated map in any of the two cases and let $\pi _k\to \pi _k'$
be the associated map in any of the two cases and let $\pi _k\to \pi _k'$![]() be the associated morphism of homotopy groups of mapping spaces. Assume that both $E^n$
be the associated morphism of homotopy groups of mapping spaces. Assume that both $E^n$![]() and $E'^n$
and $E'^n$![]() converge and that
converge and that
• $E^2_{-p,q}\to E'^2_{-p,q}$
 P-localizes for $q>p\geqslant 0$
P-localizes for $q>p\geqslant 0$ , and
, and• the torsion in $E'^2_{-q,q}$
 is P-local and $E^2_{-q,q}\to E'^2_{-q,q}$
is P-local and $E^2_{-q,q}\to E'^2_{-q,q}$ is P-injective for $q>0$
is P-injective for $q>0$ .
.
Then $\pi _k\to \pi _k'$![]() are P-localizations for all $k\geqslant 1$
are P-localizations for all $k\geqslant 1$![]() .
.
If $Y\!$![]() is connected and simple in all dimensions, we obtain a second-quadrant sequence with non-zero $E^2$
is connected and simple in all dimensions, we obtain a second-quadrant sequence with non-zero $E^2$![]() -terms given by $E^2_{-p,q}\cong \check H^p(X,\,A;\pi _q(Y))$
-terms given by $E^2_{-p,q}\cong \check H^p(X,\,A;\pi _q(Y))$![]() for $q\geqslant p\geqslant 0$
for $q\geqslant p\geqslant 0$![]() .
.
The theorem is proved in § 5 as a consequence of theorem 3.1 and the results in § 4; theorem 3.1 also contains a precise description of the first differential in terms of the $k$![]() -invariants of $Y$
-invariants of $Y$![]() . We emphasize that in the absolute case (i.e., $A=\emptyset$
. We emphasize that in the absolute case (i.e., $A=\emptyset$![]() ), the result always depends only on the homotopy type of $Y$
), the result always depends only on the homotopy type of $Y$![]() , while if $A$
, while if $A$![]() is nonempty and not cofibred in $X$
is nonempty and not cofibred in $X$![]() , then the topology of $Y$
, then the topology of $Y$![]() will play a role (§ 7 contains details for the ‘twisted’ relative case). For example, $Y$
will play a role (§ 7 contains details for the ‘twisted’ relative case). For example, $Y$![]() is an ANR if it is a smooth manifold or a locally finite CW complex.
is an ANR if it is a smooth manifold or a locally finite CW complex.
The nilpotency of $\mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() and convergence of the spectral sequence are automatic if $Y$
and convergence of the spectral sequence are automatic if $Y$![]() is a Postnikov section; this is a feature of our approach. The applications of [Reference Klein, Schochet and Smith16] include cases where $Y=K_{(0)}$
is a Postnikov section; this is a feature of our approach. The applications of [Reference Klein, Schochet and Smith16] include cases where $Y=K_{(0)}$![]() is the rationalization of a finite CW complex $K$
is the rationalization of a finite CW complex $K$![]() ; if $K$
; if $K$![]() is rationally elliptic, then $Y$
is rationally elliptic, then $Y$![]() will be a Postnikov section, guaranteeing convergence for any $X\in {\rm PHK}$
will be a Postnikov section, guaranteeing convergence for any $X\in {\rm PHK}$![]() . (Compare also with [Reference Farjoun and Schochet7, Theorem A].)
. (Compare also with [Reference Farjoun and Schochet7, Theorem A].)
The following is a formal consequence of the naturality in theorem 1.1.
Corollary 1.2 Assume the conditions for convergence in theorem 1.1. If the canonical morphisms $\check H^i(X,\,A;\pi ^q)\to \check H^i(X,\,A;\pi ^q\otimes {\mathbb {Z}}_{(P)})$![]() are localizations at P for all $q$
are localizations at P for all $q$![]() and all $i\leqslant n_q$
and all $i\leqslant n_q$![]() , then $\mathop {\rm map}\nolimits _\phi (X,\,Y)\to \mathop {\rm map}\nolimits _\phi (X,\,Y_{(P)})$
, then $\mathop {\rm map}\nolimits _\phi (X,\,Y)\to \mathop {\rm map}\nolimits _\phi (X,\,Y_{(P)})$![]() localizes homotopy groups at all basepoints. (Here, $Y_{(P)}$
localizes homotopy groups at all basepoints. (Here, $Y_{(P)}$![]() is required to be an ANR if $Y\!$
is required to be an ANR if $Y\!$![]() is.)
is.)
Universal coefficients for Čech cohomology of compact spaces immediately imply
Corollary 1.3 Suppose that $X$![]() is compact Hausdorff and Y has the homotopy type of a nilpotent CW complex. If $\mathop {\rm dim}\nolimits X<\infty$
is compact Hausdorff and Y has the homotopy type of a nilpotent CW complex. If $\mathop {\rm dim}\nolimits X<\infty$![]() or $Y$
or $Y$![]() is a Postnikov section, the induced map (1.1) is localization on each path component.
is a Postnikov section, the induced map (1.1) is localization on each path component.
Example 1.4 In [Reference Kahn15], D. S. Kahn constructed a compact metric space $X$![]() with trivial integral Čech cohomology groups $\check H^q(X;{\mathbb {Z}})$
with trivial integral Čech cohomology groups $\check H^q(X;{\mathbb {Z}})$![]() for $q>1$
for $q>1$![]() but with essential maps $X\to {\mathbb {S}}^3$
but with essential maps $X\to {\mathbb {S}}^3$![]() . Let $Y=B{\mathbb {S}}^3$
. Let $Y=B{\mathbb {S}}^3$![]() be the classifying space of the sphere ${\mathbb {S}}^3$
be the classifying space of the sphere ${\mathbb {S}}^3$![]() with basepoint $y_0$
with basepoint $y_0$![]() . Then $\pi _1(\mathop {\rm map}\nolimits (X,\,Y),\,\mathop {\rm const}\nolimits _{y_0})\cong \pi _1(\mathop {\rm map}\nolimits _*(X,\,Y),\,\mathop {\rm const}\nolimits _{y_0})\cong [X,\,\Omega B{\mathbb {S}}^3]$
. Then $\pi _1(\mathop {\rm map}\nolimits (X,\,Y),\,\mathop {\rm const}\nolimits _{y_0})\cong \pi _1(\mathop {\rm map}\nolimits _*(X,\,Y),\,\mathop {\rm const}\nolimits _{y_0})\cong [X,\,\Omega B{\mathbb {S}}^3]$![]() is nontrivial. Therefore, the spectral sequence associated to $\mathop {\rm map}\nolimits (X,\,Y)$
is nontrivial. Therefore, the spectral sequence associated to $\mathop {\rm map}\nolimits (X,\,Y)$![]() cannot converge to $\pi _*(\mathop {\rm map}\nolimits (X,\,Y))$
cannot converge to $\pi _*(\mathop {\rm map}\nolimits (X,\,Y))$![]() . In particular, $X$
. In particular, $X$![]() is infinite-dimensional (as noted by Kahn).
is infinite-dimensional (as noted by Kahn).
We need to impose restrictions on a noncompact $X$![]() for $\mathop {\rm map}\nolimits (X,\,Y)$
for $\mathop {\rm map}\nolimits (X,\,Y)$![]() to be amenable to our methods. Presumably, it would be sufficient to have a regular complete lattice of zero sets on $X$
to be amenable to our methods. Presumably, it would be sufficient to have a regular complete lattice of zero sets on $X$![]() that determines the topology and is generated by compact zero sets (see [Reference Smrekar28, pp. 1 and 2] for the definition of a regular lattice). To avoid technicalities, we content ourselves with the ‘countable case’ as follows.
that determines the topology and is generated by compact zero sets (see [Reference Smrekar28, pp. 1 and 2] for the definition of a regular lattice). To avoid technicalities, we content ourselves with the ‘countable case’ as follows.
Definition 1.5 A topological pair $(X,\,A)$![]() will be called proper if $A\in {\rm PHK}$
will be called proper if $A\in {\rm PHK}$![]() and $X$
and $X$![]() is the union of an ascending chain of subspaces $A=X_0\subset X_1\subset X_2\subset \dots$
is the union of an ascending chain of subspaces $A=X_0\subset X_1\subset X_2\subset \dots$![]() (called an admissible chain) such that for all $i\geqslant 1$
(called an admissible chain) such that for all $i\geqslant 1$![]() there is a pushout
there is a pushout

where $S_i$![]() is a zero set in the compact Hausdorff space $C_i$
is a zero set in the compact Hausdorff space $C_i$![]() and $X$
and $X$![]() has the weak (colimit) topology with respect to $\left \{X_i\right \}$
has the weak (colimit) topology with respect to $\left \{X_i\right \}$![]() . Each $X_i$
. Each $X_i$![]() is paracompact and it follows that $X\in {\rm PHK}$
is paracompact and it follows that $X\in {\rm PHK}$![]() by Michael [Reference Michael21, Theorem 8.2]. Also, the $X_i$
by Michael [Reference Michael21, Theorem 8.2]. Also, the $X_i$![]() are zero sets in $X$
are zero sets in $X$![]() .
.
We call $X$![]() a proper space if $(X,\,\emptyset )$
a proper space if $(X,\,\emptyset )$![]() is a proper pair. In this case, the $X_i$
is a proper pair. In this case, the $X_i$![]() are compact Hausdorff. Examples include countable CW complexes and proper metric spaces (i.e. closed balls are compact). Also, locally compact subspaces of Euclidean spaces ${\mathbb {R}}^d$
are compact Hausdorff. Examples include countable CW complexes and proper metric spaces (i.e. closed balls are compact). Also, locally compact subspaces of Euclidean spaces ${\mathbb {R}}^d$![]() are proper. More generally, if $X$
are proper. More generally, if $X$![]() is a Hausdorff k-space that admits a proper function $\phi \colon X\to [0,\,\infty )$
is a Hausdorff k-space that admits a proper function $\phi \colon X\to [0,\,\infty )$![]() (the preimages of compact sets are compact), then one sees that $X$
(the preimages of compact sets are compact), then one sees that $X$![]() is proper by setting $X_i=\phi ^{-1}([0,\,i])$
is proper by setting $X_i=\phi ^{-1}([0,\,i])$![]() .
.
Observe that if $(X,\,A)$![]() is a proper pair with admissible chain $\left \{X_i\right \}$
is a proper pair with admissible chain $\left \{X_i\right \}$![]() and $B$
and $B$![]() is a zero set in $X$
is a zero set in $X$![]() , then $(X,\,A\cup B)$
, then $(X,\,A\cup B)$![]() is a proper pair with admissible chain $\left \{X_i\cup B\right \}$
is a proper pair with admissible chain $\left \{X_i\cup B\right \}$![]() . In particular, if $X$
. In particular, if $X$![]() is a proper space, then $(X,\,B)$
is a proper space, then $(X,\,B)$![]() is a proper pair for any zero set $B$
is a proper pair for any zero set $B$![]() .
.
A proper pair $(X,\,A)$![]() will be called locally finite-dimensional if the $C_i$
will be called locally finite-dimensional if the $C_i$![]() have finite covering dimension. Every countable relative CW complex is then a locally finite-dimensional proper pair. We write $\mathop {\rm dim}\nolimits (X,\,A)\leqslant d$
have finite covering dimension. Every countable relative CW complex is then a locally finite-dimensional proper pair. We write $\mathop {\rm dim}\nolimits (X,\,A)\leqslant d$![]() if $\mathop {\rm dim}\nolimits C_i\leqslant d$
if $\mathop {\rm dim}\nolimits C_i\leqslant d$![]() for all $i$
for all $i$![]() and call such a pair finite-dimensional.
and call such a pair finite-dimensional.
Any admissible chain of a compact proper space (or pair) is essentially finite. In particular, a locally finite-dimensional compact proper space is finite-dimensional.
Hilton, Mislin, Roitberg, and Steiner pointed out in [Reference Hilton, Mislin, Roitberg and Steiner13] that the natural class of CW complexes $X$![]() for which (1.1) always localizes is that of globally homologically finite ones; $X$
for which (1.1) always localizes is that of globally homologically finite ones; $X$![]() is such when $\oplus _{n=0}^\infty H_n(X)$
is such when $\oplus _{n=0}^\infty H_n(X)$![]() is finitely generated. From our point of view, that is precisely because a CW complex $X$
is finitely generated. From our point of view, that is precisely because a CW complex $X$![]() is globally homologically finite if and only if $\mathop {\rm map}\nolimits (X,\,Y)$
is globally homologically finite if and only if $\mathop {\rm map}\nolimits (X,\,Y)$![]() has the homotopy type of a CW complex for every nilpotent CW complex $Y$
has the homotopy type of a CW complex for every nilpotent CW complex $Y$![]() . (For sufficiency, use [Reference Smrekar28, Proposition 2.6.4] and [Reference Smrekar30, Corollary 1.2]. For necessity, use the proof of [Reference Smrekar28, c. of Theorem 4.5.3].) Thus in this case, (1.1) is actually localization in the category of nilpotent spaces of CW homotopy type.
. (For sufficiency, use [Reference Smrekar28, Proposition 2.6.4] and [Reference Smrekar30, Corollary 1.2]. For necessity, use the proof of [Reference Smrekar28, c. of Theorem 4.5.3].) Thus in this case, (1.1) is actually localization in the category of nilpotent spaces of CW homotopy type.
The following is a generalization of Theorems A and B of [Reference Hilton, Mislin, Roitberg and Steiner13].
Theorem 1.6 Let $(X,\,A)$![]() be a proper pair and let $Y$
be a proper pair and let $Y$![]() be a nilpotent CW complex. Fix a map $\phi \colon A\to Y$
be a nilpotent CW complex. Fix a map $\phi \colon A\to Y$![]() . If $\mathop {\rm map}\nolimits _\phi (X,\,Y)$
. If $\mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() and $\mathop {\rm map}\nolimits _{l\phi }(X,\,Y_{(P)})$
and $\mathop {\rm map}\nolimits _{l\phi }(X,\,Y_{(P)})$![]() have CW homotopy type, then they are nilpotent and (1.1) is CW localization at P on path components.
have CW homotopy type, then they are nilpotent and (1.1) is CW localization at P on path components.
It turns out that the question of whether or not $\mathop {\rm map}\nolimits (X,\,Y)$![]() has CW homotopy type is intimately related to the behaviour of the spectral sequence of theorem 1.1.
has CW homotopy type is intimately related to the behaviour of the spectral sequence of theorem 1.1.
Definition 1.7 Let $A$![]() be a closed subspace of $X\in {\rm PHK}$
be a closed subspace of $X\in {\rm PHK}$![]() . The pair $(X,\,A)$
. The pair $(X,\,A)$![]() is quasi-finite, $(X,\,A)\in {\mathcal {Q}}{\mathcal {F}}$
is quasi-finite, $(X,\,A)\in {\mathcal {Q}}{\mathcal {F}}$![]() , if for each abelian group $G$
, if for each abelian group $G$![]() and all $n\geqslant 1$
and all $n\geqslant 1$![]() , the space $\mathop {\rm map}\nolimits _{A\to *}(X,\,K(G,\,n))$
, the space $\mathop {\rm map}\nolimits _{A\to *}(X,\,K(G,\,n))$![]() has the homotopy type of a CW complex. (We assume $K(G,\,n)$
has the homotopy type of a CW complex. (We assume $K(G,\,n)$![]() to be well-pointed.) We call $X$
to be well-pointed.) We call $X$![]() quasi-finite if $(X,\,\emptyset )$
quasi-finite if $(X,\,\emptyset )$![]() is a quasi-finite pair.
is a quasi-finite pair.
By [Reference Smrekar28, Theorem 4.5.3, a.], a CW complex belongs to ${\mathcal {Q}}{\mathcal {F}}$![]() if and only if all its homology groups are finitely generated.
if and only if all its homology groups are finitely generated.
Proposition 1.8 Let $(X,\,A)$![]() be a quasi-finite and locally finite-dimensional proper pair, and let $Y$
be a quasi-finite and locally finite-dimensional proper pair, and let $Y$![]() have the homotopy type of a nilpotent CW complex; if $A$
have the homotopy type of a nilpotent CW complex; if $A$![]() is nonempty and not cofibred in $X$
is nonempty and not cofibred in $X$![]() , we assume that $Y$
, we assume that $Y$![]() is an ANR. Let $\phi \colon A\to Y$
is an ANR. Let $\phi \colon A\to Y$![]() be any map.
be any map.
If $\mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() has the homotopy type of a CW complex, then the spectral sequence of theorem 1.1 converges to $\pi _*(\mathop {\rm map}\nolimits _\phi (X,\,Y),\,f)$
has the homotopy type of a CW complex, then the spectral sequence of theorem 1.1 converges to $\pi _*(\mathop {\rm map}\nolimits _\phi (X,\,Y),\,f)$![]() for any $f\in \mathop {\rm map}\nolimits _\phi (X,\,Y)$
for any $f\in \mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() .
.
We note that if $(X,\,A)$![]() is a skeleton-finite relative CW pair, then it is a quasi-finite and locally finite-dimensional proper pair.
is a skeleton-finite relative CW pair, then it is a quasi-finite and locally finite-dimensional proper pair.
For proper pairs, quasi-finiteness is actually a cohomological property as follows. Recall that a tower of groups $\dots \to G_2\to G_1$![]() is Mittag-Leffler if for each $i$
is Mittag-Leffler if for each $i$![]() , the images of $G_j\to G_i$
, the images of $G_j\to G_i$![]() stabilize for all big enough $j\geqslant i$
stabilize for all big enough $j\geqslant i$![]() .
.
Proposition 1.9 Let $(X,\,A)$![]() be a proper pair with an admissible chain $\left \{X_i\right \}$
be a proper pair with an admissible chain $\left \{X_i\right \}$![]() . Then $(X,\,A)\in {\mathcal {Q}}{\mathcal {F}}$
. Then $(X,\,A)\in {\mathcal {Q}}{\mathcal {F}}$![]() if and only if for each abelian group $G$
if and only if for each abelian group $G$![]() , the towers of abelian groups
, the towers of abelian groups
are Mittag-Leffler for $0\leqslant k<\infty$![]() and, in addition, for each $k$
and, in addition, for each $k$![]() there exists $i$
there exists $i$![]() such that restriction $\check {H}^k(X,\,A;G)\to \check {H}^k(X_i,\,A;G)$
such that restriction $\check {H}^k(X,\,A;G)\to \check {H}^k(X_i,\,A;G)$![]() is injective.
is injective.
We turn to spaces of sections.
Let $X$![]() be connected and let $Q\to X$
be connected and let $Q\to X$![]() be a Hurewicz fibration with space of sections $\Gamma (X,\,Q)\subset \mathop {\rm map}\nolimits (X,\,Q)$
be a Hurewicz fibration with space of sections $\Gamma (X,\,Q)\subset \mathop {\rm map}\nolimits (X,\,Q)$![]() . Assume that $Q\to X$
. Assume that $Q\to X$![]() is a pullback of a fibration $p\colon E\to B$
is a pullback of a fibration $p\colon E\to B$![]() of spaces of CW homotopy type where $B$
of spaces of CW homotopy type where $B$![]() is connected and the typical fibre of $p$
is connected and the typical fibre of $p$![]() , call it $Y$
, call it $Y$![]() , is nilpotent. Let $P$
, is nilpotent. Let $P$![]() be a set of primes and let $\ell \colon E\to E_{(P)}$
be a set of primes and let $\ell \colon E\to E_{(P)}$![]() be the fibrewise localization at $P$
be the fibrewise localization at $P$![]() over $B$
over $B$![]() . By pulling back, we obtain a fibrewise localization $\ell \colon Q\to Q_{(P)}$
. By pulling back, we obtain a fibrewise localization $\ell \colon Q\to Q_{(P)}$![]() over $X$
over $X$![]() . Note that $\ell$
. Note that $\ell$![]() induces a map
induces a map
In [Reference Schochet and Smith26], the authors studied the effect of $\ell _*$![]() for compact $X$
for compact $X$![]() provided $\Gamma (X,\,Q)$
provided $\Gamma (X,\,Q)$![]() is known, a priori, to be nilpotent. We give conditions for nilpotency and enhance their localization result [Reference Schochet and Smith26, Theorem 3] as follows.
is known, a priori, to be nilpotent. We give conditions for nilpotency and enhance their localization result [Reference Schochet and Smith26, Theorem 3] as follows.
Theorem 1.10 Suppose $X$![]() is a connected proper space and assume that, in addition, $X$
is a connected proper space and assume that, in addition, $X$![]() is locally finite-dimensional or $Y$
is locally finite-dimensional or $Y$![]() is a Postnikov section.
is a Postnikov section.
(a) If X is compact, then $\Gamma (X,\,Q)$
 and $\Gamma (X,\,Q_{(P)})$
and $\Gamma (X,\,Q_{(P)})$ are nilpotent spaces of CW type and (1.3) is CW localization at $P$
are nilpotent spaces of CW type and (1.3) is CW localization at $P$ on each path component.
on each path component.(b) If $\Gamma (X,\,Q)$
 has CW type, then $\Gamma (X,\,Q)$
has CW type, then $\Gamma (X,\,Q)$ and $\Gamma (X,\,Q_{(P)})$
and $\Gamma (X,\,Q_{(P)})$ are nilpotent and (1.3) localizes at $P$
are nilpotent and (1.3) localizes at $P$ on path components. If, in addition, Y is a Postnikov section, also $\Gamma (X,\,Q_{(P)})$
on path components. If, in addition, Y is a Postnikov section, also $\Gamma (X,\,Q_{(P)})$ has CW type and (1.3) is CW localization at $P$
has CW type and (1.3) is CW localization at $P$ .
.
A relative version for sections prescribed on $A\subset X$![]() , which also generalizes the main results of [Reference Møller24], is stated in § 7.
, which also generalizes the main results of [Reference Møller24], is stated in § 7.
Underlying categories and techniques. Our results are valid in the category ${\mathcal {K}}$![]() of k-spaces and in the category ${\mathcal {T}}\!\!{op}$
of k-spaces and in the category ${\mathcal {T}}\!\!{op}$![]() of all topological spaces (see [Reference May and Sigurdsson20, Sections 1.1 and 4.1]). There are the underlying Strø m closed model category structures on ${\mathcal {K}}$
of all topological spaces (see [Reference May and Sigurdsson20, Sections 1.1 and 4.1]). There are the underlying Strø m closed model category structures on ${\mathcal {K}}$![]() and ${\mathcal {T}}\!\!{op}$
and ${\mathcal {T}}\!\!{op}$![]() with Hurewicz fibrations, closed Hurewicz cofibrations, and homotopy equivalences (called h-equivalences in [Reference May and Sigurdsson20]). While for some of our results, Serre fibrations would be sufficient, we also lean on the results of Stasheff [Reference Stasheff33] and Brown and Heath [Reference Brown and Heath4] that require Hurewicz fibrations, so we stick to the latter. Our mapping spaces, which have the (k-ified) compact open topology, are homotopy metrizable in case of a proper domain, and remarks of [Reference Smrekar29, Section 2.3] apply. Some of our key technical results have been obtained by replacing the target space with a homotopy equivalent absolute neighbourhood retract; Milnor [Reference Milnor22] proved that ANRs and CW complexes contain the same homotopy types. The fact that ANRs together with homotopy equivalences and Hurewicz fibrations form a fibration category in the sense of Baues [Reference Baues2] (see Miyata [Reference Miyata23] as well as remark 7.1) is of importance.
with Hurewicz fibrations, closed Hurewicz cofibrations, and homotopy equivalences (called h-equivalences in [Reference May and Sigurdsson20]). While for some of our results, Serre fibrations would be sufficient, we also lean on the results of Stasheff [Reference Stasheff33] and Brown and Heath [Reference Brown and Heath4] that require Hurewicz fibrations, so we stick to the latter. Our mapping spaces, which have the (k-ified) compact open topology, are homotopy metrizable in case of a proper domain, and remarks of [Reference Smrekar29, Section 2.3] apply. Some of our key technical results have been obtained by replacing the target space with a homotopy equivalent absolute neighbourhood retract; Milnor [Reference Milnor22] proved that ANRs and CW complexes contain the same homotopy types. The fact that ANRs together with homotopy equivalences and Hurewicz fibrations form a fibration category in the sense of Baues [Reference Baues2] (see Miyata [Reference Miyata23] as well as remark 7.1) is of importance.
2. A generalized Federer's spectral sequence
Assume a tower of Hurewicz fibrations
We consider a spectral sequence converging to the homotopy groups of the inverse limit, taking on the approach of Federer [Reference Federer10]. He considered only the special case where $Z_i=\mathop {\rm map}\nolimits (X^{(i)},\,Y)$![]() is the space of maps from the $i$
is the space of maps from the $i$![]() -skeleton of a CW complex $X$
-skeleton of a CW complex $X$![]() to a simple CW complex $Y$
to a simple CW complex $Y$![]() , and the maps $Z_i\to Z_{i-1}$
, and the maps $Z_i\to Z_{i-1}$![]() are restriction fibrations. However, his treatment applies to a fairly general setting as we proceed to explain.
are restriction fibrations. However, his treatment applies to a fairly general setting as we proceed to explain.
Let the space $Z_\infty$![]() , together with projections $P^i\colon Z_\infty \to Z_i$
, together with projections $P^i\colon Z_\infty \to Z_i$![]() , be the (topological) inverse limit of (2.1). Let $R\colon Z\to Z_\infty$
, be the (topological) inverse limit of (2.1). Let $R\colon Z\to Z_\infty$![]() be a map of another space $Z$
be a map of another space $Z$![]() into $Z_\infty$
into $Z_\infty$![]() and denote $R^i=P^i\circ R\colon Z\to Z_i$
and denote $R^i=P^i\circ R\colon Z\to Z_i$![]() . In our applications, $Z\to Z_\infty$
. In our applications, $Z\to Z_\infty$![]() typically would not be a homotopy equivalence (i.e., it would not have a homotopy inverse), but it will induce isomorphisms on homotopy groups in favourable circumstances.
typically would not be a homotopy equivalence (i.e., it would not have a homotopy inverse), but it will induce isomorphisms on homotopy groups in favourable circumstances.
Finally, pick $\zeta \in Z$![]() and set $\zeta _i=R^i(\zeta )$
and set $\zeta _i=R^i(\zeta )$![]() for all $i$
for all $i$![]() . Let $Z_i'$
. Let $Z_i'$![]() denote the path component of $\zeta _i$
denote the path component of $\zeta _i$![]() in $Z_i$
in $Z_i$![]() , and let $F_i'$
, and let $F_i'$![]() denote the fibre of $Z_i'\to Z_{i-1}'$
denote the fibre of $Z_i'\to Z_{i-1}'$![]() over $\zeta _{i-1}$
over $\zeta _{i-1}$![]() . Note that $F_i'$
. Note that $F_i'$![]() may be disconnected. In such a setting, Federer defines a generalized exact couple
may be disconnected. In such a setting, Federer defines a generalized exact couple

where $A_{p,q}=\pi _p(Z_q',\,\zeta _q)$![]() are groups (generally noncommutative for $p=1$
are groups (generally noncommutative for $p=1$![]() ), and $C_{p,q}=\pi _p(F_q',\,\zeta _q)$
), and $C_{p,q}=\pi _p(F_q',\,\zeta _q)$![]() are abelian groups for all $p\geqslant 0$
are abelian groups for all $p\geqslant 0$![]() . When $p<0$
. When $p<0$![]() or $q<0$
or $q<0$![]() , everything is trivial. Morphisms $r$
, everything is trivial. Morphisms $r$![]() , $\partial$
, $\partial$![]() , and $i$
, and $i$![]() arise from the long exact sequences of fibrations
arise from the long exact sequences of fibrations
and are morphisms of groups throughout. Federer notes that the theory of ‘abelian’ exact couples carries over to this setting. We recall that the differential is $d=\partial \circ i$![]() ; we set $(C^{(0)},\,d^{(0)})=(C,\,d)$
; we set $(C^{(0)},\,d^{(0)})=(C,\,d)$![]() and let $C^{(n)}$
and let $C^{(n)}$![]() be the homology of $(C^{(n-1)},\,d^{(n-1)})$
be the homology of $(C^{(n-1)},\,d^{(n-1)})$![]() .
.
In the following lemma we provide a sufficient condition for the existence of a Federer's exact couple in the setting of a tower of fibrations (2.1), and give an abstract identification of the groups $C_{p,q}$![]() and the first differential.
and the first differential.
Lemma 2.1 Assume that for each $q\geqslant 0$![]() , the fibration $Z_q\to Z_{q-1}$
, the fibration $Z_q\to Z_{q-1}$![]() is principal, obtained as the pullback of a fibration $EL_q\to BL_q$
is principal, obtained as the pullback of a fibration $EL_q\to BL_q$![]() along a classifying map $l_q\colon Z_{q-1}\to BL_q$
along a classifying map $l_q\colon Z_{q-1}\to BL_q$![]() where $EL_q$
where $EL_q$![]() is contractible and $BL_q$
is contractible and $BL_q$![]() is a not necessarily connected space with abelian fundamental group (in each component). (For example, $BL_q$
is a not necessarily connected space with abelian fundamental group (in each component). (For example, $BL_q$![]() may be an H-group.) By taking $A_{p,q}=\pi _p(Z_q',\,\zeta _q)$
may be an H-group.) By taking $A_{p,q}=\pi _p(Z_q',\,\zeta _q)$![]() and $C_{p,q}=\pi _p(F_q',\,\zeta _q)$
and $C_{p,q}=\pi _p(F_q',\,\zeta _q)$![]() with morphisms (2.3), one obtains an exact couple (2.2) in the sense of Federer.
with morphisms (2.3), one obtains an exact couple (2.2) in the sense of Federer.
In the associated spectral sequence we have that $C_{p,q}\cong \pi _{p+1}(BL_q,\,l_q(\zeta _{q-1}))$![]() if $p,\,q\geqslant 1$
if $p,\,q\geqslant 1$![]() , and that $C_{0,q}$
, and that $C_{0,q}$![]() is isomorphic with a subgroup of $\pi _1(BL_q,\,l_q(\zeta _{q-1}))$
is isomorphic with a subgroup of $\pi _1(BL_q,\,l_q(\zeta _{q-1}))$![]() for $q>0$
for $q>0$![]() . If $q\leqslant 0$
. If $q\leqslant 0$![]() or $p<0$
or $p<0$![]() , then $C_{p,q}=0$
, then $C_{p,q}=0$![]() . Under those isomorphisms, the first differential $d\colon C_{p,q}\to C_{p-1,q+1}$
. Under those isomorphisms, the first differential $d\colon C_{p,q}\to C_{p-1,q+1}$![]() for $p\geqslant 1$
for $p\geqslant 1$![]() corresponds to the composite
corresponds to the composite
where $\delta _q$![]() can be identified with the connecting morphism in the homotopy exact sequence of the fibration $EL_q\to BL_q$
can be identified with the connecting morphism in the homotopy exact sequence of the fibration $EL_q\to BL_q$![]() .
.
Remark 2.2 As $Z_{-1}=\left \{\mathrm {point}\right \}$![]() , $Z_0$
, $Z_0$![]() is assumed to be a loop space of $BL_0$
is assumed to be a loop space of $BL_0$![]() . Also, when $p=1$
. Also, when $p=1$![]() , the codomain of (2.4) has to be understood as the image of $(l_{q+1})_*$
, the codomain of (2.4) has to be understood as the image of $(l_{q+1})_*$![]() .
.
Remark 2.3 Under $\pi _{p+1}(BL_q,\,l_q(\zeta _{q-1}))\cong \pi _p(\Omega (BL_q,\,l_q(\zeta _{q-1})),\,\mathop {\rm const}\nolimits _{l_q(\zeta _{q-1})})$![]() , the morphism $\delta _q$
, the morphism $\delta _q$![]() from (2.4) is induced by a continuous map $\Omega (BL_q,\,l_q(\zeta _{q-1}))\to F_q$
from (2.4) is induced by a continuous map $\Omega (BL_q,\,l_q(\zeta _{q-1}))\to F_q$![]() (taking $\mathop {\rm const}\nolimits _{l_q(\zeta _{q-1})}$
(taking $\mathop {\rm const}\nolimits _{l_q(\zeta _{q-1})}$![]() to $\zeta _q$
to $\zeta _q$![]() ) if $EL_q\to BL_q$
) if $EL_q\to BL_q$![]() is a regular fibration (i.e. stationary homotopies can be lifted to stationary homotopies).
is a regular fibration (i.e. stationary homotopies can be lifted to stationary homotopies).
Remark 2.4 The spectral sequence is natural with respect to maps of towers induced by maps of the classifying spaces $BL_q$![]() . This holds also for the identification of the first differential (2.4).
. This holds also for the identification of the first differential (2.4).
Addendum 2.5 Starting with $C_{0,q}\leqslant \widetilde C_{0,q}=\pi _0(F_q,\,\zeta _q)\cong \pi _1(BL_q,\,l_q(\zeta _{q-1}))$![]() with incoming differential $\tilde d\colon C_{1,q-1}\xrightarrow {d}C_{0,q}\leqslant \widetilde C_{0,q}$
with incoming differential $\tilde d\colon C_{1,q-1}\xrightarrow {d}C_{0,q}\leqslant \widetilde C_{0,q}$![]() , each derived group $C_{0,q}^{(n)}$
, each derived group $C_{0,q}^{(n)}$![]() is a subgroup of the group $\widetilde C_{0,q}^{(n)}=\widetilde C_{0,q}^{(n-1)}/\mathop {\rm im}\nolimits \tilde d^{(n-1)}$
is a subgroup of the group $\widetilde C_{0,q}^{(n)}=\widetilde C_{0,q}^{(n-1)}/\mathop {\rm im}\nolimits \tilde d^{(n-1)}$![]() with incoming differential $\tilde d^{(n)}\colon C^{(n)}_{1,q-n-1}\xrightarrow {d^{(n)}}C^{(n)}_{0,q}\leqslant \widetilde C_{0,q}^{(n)}$
with incoming differential $\tilde d^{(n)}\colon C^{(n)}_{1,q-n-1}\xrightarrow {d^{(n)}}C^{(n)}_{0,q}\leqslant \widetilde C_{0,q}^{(n)}$![]() . Moreover, $\widetilde C^{(n)}_{0,q}$
. Moreover, $\widetilde C^{(n)}_{0,q}$![]() and $\tilde d^{(n)}$
and $\tilde d^{(n)}$![]() are natural with respect to morphisms of towers induced by maps of classifying spaces $BL_q$
are natural with respect to morphisms of towers induced by maps of classifying spaces $BL_q$![]() . The exact couple $(A,\,C)$
. The exact couple $(A,\,C)$![]() together with natural subgroup inclusions $C^{(n)}_{0,q}\leqslant \widetilde C^{(n)}_{0,q}$
together with natural subgroup inclusions $C^{(n)}_{0,q}\leqslant \widetilde C^{(n)}_{0,q}$![]() will be called an augmented Federer's exact couple and denoted $(A,\,C,\,\widetilde C)$
will be called an augmented Federer's exact couple and denoted $(A,\,C,\,\widetilde C)$![]() .
.
Proof. As $Z_q\to Z_{q-1}\xrightarrow {l_q}BL_q$![]() is a homotopy fibration, $\partial \colon \pi _{p+1}(Z_{q-1},\,\zeta _{q-1})\to \pi _{p}(F_q',\,\zeta _q)=C_{p,q}$
is a homotopy fibration, $\partial \colon \pi _{p+1}(Z_{q-1},\,\zeta _{q-1})\to \pi _{p}(F_q',\,\zeta _q)=C_{p,q}$![]() can be viewed as $(l_q)_*\colon \pi _{p+1}(Z_{q-1},\,\zeta _{q-1})\to \pi _{p+1}(BL_q,\,l_q(\zeta _{q-1}))$
can be viewed as $(l_q)_*\colon \pi _{p+1}(Z_{q-1},\,\zeta _{q-1})\to \pi _{p+1}(BL_q,\,l_q(\zeta _{q-1}))$![]() . Moreover, $C_{0,q}$
. Moreover, $C_{0,q}$![]() can be identified with the image of $(l_q)_*$
can be identified with the image of $(l_q)_*$![]() in $\pi _1(BL_q,\,l_q(\zeta _{q-1}))$
in $\pi _1(BL_q,\,l_q(\zeta _{q-1}))$![]() which is abelian by our assumption on $BL_q$
which is abelian by our assumption on $BL_q$![]() . This provides the identification of $C_{p,q}$
. This provides the identification of $C_{p,q}$![]() and that of $\partial$
and that of $\partial$![]() in the differential $\partial \circ i\colon C_{p,q}\to C_{p-1,q+1}$
in the differential $\partial \circ i\colon C_{p,q}\to C_{p-1,q+1}$![]() . More precisely, as the fibration $Z_q\to Z_{q-1}$
. More precisely, as the fibration $Z_q\to Z_{q-1}$![]() is principal, $F_q$
is principal, $F_q$![]() is homotopy equivalent to the loop-space $\Omega (BL_q,\,l_q(\zeta _{q-1}))$
is homotopy equivalent to the loop-space $\Omega (BL_q,\,l_q(\zeta _{q-1}))$![]() , and the connecting morphism in the homotopy exact sequence of $EL_q\to BL_q$
, and the connecting morphism in the homotopy exact sequence of $EL_q\to BL_q$![]() induces the isomorphism $\delta _q\colon \pi _{p+1}(BL_q,\,l_q(\zeta _{q-1}))\to \pi _p(F_q,\,\zeta _q)$
induces the isomorphism $\delta _q\colon \pi _{p+1}(BL_q,\,l_q(\zeta _{q-1}))\to \pi _p(F_q,\,\zeta _q)$![]() . Noting that $\partial =(\delta _q)^{-1}\circ (l_q)_*\colon \pi _{p+1}(Z_{q-1},\,\zeta _{q-1})\to \pi _p(F_q,\,\zeta _q)$
. Noting that $\partial =(\delta _q)^{-1}\circ (l_q)_*\colon \pi _{p+1}(Z_{q-1},\,\zeta _{q-1})\to \pi _p(F_q,\,\zeta _q)$![]() completes the proof of the main statement.
completes the proof of the main statement.
For remark 2.3, consider a general fibration $f\colon E\to B$![]() and let $f(e_0)=b_0$
and let $f(e_0)=b_0$![]() be any coherent pair of basepoints. The connecting morphism $\pi _*(\Omega B,\,\mathop {\rm const}\nolimits _{b_0})\to \pi _{*}(F,\,e_0)$
be any coherent pair of basepoints. The connecting morphism $\pi _*(\Omega B,\,\mathop {\rm const}\nolimits _{b_0})\to \pi _{*}(F,\,e_0)$![]() is induced by a map $\Omega (B,\,b_0)\to F$
is induced by a map $\Omega (B,\,b_0)\to F$![]() which is most easily constructed by means of a lifting function that continuously lifts loops at $b_0$
which is most easily constructed by means of a lifting function that continuously lifts loops at $b_0$![]() to paths in $E$
to paths in $E$![]() beginning at $e_0$
beginning at $e_0$![]() and takes the end point (in $F$
and takes the end point (in $F$![]() ). A regular fibration admits a lifting function sending constant paths to constant paths, forcing $\mathop {\rm const}\nolimits _{b_0}$
). A regular fibration admits a lifting function sending constant paths to constant paths, forcing $\mathop {\rm const}\nolimits _{b_0}$![]() to map to $e_0$
to map to $e_0$![]() .
.
To prove the addendum by induction, note that if $\tilde d^{(n-1)}\colon C^{(n-1)}_{1,q-n}\to \widetilde C^{(n-1)}_{0,q}$![]() is just $d^{(n-1)}$
is just $d^{(n-1)}$![]() followed by the inclusion $C^{(n-1)}_{0,q}\leqslant \widetilde C^{(n-1)}_{0,q}$
followed by the inclusion $C^{(n-1)}_{0,q}\leqslant \widetilde C^{(n-1)}_{0,q}$![]() , the images of $\tilde d^{(n-1)}$
, the images of $\tilde d^{(n-1)}$![]() and $d^{(n-1)}$
and $d^{(n-1)}$![]() in $\widetilde C^{(n-1)}_{0,q}$
in $\widetilde C^{(n-1)}_{0,q}$![]() coincide, yielding subgroup inclusion $C^{(n)}_{(0,q)}=C^{(n-1)}_{0,q}/\mathop {\rm im}\nolimits d^{(n-1)}\leqslant \widetilde C^{(n-1)}_{0,q}/\mathop {\rm im}\nolimits \tilde d^{(n-1)}=\widetilde C^{(n)}_{(0,q)}$
coincide, yielding subgroup inclusion $C^{(n)}_{(0,q)}=C^{(n-1)}_{0,q}/\mathop {\rm im}\nolimits d^{(n-1)}\leqslant \widetilde C^{(n-1)}_{0,q}/\mathop {\rm im}\nolimits \tilde d^{(n-1)}=\widetilde C^{(n)}_{(0,q)}$![]() .
.
Let $G_{p,q}$![]() denote the kernel of the induced morphism $R^q_{*}\colon \pi _p(Z,\,\zeta )\to A_{p,q}=\pi _p(Z_q',\,\zeta _q)$
denote the kernel of the induced morphism $R^q_{*}\colon \pi _p(Z,\,\zeta )\to A_{p,q}=\pi _p(Z_q',\,\zeta _q)$![]() and consider the normal chain for $\pi _p(Z,\,\zeta )$
and consider the normal chain for $\pi _p(Z,\,\zeta )$![]() :
:
The question of convergence is covered by the following proposition which is a straightforward generalization of the argument of Federer (see [Reference Federer10, pp. 351–352]).
Proposition 2.6 Suppose that for each pair $(p,\,q)$![]() , where $p\geqslant 1$
, where $p\geqslant 1$![]() , there exists an integer $j(p,\,q)\geqslant q$
, there exists an integer $j(p,\,q)\geqslant q$![]() for which the images of
for which the images of
coincide. Then for $n\geqslant \max \left \{j(p,\,q)+1-q,\,q\right \}$![]() , the derived terms $C_{p,q}^{(n)}$
, the derived terms $C_{p,q}^{(n)}$![]() are stable:
are stable:
Corollary 2.7 Fix $p\geqslant 1$![]() . If, in addition to the assumption of proposition 2.6, $G_{p,q}$
. If, in addition to the assumption of proposition 2.6, $G_{p,q}$![]() is trivial for $q\geqslant Q=Q(p)$
is trivial for $q\geqslant Q=Q(p)$![]() , then the normal chain (2.5) terminates and its successive quotients are given by (2.6) for all $n\geqslant \max \left \{j(p,\,Q),\,Q\right \}$
, then the normal chain (2.5) terminates and its successive quotients are given by (2.6) for all $n\geqslant \max \left \{j(p,\,Q),\,Q\right \}$![]() . In this sense the spectral sequence converges classically to $\pi _p(Z,\,\zeta )$
. In this sense the spectral sequence converges classically to $\pi _p(Z,\,\zeta )$![]() .
.
In practice, it is difficult to verify the assumptions of proposition 2.6 and corollary 2.7 (when they are not ‘automatic’). The entire § 4 is devoted to verifying those assumptions in a particular case, while proposition 1.8 shows they are implied by strong assumptions on homotopy type.
Routine diagram chasing coupled with exactness properties of localization of nilpotent groups yield the following theorem and its corollary.
Theorem 2.8 Assume an abstract morphism of augmented Federer's exact couples $(A,\,C,\,\widetilde C)\to (A',\,C',\,\widetilde C')$![]() . Fix a set of primes $P$
. Fix a set of primes $P$![]() (allowed to be the set of all primes). Assume that the following two conditions hold for some $n\geqslant 1$
(allowed to be the set of all primes). Assume that the following two conditions hold for some $n\geqslant 1$![]() .
.
(i) The morphisms $C^{(n-1)}_{p,q}\to C'^{(n-1)}_{p,q}$
 are localizations at $P$
are localizations at $P$ for $p,\,q\geqslant 1$
for $p,\,q\geqslant 1$ .
.(ii) The torsion in $\widetilde C'^{(n-1)}_{0,q}$
 is P-local and the morphisms $\widetilde C^{(n-1)}_{0,q}\to \widetilde C'^{(n-1)}_{0,q}$
is P-local and the morphisms $\widetilde C^{(n-1)}_{0,q}\to \widetilde C'^{(n-1)}_{0,q}$ are P-injective for $q>0$
are P-injective for $q>0$ .
.
Then the same holds on level $n$![]() .
.
3. The homotopy spectral sequence of a function space
In this section, we associate to the function space $\mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() a tower of principal fibrations as studied above. We carry out the construction of the ensuing spectral sequence and the identification of the first differential. The questions of convergence and nilpotency will be addressed in the following sections.
a tower of principal fibrations as studied above. We carry out the construction of the ensuing spectral sequence and the identification of the first differential. The questions of convergence and nilpotency will be addressed in the following sections.
Let $\check {H}^i(X,\,A;G)$![]() denote the $i$
denote the $i$![]() -th Čech cohomology group of the pair $(X,\,A)$
-th Čech cohomology group of the pair $(X,\,A)$![]() with coefficients in the discrete group $G$
with coefficients in the discrete group $G$![]() . We refer to Dowker [Reference Dowker6] and Bredon [Reference Bredon3] for properties of Čech cohomology.
. We refer to Dowker [Reference Dowker6] and Bredon [Reference Bredon3] for properties of Čech cohomology.
Let $Y$![]() have the homotopy type of a connected nilpotent CW complex. Assume that $Y$
have the homotopy type of a connected nilpotent CW complex. Assume that $Y$![]() is approximated (up to weak homotopy type) with the inverse limit of successive principal fibrations with fibres $K(\pi ^q,\,n_q)$
is approximated (up to weak homotopy type) with the inverse limit of successive principal fibrations with fibres $K(\pi ^q,\,n_q)$![]() where $1=n_1\leqslant n_2\leqslant \dots$
where $1=n_1\leqslant n_2\leqslant \dots$![]() . Precisely, we assume a tower of fibrations
. Precisely, we assume a tower of fibrations
where $Y_1=K(\pi ^1,\,1)=:K_1$![]() for an abelian group $\pi ^1$
for an abelian group $\pi ^1$![]() , and each map $\eta _q\colon Y_q\to Y_{q-1}$
, and each map $\eta _q\colon Y_q\to Y_{q-1}$![]() is a principal fibration obtained from the $k$
is a principal fibration obtained from the $k$![]() -invariant $k_q\colon Y_{q-1}\to K(\pi ^q,\,n_q+1)=BK_q$
-invariant $k_q\colon Y_{q-1}\to K(\pi ^q,\,n_q+1)=BK_q$![]() where $\pi ^q$
where $\pi ^q$![]() is abelian. This is to say that $Y_q\to Y_{q-1}$
is abelian. This is to say that $Y_q\to Y_{q-1}$![]() is obtained by pulling back the path fibration $\varepsilon \colon P(BK_q)\to BK_q$
is obtained by pulling back the path fibration $\varepsilon \colon P(BK_q)\to BK_q$![]() along $k_q$
along $k_q$![]() . We also assume that the $BK_q$
. We also assume that the $BK_q$![]() and consequently $P(BK_q)$
and consequently $P(BK_q)$![]() are ANRs; it follows that so are $Y_q$
are ANRs; it follows that so are $Y_q$![]() (see [Reference Miyata23] and remark 7.1). There are compatible maps $\eta ^q\colon Y\to Y_q$
(see [Reference Miyata23] and remark 7.1). There are compatible maps $\eta ^q\colon Y\to Y_q$![]() whose connectivity tends to infinity with $q$
whose connectivity tends to infinity with $q$![]() . These induce a continuous map $\eta \colon Y\to Y_\infty$
. These induce a continuous map $\eta \colon Y\to Y_\infty$![]() where $Y_\infty$
where $Y_\infty$![]() is the inverse limit of the tower. The map $\eta$
is the inverse limit of the tower. The map $\eta$![]() is a weak homotopy equivalence.
is a weak homotopy equivalence.
Let $(X,\,A)$![]() be a pair where $X$
be a pair where $X$![]() is a Hausdorff k-space and let $\phi \colon A\to Y$
is a Hausdorff k-space and let $\phi \colon A\to Y$![]() be a map. Set $\phi _q=\eta ^q\circ \phi \colon A\to Y_q$
be a map. Set $\phi _q=\eta ^q\circ \phi \colon A\to Y_q$![]() ; the maps $\phi _q$
; the maps $\phi _q$![]() induce a continuous map $\phi _\infty \colon A\to Y_\infty$
induce a continuous map $\phi _\infty \colon A\to Y_\infty$![]() . We may form an associated tower as follows.
. We may form an associated tower as follows.
Using the fact that the $\eta _q$![]() are regular fibrations, the proof of [Reference Smrekar29, Lemma A.4] may be amended to render (3.2) a tower of fibrations (without conditions on $A$
are regular fibrations, the proof of [Reference Smrekar29, Lemma A.4] may be amended to render (3.2) a tower of fibrations (without conditions on $A$![]() ). The maps $\eta ^q\colon Y\to Y_q$
). The maps $\eta ^q\colon Y\to Y_q$![]() induce compatible maps $R^q\colon \mathop {\rm map}\nolimits _\phi (X,\,Y)\to \mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)$
induce compatible maps $R^q\colon \mathop {\rm map}\nolimits _\phi (X,\,Y)\to \mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)$![]() and thus a limit map $R\colon \mathop {\rm map}\nolimits _\phi (X,\,Y)\to \lim _q\mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)=\mathop {\rm map}\nolimits _{\phi _\infty }(X,\,Y_\infty )$
and thus a limit map $R\colon \mathop {\rm map}\nolimits _\phi (X,\,Y)\to \lim _q\mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)=\mathop {\rm map}\nolimits _{\phi _\infty }(X,\,Y_\infty )$![]() . Set $Z_q=\mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)$
. Set $Z_q=\mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)$![]() and $Z=\mathop {\rm map}\nolimits _\phi (X,\,Y)$
and $Z=\mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() . Pick $\zeta \in Z$
. Pick $\zeta \in Z$![]() and let $\zeta _q=R^q(\zeta )$
and let $\zeta _q=R^q(\zeta )$![]() for all $q$
for all $q$![]() .
.
Finally assume that, in addition, $A\hookrightarrow X$![]() is a closed cofibration or $(X,\,A)$
is a closed cofibration or $(X,\,A)$![]() is a proper pair. One can use [Reference Smrekar29, Lemma A.2] in the first case and proposition 6.1 in the second to infer that restrictions $\mathop {\rm map}\nolimits (X,\,T)\to \mathop {\rm map}\nolimits (A,\,T)$
is a proper pair. One can use [Reference Smrekar29, Lemma A.2] in the first case and proposition 6.1 in the second to infer that restrictions $\mathop {\rm map}\nolimits (X,\,T)\to \mathop {\rm map}\nolimits (A,\,T)$![]() are fibrations for all $T$
are fibrations for all $T$![]() , respectively all $T$
, respectively all $T$![]() which are ANRs.
which are ANRs.
Theorem 3.1 The tower $\left \{Z_i\right \}$![]() satisfies the assumptions of lemma 2.1. In the associated spectral sequence we have that $C_{p,q}\cong \check H^{n_q-p}(X,\,A;\pi ^q)$
satisfies the assumptions of lemma 2.1. In the associated spectral sequence we have that $C_{p,q}\cong \check H^{n_q-p}(X,\,A;\pi ^q)$![]() if $p,\,q\geqslant 1$
if $p,\,q\geqslant 1$![]() , and $\widetilde C_{0,q}\cong \check H^{n_q}(X,\,A;\pi ^q)$
, and $\widetilde C_{0,q}\cong \check H^{n_q}(X,\,A;\pi ^q)$![]() for $q>0$
for $q>0$![]() . If $q\leqslant 0$
. If $q\leqslant 0$![]() or $p<0$
or $p<0$![]() , then $C_{p,q}=\widetilde C_{0,q}=0$
, then $C_{p,q}=\widetilde C_{0,q}=0$![]() . These identifications are natural in $(X,\,A)$
. These identifications are natural in $(X,\,A)$![]() (i.e. with respect to maps over $Y$
(i.e. with respect to maps over $Y$![]() ) as well as with respect to maps of towers (3.1) induced by maps $K(\pi ^q_{(1)},\,n_q+1)\to K(\pi ^q_{(2)},\,n_q+1)$
) as well as with respect to maps of towers (3.1) induced by maps $K(\pi ^q_{(1)},\,n_q+1)\to K(\pi ^q_{(2)},\,n_q+1)$![]() for $q\geqslant 1$
for $q\geqslant 1$![]() .
.
Proof. There are induced pullback diagrams as follows. (Amend [Reference Smrekar29, Lemma A.3].)

Here, $\psi _q$![]() denotes the composite $A\xrightarrow {\phi _q}Y_q\to P(BK_q)$
denotes the composite $A\xrightarrow {\phi _q}Y_q\to P(BK_q)$![]() . Also, let $\Psi _q$
. Also, let $\Psi _q$![]() denote the composite $X\xrightarrow {\zeta _q}Y_q\to P(BK_q)$
denote the composite $X\xrightarrow {\zeta _q}Y_q\to P(BK_q)$![]() . Note that $\varepsilon \psi _q=k_q\phi _{q-1}$
. Note that $\varepsilon \psi _q=k_q\phi _{q-1}$![]() and $\varepsilon \Psi _q=k_q\zeta _{q-1}$
and $\varepsilon \Psi _q=k_q\zeta _{q-1}$![]() . As mentioned above, the vertical arrows in (3.3) are fibrations. As $P(BK_q)$
. As mentioned above, the vertical arrows in (3.3) are fibrations. As $P(BK_q)$![]() is contractible, $\mathop {\rm map}\nolimits (X,\,P(BK_q))\to \mathop {\rm map}\nolimits (A,\,P(BK_q))$
is contractible, $\mathop {\rm map}\nolimits (X,\,P(BK_q))\to \mathop {\rm map}\nolimits (A,\,P(BK_q))$![]() is a fibration and homotopy equivalence. Thus $EL_q=\mathop {\rm map}\nolimits _{\psi _q}(X,\,P(BK_q))$
is a fibration and homotopy equivalence. Thus $EL_q=\mathop {\rm map}\nolimits _{\psi _q}(X,\,P(BK_q))$![]() , its fibre over $\psi _q$
, its fibre over $\psi _q$![]() , is also contractible, rendering $(\eta _q)_*$
, is also contractible, rendering $(\eta _q)_*$![]() in diagram (3.3) a principal fibration. Set $BL_q=\mathop {\rm map}\nolimits _{\varepsilon \psi _q}(X,\,BK_q)$
in diagram (3.3) a principal fibration. Set $BL_q=\mathop {\rm map}\nolimits _{\varepsilon \psi _q}(X,\,BK_q)$![]() . Assuming an H-group multiplication on $BK_q$
. Assuming an H-group multiplication on $BK_q$![]() with strict unit $\mathbb {1}$
with strict unit $\mathbb {1}$![]() , we get induced H-group structures on $\mathop {\rm map}\nolimits (X,\,BK_q)$
, we get induced H-group structures on $\mathop {\rm map}\nolimits (X,\,BK_q)$![]() and $\mathop {\rm map}\nolimits (A,\,BK_q)$
and $\mathop {\rm map}\nolimits (A,\,BK_q)$![]() and, therefore, an induced map of fibrations as follows.
and, therefore, an induced map of fibrations as follows.

The horizontal arrows are homotopy equivalences and by coglueing homotopy equivalences (see [Reference Brown and Heath4, Corollary 1.5] or [Reference May and Ponto19, Lemma 2.2.4]), so are the maps on the fibres. In particular,
is a homotopy equivalence. This shows that, in fact, $BL_q$![]() is an H-group and so lemma 2.1 can be applied. The identification of $C_{p,q}$
is an H-group and so lemma 2.1 can be applied. The identification of $C_{p,q}$![]() as (a subgroup of) $\check H^{n_q-p}(X,\,A;\pi ^q)$
as (a subgroup of) $\check H^{n_q-p}(X,\,A;\pi ^q)$![]() comes via (3.5) through the obvious homeomorphism of loop spaces
comes via (3.5) through the obvious homeomorphism of loop spaces
and representability of Čech cohomology over paracompact Hausdorff pairs (see [Reference Huber14] and [Reference Goto11]). The reader may check that this identification is natural with respect to maps of pairs $(X,\,A)\to (X',\,A')$![]() over $Y\!$
over $Y\!$![]() .
.
For full naturality with respect to maps of towers (3.1), we assume that
are strict H-maps of ANR H-groups with strict units. To achieve that, we deloop a given homotopy representative for (3.6) to a based map $K(\pi ^q_{(1)},\,n_q+2)\to K(\pi ^q_{(2)},\,n_q+2)$![]() between ANRs and take the induced map between the associated Moore loop spaces (which will also be ANRs).
between ANRs and take the induced map between the associated Moore loop spaces (which will also be ANRs).
Addendum 3.2 The first differential $C_{p,q}\to C_{p-1,q+1}$![]() for $p\geqslant 1$
for $p\geqslant 1$![]() is obtained by applying $\pi _p$
is obtained by applying $\pi _p$![]() to the composite of (based) continuous maps
to the composite of (based) continuous maps

The first map is induced by the self-homotopy equivalence $\mathop {\rm map}\nolimits _{A\to \mathbb {1}}(X,\,BK_q)\to \mathop {\rm map}\nolimits _{k_q\phi _{q-1}}(X,\,BK_q)$![]() sending the map $\mathop {\rm const}\nolimits _{\mathbb {1}}$
sending the map $\mathop {\rm const}\nolimits _{\mathbb {1}}$![]() to $k_q\zeta _{q-1}$
to $k_q\zeta _{q-1}$![]() that is in turn induced by an H-group multiplication on $BK_q$
that is in turn induced by an H-group multiplication on $BK_q$![]() with strict unit $\mathbb {1}$
with strict unit $\mathbb {1}$![]() . The following 3 maps correspond to the sequence (2.4) in conjunction with remark 2.3. This identification of the differential is natural in $(X,\,A)$
. The following 3 maps correspond to the sequence (2.4) in conjunction with remark 2.3. This identification of the differential is natural in $(X,\,A)$![]() and $Y\!$
and $Y\!$![]() .
.
4. An auxiliary result for finite-dimensional domain
The results of this section will be used in § 5 to establish the convergence of the spectral sequence of theorem 1.1 in case of a finite dimensional domain.
In [Reference Klein, Schochet and Smith16], the authors establish natural isomorphisms $\mathop {\rm colim}\nolimits _j\pi _k(\mathop {\rm map}\nolimits (X_j,\,Y),\,f_j)\to \pi _k(\mathop {\rm map}\nolimits (X,\,Y),\,f)$![]() where $X$
where $X$![]() is a compactum and $\left \{X_j\right \}$
is a compactum and $\left \{X_j\right \}$![]() an inverse system of compact polyhedra with limit $X$
an inverse system of compact polyhedra with limit $X$![]() . They use a method of Spanier [Reference Spanier32, Theorem 13.4] and a clever trick to show validity for any map $f\colon X\to Y$
. They use a method of Spanier [Reference Spanier32, Theorem 13.4] and a clever trick to show validity for any map $f\colon X\to Y$![]() as basepoint.
as basepoint.
We note that a generalization to any paracompact space $X$![]() (pair, even) is possible, using methods of Barratt (see [Reference Barratt1, Section 12]) and the same trick to allow for general basepoints in $\mathop {\rm map}\nolimits (X,\,Y)$
(pair, even) is possible, using methods of Barratt (see [Reference Barratt1, Section 12]) and the same trick to allow for general basepoints in $\mathop {\rm map}\nolimits (X,\,Y)$![]() . To begin, let $X$
. To begin, let $X$![]() be a paracompact Hausdorff space with closed subset $A$
be a paracompact Hausdorff space with closed subset $A$![]() . For each locally finite open covering $\lambda$
. For each locally finite open covering $\lambda$![]() of $X$
of $X$![]() , let $N_\lambda$
, let $N_\lambda$![]() denote the nerve of $\lambda$
denote the nerve of $\lambda$![]() and $L_\lambda$
and $L_\lambda$![]() the subcomplex of $N_\lambda$
the subcomplex of $N_\lambda$![]() obtained by the embedding of the nerve of $\lambda \cap A$
obtained by the embedding of the nerve of $\lambda \cap A$![]() . A simplicial map $p_{\mu \lambda }\colon N_\mu \to N_\lambda$
. A simplicial map $p_{\mu \lambda }\colon N_\mu \to N_\lambda$![]() exists whenever $\mu$
exists whenever $\mu$![]() refines $\lambda$
refines $\lambda$![]() , and partitions of unity provide for maps $h_\lambda \colon X\to N_\lambda$
, and partitions of unity provide for maps $h_\lambda \colon X\to N_\lambda$![]() . Finally, we assume that $(Y,\,y_0)$
. Finally, we assume that $(Y,\,y_0)$![]() has the homotopy type of a pointed CW complex and allow for an additional compact Hausdorff parameter space $T$
has the homotopy type of a pointed CW complex and allow for an additional compact Hausdorff parameter space $T$![]() . Our auxiliary result is the following.
. Our auxiliary result is the following.
Theorem 4.1 Product maps $h_\lambda \times \mathop {\rm id}\nolimits _T$![]() and $p_{\lambda \mu }\times \mathop {\rm id}\nolimits _T$
and $p_{\lambda \mu }\times \mathop {\rm id}\nolimits _T$![]() yield a natural bijection
yield a natural bijection
Essentially, this follows by an application of [Reference Barratt1, Theorem 12.32] to the codomain $(\mathop {\rm map}\nolimits (T,\,Y),\,\mathop {\rm const}\nolimits _{y_0})$![]() , which has the homotopy type of a pointed CW complex if $(Y,\,y_0)$
, which has the homotopy type of a pointed CW complex if $(Y,\,y_0)$![]() has, and the exponential law. Barratt's restriction to locally finite targets is not necessary (the straight-line homotopy used implicitly in his Lemma 12.31 should be replaced with one in the sense of [Reference Sakai25, Proposition 4.9.7]). Note that if $A$
has, and the exponential law. Barratt's restriction to locally finite targets is not necessary (the straight-line homotopy used implicitly in his Lemma 12.31 should be replaced with one in the sense of [Reference Sakai25, Proposition 4.9.7]). Note that if $A$![]() is empty, we do not need a basepoint in $Y\!$
is empty, we do not need a basepoint in $Y\!$![]() .
.
To apply theorem 4.1, let $P^nY$![]() be the $n$
be the $n$![]() -th Postnikov section (up to homotopy) together with the projection $p\colon Y\to P^nY$
-th Postnikov section (up to homotopy) together with the projection $p\colon Y\to P^nY$![]() (pointed if $Y$
(pointed if $Y$![]() is pointed).
is pointed).
Proposition 4.2 If $\mathop {\rm dim}\nolimits X\leqslant d< n$![]() , then $p_*\colon \mathop {\rm map}\nolimits (X,\,Y)\to \mathop {\rm map}\nolimits (X,\,P^nY)$
, then $p_*\colon \mathop {\rm map}\nolimits (X,\,Y)\to \mathop {\rm map}\nolimits (X,\,P^nY)$![]() and $p_*\colon \mathop {\rm map}\nolimits _{A\to y_0}(X,\,Y)\to \mathop {\rm map}\nolimits _{A\to y_0}(X,\,P^nY)$
and $p_*\colon \mathop {\rm map}\nolimits _{A\to y_0}(X,\,Y)\to \mathop {\rm map}\nolimits _{A\to y_0}(X,\,P^nY)$![]() are $(n-d+1)$
are $(n-d+1)$![]() -equivalences.
-equivalences.
Proof. The dimension assumption guarantees a cofinal subfamily $\{\lambda \}$![]() with $\mathop {\rm dim}\nolimits N_\lambda \leqslant d$
with $\mathop {\rm dim}\nolimits N_\lambda \leqslant d$![]() . Let $N_\lambda$
. Let $N_\lambda$![]() be such and let $T$
be such and let $T$![]() be a compact $k$
be a compact $k$![]() -dimensional polyhedron. Consider
-dimensional polyhedron. Consider
By relative cellular approximation, (4.1) is a surjection if $k+d\leqslant n+1$![]() and an injection if $k+d\leqslant n$
and an injection if $k+d\leqslant n$![]() . By theorem 4.1, $[X\times T,\,Y]\to [X\times T,\,P^nY]$
. By theorem 4.1, $[X\times T,\,Y]\to [X\times T,\,P^nY]$![]() has the same properties. In particular, taking $T=\left \{*\right \}$
has the same properties. In particular, taking $T=\left \{*\right \}$![]() we infer that $[X,\,Y]\to [X,\,P^nY]$
we infer that $[X,\,Y]\to [X,\,P^nY]$![]() is a bijection. Let $f\colon X\to Y$
is a bijection. Let $f\colon X\to Y$![]() be a basepoint in $\mathop {\rm map}\nolimits (X,\,Y)$
be a basepoint in $\mathop {\rm map}\nolimits (X,\,Y)$![]() and let $*$
and let $*$![]() denote a basepoint in the sphere $S^k$
denote a basepoint in the sphere $S^k$![]() . Making use of the projection retraction $X\times S^k\to X\times \left \{*\right \}\equiv X$
. Making use of the projection retraction $X\times S^k\to X\times \left \{*\right \}\equiv X$![]() as in the proof of [Reference Klein, Schochet and Smith16, Theorem 6.4], we infer that
as in the proof of [Reference Klein, Schochet and Smith16, Theorem 6.4], we infer that
is a split short exact sequence of pointed sets. Here, $[X\times S^k,\,Y]_{f}$![]() is the set of homotopy classes of maps $X\times S^k\to Y$
is the set of homotopy classes of maps $X\times S^k\to Y$![]() that restrict to $f\colon X\times \left \{*\right \}\to Y$
that restrict to $f\colon X\times \left \{*\right \}\to Y$![]() . Applying naturality of (4.2) to $p\colon Y\to P^nY$
. Applying naturality of (4.2) to $p\colon Y\to P^nY$![]() , a diagram chase shows that $p_*\colon [X\times S^k,\,Y]_f\to [X\times S^k,\,P^nY]_{pf}$
, a diagram chase shows that $p_*\colon [X\times S^k,\,Y]_f\to [X\times S^k,\,P^nY]_{pf}$![]() , which can clearly be identified with $p_*\colon \pi _k(\mathop {\rm map}\nolimits (X,\,Y),\,f)\to \pi _k(\mathop {\rm map}\nolimits (X,\,P^nY),\,pf)$
, which can clearly be identified with $p_*\colon \pi _k(\mathop {\rm map}\nolimits (X,\,Y),\,f)\to \pi _k(\mathop {\rm map}\nolimits (X,\,P^nY),\,pf)$![]() , is bijective for $k< n-d+1$
, is bijective for $k< n-d+1$![]() and surjective for $k=(n-d+1)$
and surjective for $k=(n-d+1)$![]() .
.
For $p_*\colon \mathop {\rm map}\nolimits _{A\to y_0}(X,\,Y)\to \mathop {\rm map}\nolimits _{A\to p(y_0)}(X,\,P^nY)$![]() , use pairs everywhere.
, use pairs everywhere.
We apply proposition 4.2 to the relative case as follows. Let $A$![]() be closed in $X$
be closed in $X$![]() and let $\phi \colon A\to Y$
and let $\phi \colon A\to Y$![]() be a map. Consider the induced map
be a map. Consider the induced map
Corollary 4.3 Assume that $n$![]() is big enough.
is big enough.
We call a map a weak $n$![]() -equivalence if it induces an injection on $\pi _0$
-equivalence if it induces an injection on $\pi _0$![]() , isomorphisms on $\pi _k$
, isomorphisms on $\pi _k$![]() for $1\leqslant k< n$
for $1\leqslant k< n$![]() , and epimorphisms on $\pi _n$
, and epimorphisms on $\pi _n$![]() for all choices of basepoint.
for all choices of basepoint.
Proof. Case (i) follows from proposition 4.2 applied to the morphism of the homotopy exact sequences of fibrations $\mathop {\rm map}\nolimits (X,\,Y)\to \mathop {\rm map}\nolimits (A,\,Y)$![]() and $\mathop {\rm map}\nolimits (X,\,P^nY)\to \mathop {\rm map}\nolimits (A,\,P^nY)$
and $\mathop {\rm map}\nolimits (X,\,P^nY)\to \mathop {\rm map}\nolimits (A,\,P^nY)$![]() . For (ii), consider the pullback diagrams induced by (1.2):
. For (ii), consider the pullback diagrams induced by (1.2):

Using proposition 6.1, it follows that the vertical arrows in (4.4) are fibrations. Reasoning as in case (i), it follows that the mapping induced on the fibres of

is an $(n-d)$![]() -equivalence. By naturality of (4.4) in $Y\!$
-equivalence. By naturality of (4.4) in $Y\!$![]() ,
,
is a weak $(n-d)$![]() -equivalence for all $i$
-equivalence for all $i$![]() . Now $\mathop {\rm map}\nolimits _\phi (X,\,Y)$
. Now $\mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() is the inverse limit of $\left \{\mathop {\rm map}\nolimits _\phi (X_{i},\,Y)\right \}$
is the inverse limit of $\left \{\mathop {\rm map}\nolimits _\phi (X_{i},\,Y)\right \}$![]() (see corollary 6.2) and there are the associated $\lim ^1--\lim$
(see corollary 6.2) and there are the associated $\lim ^1--\lim$![]() short exact sequences (see [Reference Bousfield and Kan5, Chapter IX] and also [Reference Mardešić and Segal17, p. 178, Theorem 1]). By naturality in $Y$
short exact sequences (see [Reference Bousfield and Kan5, Chapter IX] and also [Reference Mardešić and Segal17, p. 178, Theorem 1]). By naturality in $Y$![]() , we get morphisms of those exact sequences identifying the morphisms $\pi _k(\mathop {\rm map}\nolimits _\phi (X,\,Y),\,f)\to \pi _k(\mathop {\rm map}\nolimits _\phi (X,\,P^nY),\,pf)$
, we get morphisms of those exact sequences identifying the morphisms $\pi _k(\mathop {\rm map}\nolimits _\phi (X,\,Y),\,f)\to \pi _k(\mathop {\rm map}\nolimits _\phi (X,\,P^nY),\,pf)$![]() . From those we infer (ii).
. From those we infer (ii).
5. Convergence, nilpotency and localization
Definition 5.1 A topological space $Z$![]() (not necessarily of CW homotopy type) is nilpotent if, for any choice of basepoint $z_0$
(not necessarily of CW homotopy type) is nilpotent if, for any choice of basepoint $z_0$![]() , the fundamental group $\pi _1(Z,\,z_0)$
, the fundamental group $\pi _1(Z,\,z_0)$![]() is nilpotent and operates nilpotently on all higher homotopy groups $\pi _n(Z,\,z_0)$
is nilpotent and operates nilpotently on all higher homotopy groups $\pi _n(Z,\,z_0)$![]() , $n\geqslant 2$
, $n\geqslant 2$![]() .
.
Proof of theorem 1.1 Assume the notation of theorem 3.1. Diagram (3.3) exhibits $\mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)$![]() as the homotopy fibre of $(k_q)_*\colon \mathop {\rm map}\nolimits _{\phi _{q-1}}(X,\,Y_{q-1})\to BL_q$
as the homotopy fibre of $(k_q)_*\colon \mathop {\rm map}\nolimits _{\phi _{q-1}}(X,\,Y_{q-1})\to BL_q$![]() where $BL_q$
where $BL_q$![]() is an H-group and hence nilpotent. As $\mathop {\rm map}\nolimits _{\phi _{0}}(X,\,Y_{0})=\left \{*\right \}$
is an H-group and hence nilpotent. As $\mathop {\rm map}\nolimits _{\phi _{0}}(X,\,Y_{0})=\left \{*\right \}$![]() , it follows by induction that $\mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)$
, it follows by induction that $\mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)$![]() are nilpotent for all $q$
are nilpotent for all $q$![]() (see [Reference Hilton, Mislin and Roitberg12, Theorem II.2.2] together with the final remark of the proof, as well as the proof of [Reference Hilton, Mislin, Roitberg and Steiner13, Theorem A]).
(see [Reference Hilton, Mislin and Roitberg12, Theorem II.2.2] together with the final remark of the proof, as well as the proof of [Reference Hilton, Mislin, Roitberg and Steiner13, Theorem A]).
Case 1. $Y$![]() has finitely many nontrivial homotopy groups. Then $Y\to Y_q$
has finitely many nontrivial homotopy groups. Then $Y\to Y_q$![]() is a homotopy equivalence for some $q$
is a homotopy equivalence for some $q$![]() . This finishes the proof if $A=\emptyset$
. This finishes the proof if $A=\emptyset$![]() or if $\phi$
or if $\phi$![]() maps the entire $A$
maps the entire $A$![]() to a nondegenerate $y_0\in Y$
to a nondegenerate $y_0\in Y$![]() , for then we have homotopy equivalences $\mathop {\rm map}\nolimits (X,\,Y)\to \mathop {\rm map}\nolimits (X,\,Y_q)$
, for then we have homotopy equivalences $\mathop {\rm map}\nolimits (X,\,Y)\to \mathop {\rm map}\nolimits (X,\,Y_q)$![]() and $\mathop {\rm map}\nolimits _{A\to y_0}(X,\,Y)\to \mathop {\rm map}\nolimits _{A\to \eta ^q(y_0)}(X,\,Y_q)$
and $\mathop {\rm map}\nolimits _{A\to y_0}(X,\,Y)\to \mathop {\rm map}\nolimits _{A\to \eta ^q(y_0)}(X,\,Y_q)$![]() . (See the proof of (1) in the discussion on page 7.)
. (See the proof of (1) in the discussion on page 7.)
Suppose that $A\hookrightarrow X$![]() is a cofibration or $(X,\,A)$
is a cofibration or $(X,\,A)$![]() is a proper pair and $Y$
is a proper pair and $Y$![]() is an ANR. Then we have restriction fibrations $\mathop {\rm map}\nolimits (X,\,Y)\to \mathop {\rm map}\nolimits (A,\,Y)$
is an ANR. Then we have restriction fibrations $\mathop {\rm map}\nolimits (X,\,Y)\to \mathop {\rm map}\nolimits (A,\,Y)$![]() and $\mathop {\rm map}\nolimits (X,\,Y_q)\to \mathop {\rm map}\nolimits (A,\,Y_q)$
and $\mathop {\rm map}\nolimits (X,\,Y_q)\to \mathop {\rm map}\nolimits (A,\,Y_q)$![]() (note $Y_q$
(note $Y_q$![]() is an ANR by construction), and a morphism between them induced by the homotopy equivalence $Y\to Y_q$
is an ANR by construction), and a morphism between them induced by the homotopy equivalence $Y\to Y_q$![]() . By [Reference Brown and Heath4, Corollary 1.5], we get the homotopy equivalence $\mathop {\rm map}\nolimits _\phi (X,\,Y)\to \mathop {\rm map}\nolimits _{\phi _q}(X,\,Y)$
. By [Reference Brown and Heath4, Corollary 1.5], we get the homotopy equivalence $\mathop {\rm map}\nolimits _\phi (X,\,Y)\to \mathop {\rm map}\nolimits _{\phi _q}(X,\,Y)$![]() between the fibres. Thus in Case 1, the assumptions of proposition 2.6 and corollary 2.7 are met trivially.
between the fibres. Thus in Case 1, the assumptions of proposition 2.6 and corollary 2.7 are met trivially.
Case 2. $Y$![]() has infinitely many nontrivial homotopy groups. By proposition 4.2 and corollary 4.3, the connectivity of $\mathop {\rm map}\nolimits _\phi (X,\,Y)\to \mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)$
has infinitely many nontrivial homotopy groups. By proposition 4.2 and corollary 4.3, the connectivity of $\mathop {\rm map}\nolimits _\phi (X,\,Y)\to \mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)$![]() tends to infinity with $q$
tends to infinity with $q$![]() , implying nilpotency of $\mathop {\rm map}\nolimits _\phi (X,\,Y)$
, implying nilpotency of $\mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() as well as the assumptions of proposition 2.6 and corollary 2.7.
as well as the assumptions of proposition 2.6 and corollary 2.7.
Finally, we set $E^2_{-k,q}=C_{q-k,q}$![]() for $k< q$
for $k< q$![]() and $E^2_{-q,q}=\widetilde C_{0,q}$
and $E^2_{-q,q}=\widetilde C_{0,q}$![]() to obtain the upper half-plane spectral sequence with homology-type differentials as claimed. Localization on the level of $E^2$
to obtain the upper half-plane spectral sequence with homology-type differentials as claimed. Localization on the level of $E^2$![]() implies localization in the limit in case of convergence by theorem 2.8.
implies localization in the limit in case of convergence by theorem 2.8.
Example 5.2 By way of example, Federer [Reference Federer10] studied the rationalized higher homotopy groups of $\mathop {\rm map}\nolimits _*(X,\,S^n)$![]() for a finite-dimensional CW complex $X$
for a finite-dimensional CW complex $X$![]() . To illustrate the usefulness of addendum 3.2, we also treat $\mathop {\rm map}\nolimits _*(X,\,S^n_{(0)})$
. To illustrate the usefulness of addendum 3.2, we also treat $\mathop {\rm map}\nolimits _*(X,\,S^n_{(0)})$![]() where $S^n_{(0)}$
where $S^n_{(0)}$![]() is the rationalized sphere. Our treatment is valid for $X\in {\rm PHK}$
is the rationalized sphere. Our treatment is valid for $X\in {\rm PHK}$![]() ; by corollary 1.3, $\mathop {\rm map}\nolimits _*(X,\,S^n)\to \mathop {\rm map}\nolimits _*(X,\,S^n_{(0)})$
; by corollary 1.3, $\mathop {\rm map}\nolimits _*(X,\,S^n)\to \mathop {\rm map}\nolimits _*(X,\,S^n_{(0)})$![]() is rationalization on path components when $X$
is rationalization on path components when $X$![]() is compact of finite covering dimension.
is compact of finite covering dimension.
The interesting case is of an even $n>2$![]() . Then, $Y=S^n_{(0)}$
. Then, $Y=S^n_{(0)}$![]() can be represented as the homotopy fibre of a single Postnikov invariant $k\colon K({\mathbb {Q}},\,n)\to K({\mathbb {Q}},\,2n)$
can be represented as the homotopy fibre of a single Postnikov invariant $k\colon K({\mathbb {Q}},\,n)\to K({\mathbb {Q}},\,2n)$![]() whose associated cohomology class in $H^{2n}(K({\mathbb {Q}},\,n);{\mathbb {Q}})$
whose associated cohomology class in $H^{2n}(K({\mathbb {Q}},\,n);{\mathbb {Q}})$![]() is the square of the fundamental class $\iota _n\in H^n(K({\mathbb {Q}},\,n);{\mathbb {Q}})$
is the square of the fundamental class $\iota _n\in H^n(K({\mathbb {Q}},\,n);{\mathbb {Q}})$![]() .
.
First we consider $[X,\,Y]_*$![]() . To this end, we investigate the Puppe sequence
. To this end, we investigate the Puppe sequence
Here, $\Rightarrow$![]() is employed to imply that the group $[X,\,K({\mathbb {Q}},\,2n-1)]_*$
is employed to imply that the group $[X,\,K({\mathbb {Q}},\,2n-1)]_*$![]() acts on the set $[X,\,Y]_*$
acts on the set $[X,\,Y]_*$![]() , and that $[X,\,Y]_*\to [X,\,K({\mathbb {Q}},\,n)]_*$
, and that $[X,\,Y]_*\to [X,\,K({\mathbb {Q}},\,n)]_*$![]() collapses precisely the orbits.
collapses precisely the orbits.
By definition, $k_\#[f]=[k\circ f]$![]() which we may view as $f^*(\iota _n^2)=(f^*(\iota _n))^2$
which we may view as $f^*(\iota _n^2)=(f^*(\iota _n))^2$![]() . Therefore, $k_\#\colon [X,\,K({\mathbb {Q}},\,n)]_*\to [X,\,K({\mathbb {Q}},\,2n)]_*$
. Therefore, $k_\#\colon [X,\,K({\mathbb {Q}},\,n)]_*\to [X,\,K({\mathbb {Q}},\,2n)]_*$![]() translates into the squaring operation $\check {H}^n(X,\,*;{\mathbb {Q}})\to \check {H}^{2n}(X,\,*;{\mathbb {Q}})$
translates into the squaring operation $\check {H}^n(X,\,*;{\mathbb {Q}})\to \check {H}^{2n}(X,\,*;{\mathbb {Q}})$![]() . This holds for any $X$
. This holds for any $X$![]() , implying that $\Omega k_\#$
, implying that $\Omega k_\#$![]() is trivial as it corresponds, by adjunction, to squaring in a suspension
is trivial as it corresponds, by adjunction, to squaring in a suspension
This gives the short exact sequence
We consider the path component of a map $\zeta \colon X\to Y$![]() . Diagram (3.3) reads
. Diagram (3.3) reads

We assume that $K({\mathbb {Q}},\,n)$![]() and $K({\mathbb {Q}},\,2n)$
and $K({\mathbb {Q}},\,2n)$![]() are well-pointed and that $k$
are well-pointed and that $k$![]() is a fibration between well-pointed spaces. Next we assume that $\mu \colon K({\mathbb {Q}},\,n)\times K({\mathbb {Q}},\,n)\to K({\mathbb {Q}},\,n)$
is a fibration between well-pointed spaces. Next we assume that $\mu \colon K({\mathbb {Q}},\,n)\times K({\mathbb {Q}},\,n)\to K({\mathbb {Q}},\,n)$![]() is an H-group multiplication with strict unit $\mathbb {1}$
is an H-group multiplication with strict unit $\mathbb {1}$![]() . By virtue of the homotopy lifting property, we may also assume that $kp\zeta$
. By virtue of the homotopy lifting property, we may also assume that $kp\zeta$![]() is the constant map.
is the constant map.
For our spectral sequence, we assume that $Y_i=*$![]() for $1\leqslant i\leqslant n-1$
for $1\leqslant i\leqslant n-1$![]() , next $Y_n=\Omega (K({\mathbb {Q}},\,n+1),\,*)=K({\mathbb {Q}},\,n)$
, next $Y_n=\Omega (K({\mathbb {Q}},\,n+1),\,*)=K({\mathbb {Q}},\,n)$![]() , then $Y_i=Y_n$
, then $Y_i=Y_n$![]() for $n+1\leqslant i\leqslant 2n-2$
for $n+1\leqslant i\leqslant 2n-2$![]() , and finally $Y=Y_{2n-1}$
, and finally $Y=Y_{2n-1}$![]() is the homotopy fibre of $k\colon Y_n\to K({\mathbb {Q}},\,2n)$
is the homotopy fibre of $k\colon Y_n\to K({\mathbb {Q}},\,2n)$![]() . The only nontrivial differential is $d^{(n-1)}$
. The only nontrivial differential is $d^{(n-1)}$![]() . The fibre $F_n$
. The fibre $F_n$![]() is equal to $\mathop {\rm map}\nolimits _*(X,\,\Omega (K({\mathbb {Q}},\,n+1),\,*))=\mathop {\rm map}\nolimits _*(X,\,Y_n)$
is equal to $\mathop {\rm map}\nolimits _*(X,\,\Omega (K({\mathbb {Q}},\,n+1),\,*))=\mathop {\rm map}\nolimits _*(X,\,Y_n)$![]() (with basepoint $\zeta _n=p\circ \zeta$
(with basepoint $\zeta _n=p\circ \zeta$![]() ). In this sense, $\delta _n$
). In this sense, $\delta _n$![]() in (2.4) can be viewed as the identity morphism, and therefore $d^{(n-1)}$
in (2.4) can be viewed as the identity morphism, and therefore $d^{(n-1)}$![]() is obtained by applying $\pi _p(\_,\,p\circ \zeta )$
is obtained by applying $\pi _p(\_,\,p\circ \zeta )$![]() to $k_*\colon \mathop {\rm map}\nolimits _*(X,\,K({\mathbb {Q}},\,n))\to \mathop {\rm map}\nolimits _*(X,\,K({\mathbb {Q}},\,2n))$
to $k_*\colon \mathop {\rm map}\nolimits _*(X,\,K({\mathbb {Q}},\,n))\to \mathop {\rm map}\nolimits _*(X,\,K({\mathbb {Q}},\,2n))$![]() (see also (3.7)). For our identification $C_{p,q}\cong \check {H}^{q-p}(X,\,*;\pi _q)$
(see also (3.7)). For our identification $C_{p,q}\cong \check {H}^{q-p}(X,\,*;\pi _q)$![]() , we need to precompose $k_*$
, we need to precompose $k_*$![]() with the natural homotopy equivalence $\mathop {\rm map}\nolimits _*(X,\,K({\mathbb {Q}},\,n))\to \mathop {\rm map}\nolimits _*(X,\,K({\mathbb {Q}},\,n))$
with the natural homotopy equivalence $\mathop {\rm map}\nolimits _*(X,\,K({\mathbb {Q}},\,n))\to \mathop {\rm map}\nolimits _*(X,\,K({\mathbb {Q}},\,n))$![]() , induced by $\mu$
, induced by $\mu$![]() , that sends the path component of $\mathop {\rm const}\nolimits _{\mathbb {1}}$
, that sends the path component of $\mathop {\rm const}\nolimits _{\mathbb {1}}$![]() to that of $p\circ \zeta$
to that of $p\circ \zeta$![]() . Thus, the nontrivial differential corresponds to the map induced on $\pi _p(\_,\,\mathop {\rm const}\nolimits _{\mathbb {1}})$
. Thus, the nontrivial differential corresponds to the map induced on $\pi _p(\_,\,\mathop {\rm const}\nolimits _{\mathbb {1}})$![]() by
by
We view the latter as the morphism $[S^p\wedge X,\,K({\mathbb {Q}},\,n)]_*\to [S^p\wedge X,\,K({\mathbb {Q}},\,2n)]_*$![]() between sets of pointed homotopy classes. In light of the isomorphism $\check H^*(S^p\wedge X,\,*;{\mathbb {Q}})\cong \check H^*(S^p\times X,\,S^p\vee X;{\mathbb {Q}})$
between sets of pointed homotopy classes. In light of the isomorphism $\check H^*(S^p\wedge X,\,*;{\mathbb {Q}})\cong \check H^*(S^p\times X,\,S^p\vee X;{\mathbb {Q}})$![]() and the split short exact sequence
and the split short exact sequence
we consider the composite
The cross product with a generator $E^p\in \check H^p(S^p,\,*;{\mathbb {Q}})=[S^p,\,K({\mathbb {Q}},\,p)]_*$![]() realizes the iterated suspension isomorphism $[X,\,K({\mathbb {Q}},\,n-p)]_*\to [(S^p\times X,\,S^p\vee X),\,(K({\mathbb {Q}},\,n),\,*)]$
realizes the iterated suspension isomorphism $[X,\,K({\mathbb {Q}},\,n-p)]_*\to [(S^p\times X,\,S^p\vee X),\,(K({\mathbb {Q}},\,n),\,*)]$![]() , hence we compute the effect of (5.2) on $E^p\vert \times x\vert$
, hence we compute the effect of (5.2) on $E^p\vert \times x\vert$![]() where $E^p\vert \in \check H^p(S^p;{\mathbb {Q}})$
where $E^p\vert \in \check H^p(S^p;{\mathbb {Q}})$![]() and $x\vert \in \check H^{n-p}(X;{\mathbb {Q}})$
and $x\vert \in \check H^{n-p}(X;{\mathbb {Q}})$![]() are restrictions. For general $A\colon S^p\times X\to K({\mathbb {Q}},\,n)$
are restrictions. For general $A\colon S^p\times X\to K({\mathbb {Q}},\,n)$![]() with $A(S^p\vee X)=\left \{\mathbb {1}\right \}$
with $A(S^p\vee X)=\left \{\mathbb {1}\right \}$![]() , the class of $A$
, the class of $A$![]() maps to $[k\circ \mu \circ (A,\,p\zeta \circ \mathop {\rm pr}\nolimits _X)]$
maps to $[k\circ \mu \circ (A,\,p\zeta \circ \mathop {\rm pr}\nolimits _X)]$![]() ; the latter can be viewed as
; the latter can be viewed as

Here, $(p\zeta )^*(\iota _n^2)$![]() corresponds to $[k\circ p\zeta ]$
corresponds to $[k\circ p\zeta ]$![]() which is trivial. Finally, if $A^*(\iota _n)=E^p\vert \times x\vert$
which is trivial. Finally, if $A^*(\iota _n)=E^p\vert \times x\vert$![]() , we have $A^*(\iota _n^2)=(E^p\vert \times x\vert )^2=0$
, we have $A^*(\iota _n^2)=(E^p\vert \times x\vert )^2=0$![]() . Setting $I_n=p^*(\iota _n)\in \check H^n(Y;{\mathbb {Q}})$
. Setting $I_n=p^*(\iota _n)\in \check H^n(Y;{\mathbb {Q}})$![]() , we express
, we express
Thus, $d^{(n-1)}\colon \check H^{n-p}(X,\,*;{\mathbb {Q}})\to \check H^{2n-p}(X,\,*;{\mathbb {Q}})$![]() reads $\xi \mapsto 2\xi \cup \zeta ^*(I_n)$
reads $\xi \mapsto 2\xi \cup \zeta ^*(I_n)$![]() ; termination after $d^{(n-1)}$
; termination after $d^{(n-1)}$![]() yields exact sequences
yields exact sequences
where all cohomology is based with rational coefficients and $\pi _p=\pi _p(\mathop {\rm map}\nolimits _*(X,\,Y);\zeta )$![]() .
.
6. Proper domain
A useful approach to studying mapping spaces $\mathop {\rm map}\nolimits (X,\,Y)$![]() where $X$
where $X$![]() is a CW complex is to view $\mathop {\rm map}\nolimits (X,\,Y)$
is a CW complex is to view $\mathop {\rm map}\nolimits (X,\,Y)$![]() as the inverse limit of the system $\left \{\mathop {\rm map}\nolimits (K,\,Y)\right \}$
as the inverse limit of the system $\left \{\mathop {\rm map}\nolimits (K,\,Y)\right \}$![]() where $K$
where $K$![]() ranges over the finite subcomplexes of $X$
ranges over the finite subcomplexes of $X$![]() and restriction mappings
and restriction mappings
are associated to subcomplex inclusions $K\leqslant L$![]() . As the latter are closed cofibrations, the restriction mappings (6.1) are Hurewicz fibrations for any space $Y$
. As the latter are closed cofibrations, the restriction mappings (6.1) are Hurewicz fibrations for any space $Y$![]() .
.
We cannot expect a general paracompact domain space $X$![]() to be expressible as colimit of a suitable system of cofibrations. However, since we are interested in the homotopy type of $\mathop {\rm map}\nolimits (X,\,Y)$
to be expressible as colimit of a suitable system of cofibrations. However, since we are interested in the homotopy type of $\mathop {\rm map}\nolimits (X,\,Y)$![]() , it is enough to replace the target space $Y$
, it is enough to replace the target space $Y$![]() with a homotopy equivalent space in a way that renders restrictions (6.1) Hurewicz fibrations for sufficiently general compact pairs $(L,\,K)$
with a homotopy equivalent space in a way that renders restrictions (6.1) Hurewicz fibrations for sufficiently general compact pairs $(L,\,K)$![]() . To this end, we replace $Y$
. To this end, we replace $Y$![]() with a homotopy equivalent ANR; for example, we may take a simplicial complex with the metric topology. This can be done by Milnor [Reference Milnor22, Theorem 2].
with a homotopy equivalent ANR; for example, we may take a simplicial complex with the metric topology. This can be done by Milnor [Reference Milnor22, Theorem 2].
We say that $A\subset X$![]() is $P$
is $P$![]() -embedded if continuous pseudo-metrics on $A$
-embedded if continuous pseudo-metrics on $A$![]() extend to $X$
extend to $X$![]() . If, in addition, $A$
. If, in addition, $A$![]() is a zero set, then it is called $P_0$
is a zero set, then it is called $P_0$![]() -embedded. We refer to Stramaccia [Reference Stramaccia34] for more details; we need $P$
-embedded. We refer to Stramaccia [Reference Stramaccia34] for more details; we need $P$![]() -embeddings in the context of Morita's homotopy extension theorem used in the proof of proposition 6.1.
-embeddings in the context of Morita's homotopy extension theorem used in the proof of proposition 6.1.
Recall that an absolute retract, with shorthand AR, is a contractible ANR.
Proposition 6.1 Let $(X,\,A)$![]() be a compact proper pair and let $Y$
be a compact proper pair and let $Y$![]() be an ANR.
be an ANR.
(i) Restriction $R\colon \mathop {\rm map}\nolimits (X,\,Y)\to \mathop {\rm map}\nolimits (A,\,Y)$
 is a Hurewicz fibration.
is a Hurewicz fibration.(ii) Further let $B$
 be an AR, $f\colon X\to B$
be an AR, $f\colon X\to B$ a given map, and $p\colon Y\to B$
a given map, and $p\colon Y\to B$ a Hurewicz fibration. For $L\subset X$
a Hurewicz fibration. For $L\subset X$ denote $\Gamma (L)=\left \{s\colon L\to Y\,\vert \,p\circ s=f\vert _L\right \}\subset \mathop {\rm map}\nolimits (L,\,Y)$
denote $\Gamma (L)=\left \{s\colon L\to Y\,\vert \,p\circ s=f\vert _L\right \}\subset \mathop {\rm map}\nolimits (L,\,Y)$ . Then $R\vert _{\Gamma (X)}\colon \Gamma (X)\to \Gamma (A)$
. Then $R\vert _{\Gamma (X)}\colon \Gamma (X)\to \Gamma (A)$ is a Hurewicz fibration.
is a Hurewicz fibration.
Proof. As $R$![]() and $R\vert _{\Gamma (X)}$
and $R\vert _{\Gamma (X)}$![]() are maps between metrizable spaces, it suffices to prove the homotopy lifting property for metrizable spaces (see [Reference Dugundji9, XX.2.3]).
are maps between metrizable spaces, it suffices to prove the homotopy lifting property for metrizable spaces (see [Reference Dugundji9, XX.2.3]).
To prove (i), we take a metric space $Z$![]() . The solid part of the lifting diagram
. The solid part of the lifting diagram

induces a map $\eta \colon Z\times X\times \left \{0\right \}\cup Z\times A\times [0,\,1]\to Y$![]() . Being the product of a paracompact and a compact space, $Z\times X$
. Being the product of a paracompact and a compact space, $Z\times X$![]() is paracompact (Barratt [Reference Barratt1, Lemma 12.43]) and hence collection-wise normal. Therefore its $P_0$
is paracompact (Barratt [Reference Barratt1, Lemma 12.43]) and hence collection-wise normal. Therefore its $P_0$![]() -embedded subsets are precisely its zero sets ([Reference Stramaccia34, Examples 1.2]). Thus, $Z\times A$
-embedded subsets are precisely its zero sets ([Reference Stramaccia34, Examples 1.2]). Thus, $Z\times A$![]() is $P_0$
is $P_0$![]() -embedded in $Z\times X$
-embedded in $Z\times X$![]() , and Morita's extension theorem (see [Reference Stramaccia34, Theorem 2.2]) yields a map $Z\times X\times [0,\,1]\to Y$
, and Morita's extension theorem (see [Reference Stramaccia34, Theorem 2.2]) yields a map $Z\times X\times [0,\,1]\to Y$![]() extending $\eta$
extending $\eta$![]() . Its adjoint is the lifting sought in (6.2).
. Its adjoint is the lifting sought in (6.2).
We turn to (ii). The lifting problem analogous to (6.2) but with $\mathop {\rm map}\nolimits (X,\,Y)$![]() and $\mathop {\rm map}\nolimits (A,\,Y)$
and $\mathop {\rm map}\nolimits (A,\,Y)$![]() replaced by, respectively, $\Gamma (X)$
replaced by, respectively, $\Gamma (X)$![]() and $\Gamma (A)$
and $\Gamma (A)$![]() , is equivalent to
, is equivalent to

By the proof of (i), $\eta$![]() extends to a map $\bar \eta \colon Z\times X\times [0,\,1]\to Y$
extends to a map $\bar \eta \colon Z\times X\times [0,\,1]\to Y$![]() . We remedy the possible difference between $p\circ \bar \eta$
. We remedy the possible difference between $p\circ \bar \eta$![]() and $f\circ \mathop {\rm pr}\nolimits _X$
and $f\circ \mathop {\rm pr}\nolimits _X$![]() (where $\mathop {\rm pr}\nolimits _X$
(where $\mathop {\rm pr}\nolimits _X$![]() is projection onto $X$
is projection onto $X$![]() ) as follows. Let a partial map into $B$
) as follows. Let a partial map into $B$![]() be defined by $p\circ \bar \eta$
be defined by $p\circ \bar \eta$![]() on $Z\times X\times [0,\,1]\times \left \{0\right \}$
on $Z\times X\times [0,\,1]\times \left \{0\right \}$![]() and $f\circ \mathop {\rm pr}\nolimits _X$
and $f\circ \mathop {\rm pr}\nolimits _X$![]() on $Z\times X\times [0,\,1]\times \left \{1\right \}\cup (Z\times X\times \left \{0\right \}\sqcup Z\times A\times [0,\,1])\times [0,\,1]$
on $Z\times X\times [0,\,1]\times \left \{1\right \}\cup (Z\times X\times \left \{0\right \}\sqcup Z\times A\times [0,\,1])\times [0,\,1]$![]() . This partial map is defined on a zero (hence $P_0$
. This partial map is defined on a zero (hence $P_0$![]() -embedded) set in $Z\times X\times [0,\,1]\times [0,\,1]$
-embedded) set in $Z\times X\times [0,\,1]\times [0,\,1]$![]() and since $B$
and since $B$![]() is an AR, there exists an extension over all $Z\times X\times [0,\,1]\times [0,\,1]$
is an AR, there exists an extension over all $Z\times X\times [0,\,1]\times [0,\,1]$![]() (see [Reference Stramaccia34, Theorem 2.1]). We consider the lifting problem
(see [Reference Stramaccia34, Theorem 2.1]). We consider the lifting problem

By construction, the homotopy into $B$![]() is stationary on $Z\times X\times \left \{0\right \}\cup Z\times A\times [0,\,1]$
is stationary on $Z\times X\times \left \{0\right \}\cup Z\times A\times [0,\,1]$![]() . By regularity of $p$
. By regularity of $p$![]() (see [Reference Dugundji9, XX.2.4]), the lifting into $Y$
(see [Reference Dugundji9, XX.2.4]), the lifting into $Y$![]() can also be assumed to be stationary there. Level 1 of that lifting is a map $Z\times X\times [0,\,1]\to Y$
can also be assumed to be stationary there. Level 1 of that lifting is a map $Z\times X\times [0,\,1]\to Y$![]() that extends $\eta$
that extends $\eta$![]() and projects to $f\circ \mathop {\rm pr}\nolimits _X$
and projects to $f\circ \mathop {\rm pr}\nolimits _X$![]() by $p$
by $p$![]() , and thus it constitutes the lifting sought in (6.3).
, and thus it constitutes the lifting sought in (6.3).
Corollary 6.2 Let $(X,\,A)$![]() be a proper pair with an admissible chain $A=X_0\subset X_1\subset X_2\subset \dots$
be a proper pair with an admissible chain $A=X_0\subset X_1\subset X_2\subset \dots$![]() , let $Y$
, let $Y$![]() be an ANR, and let $\phi \colon A\to Y$
be an ANR, and let $\phi \colon A\to Y$![]() be a map. The induced tower
be a map. The induced tower
is one of Hurewicz fibrations and the terms $\mathop {\rm map}\nolimits _\phi (X_i,\,Y)$![]() have CW homotopy type. Restrictions $R^i\colon \mathop {\rm map}\nolimits _\phi (X,\,Y)\to \mathop {\rm map}\nolimits _\phi (X_i,\,Y)$
have CW homotopy type. Restrictions $R^i\colon \mathop {\rm map}\nolimits _\phi (X,\,Y)\to \mathop {\rm map}\nolimits _\phi (X_i,\,Y)$![]() , which are also Hurewicz fibrations, exhibit $\mathop {\rm map}\nolimits _\phi (X,\,Y)$
, which are also Hurewicz fibrations, exhibit $\mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() as the inverse limit.
as the inverse limit.
Proof. The canonical inverse limit is the subspace $Z'\subset \prod _{i=1}^\infty \mathop {\rm map}\nolimits _\phi (X_i,\,Y)$![]() consisting of compatible sequences of maps $f_i\colon X_i\to Y$
consisting of compatible sequences of maps $f_i\colon X_i\to Y$![]() with $f_i\vert _A=\phi$
with $f_i\vert _A=\phi$![]() . Restrictions $R^i$
. Restrictions $R^i$![]() furnish the obvious homeomorphism $R\colon \mathop {\rm map}\nolimits _\phi (X,\,Y)\to Z'$
furnish the obvious homeomorphism $R\colon \mathop {\rm map}\nolimits _\phi (X,\,Y)\to Z'$![]() ; it is an embedding since the $X_i$
; it is an embedding since the $X_i$![]() dominate compact sets in $X$
dominate compact sets in $X$![]() and onto because $X=\mathop {\rm colim}\nolimits _iX_i$
and onto because $X=\mathop {\rm colim}\nolimits _iX_i$![]() . In diagram (4.4), restriction $\mathop {\rm map}\nolimits (C_i,\,Y)\to \mathop {\rm map}\nolimits (S_i,\,Y)$
. In diagram (4.4), restriction $\mathop {\rm map}\nolimits (C_i,\,Y)\to \mathop {\rm map}\nolimits (S_i,\,Y)$![]() is a fibration by (i) of proposition 6.1, and hence so is the pullback restriction $\mathop {\rm map}\nolimits _\phi (X_i,\,Y)\to \mathop {\rm map}\nolimits _\phi (X_{i-1},\,Y)$
is a fibration by (i) of proposition 6.1, and hence so is the pullback restriction $\mathop {\rm map}\nolimits _\phi (X_i,\,Y)\to \mathop {\rm map}\nolimits _\phi (X_{i-1},\,Y)$![]() . The spaces $\mathop {\rm map}\nolimits (C_i,\,Y)$
. The spaces $\mathop {\rm map}\nolimits (C_i,\,Y)$![]() and $\mathop {\rm map}\nolimits (S_i,\,Y)$
and $\mathop {\rm map}\nolimits (S_i,\,Y)$![]() have CW homotopy type by [Reference Milnor22, Theorem 3]. Now $\mathop {\rm map}\nolimits _\phi (X_0,\,Y)$
have CW homotopy type by [Reference Milnor22, Theorem 3]. Now $\mathop {\rm map}\nolimits _\phi (X_0,\,Y)$![]() is a point and it follows from [Reference Smrekar29, Proposition 4.2] that all $\mathop {\rm map}\nolimits _\phi (X_i,\,Y)$
is a point and it follows from [Reference Smrekar29, Proposition 4.2] that all $\mathop {\rm map}\nolimits _\phi (X_i,\,Y)$![]() have CW homotopy type.
have CW homotopy type.
By way of composition, $\mathop {\rm map}\nolimits _\phi (X_j,\,Y)\to \mathop {\rm map}\nolimits _\phi (X_i,\,Y)$![]() are fibrations for all $j\geqslant i$
are fibrations for all $j\geqslant i$![]() . The universal property of the limit implies that also the $R^i$
. The universal property of the limit implies that also the $R^i$![]() are fibrations.
are fibrations.
Proof of theorem 1.6 Corollary 1.3 guarantees that the maps
localize homotopy groups. Corollary 6.2 identifies the inverse limit of maps (6.4) as $\mathop {\rm map}\nolimits _\phi (X,\,Y)\to \mathop {\rm map}\nolimits _{l\phi }(X,\,Y_{(P)})$![]() . By [Reference Smrekar31, Theorem 6.1], the spaces $\mathop {\rm map}\nolimits (X,\,Y)$
. By [Reference Smrekar31, Theorem 6.1], the spaces $\mathop {\rm map}\nolimits (X,\,Y)$![]() and $\mathop {\rm map}\nolimits (X,\,Y_{(P)})$
and $\mathop {\rm map}\nolimits (X,\,Y_{(P)})$![]() are nilpotent and this latter map localizes homotopy groups.
are nilpotent and this latter map localizes homotopy groups.
Proof of proposition 1.8 Assume the notation of § 3. Diagram (3.3) exhibits $Z_q=\mathop {\rm map}\nolimits _{\phi _q}(X,\,Y_q)$![]() as the homotopy fibre of $(k_q)_*\colon Z_{q-1}\to \mathop {\rm map}\nolimits _{A\to *}(X,\,BK_q)$
as the homotopy fibre of $(k_q)_*\colon Z_{q-1}\to \mathop {\rm map}\nolimits _{A\to *}(X,\,BK_q)$![]() where $BK_q$
where $BK_q$![]() is an Eilenberg–MacLane space. Now $\mathop {\rm map}\nolimits _{A\to *}(X,\,BK_q)$
is an Eilenberg–MacLane space. Now $\mathop {\rm map}\nolimits _{A\to *}(X,\,BK_q)$![]() has CW type since $(X,\,A)$
has CW type since $(X,\,A)$![]() is quasi-finite, and as $Z_0=\left \{*\right \}$
is quasi-finite, and as $Z_0=\left \{*\right \}$![]() , an inductive application of [Reference Stasheff33, Proposition 0] shows that all $Z_q$
, an inductive application of [Reference Stasheff33, Proposition 0] shows that all $Z_q$![]() have CW homotopy type.
have CW homotopy type.
Set $Z^i=\mathop {\rm map}\nolimits _\phi (X_i,\,Y)$![]() , $\zeta ^i=\zeta \vert _{X_i}$
, $\zeta ^i=\zeta \vert _{X_i}$![]() , $Z^i_q=\mathop {\rm map}\nolimits _\phi (X_i,\,Y_q)$
, $Z^i_q=\mathop {\rm map}\nolimits _\phi (X_i,\,Y_q)$![]() , and $\zeta ^i_q=\zeta _q\vert _{X_i}$
, and $\zeta ^i_q=\zeta _q\vert _{X_i}$![]() . By corollary 6.2, $Z=\mathop {\rm map}\nolimits _\phi (X,\,Y)$
. By corollary 6.2, $Z=\mathop {\rm map}\nolimits _\phi (X,\,Y)$![]() is the limit of $Z^i$
is the limit of $Z^i$![]() and $Z_q$
and $Z_q$![]() is the limit of $Z^i_q$
is the limit of $Z^i_q$![]() for all $q$
for all $q$![]() , and all $Z^i$
, and all $Z^i$![]() and $Z^i_q$
and $Z^i_q$![]() have CW homotopy type. To establish the (additional) assumption of corollary 2.7, we show that for every $p\geqslant 1$
have CW homotopy type. To establish the (additional) assumption of corollary 2.7, we show that for every $p\geqslant 1$![]() , restrictions $\pi _p(Z,\,\zeta )\to \pi _p(Z_q,\,\zeta _q)$
, restrictions $\pi _p(Z,\,\zeta )\to \pi _p(Z_q,\,\zeta _q)$![]() are injective for all big enough $q$
are injective for all big enough $q$![]() . By [Reference Smrekar29, Corollary 3.4,(i)], applied to $Z=\lim _iZ^i$
. By [Reference Smrekar29, Corollary 3.4,(i)], applied to $Z=\lim _iZ^i$![]() , there exists an $i$
, there exists an $i$![]() such that $\pi _p(Z,\,\zeta )\to \pi _p(Z^i,\,\zeta ^i)$
such that $\pi _p(Z,\,\zeta )\to \pi _p(Z^i,\,\zeta ^i)$![]() are injective for all $p\geqslant 1$
are injective for all $p\geqslant 1$![]() . Fix some $p\geqslant 1$
. Fix some $p\geqslant 1$![]() . By corollary 4.3, $\pi _p(Z^i,\,\zeta ^i)\to \pi _p(Z^i_q,\,\zeta ^i_q)$
. By corollary 4.3, $\pi _p(Z^i,\,\zeta ^i)\to \pi _p(Z^i_q,\,\zeta ^i_q)$![]() is an isomorphism for all big enough $q$
is an isomorphism for all big enough $q$![]() . Thus, $\pi _p(Z,\,\zeta )\to \pi _p(Z_q,\,\zeta _q)$
. Thus, $\pi _p(Z,\,\zeta )\to \pi _p(Z_q,\,\zeta _q)$![]() must be injective for those $q$
must be injective for those $q$![]() .
.
To establish the assumptions of proposition 2.6, fix some $q$![]() . By another application of [Reference Smrekar29, Corollary 3.4,(i)], this time to $Z_q=\lim _iZ^i_q$
. By another application of [Reference Smrekar29, Corollary 3.4,(i)], this time to $Z_q=\lim _iZ^i_q$![]() , there exists an $i$
, there exists an $i$![]() such that $\pi _p(Z_q,\,\zeta _q)\to \pi _p(Z^i_q,\,\zeta ^i_q)$
such that $\pi _p(Z_q,\,\zeta _q)\to \pi _p(Z^i_q,\,\zeta ^i_q)$![]() are injective for all $p\geqslant 1$
are injective for all $p\geqslant 1$![]() . By [Reference Smrekar29, Corollary 3.4,(ii)], applied to $Z=\lim _iZ^i$
. By [Reference Smrekar29, Corollary 3.4,(ii)], applied to $Z=\lim _iZ^i$![]() , there exists a $j\geqslant i$
, there exists a $j\geqslant i$![]() such that the image of $\pi _p(Z,\,\zeta )\to \pi _p(Z^i,\,\zeta ^i)$
such that the image of $\pi _p(Z,\,\zeta )\to \pi _p(Z^i,\,\zeta ^i)$![]() coincides with that of $\pi _p(Z^j,\,\zeta ^j)\to \pi _p(Z^i,\,\zeta ^i)$
coincides with that of $\pi _p(Z^j,\,\zeta ^j)\to \pi _p(Z^i,\,\zeta ^i)$![]() for all $p$
for all $p$![]() . Finally, we fix some $p\geqslant 1$
. Finally, we fix some $p\geqslant 1$![]() . By corollary 4.3, there exists a $t$
. By corollary 4.3, there exists a $t$![]() such that $\pi _p(Z^j,\,\zeta ^j)\to \pi _p(Z^j_t,\,\zeta ^j_t)$
such that $\pi _p(Z^j,\,\zeta ^j)\to \pi _p(Z^j_t,\,\zeta ^j_t)$![]() is an isomorphism. A straightforward diagram chase shows that every element in the image of $\pi _p(Z_t,\,\zeta _t)\to \pi _p(Z_q,\,\zeta _q)$
is an isomorphism. A straightforward diagram chase shows that every element in the image of $\pi _p(Z_t,\,\zeta _t)\to \pi _p(Z_q,\,\zeta _q)$![]() is also in the image of $\pi _p(Z,\,\zeta )\to \pi _p(Z_q,\,\zeta _q)$
is also in the image of $\pi _p(Z,\,\zeta )\to \pi _p(Z_q,\,\zeta _q)$![]() .
.
Proof of proposition 1.9 By homotopy invariance of $\mathop {\rm map}\nolimits _{A\to *}(X,\,Y)$![]() for a well-pointed $Y$
for a well-pointed $Y$![]() , we may assume that $Y=K(G,\,n)$
, we may assume that $Y=K(G,\,n)$![]() is an H-group with strict unit $\mathbb {1}$
is an H-group with strict unit $\mathbb {1}$![]() and an ANR. If $\left \{X_i\right \}$
and an ANR. If $\left \{X_i\right \}$![]() is any admissible chain for $(X,\,A)$
is any admissible chain for $(X,\,A)$![]() , then by corollary 6.2, $Z^i=\mathop {\rm map}\nolimits _{A\to \mathbb {1}}(X_i,\,Y)$
, then by corollary 6.2, $Z^i=\mathop {\rm map}\nolimits _{A\to \mathbb {1}}(X_i,\,Y)$![]() defines a tower of fibrations whose terms have CW homotopy type and whose limit is $Z=\mathop {\rm map}\nolimits _{A\to \mathbb {1}}(X,\,Y)$
defines a tower of fibrations whose terms have CW homotopy type and whose limit is $Z=\mathop {\rm map}\nolimits _{A\to \mathbb {1}}(X,\,Y)$![]() . Homotopical representation of Čech cohomology directly implies that restriction $Z\to Z^i$
. Homotopical representation of Čech cohomology directly implies that restriction $Z\to Z^i$![]() induces the cohomological restriction $\check H^n(X,\,A;G)\to \check H^n(X_i,\,A;G)$
induces the cohomological restriction $\check H^n(X,\,A;G)\to \check H^n(X_i,\,A;G)$![]() .
.
Let $\zeta \colon X\to Y$![]() be a map with restrictions $\zeta ^i=\zeta \vert _{X_i}$
be a map with restrictions $\zeta ^i=\zeta \vert _{X_i}$![]() . Pointwise multiplications by $\zeta$
. Pointwise multiplications by $\zeta$![]() , respectively $\zeta ^i$
, respectively $\zeta ^i$![]() , comprise a homotopy auto-equivalence of the tower $\left \{Z^i\right \}$
, comprise a homotopy auto-equivalence of the tower $\left \{Z^i\right \}$![]() and its limit that maps the components of $\mathop {\rm const}\nolimits _{\mathbb {1}}$
and its limit that maps the components of $\mathop {\rm const}\nolimits _{\mathbb {1}}$![]() to those of $\zeta$
to those of $\zeta$![]() , respectively $\zeta ^i$
, respectively $\zeta ^i$![]() . Thus we can identify the morphisms $\pi _k(Z^j,\,\zeta ^j)\to \pi _k(Z^i,\,\zeta ^i)$
. Thus we can identify the morphisms $\pi _k(Z^j,\,\zeta ^j)\to \pi _k(Z^i,\,\zeta ^i)$![]() with $\check H^{n-k}(X_j,\,A;G)\to \check H^{n-k}(X_i,\,A;G)$
with $\check H^{n-k}(X_j,\,A;G)\to \check H^{n-k}(X_i,\,A;G)$![]() . An application of [Reference Smrekar31, Theorem 4.1] concludes the proof.
. An application of [Reference Smrekar31, Theorem 4.1] concludes the proof.
Example 6.3 Assume the notation of definition 1.5 for a proper space $X$![]() and set
and set
We claim that if $c(i)\geqslant n+2$![]() for $i\geqslant i_0$
for $i\geqslant i_0$![]() , then restriction $\mathop {\rm map}\nolimits (X,\,K(G,\,n))\to \mathop {\rm map}\nolimits (X_{i_0},\,K(G,\,n))$
, then restriction $\mathop {\rm map}\nolimits (X,\,K(G,\,n))\to \mathop {\rm map}\nolimits (X_{i_0},\,K(G,\,n))$![]() is a homotopy equivalence for every abelian group $G$
is a homotopy equivalence for every abelian group $G$![]() . To verify this claim, note first that if $i\geqslant i_0$
. To verify this claim, note first that if $i\geqslant i_0$![]() , universal coefficients imply $\check H^k(C_{i+1},\,S_i;G)=0$
, universal coefficients imply $\check H^k(C_{i+1},\,S_i;G)=0$![]() for any $G$
for any $G$![]() and all $k\leqslant n+1$
and all $k\leqslant n+1$![]() . Next, Wallace's theorem implies cohomology isomorphisms $\check H^*(X_{i+1},\,X_i;G)\to \check H^*(C_{i+1},\,S_i;G)$
. Next, Wallace's theorem implies cohomology isomorphisms $\check H^*(X_{i+1},\,X_i;G)\to \check H^*(C_{i+1},\,S_i;G)$![]() . Arguing as in the above proof, we use the cohomology exact sequence of the pair $(X_{i+1},\,X_i)$
. Arguing as in the above proof, we use the cohomology exact sequence of the pair $(X_{i+1},\,X_i)$![]() to infer that if $i\geqslant i_0$
to infer that if $i\geqslant i_0$![]() , then restriction $\mathop {\rm map}\nolimits (X_{i+1},\,K(G,\,n))\to \mathop {\rm map}\nolimits (X_{i},\,K(G,\,n))$
, then restriction $\mathop {\rm map}\nolimits (X_{i+1},\,K(G,\,n))\to \mathop {\rm map}\nolimits (X_{i},\,K(G,\,n))$![]() is a homotopy equivalence. It follows that so also is $\mathop {\rm map}\nolimits (X,\,K(G,\,n))\to \mathop {\rm map}\nolimits (X_{i_0},\,K(G,\,n))$
is a homotopy equivalence. It follows that so also is $\mathop {\rm map}\nolimits (X,\,K(G,\,n))\to \mathop {\rm map}\nolimits (X_{i_0},\,K(G,\,n))$![]() (see [Reference Smrekar29, Corollary 3.7]), rendering $\mathop {\rm map}\nolimits (X,\,K(G,\,n))$
(see [Reference Smrekar29, Corollary 3.7]), rendering $\mathop {\rm map}\nolimits (X,\,K(G,\,n))$![]() homotopy equivalent to a CW complex. In particular, if $\liminf _{i\to \infty }c(i)=\infty$
homotopy equivalent to a CW complex. In particular, if $\liminf _{i\to \infty }c(i)=\infty$![]() , then $\mathop {\rm map}\nolimits (X,\,K(G,\,n))$
, then $\mathop {\rm map}\nolimits (X,\,K(G,\,n))$![]() has CW homotopy type for every $G$
has CW homotopy type for every $G$![]() and $n$
and $n$![]() . For a simple-minded concrete example of a proper quasi-finite space that does not have the homotopy type of a CW complex, one can take the infinite wedge $X=\vee _{n=1}^\infty {\mathbb {H}}_n$
. For a simple-minded concrete example of a proper quasi-finite space that does not have the homotopy type of a CW complex, one can take the infinite wedge $X=\vee _{n=1}^\infty {\mathbb {H}}_n$![]() where ${\mathbb {H}}_n$
where ${\mathbb {H}}_n$![]() is the $n$
is the $n$![]() -dimensional Hawaiian earring.
-dimensional Hawaiian earring.
7. Spaces of sections
Let $X\in {\rm PHK}$![]() be connected and let $\pi \colon Q\to X$
be connected and let $\pi \colon Q\to X$![]() be a Hurewicz fibration with typical fibre of the homotopy type of a nilpotent CW complex. Let $\Gamma (\pi )$
be a Hurewicz fibration with typical fibre of the homotopy type of a nilpotent CW complex. Let $\Gamma (\pi )$![]() denote the space of sections of $\pi$
denote the space of sections of $\pi$![]() . We assume that $\pi =f^*(p')$
. We assume that $\pi =f^*(p')$![]() is the pullback of a fibration $p'\colon E'\to B$
is the pullback of a fibration $p'\colon E'\to B$![]() of spaces of CW homotopy type along the continuous map $f\colon X\to B$
of spaces of CW homotopy type along the continuous map $f\colon X\to B$![]() . We can change $\pi$
. We can change $\pi$![]() up to fibre homotopy equivalence (over $X$
up to fibre homotopy equivalence (over $X$![]() ) and keep the homotopy type of $\Gamma (\pi )$
) and keep the homotopy type of $\Gamma (\pi )$![]() . Thus we assume that $B$
. Thus we assume that $B$![]() is in fact a simplicial complex with the strong topology; $B$
is in fact a simplicial complex with the strong topology; $B$![]() is then an ANR with a covering of contractible open subsets (which are ANRs), see Milnor [Reference Milnor22]. The corresponding total space $E''$
is then an ANR with a covering of contractible open subsets (which are ANRs), see Milnor [Reference Milnor22]. The corresponding total space $E''$![]() will still have CW homotopy type by results of Stasheff [Reference Stasheff33]. Choosing a homotopy equivalent ANR $E'''$
will still have CW homotopy type by results of Stasheff [Reference Stasheff33]. Choosing a homotopy equivalent ANR $E'''$![]() we split the resulting map $E'''\to B$
we split the resulting map $E'''\to B$![]() into the composite of a homotopy equivalence and a fibration $p\colon E\to B$
into the composite of a homotopy equivalence and a fibration $p\colon E\to B$![]() where $E$
where $E$![]() is an ANR. The ‘usual’ splitting in the sense of the Hurewicz model structure has this property; see also Miyata [Reference Miyata23]. Consequently, each fibre of $p$
is an ANR. The ‘usual’ splitting in the sense of the Hurewicz model structure has this property; see also Miyata [Reference Miyata23]. Consequently, each fibre of $p$![]() is an ANR (being cofibred in $E$
is an ANR (being cofibred in $E$![]() by [Reference Strøm35, Theorem 12]) and we will use $Y$
by [Reference Strøm35, Theorem 12]) and we will use $Y$![]() to denote the fibre over a point understood from the context. As $\pi$
to denote the fibre over a point understood from the context. As $\pi$![]() is fibre homotopy equivalent to $f^*(p)$
is fibre homotopy equivalent to $f^*(p)$![]() , we identify $\Gamma (\pi )$
, we identify $\Gamma (\pi )$![]() with the space of maps $X\to E$
with the space of maps $X\to E$![]() whose composite with $p$
whose composite with $p$![]() equals $f$
equals $f$![]() .
.
Remark 7.1 In the fibration category on ANRs studied by [Reference Miyata23], the fibrations are what we call regular Hurewicz fibrations (and the author calls maps with the strong homotopy lifting property). As remarked above, every Hurewicz fibration $E\to B$![]() between ANRs is regular on the ground of metrizability of $B$
between ANRs is regular on the ground of metrizability of $B$![]() ; this remark makes certain parts of [Reference Miyata23] superfluous.
; this remark makes certain parts of [Reference Miyata23] superfluous.
More generally, assume that $(X,\,A)$![]() is a proper pair with an admissible chain $\left \{X_i\right \}$
is a proper pair with an admissible chain $\left \{X_i\right \}$![]() and that $\phi \colon A\to E$
and that $\phi \colon A\to E$![]() is a map over $f\vert _A$
is a map over $f\vert _A$![]() . For $A\subset L\subset X$
. For $A\subset L\subset X$![]() , we set
, we set
viewed as a subspace of $\mathop {\rm map}\nolimits (L,\,E)$![]() . For $A\subset K\subset L$
. For $A\subset K\subset L$![]() we have a restriction map $\Gamma _\phi (L,\,E)\to \Gamma _\phi (K,\,E)$
we have a restriction map $\Gamma _\phi (L,\,E)\to \Gamma _\phi (K,\,E)$![]() . As noted above, if $A=\emptyset$
. As noted above, if $A=\emptyset$![]() , then the homotopy type of $\Gamma (X,\,E)$
, then the homotopy type of $\Gamma (X,\,E)$![]() is an invariant of the homotopy type of $p\colon E\to B$
is an invariant of the homotopy type of $p\colon E\to B$![]() . Invariance in the relative version will be discussed after the following result.
. Invariance in the relative version will be discussed after the following result.
Theorem 7.2
(i) Restriction maps $\Gamma _\phi (X_i,\,E)\to \Gamma _\phi (X_{i-1},\,E)$
 are fibrations between spaces of CW homotopy type.
are fibrations between spaces of CW homotopy type.(ii) Let $l\colon E\to E_{(P)}$
 be a fibrewise localization at the set of primes $P$
be a fibrewise localization at the set of primes $P$ where we assume that $E_{(P)}$
where we assume that $E_{(P)}$ is an ANR. If $(X,\,A)$
is an ANR. If $(X,\,A)$ is locally finite dimensional or $Y$
is locally finite dimensional or $Y$ is a Postnikov section, then $\Gamma _\phi (X_{i},\,E)$
is a Postnikov section, then $\Gamma _\phi (X_{i},\,E)$ are nilpotent and $\Gamma _\phi (X_{i},\,E)\to \Gamma _\phi (X_{i},\,E_{(P)})$
are nilpotent and $\Gamma _\phi (X_{i},\,E)\to \Gamma _\phi (X_{i},\,E_{(P)})$ are localizations at $P$
are localizations at $P$ on path components.
on path components.
Proof. (i) By the assumption on $B$![]() and normality of the $C_i$
and normality of the $C_i$![]() in (1.2), we may refine each step $X_{i-1}\subset X_i$
in (1.2), we may refine each step $X_{i-1}\subset X_i$![]() into a finite chain of adjunctions to assume, after reindexing, that $f(\gamma _i(C_i))\subset K_i$
into a finite chain of adjunctions to assume, after reindexing, that $f(\gamma _i(C_i))\subset K_i$![]() for a contractible open set $K_i$
for a contractible open set $K_i$![]() in $B$
in $B$![]() . We get induced pullbacks
. We get induced pullbacks

By proposition 6.1, the vertical arrow on the right is a fibration, and hence so is the one on the left. Consider $p_*\colon \mathop {\rm map}\nolimits (C_i,\,E\vert _{K_i})\to \mathop {\rm map}\nolimits (C_i,\,K_i)$![]() . As $C_i$
. As $C_i$![]() is compact, this is a fibration between spaces of CW homotopy type. In fact $\mathop {\rm map}\nolimits (C_i,\,K_i)$
is compact, this is a fibration between spaces of CW homotopy type. In fact $\mathop {\rm map}\nolimits (C_i,\,K_i)$![]() is contractible and hence fibre inclusion $\Gamma (C_i,\,E\vert _{K_i})\hookrightarrow \mathop {\rm map}\nolimits (C_i,\,E\vert _{K_i})$
is contractible and hence fibre inclusion $\Gamma (C_i,\,E\vert _{K_i})\hookrightarrow \mathop {\rm map}\nolimits (C_i,\,E\vert _{K_i})$![]() is a homotopy equivalence. On the other hand, $Y\hookrightarrow E\vert _{K_i}$
is a homotopy equivalence. On the other hand, $Y\hookrightarrow E\vert _{K_i}$![]() is also a homotopy equivalence, hence $\mathop {\rm map}\nolimits (C_i,\,Y)\simeq \Gamma (C_i,\,E\vert _{K_i})$
is also a homotopy equivalence, hence $\mathop {\rm map}\nolimits (C_i,\,Y)\simeq \Gamma (C_i,\,E\vert _{K_i})$![]() is nilpotent (under the additional hypothesis) by theorem 1.1. The same holds for $S_i$
is nilpotent (under the additional hypothesis) by theorem 1.1. The same holds for $S_i$![]() in place of $C_i$
in place of $C_i$![]() and since $\Gamma _\phi (X_0,\,E)$
and since $\Gamma _\phi (X_0,\,E)$![]() is a one point-space, it follows by induction that all $\Gamma _\phi (X_{i},\,E)$
is a one point-space, it follows by induction that all $\Gamma _\phi (X_{i},\,E)$![]() are nilpotent (see May and Ponto [Reference May and Ponto19, Proposition 4.4.3]) of CW type (see Stasheff [Reference Stasheff33, Propositions 0 and 12]).
are nilpotent (see May and Ponto [Reference May and Ponto19, Proposition 4.4.3]) of CW type (see Stasheff [Reference Stasheff33, Propositions 0 and 12]).
(ii) We apply the same reasoning to $\Gamma _{l\phi }(X_i,\,E_{(P)})$![]() and note that $\Gamma (C_i,\,E\vert _{K_i})\to \Gamma (C_i,\,E_{(P)}\vert _{K_i})$
and note that $\Gamma (C_i,\,E\vert _{K_i})\to \Gamma (C_i,\,E_{(P)}\vert _{K_i})$![]() and $\Gamma (S_i,\,E\vert _{K_i})\to \Gamma (S_i,\,E_{(P)}\vert _{K_i})$
and $\Gamma (S_i,\,E\vert _{K_i})\to \Gamma (S_i,\,E_{(P)}\vert _{K_i})$![]() may be identified with, respectively, $\mathop {\rm map}\nolimits (C_i,\,Y)\to \mathop {\rm map}\nolimits (C_i,\,Y_{(P)})$
may be identified with, respectively, $\mathop {\rm map}\nolimits (C_i,\,Y)\to \mathop {\rm map}\nolimits (C_i,\,Y_{(P)})$![]() and $\mathop {\rm map}\nolimits (S_i,\,Y)\to \mathop {\rm map}\nolimits (S_i,\,Y_{(P)})$
and $\mathop {\rm map}\nolimits (S_i,\,Y)\to \mathop {\rm map}\nolimits (S_i,\,Y_{(P)})$![]() that localize by corollary 1.3. Thus if $\Gamma _\phi (X_{i-1},\,E)\to \Gamma _\phi (X_{i-1},\,E_{(P)})$
that localize by corollary 1.3. Thus if $\Gamma _\phi (X_{i-1},\,E)\to \Gamma _\phi (X_{i-1},\,E_{(P)})$![]() localizes (on path components), then so does $\Gamma _\phi (X_{i},\,E)\to \Gamma _\phi (X_{i},\,E_{(P)})$
localizes (on path components), then so does $\Gamma _\phi (X_{i},\,E)\to \Gamma _\phi (X_{i},\,E_{(P)})$![]() by [Reference May and Ponto19, Proposition 6.2.5].
by [Reference May and Ponto19, Proposition 6.2.5].
We turn to the question of homotopy invariance of $\Gamma _\phi (X,\,E)$![]() under changes of $p\colon E\to B$
under changes of $p\colon E\to B$![]() for general $X\in {\rm PHK}$
for general $X\in {\rm PHK}$![]() with closed subspace $A$
with closed subspace $A$![]() . To this end, assume that $p$
. To this end, assume that $p$![]() is homotopy equivalent to $p'\colon E'\to B'$
is homotopy equivalent to $p'\colon E'\to B'$![]() , i.e., there are homotopy equivalences $\eta \colon E\to E'$
, i.e., there are homotopy equivalences $\eta \colon E\to E'$![]() and $\beta \colon B\to B'$
and $\beta \colon B\to B'$![]() for which $p'\eta =\beta p$
for which $p'\eta =\beta p$![]() . Think of
. Think of
as the restriction to the fibre of the transformation $p_*\to p'_*$![]() :
:

Assume that $p_*$![]() and $p_*'$
and $p_*'$![]() are fibrations. If $\eta _*$
are fibrations. If $\eta _*$![]() and $\beta _*$
and $\beta _*$![]() are homotopy equivalences, so is (7.2) by coglueing [Reference Brown and Heath4, Corollary 1.5]. This will be true in the following cases.
are homotopy equivalences, so is (7.2) by coglueing [Reference Brown and Heath4, Corollary 1.5]. This will be true in the following cases.
(i) $\phi =\mathop {\rm const}\nolimits _{e_0}$
 (forcing $f\vert _A=\mathop {\rm const}\nolimits _{b_0}$
(forcing $f\vert _A=\mathop {\rm const}\nolimits _{b_0}$ where $b_0=p(e_0)$
where $b_0=p(e_0)$ ) and $p,\,p',\,\eta,\,\beta$
) and $p,\,p',\,\eta,\,\beta$ are pointed maps of well-pointed spaces,
are pointed maps of well-pointed spaces,(ii) $\phi =\mathop {\rm const}\nolimits _{e_0}$
 and $p$
and $p$ and $p'$
and $p'$ are regular fibrations (for example if $B$
are regular fibrations (for example if $B$ and $B'$
and $B'$ are metrizable) and $\eta$
are metrizable) and $\eta$ and $\beta$
and $\beta$ are homotopy equivalences in the pointed category,
are homotopy equivalences in the pointed category,(iii) $E,\,E',\,B,\,B'$
 are ANRs and $(X,\,A)$
are ANRs and $(X,\,A)$ is a proper pair,
is a proper pair,(iv) $A$
 is cofibred (in particular, $A$
is cofibred (in particular, $A$ may be empty).
may be empty).
For (1), the proof of [Reference Smrekar29, Lemma A.4] shows that $p_*$![]() and $p_*'$
and $p_*'$![]() are fibrations, while if $\eta '\colon E'\to E$
are fibrations, while if $\eta '\colon E'\to E$![]() is a pointed inverse for $\eta$
is a pointed inverse for $\eta$![]() and $\eta '\eta \simeq \mathop {\rm id}\nolimits _E$
and $\eta '\eta \simeq \mathop {\rm id}\nolimits _E$![]() and $\eta \eta '\simeq \mathop {\rm id}\nolimits _{E'}$
and $\eta \eta '\simeq \mathop {\rm id}\nolimits _{E'}$![]() are pointed homotopies, then the standard proof that $\eta _*\colon \mathop {\rm map}\nolimits (X,\,E)\to \mathop {\rm map}\nolimits (X,\,E')$
are pointed homotopies, then the standard proof that $\eta _*\colon \mathop {\rm map}\nolimits (X,\,E)\to \mathop {\rm map}\nolimits (X,\,E')$![]() is a homotopy equivalence (as for example [Reference Maunder18, Theorem 6.2.25]) will show its restriction $\mathop {\rm map}\nolimits (X,\,E)_{A\to e_0}\to \mathop {\rm map}\nolimits (X,\,E')_{A\to \eta (e_0)}$
is a homotopy equivalence (as for example [Reference Maunder18, Theorem 6.2.25]) will show its restriction $\mathop {\rm map}\nolimits (X,\,E)_{A\to e_0}\to \mathop {\rm map}\nolimits (X,\,E')_{A\to \eta (e_0)}$![]() is also a homotopy equivalence.
is also a homotopy equivalence.
For (2), the proof of [Reference Smrekar29, Lemma A.4] may be amended using regular lifting functions (as in Definition 2.1 in [Reference Dugundji9, Chapter XX]) to show that $p_*$![]() and $p_*'$
and $p_*'$![]() are fibrations, while the proof that $\eta _*$
are fibrations, while the proof that $\eta _*$![]() and $\beta _*$
and $\beta _*$![]() are homotopy equivalences is as above.
are homotopy equivalences is as above.
For (3), we note that $p_*$![]() and $p_*'$
and $p_*'$![]() are fibrations because $p$
are fibrations because $p$![]() and $p'$
and $p'$![]() are regular on the ground of metrizability of $B$
are regular on the ground of metrizability of $B$![]() . We consider $\eta _*\colon \mathop {\rm map}\nolimits _\phi (X,\,E)\to \mathop {\rm map}\nolimits _{\eta \phi }(X,\,E')$
. We consider $\eta _*\colon \mathop {\rm map}\nolimits _\phi (X,\,E)\to \mathop {\rm map}\nolimits _{\eta \phi }(X,\,E')$![]() as the map between the fibres induced by the transformation of restrictions:
as the map between the fibres induced by the transformation of restrictions:

The horizontal arrows in (7.4) are homotopy equivalences ([Reference Maunder18, ibid.]) and since $E$![]() and $E'$
and $E'$![]() are ANRs, the restrictions (i.e., the vertical arrows) are fibrations by proposition 6.1. Thus, the coglueing theorem will guarantee that the maps between the fibres will be homotopy equivalences as well. The same argument applies to $\beta _*$
are ANRs, the restrictions (i.e., the vertical arrows) are fibrations by proposition 6.1. Thus, the coglueing theorem will guarantee that the maps between the fibres will be homotopy equivalences as well. The same argument applies to $\beta _*$![]() , using the fact that $B$
, using the fact that $B$![]() and $B'$
and $B'$![]() are ANRs.
are ANRs.
For (4), the argument that $p_*$![]() and $p_*'$
and $p_*'$![]() are Hurewicz fibrations is standard. In ${\mathcal {K}}$
are Hurewicz fibrations is standard. In ${\mathcal {K}}$![]() , we simply use the exponential law in ${\mathcal {K}}$
, we simply use the exponential law in ${\mathcal {K}}$![]() , the fact that inclusion $X\times \left \{0\right \}\cup A\times [0,\,1]\hookrightarrow X\times [0,\,1]$
, the fact that inclusion $X\times \left \{0\right \}\cup A\times [0,\,1]\hookrightarrow X\times [0,\,1]$![]() is a closed cofibration and the lifting properties of $p_*$
is a closed cofibration and the lifting properties of $p_*$![]() and $p_*'$
and $p_*'$![]() . For ${\mathcal {T}}\!\!{op}$
. For ${\mathcal {T}}\!\!{op}$![]() , we extend the proof of [Reference Smrekar29, Lemma A.4]. When $A$
, we extend the proof of [Reference Smrekar29, Lemma A.4]. When $A$![]() is cofibred in $X$
is cofibred in $X$![]() , the vertical arrows in (7.4) are fibrations for all $E$
, the vertical arrows in (7.4) are fibrations for all $E$![]() and $E'$
and $E'$![]() .
.
Proof of theorem 1.10 The theorem deals with absolute sections ($A=\emptyset$![]() ), and we may take a representative for $p$
), and we may take a representative for $p$![]() as specified prior to the statement of theorem 7.2. Thus, statement (a) follows directly from theorem 7.2 as then $X=X_i$
as specified prior to the statement of theorem 7.2. Thus, statement (a) follows directly from theorem 7.2 as then $X=X_i$![]() for some $i$
for some $i$![]() .
.
For (b), note that $\Gamma (X,\,E)\to \Gamma (X,\,E_{(P)})$![]() is the limit of maps $\Gamma (X_i,\,E)\to \Gamma (X_i,\,E_{(P)})$
is the limit of maps $\Gamma (X_i,\,E)\to \Gamma (X_i,\,E_{(P)})$![]() (which localize by theorem 7.2). Apply [Reference Smrekar31, Theorems 6.1 and 6.2].
(which localize by theorem 7.2). Apply [Reference Smrekar31, Theorems 6.1 and 6.2].
We remark that theorem 7.2 also contains [Reference Møller24, Theorem 5.3] as a special case.
Acknowledgements
The author was supported in part by the Slovenian Research Agency grants N1-0237 and P1-0291.