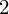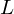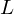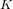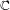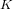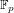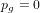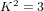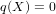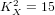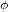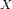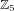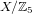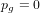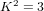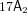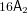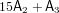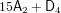36 results in 14Qxx
On the effective, nef, and semi-ample monoids of blowups of Hirzebruch surfaces at collinear points
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1179-1193
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
IWASAWA THEORY FOR p-TORSION CLASS GROUP SCHEMES IN CHARACTERISTIC p
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 250 / June 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 298-351
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Functional norms, condition numbers and numerical algorithms in algebraic geometry
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 22 November 2022, e103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arquile Varieties – Varieties Consisting of Power Series in a Single Variable
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 01 December 2021, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Linear PDE with constant coefficients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. S2-S27
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SMOOTH FANO 4-FOLDS IN GORENSTEIN FORMATS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 31 May 2021, pp. 424-433
- Print publication:
- December 2021
-
- Article
- Export citation
CATEGORICAL COMPLEXITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e34
-
- Article
-
- You have access
- Open access
- Export citation
SOLVING DIFFERENCE EQUATIONS IN SEQUENCES: UNIVERSALITY AND UNDECIDABILITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e33
-
- Article
-
- You have access
- Open access
- Export citation
Variation of Mixed Hodge Structures Associated to an Equisingular One-dimensional Family of Calabi-Yau Threefolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 16 January 2020, pp. 441-464
- Print publication:
- April 2021
-
- Article
- Export citation
Primes Dividing Invariants of CM Picard Curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 May 2019, pp. 480-504
- Print publication:
- April 2020
-
- Article
- Export citation
VARIETIES OF SIGNATURE TENSORS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 04 April 2019, e10
-
- Article
-
- You have access
- Open access
- Export citation
On an Enriques Surface Associated With a Quartic Hessian Surface
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 213-246
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Del Pezzo Surfaces in Weighted Projective Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 04 April 2018, pp. 545-572
-
- Article
-
- You have access
- Export citation
THE EXPECTED JAGGEDNESS OF ORDER IDEALS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 15 March 2017, e9
-
- Article
-
- You have access
- Open access
- Export citation
Picard curves over
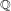 $\mathbb{Q}$ with good reduction away from 3
$\mathbb{Q}$ with good reduction away from 3
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 March 2017, pp. 382-408
-
- Article
-
- You have access
- Export citation
Divisorial Models of Normal Varieties
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 1053-1064
-
- Article
- Export citation
A database of genus-2 curves over the rational numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 235-254
-
- Article
-
- You have access
- Export citation
Constructing genus-3 hyperelliptic Jacobians with CM
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 283-300
-
- Article
-
- You have access
- Export citation
Computing cup products in integral cohomology of Hilbert schemes of points on K3 surfaces
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 78-97
-
- Article
-
- You have access
- Export citation
Cuspidal quintics and surfaces with
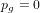 $p_{g}=0$,
$p_{g}=0$, 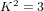 $K^{2}=3$ and 5-torsion
$K^{2}=3$ and 5-torsion
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 42-53
-
- Article
-
- You have access
- Export citation

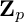
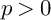
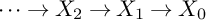
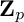
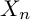
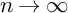
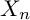
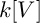
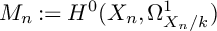
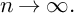
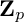
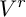
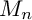
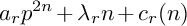
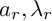
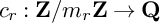
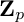
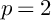
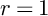
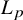
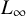
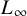
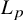
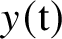
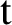
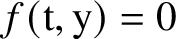
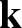
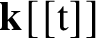

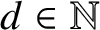
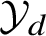
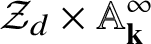
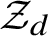
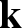
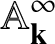
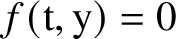

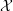
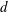
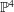
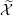
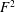
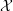
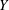
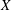
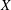
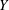
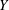
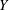
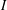
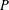
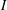
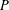
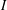
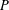

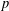
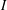
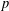
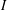
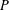
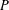
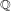
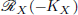 is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.
is finitely generated. We introduce a notion of nefness for non-ℚ-Gorenstein varieties and study some of its properties. We then focus on these properties for non-ℚ-Gorenstein toric varieties.