Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-05-05T21:04:29.974Z Has data issue: false hasContentIssue false
  • English
  • Français

Variation of Mixed Hodge Structures Associated to an Equisingular One-dimensional Family of Calabi-Yau Threefolds

Part of: Computational aspects in algebraic geometry Families, fibrations Cycles and subschemes Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  16 January 2020

Isidro Nieto-Baños  and
Pedro Luis del Angel-Rodriguez
Isidro Nieto-Baños
Affiliation:
C.P. 36023, Guanajuato, Gto., México Email: nietoisidrorafael@yahoo.com
Pedro Luis del Angel-Rodriguez
Affiliation:
CIMAT, A.C., Jalisco, S/N, Guanajuato, Gto., México Email: luis@cimat.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the variations of mixed Hodge structures (VMHS) associated with a pencil 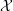${\mathcal{X}}$ of equisingular hypersurfaces of degree 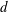$d$ in 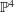$\mathbb{P}^{4}$ with only ordinary double points as singularities, as well as the variations of Hodge structures (VHS) associated with the desingularization of this family 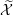$\widetilde{{\mathcal{X}}}$. The notion of a set of singular points being in homologically good position is introduced, and, by requiring that the subset of nodes in (algebraic) general position is also in homologically good position, we can extend Griffiths’ description of the 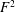$F^{2}$-term of the Hodge filtration of the desingularization to this case, where we can also determine the possible limiting mixed Hodge structures (LMHS). The particular pencil 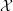${\mathcal{X}}$ of quintic hypersurfaces with 100 singular double points with 86 of them in (algebraic) general position that served as the starting point for this paper is treated with particular attention.

Keywords

variations of hodge structurescalabi-yau manifoldscomputational aspects in higher dimensional varietiestranscendental methodshodge theory

MSC classification

Primary: 14D07: Variation of Hodge structures
Secondary: 14J32: Calabi-Yau manifolds 14C30: Transcendental methods, Hodge theory , Hodge conjecture 14Q15: Higher-dimensional varieties
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 2 , April 2021 , pp. 441 - 464
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author acknowledges partial support from CIMAT as well as from the CMO congress “Primer Congreso Nacional de Geometría Algebraica” in the year 2016 in Oaxaca where part of these results were presented. Both authors had fruitful discussions at various stages of this work with D. Van Straten, Ch. Peters, J. Carlson, X. Gomez-Mont, and H. Kanarek and thank them for it. We acknowledge partial support from CONACyT Grant 0181730.

References

Barth, W. and Nieto, I., Abelian surfaces of type (1, 3) and quartic surfaces with 16 skew lines. J. Algebraic Geom. 3(1994), 173–222.Google Scholar
Bertin, J., Demailly, J. P., Illusie, L., and Peters, C., Introduction to Hodge theory. SMF-AMS texts and Monographs, 8, Panoramas et Syntheses, Num. 3, American Mathematical Society, Providence, RI, 2002.Google Scholar
Bott, R., Homogeneous vector bundles. Ann. of Math. (2) 2(1957), 203–248. https://doi.org/10.2307/1969996CrossRefGoogle Scholar
Candelas, P., De La Ossa, X. C., Green, P. S., and Parkes, L., A pair of Calabi-Yau manifolds as an exactly soluble superconformal theory. Nuclear Phys. B 359(1991), 21–74. https://doi.org/10.1016/0550-3213(91)90292-6CrossRefGoogle Scholar
Clemens, C. H., Double solids. Adv. Math. 47(1983), 107–230. https://doi.org/10.1016/0001-8708(83)90025-7CrossRefGoogle Scholar
Danilov, I. V. and Khovanskii, G. A., Newton Polyhedra and an algorithm for computing Hodge-Deligne numbers. Math. of the USSR Izvestiya. 29(1987), 279–298. https://doi.org/10.1070/IM1987V029n02ABEH000970CrossRefGoogle Scholar
Decker, W., Greuel, G.-M., Pfister, G., and Schönemann, H., Singular 2-0-6—A computer algebra system for polynomial computations. http://www.singular.uni-kl.de (2017)Google Scholar
Deligne, P., Equations différentielles à points singulieres régulieres. Lecture Notes in Math., 163, Springer Verlag, 1970. https://doi.org/10.1007/Bfb0061194CrossRefGoogle Scholar
Deligne, P., Thèorie de Hodge II. Institut des Hautes Études Scientifiques Publications Mathématiques 40(1971), 5–57.10.1007/BF02684692CrossRefGoogle Scholar
Eisenbud, D., Green, M., and Harris, J., Cayley-Bacharach theorems and conjectures. Bull. Amer. Math. Soc. (N.S.) 33(1996), 295–324. https://doi.org/10.1090/S0273-0979-96-00666-0CrossRefGoogle Scholar
Griffiths, P., On the periods of certain rational integrals I. Ann. of Math. (2) 90(1969), 460–495.10.2307/1970746CrossRefGoogle Scholar
Griffiths, P., On the periods of certain rational integrals II. Ann. of Math. (2) 90(1969), 496–541.10.2307/1970747CrossRefGoogle Scholar
P. Griffiths (ed.), Topics in trascendental algebraic geometry. Ann. of Math. Stud., 106, Princeton University Press, 1984.Google Scholar
Griffiths, P., Periods of integrals on algebraic manifolds: Summary of main results and discussion of open problems. Bull. Amer. Math. Soc. (N.S.) 76(1970), 228–296. https://projecteuclid.org/euclid.bams/1183531477 10.1090/S0002-9904-1970-12444-2CrossRefGoogle Scholar
Guillen, F., Navarro Aznar, V., Pascual-Gainza, P., and Puerta, F., Hyperresolutions cubiques et descente cohomologique. Lecture Notes in Math., 1335, Springer Verlag, 1988. https://doi.org/10.1007/BFb0085054CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer Verlag, 1977. https://doi.org/10.1007/978-1-4757-3849-0CrossRefGoogle Scholar
Hodge, W. V. D., The theory and applications of harmonic integrals. Cambridge University Press, Cambridge, 1941.Google Scholar
Kulikov, V. S., Mixed Hodge structures and singularities. Cambridge Tracts in Mathematics, 132, Cambridge University Press, Cambridge, 1998. https://doi.org/10.1017/CB09780511758928CrossRefGoogle Scholar
Nieto, I., Invariante Quartiken unter der Heisenberg Gruppe T. Thesis, Naturwissenschaftliche Fakultaet der Friedrich-Alexander-Universitaet Erlangen-Nuernberg, Erlangen 1989.Google Scholar
Peters, C. and Steenbrik, J., Mixed Hodge structures. Ergeb. Math. Grenzgeb. (3), 52, Springer Verlag, Berlin-Heidelberg, 2008. https://doi.org/10.1007/978-3-540-77017-6Google Scholar
Steenbrik, J., Adjunction conditions for 1-forms on surfaces in projective three-space. In: Singularities and computer algebra, London Math. Soc. Lecture Note Ser., 324, 2006, pp. 301–314.http://hdl.handlenet.net/2066/60197 10.1017/CBO9780511526374.015CrossRefGoogle Scholar
Steenbrink, J. and Zucker, S., Variation of mixed Hodge structure I. Invent. Math. 80(1985), 489–542. https://doi.org/10.1007/BF01388729CrossRefGoogle Scholar
Van Straten, D., A quintic hypersurface in ℙ4 with 130 nodes. Topology 32(1993), 857–864. https://doi.org/10.1016/0040-9383(93)90054-YCrossRefGoogle Scholar
Werner, J., Kleine Aufloesungen spezieller drei-dimensionaler Varietaeten. Bonner Mathematische Schriften, Nr. 186, Bonn, 1987.Google Scholar