9 results
2 - Mathematical Terms and Notations
-
- Book:
- Mathematics for Economics and Finance
- Published online:
- 24 May 2024
- Print publication:
- 30 May 2024, pp 11-22
-
- Chapter
- Export citation
Chapter 16 - Puccini’s Theatrical Vision
- from Part IV - Bringing Puccini to the Stage
-
-
- Book:
- Puccini in Context
- Published online:
- 31 August 2023
- Print publication:
- 14 September 2023, pp 130-136
-
- Chapter
- Export citation
Integrating Logic Rules with Everything Else, Seamlessly
-
- Journal:
- Theory and Practice of Logic Programming / Volume 23 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 06 July 2023, pp. 678-695
-
- Article
- Export citation

Set Theory
-
- Published online:
- 21 January 2022
- Print publication:
- 10 March 2022
-
- Element
- Export citation
Appendix - A Rapid Review of Sets and Probability
-
- Book:
- Invitation to Linear Programming and Game Theory
- Published online:
- 11 March 2021
- Print publication:
- 11 March 2021, pp 480-517
-
- Chapter
- Export citation
2 - Elements of a Computable General Equilibrium Model
-
- Book:
- Introduction to Computable General Equilibrium Models
- Published online:
- 11 December 2020
- Print publication:
- 07 January 2021, pp 25-65
-
- Chapter
- Export citation
1 - Formal Preliminaries
- from Part I - Formal Background
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 3-22
-
- Chapter
- Export citation
CLAIRE: combining sets, search and rules to better express algorithms
-
- Journal:
- Theory and Practice of Logic Programming / Volume 2 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 13 November 2002, pp. 769-805
-
- Article
- Export citation
A note on the union-closed sets conjecture
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 2 / October 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 230-236
- Print publication:
- October 1994
-
- Article
-
- You have access
- Export citation



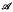 there exists some element which is contained in at least half the sets in
there exists some element which is contained in at least half the sets in 