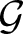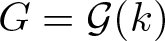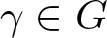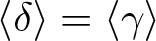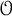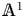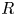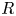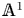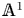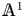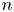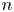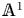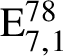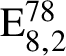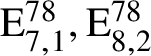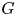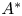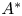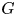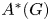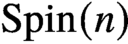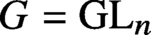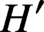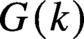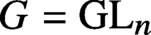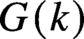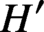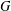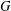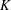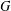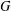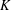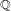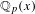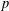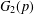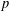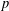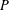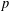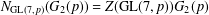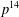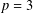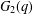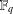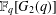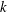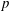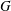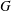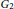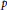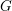50 results
Powers of commutators in linear algebraic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MODEL-THEORETIC CONNECTED GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 50-79
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Grassmanniennes affines tordues sur les entiers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 February 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A parametrization of sheets of conjugacy classes in bad characteristic
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 26 January 2023, pp. 976-983
- Print publication:
- September 2023
-
- Article
- Export citation
Localization and nilpotent spaces in
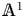 ${\mathbb {A}}^1$-homotopy theory
${\mathbb {A}}^1$-homotopy theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 3 / March 2022
- Published online by Cambridge University Press:
- 27 May 2022, pp. 654-720
- Print publication:
- March 2022
-
- Article
- Export citation
Overgroups of regular unipotent elements in reductive groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 24 February 2022, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOHR COMPACTIFICATIONS OF GROUPS AND RINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 04 February 2022, pp. 1103-1137
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On multiplicative energy of subsets of varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 January 2022, pp. 322-340
- Print publication:
- February 2023
-
- Article
- Export citation
On the Tits–Weiss conjecture and the Kneser–Tits conjecture for
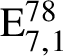 $\mathrm {E}^{78}_{7,1}$
and
$\mathrm {E}^{78}_{7,1}$
and 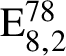 $\mathrm {E}^{78}_{8,2}$
(With an Appendix by R. M. Weiss)
$\mathrm {E}^{78}_{8,2}$
(With an Appendix by R. M. Weiss)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 23 November 2021, e75
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hopf-theoretic approach to motives of twisted flag varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 963-996
- Print publication:
- May 2021
-
- Article
- Export citation
Maximal indexes of flag varieties for spin groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 April 2021, e34
-
- Article
-
- You have access
- Open access
- Export citation
GROUPS OF WORLDVIEW TRANSFORMATIONS IMPLIED BY EINSTEIN’S SPECIAL PRINCIPLE OF RELATIVITY OVER ARBITRARY ORDERED FIELDS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 334-361
- Print publication:
- June 2022
-
- Article
- Export citation
Semisimplification for subgroups of reductive algebraic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 November 2020, e43
-
- Article
-
- You have access
- Open access
- Export citation
RELATIVE COMPLETE REDUCIBILITY AND NORMALIZED SUBGROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e30
-
- Article
-
- You have access
- Open access
- Export citation
LARGE FIELDS IN DIFFERENTIAL GALOIS THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 27 January 2020, pp. 1931-1946
- Print publication:
- November 2021
-
- Article
- Export citation
ON
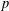 $p$-GROUPS WITH AUTOMORPHISM GROUPS RELATED TO THE CHEVALLEY GROUP
$p$-GROUPS WITH AUTOMORPHISM GROUPS RELATED TO THE CHEVALLEY GROUP 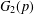 $G_{2}(p)$
$G_{2}(p)$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 321-331
- Print publication:
- June 2020
-
- Article
- Export citation
Retract Rationality and Algebraic Tori
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 173-186
- Print publication:
- March 2020
-
- Article
- Export citation
Order 3 Elements in G2 and Idempotents in Symmetric Composition Algebras
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 5 / 01 October 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1038-1075
- Print publication:
- 01 October 2018
-
- Article
-
- You have access
- Export citation
A Factorization Result for Classical and Similitude Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 1 / 01 March 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 174-190
- Print publication:
- 01 March 2018
-
- Article
-
- You have access
- Export citation
ON EXISTENCE OF CANONICAL
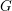 $G$-BASES
$G$-BASES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 15 September 2017, pp. 1-31
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation