12 results
VISCOSITY SOLUTIONS TO THE INFINITY LAPLACIAN EQUATION WITH SINGULAR NONLINEAR TERMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 March 2024, pp. 1-30
-
- Article
- Export citation
Solvability of Hessian quotient equations in exterior domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 14 December 2023, pp. 1-31
-
- Article
- Export citation
On large solutions for fractional Hamilton–Jacobi equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 July 2023, pp. 1-23
-
- Article
- Export citation
Propagation of minima for nonlocal operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 23 May 2023, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A continuum limit for the PageRank algorithm
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 27 April 2021, pp. 472-504
-
- Article
-
- You have access
- Open access
- Export citation
LYAPUNOV-TYPE INEQUALITY FOR EXTREMAL PUCCI’S EQUATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 29 January 2020, pp. 416-430
- Print publication:
- December 2020
-
- Article
- Export citation
Cauchy problem and periodic homogenization for nonlocal Hamilton–Jacobi equations with coercive gradient terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 17 September 2019, pp. 3028-3059
- Print publication:
- December 2020
-
- Article
- Export citation
A pointwise characterisation of the PDE system of vectorial calculus of variations in L∞
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1653-1669
- Print publication:
- August 2020
-
- Article
- Export citation
An application of the theorem on Sums to viscosity solutions of degenerate fully nonlinear equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 975-992
- Print publication:
- April 2020
-
- Article
- Export citation
Asymptotic behaviour as p → ∞ of least energy solutions of a (p, q(p))-Laplacian problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1493-1522
- Print publication:
- December 2019
-
- Article
- Export citation
Continuous solutions and approximating scheme for fractional Dirichlet problems on Lipschitz domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 533-560
- Print publication:
- April 2019
-
- Article
- Export citation
A convergence result for the ergodic problem for Hamilton–Jacobi equations with Neumann-type boundary conditions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 225-242
- Print publication:
- April 2016
-
- Article
- Export citation



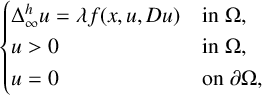

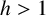
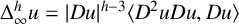
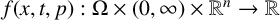
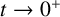
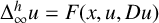
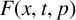
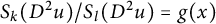
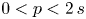
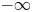
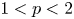
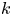

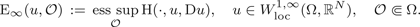
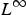
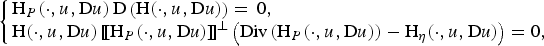
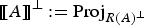
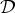
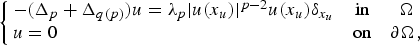
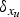
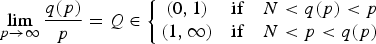
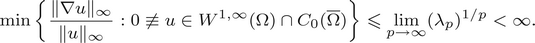
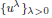 to a solution of the ergodic problem as λ → 0, and give a representation formula for the limit function via the Mather measures and Peierls function. As an interesting by-product, we introduce Mather measures associated with Hamilton–Jacobi equations with the Neumann-type boundary conditions. These results are variants of the main results in a recent paper by Davini
to a solution of the ergodic problem as λ → 0, and give a representation formula for the limit function via the Mather measures and Peierls function. As an interesting by-product, we introduce Mather measures associated with Hamilton–Jacobi equations with the Neumann-type boundary conditions. These results are variants of the main results in a recent paper by Davini 