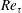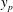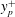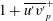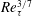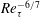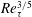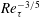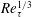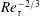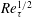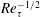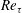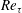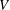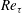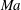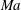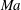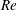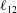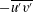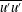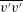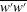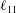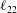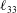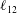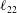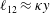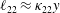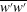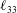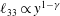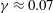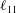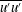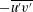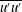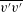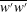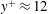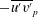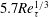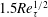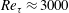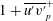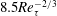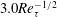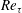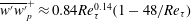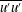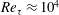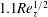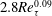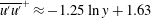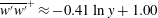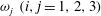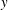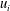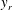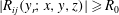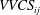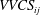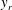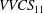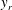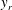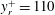We present new scaling expressions, including high-Reynolds-number (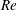 $Re$) predictions, for all Reynolds stress components in the entire flow domain of turbulent channel and pipe flows. In Part 1 (She et al., J. Fluid Mech., vol. 827, 2017, pp. 322–356), based on the dilation symmetry of the mean Navier–Stokes equation a four-layer formula of the Reynolds shear stress length
$Re$) predictions, for all Reynolds stress components in the entire flow domain of turbulent channel and pipe flows. In Part 1 (She et al., J. Fluid Mech., vol. 827, 2017, pp. 322–356), based on the dilation symmetry of the mean Navier–Stokes equation a four-layer formula of the Reynolds shear stress length 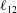 $\ell _{12}$ – and hence also the entire mean velocity profile (MVP) – was obtained. Here, random dilations on the second-order balance equations for all the Reynolds stresses (shear stress
$\ell _{12}$ – and hence also the entire mean velocity profile (MVP) – was obtained. Here, random dilations on the second-order balance equations for all the Reynolds stresses (shear stress 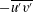 $-\overline{u^{\prime }v^{\prime }}$, and normal stresses
$-\overline{u^{\prime }v^{\prime }}$, and normal stresses 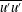 $\overline{u^{\prime }u^{\prime }}$,
$\overline{u^{\prime }u^{\prime }}$, 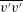 $\overline{v^{\prime }v^{\prime }}$,
$\overline{v^{\prime }v^{\prime }}$, 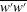 $\overline{w^{\prime }w^{\prime }}$) are analysed layer by layer, and similar four-layer formulae of the corresponding stress length functions
$\overline{w^{\prime }w^{\prime }}$) are analysed layer by layer, and similar four-layer formulae of the corresponding stress length functions 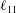 $\ell _{11}$,
$\ell _{11}$, 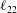 $\ell _{22}$,
$\ell _{22}$, 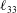 $\ell _{33}$ (hence the three turbulence intensities) are obtained for turbulent channel and pipe flows. In particular, direct numerical simulation (DNS) data are shown to agree well with the four-layer formulae for
$\ell _{33}$ (hence the three turbulence intensities) are obtained for turbulent channel and pipe flows. In particular, direct numerical simulation (DNS) data are shown to agree well with the four-layer formulae for 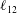 $\ell _{12}$ and
$\ell _{12}$ and 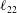 $\ell _{22}$ – which have the celebrated linear scalings in the logarithmic layer, i.e.
$\ell _{22}$ – which have the celebrated linear scalings in the logarithmic layer, i.e. 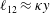 $\ell _{12}\approx \unicode[STIX]{x1D705}y$ and
$\ell _{12}\approx \unicode[STIX]{x1D705}y$ and 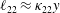 $\ell _{22}\approx \unicode[STIX]{x1D705}_{22}y$. However, data show an invariant peak location for
$\ell _{22}\approx \unicode[STIX]{x1D705}_{22}y$. However, data show an invariant peak location for 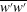 $\overline{w^{\prime }w^{\prime }}$, which theoretically leads to an anomalous scaling in
$\overline{w^{\prime }w^{\prime }}$, which theoretically leads to an anomalous scaling in 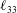 $\ell _{33}$ in the log layer only, namely
$\ell _{33}$ in the log layer only, namely 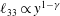 $\ell _{33}\propto y^{1-\unicode[STIX]{x1D6FE}}$ with
$\ell _{33}\propto y^{1-\unicode[STIX]{x1D6FE}}$ with 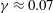 $\unicode[STIX]{x1D6FE}\approx 0.07$. Furthermore, another mesolayer modification of
$\unicode[STIX]{x1D6FE}\approx 0.07$. Furthermore, another mesolayer modification of 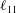 $\ell _{11}$ yields the experimentally observed location and magnitude of the outer peak of
$\ell _{11}$ yields the experimentally observed location and magnitude of the outer peak of 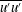 $\overline{u^{\prime }u^{\prime }}$. The resulting
$\overline{u^{\prime }u^{\prime }}$. The resulting 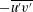 $-\overline{u^{\prime }v^{\prime }}$,
$-\overline{u^{\prime }v^{\prime }}$, 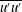 $\overline{u^{\prime }u^{\prime }}$,
$\overline{u^{\prime }u^{\prime }}$, 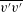 $\overline{v^{\prime }v^{\prime }}$ and
$\overline{v^{\prime }v^{\prime }}$ and 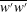 $\overline{w^{\prime }w^{\prime }}$ are all in good agreement with DNS and experimental data in the entire flow domain. Our additional results include: (1) the maximum turbulent production is located at
$\overline{w^{\prime }w^{\prime }}$ are all in good agreement with DNS and experimental data in the entire flow domain. Our additional results include: (1) the maximum turbulent production is located at 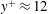 $y^{+}\approx 12$; (2) the location of peak value
$y^{+}\approx 12$; (2) the location of peak value 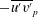 $-\overline{u^{\prime }v^{\prime }}_{p}$ has a scaling transition from
$-\overline{u^{\prime }v^{\prime }}_{p}$ has a scaling transition from 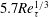 $5.7Re_{\unicode[STIX]{x1D70F}}^{1/3}$ to
$5.7Re_{\unicode[STIX]{x1D70F}}^{1/3}$ to 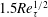 $1.5Re_{\unicode[STIX]{x1D70F}}^{1/2}$ at
$1.5Re_{\unicode[STIX]{x1D70F}}^{1/2}$ at 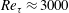 $Re_{\unicode[STIX]{x1D70F}}\approx 3000$, with a
$Re_{\unicode[STIX]{x1D70F}}\approx 3000$, with a 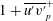 $1+\overline{u^{\prime }v^{\prime }}_{p}^{+}$ scaling transition from
$1+\overline{u^{\prime }v^{\prime }}_{p}^{+}$ scaling transition from 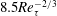 $8.5Re_{\unicode[STIX]{x1D70F}}^{-2/3}$ to
$8.5Re_{\unicode[STIX]{x1D70F}}^{-2/3}$ to 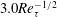 $3.0Re_{\unicode[STIX]{x1D70F}}^{-1/2}$ (
$3.0Re_{\unicode[STIX]{x1D70F}}^{-1/2}$ (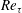 $Re_{\unicode[STIX]{x1D70F}}$ the friction Reynolds number); (3) the peak value
$Re_{\unicode[STIX]{x1D70F}}$ the friction Reynolds number); (3) the peak value 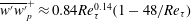 $\overline{w^{\prime }w^{\prime }}_{p}^{+}\approx 0.84Re_{\unicode[STIX]{x1D70F}}^{0.14}(1-48/Re_{\unicode[STIX]{x1D70F}})$; (4) the outer peak of
$\overline{w^{\prime }w^{\prime }}_{p}^{+}\approx 0.84Re_{\unicode[STIX]{x1D70F}}^{0.14}(1-48/Re_{\unicode[STIX]{x1D70F}})$; (4) the outer peak of 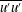 $\overline{u^{\prime }u^{\prime }}$ emerges above
$\overline{u^{\prime }u^{\prime }}$ emerges above 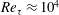 $Re_{\unicode[STIX]{x1D70F}}\approx 10^{4}$ with its location scaling as
$Re_{\unicode[STIX]{x1D70F}}\approx 10^{4}$ with its location scaling as 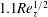 $1.1Re_{\unicode[STIX]{x1D70F}}^{1/2}$ and its magnitude scaling as
$1.1Re_{\unicode[STIX]{x1D70F}}^{1/2}$ and its magnitude scaling as 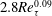 $2.8Re_{\unicode[STIX]{x1D70F}}^{0.09}$; (5) an alternative derivation of the log law of Townsend (1976, The Structure of Turbulent Shear Flow, Cambridge University Press), namely,
$2.8Re_{\unicode[STIX]{x1D70F}}^{0.09}$; (5) an alternative derivation of the log law of Townsend (1976, The Structure of Turbulent Shear Flow, Cambridge University Press), namely, 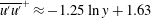 $\overline{u^{\prime }u^{\prime }}^{+}\approx -1.25\ln y+1.63$ and
$\overline{u^{\prime }u^{\prime }}^{+}\approx -1.25\ln y+1.63$ and 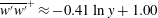 $\overline{w^{\prime }w^{\prime }}^{+}\approx -0.41\ln y+1.00$ in the bulk.
$\overline{w^{\prime }w^{\prime }}^{+}\approx -0.41\ln y+1.00$ in the bulk.