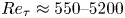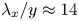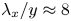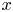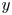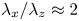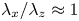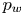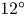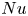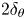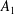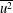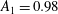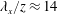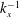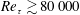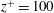8 results
Reynolds-number scaling of wall-pressure–velocity correlations in wall-bounded turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 981 / 25 February 2024
- Published online by Cambridge University Press:
- 21 February 2024, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unsteady flow behaviour of multi-rotors in ground proximity
-
- Journal:
- Flow: Applications of Fluid Mechanics / Volume 3 / 2023
- Published online by Cambridge University Press:
- 04 October 2023, E30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scale-dependent inclination angle of turbulent structures in stratified atmospheric surface layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 942 / 10 July 2022
- Published online by Cambridge University Press:
- 23 May 2022, A38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A proper framework for studying noise from jets with non-compact sources
-
- Journal:
- Journal of Fluid Mechanics / Volume 929 / 25 December 2021
- Published online by Cambridge University Press:
- 27 October 2021, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The large-scale footprint in small-scale Rayleigh–Bénard turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 911 / 25 March 2021
- Published online by Cambridge University Press:
- 03 February 2021, A62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 2. Integrated energy and
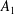 $A_{1}$
$A_{1}$
-
- Journal:
- Journal of Fluid Mechanics / Volume 882 / 10 January 2020
- Published online by Cambridge University Press:
- 12 November 2019, A26
-
- Article
- Export citation
Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 1. Energy spectra
-
- Journal:
- Journal of Fluid Mechanics / Volume 882 / 10 January 2020
- Published online by Cambridge University Press:
- 12 November 2019, A25
-
- Article
- Export citation
Self-similarity of wall-attached turbulence in boundary layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 823 / 25 July 2017
- Published online by Cambridge University Press:
- 15 June 2017, R2
-
- Article
- Export citation