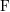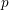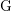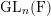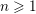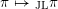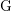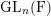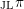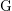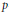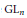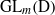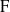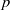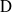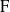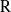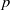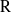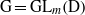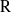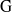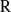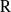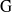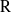4 results
Towards an explicit local Jacquet–Langlands correspondence beyond the cuspidal case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 10 / October 2019
- Published online by Cambridge University Press:
- 27 August 2019, pp. 1853-1887
- Print publication:
- October 2019
-
- Article
- Export citation
Types et contragrédientes
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 6 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1287-1304
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
Représentations banales de
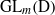 ${\rm GL}_{m}({\rm D})$
${\rm GL}_{m}({\rm D})$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 02 January 2013, pp. 679-704
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Représentations lisses de GL(m, D) II : β-extensions
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 6 / November 2005
- Published online by Cambridge University Press:
- 04 December 2007, pp. 1531-1550
- Print publication:
- November 2005
-
- Article
-
- You have access
- Export citation