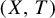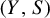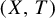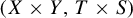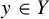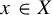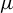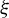37 results
Lifting generic points
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 05 February 2024, pp. 1-16
-
- Article
- Export citation
Zero-dimensional isomorphic dynamical models
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 11 December 2018, pp. 2116-2130
- Print publication:
- August 2020
-
- Article
- Export citation
Modeling potential as fiber entropy and pressure as entropy
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 35 / Issue 4 / June 2015
- Published online by Cambridge University Press:
- 26 February 2014, pp. 1165-1186
- Print publication:
- June 2015
-
- Article
- Export citation
Measure-theoretic chaos
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 34 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 31 August 2012, pp. 110-131
- Print publication:
- February 2014
-
- Article
- Export citation
Contents
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp vii-x
-
- Chapter
- Export citation
1 - Shannon information and entropy
- from PART I - Entropy in ergodic theory
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 23-52
-
- Chapter
- Export citation
References
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 379-385
-
- Chapter
- Export citation
2 - Dynamical entropy of a process
- from PART I - Entropy in ergodic theory
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 53-79
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp i-vi
-
- Chapter
- Export citation
5 - The Ergodic Law of Series*
- from PART I - Entropy in ergodic theory
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 132-156
-
- Chapter
- Export citation
8 - The entropy structure
- from PART II - Entropy in topological dynamics
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 227-271
-
- Chapter
- Export citation
13 - Open problems in operator entropy
- from PART III - Entropy theory for operators
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 344-346
-
- Chapter
- Export citation
10 - A touch of smooth dynamics*
- from PART II - Entropy in topological dynamics
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 303-310
-
- Chapter
- Export citation
List of symbols
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 374-378
-
- Chapter
- Export citation
7 - Dynamics in dimension zero
- from PART II - Entropy in topological dynamics
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 201-226
-
- Chapter
- Export citation
9 - Symbolic extensions
- from PART II - Entropy in topological dynamics
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 272-302
-
- Chapter
- Export citation
4 - Kolmogorov–Sinai Entropy
- from PART I - Entropy in ergodic theory
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 102-131
-
- Chapter
- Export citation
PART II - Entropy in topological dynamics
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp 157-158
-
- Chapter
- Export citation

Entropy in Dynamical Systems
-
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011
Preface
-
- Book:
- Entropy in Dynamical Systems
- Published online:
- 07 October 2011
- Print publication:
- 12 May 2011, pp xi-xii
-
- Chapter
- Export citation