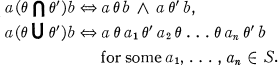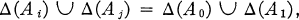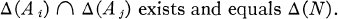17 results
Spring Meeting of the Association for Symbolic Logic, Toronto, 1993
-
- Journal:
- The Journal of Symbolic Logic / Volume 59 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 12 March 2014, pp. 346-349
- Print publication:
- March 1994
-
- Article
- Export citation
The extensions of the modal logic K5
-
- Journal:
- The Journal of Symbolic Logic / Volume 50 / Issue 1 / March 1985
- Published online by Cambridge University Press:
- 12 March 2014, pp. 102-109
- Print publication:
- March 1985
-
- Article
- Export citation
Peter Aczel. Quantifiers, games and inductive definitions. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 1–14. - Kit Fine. Some connections between elementary and modal logic. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 15–31. - Bengt Hansson and Peter Gärdenfors. Filtations and the finite frame property in Boolean semantics. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 32–39. - Jaakko Hintikka and Veikko Rantala. Systematizing definability theory. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 40–62. - Herman Ruge Jervell. Conservative endextensions and the quantifier ‘there exist uncountably many.’Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 63–80. - Per Martin-Löf. About models for intuitionistic type theories and the notion of definitional equality. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 81–109. - Henrik Sahlqvist. Completeness and correspondence in the first and second order semantics for modal logic. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 110–143. - Arto Salomaa. On some decidability problems concerning developmental languages. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 144–153.
-
- Journal:
- The Journal of Symbolic Logic / Volume 43 / Issue 2 / June 1978
- Published online by Cambridge University Press:
- 12 March 2014, pp. 373-376
- Print publication:
- June 1978
-
- Article
- Export citation
Modal operators and functional completeness, II1
-
- Journal:
- The Journal of Symbolic Logic / Volume 42 / Issue 3 / September 1977
- Published online by Cambridge University Press:
- 12 March 2014, pp. 391-399
- Print publication:
- September 1977
-
- Article
- Export citation
Categories of frames for modal logic1
-
- Journal:
- The Journal of Symbolic Logic / Volume 40 / Issue 3 / September 1975
- Published online by Cambridge University Press:
- 12 March 2014, pp. 439-442
- Print publication:
- September 1975
-
- Article
- Export citation
Reduction of tense logic to modal logic. I
-
- Journal:
- The Journal of Symbolic Logic / Volume 39 / Issue 3 / September 1974
- Published online by Cambridge University Press:
- 12 March 2014, pp. 549-551
- Print publication:
- September 1974
-
- Article
- Export citation
David Makinson. Some embedding theorems for modal logic. Notre Dame journal of formal logic, vol. 12 (1971), pp. 252–254.
-
- Journal:
- The Journal of Symbolic Logic / Volume 39 / Issue 2 / June 1974
- Published online by Cambridge University Press:
- 12 March 2014, p. 351
- Print publication:
- June 1974
-
- Article
- Export citation
David Makinson. A generalisation of the concept of a relational model for modal logic. Theoria (Lund), vol. 36 (for 1970, pub. 1971), pp. 331–335.
-
- Journal:
- The Journal of Symbolic Logic / Volume 38 / Issue 3 / September 1973
- Published online by Cambridge University Press:
- 12 March 2014, p. 520
- Print publication:
- September 1973
-
- Article
- Export citation
Noncompactness in propositional modal logic
-
- Journal:
- The Journal of Symbolic Logic / Volume 37 / Issue 4 / December 1972
- Published online by Cambridge University Press:
- 12 March 2014, pp. 716-720
- Print publication:
- December 1972
-
- Article
- Export citation
J. R. Shoenheld. Some applications of degrees. Logic, methodology and philosophy of science, Proceedings of the 1960 International Congress, edited by Ernest Nagel, Patrick Suppes, and Alfred Tarski, Stanford University Press, Stanford, Calif., 1962, pp. 56–59.
-
- Journal:
- The Journal of Symbolic Logic / Volume 37 / Issue 3 / September 1972
- Published online by Cambridge University Press:
- 12 March 2014, p. 610
- Print publication:
- September 1972
-
- Article
- Export citation
Semantic analysis of tense logics1
-
- Journal:
- The Journal of Symbolic Logic / Volume 37 / Issue 1 / March 1972
- Published online by Cambridge University Press:
- 12 March 2014, pp. 150-158
- Print publication:
- March 1972
-
- Article
- Export citation
C. E. M. Yates. Recursively enumerable degrees and the degrees less than 0(1). Sets, models and recursion theory, Proceedings of the Summer School in Mathematical Logic and Tenth Logic Colloquium, Leicester, August-September 1965, edited by John N. Crossley, Studies in logic and the foundations of mathematics, North-Holland Publishing Company, Amsterdam, and Humanities Press, New York, 1967, pp. 264–271.
-
- Journal:
- The Journal of Symbolic Logic / Volume 35 / Issue 4 / December 1970
- Published online by Cambridge University Press:
- 12 March 2014, p. 589
- Print publication:
- December 1970
-
- Article
- Export citation
Sublattices and Initial Segments of the Degrees of Unsolvability
-
- Journal:
- Canadian Journal of Mathematics / Volume 22 / Issue 3 / 01 June 1970
- Published online by Cambridge University Press:
- 20 November 2018, pp. 569-581
- Print publication:
- 01 June 1970
-
- Article
-
- You have access
- Export citation
On initial segments of hyperdegrees1
-
- Journal:
- The Journal of Symbolic Logic / Volume 35 / Issue 2 / June 1970
- Published online by Cambridge University Press:
- 12 March 2014, pp. 189-197
- Print publication:
- June 1970
-
- Article
- Export citation
A theorem on initial segments of degrees 1
-
- Journal:
- The Journal of Symbolic Logic / Volume 35 / Issue 1 / March 1970
- Published online by Cambridge University Press:
- 12 March 2014, pp. 41-45
- Print publication:
- March 1970
-
- Article
- Export citation
Dieter Titgemeyer. Untersuchungen über die Struktur des Kleene-Postschen Halbverbandes der Grade der rekursiven Unlösbarkeit. Archiv für mathematische Logik und Grundlagenforschung, vol. 8 no. 1–2 (1965), pp. 45–62.
-
- Journal:
- The Journal of Symbolic Logic / Volume 35 / Issue 1 / March 1970
- Published online by Cambridge University Press:
- 12 March 2014, pp. 155-156
- Print publication:
- March 1970
-
- Article
- Export citation
A Note on Non-Distributive Sublattices of Degrees and Hyperdegrees
-
- Journal:
- Canadian Journal of Mathematics / Volume 21 / 1969
- Published online by Cambridge University Press:
- 20 November 2018, pp. 147-148
- Print publication:
- 1969
-
- Article
-
- You have access
- Export citation



 is a frame, then
is a frame, then 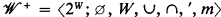 is a CAMA, where
is a CAMA, where 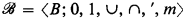 is a CAMA then
is a CAMA then 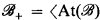 is a frame, where
is a frame, where 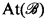 is the set of atoms of
is the set of atoms of 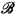 and
and 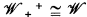 , and
, and 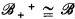 the validity of a modal formula on
the validity of a modal formula on 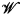 is equivalent to the satisfaction of a modal algebra polynomial identity by
is equivalent to the satisfaction of a modal algebra polynomial identity by 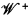 and conversely, so the validity-preserving constructions on frames ought to be in some sense equivalent to the identity-preserving constructions on CAMA's. The former are important for modal logic, and many of the results of universal algebra apply to the latter, so it is worthwhile to fix precisely the sense of the equivalence.
and conversely, so the validity-preserving constructions on frames ought to be in some sense equivalent to the identity-preserving constructions on CAMA's. The former are important for modal logic, and many of the results of universal algebra apply to the latter, so it is worthwhile to fix precisely the sense of the equivalence.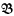 and
and 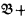 be the categories of CAMA's with homomorphisms and complete homomorphisms, respectively. We shall define categories
be the categories of CAMA's with homomorphisms and complete homomorphisms, respectively. We shall define categories 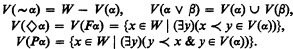
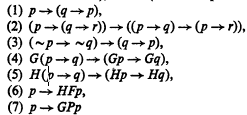
 ⊧
⊧  , possibly from different semantics, are called
, possibly from different semantics, are called  of the set
of the set