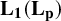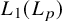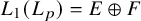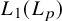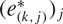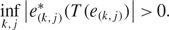2 results
The space
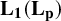 $\mathbf {L_1(L_p)}$
is primary for 1 < p < ∞
$\mathbf {L_1(L_p)}$
is primary for 1 < p < ∞
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 30 May 2022, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The factorisation property of l∞(Xk)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 10 December 2020, pp. 421-448
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation