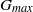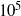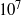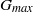Perturbations in a non-normal system can grow transiently even if the system is linearly stable. If this transient growth is sufficiently large, it can trigger self-sustained oscillations from small initial disturbances. This has important practical consequences for combustion–acoustic oscillations, which are a persistent problem in rocket and aircraft engines. Balasubramanian & Sujith (J. Fluid Mech., vol. 594, 2008, pp. 29–57) modelled an infinite-rate chemistry diffusion flame in an acoustic duct and found that the transient growth in this system can amplify the initial energy by a factor, 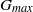${G}_{max} $ , of the order of 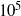$1{0}^{5} $ to 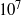$1{0}^{7} $ . However, recent investigations by L. Magri and M. P. Juniper have brought to light certain errors in that paper. When the errors are corrected, 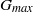${G}_{max} $ is found to be of the order of 1 to 10, revealing that non-normality is not as influential as it was thought to be.

The local environment of light emitting silicon nanocrystals (Si-nc) embedded in amorphous SiO2 has been studied by x-ray absorption spectroscopy (XAS) and by ab-initio total energy calculations. Si-nc have been formed by PECVD deposition of SiOx with different Si content (from 35 to 42 at.%) and thermal annealing at high temperature (1250 °C). The comparison between total electron yield (TEY) and photoluminescence yield (PLY) spectra has allowed the identification of a modified region of SiO2 (about 1 nm thick) surrounding the Si-nc, which participates to the light emission of Si-nc. Total energy calculations, within the density functional theory, clearly show that Si-nc are surrounded by a cap-shell of stressed SiO2 with a thickness of about 1 nm. The optoelectronic properties show the appearance of localized states not only in the Si-nc core region but also in the modified SiO2 region.

The aim of this work is to investigate the structural, electronic and optical properties of hydrogenated Si nanoclusters (H-Si-nc) in their ground and excited state configurations. Structural relaxations have been fully taken into account in all cases through total energy pseudopotential calculations. Recent results about ab-initio calculations of Stokes shift as a function of the cluster dimension and of optical gain will be presented here. A structural model that can be linked to the four level scheme recently invoked to explain the experimental outcomes relative to the observed optical gain in Si-nc embedded in a SiO2 matrix will be suggested too.