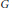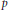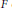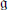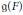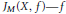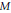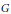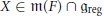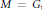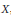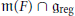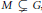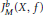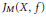Cet article est une contribution à la fois au calcul du nombre de fibrés de Hitchin sur une courbe projective et à l’explicitation de la partie nilpotente de la formule des traces d’Arthur-Selberg pour une fonction test très simple. Le lien entre les deux questions a été établi dans [Chaudouard, Sur le comptage des fibrés de Hitchin. À paraître aux actes de la conférence en l’honneur de Gérard Laumon]. On décompose cette partie nilpotente en une somme d’intégrales adéliques indexées par les orbites nilpotentes. Pour les orbites de type «régulières par blocs», on explicite complètement ces intégrales en termes de la fonction zêta de la courbe.

This work is the geometric part of our proof of the weighted fundamental lemma, which is an extension of Ngô Bao Châu’s proof of the Langlands–Shelstad fundamental lemma. Ngô’s approach is based on a study of the elliptic part of the Hichin fibration. The total space of this fibration is the algebraic stack of Hitchin bundles and its base space is the affine space of ‘characteristic polynomials’. Over the elliptic set, the Hitchin fibration is proper and the number of points of its fibers over a finite field can be expressed in terms of orbital integrals. In this paper, we study the Hitchin fibration over an open set larger than the elliptic set, namely the ‘generically regular semi-simple set’. The fibers are in general neither of finite type nor separated. By analogy with Arthur’s truncation, we introduce the substack of ξ-stable Hitchin bundles. We show that it is a Deligne–Mumford stack, smooth over the base field and proper over the base space of ‘characteristic polynomials’. Moreover, the number of points of the ξ-stable fibers over a finite field can be expressed as a sum of weighted orbital integrals, which appear in the Arthur–Selberg trace formula.

Soit 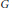$G$ un groupe réductif connexe défini sur un corps 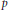$p$ -adique 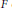$F$ et 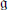$\mathfrak{g}$ son algèbre de Lie. Les intégrales orbitales pondérées sur 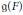$\mathfrak{g}\left( F \right)$ sont des distributions 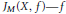${{J}_{M}}\left( X,\,f \right)-f$ est une fonction test—indexées par les sous-groupes de Lévi 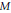$M$ de 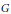$G$ et les éléments semi-simples réguliers 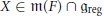$X\,\in \,\mathfrak{m}\left( F \right)\,\cap \,{{\mathfrak{g}}_{\text{reg}}}$ . Leurs analogues sur 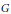$G$ sont les principales composantes du côté géométrique des formules des traces locale et globale d’Arthur.

Si 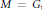$M=G$ , on retrouve les intégrales orbitales invariantes qui, vues comme fonction de 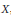$X$ , sont borńees sur 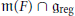$\mathfrak{m}\left( F \right)\,\cap \,{{\mathfrak{g}}_{\text{reg}}}$ : c’est un résultat bien connu de Harish-Chandra. Si 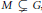$M\subsetneq G$ , les intégrales orbitales pondérées explosent au voisinage des éléments singuliers. Nous construisons dans cet article de nouvelles intégrales orbitales pondérées 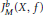$J_{M}^{b}\left( X,f \right)$ , égales à 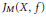${{J}_{M}}\left( X,f \right)$ à un terme correctif près, qui tout en conservant les principales propriétés des précédentes (comportement par conjugaison, développement en germes, etc.) restent borńees quand $X$ parcourt 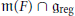$\mathfrak{m}\left( F \right)\,\cap \,{{\mathfrak{g}}_{\text{reg}}}$ . Nous montrons également que les intégrales orbitales pondérées globales, associées à des éléments semi-simples réguliers, se décomposent en produits de ces nouvelles intégrales locales.