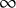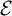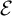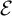7 results
The effective model structure and
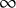 $\infty $
-groupoid objects
$\infty $
-groupoid objects
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODELS OF MARTIN-LÖF TYPE THEORY FROM ALGEBRAIC WEAK FACTORISATION SYSTEMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 08 June 2021, pp. 242-289
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Introduction – from type theory and homotopy theory to univalent foundations
-
- Journal:
- Mathematical Structures in Computer Science / Volume 25 / Issue 5 / June 2015
- Published online by Cambridge University Press:
- 10 March 2015, pp. 1005-1009
-
- Article
-
- You have access
- Export citation
Polynomial functors and polynomial monads
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 154 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 06 September 2012, pp. 153-192
- Print publication:
- January 2013
-
- Article
- Export citation
Homotopy limits for 2-categories
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 145 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 43-63
- Print publication:
- July 2008
-
- Article
- Export citation
Spatiality for formal topologies
-
- Journal:
- Mathematical Structures in Computer Science / Volume 17 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 01 February 2007, pp. 65-80
-
- Article
- Export citation
The generalised type-theoretic interpretation of constructive set theory
-
- Journal:
- The Journal of Symbolic Logic / Volume 71 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 12 March 2014, pp. 67-103
- Print publication:
- March 2006
-
- Article
- Export citation