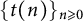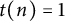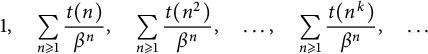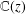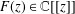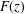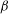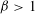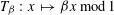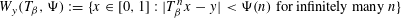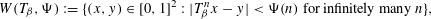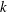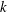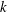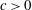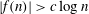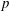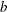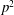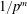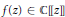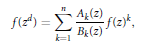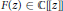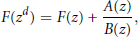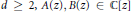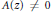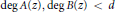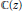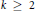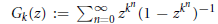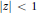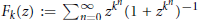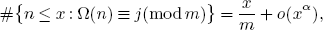20 results
RADIAL ASYMPTOTICS OF GENERATING FUNCTIONS OF k-REGULAR SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1-7
-
- Article
- Export citation
Linear independence of series related to the Thue–Morse sequence along powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 06 March 2024, pp. 1-11
-
- Article
- Export citation
ZAREMBA, SALEM AND THE FRACTAL NATURE OF GHOST DISTRIBUTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 374-389
- Print publication:
- June 2023
-
- Article
- Export citation
DEGREE-ONE MAHLER FUNCTIONS: ASYMPTOTICS, APPLICATIONS AND SPECULATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 399-409
- Print publication:
- December 2020
-
- Article
- Export citation
Hierarchy effects in copula constructions
-
- Journal:
- Canadian Journal of Linguistics/Revue canadienne de linguistique / Volume 64 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 23 October 2019, pp. 617-648
-
- Article
- Export citation
TRANSCENDENCE OVER MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 393-399
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
A DICHOTOMY LAW FOR THE DIOPHANTINE PROPERTIES IN
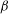 $\unicode[STIX]{x1D6FD}$-DYNAMICAL SYSTEMS
$\unicode[STIX]{x1D6FD}$-DYNAMICAL SYSTEMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 884-897
- Print publication:
- 2016
-
- Article
- Export citation
THE MINIMAL GROWTH OF A
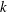 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 22 May 2014, pp. 195-203
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
AN ARITHMETICAL EXCURSION VIA STONEHAM NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 27 March 2014, pp. 303-315
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Transcendental Solutions of a Class of Minimal Functional Equations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 56 / Issue 2 / 01 June 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 283-291
- Print publication:
- 01 June 2013
-
- Article
-
- You have access
- Export citation
Index
-
- Book:
- Paternalism
- Published online:
- 05 February 2013
- Print publication:
- 14 February 2013, pp 281-283
-
- Chapter
- Export citation
Introduction - Paternalism – Issues and trends
-
-
- Book:
- Paternalism
- Published online:
- 05 February 2013
- Print publication:
- 14 February 2013, pp 1-24
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Paternalism
- Published online:
- 05 February 2013
- Print publication:
- 14 February 2013, pp 266-280
-
- Chapter
- Export citation
Contents
-
- Book:
- Paternalism
- Published online:
- 05 February 2013
- Print publication:
- 14 February 2013, pp v-vi
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Paternalism
- Published online:
- 05 February 2013
- Print publication:
- 14 February 2013, pp i-iv
-
- Chapter
- Export citation
Contributors
-
- Book:
- Paternalism
- Published online:
- 05 February 2013
- Print publication:
- 14 February 2013, pp vii-viii
-
- Chapter
- Export citation

Paternalism
- Theory and Practice
-
- Published online:
- 05 February 2013
- Print publication:
- 14 February 2013
Extension of Some Theorems of W. Schwarz
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 1 / 01 March 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 60-66
- Print publication:
- 01 March 2012
-
- Article
-
- You have access
- Export citation
On the residue class distribution of the number of prime divisors of an integer
-
- Journal:
- Nagoya Mathematical Journal / Volume 202 / June 2011
- Published online by Cambridge University Press:
- 11 January 2016, pp. 15-22
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Growth of SiO2 on Si(111)7×7 Using SiCl4 and H2O
-
- Journal:
- MRS Online Proceedings Library Archive / Volume 282 / 1992
- Published online by Cambridge University Press:
- 22 February 2011, 499
- Print publication:
- 1992
-
- Article
- Export citation