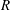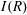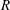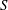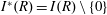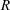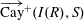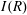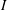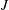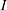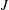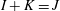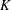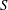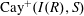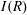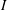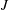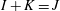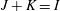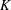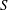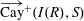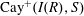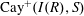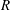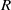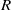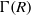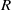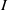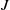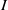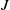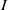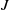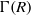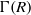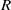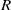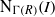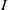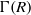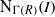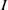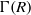Let 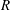 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}R$ be a commutative ring,
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}R$ be a commutative ring, 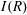 $I(R)$ be the set of all ideals of
$I(R)$ be the set of all ideals of 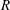 $R$ and
$R$ and 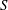 $S$ be a subset of
$S$ be a subset of 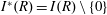 $I^*(R)=I(R)\setminus \{0\}$. We define a Cayley sum digraph of ideals of
$I^*(R)=I(R)\setminus \{0\}$. We define a Cayley sum digraph of ideals of 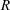 $R$, denoted by
$R$, denoted by 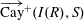 $\overrightarrow{\mathrm{Cay}}^+ (I(R),S)$, as a directed graph whose vertex set is the set
$\overrightarrow{\mathrm{Cay}}^+ (I(R),S)$, as a directed graph whose vertex set is the set 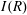 $I(R)$ and, for every two distinct vertices
$I(R)$ and, for every two distinct vertices 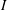 $I$ and
$I$ and 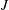 $J$, there is an arc from
$J$, there is an arc from 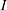 $I$ to
$I$ to 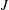 $J$, denoted by
$J$, denoted by  $I\longrightarrow J$, whenever
$I\longrightarrow J$, whenever 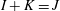 $I+K=J$, for some ideal
$I+K=J$, for some ideal 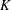 $K $ in
$K $ in 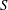 $S$. Also, the Cayley sum graph
$S$. Also, the Cayley sum graph 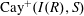 $ \mathrm{Cay}^+ (I(R), S)$ is an undirected graph whose vertex set is the set
$ \mathrm{Cay}^+ (I(R), S)$ is an undirected graph whose vertex set is the set 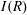 $I(R)$ and two distinct vertices
$I(R)$ and two distinct vertices 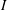 $I$ and
$I$ and 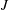 $J$ are adjacent whenever
$J$ are adjacent whenever 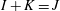 $I+K=J$ or
$I+K=J$ or 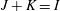 $J+K=I$, for some ideal
$J+K=I$, for some ideal 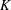 $K $ in
$K $ in 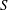 $ S$. In this paper, we study some basic properties of the graphs
$ S$. In this paper, we study some basic properties of the graphs 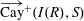 $\overrightarrow{\mathrm{Cay}}^+ (I(R),S)$ and
$\overrightarrow{\mathrm{Cay}}^+ (I(R),S)$ and 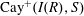 $ \mathrm{Cay}^+ (I(R), S)$ such as connectivity, girth and clique number. Moreover, we investigate the planarity, outerplanarity and ring graph of
$ \mathrm{Cay}^+ (I(R), S)$ such as connectivity, girth and clique number. Moreover, we investigate the planarity, outerplanarity and ring graph of 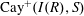 $ \mathrm{Cay}^+ (I(R), S)$ and also we provide some characterization for rings
$ \mathrm{Cay}^+ (I(R), S)$ and also we provide some characterization for rings  $R$ whose Cayley sum graphs have genus one.
$R$ whose Cayley sum graphs have genus one.