8 results
On the Digits of Sumsets
-
- Journal:
- Canadian Journal of Mathematics / Volume 69 / Issue 3 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 595-612
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
PROPRIÉTÉS LOCALES DES CHIFFRES DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 04 April 2017, pp. 189-224
- Print publication:
- January 2019
-
- Article
- Export citation
ON THE GOWERS NORM OF PSEUDORANDOM BINARY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 259-271
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Primes with an average sum of digits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 271-292
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
the sum-of-digits function of squares
-
- Journal:
- Journal of the London Mathematical Society / Volume 72 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 04 October 2005, pp. 273-292
- Print publication:
- October 2005
-
- Article
- Export citation
On the pseudorandomness of the signs of Kloosterman sums
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-436
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
Nombres premiers de la forme ⌊nc⌋
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 2 / 01 April 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 414-433
- Print publication:
- 01 April 2001
-
- Article
-
- You have access
- Export citation
Primes of the form [pc] and related questions
-
- Journal:
- Glasgow Mathematical Journal / Volume 37 / Issue 2 / May 1995
- Published online by Cambridge University Press:
- 18 May 2009, pp. 131-141
- Print publication:
- May 1995
-
- Article
-
- You have access
- Export citation

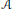
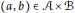
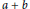
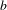
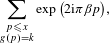
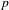
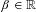
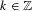
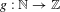
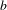
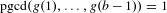
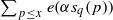 (where the sum is restricted to
(where the sum is restricted to