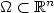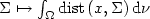7 results
Flows of measures generated by vector fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 773-818
- Print publication:
- August 2018
-
- Article
- Export citation
Long-term planning versus short-term planning in the asymptotical location problem
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 15 / Issue 3 / July 2009
- Published online by Cambridge University Press:
- 30 May 2008, pp. 509-524
- Print publication:
- July 2009
-
- Article
- Export citation
REPRESENTATION OF ATOMIC OPERATORS AND EXTENSION PROBLEMS
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 47 / Issue 3 / October 2004
- Published online by Cambridge University Press:
- 09 November 2004, pp. 695-707
-
- Article
-
- You have access
- Export citation
ON SOME CLASSES OF OPERATORS DETERMINED BY THE STRUCTURE OF THEIR MEMORY
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 45 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 17 June 2002, pp. 467-490
-
- Article
-
- You have access
- Export citation
On the Dirichlet problem with several volume constraints on the level sets
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 132 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 12 July 2007, pp. 437-461
- Print publication:
- April 2002
-
- Article
- Export citation
Thermodynamics of Co-Existing Phases at Phase Transitions in Fullerenes
-
- Journal:
- MRS Online Proceedings Library Archive / Volume 359 / 1994
- Published online by Cambridge University Press:
- 15 February 2011, 573
- Print publication:
- 1994
-
- Article
- Export citation
Diffusion Separation of Fullerenes in Solution
-
- Journal:
- MRS Online Proceedings Library Archive / Volume 359 / 1994
- Published online by Cambridge University Press:
- 15 February 2011, 567
- Print publication:
- 1994
-
- Article
- Export citation