18 results
NEW CONSTRUCTIONS OF SELF-COMPLEMENTARY CAYLEY GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 12 January 2021, pp. 372-385
- Print publication:
- December 2021
-
- Article
- Export citation
RELATIVE ELEMENTARY ABELIAN GROUPS AND A CLASS OF EDGE-TRANSITIVE CAYLEY GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 241-251
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON ISOMORPHISMS OF VERTEX-TRANSITIVE CUBIC GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 13 August 2015, pp. 341-349
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
SELF-COMPLEMENTARY VERTEX-TRANSITIVE GRAPHS OF ORDER A PRODUCT OF TWO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 13 June 2013, pp. 322-330
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
LOCALLY PRIMITIVE GRAPHS AND BIDIRECT PRODUCTS OF GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 14 October 2011, pp. 231-242
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
LOCALLY PRIMITIVE GRAPHS OF PRIME-POWER ORDER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 111-122
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
On the Weiss conjecture for finite locally primitive graphs
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 43 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 20 January 2009, pp. 129-138
-
- Article
-
- You have access
- Export citation
The Finite Primitive Permutation Groups Containing an Abelian Regular Subgroup
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 87 / Issue 3 / November 2003
- Published online by Cambridge University Press:
- 23 October 2003, pp. 725-747
- Print publication:
- November 2003
-
- Article
- Export citation
THE PRIMITIVE PERMUTATION GROUPS OF SQUAREFREE DEGREE
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 5 / September 2003
- Published online by Cambridge University Press:
- 13 August 2003, pp. 635-644
- Print publication:
- September 2003
-
- Article
- Export citation
SELF-COMPLEMENTARY VERTEX-TRANSITIVE GRAPHS NEED NOT BE CAYLEY GRAPHS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 33 / Issue 6 / November 2001
- Published online by Cambridge University Press:
- 28 November 2001, pp. 653-661
- Print publication:
- November 2001
-
- Article
- Export citation
FINITE s-ARC TRANSITIVE GRAPHS OF PRIME-POWER ORDER
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 33 / Issue 2 / March 2001
- Published online by Cambridge University Press:
- 09 April 2001, pp. 129-137
- Print publication:
- March 2001
-
- Article
- Export citation
A class of finite symmetric graphs with 2-arc transitive quotients
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 129 / Issue 1 / July 2000
- Published online by Cambridge University Press:
- 01 July 2000, pp. 19-34
- Print publication:
- July 2000
-
- Article
- Export citation
A complete classification of finite homogeneous groups
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 60 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 17 April 2009, pp. 331-334
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
FINITE CI-GROUPS ARE SOLUBLE
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 31 / Issue 4 / July 1999
- Published online by Cambridge University Press:
- 01 July 1999, pp. 419-423
- Print publication:
- July 1999
-
- Article
- Export citation
On isomorphisms of connected Cayley graphs, III
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 58 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-145
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
Isomorphisms of Cayley digraphs of Abelian groups
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 57 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 17 April 2009, pp. 181-188
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
On finite groups with the Cayley invariant property
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 56 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 17 April 2009, pp. 253-261
- Print publication:
- October 1997
-
- Article
-
- You have access
- Export citation
Isomorphisms of finite Cayley graphs
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 56 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-172
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation

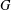
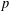
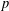
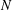

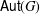
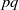
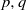
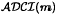 of Abelian groups. First we reduce the problem of determining Abelian
of Abelian groups. First we reduce the problem of determining Abelian 