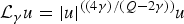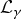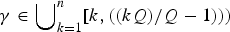39 results
Nodal solutions for the fractional Yamabe problem on Heisenberg groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 771-788
- Print publication:
- April 2020
-
- Article
- Export citation
Low-dimensional compact embeddings of symmetric Sobolev spaces with applications
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 141 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 04 April 2011, pp. 383-395
- Print publication:
- April 2011
-
- Article
- Export citation
Multiple Solutions for a Class of Neumann Elliptic Problems on Compact Riemannian Manifolds with Boundary
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 4 / 01 December 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 674-683
- Print publication:
- 01 December 2010
-
- Article
-
- You have access
- Export citation
Part II - Variational principles in geometry
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 215-216
-
- Chapter
- Export citation
Appendix C - Category and genus
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 337-338
-
- Chapter
- Export citation
14 - Minimization of cost-functions on manifolds
- from Part III - Variational principles in economics
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 278-288
-
- Chapter
- Export citation
7 - Competition phenomena in Dirichlet problems
- from Part I - Variational principles in mathematical physics
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 183-209
-
- Chapter
- Export citation
11 - Equations with critical exponent
- from Part II - Variational principles in geometry
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 248-260
-
- Chapter
- Export citation
1 - Variational principles
- from Part I - Variational principles in mathematical physics
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 3-41
-
- Chapter
- Export citation
16 - A variational approach to Nash equilibria
- from Part III - Variational principles in economics
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 304-319
-
- Chapter
- Export citation
3 - Nonlinear eigenvalue problems
- from Part I - Variational principles in mathematical physics
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 81-116
-
- Chapter
- Export citation
Part I - Variational principles in mathematical physics
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 1-2
-
- Chapter
- Export citation
Appendix D - Clarke and Degiovanni gradients
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 339-345
-
- Chapter
- Export citation
Notation index
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 361-362
-
- Chapter
- Export citation
15 - Best approximation problems on manifolds
- from Part III - Variational principles in economics
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 289-303
-
- Chapter
- Export citation
8 - Problems to Part I
- from Part I - Variational principles in mathematical physics
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 210-214
-
- Chapter
- Export citation
5 - Systems with arbitrary growth nonlinearities
- from Part I - Variational principles in mathematical physics
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 146-161
-
- Chapter
- Export citation
References
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 349-360
-
- Chapter
- Export citation
17 - Problems to Part III
- from Part III - Variational principles in economics
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 320-321
-
- Chapter
- Export citation
10 - Asymptotically critical problems on spheres
- from Part II - Variational principles in geometry
-
- Book:
- Variational Principles in Mathematical Physics, Geometry, and Economics
- Published online:
- 05 June 2013
- Print publication:
- 19 August 2010, pp 228-247
-
- Chapter
- Export citation