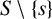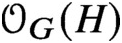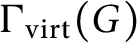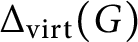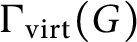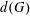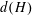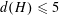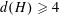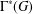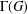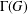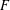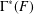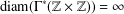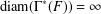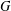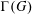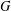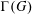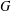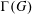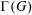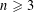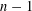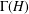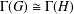16 results
FINITE GROUPS WITH INDEPENDENT GENERATING SETS OF ONLY TWO SIZES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 449-458
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Boolean lattices in finite alternating and symmetric groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e55
-
- Article
-
- You have access
- Open access
- Export citation
The virtually generating graph of a profinite group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 15 October 2020, pp. 808-819
- Print publication:
- December 2021
-
- Article
- Export citation
FINITE GROUPS WITH THE SAME JOIN GRAPH AS A FINITE NILPOTENT GROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 17 August 2020, pp. 640-650
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
GENERATING MAXIMAL SUBGROUPS OF FINITE ALMOST SIMPLE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e32
-
- Article
-
- You have access
- Open access
- Export citation
Bounding the maximal size of independent generating sets of finite groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 January 2020, pp. 133-150
- Print publication:
- February 2021
-
- Article
-
- You have access
- Open access
- Export citation
THE GENERATING GRAPH OF INFINITE ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 68-75
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
ALTERNATING AND SYMMETRIC GROUPS WITH EULERIAN GENERATING GRAPH
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 10 November 2017, e24
-
- Article
-
- You have access
- Open access
- Export citation
ON THE GENERATING GRAPH OF A SIMPLE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 91-103
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Probability and Bias in Generating Supersoluble Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 899-909
-
- Article
- Export citation
LARGE P-GROUPS WITHOUT PROPER SUBGROUPS WITH THE SAME DERIVED LENGTH
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 23 July 2015, pp. 445-459
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
RECOGNIZING SOLUBLE GROUPS FROM THEIR PROBABILISTIC ZETA FUNCTIONS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 5 / September 2003
- Published online by Cambridge University Press:
- 13 August 2003, pp. 659-664
- Print publication:
- September 2003
-
- Article
- Export citation
SOME REMARKS ON THE PROBABILITY OF GENERATING AN ALMOST SIMPLE GROUP
-
- Journal:
- Glasgow Mathematical Journal / Volume 45 / Issue 2 / May 2003
- Published online by Cambridge University Press:
- 31 July 2003, pp. 281-291
- Print publication:
- May 2003
-
- Article
-
- You have access
- Export citation
ENUMERATING TRANSITIVE FINITE PERMUTATION GROUPS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 30 / Issue 6 / November 1998
- Published online by Cambridge University Press:
- 01 November 1998, pp. 569-577
- Print publication:
- November 1998
-
- Article
- Export citation
Finite groups that need more generators than any proper quotient
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 82-91
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
A BOUND ON THE PRESENTATION RANK OF A FINITE GROUP
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 29 / Issue 4 / July 1997
- Published online by Cambridge University Press:
- 01 July 1997, pp. 389-394
- Print publication:
- July 1997
-
- Article
- Export citation