1. Introduction
The occurrence of periodic surge events at roughly 10 kyear intervals during the last ice-age cycle has now been clearly documented in the ice-rafted debris (IRD) layers of North Atlantic deep-sea cores (Heinrich, 1988; Grousset and others, 1993). Here, as an extension of our previous studies (Verbitsky and Saltzman, 1994, 1995), we present a simple horizontally averaged dynamical model of ice-sheet behavior in which we determine a set of the unknown rate constants required for the existence of internal oscillations that may bear some relation to these “Heinrich events”.
This dynamical model has some physical similarities to a previous model for oscillatory ice-sheet behavior on the scale of 100 kyear, developed by Oerlemans (1983), that involves basal water-layer development due to melting caused primarily by frictional heating. The dominance of both advectional and frictional effects over geothermal effects in generating basal melting and surge events was emphasized in our previous studies (Verbitsky and Saltzman, 1994, 1995). Another model of Heinrich oscillations, in which the geothermal heat flux plays a more dominant role during the growth phase of the ice-sheet oscillations, was presented by MacAyeal (1993). Reviews of earlier discussions of basal sliding and oscillatory glacial behavior as well as some ideas similar to those discussed here and in Verbitsky and Saltzman (1994, 1995) can be found in Paterson (1994) and Payne (1995).
2. Basic Equations
Let us consider the idealized two-dimensional ice sheet shown in Figure 1, characterized by a horizontal length scale L, mean height H at which the mean temperature is T H and a constant net accumulation rate a. The base of this ice sheet has a mean temperature T B, which, if it reaches the pressure-melting point T M, may generate liquid water of mean equivalent thickness W that is likely to be distributed unevenly through some basal layer mainly in channels. Such a mean water layer is assumed to make the outer pans of the ice sheet vulnerable to a surging discharge flux of ice. The flow of ice has characteristic horizontal and downward velocity components U(≈ aL/H) and W(≈ a), respectively. The characteristic area and volume of the ice sheet are A = L 2 and V = AH, respectively.
The basic internal dynamics of this two-dimensional ice sheet is governed by the motion equations

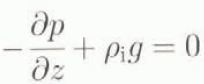
and the continuity equation
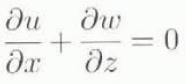
where (x, z) and (u, w) are the horizontal and vertical coordinates and velocity components, respectively, p is pressure, g is the acceleration due to gravity, μi and ρi are the ice viscosity and density, respectively, and n is the power degree of Glen’s rheological law. From these equations, we can show (Verbitsky, 1992) that to first-order scaling


Fig. 1. Idealized cross-section of a two-dimensional ice sheet of characteristic horizontal size L, thickness H, creeping velocity components U and W, and surface and basal temperature T H and T B.
The basic thermodynamics of the ice sheet is governed by the equation

where t is time, c is the specific beat capacity of ice, λ(~ ρi ck) is the thermal conductivity of ice, k is the thermal diffusivity of ice and qf is the heat added per unit volume due to internal friction expressible in the form

The lower boundary condition (z = 0) depends on whether the basal temperature T B is below or at the pressure-melting point (Shumskii, 1955)

in which latter case melting and basal sliding can occur, Thus, at z = 0 we have two types of boundary conditions; if T B < T M, i.e. no melting,
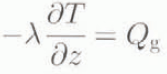
but, if melting occurs, the basal temperature is fixed at the melting point

where Q g is the geothermal heat flux, D(= σ xz u 0) is the rate of heat addition per unit area due to basal sliding, of velocity u 0, σ xz is the basal shear stress. L f is the latent heat of fusion and M B is the rate of basal melting.
At the upper boundary of the ice sheet (z = H), we assume here that the temperature is given by
where T s is the annual mean sea-level air temperature near the edge of the ice sheet, which we take to be a constant, 273 K, and γ is the atmospheric lapse rate.

Fig. 2. Thermal balances in three main domains of an ice sheet, the central (summit) region (L < L c), the basal boundary layer (z < z b) and the main domain above the bottom boundary layer where thermal advection dominates.
In Figure 2, we show the special thermodynamic balances for the three main regions of an ice sheet: (1) The summit (x < L c), where L c, represents the characteristic distance from the center beyond which the horizontal flow becomes large enough to control the advective heat flux and friction. (2) The region above the bottom boundary layer (z > t b, z b ≈ k/a is the thickness of the boundary layer) where advection dominates, conveying the temperature at the upper surface (T H) to the basal layer with an advective time delay t* ≈ H(t)/a, i.e. the temperature at the top of the bottom boundary layer (z = z b) is T b = T<H(t – t*). (3) The bottom boundary layer (z ≤ z b) where vertical diffusion balances heat added due to internal friction.
In Verbitsky and Saltzman (1994, 1995), we showed that the solution for the basal temperature, T B, obtained by matching all the boundary conditions, is of the following form (assuming the presence of ice of thickness greater than z b, i.e. H > z b):
where



To derive an equation for the melting rate. M B, as given by the boundary condition (8b).

we use the thermal balance in the bottom boundary layer (z ≤ z b) to evaluate

where q fb the frictional heating pet unit volume in the bottom boundary layer, given by Equation (6), which from Verbitsky and Saltzman (1994, 1995) can be written in the form

The steady-state solution of Equation (12) (implying that we are considering processes longer than the characteristic time-scale ![]() , with boundary conditions T = T
b = T
B(adv) = T
H(t – t*) at z = z
b, and T = T
B = T
M at z = 0, is
, with boundary conditions T = T
b = T
B(adv) = T
H(t – t*) at z = z
b, and T = T
B = T
M at z = 0, is

from which

Since basal ice physics is as yet poorly understood and, in view of the uncertainties regarding the basal buoyancy process, a sliding law (i.e. a relationship between the basal sliding velocity u 0 and the basal shear stress σ xz ) is very uncertain. Therefore, to estimate the amount of heat released due to the bottm sliding, we simply suppose that the frictional heating per unit volume due to normal creep in the lower boundary layer given by Equation (13) can be used in this sliding case also, so that

From Equation (16), we can write Equation (11) final form in terms of the variable H(t)

3. The Dynamical Model
We now postulate what we suppose is the simplest dynamical system that may govern the variation of H (on which T B and M B depend), coupled with the variations of the basal-water amount W and the ice-surge flux S(= ρi AS, where A is the area of the ice sheet (assumed constant) and S is the rate of ice-thickness loss due to the surge flux). All of these variations are assumed to represent relatively small fluctuations of a massive ice sheet such as the Laurentide ice sheet. This system has the form
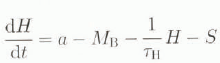


where τH is the characteristic time-scale of ice-flow creep, and τS and τ W are dissipative time constants. These latter two time constants are only weakly constrained but plausibility arguments have been made by MacAyeal (1993) that τS is of the order of 1 kyear and by Oerlemans and Van der Veen (1984) that (in accordance with a diffusive approximation for basal-water flow) τ W is also of this same order (1 kyear). The rate constant α in Equation (19), relating the surge changes to the basal Equation-water amount, is even more weakly constrained. We consider τS, τ W and α, which must appear in some form in all models of ice-sheet surging, to be free parameters to be determined as a (non-unique) set of predicted values required to account for the observed variations (in our case the Heinrich oscillations). To close the system, we must add the formula for M B embodied in Equation (17), together with the formulas (7) and (10) for T M and T B. A schematic feed-back loop diagram showing the cyclical coupling of the main variables of the model is given in Figure 3.
It may be recognized that the ice volume V(H), the surge loss (S) and basal-water amount (W) are also the main variables of the more complex model described by Oerlemans (1983) in which he demonstrated the possibility for oscillatory behavior, albeit for a much longer time-scale (100 kyear) than Heinrich events (10 kyear). To illustrate the possibility that our present much simpler system can exhibit fluctuations of the Heinrich time-scale, we take the following plausible values of physical constants and parameters: ρi = 917 kg m−3, n = 3, g = 9.8 m s−2, c = 2 × 103 J kg−1°C−1, k = 1 ° 10−6 m2 s−1. Q g = 0.04 Wm−2, γ = 10−2°C m−1 and a = 14 cm year−1 (the low accumulation rate characteristic of the central parts of an ice sheet, where we presume ice trajectories, delivering the surface temperature T H to the bottom, originate), and τH = 50 kyear. For the more weakly constrained parameters, we assign the set of values, τS = τW = 1.5 kyear and α = 10−5 year−2.

Fig. 3. Fig. 3. Schematic feed-bad loop diagram for the present simplified model, showing the internal couplings between the height of the ice sheet (H), basal water depth (W) and surge loss (S) under the influence of steady forcing due to net snow accumulation (a) and geothermal flux (Q g). A wiggly arrow denotes a time-delayed (inertial) influence of changes in one variable on another, in the direction of the arrow.

Fig. 4. Time-dependent solution of the dynamical system, showing in the top panel the fluctuation of the upper surface temperature (T H) and the temperature at z = zb(T b), in the middle panel the pressure-melting point (T M), the basal temperature (T B), the basal-melting rate (M B) as black bars, and in the bottom panel the surge discharge in units of ice thickness loss (5) and ice-sheet thickness H.
The solution is shown in Figure 4 starting from an arbitrary initial condition. We note that an oscillation of roughly a 14 kyear period occurs, characterized by lagged variations of T H, T b, T B, H and S, that go along with episodes of melting (M B > 0) when T B = T M. The results are not qualitatively changed for small changes in the parameters; more extensive calculations will be made to determine the limits of applicability for larger parameter changes and for different accumulation rates.
5. Conclusions
Using a dynamical model based on fundamental thermomechanical properties of an ice sheet, we have shown that such a model can exhibit periodic fluctuations of roughly the same scale as observed Heinrich events, providing the unknown rate constants are assigned certain values. This model embodies in its simplest form the essential physical processes governing the coupled variation of ice volume, mean basal water amount and the surge of ice. The system is influenced mainly by the internal thermodynamic processes in ice sheets and the instability engendered by basal friction beating, as regulated by both cold advection from the upper ice surface and a much weaker influence of geothermal healing. In this respect, the mechanism involved is akin to that in Oerlemans’ (1983) and Payne’s (1995) models but only to the discharge phase of MacAyeal’s (1993) “binge purge” model.
Acknowledgements
This work has been supported by the U.S. National Science Foundation under grants ATM-9222591 (Division of Atmospheric Sciences, Climate Dynamics Program) and OPP-9319674 (Office of Polar Programs, Polar Glaciology Program), and by NASA under grant NAGW-4197 (Polar Research Program) at Yale University.








