1 Introduction
Micrometric particles can adsorb to fluid–fluid interfaces and impart stability to emulsions and foams (Binks Reference Binks2002). The mechanism by which a colloidal particle adsorbs on an interface is a significant decrease in free energy, which can be of the order of
![]() $10^{6}k_{B}T$
, where
$10^{6}k_{B}T$
, where
![]() $k_{B}$
is the Boltzmann constant and
$k_{B}$
is the Boltzmann constant and
![]() $T$
the temperature, in the case of micrometric spheres (Binks & Horozov Reference Binks and Horozov2006). The stability and behaviour of the particle-laden interface strongly depend on the microstructure formed by the adsorbed particles (Fuller & Vermant Reference Fuller and Vermant2012). This microstructure is determined by the interactions between the particles at the interface, which can differ from those in the bulk. Indeed, in addition to the colloidal forces that particles experience in the bulk, particles adsorbed on an interface experience lateral capillary forces due to important interface deformations generated by their presence (Oettel & Dietrich Reference Oettel and Dietrich2008).
$T$
the temperature, in the case of micrometric spheres (Binks & Horozov Reference Binks and Horozov2006). The stability and behaviour of the particle-laden interface strongly depend on the microstructure formed by the adsorbed particles (Fuller & Vermant Reference Fuller and Vermant2012). This microstructure is determined by the interactions between the particles at the interface, which can differ from those in the bulk. Indeed, in addition to the colloidal forces that particles experience in the bulk, particles adsorbed on an interface experience lateral capillary forces due to important interface deformations generated by their presence (Oettel & Dietrich Reference Oettel and Dietrich2008).
The self-assembly of colloidal particles due to capillary forces on planar and curved interfaces has been investigated in quasi-static configurations and in the limit of small deformations (Kralchevsky, Paunov & Nagayama Reference Kralchevsky, Paunov and Nagayama1995; Kralchevsky & Nagayama Reference Kralchevsky and Nagayama2000; Saif Reference Saif2002; Danov & Kralchevsky Reference Danov and Kralchevsky2010; Guzowski, Tasinkevych & Dietrich Reference Guzowski, Tasinkevych and Dietrich2011a ,Reference Guzowski, Tasinkevych and Dietrich b ). At equilibrium, buoyant (or heavy) particles trapped at an interface induce deformations that decay over distances of the order of the capillary length (Chan, Henry & White Reference Chan, Henry and White1981). Such deformations give rise to long-range attractive forces between particles, which drive aggregation of the interfacial suspension (Vassileva et al. Reference Vassileva, van den Ende, Mugele and Mellema2005; Vella, Metcalfe & Whittaker Reference Vella, Metcalfe and Whittaker2006; Bleibel et al. Reference Bleibel, Dietrich, Domínguez and Oettel2011; Lee, Cicuta & Vella Reference Lee, Cicuta and Vella2017). For micrometric particles, the weight of the particle is too small to appreciably deform the interface, but interface deformations can arise due to pinning of the three-phase contact line on surface roughness (Stamou, Duschl & Johannsmann Reference Stamou, Duschl and Johannsmann2000; Sharifi-Mood, Liu & Stebe Reference Sharifi-Mood, Liu and Stebe2015; Zanini et al. Reference Zanini, Marschelke, Anachkov, Marini, Synytska and Isa2017), anisotropic shape of the particles leading to an undulated contact line (Van Nierop, Stijnman & Hilgenfeldt Reference Van Nierop, Stijnman and Hilgenfeldt2005; Botto et al. Reference Botto, Lewandowski, Cavallaro and Stebe2012) or external forces (Vella Reference Vella2015) and torques (Davies et al. Reference Davies, Krüger, Coveney, Harting and Bresme2014). In the limit of small deformations and in the absence of dynamic effects, lateral capillary interactions between adsorbed particles can be represented in terms of interactions between two-dimensional multipole moments (Danov et al. Reference Danov, Kralchevsky, Naydenov and Brenn2005; Danov & Kralchevsky Reference Danov and Kralchevsky2010), in analogy with two-dimensional electrostatics (Domínguez, Oettel & Dietrich Reference Domínguez, Oettel and Dietrich2008). In such an analogy, a particle exerting a net force normal to the interface is represented by a capillary ‘monopole’, a particle exerting a torque in the plane of the interface is represented by a capillary ‘dipole’, while higher-order capillary multipoles describe an undulated three-phase contact line.
In practical situations, particle-laden interfaces are driven out of equilibrium by an external flow (Stancik et al. Reference Stancik, Widenbrant, Laschitsch, Vermant and Fuller2002, Reference Stancik, Gavranovic, Widenbrant, Laschitsch, Vermant and Fuller2003; Lishchuk, Halliday & Care Reference Lishchuk, Halliday and Care2006; Lishchuk Reference Lishchuk2016; Vidal & Botto Reference Vidal and Botto2017), by dynamic external fields (Grzybowski, Stone & Whitesides Reference Grzybowski, Stone and Whitesides2000; Belkin et al. Reference Belkin, Snezhko, Aranson and Kwok2007; Snezhko & Aranson Reference Snezhko and Aranson2011; Wang et al. Reference Wang, Giltinan, Zakharchenko and Sitti2017) or by acoustic waves (Poulichet & Garbin Reference Poulichet and Garbin2015; Poulichet, Huerre & Garbin Reference Poulichet, Huerre and Garbin2017). Recent work on the dynamics of particles adsorbed on an interface focused on the mobility coefficients of a single (Danov et al. Reference Danov, Aust, Durst and Lange1995; Danov, Dimova & Pouligny Reference Danov, Dimova and Pouligny2000; Fischer, Dhar & Heinig Reference Fischer, Dhar and Heinig2006; Pozrikidis Reference Pozrikidis2007; Boniello et al. Reference Boniello, Stocco, Gross, In, Blanc and Nobili2016; Dörr et al. Reference Dörr, Hardt, Masoud and Stone2016; Koplik & Maldarelli Reference Koplik and Maldarelli2017) or a pair of colloidal particles (Dani et al. Reference Dani, Keiser, Yeganeh and Maldarelli2015) that move tangentially to the interface without deforming it.
However, colloidal particles driven by an external force can significantly deform the interface. In such a dynamic situation, much less is known about the interfacial deformation induced by the forced particles, and the resulting lateral capillary interactions. Singh et al. (Reference Singh, Joseph, Gurupatham, Dalal and Nudurupati2009, Reference Singh, Joseph, Fischer and Dalal2011) showed that dynamic effects are significant during adsorption of micrometric particles onto a free surface, leading to large underdamped oscillations about the final equilibrium position. Such oscillations generate nonlinear flows that disperse tracer particles. Dörr & Hardt (Reference Dörr and Hardt2015) considered the problem of spherical colloidal particles moving on a free surface due to an external tangential force and found that they experience a torque in the plane of the interface, thus behaving as capillary dipoles. Dynamic capillary forces are responsible for the lateral drift of spheres floating on Faraday waves (Falkovich et al. Reference Falkovich, Weinberg, Denissenko and Lukaschuk2005; Sanlı, Lohse & van der Meer Reference Sanlı, Lohse and van der Meer2014). Ledesma-Alonso, Tordjeman & Legendre (Reference Ledesma-Alonso, Tordjeman and Legendre2014) and Wdołowski & Napiórkowski (Reference Wdołowski and Napiórkowski2015) studied the dynamic deformation of liquid films induced by van der Waals interactions with a single oscillating nanoparticle, as a model for a vibrating atomic force microscopy tip. They found that the dynamic motion of the nanoparticle can generate capillary waves on the surface of the film. Protière et al. (Reference Protière, Couder, Fort and Boudaoud2005), Protière, Boudaoud & Couder (Reference Protière, Boudaoud and Couder2006) and Moláček & Bush (Reference Moláček and Bush2013) found that the interactions between drops bouncing on an interface and the capillary waves generated during each impact are responsible for a range of drop dynamics such as inter-drop attraction, repulsion and orbiting. Dynamic capillary interactions could be relevant for the self-assembly of colloids on the interface bubbles and drops deformed by unsteady and dynamic stresses (Mulligan & Rothstein Reference Mulligan and Rothstein2011; Poulichet & Garbin Reference Poulichet and Garbin2015; Prabhudesai et al. Reference Prabhudesai, Bihi, Zoueshtiagh, Jose and Baudoin2017).
Despite their relevance, the interface deformations due to dynamic forces at the colloidal scale, and the capillary interactions between dynamically driven particles, have not been investigated as extensively as those occurring in the quasi-static regime. In this paper, we evaluate the far-field deformation of a gas–liquid interface induced by a micrometric adsorbed particle that is dynamically forced in the direction normal to the unperturbed surface, in the limit of small deformations, point-like particle and negligible viscous effects. The case of a planar interface and of a bubble are considered. Finally, we evaluate the lateral capillary forces between two forced particles by linearly superimposing the two deformation fields. In contrast to the quasi-static case, we find that capillary interactions between identically forced particles can be repulsive and can prevent aggregation. The results have general applicability to different particle forcing mechanisms such as electric, magnetic or acoustic fields.

Figure 1. Schematic picture of the problems considered in the present paper: (a) dynamic point force acting on a planar gas–liquid interface, (b) dynamic point force acting on a bubble. The deformation of the free surface (dashed line) and the size of the particle are exaggerated for clarity.
2 Model for dynamic interface deformation and capillary interactions
2.1 Problem formulation
We consider micrometric particles straddling the interface between a liquid phase of viscosity
![]() $\unicode[STIX]{x1D702}$
and density
$\unicode[STIX]{x1D702}$
and density
![]() $\unicode[STIX]{x1D70C}$
, and a gas phase whose density and viscosity are negligible compared to the liquid phase. The surface tension between the liquid and the gas phase is given by
$\unicode[STIX]{x1D70C}$
, and a gas phase whose density and viscosity are negligible compared to the liquid phase. The surface tension between the liquid and the gas phase is given by
![]() $\unicode[STIX]{x1D6FE}$
. We consider two geometries: a planar interface (figure 1
a), and the interface of a bubble with equilibrium radius
$\unicode[STIX]{x1D6FE}$
. We consider two geometries: a planar interface (figure 1
a), and the interface of a bubble with equilibrium radius
![]() $R_{0}$
(figure 1
b). We are interested in the interface deformation caused by particles driven by an external dynamic force
$R_{0}$
(figure 1
b). We are interested in the interface deformation caused by particles driven by an external dynamic force
![]() $F(t)=F_{0}\cos (\unicode[STIX]{x1D714}t)$
, with the angular frequency
$F(t)=F_{0}\cos (\unicode[STIX]{x1D714}t)$
, with the angular frequency
![]() $\unicode[STIX]{x1D714}$
, and the resulting capillary interactions. We consider a particle as a dynamic point force acting on the gas–liquid interface. The external force is applied in a direction normal to the undisturbed the interface, that is, in the
$\unicode[STIX]{x1D714}$
, and the resulting capillary interactions. We consider a particle as a dynamic point force acting on the gas–liquid interface. The external force is applied in a direction normal to the undisturbed the interface, that is, in the
![]() $z$
direction in the case of a planar interface, and in the radial direction in the case of a bubble, as shown schematically in figure 1.
$z$
direction in the case of a planar interface, and in the radial direction in the case of a bubble, as shown schematically in figure 1.
This problem involves multiple length scales: a characteristic particle size
![]() $l_{p}$
, a characteristic inter-particle distance
$l_{p}$
, a characteristic inter-particle distance
![]() $d$
, the thickness of the boundary layer
$d$
, the thickness of the boundary layer
![]() $\unicode[STIX]{x1D6FF}=\sqrt{\unicode[STIX]{x1D702}/(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714})}$
, the wavelength
$\unicode[STIX]{x1D6FF}=\sqrt{\unicode[STIX]{x1D702}/(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714})}$
, the wavelength
![]() $\unicode[STIX]{x1D706}=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}^{1/3}/(\unicode[STIX]{x1D714}^{2/3}\unicode[STIX]{x1D70C}^{1/3})$
of capillary waves, the bubble radius
$\unicode[STIX]{x1D706}=2\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}^{1/3}/(\unicode[STIX]{x1D714}^{2/3}\unicode[STIX]{x1D70C}^{1/3})$
of capillary waves, the bubble radius
![]() $R_{0}$
and a characteristic deformation of the interface
$R_{0}$
and a characteristic deformation of the interface
![]() $F_{0}/\unicode[STIX]{x1D6FE}$
. In the case of colloidal systems, typical particle separations and bubble radii are much smaller than the capillary length,
$F_{0}/\unicode[STIX]{x1D6FE}$
. In the case of colloidal systems, typical particle separations and bubble radii are much smaller than the capillary length,
![]() $\sqrt{\unicode[STIX]{x1D6FE}/(\unicode[STIX]{x1D70C}g)}$
, hence we neglect the effects of the gravitational acceleration
$\sqrt{\unicode[STIX]{x1D6FE}/(\unicode[STIX]{x1D70C}g)}$
, hence we neglect the effects of the gravitational acceleration
![]() $g$
. The motion of macroscopic bodies on gas–liquid interfaces, for which gravity effects are important, has been studied by Raphaël & De Gennes (Reference Raphaël and De Gennes1996), Chepelianskii, Chevy & Raphaël (Reference Chepelianskii, Chevy and Raphaël2008) and Le Merrer et al. (Reference Le Merrer, Clanet, Quéré, Raphaël and Chevy2011), while the case of negligible surface tension has been studied by Ursell (Reference Ursell1953, Reference Ursell1954), Davis (Reference Davis1976, Reference Davis1977) and Hulme (Reference Hulme1982).
$g$
. The motion of macroscopic bodies on gas–liquid interfaces, for which gravity effects are important, has been studied by Raphaël & De Gennes (Reference Raphaël and De Gennes1996), Chepelianskii, Chevy & Raphaël (Reference Chepelianskii, Chevy and Raphaël2008) and Le Merrer et al. (Reference Le Merrer, Clanet, Quéré, Raphaël and Chevy2011), while the case of negligible surface tension has been studied by Ursell (Reference Ursell1953, Reference Ursell1954), Davis (Reference Davis1976, Reference Davis1977) and Hulme (Reference Hulme1982).
In this paper, we consider the case of micrometric particles whose separation distance is comparable to the capillary wavelength and to the bubble radius,
![]() $d\approx R_{0}\approx \unicode[STIX]{x1D706}$
, while their size
$d\approx R_{0}\approx \unicode[STIX]{x1D706}$
, while their size
![]() $l_{p}$
, the thickness of the boundary layer
$l_{p}$
, the thickness of the boundary layer
![]() $\unicode[STIX]{x1D6FF}$
and the characteristic interface deformation
$\unicode[STIX]{x1D6FF}$
and the characteristic interface deformation
![]() $F_{0}/\unicode[STIX]{x1D6FE}$
, are much smaller. The relevant length scale in our problem is then given by the wavelength,
$F_{0}/\unicode[STIX]{x1D6FE}$
, are much smaller. The relevant length scale in our problem is then given by the wavelength,
![]() $\unicode[STIX]{x1D706}$
. Thus, we base the non-dimensional numbers on this characteristic length.
$\unicode[STIX]{x1D706}$
. Thus, we base the non-dimensional numbers on this characteristic length.
As viscous dissipation only takes place within the boundary layer, the assumption that
![]() $\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D706}$
implies that inertial effects dominate over viscous dissipation and the Reynolds number is large
$\unicode[STIX]{x1D6FF}\ll \unicode[STIX]{x1D706}$
implies that inertial effects dominate over viscous dissipation and the Reynolds number is large
![]() $Re=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x1D702}=\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x1D6FF}^{2}\gg 1$
. This assumption is satisfied for angular frequencies
$Re=\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x1D702}=\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x1D6FF}^{2}\gg 1$
. This assumption is satisfied for angular frequencies
![]() $\unicode[STIX]{x1D714}$
up to
$\unicode[STIX]{x1D714}$
up to
![]() $10^{6}~\text{rad}~\text{s}^{-1}$
, in the case of water–air interfaces. In the same conditions viscous forces are much smaller than surface tension ones, and the capillary number is negligible
$10^{6}~\text{rad}~\text{s}^{-1}$
, in the case of water–air interfaces. In the same conditions viscous forces are much smaller than surface tension ones, and the capillary number is negligible
![]() $Ca=\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D6FE}=Re^{-1}\ll 1$
. Since viscous forces are negligible compared to inertial and surface tension ones,
$Ca=\unicode[STIX]{x1D702}\unicode[STIX]{x1D714}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D6FE}=Re^{-1}\ll 1$
. Since viscous forces are negligible compared to inertial and surface tension ones,
![]() $Re\gg 1$
and
$Re\gg 1$
and
![]() $Ca\ll 1$
, we neglect viscosity in the fluid phase. The assumption
$Ca\ll 1$
, we neglect viscosity in the fluid phase. The assumption
![]() $l_{p}\ll \unicode[STIX]{x1D706}$
is satisfied in the case of micrometre-sized particles adsorbed on water–air interfaces, for
$l_{p}\ll \unicode[STIX]{x1D706}$
is satisfied in the case of micrometre-sized particles adsorbed on water–air interfaces, for
![]() $\unicode[STIX]{x1D714}$
up to
$\unicode[STIX]{x1D714}$
up to
![]() $10^{6}~\text{rad}~\text{s}^{-1}$
.
$10^{6}~\text{rad}~\text{s}^{-1}$
.
Finally, we remark that forces
![]() $F_{0}$
larger than 1 nN are rarely exceeded at the colloidal scale even with strong external fields (Ashkin Reference Ashkin1980; Baresch, Thomas & Marchiano Reference Baresch, Thomas and Marchiano2016). It follows that the characteristic deformation of the interface,
$F_{0}$
larger than 1 nN are rarely exceeded at the colloidal scale even with strong external fields (Ashkin Reference Ashkin1980; Baresch, Thomas & Marchiano Reference Baresch, Thomas and Marchiano2016). It follows that the characteristic deformation of the interface,
![]() $F_{0}/\unicode[STIX]{x1D6FE}$
, is typically small compared to both the capillary wavelength
$F_{0}/\unicode[STIX]{x1D6FE}$
, is typically small compared to both the capillary wavelength
![]() $\unicode[STIX]{x1D706}$
, and the micrometric particle size
$\unicode[STIX]{x1D706}$
, and the micrometric particle size
![]() $l_{p}$
. In the small deformation limit,
$l_{p}$
. In the small deformation limit,
![]() $F_{0}/\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D706}\ll 1$
and
$F_{0}/\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D706}\ll 1$
and
![]() $F_{0}/\unicode[STIX]{x1D6FE}l_{p}\ll 1$
, we can linearise the balance equations around the equilibrium state. Under this hypothesis, the surface deformations induced by multiple particles are obtained by superimposing the deformation independently caused by each particle.
$F_{0}/\unicode[STIX]{x1D6FE}l_{p}\ll 1$
, we can linearise the balance equations around the equilibrium state. Under this hypothesis, the surface deformations induced by multiple particles are obtained by superimposing the deformation independently caused by each particle.
In summary, our analysis is concerned with the far-field interface deformations induced by dynamically driven particles and the resulting far-field lateral capillary interactions. In the far-field limit the details of the shape of the particle and its contact angle have no effect. Likewise, the details of the flow field in the proximity of the particles have no effect over the length scale
![]() $\unicode[STIX]{x1D706}$
. However, our analysis is not applicable at distances from the particles that are much smaller than the capillary wavelength, where our assumptions of an inviscid fluid and a point particle break down. Addressing the near-field deformation of the interface and the near-field capillary interactions requires a separate numerical investigation.
$\unicode[STIX]{x1D706}$
. However, our analysis is not applicable at distances from the particles that are much smaller than the capillary wavelength, where our assumptions of an inviscid fluid and a point particle break down. Addressing the near-field deformation of the interface and the near-field capillary interactions requires a separate numerical investigation.
In §§ 2.2 and 2.3 we summarise the equations and the boundary conditions governing the hydrodynamic problem of a single time-dependent point force acting on a gas–liquid interface. In § 2.4, we make use of the assumption of small deformations to derive an expression for the lateral capillary force acting between two dynamically driven point forces.
2.2 Equations for the velocity and pressure fields
Under the hypothesis of linearity, the convective term in the momentum balance can be neglected, hence the velocity
![]() $\boldsymbol{v}$
and pressure
$\boldsymbol{v}$
and pressure
![]() $p$
disturbances induced by a single driven particle in the liquid phase are given by:
$p$
disturbances induced by a single driven particle in the liquid phase are given by:
The effects of viscosity in (2.2) have been neglected, as discussed in § 2.1. In the inviscid limit the velocity field can be expressed as the gradient of a scalar potential function,
![]() $\boldsymbol{v}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
, and the above equations can be rewritten in terms of the velocity potential
$\boldsymbol{v}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
, and the above equations can be rewritten in terms of the velocity potential
![]() $\unicode[STIX]{x1D719}$
:
$\unicode[STIX]{x1D719}$
:
2.3 Boundary conditions and effects of particle forcing
The equations reported in § 2.2 are valid for both geometries considered in this work. The difference between the case of a planar interface and the case of a bubble is represented by the boundary conditions, which are reported in detail in the next two subsections. Since we neglected the effects of viscosity, it is not necessary to consider a tangential stress balance on the interface as it is automatically satisfied in the inviscid limit. Within the linear approximation, the boundary conditions on the free surface only involve quantities and differential operators evaluated on the undeformed interface, that is to say, at
![]() $z=0$
in the case of a planar interface and at
$z=0$
in the case of a planar interface and at
![]() $r=R_{0}$
in the case of a bubble.
$r=R_{0}$
in the case of a bubble.
2.3.1 Boundary conditions for a planar interface
In the case of a point force acting on a planar interface, we adopt a Cartesian reference frame with origin on the undeformed surface
![]() $z=0$
(see figure 1
a) and we define
$z=0$
(see figure 1
a) and we define
![]() $u(x,y,t)$
the deformation field of the interface. Due to the translational invariance of the problem, we consider the point force acting at the origin. The normal stress balance on the free surface is thus given by:
$u(x,y,t)$
the deformation field of the interface. Due to the translational invariance of the problem, we consider the point force acting at the origin. The normal stress balance on the free surface is thus given by:
where
![]() $\unicode[STIX]{x1D6FB}_{\Vert }^{2}$
is the Laplacian operator on the undeformed interface,
$\unicode[STIX]{x1D6FB}_{\Vert }^{2}$
is the Laplacian operator on the undeformed interface,
![]() $\unicode[STIX]{x1D6FB}_{\Vert }^{2}=(\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}x^{2})+(\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}y^{2})$
. The pressure in the gas above the free surface is assumed to be zero. The effect of the forced particle is represented by a time-dependent point force of amplitude
$\unicode[STIX]{x1D6FB}_{\Vert }^{2}=(\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}x^{2})+(\unicode[STIX]{x2202}^{2}/\unicode[STIX]{x2202}y^{2})$
. The pressure in the gas above the free surface is assumed to be zero. The effect of the forced particle is represented by a time-dependent point force of amplitude
![]() $F_{0}\cos (\unicode[STIX]{x1D714}t)$
in (2.5) (Havelock Reference Havelock1919; Morse & Witten Reference Morse and Witten1993; Raphaël & De Gennes Reference Raphaël and De Gennes1996; Guzowski et al.
Reference Guzowski, Tasinkevych and Dietrich2011a
,Reference Guzowski, Tasinkevych and Dietrich
b
).
$F_{0}\cos (\unicode[STIX]{x1D714}t)$
in (2.5) (Havelock Reference Havelock1919; Morse & Witten Reference Morse and Witten1993; Raphaël & De Gennes Reference Raphaël and De Gennes1996; Guzowski et al.
Reference Guzowski, Tasinkevych and Dietrich2011a
,Reference Guzowski, Tasinkevych and Dietrich
b
).
In the linear regime the kinematic boundary condition at the free surface is given by:
Finally, at infinity the fluid is quiescent:
2.3.2 Boundary conditions for a bubble
We consider a point force acting on the north pole (see figure 1
b) of a bubble of equilibrium radius
![]() $R_{0}$
, and we define
$R_{0}$
, and we define
![]() $u(\unicode[STIX]{x1D703},t)$
to be the axisymmetric deformation field of the interface. The normal stress balance at the bubble surface reads (Landau & Lifshits Reference Landau and Lifshits1999):
$u(\unicode[STIX]{x1D703},t)$
to be the axisymmetric deformation field of the interface. The normal stress balance at the bubble surface reads (Landau & Lifshits Reference Landau and Lifshits1999):
where the Laplacian operator on the undeformed interface of a sphere takes the form
![]() $\unicode[STIX]{x1D6FB}_{\Vert }^{2}=(1/R_{0}^{2}\sin \unicode[STIX]{x1D703})(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})(\sin \unicode[STIX]{x1D703}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}))$
, and the effect of the forced particle is represented by the last term in (2.8).
$\unicode[STIX]{x1D6FB}_{\Vert }^{2}=(1/R_{0}^{2}\sin \unicode[STIX]{x1D703})(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})(\sin \unicode[STIX]{x1D703}(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}))$
, and the effect of the forced particle is represented by the last term in (2.8).
Compared to the case of a planar interface, the normal stress balance for the spherical surface includes an additional term proportional to the pressure inside the bubble
![]() $p_{gas}$
, for which a compression law has to be specified. We assume an isothermal compression law, however a polytropic exponent different from one does not change qualitatively our results. Hence, we consider that
$p_{gas}$
, for which a compression law has to be specified. We assume an isothermal compression law, however a polytropic exponent different from one does not change qualitatively our results. Hence, we consider that
![]() $p_{gas}$
is given by:
$p_{gas}$
is given by:
with
![]() $V$
the volume of the deformed bubble at a time
$V$
the volume of the deformed bubble at a time
![]() $t$
. The constant
$t$
. The constant
![]() $p_{gas,0}$
is the gas pressure within the bubble at equilibrium and it is given by the Laplace pressure for a spherical bubble
$p_{gas,0}$
is the gas pressure within the bubble at equilibrium and it is given by the Laplace pressure for a spherical bubble
![]() $p_{gas,0}=p_{0}+(2\unicode[STIX]{x1D6FE}/R_{0})$
, with
$p_{gas,0}=p_{0}+(2\unicode[STIX]{x1D6FE}/R_{0})$
, with
![]() $p_{0}$
the equilibrium pressure in the liquid. The kinematic condition on the bubble surface is given by:
$p_{0}$
the equilibrium pressure in the liquid. The kinematic condition on the bubble surface is given by:
Finally, far from the bubble the fluid is quiescent:
In contrast to the case of a planar interface, the centre of mass of the bubble is displaced by the point force. It follows that not only the interface deformation, but also the bubble displacement is required to be small for the assumption of linearity to be valid. The condition of small interface deformation and bubble displacement implies that
![]() $(F_{0}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D6FE}R_{0}^{2})\ll 1$
. Since in § 2.1 we have already assumed small deformations of the interface,
$(F_{0}\unicode[STIX]{x1D706}/\unicode[STIX]{x1D6FE}R_{0}^{2})\ll 1$
. Since in § 2.1 we have already assumed small deformations of the interface,
![]() $F_{0}/\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D706}\ll 1$
, it follows that the capillary wavelength
$F_{0}/\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D706}\ll 1$
, it follows that the capillary wavelength
![]() $\unicode[STIX]{x1D706}$
has to be, at most, comparable to the bubble radius
$\unicode[STIX]{x1D706}$
has to be, at most, comparable to the bubble radius
![]() $R_{0}$
, that is
$R_{0}$
, that is
![]() $\unicode[STIX]{x1D706}^{2}/R_{0}^{2}\approx (\unicode[STIX]{x1D6FE}^{2/3})/(\unicode[STIX]{x1D70C}^{2/3}\unicode[STIX]{x1D714}^{4/3}R_{0}^{2})$
is at most
$\unicode[STIX]{x1D706}^{2}/R_{0}^{2}\approx (\unicode[STIX]{x1D6FE}^{2/3})/(\unicode[STIX]{x1D70C}^{2/3}\unicode[STIX]{x1D714}^{4/3}R_{0}^{2})$
is at most
![]() $\mathit{O}(1)$
. This condition suggests that it is not possible to fulfil the condition of small interface deformation and bubble displacements, as the forcing frequency goes to zero, because a steady point force would displace the centre of mass of the bubble indefinitely far from its equilibrium position.
$\mathit{O}(1)$
. This condition suggests that it is not possible to fulfil the condition of small interface deformation and bubble displacements, as the forcing frequency goes to zero, because a steady point force would displace the centre of mass of the bubble indefinitely far from its equilibrium position.
2.4 Capillary interactions between dynamic point forces
When the interface deformation fields induced by multiple particles overlap, the particles experience a lateral capillary force (Kralchevsky & Nagayama Reference Kralchevsky and Nagayama2000). In the case of deformations generated by multiple steady forces (e.g. heavy particles) an attractive lateral capillary force arises, causing aggregation of the particles. In this section we extend our study to consider the far-field capillary interactions between two particles.
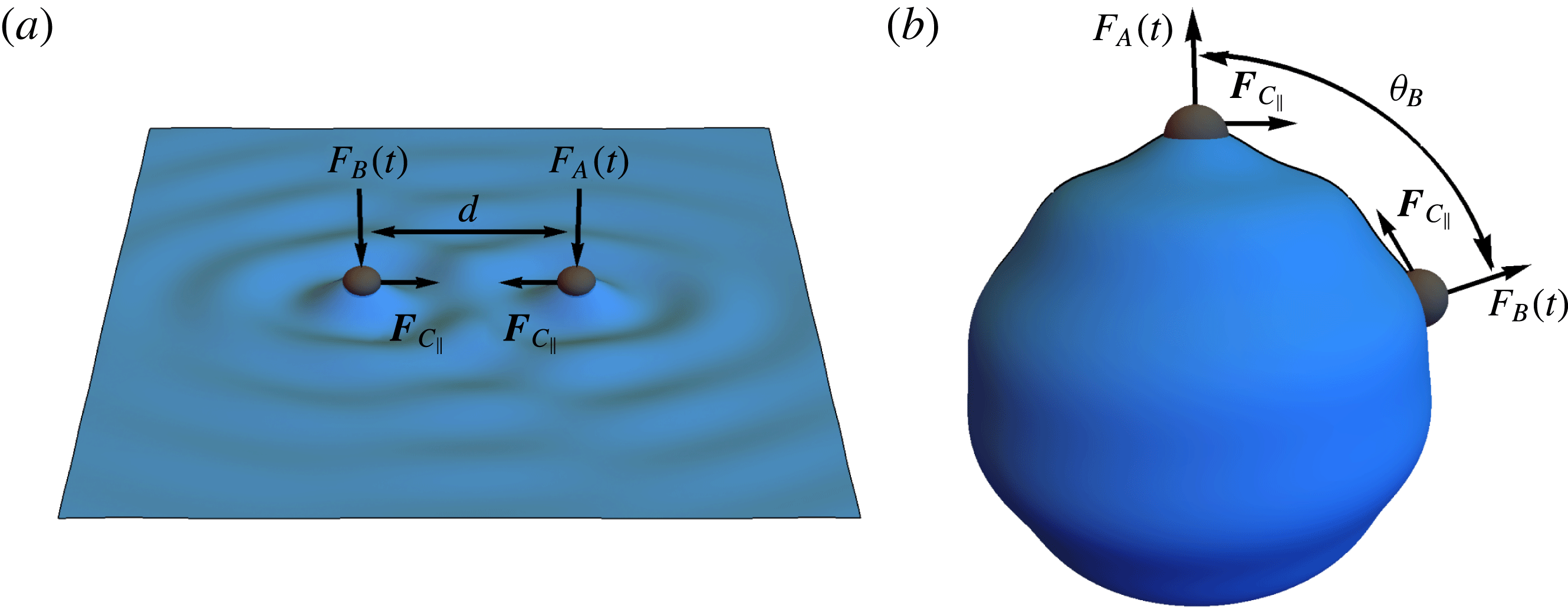
Figure 2. Schematic picture of two dynamically driven particles,
![]() $A$
and
$A$
and
![]() $B$
, adsorbed on: (a) a planar interface, (b) surface of a bubble. The particles interact through lateral capillary forces
$B$
, adsorbed on: (a) a planar interface, (b) surface of a bubble. The particles interact through lateral capillary forces
![]() $\boldsymbol{F}_{C_{\Vert }}$
that are tangent to the undeformed interface. The size of the particles and of the interface deformation is exaggerated for clarity.
$\boldsymbol{F}_{C_{\Vert }}$
that are tangent to the undeformed interface. The size of the particles and of the interface deformation is exaggerated for clarity.
We seek an equation for the lateral capillary force
![]() $\boldsymbol{F}_{C_{\Vert }}$
acting between two point-like particles driven by a dynamic force on a planar interface or a bubble, as reported schematically in figure 2. For simplicity, we consider that both particles exert the same total force
$\boldsymbol{F}_{C_{\Vert }}$
acting between two point-like particles driven by a dynamic force on a planar interface or a bubble, as reported schematically in figure 2. For simplicity, we consider that both particles exert the same total force
![]() $F_{A}(t)=F_{B}(t)=F_{0}\cos (\unicode[STIX]{x1D714}t)$
in the direction normal to the undisturbed interface, which corresponds to the case of particles driven by the same external field. For the case of a planar interface we consider particle
$F_{A}(t)=F_{B}(t)=F_{0}\cos (\unicode[STIX]{x1D714}t)$
in the direction normal to the undisturbed interface, which corresponds to the case of particles driven by the same external field. For the case of a planar interface we consider particle
![]() $A$
and particle
$A$
and particle
![]() $B$
separated by a distance
$B$
separated by a distance
![]() $d$
. The angular separation between the two point forces on a bubble is given by
$d$
. The angular separation between the two point forces on a bubble is given by
![]() $\unicode[STIX]{x1D703}_{B}$
. Without loss of generality we assume particle
$\unicode[STIX]{x1D703}_{B}$
. Without loss of generality we assume particle
![]() $A$
is positioned at the origin in the planar case, and at the north pole in the case of the bubble.
$A$
is positioned at the origin in the planar case, and at the north pole in the case of the bubble.
If only particle
![]() $A$
is driven by the external force, the deformation of the interface is axisymmetric and the capillary force on the particle has no lateral component. However, if particle
$A$
is driven by the external force, the deformation of the interface is axisymmetric and the capillary force on the particle has no lateral component. However, if particle
![]() $B$
produces a distortion of the interface at the position where particle
$B$
produces a distortion of the interface at the position where particle
![]() $A$
is located, the axial symmetry is broken and particle
$A$
is located, the axial symmetry is broken and particle
![]() $A$
experiences a lateral capillary force. By superimposing the distortion of the interface induced by the two particles, it can be shown that the capillary force on particle
$A$
experiences a lateral capillary force. By superimposing the distortion of the interface induced by the two particles, it can be shown that the capillary force on particle
![]() $A$
has a lateral component,
$A$
has a lateral component,
![]() $\boldsymbol{F}_{C_{\Vert }}$
, that is proportional to the gradient of the surface distortion generated by particle
$\boldsymbol{F}_{C_{\Vert }}$
, that is proportional to the gradient of the surface distortion generated by particle
![]() $B$
,
$B$
,
![]() $\unicode[STIX]{x1D735}_{\Vert }u_{B}$
(Domínguez et al.
Reference Domínguez, Oettel and Dietrich2008). In the case of a planar interface
$\unicode[STIX]{x1D735}_{\Vert }u_{B}$
(Domínguez et al.
Reference Domínguez, Oettel and Dietrich2008). In the case of a planar interface
![]() $\boldsymbol{F}_{C_{\Vert }}$
is given by:
$\boldsymbol{F}_{C_{\Vert }}$
is given by:
In the case of a bubble it is given by:
The lateral capillary force
![]() $\boldsymbol{F}_{C_{\Vert }}$
between dynamically forced particles can be computed through (2.12)–(2.13), in which the only unknown is the gradient of the interface deformation induced by particle
$\boldsymbol{F}_{C_{\Vert }}$
between dynamically forced particles can be computed through (2.12)–(2.13), in which the only unknown is the gradient of the interface deformation induced by particle
![]() $B$
, evaluated at the position of particle
$B$
, evaluated at the position of particle
![]() $A$
. Interestingly, the lateral capillary force, given by (2.12), between particles adsorbed on a planar interface is the same as that acting between drops bouncing on a liquid bath, in the limit of short drop–interface contact times (Moláček & Bush Reference Moláček and Bush2013). Hence, some similarity between the two systems can be expected.
$A$
. Interestingly, the lateral capillary force, given by (2.12), between particles adsorbed on a planar interface is the same as that acting between drops bouncing on a liquid bath, in the limit of short drop–interface contact times (Moláček & Bush Reference Moláček and Bush2013). Hence, some similarity between the two systems can be expected.
3 Dynamic deformation of a planar interface
We solve (2.3)–(2.4), for the case of a planar interface. Given the time periodic nature of the forcing it is natural to express the time dependence of all the fields as a Fourier series,
with the unknowns being the modes
![]() $\unicode[STIX]{x1D719}_{n}$
,
$\unicode[STIX]{x1D719}_{n}$
,
![]() $p_{n}$
and
$p_{n}$
and
![]() $u_{n}$
. Due to the linearity of the problem, no mode coupling occurs. Furthermore, as the forcing is represented simply by a cosine, all the modes
$u_{n}$
. Due to the linearity of the problem, no mode coupling occurs. Furthermore, as the forcing is represented simply by a cosine, all the modes
![]() $n$
other than 1 or
$n$
other than 1 or
![]() $-1$
are identically zero, and the modes 1 and
$-1$
are identically zero, and the modes 1 and
![]() $-1$
of all the fields are complex conjugates
$-1$
of all the fields are complex conjugates
![]() $\unicode[STIX]{x1D719}_{1}=\overline{\unicode[STIX]{x1D719}}_{-1}$
,
$\unicode[STIX]{x1D719}_{1}=\overline{\unicode[STIX]{x1D719}}_{-1}$
,
![]() $p_{1}=\overline{p}_{-1}$
and
$p_{1}=\overline{p}_{-1}$
and
![]() $u_{1}=\overline{u}_{-1}$
. It is thus clear that the specification of the modes
$u_{1}=\overline{u}_{-1}$
. It is thus clear that the specification of the modes
![]() $\unicode[STIX]{x1D719}_{1}$
,
$\unicode[STIX]{x1D719}_{1}$
,
![]() $p_{1}$
and
$p_{1}$
and
![]() $u_{1}$
completely determines the solution.
$u_{1}$
completely determines the solution.
We further define the two-dimensional Fourier transform in the
![]() $x$
–
$x$
–
![]() $y$
plane of the fields
$y$
plane of the fields
![]() $\unicode[STIX]{x1D719}_{1}(x,y,z)$
,
$\unicode[STIX]{x1D719}_{1}(x,y,z)$
,
![]() $u_{1}(x,y,z)$
,
$u_{1}(x,y,z)$
,
![]() $p_{1}(x,y,z)$
and of the Dirac delta distribution
$p_{1}(x,y,z)$
and of the Dirac delta distribution
![]() $\unicode[STIX]{x1D6FF}(x)\unicode[STIX]{x1D6FF}(y)$
, as:
$\unicode[STIX]{x1D6FF}(x)\unicode[STIX]{x1D6FF}(y)$
, as:
with
![]() $\boldsymbol{k}=(k_{x},k_{y})$
and
$\boldsymbol{k}=(k_{x},k_{y})$
and
![]() $\boldsymbol{x}=(x,y)$
. Substituting the Fourier series given by (3.1) and the Fourier transform given by (3.4) in (2.3) we obtain:
$\boldsymbol{x}=(x,y)$
. Substituting the Fourier series given by (3.1) and the Fourier transform given by (3.4) in (2.3) we obtain:
where
![]() $k^{2}=\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{k}$
. The only solution compatible with the quiescent condition at
$k^{2}=\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{k}$
. The only solution compatible with the quiescent condition at
![]() $z\rightarrow -\infty$
is:
$z\rightarrow -\infty$
is:
The function
![]() $\hat{q}_{1}(k_{x},k_{y})$
is determined using the normal stress boundary condition. By substituting (2.4) into (2.5) and taking the time derivative we obtain:
$\hat{q}_{1}(k_{x},k_{y})$
is determined using the normal stress boundary condition. By substituting (2.4) into (2.5) and taking the time derivative we obtain:
Substituting the kinematic condition equation (2.6), we obtain:
By inserting the Fourier series given by (3.1) and the Fourier transforms given by (3.4)–(3.7) into (3.11), we obtain:
Further replacing
![]() $\hat{\unicode[STIX]{x1D719}}_{1}$
as obtained from (3.9):
$\hat{\unicode[STIX]{x1D719}}_{1}$
as obtained from (3.9):
The solution is trivially:
The first Fourier mode of the interface deformation is obtained considering the kinematic condition:
To obtain the interfacial deformation field
![]() $u_{1}$
in real space we evaluate the integral in (3.6) with
$u_{1}$
in real space we evaluate the integral in (3.6) with
![]() $\hat{u} _{1}$
given by (3.15). The details are reported in appendix A. The solution reads:
$\hat{u} _{1}$
given by (3.15). The details are reported in appendix A. The solution reads:
 $$\begin{eqnarray}\displaystyle u_{1}(r) & = & \displaystyle \frac{-F_{0}}{24\unicode[STIX]{x1D6FE}} [\!H_{0}((-a)^{1/3}r)+H_{0}(\overline{(-a)^{1/3}}r)-H_{0}(a^{1/3}r)-Y_{0}((-a)^{1/3}r)\nonumber\\ \displaystyle & & \displaystyle -\,Y_{0}(\overline{(-a)^{1/3}}r)-Y_{0}((a^{1/3}r))\!],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{1}(r) & = & \displaystyle \frac{-F_{0}}{24\unicode[STIX]{x1D6FE}} [\!H_{0}((-a)^{1/3}r)+H_{0}(\overline{(-a)^{1/3}}r)-H_{0}(a^{1/3}r)-Y_{0}((-a)^{1/3}r)\nonumber\\ \displaystyle & & \displaystyle -\,Y_{0}(\overline{(-a)^{1/3}}r)-Y_{0}((a^{1/3}r))\!],\end{eqnarray}$$
with
![]() $a=(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}^{2}/\unicode[STIX]{x1D6FE})$
and the overbar denotes the complex conjugate. The dynamic deformation of the interface is finally given by:
$a=(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}^{2}/\unicode[STIX]{x1D6FE})$
and the overbar denotes the complex conjugate. The dynamic deformation of the interface is finally given by:
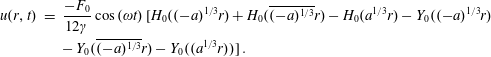 $$\begin{eqnarray}\displaystyle u(r,t) & = & \displaystyle \frac{-F_{0}}{12\unicode[STIX]{x1D6FE}}\cos (\unicode[STIX]{x1D714}t)[\!H_{0}((-a)^{1/3}r)+H_{0}(\overline{(-a)^{1/3}}r)-H_{0}(a^{1/3}r)-Y_{0}((-a)^{1/3}r)\nonumber\\ \displaystyle & & \displaystyle -\,Y_{0}(\overline{(-a)^{1/3}}r)-Y_{0}((a^{1/3}r))\!].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u(r,t) & = & \displaystyle \frac{-F_{0}}{12\unicode[STIX]{x1D6FE}}\cos (\unicode[STIX]{x1D714}t)[\!H_{0}((-a)^{1/3}r)+H_{0}(\overline{(-a)^{1/3}}r)-H_{0}(a^{1/3}r)-Y_{0}((-a)^{1/3}r)\nonumber\\ \displaystyle & & \displaystyle -\,Y_{0}(\overline{(-a)^{1/3}}r)-Y_{0}((a^{1/3}r))\!].\end{eqnarray}$$
The pressure field is given by:
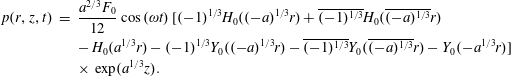 $$\begin{eqnarray}\displaystyle p(r,z,t) & = & \displaystyle \frac{a^{2/3}F_{0}}{12}\cos (\unicode[STIX]{x1D714}t)[(-1)^{1/3}H_{0}((-a)^{1/3}r)+\overline{(-1)^{1/3}}H_{0}(\overline{(-a)^{1/3}}r)\nonumber\\ \displaystyle & & \displaystyle -\,H_{0}(a^{1/3}r)-(-1)^{1/3}Y_{0}((-a)^{1/3}r)-\overline{(-1)^{1/3}}Y_{0}(\overline{(-a)^{1/3}}r)-Y_{0}(-a^{1/3}r)\!]\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (a^{1/3}z).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle p(r,z,t) & = & \displaystyle \frac{a^{2/3}F_{0}}{12}\cos (\unicode[STIX]{x1D714}t)[(-1)^{1/3}H_{0}((-a)^{1/3}r)+\overline{(-1)^{1/3}}H_{0}(\overline{(-a)^{1/3}}r)\nonumber\\ \displaystyle & & \displaystyle -\,H_{0}(a^{1/3}r)-(-1)^{1/3}Y_{0}((-a)^{1/3}r)-\overline{(-1)^{1/3}}Y_{0}(\overline{(-a)^{1/3}}r)-Y_{0}(-a^{1/3}r)\!]\nonumber\\ \displaystyle & & \displaystyle \times \,\exp (a^{1/3}z).\end{eqnarray}$$
In (3.16)–(3.18)
![]() $H_{0}$
is the zeroth-order Struve function (Abramowitz & Stegun Reference Abramowitz and Stegun1964), and
$H_{0}$
is the zeroth-order Struve function (Abramowitz & Stegun Reference Abramowitz and Stegun1964), and
![]() $Y_{0}$
is the zeroth-order Bessel function of the second kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964). The argument
$Y_{0}$
is the zeroth-order Bessel function of the second kind (Abramowitz & Stegun Reference Abramowitz and Stegun1964). The argument
![]() $r$
is the radial distance from the origin
$r$
is the radial distance from the origin
![]() $r=\sqrt{x^{2}+y^{2}}$
.
$r=\sqrt{x^{2}+y^{2}}$
.
The dynamic deformation field generated by the point force, given by (3.17), is a standing capillary wave whose wavenumber is given by
![]() $a^{1/3}=(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}^{2}/\unicode[STIX]{x1D6FE})^{1/3}$
. As expected, the deformation of the interface has a characteristic wavenumber that fulfils the dispersion relation for capillary waves at the free surface of an inviscid fluid (Landau & Lifshits Reference Landau and Lifshits1999). We remark that the solution equation (3.17) for a periodic point force can be used to evaluate the interface deformation caused by more complex dynamic distributions of pressure. Specifically, the interface deformation induced by dynamic pressure dipoles, quadrupoles or higher-order multipoles is easily obtained by taking gradients of (3.17).
$a^{1/3}=(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}^{2}/\unicode[STIX]{x1D6FE})^{1/3}$
. As expected, the deformation of the interface has a characteristic wavenumber that fulfils the dispersion relation for capillary waves at the free surface of an inviscid fluid (Landau & Lifshits Reference Landau and Lifshits1999). We remark that the solution equation (3.17) for a periodic point force can be used to evaluate the interface deformation caused by more complex dynamic distributions of pressure. Specifically, the interface deformation induced by dynamic pressure dipoles, quadrupoles or higher-order multipoles is easily obtained by taking gradients of (3.17).
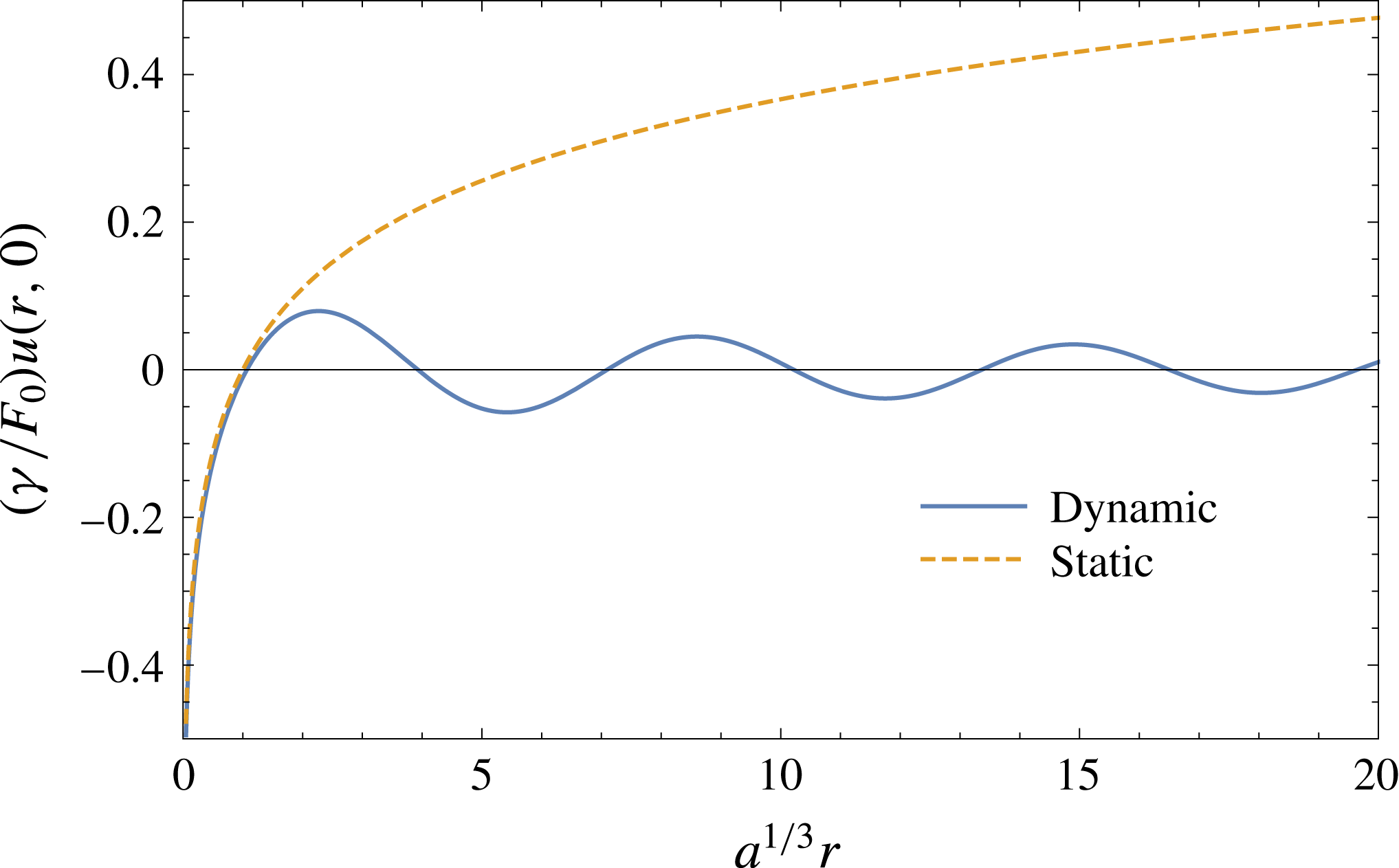
Figure 3. Deformation of the planar interface induced by a dynamic point force, equation (3.17), at time
![]() $t=0$
(solid line), and by a static point force (dashed line). Note that the static deformation (dashed line), given by
$t=0$
(solid line), and by a static point force (dashed line). Note that the static deformation (dashed line), given by
![]() $\unicode[STIX]{x1D6FE}/F_{0}u(r)=(1/2\unicode[STIX]{x03C0})\ln (r)$
, is plotted as a function of
$\unicode[STIX]{x1D6FE}/F_{0}u(r)=(1/2\unicode[STIX]{x03C0})\ln (r)$
, is plotted as a function of
![]() $r$
as it does not depend on the wavenumber.
$r$
as it does not depend on the wavenumber.
It is useful to inspect the asymptotic behaviour of the interface deformation field given by (3.17) as
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
. In this limit, the leading-order correction to the interface deformation given by (3.17) results in a logarithmic dependence
$\unicode[STIX]{x1D714}\rightarrow 0$
. In this limit, the leading-order correction to the interface deformation given by (3.17) results in a logarithmic dependence
![]() $u(r)\propto \text{ln}(r)$
. This behaviour is explained by considering the normal stress balance in (2.5) in absence of bulk dynamic effects (i.e.
$u(r)\propto \text{ln}(r)$
. This behaviour is explained by considering the normal stress balance in (2.5) in absence of bulk dynamic effects (i.e.
![]() $p=0$
). In this limit, equation (2.5) reduces to a two-dimensional Laplace equation with a point force, whose solution is well known (Prosperetti Reference Prosperetti2011) to be
$p=0$
). In this limit, equation (2.5) reduces to a two-dimensional Laplace equation with a point force, whose solution is well known (Prosperetti Reference Prosperetti2011) to be
![]() $u(r)=(F_{0}/2\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE})\ln (r)$
. Such asymptotic behaviour of the free surface deformation is identical to that obtained for a heavy particle adsorbed on a planar interface, at distances much smaller than the capillary length (Chan et al.
Reference Chan, Henry and White1981; Domínguez et al.
Reference Domínguez, Oettel and Dietrich2008). Hence, in the limit
$u(r)=(F_{0}/2\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE})\ln (r)$
. Such asymptotic behaviour of the free surface deformation is identical to that obtained for a heavy particle adsorbed on a planar interface, at distances much smaller than the capillary length (Chan et al.
Reference Chan, Henry and White1981; Domínguez et al.
Reference Domínguez, Oettel and Dietrich2008). Hence, in the limit
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
the dynamic solution given by (3.17) recovers the interface deformation induced by a static point force, as expected.
$\unicode[STIX]{x1D714}\rightarrow 0$
the dynamic solution given by (3.17) recovers the interface deformation induced by a static point force, as expected.
The dynamic deformation of the planar free surface
![]() $u(r,0)$
at time
$u(r,0)$
at time
![]() $t=0$
is plotted in figure 3 together with the deformation induced by a static point force (e.g. a heavy particle). It is evident that the dynamic interface deformation is qualitatively different from the case of a static forcing. The interface shape is non-monotonic and is characterised by a wavenumber
$t=0$
is plotted in figure 3 together with the deformation induced by a static point force (e.g. a heavy particle). It is evident that the dynamic interface deformation is qualitatively different from the case of a static forcing. The interface shape is non-monotonic and is characterised by a wavenumber
![]() $a^{-1/3}$
. Nevertheless, as clearly observed in figure 3, close to the origin the dynamic deformation shows the same logarithmic dependence of the case of a static point force. This behaviour is explained by considering that in the proximity of the point force we have
$a^{-1/3}$
. Nevertheless, as clearly observed in figure 3, close to the origin the dynamic deformation shows the same logarithmic dependence of the case of a static point force. This behaviour is explained by considering that in the proximity of the point force we have
![]() $p\ll \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FB}^{2}u$
. As a consequence, locally around
$p\ll \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FB}^{2}u$
. As a consequence, locally around
![]() $r=0$
, the interface deformation is governed by a Laplace equation with a point force, similarly to the static case. Note that a particle exerting the dynamic force on the interface has a finite size thus the deformation is finite everywhere. Indeed, as
$r=0$
, the interface deformation is governed by a Laplace equation with a point force, similarly to the static case. Note that a particle exerting the dynamic force on the interface has a finite size thus the deformation is finite everywhere. Indeed, as
![]() $r\rightarrow 0$
the assumptions of a point particle and an inviscid fluid are not valid; the divergence of the interface deformation is the signature of their breakdown. The markedly different interface deformations induced by dynamic and static point forces are expected to induce lateral capillary interactions between two particles that also differ significantly in the two cases. We compute the lateral capillary force in the next section.
$r\rightarrow 0$
the assumptions of a point particle and an inviscid fluid are not valid; the divergence of the interface deformation is the signature of their breakdown. The markedly different interface deformations induced by dynamic and static point forces are expected to induce lateral capillary interactions between two particles that also differ significantly in the two cases. We compute the lateral capillary force in the next section.
3.1 Lateral capillary force
To evaluate the lateral capillary force through (2.12) we have to compute the gradient of the deformation field induced by particle
![]() $B$
, evaluated at the position of particle
$B$
, evaluated at the position of particle
![]() $A$
. Due to the translational invariance of the problem, the deformation field induced by particle
$A$
. Due to the translational invariance of the problem, the deformation field induced by particle
![]() $B$
is the same as that generated by particle
$B$
is the same as that generated by particle
![]() $A$
. Hence, the term
$A$
. Hence, the term
![]() $\unicode[STIX]{x1D735}_{\Vert }u_{B}|_{x=0}$
in (2.12) is simply given by (3.17) with
$\unicode[STIX]{x1D735}_{\Vert }u_{B}|_{x=0}$
in (2.12) is simply given by (3.17) with
![]() $r=d$
. The lateral capillary force
$r=d$
. The lateral capillary force
![]() $\boldsymbol{F}_{C_{\Vert }}$
acting on particle
$\boldsymbol{F}_{C_{\Vert }}$
acting on particle
![]() $A$
is given by:
$A$
is given by:
Substituting the expression for the interface deformation, equation (3.17), we have:
 $$\begin{eqnarray}\displaystyle \boldsymbol{F}_{C_{\Vert }} & = & \displaystyle \hat{\boldsymbol{d}}_{AB}\frac{F_{0}^{2}a^{1/3}\cos (\unicode[STIX]{x1D714}t)^{2}}{12\unicode[STIX]{x1D6FE}} [\!H_{-1}(a^{1/3}d)-Y_{1}(a^{1/3}d)+(-1)^{1/3} (\!-H_{-1}((-a)^{1/3}d)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{1/3}(H_{-1}(\overline{(-a)^{1/3}}d)+Y_{1}(-\overline{(-a)^{1/3}}d))-Y_{1}((-a)^{1/3}d)\!)\!],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{F}_{C_{\Vert }} & = & \displaystyle \hat{\boldsymbol{d}}_{AB}\frac{F_{0}^{2}a^{1/3}\cos (\unicode[STIX]{x1D714}t)^{2}}{12\unicode[STIX]{x1D6FE}} [\!H_{-1}(a^{1/3}d)-Y_{1}(a^{1/3}d)+(-1)^{1/3} (\!-H_{-1}((-a)^{1/3}d)\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{1/3}(H_{-1}(\overline{(-a)^{1/3}}d)+Y_{1}(-\overline{(-a)^{1/3}}d))-Y_{1}((-a)^{1/3}d)\!)\!],\end{eqnarray}$$
with
![]() $\hat{\boldsymbol{d}}_{AB}$
the unit vector from particle
$\hat{\boldsymbol{d}}_{AB}$
the unit vector from particle
![]() $A$
to particle
$A$
to particle
![]() $B$
and tangent to the undeformed planar interface. When the term in square brackets of (3.20) is positive the force is attractive.
$B$
and tangent to the undeformed planar interface. When the term in square brackets of (3.20) is positive the force is attractive.
Interestingly, the lateral capillary force given by (3.20) is quadratic in the point force amplitude. It follows that its mean over a period is non-zero, even if the average force individually applied by the two particles over one period is zero. Equation (3.20) also shows that the lateral interaction force scales with the wavenumber of the interface deformation
![]() $a^{1/3}$
.
$a^{1/3}$
.

Figure 4. Lateral capillary force
![]() $\langle F_{C_{\Vert }}\rangle$
, averaged over one period, between two dynamic (a) and static (b) point forces acting in the direction normal to a planar free surface, as a function of their separation distance
$\langle F_{C_{\Vert }}\rangle$
, averaged over one period, between two dynamic (a) and static (b) point forces acting in the direction normal to a planar free surface, as a function of their separation distance
![]() $d$
. In the dynamic case, the lateral capillary interaction has multiple equilibrium points, both stable and unstable, as the sign of the force oscillates between attractive and repulsive.
$d$
. In the dynamic case, the lateral capillary interaction has multiple equilibrium points, both stable and unstable, as the sign of the force oscillates between attractive and repulsive.
The component of the capillary interaction force along
![]() $\hat{\boldsymbol{d}}_{AB}$
, given by (3.20), and averaged over one period, is reported in figure 4(a) as a function of the particle separation distance
$\hat{\boldsymbol{d}}_{AB}$
, given by (3.20), and averaged over one period, is reported in figure 4(a) as a function of the particle separation distance
![]() $d$
(see figure 2
a). For comparison, the interaction force between two static point forces given by
$d$
(see figure 2
a). For comparison, the interaction force between two static point forces given by
![]() $F_{0}^{2}/2\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}d$
(Domínguez et al.
Reference Domínguez, Oettel and Dietrich2008) is shown in figure 4(b). The lateral capillary force between identical static point forces is attractive at all particle separations
$F_{0}^{2}/2\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}d$
(Domínguez et al.
Reference Domínguez, Oettel and Dietrich2008) is shown in figure 4(b). The lateral capillary force between identical static point forces is attractive at all particle separations
![]() $d$
. Conversely, in the dynamic case the interaction force is non-monotonic and for certain distances it becomes repulsive. Figure 4(a) shows that there exist multiple equilibrium positions for which the particles do not move laterally. These equilibrium positions correspond to the antinodes of the standing wave and can be either stable of unstable depending on the inter-particle distance. This suggests that two dynamically driven particles, would attract or repel each other until the closest stable equilibrium distance is reached. This behaviour is in contrast to the static case where the two particles approach until contact. In figure 4(a) it is seen that dynamic effects become important for inter-particle distances of the order of the inverse of the wavenumber,
$d$
. Conversely, in the dynamic case the interaction force is non-monotonic and for certain distances it becomes repulsive. Figure 4(a) shows that there exist multiple equilibrium positions for which the particles do not move laterally. These equilibrium positions correspond to the antinodes of the standing wave and can be either stable of unstable depending on the inter-particle distance. This suggests that two dynamically driven particles, would attract or repel each other until the closest stable equilibrium distance is reached. This behaviour is in contrast to the static case where the two particles approach until contact. In figure 4(a) it is seen that dynamic effects become important for inter-particle distances of the order of the inverse of the wavenumber,
![]() $da^{1/3}\approx 1$
, and the average lateral force becomes repulsive already at
$da^{1/3}\approx 1$
, and the average lateral force becomes repulsive already at
![]() $da^{1/3}\approx 2$
. The results reported in figure 4 suggest that dynamically driving an interfacial suspension of colloidal particles with a suitable wavenumber
$da^{1/3}\approx 2$
. The results reported in figure 4 suggest that dynamically driving an interfacial suspension of colloidal particles with a suitable wavenumber
![]() $a^{1/3}$
can prevent particle aggregation on planar surfaces. Interestingly, a behaviour similar to that predicted by our theory has been observed in the experiments of Protière et al. (Reference Protière, Couder, Fort and Boudaoud2005) and Protière et al. (Reference Protière, Boudaoud and Couder2006) for bouncing drops. The authors found that multiple identical drops bouncing on a planar interface aggregated, when the capillary waves generated during impacts were damped, while they moved towards a stable equilibrium distance when the waves were not damped. This behaviour is remarkably similar to that predicted by (3.20) and shown in figure 4.
$a^{1/3}$
can prevent particle aggregation on planar surfaces. Interestingly, a behaviour similar to that predicted by our theory has been observed in the experiments of Protière et al. (Reference Protière, Couder, Fort and Boudaoud2005) and Protière et al. (Reference Protière, Boudaoud and Couder2006) for bouncing drops. The authors found that multiple identical drops bouncing on a planar interface aggregated, when the capillary waves generated during impacts were damped, while they moved towards a stable equilibrium distance when the waves were not damped. This behaviour is remarkably similar to that predicted by (3.20) and shown in figure 4.
4 Dynamic deformation of a bubble
In this section we provide the solution of (2.3)–(2.4), for a point force acting on the north pole of a bubble, i.e. with boundary conditions given by (2.8)–(2.11). Similarly to the case of a planar interface, all the fields, and the pressure inside the bubble are expressed as a Fourier series:
where the unknowns are the modes
![]() $\unicode[STIX]{x1D719}_{n}$
,
$\unicode[STIX]{x1D719}_{n}$
,
![]() $u_{n}$
,
$u_{n}$
,
![]() $p_{n}$
and
$p_{n}$
and
![]() $p_{gas,n}$
. As the governing equations (2.3)–(2.4) and the boundary conditions (2.8)–(2.11) are linear, no mode coupling occurs. In addition, the time dependence of the point force is simply a cosine, and therefore all the modes
$p_{gas,n}$
. As the governing equations (2.3)–(2.4) and the boundary conditions (2.8)–(2.11) are linear, no mode coupling occurs. In addition, the time dependence of the point force is simply a cosine, and therefore all the modes
![]() $n$
larger than 1 and smaller than
$n$
larger than 1 and smaller than
![]() $-1$
are identically zero. The zeroth mode for the gas pressure
$-1$
are identically zero. The zeroth mode for the gas pressure
![]() $p_{gas,0}$
is given by the equilibrium Laplace pressure
$p_{gas,0}$
is given by the equilibrium Laplace pressure
![]() $p_{gas,0}=p_{0}+(2\unicode[STIX]{x1D6FE}/R_{0})$
with
$p_{gas,0}=p_{0}+(2\unicode[STIX]{x1D6FE}/R_{0})$
with
![]() $p_{0}$
the equilibrium pressure in the liquid. Furthermore, the fields
$p_{0}$
the equilibrium pressure in the liquid. Furthermore, the fields
![]() $\unicode[STIX]{x1D719}$
,
$\unicode[STIX]{x1D719}$
,
![]() $u$
,
$u$
,
![]() $p$
and the pressure inside the gas
$p$
and the pressure inside the gas
![]() $p_{gas}$
are real variables, hence the modes 1 and
$p_{gas}$
are real variables, hence the modes 1 and
![]() $-1$
must be complex conjugates:
$-1$
must be complex conjugates:
![]() $\unicode[STIX]{x1D719}_{1}=\overline{\unicode[STIX]{x1D719}}_{-1}$
,
$\unicode[STIX]{x1D719}_{1}=\overline{\unicode[STIX]{x1D719}}_{-1}$
,
![]() $u_{1}=\overline{u}_{-1}$
,
$u_{1}=\overline{u}_{-1}$
,
![]() $p_{1}=\overline{p}_{-1}$
and
$p_{1}=\overline{p}_{-1}$
and
![]() $p_{gas,1}=\overline{p}_{gas,1}$
. The specification of the modes
$p_{gas,1}=\overline{p}_{gas,1}$
. The specification of the modes
![]() $\unicode[STIX]{x1D719}_{1}$
,
$\unicode[STIX]{x1D719}_{1}$
,
![]() $u_{1}$
,
$u_{1}$
,
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{gas,1}$
completely determines the solution of the problem.
$p_{gas,1}$
completely determines the solution of the problem.
Laplace’s equation, equation (2.3), for the first mode of the velocity potential reads:
whose solution can be expressed as a sum of Legendre polynomials
![]() $P_{l}(\cos \unicode[STIX]{x1D703})$
:
$P_{l}(\cos \unicode[STIX]{x1D703})$
:
with
![]() $C_{l}$
constants to be determined through the boundary conditions. The pressure in the bulk is found by substituting the Fourier series in (4.2) into (2.4):
$C_{l}$
constants to be determined through the boundary conditions. The pressure in the bulk is found by substituting the Fourier series in (4.2) into (2.4):
By substituting the Fourier series in (4.3) and (4.6) in the kinematic boundary condition equation (2.10) we obtain a relation between interface deformation,
![]() $u_{1}$
, and the velocity potential evaluated on the undeformed sphere:
$u_{1}$
, and the velocity potential evaluated on the undeformed sphere:
Equation (4.8) represents a decomposition in Legendre polynomials of the deformation of the bubble interface, which can be used to evaluate the time-dependent volume of the bubble:
The pressure inside the gas,
![]() $p_{gas}$
, is obtained by substituting the equation for the volume, equation (4.9), into (2.9):
$p_{gas}$
, is obtained by substituting the equation for the volume, equation (4.9), into (2.9):
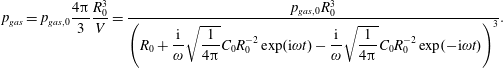 $$\begin{eqnarray}p_{gas}=p_{gas,0}\frac{4\unicode[STIX]{x03C0}}{3}\frac{R_{0}^{3}}{V}=\frac{p_{gas,0}R_{0}^{3}}{\left(R_{0}+{\displaystyle \frac{\text{i}}{\unicode[STIX]{x1D714}}}\sqrt{{\displaystyle \frac{1}{4\unicode[STIX]{x03C0}}}}C_{0}R_{0}^{-2}\exp (\text{i}\unicode[STIX]{x1D714}t)-{\displaystyle \frac{\text{i}}{\unicode[STIX]{x1D714}}}\sqrt{{\displaystyle \frac{1}{4\unicode[STIX]{x03C0}}}}C_{0}R_{0}^{-2}\exp (-\text{i}\unicode[STIX]{x1D714}t)\right)^{3}}.\end{eqnarray}$$
$$\begin{eqnarray}p_{gas}=p_{gas,0}\frac{4\unicode[STIX]{x03C0}}{3}\frac{R_{0}^{3}}{V}=\frac{p_{gas,0}R_{0}^{3}}{\left(R_{0}+{\displaystyle \frac{\text{i}}{\unicode[STIX]{x1D714}}}\sqrt{{\displaystyle \frac{1}{4\unicode[STIX]{x03C0}}}}C_{0}R_{0}^{-2}\exp (\text{i}\unicode[STIX]{x1D714}t)-{\displaystyle \frac{\text{i}}{\unicode[STIX]{x1D714}}}\sqrt{{\displaystyle \frac{1}{4\unicode[STIX]{x03C0}}}}C_{0}R_{0}^{-2}\exp (-\text{i}\unicode[STIX]{x1D714}t)\right)^{3}}.\end{eqnarray}$$
By employing the assumption of small interface deformations, we can linearise the expression above to obtain:
From (4.11) it is immediately clear that the pressure in the gas phase
![]() $p_{gas}$
is the sum of three Fourier modes: a zeroth mode
$p_{gas}$
is the sum of three Fourier modes: a zeroth mode
![]() $p_{gas,0}$
, a mode
$p_{gas,0}$
, a mode
![]() $-1$
and a mode 1. The latter is given by:
$-1$
and a mode 1. The latter is given by:
with
![]() $\unicode[STIX]{x1D6FF}_{l0}$
the Kronecker delta. It is clear from (4.12), (4.8), (4.7), (4.6), that the specification of the constants
$\unicode[STIX]{x1D6FF}_{l0}$
the Kronecker delta. It is clear from (4.12), (4.8), (4.7), (4.6), that the specification of the constants
![]() $C_{l}$
completely determines the solution to the problem. An equation for
$C_{l}$
completely determines the solution to the problem. An equation for
![]() $C_{l}$
is obtained considering the normal stress balance. Substituting the Fourier series given by (4.1)–(4.4) in the normal stress balance equation (2.8) and considering the first Fourier mode, we obtain:
$C_{l}$
is obtained considering the normal stress balance. Substituting the Fourier series given by (4.1)–(4.4) in the normal stress balance equation (2.8) and considering the first Fourier mode, we obtain:
Inserting (4.12), (4.8), (4.7), (4.6), in the normal stress balance (4.13), and using the fact that
![]() $\unicode[STIX]{x1D6FB}_{\Vert }^{2}P_{l}(\cos \unicode[STIX]{x1D703})=-l(l+1)P_{l}(\cos \unicode[STIX]{x1D703})$
, we obtain an equation for each constant
$\unicode[STIX]{x1D6FB}_{\Vert }^{2}P_{l}(\cos \unicode[STIX]{x1D703})=-l(l+1)P_{l}(\cos \unicode[STIX]{x1D703})$
, we obtain an equation for each constant
![]() $C_{l}$
:
$C_{l}$
:
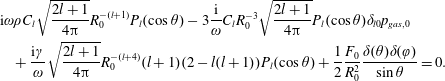 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D70C}C_{l}\sqrt{\frac{2l+1}{4\unicode[STIX]{x03C0}}}R_{0}^{-(l+1)}P_{l}(\cos \unicode[STIX]{x1D703})-3\frac{\text{i}}{\unicode[STIX]{x1D714}}C_{l}R_{0}^{-3}\sqrt{\frac{2l+1}{4\unicode[STIX]{x03C0}}}P_{l}(\cos \unicode[STIX]{x1D703})\unicode[STIX]{x1D6FF}_{l0}p_{gas,0}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\text{i}\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D714}}\sqrt{\frac{2l+1}{4\unicode[STIX]{x03C0}}}R_{0}^{-(l+4)}(l+1)(2-l(l+1))P_{l}(\cos \unicode[STIX]{x1D703})+\frac{1}{2}\frac{F_{0}}{R_{0}^{2}}\frac{\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D703})\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D711})}{\sin \unicode[STIX]{x1D703}}=0.\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D70C}C_{l}\sqrt{\frac{2l+1}{4\unicode[STIX]{x03C0}}}R_{0}^{-(l+1)}P_{l}(\cos \unicode[STIX]{x1D703})-3\frac{\text{i}}{\unicode[STIX]{x1D714}}C_{l}R_{0}^{-3}\sqrt{\frac{2l+1}{4\unicode[STIX]{x03C0}}}P_{l}(\cos \unicode[STIX]{x1D703})\unicode[STIX]{x1D6FF}_{l0}p_{gas,0}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\frac{\text{i}\unicode[STIX]{x1D6FE}}{\unicode[STIX]{x1D714}}\sqrt{\frac{2l+1}{4\unicode[STIX]{x03C0}}}R_{0}^{-(l+4)}(l+1)(2-l(l+1))P_{l}(\cos \unicode[STIX]{x1D703})+\frac{1}{2}\frac{F_{0}}{R_{0}^{2}}\frac{\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D703})\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D711})}{\sin \unicode[STIX]{x1D703}}=0.\quad\end{eqnarray}$$
We substitute in (4.14) the expression of the Dirac delta in terms of a sum of Legendre polynomials
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D703})\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D711})/\text{sin}\unicode[STIX]{x1D703}=\sum _{l=0}^{\infty }((2l+1)/4\unicode[STIX]{x03C0})P_{l}(\cos \unicode[STIX]{x1D703})$
:
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D703})\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D711})/\text{sin}\unicode[STIX]{x1D703}=\sum _{l=0}^{\infty }((2l+1)/4\unicode[STIX]{x03C0})P_{l}(\cos \unicode[STIX]{x1D703})$
:
which gives as solution:
 $$\begin{eqnarray}C_{l}=\frac{\text{i}\unicode[STIX]{x1D714}F_{0}R_{0}^{l-1}\sqrt{{\displaystyle \frac{2l+1}{4\unicode[STIX]{x03C0}}}}}{2\left(\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}-{\displaystyle \frac{3}{R_{0}^{2}}}\unicode[STIX]{x1D6FF}_{l0}p_{gas,0}+{\displaystyle \frac{\unicode[STIX]{x1D6FE}}{R_{0}^{3}}}(l+1)(2-l(l+1))\right)}.\end{eqnarray}$$
$$\begin{eqnarray}C_{l}=\frac{\text{i}\unicode[STIX]{x1D714}F_{0}R_{0}^{l-1}\sqrt{{\displaystyle \frac{2l+1}{4\unicode[STIX]{x03C0}}}}}{2\left(\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}-{\displaystyle \frac{3}{R_{0}^{2}}}\unicode[STIX]{x1D6FF}_{l0}p_{gas,0}+{\displaystyle \frac{\unicode[STIX]{x1D6FE}}{R_{0}^{3}}}(l+1)(2-l(l+1))\right)}.\end{eqnarray}$$
The pressure field is obtained by substituting the coefficients in (4.16) into (4.6) and the resulting expression into (4.7). The final result reads:
 $$\begin{eqnarray}p(r,\unicode[STIX]{x1D703},t)=\frac{F_{0}R_{0}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}\cos (\unicode[STIX]{x1D714}t)\mathop{\sum }_{l=0}^{\infty }\frac{(2l+1)P_{l}(\cos \unicode[STIX]{x1D703})}{{\displaystyle \frac{R_{0}^{3}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D6FE}}}-{\displaystyle \frac{3R_{0}}{\unicode[STIX]{x1D6FE}}}p_{gas,0}\unicode[STIX]{x1D6FF}_{l0}+(l+1)(2-l(l+1))}\left(\frac{r}{R_{0}}\right)^{l+1}.\end{eqnarray}$$
$$\begin{eqnarray}p(r,\unicode[STIX]{x1D703},t)=\frac{F_{0}R_{0}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}\cos (\unicode[STIX]{x1D714}t)\mathop{\sum }_{l=0}^{\infty }\frac{(2l+1)P_{l}(\cos \unicode[STIX]{x1D703})}{{\displaystyle \frac{R_{0}^{3}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D6FE}}}-{\displaystyle \frac{3R_{0}}{\unicode[STIX]{x1D6FE}}}p_{gas,0}\unicode[STIX]{x1D6FF}_{l0}+(l+1)(2-l(l+1))}\left(\frac{r}{R_{0}}\right)^{l+1}.\end{eqnarray}$$
By substituting the coefficients (4.16) into (4.8), and the resulting first modes
![]() $u_{1}$
, and
$u_{1}$
, and
![]() $u_{-1}$
into the Fourier series expansion given by (4.3), we obtain the solution for the dynamic interface deformation:
$u_{-1}$
into the Fourier series expansion given by (4.3), we obtain the solution for the dynamic interface deformation:
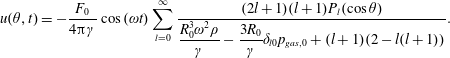 $$\begin{eqnarray}u(\unicode[STIX]{x1D703},t)=-\frac{F_{0}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}\cos (\unicode[STIX]{x1D714}t)\mathop{\sum }_{l=0}^{\infty }\frac{(2l+1)(l+1)P_{l}(\cos \unicode[STIX]{x1D703})}{{\displaystyle \frac{R_{0}^{3}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D6FE}}}-{\displaystyle \frac{3R_{0}}{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6FF}_{l0}p_{gas,0}+(l+1)(2-l(l+1))}.\end{eqnarray}$$
$$\begin{eqnarray}u(\unicode[STIX]{x1D703},t)=-\frac{F_{0}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}\cos (\unicode[STIX]{x1D714}t)\mathop{\sum }_{l=0}^{\infty }\frac{(2l+1)(l+1)P_{l}(\cos \unicode[STIX]{x1D703})}{{\displaystyle \frac{R_{0}^{3}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D6FE}}}-{\displaystyle \frac{3R_{0}}{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6FF}_{l0}p_{gas,0}+(l+1)(2-l(l+1))}.\end{eqnarray}$$
It is interesting to examine the first two terms in (4.18). The term
![]() $l=0$
represents radially symmetric oscillations of the bubble. From (4.18) it is clear that this term has a resonance frequency
$l=0$
represents radially symmetric oscillations of the bubble. From (4.18) it is clear that this term has a resonance frequency
![]() $\unicode[STIX]{x1D714}^{2}=-(2\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}R_{0}^{3})+(3p_{gas,0}/\unicode[STIX]{x1D70C}R_{0}^{2})$
, which is the well-known resonance frequency of a bubble in an inviscid fluid (Plesset & Prosperetti Reference Plesset and Prosperetti1977). The term
$\unicode[STIX]{x1D714}^{2}=-(2\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}R_{0}^{3})+(3p_{gas,0}/\unicode[STIX]{x1D70C}R_{0}^{2})$
, which is the well-known resonance frequency of a bubble in an inviscid fluid (Plesset & Prosperetti Reference Plesset and Prosperetti1977). The term
![]() $l=1$
represents periodic rigid body displacements of the bubble in the direction of the point force. From (4.18) we observe that the amplitude of this term is proportional to
$l=1$
represents periodic rigid body displacements of the bubble in the direction of the point force. From (4.18) we observe that the amplitude of this term is proportional to
![]() $\unicode[STIX]{x1D6FE}/R_{0}^{3}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}$
, which has to be at most
$\unicode[STIX]{x1D6FE}/R_{0}^{3}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}$
, which has to be at most
![]() $\mathit{O}(1)$
for our linear theory to be valid, as discussed in § 2.3.2. The terms
$\mathit{O}(1)$
for our linear theory to be valid, as discussed in § 2.3.2. The terms
![]() $l\geqslant 2$
represent shape oscillations of the bubble interface. In (4.18) it is clear that the amplitude of each Legendre polynomial has a resonance frequency
$l\geqslant 2$
represent shape oscillations of the bubble interface. In (4.18) it is clear that the amplitude of each Legendre polynomial has a resonance frequency
![]() $\unicode[STIX]{x1D714}^{2}=-(\unicode[STIX]{x1D6FE}/R_{0}^{3}\unicode[STIX]{x1D70C})(l+1)(2-l(l+1))$
(Lamb Reference Lamb1932). It follows that a dynamic point force acting at the north pole of a bubble induces shape oscillations of the interface mainly described by some dominating Legendre polynomial that is close to resonance. Note that for a fixed set of parameters, if the particle forcing frequency approaches the resonance frequency of a specific Legendre mode, the bubble deformation formally becomes infinite. In practice, close to resonance, viscous damping and possibly nonlinear effects that have been neglected in the present theory become important. This behaviour of the interface deformation is not observed in the case of a planar surface, because it is induced by the different topology of a sphere compared to a plane. For a planar surface, a change in the driving frequency only modifies the wavenumber of the deformation. In the limit
$\unicode[STIX]{x1D714}^{2}=-(\unicode[STIX]{x1D6FE}/R_{0}^{3}\unicode[STIX]{x1D70C})(l+1)(2-l(l+1))$
(Lamb Reference Lamb1932). It follows that a dynamic point force acting at the north pole of a bubble induces shape oscillations of the interface mainly described by some dominating Legendre polynomial that is close to resonance. Note that for a fixed set of parameters, if the particle forcing frequency approaches the resonance frequency of a specific Legendre mode, the bubble deformation formally becomes infinite. In practice, close to resonance, viscous damping and possibly nonlinear effects that have been neglected in the present theory become important. This behaviour of the interface deformation is not observed in the case of a planar surface, because it is induced by the different topology of a sphere compared to a plane. For a planar surface, a change in the driving frequency only modifies the wavenumber of the deformation. In the limit
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
and neglecting the terms
$\unicode[STIX]{x1D714}\rightarrow 0$
and neglecting the terms
![]() $l=0$
and
$l=0$
and
![]() $l=1$
, the deformation of the bubble due to a dynamic point force given by (4.18), reduces to that obtained by Morse & Witten (Reference Morse and Witten1993) and Guzowski et al. (Reference Guzowski, Tasinkevych and Dietrich2011a
) in the case of a static point force acting on a stationary and incompressible droplet.
$l=1$
, the deformation of the bubble due to a dynamic point force given by (4.18), reduces to that obtained by Morse & Witten (Reference Morse and Witten1993) and Guzowski et al. (Reference Guzowski, Tasinkevych and Dietrich2011a
) in the case of a static point force acting on a stationary and incompressible droplet.
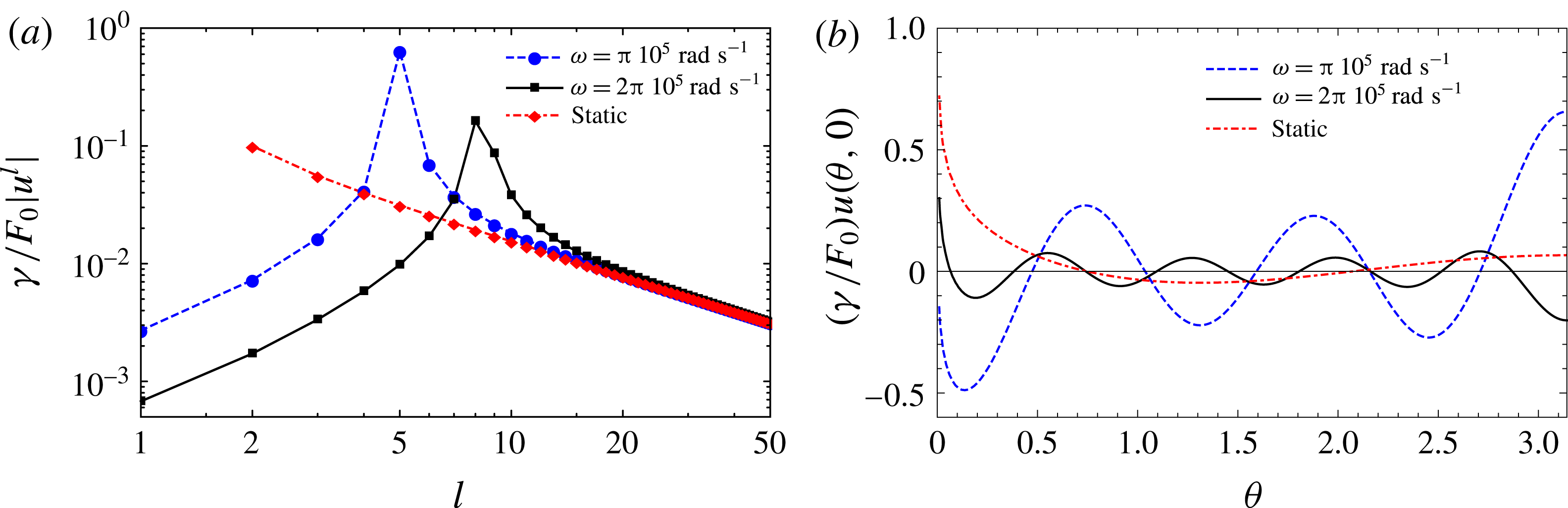
Figure 5. (a) Absolute value of the coefficients
![]() $u^{l}$
of each Legendre polynomial in (4.18) as a function of the Legendre polynomial index
$u^{l}$
of each Legendre polynomial in (4.18) as a function of the Legendre polynomial index
![]() $l$
; lines are guides for the eye. (b) Interfacial deformation
$l$
; lines are guides for the eye. (b) Interfacial deformation
![]() $u(\unicode[STIX]{x1D703},0)$
as a function of the angle
$u(\unicode[STIX]{x1D703},0)$
as a function of the angle
![]() $\unicode[STIX]{x1D703}$
at time equal to zero. The parameters used in this figure are
$\unicode[STIX]{x1D703}$
at time equal to zero. The parameters used in this figure are
![]() $R_{0}=50~\unicode[STIX]{x03BC}\text{m}$
,
$R_{0}=50~\unicode[STIX]{x03BC}\text{m}$
,
![]() $\unicode[STIX]{x1D6FE}=0.07~\text{N}~\text{m}^{-1}$
,
$\unicode[STIX]{x1D6FE}=0.07~\text{N}~\text{m}^{-1}$
,
![]() $\unicode[STIX]{x1D70C}=10^{3}~\text{kg}~\text{m}^{-3}$
and
$\unicode[STIX]{x1D70C}=10^{3}~\text{kg}~\text{m}^{-3}$
and
![]() $p_{0}=1~\text{atm}$
. Note that the terms
$p_{0}=1~\text{atm}$
. Note that the terms
![]() $l=0$
and
$l=0$
and
![]() $l=1$
are neglected in the static curves (see text).
$l=1$
are neglected in the static curves (see text).
To highlight the dominating terms in the sum equation (4.18), we plot in figure 5(a) the absolute value of the coefficients of each Legendre polynomial
 $$\begin{eqnarray}|u^{l}|=\left|\frac{-(2l+1)(l+1)}{4\unicode[STIX]{x03C0}\left({\displaystyle \frac{R_{0}^{3}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D6FE}}}-{\displaystyle \frac{3R_{0}}{\unicode[STIX]{x1D6FE}}}p_{gas,0}\unicode[STIX]{x1D6FF}_{l0}+(l+1)(2-l(l+1))\right)}\right|,\end{eqnarray}$$
$$\begin{eqnarray}|u^{l}|=\left|\frac{-(2l+1)(l+1)}{4\unicode[STIX]{x03C0}\left({\displaystyle \frac{R_{0}^{3}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D6FE}}}-{\displaystyle \frac{3R_{0}}{\unicode[STIX]{x1D6FE}}}p_{gas,0}\unicode[STIX]{x1D6FF}_{l0}+(l+1)(2-l(l+1))\right)}\right|,\end{eqnarray}$$
for an air bubble of equilibrium radius
![]() $R_{0}=50~\unicode[STIX]{x03BC}\text{m}$
immersed in water at atmospheric pressure, and for different frequencies of the point force. The parameters have been selected in the range of those employed in the experiments of Poulichet & Garbin (Reference Poulichet and Garbin2015). For comparison, the values of the coefficients
$R_{0}=50~\unicode[STIX]{x03BC}\text{m}$
immersed in water at atmospheric pressure, and for different frequencies of the point force. The parameters have been selected in the range of those employed in the experiments of Poulichet & Garbin (Reference Poulichet and Garbin2015). For comparison, the values of the coefficients
![]() $|u^{l}|$
, for a static point force acting on an incompressible and stationary droplet are also displayed in figure 5(a). Note that, in the case of a static point force, the sum in (4.18) starts from
$|u^{l}|$
, for a static point force acting on an incompressible and stationary droplet are also displayed in figure 5(a). Note that, in the case of a static point force, the sum in (4.18) starts from
![]() $l=2$
. Figure 5(a) shows that in the case of a static point force (
$l=2$
. Figure 5(a) shows that in the case of a static point force (
![]() $\unicode[STIX]{x1D714}\rightarrow 0$
) the largest amplitude
$\unicode[STIX]{x1D714}\rightarrow 0$
) the largest amplitude
![]() $|u^{l}|$
is obtained for
$|u^{l}|$
is obtained for
![]() $l=2$
and then it decreases monotonically as
$l=2$
and then it decreases monotonically as
![]() $|u^{l}|\propto l^{-1}$
. In the case of a dynamic point force, a qualitatively different behaviour is observed. Figure 5(a) shows that the amplitude of each Legendre polynomial
$|u^{l}|\propto l^{-1}$
. In the case of a dynamic point force, a qualitatively different behaviour is observed. Figure 5(a) shows that the amplitude of each Legendre polynomial
![]() $|u^{l}|$
is non-monotonic, it has a maximum for some value of
$|u^{l}|$
is non-monotonic, it has a maximum for some value of
![]() $l$
, and then decreases as
$l$
, and then decreases as
![]() $|u^{l}|\propto l^{-1}$
. We remark that the Legendre polynomial with the largest amplitude is expected to dominate in the sum given by (4.18). Figure 5(a) also shows that as
$|u^{l}|\propto l^{-1}$
. We remark that the Legendre polynomial with the largest amplitude is expected to dominate in the sum given by (4.18). Figure 5(a) also shows that as
![]() $\unicode[STIX]{x1D714}$
increases the largest amplitude
$\unicode[STIX]{x1D714}$
increases the largest amplitude
![]() $|u^{l}|$
occurs at larger index
$|u^{l}|$
occurs at larger index
![]() $l$
. It follows that Legendre polynomials of larger order
$l$
. It follows that Legendre polynomials of larger order
![]() $l$
dominate the interface deformation equation (4.18), as the frequency increases.
$l$
dominate the interface deformation equation (4.18), as the frequency increases.
The interface deformation
![]() $u(\unicode[STIX]{x1D703},0)$
, shown in figure 5(b), is obtained by numerically evaluating the sum in (4.18), for the same parameters used in figure 5(a). Figure 5(b) clearly shows that the free interface deformation induced by a dynamic point force is significantly different from that obtained for a steady point force. As discussed above, the bubble interface undergoes shape oscillations whose amplitude is approximately given by the dominant Legendre polynomial
$u(\unicode[STIX]{x1D703},0)$
, shown in figure 5(b), is obtained by numerically evaluating the sum in (4.18), for the same parameters used in figure 5(a). Figure 5(b) clearly shows that the free interface deformation induced by a dynamic point force is significantly different from that obtained for a steady point force. As discussed above, the bubble interface undergoes shape oscillations whose amplitude is approximately given by the dominant Legendre polynomial
![]() $P_{l}(\cos \unicode[STIX]{x1D703})$
. In the limit of
$P_{l}(\cos \unicode[STIX]{x1D703})$
. In the limit of
![]() $\unicode[STIX]{x1D703}\rightarrow 0$
the behaviour of the interface deformation is similar, regardless of the frequency of the point force. Indeed, in a small region around the point force, the deformation is insensitive to the global curvature of the bubble. It follows that in this small area the bubble deformation is similar to that observed in the case a planar interface, in other words
$\unicode[STIX]{x1D703}\rightarrow 0$
the behaviour of the interface deformation is similar, regardless of the frequency of the point force. Indeed, in a small region around the point force, the deformation is insensitive to the global curvature of the bubble. It follows that in this small area the bubble deformation is similar to that observed in the case a planar interface, in other words
![]() $u(\unicode[STIX]{x1D703})\propto -\ln (\unicode[STIX]{x1D703})$
as
$u(\unicode[STIX]{x1D703})\propto -\ln (\unicode[STIX]{x1D703})$
as
![]() $\unicode[STIX]{x1D703}\rightarrow 0$
. The divergence of the deformation is the signature of the breakdown of our assumptions in a small region around the north pole where the effects of a finite particle size and of viscosity are no longer negligible, thus our results are not valid as
$\unicode[STIX]{x1D703}\rightarrow 0$
. The divergence of the deformation is the signature of the breakdown of our assumptions in a small region around the north pole where the effects of a finite particle size and of viscosity are no longer negligible, thus our results are not valid as
![]() $\unicode[STIX]{x1D703}\rightarrow 0$
. In fact, even if our results predict that the interface deformation is formally unbounded at
$\unicode[STIX]{x1D703}\rightarrow 0$
. In fact, even if our results predict that the interface deformation is formally unbounded at
![]() $\unicode[STIX]{x1D703}=0$
, in practice the finite size of the driven particle keeps the deformation finite for all
$\unicode[STIX]{x1D703}=0$
, in practice the finite size of the driven particle keeps the deformation finite for all
![]() $\unicode[STIX]{x1D703}$
.
$\unicode[STIX]{x1D703}$
.
4.1 Lateral capillary force
The lateral capillary force given by (2.13) is obtained by evaluating the gradient of the deformation field induced by particle
![]() $B$
, evaluated at the position of particle
$B$
, evaluated at the position of particle
![]() $A$
. The deformation induced by particle
$A$
. The deformation induced by particle
![]() $B$
is identical to that induced by a particle placed at the north pole, due to the rotational invariance of the problem of a single dynamic point force. Hence, the deformation field
$B$
is identical to that induced by a particle placed at the north pole, due to the rotational invariance of the problem of a single dynamic point force. Hence, the deformation field
![]() $u_{B}$
is also given by (4.18), and the lateral capillary force equation (2.13) is rewritten as:
$u_{B}$
is also given by (4.18), and the lateral capillary force equation (2.13) is rewritten as:
Substituting
![]() $u(\unicode[STIX]{x1D703},t)$
as given by (4.18) into (4.20) we obtain:
$u(\unicode[STIX]{x1D703},t)$
as given by (4.18) into (4.20) we obtain:
 $$\begin{eqnarray}\boldsymbol{F}_{C_{\Vert }}=\hat{\boldsymbol{d}}_{AB}\frac{F_{0}^{2}\cos (\unicode[STIX]{x1D714}t)^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}R_{0}}\mathop{\sum }_{l=0}^{\infty }\frac{\sin {\unicode[STIX]{x1D703}_{B}}^{-1}(2l+1)(l+1)^{2}(\cos \unicode[STIX]{x1D703}_{B}P_{l}(\cos \unicode[STIX]{x1D703}_{B})-P_{l+1}(\cos \unicode[STIX]{x1D703}_{B}))}{{\displaystyle \frac{R_{0}^{3}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D6FE}}}-{\displaystyle \frac{3R_{0}}{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6FF}_{l0}p_{gas,0}+(l+1)(2-l(l+1))},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{F}_{C_{\Vert }}=\hat{\boldsymbol{d}}_{AB}\frac{F_{0}^{2}\cos (\unicode[STIX]{x1D714}t)^{2}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}R_{0}}\mathop{\sum }_{l=0}^{\infty }\frac{\sin {\unicode[STIX]{x1D703}_{B}}^{-1}(2l+1)(l+1)^{2}(\cos \unicode[STIX]{x1D703}_{B}P_{l}(\cos \unicode[STIX]{x1D703}_{B})-P_{l+1}(\cos \unicode[STIX]{x1D703}_{B}))}{{\displaystyle \frac{R_{0}^{3}\unicode[STIX]{x1D714}^{2}\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D6FE}}}-{\displaystyle \frac{3R_{0}}{\unicode[STIX]{x1D6FE}}}\unicode[STIX]{x1D6FF}_{l0}p_{gas,0}+(l+1)(2-l(l+1))},\end{eqnarray}$$
with
![]() $\hat{\boldsymbol{d}}_{AB}$
the unit vector tangent to the undeformed sphere directed from particle
$\hat{\boldsymbol{d}}_{AB}$
the unit vector tangent to the undeformed sphere directed from particle
![]() $A$
to particle
$A$
to particle
![]() $B$
. As a consequence, if the summation on the right-hand side of (4.21) is positive, the capillary force is attractive. As expected, the lateral capillary force
$B$
. As a consequence, if the summation on the right-hand side of (4.21) is positive, the capillary force is attractive. As expected, the lateral capillary force
![]() $\boldsymbol{F}_{C_{\Vert }}$
is proportional to the product of the force induced by the each particle, thus displaying a non-zero mean component over a period, similarly to the case of a planar interface.
$\boldsymbol{F}_{C_{\Vert }}$
is proportional to the product of the force induced by the each particle, thus displaying a non-zero mean component over a period, similarly to the case of a planar interface.
The component of the lateral capillary force acting between two dynamic point forces along
![]() $\hat{\boldsymbol{d}}_{AB}$
, averaged over one period, is reported in figure 6 as a function of the angular separation
$\hat{\boldsymbol{d}}_{AB}$
, averaged over one period, is reported in figure 6 as a function of the angular separation
![]() $\unicode[STIX]{x1D703}_{B}$
(see figure 2
b). The same parameters used in figure 5 are considered. For comparison also the lateral capillary force experienced by two static point forces acting on an incompressible and stationary droplet is reported in the same plot (Guzowski et al.
Reference Guzowski, Tasinkevych and Dietrich2011a
).
$\unicode[STIX]{x1D703}_{B}$
(see figure 2
b). The same parameters used in figure 5 are considered. For comparison also the lateral capillary force experienced by two static point forces acting on an incompressible and stationary droplet is reported in the same plot (Guzowski et al.
Reference Guzowski, Tasinkevych and Dietrich2011a
).

Figure 6. Lateral capillary force
![]() $\langle F_{C_{\Vert }}\rangle$
, averaged over one period, between two dynamic point forces acting in direction normal to the bubble interface, plotted as a function of the angular separation
$\langle F_{C_{\Vert }}\rangle$
, averaged over one period, between two dynamic point forces acting in direction normal to the bubble interface, plotted as a function of the angular separation
![]() $\unicode[STIX]{x1D703}_{B}$
. The force is attractive when positive, and repulsive otherwise. The parameters used in this figure are
$\unicode[STIX]{x1D703}_{B}$
. The force is attractive when positive, and repulsive otherwise. The parameters used in this figure are
![]() $R_{0}=50~\unicode[STIX]{x03BC}\text{m}$
,
$R_{0}=50~\unicode[STIX]{x03BC}\text{m}$
,
![]() $\unicode[STIX]{x1D6FE}=0.07~\text{N}~\text{m}^{-1}$
,
$\unicode[STIX]{x1D6FE}=0.07~\text{N}~\text{m}^{-1}$
,
![]() $\unicode[STIX]{x1D70C}=10^{3}~\text{kg}~\text{m}^{-3}$
and
$\unicode[STIX]{x1D70C}=10^{3}~\text{kg}~\text{m}^{-3}$
and
![]() $p_{0}=1~\text{atm}$
.
$p_{0}=1~\text{atm}$
.
Figure 6 shows that the interaction force between two dynamically forced particles is significantly different from the static case. The static capillary force has two equilibrium points, an unstable one at
![]() $\unicode[STIX]{x1D703}_{B}\approx \unicode[STIX]{x03C0}/2$
and a stable one at
$\unicode[STIX]{x1D703}_{B}\approx \unicode[STIX]{x03C0}/2$
and a stable one at
![]() $\unicode[STIX]{x1D703}_{B}=\unicode[STIX]{x03C0}$
. Instead, the dynamic capillary force displays multiple stable and unstable equilibrium points. As a consequence, two static point forces either move to contact or attain a separation angle
$\unicode[STIX]{x1D703}_{B}=\unicode[STIX]{x03C0}$
. Instead, the dynamic capillary force displays multiple stable and unstable equilibrium points. As a consequence, two static point forces either move to contact or attain a separation angle
![]() $\unicode[STIX]{x1D703}_{B}=\unicode[STIX]{x03C0}$
, whereas two dynamic point forces move to the closest stable equilibrium separation
$\unicode[STIX]{x1D703}_{B}=\unicode[STIX]{x03C0}$
, whereas two dynamic point forces move to the closest stable equilibrium separation
![]() $\unicode[STIX]{x1D703}_{B}$
. In the dynamic case, figure 6 suggests that for small particle separations there exists a critical distance below which particles on the bubble surface aggregate, while particles whose separation is larger than such critical value experience a repulsive capillary force and move towards a stable equilibrium distance. Finally, in the limit of small angular separations
$\unicode[STIX]{x1D703}_{B}$
. In the dynamic case, figure 6 suggests that for small particle separations there exists a critical distance below which particles on the bubble surface aggregate, while particles whose separation is larger than such critical value experience a repulsive capillary force and move towards a stable equilibrium distance. Finally, in the limit of small angular separations
![]() $\unicode[STIX]{x1D703}_{B}\rightarrow 0$
the capillary force scales as the separation distance
$\unicode[STIX]{x1D703}_{B}\rightarrow 0$
the capillary force scales as the separation distance
![]() $(R_{0}\unicode[STIX]{x1D703}_{B})^{-1}$
regardless of the dynamic or static nature of the forcing. Indeed, if the angular separation is small, the effects of the bubble curvature are negligible and the lateral capillary force behaves as in the case of a planar interface.
$(R_{0}\unicode[STIX]{x1D703}_{B})^{-1}$
regardless of the dynamic or static nature of the forcing. Indeed, if the angular separation is small, the effects of the bubble curvature are negligible and the lateral capillary force behaves as in the case of a planar interface.
5 Conclusions
We have investigated the dynamic deformation of a gas–liquid interface induced by a micrometric particle adsorbed either on a planar surface or on a bubble, and driven by a periodic force in the direction normal to the surface. By modelling the effects of the particle as a point force we analytically calculated the far-field deformation of the surface assuming negligible liquid viscosity, small interfacial deformation and small displacement in the case of a bubble. The dynamic interface deformation field induced by a single particle has been employed to evaluate the lateral capillary force between two driven particles, assuming a linear superposition of the individual deformations.
A dynamic point force acting on a planar interface generates a capillary wave with the wavenumber set by the dispersion relation for the surface waves of an inviscid fluid. We found that the lateral capillary force resulting from the dynamic deformation can be attractive or repulsive depending on the inter-particle separation distance thus showing multiple equilibrium points, in contrast to the static case in which the capillary interaction is always attractive. The solution obtained for a periodic point force acting on a planar interface can be used to evaluate the interface deformation generated by more complex dynamic distributions of pressure, e.g. dynamic pressure dipoles, quadrupoles or higher-order multipoles. Non-monotonic capillary interactions have been observed in the experiments of Protière et al. (Reference Protière, Boudaoud and Couder2006) and Eddi et al. (Reference Eddi, Decelle, Fort and Couder2009) on drops bouncing on a planar gas–liquid interface and interacting through capillary waves. The authors observed that multiple drops attained a stable lateral equilibrium distance, similarly to that predicted by our theory for periodic point forces.
A dynamic point force acting on a bubble induces deformations of the interface described by a sum of Legendre polynomials with a dominating term that is selected by the dispersion relation for the shape oscillations of a bubble in an inviscid liquid. As a consequence, the lateral capillary force experienced by two particles adsorbed on a bubble is found to qualitatively differ from the static case. Depending on the forcing frequency, the bubble radius, the fluid density and the surface tension, multiple stable and unstable equilibrium distances occur. At small inter-particle separations, the lateral force can be repulsive, and therefore the critical separation distance for particle aggregation on a bubble is significantly decreased by dynamic effects. Dynamic capillary interactions between colloidal particles oscillating at an interface have not yet been observed, likely because of the high surface coverage in typical experiments, resulting in small inter-particle distances such that this theory is not applicable (Poulichet & Garbin Reference Poulichet and Garbin2015; Prabhudesai et al. Reference Prabhudesai, Bihi, Zoueshtiagh, Jose and Baudoin2017). This work therefore motivates future controlled experiments with sufficiently large inter-particle distances.
Our results suggest that the interaction between dynamically forced particles on a planar interface or a bubble can lead to markedly different microstructures compared to particles interacting statically. Dynamic effects can promote interfacial stability by preventing aggregation of a monolayer of colloidal particles. We have shown that micrometric particles, whose weight is negligible compared to surface forces, can impart dynamic deformations of the interface when driven by time-dependent external fields, such as magnetic or electric fields. The analytical results for the dynamic interface deformation and lateral capillary forces developed in the present paper have wide applicability to different time-dependent forcing mechanisms and open new possibilities for self-assembly of colloids on fluid interfaces. Finally, the linear analysis presented in this paper represents a first step in the investigation of the nonlinear regime that is relevant when the driving force and the deformation of the interface are large.
Acknowledgements
The authors thank D. Baresch, L. Botto, F. Greco, A. Huerre and E. E. Keaveny for helpful discussions. We thank an anonymous reviewer for correcting the derivation in § 2.4. This work is supported by European Research Council Starting grant no. 639221.
Appendix A. First Fourier mode of planar interface deformation in real space
The solution for the interface dynamics in real space is obtained by evaluating the integral in (3.6) with
![]() $\hat{u} _{1}$
given by (3.15):
$\hat{u} _{1}$
given by (3.15):
As the above integral contains only quantities depending on
![]() $k=\sqrt{k_{x}^{2}+k_{y}^{2}}$
, the argument is invariant under rotations around
$k=\sqrt{k_{x}^{2}+k_{y}^{2}}$
, the argument is invariant under rotations around
![]() $z$
, thus we can choose
$z$
, thus we can choose
![]() $\boldsymbol{k}=k_{x}\hat{\boldsymbol{x}}+k_{y}\hat{\boldsymbol{y}}$
. The dot product in the exponential can now be expressed as
$\boldsymbol{k}=k_{x}\hat{\boldsymbol{x}}+k_{y}\hat{\boldsymbol{y}}$
. The dot product in the exponential can now be expressed as
![]() $\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}=kr\cos \unicode[STIX]{x1D703}$
, with
$\boldsymbol{k}\boldsymbol{\cdot }\boldsymbol{x}=kr\cos \unicode[STIX]{x1D703}$
, with
![]() $r$
the radial distance from the origin and
$r$
the radial distance from the origin and
![]() $\unicode[STIX]{x1D703}$
the angle between the two vectors
$\unicode[STIX]{x1D703}$
the angle between the two vectors
![]() $\boldsymbol{k}$
and
$\boldsymbol{k}$
and
![]() $\boldsymbol{x}$
. Rewriting the integral in cylindrical coordinates we have:
$\boldsymbol{x}$
. Rewriting the integral in cylindrical coordinates we have:
The angular integration can be carried out and it gives:
 $$\begin{eqnarray}u_{1}(r)=\frac{-F_{0}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}\int _{0}^{\infty }\frac{k^{2}}{\left(-{\displaystyle \frac{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D6FE}}}+k^{3}\right)}\text{J}_{0}(kr)\,\text{d}k,\end{eqnarray}$$
$$\begin{eqnarray}u_{1}(r)=\frac{-F_{0}}{4\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}}\int _{0}^{\infty }\frac{k^{2}}{\left(-{\displaystyle \frac{\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D6FE}}}+k^{3}\right)}\text{J}_{0}(kr)\,\text{d}k,\end{eqnarray}$$
with
![]() $\text{J}_{0}$
the Bessel function of the first kind and zeroth order. The solution of the above integral proceeds through partial fraction decomposition to give:
$\text{J}_{0}$
the Bessel function of the first kind and zeroth order. The solution of the above integral proceeds through partial fraction decomposition to give:
with
![]() $a=(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}^{2}/\unicode[STIX]{x1D6FE})$
. The above integrals are known, see formulas (2.12.3.6) and (2.12.3.12) in Prudnikov et al. (Reference Prudnikov, Brychkov, Marichev and Romer1988). Their evaluation gives:
$a=(\unicode[STIX]{x1D70C}\unicode[STIX]{x1D714}^{2}/\unicode[STIX]{x1D6FE})$
. The above integrals are known, see formulas (2.12.3.6) and (2.12.3.12) in Prudnikov et al. (Reference Prudnikov, Brychkov, Marichev and Romer1988). Their evaluation gives:
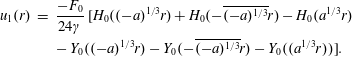 $$\begin{eqnarray}\displaystyle u_{1}(r) & = & \displaystyle \frac{-F_{0}}{24\unicode[STIX]{x1D6FE}} [\!H_{0}((-a)^{1/3}r)+H_{0}(-\overline{(-a)^{1/3}}r)-H_{0}(a^{1/3}r)\nonumber\\ \displaystyle & & \displaystyle -\,Y_{0}((-a)^{1/3}r)-Y_{0}(-\overline{(-a)^{1/3}}r)-Y_{0}((a^{1/3}r))\!]\!.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle u_{1}(r) & = & \displaystyle \frac{-F_{0}}{24\unicode[STIX]{x1D6FE}} [\!H_{0}((-a)^{1/3}r)+H_{0}(-\overline{(-a)^{1/3}}r)-H_{0}(a^{1/3}r)\nonumber\\ \displaystyle & & \displaystyle -\,Y_{0}((-a)^{1/3}r)-Y_{0}(-\overline{(-a)^{1/3}}r)-Y_{0}((a^{1/3}r))\!]\!.\end{eqnarray}$$











