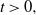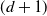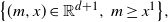1. Introduction
The goal of this paper is to study the law of the pair
![]() $(M_t, X_t)$
where X is a d-dimensional diffusion and M is the running maximum of the first component. In a previous work [Reference Coutin and Pontier9], using Malliavin calculus and specifically Nualart’s seminal book [Reference Nualart21], we have proved that, for any
$(M_t, X_t)$
where X is a d-dimensional diffusion and M is the running maximum of the first component. In a previous work [Reference Coutin and Pontier9], using Malliavin calculus and specifically Nualart’s seminal book [Reference Nualart21], we have proved that, for any
![]() $t> 0$
, the law of
$t> 0$
, the law of
![]() $V_t\,:\!=\,\big(M_t,X_t\big)$
is absolutely continuous with respect to the Lebesgue measure with density
$V_t\,:\!=\,\big(M_t,X_t\big)$
is absolutely continuous with respect to the Lebesgue measure with density
![]() $p_V(.;\,t)$
, and that the support of this density is included in the set
$p_V(.;\,t)$
, and that the support of this density is included in the set
![]() ${\big\{(m,x)\in \mathbb{R}^{d+1},\,m\geq x^1\big\}}$
.
${\big\{(m,x)\in \mathbb{R}^{d+1},\,m\geq x^1\big\}}$
.
In the present work, we prove that the density
![]() $p_V$
is a weak solution of a partial differential equation (PDE). Furthermore, we exhibit a boundary condition on the set
$p_V$
is a weak solution of a partial differential equation (PDE). Furthermore, we exhibit a boundary condition on the set
![]() $\{(m,x)\in \mathbb{R}^{d+1},\,m=x^1\}.$
This work extends the results given in [Reference Coutin, Ngom and Pontier8] and in Ngom’s thesis [Reference Ngom20], obtained in the case where X is a Lévy process, where it is proved that the density is a weak solution to an integro-differential equation.
$\{(m,x)\in \mathbb{R}^{d+1},\,m=x^1\}.$
This work extends the results given in [Reference Coutin, Ngom and Pontier8] and in Ngom’s thesis [Reference Ngom20], obtained in the case where X is a Lévy process, where it is proved that the density is a weak solution to an integro-differential equation.
In the literature, there exist many studies of the law of
![]() $V_t$
. When the process X is a Brownian motion, one can refer to [Reference He, Keirstead and Rebholz15, Reference Jeanblanc, Yor and Chesney17], where an explicit expression for
$V_t$
. When the process X is a Brownian motion, one can refer to [Reference He, Keirstead and Rebholz15, Reference Jeanblanc, Yor and Chesney17], where an explicit expression for
![]() $p_V$
is given. When X is a one-dimensional linear diffusion, [Reference Csáki, Földes and Salminen11] provides an expression for
$p_V$
is given. When X is a one-dimensional linear diffusion, [Reference Csáki, Földes and Salminen11] provides an expression for
![]() $p_V$
using the scale function, the speed measure, and the density of the law of some hitting times. See also [Reference Alili, Patie and Pedersen1, Reference Blanchet-Scalliet, Dorobantu and Gay4] for the particular case of an Ornstein–Uhlenbeck process. For some applications to the local score of a biological sequence, see [Reference Lagnoux, Mercier and Vallois19], which presents the case of reflected Brownian motion. The law of the maximum
$p_V$
using the scale function, the speed measure, and the density of the law of some hitting times. See also [Reference Alili, Patie and Pedersen1, Reference Blanchet-Scalliet, Dorobantu and Gay4] for the particular case of an Ornstein–Uhlenbeck process. For some applications to the local score of a biological sequence, see [Reference Lagnoux, Mercier and Vallois19], which presents the case of reflected Brownian motion. The law of the maximum
![]() $M_t$
is studied in [Reference Azaïs and Wschebor2] for general Gaussian processes. The case of a Lévy process X has been deeply investigated in the literature; see for instance [Reference Doney and Kyprianou12, Reference Ngom20]. Moreover, Section 2.4 in Ngom’s thesis [Reference Ngom20] provides the existence and the regularity of the joint law density of the process
$M_t$
is studied in [Reference Azaïs and Wschebor2] for general Gaussian processes. The case of a Lévy process X has been deeply investigated in the literature; see for instance [Reference Doney and Kyprianou12, Reference Ngom20]. Moreover, Section 2.4 in Ngom’s thesis [Reference Ngom20] provides the existence and the regularity of the joint law density of the process
![]() $\big(M_t,X_t\big)$
for a Lévy process X. In the case where X is a martingale (see e.g. [Reference Duembgen and Rogers13, Reference Rogers22] or [Reference Cox and Obloj10, Reference Henry-Labordère, Obloj, Spoida and Touzi16]), the law of the running maximum is provided.
$\big(M_t,X_t\big)$
for a Lévy process X. In the case where X is a martingale (see e.g. [Reference Duembgen and Rogers13, Reference Rogers22] or [Reference Cox and Obloj10, Reference Henry-Labordère, Obloj, Spoida and Touzi16]), the law of the running maximum is provided.
Such studies concerning this running maximum are useful in the areas of finance which involve hitting times, for instance for the pricing of barrier options. It is known that the law of hitting times is closely related to that of the running maximum; see [Reference Brown, Hobson and Rogers6, Reference Coutin and Dorobantu7, Reference Roynette, Vallois and Volpi23]. As an application of our work, consider a firm whose activity is characterized by a set of processes
![]() $\big(X^1,\ldots,X^d\big)$
, one of which, e.g.
$\big(X^1,\ldots,X^d\big)$
, one of which, e.g.
![]() $X^1$
, is linked to an alarm; namely, when there exists
$X^1$
, is linked to an alarm; namely, when there exists
![]() $s\leq t$
such that
$s\leq t$
such that
![]() $X^1_s$
exceeds a threshold a, which is equivalent to
$X^1_s$
exceeds a threshold a, which is equivalent to
![]() $M_t=\sup_{0\leq s\leq t} {{X_s^1}}\geq a,$
it is important to perform some action. So the firm needs to know the law of such a pair
$M_t=\sup_{0\leq s\leq t} {{X_s^1}}\geq a,$
it is important to perform some action. So the firm needs to know the law of such a pair
![]() $\big(M_t,X_t\big)$
; more specifically, the law of the stopping time
$\big(M_t,X_t\big)$
; more specifically, the law of the stopping time
![]() $\tau_a= \inf\big\{u, X^1_u \geq a\big\}$
is linked to the law of M as follows:
$\tau_a= \inf\big\{u, X^1_u \geq a\big\}$
is linked to the law of M as follows:
![]() $\{\tau_a\leq t\}=\{M_t\geq a\}.$
To know the probability of such an alarm, it is useful to know the law of the pair
$\{\tau_a\leq t\}=\{M_t\geq a\}.$
To know the probability of such an alarm, it is useful to know the law of the pair
![]() $\big(M_t,X_t\big)$
.
$\big(M_t,X_t\big)$
.
We provide an infinite expansion of the density of the law of the pair
![]() $\big(M_t,X_t\big)$
, which can lead to a numerical approximation.
$\big(M_t,X_t\big)$
, which can lead to a numerical approximation.
Let
![]() $(\Omega,{\mathcal{F}}, {\mathbb P})$
be a probability space endowed with a d-dimensional Brownian motion
$(\Omega,{\mathcal{F}}, {\mathbb P})$
be a probability space endowed with a d-dimensional Brownian motion
![]() $W$
. Let X be the diffusion process with values in
$W$
. Let X be the diffusion process with values in
![]() $\mathbb{R}^d$
which solves
$\mathbb{R}^d$
which solves
where
![]() $X_0$
is a random variable independent of the Brownian motion W, with law
$X_0$
is a random variable independent of the Brownian motion W, with law
![]() $ \mu_0$
, and A (resp. B) is a map from
$ \mu_0$
, and A (resp. B) is a map from
![]() $\mathbb{R}^d$
to the set of
$\mathbb{R}^d$
to the set of
![]() $(d\times d)$
matrices (resp. to
$(d\times d)$
matrices (resp. to
![]() $\mathbb{R}^d).$
Let us denote by
$\mathbb{R}^d).$
Let us denote by
![]() $C^i_b\big(\mathbb{R}^d,\mathbb{R}^n\big)$
the set of functions on
$C^i_b\big(\mathbb{R}^d,\mathbb{R}^n\big)$
the set of functions on
![]() $\mathbb{R}^d$
which are i times differentiable, bounded, with bounded derivatives, taking their values in
$\mathbb{R}^d$
which are i times differentiable, bounded, with bounded derivatives, taking their values in
![]() $\mathbb{R}^n$
. Let
$\mathbb{R}^n$
. Let
![]() ${\mathbb{F}}=({\mathcal{F}}_t,t\geq 0)$
be the completed right-continuous filtration defined by
${\mathbb{F}}=({\mathcal{F}}_t,t\geq 0)$
be the completed right-continuous filtration defined by
![]() $ {\mathcal{F}}_t\,:\!=\,\sigma\{X_0,\,W_s,s\leq t\}\vee {\mathcal N}$
, where
$ {\mathcal{F}}_t\,:\!=\,\sigma\{X_0,\,W_s,s\leq t\}\vee {\mathcal N}$
, where
![]() ${\mathcal N}$
is the set of negligible sets of
${\mathcal N}$
is the set of negligible sets of
![]() ${\mathcal F}.$
${\mathcal F}.$
Under classical assumptions on A and B (cf. (4) and (5) below), according to [Reference Coutin and Pontier9], for all
![]() $t>0$
, the law of
$t>0$
, the law of
![]() $V_t=\big(\!\sup_{u\leq t} X^1_t,X_t\big)$
has a density with respect to the Lebesgue measure on
$V_t=\big(\!\sup_{u\leq t} X^1_t,X_t\big)$
has a density with respect to the Lebesgue measure on
![]() ${\mathbb R}^{d+1}.$
${\mathbb R}^{d+1}.$
The main results and notation are given in Section 2: in the d-dimensional case, under a quite natural assumption (namely, Hypothesis 2.1 below) on the regularity of
![]() $p_V$
around the boundary of
$p_V$
around the boundary of
![]() $\Delta,$
we have that
$\Delta,$
we have that
![]() $p_V$
is a weak solution of a Fokker–Planck PDE on the subset of
$p_V$
is a weak solution of a Fokker–Planck PDE on the subset of
![]() $\mathbb{R}^{d+1}$
defined by
$\mathbb{R}^{d+1}$
defined by
![]() $\big\{(m,x),\,m\geq x^1\big\}.$
When
$\big\{(m,x),\,m\geq x^1\big\}.$
When
![]() $A=I_d,$
this assumption is satisfied; see Theorem 2.4. The main results are proved in Section 3 under Hypothesis 2.1. Section 4 is devoted to proving that Hypothesis 2.1 is satisfied when
$A=I_d,$
this assumption is satisfied; see Theorem 2.4. The main results are proved in Section 3 under Hypothesis 2.1. Section 4 is devoted to proving that Hypothesis 2.1 is satisfied when
![]() $A= I_d.$
The main tool is an infinite expansion of
$A= I_d.$
The main tool is an infinite expansion of
![]() $p_V$
given in Proposition 3.2 In Section 5, which treats the one-dimensional case, a Lamperti transformation [Reference Lamperti18] allows us to get the main result for any
$p_V$
given in Proposition 3.2 In Section 5, which treats the one-dimensional case, a Lamperti transformation [Reference Lamperti18] allows us to get the main result for any
![]() $A\in C^2_b(\mathbb{R},\mathbb{R}).$
Finally, the appendix contains some technical tools that are useful for the proofs of main results.
$A\in C^2_b(\mathbb{R},\mathbb{R}).$
Finally, the appendix contains some technical tools that are useful for the proofs of main results.
2. Main results and some notation
In this section, we give our main results. (As mentioned in the introduction, the proofs will be given later on.)
2.1. Notation
Let
![]() $\Delta$
be the open set of
$\Delta$
be the open set of
![]() $\mathbb{R}^{D+1}$
given by
$\mathbb{R}^{D+1}$
given by
![]() $\Delta\,:\!=\, \big\{(m,x),\ m\in \mathbb{R},\ x \in\mathbb{R}^{d},\ m> x^1,\ x=\big(x^1,\ldots,x^d\big)\big\}.$
From now on, we use Einstein’s convention. The infinitesimal generator
$\Delta\,:\!=\, \big\{(m,x),\ m\in \mathbb{R},\ x \in\mathbb{R}^{d},\ m> x^1,\ x=\big(x^1,\ldots,x^d\big)\big\}.$
From now on, we use Einstein’s convention. The infinitesimal generator
![]() ${\mathcal L}$
of the diffusion X defined in (1) is the partial differential operator on the space
${\mathcal L}$
of the diffusion X defined in (1) is the partial differential operator on the space
![]() $C^2(\mathbb{R}^d,\mathbb{R})$
given by
$C^2(\mathbb{R}^d,\mathbb{R})$
given by
where
![]() $A^t$
denotes the transposed matrix.
$A^t$
denotes the transposed matrix.
Its adjoint operator is
![]() ${{\mathcal{L}}^*f= {\frac{1}{2}} \Sigma^{ij}\partial^2_{ij}f -\big[B^i-\partial_j\big(\Sigma^{ij}\big)\big]\partial_if -\big[\partial_iB^i-{\frac{1}{2}}\partial^2_{ij} \big(\Sigma^{ij}\big)\big]f}$
, where
${{\mathcal{L}}^*f= {\frac{1}{2}} \Sigma^{ij}\partial^2_{ij}f -\big[B^i-\partial_j\big(\Sigma^{ij}\big)\big]\partial_if -\big[\partial_iB^i-{\frac{1}{2}}\partial^2_{ij} \big(\Sigma^{ij}\big)\big]f}$
, where
![]() $\Sigma\,:\!=\,AA^t.$
In what follows, the operators
$\Sigma\,:\!=\,AA^t.$
In what follows, the operators
![]() ${\mathcal{L}}$
and
${\mathcal{L}}$
and
![]() ${\mathcal{L}}^* $
are extended to the space
${\mathcal{L}}^* $
are extended to the space
![]() $C^2\big(\mathbb{R}^{d+1},\mathbb{R}\big)$
, for
$C^2\big(\mathbb{R}^{d+1},\mathbb{R}\big)$
, for
![]() $\Phi \in C^2\big(\mathbb{R}^{d+1},\mathbb{R}\big)$
, as
$\Phi \in C^2\big(\mathbb{R}^{d+1},\mathbb{R}\big)$
, as
and
 \begin{align*} {\mathcal{L}}^*&(\Phi)(m,x)= \\ &{\frac{1}{2}}\Sigma^{ij}(x) \partial^2_{ij} \Phi(m,x)-[B^i-\partial_j\big(\Sigma^{ij}\big)](x)\partial_{x_i}\Phi(m,x)+\left[{\frac{1}{2}} \partial^2_{x_i,x_j}\Sigma^{ij}-\partial_{x_i}B^i\right](x)\Phi(m,x).\end{align*}
\begin{align*} {\mathcal{L}}^*&(\Phi)(m,x)= \\ &{\frac{1}{2}}\Sigma^{ij}(x) \partial^2_{ij} \Phi(m,x)-[B^i-\partial_j\big(\Sigma^{ij}\big)](x)\partial_{x_i}\Phi(m,x)+\left[{\frac{1}{2}} \partial^2_{x_i,x_j}\Sigma^{ij}-\partial_{x_i}B^i\right](x)\Phi(m,x).\end{align*}
We stress that these operators are degenerate, since no derivative with respect to the variable m appears.
Let
![]() $A^1(x)$
be the d-dimensional vector
$A^1(x)$
be the d-dimensional vector
![]() $A^1(x)=\big(A^1_j(x),\ j=1,\ldots,d\big)\in \mathbb{R}^d$
corresponding to the first column of A(x); similarly
$A^1(x)=\big(A^1_j(x),\ j=1,\ldots,d\big)\in \mathbb{R}^d$
corresponding to the first column of A(x); similarly
![]() $A_j(x)$
denotes its jth row.
$A_j(x)$
denotes its jth row.
Recall that M denotes the running maximum of the first component of X, meaning
![]() $M_t=\sup_{0\leq s\leq t} \big\{X^1_s\big\}$
, and V is the
$M_t=\sup_{0\leq s\leq t} \big\{X^1_s\big\}$
, and V is the
![]() $\mathbb{R}^{d+1}$
-valued process defined by
$\mathbb{R}^{d+1}$
-valued process defined by
![]() $(V_t=(M_t, X_t), \forall t\geq 0).$
Finally,
$(V_t=(M_t, X_t), \forall t\geq 0).$
Finally,
![]() $\tilde x\in\mathbb{R}^{d-1}$
denotes the vector
$\tilde x\in\mathbb{R}^{d-1}$
denotes the vector
![]() $(x_2,\ldots,x_d).$
$(x_2,\ldots,x_d).$
In [Reference Coutin and Pontier9], under Assumptions (4) and (5) below, when the initial value is deterministic,
![]() $X_0=x_0 \in {\mathbb R}^d$
, the density of
$X_0=x_0 \in {\mathbb R}^d$
, the density of
![]() $V_t$
exists and is denoted by
$V_t$
exists and is denoted by
![]() $p_V(.;\,t,x_0)$
. If
$p_V(.;\,t,x_0)$
. If
![]() $\mu_0$
is the distribution of
$\mu_0$
is the distribution of
![]() $X_0$
, the density of the law of
$X_0$
, the density of the law of
![]() $V_t$
with respect to the Lebesgue measure on
$V_t$
with respect to the Lebesgue measure on
![]() ${\mathbb R}^{d+1} $
is
${\mathbb R}^{d+1} $
is
When there is no ambiguity, the dependency on
![]() $\mu_0$
is omitted.
$\mu_0$
is omitted.
Since
![]() $M_t \geq X^1_t,$
the support of
$M_t \geq X^1_t,$
the support of
![]() $p_V(.;\,t,\mu_0)$
is contained in
$p_V(.;\,t,\mu_0)$
is contained in
![]() $\bar{\Delta}\,:\!=\,\left\{(m,x)\in {\mathbb R}^{d+1} | m\geq x^1\right\}.$
$\bar{\Delta}\,:\!=\,\left\{(m,x)\in {\mathbb R}^{d+1} | m\geq x^1\right\}.$
2.2. Main results
The aim of this article is to show that the density
![]() $p_V$
is a weak solution of a Fokker–Planck PDE. We assume that the coefficients B and A satisfy
$p_V$
is a weak solution of a Fokker–Planck PDE. We assume that the coefficients B and A satisfy
and that there exists a constant
![]() $c>0$
such that the Euclidean norm of any vector v satisfies
$c>0$
such that the Euclidean norm of any vector v satisfies
Our first result will be established under the following hypothesis, which is a quite natural assumption on the regularity of
![]() $p_V$
in the neighborhood of the boundary of
$p_V$
in the neighborhood of the boundary of
![]() $\Delta$
, since the set of times where the process M increases is included in the set
$\Delta$
, since the set of times where the process M increases is included in the set
![]() $\{t,\,\,M_t=X_t\}$
.
$\{t,\,\,M_t=X_t\}$
.
Hypothesis 2.1.
The density of the law of
![]() $V_t=\big(M_t,X_t\big),$
denoted by
$V_t=\big(M_t,X_t\big),$
denoted by
![]() $p_V$
(see (3)), satisfies the following:
$p_V$
(see (3)), satisfies the following:
-
(i) The map
 $(t,m,\tilde{x})\mapsto \sup_{u >0} p_V(m,m-u,\tilde{x};\,t)$
belongs to
$(t,m,\tilde{x})\mapsto \sup_{u >0} p_V(m,m-u,\tilde{x};\,t)$
belongs to
 $L^1([0,T] \times {\mathbb R}^d,dtdmd\tilde{x}).$
$L^1([0,T] \times {\mathbb R}^d,dtdmd\tilde{x}).$
-
(ii) For all
 $t>0$
, almost surely in
$t>0$
, almost surely in
 $(m,\tilde{x}) \in {\mathbb R}^d,$
$(m,\tilde{x}) \in {\mathbb R}^d,$
 $\lim_{u\rightarrow 0^+} p_V(m,m-u,\tilde{x};\,t)$
exists and is denoted by
$\lim_{u\rightarrow 0^+} p_V(m,m-u,\tilde{x};\,t)$
exists and is denoted by
 $ p_V(m,m,\tilde{x};\,t).$
$ p_V(m,m,\tilde{x};\,t).$
Theorem 2.2.
Assume that A and B fulfil (4) and (5) and that (M, X) fulfils Hypothesis 2.1. Then, for any initial law
![]() $\mu_0$
and
$\mu_0$
and
![]() $F \in C^2_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
,
$F \in C^2_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
,
 \begin{align}{\mathbb E}\left[F\big(M_t,X_t\big)\right)& ={\mathbb E} \left[ F\big(X^1_0,X_0\big)\right] + \int_0^t {\mathbb E} \left[ {\mathcal L}\left(F\right)(M_s,X_s)\right] ds\nonumber\\&+\frac{1}{2} {\int_0^t{\mathbb E}\left[\partial_mF\big(X^1_s,{X_s}\big)\|A^{1}(X_s)\|^2\frac{p_V\big(X^1_s,{X_s};\,s\big)}{p_{X}(X_s;\,s)}\right] ds.}\end{align}
\begin{align}{\mathbb E}\left[F\big(M_t,X_t\big)\right)& ={\mathbb E} \left[ F\big(X^1_0,X_0\big)\right] + \int_0^t {\mathbb E} \left[ {\mathcal L}\left(F\right)(M_s,X_s)\right] ds\nonumber\\&+\frac{1}{2} {\int_0^t{\mathbb E}\left[\partial_mF\big(X^1_s,{X_s}\big)\|A^{1}(X_s)\|^2\frac{p_V\big(X^1_s,{X_s};\,s\big)}{p_{X}(X_s;\,s)}\right] ds.}\end{align}
Actually,
![]() $p_X$
is the solution of the PDE
$p_X$
is the solution of the PDE
![]() $ \partial_t p= {\mathcal L}^* p,\ p(.;\,0)=\mu_0,$
where
$ \partial_t p= {\mathcal L}^* p,\ p(.;\,0)=\mu_0,$
where
![]() ${{\mathcal{L}}^*f= {\frac{1}{2}} \Sigma^{ij}\partial^2_{ij}f -\big[B^i-\partial_j\big(\Sigma^{ij}\big)\big]\partial_if -\big[\partial_iB^i-{\frac{1}{2}}\partial^2_{ij} \big(\Sigma^{ij}\big)\big]f}$
. Let
${{\mathcal{L}}^*f= {\frac{1}{2}} \Sigma^{ij}\partial^2_{ij}f -\big[B^i-\partial_j\big(\Sigma^{ij}\big)\big]\partial_if -\big[\partial_iB^i-{\frac{1}{2}}\partial^2_{ij} \big(\Sigma^{ij}\big)\big]f}$
. Let
![]() $a_{ij}\,:\!=\,\Sigma^{ij},$
$a_{ij}\,:\!=\,\Sigma^{ij},$
![]() $a_i\,:\!=\,\big[B^i-\partial_j\big(\Sigma^{ij}\big)\big]\partial_i,$
and
$a_i\,:\!=\,\big[B^i-\partial_j\big(\Sigma^{ij}\big)\big]\partial_i,$
and
![]() $ {a_0\,:\!=\,\partial_iB^i-{\frac{1}{2}}\partial^2_{ij}\big(\Sigma^{ij}\big)}.$
Under Assumptions (4) and (5), the operator
$ {a_0\,:\!=\,\partial_iB^i-{\frac{1}{2}}\partial^2_{ij}\big(\Sigma^{ij}\big)}.$
Under Assumptions (4) and (5), the operator
![]() ${\mathcal{L}}^*$
satisfies all the assumptions of [Reference Garroni and Menaldi14, Theorem 3.5] (see (3.2), (3.3), and (3.4) on p. 177). As a consequence of [Reference Garroni and Menaldi14, Theorem 3.5], line 14, we have
${\mathcal{L}}^*$
satisfies all the assumptions of [Reference Garroni and Menaldi14, Theorem 3.5] (see (3.2), (3.3), and (3.4) on p. 177). As a consequence of [Reference Garroni and Menaldi14, Theorem 3.5], line 14, we have
![]() $p_X(x;\,s)>0$
.
$p_X(x;\,s)>0$
.
Remark 2.1. (i) When A is the identity matrix of
![]() ${\mathbb R}^d$
(denoted by
${\mathbb R}^d$
(denoted by
![]() $I_d$
) and
$I_d$
) and
![]() $B\in C^1_b\big(\mathbb{R}^d,\mathbb{R}^d\big)$
, Hypothesis 2.1 is fulfilled; see Theorem 2.4 below. When
$B\in C^1_b\big(\mathbb{R}^d,\mathbb{R}^d\big)$
, Hypothesis 2.1 is fulfilled; see Theorem 2.4 below. When
![]() $d=1$
, using a Lamperti transformation [Reference Lamperti18], one can prove that Hypothesis 2.1 is always fulfilled; see Section 5.
$d=1$
, using a Lamperti transformation [Reference Lamperti18], one can prove that Hypothesis 2.1 is always fulfilled; see Section 5.
(ii) This result is similar to [Reference Coutin, Ngom and Pontier8, Theorem 2.1], where the process X is a Lévy process. Proposition 4 in [Reference Coutin, Ngom and Pontier8] gives a key to the last term in (6) with factor
![]() ${\frac{1}{2}}$
. First, roughly speaking, the local behavior of
${\frac{1}{2}}$
. First, roughly speaking, the local behavior of
![]() $X_t^1-X_s^1$
conditionally on
$X_t^1-X_s^1$
conditionally on
![]() ${\mathcal F}_s$
is that of
${\mathcal F}_s$
is that of
![]() $\|A^{1}(X_s)\|\big(W^1_{t}-X_s^1\big).$
So, as in the Brownian case, the running maximum M of
$\|A^{1}(X_s)\|\big(W^1_{t}-X_s^1\big).$
So, as in the Brownian case, the running maximum M of
![]() $X^1$
is increasing as soon as it is equal to
$X^1$
is increasing as soon as it is equal to
![]() $X^1$
and both M and
$X^1$
and both M and
![]() $X^1$
are increasing. It is well known that the Brownian process
$X^1$
are increasing. It is well known that the Brownian process
![]() $W^1$
is increasing with probability
$W^1$
is increasing with probability
![]() ${\frac{1}{2}}$
; more specifically, we have
${\frac{1}{2}}$
; more specifically, we have
![]() $\mathbb{P}\Big\{\lim_{t\rightarrow s+}\frac{W^1_t -W_s^1}{t-s}=-\infty\Big\}=\mathbb{P}\Big\{\lim_{t\rightarrow s+}\frac{W^1_t -W_s^1}{t-s}=+\infty\Big\} ={\frac{1}{2}}$
.
$\mathbb{P}\Big\{\lim_{t\rightarrow s+}\frac{W^1_t -W_s^1}{t-s}=-\infty\Big\}=\mathbb{P}\Big\{\lim_{t\rightarrow s+}\frac{W^1_t -W_s^1}{t-s}=+\infty\Big\} ={\frac{1}{2}}$
.
The starting point of the proof of Theorem 2.2 is Itô’s formula: let F belong to
![]() $C^2_b\big(\mathbb{R}^{d+1},\mathbb{R}\big)$
. The process M is increasing; hence
$C^2_b\big(\mathbb{R}^{d+1},\mathbb{R}\big)$
. The process M is increasing; hence
![]() $V=(M, X)$
is a semi-martingale. Applying Itô’s formula to F(V) and taking the expectation of both sides, we have
$V=(M, X)$
is a semi-martingale. Applying Itô’s formula to F(V) and taking the expectation of both sides, we have
The novelty comes from the third term in the right-hand side of the equation above. The following theorem, proved in Section 3, completes the proof of Theorem 2.2.
Theorem 2.3.
Assume that A and B fulfil (4) and (5) and that (M, X) fulfils Hypothesis 2.1. For every
![]() $\Psi \in C^1_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
, let
$\Psi \in C^1_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
, let
![]() $F_\psi$
be the map
$F_\psi$
be the map
Then
![]() $F_{\Psi}$
is absolutely continuous with respect to the Lebesgue measure, and its derivative is
$F_{\Psi}$
is absolutely continuous with respect to the Lebesgue measure, and its derivative is
Observe that, as expressed in Theorem 2.2, this derivative can be written as
 \begin{equation*}\frac{1}{2}{\mathbb E}\left[\Psi\big(X^1_t,{X_t}\big)\|A^{1}({X_t})\|^2\frac{p_V\big(X^1_t,{X_t};\,t\big)}{p_{X}( X_t;\,t)}\right].\end{equation*}
\begin{equation*}\frac{1}{2}{\mathbb E}\left[\Psi\big(X^1_t,{X_t}\big)\|A^{1}({X_t})\|^2\frac{p_V\big(X^1_t,{X_t};\,t\big)}{p_{X}( X_t;\,t)}\right].\end{equation*}
Remark 2.2. The above proposition provides an explicit formulation of the derivative of the function
![]() $F_\Psi.$
Note that the absolute continuity of
$F_\Psi.$
Note that the absolute continuity of
![]() $F_\psi$
could be established as a direct consequence of the existence of the density of the law of the hitting time
$F_\psi$
could be established as a direct consequence of the existence of the density of the law of the hitting time
![]() $\tau_a=\inf\!\big\{s\,:\,X^1_s\geq a\big\}$
when it exists, using the identity
$\tau_a=\inf\!\big\{s\,:\,X^1_s\geq a\big\}$
when it exists, using the identity
![]() $\{\tau_a\leq t\}=\{M_t\geq a\}.$
Conversely, it could be proved that the absolute continuity of
$\{\tau_a\leq t\}=\{M_t\geq a\}.$
Conversely, it could be proved that the absolute continuity of
![]() $F_\Psi$
yields the existence of the density of the law of the hitting time
$F_\Psi$
yields the existence of the density of the law of the hitting time
![]() $\tau_a$
, using a sequence of
$\tau_a$
, using a sequence of
![]() $C^2_b(\mathbb{R},\mathbb{R})$
functions
$C^2_b(\mathbb{R},\mathbb{R})$
functions
![]() $(F_n)$
approximating the indicator function
$(F_n)$
approximating the indicator function
![]() ${{\mathbf 1}}_{[a,\infty)}$
; namely, this density satisfies
${{\mathbf 1}}_{[a,\infty)}$
; namely, this density satisfies
![]() $f_{\tau_a}(t)={\frac{1}{2}} \int_{\mathbb{R}^{d-1}}p_V(a,a,\tilde x;\,t)d\tilde x.$
$f_{\tau_a}(t)={\frac{1}{2}} \int_{\mathbb{R}^{d-1}}p_V(a,a,\tilde x;\,t)d\tilde x.$
Theorem 2.4.
Assume that
![]() $A=I_d$
and B satisfies Assumption (4). Then, for all
$A=I_d$
and B satisfies Assumption (4). Then, for all
![]() $t>0$
, the distribution of the pair
$t>0$
, the distribution of the pair
![]() $\big(M_t,X_t\big)$
fulfils Hypothesis 2.1. As a consequence, for all
$\big(M_t,X_t\big)$
fulfils Hypothesis 2.1. As a consequence, for all
![]() $F\in C^2_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
,
$F\in C^2_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
,
 \begin{align*}&{\mathbb E}\left[F\big(M_t,X_t\big)\right] ={\mathbb E} \left[ F\big(X^1_0,X_0\big)\right] + \int_0^t {\mathbb E} \left[ {\mathcal L}\left(F\right)(M_s,X_s)\right] ds\\&+\frac{1}{2} \int_0^t{\mathbb E}\left[\partial_mF\big(X^1_s,{X_s}\big)\frac{p_V\big(X^1_s,{X_s};\,s\big)}{p_{X}( X_s;\,s)}\right] ds.\end{align*}
\begin{align*}&{\mathbb E}\left[F\big(M_t,X_t\big)\right] ={\mathbb E} \left[ F\big(X^1_0,X_0\big)\right] + \int_0^t {\mathbb E} \left[ {\mathcal L}\left(F\right)(M_s,X_s)\right] ds\\&+\frac{1}{2} \int_0^t{\mathbb E}\left[\partial_mF\big(X^1_s,{X_s}\big)\frac{p_V\big(X^1_s,{X_s};\,s\big)}{p_{X}( X_s;\,s)}\right] ds.\end{align*}
When
![]() $d=1$
, a Lamperti transformation leads to the following corollary.
$d=1$
, a Lamperti transformation leads to the following corollary.
Corollary 1.
Assume that
![]() $d=1$
, and A and B satisfy (4) and (5). Then the density
$d=1$
, and A and B satisfy (4) and (5). Then the density
![]() $p_V$
satisfies Hypothesis 2.1, so
$p_V$
satisfies Hypothesis 2.1, so
 \begin{align*}&{\mathbb E}\left[F\big(M_t,X_t\big)\right] ={\mathbb E} \left[ F(X_0,X_0)\right] + \int_0^t {\mathbb E} \left[ {\mathcal L}\left(F\right)(M_s,X_s)\right] ds\\&+\frac{1}{2} \int_0^t{\mathbb E}\left[A^2(X_s)\partial_mF(X_s,{X_s})\frac{p_V(X_s,{X_s};\,s)}{p_{X}( X_s;\,s)}\right] ds.\end{align*}
\begin{align*}&{\mathbb E}\left[F\big(M_t,X_t\big)\right] ={\mathbb E} \left[ F(X_0,X_0)\right] + \int_0^t {\mathbb E} \left[ {\mathcal L}\left(F\right)(M_s,X_s)\right] ds\\&+\frac{1}{2} \int_0^t{\mathbb E}\left[A^2(X_s)\partial_mF(X_s,{X_s})\frac{p_V(X_s,{X_s};\,s)}{p_{X}( X_s;\,s)}\right] ds.\end{align*}
Remark 2.3. If
![]() $p_V$
is regular enough, and if the initial law of
$p_V$
is regular enough, and if the initial law of
![]() $X_0$
satisfies
$X_0$
satisfies
![]() $\mu_0(dx)=f_0(x)dx$
, then Theorem 2.2 means that
$\mu_0(dx)=f_0(x)dx$
, then Theorem 2.2 means that
![]() $p_V$
is a weak solution in the set
$p_V$
is a weak solution in the set
![]() $\Delta$
of
$\Delta$
of
![]() $\partial_t p= {\mathcal{L}}^*p,$
where
$\partial_t p= {\mathcal{L}}^*p,$
where
![]() ${\mathcal{L}}^*f= {\frac{1}{2}} \Sigma^{ij}\partial^2_{ij}f -\big[B^i-\partial_j\big(\Sigma^{ij}\big)\big] \partial_if -\partial_iB^i-{\frac{1}{2}}\partial^2_{ij} \big(\Sigma^{ij}\big))f$
with boundary condition
${\mathcal{L}}^*f= {\frac{1}{2}} \Sigma^{ij}\partial^2_{ij}f -\big[B^i-\partial_j\big(\Sigma^{ij}\big)\big] \partial_if -\partial_iB^i-{\frac{1}{2}}\partial^2_{ij} \big(\Sigma^{ij}\big))f$
with boundary condition
This result is proved in Appendix A.3.
This boundary condition also appears in [Reference Blanchet-Scalliet, Dorobantu and Gay4, Proposition 4, Equation (11)] (Ornstein–Uhlenbeck process). Finally, a similar PDE is studied in [Reference Garroni and Menaldi14, Chapter 1.2], where the authors establish the existence of a unique strong solution of the PDE, but in the case of a non-degenerate elliptic operator.
3. Proof of Theorem 2.3
We start this section with a roadmap for the proof of Theorem 2.3. First we compute the right derivative of the map
![]() $F_\Psi\,:\,t\mapsto \mathbb{E}\big[\!\int_0^t\Psi(M_s,X_s)dM_s\big],$
namely
$F_\Psi\,:\,t\mapsto \mathbb{E}\big[\!\int_0^t\Psi(M_s,X_s)dM_s\big],$
namely
![]() $\lim_{h\to 0^+}T_{h,t}$
with
$\lim_{h\to 0^+}T_{h,t}$
with
![]() $T_{h,t}=\frac{1}{h}\mathbb{E}_{\mathbb{P}}\big[\int_t^{t+h}\psi(V_s)dM_s\big].$
A first step is the decomposition
$T_{h,t}=\frac{1}{h}\mathbb{E}_{\mathbb{P}}\big[\int_t^{t+h}\psi(V_s)dM_s\big].$
A first step is the decomposition
 \begin{align}T_{h,t}=\frac{1}{h}\mathbb{E}_\mathbb{P}\Bigg[\int_t^{t+h}(\psi(V_s)-\psi(V_t))dM_s\Bigg]+\frac{1}{h}\mathbb{E}_\mathbb{P}[\psi(V_t)\big(M_{t+h}-M_t\big)].\end{align}
\begin{align}T_{h,t}=\frac{1}{h}\mathbb{E}_\mathbb{P}\Bigg[\int_t^{t+h}(\psi(V_s)-\psi(V_t))dM_s\Bigg]+\frac{1}{h}\mathbb{E}_\mathbb{P}[\psi(V_t)\big(M_{t+h}-M_t\big)].\end{align}
Since
![]() $\psi\in C^1_b\big(\mathbb{R}^{d+1},\mathbb{R}\big)$
and the process M is increasing, the first term in (8) is dominated by
$\psi\in C^1_b\big(\mathbb{R}^{d+1},\mathbb{R}\big)$
and the process M is increasing, the first term in (8) is dominated by
 \begin{equation*}\mathbb{E}\left[\int_t^{t+h}(\psi(V_s)-\psi(V_t))dM_s\right]\leq\|\nabla\psi\|_\infty \mathbb{E}\left[\sup_{t\leq s\leq t+h}\|V_s-V_t\|\big(M_{t+h}-M_t\big)\right].\end{equation*}
\begin{equation*}\mathbb{E}\left[\int_t^{t+h}(\psi(V_s)-\psi(V_t))dM_s\right]\leq\|\nabla\psi\|_\infty \mathbb{E}\left[\sup_{t\leq s\leq t+h}\|V_s-V_t\|\big(M_{t+h}-M_t\big)\right].\end{equation*}
Lemma 3.1 states that
![]() $\sup_{t\leq s\leq t+h}\|X_s-X_t\|_p= {O\big(\sqrt h\big)} $
, and Lemma 3.2 yields
$\sup_{t\leq s\leq t+h}\|X_s-X_t\|_p= {O\big(\sqrt h\big)} $
, and Lemma 3.2 yields
![]() $\|M_{t+h}-M_t\|_p={o\big(\sqrt h\big)}$
, so that that this first term is o(h).
$\|M_{t+h}-M_t\|_p={o\big(\sqrt h\big)}$
, so that that this first term is o(h).
Concerning the second term in (8),
![]() $M_{t+h}-M_t$
can be written as
$M_{t+h}-M_t$
can be written as
![]() $\sup_{0\leq u\leq h} \big(X^1_{t+h}-X^1_t-M_t+X^1_t\big)_+$
. In order to use the independence of the increments of Brownian motion, we introduce a new process, independent of
$\sup_{0\leq u\leq h} \big(X^1_{t+h}-X^1_t-M_t+X^1_t\big)_+$
. In order to use the independence of the increments of Brownian motion, we introduce a new process, independent of
![]() ${\mathcal{F}}_t$
, which is an approximation of
${\mathcal{F}}_t$
, which is an approximation of
![]() $X^1_{t+u}-X^1_t:$
$X^1_{t+u}-X^1_t:$
Lemma 3.4(ii) will set
![]() ${\mathbb{E}\left[|M_{t+h}-M_t- \left(M_{t,h}-M_t+X_t^1\right)_+| \right]=o(h),}$
where
${\mathbb{E}\left[|M_{t+h}-M_t- \left(M_{t,h}-M_t+X_t^1\right)_+| \right]=o(h),}$
where
![]() $(x)_+=\max\!(x,0)$
. Thus,
$(x)_+=\max\!(x,0)$
. Thus,
Observe that the law of
![]() $M_{t,h}$
given
$M_{t,h}$
given
![]() ${\mathcal{F}}_t$
is the law of
${\mathcal{F}}_t$
is the law of
![]() $\|A^1(X_t)\| \sup_{0\leq u\leq h} \hat W^1_u$
; then, using the function
$\|A^1(X_t)\| \sup_{0\leq u\leq h} \hat W^1_u$
; then, using the function
![]() ${{\mathcal{H}}}$
from (13), an
${{\mathcal{H}}}$
from (13), an
![]() ${\mathcal{F}}_t$
-conditioning yields
${\mathcal{F}}_t$
-conditioning yields
Then
as given in Proposition 3.1(ii). In Proposition 3.2, under Hypothesis 2.1, we compute
![]() $\lim_{h\to 0}T_{h;\,t}.$
$\lim_{h\to 0}T_{h;\,t}.$
Finally in Section 3.4 we prove that
![]() $F_\psi\,:\, t\mapsto E\big[\int_0^t \psi(V_s)dM_s\big]$
is an absolutely continuous function with respect to the Lebesgue measure, integral of its right derivative. Actually we prove that
$F_\psi\,:\, t\mapsto E\big[\int_0^t \psi(V_s)dM_s\big]$
is an absolutely continuous function with respect to the Lebesgue measure, integral of its right derivative. Actually we prove that
![]() $F_\psi$
is a continuous function belonging to the Sobolev space
$F_\psi$
is a continuous function belonging to the Sobolev space
![]() $W^{1,1}(I),\,I=(0,T).$
This completes the proof of Theorem 2.3.
$W^{1,1}(I),\,I=(0,T).$
This completes the proof of Theorem 2.3.
The main propositions to prove are the following.
Proposition 3.1.
Let B and A fulfil (4) and (5), and let
![]() $\Psi \in C_b^1\big({\mathbb R}^{d+1},{\mathbb R}\big)$
. Recall that
$\Psi \in C_b^1\big({\mathbb R}^{d+1},{\mathbb R}\big)$
. Recall that
![]() $A^1$
is the vector
$A^1$
is the vector
![]() $\big(A^1_j,\ j=1,\ldots,d\big),$
and
$\big(A^1_j,\ j=1,\ldots,d\big),$
and
![]() $\|A^{1}(x)\|^2=\sum_{j=1}^d \big(A^{1}_j(x)\big)^2$
.
$\|A^{1}(x)\|^2=\sum_{j=1}^d \big(A^{1}_j(x)\big)^2$
.
-
(i) For every
 $T>0$
, there exists a constant
$T>0$
, there exists a constant
 $C>0$
(depending on
$C>0$
(depending on
 $\|A\|_{\infty},$
$\|A\|_{\infty},$
 $\|B\|_{\infty}$
,
$\|B\|_{\infty}$
,
 $ \|\nabla A\|_{\infty},$
$ \|\nabla A\|_{\infty},$
 $\|\Psi\|_{\infty},$
$\|\Psi\|_{\infty},$
 $\|\nabla \Psi\|_{\infty}$
, and T) such that for all
$\|\nabla \Psi\|_{\infty}$
, and T) such that for all
 $t\in [0,T]$
and
$t\in [0,T]$
and
 $h\in [0,1],$
(12)
$h\in [0,1],$
(12) \begin{equation} \left|\mathbb{E}\left[\int_t^{t+h}\Psi(V_s)dM_s-{2}\sqrt h \left(\Psi({V_t}){\|A^1(X_t)\|}{{\mathcal{H}}}\left(\frac{M_t-X^1_t}{\sqrt h \|A^1(X_t)\|}\right)\right)\right]\right|\leq C h {\|\nabla \Psi\|_\infty}.\end{equation}
\begin{equation} \left|\mathbb{E}\left[\int_t^{t+h}\Psi(V_s)dM_s-{2}\sqrt h \left(\Psi({V_t}){\|A^1(X_t)\|}{{\mathcal{H}}}\left(\frac{M_t-X^1_t}{\sqrt h \|A^1(X_t)\|}\right)\right)\right]\right|\leq C h {\|\nabla \Psi\|_\infty}.\end{equation}
-
(ii) For all
 $t>0$
and
$t>0$
and
 $h\in [0,1],$
$h\in [0,1],$
 \begin{equation*}\lim_{h\to 0+}\frac{1}{h} \left|\mathbb{E}\left[\int_t^{t+h}\Psi(V_s)dM_s\right]-{2}\sqrt h\mathbb{E}\left[\Psi({V_t}){\|A^{1}({X_t})\|}{{\mathcal{H}}}\left(\frac{M_t-X^1_t}{\sqrt h \|A^{1}({X_t})\|}\right)\right]\right|=0,\end{equation*}
\begin{equation*}\lim_{h\to 0+}\frac{1}{h} \left|\mathbb{E}\left[\int_t^{t+h}\Psi(V_s)dM_s\right]-{2}\sqrt h\mathbb{E}\left[\Psi({V_t}){\|A^{1}({X_t})\|}{{\mathcal{H}}}\left(\frac{M_t-X^1_t}{\sqrt h \|A^{1}({X_t})\|}\right)\right]\right|=0,\end{equation*}
where, denoting by
 $\Phi_G$
the standard Gaussian cumulative distribution function, we write
(13)
$\Phi_G$
the standard Gaussian cumulative distribution function, we write
(13) \begin{align}{{\mathcal{H}}}(\theta)\,:\!=\,\int_\theta^{\infty} \frac{1}{\sqrt{2\pi}} (y-\theta)e^{-\frac{y^2}{2}} dy=\frac{e^{-\frac{\theta^2}{2}}}{\sqrt{2\pi}}-\theta\Phi_{G}({-}\theta).\end{align}
\begin{align}{{\mathcal{H}}}(\theta)\,:\!=\,\int_\theta^{\infty} \frac{1}{\sqrt{2\pi}} (y-\theta)e^{-\frac{y^2}{2}} dy=\frac{e^{-\frac{\theta^2}{2}}}{\sqrt{2\pi}}-\theta\Phi_{G}({-}\theta).\end{align}
The following remark will be useful.
Remark 3.1. The definition of
![]() ${{\mathcal{H}}} $
in (13) implies that
${{\mathcal{H}}} $
in (13) implies that
![]() $\int_0^\infty {{\mathcal{H}}}(u)du=1/4$
. Moreover,
$\int_0^\infty {{\mathcal{H}}}(u)du=1/4$
. Moreover,
![]() ${{\mathcal{H}}}^{\prime}(\theta)= -\Phi_G({-}\theta)\leq 0;$
in particular,
${{\mathcal{H}}}^{\prime}(\theta)= -\Phi_G({-}\theta)\leq 0;$
in particular,
![]() ${{\mathcal{H}}}$
is non-increasing.
${{\mathcal{H}}}$
is non-increasing.
Proposition 3.2.
Assume that A and B fulfil (4) and (5) and that (M, X) fulfils Hypothesis 2.1. Then for all
![]() $\Psi \in C^1_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
, all
$\Psi \in C^1_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
, all
![]() $T>0$
, and all
$T>0$
, and all
![]() $t\geq 0$
, the following hold:
$t\geq 0$
, the following hold:
 \begin{align*}(i) \quad &t\mapsto \sup_{h >0}\frac{{2}\sqrt h}{h}\,\mathbb{E}\left[\Psi(V_t){\|A^1(X_t)\|}{{\mathcal{H}}}\left(\frac{M_t-X^1_t}{\sqrt h \|A^1(X_t)\|}\right)\right] \in L^1([0,T],{\mathbb R}); \\ (ii) \quad & \lim_{h \rightarrow 0^+} \frac{{2}\sqrt h}{h}\,\mathbb{E}\left[\Psi(V_t){\|A^1(X_t)\|}{{\mathcal{H}}}\left(\frac{M_t-X^1_t}{\sqrt h \|A^1(X_t)\|}\right)\right] \\ & \quad ={\frac{1}{2}}\int_{{\mathbb R}^d} \Psi(m,m,\tilde{x})\|A^1(m,\tilde{x})\|{^2}p_V(m,m,\tilde{x};\,t)dmd\tilde{x} \end{align*}
\begin{align*}(i) \quad &t\mapsto \sup_{h >0}\frac{{2}\sqrt h}{h}\,\mathbb{E}\left[\Psi(V_t){\|A^1(X_t)\|}{{\mathcal{H}}}\left(\frac{M_t-X^1_t}{\sqrt h \|A^1(X_t)\|}\right)\right] \in L^1([0,T],{\mathbb R}); \\ (ii) \quad & \lim_{h \rightarrow 0^+} \frac{{2}\sqrt h}{h}\,\mathbb{E}\left[\Psi(V_t){\|A^1(X_t)\|}{{\mathcal{H}}}\left(\frac{M_t-X^1_t}{\sqrt h \|A^1(X_t)\|}\right)\right] \\ & \quad ={\frac{1}{2}}\int_{{\mathbb R}^d} \Psi(m,m,\tilde{x})\|A^1(m,\tilde{x})\|{^2}p_V(m,m,\tilde{x};\,t)dmd\tilde{x} \end{align*}
As a corollary, the function
belongs to
![]() $ L^1([0,T],\mathbb{R}).$
$ L^1([0,T],\mathbb{R}).$
The proof of Proposition 3.1 will be obtained using the lemmas in the following section.
3.1. Tools for proving Proposition 3.1
Here we provide some estimates of the expectations of the increments of the processes X and M. Assumptions (4) and (5) allow us to introduce a constant K which denotes either
![]() $ \max\!(\|A\|_{\infty},\|B\|_{\infty})$
or
$ \max\!(\|A\|_{\infty},\|B\|_{\infty})$
or
![]() $ \max\!(\|A\|_{\infty},\|B\|_{\infty},$
$ \max\!(\|A\|_{\infty},\|B\|_{\infty},$
![]() $\|\nabla A\|_\infty).$
Let
$\|\nabla A\|_\infty).$
Let
![]() $C_p$
be the constant in the Burkholder–Davis–Gundy inequality (cf. [Reference Bain and Crisan3, Theorem B.36]).
$C_p$
be the constant in the Burkholder–Davis–Gundy inequality (cf. [Reference Bain and Crisan3, Theorem B.36]).
Lemma 3.1.
Let A and B be bounded. Then, for all
![]() $ 0<h\leq 1,$
for all
$ 0<h\leq 1,$
for all
![]() $ p\geq 1$
there exists a constant
$ p\geq 1$
there exists a constant
![]() $C_{p,K}$
(depending only on p and K) such that
$C_{p,K}$
(depending only on p and K) such that
 \begin{align*}{\sup_{t>0}}\,\mathbb{E} \left[ \sup_{0\leq s \leq h}\| X_{t+s} -X_t\|^p \right] \leq C_{p,K} h^{p/2}.\end{align*}
\begin{align*}{\sup_{t>0}}\,\mathbb{E} \left[ \sup_{0\leq s \leq h}\| X_{t+s} -X_t\|^p \right] \leq C_{p,K} h^{p/2}.\end{align*}
Proof. Using the fact that
![]() $(a+b)^p \leq 2^{p-1} \left[a^p +b^p \right],\,a,b\geq 0$
, one obtains
$(a+b)^p \leq 2^{p-1} \left[a^p +b^p \right],\,a,b\geq 0$
, one obtains
 \begin{align*}0\leq \sup_{s \leq h} \| X_{t+s}-X_t \|^p \leq 2^{p-1}\left[\sup_{u \leq h} \left( \Big\|\int_t^{t+u} B(X_s) ds\Big\| \right)^p+ \sup_{u \leq h}\left( \Big\|\int_t^{t+u} A_j(X_s) dW^j_s \Big\|\right)^p \right].\end{align*}
\begin{align*}0\leq \sup_{s \leq h} \| X_{t+s}-X_t \|^p \leq 2^{p-1}\left[\sup_{u \leq h} \left( \Big\|\int_t^{t+u} B(X_s) ds\Big\| \right)^p+ \sup_{u \leq h}\left( \Big\|\int_t^{t+u} A_j(X_s) dW^j_s \Big\|\right)^p \right].\end{align*}
If we take the expectation of both sides, the Burkholder–Davis–Gundy inequality implies
 \begin{equation*}\mathbb{E}\Big[\sup_{s \leq h} \| X_{t+s}-X_t \|^p\Big] \leq 2^{p-1}(1+C_p)\mathbb{E}\left[ \left( \int_{t}^{t+h} \|B(X_s) \|ds \right)^p+\left( \int_t^{t+h} \|A(X_s)\|^2 ds\right)^{p/2} \right].\end{equation*}
\begin{equation*}\mathbb{E}\Big[\sup_{s \leq h} \| X_{t+s}-X_t \|^p\Big] \leq 2^{p-1}(1+C_p)\mathbb{E}\left[ \left( \int_{t}^{t+h} \|B(X_s) \|ds \right)^p+\left( \int_t^{t+h} \|A(X_s)\|^2 ds\right)^{p/2} \right].\end{equation*}
Assumption (4) on B and A yields
 \begin{equation*}\mathbb{E}\left[\sup_{s \leq h}{\| X_{t+s}-X_t \|^p}\right] \leq 2^{p-1}(1+C_p)\big(h^{p}K^p+ h^{p/2} K^p\big).\end{equation*}
\begin{equation*}\mathbb{E}\left[\sup_{s \leq h}{\| X_{t+s}-X_t \|^p}\right] \leq 2^{p-1}(1+C_p)\big(h^{p}K^p+ h^{p/2} K^p\big).\end{equation*}
Lemma 3.2.
Let B and A satisfy Assumptions (4) and (5). Then, for all
![]() $ 0<h\leq 1,$
for all
$ 0<h\leq 1,$
for all
![]() $ p\geq 1$
we get
$ p\geq 1$
we get
Proof. Recall that
 \begin{equation*}M_{t+h}-M_t= \left( \sup_{0 \leq u \leq h} \big(X_{t+u}^1 - X_t^1\big)+X_t^1 - M_t \right)_+,\end{equation*}
\begin{equation*}M_{t+h}-M_t= \left( \sup_{0 \leq u \leq h} \big(X_{t+u}^1 - X_t^1\big)+X_t^1 - M_t \right)_+,\end{equation*}
recalling
![]() $(x)_+=\max\!(x,0).$
For any
$(x)_+=\max\!(x,0).$
For any
![]() $a \geq 0,$
one has
$a \geq 0,$
one has
![]() ${( x-a)_+} \leq |x|{{\mathbf 1}_{\{x >a\}}}$
; thus
${( x-a)_+} \leq |x|{{\mathbf 1}_{\{x >a\}}}$
; thus
The Cauchy–Schwarz inequality yields
 \begin{align*}0 &\leq \mathbb{E} \left[ \left( M_{t+h}-M_t\right)^p \right]\\&\leq \sqrt{\mathbb{E}\left[\Big| \sup_{0 \leq u \leq h} \big(X_{t+u}^1- X_t^1\big)\Big|^{2p} \right] {\mathbb P} \bigg( \bigg\{\sup_{0 \leq u \leq h} \big(X_{t+u}^1- X_t^1\big)> M_t-X_t^1\bigg\}\bigg)}.\end{align*}
\begin{align*}0 &\leq \mathbb{E} \left[ \left( M_{t+h}-M_t\right)^p \right]\\&\leq \sqrt{\mathbb{E}\left[\Big| \sup_{0 \leq u \leq h} \big(X_{t+u}^1- X_t^1\big)\Big|^{2p} \right] {\mathbb P} \bigg( \bigg\{\sup_{0 \leq u \leq h} \big(X_{t+u}^1- X_t^1\big)> M_t-X_t^1\bigg\}\bigg)}.\end{align*}
Replacing p by 2p in Lemma 3.1 leads to the inequality in (14), and the equality
holds almost surely. According to [Reference Coutin and Pontier9, Theorem 1.1] extended to
![]() $X_0$
with law
$X_0$
with law
![]() $\mu_0$
on
$\mu_0$
on
![]() $\mathbb{R}^d$
, the pair
$\mathbb{R}^d$
, the pair
![]() $\big(M_t,X_t\big)$
admits a density; thus
$\big(M_t,X_t\big)$
admits a density; thus
![]() ${\mathbb P} \{M_t-X_t^1=0\}=0$
holds almost surely. Therefore
${\mathbb P} \{M_t-X_t^1=0\}=0$
holds almost surely. Therefore
![]() $E\! \left( \left[ M_{t+h}-M_t\right]^p \right)$
is bounded by the product of
$E\! \left( \left[ M_{t+h}-M_t\right]^p \right)$
is bounded by the product of
![]() $h^{p/2}$
and a factor going to zero when h goes to 0, and this quantity is
$h^{p/2}$
and a factor going to zero when h goes to 0, and this quantity is
![]() $o(h^{p/2})$
.
$o(h^{p/2})$
.
For any fixed t we recall the process
![]() $(X_{t,u},\ u \in [0,h])$
and the running maximum of its first component as follows:
$(X_{t,u},\ u \in [0,h])$
and the running maximum of its first component as follows:
Lemma 3.3.
Under Assumptions (4) and (5), for every
![]() $ p\geq 1$
there exists a constant
$ p\geq 1$
there exists a constant
![]() $C_{p,K}$
such that for all
$C_{p,K}$
such that for all
![]() $ t\leq T$
, for all
$ t\leq T$
, for all
![]() $ h \in [0,1]$
,
$ h \in [0,1]$
,
 \begin{align*}\mathbb{E} \left[ \sup_{s \leq h} \big| X^1_{s+t}-X^1_t - X^1_{t,s}\big|^p \right]\leq C_{p,K}h^{p}.\end{align*}
\begin{align*}\mathbb{E} \left[ \sup_{s \leq h} \big| X^1_{s+t}-X^1_t - X^1_{t,s}\big|^p \right]\leq C_{p,K}h^{p}.\end{align*}
Proof. By definition, recalling
![]() $\hat{W}_u\,:\!=\, W_{t+u} - W_t$
,
$\hat{W}_u\,:\!=\, W_{t+u} - W_t$
,
![]() $u \geq 0,$
we obtain
$u \geq 0,$
we obtain
Once again using the inequality
![]() $(a+b)^p \leq 2^{p-1}(a^p+b^p ),\ a,b\geq 0,$
we get
$(a+b)^p \leq 2^{p-1}(a^p+b^p ),\ a,b\geq 0,$
we get
 \begin{align*}&\sup_{0\leq s \leq h} \big| X^1_{s+t}-X^1_t - X^1_{t,s}\big|^p \leq\\& 2^{p-1}\left[\left( {\int_0^h} {\|B^1(X_{u+t})\|} du\right)^p +\sup_{0\leq s \leq h} \left\| {\int_0^s} \left[ A^1(X_{u+t}) - A^1(X_t)\right] d{\hat{W}}_u\right\|^p \right]. \end{align*}
\begin{align*}&\sup_{0\leq s \leq h} \big| X^1_{s+t}-X^1_t - X^1_{t,s}\big|^p \leq\\& 2^{p-1}\left[\left( {\int_0^h} {\|B^1(X_{u+t})\|} du\right)^p +\sup_{0\leq s \leq h} \left\| {\int_0^s} \left[ A^1(X_{u+t}) - A^1(X_t)\right] d{\hat{W}}_u\right\|^p \right]. \end{align*}
Taking the expectation of both sides and applying the Burkholder–Davis–Gundy inequality yields, with
![]() $D_p=2^{p-1}(1+ C_p)$
,
$D_p=2^{p-1}(1+ C_p)$
,
 \begin{align*} & \mathbb{E} \left[\sup_{0\leq s \leq h} \big| X^1_{s+t}-X^1_t - X^1_{t,s}\big|^p \right]\\& \qquad \leq D_p\left(\mathbb{E}\left[{\int_0^h} {\|B^1(X_{u+t}) \|}du\right]^p +\mathbb{E} \left| {\int_0^h} \|A^1(X_{u+t}) - A^1(X_t)\|^2 du\right|^{p/2}\right). \end{align*}
\begin{align*} & \mathbb{E} \left[\sup_{0\leq s \leq h} \big| X^1_{s+t}-X^1_t - X^1_{t,s}\big|^p \right]\\& \qquad \leq D_p\left(\mathbb{E}\left[{\int_0^h} {\|B^1(X_{u+t}) \|}du\right]^p +\mathbb{E} \left| {\int_0^h} \|A^1(X_{u+t}) - A^1(X_t)\|^2 du\right|^{p/2}\right). \end{align*}
The first term above is bounded by
![]() $K^ph^p$
, since B is bounded. The assumption that A belongs to
$K^ph^p$
, since B is bounded. The assumption that A belongs to
![]() $C^1_b\big(\mathbb{R}^d,\mathbb{R}^{d\times d}\big)$
and Jensen’s inequality imply that the second term is bounded by
$C^1_b\big(\mathbb{R}^d,\mathbb{R}^{d\times d}\big)$
and Jensen’s inequality imply that the second term is bounded by
![]() $K^ph^{p/2-1}{\int_0^h}E\|X_{u+t}-X_t\|^pdu$
; thus
$K^ph^{p/2-1}{\int_0^h}E\|X_{u+t}-X_t\|^pdu$
; thus
 \begin{equation*}\mathbb{E}\left[\sup_{0\leq s \leq h} \big| X^1_{s+t}-X^1_t - X^1_{t,s}\big|^p \right] \leq D_p{K^ph^{p/2-1}\left(h^{p/2+1} + {\int_0^h}\mathbb{E} \|X_{u+t}- X_t\|^pdu\right).}\end{equation*}
\begin{equation*}\mathbb{E}\left[\sup_{0\leq s \leq h} \big| X^1_{s+t}-X^1_t - X^1_{t,s}\big|^p \right] \leq D_p{K^ph^{p/2-1}\left(h^{p/2+1} + {\int_0^h}\mathbb{E} \|X_{u+t}- X_t\|^pdu\right).}\end{equation*}
From Lemma 3.1 we obtain the uniform upper bound
![]() $\mathbb{E} [\|X_{u+t}- X_t\|^p]\leq C_{p,K} u^{p/2}$
; hence,
$\mathbb{E} [\|X_{u+t}- X_t\|^p]\leq C_{p,K} u^{p/2}$
; hence,
 \begin{equation*}\mathbb{E} \left[\sup_{s \leq h} \big| X^1_{s+t}-X^1_t - X^1_{t,s}\big| ^p \right] \leq\frac{D_pK^pC_{p,K}}{\frac{p}{2}+1}h^p.\end{equation*}
\begin{equation*}\mathbb{E} \left[\sup_{s \leq h} \big| X^1_{s+t}-X^1_t - X^1_{t,s}\big| ^p \right] \leq\frac{D_pK^pC_{p,K}}{\frac{p}{2}+1}h^p.\end{equation*}
Lemma 3.4. Under Assumptions (4) and (5), the following hold:
-
(i) There exists
 $C>0$
such that
$C>0$
such that  \begin{equation*} \sup_{0 \leq t \leq T; \,\,\,0 \leq h \leq 1} h^{-1}\mathbb{E} \left[\left| M_{t+h}- M_t - \left( M_{t,h} - M_t + X_t^1\right)_+ \right|\right] \leq C<\infty. \end{equation*}
\begin{equation*} \sup_{0 \leq t \leq T; \,\,\,0 \leq h \leq 1} h^{-1}\mathbb{E} \left[\left| M_{t+h}- M_t - \left( M_{t,h} - M_t + X_t^1\right)_+ \right|\right] \leq C<\infty. \end{equation*}
-
(ii) We have
 \begin{equation*} \qquad \lim_{h \rightarrow 0^+} h^{-1}\mathbb{E}\left[ \left| M_{t+h}- M_t - \left( M_{t,h} - M_t + X_t^1\right)_+ \right|\right]=0. \end{equation*}
\begin{equation*} \qquad \lim_{h \rightarrow 0^+} h^{-1}\mathbb{E}\left[ \left| M_{t+h}- M_t - \left( M_{t,h} - M_t + X_t^1\right)_+ \right|\right]=0. \end{equation*}
Proof. First, observe that
and if f and g are functions on [0, T], then
hence
![]() $\sup_{s \leq T} f(s) - \sup_{u \leq T}g(u) \leq \sup_{v \leq T}|f(v) - g(v)|.$
Here the roles of f and g are symmetrical, so
$\sup_{s \leq T} f(s) - \sup_{u \leq T}g(u) \leq \sup_{v \leq T}|f(v) - g(v)|.$
Here the roles of f and g are symmetrical, so
![]() $\sup_{s \leq T} g(s) - \sup_{u \leq T}f(u) \leq \sup_{v \leq T}| f(v) - g(v)|,$
and
$\sup_{s \leq T} g(s) - \sup_{u \leq T}f(u) \leq \sup_{v \leq T}| f(v) - g(v)|,$
and
 \begin{equation}\left| \sup_{s \leq T} g(s) - \sup_{u \leq T}f(u) \right| \leq \sup_{v \leq T}|f(v) - g(v)|.\end{equation}
\begin{equation}\left| \sup_{s \leq T} g(s) - \sup_{u \leq T}f(u) \right| \leq \sup_{v \leq T}|f(v) - g(v)|.\end{equation}
We now consider
![]() $M_{t+h}-M_t =\left( \sup_{0 \leq u \leq h}\big(X_{u+t}^1 -X_t^1\big) -M_t + X_t^1\right)_{+};$
using (16),
$M_{t+h}-M_t =\left( \sup_{0 \leq u \leq h}\big(X_{u+t}^1 -X_t^1\big) -M_t + X_t^1\right)_{+};$
using (16),
 \begin{align*}&\left| M_{t+h}- M_t - \left( M_{t,h} - M_t + X_t^1\right)_+ \right|\leq\\& \left| \sup_{0 \leq u \leq h}\big(X_{u+t}^1 -X_t^1\big) - M_{t,h} \right| \left[ {\mathbf 1}_{\big\{\sup_{0 \leq u \leq h}\big(X_{u+t}^1 -X_t^1\big) > M_t-{X^1_t}\big\}} + {\mathbf 1}_{\big\{M_{t,h}> M_t-X_t^1\big\}} \right].\end{align*}
\begin{align*}&\left| M_{t+h}- M_t - \left( M_{t,h} - M_t + X_t^1\right)_+ \right|\leq\\& \left| \sup_{0 \leq u \leq h}\big(X_{u+t}^1 -X_t^1\big) - M_{t,h} \right| \left[ {\mathbf 1}_{\big\{\sup_{0 \leq u \leq h}\big(X_{u+t}^1 -X_t^1\big) > M_t-{X^1_t}\big\}} + {\mathbf 1}_{\big\{M_{t,h}> M_t-X_t^1\big\}} \right].\end{align*}
Then, for any t fixed, we apply the inequality (17) to the maps
![]() $g\,:\,u\mapsto X_{{u+t}}^1 {-X_t}^1$
and
$g\,:\,u\mapsto X_{{u+t}}^1 {-X_t}^1$
and
![]() $f\,:\,u\mapsto X_{t,u}^1$
. Then
$f\,:\,u\mapsto X_{t,u}^1$
. Then
 \begin{align*} &\left| M_{t+h}- M_t - \left( M_{t,h} - M_t + X_t^1\right)_+ \right| \leq \\& \quad \sup_{0\leq u \leq h} \left|X_{u+t}^1 -X_t^1 - X_{t,u}^1\right| \left[ {\mathbf 1}_{\big\{\sup_{0 \leq u \leq h}\big(X_{u+t}^1 -X_t^1\big) > M_t-X_t^1\big\}} + {\mathbf 1}_{\big\{M_{t,h}> M_t-X_t^1\big\}} \right].\end{align*}
\begin{align*} &\left| M_{t+h}- M_t - \left( M_{t,h} - M_t + X_t^1\right)_+ \right| \leq \\& \quad \sup_{0\leq u \leq h} \left|X_{u+t}^1 -X_t^1 - X_{t,u}^1\right| \left[ {\mathbf 1}_{\big\{\sup_{0 \leq u \leq h}\big(X_{u+t}^1 -X_t^1\big) > M_t-X_t^1\big\}} + {\mathbf 1}_{\big\{M_{t,h}> M_t-X_t^1\big\}} \right].\end{align*}
From the Cauchy–Schwarz inequality and the fact that
![]() $(a+b)^2 \leq 2\big(a^2+b^2\big),$
we get
$(a+b)^2 \leq 2\big(a^2+b^2\big),$
we get
 \begin{align*}&\mathbb{E} \left[ \left| M_{t+h}- M_t - \left( M_{t,h} - M_t + X_t^1\right)_+ \right|\right]\leq\\&\sqrt{2\mathbb{E}\left[\sup_{u \leq h} \left|X_{u+t}^1 -X_t^1 - X_{t,u}^1\right| ^2\right]\left( {\mathbb P} \Big\{\sup_{0 \leq u \leq h} \big(X_{u+t}^1 -X_t^1\big) > M_t-X_t^1\Big\}+{\mathbb P} \big\{M_{t,h}> M_t-X_t^1\big\} \right)}.\end{align*}
\begin{align*}&\mathbb{E} \left[ \left| M_{t+h}- M_t - \left( M_{t,h} - M_t + X_t^1\right)_+ \right|\right]\leq\\&\sqrt{2\mathbb{E}\left[\sup_{u \leq h} \left|X_{u+t}^1 -X_t^1 - X_{t,u}^1\right| ^2\right]\left( {\mathbb P} \Big\{\sup_{0 \leq u \leq h} \big(X_{u+t}^1 -X_t^1\big) > M_t-X_t^1\Big\}+{\mathbb P} \big\{M_{t,h}> M_t-X_t^1\big\} \right)}.\end{align*}
Lemma 3.3 with
![]() $p=2$
ensures that the map
$p=2$
ensures that the map
![]() $h \mapsto h^{-1}\sqrt{2\mathbb{E} \left[ \sup_{u \leq h} \left|X_{u+t}^1-X_t^1 - X_{t,u}^1\right| ^2\right]}$
is uniformly bounded in t. Concerning the second factor, we have the following:
$h \mapsto h^{-1}\sqrt{2\mathbb{E} \left[ \sup_{u \leq h} \left|X_{u+t}^1-X_t^1 - X_{t,u}^1\right| ^2\right]}$
is uniformly bounded in t. Concerning the second factor, we have the following:
-
• First, the almost sure continuity with respect to h ensures that the quantities
 $\lim_{h\rightarrow 0} \sup_{0 \leq u \leq h}\!\big(X_{u+t}^1 -X_t^1\big) $
and
$\lim_{h\rightarrow 0} \sup_{0 \leq u \leq h}\!\big(X_{u+t}^1 -X_t^1\big) $
and
 $\lim_{h\rightarrow 0} M_{t,h}$
are equal to 0.
$\lim_{h\rightarrow 0} M_{t,h}$
are equal to 0. -
• Second, the law of the pair
 $\big(M_t,X_t\big)$
admits a density with respect to the Lebesgue measure on
$\big(M_t,X_t\big)$
admits a density with respect to the Lebesgue measure on
 $\bar\Delta$
, according to [Reference Coutin and Pontier9, Theorem 1.1], so
$\bar\Delta$
, according to [Reference Coutin and Pontier9, Theorem 1.1], so
 ${\mathbb P}\big( \big\{0= M_t-X_t^1\big\}\big)=0$
, and the limit of the second factor is equal to
${\mathbb P}\big( \big\{0= M_t-X_t^1\big\}\big)=0$
, and the limit of the second factor is equal to
 $0.$
$0.$
This concludes the proof of the lemma.
Recall Definition (15):
![]() $X_{t,h}= A_j(X_t)\big[ W_{t+h}^j-W_t^j\big],\,{M_{t,h}=\mathbf{\sup_{0\leq u\leq h}} {X_{t,u}^1},}\,h \in [0,1].$
$X_{t,h}= A_j(X_t)\big[ W_{t+h}^j-W_t^j\big],\,{M_{t,h}=\mathbf{\sup_{0\leq u\leq h}} {X_{t,u}^1},}\,h \in [0,1].$
Lemma 3.5.
Under Assumptions (4) and (5), with
![]() ${{\mathcal{H}}}$
defined in (13), we have
${{\mathcal{H}}}$
defined in (13), we have
Proof. For any t fixed, conditionally on
![]() ${\mathcal F}_t$
, the process
${\mathcal F}_t$
, the process
![]() $\big(X_{t,u}^1,\ u \in [0,h]\big)$
from (9) has the same law as
$\big(X_{t,u}^1,\ u \in [0,h]\big)$
from (9) has the same law as
![]() $\big(\sqrt{h}\|A^{1}(X_t)\|\hat W_u,\,u\in [0,1]\big)$
, where
$\big(\sqrt{h}\|A^{1}(X_t)\|\hat W_u,\,u\in [0,1]\big)$
, where
![]() $\hat W$
is a Brownian motion independent of
$\hat W$
is a Brownian motion independent of
![]() ${\mathcal F}_t$
, and for any h, the random variable
${\mathcal F}_t$
, and for any h, the random variable
![]() $M_{t,h}$
has the same law as
$M_{t,h}$
has the same law as
![]() $ \sqrt{h}\|A^{1}(X_t)\|\sup_{u \leq 1}\hat{W}_u.$
$ \sqrt{h}\|A^{1}(X_t)\|\sup_{u \leq 1}\hat{W}_u.$
Following [Reference Jeanblanc, Yor and Chesney17, Section 3.1.3], the random variable
![]() $\sup_{u \leq 1}\hat W_u$
has the same law as
$\sup_{u \leq 1}\hat W_u$
has the same law as
![]() $|G|$
, where G is a standard Gaussian variable (independent of
$|G|$
, where G is a standard Gaussian variable (independent of
![]() ${\mathcal F}_t$
) with density
${\mathcal F}_t$
) with density
![]() $\frac{2}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}{\mathbf 1}_{[0,+\infty [}(z)$
. Then, using the function
$\frac{2}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}{\mathbf 1}_{[0,+\infty [}(z)$
. Then, using the function
![]() ${{\mathcal{H}}}$
introduced in (13), we have
${{\mathcal{H}}}$
introduced in (13), we have
 \begin{align*}\mathbb{E}\left[\big(M_{t,h} -\big(M_t -X_t^1\big)\big)_+ |{\mathcal F}_t \right]&= \int_0^{\infty} \left( \|A^{1}(X_t)\|\sqrt{h} z - \big(M_t -X_t^1\big)\right)_+ \frac{2}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}dz\\&= 2 \|A^{1}(X_t)\|\sqrt{h} {{\mathcal{H}}} \left( \frac{M_t -X_t^1}{\sqrt{h}\|A^{1}(X_t)\|} \right).\end{align*}
\begin{align*}\mathbb{E}\left[\big(M_{t,h} -\big(M_t -X_t^1\big)\big)_+ |{\mathcal F}_t \right]&= \int_0^{\infty} \left( \|A^{1}(X_t)\|\sqrt{h} z - \big(M_t -X_t^1\big)\right)_+ \frac{2}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}dz\\&= 2 \|A^{1}(X_t)\|\sqrt{h} {{\mathcal{H}}} \left( \frac{M_t -X_t^1}{\sqrt{h}\|A^{1}(X_t)\|} \right).\end{align*}
3.2. Proof of Proposition 3.1
Let
![]() $t>0$
. The key in this proof is to write the quantity
$t>0$
. The key in this proof is to write the quantity
 \begin{equation*}\mathbb{E}\left[\int_t^{t+h}\Psi(V_s)dM_s\right]-{2}\sqrt h\mathbb{E}\left[\Psi({V_t}){\|A^{1}({X_t})\|}{{\mathcal{H}}}\left(\frac{M_t-X_t^1}{\sqrt h \|A^{1}({X_t})\|}\right)\right]\end{equation*}
\begin{equation*}\mathbb{E}\left[\int_t^{t+h}\Psi(V_s)dM_s\right]-{2}\sqrt h\mathbb{E}\left[\Psi({V_t}){\|A^{1}({X_t})\|}{{\mathcal{H}}}\left(\frac{M_t-X_t^1}{\sqrt h \|A^{1}({X_t})\|}\right)\right]\end{equation*}
as the sum of three terms,
 \begin{align}&\mathbb{E}\Big[\int_t^{t+h}(\Psi(V_s)-\Psi(V_t))dM_s\Big]+{\mathbb{E}\Big[\Psi(V_t)\Big(\big(M_{t+h}-M_t\big)- \mathbb{E}\left[M_{t,h}-M_t+X_t^1\big)_+| {\mathcal F}_t \right]\Big)\Big]}\\&+\mathbb{E}\left[\Psi(V_t) {\mathbb{E}} \left[\big(M_{t,h}-M_t+X_t^1\big)_+\left| \right. {\mathcal F}_{t} \right]-{2}\sqrt h\Psi(V_t){\|A^{1}(X_t)\|}{{\mathcal{H}}}\left(\frac{M_t-X_t^1}{\sqrt h \|A^{1}(X_t)\|}\right)\right].\nonumber\end{align}
\begin{align}&\mathbb{E}\Big[\int_t^{t+h}(\Psi(V_s)-\Psi(V_t))dM_s\Big]+{\mathbb{E}\Big[\Psi(V_t)\Big(\big(M_{t+h}-M_t\big)- \mathbb{E}\left[M_{t,h}-M_t+X_t^1\big)_+| {\mathcal F}_t \right]\Big)\Big]}\\&+\mathbb{E}\left[\Psi(V_t) {\mathbb{E}} \left[\big(M_{t,h}-M_t+X_t^1\big)_+\left| \right. {\mathcal F}_{t} \right]-{2}\sqrt h\Psi(V_t){\|A^{1}(X_t)\|}{{\mathcal{H}}}\left(\frac{M_t-X_t^1}{\sqrt h \|A^{1}(X_t)\|}\right)\right].\nonumber\end{align}
We now prove that each of the terms in the sum (18) are both o(h) and O(h) uniformly in time.
(a) Using Lemma 3.1, the third term is null.
(b) Concerning the second term, using the fact that
![]() $\Psi$
is bounded and Lemma 3.1(i), for all
$\Psi$
is bounded and Lemma 3.1(i), for all
![]() $ t\in [0,T]$
$ t\in [0,T]$
 \begin{align*}&\left|\mathbb{E}\left[\Psi(V_t)[\big(M_{t+h}-M_t\big)- \mathbb{E}\big[\big(M_{t,h}-M_t+X_t^1\big)_+\left| \right. {\mathcal F}_{t} \big]\right]\right|\leq\\& \quad \|\Psi\|_\infty\left|\mathbb{E}\left[M_{t+h}-M_t- \mathbb{E}\big[\big(M_{t,h}-M_t+X_t^1\big)_+| {\mathcal F}_t\big]\right]\right|{\leq Ch\|\Psi\|_\infty},\end{align*}
\begin{align*}&\left|\mathbb{E}\left[\Psi(V_t)[\big(M_{t+h}-M_t\big)- \mathbb{E}\big[\big(M_{t,h}-M_t+X_t^1\big)_+\left| \right. {\mathcal F}_{t} \big]\right]\right|\leq\\& \quad \|\Psi\|_\infty\left|\mathbb{E}\left[M_{t+h}-M_t- \mathbb{E}\big[\big(M_{t,h}-M_t+X_t^1\big)_+| {\mathcal F}_t\big]\right]\right|{\leq Ch\|\Psi\|_\infty},\end{align*}
as is required in (12). Moreover, using Lemma 3.4(ii),
(c) Since
![]() $\nabla \Psi$
is bounded and the process M is increasing, the first term is bounded:
$\nabla \Psi$
is bounded and the process M is increasing, the first term is bounded:
 \begin{equation*}\mathbb{E}\left[\int_t^{t+h}[\Psi(V_s)-\Psi(V_t)]dM_s\right]\leq\|\nabla\Psi\|_\infty \mathbb{E}\bigg[\sup_{t\leq s\leq t+h}\|V_s-V_t\|\big(M_{t+h}-M_t\big)\bigg].\end{equation*}
\begin{equation*}\mathbb{E}\left[\int_t^{t+h}[\Psi(V_s)-\Psi(V_t)]dM_s\right]\leq\|\nabla\Psi\|_\infty \mathbb{E}\bigg[\sup_{t\leq s\leq t+h}\|V_s-V_t\|\big(M_{t+h}-M_t\big)\bigg].\end{equation*}
Using the Cauchy–Schwarz inequality,
 \begin{equation*}\mathbb{E}\left[\sup_{t\leq s\leq t+h}\|V_s-V_t\|\big(M_{t+h}-M_t\big)\right]\leq \sqrt{\mathbb{E}\bigg[\sup_{t\leq s\leq t+h}\|V_s-V_t\|^2\bigg]\mathbb{E}\big[\big(M_{t+h}-M_t\big)^2\big]}.\end{equation*}
\begin{equation*}\mathbb{E}\left[\sup_{t\leq s\leq t+h}\|V_s-V_t\|\big(M_{t+h}-M_t\big)\right]\leq \sqrt{\mathbb{E}\bigg[\sup_{t\leq s\leq t+h}\|V_s-V_t\|^2\bigg]\mathbb{E}\big[\big(M_{t+h}-M_t\big)^2\big]}.\end{equation*}
Since
![]() $\|V_s-V_t\|^2=(M_s-M_t)^2+\|X_s-X_t\|^2,$
we obtain
$\|V_s-V_t\|^2=(M_s-M_t)^2+\|X_s-X_t\|^2,$
we obtain
hence
 \begin{align*}&\mathbb{E}\left[\sup_{t\leq s\leq t+h}\|V_s-V_t\|\big(M_{t+h}-M_t\big)\right]\leq\\& \quad \sqrt{\mathbb{E}\big[\big(M_{t+h}-M_t\big)^2\big]+ \mathbb{E}\left[\sup_{t\leq s\leq t+h}\|X_s-X_t\|\right]^2}\sqrt{\mathbb{E}\big[\big(M_{t+h}-M_t\big)^2\big]}.\end{align*}
\begin{align*}&\mathbb{E}\left[\sup_{t\leq s\leq t+h}\|V_s-V_t\|\big(M_{t+h}-M_t\big)\right]\leq\\& \quad \sqrt{\mathbb{E}\big[\big(M_{t+h}-M_t\big)^2\big]+ \mathbb{E}\left[\sup_{t\leq s\leq t+h}\|X_s-X_t\|\right]^2}\sqrt{\mathbb{E}\big[\big(M_{t+h}-M_t\big)^2\big]}.\end{align*}
Lemmas 3.1 and 3.2 (
![]() $p=2$
) yield the fact that the first factor is
$p=2$
) yield the fact that the first factor is
![]() $o\big(\sqrt h\big)$
and the second is
$o\big(\sqrt h\big)$
and the second is
![]() $O\big(\sqrt h\big)$
uniformly with respect to
$O\big(\sqrt h\big)$
uniformly with respect to
![]() $t\geq 0$
. Then
$t\geq 0$
. Then
![]() $\mathbb{E}\big[\sup_{t\leq s\leq t+h}\|V_s-V_t\|\big(M_{t+h}-M_t\big)\big]$
is o(h) and O(h) uniformly with respect to
$\mathbb{E}\big[\sup_{t\leq s\leq t+h}\|V_s-V_t\|\big(M_{t+h}-M_t\big)\big]$
is o(h) and O(h) uniformly with respect to
![]() $t\geq 0$
.
$t\geq 0$
.
3.3. Proof of Proposition 3.2
(i) Recall that A and B fulfil (4), (5) and (M, X) fulfils Hypothesis 2.1. Then, using the density
![]() $p_V$
of the law of the pair
$p_V$
of the law of the pair
![]() $\big(M_t,X_t\big)$
, we have
$\big(M_t,X_t\big)$
, we have
 \begin{align*}&{\mathbb E} \left[\Psi(V_t) \|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-{X^1_t}}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\leq\\&\|\Psi\|_{\infty} \|A\|_{\infty}\int_{{\mathbb R}^{d+1}}{\mathcal H}\left( \frac{m-x^1}{\sqrt{h}\|A^1(x^1,\tilde{x})\|}\right) p_V\big(m,x^1,\tilde{x};\,t\big) dm\, dx^1\,d\tilde{x}.\end{align*}
\begin{align*}&{\mathbb E} \left[\Psi(V_t) \|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-{X^1_t}}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\leq\\&\|\Psi\|_{\infty} \|A\|_{\infty}\int_{{\mathbb R}^{d+1}}{\mathcal H}\left( \frac{m-x^1}{\sqrt{h}\|A^1(x^1,\tilde{x})\|}\right) p_V\big(m,x^1,\tilde{x};\,t\big) dm\, dx^1\,d\tilde{x}.\end{align*}
The change of variable
![]() $x^1=m-u\sqrt{h}$
yields
$x^1=m-u\sqrt{h}$
yields
 \begin{align}&\frac{\sqrt{h}}{h}{\mathbb E} \left[ \Psi(V_t)\|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-{X^1_t}}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\leq \\&\|\Psi\|_{\infty} \|A^1\|_{\infty}\int_{{\mathbb R}^d\times[0,+\infty[} {\mathcal H}\left( \frac{u}{\|A^1\big(m-\sqrt{h}u,\tilde{x}\big)\|}\right) p_V\big(m,m-\sqrt{h}u,\tilde{x};\,t\big) dm\, d\tilde{x}\,du.\nonumber\end{align}
\begin{align}&\frac{\sqrt{h}}{h}{\mathbb E} \left[ \Psi(V_t)\|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-{X^1_t}}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\leq \\&\|\Psi\|_{\infty} \|A^1\|_{\infty}\int_{{\mathbb R}^d\times[0,+\infty[} {\mathcal H}\left( \frac{u}{\|A^1\big(m-\sqrt{h}u,\tilde{x}\big)\|}\right) p_V\big(m,m-\sqrt{h}u,\tilde{x};\,t\big) dm\, d\tilde{x}\,du.\nonumber\end{align}
Since
![]() ${{\mathcal{H}}}$
is decreasing (Remark 3.1) and
${{\mathcal{H}}}$
is decreasing (Remark 3.1) and
![]() $0\leq h\leq 1,$
we have
$0\leq h\leq 1,$
we have
 \begin{equation*}{{\mathcal{H}}}\left( \frac{u}{\|A^1\big(m-\sqrt{h}u,\tilde{x}\big)\|}\right)\leq {{\mathcal{H}}}\left(\frac{u}{\|A^1\|_\infty}\right),\end{equation*}
\begin{equation*}{{\mathcal{H}}}\left( \frac{u}{\|A^1\big(m-\sqrt{h}u,\tilde{x}\big)\|}\right)\leq {{\mathcal{H}}}\left(\frac{u}{\|A^1\|_\infty}\right),\end{equation*}
so
 \begin{align*}&\left|\frac{\sqrt{h}}{h}{\mathbb E} \left[\Psi(V_t) \|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-{X^1_t}}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\right|\leq\\&\|\Psi\|_{\infty} \|A^1\|_{\infty}\int_{{\mathbb R}^d\times[0,+\infty[}{{\mathcal{H}}}\left(\frac{u}{\|A^1\|_\infty}\right)\sup_{r>0}p_V(m,m-r,\tilde{x};\,t) dm\, d\tilde{x}\,du.\end{align*}
\begin{align*}&\left|\frac{\sqrt{h}}{h}{\mathbb E} \left[\Psi(V_t) \|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-{X^1_t}}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\right|\leq\\&\|\Psi\|_{\infty} \|A^1\|_{\infty}\int_{{\mathbb R}^d\times[0,+\infty[}{{\mathcal{H}}}\left(\frac{u}{\|A^1\|_\infty}\right)\sup_{r>0}p_V(m,m-r,\tilde{x};\,t) dm\, d\tilde{x}\,du.\end{align*}
Applying Tonelli’s theorem, computing the integral with respect to du in the right-hand side with
![]() $\int_0^{\infty}{{\mathcal{H}}}(v)dv=1/4$
(Remark 3.1), we obtain
$\int_0^{\infty}{{\mathcal{H}}}(v)dv=1/4$
(Remark 3.1), we obtain
 \begin{align*}&\sup_{h>0}\left|\frac{\sqrt{h}}{h}{\mathbb E} \left[\Psi(V_t) \|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-{X^1_t}}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\right|\\& \quad \leq\frac{1}{4} \|\Psi\|_{\infty} \|A^1\|^2_{\infty}\int_{{\mathbb R}^{d}}\sup_{r>0}p_V(m,m-r,\tilde{x};\,t) dm\, d\tilde{x}.\end{align*}
\begin{align*}&\sup_{h>0}\left|\frac{\sqrt{h}}{h}{\mathbb E} \left[\Psi(V_t) \|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-{X^1_t}}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\right|\\& \quad \leq\frac{1}{4} \|\Psi\|_{\infty} \|A^1\|^2_{\infty}\int_{{\mathbb R}^{d}}\sup_{r>0}p_V(m,m-r,\tilde{x};\,t) dm\, d\tilde{x}.\end{align*}
Using Hypothesis 2.1(i), we obtain that the map
 \begin{equation*}t\mapsto \sup_{h>0}\left|\frac{\sqrt{h}}{h}{\mathbb E} \left[\Psi(V_t) \|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-X^1_t}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\right|\end{equation*}
\begin{equation*}t\mapsto \sup_{h>0}\left|\frac{\sqrt{h}}{h}{\mathbb E} \left[\Psi(V_t) \|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-X^1_t}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\right|\end{equation*}
belongs to
![]() $ L^1([0,T], \mathbb{R})$
. Part (i) of Proposition 3.2 is proved.
$ L^1([0,T], \mathbb{R})$
. Part (i) of Proposition 3.2 is proved.
(ii) For the proof of Part (ii), first note that
 \begin{align*}&{\mathbb E} \left[ \Psi(V_t)\|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-X^1_t}{\sqrt{h}\|A^1(X_t)\|}\right)\right]\\&\quad =\int_{{\mathbb R}^{d+1}} \Psi(m,x) \|A^1(x)\| {\mathcal H} \left( \frac{m-x^1}{\sqrt{h}\|A^1(x)\|}\right) p_V(m,x;\,t) dm \,dx.\end{align*}
\begin{align*}&{\mathbb E} \left[ \Psi(V_t)\|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-X^1_t}{\sqrt{h}\|A^1(X_t)\|}\right)\right]\\&\quad =\int_{{\mathbb R}^{d+1}} \Psi(m,x) \|A^1(x)\| {\mathcal H} \left( \frac{m-x^1}{\sqrt{h}\|A^1(x)\|}\right) p_V(m,x;\,t) dm \,dx.\end{align*}
After the change of variable
![]() $x^1=m-u\sqrt{h},$
we obtain
$x^1=m-u\sqrt{h},$
we obtain
 \begin{align}&\frac{\sqrt{h}}{h}{\mathbb E} \left[ \Psi(V_t)\|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-{X^1_t}}{\sqrt{h}\|A^1(X_t)\|}\right) \right] =\\&\int_{{\mathbb R}^d\times\mathbb R^+} \Psi\big(m,m-u\sqrt{h},\tilde{x}\big)\|A^1\big(m-u\sqrt{h},\tilde{x}\big)\|{\mathcal H}\left( \frac{u}{\|A^1\big(m-\sqrt{h}u,\tilde{x}\big)\|}\right)\nonumber\\& p_V\big(m,m-\sqrt{h}u,\tilde{x};\,t\big) dm\, d\tilde{x}\,du.\nonumber\end{align}
\begin{align}&\frac{\sqrt{h}}{h}{\mathbb E} \left[ \Psi(V_t)\|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-{X^1_t}}{\sqrt{h}\|A^1(X_t)\|}\right) \right] =\\&\int_{{\mathbb R}^d\times\mathbb R^+} \Psi\big(m,m-u\sqrt{h},\tilde{x}\big)\|A^1\big(m-u\sqrt{h},\tilde{x}\big)\|{\mathcal H}\left( \frac{u}{\|A^1\big(m-\sqrt{h}u,\tilde{x}\big)\|}\right)\nonumber\\& p_V\big(m,m-\sqrt{h}u,\tilde{x};\,t\big) dm\, d\tilde{x}\,du.\nonumber\end{align}
Using Lebesgue’s dominated convergence theorem, we let h go to 0 in (20) for
![]() $t>0$
, and using the fact that
$t>0$
, and using the fact that
![]() $\Psi,$
A, and
$\Psi,$
A, and
![]() ${\mathcal H}$
are continuous and Hypothesis 2.1(ii), we obtain
${\mathcal H}$
are continuous and Hypothesis 2.1(ii), we obtain
 \begin{align*}&\lim_{h \rightarrow 0}\frac{\sqrt{h}}{h}{\mathbb E} \left[ \Psi(V_t)\|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-X_t}{\sqrt{h}\|A^1(X_t)\|}\right) \right]=\\&\int_{{\mathbb R}^{d}\times[0,+\infty[}\Psi(m,{m,\tilde{x}})\|A^1(m,\tilde{x})\| {{\mathcal{H}}}\left( \frac{u}{\| A^1({m,\tilde{x}})\|}\right) {p_V(m,m,\tilde{x};\,t)}dm\,d\tilde{x} \,du.\end{align*}
\begin{align*}&\lim_{h \rightarrow 0}\frac{\sqrt{h}}{h}{\mathbb E} \left[ \Psi(V_t)\|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-X_t}{\sqrt{h}\|A^1(X_t)\|}\right) \right]=\\&\int_{{\mathbb R}^{d}\times[0,+\infty[}\Psi(m,{m,\tilde{x}})\|A^1(m,\tilde{x})\| {{\mathcal{H}}}\left( \frac{u}{\| A^1({m,\tilde{x}})\|}\right) {p_V(m,m,\tilde{x};\,t)}dm\,d\tilde{x} \,du.\end{align*}
Using the change of variable
![]() $z=\frac{u}{\|A^1(m,\tilde{x})\|}$
and Remark 3.1
$z=\frac{u}{\|A^1(m,\tilde{x})\|}$
and Remark 3.1
![]() $\int_0^{\infty}{{\mathcal{H}}}(z)dz=1/4$
yields
$\int_0^{\infty}{{\mathcal{H}}}(z)dz=1/4$
yields
 \begin{align*}&\lim_{h \rightarrow 0}\frac{\sqrt{h}}{h}{\mathbb E} \left[ \Psi(V_t)\|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-X^1_t}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\\&\quad =\frac{1}{4}\int_{{\mathbb R}^{d}}\Psi(m,{m,\tilde x})\|A^1(m,\tilde{x})\|^2 p_V(m,{m,}\tilde{x};\,t)dm\,d\tilde{x}.\end{align*}
\begin{align*}&\lim_{h \rightarrow 0}\frac{\sqrt{h}}{h}{\mathbb E} \left[ \Psi(V_t)\|A^1(X_t)\| {\mathcal H} \left( \frac{M_t-X^1_t}{\sqrt{h}\|A^1(X_t)\|}\right) \right]\\&\quad =\frac{1}{4}\int_{{\mathbb R}^{d}}\Psi(m,{m,\tilde x})\|A^1(m,\tilde{x})\|^2 p_V(m,{m,}\tilde{x};\,t)dm\,d\tilde{x}.\end{align*}
3.4. End of proof of Theorem 2.3
We recall Theorem 8.2 from Brezis [Reference Brezis5, p. 204]: let
![]() $f\in W^{1,1}(0,T)$
; then f is almost surely equal to an absolutely continuous function. As a particular case, any
$f\in W^{1,1}(0,T)$
; then f is almost surely equal to an absolutely continuous function. As a particular case, any
![]() $f\in W^{1,1}(0,T)\cap C(0,T)$
is absolutely continuous. Recall
$f\in W^{1,1}(0,T)\cap C(0,T)$
is absolutely continuous. Recall
![]() $F_{\psi}\,:\,t \mapsto {{\mathbb E}\left[\int_0 ^t \Psi(V_s)dM_s \right]}.$
$F_{\psi}\,:\,t \mapsto {{\mathbb E}\left[\int_0 ^t \Psi(V_s)dM_s \right]}.$
Lemma 3.6.
Assume that A and B fulfil (4) and (5) and that
![]() $\Psi$
is a continuous bounded function. Then
$\Psi$
is a continuous bounded function. Then
![]() $F_{\Psi}$
is a continuous function on
$F_{\Psi}$
is a continuous function on
![]() $\mathbb{R}^+.$
$\mathbb{R}^+.$
Proof. Let
![]() $0 \leq s\leq t.$
Since
$0 \leq s\leq t.$
Since
![]() $\Psi$
is bounded and M is non-decreasing,
$\Psi$
is bounded and M is non-decreasing,
The map
![]() $t\mapsto {\mathbb E}[M_t]$
being continuous,
$t\mapsto {\mathbb E}[M_t]$
being continuous,
![]() $F_{\Psi}$
is a continuous function on
$F_{\Psi}$
is a continuous function on
![]() $\mathbb{R}^+.$
$\mathbb{R}^+.$
Lemma 3.7.
Assume that A and B fulfil (4) and (5), (M, X) fulfils Hypothesis 2.1, and
![]() $\Psi \in C^1_b.$
Then for all
$\Psi \in C^1_b.$
Then for all
![]() $T>0$
, the map
$T>0$
, the map
![]() $F_{\psi}$
belongs to the Sobolev space
$F_{\psi}$
belongs to the Sobolev space
![]() $W^{1,1}(]0,T[)$
, and its weak derivative is
$W^{1,1}(]0,T[)$
, and its weak derivative is
Proof. Let
![]() $g\,:\, [0,T]\rightarrow \mathbb{R}$
be
$g\,:\, [0,T]\rightarrow \mathbb{R}$
be
![]() $C^1$
with compact support
$C^1$
with compact support
![]() $[\alpha,\beta]\subset(0,T).$
This means both functions g and
$[\alpha,\beta]\subset(0,T).$
This means both functions g and
![]() $\dot g$
are continuous, hence bounded, and that moreover
$\dot g$
are continuous, hence bounded, and that moreover
![]() $g(\alpha)=g(\beta)=0.$
Note that
$g(\alpha)=g(\beta)=0.$
Note that
Moreover,
Observe that, since M is non-decreasing and the coefficients A and B are bounded,
Then, using Lebesgue’s dominated convergence theorem, we have
Using the change of variable
![]() $u=s-h$
in the last integral, we have
$u=s-h$
in the last integral, we have
 \begin{align*}\int_0^T &\frac{g(s) -g(s-h)}{h}F_{\Psi}(s)ds=h^{-1}\int_0^T g(s) F_{\Psi}(s) ds -h^{-1}\int_{-h}^{T-h} g(u) F_{\Psi}(u+h)du\\&= \int_{0}^T g(s) \frac{F_{\Psi}(s) -F_{\Psi}(s+h)}{h}ds{-}h^{-1}\int_{-h}^0 g(s)F_{\Psi}(s+h) ds {+}h^{-1}\int_{T-h}^Tg(s) F_{\Psi}(s+h) ds.\end{align*}
\begin{align*}\int_0^T &\frac{g(s) -g(s-h)}{h}F_{\Psi}(s)ds=h^{-1}\int_0^T g(s) F_{\Psi}(s) ds -h^{-1}\int_{-h}^{T-h} g(u) F_{\Psi}(u+h)du\\&= \int_{0}^T g(s) \frac{F_{\Psi}(s) -F_{\Psi}(s+h)}{h}ds{-}h^{-1}\int_{-h}^0 g(s)F_{\Psi}(s+h) ds {+}h^{-1}\int_{T-h}^Tg(s) F_{\Psi}(s+h) ds.\end{align*}
Recalling that
![]() $supp(g)=[\alpha,\beta]\subset(0,T)$
,
$supp(g)=[\alpha,\beta]\subset(0,T)$
,
![]() $gF_{\Psi}$
extended by 0 on
$gF_{\Psi}$
extended by 0 on
![]() $[\alpha,\beta]^c$
is bounded on [0, T], so
$[\alpha,\beta]^c$
is bounded on [0, T], so
![]() $\lim_{s\rightarrow 0} g(s)=\lim_{s\rightarrow T} g(s)=0$
. Then
$\lim_{s\rightarrow 0} g(s)=\lim_{s\rightarrow T} g(s)=0$
. Then
as soon as
![]() $0<h\leq T-\beta$
; thus
$0<h\leq T-\beta$
; thus
 \begin{equation*}\lim_{h \rightarrow 0} \left[h^{-1}\int_{-h}^0 g(s)F_{\Psi}(s+h) ds\right] = \lim_{h \rightarrow 0}\left[ h^{-1}\int_{T-h}^Tg(s) F_{\psi}(s+h) ds\right]=0.\end{equation*}
\begin{equation*}\lim_{h \rightarrow 0} \left[h^{-1}\int_{-h}^0 g(s)F_{\Psi}(s+h) ds\right] = \lim_{h \rightarrow 0}\left[ h^{-1}\int_{T-h}^Tg(s) F_{\psi}(s+h) ds\right]=0.\end{equation*}
Applying Lebesgue’s dominated convergence theorem yields that F admits a weak derivative:
Using Proposition 3.1(ii), we have
Using Proposition 3.2(ii),
and by Propositions 3.1(i) and 3.2(i),
so
![]() $\dot{F}_{\Psi}\in L^1([0,T],\mathbb{R}).$
By [Reference Brezis5, Chapter 8, Section 2, p. 202],
$\dot{F}_{\Psi}\in L^1([0,T],\mathbb{R}).$
By [Reference Brezis5, Chapter 8, Section 2, p. 202],
![]() $F_{\Psi}$
belongs to
$F_{\Psi}$
belongs to
![]() $W^{1,1}(]0,T[,{\mathbb R}).$
$W^{1,1}(]0,T[,{\mathbb R}).$
We now finish the proof of Theorem 2.3. According to [Reference Brezis5, Theorem 8.2, p. 204],
![]() $F_{\psi}$
is equal almost surely to an absolutely continuous function. Since
$F_{\psi}$
is equal almost surely to an absolutely continuous function. Since
![]() $F_{\Psi}$
is continuous (Lemma 3.6), the equality holds everywhere. Thus
$F_{\Psi}$
is continuous (Lemma 3.6), the equality holds everywhere. Thus
![]() $F_{\Psi}$
is an absolutely continuous function, and its derivative is its right derivative.
$F_{\Psi}$
is an absolutely continuous function, and its derivative is its right derivative.
4. The case
 $\boldsymbol{{A}}=\boldsymbol{{I}}_{\boldsymbol{{d}}}$
$\boldsymbol{{A}}=\boldsymbol{{I}}_{\boldsymbol{{d}}}$
In this rather technical section, we first prove that the density of the pair
![]() $\big(M_t,X_t\big)$
fulfils Hypothesis 2.1:
$\big(M_t,X_t\big)$
fulfils Hypothesis 2.1:
![]() $p_V$
(from (3)) is continuous on the boundary of
$p_V$
(from (3)) is continuous on the boundary of
![]() $\bar{\Delta}$
and is dominated by an integrable function.
$\bar{\Delta}$
and is dominated by an integrable function.
Proposition 4.1. Assume that B fulfils Assumption (4) and
![]() $A=I_d$
. Then (M, X) fulfils Hypothesis 2.1, meaning that for any probability measure
$A=I_d$
. Then (M, X) fulfils Hypothesis 2.1, meaning that for any probability measure
![]() $\mu_0$
on
$\mu_0$
on
![]() ${\mathbb R}^d$
, the following hold:
${\mathbb R}^d$
, the following hold:
-
(i) For every
 $T>0$
,
$T>0$
,  \begin{equation*}\sup_{(h,u) \in [0,1]\times {\mathbb R}_+}p_V(b,b-hu,\tilde{a};\,t,{\mu_0}) \in L^1\big([0,T] \times {\mathbb R}^d, dtdbd\tilde{a}\big).\end{equation*}
\begin{equation*}\sup_{(h,u) \in [0,1]\times {\mathbb R}_+}p_V(b,b-hu,\tilde{a};\,t,{\mu_0}) \in L^1\big([0,T] \times {\mathbb R}^d, dtdbd\tilde{a}\big).\end{equation*}
-
(ii) Almost surely in
 $(m, \tilde{x}) \in {\mathbb R}^d$
, for every
$(m, \tilde{x}) \in {\mathbb R}^d$
, for every
 $t>0$
,
$t>0$
,  \begin{equation*}\lim_{u \rightarrow 0,\ u>0} p_V\big(m,m-u,\tilde{x};\,t,{\mu_0}\big)=p_V\big(m,m,\tilde{x};\,t,{\mu_0}\big).\end{equation*}
\begin{equation*}\lim_{u \rightarrow 0,\ u>0} p_V\big(m,m-u,\tilde{x};\,t,{\mu_0}\big)=p_V\big(m,m,\tilde{x};\,t,{\mu_0}\big).\end{equation*}
As a by-product, using Theorems 2.2 and 2.3, this proposition completes the proof of Theorem 2.4. The main tool for the proof of this proposition is an integral representation of the density.
Proposition 4.2
For any probability measure
![]() $\mu_0$
on
$\mu_0$
on
![]() ${\mathbb R}^d,$
for all
${\mathbb R}^d,$
for all
![]() $t>0$
,
$t>0$
,
where the various p terms are defined as follows (here
![]() $\partial_k$
is the derivative with respect to
$\partial_k$
is the derivative with respect to
![]() $k= m, x^1,\ldots,x^d$
and
$k= m, x^1,\ldots,x^d$
and
![]() $B^m=B^1$
):
$B^m=B^1$
):
 \begin{align*} &p^0(m,x;\,t)\,:\!=\,{\int_{{\mathbb R}^d}p_{W^{*1},W}\big(m-x_0^1,x-x_0;\,t\big)\mu_0(dx_0)}, \\&{p^{k,\alpha}}(m,x;\,t)\,:\!=\,\int_0^t{\int_{\mathbb{R}^{d+1}} {\mathbf 1}_{b <m}B^{k}(a)\partial_{k}p_{W^{*1},W}\big(m-a^1,x-a;\,t-s\big)p_V(b,a;\,s)dbda}ds,\\&{p^{k,\beta}}(m,x;\,t)\,:\!=\,\int_0^t \int_{{\mathbb R}^{(d+1)}}{\mathbf 1}_{b<m} B^{k}(a)\partial_{k}p_{W^{*1},W}\big(b-a^1,x-a;\,t-s\big)p_V(m,a;\,s)dbda ds,\end{align*}
\begin{align*} &p^0(m,x;\,t)\,:\!=\,{\int_{{\mathbb R}^d}p_{W^{*1},W}\big(m-x_0^1,x-x_0;\,t\big)\mu_0(dx_0)}, \\&{p^{k,\alpha}}(m,x;\,t)\,:\!=\,\int_0^t{\int_{\mathbb{R}^{d+1}} {\mathbf 1}_{b <m}B^{k}(a)\partial_{k}p_{W^{*1},W}\big(m-a^1,x-a;\,t-s\big)p_V(b,a;\,s)dbda}ds,\\&{p^{k,\beta}}(m,x;\,t)\,:\!=\,\int_0^t \int_{{\mathbb R}^{(d+1)}}{\mathbf 1}_{b<m} B^{k}(a)\partial_{k}p_{W^{*1},W}\big(b-a^1,x-a;\,t-s\big)p_V(m,a;\,s)dbda ds,\end{align*}
where
![]() $p_{W^{*1},W}(.,.;\,t)$
is the density of the distribution of
$p_{W^{*1},W}(.,.;\,t)$
is the density of the distribution of
![]() $\big(\!\sup_{s\leq t}W^1_s,W_t\big)$
for
$\big(\!\sup_{s\leq t}W^1_s,W_t\big)$
for
![]() $t \geq 0$
; see Appendix A.2.
$t \geq 0$
; see Appendix A.2.
4.1. Integral representation of the density: proof of Proposition 4.2
Let
![]() $t >0$
be fixed. First, we assume that
$t >0$
be fixed. First, we assume that
![]() $\mu_0=\delta_{x_0}$
,
$\mu_0=\delta_{x_0}$
,
![]() $x_0$
being fixed in
$x_0$
being fixed in
![]() ${\mathbb R}^d.$
By Lemma 4.2 below, and using the fact that B is bounded, for all
${\mathbb R}^d.$
By Lemma 4.2 below, and using the fact that B is bounded, for all
![]() $t\in [0,T]$
, the functions
$t\in [0,T]$
, the functions
![]() $ p^{k,\gamma}\in^\infty L\left([0,T], L^1\big(\mathbb{R}^{d+1}\big)\right)$
for
$ p^{k,\gamma}\in^\infty L\left([0,T], L^1\big(\mathbb{R}^{d+1}\big)\right)$
for
![]() $\gamma=\alpha,\beta$
.
$\gamma=\alpha,\beta$
.
Let
![]() $F\in C^1_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
with compact support. We will prove that
$F\in C^1_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
with compact support. We will prove that
 \begin{equation}\mathbb{E}_\mathbb{P}[F\big(M_t,X_t\big)]=\int_{\mathbb{R}^{d+1}}F(m,x)\left(p^0-\sum_{k=m,x^1,\ldots,x^d}\big(p^{k,\alpha}+p^{k,\beta}\big)(m,x,t)\right)dmdx.\end{equation}
\begin{equation}\mathbb{E}_\mathbb{P}[F\big(M_t,X_t\big)]=\int_{\mathbb{R}^{d+1}}F(m,x)\left(p^0-\sum_{k=m,x^1,\ldots,x^d}\big(p^{k,\alpha}+p^{k,\beta}\big)(m,x,t)\right)dmdx.\end{equation}
Using Malliavin calculus we obtain the following decomposition.
Lemma 4.1. We have
 \begin{align*}{\mathbb E}_\mathbb{P} &\left[F\big(M_t,X_t\big)\right]= \int_{{\mathbb R}^{d+1}} F\big(x_0^1+b,x_0+a\big)p_{W^{*1},W}(b,a;\,t)dbda\nonumber\\&+ \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}\partial_mF \left(X^1_s + b,X_s+ a\right){\mathbf 1}_{\big\{M_s <X^1_s + b\big\}} B^1(X_s)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds\nonumber\\&+ \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{\partial_{k}} F\!\left(\max\! \left( M_s, X_s^1 + b\right),X_s+ a\right) B^k(X_s)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds.\end{align*}
\begin{align*}{\mathbb E}_\mathbb{P} &\left[F\big(M_t,X_t\big)\right]= \int_{{\mathbb R}^{d+1}} F\big(x_0^1+b,x_0+a\big)p_{W^{*1},W}(b,a;\,t)dbda\nonumber\\&+ \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}\partial_mF \left(X^1_s + b,X_s+ a\right){\mathbf 1}_{\big\{M_s <X^1_s + b\big\}} B^1(X_s)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds\nonumber\\&+ \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{\partial_{k}} F\!\left(\max\! \left( M_s, X_s^1 + b\right),X_s+ a\right) B^k(X_s)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds.\end{align*}
Proof. Let Z be the exponential martingale solution of
As before, Einstein’s convention is used. Let
![]() ${\mathbb Q}=Z{\mathbb P}$
; according to Girsanov’s theorem, using (23),
${\mathbb Q}=Z{\mathbb P}$
; according to Girsanov’s theorem, using (23),
![]() $W_B\,:\!=\,\left(W_t^k-\int_0^t B^k\big(x_0+W_s\big) ds;\, k=1,\ldots,d\right)_{t\geq 0}$
is a
$W_B\,:\!=\,\left(W_t^k-\int_0^t B^k\big(x_0+W_s\big) ds;\, k=1,\ldots,d\right)_{t\geq 0}$
is a
![]() ${\mathbb Q}$
-continuous martingale such that
${\mathbb Q}$
-continuous martingale such that
![]() $\langle W_B\rangle_t=t$
for all
$\langle W_B\rangle_t=t$
for all
![]() $t \geq 0.$
That means that under
$t \geq 0.$
That means that under
![]() ${\mathbb Q},$
${\mathbb Q},$
![]() $W_B$
is a d-dimensional Brownian motion. Then the distribution of X (resp. (M, X)) under
$W_B$
is a d-dimensional Brownian motion. Then the distribution of X (resp. (M, X)) under
![]() ${\mathbb P}$
is the distribution of
${\mathbb P}$
is the distribution of
![]() $W+x_0$
(resp.
$W+x_0$
(resp.
![]() $(W^{1*}+x_0,W+x_0))$
under
$(W^{1*}+x_0,W+x_0))$
under
![]() ${\mathbb Q}$
, and
${\mathbb Q}$
, and
Let
![]() $G\,:\!=\, F\big(x_0^1+W^{1*}_t,x_0+W_t\big)$
and
$G\,:\!=\, F\big(x_0^1+W^{1*}_t,x_0+W_t\big)$
and
![]() $u\,:\!=\,ZB(x_0+W)$
; using (23),
$u\,:\!=\,ZB(x_0+W)$
; using (23),
As a first step we will apply (50) (see the appendix) to the second term in (25). Thus we have to check that the pair
![]() $(G,u)\in {\mathbb D}^{1,2}\times {\mathbb L}^{1,2}$
. Since F is bounded and smooth, we have
$(G,u)\in {\mathbb D}^{1,2}\times {\mathbb L}^{1,2}$
. Since F is bounded and smooth, we have
![]() $G\in {\mathbb D}^{1,2}$
; and according to Lemma A.1, the process u belongs to
$G\in {\mathbb D}^{1,2}$
; and according to Lemma A.1, the process u belongs to
![]() ${\mathbb L}^{1,2}$
.
${\mathbb L}^{1,2}$
.
Using (53)
![]() $\big({\tau\,:\!=\,\inf\big\{s, W_s^{1*} =W^{1*}_t\big\}}\big)$
, the pair
$\big({\tau\,:\!=\,\inf\big\{s, W_s^{1*} =W^{1*}_t\big\}}\big)$
, the pair
![]() $\big(W^{1*}_t,W_t\big)$
belongs to
$\big(W^{1*}_t,W_t\big)$
belongs to
![]() ${\mathbb D}^{1,2}$
with Malliavin gradient
${\mathbb D}^{1,2}$
with Malliavin gradient
Using the chain rule,
 \begin{align*} \langle DG,u\rangle_{{\mathbb H}}&= \int_0^{t}\partial_m F\big({x^1_0}+W^{*1}_t,x_0+W_t\big) {\mathbf 1}_{\big\{W^{1*}_s<W^{1*}_t\big\}}B^1\big(x_0+W_s\big){Z_s} ds \\ &+ \int_0^{t}{\partial_{k}} F\big({x^1_0}+W^{*1}_t,x_0+W_t\big)B^k\big(x_0+W_s\big){Z_s}ds.\end{align*}
\begin{align*} \langle DG,u\rangle_{{\mathbb H}}&= \int_0^{t}\partial_m F\big({x^1_0}+W^{*1}_t,x_0+W_t\big) {\mathbf 1}_{\big\{W^{1*}_s<W^{1*}_t\big\}}B^1\big(x_0+W_s\big){Z_s} ds \\ &+ \int_0^{t}{\partial_{k}} F\big({x^1_0}+W^{*1}_t,x_0+W_t\big)B^k\big(x_0+W_s\big){Z_s}ds.\end{align*}
We are now in a position to apply (50),
![]() $E_\mathbb{P}[G\delta(u)]=E_\mathbb{P}[\langle DG,u\rangle_{\mathbb{H}}]$
:
$E_\mathbb{P}[G\delta(u)]=E_\mathbb{P}[\langle DG,u\rangle_{\mathbb{H}}]$
:
 \begin{eqnarray}& & \mathbb{E}_\mathbb{P}[G\delta(u)]=\mathbb{E}_\mathbb{P}\left[\int_0^t \partial_m F \big(x_0^1+W^{1*}_t,x_0+W_t\big){\mathbf 1}_{\{W^{1*}_s <W^{1*}_t \}} B^1\big(x_0+W_s\big)Z_sds\right]\nonumber \\ & +\, &\mathbb{E}_\mathbb{P}\left[\int_0^t {\partial_{k}} F \big(x_0^1+ W^{1*}_t,x_0+W_t\big)B^k\big(x_0+W_s\big) Z_s ds\right].\end{eqnarray}
\begin{eqnarray}& & \mathbb{E}_\mathbb{P}[G\delta(u)]=\mathbb{E}_\mathbb{P}\left[\int_0^t \partial_m F \big(x_0^1+W^{1*}_t,x_0+W_t\big){\mathbf 1}_{\{W^{1*}_s <W^{1*}_t \}} B^1\big(x_0+W_s\big)Z_sds\right]\nonumber \\ & +\, &\mathbb{E}_\mathbb{P}\left[\int_0^t {\partial_{k}} F \big(x_0^1+ W^{1*}_t,x_0+W_t\big)B^k\big(x_0+W_s\big) Z_s ds\right].\end{eqnarray}
Plugging the identity (26) into the right-hand side of (25) and using Fubini’s theorem to commute the integrals in ds and
![]() $d\mathbb{P}$
, we obtain
$d\mathbb{P}$
, we obtain
 \begin{eqnarray}&&{\mathbb E}_\mathbb{P} \left [F\big(M_t,X_t\big)\right]={\mathbb E}_\mathbb{P} \left [ F\big(x_0^1+W^{1*}_t,x_0+W_t\big)\right]\\&+& \int_0^t {\mathbb E}_\mathbb{P}\left[\partial_m F \big(x_0^1+W^{1*}_t,x_0+W_t\big){\mathbf 1}_{\big\{W^{1*}_s <W^{1*}_t \big\}} Z_sB^1\big(x_0+W_s\big) \right]ds\nonumber \nonumber\\&+& \int_0^t {\mathbb E}_\mathbb{P}\left[ \partial_k F \big(x_0^1+W^{1*}_t,x_0+W_t\big)Z_sB^k\big(x_0+W_s\big) \right]ds.\nonumber\end{eqnarray}
\begin{eqnarray}&&{\mathbb E}_\mathbb{P} \left [F\big(M_t,X_t\big)\right]={\mathbb E}_\mathbb{P} \left [ F\big(x_0^1+W^{1*}_t,x_0+W_t\big)\right]\\&+& \int_0^t {\mathbb E}_\mathbb{P}\left[\partial_m F \big(x_0^1+W^{1*}_t,x_0+W_t\big){\mathbf 1}_{\big\{W^{1*}_s <W^{1*}_t \big\}} Z_sB^1\big(x_0+W_s\big) \right]ds\nonumber \nonumber\\&+& \int_0^t {\mathbb E}_\mathbb{P}\left[ \partial_k F \big(x_0^1+W^{1*}_t,x_0+W_t\big)Z_sB^k\big(x_0+W_s\big) \right]ds.\nonumber\end{eqnarray}
As a second step, we use the independence of the increments of the Brownian motion in order to obtain the density of
![]() $\big(W^{1*}_{t-s},W_{t-s}\big)$
. Recall (9):
$\big(W^{1*}_{t-s},W_{t-s}\big)$
. Recall (9):
![]() $\hat W_{t-s}\,:\!=\,W_t-W_s$
and
$\hat W_{t-s}\,:\!=\,W_t-W_s$
and
![]() $\big(\hat W^1\big)^*_{t-s}= \max_{s \leq u \leq t} \left(W^1_u-W^1_s\right).$
Then
$\big(\hat W^1\big)^*_{t-s}= \max_{s \leq u \leq t} \left(W^1_u-W^1_s\right).$
Then
so the expression (27) becomes
 \begin{align*}&{\mathbb E}_\mathbb{P} \left [ F\big(M_t,X_t\big)\right]= {\mathbb E}_\mathbb{P} \left [F\big(x_0^1+W^{1*}_tx_0\,+,W_t\big)\right]+ \\& \int_0^t {\mathbb E}_\mathbb{P}\left[\partial_m F \left(x_0^1+ W^1_s +\big(\hat W^1\big)_{t-s}^*,x_0+W_s+ \hat W_{t-s}\right){\mathbf 1}_{\big\{W^{1*}_s <W^1_s + \big(\hat W^1\big)_{t-s}^*\big\}} Z_sB^1\big(x_0+W_s\big) \right]ds\nonumber\\&+ \int_0^t {\mathbb E}_\mathbb{P}\left[{\partial_{k}} F\!\left(\max\! \left( x_0^1+W^{1*}_s, x^1_0+W^1_s +\big(\hat W^1\big)_{t-s}^* \right),x_0+W_s+\hat W_{t-s}\right) Z_sB^k\big(x_0+W_s\big) \right]ds.\end{align*}
\begin{align*}&{\mathbb E}_\mathbb{P} \left [ F\big(M_t,X_t\big)\right]= {\mathbb E}_\mathbb{P} \left [F\big(x_0^1+W^{1*}_tx_0\,+,W_t\big)\right]+ \\& \int_0^t {\mathbb E}_\mathbb{P}\left[\partial_m F \left(x_0^1+ W^1_s +\big(\hat W^1\big)_{t-s}^*,x_0+W_s+ \hat W_{t-s}\right){\mathbf 1}_{\big\{W^{1*}_s <W^1_s + \big(\hat W^1\big)_{t-s}^*\big\}} Z_sB^1\big(x_0+W_s\big) \right]ds\nonumber\\&+ \int_0^t {\mathbb E}_\mathbb{P}\left[{\partial_{k}} F\!\left(\max\! \left( x_0^1+W^{1*}_s, x^1_0+W^1_s +\big(\hat W^1\big)_{t-s}^* \right),x_0+W_s+\hat W_{t-s}\right) Z_sB^k\big(x_0+W_s\big) \right]ds.\end{align*}
The random vector
![]() $\left(\big(\hat W^1\big)_{t-s}^*,\hat W_{t-s}\right)$
is independent of the
$\left(\big(\hat W^1\big)_{t-s}^*,\hat W_{t-s}\right)$
is independent of the
![]() $\sigma$
-field
$\sigma$
-field
![]() ${\mathcal{F}}_s$
and has the same distribution as the pair
${\mathcal{F}}_s$
and has the same distribution as the pair
![]() $\big(W^{1*}_{t-s},W_{t-s}\big).$
Let
$\big(W^{1*}_{t-s},W_{t-s}\big).$
Let
![]() $p_{W^{*1},W}(.,.;\,t-s)$
be the density of its law, and express the expectation with this density:
$p_{W^{*1},W}(.,.;\,t-s)$
be the density of its law, and express the expectation with this density:
 \begin{align*}{\mathbb E}_\mathbb{P} \left [ F\big(M_t,X_t\big)\right] & = \int_{{\mathbb R}^{d+1}} F\big(x_0^1+b,x_0+a\big)p_{W^{*1},W}(b,a;\,t)dbda\\& \quad + \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}\partial_m F \big(x_0^1+ W^1_s + b,x_0\right.\\& \left. \qquad +\,W_s+ a\big){\mathbf 1}_{\big\{W^{1*}_s <W^1_s + b\big\}} Z_sB^1\big(x_0+W_s\big)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds\\& \quad + \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{\partial_{k}} F\big(x_0^1+\max\! \left( W^{1*}_s, W^1_s + b\right),x_0\right.\\& \left. \qquad +\,W_s+ a\big) Z_sB^k\big(x_0+W_s\big)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds. \end{align*}
\begin{align*}{\mathbb E}_\mathbb{P} \left [ F\big(M_t,X_t\big)\right] & = \int_{{\mathbb R}^{d+1}} F\big(x_0^1+b,x_0+a\big)p_{W^{*1},W}(b,a;\,t)dbda\\& \quad + \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}\partial_m F \big(x_0^1+ W^1_s + b,x_0\right.\\& \left. \qquad +\,W_s+ a\big){\mathbf 1}_{\big\{W^{1*}_s <W^1_s + b\big\}} Z_sB^1\big(x_0+W_s\big)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds\\& \quad + \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{\partial_{k}} F\big(x_0^1+\max\! \left( W^{1*}_s, W^1_s + b\right),x_0\right.\\& \left. \qquad +\,W_s+ a\big) Z_sB^k\big(x_0+W_s\big)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds. \end{align*}
Using Girsanov’s Theorem for
![]() $Z.\mathbb{P}=\mathbb{Q},$
since the law of (M, X) under
$Z.\mathbb{P}=\mathbb{Q},$
since the law of (M, X) under
![]() $\mathbb{P}$
is the law of
$\mathbb{P}$
is the law of
![]() $\big(x^1_0+W^{1*},x_0+W\big)$
, under
$\big(x^1_0+W^{1*},x_0+W\big)$
, under
![]() $\mathbb{Q}$
, using the equality (24), we have:
$\mathbb{Q}$
, using the equality (24), we have:
 \begin{align*}{\mathbb E}_\mathbb{P} \left[F\big(M_t,X_t\big)\right]&= \int_{{\mathbb R}^{d+1}} F\big(x_0^1+b,x_0+a\big)p_{W^{*1},W}(b,a;\,t)dbda\nonumber\\&+ \int_0^t {\mathbb E}_\mathbb{P} \left[\int_{{\mathbb R}^{d+1}}\partial_mF \left(X^1_s + b,X_s+ a\right){\mathbf 1}_{\big\{M_s <X^1_s + b\big\}} B^1(X_s)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds\nonumber\\&+ \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{\partial_{k}} F\!\left(\max\! \left( M_s, X_s^1 + b\right),X_s+ a\right) B^k(X_s)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds.\end{align*}
\begin{align*}{\mathbb E}_\mathbb{P} \left[F\big(M_t,X_t\big)\right]&= \int_{{\mathbb R}^{d+1}} F\big(x_0^1+b,x_0+a\big)p_{W^{*1},W}(b,a;\,t)dbda\nonumber\\&+ \int_0^t {\mathbb E}_\mathbb{P} \left[\int_{{\mathbb R}^{d+1}}\partial_mF \left(X^1_s + b,X_s+ a\right){\mathbf 1}_{\big\{M_s <X^1_s + b\big\}} B^1(X_s)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds\nonumber\\&+ \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{\partial_{k}} F\!\left(\max\! \left( M_s, X_s^1 + b\right),X_s+ a\right) B^k(X_s)p_{W^{*1},W}(b,a;\,t-s)dbda \right]ds.\end{align*}
We are now in a position to complete the proof of Proposition 4.2. Using some suitable translations of the variables (a, b), we have
![]() ${\mathbb E}_\mathbb{P} \left [F\big(M_t,X_t\big)\right]= {\sum_{k=0}^{d} I_k}+I_m,$
where
${\mathbb E}_\mathbb{P} \left [F\big(M_t,X_t\big)\right]= {\sum_{k=0}^{d} I_k}+I_m,$
where
 \begin{align}&I_0=\int_{{\mathbb R}^{d+1}} F(b,a)p_{W^{*1},W}\big(b-x_0^1,a-x_0;\,t\big)dbda,\\&I_m=\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}\partial_m F(b,a){\mathbf 1}_{\{M_s < b\}} B^1(X_s)p_{W^{*1},W}\left(b-X_s^1,a-X_s;\,t-s\right)dbda \right]ds, \nonumber\end{align}
\begin{align}&I_0=\int_{{\mathbb R}^{d+1}} F(b,a)p_{W^{*1},W}\big(b-x_0^1,a-x_0;\,t\big)dbda,\\&I_m=\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}\partial_m F(b,a){\mathbf 1}_{\{M_s < b\}} B^1(X_s)p_{W^{*1},W}\left(b-X_s^1,a-X_s;\,t-s\right)dbda \right]ds, \nonumber\end{align}
and for
![]() $k=1,\ldots,d,$
$k=1,\ldots,d,$
Since B, F, and its derivatives are bounded, all these integrals are finite. Using (54) in the appendix, the function
![]() $p_{W^{*1},W}(.,.;\,t)$
is
$p_{W^{*1},W}(.,.;\,t)$
is
![]() $C^{\infty}$
on
$C^{\infty}$
on
![]() $\bar{\Delta}=\big\{(b,a),\,\,b{\geq} a^1_+, \,\,(a,b) \in {\mathbb R}^{d+1}\big\}$
. The aim is now to identify the terms
$\bar{\Delta}=\big\{(b,a),\,\,b{\geq} a^1_+, \,\,(a,b) \in {\mathbb R}^{d+1}\big\}$
. The aim is now to identify the terms
![]() $p^0$
,
$p^0$
,
![]() $p^{k,\alpha}$
,
$p^{k,\alpha}$
,
![]() $p^{k,\beta}$
,
$p^{k,\beta}$
,
![]() ${\mathbf k=m,1,\ldots, d}$
, defined in Proposition 4.2.
${\mathbf k=m,1,\ldots, d}$
, defined in Proposition 4.2.
Step 1. First we identify
![]() $p^0(b,a;\,t) $
as the factor of F(b, a) in the integrand of
$p^0(b,a;\,t) $
as the factor of F(b, a) in the integrand of
![]() $I_0:$
$I_0:$
Step 2. We now deal with
![]() $I_k$
,
$I_k$
,
![]() $k=2,\ldots,d.$
Integrating by parts with respect to
$k=2,\ldots,d.$
Integrating by parts with respect to
![]() $a^k$
between
$a^k$
between
![]() $-\infty $
and
$-\infty $
and
![]() $\infty$
in
$\infty$
in
![]() $I_k$
for
$I_k$
for
![]() $k=2,\ldots,d$
yields
$k=2,\ldots,d$
yields
 \begin{align*}I_k&=-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}} F\!\left(\max\! \left( M_s,b\right),a\right) B^{k}(X_s)\partial_{k}p_{W^{*1},W}\big(b-{X^1_s},a-X_s;\,t-s\big)dbda \right]ds\nonumber \\ &=-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{{\mathbf 1}}_{\{b> M_s\}} F\!\left(b,a\right) B^{k}(X_s)\partial_{k}p_{W^{*1},W}\big(b-{X^1_s},a-X_s;\,t-s\big)dbda \right]ds \\ &-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}} {{\mathbf 1}}_{\{b< M_s\}}F\!\left( M_s,a\right) B^{k}(X_s)\partial_{k}p_{W^{*1},W}\big(b-{X^1_s},a-X_s;\,t-s\big)dbda \right]ds. \nonumber\end{align*}
\begin{align*}I_k&=-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}} F\!\left(\max\! \left( M_s,b\right),a\right) B^{k}(X_s)\partial_{k}p_{W^{*1},W}\big(b-{X^1_s},a-X_s;\,t-s\big)dbda \right]ds\nonumber \\ &=-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{{\mathbf 1}}_{\{b> M_s\}} F\!\left(b,a\right) B^{k}(X_s)\partial_{k}p_{W^{*1},W}\big(b-{X^1_s},a-X_s;\,t-s\big)dbda \right]ds \\ &-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}} {{\mathbf 1}}_{\{b< M_s\}}F\!\left( M_s,a\right) B^{k}(X_s)\partial_{k}p_{W^{*1},W}\big(b-{X^1_s},a-X_s;\,t-s\big)dbda \right]ds. \nonumber\end{align*}
We identify
![]() $-p^{k,\alpha}(b,a,t)$
inside the integral on the set
$-p^{k,\alpha}(b,a,t)$
inside the integral on the set
![]() $\{b>M_s\}.$
For the integral on the set
$\{b>M_s\}.$
For the integral on the set
![]() $\{b<M_s\}$
, we introduce the density of
$\{b<M_s\}$
, we introduce the density of
![]() $(M_s,X_s)$
and identify
$(M_s,X_s)$
and identify
![]() $-p^{k,\beta}(m,a;\,t)$
as the factor of F(m, a).
$-p^{k,\beta}(m,a;\,t)$
as the factor of F(m, a).
Step 3. Finally, we identify the terms
![]() $p^{m,\gamma}$
and
$p^{m,\gamma}$
and
![]() $p^{1,\gamma}$
,
$p^{1,\gamma}$
,
![]() $\gamma=\alpha, \beta$
, which come from the sum of
$\gamma=\alpha, \beta$
, which come from the sum of
![]() $I_m$
and
$I_m$
and
![]() $I_1$
. Note that
$I_1$
. Note that
![]() $p_{W^{*1},W}\!\left(b-X_s^1,a-X_s;\,t-s\right)=0$
on the set
$p_{W^{*1},W}\!\left(b-X_s^1,a-X_s;\,t-s\right)=0$
on the set
![]() ${\big\{b<a^1\big\}}.$
Integrating by parts with respect to b between
${\big\{b<a^1\big\}}.$
Integrating by parts with respect to b between
![]() $\max\left({a^1},M_s\right) $
and
$\max\left({a^1},M_s\right) $
and
![]() $\infty$
in
$\infty$
in
![]() $I_m$
yields
$I_m$
yields
 \begin{align}&I_m=-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^d}F\big( \max\!\big({a^1}, M_s\big),a\big)B^1(X_s)p_{W^{*1},W}\big(\max\!\big({a^1},M_s\big)-X_s^1,a-X_s;\,t-s\big)da\right]ds\nonumber\\[4pt]&-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{\mathbf 1}_{M_s<b}F\!\left( b,a\right)B^1(X_s)\partial_{m}p_{W^{*1},W}\left(b-X_s^1,a-X_s;\,t-s\right)dbda\right]ds.\end{align}
\begin{align}&I_m=-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^d}F\big( \max\!\big({a^1}, M_s\big),a\big)B^1(X_s)p_{W^{*1},W}\big(\max\!\big({a^1},M_s\big)-X_s^1,a-X_s;\,t-s\big)da\right]ds\nonumber\\[4pt]&-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{\mathbf 1}_{M_s<b}F\!\left( b,a\right)B^1(X_s)\partial_{m}p_{W^{*1},W}\left(b-X_s^1,a-X_s;\,t-s\right)dbda\right]ds.\end{align}
Integrating by parts with respect to
![]() $a^1$
between
$a^1$
between
![]() $-\infty $
and b in
$-\infty $
and b in
![]() $I_1$
yields
$I_1$
yields
 \begin{align}I_1&= \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d}}F\!\left( \max\left( M_s,b\right),b,\tilde a\right) B^1(X_s)p_{W^{*1},W}\big(b- X^1_s,b- X^1_s,\tilde a-\tilde X_s;\,t-s\big)dbd\tilde a \right]ds \nonumber \\&-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}} F\!\left(\max\! \left( M_s,b\right),a\right) B^1(X_s)\partial_{1}p_{W^{*1},W}\big(b- X^1_s,a-X_s;\,t-s\big)dbda \right]ds.\nonumber\\\end{align}
\begin{align}I_1&= \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d}}F\!\left( \max\left( M_s,b\right),b,\tilde a\right) B^1(X_s)p_{W^{*1},W}\big(b- X^1_s,b- X^1_s,\tilde a-\tilde X_s;\,t-s\big)dbd\tilde a \right]ds \nonumber \\&-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}} F\!\left(\max\! \left( M_s,b\right),a\right) B^1(X_s)\partial_{1}p_{W^{*1},W}\big(b- X^1_s,a-X_s;\,t-s\big)dbda \right]ds.\nonumber\\\end{align}
We then have the following:
-
(i) The term
 $p^{m,\beta}{(b,a,t)}$
comes from the second term in
$p^{m,\beta}{(b,a,t)}$
comes from the second term in
 $I_m$
(Equation (29)) as the factor of F(b, a):
$I_m$
(Equation (29)) as the factor of F(b, a):  \begin{equation*}-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{\mathbf 1}_{M_s<b}F\!\left( b,a\right)B^1(X_s){\partial_m}p_{W^{*1},W}\big(b-X_s^1,a-X_s;\,t-s\big)dbda\right]ds\end{equation*}
\begin{equation*}-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}}{\mathbf 1}_{M_s<b}F\!\left( b,a\right)B^1(X_s){\partial_m}p_{W^{*1},W}\big(b-X_s^1,a-X_s;\,t-s\big)dbda\right]ds\end{equation*}
-
(ii) The terms
 $-p^{1,\alpha}(b,a,t)$
and
$-p^{1,\alpha}(b,a,t)$
and
 $-p^{1,\beta}(b,a;\,t)$
come from the second term in
$-p^{1,\beta}(b,a;\,t)$
come from the second term in
 $I_1$
(Equation (30)): Inside the integral on the set
$I_1$
(Equation (30)): Inside the integral on the set \begin{equation*}-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}} F\!\left(\max\! \left( b,M_s\right),a\right) B^1(X_s)\partial_{1}p_{W^{*1},W}\big(b-{X^1_s},a-X_s;\,t-s\big)dbda \right]ds.\end{equation*}
\begin{equation*}-\int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d+1}} F\!\left(\max\! \left( b,M_s\right),a\right) B^1(X_s)\partial_{1}p_{W^{*1},W}\big(b-{X^1_s},a-X_s;\,t-s\big)dbda \right]ds.\end{equation*}
 $\{M_s<b\}$
we identify
$\{M_s<b\}$
we identify
 $-p^{1,\alpha}(b,a,t)$
as the factor of
$-p^{1,\alpha}(b,a,t)$
as the factor of
 $F(b,a)$
, and inside the integral on the set
$F(b,a)$
, and inside the integral on the set
 $\{M_s>b\}$
we identify
$\{M_s>b\}$
we identify
 $-p^{1,\beta}(b,a;t)$
as the factor of
$-p^{1,\beta}(b,a;t)$
as the factor of
 $F(M_s,a)$
.
$F(M_s,a)$
.
-
(iii) The term
 $-p^{m,\alpha}(b,a,t)$
comes from the sum of first terms in
$-p^{m,\alpha}(b,a,t)$
comes from the sum of first terms in
 $I_1$
(Equation (30)) and
$I_1$
(Equation (30)) and
 $I_m$
(Equation (29)).
$I_m$
(Equation (29)).
Now we replace the variable b by
![]() $a_1$
and replace
$a_1$
and replace
![]() $dbd\tilde a$
by da in the first terms of
$dbd\tilde a$
by da in the first terms of
![]() $I_m$
and
$I_m$
and
![]() $I_1$
:
$I_1$
:
 \begin{align*}I^1_m&=-\!\int_0^t {\mathbb E}_\mathbb{P}\!\left[\int_{{\mathbb R}^d}\!F\big( \max\!\big({a^1}, M_s\big),a\big)B^1(X_s)p_{W^{*1},W}\big(\max\!\big({a^1},M_s\big)-X_s^1,a-X_s;\,t-s\big)da\right]ds,\\I^1_1&= \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d}}F\big( \max\!\big( M_s,a^1\big),a\big) B^1(X_s)p_{W^{*1},W}\big(a^1-{X^1_s},a-X_s;\,t-s\big)d a \right]ds.\end{align*}
\begin{align*}I^1_m&=-\!\int_0^t {\mathbb E}_\mathbb{P}\!\left[\int_{{\mathbb R}^d}\!F\big( \max\!\big({a^1}, M_s\big),a\big)B^1(X_s)p_{W^{*1},W}\big(\max\!\big({a^1},M_s\big)-X_s^1,a-X_s;\,t-s\big)da\right]ds,\\I^1_1&= \int_0^t {\mathbb E}_\mathbb{P}\left[\int_{{\mathbb R}^{d}}F\big( \max\!\big( M_s,a^1\big),a\big) B^1(X_s)p_{W^{*1},W}\big(a^1-{X^1_s},a-X_s;\,t-s\big)d a \right]ds.\end{align*}
Note that
 \begin{align*}&-p_{W^{*1},W}\big(\max\!\big(a^1, M_s\big)-X_s^1,a-X_s;\,t-s\big)+p_{W^{*1},W}\big(a^1-X^1_s,a-X_s;\,t-s\big)\\&=\left[-p_{W^{*1},W}\big(M_s-X_s^1,a-X_s;\,t-s\big)+p_{W^{*1},W}\big(a^1-X_s^1,a-X_s;\,t-s\big)\right] {\mathbf 1}_{M_s >a^1}\\&=-\int_{a^1}^{M_s}{\partial_m}p_{W^{*1},W}\big(b-X^1_s, a-X_s,t-s\big){db} {\mathbf 1}_{M_s >a^1}.\end{align*}
\begin{align*}&-p_{W^{*1},W}\big(\max\!\big(a^1, M_s\big)-X_s^1,a-X_s;\,t-s\big)+p_{W^{*1},W}\big(a^1-X^1_s,a-X_s;\,t-s\big)\\&=\left[-p_{W^{*1},W}\big(M_s-X_s^1,a-X_s;\,t-s\big)+p_{W^{*1},W}\big(a^1-X_s^1,a-X_s;\,t-s\big)\right] {\mathbf 1}_{M_s >a^1}\\&=-\int_{a^1}^{M_s}{\partial_m}p_{W^{*1},W}\big(b-X^1_s, a-X_s,t-s\big){db} {\mathbf 1}_{M_s >a^1}.\end{align*}
Then the sum of
![]() $I_m^1$
and
$I_m^1$
and
![]() $I_1^1$
is
$I_1^1$
is
We introduce the density of the law of the pair
![]() $(M_s,X_s)$
and we identify
$(M_s,X_s)$
and we identify
![]() $-p^{m,\alpha}(m,a;\,t)$
as the factor of
$-p^{m,\alpha}(m,a;\,t)$
as the factor of
![]() $F(m,a).$
$F(m,a).$
These three steps complete the proof of Proposition 4.2 when
![]() $\mu_0=\delta_{x_0}.$
$\mu_0=\delta_{x_0}.$
Finally, when
![]() $\mu_0$
is the law of
$\mu_0$
is the law of
![]() $X_0,$
we have
$X_0,$
we have
![]() $ p_V(m,w;\,t,\mu_0)=\int_{{\mathbb R}^d} p_V(m,x;\,t,\delta_{x_0}) \mu_0(dx_0).$
Then we can complete the proof of Proposition 4.2 for any initial law
$ p_V(m,w;\,t,\mu_0)=\int_{{\mathbb R}^d} p_V(m,x;\,t,\delta_{x_0}) \mu_0(dx_0).$
Then we can complete the proof of Proposition 4.2 for any initial law
![]() $\mu_0$
by integrating with respect to
$\mu_0$
by integrating with respect to
![]() $\mu_0$
the expression obtained in (21) for
$\mu_0$
the expression obtained in (21) for
![]() $p_V\big(m,x;\,t,\delta_{x_0}\big)$
.
$p_V\big(m,x;\,t,\delta_{x_0}\big)$
.
4.2. Proof of Proposition 4.1
Using some ideas used in [Reference Garroni and Menaldi14, Section V.3.2], let us introduce the following linear maps on
![]() $L^{\infty}\big([0, T],dt, L^1\big({\mathbb R}^{d+1},dmdx\big)\big),$
for
$L^{\infty}\big([0, T],dt, L^1\big({\mathbb R}^{d+1},dmdx\big)\big),$
for
![]() $k=m,1,\ldots,d$
:
$k=m,1,\ldots,d$
:
 \begin{align}&{{\mathcal{I}}^{k,\alpha}}[p](m,x;\,t)\,:\!=\,\int_0^t{\int_{\mathbb{R}^{d+1}} {\mathbf 1}_{b <m}B^{k}(a)\partial_{k}p_{W^{*1},W}\big(m-a^1,x-a;\,t-s\big)}p(b,a;\,s)dbdads,\\&{{\mathcal{I}}^{k,\beta}}[p](m,x;\,t)\,:\!=\,\int_0^t \int_{{\mathbb R}^{d+1}}{\mathbf 1}_{b<m} B^{k}(a)\partial_{k}p_{W^{*1},W}\big(b-a^1,x-a;\,t-s\big)p(m,a;\,s)dbda ds.\nonumber\end{align}
\begin{align}&{{\mathcal{I}}^{k,\alpha}}[p](m,x;\,t)\,:\!=\,\int_0^t{\int_{\mathbb{R}^{d+1}} {\mathbf 1}_{b <m}B^{k}(a)\partial_{k}p_{W^{*1},W}\big(m-a^1,x-a;\,t-s\big)}p(b,a;\,s)dbdads,\\&{{\mathcal{I}}^{k,\beta}}[p](m,x;\,t)\,:\!=\,\int_0^t \int_{{\mathbb R}^{d+1}}{\mathbf 1}_{b<m} B^{k}(a)\partial_{k}p_{W^{*1},W}\big(b-a^1,x-a;\,t-s\big)p(m,a;\,s)dbda ds.\nonumber\end{align}
Let us introduce the following inductively defined functions:
and for
![]() $k=m,1,\ldots,d$
,
$k=m,1,\ldots,d$
,
![]() $j=\alpha,\beta$
, and
$j=\alpha,\beta$
, and
![]() $n \geq 1$
,
$n \geq 1$
,
Let us define the operator
Moreover, one can observe that this means
![]() $p_{n+1}={\mathcal{I}}(p_n)$
, and Proposition 4.2 leads to
$p_{n+1}={\mathcal{I}}(p_n)$
, and Proposition 4.2 leads to
![]() $p_V=p_0+{\mathcal{I}}(p_V).$
Let
$p_V=p_0+{\mathcal{I}}(p_V).$
Let
Proposition 4.3.
Assume the vector B is bounded; then for all T the sequence
![]() $(P_n)_n$
converges in
$(P_n)_n$
converges in
![]() $L^{\infty} ( [0,T],L^1 ({\mathbb R}^{d+1},dxdm))$
to
$L^{\infty} ( [0,T],L^1 ({\mathbb R}^{d+1},dxdm))$
to
![]() $p_V$
. Moreover,
$p_V$
. Moreover,
![]() $p_V=\sum_{n=0}^{\infty} p_n.$
$p_V=\sum_{n=0}^{\infty} p_n.$
The proof is a consequence of the following two lemmas.
Lemma 4.2. Let
![]() $j=\alpha,\beta$
,
$j=\alpha,\beta$
,
![]() $k=m,1,\ldots,d$
, and
$k=m,1,\ldots,d$
, and
![]() $T>0$
. The linear maps
$T>0$
. The linear maps
![]() ${\mathcal I}^{k,j}$
are continuous on
${\mathcal I}^{k,j}$
are continuous on
![]() $L^{\infty}\big([0, T],dt, L^1\big({\mathbb R}^{d+1},dmdx\big)\big)$
: there exists a constant C such that for all
$L^{\infty}\big([0, T],dt, L^1\big({\mathbb R}^{d+1},dmdx\big)\big)$
: there exists a constant C such that for all
![]() $p \in L^{\infty}\big([0, T],dt, L^1\big({\mathbb R}^{d+1},dmdx\big)\big)$
,
$p \in L^{\infty}\big([0, T],dt, L^1\big({\mathbb R}^{d+1},dmdx\big)\big)$
,
As a consequence,
Proof. Let
![]() $T>0,$
$T>0,$
![]() $p \in L^{\infty}\big([0, T] \times L^1\big({\mathbb R}^{d+1},dmdx\big)\big)$
, and
$p \in L^{\infty}\big([0, T] \times L^1\big({\mathbb R}^{d+1},dmdx\big)\big)$
, and
![]() $t \in [0,T]$
, and let
$t \in [0,T]$
, and let
![]() $\phi_{d+1}$
be the Gaussian law density restricted to the subset
$\phi_{d+1}$
be the Gaussian law density restricted to the subset
![]() $\big\{b>a^1_+\big\}$
(up to a constant):
$\big\{b>a^1_+\big\}$
(up to a constant):
 \begin{align} \phi_{d+1}\big(b,b-a^1,\tilde a;\,2t\big) \,:\!=\,\frac{1}{{\sqrt{2 \pi t}^{d+1}}}{\mathbf 1}_{b>a^1_+}e^{- \frac{b^2 + \big(b-a^1\big)^2 + \|\tilde{a}\|^2}{4t}}. \end{align}
\begin{align} \phi_{d+1}\big(b,b-a^1,\tilde a;\,2t\big) \,:\!=\,\frac{1}{{\sqrt{2 \pi t}^{d+1}}}{\mathbf 1}_{b>a^1_+}e^{- \frac{b^2 + \big(b-a^1\big)^2 + \|\tilde{a}\|^2}{4t}}. \end{align}
(i) Let
![]() $j=\alpha$
and
$j=\alpha$
and
![]() $k=m,1,\ldots,d$
; according to the definition of
$k=m,1,\ldots,d$
; according to the definition of
![]() ${\mathcal I}^{k,\alpha}$
and the boundedness of B,
${\mathcal I}^{k,\alpha}$
and the boundedness of B,
Using Lemma A.2, there exists a constant D such that for
![]() $k=m,1,\ldots,d$
,
$k=m,1,\ldots,d$
,
So
 \begin{align*} &\left| {\mathcal I}^{k,\alpha}[p](m,x;\,t)\right| \\ & \quad \leq \|B\|_{\infty} \int_0^t \int_{{\mathbb R}^{d+1}} \frac{D}{\sqrt{t-s}}\phi_{d+1}\big(m-a^1,m-x^1,\tilde x-\tilde a;\,t-s\big)|p(b,a;\,s)|dbdads. \end{align*}
\begin{align*} &\left| {\mathcal I}^{k,\alpha}[p](m,x;\,t)\right| \\ & \quad \leq \|B\|_{\infty} \int_0^t \int_{{\mathbb R}^{d+1}} \frac{D}{\sqrt{t-s}}\phi_{d+1}\big(m-a^1,m-x^1,\tilde x-\tilde a;\,t-s\big)|p(b,a;\,s)|dbdads. \end{align*}
We perform an integration with respect to (m, x) using Tonelli’s theorem and omitting the indicator functions. Since
![]() $\phi_{d+1}$
is the density of a Gaussian law, we get the bound
$\phi_{d+1}$
is the density of a Gaussian law, we get the bound
 \begin{align*} \left\| {\mathcal I}^{k,\alpha}[p](.,.;\,t)\right\|_{L^1\big({\mathbb R}^{d+1},dmdx\big)} \leq\, & D\|B\|_{\infty} \int_0^t \int_{{\mathbb R}^{d+1}}\frac{1}{\sqrt{t-s}}| p(b,a;\,s)|{db}dads \\ \leq\, & 2^{(d+1)/2}D\|B\|_{\infty} \int_0^t \frac{1}{\sqrt{t-s}}\sup_{u\leq s}\| p(.,.;\,u)\|_{L^1\big(\mathbb{R}^{d+1},dbda\big)}ds, \end{align*}
\begin{align*} \left\| {\mathcal I}^{k,\alpha}[p](.,.;\,t)\right\|_{L^1\big({\mathbb R}^{d+1},dmdx\big)} \leq\, & D\|B\|_{\infty} \int_0^t \int_{{\mathbb R}^{d+1}}\frac{1}{\sqrt{t-s}}| p(b,a;\,s)|{db}dads \\ \leq\, & 2^{(d+1)/2}D\|B\|_{\infty} \int_0^t \frac{1}{\sqrt{t-s}}\sup_{u\leq s}\| p(.,.;\,u)\|_{L^1\big(\mathbb{R}^{d+1},dbda\big)}ds, \end{align*}
which implies the inequality (35) when
![]() $j=\alpha.$
$j=\alpha.$
(ii) Let
![]() $j=\beta$
and
$j=\beta$
and
![]() $k=m,1,\ldots,d.$
According to the definition of
$k=m,1,\ldots,d.$
According to the definition of
![]() ${\mathcal I}^{k,\beta}$
and the boundedness of B,
${\mathcal I}^{k,\beta}$
and the boundedness of B,
Using (38) yields
We integrate with respect to x, then with respect to b, using Tonelli’s theorem and omitting the indicator functions, and using the fact that
![]() $\phi$
is the density of a Gaussian law. So the bound with respect to a multiplicative constant is
$\phi$
is the density of a Gaussian law. So the bound with respect to a multiplicative constant is
 \begin{align*} \left\| {\mathcal I}^{k,\beta}[p](.,.;\,t)\right\|_{L^1\big({\mathbb R}^{d+1},dmdx\big)} \leq\, & D \|B\|_{\infty}2^{(d+1)/2} \int_0^t \int_{{\mathbb R}^{d+1}}\frac{1}{\sqrt{t-s}}| p(m,a;\,s)|dmdads\\ \leq\, & D \|B\|_{\infty}2^{(d+1)/2} \int_0^t \frac{1}{\sqrt{t-s}}\sup_{u\leq s}\| p(.,.;\,u)\|_{L^1\big(\mathbb{R}^{d+1},dmda\big)}ds, \end{align*}
\begin{align*} \left\| {\mathcal I}^{k,\beta}[p](.,.;\,t)\right\|_{L^1\big({\mathbb R}^{d+1},dmdx\big)} \leq\, & D \|B\|_{\infty}2^{(d+1)/2} \int_0^t \int_{{\mathbb R}^{d+1}}\frac{1}{\sqrt{t-s}}| p(m,a;\,s)|dmdads\\ \leq\, & D \|B\|_{\infty}2^{(d+1)/2} \int_0^t \frac{1}{\sqrt{t-s}}\sup_{u\leq s}\| p(.,.;\,u)\|_{L^1\big(\mathbb{R}^{d+1},dmda\big)}ds, \end{align*}
which implies the inequality (35) for
![]() $j=\beta.$
$j=\beta.$
Finally, the estimate (36) is obtained by adding the estimates (35) for
![]() $j=\alpha, \beta$
and
$j=\alpha, \beta$
and
![]() $k=m, 1,\ldots,d.$
$k=m, 1,\ldots,d.$
The following lemma is a consequence of (36) in Lemma 4.2.
Lemma 4.3. For all n,
Proof. (i) For all
![]() $t>0,$
$t>0,$
![]() $p_0(.;\,t)$
is a probability density function, so (39) is satisfied for
$p_0(.;\,t)$
is a probability density function, so (39) is satisfied for
![]() $n=0.$
We now assume that (39) is satisfied for n. Using
$n=0.$
We now assume that (39) is satisfied for n. Using
![]() $p_{n+1}={\mathcal{I}} [p_n]$
, (36), and the inductive assumption,
$p_{n+1}={\mathcal{I}} [p_n]$
, (36), and the inductive assumption,
We perform the change of variable
![]() $s=tu$
and use
$s=tu$
and use
to obtain
which proves (39) for all n.
(ii) Noting that
![]() $P_0=p_0$
and
$P_0=p_0$
and
![]() $p_V-p_0= {\mathcal{I}}[p_V]$
and applying (36) to
$p_V-p_0= {\mathcal{I}}[p_V]$
and applying (36) to
![]() $p_V$
, we obtain
$p_V$
, we obtain
But
![]() $\Gamma(1/2) / \Gamma(3/2)=2$
, so (40) is satisfied for
$\Gamma(1/2) / \Gamma(3/2)=2$
, so (40) is satisfied for
![]() $n=0.$
$n=0.$
We now suppose that (40) is satisfied for n. Using
the bound (36), and the induction assumption, we have
We now perform the change of variable
![]() $s=tu$
and
$s=tu$
and
with
![]() $a=(n+3)/2$
,
$a=(n+3)/2$
,
![]() $b={\frac{1}{2}}$
, to obtain
$b={\frac{1}{2}}$
, to obtain
which proves (40) for
![]() $n+1$
and thus for all n.
$n+1$
and thus for all n.
The series
![]() $\sum_n \frac{x^n}{\Gamma(n/2 +1)}$
is convergent for any x, so Proposition 4.3 is a consequence of Lemmas 4.2 and 4.3.
$\sum_n \frac{x^n}{\Gamma(n/2 +1)}$
is convergent for any x, so Proposition 4.3 is a consequence of Lemmas 4.2 and 4.3.
4.2.1. Upper bound of
 $p_V$
(i.e., Hypothesis 2.1(i)).
$p_V$
(i.e., Hypothesis 2.1(i)).
For all
![]() $T>0,$
$T>0,$
![]() $x_0 \in \mathbb{R}^d,$
and
$x_0 \in \mathbb{R}^d,$
and
![]() $p \in L^{\infty}([0,T], L^{1}\big(\mathbb{R}^{d+1},dmdx\big))$
whose support is contained in
$p \in L^{\infty}([0,T], L^{1}\big(\mathbb{R}^{d+1},dmdx\big))$
whose support is contained in
![]() $\big\{(m,x),\ m>x_0^1, m>x^1\big\}$
, let us define
$\big\{(m,x),\ m>x_0^1, m>x^1\big\}$
, let us define
Proposition 4.4.
For every
![]() $T>0$
there exists a constant
$T>0$
there exists a constant
![]() $C_T$
, and for all n there exist constants
$C_T$
, and for all n there exist constants
![]() $C_n= \frac{\left[\|B\|_\infty D{(2(d+1)) 2^{d/2}}{\Gamma(1/2)}\right]^n}{\Gamma(1+n/2)}$
, such that for all
$C_n= \frac{\left[\|B\|_\infty D{(2(d+1)) 2^{d/2}}{\Gamma(1/2)}\right]^n}{\Gamma(1+n/2)}$
, such that for all
![]() $x_0 \in \mathbb{R}^d$
,
$x_0 \in \mathbb{R}^d$
,
![]() ${0<t\leq T},$
the following hold:
${0<t\leq T},$
the following hold:
-
(i)
 $\left| p_n\big(m,x;\,t,x_0\big) \right| \leq C_nt^{n/2}\phi_{d+1}\big( m-x^1_0,m-x^1,\tilde{x}-\tilde{x}_0, 2t\big){\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)}$
;
$\left| p_n\big(m,x;\,t,x_0\big) \right| \leq C_nt^{n/2}\phi_{d+1}\big( m-x^1_0,m-x^1,\tilde{x}-\tilde{x}_0, 2t\big){\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)}$
; -
(ii)
 $\left|p_V\big(m,x;\,t,x_0\big) \right| \leq C_T\phi_{d+1}\big( m-x^1_0,m-x^1,\tilde{x}-\tilde{x}_0, 2t\big){\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)}$
;
$\left|p_V\big(m,x;\,t,x_0\big) \right| \leq C_T\phi_{d+1}\big( m-x^1_0,m-x^1,\tilde{x}-\tilde{x}_0, 2t\big){\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)}$
; -
(iii) for every initial probability measure
 $\mu_0$
on
$\mu_0$
on
 ${\mathbb R}^d$
,
${\mathbb R}^d$
,  \begin{equation*}\sup_{u >0} p_V(m,m-u,\tilde{x},t;\, \mu_0) \in L^1([0,T] \times \mathbb{R}^d, dtdmd\tilde{x}).\end{equation*}
\begin{equation*}\sup_{u >0} p_V(m,m-u,\tilde{x},t;\, \mu_0) \in L^1([0,T] \times \mathbb{R}^d, dtdmd\tilde{x}).\end{equation*}
Note that Part (iii) is actually Hypothesis 2.1(i).
Proof. Part (ii) is a consequence of Part (i), since
![]() $p_V=\sum_{n=0}^{\infty}p_n,$
and the series
$p_V=\sum_{n=0}^{\infty}p_n,$
and the series
![]() $\sum_n \frac{1}{{\Gamma (1+n/2)}}x^n$
has an infinite radius of convergence (Proposition 4.3).
$\sum_n \frac{1}{{\Gamma (1+n/2)}}x^n$
has an infinite radius of convergence (Proposition 4.3).
We prove Part (i) by induction on n, using Part (ii) of Lemma A.2:
 \begin{align*} p_0\big(m,x;\,t,x_0\big) &\leq\frac{e^{-\frac{\big(m-x^1\big)^2}{4t}-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t} {- \frac{\big(m-x_0^1\big)^2}{4t}}}}{\sqrt{(2 \pi )^{d+1}{t^{d+1}}}}{\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)}\\&= \phi_{d+1}(m-x^1,m-x_0^1,\tilde x-\tilde x_0;\,2t){\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)},\end{align*}
\begin{align*} p_0\big(m,x;\,t,x_0\big) &\leq\frac{e^{-\frac{\big(m-x^1\big)^2}{4t}-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t} {- \frac{\big(m-x_0^1\big)^2}{4t}}}}{\sqrt{(2 \pi )^{d+1}{t^{d+1}}}}{\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)}\\&= \phi_{d+1}(m-x^1,m-x_0^1,\tilde x-\tilde x_0;\,2t){\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)},\end{align*}
so
![]() $N(p_0;\,t,x_0) \leq 1,$
which is Part (i) for
$N(p_0;\,t,x_0) \leq 1,$
which is Part (i) for
![]() $n=0,$
$n=0,$
![]() $C_0=1$
.
$C_0=1$
.
We assume Part (i) is true for
![]() $p_n,$
meaning
$p_n,$
meaning
![]() $N(p_n;\,t,x_0) \leq C_nt^{n/2}.$
By definition,
$N(p_n;\,t,x_0) \leq C_nt^{n/2}.$
By definition,
![]() $p_{n+1}= {\mathcal I}[p_n]$
; Lemma 4.4, proved below, yields
$p_{n+1}= {\mathcal I}[p_n]$
; Lemma 4.4, proved below, yields
We perform the change of variable
![]() $s=tu$
to obtain
$s=tu$
to obtain
Using
and the definition of
![]() $C_n$
, we have
$C_n$
, we have
this completes the proof of Proposition 4.4(i).
Then, for all
![]() $x_0 \in \mathbb{R}^d$
and using
$x_0 \in \mathbb{R}^d$
and using
![]() $x^1=m-u,$
$x^1=m-u,$
Since
![]() $p_V(m,x;\,t,\mu_0)=\int_{\mathbb{R}^d} p_V\big(m,x;\,t,x_0\big) \mu_0(dx_0)$
, Part (iii) is true.
$p_V(m,x;\,t,\mu_0)=\int_{\mathbb{R}^d} p_V\big(m,x;\,t,x_0\big) \mu_0(dx_0)$
, Part (iii) is true.
Lemma 4.4.
Let
![]() $T>0, $
$T>0, $
![]() $x_0 \in \mathbb{R}^d,$
$x_0 \in \mathbb{R}^d,$
![]() $p \in L^{\infty}\big([0,T], dt, L^{1}\big(\mathbb{R}^{d+1},dmdx\big)\big)$
be such that the support of
$p \in L^{\infty}\big([0,T], dt, L^{1}\big(\mathbb{R}^{d+1},dmdx\big)\big)$
be such that the support of
![]() $p(.,.;\,t)$
is included in
$p(.,.;\,t)$
is included in
![]() $\big\{(m,x),\ m>x_0^1, m>x^1\big\}$
and for all
$\big\{(m,x),\ m>x_0^1, m>x^1\big\}$
and for all
![]() $s\in ]0,T]$
$s\in ]0,T]$
![]() $N(p;\,s,x_0) <\infty. $
Then for
$N(p;\,s,x_0) <\infty. $
Then for
![]() $j=\alpha,$
$j=\alpha,$
![]() $k=m,1,\ldots,d,$
the support of the function
$k=m,1,\ldots,d,$
the support of the function
![]() ${\mathcal I}^{j,k}[p](.;\,t)$
is included in
${\mathcal I}^{j,k}[p](.;\,t)$
is included in
![]() $\big\{(m,x),\ m>x_0^1, m>x^1\big\}.$
Moreover, for all
$\big\{(m,x),\ m>x_0^1, m>x^1\big\}.$
Moreover, for all
![]() $t\in [0,T]$
, we have
$t\in [0,T]$
, we have
Proof. Let
![]() $T>0,$
$T>0,$
![]() $x_0\in\mathbb{R}^d,$
$x_0\in\mathbb{R}^d,$
![]() $p \in L^{\infty}\big([0,T], dt,L^{1}\big(\mathbb{R}^{d+1},dmdx\big)\big)$
be such that for all
$p \in L^{\infty}\big([0,T], dt,L^{1}\big(\mathbb{R}^{d+1},dmdx\big)\big)$
be such that for all
![]() $t>0$
, the support of
$t>0$
, the support of
![]() $p(.;\,t)$
is included in
$p(.;\,t)$
is included in
![]() $\big\{(m,x),\ m>x_0^1, m>x^1\big\}.$
$\big\{(m,x),\ m>x_0^1, m>x^1\big\}.$
(i) For
![]() $j=\alpha,$
$j=\alpha,$
![]() $k=m, 1,\ldots,d,$
using the definition of
$k=m, 1,\ldots,d,$
using the definition of
![]() ${\mathcal I}^{\alpha,k}$
yields
${\mathcal I}^{\alpha,k}$
yields
 \begin{align*} &{{\mathcal I}^{k,\alpha}}[p](m,x;\,t)\,:\!=\, \\ & \quad \int_0^t{\int_{\mathbb{R}^{d+1}} B^{k}(a)\partial_{k}p_{W^{*1},W}\big(m-a^1,x-a;\,t-s\big){\mathbf 1}_{x_0^1<b <m,m>x^1}p(b,a;\,s)dbda}ds. \end{align*}
\begin{align*} &{{\mathcal I}^{k,\alpha}}[p](m,x;\,t)\,:\!=\, \\ & \quad \int_0^t{\int_{\mathbb{R}^{d+1}} B^{k}(a)\partial_{k}p_{W^{*1},W}\big(m-a^1,x-a;\,t-s\big){\mathbf 1}_{x_0^1<b <m,m>x^1}p(b,a;\,s)dbda}ds. \end{align*}
So the support of
![]() ${\mathcal I}^{\alpha,k}[p](.;\,t)$
is included in
${\mathcal I}^{\alpha,k}[p](.;\,t)$
is included in
![]() $\big\{(m,x) \in \mathbb{R}^{d+1},\ m>\max\!\big(x^1_0,x^1\big)\big\}.$
From now on, we consider only (m, x) such that
$\big\{(m,x) \in \mathbb{R}^{d+1},\ m>\max\!\big(x^1_0,x^1\big)\big\}.$
From now on, we consider only (m, x) such that
![]() $m >\max\!\big(x^1,x^1_0\big).$
$m >\max\!\big(x^1,x^1_0\big).$
Let p be a function such that for all
![]() $s \in ]0,T]$
,
$s \in ]0,T]$
,
![]() $N(p;\,x_0,s)<\infty.$
The definition of
$N(p;\,x_0,s)<\infty.$
The definition of
![]() ${\mathcal I}^{k,\alpha},$
the boundedness of B, the fact that
${\mathcal I}^{k,\alpha},$
the boundedness of B, the fact that
![]() $\partial_kp_{W^*,W}$
satisfies (38), and the definition (41) of
$\partial_kp_{W^*,W}$
satisfies (38), and the definition (41) of
![]() $N(p;\,t,x_0)$
imply that
$N(p;\,t,x_0)$
imply that
 \begin{align*} \left| {\mathcal I}^{k,\alpha}[p](m,x;\,t) \right| \leq \|B\|_{\infty}\int_0^t\int_{{\mathbb R}^{d+1}}N(p;\,s,x_0) \frac{D}{\sqrt{(t-s)}} {\mathbf 1}_{m>x_1}{\mathbf 1}_{m>b>\max\!\big(a^1,x_0^1\big)} \\ \,\,\,\,\,\, \phi_{d+1}\big(m-a^1, m-x^1,\tilde{x}-\tilde{a};\,t-s\big) \phi_{d+1}\big(b-x_0^1,b-a^1,\tilde{a}-\tilde{x_0};\,s\big) db da ds. \end{align*}
\begin{align*} \left| {\mathcal I}^{k,\alpha}[p](m,x;\,t) \right| \leq \|B\|_{\infty}\int_0^t\int_{{\mathbb R}^{d+1}}N(p;\,s,x_0) \frac{D}{\sqrt{(t-s)}} {\mathbf 1}_{m>x_1}{\mathbf 1}_{m>b>\max\!\big(a^1,x_0^1\big)} \\ \,\,\,\,\,\, \phi_{d+1}\big(m-a^1, m-x^1,\tilde{x}-\tilde{a};\,t-s\big) \phi_{d+1}\big(b-x_0^1,b-a^1,\tilde{a}-\tilde{x_0};\,s\big) db da ds. \end{align*}
We integrate in
![]() $\tilde{a}$
using Lemma A.3(ii) with
$\tilde{a}$
using Lemma A.3(ii) with
![]() $u=\tilde{x},$
$u=\tilde{x},$
![]() $v=\tilde{a},$
$v=\tilde{a},$
![]() $w=\tilde{x}_0$
and the fact that
$w=\tilde{x}_0$
and the fact that
![]() $\phi_{d+1}$
is a Gaussian probability density function:
$\phi_{d+1}$
is a Gaussian probability density function:
 \begin{align} & \left| {\mathcal I}^{\alpha,k}[p](m,x;\,t) \right| \leq 2^{(d-1)/2}\|B\|_{\infty}D \\& \int_0^t\int_{{\mathbb R}^{2}}N(p;\,s,x_0) {\mathbf 1}_{m>b>\max\!\big(a^1,x_0^1\big)} \frac{e^{-\frac{\|\tilde{x}-\tilde{x_0}\|^2}{4t}}}{\sqrt{(2 \pi t)^{d-1}}} \frac{e^{-\frac{\big(m-a^1\big)^2}{4(t-s)}-\frac{\big(m-x^1\big)^2}{4(t-s)}}}{\sqrt{(2\pi)^2(t-s)^3}} \frac{e^{-\frac{\big(b-x_0^1\big)^2}{4s}-\frac{\big(b-a^1\big)^2}{4s}}}{\sqrt{(2\pi)^2 {s^2}}}db da^1 ds. \nonumber \end{align}
\begin{align} & \left| {\mathcal I}^{\alpha,k}[p](m,x;\,t) \right| \leq 2^{(d-1)/2}\|B\|_{\infty}D \\& \int_0^t\int_{{\mathbb R}^{2}}N(p;\,s,x_0) {\mathbf 1}_{m>b>\max\!\big(a^1,x_0^1\big)} \frac{e^{-\frac{\|\tilde{x}-\tilde{x_0}\|^2}{4t}}}{\sqrt{(2 \pi t)^{d-1}}} \frac{e^{-\frac{\big(m-a^1\big)^2}{4(t-s)}-\frac{\big(m-x^1\big)^2}{4(t-s)}}}{\sqrt{(2\pi)^2(t-s)^3}} \frac{e^{-\frac{\big(b-x_0^1\big)^2}{4s}-\frac{\big(b-a^1\big)^2}{4s}}}{\sqrt{(2\pi)^2 {s^2}}}db da^1 ds. \nonumber \end{align}
Using Part (i′) of Lemma A.2 with
![]() $u=m,$
$u=m,$
![]() $v=a^1,$
$v=a^1,$
![]() $w=b,$
$w=b,$
![]() $k=1$
, we integrate in
$k=1$
, we integrate in
![]() $da^1$
up to b:
$da^1$
up to b:
 \begin{align*}&\int_{-\infty}^b \frac{e^{-\frac{\big(m-a^1\big)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)}}\frac{e^{-\frac{\big(b-a^1\big)^2}{4s}}}{\sqrt{(2\pi s)}}da^1=\frac{e^{\frac{-(m-b)^2}{4t}}}{\sqrt{2\pi t}}\Phi_G\left( \sqrt{\frac{s}{2t(t-s)}}(b-m)\right),\end{align*}
\begin{align*}&\int_{-\infty}^b \frac{e^{-\frac{\big(m-a^1\big)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)}}\frac{e^{-\frac{\big(b-a^1\big)^2}{4s}}}{\sqrt{(2\pi s)}}da^1=\frac{e^{\frac{-(m-b)^2}{4t}}}{\sqrt{2\pi t}}\Phi_G\left( \sqrt{\frac{s}{2t(t-s)}}(b-m)\right),\end{align*}
where
for
![]() $u=b-m<0$
by Lemma A.3(iii). This yields the bound
$u=b-m<0$
by Lemma A.3(iii). This yields the bound
 \begin{equation*}\frac{e^{\frac{-(m-b)^2}{4t}}}{\sqrt{2\pi t}}e^{-\frac{s(b-m)^2}{4t(t-s)}}\end{equation*}
\begin{equation*}\frac{e^{\frac{-(m-b)^2}{4t}}}{\sqrt{2\pi t}}e^{-\frac{s(b-m)^2}{4t(t-s)}}\end{equation*}
and
 \begin{align*}2\int_{-\infty}^b \frac{e^{-\frac{\big(m-a^1\big)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)}}\frac{e^{-\frac{\big(b-a^1\big)^2}{4s}}}{\sqrt{(2\pi s)}}da^1&\leq\frac{e^{-\frac{(m-b)^2}{4t}}}{\sqrt{2\pi t}}e^{-\frac{s(m-b)^2}{4t(t-s)}}= \frac{e^{-\frac{(m-b)^2}{4(t-s)}}}{\sqrt{2\pi t}}.\end{align*}
\begin{align*}2\int_{-\infty}^b \frac{e^{-\frac{\big(m-a^1\big)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)}}\frac{e^{-\frac{\big(b-a^1\big)^2}{4s}}}{\sqrt{(2\pi s)}}da^1&\leq\frac{e^{-\frac{(m-b)^2}{4t}}}{\sqrt{2\pi t}}e^{-\frac{s(m-b)^2}{4t(t-s)}}= \frac{e^{-\frac{(m-b)^2}{4(t-s)}}}{\sqrt{2\pi t}}.\end{align*}
Plugging this inequality into (42) yields the following, with
![]() $C_{d,B}=2^{(d+1)/2}\|B\|_{\infty}D$
:
$C_{d,B}=2^{(d+1)/2}\|B\|_{\infty}D$
:
 \begin{align*} \frac{\left| {\mathcal I}^{\alpha,k}[p](m,x;\,t)\right|}{C_{d,B}} \leq\int_0^t\int_{{\mathbb R}}N(p;\,s,x_0) {\mathbf 1}_{m>b>x_0^1} \frac{e^{-\frac{\|\tilde{x}-\tilde{x_0}\|^2}{4t}}}{\sqrt{(2 \pi t)^d}} \frac{e^{-\frac{(m-b)^2}{4(t-s)}-\frac{\big(m-x^1\big)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)^2{s}}} e^{-\frac{\big(b-x_0^1\big)^2}{4s}}db ds. \end{align*}
\begin{align*} \frac{\left| {\mathcal I}^{\alpha,k}[p](m,x;\,t)\right|}{C_{d,B}} \leq\int_0^t\int_{{\mathbb R}}N(p;\,s,x_0) {\mathbf 1}_{m>b>x_0^1} \frac{e^{-\frac{\|\tilde{x}-\tilde{x_0}\|^2}{4t}}}{\sqrt{(2 \pi t)^d}} \frac{e^{-\frac{(m-b)^2}{4(t-s)}-\frac{\big(m-x^1\big)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)^2{s}}} e^{-\frac{\big(b-x_0^1\big)^2}{4s}}db ds. \end{align*}
Omitting the indicator functions, Lemma A.3(ii) with
![]() $u=m,\,v=b,\,w=x_0^1,\,k=1$
implies
$u=m,\,v=b,\,w=x_0^1,\,k=1$
implies
 \begin{equation*}\int_{b<m}\frac{e^{-\frac{(m-b)^2}{4(t-s)}}e^{-\frac{\big(b-x_0^1\big)^2}{4s}}}{\sqrt{2\pi(t-s)2\pi s}} db \leq\sqrt{\frac{2}{2\pi t}}e^{-\frac{\big(m-x_0^1\big)^2}{4t}}.\end{equation*}
\begin{equation*}\int_{b<m}\frac{e^{-\frac{(m-b)^2}{4(t-s)}}e^{-\frac{\big(b-x_0^1\big)^2}{4s}}}{\sqrt{2\pi(t-s)2\pi s}} db \leq\sqrt{\frac{2}{2\pi t}}e^{-\frac{\big(m-x_0^1\big)^2}{4t}}.\end{equation*}
Inserting this result, we obtain
 \begin{align*} \left| {\mathcal I}^{\alpha,k}[p](m,x;\,t) \right| \leq \sqrt{2}C_{d,B}\int_0^tN(p;\,s,x_0) \frac{e^{-\frac{\|\tilde{x}-\tilde{x_0}\|^2}{4t}}}{\sqrt{(2 \pi t)^{d+1}}} \frac{e^{-\frac{\big(m-x_0^1\big)^2}{4t}-\frac{\big(m-x^1\big)^2}{4(t-s)}}}{\sqrt{2\pi{(t-s)}}} ds. \end{align*}
\begin{align*} \left| {\mathcal I}^{\alpha,k}[p](m,x;\,t) \right| \leq \sqrt{2}C_{d,B}\int_0^tN(p;\,s,x_0) \frac{e^{-\frac{\|\tilde{x}-\tilde{x_0}\|^2}{4t}}}{\sqrt{(2 \pi t)^{d+1}}} \frac{e^{-\frac{\big(m-x_0^1\big)^2}{4t}-\frac{\big(m-x^1\big)^2}{4(t-s)}}}{\sqrt{2\pi{(t-s)}}} ds. \end{align*}
For
![]() $0<s<t,$
we have
$0<s<t,$
we have
so
 \begin{align*} \left| {\mathcal I}^{\alpha,k}[p](m,x;\,t) \right| \leq \sqrt{2} C_{d,B}\int_0^tN(p;\,s,x_0) \frac{e^{-\frac{\|\tilde{x}-\tilde{x_0}\|^2}{4t}}}{\sqrt{(2 \pi t)^{d+1}}} \frac{e^{-\frac{\big(m-x_0^1\big)^2}{4t}-\frac{\big(m-x^1\big)^2}{4t}}}{\sqrt{2\pi{(t-s)}}} ds. \end{align*}
\begin{align*} \left| {\mathcal I}^{\alpha,k}[p](m,x;\,t) \right| \leq \sqrt{2} C_{d,B}\int_0^tN(p;\,s,x_0) \frac{e^{-\frac{\|\tilde{x}-\tilde{x_0}\|^2}{4t}}}{\sqrt{(2 \pi t)^{d+1}}} \frac{e^{-\frac{\big(m-x_0^1\big)^2}{4t}-\frac{\big(m-x^1\big)^2}{4t}}}{\sqrt{2\pi{(t-s)}}} ds. \end{align*}
Using the definition of
![]() $\phi_{d+1}$
we find
$\phi_{d+1}$
we find
and with the definition of N, with respect to a multiplicative constant we have
(ii) For
![]() $j=\beta,$
$j=\beta,$
![]() $k=m,1,\ldots,d$
, using the definition of
$k=m,1,\ldots,d$
, using the definition of
![]() ${\mathcal I}^{\beta,k}$
and the fact that the support of p is included in
${\mathcal I}^{\beta,k}$
and the fact that the support of p is included in
![]() $\big\{(m,x),\ m>\max\!\big(x_0^1,x^1\big)\big\}$
yields
$\big\{(m,x),\ m>\max\!\big(x_0^1,x^1\big)\big\}$
yields
 \begin{align*} &{\mathcal I}^{\beta,k}[p](m,x;\,t)= \\& \quad \int_0^t \int_{\mathbb{R}^{d+1}}{\mathbf 1}_{m>b>x^1, m>x_0^1,b>a^1} B^{k}(a) \partial_k p_{W^{1*},W}\big(b-a^1,x-a,t-s\big)p(m,a,s) da db ds. \end{align*}
\begin{align*} &{\mathcal I}^{\beta,k}[p](m,x;\,t)= \\& \quad \int_0^t \int_{\mathbb{R}^{d+1}}{\mathbf 1}_{m>b>x^1, m>x_0^1,b>a^1} B^{k}(a) \partial_k p_{W^{1*},W}\big(b-a^1,x-a,t-s\big)p(m,a,s) da db ds. \end{align*}
Thus the support of
![]() $ {\mathcal I}^{\beta,k}[p](.;\,t)$
is included in
$ {\mathcal I}^{\beta,k}[p](.;\,t)$
is included in
![]() $\big\{(m,x),\ m>\max\!\big(x^1,x^0\big)\big\}.$
From now on we consider only (m, x) satisfying
$\big\{(m,x),\ m>\max\!\big(x^1,x^0\big)\big\}.$
From now on we consider only (m, x) satisfying
![]() $m>\max\!\big(x^1,x_0^1\big).$
From the definition of
$m>\max\!\big(x^1,x_0^1\big).$
From the definition of
![]() ${\mathcal I}^{\beta,k}$
and the boundedness of B, as well as the inequality (38) satisfied by
${\mathcal I}^{\beta,k}$
and the boundedness of B, as well as the inequality (38) satisfied by
![]() $\partial_kp_{W^*,W}$
, namely
$\partial_kp_{W^*,W}$
, namely
and the definition of
![]() $N(p;\,t,x_0)$
, we obtain
$N(p;\,t,x_0)$
, we obtain
 \begin{align*} \left| {\mathcal I}^{\beta,k}[p](m,x;\,t)\right|\leq \|B\|_{\infty} D \int_0^t \int_{\mathbb{R}^{d+1}}{\mathbf 1}_{m>b>x^1, b>a^1} N(p;\,s,x_0)\\\frac{e^{- \frac{\big(b-a^1\big)^2}{4(t-s)}- \frac{\big(b-x^1\big)^2}{4(t-s)} - \frac{\|\tilde{x}-\tilde{a}\|^2}{4(t-s)}}}{\sqrt{(2\pi)^{d+1}(t-s)^{d+2}}}\frac{e^{- \frac{\big(m-x_0^1\big)^2}{4s}- \frac{\big(m-a^1\big)^2}{4s} -\frac{\|\tilde{x}_0 -\tilde{a}\|^2}{4s}}}{\sqrt{(2\pi)^{d+1}{s^{d+1}}}}da db ds. \end{align*}
\begin{align*} \left| {\mathcal I}^{\beta,k}[p](m,x;\,t)\right|\leq \|B\|_{\infty} D \int_0^t \int_{\mathbb{R}^{d+1}}{\mathbf 1}_{m>b>x^1, b>a^1} N(p;\,s,x_0)\\\frac{e^{- \frac{\big(b-a^1\big)^2}{4(t-s)}- \frac{\big(b-x^1\big)^2}{4(t-s)} - \frac{\|\tilde{x}-\tilde{a}\|^2}{4(t-s)}}}{\sqrt{(2\pi)^{d+1}(t-s)^{d+2}}}\frac{e^{- \frac{\big(m-x_0^1\big)^2}{4s}- \frac{\big(m-a^1\big)^2}{4s} -\frac{\|\tilde{x}_0 -\tilde{a}\|^2}{4s}}}{\sqrt{(2\pi)^{d+1}{s^{d+1}}}}da db ds. \end{align*}
We integrate in
![]() $\tilde{a} $
using Lemma A.3(ii) with
$\tilde{a} $
using Lemma A.3(ii) with
![]() $u=\tilde{x},$
$u=\tilde{x},$
![]() $v=\tilde{a}$
, and
$v=\tilde{a}$
, and
![]() $w=\tilde{x}_0$
:
$w=\tilde{x}_0$
:
 \begin{align} & \left| {\mathcal I}^{\beta,k}[p](m,x;\,t)\right|\leq C_{d,B}. \\ & \int_0^t \int_{\mathbb{R}^{2}}{\mathbf 1}_{m>b>x^1, b>a^1}\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{(2 \pi t)^{d-1}}}N(p;\,s,x_0)\nonumber.\frac{e^{- \frac{\big(b-a^1\big)^2}{4(t-s)}- \frac{\big(b-x^1\big)^2}{4(t-s)}}}{\sqrt{(2\pi)^2(t-s)^{3}}}\frac{e^{- \frac{\big(m-x_0^1\big)^2}{4s}- \frac{\big(m-a^1\big)^2}{4s}}}{\sqrt{(2\pi)^{2}{s^{2}}}}da^1 db ds. \end{align}
\begin{align} & \left| {\mathcal I}^{\beta,k}[p](m,x;\,t)\right|\leq C_{d,B}. \\ & \int_0^t \int_{\mathbb{R}^{2}}{\mathbf 1}_{m>b>x^1, b>a^1}\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{(2 \pi t)^{d-1}}}N(p;\,s,x_0)\nonumber.\frac{e^{- \frac{\big(b-a^1\big)^2}{4(t-s)}- \frac{\big(b-x^1\big)^2}{4(t-s)}}}{\sqrt{(2\pi)^2(t-s)^{3}}}\frac{e^{- \frac{\big(m-x_0^1\big)^2}{4s}- \frac{\big(m-a^1\big)^2}{4s}}}{\sqrt{(2\pi)^{2}{s^{2}}}}da^1 db ds. \end{align}
Using Lemma A.3(i′) for
![]() $u=b,$
$u=b,$
![]() $v=a^1,$
$v=a^1,$
![]() $w=m$
,
$w=m$
,
![]() $k=1$
, we have
$k=1$
, we have
 \begin{align*} & \int_{-\infty}^b \frac{e^{- \frac{\big(b-a^1\big)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)}}\frac{e^{- \frac{\big(m-a^1\big)^2}{4s}}}{\sqrt{2\pi s}}da^1= \sqrt{2}\frac{e^{- \frac{(b-m)^2}{4t}}}{\sqrt{2 \pi t}}\Phi_G\left( \sqrt{\frac{t}{4s(t-s)}}\left[ b - \left(\frac{s}{t} b + \frac{t-s}{t} m\right)\right] \right)\\ &= \frac{e^{- \frac{(b-m)^2}{4t}}}{\sqrt{2 \pi t}}\Phi_G\left( \sqrt{\frac{t-s}{4st}}[ b - m] \right)\leq \frac{e^{- \frac{(b-m)^2}{4t}}}{\sqrt{2 \pi t}}e^{- \frac{t-s}{4st}[ b - m]^2}= \frac{e^{- \frac{(b-m)^2}{4s}}}{\sqrt{2 \pi t}}, \end{align*}
\begin{align*} & \int_{-\infty}^b \frac{e^{- \frac{\big(b-a^1\big)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)}}\frac{e^{- \frac{\big(m-a^1\big)^2}{4s}}}{\sqrt{2\pi s}}da^1= \sqrt{2}\frac{e^{- \frac{(b-m)^2}{4t}}}{\sqrt{2 \pi t}}\Phi_G\left( \sqrt{\frac{t}{4s(t-s)}}\left[ b - \left(\frac{s}{t} b + \frac{t-s}{t} m\right)\right] \right)\\ &= \frac{e^{- \frac{(b-m)^2}{4t}}}{\sqrt{2 \pi t}}\Phi_G\left( \sqrt{\frac{t-s}{4st}}[ b - m] \right)\leq \frac{e^{- \frac{(b-m)^2}{4t}}}{\sqrt{2 \pi t}}e^{- \frac{t-s}{4st}[ b - m]^2}= \frac{e^{- \frac{(b-m)^2}{4s}}}{\sqrt{2 \pi t}}, \end{align*}
the last bound coming from Lemma A.3(iii) since
![]() $b-m<0.$
$b-m<0.$
We plug this estimate into (43):
 \begin{align*}& \left| {\mathcal I}^{\beta,k}[p](m,x;\,t)\right|\leq \\& C_{d,B}\int_0^t \int_{\mathbb{R}}{\mathbf 1}_{m>b>x^1}\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{(2 \pi t)^{d}}}N(p;\,s,x_0)\frac{e^{-\frac{(b-x^1)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)^{2}}} \frac{e^{- \frac{\big(m-x_0^1\big)^2}{4s}-\frac{(b-m)^2}{4s}}}{\sqrt{2\pi s}} db ds. \end{align*}
\begin{align*}& \left| {\mathcal I}^{\beta,k}[p](m,x;\,t)\right|\leq \\& C_{d,B}\int_0^t \int_{\mathbb{R}}{\mathbf 1}_{m>b>x^1}\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{(2 \pi t)^{d}}}N(p;\,s,x_0)\frac{e^{-\frac{(b-x^1)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)^{2}}} \frac{e^{- \frac{\big(m-x_0^1\big)^2}{4s}-\frac{(b-m)^2}{4s}}}{\sqrt{2\pi s}} db ds. \end{align*}
We integrate with respect to b on
![]() $\mathbb{R}$
, and we use Lemma A.3(ii) with
$\mathbb{R}$
, and we use Lemma A.3(ii) with
![]() $u=x^1,$
$u=x^1,$
![]() $v=b$
,
$v=b$
,
![]() $w=m,$
$w=m,$
![]() $k=1$
:
$k=1$
:
 \begin{align*}{\left| {\mathcal I}^{\beta,k}[p](m,x;\,t)\right|\leq \sqrt{2}C_{d,B} \int_0^t\frac{e^{-\frac{\big(m-x^1\big)^2}{4t}-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{(2 \pi t)^{d+1}}}N(p;\,s,x_0) \frac{e^{- \frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{2\pi (t-s)}} ds}. \end{align*}
\begin{align*}{\left| {\mathcal I}^{\beta,k}[p](m,x;\,t)\right|\leq \sqrt{2}C_{d,B} \int_0^t\frac{e^{-\frac{\big(m-x^1\big)^2}{4t}-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{(2 \pi t)^{d+1}}}N(p;\,s,x_0) \frac{e^{- \frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{2\pi (t-s)}} ds}. \end{align*}
When
![]() $0<s<t,$
we have
$0<s<t,$
we have
so
 \begin{align*} \left| {\mathcal I}^{\beta,k}[p](m,x;\,t)\right|\leq \sqrt{2}C_{d,B}\int_0^t \frac{e^{-\frac{\big(m-x^1\big)^2}{4t}-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t} {- \frac{\big(m-x_0^1\big)^2}{4t}}}}{\sqrt{(2 \pi t)^{d+1}}}N(p;\,s,x_0) \frac{1}{\sqrt{2\pi (t-s)}} ds. \end{align*}
\begin{align*} \left| {\mathcal I}^{\beta,k}[p](m,x;\,t)\right|\leq \sqrt{2}C_{d,B}\int_0^t \frac{e^{-\frac{\big(m-x^1\big)^2}{4t}-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t} {- \frac{\big(m-x_0^1\big)^2}{4t}}}}{\sqrt{(2 \pi t)^{d+1}}}N(p;\,s,x_0) \frac{1}{\sqrt{2\pi (t-s)}} ds. \end{align*}
Under the integral we identify the factor
![]() $\phi_{d+1}\big(m-x^1_0,m-x^1, \tilde{x}-\tilde{x_0};\,2t\big)$
, so
$\phi_{d+1}\big(m-x^1_0,m-x^1, \tilde{x}-\tilde{x_0};\,2t\big)$
, so
Finally, using the definition of N (Equation (41)), we have proved
which completes the proof of Lemma 4.4.
4.2.2. Proof of Hypothesis 2.1(ii), case
 $A=I_d$
.
$A=I_d$
.
Proposition 4.5.
For any probability measure
![]() $\mu_0$
on
$\mu_0$
on
![]() ${\mathbb R}^d,$
for all
${\mathbb R}^d,$
for all
![]() $(m, \tilde{x},t)\in \mathbb{R}^d\times ]0,T],$
$(m, \tilde{x},t)\in \mathbb{R}^d\times ]0,T],$
![]() $u \mapsto p_V(m,m-u,\tilde{x},t)$
admits a limit when u goes to 0,
$u \mapsto p_V(m,m-u,\tilde{x},t)$
admits a limit when u goes to 0,
![]() $u>0.$
$u>0.$
Proof. The proof is a consequence of the following three lemmas.
Lemma 4.5.
Recall that
![]() $p^0(m,x;\,t)=\int_{{\mathbb R}^d}p_{W^{*1},W}\big(m-x_0^1,x-x_0;\,t\big)\mu_0(dx_0).$
We have
$p^0(m,x;\,t)=\int_{{\mathbb R}^d}p_{W^{*1},W}\big(m-x_0^1,x-x_0;\,t\big)\mu_0(dx_0).$
We have
Proof. We have
 \begin{equation*}p^0(b,b-u,\tilde{x};\,t)={\int_{{\mathbb R}^d}} {2\frac{b+u-x_0^1}{\sqrt{(2\pi)^d{\mathbf{t^{d+1}}}}}e^{-\frac{\big(b+u-x_0^1\big)^2}{2t} -\frac{\|\tilde{x}-\tilde{x}_0\|^2}{2t}}}{{\mathbf 1}_{b \geq x_0^1,\,\,u \geq 0}\mu_0(dx_0)}.\end{equation*}
\begin{equation*}p^0(b,b-u,\tilde{x};\,t)={\int_{{\mathbb R}^d}} {2\frac{b+u-x_0^1}{\sqrt{(2\pi)^d{\mathbf{t^{d+1}}}}}e^{-\frac{\big(b+u-x_0^1\big)^2}{2t} -\frac{\|\tilde{x}-\tilde{x}_0\|^2}{2t}}}{{\mathbf 1}_{b \geq x_0^1,\,\,u \geq 0}\mu_0(dx_0)}.\end{equation*}
Then, since the integrand is dominated by
and
![]() $\mu_0$
is a probability measure, using Lebesgue’s dominated convergence theorem yields
$\mu_0$
is a probability measure, using Lebesgue’s dominated convergence theorem yields
Lemma 4.6.
For
![]() $k=m,1,\ldots,d$
, recall that
$k=m,1,\ldots,d$
, recall that
The map
![]() $u \mapsto p^{k,\alpha}(m,m-u,\tilde{x};\,t)$
converges to
$u \mapsto p^{k,\alpha}(m,m-u,\tilde{x};\,t)$
converges to
![]() $p^{k,\alpha}\big(m,m,\tilde{x};\,t\big)$
when u goes to
$p^{k,\alpha}\big(m,m,\tilde{x};\,t\big)$
when u goes to
![]() $0^+.$
$0^+.$
Proof. The proof will be a consequence of Lebesgue’s dominated convergence theorem. First, the map
![]() $u \mapsto {\mathbf 1}_{b<m} \partial_{k}p_{W^{*1}, W} \big(m-a^1,m-u-a^1,\tilde{x}-\tilde{a};\, t-s\big) p_V(b,a;\,s)$
converges to
$u \mapsto {\mathbf 1}_{b<m} \partial_{k}p_{W^{*1}, W} \big(m-a^1,m-u-a^1,\tilde{x}-\tilde{a};\, t-s\big) p_V(b,a;\,s)$
converges to
![]() ${\mathbf 1}_{b<m} \partial_{k}p_{W^{*1}, W} \big(m-a^1,ma^1,\tilde{x}-\tilde{a};\, t-s\big) p_V(b,a;\,s)$
when u goes to
${\mathbf 1}_{b<m} \partial_{k}p_{W^{*1}, W} \big(m-a^1,ma^1,\tilde{x}-\tilde{a};\, t-s\big) p_V(b,a;\,s)$
when u goes to
![]() $0^+.$
$0^+.$
Second, it is dominated by
 \begin{align*} &q^{k,\alpha}(m,\tilde{x},a,b;\,s,x_0)\,:\!=\, \\& \quad |B^k(a)|{\mathbf 1}_{b<m}\sup_{u>0} \left|\partial_{k}p_{W^{*1}, W} \big(m-a^1,m-u-a^1,\tilde{x}-\tilde{a};\, t-s\big) p_V(b,a;\,s,x_0)\right|.\end{align*}
\begin{align*} &q^{k,\alpha}(m,\tilde{x},a,b;\,s,x_0)\,:\!=\, \\& \quad |B^k(a)|{\mathbf 1}_{b<m}\sup_{u>0} \left|\partial_{k}p_{W^{*1}, W} \big(m-a^1,m-u-a^1,\tilde{x}-\tilde{a};\, t-s\big) p_V(b,a;\,s,x_0)\right|.\end{align*}
We seek to prove that
According to the estimate (38) of
![]() $\partial_k p_{W^{*1},W}$
and the estimate (ii) of Proposition 4.4, we obtain
$\partial_k p_{W^{*1},W}$
and the estimate (ii) of Proposition 4.4, we obtain
 \begin{align*}q^{k,\alpha}\big(m,\tilde{x},a,b;\,s,x_0\big)&\leq\|B\|_{\infty}{\mathbf 1}_{m>b>a^1}\frac{D}{\sqrt{t-s} \sqrt{2\pi(t-s)}^{d+1}} \exp \bigg[ -\frac{\big(m-a^1\big)^2}{4(t-s)} -\frac{\|\tilde{x}-\tilde{a}\|^2}{4(t-s)} \bigg] \\ &\frac{C_T}{\sqrt{2\pi s}^{d+1}}\exp\bigg[- \frac{\big(b-x_0^1\big)^2}{4s} - \frac{\big(b-a^1\big)}{4s} - \frac{\|\tilde{x}_0-\tilde{a}\|^2}{4s}\bigg].\end{align*}
\begin{align*}q^{k,\alpha}\big(m,\tilde{x},a,b;\,s,x_0\big)&\leq\|B\|_{\infty}{\mathbf 1}_{m>b>a^1}\frac{D}{\sqrt{t-s} \sqrt{2\pi(t-s)}^{d+1}} \exp \bigg[ -\frac{\big(m-a^1\big)^2}{4(t-s)} -\frac{\|\tilde{x}-\tilde{a}\|^2}{4(t-s)} \bigg] \\ &\frac{C_T}{\sqrt{2\pi s}^{d+1}}\exp\bigg[- \frac{\big(b-x_0^1\big)^2}{4s} - \frac{\big(b-a^1\big)}{4s} - \frac{\|\tilde{x}_0-\tilde{a}\|^2}{4s}\bigg].\end{align*}
We integrate with respect to
![]() $\tilde{a}$
using Lemma A.3(ii) for
$\tilde{a}$
using Lemma A.3(ii) for
![]() $k=d+1,$
$k=d+1,$
![]() $u=\tilde{x},$
$u=\tilde{x},$
![]() $v=\tilde{a}$
, and
$v=\tilde{a}$
, and
![]() $w=\tilde{x}_0:$
$w=\tilde{x}_0:$
 \begin{align*}\int_{\mathbb{R}^{d-1}}q^{k,\alpha}\big(m,\tilde{x},a^1,b;\,s,x_0^1\big)d\tilde{a} &\leq {\mathbf 1}_{m>b>a^1}\frac{\|B\|_{\infty} C_T D2^{(d-1)/2}}{\sqrt{t-s} \sqrt{2\pi(t-s)}^{2} \sqrt{2\pi s}^{2}}\frac{e^{-\frac{|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d-1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,& \exp \bigg[ -\frac{\big(m-a^1\big)^2}{4(t-s)} - \frac{\big(b-x_0^1\big)^2}{4s} - \frac{\big(b-a^1\big)^2}{4s} \bigg].\end{align*}
\begin{align*}\int_{\mathbb{R}^{d-1}}q^{k,\alpha}\big(m,\tilde{x},a^1,b;\,s,x_0^1\big)d\tilde{a} &\leq {\mathbf 1}_{m>b>a^1}\frac{\|B\|_{\infty} C_T D2^{(d-1)/2}}{\sqrt{t-s} \sqrt{2\pi(t-s)}^{2} \sqrt{2\pi s}^{2}}\frac{e^{-\frac{|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d-1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,& \exp \bigg[ -\frac{\big(m-a^1\big)^2}{4(t-s)} - \frac{\big(b-x_0^1\big)^2}{4s} - \frac{\big(b-a^1\big)^2}{4s} \bigg].\end{align*}
We integrate with respect to
![]() $a_1$
between
$a_1$
between
![]() $-\infty$
and b using Lemma A.3(i′) for
$-\infty$
and b using Lemma A.3(i′) for
![]() $u=m,$
$u=m,$
![]() $v=a^1$
, and
$v=a^1$
, and
![]() $w=b$
:
$w=b$
:
 \begin{align*}\int_{\mathbb{R}^{d}}{\mathbf 1}_{a^1<b}q^{k,\alpha}(m,\tilde{x},b,a;\,s;\,x_0)da &\leq {\mathbf 1}_{b<m}\frac{\|B\|_{\infty} C_T D2^{d/2}}{\sqrt{t-s} \sqrt{2\pi(t-s)} \sqrt{2\pi s}}\frac{e^{-\frac{|\tilde{x}-\tilde{x}_0\|^2}{4t}}-\frac{(b-m)^2}{4t}}{\sqrt{2 \pi t}^{d}}\\& \!\!\!\!\exp \bigg[ - \frac{\big(b-x_0^1\big)^2}{4s} \bigg]\Phi_G\left(\sqrt{\frac{t}{2s(t-s)}}\Big( b- \Big[\frac{s}{t}m + \frac{(t-s)}{t}b\Big]\Big)\right).\end{align*}
\begin{align*}\int_{\mathbb{R}^{d}}{\mathbf 1}_{a^1<b}q^{k,\alpha}(m,\tilde{x},b,a;\,s;\,x_0)da &\leq {\mathbf 1}_{b<m}\frac{\|B\|_{\infty} C_T D2^{d/2}}{\sqrt{t-s} \sqrt{2\pi(t-s)} \sqrt{2\pi s}}\frac{e^{-\frac{|\tilde{x}-\tilde{x}_0\|^2}{4t}}-\frac{(b-m)^2}{4t}}{\sqrt{2 \pi t}^{d}}\\& \!\!\!\!\exp \bigg[ - \frac{\big(b-x_0^1\big)^2}{4s} \bigg]\Phi_G\left(\sqrt{\frac{t}{2s(t-s)}}\Big( b- \Big[\frac{s}{t}m + \frac{(t-s)}{t}b\Big]\Big)\right).\end{align*}
Note that
and using Lemma A.3(iii),
 \begin{align*}\int_{\mathbb{R}^{d}}q^{k,\alpha}(m,\tilde{x},b,a;\,s,x_0)da &\leq {\mathbf 1}_{b<m}\frac{\|B\|_{\infty} C_T D2^{d/2}}{\sqrt{t-s} \sqrt{2\pi(t-s)} \sqrt{2\pi s}}\frac{e^{-\frac{|\tilde{x}-\tilde{x}_0\|^2}{4t}-\frac{(b-m)^2}{4t}}}{\sqrt{2 \pi t}^{d}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,& \exp \left[ - \frac{\big(b-x_0^1\big)^2}{4s}\right]\exp\left[ -\frac{s}{t(t-s)}\frac{(b-m)^2}{4}\right].\end{align*}
\begin{align*}\int_{\mathbb{R}^{d}}q^{k,\alpha}(m,\tilde{x},b,a;\,s,x_0)da &\leq {\mathbf 1}_{b<m}\frac{\|B\|_{\infty} C_T D2^{d/2}}{\sqrt{t-s} \sqrt{2\pi(t-s)} \sqrt{2\pi s}}\frac{e^{-\frac{|\tilde{x}-\tilde{x}_0\|^2}{4t}-\frac{(b-m)^2}{4t}}}{\sqrt{2 \pi t}^{d}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,& \exp \left[ - \frac{\big(b-x_0^1\big)^2}{4s}\right]\exp\left[ -\frac{s}{t(t-s)}\frac{(b-m)^2}{4}\right].\end{align*}
We observe that
![]() $\frac{1}{t} +\frac{s}{t(t-s)}=\frac{1}{t-s}$
, so that
$\frac{1}{t} +\frac{s}{t(t-s)}=\frac{1}{t-s}$
, so that
We integrate with respect to b (neglecting the indicator function) using Lemma A.3(ii) for
![]() $u=m,$
$u=m,$
![]() $v=b$
, and
$v=b$
, and
![]() $w=x_0^1$
, and
$w=x_0^1$
, and
 $\exp\left[-\frac{\big(m-x^1_0\big)^2}{4t}\right]\leq 1$
:
$\exp\left[-\frac{\big(m-x^1_0\big)^2}{4t}\right]\leq 1$
:
 \begin{align*}\int_{\mathbb{R}^{d+1}}q^{k,\alpha}(m,\tilde{x},b,a;\,s,x_0)dadb &\leq {\mathbf 1}_{m>x_0^1}\frac{\|B\|_{\infty} C_T D2^{(d+1)/2}}{\sqrt{t-s}}\frac{e^{-\frac{|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{t}^{d+1}}.\end{align*}
\begin{align*}\int_{\mathbb{R}^{d+1}}q^{k,\alpha}(m,\tilde{x},b,a;\,s,x_0)dadb &\leq {\mathbf 1}_{m>x_0^1}\frac{\|B\|_{\infty} C_T D2^{(d+1)/2}}{\sqrt{t-s}}\frac{e^{-\frac{|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{t}^{d+1}}.\end{align*}
Since
![]() $\mu_0$
is a probability measure, we have
$\mu_0$
is a probability measure, we have
Lemma 4.7. For
![]() $k=m,1,\ldots,d$
, recall that
$k=m,1,\ldots,d$
, recall that
The map
![]() $u \mapsto p^{k,\beta}(m,m-u,\tilde{x};\,t)$
converges to 0 when u goes to
$u \mapsto p^{k,\beta}(m,m-u,\tilde{x};\,t)$
converges to 0 when u goes to
![]() $0^+.$
$0^+.$
Proof. Using the estimate (38) of
![]() $\partial_kp_{W^{*1},W}$
and the estimate (ii) of Proposition 4.4 for
$\partial_kp_{W^{*1},W}$
and the estimate (ii) of Proposition 4.4 for
![]() $p_V,$
we dominate the integrand which defines
$p_V,$
we dominate the integrand which defines
![]() $p^{k,\beta}(m,m-u,\tilde{x};\,t)$
by
$p^{k,\beta}(m,m-u,\tilde{x};\,t)$
by
 \begin{align*} &q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s)\,:\!=\, \\& \quad {\mathbf 1}_{m-u<b<m,a^1<b}\frac{e^{-\frac{\big(b-a^1\big)^2}{4(t-s)} -\frac{(b-m+u)^2}{4(t-s)} -\frac{\|\tilde{x}-\tilde{a}\|^2}{4(t-s)} -\frac{\big(m-x_0^1\big)^2}{4s} - \frac{\big(m-a^1\big)}{4s} -\frac{\|\tilde{x}_0 -\tilde{a}\|^2}{4s}}}{\sqrt{t-s}\sqrt{2 \pi (t-s)}^{d+1}\sqrt{2 \pi s}^{d+1}}\end{align*}
\begin{align*} &q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s)\,:\!=\, \\& \quad {\mathbf 1}_{m-u<b<m,a^1<b}\frac{e^{-\frac{\big(b-a^1\big)^2}{4(t-s)} -\frac{(b-m+u)^2}{4(t-s)} -\frac{\|\tilde{x}-\tilde{a}\|^2}{4(t-s)} -\frac{\big(m-x_0^1\big)^2}{4s} - \frac{\big(m-a^1\big)}{4s} -\frac{\|\tilde{x}_0 -\tilde{a}\|^2}{4s}}}{\sqrt{t-s}\sqrt{2 \pi (t-s)}^{d+1}\sqrt{2 \pi s}^{d+1}}\end{align*}
up to a multiplicative constant, meaning that
We integrate with respect to
![]() $\tilde{a} $
using Lemma A.3(ii) with
$\tilde{a} $
using Lemma A.3(ii) with
![]() $u=\tilde{x},$
$u=\tilde{x},$
![]() $v=\tilde{a}$
, and
$v=\tilde{a}$
, and
![]() $w=\tilde{x}_0$
:
$w=\tilde{x}_0$
:
 \begin{align*}\int_{R^{d-1}} q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s) d\tilde{a} \leq \sqrt{2}^{d-1} \frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d-1}}\frac{e^{-\frac{\big(b-a^1\big)^2}{4(t-s)} -\frac{(b-m+u)^2}{4(t-s)} -\frac{\big(m-x_0^1\big)^2}{4s} - \frac{\big(m-a^1\big)}{4s}}}{\sqrt{t-s}\sqrt{2 \pi (t-s)}^{2}\sqrt{2 \pi s}^{2}}.\end{align*}
\begin{align*}\int_{R^{d-1}} q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s) d\tilde{a} \leq \sqrt{2}^{d-1} \frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d-1}}\frac{e^{-\frac{\big(b-a^1\big)^2}{4(t-s)} -\frac{(b-m+u)^2}{4(t-s)} -\frac{\big(m-x_0^1\big)^2}{4s} - \frac{\big(m-a^1\big)}{4s}}}{\sqrt{t-s}\sqrt{2 \pi (t-s)}^{2}\sqrt{2 \pi s}^{2}}.\end{align*}
We integrate with respect to
![]() $a^1$
between
$a^1$
between
![]() $-\infty$
and b using Lemma A.3(i′) for
$-\infty$
and b using Lemma A.3(i′) for
![]() $u=b,$
$u=b,$
![]() $v=a^{1}$
, and
$v=a^{1}$
, and
![]() $w=m$
:
$w=m$
:
 \begin{align*}&\int_{R^{d}} {\mathbf 1}_{b>a^1}q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s) da \leq\\&\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d}}\frac{e^{-\frac{(b-m)^2}{4t} -\frac{(b-m+u)^2}{4(t-s)} -\frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{t-s}\sqrt{2 \pi (t-s)}\sqrt{2 \pi s}}\Phi_G\left(\sqrt{\frac{t}{s(t-s)2}}( b-\frac{s}{t}b-\frac{t-s}{t}m)\right)\\&= \frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d}}\frac{e^{-\frac{(b-m)^2}{4t} -\frac{(b-m+u)^2}{4(t-s)} -\frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{t-s}\sqrt{2 \pi (t-s)}\sqrt{2 \pi s}}\Phi_G\left(\sqrt{\frac{t-s}{2st}}( b-m)\right).\end{align*}
\begin{align*}&\int_{R^{d}} {\mathbf 1}_{b>a^1}q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s) da \leq\\&\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d}}\frac{e^{-\frac{(b-m)^2}{4t} -\frac{(b-m+u)^2}{4(t-s)} -\frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{t-s}\sqrt{2 \pi (t-s)}\sqrt{2 \pi s}}\Phi_G\left(\sqrt{\frac{t}{s(t-s)2}}( b-\frac{s}{t}b-\frac{t-s}{t}m)\right)\\&= \frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d}}\frac{e^{-\frac{(b-m)^2}{4t} -\frac{(b-m+u)^2}{4(t-s)} -\frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{t-s}\sqrt{2 \pi (t-s)}\sqrt{2 \pi s}}\Phi_G\left(\sqrt{\frac{t-s}{2st}}( b-m)\right).\end{align*}
Since
![]() $b-m<0$
, using Lemma A.3(iii) we have
$b-m<0$
, using Lemma A.3(iii) we have
 \begin{align*}\int_{R^{d}}{\mathbf 1}_{b>a^1} q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s) da \leq\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d}}\frac{e^{-\frac{(b-m)^2}{4t} -\frac{(b-m+u)^2}{4(t-s)} -\frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{t-s}\sqrt{2 \pi (t-s)}\sqrt{2 \pi s}}e^{-\frac{t-s}{4st}( b-m)^2}.\end{align*}
\begin{align*}\int_{R^{d}}{\mathbf 1}_{b>a^1} q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s) da \leq\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d}}\frac{e^{-\frac{(b-m)^2}{4t} -\frac{(b-m+u)^2}{4(t-s)} -\frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{t-s}\sqrt{2 \pi (t-s)}\sqrt{2 \pi s}}e^{-\frac{t-s}{4st}( b-m)^2}.\end{align*}
Note that
We integrate this last bound with respect to b between
![]() $m-u$
and m using Lemma A.3(i′) for the triplet
$m-u$
and m using Lemma A.3(i′) for the triplet
![]() $(m-u,b,m)$
and the fact that
$(m-u,b,m)$
and the fact that
to obtain
 \begin{eqnarray*}&\int_{R^{d+1}}{\mathbf 1}_{m-u<b<m,b<a^1} q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s) da db\leq\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d+1}}\frac{e^{-\frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{t-s}}.\\&\left[\Phi_G\left(\sqrt{\frac{t}{2s(t-s)}}\left( m-\frac{s(m-u)+m(t-s)}{t}\right) \right)- \Phi_G\left( \sqrt{\frac{t}{2s(t-s)}}\left( m-u-\frac{s(m-u)+m(t-s)}{t}\right) \right)\right].\end{eqnarray*}
\begin{eqnarray*}&\int_{R^{d+1}}{\mathbf 1}_{m-u<b<m,b<a^1} q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s) da db\leq\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d+1}}\frac{e^{-\frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{t-s}}.\\&\left[\Phi_G\left(\sqrt{\frac{t}{2s(t-s)}}\left( m-\frac{s(m-u)+m(t-s)}{t}\right) \right)- \Phi_G\left( \sqrt{\frac{t}{2s(t-s)}}\left( m-u-\frac{s(m-u)+m(t-s)}{t}\right) \right)\right].\end{eqnarray*}
Then,
 \begin{align*}&\int_{R^{d+1}}q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s) da db\leq\\&\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d+1}}\frac{e^{-\frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{t-s}}\left[\Phi_G\left( \sqrt{\frac{s}{2t(t-s)}}u \right)- \Phi_G\left({-} \sqrt{\frac{t-s}{2t(t-s)}} u \right)\right].\end{align*}
\begin{align*}&\int_{R^{d+1}}q^{k,\beta}(m,u,\tilde{x},a,b,x_0,s) da db\leq\\&\frac{e^{-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t}}}{\sqrt{2 \pi t}^{d+1}}\frac{e^{-\frac{\big(m-x_0^1\big)^2}{4s}}}{\sqrt{t-s}}\left[\Phi_G\left( \sqrt{\frac{s}{2t(t-s)}}u \right)- \Phi_G\left({-} \sqrt{\frac{t-s}{2t(t-s)}} u \right)\right].\end{align*}
Note that
and
Since
![]() $\mu$
is a probability measure, using Lebesgue’s dominated convergence theorem,
$\mu$
is a probability measure, using Lebesgue’s dominated convergence theorem,
Finally, the estimate (45) yields
![]() $\lim_{u\rightarrow 0^+} p^{k,\beta}(m,m-u, \tilde x;\,t)=0.$
$\lim_{u\rightarrow 0^+} p^{k,\beta}(m,m-u, \tilde x;\,t)=0.$
5. The case
 $\boldsymbol{{d}}=1$
$\boldsymbol{{d}}=1$
Proposition 5.1.
Consider the real diffusion X given by
![]() $dX_t=B(X_t)dt+A(X_t)dW_t$
where A,B fulfil (4) and (5). Then the probability density function
$dX_t=B(X_t)dt+A(X_t)dW_t$
where A,B fulfil (4) and (5). Then the probability density function
![]() $p_V$
satisfies Hypothesis 2.1, so for any initial law
$p_V$
satisfies Hypothesis 2.1, so for any initial law
![]() $\mu_0$
and
$\mu_0$
and
![]() $F\in C^2_b(\mathbb{R}^2,\mathbb{R}),$
$F\in C^2_b(\mathbb{R}^2,\mathbb{R}),$
 \begin{align}{\mathbb E}\left[F\big(M_t,X_t\big)\right)& ={\mathbb E} \left[ F(X_0,X_0)\right] + \int_0^t {\mathbb E} \left[ {\mathcal L}\left(F\right)(M_s,X_s)\right] ds\nonumber\\&+\frac{1}{2} {\int_0^t{\mathbb E}\left[\partial_mF(X_s,{X_s})\|A(X_s)\|^2\frac{p_V(X_s,{X_s};\,s)}{p_{X}(X_s;\,s)}\right] ds.}\end{align}
\begin{align}{\mathbb E}\left[F\big(M_t,X_t\big)\right)& ={\mathbb E} \left[ F(X_0,X_0)\right] + \int_0^t {\mathbb E} \left[ {\mathcal L}\left(F\right)(M_s,X_s)\right] ds\nonumber\\&+\frac{1}{2} {\int_0^t{\mathbb E}\left[\partial_mF(X_s,{X_s})\|A(X_s)\|^2\frac{p_V(X_s,{X_s};\,s)}{p_{X}(X_s;\,s)}\right] ds.}\end{align}
Proof. We perform a Lamperti transformation [Reference Lamperti18]. Without loss of generality, A can be chosen positive. In the case
![]() $d=1$
, Assumption (5), which states that there exists
$d=1$
, Assumption (5), which states that there exists
![]() $c>0$
such that for any
$c>0$
such that for any
![]() $x\in\mathbb{R},$
$x\in\mathbb{R},$
![]() $A^2(x)\geq c$
, can be expressed as follows:
$A^2(x)\geq c$
, can be expressed as follows:
Let
![]() $\varphi$
be such that
$\varphi$
be such that
![]() $\varphi^{\prime}=\frac{1}{A}$
and
$\varphi^{\prime}=\frac{1}{A}$
and
![]() $\varphi(0)=0$
, so that
$\varphi(0)=0$
, so that
![]() $\varphi^{\prime}$
is uniformly bounded and
$\varphi^{\prime}$
is uniformly bounded and
![]() $\varphi\in C^2(\mathbb{R})$
, as is the function A. Moreover,
$\varphi\in C^2(\mathbb{R})$
, as is the function A. Moreover,
![]() $\varphi^{\prime}$
being strictly positive,
$\varphi^{\prime}$
being strictly positive,
![]() $\varphi$
is strictly increasing, hence invertible, and we denote by
$\varphi$
is strictly increasing, hence invertible, and we denote by
![]() $\varphi^{-1}$
its inverse function. Under the initial condition
$\varphi^{-1}$
its inverse function. Under the initial condition
![]() $\varphi(0)=0$
, using Itô’s formula,
$\varphi(0)=0$
, using Itô’s formula,
![]() $Y=\varphi(X)$
satisfies
$Y=\varphi(X)$
satisfies
Let
![]() $A_\varphi=1$
and
$A_\varphi=1$
and
![]() $B_\varphi\,:\!=\,\frac{B}{A}\circ\varphi^{-1}-{\frac{1}{2}} A^{\prime}\circ\varphi^{-1}$
, which belongs to
$B_\varphi\,:\!=\,\frac{B}{A}\circ\varphi^{-1}-{\frac{1}{2}} A^{\prime}\circ\varphi^{-1}$
, which belongs to
![]() $ C^1_b(\mathbb{R})$
as a consequence of the fact that
$ C^1_b(\mathbb{R})$
as a consequence of the fact that
![]() $B\in C^1_b$
and
$B\in C^1_b$
and
![]() $A\in C^2_b.$
Obviously,
$A\in C^2_b.$
Obviously,
![]() $\varphi^{\prime}>0$
implies that
$\varphi^{\prime}>0$
implies that
![]() $\varphi$
is increasing, and
$\varphi$
is increasing, and
![]() $Y^*_t=\varphi\big(X_t^*\big)=\varphi(M_t)$
.
$Y^*_t=\varphi\big(X_t^*\big)=\varphi(M_t)$
.
Theorem 1.1 in [Reference Coutin and Pontier9] can easily be extended to the case where X admits an initial law
![]() $\mu_0$
; thus the law of the pair
$\mu_0$
; thus the law of the pair
![]() $(Y^*_t,Y_t)$
admits a density with respect to the Lebesgue measure. Moreover, [Reference Coutin and Pontier9, Lemma 2.2] sets out
$(Y^*_t,Y_t)$
admits a density with respect to the Lebesgue measure. Moreover, [Reference Coutin and Pontier9, Lemma 2.2] sets out
Now, applying Theorem 2.4 to the pair
![]() $(B_\varphi,1)$
, we find that the density
$(B_\varphi,1)$
, we find that the density
![]() $p_{Y^*,Y}$
satisfies Hypothesis 2.1.
$p_{Y^*,Y}$
satisfies Hypothesis 2.1.
Since the functions A and
![]() $\varphi$
are continuous,
$\varphi$
are continuous,
which means
![]() $p_V$
satisfies Hypothesis 2.1(ii).
$p_V$
satisfies Hypothesis 2.1(ii).
Now, using (47),
Since
![]() $\varphi$
is increasing, if
$\varphi$
is increasing, if
![]() $u>0$
, then
$u>0$
, then
![]() $\varphi(b-u)<\varphi(b)$
; writing
$\varphi(b-u)<\varphi(b)$
; writing
![]() $v=\varphi(b)-\varphi(b-u)$
, we have
$v=\varphi(b)-\varphi(b-u)$
, we have
![]() $v>0,$
and
$v>0,$
and
After the change of variable
![]() $m=\varphi(b)$
, so that
$m=\varphi(b)$
, so that
![]() $db=A(b)dm,$
we have
$db=A(b)dm,$
we have
Since A is bounded and
![]() $p_{Y^*,Y}$
satisfies Hypothesis 2.11(i),
$p_{Y^*,Y}$
satisfies Hypothesis 2.11(i),
and
![]() $p_V$
satisfies Hypothesis 2.1(i)–(ii).
$p_V$
satisfies Hypothesis 2.1(i)–(ii).
6. Conclusion
This paper establishes a PDE of which the density of the running-maximum–diffusion-process pair
![]() $[M_t, X_t]$
is a weak solution, under a quite natural assumption on the regularity of
$[M_t, X_t]$
is a weak solution, under a quite natural assumption on the regularity of
![]() $p_V$
around the boundary of
$p_V$
around the boundary of
![]() $\Delta.$
This assumption is fulfilled when the matrix coefficient of the diffusion A is the identity matrix or when the dimension
$\Delta.$
This assumption is fulfilled when the matrix coefficient of the diffusion A is the identity matrix or when the dimension
![]() $d=1$
. This PDE is degenerate; thus, the classical results on uniqueness cannot be applied here. The case of a non-constant matrix A is an open problem. Such a generalization could be useful in practical applications, such as the management of barrier options, in models including stochastic volatility.
$d=1$
. This PDE is degenerate; thus, the classical results on uniqueness cannot be applied here. The case of a non-constant matrix A is an open problem. Such a generalization could be useful in practical applications, such as the management of barrier options, in models including stochastic volatility.
Appendix A. Tools
A.1. Malliavin calculus tools
The material in this subsection is taken from [Reference Nualart21, Section 1.2].
Let
![]() ${\mathbb H}=L^2([0,T],{\mathbb R}^d)$
be endowed with the usual scalar product
${\mathbb H}=L^2([0,T],{\mathbb R}^d)$
be endowed with the usual scalar product
![]() $\langle.,.\rangle_{{\mathbb H}}$
and the associated norm
$\langle.,.\rangle_{{\mathbb H}}$
and the associated norm
![]() $\|.\|_{\mathbb H}.$
For all
$\|.\|_{\mathbb H}.$
For all
![]() $h \in {\mathbb H},$
$h \in {\mathbb H},$
![]() $W(h)\,:\!=\, \int_0^T h(t) dW_t$
is a centered Gaussian variable with variance equal to
$W(h)\,:\!=\, \int_0^T h(t) dW_t$
is a centered Gaussian variable with variance equal to
![]() $\|h\|^2_{{\mathbb H}}.$
If
$\|h\|^2_{{\mathbb H}}.$
If
![]() $(h_1,h_2 )\in {\mathbb H}^2$
and
$(h_1,h_2 )\in {\mathbb H}^2$
and
![]() $\langle h_1,h_2\rangle_{{\mathbb H}}=0$
, then the random variables
$\langle h_1,h_2\rangle_{{\mathbb H}}=0$
, then the random variables
![]() $W(h_i),\,i=1,2,$
are independent.
$W(h_i),\,i=1,2,$
are independent.
Let
![]() ${\mathcal S}$
denote the class of smooth random variables F defined by
${\mathcal S}$
denote the class of smooth random variables F defined by
Definition A.1. The derivative of the smooth variable F defined in (49) is the
![]() ${\mathbb H}$
-valued random variable given by
${\mathbb H}$
-valued random variable given by
![]() $DF\,:\!=\,\sum_{i=1}^n \partial_i f(W(h_1),\ldots,W(h_n)) h_i.$
$DF\,:\!=\,\sum_{i=1}^n \partial_i f(W(h_1),\ldots,W(h_n)) h_i.$
We denote the domain of the operator D in
![]() $L^2(\Omega)$
by
$L^2(\Omega)$
by
![]() ${\mathbb D}^{1,2}$
, meaning that
${\mathbb D}^{1,2}$
, meaning that
![]() ${\mathbb D}^{1,2}$
is the closure of the class of smooth random variables
${\mathbb D}^{1,2}$
is the closure of the class of smooth random variables
![]() ${\mathcal S}$
with respect to the norm
${\mathcal S}$
with respect to the norm
Definition A.2.
![]() ${\mathbb L}^{1,2}$
is the set of processes
${\mathbb L}^{1,2}$
is the set of processes
![]() $(u_s,s\in [0,T])$
such that
$(u_s,s\in [0,T])$
such that
and for all
![]() $s\in [0,T],$
$s\in [0,T],$
![]() $u_s$
belongs to
$u_s$
belongs to
![]() ${\mathbb D}^{1,2}$
and
${\mathbb D}^{1,2}$
and
Definition A.3. Let
![]() $u \in {\mathbb L}^{1,2};$
then the divergence
$u \in {\mathbb L}^{1,2};$
then the divergence
![]() $\delta(u)$
is the unique random variable of
$\delta(u)$
is the unique random variable of
![]() $L^2(\Omega)$
such that
$L^2(\Omega)$
such that
![]() ${\mathbb E} \left[ F\delta(u)\right]= {\mathbb E}\left[\langle DF,u\rangle_{{\mathbb H}} \right]$
for every smooth random variable
${\mathbb E} \left[ F\delta(u)\right]= {\mathbb E}\left[\langle DF,u\rangle_{{\mathbb H}} \right]$
for every smooth random variable
![]() ${F\in {\mathcal S}}$
. We apply [Reference Nualart21, Definition 1.3.1] with
${F\in {\mathcal S}}$
. We apply [Reference Nualart21, Definition 1.3.1] with
![]() $u\in {\mathbb L}^{1,2}$
and
$u\in {\mathbb L}^{1,2}$
and
![]() $G\in{\mathbb D}^{1,2}$
:
$G\in{\mathbb D}^{1,2}$
:
Let
![]() $x_0\in {\mathbb R}^d.$
We introduce the exponential martingale
$x_0\in {\mathbb R}^d.$
We introduce the exponential martingale
 \begin{align}{Z_t^{x_0}}\,:\!=\,\exp \left[ \sum_{k=1}^d\left(\int_0^t B^k({x_0+}W_s) dW^k_s - \frac{1}{2}\int_0^t \big(B^k\big({x_0+}W_s\big)\big)^2ds\right)\right].\end{align}
\begin{align}{Z_t^{x_0}}\,:\!=\,\exp \left[ \sum_{k=1}^d\left(\int_0^t B^k({x_0+}W_s) dW^k_s - \frac{1}{2}\int_0^t \big(B^k\big({x_0+}W_s\big)\big)^2ds\right)\right].\end{align}
When there is no ambiguity, we will omit the exponent
![]() $x_0.$
$x_0.$
Lemma A.1.
Let
![]() $B\in {C^1_b({\mathbb R}^{d},{\mathbb R})};$
then for all
$B\in {C^1_b({\mathbb R}^{d},{\mathbb R})};$
then for all
![]() $x_0\in {\mathbb R}^d$
, the process
$x_0\in {\mathbb R}^d$
, the process
belongs to
![]() ${\mathbb L}^{1,2}.$
${\mathbb L}^{1,2}.$
Proof. Let
![]() $x_0$
be fixed. In this proof we omit the exponent
$x_0$
be fixed. In this proof we omit the exponent
![]() $x_0.$
Note that
$x_0.$
Note that
 \begin{align*} &Z_t^2 = \exp\left(2 \sum_{k=1}^d\int_0^t\! B^k\big(x_0+W_s\big)dW^k_s- \frac{4}{2}\int_0^t\!\|B\big(x_0+W_s\big)\|^2 ds+ \frac{4-2}{2}\int_0^t\!\|B\big(x_0+W_s\big)\|^2 ds\right)\\&\quad \leq e^{T\|B\|_{\infty}^2}\exp\left( 2 \sum_{k=1}^d \int_0^tB^k\big(x_0+W_s\big)dW^k_s- \frac{4}{2}\int_0^t\|B\big(x_0+W_s\big)\|^2 ds\right).\end{align*}
\begin{align*} &Z_t^2 = \exp\left(2 \sum_{k=1}^d\int_0^t\! B^k\big(x_0+W_s\big)dW^k_s- \frac{4}{2}\int_0^t\!\|B\big(x_0+W_s\big)\|^2 ds+ \frac{4-2}{2}\int_0^t\!\|B\big(x_0+W_s\big)\|^2 ds\right)\\&\quad \leq e^{T\|B\|_{\infty}^2}\exp\left( 2 \sum_{k=1}^d \int_0^tB^k\big(x_0+W_s\big)dW^k_s- \frac{4}{2}\int_0^t\|B\big(x_0+W_s\big)\|^2 ds\right).\end{align*}
Then,
![]() $Z_t$
belongs to
$Z_t$
belongs to
![]() $L^2(\Omega)$
for all
$L^2(\Omega)$
for all
![]() $t\in [0,T]$
, since
$t\in [0,T]$
, since
Note that
![]() $Z_t= 1+\sum_{k=1}^d\int_0^t B^k\big(x_0+W_s\big) Z_s dW^k_s$
,
$Z_t= 1+\sum_{k=1}^d\int_0^t B^k\big(x_0+W_s\big) Z_s dW^k_s$
,
![]() $t\in [0,T].$
Using Lemma 2.2.1 and Theorem 2.2.1 of [Reference Nualart21], as well as the definition of
$t\in [0,T].$
Using Lemma 2.2.1 and Theorem 2.2.1 of [Reference Nualart21], as well as the definition of
![]() ${\mathbb L}^{1,2}$
applied to the
${\mathbb L}^{1,2}$
applied to the
![]() $\mathbb{R}^{d+1}$
-valued process
$\mathbb{R}^{d+1}$
-valued process
![]() $Y=(W,Z)$
with a null drift coefficient, the
$Y=(W,Z)$
with a null drift coefficient, the
![]() $(d+1)\times d$
matrix
$(d+1)\times d$
matrix
![]() $\Sigma$
defined by
$\Sigma$
defined by
we obtain that Z belongs to
![]() ${\mathbb L}^{1,2}.$
Since B is continuously differentiable with bounded derivatives, the process
${\mathbb L}^{1,2}.$
Since B is continuously differentiable with bounded derivatives, the process
![]() $\left(B(W_s+x_0) Z_s,\ s\in [0,T]\right)$
belongs to
$\left(B(W_s+x_0) Z_s,\ s\in [0,T]\right)$
belongs to
![]() ${\mathbb L}^{1,2}.$
${\mathbb L}^{1,2}.$
The following remark will frequently be used: by [Reference Coutin and Pontier9, p. 135, line 15] or [Reference Nualart21, Exercise 1.2.11, p. 36], we have
A.2. Estimates for the Brownian motion case
Let us recall the density of the distribution of the pair
![]() $\big(W^{*,1}_t,W_t^1\big)$
, where
$\big(W^{*,1}_t,W_t^1\big)$
, where
![]() $W^1$
is a one-dimensional Brownian motion and
$W^1$
is a one-dimensional Brownian motion and
![]() $W^{*,1}$
its running maximum (see, e.g., [Reference Jeanblanc, Yor and Chesney17, Section 3.2] or [Reference He, Keirstead and Rebholz15]):
$W^{*,1}$
its running maximum (see, e.g., [Reference Jeanblanc, Yor and Chesney17, Section 3.2] or [Reference He, Keirstead and Rebholz15]):
Thus, using the independence of the components of the process W, the law of
![]() $\big(W^{1*}_t,W_t\big)$
has a density with respect to the Lebesgue measure on
$\big(W^{1*}_t,W_t\big)$
has a density with respect to the Lebesgue measure on
![]() ${\mathbb R}^{d+1}$
, denoted by
${\mathbb R}^{d+1}$
, denoted by
![]() $p_{W^{1*},W}(.;\,t):$
$p_{W^{1*},W}(.;\,t):$
 \begin{align}p_{W^{1*},W}(b,a;\,t)= 2\frac{\big(2b-a^1\big)}{\sqrt{(2\pi)^d t^{d+2}}}e^{-\frac{\big(2b-a^1\big)^2}{2t}-\frac{\sum_{k=2}^d |a^k|^2}{2t}}&{\mathbf 1}_{b\geq 0,b\geq a^1}, \nonumber\\&b\in {\mathbb R},\,a=\big(a^1,\ldots,a^d\big)\in {\mathbb R}^d.\end{align}
\begin{align}p_{W^{1*},W}(b,a;\,t)= 2\frac{\big(2b-a^1\big)}{\sqrt{(2\pi)^d t^{d+2}}}e^{-\frac{\big(2b-a^1\big)^2}{2t}-\frac{\sum_{k=2}^d |a^k|^2}{2t}}&{\mathbf 1}_{b\geq 0,b\geq a^1}, \nonumber\\&b\in {\mathbb R},\,a=\big(a^1,\ldots,a^d\big)\in {\mathbb R}^d.\end{align}
Lemma A.2.
(i) For all
![]() $t{>0},$
$t{>0},$
![]() $p_{W^{*1},W}(.;\,t)$
is the restriction to
$p_{W^{*1},W}(.;\,t)$
is the restriction to
![]() $\bar\Delta$
of a
$\bar\Delta$
of a
![]() $C^{\infty}\big(\mathbb{R}^{d+1}\big)$
function, and there exists a universal constant D such that for
$C^{\infty}\big(\mathbb{R}^{d+1}\big)$
function, and there exists a universal constant D such that for
![]() $x=b,a^1,a^2,\ldots,a^d,$
$x=b,a^1,a^2,\ldots,a^d,$
 \begin{align}\left|\partial_xp_{W^{*1},W}(b,a;\,t)\right|\leq \frac{D}{\sqrt{(4\pi)^d t^{d+2}}}e^{-\frac{b^2+\big(b-a^1\big)^2}{4t} -\sum_{k=2}^d \frac{\big(a^k\big)^2}{4t}}{\mathbf 1}_{b>\max\!\big(a^1,0\big)}.\end{align}
\begin{align}\left|\partial_xp_{W^{*1},W}(b,a;\,t)\right|\leq \frac{D}{\sqrt{(4\pi)^d t^{d+2}}}e^{-\frac{b^2+\big(b-a^1\big)^2}{4t} -\sum_{k=2}^d \frac{\big(a^k\big)^2}{4t}}{\mathbf 1}_{b>\max\!\big(a^1,0\big)}.\end{align}
As a consequence,
(ii) We have
 \begin{align*}p_0(m,x;\,\,t,x_0)& \leq \frac{e^{-\frac{\big(m-x^1\big)^2}{4t}-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t} {- \frac{\big(m-x_0^1\big)^2}{4t}}}}{\sqrt{(2 \pi )^{d+1}t^{d+1}}}{\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)}\\&= 2^{(d+1)/2}\phi_{d+1}\big(m-x^1,m-x_0^1,\tilde x-\tilde x_0;\,\,2t\big){\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)},\end{align*}
\begin{align*}p_0(m,x;\,\,t,x_0)& \leq \frac{e^{-\frac{\big(m-x^1\big)^2}{4t}-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t} {- \frac{\big(m-x_0^1\big)^2}{4t}}}}{\sqrt{(2 \pi )^{d+1}t^{d+1}}}{\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)}\\&= 2^{(d+1)/2}\phi_{d+1}\big(m-x^1,m-x_0^1,\tilde x-\tilde x_0;\,\,2t\big){\mathbf 1}_{m>\max\!\big(x^1,x^1_0\big)},\end{align*}
Proof. (i) Let
![]() $p_W$
be the density of a d-dimensional Brownian motion, and the density of the law of
$p_W$
be the density of a d-dimensional Brownian motion, and the density of the law of
![]() $W_t$
for all
$W_t$
for all
![]() $t>0$
, with
$t>0$
, with
![]() $p_W(.;\,t)\in C^\infty(\mathbb{R}^d)$
given by
$p_W(.;\,t)\in C^\infty(\mathbb{R}^d)$
given by
 \begin{align*}p_W(x;\,t)= \frac{1}{\sqrt{2^d \pi^d t^d}}e^{- \sum_{k=1}^d \frac{\big(x^k\big)^2}{2t}},\,\,t>0,\,\,x=\big(x^1,\ldots,x^d\big) \in {\mathbb R}^d.\end{align*}
\begin{align*}p_W(x;\,t)= \frac{1}{\sqrt{2^d \pi^d t^d}}e^{- \sum_{k=1}^d \frac{\big(x^k\big)^2}{2t}},\,\,t>0,\,\,x=\big(x^1,\ldots,x^d\big) \in {\mathbb R}^d.\end{align*}
Its derivative with respect to
![]() $x^1$
is
$x^1$
is
 \begin{align*}\partial_{x^1}p_W(x;\,t)= -\frac{x^1}{\sqrt{2^d \pi^d t^{d+2}}}e^{- \sum_{k=1}^d \frac{\big(x^k\big)^2}{2t}},\,\,t>0,\,\,x=\big(x^1,\ldots,x^d\big) \in {\mathbb R}^d.\end{align*}
\begin{align*}\partial_{x^1}p_W(x;\,t)= -\frac{x^1}{\sqrt{2^d \pi^d t^{d+2}}}e^{- \sum_{k=1}^d \frac{\big(x^k\big)^2}{2t}},\,\,t>0,\,\,x=\big(x^1,\ldots,x^d\big) \in {\mathbb R}^d.\end{align*}
Its second derivatives are
 \begin{align*}\partial_{x^1 x^k}^2p_W(x;\,t)&= \frac{x^1x^k}{\sqrt{2^d \pi^d t^{d+4}}}e^{- \sum_{k=1}^d \frac{\big(x^k\big)^2}{2t}},\,\,t>0,\,\,x=\big(x^1,\ldots,x^d\big) \in {\mathbb R}^d, \,\,k=2,\ldots,d,\\\partial_{x^1 x^1}^2p_W(x;\,t)&= \frac{(x^1)^2-t}{\sqrt{2^d \pi^d t^{d+4}}}e^{- \sum_{k=1}^d \frac{\big(x^k\big)^2}{2t}},\,\,t>0,\,\,x=\big(x^1,\ldots,x^d\big) \in {\mathbb R}^d.\end{align*}
\begin{align*}\partial_{x^1 x^k}^2p_W(x;\,t)&= \frac{x^1x^k}{\sqrt{2^d \pi^d t^{d+4}}}e^{- \sum_{k=1}^d \frac{\big(x^k\big)^2}{2t}},\,\,t>0,\,\,x=\big(x^1,\ldots,x^d\big) \in {\mathbb R}^d, \,\,k=2,\ldots,d,\\\partial_{x^1 x^1}^2p_W(x;\,t)&= \frac{(x^1)^2-t}{\sqrt{2^d \pi^d t^{d+4}}}e^{- \sum_{k=1}^d \frac{\big(x^k\big)^2}{2t}},\,\,t>0,\,\,x=\big(x^1,\ldots,x^d\big) \in {\mathbb R}^d.\end{align*}
Using [Reference Garroni and Menaldi14, (2.1), p. 106] we obtain the analogue of [Reference Garroni and Menaldi14, (2.2), p. 107]: there exists a constant C such that
Recall (54):
 \begin{align*}p_{W^{*1},W}(b,a;\,t)=2\frac{2b-a^1}{\sqrt{(2\pi)^d t^{d+2}}}e^{-\frac{\big(2b-a^1\big)^2}{2t} -\sum_{k=2}^d \frac{\big(a^k\big)^2}{2t}}{\mathbf 1}_{b\geq a^1_+},\,\,\forall (b,a)\in {\mathbb R}^{d+1},\,\,t >0.\end{align*}
\begin{align*}p_{W^{*1},W}(b,a;\,t)=2\frac{2b-a^1}{\sqrt{(2\pi)^d t^{d+2}}}e^{-\frac{\big(2b-a^1\big)^2}{2t} -\sum_{k=2}^d \frac{\big(a^k\big)^2}{2t}}{\mathbf 1}_{b\geq a^1_+},\,\,\forall (b,a)\in {\mathbb R}^{d+1},\,\,t >0.\end{align*}
We observe that
Then
![]() $p_{W^{*1},W}(.,.;\,t)$
is the restriction to
$p_{W^{*1},W}(.,.;\,t)$
is the restriction to
![]() $\overline{\Delta}$
of a
$\overline{\Delta}$
of a
![]() $C^{\infty} $
function. Moreover, using the chain rule, with x being
$C^{\infty} $
function. Moreover, using the chain rule, with x being
![]() $\big(b,a^1,\ldots,a^d\big)$
, we have
$\big(b,a^1,\ldots,a^d\big)$
, we have
On the set
![]() $\big\{(b,a),\ b{>}\max\!\big(0,a^1\big)\big\}$
we have
$\big\{(b,a),\ b{>}\max\!\big(0,a^1\big)\big\}$
we have
Plugging the estimate (59) into (58) yields (55) with
![]() $D=2^3 C.$
$D=2^3 C.$
(ii) Recalling the definition
 \begin{align*}p_0(m,x;\,t,x_0)&= p_{W^{1*},W}\big(m-x_0^1,x-x_0;\,t\big) \\ &= 2\frac{m-x^1+m-x_0^1}{\sqrt{(2\pi)^d t^{d+2}}} e^{-\frac{\big(m-x^1+m-x_0^1\big)^2}{2t}- \frac{|\tilde x- \tilde x_0\|^2}{2t}} {\mathbf 1}_{m\geq x^1\vee x_0^1}, \end{align*}
\begin{align*}p_0(m,x;\,t,x_0)&= p_{W^{1*},W}\big(m-x_0^1,x-x_0;\,t\big) \\ &= 2\frac{m-x^1+m-x_0^1}{\sqrt{(2\pi)^d t^{d+2}}} e^{-\frac{\big(m-x^1+m-x_0^1\big)^2}{2t}- \frac{|\tilde x- \tilde x_0\|^2}{2t}} {\mathbf 1}_{m\geq x^1\vee x_0^1}, \end{align*}
we deduce the standard bound which uses
![]() $xe^{-x^2}\leq e^{-x^2/2}$
and
$xe^{-x^2}\leq e^{-x^2/2}$
and
![]() $\big(m-x^1+m-x_0^1\big)^2\geq \big(m-x^1\big)^2+\big(m-x_0^1\big)^2$
:
$\big(m-x^1+m-x_0^1\big)^2\geq \big(m-x^1\big)^2+\big(m-x_0^1\big)^2$
:
 \begin{align*}p_0(m,x;\,t,x_0) &\leq \frac{e^{-\frac{\big(m-x^1\big)^2}{4t}-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t} {- \frac{\big(m-x_0^1\big)^2}{4t}}}}{\sqrt{(2 \pi )^{d+1}t^{d+1}}}{\mathbf 1}_{m>x^1\vee x_0^1}\\&=2^{(d+1)/2} \phi_{d+1}\big(m-x^1,m-x_0^1,\tilde x-\tilde x_0;\,2t\big){\mathbf 1}_{m>x^1\vee x_0^1}.\end{align*}
\begin{align*}p_0(m,x;\,t,x_0) &\leq \frac{e^{-\frac{\big(m-x^1\big)^2}{4t}-\frac{\|\tilde{x}-\tilde{x}_0\|^2}{4t} {- \frac{\big(m-x_0^1\big)^2}{4t}}}}{\sqrt{(2 \pi )^{d+1}t^{d+1}}}{\mathbf 1}_{m>x^1\vee x_0^1}\\&=2^{(d+1)/2} \phi_{d+1}\big(m-x^1,m-x_0^1,\tilde x-\tilde x_0;\,2t\big){\mathbf 1}_{m>x^1\vee x_0^1}.\end{align*}
Lemma A.3.
For all
![]() $0<s<t,$
$0<s<t,$
![]() $k\geq 1$
and all
$k\geq 1$
and all
![]() $u,v,w\in \mathbb{R}^k$
, the following hold:
$u,v,w\in \mathbb{R}^k$
, the following hold:
 \begin{align*} &(i)\,\, \frac{\|u-v\|^2}{t-s}+\frac{\|v-w\|^2}{s}= \frac{t}{s(t-s)} \left\|v-\left(\frac{s}{t}u+\frac{t-s}{t} w \right)\right\|^2 + \frac{\|u-w\|^2}{t};\\&(i^{\prime})\,\,k=1,\int_{-\infty}^b\frac{e^{-\frac{(u-v)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)}}\frac{e^{-\frac{(w-v)^2}{4s}}}{\sqrt{2\pi s}}dv=\sqrt 2\frac{e^{-\frac{(u-w)^2}{4t}}}{\sqrt{2\pi t)}}\Phi_G\left(\sqrt{\frac{t}{s(t-s)}}\left[b-\left(\frac{s}{t}u+\frac{t-s}{t} w\right)\right]\right);\\&(ii)\,\,\int_{\mathbb{R}^k} \frac{e^{-\frac{\|u-v\|^2}{4(t-s)}}}{\sqrt{(2\pi(t-s))^k}}\frac{e^{-\frac{\|w-v\|^2}{4s}}}{\sqrt{(2\pi s)^k}}dv= 2^{k/2}\frac{e^{-\frac{\|u-w\|^2}{4t}}}{\sqrt{(2\pi t)^k}};\\&(iii)\,\,\mbox{for } u>0,\,1-\Phi_G(u)\,:\!=\, \int^{+\infty}_u \frac{e^{-\frac{z^2}{2\,}}}{\sqrt{2\pi}}dz =\Phi_G({-}u)\leq \frac{e^{- \frac{u^2}{2}}}{2}.\end{align*}
\begin{align*} &(i)\,\, \frac{\|u-v\|^2}{t-s}+\frac{\|v-w\|^2}{s}= \frac{t}{s(t-s)} \left\|v-\left(\frac{s}{t}u+\frac{t-s}{t} w \right)\right\|^2 + \frac{\|u-w\|^2}{t};\\&(i^{\prime})\,\,k=1,\int_{-\infty}^b\frac{e^{-\frac{(u-v)^2}{4(t-s)}}}{\sqrt{2\pi(t-s)}}\frac{e^{-\frac{(w-v)^2}{4s}}}{\sqrt{2\pi s}}dv=\sqrt 2\frac{e^{-\frac{(u-w)^2}{4t}}}{\sqrt{2\pi t)}}\Phi_G\left(\sqrt{\frac{t}{s(t-s)}}\left[b-\left(\frac{s}{t}u+\frac{t-s}{t} w\right)\right]\right);\\&(ii)\,\,\int_{\mathbb{R}^k} \frac{e^{-\frac{\|u-v\|^2}{4(t-s)}}}{\sqrt{(2\pi(t-s))^k}}\frac{e^{-\frac{\|w-v\|^2}{4s}}}{\sqrt{(2\pi s)^k}}dv= 2^{k/2}\frac{e^{-\frac{\|u-w\|^2}{4t}}}{\sqrt{(2\pi t)^k}};\\&(iii)\,\,\mbox{for } u>0,\,1-\Phi_G(u)\,:\!=\, \int^{+\infty}_u \frac{e^{-\frac{z^2}{2\,}}}{\sqrt{2\pi}}dz =\Phi_G({-}u)\leq \frac{e^{- \frac{u^2}{2}}}{2}.\end{align*}
Proof. Part (i) is proved by a development of both sides, then an identification of the coefficients of the squared norms and scalar products
![]() $\|u\|^2,\|v\|^2,\|w\|^2,u.v,u.w,v.w.$
So we deduce (i′) as the integral of
$\|u\|^2,\|v\|^2,\|w\|^2,u.v,u.w,v.w.$
So we deduce (i′) as the integral of
 \begin{equation*}\frac{e^{-\frac{t}{4s(t-s)} \left(v-\left(\frac{s}{t}u+\frac{t-s}{t} w \right)\right)^2 - \frac{(u-w)^2}{4t}}}{\sqrt{2\pi(t-s)}\sqrt{2\pi s}}\end{equation*}
\begin{equation*}\frac{e^{-\frac{t}{4s(t-s)} \left(v-\left(\frac{s}{t}u+\frac{t-s}{t} w \right)\right)^2 - \frac{(u-w)^2}{4t}}}{\sqrt{2\pi(t-s)}\sqrt{2\pi s}}\end{equation*}
with respect to v up to b.
Part (ii) is a consequence of Part (i), then an integration on
![]() $\mathbb{R}^k$
of the Gaussian density with respect to dv.
$\mathbb{R}^k$
of the Gaussian density with respect to dv.
(iii) The function
is null at 0, it has a null limit when u goes to
![]() $ -\infty$
, and its derivative is
$ -\infty$
, and its derivative is
 \begin{equation*}u\mapsto -\frac{e^{-\frac{u^2}{2}}}{\sqrt{2\pi}} +u\frac{e^{-\frac{u^2}{2}}}{2}.\end{equation*}
\begin{equation*}u\mapsto -\frac{e^{-\frac{u^2}{2}}}{\sqrt{2\pi}} +u\frac{e^{-\frac{u^2}{2}}}{2}.\end{equation*}
Its derivative vanishes at
![]() $ \sqrt{2/\pi}$
and is negative for
$ \sqrt{2/\pi}$
and is negative for
![]() $u \leq \sqrt{2/\pi}$
and positive after. Thus,
$u \leq \sqrt{2/\pi}$
and positive after. Thus,
![]() $u \mapsto \Phi_G(u) -\frac{e^{-\frac{u^2}{2}}}{2}$
is negative for
$u \mapsto \Phi_G(u) -\frac{e^{-\frac{u^2}{2}}}{2}$
is negative for
![]() $u \leq 0.$
$u \leq 0.$
A.3. Proof of Remark 2.3, boundary conditions of the PDE
Here we assume that
![]() $p_V$
is regular enough. Let
$p_V$
is regular enough. Let
![]() $\mu_0(dx)= f_0(x)dx.$
Using Theorem 2.2, (6) means that for all
$\mu_0(dx)= f_0(x)dx.$
Using Theorem 2.2, (6) means that for all
![]() $F\in C^2_b\big({\mathbb R}^{d+1},{\mathbb R}^d\big)$
,
$F\in C^2_b\big({\mathbb R}^{d+1},{\mathbb R}^d\big)$
,
 \begin{align}{\int_{\bar\Delta}} F(m,x)p_V(m,x;\,t)dmdx = &\int_{\mathbb{R}^d} F(m,m,\tilde x)f_0(m,\tilde x)dmd\tilde x\nonumber \\&+ \int_0^t{\int_{\bar\Delta}}{\mathcal{L}}F(m,x) p_V(m,x;\,s)dmdxds\nonumber \\&+{\frac{1}{2}}\int_0^t\int_{\mathbb{R}^d} {\|A^1(m,\tilde x)\|^2}\partial_mF(m,m,\tilde x ){p_V(m,m,\tilde x;\,s)}dmd\tilde xds,\end{align}
\begin{align}{\int_{\bar\Delta}} F(m,x)p_V(m,x;\,t)dmdx = &\int_{\mathbb{R}^d} F(m,m,\tilde x)f_0(m,\tilde x)dmd\tilde x\nonumber \\&+ \int_0^t{\int_{\bar\Delta}}{\mathcal{L}}F(m,x) p_V(m,x;\,s)dmdxds\nonumber \\&+{\frac{1}{2}}\int_0^t\int_{\mathbb{R}^d} {\|A^1(m,\tilde x)\|^2}\partial_mF(m,m,\tilde x ){p_V(m,m,\tilde x;\,s)}dmd\tilde xds,\end{align}
recalling
![]() ${\mathcal{L}}= B^i\partial_{x_i}+{\frac{1}{2}} \Sigma^{ij}\partial^2_{x_i,x_j}$
, where
${\mathcal{L}}= B^i\partial_{x_i}+{\frac{1}{2}} \Sigma^{ij}\partial^2_{x_i,x_j}$
, where
![]() $\Sigma=AA^t$
.
$\Sigma=AA^t$
.
(i) Integrating by parts with respect to a convenient
![]() $dx_k$
in
$dx_k$
in
and noting that the support of
![]() $p_V(.,.;\,s)$
is
$p_V(.,.;\,s)$
is
![]() $\bar\Delta, $
we see that the boundary terms concern only the component
$\bar\Delta, $
we see that the boundary terms concern only the component
![]() $x^1$
:
$x^1$
:
 \begin{align*}&\int_0^t{\int_{\bar\Delta}}{\mathcal{L}}F(m,x)p_V(m,x;\,s)dmdxds=-\int_0^t{\int_{\bar\Delta}} F(m,x)\partial_{x^k}\big(B^kp_V\big)(m,x;\,s)dmdxds\\&\quad -{\frac{1}{2}} \int_0^t{\int_{\bar\Delta}}\partial_{x^l} F(m,x)\partial_{x^k}[\Sigma^{{k,l}}(m,x) p_V(m,x;\,s)]dmdxds\\& \quad+\int_0^t \int_{{\mathbb R}^d}\left(F(m,m,\tilde x)B^1(m,\tilde x)+{\frac{1}{2}}\partial_{x^k}F(m,m,\tilde x)\Sigma^{1,k}(m,\tilde x)\right)p_V(m,m,\tilde x;\,s) dmd\tilde x ds.\end{align*}
\begin{align*}&\int_0^t{\int_{\bar\Delta}}{\mathcal{L}}F(m,x)p_V(m,x;\,s)dmdxds=-\int_0^t{\int_{\bar\Delta}} F(m,x)\partial_{x^k}\big(B^kp_V\big)(m,x;\,s)dmdxds\\&\quad -{\frac{1}{2}} \int_0^t{\int_{\bar\Delta}}\partial_{x^l} F(m,x)\partial_{x^k}[\Sigma^{{k,l}}(m,x) p_V(m,x;\,s)]dmdxds\\& \quad+\int_0^t \int_{{\mathbb R}^d}\left(F(m,m,\tilde x)B^1(m,\tilde x)+{\frac{1}{2}}\partial_{x^k}F(m,m,\tilde x)\Sigma^{1,k}(m,\tilde x)\right)p_V(m,m,\tilde x;\,s) dmd\tilde x ds.\end{align*}
We again perform integration by parts on the second term on the right-hand side above:
 \begin{align*}&-{\frac{1}{2}} \int_0^t{\int_{\bar\Delta}}\partial_{x^l} F(m,x)\partial_{x^k}\Sigma^{{k,l}}(m,x) p_V(m,x;\,s)]dmdxds\\&\qquad = {\frac{1}{2}} \int_0^t{\int_{\bar\Delta}} F(m,x)\partial^2_{x^k,x^l}\big[\Sigma^{k,l} p_V\big](m,x;\,s)dmdxds\\&\qquad \quad -{\frac{1}{2}} \int_0^t\int_{{\mathbb R}^d} F(m,m,\tilde{x}) \partial_{x^k} \big[ \Sigma^{1,k} p_V\big](m,m,\tilde{x};\,s) dm d\tilde{x} ds. \end{align*}
\begin{align*}&-{\frac{1}{2}} \int_0^t{\int_{\bar\Delta}}\partial_{x^l} F(m,x)\partial_{x^k}\Sigma^{{k,l}}(m,x) p_V(m,x;\,s)]dmdxds\\&\qquad = {\frac{1}{2}} \int_0^t{\int_{\bar\Delta}} F(m,x)\partial^2_{x^k,x^l}\big[\Sigma^{k,l} p_V\big](m,x;\,s)dmdxds\\&\qquad \quad -{\frac{1}{2}} \int_0^t\int_{{\mathbb R}^d} F(m,m,\tilde{x}) \partial_{x^k} \big[ \Sigma^{1,k} p_V\big](m,m,\tilde{x};\,s) dm d\tilde{x} ds. \end{align*}
Gathering these equalities yields
 \begin{eqnarray}&&\int_0^t{\int_{\bar\Delta}}{\mathcal{L}}F(m,x)p_V(m,x;\,s)dmdxds=\int_0^t{\int_{\bar\Delta}} F(m,x){\mathcal{L}}^* p_V(m,x;\,s)dmdxds \nonumber\\&& \qquad {-{\frac{1}{2}} \int_0^t\int_{{\mathbb R}^d} F(m,m,\tilde{x}) \partial_{x^k} \big[ \Sigma^{1,k} p_V\big](m,m,\tilde{x};\,s) dm d\tilde{x} ds}\\&&\qquad +\int_0^t \int_{\mathbb{R}^d}\left(F(m,m,\tilde x)B^1(m,\tilde x)p_V(m,m,\tilde x;\,s) +{\frac{1}{2}}\big[\partial_{x^k}F\Sigma^{1,k} p_V\big](m,m,\tilde x;\,s)\right) dmd\tilde{x} ds.\nonumber\end{eqnarray}
\begin{eqnarray}&&\int_0^t{\int_{\bar\Delta}}{\mathcal{L}}F(m,x)p_V(m,x;\,s)dmdxds=\int_0^t{\int_{\bar\Delta}} F(m,x){\mathcal{L}}^* p_V(m,x;\,s)dmdxds \nonumber\\&& \qquad {-{\frac{1}{2}} \int_0^t\int_{{\mathbb R}^d} F(m,m,\tilde{x}) \partial_{x^k} \big[ \Sigma^{1,k} p_V\big](m,m,\tilde{x};\,s) dm d\tilde{x} ds}\\&&\qquad +\int_0^t \int_{\mathbb{R}^d}\left(F(m,m,\tilde x)B^1(m,\tilde x)p_V(m,m,\tilde x;\,s) +{\frac{1}{2}}\big[\partial_{x^k}F\Sigma^{1,k} p_V\big](m,m,\tilde x;\,s)\right) dmd\tilde{x} ds.\nonumber\end{eqnarray}
(ii) Using
![]() $F\in C^2_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
with compact support in
$F\in C^2_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
with compact support in
![]() $\Delta$
(so
$\Delta$
(so
![]() $F(m,m,\tilde x)=0$
), we deduce the equality in
$F(m,m,\tilde x)=0$
), we deduce the equality in
![]() $\Delta$
:
$\Delta$
:
We use (60), (61), and (62) applied to
![]() $F\in C^2_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
with compact support in
$F\in C^2_b\big({\mathbb R}^{d+1},{\mathbb R}\big)$
with compact support in
![]() $\bar\Delta$
:
$\bar\Delta$
:
 \begin{align}0&= \int_{\mathbb{R}^d} F(m,m,\tilde x)f_0(m,\tilde x)dmd\tilde x {-{\frac{1}{2}} \int_0^t\int_{{\mathbb R}^d} F(m,m,\tilde{x}) \partial_{x^k} \big[ \Sigma^{1,k} p_V\big](m,m,\tilde{x};\,s) dm d\tilde{x} ds}\nonumber \\ & +\int_0^t \int_{{\mathbb R}^d} \left(F(m,m,\tilde x)B^1(m,\tilde x)p_V(m,m,\tilde x;\,s) +{\frac{1}{2}} \big[\partial_{x^k}F\Sigma^{1,k} p_V\big](m,m,\tilde x;\,s)\right) dmd\tilde{x} ds\nonumber \\ & +{\frac{1}{2}}\int_0^t\int_{\mathbb{R}^d} {\|A^1(m,\tilde x)\|^2}\partial_mF(m,m,\tilde x ){p(m,m,\tilde x;\,s)}dmd\tilde xds.\end{align}
\begin{align}0&= \int_{\mathbb{R}^d} F(m,m,\tilde x)f_0(m,\tilde x)dmd\tilde x {-{\frac{1}{2}} \int_0^t\int_{{\mathbb R}^d} F(m,m,\tilde{x}) \partial_{x^k} \big[ \Sigma^{1,k} p_V\big](m,m,\tilde{x};\,s) dm d\tilde{x} ds}\nonumber \\ & +\int_0^t \int_{{\mathbb R}^d} \left(F(m,m,\tilde x)B^1(m,\tilde x)p_V(m,m,\tilde x;\,s) +{\frac{1}{2}} \big[\partial_{x^k}F\Sigma^{1,k} p_V\big](m,m,\tilde x;\,s)\right) dmd\tilde{x} ds\nonumber \\ & +{\frac{1}{2}}\int_0^t\int_{\mathbb{R}^d} {\|A^1(m,\tilde x)\|^2}\partial_mF(m,m,\tilde x ){p(m,m,\tilde x;\,s)}dmd\tilde xds.\end{align}
We now perform integration by parts on the last two terms:
 \begin{align}& \int_0^t\int_{\mathbb{R}^d} \left(\big[\partial_{x^k}F.\Sigma^{1,k}. p_V\big](m,m,\tilde x;\,s) +{\|A^1(m,\tilde x)\|^2}\partial_mF(m,m,\tilde x ){p_V(m,m,\tilde x;\,s)}\right)dmd\tilde xds=\nonumber\\&- \int_0^t\int_{\mathbb{R}^d}\left(\big[ F.\partial_{x^k}(\Sigma^{1,k} p_V)\big]\big(m,m,\tilde x;\,s\big)+\partial_m\big(\|A^1\|^2 p_V\big)(m,m,\tilde x;\,s)\right)dmd\tilde xds\end{align}
\begin{align}& \int_0^t\int_{\mathbb{R}^d} \left(\big[\partial_{x^k}F.\Sigma^{1,k}. p_V\big](m,m,\tilde x;\,s) +{\|A^1(m,\tilde x)\|^2}\partial_mF(m,m,\tilde x ){p_V(m,m,\tilde x;\,s)}\right)dmd\tilde xds=\nonumber\\&- \int_0^t\int_{\mathbb{R}^d}\left(\big[ F.\partial_{x^k}(\Sigma^{1,k} p_V)\big]\big(m,m,\tilde x;\,s\big)+\partial_m\big(\|A^1\|^2 p_V\big)(m,m,\tilde x;\,s)\right)dmd\tilde xds\end{align}
Plugging (64) into (63) yields the boundary condition, namely a PDE of which
![]() $p_V$
is a solution in the weak sense:
$p_V$
is a solution in the weak sense:
 \begin{eqnarray*}&B^1(m,\tilde x) p_V(m,m,\tilde x;\,s)={\frac{1}{2}}\sum_{k\geq 1}\partial_{x^k}\big(\Sigma^{1,k} p_V\big)(m,m,\tilde x;\,s)\\&\qquad \qquad +\, {\frac{1}{2}} {\sum_{k\geq 1}} \partial_{x^k}\big(\Sigma^{1,k} p_V\big)(m,m,\tilde x;\,s)+{\frac{1}{2}} {\partial_{m}\big(\|A^1\|^2{p_V}\big)}(m,m,\tilde x;\,s),\end{eqnarray*}
\begin{eqnarray*}&B^1(m,\tilde x) p_V(m,m,\tilde x;\,s)={\frac{1}{2}}\sum_{k\geq 1}\partial_{x^k}\big(\Sigma^{1,k} p_V\big)(m,m,\tilde x;\,s)\\&\qquad \qquad +\, {\frac{1}{2}} {\sum_{k\geq 1}} \partial_{x^k}\big(\Sigma^{1,k} p_V\big)(m,m,\tilde x;\,s)+{\frac{1}{2}} {\partial_{m}\big(\|A^1\|^2{p_V}\big)}(m,m,\tilde x;\,s),\end{eqnarray*}
simplified as
with the initial condition
![]() $p_V(m,m,\tilde x;\,0)=f_0(m,\tilde x).$
$p_V(m,m,\tilde x;\,0)=f_0(m,\tilde x).$
Acknowledgements
The authors would like to thank Monique Jeanblanc, who gave us valuable help in writing this paper. The authors would also like to thank the anonymous referees for their constructive comments, which improved the quality of this paper.
Funding information
There are no funding bodies to thank in relation to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.