The energy line of a flowing snow avalanche

In Figure 1, an avalanche occurrence is illustrated by means of a profile of the path of the avalanche, the top left-hand corner of the figure being taken as the break-away point of the avalanche. Accelerated by gravity, the masses travelled down-hill on the steep sections and, braked in flatter parts of the slope and by other obstacles, were deposited at the foot of the slope. The movement involved is a non-steady state process (owing to the continuous change in the magnitude of accelerating and braking forces) and also non-uniform (as narrowing and widening and changes in the height of the flow alter the flow crosssection). The total mass, the density of the snow, and the flow-resistance coefficients also change, as a rule, in the course of the movement.

It is difficult to take stock of and calculate the totality of these complicated processes. With the help of the energy-line method, the entire course of the movement can be made easier to understand. In this method, the flow height D _f of the avalanche snow is entered on the longitudinal profile of the slide path (line A'B'PTC'E' in Fig. 1) at point any P as a line PQ normal to the path, and the velocity head hv'

as a line QL vertically above Q (v is the flow velocity at the point P on the path, and g the acceleration due to gravity = 9.81 m/s²). The point L which is thus obtained lies on the energy line. The flow height D_t is usually much smaller than the velocity head and can then be neglected.

The energy line results from the graphical representation of the law of the conservation of energy, as is familiar in hydraulics. Applied to avalanches, this law states that for any point P on the path, the sum of potential energy (due to elevation) plus kinetic energy (the velocity head) plus energy losses which occur (the energy-loss head) is constant. The energy-loss head Δh' (the line LK in Fig. 1) is that part of the original overall energy, shown in Figure 1 as energy head Ha' of the initial position of rest, which is dissipated on the way from A' to P, i.e. is no longer convertible into velocity. The energy losses determine how the energy line runs.

From measured values for flow height D_t and flow velocity v of avalanches, continuously falling, more or less dipping, sometimes undulating curves, or even curves with kinks (see, for instance, the dashed-line curve in Fig. 2a) are obtained as energy lines. In those cases when the slide path has little dip, these lines can usually be replaced by a straight line.

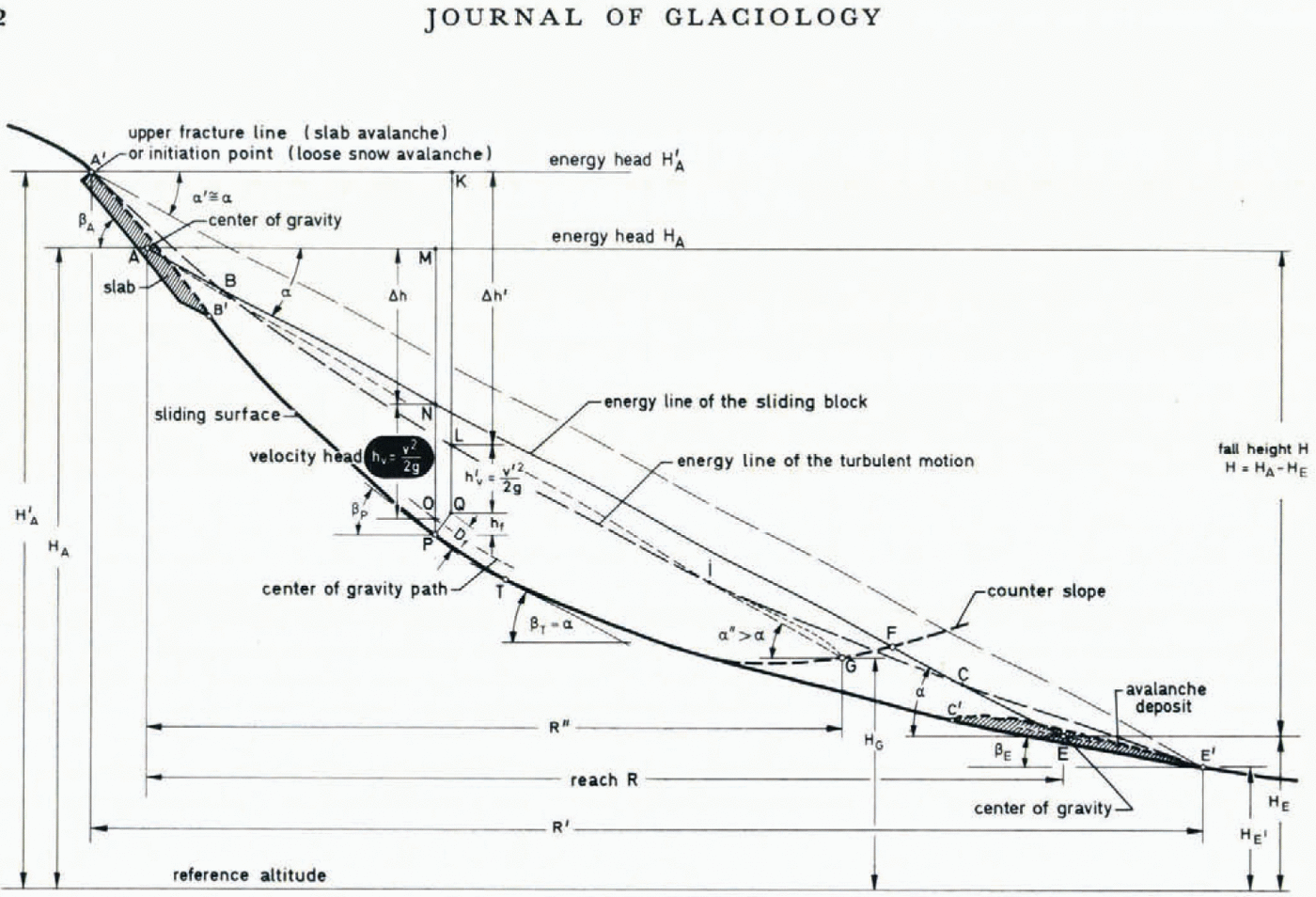
Fig. 1. Avalanche-path profile with the energy lines for the one-coefficient and two-coifficient models.

The energy line of the one-coefficient model

For a rigid body like a sled which slides over the slide path with a constant coefficient of friction fr a straight energy line corresponding to the line AE in Figure 1 at an angle α to the horizontal is obtained (Reference Heim and KörnerHeim, 1932). The points A and E mark the position of rest of the centres of gravity of the plunging mass before and after the plunge. The velocity v of the sled for every point on the path is particularly easy to determine with this straight energy line AE. By measuring to scale the distance ON in Figure 1, i.e. the distance between the path of the centre of gravity and the energy line AE, as the velocity head h_v, it is possible to obtain

The slope angle α of the straight energy line AE was designated by Heim (1932, p. 113) the “centre- of-gravity slope” and the tangent of this angle α

Scheller (unpublished) called the “average slope”. Geometrically, the average slope is the mean slope of all curves connecting the points A and E. Physically, the average slope is equivalent to the constant coefficient of friction f _r between the sled and the slide path:

(Reference Heim and KörnerHeim, 1932; Reference ScheideggerScheidegger, 1973; Reference KörnerKörner, 1977). Empirical values of α can be used to determine the reach R of the movement by plotting a line making an angle α to the horizontal from the starting point A. The terminal point E of the movement of the sled is always where the centre-of-gravity path (or the slide path as an approximation) intersects the energy line. On a counter-slope, the movement would thus terminate at point F in Figure 1 at the latest, and probably sooner, roughly at point G.

The average slope of avalanches

In the case of avalanches with a free run-out, the slope angle α of the centre-of-gravity straight line AE is adequately equal to the slope angle α' of the line A'E' in Figure 1. The line A'E' is designated the “travel slope” (Reference Heim and KörnerHeim, 1932, p. 113). A' is the highest breakaway point and E' is the furthest removed terminal point of the deposit. These two points can always be unambiguously determined on the terrain. The average slope

is the first and most important factor determining any avalanche descent because, by analogy with the sled model, it provides empirical data on the reach and run-out distance and initial pointers to the velocity of avalanches. It is on this account that the energy-line method is chiefly used for avalanche dynamics.

The average slope tan α' of large snow avalanches is between 0.3 and 0.6 (α = 17-31°), usually between 0.4 and 0.5 (α' = 22-27°). These figures depend on the snow conditions, the volume of descending snow, and the properties of the path (shape of the profile, roughness, etc.). Empirical figures for snow avalanches are given by Reference LiedLied and Bakkehøi (1980).

The energy lines and coefficients of the Voellmy model

With smooth-transition slope paths, predominantly concave dipping energy lines corresponding to the line A'BLiCE' in Figure 1 are obtained for the two-coefficient model of Reference VoellmyVoellmy (1955). These curves are obtained section by section, as described by Reference KörnerKörner (1976), with the help of the equation:

where v _i is the velocity at path station i, v_i+1 the velocity at the path station i+1, Δs _i the length of section i between path station i and i+ 1,

and represents Voellmy’s equation for terminal velocity on a path with constant slope β_i, D _fi is the mean flow height in section i, β _i the path slope in section i, μ and ξare the coefficients of the Voellmy model, and k _i= D _fiξ / g is the characteristic flow length in section i.

In Equations (6), the second term in the brackets acts as a corrective term to Equations (7) for short sections Δs of a bending path within which the variables β, D _f, μ, and ξ can be assumed to be constant. For the final path section Δs_u, that is to say for the so-called run-out distance, it follows from (6) that

For every possible terminal point E' of an avalanche, there is a set of related pairs of values for the coefficients μ and ξ (μ being the sliding friction coefficients and ξ the flow-resistance coefficient). For each of these pairs of values of μ and ξ an energy line and a velocity distribution along the path can also be calculated (see Fig, 2), For ξ→ ∞ the two-coefficient model changes into the sled model.

When the calculated velocity distributions are compared with the velocities measured in Nature, the significant pair of coefficients μ and ξ for the overall process can be assessed.

Example of application: flowing snow avalanche after Bryukhanov and others(1967, 1968)

Flowing snow avalanche No. 1 triggered by mortar shell explosions on 30 March 1965 was selected as an example, because very precise photogrammetric measurements of the front velocities of this avalanche by Bryukhanov (1967, 1968) are available. Involving a volume of 10 000 m³, this is also the largest avalanche measured by Bryukhanov. The path profile and the velocities measured were taken from the 1967 paper. Unfortunately, Bryukhanov provides no information on the flow heights of this avalanche. For this reason, a flow height of D _f = 1 m was assumed for the calculations. As can be seen, the path profile shown in Figure 2 is a rather gentle slope in the upper part and then starts to dip more steeply. The measured velocities are shown in Figure 2b as a dashed, undulating line. These measured velocities are used to work out the energy line shown as a dashed line in Figure 2a.

All avalanches measured by Bryukhanov exhibit this conspicuous pulsation of the front velocities. Owing to unevennesses in the path, the calculated velocity curves admittedly also undulate slightly along the path, as can be seen from Figure 2b. However, the measured front velocities obviously show a great deal more pronounced a reaction and the frequency is out of phase with calculated velocity fluctuations. This phenomenon points to a complication which cannot be covered by the available models for avalanche dynamics.

Fig. 2. Example of application: flowing snow avalanche of 30 March 1965, to 10000 m ³ in volume; profile and measured velocity data after Bryukhanov. Calculated energy lines and velocity distribution.

The average slope in the example in Figure 2 is

From point A to point A₀ (path station 12), the measured velocities agree quite well with the figures resulting from the straight energy line of the sled model. On this basis, maximum velocity should occur where the tangent parallel to the travel slope touches the slide path (at point T in Fig. 1). In the example in Figure 2, this would be the case at path station 16, for which the velocity head h _v max = 28.5 m can be measured. It follows that

The actual maximum velocity measured, however, was below path station 13, where v = 21.3 m/s was observed (see Fig. 2b). At point A ₀ (path station 12), where the steeper profile dip begins and where the curve of measured velocities intersects that of the velocity distribution for the sled model (v₁₂= 12.7 m/s), the calculation was started on the basis of the two-coefficient model, as described by Reference Heim and KörnerKörner (1976). The calculated energy lines can be seen in Figure 2a and the velocity distributions with their pairs of values of p. and D _fξ in Figure 2b.

The agreement between the measured and calculated lines is not satisfactory, owing to the pulsation of the front velocities. In order to assess the significant coefficients for the calculation section A₀-E, the velocity distribution for the measured values must therefore be smoothed out. With D _f = 1 m, the following estimated values are then obtained:

From the velocity distribution which can be worked out on the basis of these values, a fairly constant maximum flow velocity of 19 m/s is obtained between path stations 13 and 17.

Final remarks

The energy-line method shows clearly the effect of the path profile shape on avalanche movement. It shows that the models for avalanche dynamics are not in competition but complement each other without inconsistencies. Moreover, the method is useful for model-making, as two movement processes are similar to one another if their energy lines are similar.