1. Introduction
Although very rare, icefalls can be extremely dangerous and they pose a real threat to humans, settlements and infrastructures. The destructive power of this natural phenomenon is usually greater in winter as it may drag snow and ice in its train. One of the most potentially endangered places in the Alps is the village of Randa in the Mattertal, below Weisshorn hanging glacier, canton Valais, Switzerland. This village has been damaged several times in the past by combined snow and ice avalanches triggered by icefalls from hanging glaciers on the northeast face of Weisshorn mountain. The first recorded event of this kind occurred in 1636, when an avalanche buried the village, killing 37 inhabitants. Since then, 19 further events have been recorded, the largest in 1819 with a volume of ∼13 × 106 m3. These events destroyed or damaged roads, railways and settlements. Moreover, because of the natural dam formed by snow and ice accumulation in the valley, a lake formed on three occasions, posing the risk of flooding (Reference Raymond, Wegmann and FunkRaymond and others, 2003). Other hanging glaciers such as Mönch glacier present a less dangerous situation because of their isolated geographical locations. Nevertheless, ice avalanches from the Mönch hanging glacier remain hazardous as mountaineers walk daily along the lower edge of the glacier to reach a mountain refuge.
In order to better understand this phenomenon and investigate precursors of the rupture, we monitored the break-off of ice masses from two unstable hanging glaciers, namely Weisshorn and Mönch. Motion was recorded at the surface of both glaciers. In addition, passive seismic activity was monitored on Weisshorn glacier. Final rupture occurred 30 and 100 days after the start of monitoring at Weisshorn and Mönch glaciers, respectively.
The break-off of ice from glaciers is a gravity-driven rupture. At the microscale, this is a rather complex process due to the polycrystalline nature of the ice, which makes the material heterogeneous. Furthermore, the information pertaining to the heterogeneity of the ice is difficult to quantify and remains mostly qualitative.
In 1973, Flotron and Röthlisberger performed the first icefall prediction on Weisshorn glacier by proposing an empirical function to fit the increasing surface velocity measurements before break-off (Reference FlotronFlotron, 1977; Reference RöthlisbergerRöthlisberger, 1981). This function describes an acceleration of the velocity following a power law up to infinity at a finite time t c, referred to as ‘critical time’ or ‘finite time singularity’ (Equation (1)). This infinite velocity is obviously not realistic in nature, and the effective time of failure necessarily occurs before t c. However, in the case of predictions, the effective time of failure referred to as t f is usually assimilated to t c, for lack of a better rule.
Recently, Reference LüthiLüthi (2003) re-analyzed the Weisshorn data-set and showed evidence of an oscillatory behaviour superimposed on the power-law acceleration. The frequency of these so-called ‘log-periodic oscillations’ is proportional to ln(t c − t), the logarithm of the time before failure. Reference Pralong, Birrer, Stahel and FunkPralong and others (2005) also discovered this log-periodic oscillatory behaviour for other glaciers such as Mönch glacier and possibly Gruben glacier. They also pointed out that rupture predictions for hanging glaciers are significantly improved if log-periodic oscillations are accounted for in the function that fits the measurements.
Observations of various other heterogeneous materials prior to the final rupture reveal the same power-law behaviour for several control parameters, such as displacement, velocity or acoustic emissions (Reference VoightVoight, 1989). Examples of such critical behaviour can be found in a wide range of non-linear processes such as natural ruptures (e.g. rockfalls (Reference Amitrano, Grasso and SenfauteAmitrano and others, 2005), landslides (Reference Sornette, Helmstetter, Andersen, Gluzman, Grasso and PisarenkoSornette and others, 2004), volcanic eruptions (Reference VoightVoight, 1988), earthquakes (Reference Bowman, Ouillon, Sammis, Sornette and SornetteBowman and others, 1998) and the break-off of ice from hanging glaciers (Reference FlotronFlotron, 1977; Reference RöthlisbergerRöthlisberger, 1981; Reference LüthiLüthi, 2003; Reference Pralong and FunkPralong and Funk, 2005; Reference Pralong, Birrer, Stahel and FunkPralong and others, 2005)), but also in finance, economics and population dynamics (Reference Johansen and SornetteJohansen and Sornette, 2001; Reference Ide and SornetteIde and Sornette, 2002). Moreover, log-periodic corrections can be found in other scientific fields such as earthquakes (Reference Sornette and SammisSornette and Sammis, 1995; Reference SornetteSornette, 2006), rupture in composite materials (Reference Anifrani, Le Floc’h, Sornette and SouillardAnifrani and others, 1995), finance and population dynamics (Reference Ide and SornetteIde and Sornette, 2002). This common behaviour could be linked to a common process.
For hanging glaciers, it seems that small cracks could initiate in the shear band close to the glacier bed because of the high strain rate at the base of the glacier. These cracks could then develop and propagate, leading to an acceleration of the whole ice mass. If the crack density is large enough, these cracks could then interact and percolate, leading to this characteristic oscillatory behaviour. The physical origin of this behaviour is still a subject of debate, however.
This paper presents an analysis of measurements performed prior to the catastrophic rupture of ice from hanging glaciers. The study, based on in situ measurements, strives to improve the time prediction of the failure. We will show that ice motion fulfils some scaling laws, as is also the case for the fracture of other heterogeneous materials. This enables an initial estimation of the time of rupture. Moreover, some log-periodic oscillations accompanying this power-law behaviour are also detected on the analyzed datasets. We will show the implications that they have for the forecasting of the failure time and also for the rupture processes occurring in hanging glaciers. In addition, increasing icequake activity is also observed prior to the final rupture. These results have important implications for the prediction of the break-off of hanging glaciers, and provide an indication of the origin of log-periodic oscillations.
2. Study Sites
2.1. Weisshorn glacier
The northeast face of the Weisshorn is covered with unbalanced cold ramp glaciers (i.e. the snow accumulation is mostly compensated with break-off; Reference Pralong and FunkPralong and Funk, 2006) located between 4500 and 3800 m a.s.l. on a steep slope of 45–50°. In winter, snow avalanches triggered by icefalls pose a threat to the village of Randa located some 2500 m below the glacier, and to transport routes to Zermatt (Figs 1 and 2). In a compilation of historical records, Reference Raymond, Wegmann and FunkRaymond and others (2003) showed that Randa was damaged repeatedly during the past few centuries. Of the nineteen events recorded since 1636, three caused a total of 51 fatalities and six caused damage to property. Weisshorn hanging glacier broke off five times in the last 35 years (1973, 1980, 1986, 1999 and 2005; see Reference Raymond, Wegmann and FunkRaymond and others, 2003). Two of these events (in 1973 and 2005) were monitored in detail (Reference FlotronFlotron, 1977).

Fig. 1. The east face of the Weisshorn with the hanging glacier. The village of Randa and transit routes are visible in the valley. The asterisk indicates the location of the hanging glacier. The inset shows the location of Weisshorn and Mönch glaciers in Switzerland.

Fig. 2. General schematic view of Weisshorn hanging glacier (dashed zone) and the monitoring setting (theodolite and automatic camera). Thick black lines indicate the mountain ridges, and the thin line represents the bottom of the valley.
2.2. Mönch glacier
This hanging glacier located between 4100 and 3600 m a.s.l. on the southern face of Mönch glacier, Bernese Alps, Switzerland, (Figs 1 and 3) is an unbalanced terraced glacier (i.e. with significant increase in the slope bedrock at the glacier margin; Reference Pralong and FunkPralong and Funk, 2006). The Mönch break-off mechanism is very different to that of Weisshorn glacier, as Mönch shows a wedge fracture (Figs 3 and 4) and the Weisshorn a slab fracture (Fig. 4). The bedrock topography was measured in 2001 by drilling six boreholes down to the bed along two flowlines. Temperature records in the boreholes showed that this glacier is temperate (only one thermistor indicated a cold temperature of −0.6 ± 0.05°C; Reference Pralong and FunkPralong and Funk, 2006) in contrast to Weisshorn glacier which is cold.

Fig. 3. Left: general situation of the south face of Mönch. The picture shows the relics of an ice avalanche which occurred on 5 July 1984 (photograph courtesy of J. Alean). Right: side view of the unstable part of the glacier. The unstable mass is approximately 50 m high, 300 m long and 40 m wide.

Fig. 4. Sketch of Mönch (left; wedge fracture) and Weisshorn (right; slab fracture) break-off. The unstable ice masses are depicted in grey. The mass-balance regime is indicated with arrows (after Reference Pralong and FunkPralong and Funk, 2006).
3. Measurements
3.1. Weisshorn 1973 break-off
An unstable ice mass of 500 000 m3 was detected in summer 1972. Velocity measurements were performed for the first time on the unstable ice mass by Reference FlotronFlotron (1977) and Reference RöthlisbergerRöthlisberger (1981) to predict its failure time. They monitored the unstable portions of the glacier by means of theodolite measurements and photogrammetry. The theodolite measurements were interrupted 37 days prior to the break-off after 266 days of monitoring (Fig. 5). An extensometer was then installed at the highest crevasse, which measured the velocity difference between the stable and unstable parts as ∼120 cm d−1 just before rupture (see inset in Fig. 5).

Fig. 5. Velocity of Weisshorn glacier before the 1973 break-off. The vertical thick dashed line represents the observed time of failure (at day 306). The thin dashed curve is a fit of the data with Equation (1). The inset shows extensometer measurements a few days before break-off.
In order to predict the failure time, Reference FlotronFlotron (1977) analyzed these data and proposed an empirical power-law function to fit the measurements, i.e.
where v(t) is the velocity at time t, v 0 a constant velocity, t c the critical time and a and m < 1 are the parameters characterizing the acceleration.
By fitting velocity data with Equation (1), Reference FlotronFlotron (1977) found a time of failure t c at day 322, 2 weeks after the observed break-off which occurred at day t f = 306 days (Fig. 5). The volume of the falling ice mass was one-third of that expected (only the frontal part broke off). The sketch of the 1973 break-off (Fig. 6) shows a progressive disaggregation of the glacier, resulting in many small failures. On the basis of aerial photographs, Reference RöthlisbergerRöthlisberger (1981) estimated that the ice mass started to accelerate 5 years before breaking off (i.e. in 1968). Simulations by Reference Pralong and FunkPralong and Funk (2006) on the south Grandes Jorasses hanging glacier (unbalanced cold ramp hanging glacier) suggest an initial acceleration resulting from the thickening of the ice mass because of snow accumulation followed by an acceleration due to the fracture process.

Fig. 6. Comparison of the evolution of glacier geometry for the 1973 break-off (left column, VAW, unpublished) with the glacier geometry evolution for the 2005 break-off (right column; source VAW). The grey zones represent lost sections of the glacier from one picture to the next.
After this event, a monitoring programme was set up by the VAW (Laboratory of Hydraulics, Hydrology and Glaciology) in collaboration with canton Valais. Aerial photographs of the glacier were taken every year by Swisstopo. The evolution of the hanging glacier between 1980 and 2005 is shown in Figure 7. Note a progressive build-up of the hanging glacier. Frontal crevasses were recognizable from 2000, indicating a separation of the frontal part from the rear part of the glacier. Crevasses were fully open in March 2005, suggesting the imminent rupture which occurred in April 2005. According to the evidence of these aerial photographs, the ice mass started to accelerate around 5 years before the rupture in 2000, as Röthlisberger noticed in the case of the 1973 break-off.

Fig. 7. Aerial view of Weisshorn hanging glacier in (a) September 1980, (b) September 1996, (c) September 2000 and (d) March 2005 (Swisstopo). Ellipses indicate the unstable part of the glacier.
3.2. Weisshorn 2005 break-off
An automatic camera was installed on the Bishorn (Fig. 2) in September 2003, in order to monitor the evolution of the hanging glacier as it approached the final break-off. The formation of a crevasse could be observed from daily photographs, in particular just before the rupture (Fig. 6). The total volume of the unstable ice mass was estimated to be 500 000 m3. Because of the dangerous situation for the village of Randa, a monitoring system was installed to alert the population to an impending icefall.
The measurement equipment consisted of a total station (Leica theodolite TM1800 combined with the DI3000S Distometer) installed at a fixed position above Randa on the other side of the valley and seven reflectors mounted on stakes drilled into the unstable ice mass. A reference reflector was installed (point 108, Fig. 8) on a rock for the correction of the measurements due to varying meteorological conditions. This fully autonomous apparatus performed the measurements every 2 hours. The motion of the reflectors (see Fig. 8) could only be monitored if the visibility conditions were good enough.

Fig. 8. Orthophotograph of Weisshorn glacier on 16 March 2005 (left; before the break-off) and on 3 April 2005 (right; after the break-off) (Swisstopo). The monitored points (black dots) and the geophone (black square) on the east face of the Weisshorn are highlighted. The black line indicates the location of the cross-sectional view (Fig. 9).
A geophone was also installed near the upper crevasse (Fig. 8) in order to record icequake activity before the final rupture. This signal is assumed to describe the crack evolution within the ice mass during the failure process. These results are discussed in section 4.1.4. Unfortunately, due to bad weather, no theodolite measurements are available for the week preceding the final rupture. Moreover, the seismic recorder failed to function after the first break-off.
The automatic camera provided a detailed movie of the destabilization of the glacier. A first break-off occurred on 24 March 2005 (point 106, after 26.5 days of monitoring). Its estimated volume amounted to 120 000 m3 (comparable to the 1973 break-off with 160 000 m3). A second rupture occurred on 31 March 2005, during which the major part of the glacier fell (after 33.5 days of monitoring). The volume of this second ice avalanche was estimated to be 400 000 m3. Figure 6 depicts the 2005 break-off. Figure 9 depicts the cross-sectional view of the glacier before and after break-off. The 1973 and 2005 break-offs appear to be almost identical.

Fig. 9. Cross-sectional view of Weisshorn glacier along the flowline drawn in Figure 8 in March 2005 (thick line) and in April 2005 (thin dashed line).
3.3. Mönch 2003 break-off
Displacement measurements of the unstable part of Mönch glacier were performed in 2003 using the same equipment as for Weisshorn hanging glacier (Reference Pralong, Birrer, Stahel and FunkPralong and others, 2005), i.e. with reflectors on stakes. Data were recorded during more than 90 days before the rupture, which is significantly longer than for the Weisshorn. The time of failure of the unstable mass is not precisely known, as sub-failures occurred prior to the main one and caused the measuring equipment on the glacier to be lost. Nevertheless, the break-off was estimated to occur after 107 days.
In contrast to the work done by Reference RöthlisbergerRöthlisberger (1981), who analyzed the ice mass velocity, Reference Pralong, Birrer, Stahel and FunkPralong and others (2005) analyzed its displacement (i.e. the integral of the velocity) which is the direct measurement. They discovered an acceleration of the displacement prior to rupture, as did Reference FlotronFlotron (1977). Moreover, they detected log-periodic oscillations superimposed on this acceleration. The corresponding equation for the displacement takes the form (Reference Pralong, Birrer, Stahel and FunkPralong and others, 2005):
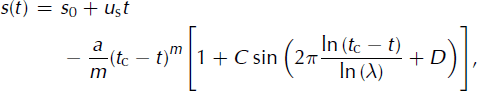
where u s is a steady motion, t c the critical time, m < 1 the power-law exponent, a a constant, C the relative amplitude, λ the logarithmic frequency and D the phase shift of the log-periodic oscillation.
4. Results
4.1. Weisshorn
4.1.1. Displacement measurements
The automatic total station used for our measurements has an accuracy of 9 mm and (1.4 × 10 − 4)°. It was installed close to Randa (Fig. 2) at a distance of ∼6 km from the hanging glacier. It stores the last position of each monitored point and tracks the new position in the vicinity of the last stored position. Nevertheless, because of the large distance between the theodolite and the reflectors, a small error in angle measurement has considerable impact on the accuracy of the calculated position. In our case, the imprecision in the angle measurement leads to an error of 40 cm in the determination of the stake position. To improve the accuracy, two corrections were applied to the measurements.
First, the distance measurements were corrected in order to compensate for the meteorological disturbances of the air temperature, humidity and pressure. The reference point 108 (Fig. 8) located on the rock (fixed position) was used for this correction, as its distance to the theodolite is constant. Second, we assume that a material point moves along a straight stream line. The trajectory is estimated by fitting a line through the measurements (Fig. 10). This assumption is justified, as the slope is homogeneous. However, one can argue that this correction procedure can introduce undesired side effects into the measured displacements. As no oscillating behaviour was observed on the secured side of the glacier (points 107, 109 and 110), we conclude that this is a real signal. Once this line is fitted, it is possible to determine the position by using only the measured distance, as each measurement is associated with a unique position on the line. This method allows the position of the reflectors to be determined with an accuracy of the same order as the corrected distance measurement (about 9 mm). Figure 11 shows the displacement of point 103 after these corrections.

Fig. 10. Position of point 103 before correction, projected on the horizontal plane. The arrow indicates the direction of motion. The inset shows the raw displacement before correction as a function of time. This inset can be compared with the displacement after correction (Fig. 11).

Fig. 11. Displacement of point 103 after corrections. The dotted line shows the first break-off (26.5 days) and the dashed line indicates the final rupture (33.5 days).
Velocities have been derived from the position measurements for seven reflectors (Fig. 12). They show two distinct zones: the upper with constant velocities (points 107, 109 and 110) and the lower with increasing velocities (points 103–106). The zone with constant low velocities did not break off, whereas the other experienced a catastrophic rupture (Fig. 8). This velocity analyzis enables a prior estimation of the volume of the unstable ice.

Fig. 12. Smoothed velocities of the monitored stakes.
4.1.2. Evidence of log-periodic oscillations
In order to illustrate the existence of log-periodic oscillations, we fit the corrected displacement of point 103 with the integral of Equation (1). Figure 13 shows the overall motion of point 103 and its residuals to the power-law fit. Residuals present oscillations with an amplitude one order of magnitude larger than the accuracy of the measurements. We therefore expect these residuals to contain a log-periodic oscillation signature. Our next step is to fit Equation (2) (which contains the log-periodicity) with the displacement of the four points (points 103–106) showing a dramatic acceleration. We adopt the same fit procedure as Reference Pralong, Birrer, Stahel and FunkPralong and others (2005). For the sake of visibility, we subtract the power-law acceleration from the measurements and the fit in Figure 14 (Table 1). We therefore show only the oscillatory behaviour. The fits show good agreement with the measurements except after the first break-off (t = 26.5 days).

Fig. 13. (a) Corrected displacement of Weisshorn glacier at point 103. The grey curve represents the power-law fit (time integral of Equation (1)). (b) Residual of the power-law fit. The two vertical dashed lines show the two successive break-offs (after 26.5 and 33.5 days of monitoring).

Fig. 14. Oscillating part of the four points showing a dramatic acceleration. The solid grey lines indicate the fit of the log-periodic oscillations with parameters of Table 1. The two vertical dashed lines represent the two successive break-off events which occurred on the Weisshorn glacier (after 26.5 and 33.5 days of monitoring). See Figure 8 for point location.
Table 1. Values of the estimated coefficients of Equation (2) with λ = 1.93 and u s = 0.1 m d−1 and the root-mean-square error (RMSE) of the fit
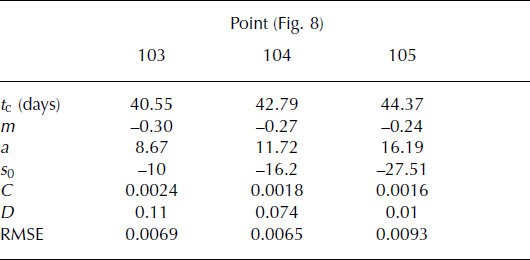
Table 2 shows the values of the estimated coefficients, corresponding to Equation (2). To simplify the fitting procedure, we assume a constant velocity u s = 0.1 m d−1, approximated from the velocity of point 109 located slightly upstream.
Table 2. Estimated coefficients of Equation (2) for the four analyzed datasets, assuming u s = 0.1 m d−1, and RMSE of the fit

4.1.3. Lomb periodogram analysis
The identification of the log-frequency is difficult to perform with a fit since the log-frequency is strongly correlated to other parameters of the fitting function. A periodic component of a time series is usually detected by Fourier analysis. Unfortunately, the sampling rate of our data is not constant, as the theodolite measurements depend upon the visibility conditions, making a Fourier analysis impossible. We use the Lomb periodogram analysis, which is designed to analyze non-uniformly sampled time series. In this method, these time series are fitted by means of the least-squares method to a sine function of varying frequency (f Lomb) on a non-uniform grid (Press and others, 1994; Reference Zhou and SornetteZhou and Sornette, 2002b). This method enables us to determine f Lomb as a function of cos(2πf Lomb t). The parameter λ in Equation (2) can then be evaluated easily as λ = exp(1/f Lomb). Unfortunately, the critical time t c has to be known to perform this analysis, i.e. this analysis can only be an a posteriori analysis.
This analysis clearly shows two main peaks in Lomb power (power spectral density) (f Lomb ∼ 1.52 and 0.69) with the same log-frequency for points 103, 104 and 105, whereas there are no clear peaks for point 106 (Fig. 15). Their existence is statistically significant, as the difference between the maximum and the minimum is larger than two standard deviations (Reference Sornette, Johansen, Arneodo, Muzy and SaleurSornette and others, 1996).

Fig. 15. Lomb periodogram for the different points and the corresponding log frequencies (λ) of the peaks (see Fig. 8 for point location).
As this analysis is independent of the phase angle, it is possible to total and average these periodograms, leading to the global Lomb periodogram for points 103–105 (Fig. 16). Again, the two main peaks appear. These two log-frequencies correspond to λ 1 = 1.93 and λ 2 = 4.2, with λ 2 ∼ 2λ 1. The existence of such subharmonic log-frequencies is discussed in section 5.1.3. These results with a value of λ ∼ 1.93 are consistent with our previous fits. The exception of point 106 (the corresponding glacier segment which broke off earlier) is discussed in section 5.3.

Fig. 16. Mean Lomb periodogram for points 103–105.
The same analysis was performed for Mönch glacier, resulting in the same λ value (section 4.2). Figure 16 also shows two secondary peaks corresponding to λ = 1.37 and λ = 1.32. These peaks are not taken into account for two reasons. First, their amplitudes are small compared to those of the mean peaks. Second, these low λ values would induce less than a single oscillation during our data acquisition (from 1 month to 1 week before rupture, since we failed to conduct measurements during the week before the break-off). Table 1 shows the result of the new fit that takes Lomb analysis into account (i.e. with λ ∼ 1.93). The results are similar for the three points re-analyzed. It can be seen that m is relatively constant (−0.24 to −0.30) and C has the same order of magnitude (between 1.6 × 10 − 3 and 2.4 × 10 − 3).
4.1.4. Icequake analysis
As mentioned in section 3.2, a geophone (Lennartz LE-3Dlite Mkll, three orthogonal sensors, eigenfrequency 1 Hz) was installed in compact ice 30 cm beneath the ice surface next to point 107 (Fig. 8). A Taurus portable seismograph (Nanometrics Inc.) was used to record the seismic activity of the glacier prior to its rupture. As seismic waves are produced by crack initiation or crack propagation in an elastic medium, monitoring icequake activity was expected to quantify the evolution of cracks within the glacier (e.g. Reference Deichmann, Ansorge, Scherbaum, Aschwanden, Bernardi and GudmundssonDeichmann and others, 2000; Reference Métaxian, Araujo, Mora and LesageMétaxian and others, 2003). Unfortunately, the instrument stopped recording after the first break-off event, so no data are available for the period between the two major break-off events.
In order to detect an evolution in seismic activity, and therefore the progression of the failure process, we simply count the number of icequakes per day with an amplitude greater than a given threshold (eliminating background noise). The results are shown in Figure 17 and indicate an increase in seismic activity before the rupture. Indeed, 2 days before the first break-off, the number of icequakes with amplitudes greater than a given threshold increased by a factor of ten. If confirmed, this result is very promising for the prediction of icefalls, since this analysis can be performed in real time and can be used as a warning signal of an imminent rupture. Just before the rupture, the number of icequakes with low amplitudes decreases whereas the number of stronger icequakes increases. The mean size of icequakes therefore seems to increase just before the final rupture. This suggests that small cracks appear first and start to propagate just before rupture, giving rise to larger events.

Fig. 17. Threshold analysis: number of events per day with an amplitude greater than a given threshold as a function of time. The vertical dotted line indicates the first observed rupture.
A recent study on hanging glaciers at Iliamna volcano, Alaska, USA (Reference Caplan-Auerbach and HuggelCaplan-Auerbach and Huggel, 2007) demonstrated that precursory seismic signals also exist for slab fractures in glaciers sliding on their base. Caplan-Auerbach and Huggel distinguished four basic phases in the failure process: (1) crevasse opening, a process that can be initiated months before failure; (2) acceleration of the glacier motion; (3) discrete sliding episodes; and (4) continuous sliding.
4.2. Mönch
We perform the same analysis as for the Weisshorn measurements. A clear power-law behaviour with log-periodic oscillations was found before the break-off, as Reference Pralong, Birrer, Stahel and FunkPralong and others (2005) already showed. These results (Figs 18 and 19; Table 3) show the same oscillating behaviour before the rupture as for Weisshorn glacier, with increasing amplitude and frequency when approaching break-off. It is not surprising to observe sub-failures prior to the main break-off; extrapolation of the log-periodic fit suggests very large amplitudes of oscillation, which are able to promote sub-failures, when approaching the final break-off.

Fig. 18. Lomb periodogram for one measured point on Mönch hanging glacier.

Fig. 19. Oscillating part of one measured point on Mönch hanging glacier. Solid line indicates the fit of the log-periodic oscillations. The dashed vertical line shows the break-off occurrence after 107 days of measurements.
Table 3. Values of the estimated coefficients of Equation (2) with λ = 1.93 and the RMSE of the fit
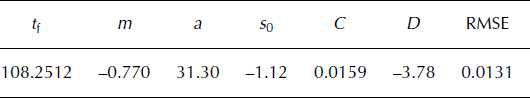
The Lomb periodogram analysis gives a similar peak at λ = 1.94 despite a different release mechanism (see Fig. 4). The value λ ∼ 1.93 seems to be a universal value for a hanging-glacier break-off mechanism. The subharmonic frequency (λ ∼ 4.2) found in the Weisshorn analysis does not appear at Mönch glacier.
5. Discussion
The possible mechanisms leading to this oscillatory behaviour superimposed on the general acceleration of the unstable ice mass are examined. Implications of these results for rupture forecasting are discussed.
5.1. What causes log-periodic oscillations to be superimposed on the overall acceleration?
Before proposing an explanation for the appearance of log-periodic oscillations, the concept and the definition of continuous scale invariance (CSI) is introduced. An object is said to be ‘scale invariant’ if it remains the same when changing the scale of observation. Mathematically speaking, an observable ![]() which depends on a control parameter x is scale-invariant under an arbitrary change x → νx if there is a number μ(ν) such that
which depends on a control parameter x is scale-invariant under an arbitrary change x → νx if there is a number μ(ν) such that
The solution of Equation (3) is simply a power law:
Power laws are therefore the hallmark of scale invariance, as the ratio ![]() does not depend upon x (Reference SornetteSornette, 2006).
does not depend upon x (Reference SornetteSornette, 2006).
It is now possible to generalize this concept of CSI by taking a complex exponent α. This concept is referred to as discrete scale invariance (DSI). This is a weaker type where the system obeys scale invariance only for a specific choice of ν; see Equation (3) for definition. The signature of DSI is the presence of power laws with complex exponents α. The existence of DSI manifests itself in data by log-periodic oscillations superimposed on a power law (Reference SornetteSornette, 2006).
The best way to understand this weaker form of scale invariance is to look at the construction of the triadic Cantor set (Fig. 20). It is usually stated that the triadic Cantor set has the fractal dimension D 0 = ln 2 / ln 3. The number of intervals grows as 2 n , while their length shrinks as 3 −n at the nth iteration. It is obvious to see that, by construction, this triadic Cantor set is geometrically identical to itself only with a magnification by a factor νp = 3 p . Thus, the triadic Cantor set does not possess the property of CSI but only that of DSI under the fundamental scaling ratio of 3 (Reference SornetteSornette, 2006).

Fig. 20. The triadic Cantor set is created by repeatedly deleting the open middle thirds of a set of line segments. One starts by deleting the middle third from the interval [0,1], leaving two line segments. Next, the middle third of each of the remaining segments is deleted. This process is continued ad infinitum. The Cantor set contains all points that are not deleted at any step in this infinite process.
Mathematically speaking, if we look for a solution to Equation (3) in the form of Equation (4), we obtain the equation 1 = μνα . As 1 = exp i2πn, where n is an arbitrary integer, this leads to
The value of α in Equation (5) is complex and, if n = 0, CSI is recovered. DSI is also a generalization of the concept of CSI, where a preferred scaling factor ν exists. The general real part of Equation (4) leads to Equation (2) (where λ plays the same role as ν).
DSI is therefore a partial breaking of a continuous symmetry. Many physical mechanisms can lead to a breaking of continuous symmetry. Mechanisms which possibly occur in a hanging glacier are described in section 5.1.1.
5.1.1. Continuum damage mechanics argument
A possible explanation for such an oscillating behaviour is the damage anisotropy evolution in the case of a shearing fracture, as proposed by Reference PralongPralong (2006). The anisotropy of the damage evolution near the glacier bed, coupled with the rotation of the ice, induces oscillations of the anisotropic components of the damage projected in the flow direction. The rotation is caused by the shearing deformation of the ice, concentrated just above the bedrock (Fig. 21). The oscillations of the damage are transmitted to the glacier surface velocity. This transfer results in power-periodic oscillations accompanying the global power-law acceleration of the glacier.

Fig. 21. Motion of the serac of Weisshorn glacier, obtained from a photogrammetric analysis of terrestrial pictures taken prior to the 1973 rupture (see also Fig. 6). The deformations are concentrated in the vicinity of the glacier bed, where the formation of the cracks is concentrated (VAW, unpublished).
The power-periodic oscillations generalize the log-periodic oscillations, since the power-periodicity converges to the log-periodicity when the exponent of the power-periodicity equals 1. Reference PralongPralong (2006) identified this exponent to be close to 1 for Weisshorn glacier. This approach shows the natural emergence of log-periodic oscillations from the classical constitutive equations of anisotropic damage evolution and ice deformation in the case of shearing flow. The log-periodic oscillations are thus quantitatively related to the parameters of the constitutive equations. Similar relations have been found by Reference Ide and SornetteIde and Sornette (2002) (section 5.1.2). What is new is that the log-periodic oscillations naturally accompany the global power-law acceleration. In Reference Ide and SornetteIde and Sornette (2002) the log-periodic oscillations which emerge from their analysis are not superimposed on any power-law acceleration.
The modelling of the cracks using the theory of the continuum damage mechanics homogenizes the crack effects below a certain scale. This possibly hides discrete fractures which could extend at larger scales and therefore have a macroscopic influence on the fracture.
5.1.2. Relaxation mechanism
Several attempts have been made to link log-periodic oscillations to a system that contains a relaxation mechanism reducing the damage (Reference Ide and SornetteIde and Sornette, 2002). In our case, the development of cracks at the base of the hanging glacier is obvious (Reference Pralong and FunkPralong and Funk, 2005, observations (Fig. 21) and numerical experiments), but the existence of a relaxation mechanism that reduces damage in ice (negative feedback) is rather uncertain.
Healing could indeed play this role, as it can reduce damage by healing cracks (or microcracks) in ice. Healing processes in ice are poorly understood. Healing depends on the ice temperature (Reference Pralong, Hutter and FunkPralong and others, 2006) and is therefore expected to be less effective for low temperatures. If healing processes influence the frequency λ of the log-periodic oscillations (Reference Ide and SornetteIde and Sornette, 2002), glaciers with different temperatures should have different values of λ. As demonstrated in this study, log-periodic oscillations have been detected in both cold and temperate hanging glaciers (for Weisshorn and the Mönch hanging glaciers, respectively) with the same λ value. Thus, healing does not seem to play a role in the occurrence of such oscillations.
Nevertheless, the amplitude of these oscillations (C), the rupture mechanism and the shape of these glaciers are very different, as shown in Figure 4. The amplitude of the oscillations varies from C ∼ 0.001 for Weisshorn glacier to C ∼ 0.01 for Mönch glacier, which is significantly less than the usual values for rupture and growth processes (typically 10−1 according to Reference SornetteSornette, 1998). As explained previously, healing processes are expected to be more effective in the case of Mönch glacier. This negative feedback that possibly heals pre-existing cracks in ice could lead to greater oscillations, thus explaining the difference in the C values in the case of Mönch and Weisshorn glaciers.
5.1.3. Dynamic crack interaction
Dynamic crack interaction could be another mechanism leading to log-periodic oscillations, as argued by Reference Sahimi and ArbabiSahimi and Arbabi (1996) and Reference Huang, Ouillon, Saleur and SornetteHuang and others (1997). Due to the strain rate at the base of the glacier, small cracks develop in a shear band close to the glacier bed. As a result of fracture mechanics, the stress is enhanced near the crack tip (inducing crack growth) and reduced near the crack edge (leading to a screening effect in this zone).
When considering a set of parallel cracks, the largest cracks will be less screened and will therefore grow faster, eventually stopping the smaller cracks. Reference Huang, Ouillon, Saleur and SornetteHuang and others (1997) showed that, for the growth of a population of cracks oriented in one direction, this mechanism leads to a spontaneous generation of discrete scale invariance with a preferred scale of λ = 2 (see fig. 1 in Reference Huang, Ouillon, Saleur and SornetteHuang and others, 1997 for a schematic drawing of the period-doubling cascade of the growth of a system of parallel cracks). Moreover, subharmonic frequencies appear naturally and are arbitrary powers λn of the preferred scaling ratio λ. This corresponds to what we found in section 4.1.3 for Weisshorn hanging glacier, where two preferred scales were detected (λ = 1.93 and λ = 4.2). However, we do not have a satisfactory explanation as to why subharmonic frequencies are observed for Weisshorn and not for Mönch hanging glacier.
Another argument in favour of dynamic crack interaction lies in the analysis of icequakes. As shown in section 4.1.4, the mean size of icequakes increased just before the final rupture. This means that small cracks interact to form larger cracks during the rupture process. This process could break the continuous symmetry of the cracks and lead to DSI.
5.1.4. Value of λ for other phenomena
Scaling laws with log-periodic corrections appear in various phenomena. The parameter λ can have different values, as listed in Table 4 (Reference Sornette and SammisSornette and Sammis, 1995; Reference SornetteSornette, 1998; Reference Zhou and SornetteZhou and Sornette, 2002b).
Table 4. Estimated values of coefficient λ (Equation (2)) for various phenomena (Reference Sornette and SammisSornette and Sammis, 1995; Reference SornetteSornette, 1998; Reference Sornette and JohansenSornette and Johansen, 2001; Reference Zhou and SornetteZhou and Sornette, 2002a)

According to Reference SornetteSornette (1998), usual values for λ are ∼2 for growth processes, ruptures, earthquakes and financial crashes. Our results are in agreement with this mean value. The reason for such a preferred scale is not yet clear, but Reference Huang, Ouillon, Saleur and SornetteHuang and others (1997) suggested that the short-wavelength Mullins–Sekerka instability, together with strong screening effects, could generate DSI spontaneously with a preferred scaling ratio λ = 2 for rupture and growth processes.
5.2. Implication for rupture forecasting
5.2.1. Power-law fit versus log-periodic fit
In order to investigate how the time between the end of the measurements and the time of failure influence the quality of the fit and the predicted time of failure t f, we use the measurements of the Weisshorn 2005 break-off to perform a prediction on truncated datasets using both the power-law and the log-periodic functions.
We removed the last records one by one and evaluated the predicted time of failure and the RMSE of the fit for each truncated dataset (Fig. 22). In this way, it was possible to determine the accuracy of the prediction as a function of the time before failure. This result highlights the variability of the predicted time of failure using the power-law fit without log-periodic oscillations, compared to the fit with log-periodic oscillations. Reference Pralong, Birrer, Stahel and FunkPralong and others (2005) obtained similar results for the failure of Mönch hanging glacier. Note also that the RMSE of the fit without log-periodic oscillations is greater than the fit with log-periodic oscillations.

Fig. 22. Predicted failure time as a function of the number of days of observation for the Weisshorn 2005 break-off. The dashed curve shows the prediction obtained by fitting Equation (1) and the solid curve the prediction obtained by fitting Equation (2). The inset shows the corresponding RMSE.
A large discontinuity in the predicted time of failure and in the RMSE appears when the measurements after the first break-off are taken into account (i.e. after t = 26.5 days; see Fig. 14). This discontinuity results from the first break-off that modifies the dynamics of the failure of the remaining unstable part. If the predicted time of failure t c is adjusted to that observed and the other parameters are left unchanged, the measured motion is well fitted between the two break-off events, but not for the time before the first failure. A re-initialization of the parameters may therefore be necessary after the first break-off. This example highlights the difficulty in performing an accurate prediction after a partial failure.
5.2.2. Rupture in a rising phase
For the fractures described in this paper, the final rupture always appears during a rising phase of the oscillation (Fig. 14). If confirmed, this observation can be very useful for forecasts and mitigation strategies. If oscillations can be detected, it would be possible to determine some periods (of rising phases) when rupture is more likely.
5.2.3. Icequake activity
Seismic activity at Weisshorn glacier increased significantly 3 days before rupture. This signal provided a clear indication of the imminence of the break-off. This warning method can be applied easily in real time and is independent of weather conditions. Icequake analysis therefore seems to be a simple method for detecting precursors of break-off, in contrast to power-law and log-periodic analysis which require much processing of the field data. However, the icequake analysis does not provide information on the volume of the unstable part. Monitoring the surface velocities remains necessary in order to obtain this information.
5.3. Behaviour of point 106
If the λ value is universal, it should also be valid for point 106. However, it has been shown in the Lomb periodogram analysis that λ 106 is significantly different. The displacement of point 106 may result from a combination of two dynamical motions: one due to the dynamics of the major failure (as for points 103–105) with λ = 1.93, and the other due to the first smaller break-off. In this case, the motion of 106 should be described by the equation:
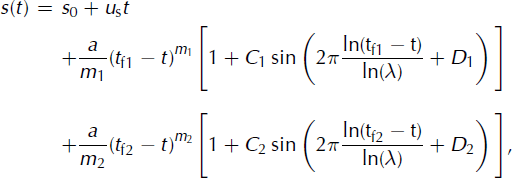
where m 1 ≠ m 2, C 1 ≠ C 2, t f1 ≠ t f2 and D 1 ≠ D 2 in the general case. Figure 23 indicates that there is no significant difference between the fit performed with Equation (6) and with Equation (2). Unfortunately, due to the lack of data for the period immediately prior to the rupture, it is not possible to fit the motion of point 106 more precisely. This approach, which considers a superposition of two dynamical motions, would be valid only if λ is an intrinsic parameter of ice break-off, i.e. if λ is universal. Although verified for Weisshorn and Mönch glaciers, the universality of the λ value should be confirmed by studying other ice break-off events.

Fig. 23. Displacement of point 106 (up) and the oscillating part as a combination of two different log-periodic oscillations.
6. Conclusion
Recent in situ measurements on Weisshorn and Mönch hanging glaciers in the Swiss Alps show an acceleration in both the displacement and the icequake activity of unstable large ice masses prior to their failure.
The general power-law acceleration is accompanied by oscillations which increase logarithmically in frequency as the time of failure is approached (referred to as log-periodic oscillations). We show that rupture always occurs in a rising phase of these oscillations. The origin of such oscillations is not yet fully understood, but the log-periodic frequency seems to be universal for the break-off of large ice masses. A Lomb analysis was performed and gives similar log-periodic frequency parameters for both the ramp rupture at Weisshorn and the wedge rupture at Mönch hanging glacier. Different processes are discussed on the basis of our measurements, and dynamic crack interactions are hypothesized as a possible mechanism leading to such log-periodic oscillations.
In addition, the icequake activity of Weisshorn hanging glacier was monitored. Seismic activity strongly increased 3 days prior to the first failure. This method opens new perspectives for predictions, since the seismic signal provides clear indications of an immediate failure and the method can be applied easily in real time and is independent of weather conditions.
By combining the analysis of the motion with log-periodic oscillations and icequake evolution, the prediction of the final break-off time can be improved significantly. Further in situ studies with measurements taken up to the point of final rupture would be useful to confirm our results.
Acknowledgements
We are grateful to C. Wuilloud (natural hazards, Valais) for logistic and financial support and to L. Jörger (mayor of Randa) and D. Giardini for their help during fieldwork. Our thanks are extended to D. Sornette and M. Lüthi for constructive discussions. We acknowledge W.-X. Zhou for his help on Lomb periodogram analysis, P. Zweifel for preparing the seismic equipment, Swisstopo for providing the aerial photographs and H. Bösch for preparing the orthophotos in Figure 8. S. Braun-Clarke corrected the English.































