1. Introduction
One of the largest ice sheets that are now retreating is the West Antarctic ice sheet, which contains 3.8×106 km3 of ice, equivalent to a 5–6 m sea-level rise (Reference OppenheimerOppenheimer, 1998; Reference Vaughan and SpougeVaughan and Spouge, 2002). Because of the Earth’s crust isostatic response, the bedrock underneath the ice sheet is below the sea surface and is sloping up away from the ice-sheet centre. In order to get an insight into whether the retreat has been caused by the ice sheet’s intrinsic instability, Reference WeertmanWeertman (1974) used a simplified analysis that treated ice as a plastic material and concluded that ice sheets that flow into the ocean and then readjust their flow to become ice shelves should be unstable when the bed is sloping up along the flow and stable when it slopes down. Despite the great insight provided by that work, many simplifications and the use of a plastic model of ice have led to doubts that the above conclusion is applicable to real ice sheets and, if it is, to what extent. Reference Thomas and BentleyThomas and Bentley (1978) used another approach, where they derived the grounding-line dynamics equation from the mass balance, together with an estimate for the mass supply from the catchment area of the grounded ice sheet. The velocity gradient appearing in the mass balance was found by equating it to vertical strain rate in the ice shelf. Calculations performed by Reference Thomas and BentleyThomas and Bentley (1978) supported the view that ascending slopes imply instability, while descending slopes imply stability. Reference SalamatinSalamatin (1989) followed Reference Thomas and BentleyThomas and Bentley (1978) in identifying the grounding-line dynamics equation, but additionally introduced a constant correction factor for the ice-shelf strain rate that accounts for the complexity of the transition zone flow, and also used the velocity found through the shallow-ice approximation.
The simplified nature of the above models has left space for doubts in their conclusions. In particular, Reference HindmarshHindmarsh (1996) claimed that as the stress in the ice shelf is much smaller than that in the ice sheet, the ice-shelf effects should be disregarded. The controversy surrounding the ice-sheet/ice-shelf junction was important to resolve, as the problem of stability of ice sheets flowing into the ocean would crucially depend on the boundary conditions used at the grounding line for the ice sheet. The first attempt to find such conditions in a more rigorous way was made by Reference Chugunov and WilchinskyChugunov and Wilchinsky (1996), who concluded that the mass flow rate is related to the ice thickness at the grounding line. As the use of a sigma coordinate transformation in the ice shelf leads to a third-order differential equation for the bottom elevation, they also imposed additional conditions of its smoothness at the grounding line in order to obtain a unique solution to the problem. It can be argued, however, that the need to impose these extraneous conditions may have arisen due to the use of the sigma transformation together with numerical solution of the problem, while in reality only one condition for the bottom elevation at the grounding line is required since the original mass-balance condition contains only a first-order derivative. Assuming this to be correct, Reference Chugunov and WilchinskyChugunov and Wilchinsky (1996) still had to impose an additional condition of continuity of the ice bottom slope at the grounding line in order to find a unique value of the parameter relating the mass flow rate and the ice thickness at the grounding line. The physical condition for the ice sheet to stay grounded, namely that the water pressure could not lift it, was overlooked by the authors (below, this condition is frequently referred to as the grounding condition). The reason for this was that when the shallow-ice approximation is considered, matching the ice-shelf and ice-sheet thicknesses at the grounding line involves imposing the condition of hydrostatic equilibrium at the grounding line for the ice-sheet thickness. This usually automatically satisfies the condition of grounding of ice in the rest of the ice sheet, as its upper surface elevation at the grounding line is the lowest. As the condition of hydrostatic equilibrium of the ice shelf arises naturally when solving the Stokes equation (due to its small aspect ratio) and solution of the transition-zone problem determines a single solution valid in both the ice sheet and the ice shelf, which is analogous to matching, the authors erroneously assumed that solving the Stokes equations in the transition zone would automatically satisfy all relevant conditions. Generally, as the full system of Stokes equations needs to be solved in the transition zone, the condition of hydrostatic equilibrium of ice in water does not automatically hold there. Reference Chugunov and WilchinskyChugunov and Wilchinsky (1996) found that deviation from hydrostatic equilibrium depended on the imposed bottom slope at the grounding line that identifies a particular solution. If a solution is chosen, then the ensuing grounding condition is automatically satisfied for the far-field solutions (shallow-ice approximation) that made the issue difficult to recognize. The problem of existence of the solution with zero bottom slope at the grounding line was recently considered by Reference Fontelos and MuñozFontelos and Muñoz (2007).
In an attempt to avoid the issue of the complexity of the ice-sheet/ice-shelf transition zone, Reference SchoofSchoof (2007b) adopted a rapid-sliding ice-sheet model and asserted that, as plug flow prevails everywhere in the ice, a direct solution of a reduced problem is possible in the transition zone. This approach included considering two zones in the ice sheet, the main one away from the grounding line, where the pressure gradient was balanced only by the bottom drag, and a so-called ‘shelfy stream’ zone closer to the grounding line (Reference Muszynski and BirchfieldMuszynski and Birchfield, 1987), where increase of the thickness gradient leads to the appearance of the longitudinal deviatoric stress term in the momentum equation. The performed analysis determined a unique solution of the problem (on a monotonic bed) and a condition at the grounding line relating the mass flux and the ice thickness. Despite its mathematical rigor, this approach resulted in several physical inconsistencies. In particular, the found solution describes an upper surface slope discontinuity at the grounding line that renders the solution unphysical near the grounding line which was the area of main interest. This issue was predicted earlier by Reference Wilchinsky and ChugunovWilchinsky and Chugunov (2000), who argued that flow in the transition zone cannot be reduced even if there is free slip, due to the jump in the normal condition at the bottom, i.e. from zero vertical velocity on the ground to free floating in the ocean. Furthermore, even if one assumes that the transition zone singularity does not affect the continuity of integral fields such as velocity, thickness and longitudinal stress, then with the typical ice-sheet characteristics used in the paper the theory predicts that the typical thickness of the ‘shelfy’ ice-stream part is scaled to be around 40 times smaller (≲30 m) than that of the main ice sheet, which makes the ‘shelfy’ ice-stream thinner than the ice shelf, and this cannot be expected in real situations. Although this transition-zone thickness scale can be increased by choosing different flow parameters (Reference SchoofSchoof, 2007a), the theory was developed to work in all cases when the ratio of the normal stress deviator to the hydrostatic pressure, to which the scale is related, is small. This again is in line with the conclusions of Reference Wilchinsky and ChugunovWilchinsky and Chugunov (2000) that existence of two-dimensional (with no lateral drag) shelfy streams interacting with ice shelves is doubtful as they would be thinner than the ice shelves themselves. A simple explanation of this effect is that, given the same typical ice thickness and its gradient determining the longitudinal stress deviator around the transition zone, the upper surface slope, and hence the pressure gradient, in the stream would be ten times larger than that in the ice shelf, thereby making the horizontal momentum terms unbalanced.
Acknowledging the lack of real progress in treating the uniqueness problem, Reference WilchinskyWilchinsky (2007) stated the importance of using the condition of ice grounding in closing the transition-zone problem, and explored an unconventional but physically intuitive approach. He argued that, firstly, if one assumes that in real, physical ice sheets the stress is continuous across the grounding line, then the condition of bottom slope continuity at the grounding line is equivalent to the condition of ice grounding there, regardless of the material properties of the ice. Secondly, as the mathematical solution of this problem with a jump in the bottom boundary conditions is singular (i.e. it has infinite stresses at the grounding line), using the grounding condition directly (i.e. comparing an infinite ice normal stress to the finite water pressure) becomes meaningless in the vicinity of the grounding line and is unlikely to lead to a valid conclusion about the uniqueness of the solution. The condition of bottom slope continuity, however, can still be applied, since the bottom slope remains finite even in the presence of the singularity. Thirdly, consideration of an elasticity problem may yield useful insights: in particular, it exemplifies how disregarding the grounding condition gives rise to multiple solutions with non-zero bottom slopes. It should be said, however, that the validity of the comparison of ice-sheet flow with an elasticity problem has been frequently questioned.
Reference Nowicki and WinghamNowicki and Wingham (2008) were the first to test the grounding condition in their modelling of the transition-zone problem with a finite-element technique using no-slip and slip conditions at the bottom. As a sigma transformation was not used, their calculations showed that, indeed, no additional conditions except for the bottom elevation continuity were required at the grounding line to solve the problem. The condition of ice grounding was checked at the distance from the grounding line where, for the adopted grid, the presence of the singularity had ceased to affect the numerical solution convergence. This approach determined a continuous range of solutions satisfying the grounding condition when the mass flow rate was within a certain range. Many of these solutions had a bottom slope discontinuity, which led to questioning of the assumption of continuity of the ice bottom slope at the grounding line. However, as the singular solution involves an infinite normal stress at the grounding line, the limits of this mass flow range, and therefore the number of solutions, would crucially depend on how far from the grounding line the grounding condition is applied.
To date, there is no rigorous solution of the uniqueness problem; in this work we base our analysis on the assumption that the solution is unique. In support of the conclusion of Reference WeertmanWeertman (1974), Reference Wilchinsky, Chugunov, Glazovskiy and MacheretWilchinsky and others (1998) observed that steady states cannot be reached on bottoms that slope downwards while simulating glacier dynamics with the derived grounding-line conditions. The same conclusion was reached by Reference SchoofSchoof (2007a), employing his rapidly sliding ice-mass model. He compared the magnitude of the ice accumulation rate with the ice mass flow rate at the grounding line of perturbed solutions and asserted that, when the former is larger than the latter, the ice sheet is unstable. The latter condition was proposed by Reference SchoofSchoof (2007b) while disregarding the effect of the ice-sheet thickness evolution on the ice mass flux.
Although the method of comparing the grounding-line mass flow rate with the cumulative accumulation rate in order to make conclusions about ice-sheet stability is intuitively physical, it lacks a mathematically rigorous justification. Therefore our aim here is to perform a linear stability analysis of ice sheets with regard to surface and grounding-line position perturbations, in order to obtain a more rigorous stability criterion. The latter is in contrast to this author’s previous study of ice-sheet stability, where the grounding-line motion was disregarded (Reference WilchinskyWilchinsky, 2001) due to misinterpretation of the necessary conditions of existence of the solution, as was discussed by Reference Wilchinsky and FelthamWilchinsky and Feltham (2004).
2. Ice-Sheet Model
Ice sheets accumulate ice through snowfall. They spread under their own weight and drain into the ocean, where they become ice shelves. A typical timescale for ice-sheet and glacier motion varies from 10 to 10 000 years (Reference PatersonPaterson, 1994). On these timescales the ice flow can be modelled by fluid mechanics and laboratory experiments. Reference GlenGlen (1955) showed that the power-law rheology of ice flow has an exponent, n, close to 3. Other approaches to the determination of n (e.g. Reference Rémy, Ritz and BrissetRémy and others, 1996; Reference Lipenkov, Salamatin and DuvalLipenkov and others, 1997; Reference Salamatin, Lipenkov and DuvalSalamatin and others, 1997) give n varying from 1 to 3. In this work we consider a linear, Newtonian rheology, and assume n = 1. We also assume that the ice-sheet bed is stationary.
Ice flow in ice sheets is described by the Stokes equations taking into account the incompressibility of ice. In order to make the problem more tractable using analytical tools, here we disregard any temperature effects, and study a two-dimensional flow only. At the ice-sheet bed where the ice is assumed not to melt, the no-slip condition is applied.
Ice sheets are characterized by a small ratio of the typical ice thickness to the ice-sheet length: the aspect ratio, Δ, usually ranges between 0.01 and 0.001. Therefore the Stokes equations can be simplified by a lubrication approximation, which determines the ice-sheet evolution equation (Reference Fowler and LarsonFowler and Larson, 1978; Reference Morland and JohnsonMorland and Johnson, 1980; Reference HutterHutter, 1983; Reference Salamatin and MazoSalamatin and Mazo, 1989). In order to scale the problem in an efficient way, we briefly review this inference and the problem scaling.
The ice-sheet geometry is sketched in Figure 1. Let us denote the dimensional horizontal and upward vertical spatial coordinates by (X, Z), time by T, horizontal and vertical velocities by U and W, pressure by P, bed and surface elevations by B and S, ice thickness by H = S − B, gravitational acceleration by g, ice accumulation rate at the upper surface by A, ice and water densities by ρ
i and ρ
w, and ice viscosity by μ. Considering that the ice sheet is in a quasi-equilibrium state, we equate the vertical velocity scale to the accumulation-rate scale [W] = [A], as the latter would be balanced by the ice descent at the ice divide, provided the upper surface is stationary. The horizontal velocity scale is then determined from the mass balance, [U] = [W]/Δ, where Δ = [Z]/[X] is the ice-sheet aspect ratio. The pressure scale is hydrostatic, [P] = [Z]ρ
i
g, and the time scale is enough for an ice particle to reach the bottom, [T] = [Z]/[W]. To make our scaling in an efficient way, we choose the horizontal scale to be exactly equal to the steady-state ice-sheet length, L
0, and the ice accumulation scale to be exactly equal to the mean accumulation rate, ![]() .
.

Fig. 1. An ice sheet interacting with the ocean.
If we denote our non-dimensional variables by lower-case letters, we can reduce the Stokes equations to the form
where η = μ[A]/ (Δ4 ρ i g[X]2). The stress-free conditions at the upper surface imply
The mass conservation integrated over the thickness yields
where q is the horizontal mass flow rate. Balancing the terms in Equation (1) implies that η is of order unity. Equating η = 1, we can find the typical ice thickness, [Z], when the ice-sheet length, [X], is known (Reference Salamatin and MazoSalamatin and Mazo, 1989). The ice-sheet aspect ratio is then
Neglecting terms of order Δ2 from Equations (1) and (2) we obtain a linear, hydrostatic pressure, and a parabolic horizontal velocity,
Substitution of Equation (5) 2 into Equation (3) yields the evolution equation for the ice-sheet thickness:
where x = x g(t) is the unknown grounding-line position that, because of our scaling, is equal to unity if a steady-state solution is considered.
Equation (6) is a parabolic, non-linear, second-order partial differential equation. It requires an initial condition, two boundary conditions and one more condition to determine the grounding-line position, x g. The initial condition is arbitrary. Here we take our coordinate system to originate at the ice divide, where the mass flow rate is zero,
Another boundary condition usually assumed for ice sheets interacting with the ocean is that of hydrostatic equilibrium of ice in water,
where k = ρ w /ρ i and h w is the water depth. Although this condition is strictly valid only when shear stress can be neglected in the vertical momentum balance, which is not the case near the grounding line, numerical calculations by Reference Chugunov and WilchinskyChugunov and Wilchinsky (1996) showed that to a certain degree of accuracy this condition holds, if applied to the above approximate grounded-ice-sheet model.
The second boundary condition imposed at the grounding line has been a matter of controversy up to this time. The common understanding is that it effectively arises through the balance of stresses around the grounding line: between the grounded and floating parts of the ice sheets (Reference WeertmanWeertman, 1974; Reference Thomas and BentleyThomas and Bentley, 1978; Reference SalamatinSalamatin, 1989). Modelling the full stationary transition-zone problem, Reference Wilchinsky and ChugunovWilchinsky and Chugunov (2001) assumed the uniqueness of the solution and arrived at the following relationship between the mass flow rate at the grounding line and the ice thickness there,
where r 3 = δ/(Δβ), δ = (ρw − ρi) /ρw ≈ 0.1 is the relative difference between the water and ice densities (fraction of ice above the water in hydrostatic equilibrium) and β is a constant of order one. In dimensional terms, where Q is the mass flow rate, this condition takes the form
Note that δρ i gH describes the typical normal stress deviator in the ice shelf at the grounding line, while μQ/H 2 describes the typical shear stress in the grounded ice sheet. Therefore, β effectively describes the ratio of the typical shear stress to the normal stress at the grounding line. Numerical modelling found β to be between 1 and 2 (Reference Chugunov and WilchinskyChugunov and Wilchinsky, 1996). Later, higher-resolution simulations by this author (unpublished) showed that β may be closer to 2. If sliding is present, then the scale used in terms of mass flow rate overestimates the shear stress, and we expect β to be smaller (Reference Wilchinsky and ChugunovWilchinsky and Chugunov, 2000). As Δ normally ranges between 0.01 and 0.001, while δ ≈ 0.1, then for β ≈ 2, r 3 ranges between 5 and 50 for an ice sheet with negligible sliding. It may take even larger values if sliding is present.
Equation (9) was derived for a steady-state two-dimensional flow. If the ice-shelf length is much shorter than the ice-sheet length, then the boundary condition, Equation (9), still holds for an axisymmetric flow, as the stresses across the grounding line are much larger than those along it (Reference WilchinskyWilchinsky 1997), and the effect of the transverse normal stress is negligible when the ice shelf is short. If small timescale perturbations in the sea-surface elevation are neglected, then for a non-stationary ice-sheet motion time dependence enters only through the mass balance at the free surfaces. In this case, positioning the coordinate system onto the moving grounding line (cf. Reference Fontelos and MuñozFontelos and Muñoz, 2007) leads to the appearance of additional ter (s in the)surface mass balance that can be evaluated as O (h(x g)Δs)(Reference WilchinskyWilchinsky, 1997), where Δs is the typical ice-thickness gradient in the ice shelf near the grounding line. For a power flow law rheology Δs ≈ 2− 2n−1, where n is the power flow law exponent (Reference Wilchinsky and ChugunovWilchinsky and Chugunov, 2001). In our case of a linear rheology, Δs ≈ 1/8, while from Equation (9) we have h g(x g) ≈ r − 1 ≲ 0.6, so the correction to the boundary condition due to non-stationarity is <10%. For a power flow law fluid this estimate decreases significantly, therefore here we assume that Equation (9) also holds for non-steady-state solutions. In this case, with the chosen scaling, different steady-state ice sheets are distinguished only by different values of r, accumulation rate, a, and the bed elevation, b. Due to our non-dimensionalization a steady-state solution is always described by x g = 1 so the water depth at the grounding line, h w(1), is no longer a free parameter. It can be determined from the ice thickness at the grounding line, Equation (8), (note that, due to our non-dimensionalization, q(1) = 1) and the hydrostatic equilibrium condition, Equation (9),
It follows from Equation (9) that at the grounding line of a steady-state ice sheet h = k− 1, and the ice mass flux through the grounding line, q/h, is given by r. We therefore call parameter r the normalized grounding-line mass flux.
The conventional understanding of ice-sheet instability then follows from Equation (6) integrated from the ice divide up to the grounding line where Equation (9) is used:
where ![]() is the ice-thickness anomaly relative to a steady-state ice thickness and the mass flow rate at the grounding line, q(x
g), is given by Equation (9). If the cumulative accumulation rate (first term on the right-hand side) is smaller than the mass flow rate through the ice-heet/ice-shelf junction (second term on the right-hand side), then
is the ice-thickness anomaly relative to a steady-state ice thickness and the mass flow rate at the grounding line, q(x
g), is given by Equation (9). If the cumulative accumulation rate (first term on the right-hand side) is smaller than the mass flow rate through the ice-heet/ice-shelf junction (second term on the right-hand side), then ![]() . This would imply stability if
. This would imply stability if ![]() is positive everywhere. However, the initial perturbation,
is positive everywhere. However, the initial perturbation, ![]() , may be taken to be positive only in the vicinity of the grounding line in order to ensure that the grounding line advances when the bottom slopes down, while
, may be taken to be positive only in the vicinity of the grounding line in order to ensure that the grounding line advances when the bottom slopes down, while ![]() can be negative everywhere else. In this case
can be negative everywhere else. In this case ![]() would imply instability. Therefore such a stability criterion can be questioned, and a more rigorous analysis must be performed in order to determine the stability condition. Note, however, that if the grounding-line position is close to its steady-state position (x
g + Δx
g), then, due to the steady-state mass balance, the right-hand side of Equation (12) is
would imply instability. Therefore such a stability criterion can be questioned, and a more rigorous analysis must be performed in order to determine the stability condition. Note, however, that if the grounding-line position is close to its steady-state position (x
g + Δx
g), then, due to the steady-state mass balance, the right-hand side of Equation (12) is ![]() . Therefore, if we equate the above expression to zero and denote all values at the grounding line by subscript ‘g’, we obtain a necessary condition for neutral equilibrium in the form
. Therefore, if we equate the above expression to zero and denote all values at the grounding line by subscript ‘g’, we obtain a necessary condition for neutral equilibrium in the form
where the last equality appears due to Equations (8), (9) and (11) and because dh
w/db = −1. If ![]() then the right-hand side of Equation (12) is negative, which would correspond to stability according to the conventional approach (Reference SchoofSchoof, 2007b).
then the right-hand side of Equation (12) is negative, which would correspond to stability according to the conventional approach (Reference SchoofSchoof, 2007b).
3. Linear Stability Analysis
To find a time-dependent solution of Equation (6) as a perturbation about a steady-state solution, h 0, we expand all the functions on the small parameter, ε, determining the amplitude of the surface and grounding-line position perturbations
3.1. The leading-order steady-state problem
After substitution of Equations (14) and (15) into Equations (6), (8) and (9) for the leading-order terms we derive
where s 0 = h 0 + b and the primes denote derivatives. The ice-thickness gradient and curvature at the grounding line are
so that as ![]() and
and ![]() , determining high thickness gradient and curvature at the grounding line for 5 ≲ r
3 ≲ 50.
, determining high thickness gradient and curvature at the grounding line for 5 ≲ r
3 ≲ 50.
When the bed is a horizontal plane (b ≡ 0), the solution of Equations (16–18) can be easily found (Reference VialovVialov, 1958; Reference NyeNye, 1959):
3.2. The first-order perturbation problem
For the first-order problem in terms of the function ![]() , we obtain
, we obtain
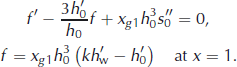
The perturbation function is determined to order of a constant factor, therefore we choose f (1) = 1 at the grounding line. Excluding xg
1 from Equation (24) and taking into account that ![]() and f = 1, we obtain the grounding-line conditions in closed form,
and f = 1, we obtain the grounding-line conditions in closed form,
In this case the perturbation solution can be sought by solving Equation (22) with two boundary conditions: Equation (23) at the ice divide and any one from Equations (25) at the grounding line, x = 1. The eigenvalue, λ, is then found by satisfying the remaining condition at the grounding line, Equation (25).
3.2.1. Zero-growth condition
Here we are interested in determining which values of the bedrock slope at the grounding line and the normalized grounding-line mass flux, r, determine stable and unstable solutions. In order to do this we ask, firstly, which of these values would determine λ = 0. Putting λ = 0 in the perturbation equation (22), we can integrate it from the ice divide (x = 0) with the help of the boundary condition, Equation (23). The zero-growth solution then satisfies
Considering Equation (26) as x → 1 and substituting the two boundary conditions, Equations (27), into Equation (26) leads to an equation relating ![]() and r that ensures zero perturbation growth (λ = 0),
and r that ensures zero perturbation growth (λ = 0),
With the help of Equations (19) and (20), this can be written as
The physical solution to the above equation is given by Equation (13), which was derived using simple physical arguments (Reference SchoofSchoof, 2007b). The denominator in Equation (29) is then zero if
For a
g > 0 and k > 1 the right-hand side is always negative, so that the denominator in Equation (29) is never zero, and Equation (13) is always the solution of Equation (29). Generally speaking, while a particular choice of ![]() and r satisfying Equation (13) ensures the existence of λ = 0, it does not necessarily follow that this also describes the state of neutral equilibrium, as lower, negative eigenvalues may still exist at the same time. Proving with mathematical rigour that the latter is not the case is outside the scope of this work. However, in order to get some insight as to whether Equation (13) may determine the neutral equilibrium that separates stable and unstable solutions, we describe several intuitive considerations.
and r satisfying Equation (13) ensures the existence of λ = 0, it does not necessarily follow that this also describes the state of neutral equilibrium, as lower, negative eigenvalues may still exist at the same time. Proving with mathematical rigour that the latter is not the case is outside the scope of this work. However, in order to get some insight as to whether Equation (13) may determine the neutral equilibrium that separates stable and unstable solutions, we describe several intuitive considerations.
Firstly we assume that a solution to the problem exists and the eigenvalues are smooth functions of the independent problem parameters, namely r, k, the bedrock elevation, b(x), and the ice accumulation rate, a(x), together with their derivatives; and that the eigenvalues do not bifurcate. Furthermore, we consider only such families of solutions whose independent parameters satisfy the following conditions: each of the regions described by ![]() ,
, ![]() and
and ![]() is connected, and any set of the problem parameters, [b(x), r, k, a(x)], can be attained by continuous variation of any other belonging to the same region.
is connected, and any set of the problem parameters, [b(x), r, k, a(x)], can be attained by continuous variation of any other belonging to the same region.
If negative eigenvalues existed when one eigenvalue is zero for a particular set [b
0(x), r
0, k
0, a
0(x)], such that its grounding-line values ![]() and a
g0 satisfy Equation (13), then the continuous form of Equation (13) would imply that the ice sheets from this family of solutions are always unstable when one of their eigenvalues is zero. The latter is because any other choice of [b
1(x), r
1, k
1, a
1(x)] whose grounding line values
and a
g0 satisfy Equation (13), then the continuous form of Equation (13) would imply that the ice sheets from this family of solutions are always unstable when one of their eigenvalues is zero. The latter is because any other choice of [b
1(x), r
1, k
1, a
1(x)] whose grounding line values ![]() satisfy Equation (13) (that determines λ = 0) can be attained by a continuous variation of [b(x), r, k, a(x)] between these two sets of independent parameters in such a way that
satisfy Equation (13) (that determines λ = 0) can be attained by a continuous variation of [b(x), r, k, a(x)] between these two sets of independent parameters in such a way that ![]() always lies on the zero-growth surface, since Equation (13) describes a connected region (Fig. 2). The assumed absence of bifurcation will prevent the negative eigenvalue from disappearing. This, in turn, will mean that stable solutions would not exist in any case, since, in order for them to exist, the most negative eigenvalue should gradually become positive when the problem parameters gradually vary. This is, however, not possible without it becoming zero, and that will, in turn, mean that another negative λ exists. Therefore, finding a stable solution for the considered family may be sufficient to show that λ = 0 indeed describes a neutral equilibrium.
always lies on the zero-growth surface, since Equation (13) describes a connected region (Fig. 2). The assumed absence of bifurcation will prevent the negative eigenvalue from disappearing. This, in turn, will mean that stable solutions would not exist in any case, since, in order for them to exist, the most negative eigenvalue should gradually become positive when the problem parameters gradually vary. This is, however, not possible without it becoming zero, and that will, in turn, mean that another negative λ exists. Therefore, finding a stable solution for the considered family may be sufficient to show that λ = 0 indeed describes a neutral equilibrium.

Fig. 2. The zero-growth line, ![]() , for a = 1. Two points (b
2, r
2) and (b, r) that can be connected by a curve that does not intersect the zero-growth line have eigenvalues of the same sign.
, for a = 1. Two points (b
2, r
2) and (b, r) that can be connected by a curve that does not intersect the zero-growth line have eigenvalues of the same sign.
Furthermore, even if a stable solution is found only for a particular set of parameters [b
2(x), r
2, k
2, a
2(x)] satisfying, say, ![]() (see Fig. 2), then any other solution with [b(x), r, k, a(x)] satisfying
(see Fig. 2), then any other solution with [b(x), r, k, a(x)] satisfying ![]() would also be stable because it can be attained by continuous variation of [b
2(x), r
2, k
2, a
2(x)] in such a way that
would also be stable because it can be attained by continuous variation of [b
2(x), r
2, k
2, a
2(x)] in such a way that ![]() does not cross the surface
does not cross the surface ![]() due to the connectedness of this region. In this case the minimum eigenvalue would stay positive. Similarly, if an unstable solution is found when
due to the connectedness of this region. In this case the minimum eigenvalue would stay positive. Similarly, if an unstable solution is found when ![]() , then all solutions satisfying this condition would be unstable. In the latter case such a solution can be found analytically for non-singular bed elevations and accumulation rates (section 3.2.2) and, hence, all solutions of the family satisfying the imposed conditions would be unstable when
, then all solutions satisfying this condition would be unstable. In the latter case such a solution can be found analytically for non-singular bed elevations and accumulation rates (section 3.2.2) and, hence, all solutions of the family satisfying the imposed conditions would be unstable when ![]() . Numerical, stable solutions can also be found for linear bed profiles and constant accumulation rates (section 3.2.3), so that we assume all solutions belonging to the same family that satisfy
. Numerical, stable solutions can also be found for linear bed profiles and constant accumulation rates (section 3.2.3), so that we assume all solutions belonging to the same family that satisfy ![]() are stable. As the analytical solution described in section 3.2 is also valid for linear bed profiles and constant accumulation rates, we presume that the existence of these two stable and unstable solutions may imply that Equation (13) separates stable solutions from unstable solutions for many useful scenarios.
are stable. As the analytical solution described in section 3.2 is also valid for linear bed profiles and constant accumulation rates, we presume that the existence of these two stable and unstable solutions may imply that Equation (13) separates stable solutions from unstable solutions for many useful scenarios.
3.2.2. An unstable solution
Our aim is to find an unstable solution. Let us choose ![]() , b′(x) = O(1), a(x) = 1. In this case it follows from Equations (19) and (20) that
, b′(x) = O(1), a(x) = 1. In this case it follows from Equations (19) and (20) that ![]() ,
, ![]() , so that Equation (25) becomes
, so that Equation (25) becomes
Let us now abstract from the physical problem and consider k → 0. In this case, as f(1) = 1, f′(1) = 1/k is possible only if f change significantly within 1 − k ≲ x ≲ 1. This implies f″ =O (k −2), so Equation (22) implies λ = O (k− 2). If we introduce Λ = k 2 λ, then Equations (22) and (23) take the form
If we consider only non-oscillating solutions, then as k → 0 we can find the outer solution valid away from the grounding line to order k 2 as zero. Now if we introduce an inner coordinate, ξ = (1 − x)/k, then the perturbation problem can be written as (the primes now define derivatives in ξ)
As in these coordinates b′ = O(3r 3 k), while h 0 ∼ r− 1, the second term in the parenthesis of Equation (34) is negligible in comparison with the first term provided
Note that ![]() , so Equation (37) implies
, so Equation (37) implies ![]() as both are negative. Neglecting the second term in Equation (34), we can find the inner solution that matches the zero outer solution and satisfies boundary conditions, Equation (36), as
as both are negative. Neglecting the second term in Equation (34), we can find the inner solution that matches the zero outer solution and satisfies boundary conditions, Equation (36), as
Therefore, an unstable solution exists that also satisfies ![]() so
so ![]() implies instability.
implies instability.
3.2.3. A stable solution
Finding a stable solution analytically is a complex task, therefore here we resort to numerical solution of the perturbation problem, Equation (22), with boundary conditions Equations (23) and (25). Only linear bed profiles and a = 1 were considered and we used ρ
w = 1.025 kg m−
3 and ρ
i = 0.9167 kg m−
3. Together with the leading-order problem, Equations (16–18), this set of equations was solved using Mathematica 6.0. In particular, Equation (23) was solved satisfying the ice-divide condition and f(1) = 1 at the grounding line. For an arbitrary λ the second grounding-line condition, Equation (25)
2, is not generally satisfied. If we denote the difference between the calculated f′(1) and that given by Equation (25)
2 by df′, then the eigenvalues will be determined by df′ = 0. In Figures 3 and 4 we plot df′(λ) for the bed slope, b′ = −0.2. Figure 4 is a zoomed-out version of Figure 3. The corresponding value of the grounding-line mass flux, r
n, that ensures zero growth is ∼3.3. The sought eigenvalues are given by the intersection of the curves with the line df′ = 0. Three curves are shown: the solid curve is determined by r = r
n, the dashed curve by r being two times larger and the dot–dashed curve by r being two times smaller. As the solid line passes through the origin of the coordinate system, this numerical solution found with the zero-growth values of the parameters is adequate. From Figure 3 it can be seen that an increase of r leads to stability, while a decrease leads to instability. Furthermore, from Figure 4 it can be seen that the eigenvalues shown in Figure 3 are the lowest eigenvalues within the shown range. Therefore, if no eigen-values that are even lower than the shown lower limit exist, then a stable solution exists when ![]() . In order to ascertain that no such lower eigenvalues exist, we can perform an asymptotic analysis similar to that determining the unstable solution. We consider only negative eigenvalues with a large magnitude, λ → −∞. Firstly, by considering a non-oscillating solution we can again determine a zero outer solution. In the boundary layer near x = 1 the second term in Equation (22) is small and h
0 ∼ 1/r, so we can find the solution in the form
. In order to ascertain that no such lower eigenvalues exist, we can perform an asymptotic analysis similar to that determining the unstable solution. We consider only negative eigenvalues with a large magnitude, λ → −∞. Firstly, by considering a non-oscillating solution we can again determine a zero outer solution. In the boundary layer near x = 1 the second term in Equation (22) is small and h
0 ∼ 1/r, so we can find the solution in the form
which implies
where subscript ‘a’ identifies the asymptotic value. If we also assume that for the same value of λ, other, oscillating solutions exist then in this case the second term is still negligible and the difference between these two leading-order solutions satisfies Equation (22) without the second term as well as boundary conditions, Equation (23) and f(1) = 0. Multiplying this equation by the solution difference and integrating between 0 and 1, one can easily show that the solution difference is zero, so that the leading-order solution is non-oscillating and unique.

Fig. 3. The dependence of the perturbation gradient error at the grounding line, df′, on λ. The sought eigenvalues are determined by df′(λ) = 0.
The form of Equation (40) implies that df′ is monotonically increasing as λ → −∞ and therefore will not cross the axis while λ is increasing. Let us denote the normalized difference between the exact and asymptotic values of the first-order gradients as ![]() . For r = r
n, the value of D
n is plotted in Figure 5.
. For r = r
n, the value of D
n is plotted in Figure 5.

Fig. 5. The normalized difference between the exact and asymptotic first-order perturbation gradients at the grounding line, D n.
It can be seen that D n gradually decreases. The decrease is, however, slow, due to the large ice-thickness gradient at the grounding line while the boundary layer thickness is proportional to λ− 1/2. Therefore, for the considered discretized version of the problem, the zero-growth surface, Equation (13), indeed describes neutral equilibrium and separates stable and unstable solutions.
4. Concluding Remarks
We have considered a linear stability analysis of an ice sheet interacting with the ocean. As the no-slip condition was assumed at the bedrock, a cubic dependence of the mass flow rate on the ice thickness at the grounding line was adopted. Using simple arguments combined with analytical unstable and numerical stable solutions we argued that a zero-growth (zero-eigenvalue) mode is determined by a relationship between the bed slope, the ice accumulation rate and the water depth at the grounding line. In dimensional variables this relationship takes the form
which describes neutral equilibrium and separates stable and unstable steady-state ice-sheet solutions for many useful scenarios. In a more generic form the above equation can be written as (Reference SchoofSchoof, 2007b)
If the bed slope is higher than ![]() , then the ice sheet is unstable; and if it is lower, then it is stable. This supports the conventional, intuitive understanding of ice-sheet instability, as in the former case the cumulative ice accumulation rate is larger than the ice mass flow rate at the grounding line of the perturbed ice sheet and the ice sheet will advance through a runaway mechanism; while in the latter case the opposite applies.
, then the ice sheet is unstable; and if it is lower, then it is stable. This supports the conventional, intuitive understanding of ice-sheet instability, as in the former case the cumulative ice accumulation rate is larger than the ice mass flow rate at the grounding line of the perturbed ice sheet and the ice sheet will advance through a runaway mechanism; while in the latter case the opposite applies.
Acknowledgements
We thank an unknown reviewer and C. Schoof for suggestions that helped improve the manuscript.










