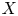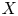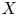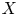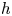1. Introduction
If ![]() $X$ is a projective variety and
$X$ is a projective variety and ![]() $Y$ is a quasi-projective variety over a field
$Y$ is a quasi-projective variety over a field ![]() $k$, then it is well known that there is a quasi-projective variety
$k$, then it is well known that there is a quasi-projective variety ![]() $\operatorname {Map}(X,Y)$ parameterizing morphisms from
$\operatorname {Map}(X,Y)$ parameterizing morphisms from ![]() $X$ to
$X$ to ![]() $Y$. The properness hypothesis on
$Y$. The properness hypothesis on ![]() $X$ is necessary:
$X$ is necessary:
Example 1.0.1 The functor ![]() $\operatorname {Map}(\mathbf {A}^{1}_k,\mathbf {A}^{1}_k)$ parameterizing families of maps from
$\operatorname {Map}(\mathbf {A}^{1}_k,\mathbf {A}^{1}_k)$ parameterizing families of maps from ![]() $\mathbf {A}^{1}_k$ to itself is not representable by an algebraic space. If it were, then any compatible family of
$\mathbf {A}^{1}_k$ to itself is not representable by an algebraic space. If it were, then any compatible family of ![]() $k[\![x]\!] / x^{n}$-points for
$k[\![x]\!] / x^{n}$-points for ![]() $n \geqslant 1$ would extend to a unique
$n \geqslant 1$ would extend to a unique ![]() $k[\![x]\!]$-point. But letting
$k[\![x]\!]$-point. But letting ![]() $t$ denote the coordinate on
$t$ denote the coordinate on ![]() $\mathbf {A}^{1}$, the compatible family of morphisms
$\mathbf {A}^{1}$, the compatible family of morphisms ![]() $e^{tx} \colon \mathbf {A}^{1}_{k[x]/x^{n}} \to \mathbf {A}^{1}_k$ does not extend to a morphism
$e^{tx} \colon \mathbf {A}^{1}_{k[x]/x^{n}} \to \mathbf {A}^{1}_k$ does not extend to a morphism ![]() $\mathbf {A}^{1}_{k[\![x]\!]} \to \mathbf {A}^{1}_{k}$, because
$\mathbf {A}^{1}_{k[\![x]\!]} \to \mathbf {A}^{1}_{k}$, because ![]() $e^{tx}$ is not a polynomial in
$e^{tx}$ is not a polynomial in ![]() $t$ unless
$t$ unless ![]() $x$ is nilpotent.
$x$ is nilpotent.
On the other hand, if ![]() $Y$ is equipped with a linearizable
$Y$ is equipped with a linearizable ![]() $\mathbf {G}_m$-action, then the functor parameterizing families of
$\mathbf {G}_m$-action, then the functor parameterizing families of ![]() $\mathbf {G}_m$-equivariant maps is representable by a scheme,
$\mathbf {G}_m$-equivariant maps is representable by a scheme, ![]() $\operatorname {Map}(\mathbf {A}^{1}_k,Y)^{\mathbf {G}_m}$. The scheme
$\operatorname {Map}(\mathbf {A}^{1}_k,Y)^{\mathbf {G}_m}$. The scheme ![]() $\operatorname {Map}(\mathbf {A}^{1}_k,Y)^{\mathbf {G}_m}$ is the disjoint union of the Białynicki-Birula strata [Reference Białynicki-BirulaBB73] for the action of
$\operatorname {Map}(\mathbf {A}^{1}_k,Y)^{\mathbf {G}_m}$ is the disjoint union of the Białynicki-Birula strata [Reference Białynicki-BirulaBB73] for the action of ![]() $\mathbf {G}_m$ on
$\mathbf {G}_m$ on ![]() $Y$.
$Y$.
This illustrates a common phenomenon in equivariant algebraic geometry (see, for instance, [Reference Haiman and SturmfelsHS04, Reference Alexeev and BrionAB05]): certain non-proper schemes behave as if they are proper if one takes into account equivariance. This paper is dedicated to the systematic development of this concept, and its consequences.
In the example above, we will deduce the representability of ![]() $\underline {\operatorname {Map}}(\mathbf {A}^{1}_k,Y)^{\mathbf {G}_m}$ from the fact that the functor
$\underline {\operatorname {Map}}(\mathbf {A}^{1}_k,Y)^{\mathbf {G}_m}$ from the fact that the functor ![]() $\underline {\operatorname {Map}}(\mathbf {A}^{1}_k / \mathbf {G}_{m,k}, Y / \mathbf {G}_{m,k})$ parameterizing flat families of morphisms of algebraic stacks is itself representable by an algebraic stack (see Example 1.2.3 below). However, the stack
$\underline {\operatorname {Map}}(\mathbf {A}^{1}_k / \mathbf {G}_{m,k}, Y / \mathbf {G}_{m,k})$ parameterizing flat families of morphisms of algebraic stacks is itself representable by an algebraic stack (see Example 1.2.3 below). However, the stack ![]() $\mathbf {A}^{1}_k / \mathbf {G}_{m,k}$ is still not proper in the sense of [Reference Laumon and Moret-BaillyLMB00] (i.e. separated, of finite type, and universally closed). The problem is that points in a separated stack must have proper automorphism groups, so the quotient of a scheme
$\mathbf {A}^{1}_k / \mathbf {G}_{m,k}$ is still not proper in the sense of [Reference Laumon and Moret-BaillyLMB00] (i.e. separated, of finite type, and universally closed). The problem is that points in a separated stack must have proper automorphism groups, so the quotient of a scheme ![]() $X$ by a linear algebraic group
$X$ by a linear algebraic group ![]() $G$ cannot be proper unless
$G$ cannot be proper unless ![]() $G$ acts with finite stabilizers on
$G$ acts with finite stabilizers on ![]() $X$.
$X$.
Our aim is thus to propose an alternative to the notion of properness for an algebraic stack ![]() $\mathscr {X}$ which applies to many of the quotient stacks which arise in practice, such as the stack
$\mathscr {X}$ which applies to many of the quotient stacks which arise in practice, such as the stack ![]() $\mathbf {A}^{1}/\mathbf {G}_m$. The resulting notion has convenient formal properties, and we establish two of the useful consequences which are familiar from the case of schemes:
$\mathbf {A}^{1}/\mathbf {G}_m$. The resulting notion has convenient formal properties, and we establish two of the useful consequences which are familiar from the case of schemes: ![]() $\operatorname {Map}(\mathscr {X},\mathscr {Y})$ is an algebraic stack, as is the stack of coherent sheaves on
$\operatorname {Map}(\mathscr {X},\mathscr {Y})$ is an algebraic stack, as is the stack of coherent sheaves on ![]() $\mathscr {X}$, when
$\mathscr {X}$, when ![]() $\mathscr {X}$ is ‘formally proper’ and flat over the base.
$\mathscr {X}$ is ‘formally proper’ and flat over the base.
1.1 Definition of a formally proper morphism
Our notion of properness makes use of the derived category of ‘almost perfect complexes’ on a stack, ![]() $\operatorname {APerf}(\mathscr {X})$. When
$\operatorname {APerf}(\mathscr {X})$. When ![]() $\mathscr {X}$ is noetherian and classical,
$\mathscr {X}$ is noetherian and classical, ![]() $\operatorname {APerf}(\mathscr {X})$ agrees with the derived category
$\operatorname {APerf}(\mathscr {X})$ agrees with the derived category ![]() $D^{-}\mathop {{\rm Coh}^{}}\nolimits (\mathscr {X})$ of right-bounded complexes of quasi-coherent sheaves with coherent homology, and more generally
$D^{-}\mathop {{\rm Coh}^{}}\nolimits (\mathscr {X})$ of right-bounded complexes of quasi-coherent sheaves with coherent homology, and more generally ![]() $\operatorname {APerf}(-)$ extends the definition of pseudo-coherent complexes [Sta19, Tag 08FS] to derived schemes and stacks.
$\operatorname {APerf}(-)$ extends the definition of pseudo-coherent complexes [Sta19, Tag 08FS] to derived schemes and stacks.
We will also use the theory of formal completion, which we review in § 2.1. If ![]() $\mathscr {X}$ is an algebraic stack and
$\mathscr {X}$ is an algebraic stack and ![]() $Z \subset |\mathscr {X}|$ a cocompact closed subset, we will denote the formal completion of
$Z \subset |\mathscr {X}|$ a cocompact closed subset, we will denote the formal completion of ![]() $\mathscr {X}$ along
$\mathscr {X}$ along ![]() $Z$ by
$Z$ by ![]() $\widehat {\mathscr {X}}_Z$.
$\widehat {\mathscr {X}}_Z$.
Definition 1.1.1 We say that ![]() $\mathscr {X}$ is complete along
$\mathscr {X}$ is complete along ![]() $Z$ if the restriction functor
$Z$ if the restriction functor ![]() $\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}}_Z)$ is an equivalence of
$\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}}_Z)$ is an equivalence of ![]() $\infty$-categories. In this case we say that
$\infty$-categories. In this case we say that ![]() $\mathscr {Z} \to \mathscr {X}$ is a complete closed immersion for any closed substack
$\mathscr {Z} \to \mathscr {X}$ is a complete closed immersion for any closed substack ![]() $\mathscr {Z} \subset \mathscr {X}$ having underlying closed subset
$\mathscr {Z} \subset \mathscr {X}$ having underlying closed subset ![]() $Z$.
$Z$.
Example 1.1.2 Let ![]() $\mathscr {X} = \operatorname {Spec}(R)$ for some noetherian ring
$\mathscr {X} = \operatorname {Spec}(R)$ for some noetherian ring ![]() $R$, and let
$R$, and let ![]() $Z \subset \operatorname {Spec}(R)$ be the closed subset corresponding to an ideal
$Z \subset \operatorname {Spec}(R)$ be the closed subset corresponding to an ideal ![]() $I \subset R$. Then by Proposition 2.1.4 we have
$I \subset R$. Then by Proposition 2.1.4 we have
and ![]() $\mathscr {X}$ is complete along
$\mathscr {X}$ is complete along ![]() $Z$ if and only if
$Z$ if and only if ![]() $R$ is
$R$ is ![]() $I$-adically complete.
$I$-adically complete.
Although this notion of completeness is formulated for derived stacks, we will see in Lemma 2.3.4 that it only depends on the underlying classical stack, and in fact only on its underlying reduced stack.
Definition 1.1.3 We say that a morphism of algebraic (derived) stacks ![]() $\pi \colon \mathscr {X} \to \mathscr {S}$ is formally proper if it is (almost) finitely presented, and, for any noetherian algebraic (derived) stack
$\pi \colon \mathscr {X} \to \mathscr {S}$ is formally proper if it is (almost) finitely presented, and, for any noetherian algebraic (derived) stack ![]() $\mathscr {Y}$ which is complete along a closed subset
$\mathscr {Y}$ which is complete along a closed subset ![]() $Z \subset |\mathscr {Y}|$ and any morphism
$Z \subset |\mathscr {Y}|$ and any morphism ![]() $\mathscr {Y} \to \mathscr {S}$, the fiber product
$\mathscr {Y} \to \mathscr {S}$, the fiber product ![]() $\mathscr {X}^{\prime } := \mathscr {X} \times _\mathscr {S} \mathscr {Y}$ is complete along the preimage of
$\mathscr {X}^{\prime } := \mathscr {X} \times _\mathscr {S} \mathscr {Y}$ is complete along the preimage of ![]() $Z$.Footnote 1
$Z$.Footnote 1
Suppose ![]() $\mathscr {Y} = \operatorname {Spec}(R)$ for a complete noetherian ring
$\mathscr {Y} = \operatorname {Spec}(R)$ for a complete noetherian ring ![]() $R$ and
$R$ and ![]() $Z$ is the closed subset defined by an ideal
$Z$ is the closed subset defined by an ideal ![]() $I \subset R$. Then
$I \subset R$. Then ![]() $\mathscr {X}' = \mathscr {X} \times _\mathscr {S} \mathscr {Y}$ being complete along the preimage of
$\mathscr {X}' = \mathscr {X} \times _\mathscr {S} \mathscr {Y}$ being complete along the preimage of ![]() $Z$ is equivalent to the restriction map giving an equivalence
$Z$ is equivalent to the restriction map giving an equivalence
When ![]() $\mathscr {X} \to \mathscr {S}$ is representable by proper algebraic spaces, then this equivalence is the Grothendieck existence theorem, or formal GAGA, for derived categories [Reference KnutsonKnu71, Chap. V]. Therefore, Definition 1.1.3 asserts that
$\mathscr {X} \to \mathscr {S}$ is representable by proper algebraic spaces, then this equivalence is the Grothendieck existence theorem, or formal GAGA, for derived categories [Reference KnutsonKnu71, Chap. V]. Therefore, Definition 1.1.3 asserts that ![]() $\pi$ universally satisfies a strong form of the Grothendieck existence theorem.
$\pi$ universally satisfies a strong form of the Grothendieck existence theorem.
At first blush, it is strange to elevate a major theorem into a definition. On the other hand, the definition of a proper scheme is also somewhat complicated: checking that a morphism is universally closed, or even checking the valuative criterion, is a priori an infinite and intractable task. We argue that the value of Definition 1.1.3 (as with any definition!) results from the availability of interesting examples, the usefulness of its formal properties, and the theorems one can prove with it.
As a first source of examples, we generalize the notion of a projective morphism of schemes to that of a cohomologically projective morphism of derived algebraic stacks in Definition 4.1.3, and we prove the following result.
Theorem (Theorem 4.2.1)
A cohomologically projective morphism of (derived) algebraic stacks is formally proper.
The proof is formally similar to the classical proof of the Grothendieck existence theorem for projective morphisms, but the framework of derived algebraic geometry offers some significant conceptual simplifications.
Example 1.1.4 (Proposition 4.2.3)
Let ![]() $S$ be a noetherian scheme over a field
$S$ be a noetherian scheme over a field ![]() $k$,
$k$, ![]() $G$ a linearly reductive algebraic
$G$ a linearly reductive algebraic ![]() $k$-group acting on a
$k$-group acting on a ![]() $k$-scheme
$k$-scheme ![]() $X$, and
$X$, and ![]() $\pi : X \to S$ a
$\pi : X \to S$ a ![]() $G$-invariant morphism which factors as a projective morphism
$G$-invariant morphism which factors as a projective morphism ![]() $X \to X'$ followed by an affine morphism
$X \to X'$ followed by an affine morphism ![]() $X' \to S$ of finite type. If
$X' \to S$ of finite type. If ![]() $\pi$ admits a relatively ample
$\pi$ admits a relatively ample ![]() $G$-equivariant invertible sheaf and
$G$-equivariant invertible sheaf and ![]() $H_0 \pi _\ast (\mathcal {O}_X)^{G}$ is a coherent
$H_0 \pi _\ast (\mathcal {O}_X)^{G}$ is a coherent ![]() $\mathcal {O}_S$-module, then
$\mathcal {O}_S$-module, then ![]() $X/G \to S$ is cohomologically projective.
$X/G \to S$ is cohomologically projective.
Example 1.1.5 (Proposition 4.2.5)
If ![]() $S$ is a noetherian scheme over a field
$S$ is a noetherian scheme over a field ![]() $k$,
$k$, ![]() $G$ is an algebraic
$G$ is an algebraic ![]() $k$-group, and
$k$-group, and ![]() $X$ is a
$X$ is a ![]() $G$-scheme which admits a good quotient [Reference SeshadriSes72] which is projective over
$G$-scheme which admits a good quotient [Reference SeshadriSes72] which is projective over ![]() $S$, then
$S$, then ![]() $X/G$ is cohomologically projective over
$X/G$ is cohomologically projective over ![]() $S$. This generalizes the formal GAGA result for good moduli spaces established in [Reference Geraschenko and Zureick-BrownGZB15].
$S$. This generalizes the formal GAGA result for good moduli spaces established in [Reference Geraschenko and Zureick-BrownGZB15].
Formally proper morphisms also enjoy some convenient formal properties.
Proposition 1.1.6 Suppose ![]() $\mathscr {X}' \to \mathscr {X}$ is a surjective and formally proper morphism of (derived)
$\mathscr {X}' \to \mathscr {X}$ is a surjective and formally proper morphism of (derived) ![]() $\mathscr {S}$-stacks. Then if
$\mathscr {S}$-stacks. Then if ![]() $\mathscr {X}' \to \mathscr {S}$ is formally proper, so is
$\mathscr {X}' \to \mathscr {S}$ is formally proper, so is ![]() $\mathscr {X} \to \mathscr {S}$. In addition, formally proper morphisms are closed under base change, composition, and fiber products.
$\mathscr {X} \to \mathscr {S}$. In addition, formally proper morphisms are closed under base change, composition, and fiber products.
Proof. The first claim follows from Theorem 4.3.1 (which holds under weaker hypotheses on the map ![]() $\mathscr {X}' \to \mathscr {X}$) and Theorem 2.4.3, and the remaining claims are immediate from Definition 1.1.3.
$\mathscr {X}' \to \mathscr {X}$) and Theorem 2.4.3, and the remaining claims are immediate from Definition 1.1.3.
As a result, any stack ![]() $\mathscr {X}$ which admits a surjective proper morphism
$\mathscr {X}$ which admits a surjective proper morphism ![]() $\mathscr {X}' \to \mathscr {X}$ from a cohomologically projective stack
$\mathscr {X}' \to \mathscr {X}$ from a cohomologically projective stack ![]() $\mathscr {X}'$ is formally proper. This allows one to construct many examples of formally proper morphisms which are not cohomologically projective. For instance, if
$\mathscr {X}'$ is formally proper. This allows one to construct many examples of formally proper morphisms which are not cohomologically projective. For instance, if ![]() $G$ is a reductive group scheme over a scheme
$G$ is a reductive group scheme over a scheme ![]() $S$, then
$S$, then ![]() $B_S G \to S$ is formally proper under suitable hypotheses (Proposition 4.3.4). See Example 4.3.3 below for more examples.
$B_S G \to S$ is formally proper under suitable hypotheses (Proposition 4.3.4). See Example 4.3.3 below for more examples.
One key technical result underlying Proposition 1.1.6 and many other results is a new ![]() $h$-descent theorem in the context of derived algebraic geometry. Recall that an
$h$-descent theorem in the context of derived algebraic geometry. Recall that an ![]() $h$-cover of locally noetherian (derived) algebraic stacks is an (almost) finitely presented morphism which is universally a topological submersion. Examples include fppfFootnote 2 morphisms, as well as proper and formally proper surjective morphisms.
$h$-cover of locally noetherian (derived) algebraic stacks is an (almost) finitely presented morphism which is universally a topological submersion. Examples include fppfFootnote 2 morphisms, as well as proper and formally proper surjective morphisms.
Theorem (Theorem 3.3.1)
The presheaf ![]() $\operatorname {APerf}(-)$ satisfies derived descent for
$\operatorname {APerf}(-)$ satisfies derived descent for ![]() $h$-covers of locally noetherian derived stacks.
$h$-covers of locally noetherian derived stacks.
Although many of the results in this paper are classical in nature, this result truly requires the setting of derived algebraic geometry. For instance the inclusion of the reduced subscheme ![]() $X^{\mathrm {red}} \to X$ is a derived
$X^{\mathrm {red}} \to X$ is a derived ![]() $h$-cover, but it has a trivial Čech nerve in the category of classical schemes and therefore this is not an effective descent morphism in this category. On the other hand, there are classical stacks for which this descent theorem provides our only method of establishing formal properness.
$h$-cover, but it has a trivial Čech nerve in the category of classical schemes and therefore this is not an effective descent morphism in this category. On the other hand, there are classical stacks for which this descent theorem provides our only method of establishing formal properness.
Finally, we note that Definition 1.1.3 is closely related to other plausible notions of properness for algebraic stacks. By Theorem 2.4.3 and Proposition 2.4.5, we have the following implications for an (almost) finitely presented morphism ![]() $\pi : \mathscr {X} \to \mathscr {S}$ of noetherian algebraic (derived) stacks:
$\pi : \mathscr {X} \to \mathscr {S}$ of noetherian algebraic (derived) stacks:

Furthermore, all of these properties hold if ![]() $\mathscr {S}$ is a noetherian scheme and
$\mathscr {S}$ is a noetherian scheme and ![]() $\pi$ is proper, by Example 4.3.3(i). However, we will see in Example 1.2.5 that (CP) alone is not sufficient for our applications to mapping stacks and coherent sheaves.
$\pi$ is proper, by Example 4.3.3(i). However, we will see in Example 1.2.5 that (CP) alone is not sufficient for our applications to mapping stacks and coherent sheaves.
1.2 Applications
Recall that, given two stacks ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $\mathscr {Y}$ over a base stack
$\mathscr {Y}$ over a base stack ![]() $\mathscr {S}$, the mapping stack
$\mathscr {S}$, the mapping stack ![]() $\underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X},\mathscr {Y})$ is the stack whose space of
$\underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X},\mathscr {Y})$ is the stack whose space of ![]() $T$-points (for any scheme
$T$-points (for any scheme ![]() $T$ over
$T$ over ![]() $\mathscr {S}$) is the space of maps
$\mathscr {S}$) is the space of maps ![]() $\underline {\operatorname {Map}}_\mathscr {S} (T \times _\mathscr {S} \mathscr {X}, \mathscr {Y})$.
$\underline {\operatorname {Map}}_\mathscr {S} (T \times _\mathscr {S} \mathscr {X}, \mathscr {Y})$.
Theorem (Theorem 5.1.1)
Let ![]() $R$ be a (simplicial commutative)
$R$ be a (simplicial commutative) ![]() $G$-ring, and let
$G$-ring, and let ![]() $\mathscr {X}$ be an algebraic (derived)
$\mathscr {X}$ be an algebraic (derived) ![]() $R$-stack which is formally proper and of finite Tor amplitude
$R$-stack which is formally proper and of finite Tor amplitude ![]() $n$ over
$n$ over ![]() $\mathscr {S}:=\operatorname {Spec}(R)$. Then for any algebraic (derived) stack
$\mathscr {S}:=\operatorname {Spec}(R)$. Then for any algebraic (derived) stack ![]() $\mathscr {Y}$ which is locally almost finitely presented with quasi-affine diagonal over
$\mathscr {Y}$ which is locally almost finitely presented with quasi-affine diagonal over ![]() $\mathscr {S}$,
$\mathscr {S}$, ![]() $\underline {\operatorname {Map}}_{\mathscr {S}}(\mathscr {X},\mathscr {Y})$ is an algebraic
$\underline {\operatorname {Map}}_{\mathscr {S}}(\mathscr {X},\mathscr {Y})$ is an algebraic ![]() $(n+1)$-stack, locally almost finitely presented over
$(n+1)$-stack, locally almost finitely presented over ![]() $\mathscr {S}$. If
$\mathscr {S}$. If ![]() $\pi$ is flat then
$\pi$ is flat then ![]() $\underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X},\mathscr {Y})$ has quasi-affine diagonal, and if
$\underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X},\mathscr {Y})$ has quasi-affine diagonal, and if ![]() $\mathscr {Y} \to \mathscr {S}$ has affine diagonal then the diagonal is affine.
$\mathscr {Y} \to \mathscr {S}$ has affine diagonal then the diagonal is affine.
Remark 1.2.1 This theorem holds under slightly weaker hypotheses. For an elaboration, see the discussion following Theorem 5.1.1.
Example 1.2.2 Let ![]() $\Theta := \mathbf {A}^{1} / \mathbf {G}_m$, then for any locally (almost) finitely presented morphism of (derived) algebraic stacks
$\Theta := \mathbf {A}^{1} / \mathbf {G}_m$, then for any locally (almost) finitely presented morphism of (derived) algebraic stacks ![]() $\mathscr {Y} \to \mathscr {S}$ with quasi-affine (respectively, affine) diagonal,
$\mathscr {Y} \to \mathscr {S}$ with quasi-affine (respectively, affine) diagonal, ![]() $\underline {\operatorname {Map}}_\mathscr {S}(\Theta _\mathscr {S},\mathscr {Y})$ is a locally almost finitely presented algebraic
$\underline {\operatorname {Map}}_\mathscr {S}(\Theta _\mathscr {S},\mathscr {Y})$ is a locally almost finitely presented algebraic ![]() $\mathscr {S}$-stack with quasi-affine (respectively, affine) diagonal (the lack of noetherian hypotheses is explained in Remark 5.1.4). This is the starting point for the theory of
$\mathscr {S}$-stack with quasi-affine (respectively, affine) diagonal (the lack of noetherian hypotheses is explained in Remark 5.1.4). This is the starting point for the theory of ![]() $\Theta$-stability developed in [Reference Halpern-LeistnerHal14], where
$\Theta$-stability developed in [Reference Halpern-LeistnerHal14], where ![]() $\underline {\operatorname {Map}}_\mathscr {S}(\Theta _\mathscr {S},\mathscr {Y})$ is regarded as the stack of ‘filtered points’ in
$\underline {\operatorname {Map}}_\mathscr {S}(\Theta _\mathscr {S},\mathscr {Y})$ is regarded as the stack of ‘filtered points’ in ![]() $\mathscr {Y}$. The fibers of the map
$\mathscr {Y}$. The fibers of the map ![]() $\underline {\operatorname {Map}}_\mathscr {S}(\Theta _\mathscr {S},\mathscr {Y}) \to \mathscr {Y}$ defined by restriction along the inclusion
$\underline {\operatorname {Map}}_\mathscr {S}(\Theta _\mathscr {S},\mathscr {Y}) \to \mathscr {Y}$ defined by restriction along the inclusion ![]() $\{1\} \to \Theta$ are regarded as generalized flag spaces for points of
$\{1\} \to \Theta$ are regarded as generalized flag spaces for points of ![]() $\mathscr {Y}$.
$\mathscr {Y}$.
Example 1.2.3 (BB strata)
As a special case of the previous example, consider a quasi-separated algebraic space ![]() $X$ locally of finite presentation over a scheme
$X$ locally of finite presentation over a scheme ![]() $S$, and let
$S$, and let ![]() $(\mathbf {G}_m)_S$ act on
$(\mathbf {G}_m)_S$ act on ![]() $X$. Then we have a cartesian square
$X$. Then we have a cartesian square

where ![]() $s$ classifies the projection
$s$ classifies the projection ![]() $(\mathbf {A}^{1}/\mathbf {G}_m)_S \to (B\mathbf {G}_m)_S$. So the fact that the mapping stacks on the right-hand side are algebraic implies that the functor
$(\mathbf {A}^{1}/\mathbf {G}_m)_S \to (B\mathbf {G}_m)_S$. So the fact that the mapping stacks on the right-hand side are algebraic implies that the functor ![]() $\operatorname {Map}_S(\mathbf {A}^{1}_S,X)^{\mathbf {G}_m}$ parameterizing families of equivariant maps from
$\operatorname {Map}_S(\mathbf {A}^{1}_S,X)^{\mathbf {G}_m}$ parameterizing families of equivariant maps from ![]() $\mathbf {A}^{1}$ to
$\mathbf {A}^{1}$ to ![]() $X$ is algebraic. This generalizes the classical theorem of Białynicki-Birula, and more recent work by Drinfeld [Reference DrinfeldDri13].
$X$ is algebraic. This generalizes the classical theorem of Białynicki-Birula, and more recent work by Drinfeld [Reference DrinfeldDri13].
Example 1.2.4 If ![]() $S$ is a scheme and
$S$ is a scheme and ![]() $G$ and
$G$ and ![]() $H$ are smooth affine
$H$ are smooth affine ![]() $S$-group-schemes, the fiber of the map
$S$-group-schemes, the fiber of the map ![]() $\underline {\operatorname {Map}}_S(BG, BH) \to \underline {\operatorname {Map}}_S(\ast,BH) \simeq BH$ over the tautological
$\underline {\operatorname {Map}}_S(BG, BH) \to \underline {\operatorname {Map}}_S(\ast,BH) \simeq BH$ over the tautological ![]() $S$-point of
$S$-point of ![]() $BH$ is the functor
$BH$ is the functor ![]() $\operatorname {Hom}_{gp/S}(G, H)$ parameterizing families of group homomorphisms. If
$\operatorname {Hom}_{gp/S}(G, H)$ parameterizing families of group homomorphisms. If ![]() $G$ is a reductive group scheme, then
$G$ is a reductive group scheme, then ![]() $\underline {\operatorname {Map}}_S(BG, BH)$ is algebraic with affine diagonal by Proposition 4.3.4 and Theorem 5.1.1 (working étale locally over
$\underline {\operatorname {Map}}_S(BG, BH)$ is algebraic with affine diagonal by Proposition 4.3.4 and Theorem 5.1.1 (working étale locally over ![]() $S$ and using relative noetherian approximation), and hence
$S$ and using relative noetherian approximation), and hence ![]() $\operatorname {Hom}_{gp/S}(G,H)$ is representable by algebraic spaces with affine diagonal. This recovers a slightly weaker form of the deep result in [Reference Demazure and GrothendieckSGA3, Exp. XXIV, Corollary 7.2.3] that
$\operatorname {Hom}_{gp/S}(G,H)$ is representable by algebraic spaces with affine diagonal. This recovers a slightly weaker form of the deep result in [Reference Demazure and GrothendieckSGA3, Exp. XXIV, Corollary 7.2.3] that ![]() $\operatorname {Hom}_{gp/S}(G,H)$ is a separated scheme whenever
$\operatorname {Hom}_{gp/S}(G,H)$ is a separated scheme whenever ![]() $H$ is a smooth quasi-projective
$H$ is a smooth quasi-projective ![]() $S$-group-scheme.
$S$-group-scheme.
Example 1.2.5 To illustrate why formal properness is the correct hypothesis in Theorem 5.1.1, suppose ![]() $S=\operatorname {Spec}(k)$ is a field of characteristic
$S=\operatorname {Spec}(k)$ is a field of characteristic ![]() $0$. Then
$0$. Then ![]() $B\mathbf {G}_a$ satisfies the ‘coherent pushforward’ property (CP), but
$B\mathbf {G}_a$ satisfies the ‘coherent pushforward’ property (CP), but ![]() $\operatorname {Hom}_{gp/S}(\mathbf {G}_a, \mathbf {G}_m)$, and thus
$\operatorname {Hom}_{gp/S}(\mathbf {G}_a, \mathbf {G}_m)$, and thus ![]() $\underline {\operatorname {Map}}_k(B\mathbf {G}_a,B\mathbf {G}_m)$, is not algebraic. If it were, then every compatible family of
$\underline {\operatorname {Map}}_k(B\mathbf {G}_a,B\mathbf {G}_m)$, is not algebraic. If it were, then every compatible family of ![]() $k[x]/x^{n}$-points would necessarily come from a
$k[x]/x^{n}$-points would necessarily come from a ![]() $k[\![x]\!]$-point, and the counterexample of Example 1.0.1 provides a counterexample here as well. Specifically, letting
$k[\![x]\!]$-point, and the counterexample of Example 1.0.1 provides a counterexample here as well. Specifically, letting ![]() $t$ denote the coordinate on
$t$ denote the coordinate on ![]() $\mathbf {G}_a$, the compatible family of group homomorphisms
$\mathbf {G}_a$, the compatible family of group homomorphisms ![]() $e^{tx} \colon (\mathbf {G}_a)_{k[x]/x^{n}} \to (\mathbf {G}_m)_{k[x]/x^{n}}$ does not extend to a morphism of group schemes
$e^{tx} \colon (\mathbf {G}_a)_{k[x]/x^{n}} \to (\mathbf {G}_m)_{k[x]/x^{n}}$ does not extend to a morphism of group schemes ![]() $(\mathbf {G}_a)_{k[\![x]\!]} \to (\mathbf {G}_m)_{k[\![x]\!]}$.
$(\mathbf {G}_a)_{k[\![x]\!]} \to (\mathbf {G}_m)_{k[\![x]\!]}$.
As another application of the notion of formal properness, we generalize the well-known fact that the stack of coherent sheaves on a proper scheme is algebraic.
Theorem (Theorem 5.2.2)
Let ![]() $R$ be a simplicial commutative
$R$ be a simplicial commutative ![]() $G$-ring, and let
$G$-ring, and let ![]() $\mathscr {X}$ be an algebraic derived stack which is flat and formally proper over
$\mathscr {X}$ be an algebraic derived stack which is flat and formally proper over ![]() $\operatorname {Spec}(R)$. Then the stack
$\operatorname {Spec}(R)$. Then the stack ![]() $\underline {\mathop {{\rm Coh}^{}}\nolimits }_{\mathscr {X}/R}$ parameterizing flat families of coherent sheaves (see Definition 5.2.1) is an algebraic derived stack locally almost finitely presented and with affine diagonal over
$\underline {\mathop {{\rm Coh}^{}}\nolimits }_{\mathscr {X}/R}$ parameterizing flat families of coherent sheaves (see Definition 5.2.1) is an algebraic derived stack locally almost finitely presented and with affine diagonal over ![]() $\operatorname {Spec}(R)$.
$\operatorname {Spec}(R)$.
1.2.1 Comparison with previous results
Artin's criteria have been used in several papers to establish the algebraicity of the mapping stack ![]() $\underline {\operatorname {Map}}_S(\mathscr {X},\mathscr {Y})$, where
$\underline {\operatorname {Map}}_S(\mathscr {X},\mathscr {Y})$, where ![]() $S$ is an algebraic space and
$S$ is an algebraic space and ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $\mathscr {Y}$ are algebraic stacks, but always under the hypothesis that
$\mathscr {Y}$ are algebraic stacks, but always under the hypothesis that ![]() $\mathscr {X} \to S$ is proper – see [Reference OlssonOls06, Theorem 1.1], [Reference LieblichLie06, § 2.3], and [Reference Hall and RydhHR19, Theorem 1.2] for the strongest result in this direction.Footnote 3 All of these approaches require a version of the Grothendieck existence theorem of proper stacks – see [Reference OlssonOls06, Theorem A.1] for coherent sheaves and [Reference LimLim19] for the case of pseudo-coherent complexes.
$\mathscr {X} \to S$ is proper – see [Reference OlssonOls06, Theorem 1.1], [Reference LieblichLie06, § 2.3], and [Reference Hall and RydhHR19, Theorem 1.2] for the strongest result in this direction.Footnote 3 All of these approaches require a version of the Grothendieck existence theorem of proper stacks – see [Reference OlssonOls06, Theorem A.1] for coherent sheaves and [Reference LimLim19] for the case of pseudo-coherent complexes.
Our approach to Artin's criteria, via the Tannakian formalism, is highly indebted to the algebraicity result [Reference LurieLur4, Theorem 3.2.1] in the context of derived (and spectral) algebraic geometry, which implies algebraicity under the hypothesis that ![]() $\mathscr {X} \to S$ is a flat and proper spectral algebraic space, and
$\mathscr {X} \to S$ is a flat and proper spectral algebraic space, and ![]() $\mathscr {Y}$ is a quasi-compact spectral Deligne–Mumford stack with affine diagonal. Our main conceptual contribution is relaxing the hypothesis that the map
$\mathscr {Y}$ is a quasi-compact spectral Deligne–Mumford stack with affine diagonal. Our main conceptual contribution is relaxing the hypothesis that the map ![]() $\mathscr {X} \to S$ is proper.
$\mathscr {X} \to S$ is proper.
In [Reference Alper, Hall and RydhAHR20] algebraicity is established when ![]() $\mathscr {X} \to S$ is a flat good moduli space morphism of classical stacks. The main contribution of [Reference Alper, Hall and RydhAHR20] is showing that a good moduli space morphism is, étale locally over
$\mathscr {X} \to S$ is a flat good moduli space morphism of classical stacks. The main contribution of [Reference Alper, Hall and RydhAHR20] is showing that a good moduli space morphism is, étale locally over ![]() $S$, cohomologically projective. From this point, one could use Theorem 5.1.1 to establish algebraicity when
$S$, cohomologically projective. From this point, one could use Theorem 5.1.1 to establish algebraicity when ![]() $\mathscr {Y}$ has quasi-affine diagonal, but [Reference Alper, Hall and RydhAHR20] makes use of a stronger version of Tannaka duality in the classical context [Reference Hall and RydhHR19] which allows one to only assume that
$\mathscr {Y}$ has quasi-affine diagonal, but [Reference Alper, Hall and RydhAHR20] makes use of a stronger version of Tannaka duality in the classical context [Reference Hall and RydhHR19] which allows one to only assume that ![]() $\mathscr {Y}$ has affine stabilizer groups (see Remark 5.1.3). The paper [Reference Alper, Hall and RydhAHR20] was developed independently of our work, and was released around the same time as the original version of this paper.
$\mathscr {Y}$ has affine stabilizer groups (see Remark 5.1.3). The paper [Reference Alper, Hall and RydhAHR20] was developed independently of our work, and was released around the same time as the original version of this paper.
1.3 Context, conventions, and authors’ note
Unless we explicitly state otherwise, all of our categories will be ![]() $\infty$-categories. The model for
$\infty$-categories. The model for ![]() $\infty$-categories we have in mind is that of quasi-categories [Reference LurieLur09], and our model for the
$\infty$-categories we have in mind is that of quasi-categories [Reference LurieLur09], and our model for the ![]() $\infty$-category of
$\infty$-category of ![]() $\infty$-groupoids or ‘spaces’ will be Kan simplicial sets, which we denote by
$\infty$-groupoids or ‘spaces’ will be Kan simplicial sets, which we denote by ![]() $\mathcal {S}$. The reader may freely substitute their favorite models for each.
$\mathcal {S}$. The reader may freely substitute their favorite models for each.
1.3.1 Context
We will mostly work in the context of derived algebraic geometry, that is, algebraic geometry over the ![]() $\infty$-site of simplicial commutative rings, which we denote by
$\infty$-site of simplicial commutative rings, which we denote by ![]() $\mathrm {SCR}$. Many of our results hold in the context of spectral algebraic geometry, that is, algebraic geometry over the
$\mathrm {SCR}$. Many of our results hold in the context of spectral algebraic geometry, that is, algebraic geometry over the ![]() $\infty$-site of connective
$\infty$-site of connective ![]() $E_\infty$-algebras
$E_\infty$-algebras ![]() $\mathrm {CAlg}^{\mathrm {cn}}$. For the most part, we indicate the intended context in the statements of our propositions, and indicate any modifications of the proof required in the different contexts. However, we only establish the algebraicity of mapping stacks, Theorem 5.1.1 in the derived context, because at the time of this writing the spectral version of Artin's criteria for stacks does not yet appear in [Reference LurieLur5].
$\mathrm {CAlg}^{\mathrm {cn}}$. For the most part, we indicate the intended context in the statements of our propositions, and indicate any modifications of the proof required in the different contexts. However, we only establish the algebraicity of mapping stacks, Theorem 5.1.1 in the derived context, because at the time of this writing the spectral version of Artin's criteria for stacks does not yet appear in [Reference LurieLur5].
1.3.2 Notation
We briefly summarize some of the terminology for the objects we use throughout the paper:

We also have the following notions for a morphism ![]() $\mathscr {X} \to \mathscr {Y}$ of derived stacks:
$\mathscr {X} \to \mathscr {Y}$ of derived stacks:

For any prestack ![]() $\mathscr {X}$, we let
$\mathscr {X}$, we let ![]() $\operatorname {QC}(\mathscr {X})$ denote the stable
$\operatorname {QC}(\mathscr {X})$ denote the stable ![]() $\infty$-category of quasi-coherent sheaves on
$\infty$-category of quasi-coherent sheaves on ![]() $\mathscr {X}$, which is the Kan extension of the functor
$\mathscr {X}$, which is the Kan extension of the functor ![]() $\operatorname {QC} : \mathrm {SCR} \to \widehat {\!\!\mathop {\rm ~Cat}\nolimits }_{\infty }$ which takes a simplicial commutative ring to its category of (differential graded (dg)) modules. The same construction allows one to define the category of almost perfect complexes
$\operatorname {QC} : \mathrm {SCR} \to \widehat {\!\!\mathop {\rm ~Cat}\nolimits }_{\infty }$ which takes a simplicial commutative ring to its category of (differential graded (dg)) modules. The same construction allows one to define the category of almost perfect complexes ![]() $\operatorname {APerf}(\mathscr {X})$, perfect complexes
$\operatorname {APerf}(\mathscr {X})$, perfect complexes ![]() $\operatorname {Perf}(\mathscr {X})$,
$\operatorname {Perf}(\mathscr {X})$, ![]() $n$-finitely presented complexes
$n$-finitely presented complexes ![]() ${\rm Coh}^{n} (\mathscr {X})$, etc. We recall these constructions and their basic properties in Appendix A.
${\rm Coh}^{n} (\mathscr {X})$, etc. We recall these constructions and their basic properties in Appendix A.
In addition to working in a derived context, we depart from the usual algebro-geometric literature in some potentially confusing notational conventions.
(i) We think of our
 $t$-structures as homologically indexed, and write
$t$-structures as homologically indexed, and write  $H_i$ for
$H_i$ for  $H^{-i}$ and, for example,
$H^{-i}$ and, for example,  $\tau _{\leqslant i}$ for
$\tau _{\leqslant i}$ for  $\tau ^{\geqslant -i}$ and
$\tau ^{\geqslant -i}$ and  $\mathcal {C}_{\leqslant i}$ for
$\mathcal {C}_{\leqslant i}$ for  $\mathcal {C}^{\geqslant -i}$. In particular, ‘bounded above’ will mean homologically bounded above (i.e. lying in
$\mathcal {C}^{\geqslant -i}$. In particular, ‘bounded above’ will mean homologically bounded above (i.e. lying in  $\mathcal {C}_{\leqslant i}$ for some
$\mathcal {C}_{\leqslant i}$ for some  $i$).
$i$).(ii) We implicitly work with
 $\infty$-categorical enhancements of various triangulated categories of sheaves.
$\infty$-categorical enhancements of various triangulated categories of sheaves.(iii) The symbols
 $f_*$,
$f_*$,  $f^{*}$, etc. will, unless otherwise stated, denote the functors of
$f^{*}$, etc. will, unless otherwise stated, denote the functors of  $\infty$-categories. We do not include extra decorations to indicate that they are ‘derived’, and will instead sometimes write, for example,
$\infty$-categories. We do not include extra decorations to indicate that they are ‘derived’, and will instead sometimes write, for example,  $H_0 \circ f_*$ for the functor on abelian categories. (The one exception: we will write
$H_0 \circ f_*$ for the functor on abelian categories. (The one exception: we will write  $R\Gamma$ for global sections, as a reminder that this is global sections of sheaves of spectra and not spaces.)
$R\Gamma$ for global sections, as a reminder that this is global sections of sheaves of spectra and not spaces.)(iv) We use
 $\operatorname {Map}$ for a mapping simplicial set in an
$\operatorname {Map}$ for a mapping simplicial set in an  $\infty$-category
$\infty$-category  $\mathcal {C}$. If
$\mathcal {C}$. If  $\mathcal {C}$ is stable, we use
$\mathcal {C}$ is stable, we use  $\operatorname {RHom}$ to denote any stable enrichment (e.g. in spectra, in chain complexes, or in complexes of sheaves). Finally, we use
$\operatorname {RHom}$ to denote any stable enrichment (e.g. in spectra, in chain complexes, or in complexes of sheaves). Finally, we use  $\operatorname {Hom}$ to denote the maps in the homotopy category of
$\operatorname {Hom}$ to denote the maps in the homotopy category of  $\mathcal {C}$.
$\mathcal {C}$.
1.3.3 Comparison with the classical context
There are natural functors of ![]() $\infty$-categories
$\infty$-categories ![]() $\mathrm {Ring} \to \mathrm {SCR} \to \mathrm {CAlg}^{\mathrm {cn}}$, which are neither fully faithful nor essentially surjective. Nevertheless, one can perform a left Kan extension of stacks along these functors, and this preserves algebraic stacks and their formal completions. Also, the formation of
$\mathrm {Ring} \to \mathrm {SCR} \to \mathrm {CAlg}^{\mathrm {cn}}$, which are neither fully faithful nor essentially surjective. Nevertheless, one can perform a left Kan extension of stacks along these functors, and this preserves algebraic stacks and their formal completions. Also, the formation of ![]() $\infty$-categories
$\infty$-categories ![]() $\operatorname {QC}(-)$,
$\operatorname {QC}(-)$, ![]() $\operatorname {APerf}(-),\operatorname {Perf}(-),$ and
$\operatorname {APerf}(-),\operatorname {Perf}(-),$ and ![]() $\operatorname {QC}(-)^{\mathrm {cn}}$ commutes with left Kan extension along these functors (see Appendix A). It follows that many statements which are proved for
$\operatorname {QC}(-)^{\mathrm {cn}}$ commutes with left Kan extension along these functors (see Appendix A). It follows that many statements which are proved for ![]() $\operatorname {QC}(-)$ for spectral algebraic stacks automatically imply the corresponding statement for
$\operatorname {QC}(-)$ for spectral algebraic stacks automatically imply the corresponding statement for ![]() $\operatorname {QC}(-)$ applied to derived or classical stacks. For instance, one can formulate Definition 1.1.1, of a complete closed immersion, in all three contexts, but a classical or derived stack is complete along a closed subset if and only if it is complete when regarded as a spectral stack via left Kan extension.
$\operatorname {QC}(-)$ applied to derived or classical stacks. For instance, one can formulate Definition 1.1.1, of a complete closed immersion, in all three contexts, but a classical or derived stack is complete along a closed subset if and only if it is complete when regarded as a spectral stack via left Kan extension.
1.3.4 Further questions
We show that formally proper morphisms have several of the common and useful properties of proper maps, but we would like to highlight some natural questions to inspire future research.
Question 1.3.1 Is the property of being formally proper local for the étale topology on the target? Also, in Definition 1.1.3, does it suffice to only consider ![]() $\mathscr {Y} = \operatorname {Spec}(R)$ for complete local noetherian rings
$\mathscr {Y} = \operatorname {Spec}(R)$ for complete local noetherian rings ![]() $R$ over
$R$ over ![]() $\mathscr {S}$?
$\mathscr {S}$?
Question 1.3.2 If ![]() $\pi : \mathscr {X} \to \operatorname {Spec}(A)$ is formally proper, is there a model for
$\pi : \mathscr {X} \to \operatorname {Spec}(A)$ is formally proper, is there a model for ![]() $\mathscr {X}$ over a finitely generated subring
$\mathscr {X}$ over a finitely generated subring ![]() $A' \subset A$ which is also formally proper?
$A' \subset A$ which is also formally proper?
Question 1.3.3 If ![]() $\mathscr {X}$ is smooth and formally proper over a field of characteristic
$\mathscr {X}$ is smooth and formally proper over a field of characteristic ![]() $0$, does the Hodge–de Rham spectral sequence for
$0$, does the Hodge–de Rham spectral sequence for ![]() $\mathscr {X}$ degenerate?
$\mathscr {X}$ degenerate?
2. Background and first properties of complete closed immersions
2.1 Recollections on formal completions
Here we review some of the key results we will use from [Reference LurieLur3, § 4,5], noting how they can be slightly strengthened in the context of simplicial commutative rings.
Definition 2.1.1 [Reference LurieLur3, 5.1.1]
Suppose that ![]() $\mathscr {X}$ is a prestack. Let
$\mathscr {X}$ is a prestack. Let ![]() $|\mathscr {X}|$ denote the underlying Zariski topological space of points of
$|\mathscr {X}|$ denote the underlying Zariski topological space of points of ![]() $\mathscr {X}$. We say that a closed subset
$\mathscr {X}$. We say that a closed subset ![]() $Z \subset |\mathscr {X}|$ is cocompact if the inclusion of the complement of
$Z \subset |\mathscr {X}|$ is cocompact if the inclusion of the complement of ![]() $Z$ is a quasi-compact open immersion. Given a cocompact
$Z$ is a quasi-compact open immersion. Given a cocompact ![]() $Z \subset |\mathscr {X}|$, define the formal completion of
$Z \subset |\mathscr {X}|$, define the formal completion of ![]() $\mathscr {X}$ along
$\mathscr {X}$ along ![]() $Z$ to be the prestack
$Z$ to be the prestack
When ![]() $Z$ is clear from context, we will sometimes simplify the notation to
$Z$ is clear from context, we will sometimes simplify the notation to ![]() $\widehat {\mathscr {X}}$.
$\widehat {\mathscr {X}}$.
Note that as ![]() $|\!\operatorname {Spec}(\pi _0(R))| \simeq |\!\operatorname {Spec}(R)|$,
$|\!\operatorname {Spec}(\pi _0(R))| \simeq |\!\operatorname {Spec}(R)|$, ![]() $|\mathscr {X}|$ only depends on the underlying classical stack of
$|\mathscr {X}|$ only depends on the underlying classical stack of ![]() $\mathscr {X}$. If
$\mathscr {X}$. If ![]() $\mathscr {X}$ is an algebraic derived stack and
$\mathscr {X}$ is an algebraic derived stack and ![]() $\mathscr {I} \subset H_0(\mathcal {O}_\mathscr {X})$ is a locally finitely generated ideal sheaf, then
$\mathscr {I} \subset H_0(\mathcal {O}_\mathscr {X})$ is a locally finitely generated ideal sheaf, then ![]() $\mathscr {I}$ defines a cocompact closed substack
$\mathscr {I}$ defines a cocompact closed substack ![]() $\mathscr {Z}(\mathscr {I})$ of the underlying classical stack of
$\mathscr {Z}(\mathscr {I})$ of the underlying classical stack of ![]() $\mathscr {X}$ and hence a cocompact closed subset
$\mathscr {X}$ and hence a cocompact closed subset ![]() $Z \subset |\mathscr {X}|$. By abuse of terminology we will call
$Z \subset |\mathscr {X}|$. By abuse of terminology we will call ![]() $\widehat {\mathscr {X}}_Z$ the formal completion of
$\widehat {\mathscr {X}}_Z$ the formal completion of ![]() $\mathscr {X}$ along
$\mathscr {X}$ along ![]() $\mathscr {I}$. When
$\mathscr {I}$. When ![]() $\mathscr {X}$ (and hence
$\mathscr {X}$ (and hence ![]() $\mathscr {Z}(\mathscr {I})$) is affine, we have an explicit description of
$\mathscr {Z}(\mathscr {I})$) is affine, we have an explicit description of ![]() $\widehat {\mathscr {X}}_Z$.
$\widehat {\mathscr {X}}_Z$.
Proposition 2.1.2 Suppose that ![]() $R \in \mathrm {SCR}$ and
$R \in \mathrm {SCR}$ and ![]() $I \subset \pi _0(R)$ is a finitely generated ideal. Let
$I \subset \pi _0(R)$ is a finitely generated ideal. Let ![]() $\mathscr {X} = \operatorname {Spec}(R)$ and
$\mathscr {X} = \operatorname {Spec}(R)$ and ![]() $\widehat {\mathscr {X}} = \operatorname {Spf}(R)$ be its formal completion along
$\widehat {\mathscr {X}} = \operatorname {Spf}(R)$ be its formal completion along ![]() $I$. Then there exists a tower
$I$. Then there exists a tower
in ![]() $\mathrm {SCR}_R$ such that there is an equivalence of prestacks over
$\mathrm {SCR}_R$ such that there is an equivalence of prestacks over ![]() $\mathscr {X}$,
$\mathscr {X}$,
Furthermore, we may suppose that ![]() $\pi _0(R_n) \to \pi _0(R_{n-1})$ is surjective for each
$\pi _0(R_n) \to \pi _0(R_{n-1})$ is surjective for each ![]() $i$, and that each
$i$, and that each ![]() $R_n$ is perfect as an
$R_n$ is perfect as an ![]() $R$-module with Tor amplitude uniformly bounded by the number of generators of
$R$-module with Tor amplitude uniformly bounded by the number of generators of ![]() $I$.
$I$.
Remark 2.1.3 [Reference LurieLur3, Lemma 5.1.5] gives an analogous statement for ![]() $R \in \mathrm {CAlg}$. The only difference in the
$R \in \mathrm {CAlg}$. The only difference in the ![]() $E_\infty$ statement is that the
$E_\infty$ statement is that the ![]() $R_n$ are almost perfect as
$R_n$ are almost perfect as ![]() $R$-modules. This is, essentially, the one statement in this paper that depends strongly on the fact that we are working with simplicial commutative rings rather than
$R$-modules. This is, essentially, the one statement in this paper that depends strongly on the fact that we are working with simplicial commutative rings rather than ![]() $E_\infty$-rings.
$E_\infty$-rings.
Proof. The proof of [Reference LurieLur3, Lemma 5.1.5] goes over essentially unchanged in simplicial commutative rings, but now the rings ![]() $R_n$ can be assumed to be perfect rather than merely almost perfect. This follows from the construction of the algebras denote
$R_n$ can be assumed to be perfect rather than merely almost perfect. This follows from the construction of the algebras denote ![]() $A(x)_n$ in [Reference LurieLur3], and the fact that in the universal example
$A(x)_n$ in [Reference LurieLur3], and the fact that in the universal example ![]() $\mathbb {Z}$ is a perfect module over
$\mathbb {Z}$ is a perfect module over ![]() $\mathbb {Z}[x]$ of Tor dimension explicitly bounded by
$\mathbb {Z}[x]$ of Tor dimension explicitly bounded by ![]() $1$, thanks to the Koszul resolution.
$1$, thanks to the Koszul resolution.
Suppose that ![]() $S = \operatorname {Spec}(R)$,
$S = \operatorname {Spec}(R)$, ![]() $I \subset \pi _0(R)$ a finitely generated ideal, and
$I \subset \pi _0(R)$ a finitely generated ideal, and ![]() $\widehat {S}$ the associated formal completion. Let
$\widehat {S}$ the associated formal completion. Let ![]() $\pi \colon \mathscr {X} \to S$ be an
$\pi \colon \mathscr {X} \to S$ be an ![]() $S$-stack,
$S$-stack, ![]() $Z \subset |\mathscr {X}|$ the preimage of
$Z \subset |\mathscr {X}|$ the preimage of ![]() $Z(I) \subset |S|$, and
$Z(I) \subset |S|$, and ![]() $\widehat {\mathscr {X}}$ the associated formal completion. Then the natural map
$\widehat {\mathscr {X}}$ the associated formal completion. Then the natural map
is an equivalence (just use the functor-of-points descriptions on both sides). Furthermore, if ![]() $\{R_n\}$ is a tower as in Proposition 2.1.2, then there is an equivalence
$\{R_n\}$ is a tower as in Proposition 2.1.2, then there is an equivalence
since fiber products preserve filtered colimits in presheaves. We will generally write ![]() $i_n \colon \mathscr {X}_n = \mathscr {X} \times _S \operatorname {Spec}(R_n) \to \mathscr {X}$ for the base-changed closed immersions.
$i_n \colon \mathscr {X}_n = \mathscr {X} \times _S \operatorname {Spec}(R_n) \to \mathscr {X}$ for the base-changed closed immersions.
A natural question is how this compares to the classical notion of formal completion. To this end, we have the following proposition.
Proposition 2.1.4 Suppose that ![]() $R$ is a noetherian classical commutative ring and that
$R$ is a noetherian classical commutative ring and that ![]() $I \subset \pi _0(R)$. Let
$I \subset \pi _0(R)$. Let ![]() $\operatorname {Spf}(R)$ denote the formal completion of the derived stack
$\operatorname {Spf}(R)$ denote the formal completion of the derived stack ![]() $\operatorname {Spec}(R)$ along
$\operatorname {Spec}(R)$ along ![]() $I$, and let
$I$, and let ![]() $\operatorname {Spf}^{\mathrm {cl}} R$ denote the left Kan extension of the (classical) prestack
$\operatorname {Spf}^{\mathrm {cl}} R$ denote the left Kan extension of the (classical) prestack ![]() $\mathop {\varinjlim }\limits _n \operatorname {Spec}(R/I^{n})$. Then the natural morphism
$\mathop {\varinjlim }\limits _n \operatorname {Spec}(R/I^{n})$. Then the natural morphism
is an equivalence.
Proof. Note first that the natural maps ![]() $\operatorname {Spec}(R/I^{n}) \to \operatorname {Spec}(R)$ factor uniquely through
$\operatorname {Spec}(R/I^{n}) \to \operatorname {Spec}(R)$ factor uniquely through ![]() $\operatorname {Spf}(R)$ – this determines the natural morphism of the proposition. Let
$\operatorname {Spf}(R)$ – this determines the natural morphism of the proposition. Let ![]() $R_n$ be the Koszul-type algebra killing the
$R_n$ be the Koszul-type algebra killing the ![]() $n$th powers of a finite set of generators for the ideal
$n$th powers of a finite set of generators for the ideal ![]() $I \subset R$ (in dg language this would be
$I \subset R$ (in dg language this would be ![]() $R[B_1,\ldots,B_r; dB_i = f_i^{n}]$) – it satisfies the conditions of Proposition 2.1.2 by the proof of [Reference LurieLur3, Lemma 5.1.5]. Note that
$R[B_1,\ldots,B_r; dB_i = f_i^{n}]$) – it satisfies the conditions of Proposition 2.1.2 by the proof of [Reference LurieLur3, Lemma 5.1.5]. Note that ![]() $\operatorname {Spf}^{\mathrm {cl}} R \simeq \mathop {\varinjlim }\limits \operatorname {Spec}(\pi _0(R_n))$ since
$\operatorname {Spf}^{\mathrm {cl}} R \simeq \mathop {\varinjlim }\limits \operatorname {Spec}(\pi _0(R_n))$ since ![]() $I^{(n-1)r+1} \subset (f_1^{n}, \ldots,f_r^{n}) \subset I^{n}$. We must thus show that the natural map
$I^{(n-1)r+1} \subset (f_1^{n}, \ldots,f_r^{n}) \subset I^{n}$. We must thus show that the natural map
is an equivalence, that is, that the map of pro-objects in (almost perfect) commutative ![]() $R$-algebras
$R$-algebras ![]() $\{R_n\} \to \{ \pi _0(R_n) \}$ is a pro-equivalence. There is almost an argument for this in [Reference LurieLur3, Lemma 5.2.17], which implies that
$\{R_n\} \to \{ \pi _0(R_n) \}$ is a pro-equivalence. There is almost an argument for this in [Reference LurieLur3, Lemma 5.2.17], which implies that
is an equivalence of pro-objects in (almost perfect) ![]() $R$-modules for all
$R$-modules for all ![]() $k$. By the bound on the Tor amplitude in Proposition 2.1.2, taking
$k$. By the bound on the Tor amplitude in Proposition 2.1.2, taking ![]() $k>r+1$ establishes the pro-equivalence at the level of
$k>r+1$ establishes the pro-equivalence at the level of ![]() $R$-modules. Furthermore, the module-level statement does in fact imply the algebra statement (i.e. potential issues with pro-algebras versus algebras in pro-objects do not get in the way) because we may restrict to
$R$-modules. Furthermore, the module-level statement does in fact imply the algebra statement (i.e. potential issues with pro-algebras versus algebras in pro-objects do not get in the way) because we may restrict to ![]() $(r+1)$-truncated algebras (cf. the proof of [Reference LurieLur3, Lemma 6.3.3]).
$(r+1)$-truncated algebras (cf. the proof of [Reference LurieLur3, Lemma 6.3.3]).
Since fppf morphisms are topological quotient morphisms, we can use this to deduce the following corollary.
Corollary 2.1.5 Suppose that ![]() $\mathscr {X}$ is a noetherian classical stack, and that
$\mathscr {X}$ is a noetherian classical stack, and that ![]() $\mathscr {I} \subset \mathcal {O}_\mathscr {X}$ is an ideal sheaf. Then the formal completion of the Kan extension of
$\mathscr {I} \subset \mathcal {O}_\mathscr {X}$ is an ideal sheaf. Then the formal completion of the Kan extension of ![]() $\mathscr {X}$ (from classical rings to derived rings) along
$\mathscr {X}$ (from classical rings to derived rings) along ![]() $\mathscr {I}$ is the Kan extension of the classical formal completion of
$\mathscr {I}$ is the Kan extension of the classical formal completion of ![]() $\mathscr {X}$ along
$\mathscr {X}$ along ![]() $\mathscr {I}$.
$\mathscr {I}$.
Remark 2.1.6 The rings ![]() $R_n$ appearing in Proposition 2.1.2 are not unique, in contrast to the
$R_n$ appearing in Proposition 2.1.2 are not unique, in contrast to the ![]() $R/I^{n}$ used to form classical formal completions – in particular, they need not globalize. This is related to the fact that our notion of formal completion
$R/I^{n}$ used to form classical formal completions – in particular, they need not globalize. This is related to the fact that our notion of formal completion ![]() $\widehat {\mathscr {X}}_Z$ depends only on the underlying subset
$\widehat {\mathscr {X}}_Z$ depends only on the underlying subset ![]() $Z$ and not on the choice of structure sheaf etc.
$Z$ and not on the choice of structure sheaf etc.
There is a notion of formal completion along a closed immersion ![]() $\mathscr {Z} \to \mathscr {X}$ in derived algebraic geometry more analogous to the usual
$\mathscr {Z} \to \mathscr {X}$ in derived algebraic geometry more analogous to the usual ![]() $\mathscr {I}$-adic completion, that is, it gives rise to a canonically defined pro-algebra
$\mathscr {I}$-adic completion, that is, it gives rise to a canonically defined pro-algebra ![]() $\widehat {\mathcal {O}_\mathscr {X}} = \text {``}\mathop {\varprojlim }\limits _n\text {''} \mathcal {O}_{\mathscr {X}_n}$ such that
$\widehat {\mathcal {O}_\mathscr {X}} = \text {``}\mathop {\varprojlim }\limits _n\text {''} \mathcal {O}_{\mathscr {X}_n}$ such that ![]() $H_0(\mathcal {O}_{\mathscr {X}_n}) = H_0(\mathcal {O}_\mathscr {X})/\mathscr {I}^{n}$ where
$H_0(\mathcal {O}_{\mathscr {X}_n}) = H_0(\mathcal {O}_\mathscr {X})/\mathscr {I}^{n}$ where ![]() $\mathscr {I} = \ker \{ H_0(\mathcal {O}_\mathscr {X}) \to H_0(\mathcal {O}_\mathscr {Z})\}$. This is constructed in characteristic
$\mathscr {I} = \ker \{ H_0(\mathcal {O}_\mathscr {X}) \to H_0(\mathcal {O}_\mathscr {Z})\}$. This is constructed in characteristic ![]() $0$ in [Reference Gaitsgory and RozenblyumGR17, Chap. 9.5]. The construction is somewhat involved, however, and we will not need it for what follows.
$0$ in [Reference Gaitsgory and RozenblyumGR17, Chap. 9.5]. The construction is somewhat involved, however, and we will not need it for what follows.
2.1.1 Almost perfect complexes and coherent sheaves
In this section we will use the ![]() $\infty$-category of almost perfect complexes
$\infty$-category of almost perfect complexes ![]() $\operatorname {APerf}(-)$, as well as the ordinary category
$\operatorname {APerf}(-)$, as well as the ordinary category ![]() ${\rm Coh} (-)$, for both a derived stack and its formal completion. We refer the reader to Appendix A for a reminder on how these categories are defined for arbitrary prestacks.
${\rm Coh} (-)$, for both a derived stack and its formal completion. We refer the reader to Appendix A for a reminder on how these categories are defined for arbitrary prestacks.
Let ![]() $R$ be a simplicial commutative ring, and let
$R$ be a simplicial commutative ring, and let ![]() $I \subset \pi _0(R)$ be a finitely generated ideal. We let
$I \subset \pi _0(R)$ be a finitely generated ideal. We let ![]() $E_\infty (R)$ denote the underlying
$E_\infty (R)$ denote the underlying ![]() $E_\infty$ algebra of
$E_\infty$ algebra of ![]() $R$, that is, the endomorphism algebra of
$R$, that is, the endomorphism algebra of ![]() $R$ in the symmetric monoidal
$R$ in the symmetric monoidal ![]() $\infty$-category
$\infty$-category ![]() $R {\rm {}\hbox{-}{\rm mod}}$, so that we have a canonical equivalence
$R {\rm {}\hbox{-}{\rm mod}}$, so that we have a canonical equivalence ![]() $R {\rm {}\hbox{-}{\rm mod}} \cong E_\infty (R) {\rm {}\hbox{-}{\rm mod}}$ and
$R {\rm {}\hbox{-}{\rm mod}} \cong E_\infty (R) {\rm {}\hbox{-}{\rm mod}}$ and ![]() $\pi _0(R) \cong \pi _0(E_\infty (R))$. We may therefore use the theory of completion of
$\pi _0(R) \cong \pi _0(E_\infty (R))$. We may therefore use the theory of completion of ![]() $R$-modules developed in the
$R$-modules developed in the ![]() $E_\infty$-context in [Reference LurieLur3, § 4].
$E_\infty$-context in [Reference LurieLur3, § 4].
Definition 2.1.7 We say that ![]() $R$ is
$R$ is ![]() $I$-complete if it is so as an object of
$I$-complete if it is so as an object of ![]() $R {\rm {}\hbox{-}{\rm mod}}$, and we say that a map
$R {\rm {}\hbox{-}{\rm mod}}$, and we say that a map ![]() $R \to \widehat {R}$ of simplicial commutative rings exhibits
$R \to \widehat {R}$ of simplicial commutative rings exhibits ![]() $\widehat {R}$ as an
$\widehat {R}$ as an ![]() $I$-completion of
$I$-completion of ![]() $R$ if this holds for the associated map of
$R$ if this holds for the associated map of ![]() $R$-modules.
$R$-modules.
It follows from [Reference LurieLur3, Corollary 4.2.12] that ![]() $R$ is
$R$ is ![]() $I$-complete if and only if it is
$I$-complete if and only if it is ![]() $(f)$-complete for any
$(f)$-complete for any ![]() $f \in I$, which is equivalent to it being
$f \in I$, which is equivalent to it being ![]() $(f_i)$-complete for some generating set
$(f_i)$-complete for some generating set ![]() $f_1,\ldots,f_n \in I$. By [Reference LurieLur3, Proposition 4.2.7], if we choose a map
$f_1,\ldots,f_n \in I$. By [Reference LurieLur3, Proposition 4.2.7], if we choose a map ![]() ${\mathbb {Z}}[x] \to R$ mapping
${\mathbb {Z}}[x] \to R$ mapping ![]() $x$ to
$x$ to ![]() $f \in \pi _0(R)$, then the canonical map
$f \in \pi _0(R)$, then the canonical map ![]() $R \to \varprojlim _k R \otimes _{{\mathbb {Z}}[x]} {\mathbb {Z}}[x]/(x^{k})$ is an
$R \to \varprojlim _k R \otimes _{{\mathbb {Z}}[x]} {\mathbb {Z}}[x]/(x^{k})$ is an ![]() $(f)$-completion. It follows that if we choose a map
$(f)$-completion. It follows that if we choose a map ![]() ${\mathbb {Z}}[x_1,\ldots,x_n] \to R$ mapping
${\mathbb {Z}}[x_1,\ldots,x_n] \to R$ mapping ![]() $x_i$ to generators of
$x_i$ to generators of ![]() $I$, then the canonical map
$I$, then the canonical map
is an ![]() $I$-completion. Furthermore, any map
$I$-completion. Furthermore, any map ![]() $R \to R'$ exhibiting
$R \to R'$ exhibiting ![]() $R'$ as an
$R'$ as an ![]() $I$-completion of
$I$-completion of ![]() $R$ becomes an isomorphism after applying the functor
$R$ becomes an isomorphism after applying the functor ![]() $\varprojlim _k (-) \otimes {\mathbb {Z}}[x_1,\ldots,x_n] / (x_1^{k},\ldots,x_n^{k})$, and one can use this to show that any
$\varprojlim _k (-) \otimes {\mathbb {Z}}[x_1,\ldots,x_n] / (x_1^{k},\ldots,x_n^{k})$, and one can use this to show that any ![]() $I$-completion of
$I$-completion of ![]() $R$ is canonically isomorphic to
$R$ is canonically isomorphic to ![]() $\widehat {R}$ defined in (1). Note also that
$\widehat {R}$ defined in (1). Note also that ![]() $E_\infty (R) \to E_\infty (\widehat {R})$ exhibits the latter as an
$E_\infty (R) \to E_\infty (\widehat {R})$ exhibits the latter as an ![]() $I$-completion of
$I$-completion of ![]() $E_\infty$-algebras, so we have
$E_\infty$-algebras, so we have ![]() $E_\infty (\widehat {R}) \cong E_\infty (R)^{\wedge }$.
$E_\infty (\widehat {R}) \cong E_\infty (R)^{\wedge }$.
Remark 2.1.8 For a noetherian commutative ring ![]() $R$, regarded as a discrete simplicial commutative ring, and a finitely generated ideal
$R$, regarded as a discrete simplicial commutative ring, and a finitely generated ideal ![]() $I \subset R$, the Koszul algebras
$I \subset R$, the Koszul algebras ![]() $R_k := R \otimes _{{\mathbb {Z}}[x_1,\ldots,x_n]} ({\mathbb {Z}}[x_1,\ldots,x_n]/(x_1^{k},\ldots,x_n^{k}))$ in (1) need not be discrete. Nevertheless the derived completion
$R_k := R \otimes _{{\mathbb {Z}}[x_1,\ldots,x_n]} ({\mathbb {Z}}[x_1,\ldots,x_n]/(x_1^{k},\ldots,x_n^{k}))$ in (1) need not be discrete. Nevertheless the derived completion ![]() $R^{\wedge } \cong \varprojlim _k R_k$ is discrete, because
$R^{\wedge } \cong \varprojlim _k R_k$ is discrete, because ![]() $R \to R^{\wedge }$ is flat [Reference LurieLur5, Corollary 7.3.6.9]. The analogous claim for formal completions is Proposition 2.1.4.
$R \to R^{\wedge }$ is flat [Reference LurieLur5, Corollary 7.3.6.9]. The analogous claim for formal completions is Proposition 2.1.4.
Remark 2.1.9 We may replace ![]() $(x_1^{k},\ldots,x_n^{k})$ with
$(x_1^{k},\ldots,x_n^{k})$ with ![]() $(x_1,\ldots,x_n)^{k}$ in (1), because this is an equivalent pro-system of ideals. Using this, one can show that
$(x_1,\ldots,x_n)^{k}$ in (1), because this is an equivalent pro-system of ideals. Using this, one can show that ![]() $\widehat {R}$ is equivalent to the following natural construction of a derived
$\widehat {R}$ is equivalent to the following natural construction of a derived ![]() $I$-adic completion: choose an equivalence of simplicial commutative rings
$I$-adic completion: choose an equivalence of simplicial commutative rings ![]() $R' \to R$, where
$R' \to R$, where ![]() $R' = {\mathbb {Z}}[X_\bullet ]$ is levelwise polynomial and there is a finite subset
$R' = {\mathbb {Z}}[X_\bullet ]$ is levelwise polynomial and there is a finite subset ![]() $S_0 \subset X_0$ that generates
$S_0 \subset X_0$ that generates ![]() $I \subset \pi _0(R)$. If
$I \subset \pi _0(R)$. If ![]() $I' \subset R'$ is the simplicial ideal generated by
$I' \subset R'$ is the simplicial ideal generated by ![]() $S_0$, then the canonical map
$S_0$, then the canonical map
exhibits the latter as an ![]() $I$-completion of
$I$-completion of ![]() $R'$, and thus the induced map
$R'$, and thus the induced map ![]() $\varprojlim _k R' / (I')^{k} \to \widehat {R}$ is an equivalence.
$\varprojlim _k R' / (I')^{k} \to \widehat {R}$ is an equivalence.
Lemma 2.1.10 (Derived Artin-Rees lemma)
Suppose ![]() $R$ is a noetherian simplicial commutative ring,
$R$ is a noetherian simplicial commutative ring, ![]() $I \subset \pi _0(R)$ is a finitely generated ideal, and
$I \subset \pi _0(R)$ is a finitely generated ideal, and ![]() $\widehat {R}$ the
$\widehat {R}$ the ![]() $I$-completion of
$I$-completion of ![]() $R$. Then the natural restriction functor
$R$. Then the natural restriction functor
is a ![]() $t$-exact equivalence of
$t$-exact equivalence of ![]() $\infty$-categories, and hence induces an equivalence of abelian categories
$\infty$-categories, and hence induces an equivalence of abelian categories ![]() ${\rm Coh} (\widehat {R}) \simeq {\rm Coh} (\operatorname {Spf}(R))$.
${\rm Coh} (\widehat {R}) \simeq {\rm Coh} (\operatorname {Spf}(R))$.
Proof. Use the fact that ![]() $E_\infty (\widehat {R}) \cong \widehat {E_\infty (R)}$, and apply [Reference LurieLur3, Theorem 5.3.2].
$E_\infty (\widehat {R}) \cong \widehat {E_\infty (R)}$, and apply [Reference LurieLur3, Theorem 5.3.2].
This globalizes as follows.
Proposition 2.1.11 Suppose ![]() $\mathscr {X}$ is a locally noetherian algebraic derived stack,
$\mathscr {X}$ is a locally noetherian algebraic derived stack, ![]() $Z \subset |\mathscr {X}|$ a cocompact closed subset, and
$Z \subset |\mathscr {X}|$ a cocompact closed subset, and ![]() $\widehat {\mathscr {X}}$ the formal completion of
$\widehat {\mathscr {X}}$ the formal completion of ![]() $\mathscr {X}$ along
$\mathscr {X}$ along ![]() $Z$. Furthermore, let
$Z$. Furthermore, let ![]() $f : \mathscr {X}' \to \mathscr {X}$ be a flat morphism from another locally noetherian algebraic derived stack and
$f : \mathscr {X}' \to \mathscr {X}$ be a flat morphism from another locally noetherian algebraic derived stack and ![]() $Z' := f^{-1}(Z)$. Then the following assertions hold.
$Z' := f^{-1}(Z)$. Then the following assertions hold.
(i) The (ordinary) category
 ${\rm Coh} (\widehat {\mathscr {X}})$ is abelian. The induced pullback functor
${\rm Coh} (\widehat {\mathscr {X}})$ is abelian. The induced pullback functor  ${\rm Coh} (\widehat {\mathscr {X}}_{Z}) \to {\rm Coh} (\widehat {\mathscr {X}'}_{Z'})$ is exact. The exactness of sequences in
${\rm Coh} (\widehat {\mathscr {X}}_{Z}) \to {\rm Coh} (\widehat {\mathscr {X}'}_{Z'})$ is exact. The exactness of sequences in  ${\rm Coh} (\widehat {\mathscr {X}})$ may be checked on a flat cover.
${\rm Coh} (\widehat {\mathscr {X}})$ may be checked on a flat cover.(ii) The
 $\infty$-category
$\infty$-category  $\operatorname {APerf}(\widehat {\mathscr {X}})$ admits a
$\operatorname {APerf}(\widehat {\mathscr {X}})$ admits a  $t$-structure. The induced pullback functor
$t$-structure. The induced pullback functor  $\operatorname {APerf}(\widehat {\mathscr {X}}_Z) \to \operatorname {APerf}(\widehat {\mathscr {X}'}_{Z'})$ is
$\operatorname {APerf}(\widehat {\mathscr {X}}_Z) \to \operatorname {APerf}(\widehat {\mathscr {X}'}_{Z'})$ is  $t$-exact. The property of being connective/coconnective in
$t$-exact. The property of being connective/coconnective in  $\operatorname {APerf}(\widehat {\mathscr {X}})$ may be checked on a flat cover of
$\operatorname {APerf}(\widehat {\mathscr {X}})$ may be checked on a flat cover of  $\mathscr {X}$. In the affine case, the
$\mathscr {X}$. In the affine case, the  $t$-structure is described in Lemma 2.1.10.
$t$-structure is described in Lemma 2.1.10.(iii) The heart of the
 $t$-structure in (ii) identifies with
$t$-structure in (ii) identifies with  ${\rm Coh} (\widehat {\mathscr {X}})$. More generally, the
${\rm Coh} (\widehat {\mathscr {X}})$. More generally, the  $\infty$-category of connective
$\infty$-category of connective  $n$-truncated objects
$n$-truncated objects  $\operatorname {APerf}(\widehat {\mathscr {X}})_{\leqslant n}^{\mathrm {cn}}$ naturally identifies with
$\operatorname {APerf}(\widehat {\mathscr {X}})_{\leqslant n}^{\mathrm {cn}}$ naturally identifies with  ${\rm Coh}^{n} (\widehat {\mathscr {X}})$.
${\rm Coh}^{n} (\widehat {\mathscr {X}})$.(iv) The
 $t$-structure on
$t$-structure on  $\operatorname {APerf}(\widehat {\mathscr {X}})$ is left
$\operatorname {APerf}(\widehat {\mathscr {X}})$ is left  $t$-complete, and (if
$t$-complete, and (if  $\mathscr {X}$ is quasi-compact) right
$\mathscr {X}$ is quasi-compact) right  $t$-bounded. There is a natural equivalence
$t$-bounded. There is a natural equivalence
 \[ \operatorname{APerf}(\widehat{\mathscr{X}})^{\mathrm{cn}} \stackrel\sim\longrightarrow \mathop{\varprojlim}\limits_n \operatorname{APerf}(\widehat{\mathscr{X}})^{\mathrm{cn}}_{\leqslant n} \simeq \mathop{\varprojlim}\limits_n \mathop{{\rm Coh}^{n}}\nolimits(\widehat{\mathscr{X}}) \]
\[ \operatorname{APerf}(\widehat{\mathscr{X}})^{\mathrm{cn}} \stackrel\sim\longrightarrow \mathop{\varprojlim}\limits_n \operatorname{APerf}(\widehat{\mathscr{X}})^{\mathrm{cn}}_{\leqslant n} \simeq \mathop{\varprojlim}\limits_n \mathop{{\rm Coh}^{n}}\nolimits(\widehat{\mathscr{X}}) \]
Proof. For (i), see [Reference ConardCon, §§ 1–2] – note that this is a statement at the level of classical stacks.
For (ii), note first that the claim is fppf local on ![]() $\mathscr {X}$: see [Reference LurieLur3, Proposition 5.2.4, Remark 5.2.13], for the case where
$\mathscr {X}$: see [Reference LurieLur3, Proposition 5.2.4, Remark 5.2.13], for the case where ![]() $\mathscr {X}$ is Deligne–Mumford and étale descent. It remains to show that the
$\mathscr {X}$ is Deligne–Mumford and étale descent. It remains to show that the ![]() $t$-structure is, in fact, fppf local in the affine case: note that the proofs of Lemmas 5.2.5 and 5.2.7 of [Reference LurieLur3] apply verbatim with ‘étale’ replaced by ‘fppf’.
$t$-structure is, in fact, fppf local in the affine case: note that the proofs of Lemmas 5.2.5 and 5.2.7 of [Reference LurieLur3] apply verbatim with ‘étale’ replaced by ‘fppf’.
For (iii) and (iv), we apply the last points of the following lemma.
We record some convenient facts on left ![]() $t$-complete
$t$-complete ![]() $t$-structures that we will use.
$t$-structures that we will use.
Lemma 2.1.12
(i) Suppose that
 $\mathcal {C}$ is a stable
$\mathcal {C}$ is a stable  $\infty$-category with a
$\infty$-category with a  $t$-structure. Then
$t$-structure. Then  $\mathcal {C}$ is left
$\mathcal {C}$ is left  $t$-complete if and only if the following condition holds. Suppose given a tower
$t$-complete if and only if the following condition holds. Suppose given a tower  $\mathscr {F}_0 \leftarrow \mathscr {F}_1 \leftarrow \cdots$ in
$\mathscr {F}_0 \leftarrow \mathscr {F}_1 \leftarrow \cdots$ in  $\mathcal {C}$ such that, for every
$\mathcal {C}$ such that, for every  $k \geqslant 0$, the tower
$k \geqslant 0$, the tower  $\tau _{\leqslant k}(\mathscr {F}_n) \in \mathcal {C}_{\leqslant k}$ is eventually constant. Then the tower has an inverse limit
$\tau _{\leqslant k}(\mathscr {F}_n) \in \mathcal {C}_{\leqslant k}$ is eventually constant. Then the tower has an inverse limit  $\mathscr {F}$, and for every
$\mathscr {F}$, and for every  $k \geqslant 0$ the natural map
$k \geqslant 0$ the natural map  $\tau _{\leqslant k} \mathscr {F} \to \tau _{\leqslant k} \mathscr {F}_n$ is an equivalence for
$\tau _{\leqslant k} \mathscr {F} \to \tau _{\leqslant k} \mathscr {F}_n$ is an equivalence for  $n \gg 0$ (depending on
$n \gg 0$ (depending on  $k$).
$k$).(ii) Suppose that
 $F \colon \mathcal {C} \to \mathcal {D}$ is an exact and right
$F \colon \mathcal {C} \to \mathcal {D}$ is an exact and right  $t$-exact functor, and that
$t$-exact functor, and that  $\{\mathscr {F}_n\}$ is a tower in
$\{\mathscr {F}_n\}$ is a tower in  $\mathcal {C}$ satisfying the above conditions. Then the tower
$\mathcal {C}$ satisfying the above conditions. Then the tower  $\{F(\mathscr {F}_n)\}$ in
$\{F(\mathscr {F}_n)\}$ in  $\mathcal {D}$ satisfies the above conditions as well.
$\mathcal {D}$ satisfies the above conditions as well.(iii) Suppose given a limit diagram
 $i \mapsto \mathcal {C}_i$ and
$i \mapsto \mathcal {C}_i$ and  $\mathcal {C} \to \mathcal {C}_i$, of small stable
$\mathcal {C} \to \mathcal {C}_i$, of small stable  $\infty$-categories with
$\infty$-categories with  $t$-structures such that all the functors are exact and right
$t$-structures such that all the functors are exact and right  $t$-exact. If each
$t$-exact. If each  $\mathcal {C}_i$ is left
$\mathcal {C}_i$ is left  $t$-complete, then so is
$t$-complete, then so is  $\mathcal {C}$.
$\mathcal {C}$.(iv) Suppose given a diagram
 $i \mapsto \mathcal {C}_i$ of small stable
$i \mapsto \mathcal {C}_i$ of small stable  $\infty$-categories with
$\infty$-categories with  $t$-structures, such that all the functors are exact and
$t$-structures, such that all the functors are exact and  $t$-exact. Then there is a unique
$t$-exact. Then there is a unique  $t$-structure on the limit
$t$-structure on the limit  $\mathcal {C} : = \mathop {\varprojlim }\limits _i \mathcal {C}_i$ such that the natural functors
$\mathcal {C} : = \mathop {\varprojlim }\limits _i \mathcal {C}_i$ such that the natural functors  $\mathcal {C} \to \mathcal {C}_i$ are
$\mathcal {C} \to \mathcal {C}_i$ are  $t$-exact. In this case, for each
$t$-exact. In this case, for each  $n \geqslant 0$, the natural functor
is an equivalence.
$n \geqslant 0$, the natural functor
is an equivalence. \begin{align*} \mathcal{C}^{\mathrm{cn}}_{\leqslant n} \longrightarrow \mathop{\varprojlim}\limits_i (\mathcal{C}_i)^{\mathrm{cn}}_{\leqslant n} \end{align*}
\begin{align*} \mathcal{C}^{\mathrm{cn}}_{\leqslant n} \longrightarrow \mathop{\varprojlim}\limits_i (\mathcal{C}_i)^{\mathrm{cn}}_{\leqslant n} \end{align*}
Proof. For (i), note first that left ![]() $t$-completeness is equivalent to the assertion for the tower
$t$-completeness is equivalent to the assertion for the tower ![]() $\mathscr {F}_n = \tau _{\leqslant n} \mathscr {F}$. It remains to suppose that
$\mathscr {F}_n = \tau _{\leqslant n} \mathscr {F}$. It remains to suppose that ![]() $\mathcal {C}$ is left
$\mathcal {C}$ is left ![]() $t$-complete and prove the desired condition. Consider the double tower
$t$-complete and prove the desired condition. Consider the double tower ![]() $\{\tau _{\leqslant m} \mathscr {F}_n\}_{m,n}$. We will show that it has a limit, and evaluate this limit in two different ways ‘rows-then-columns’ and the transpose.
$\{\tau _{\leqslant m} \mathscr {F}_n\}_{m,n}$. We will show that it has a limit, and evaluate this limit in two different ways ‘rows-then-columns’ and the transpose.
In one direction, we have that
exists since the diagram is eventually constant by hypothesis. Furthermore, ![]() $\mathscr {F}'_m \simeq \tau _{\leqslant m} \mathscr {F}'_n$ for any
$\mathscr {F}'_m \simeq \tau _{\leqslant m} \mathscr {F}'_n$ for any ![]() $n \geqslant m$ by construction. Thus,
$n \geqslant m$ by construction. Thus,
exists, and ![]() $\mathscr {F} \to \tau _{\leqslant m} \mathscr {F}'_m$ induces an equivalence on
$\mathscr {F} \to \tau _{\leqslant m} \mathscr {F}'_m$ induces an equivalence on ![]() $\tau _{\leqslant m}$, since
$\tau _{\leqslant m}$, since ![]() $\mathcal {C}$ is left
$\mathcal {C}$ is left ![]() $t$-complete. So, the inverse limit over the whole double tower exists and is also equal to
$t$-complete. So, the inverse limit over the whole double tower exists and is also equal to ![]() $\mathscr {F}$. Computing this in the other direction, we note
$\mathscr {F}$. Computing this in the other direction, we note
since ![]() $\mathcal {C}$ is left
$\mathcal {C}$ is left ![]() $t$-complete, so that
$t$-complete, so that
The assertion that ![]() $\tau _{\leqslant k} \mathscr {F} \to \tau _{\leqslant k} \mathscr {F}_n$ is an equivalence for
$\tau _{\leqslant k} \mathscr {F} \to \tau _{\leqslant k} \mathscr {F}_n$ is an equivalence for ![]() $n \gg 0$ follows by comparing it to
$n \gg 0$ follows by comparing it to ![]() $\tau _{\leqslant k} \mathscr {F} \to \tau _{\leqslant k} \mathscr {F}'_n$ for
$\tau _{\leqslant k} \mathscr {F} \to \tau _{\leqslant k} \mathscr {F}'_n$ for ![]() $n \geqslant k$. This completes the proof of (i).
$n \geqslant k$. This completes the proof of (i).
For (ii), it is enough to show that ![]() $F$ preserves
$F$ preserves ![]() $\tau _{\leqslant k}$-equivalences to
$\tau _{\leqslant k}$-equivalences to ![]() $\tau _{\leqslant k}$-equivalences. This follows from the fact that
$\tau _{\leqslant k}$-equivalences. This follows from the fact that ![]() $F$ preserves extension sequences and
$F$ preserves extension sequences and ![]() $k$-connective objects.
$k$-connective objects.
For (iii), we apply the criterion in (i). Notice that a putative limit diagram in ![]() $\mathcal {C}$ which gives a limit diagram in each
$\mathcal {C}$ which gives a limit diagram in each ![]() $\mathcal {C}_i$ is itself a limit diagram (though the converse need not hold in general!), so that (ii) completes the proof.
$\mathcal {C}_i$ is itself a limit diagram (though the converse need not hold in general!), so that (ii) completes the proof.
For (iv), note that the ![]() $t$-structure is characterized by stating that an object of
$t$-structure is characterized by stating that an object of ![]() $\mathcal {C}$ is connective (respectively, coconnective) if and only if this is true of its image in each
$\mathcal {C}$ is connective (respectively, coconnective) if and only if this is true of its image in each ![]() $\mathcal {C}_i$. Since the transition functors are
$\mathcal {C}_i$. Since the transition functors are ![]() $t$-exact, the truncation functors on each
$t$-exact, the truncation functors on each ![]() $\mathcal {C}_i$ pass to the limit to provide truncation functors on
$\mathcal {C}_i$ pass to the limit to provide truncation functors on ![]() $\mathcal {C}$. It is thus straightforward to check that this is a
$\mathcal {C}$. It is thus straightforward to check that this is a ![]() $t$-structure, and the desired description of the connective
$t$-structure, and the desired description of the connective ![]() $n$-truncated objects. Notice also that (iii) and (iv) are essentially contained in [Reference LurieLur3, Remark 5.2.9].
$n$-truncated objects. Notice also that (iii) and (iv) are essentially contained in [Reference LurieLur3, Remark 5.2.9].
2.2 Theorem on formal functions in derived algebraic geometry
Here we describe ![]() $\operatorname {QC}$ on a formal completion. This leads to a formulation of the theorem on formal functions as a base-change result, Theorem 2.2.5, which applies to arbitrary morphisms of algebraic stacks and complexes of quasi-coherent sheaves.
$\operatorname {QC}$ on a formal completion. This leads to a formulation of the theorem on formal functions as a base-change result, Theorem 2.2.5, which applies to arbitrary morphisms of algebraic stacks and complexes of quasi-coherent sheaves.
Lemma 2.2.1 Suppose ![]() $R \in \mathrm {SCR}$,
$R \in \mathrm {SCR}$, ![]() $I \subset \pi _0(R)$ is a finitely generated ideal,
$I \subset \pi _0(R)$ is a finitely generated ideal, ![]() $\widehat {R}$ is the
$\widehat {R}$ is the ![]() $I$-completion of
$I$-completion of ![]() $R$, and
$R$, and ![]() $i \colon \operatorname {Spf}(R) \to \operatorname {Spec}(R)$ is the inclusion. Then the composite functor
$i \colon \operatorname {Spf}(R) \to \operatorname {Spec}(R)$ is the inclusion. Then the composite functor
has finite left ![]() $t$-amplitude (i.e. is left
$t$-amplitude (i.e. is left ![]() $t$-exact up to a shift).
$t$-exact up to a shift).
Proof. Let ![]() $\{R_n\}$ be a tower of perfect
$\{R_n\}$ be a tower of perfect ![]() $R$-algebras having Tor amplitude at most
$R$-algebras having Tor amplitude at most ![]() $d$ as in Proposition 2.1.2. Then we may identify
$d$ as in Proposition 2.1.2. Then we may identify ![]() $\operatorname {QC}(\operatorname {Spec}(R)) \simeq R {\rm {}\hbox{-}{\rm mod}}$ and
$\operatorname {QC}(\operatorname {Spec}(R)) \simeq R {\rm {}\hbox{-}{\rm mod}}$ and ![]() $\operatorname {QC}(\operatorname {Spf}(R)) \simeq \mathop {\varprojlim }\limits _n R_n {\rm {}\hbox{-}{\rm mod}}$. Under these identifications, the functor
$\operatorname {QC}(\operatorname {Spf}(R)) \simeq \mathop {\varprojlim }\limits _n R_n {\rm {}\hbox{-}{\rm mod}}$. Under these identifications, the functor ![]() $i_* i^{*}$ is identified with
$i_* i^{*}$ is identified with
If ![]() $M \in R {\rm {}\hbox{-}{\rm mod}}_{<0}$ then
$M \in R {\rm {}\hbox{-}{\rm mod}}_{<0}$ then ![]() $R_n \otimes _R M \in R {\rm {}\hbox{-}{\rm mod}}_{< d}$ by hypothesis on
$R_n \otimes _R M \in R {\rm {}\hbox{-}{\rm mod}}_{< d}$ by hypothesis on ![]() $R_n$.
$R_n$.
We let ![]() $(R {\rm {}\hbox{-}{\rm mod}})^{I\text{-cplt}}\subset R {\rm {}\hbox{-}{\rm mod}}$ denote the subcategory of
$(R {\rm {}\hbox{-}{\rm mod}})^{I\text{-cplt}}\subset R {\rm {}\hbox{-}{\rm mod}}$ denote the subcategory of ![]() $I$-complete modules [Reference LurieLur3, Definition 4.2.1].
$I$-complete modules [Reference LurieLur3, Definition 4.2.1].
Lemma 2.2.2 Suppose ![]() $R \in \mathrm {SCR}$,
$R \in \mathrm {SCR}$, ![]() $I \subset \pi _0(R)$ is a finitely generated ideal, and
$I \subset \pi _0(R)$ is a finitely generated ideal, and ![]() $\widehat {R}$ is the
$\widehat {R}$ is the ![]() $I$-completion of
$I$-completion of ![]() $R$. Let
$R$. Let ![]() $i \colon \operatorname {Spf}(\widehat {R}) \to \operatorname {Spec}(R)$ be the natural inclusion. Then the composite
$i \colon \operatorname {Spf}(\widehat {R}) \to \operatorname {Spec}(R)$ be the natural inclusion. Then the composite
is an equivalence. In particular, the counit ![]() $i^{*} i_* \to \mathop {{\rm id}}\nolimits$ is an equivalence and the unit
$i^{*} i_* \to \mathop {{\rm id}}\nolimits$ is an equivalence and the unit ![]() $\mathop {{\rm id}}\nolimits \to i_* i^{*}$ can be identified with the
$\mathop {{\rm id}}\nolimits \to i_* i^{*}$ can be identified with the ![]() $I$-completion.
$I$-completion.
Proof. Note that this is proved, under the additional hypothesis that we restrict to connective objects on both sides, in [Reference LurieLur3, Lemma 5.1.10]. We will prove this stronger result by exploiting our stronger assumptions in the form of Lemma 2.2.1.
We note that ![]() $i^{*}$ has a right adjoint
$i^{*}$ has a right adjoint ![]() $i_*$. If we identify
$i_*$. If we identify ![]() $\operatorname {QC}(\operatorname {Spec}(R)) = R {\rm {}\hbox{-}{\rm mod}}$ and
$\operatorname {QC}(\operatorname {Spec}(R)) = R {\rm {}\hbox{-}{\rm mod}}$ and ![]() $\operatorname {QC}(\operatorname {Spf}(R)) = \mathop {\varprojlim }\limits _n R_n {\rm {}\hbox{-}{\rm mod}}$, then
$\operatorname {QC}(\operatorname {Spf}(R)) = \mathop {\varprojlim }\limits _n R_n {\rm {}\hbox{-}{\rm mod}}$, then ![]() $i_*$ is given by the inverse limit in
$i_*$ is given by the inverse limit in ![]() $R$-modules
$R$-modules
It is enough to prove two assertions.
(i) If ![]() $M \in R {\rm {}\hbox{-}{\rm mod}}$, then the natural map
$M \in R {\rm {}\hbox{-}{\rm mod}}$, then the natural map
identifies ![]() $i_* i^{*} M$ with the
$i_* i^{*} M$ with the ![]() $I$-completion of
$I$-completion of ![]() $M$. If
$M$. If ![]() $M$ is almost connective, this follows by [Reference LurieLur3, Remark 5.1.11]. Since
$M$ is almost connective, this follows by [Reference LurieLur3, Remark 5.1.11]. Since ![]() $R {\rm {}\hbox{-}{\rm mod}}$ is right
$R {\rm {}\hbox{-}{\rm mod}}$ is right ![]() $t$-complete we may write
$t$-complete we may write ![]() $M = \mathop {\varinjlim }\limits \tau _{\geqslant -k} M$, and it is enough to show that both
$M = \mathop {\varinjlim }\limits \tau _{\geqslant -k} M$, and it is enough to show that both ![]() $i_* i^{*}$ and the
$i_* i^{*}$ and the ![]() $I$-completion functor
$I$-completion functor ![]() $M \mapsto \widehat {M}$ preserve this directed colimit. By Lemma 2.1.12, it is enough to show that both
$M \mapsto \widehat {M}$ preserve this directed colimit. By Lemma 2.1.12, it is enough to show that both ![]() $i_* i^{*}$ and the
$i_* i^{*}$ and the ![]() $I$-completion functor have bounded left
$I$-completion functor have bounded left ![]() $t$-amplitude. For
$t$-amplitude. For ![]() $i_* i^{*}$ this is Lemma 2.2.1, while for the
$i_* i^{*}$ this is Lemma 2.2.1, while for the ![]() $I$-completion it is [Reference LurieLur3, Remark 5.11]. This shows that
$I$-completion it is [Reference LurieLur3, Remark 5.11]. This shows that ![]() $M \to i_* i^{*} M$ is the
$M \to i_* i^{*} M$ is the ![]() $I$-completion for all
$I$-completion for all ![]() $M \in R {\rm {}\hbox{-}{\rm mod}}$.
$M \in R {\rm {}\hbox{-}{\rm mod}}$.
(ii) Let ![]() $\{R_n\}$ be as in Proposition 2.1.2. We must show that if
$\{R_n\}$ be as in Proposition 2.1.2. We must show that if ![]() $\{M_n\} \in \mathop {\varprojlim }\limits _n R_n {\rm {}\hbox{-}{\rm mod}}$ then the unit
$\{M_n\} \in \mathop {\varprojlim }\limits _n R_n {\rm {}\hbox{-}{\rm mod}}$ then the unit
is an equivalence. More concretely, we must show that for each ![]() $k$ the natural map
$k$ the natural map
is an equivalence. Since ![]() $R_k$ is perfect over
$R_k$ is perfect over ![]() $R$,
$R$, ![]() $R_k \otimes _R$ commutes with limits, so we may identify this with the map
$R_k \otimes _R$ commutes with limits, so we may identify this with the map
Recall that ![]() $\operatorname {Spf}(\widehat {R}) \simeq \mathop {\varinjlim }\limits _n \operatorname {Spec}(R_n)$ and that fiber products preserve filtered colimits of (pre)sheaves, so that we obtain
$\operatorname {Spf}(\widehat {R}) \simeq \mathop {\varinjlim }\limits _n \operatorname {Spec}(R_n)$ and that fiber products preserve filtered colimits of (pre)sheaves, so that we obtain
Furthermore, ![]() $\operatorname {Spec}(R_k) \times _{\operatorname {Spec}(R)} \operatorname {Spf}(\widehat {R}) \simeq \operatorname {Spec}(R_k)$ since
$\operatorname {Spec}(R_k) \times _{\operatorname {Spec}(R)} \operatorname {Spf}(\widehat {R}) \simeq \operatorname {Spec}(R_k)$ since ![]() $\operatorname {Spec}(R_k) \to \operatorname {Spec}(R)$ factors through the monomorphism
$\operatorname {Spec}(R_k) \to \operatorname {Spec}(R)$ factors through the monomorphism ![]() $\operatorname {Spf}(R) \to \operatorname {Spec}(R)$. Thus, the natural map
$\operatorname {Spf}(R) \to \operatorname {Spec}(R)$. Thus, the natural map
is an equivalence by (i). This completes the proof.
Finally, we deduce the following theorem.
Theorem 2.2.3 Suppose that ![]() $\mathscr {X}$ is a derived prestack and
$\mathscr {X}$ is a derived prestack and ![]() $Z \subset |\mathscr {X}|$ is a cocompact closed subset. Let
$Z \subset |\mathscr {X}|$ is a cocompact closed subset. Let ![]() $i \colon \widehat {\mathscr {X}} \to \mathscr {X}$ be the inclusion of the formal completion along
$i \colon \widehat {\mathscr {X}} \to \mathscr {X}$ be the inclusion of the formal completion along ![]() $Z$. Then the following assertions hold:
$Z$. Then the following assertions hold:
(i)
 $i^{*}$ admits a left adjoint
$i^{*}$ admits a left adjoint  $i_+$;
$i_+$;(ii) the composite
is an equivalence, with inverse given by \[ \operatorname{QC}_Z(\mathscr{X}) \subset \operatorname{QC}(\mathscr{X}) \stackrel{i^{*}}\longrightarrow \operatorname{QC}(\widehat{\mathscr{X}}) \]
\[ \operatorname{QC}_Z(\mathscr{X}) \subset \operatorname{QC}(\mathscr{X}) \stackrel{i^{*}}\longrightarrow \operatorname{QC}(\widehat{\mathscr{X}}) \]
 $i_+$ (i.e. the essential image of
$i_+$ (i.e. the essential image of  $i_+$ is contained in
$i_+$ is contained in  $\operatorname {QC}_Z(\mathscr {X})$);
$\operatorname {QC}_Z(\mathscr {X})$);(iii)
 $i_+$ is of formation local on
$i_+$ is of formation local on  $\mathscr {X}$, and satisfies the projection formula (i.e. is a functor of
$\mathscr {X}$, and satisfies the projection formula (i.e. is a functor of  $\operatorname {QC}(\mathscr {X})$-module categories).
$\operatorname {QC}(\mathscr {X})$-module categories).
The composite ![]() $i_+ \circ i^{*}$ can be identified with the functor
$i_+ \circ i^{*}$ can be identified with the functor ![]() $R\Gamma _Z$, which fits into a fiber sequence
$R\Gamma _Z$, which fits into a fiber sequence ![]() $R\Gamma _Z \longrightarrow \mathop {{\rm id}}\nolimits \longrightarrow j_* j^{*}$, where
$R\Gamma _Z \longrightarrow \mathop {{\rm id}}\nolimits \longrightarrow j_* j^{*}$, where ![]() $j$ is the inclusion of the open complement of
$j$ is the inclusion of the open complement of ![]() $Z$.
$Z$.
Remark 2.2.4 For spectral prestacks the theorem holds as stated, but with the categories ![]() $\operatorname {QC}(\mathscr {X})$,
$\operatorname {QC}(\mathscr {X})$, ![]() $\operatorname {QC}(\widehat {\mathscr {X}})$ and
$\operatorname {QC}(\widehat {\mathscr {X}})$ and ![]() $\operatorname {QC}_Z(\mathscr {X})$ replaced with the corresponding categories of almost connective complexes,
$\operatorname {QC}_Z(\mathscr {X})$ replaced with the corresponding categories of almost connective complexes, ![]() $\operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$,
$\operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$, ![]() $\operatorname {QC}(\widehat {\mathscr {X}})^{\mathrm {acn}}$, and
$\operatorname {QC}(\widehat {\mathscr {X}})^{\mathrm {acn}}$, and ![]() $\operatorname {QC}_Z(\mathscr {X})^{\mathrm {acn}}$ – see [Reference LurieLur3, Theorem 5.1.9]. The proof is essentially the same in the derived context, combined with Lemma 2.2.2.
$\operatorname {QC}_Z(\mathscr {X})^{\mathrm {acn}}$ – see [Reference LurieLur3, Theorem 5.1.9]. The proof is essentially the same in the derived context, combined with Lemma 2.2.2.
Proof. It is enough to prove the claims when ![]() $\mathscr {X}$ is affine, for the claims are local by construction (i.e. because we required the formation of
$\mathscr {X}$ is affine, for the claims are local by construction (i.e. because we required the formation of ![]() $i_+$ to be local).
$i_+$ to be local).
Suppose now that ![]() $\mathscr {X} = \operatorname {Spec}(R)$ and
$\mathscr {X} = \operatorname {Spec}(R)$ and ![]() $Z$ is cut out by a finitely generated ideal
$Z$ is cut out by a finitely generated ideal ![]() $I \subset \pi _0(R)$. Let
$I \subset \pi _0(R)$. Let ![]() $(R {\rm {}\hbox{-}{\rm mod}})^{I\text{-nil}} \subset R {\rm {}\hbox{-}{\rm mod}}$ denote the full subcategory of locally
$(R {\rm {}\hbox{-}{\rm mod}})^{I\text{-nil}} \subset R {\rm {}\hbox{-}{\rm mod}}$ denote the full subcategory of locally ![]() $I$-nilpotent modules. By [Reference LurieLur3, Proposition 4.2.5] these are equivalent via the
$I$-nilpotent modules. By [Reference LurieLur3, Proposition 4.2.5] these are equivalent via the ![]() $I$-completion functor and the ‘local cohomology’ functor
$I$-completion functor and the ‘local cohomology’ functor ![]() $\Gamma _I$. Notice that
$\Gamma _I$. Notice that ![]() $i^{*}$ vanishes on
$i^{*}$ vanishes on ![]() $I$-local modules (i.e. those supported away from
$I$-local modules (i.e. those supported away from ![]() $Z$), so that
$Z$), so that
It thus follows from Lemma 2.2.2 and the above mentioned equivalence that the composite
is also an equivalence. Let ![]() $i_+$ be the composite of an inverse to this functor with the inclusion
$i_+$ be the composite of an inverse to this functor with the inclusion ![]() $(R {\rm {}\hbox{-}{\rm mod}})^{I\text{-nil}} \subset R {\rm {}\hbox{-}{\rm mod}}$ – more explicitly,
$(R {\rm {}\hbox{-}{\rm mod}})^{I\text{-nil}} \subset R {\rm {}\hbox{-}{\rm mod}}$ – more explicitly, ![]() $i_+ = \Gamma _I \circ i_*$. Since the inclusion is left adjoint to
$i_+ = \Gamma _I \circ i_*$. Since the inclusion is left adjoint to ![]() $\Gamma _I \colon R {\rm {}\hbox{-}{\rm mod}} \to (R {\rm {}\hbox{-}{\rm mod}})^{I\text{-nil}}$ it follows that
$\Gamma _I \colon R {\rm {}\hbox{-}{\rm mod}} \to (R {\rm {}\hbox{-}{\rm mod}})^{I\text{-nil}}$ it follows that ![]() $i_+$ is left adjoint to
$i_+$ is left adjoint to ![]() $i^{*}$.
$i^{*}$.
It is easy to check that ![]() $i_+$, so defined, is local on
$i_+$, so defined, is local on ![]() $R$: given a cartesian diagram
$R$: given a cartesian diagram

we wish to check that
is an equivalence for all ![]() $\mathscr {F} \in \operatorname {QC}(\operatorname {Spf}(R))$. But by the above we may suppose that
$\mathscr {F} \in \operatorname {QC}(\operatorname {Spf}(R))$. But by the above we may suppose that ![]() $\mathscr {F} = i^{*} \mathscr {F}'$ for some
$\mathscr {F} = i^{*} \mathscr {F}'$ for some ![]() $\mathscr {F} \in (R {\rm {}\hbox{-}{\rm mod}})^{I\text{-nil}}$, and then notice that
$\mathscr {F} \in (R {\rm {}\hbox{-}{\rm mod}})^{I\text{-nil}}$, and then notice that ![]() $\pi ^{*} \mathscr {F}' \in (R' {\rm {}\hbox{-}{\rm mod}})^{I'\text{-nil}}$. The result is then immediate from the equivalence applied upstairs and downstairs.
$\pi ^{*} \mathscr {F}' \in (R' {\rm {}\hbox{-}{\rm mod}})^{I'\text{-nil}}$. The result is then immediate from the equivalence applied upstairs and downstairs.
Finally, the projection formula assertion follows from [Reference LurieLur3, 4.1.22, 4.2.6].
As an application, we have a version of the theorem on formal functions without properness or coherence hypotheses.
Theorem 2.2.5 (Theorem on formal functions)
Suppose given a cartesian diagram of derived stacks for which ![]() $\operatorname {QC}$ is presentable (e.g.
$\operatorname {QC}$ is presentable (e.g. ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $\mathscr {Y}$ are algebraic):
$\mathscr {Y}$ are algebraic):

where ![]() $\widehat {\mathscr {Y}}$ is the formal completion of
$\widehat {\mathscr {Y}}$ is the formal completion of ![]() $\mathscr {Y}$ along a cocompact closed subset
$\mathscr {Y}$ along a cocompact closed subset ![]() $Z \subset |\mathscr {Y}|$. (It follows that
$Z \subset |\mathscr {Y}|$. (It follows that ![]() $\widehat {\mathscr {X}}$ is the formal completion of
$\widehat {\mathscr {X}}$ is the formal completion of ![]() $\mathscr {X}$ along
$\mathscr {X}$ along ![]() $\pi ^{-1}(Z)$.) Then the base-change map
$\pi ^{-1}(Z)$.) Then the base-change map
is an equivalence for all ![]() $\mathscr {F} \in \operatorname {QC}(\mathscr {X})$.
$\mathscr {F} \in \operatorname {QC}(\mathscr {X})$.
Furthermore, if ![]() $\mathscr {Y} = \operatorname {Spec}(R)$ is affine, we may take global sections and obtain that the map
$\mathscr {Y} = \operatorname {Spec}(R)$ is affine, we may take global sections and obtain that the map
is an equivalence of complete ![]() $R$-modules for every
$R$-modules for every ![]() $\mathscr {F} \in \operatorname {QC}(\mathscr {X})$.
$\mathscr {F} \in \operatorname {QC}(\mathscr {X})$.
Remark 2.2.6 For a map of spectral stacks ![]() $\pi : \mathscr {X} \to \mathscr {Y}$ which satisfies (CD) (so that
$\pi : \mathscr {X} \to \mathscr {Y}$ which satisfies (CD) (so that ![]() $\pi _\ast$ preserves almost connective complexes), the same statement is true for any almost connective
$\pi _\ast$ preserves almost connective complexes), the same statement is true for any almost connective ![]() $\mathscr {F} \in \operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$ with the same proof, using Remark 2.2.4.
$\mathscr {F} \in \operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$ with the same proof, using Remark 2.2.4.
Proof. By general non-sense, it is enough to prove that the base-change map of left adjoints
is an equivalence. By Theorem 2.2.3 the assertion is local on ![]() $\mathscr {Y}$ so that we may suppose it is affine. Also, by Theorem 2.2.3 we know that
$\mathscr {Y}$ so that we may suppose it is affine. Also, by Theorem 2.2.3 we know that ![]() $i^{*}$ is essentially surjective so that it is enough to show that map
$i^{*}$ is essentially surjective so that it is enough to show that map
is an equivalence. By another application of Theorem 2.2.3 we see that this is true (since ![]() $i_+ i^{*} \simeq \mathop {{\rm id}}\nolimits$ and similarly for
$i_+ i^{*} \simeq \mathop {{\rm id}}\nolimits$ and similarly for ![]() $i'$).
$i'$).
The affine statement follows by applying Lemma 2.2.2.
Remark 2.2.7 If ![]() $\mathscr {Y} = \operatorname {Spec}(R)$ with
$\mathscr {Y} = \operatorname {Spec}(R)$ with ![]() $R$ noetherian and
$R$ noetherian and ![]() $\pi _\ast (\mathscr {F}) \in \operatorname {APerf}(R)$, one can recover the usual statement of the theorem on formal functions, that
$\pi _\ast (\mathscr {F}) \in \operatorname {APerf}(R)$, one can recover the usual statement of the theorem on formal functions, that ![]() $\widehat {H_i R\Gamma (\mathscr {F})} \simeq H_i R\Gamma (\widehat {\mathscr {F}})$, by combining Theorem 2.2.5 with Lemma 2.1.10.
$\widehat {H_i R\Gamma (\mathscr {F})} \simeq H_i R\Gamma (\widehat {\mathscr {F}})$, by combining Theorem 2.2.5 with Lemma 2.1.10.
2.3 Criteria for completeness
Proposition 2.3.1 (Full-faithfulness criterion)
Let ![]() $\pi : \mathscr {X} \to \mathscr {S}$ be a morphism of noetherian algebraic spectral (or derived) stacks, and assume that
$\pi : \mathscr {X} \to \mathscr {S}$ be a morphism of noetherian algebraic spectral (or derived) stacks, and assume that ![]() $\mathscr {S}$ is complete along a closed subset
$\mathscr {S}$ is complete along a closed subset ![]() $Z \subset |\mathscr {S}|$. Suppose that
$Z \subset |\mathscr {S}|$. Suppose that ![]() $\pi _\ast ({\rm Coh} (\mathscr {X})) \subset \operatorname {{\mathbb {D}}APerf}(\mathscr {S})$ and that
$\pi _\ast ({\rm Coh} (\mathscr {X})) \subset \operatorname {{\mathbb {D}}APerf}(\mathscr {S})$ and that ![]() $G \in \operatorname {APerf}(\mathscr {X})$. Then the natural map
$G \in \operatorname {APerf}(\mathscr {X})$. Then the natural map
is an equivalence for any ![]() $F \in \operatorname {QC}(\mathscr {X})$, where
$F \in \operatorname {QC}(\mathscr {X})$, where ![]() $i : \widehat {\mathscr {X}} \to \mathscr {X}$ is the formal completion of
$i : \widehat {\mathscr {X}} \to \mathscr {X}$ is the formal completion of ![]() $\mathscr {X}$ along
$\mathscr {X}$ along ![]() $Z' = \pi ^{-1} (Z)$.
$Z' = \pi ^{-1} (Z)$.
Proof. The proof consists of four steps.
Step 1: reducing to ![]() $F, G$ bounded coherent. It suffices to prove the assertion under the additional hypothesis that
$F, G$ bounded coherent. It suffices to prove the assertion under the additional hypothesis that ![]() $G \in \operatorname {DCoh}(\mathscr {X})$ is bounded, because
$G \in \operatorname {DCoh}(\mathscr {X})$ is bounded, because ![]() $G = \mathop {\varprojlim }\limits \tau _{\leqslant n} G$, the limit being taken in
$G = \mathop {\varprojlim }\limits \tau _{\leqslant n} G$, the limit being taken in ![]() $\operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$, and Theorem 2.2.3 implies that
$\operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$, and Theorem 2.2.3 implies that ![]() $i^{\ast }$ preserves limits. Suppose for concreteness, shifting as needed, that
$i^{\ast }$ preserves limits. Suppose for concreteness, shifting as needed, that ![]() $G \in \operatorname {APerf}(\mathscr {X})^{\mathrm {cn}}_{\leqslant k}$. Let
$G \in \operatorname {APerf}(\mathscr {X})^{\mathrm {cn}}_{\leqslant k}$. Let ![]() $\mathcal {C} \subset \operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$ denote the full subcategory consisting of those
$\mathcal {C} \subset \operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$ denote the full subcategory consisting of those ![]() $F$ for which the map
$F$ for which the map
is an equivalence for our fixed ![]() $G$. Note that
$G$. Note that ![]() $\mathcal {C}$ is closed under extensions and arbitrary colimits which exist in
$\mathcal {C}$ is closed under extensions and arbitrary colimits which exist in ![]() $\operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$. We wish to show that
$\operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$. We wish to show that ![]() $\mathcal {C} = \operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$.
$\mathcal {C} = \operatorname {QC}(\mathscr {X})^{\mathrm {acn}}$.
Note that Theorem 2.2.3 allows us to identify the right-hand side with
Furthermore, ![]() $R\Gamma _{Z'} \mathcal {O}_X$ is almost connective, so that tensoring with it is right
$R\Gamma _{Z'} \mathcal {O}_X$ is almost connective, so that tensoring with it is right ![]() $t$-exact up to a shift. So
$t$-exact up to a shift. So ![]() $\mathcal {C} \subset \operatorname {QC}(\mathscr {X})$ is the subcategory for which the map to this is an equivalence. We see that
$\mathcal {C} \subset \operatorname {QC}(\mathscr {X})$ is the subcategory for which the map to this is an equivalence. We see that ![]() $\mathcal {C}$ is closed under arbitrary colimits and contains
$\mathcal {C}$ is closed under arbitrary colimits and contains ![]() $\operatorname {QC}(\mathscr {X})_{\geqslant d}$ for some
$\operatorname {QC}(\mathscr {X})_{\geqslant d}$ for some ![]() $d$ – since
$d$ – since ![]() $G$ is bounded and tensoring by
$G$ is bounded and tensoring by ![]() $R\Gamma _{Z'} \mathcal {O}_X$ is right
$R\Gamma _{Z'} \mathcal {O}_X$ is right ![]() $t$-exact up to a shift. By Theorem A.2.1 it is thus enough to show that
$t$-exact up to a shift. By Theorem A.2.1 it is thus enough to show that ![]() $\operatorname {APerf}(\mathscr {X})_{< d} \subset \mathcal {C}$, that is, that the map
$\operatorname {APerf}(\mathscr {X})_{< d} \subset \mathcal {C}$, that is, that the map
is an equivalence for all ![]() $F \in \operatorname {APerf}(\mathscr {X})_{< d}$.
$F \in \operatorname {APerf}(\mathscr {X})_{< d}$.
In particular, we are reduced to proving this if both ![]() $F, G \in \operatorname {DCoh}(\mathscr {X})$.
$F, G \in \operatorname {DCoh}(\mathscr {X})$.
Step 2: reducing to a fact on inner Homs. Taking shifts, we may reduce to the case ![]() $G \in \operatorname {DCoh}(\mathscr {X})_{\leqslant 0}$ and
$G \in \operatorname {DCoh}(\mathscr {X})_{\leqslant 0}$ and ![]() $F \in \operatorname {DCoh}(\mathscr {X})_{\geqslant 0}$. Let
$F \in \operatorname {DCoh}(\mathscr {X})_{\geqslant 0}$. Let
be the inner Hom for the monoidal structure on ![]() $\operatorname {QC}(\mathscr {X})$. Using the definition of inner Hom, it is enough to show that
$\operatorname {QC}(\mathscr {X})$. Using the definition of inner Hom, it is enough to show that
is an equivalence. Note that ![]() $H$ is coconnective with coherent homology sheaves by Lemma 2.3.2. Thus, it is enough to prove this assertion for any such
$H$ is coconnective with coherent homology sheaves by Lemma 2.3.2. Thus, it is enough to prove this assertion for any such ![]() $H$, not necessarily arising as an inner Hom.
$H$, not necessarily arising as an inner Hom.
Step 3: reducing to a fact on ![]() $\mathscr {S}$. Consider the fiber sequence of quasi-coherent sheaves on
$\mathscr {S}$. Consider the fiber sequence of quasi-coherent sheaves on ![]() $\mathscr {S}$,
$\mathscr {S}$, ![]() $R\Gamma _Z \mathcal {O}_\mathscr {S} \longrightarrow \mathcal {O}_\mathscr {S} \longrightarrow j_* \mathcal {O}_\mathscr {U}$, where
$R\Gamma _Z \mathcal {O}_\mathscr {S} \longrightarrow \mathcal {O}_\mathscr {S} \longrightarrow j_* \mathcal {O}_\mathscr {U}$, where ![]() $j$ is the open immersion
$j$ is the open immersion ![]() $j \colon \mathscr {U} = \mathscr {S} \setminus Z \to \mathscr {S}$. Applying
$j \colon \mathscr {U} = \mathscr {S} \setminus Z \to \mathscr {S}$. Applying ![]() $\pi ^{\ast }$ to this sequence, we can use the base-change formula to identify the third term with
$\pi ^{\ast }$ to this sequence, we can use the base-change formula to identify the third term with ![]() $(j')_\ast \mathcal {O}_{\mathscr {U}'}$, where
$(j')_\ast \mathcal {O}_{\mathscr {U}'}$, where ![]() $j' \colon \mathscr {U}' = \mathscr {X} \setminus Z' \to \mathscr {X}$ is the base-changed open immersion. It follows that
$j' \colon \mathscr {U}' = \mathscr {X} \setminus Z' \to \mathscr {X}$ is the base-changed open immersion. It follows that ![]() $R\Gamma _{Z'} \mathcal {O}_\mathscr {X} \simeq \pi ^{*}(R\Gamma _Z \mathcal {O}_\mathscr {S})$.
$R\Gamma _{Z'} \mathcal {O}_\mathscr {X} \simeq \pi ^{*}(R\Gamma _Z \mathcal {O}_\mathscr {S})$.
This lets us identify the morphism of (2) with the morphism
Since ![]() $H$ was left-bounded with coherent homology, the assumption on
$H$ was left-bounded with coherent homology, the assumption on ![]() $\pi$ ensures that has
$\pi$ ensures that has ![]() $\pi _* H$ has left-bounded, coherent, homology sheaves on
$\pi _* H$ has left-bounded, coherent, homology sheaves on ![]() $\mathscr {S}$ (see Remark 2.4.2 below).
$\mathscr {S}$ (see Remark 2.4.2 below).
It is thus enough to show that for any ![]() $H' \in \operatorname {QC}(\mathscr {S})$ having coherent homology sheaves the natural map
$H' \in \operatorname {QC}(\mathscr {S})$ having coherent homology sheaves the natural map ![]() $R\Gamma (\mathscr {S}, H') \to \operatorname {RHom}_\mathscr {S}(R\Gamma _Z \mathcal {O}_\mathscr {S}, H')$ is an equivalence.
$R\Gamma (\mathscr {S}, H') \to \operatorname {RHom}_\mathscr {S}(R\Gamma _Z \mathcal {O}_\mathscr {S}, H')$ is an equivalence.
Step 4: completing the proof. Note first that, since ![]() $R\Gamma _Z \mathcal {O}_\mathscr {S}$ is almost connective, we can reduce as above to the case where
$R\Gamma _Z \mathcal {O}_\mathscr {S}$ is almost connective, we can reduce as above to the case where ![]() $H'$ is right-bounded and hence almost perfect. Next, note that
$H'$ is right-bounded and hence almost perfect. Next, note that ![]() $i^{*} R\Gamma _Z \mathcal {O}_\mathscr {S} = \mathcal {O}_{\widehat {\mathscr {S}}}$ so that another application of Theorem 2.2.3 yields
$i^{*} R\Gamma _Z \mathcal {O}_\mathscr {S} = \mathcal {O}_{\widehat {\mathscr {S}}}$ so that another application of Theorem 2.2.3 yields
Thus, the desired assertion follows by our assumption that ![]() $\operatorname {APerf}(\mathscr {S}) \to \operatorname {APerf}(\widehat {\mathscr {S}})$ is an equivalence.
$\operatorname {APerf}(\mathscr {S}) \to \operatorname {APerf}(\widehat {\mathscr {S}})$ is an equivalence.
Lemma 2.3.2 Let ![]() $\mathscr {X}$ be a noetherian algebraic spectral (or derived) stack, and let
$\mathscr {X}$ be a noetherian algebraic spectral (or derived) stack, and let ![]() $F \in \operatorname {APerf}(\mathscr {X})_{\geqslant 0}$ and
$F \in \operatorname {APerf}(\mathscr {X})_{\geqslant 0}$ and ![]() $G \in \operatorname {{\mathbb {D}}APerf}(\mathscr {X})_{\leqslant 0}$. Let
$G \in \operatorname {{\mathbb {D}}APerf}(\mathscr {X})_{\leqslant 0}$. Let ![]() $H = \operatorname {RHom}^{\otimes _{\operatorname {QC}(\mathscr {X})}}_\mathscr {X}(F,G)$ be the inner Hom for the monoidal structure on
$H = \operatorname {RHom}^{\otimes _{\operatorname {QC}(\mathscr {X})}}_\mathscr {X}(F,G)$ be the inner Hom for the monoidal structure on ![]() $\operatorname {QC}(\mathscr {X})$. Then
$\operatorname {QC}(\mathscr {X})$. Then ![]() $H \in \operatorname {{\mathbb {D}}APerf}(\mathscr {X})_{\leqslant 0}$, and its formation is fppf local on
$H \in \operatorname {{\mathbb {D}}APerf}(\mathscr {X})_{\leqslant 0}$, and its formation is fppf local on ![]() $\mathscr {X}$.
$\mathscr {X}$.
Proof. Note that [Reference PreygelPre11, A.1.1] guarantees that the formation of ![]() $H$ is fppf local since
$H$ is fppf local since ![]() $F$ is almost perfect and
$F$ is almost perfect and ![]() $G$ is bounded above. As explained in the proof there, this does not require condition
$G$ is bounded above. As explained in the proof there, this does not require condition ![]() $(\ast )$ from [Reference PreygelPre11], since the proof reduces to the affine case. Now the claim that
$(\ast )$ from [Reference PreygelPre11], since the proof reduces to the affine case. Now the claim that ![]() $H$ is coconnective with coherent homology sheaves is flat local, so in proving it we may suppose that
$H$ is coconnective with coherent homology sheaves is flat local, so in proving it we may suppose that ![]() $\mathscr {X} = \operatorname {Spec}(A)$ is affine with
$\mathscr {X} = \operatorname {Spec}(A)$ is affine with ![]() $A$ noetherian. In this case, the proof in [Reference PreygelPre11] shows that there is a third-quadrant spectral sequence converging to the homology groups of
$A$ noetherian. In this case, the proof in [Reference PreygelPre11] shows that there is a third-quadrant spectral sequence converging to the homology groups of ![]() $H$ whose starting term consists of finite sums of the homology of
$H$ whose starting term consists of finite sums of the homology of ![]() $G$. This shows both that the homology of
$G$. This shows both that the homology of ![]() $H$ is appropriately bounded above and that each homology sheaf is coherent.
$H$ is appropriately bounded above and that each homology sheaf is coherent.
Once one knows full faithfulness, one can establish essential surjectivity with the following proposition.
Proposition 2.3.3 (Essential surjectivity criterion)
Let ![]() $\mathscr {X}$ be a noetherian algebraic derived (or spectral) stack, and let
$\mathscr {X}$ be a noetherian algebraic derived (or spectral) stack, and let ![]() $Z \subset |\mathscr {X}|$ be a cocompact closed subset. Let
$Z \subset |\mathscr {X}|$ be a cocompact closed subset. Let ![]() $\widehat {\mathscr {X}}$ be the formal completion of
$\widehat {\mathscr {X}}$ be the formal completion of ![]() $\mathscr {X}$ along
$\mathscr {X}$ along ![]() $Z$, and assume that
$Z$, and assume that ![]() $\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is fully faithful. Then the following assertions are equivalent:
$\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is fully faithful. Then the following assertions are equivalent:
(i)
 $\mathscr {X}$ is complete along
$\mathscr {X}$ is complete along  $Z$, that is,
$Z$, that is,  $\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is an equivalence;
$\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is an equivalence;(ii) for each
 $m \geqslant 0$, the induced functor of
$m \geqslant 0$, the induced functor of  $(m+1,1)$-categories,
$(m+1,1)$-categories,  ${\rm Coh}^{m} (\mathscr {X}) \to {\rm Coh}^{m} (\widehat {\mathscr {X}})$, is an equivalence;
${\rm Coh}^{m} (\mathscr {X}) \to {\rm Coh}^{m} (\widehat {\mathscr {X}})$, is an equivalence;(iii)
 ${\rm Coh} (\mathscr {X}) \to {\rm Coh} (\widehat {\mathscr {X}})$ is an equivalence;
${\rm Coh} (\mathscr {X}) \to {\rm Coh} (\widehat {\mathscr {X}})$ is an equivalence;(iv) every
 $F \in {\rm Coh} (\widehat {\mathscr {X}})$ admits a surjection from the restriction of an object of
$F \in {\rm Coh} (\widehat {\mathscr {X}})$ admits a surjection from the restriction of an object of  ${\rm Coh} (\mathscr {X})$.
${\rm Coh} (\mathscr {X})$.
Proof. It is clear that ![]() $(\mathrm {i}) \Rightarrow (\mathrm {ii}) \Rightarrow (\mathrm {iii}) \Rightarrow (\mathrm {iv})$. Now assume (iv). For any
$(\mathrm {i}) \Rightarrow (\mathrm {ii}) \Rightarrow (\mathrm {iii}) \Rightarrow (\mathrm {iv})$. Now assume (iv). For any ![]() $\widehat {F} \in {\rm Coh} (\widehat {\mathscr {X}})$, one can find
$\widehat {F} \in {\rm Coh} (\widehat {\mathscr {X}})$, one can find ![]() $G_0,G_1 \in {\rm Coh} (\mathscr {X})$ along with surjections
$G_0,G_1 \in {\rm Coh} (\mathscr {X})$ along with surjections ![]() $i^{\ast } G_0 \to \widehat {F}$ and
$i^{\ast } G_0 \to \widehat {F}$ and ![]() $i^{\ast } G_1 \to \ker (i^{\ast } G_0 \to \widehat {F})$. It follows that
$i^{\ast } G_1 \to \ker (i^{\ast } G_0 \to \widehat {F})$. It follows that ![]() $\tau _{\leqslant 0} \operatorname {cone}(i^{\ast } G_1 \to i^{\ast } G_0) \simeq \widehat {F}$. But by full faithfulness the morphism
$\tau _{\leqslant 0} \operatorname {cone}(i^{\ast } G_1 \to i^{\ast } G_0) \simeq \widehat {F}$. But by full faithfulness the morphism ![]() $i^{\ast } G_1 \to i^{\ast } G_0$ is induced by a morphism
$i^{\ast } G_1 \to i^{\ast } G_0$ is induced by a morphism ![]() $G_1 \to G_0$ and we have
$G_1 \to G_0$ and we have ![]() $\widehat {F} \simeq i^{\ast } \tau _{\leqslant 0} \operatorname {cone}(G_1 \to G_0)$. Hence, we have shown (iii), and (ii) follows from this by a simple inductive argument using the
$\widehat {F} \simeq i^{\ast } \tau _{\leqslant 0} \operatorname {cone}(G_1 \to G_0)$. Hence, we have shown (iii), and (ii) follows from this by a simple inductive argument using the ![]() $t$-structure and Proposition 2.1.11. Finally, for
$t$-structure and Proposition 2.1.11. Finally, for ![]() $(\mathrm {ii}) \Rightarrow (\mathrm {i})$, given
$(\mathrm {ii}) \Rightarrow (\mathrm {i})$, given ![]() $\widehat {F} \in \operatorname {APerf}(\widehat {\mathscr {X}})$, full faithfulness of
$\widehat {F} \in \operatorname {APerf}(\widehat {\mathscr {X}})$, full faithfulness of ![]() $i^{\ast }$ and essential surjectivity on
$i^{\ast }$ and essential surjectivity on ![]() $\operatorname {APerf}(\widehat {\mathscr {X}})_{\geqslant n}$ allow one to lift
$\operatorname {APerf}(\widehat {\mathscr {X}})_{\geqslant n}$ allow one to lift ![]() $\{\tau _{\leqslant n} \widehat {F}\}$ to a tower
$\{\tau _{\leqslant n} \widehat {F}\}$ to a tower ![]() $\cdots \to F_1 \to F_0$ in
$\cdots \to F_1 \to F_0$ in ![]() $\operatorname {APerf}(\mathscr {X})$ with
$\operatorname {APerf}(\mathscr {X})$ with ![]() $i^{\ast }(F_n) \simeq \tau _{\leqslant n} \widehat {F}$. Then part (iv) of Proposition 2.1.11 and part (ii) of Lemma 2.1.12 guarantee that
$i^{\ast }(F_n) \simeq \tau _{\leqslant n} \widehat {F}$. Then part (iv) of Proposition 2.1.11 and part (ii) of Lemma 2.1.12 guarantee that
2.3.1 Completeness is classical
The following is an application of Theorem 3.3.1 below, but we include it here for expository reasons.
Lemma 2.3.4 Let ![]() $\phi : \mathscr {X} \hookrightarrow \mathscr {X}'$ be an almost finitely presented closed immersion of algebraic derived (or spectral) stacks, and
$\phi : \mathscr {X} \hookrightarrow \mathscr {X}'$ be an almost finitely presented closed immersion of algebraic derived (or spectral) stacks, and ![]() $Z \subset |\mathscr {X}'|$ a closed subset. If
$Z \subset |\mathscr {X}'|$ a closed subset. If ![]() $\mathscr {X}'$ is complete along
$\mathscr {X}'$ is complete along ![]() $Z$ then
$Z$ then ![]() $\mathscr {X}$ is complete along
$\mathscr {X}$ is complete along ![]() $|\mathscr {X}| \cap Z \subset |\mathscr {X}|$, and the converse holds if
$|\mathscr {X}| \cap Z \subset |\mathscr {X}|$, and the converse holds if ![]() $\phi$ is surjective.
$\phi$ is surjective.
Proof. Note that ![]() $\phi _\ast (\mathcal {O}_\mathscr {X})$ is a commutative algebra object in the symmetric monoidal
$\phi _\ast (\mathcal {O}_\mathscr {X})$ is a commutative algebra object in the symmetric monoidal ![]() $\infty$-category
$\infty$-category ![]() $\operatorname {APerf}(\mathscr {X}')$, and
$\operatorname {APerf}(\mathscr {X}')$, and ![]() $\operatorname {APerf}(\mathscr {X}) \simeq \phi _\ast (\mathcal {O}_\mathscr {X}) {\rm {}\hbox{-}{\rm mod}} (\operatorname {APerf}(\mathscr {X}')^{\otimes })$. The same is true for
$\operatorname {APerf}(\mathscr {X}) \simeq \phi _\ast (\mathcal {O}_\mathscr {X}) {\rm {}\hbox{-}{\rm mod}} (\operatorname {APerf}(\mathscr {X}')^{\otimes })$. The same is true for ![]() $\widehat {\mathscr {X}'}$ and
$\widehat {\mathscr {X}'}$ and ![]() $\widehat {\mathscr {X}} = \widehat {\mathscr {X}'} \times _{\mathscr {X}'} \mathscr {X}$. So if
$\widehat {\mathscr {X}} = \widehat {\mathscr {X}'} \times _{\mathscr {X}'} \mathscr {X}$. So if ![]() $\operatorname {APerf}(\mathscr {X}') \to \operatorname {APerf}(\widehat {\mathscr {X}'})$ is an equivalence, then so is
$\operatorname {APerf}(\mathscr {X}') \to \operatorname {APerf}(\widehat {\mathscr {X}'})$ is an equivalence, then so is ![]() $\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$.
$\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$.
Conversely, assume that ![]() $\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is an equivalence. Consider the Čech nerve
$\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is an equivalence. Consider the Čech nerve ![]() ${\rm Cech}(\phi ) = \mathscr {X}^{\times _{\mathscr {X}'} \bullet + 1}$. Using descent for surjective closed immersions (Proposition 3.1.5), it suffices to show that
${\rm Cech}(\phi ) = \mathscr {X}^{\times _{\mathscr {X}'} \bullet + 1}$. Using descent for surjective closed immersions (Proposition 3.1.5), it suffices to show that
is an equivalence for all ![]() $n$. This follows from the previous paragraph, because
$n$. This follows from the previous paragraph, because ![]() $\mathscr {X}^{\times _{\mathscr {X}'} n+1} \to \mathscr {X}$ is an almost finitely presented closed immersion.
$\mathscr {X}^{\times _{\mathscr {X}'} n+1} \to \mathscr {X}$ is an almost finitely presented closed immersion.
Corollary 2.3.5 (Formal properness is classical)
An almost finitely presented morphism of algebraic derived (or spectral) stacks ![]() $\pi \colon \mathscr {X} \to \mathscr {S}$ is formally proper if and only if, for every classical noetherian algebraic
$\pi \colon \mathscr {X} \to \mathscr {S}$ is formally proper if and only if, for every classical noetherian algebraic ![]() $\mathscr {S}$-stack
$\mathscr {S}$-stack ![]() $\mathscr {S}'$ which is complete along a closed subset
$\mathscr {S}'$ which is complete along a closed subset ![]() $Z \subset |\mathscr {S}'|$, the classical fiber product
$Z \subset |\mathscr {S}'|$, the classical fiber product ![]() $(\mathscr {X} \times _{\mathscr {S}} \mathscr {S}')^{\rm cl}$ is complete along the preimage of
$(\mathscr {X} \times _{\mathscr {S}} \mathscr {S}')^{\rm cl}$ is complete along the preimage of ![]() $Z$.
$Z$.
Proof. This is an immediate consequence of Lemma 2.3.4, which implies that any noetherian algebraic derived stack ![]() $\mathscr {X}$ is complete if and only if
$\mathscr {X}$ is complete if and only if ![]() $\mathscr {X}^{\rm cl}$ is complete.
$\mathscr {X}^{\rm cl}$ is complete.
2.4 The coherent pushforward property
One property enjoyed by a proper morphism of schemes is that the pushforward and all higher direct images of a coherent sheaf are coherent. In this section we study this as an abstract property of a morphism of stacks.
Definition 2.4.1 Let ![]() $\mathscr {X}$ be a noetherian algebraic derived (or spectral) stack over a noetherian affine derived (respectively, spectral) scheme
$\mathscr {X}$ be a noetherian algebraic derived (or spectral) stack over a noetherian affine derived (respectively, spectral) scheme ![]() $\operatorname {Spec}(R)$. We introduce the following property:
$\operatorname {Spec}(R)$. We introduce the following property:
(CP)R: For any
 $F \in \operatorname {DCoh}(\mathscr {X})$ and
$F \in \operatorname {DCoh}(\mathscr {X})$ and  $i \in \mathbb {Z}$ the sheaf
$i \in \mathbb {Z}$ the sheaf  $H_i \circ R\Gamma (F) \in \operatorname {QC}(R)^{\heartsuit }$ is coherent.
$H_i \circ R\Gamma (F) \in \operatorname {QC}(R)^{\heartsuit }$ is coherent.
We say that a morphism ![]() $\pi : \mathscr {X} \to \mathscr {S}$ between derived prestacks satisfies the coherent pushforward property, or (CP), if
$\pi : \mathscr {X} \to \mathscr {S}$ between derived prestacks satisfies the coherent pushforward property, or (CP), if ![]() $\pi$ is relatively algebraic and almost of finite presentation, and for any morphism
$\pi$ is relatively algebraic and almost of finite presentation, and for any morphism ![]() $\operatorname {Spec}(R) \to \mathscr {S}$ with
$\operatorname {Spec}(R) \to \mathscr {S}$ with ![]() $R$ noetherian, the base change
$R$ noetherian, the base change ![]() $\mathscr {X}_R$ satisfies (CP)R.
$\mathscr {X}_R$ satisfies (CP)R.
Remark 2.4.2 Because any ![]() $F \in \operatorname {DCoh}(\mathscr {X})$ is a finite sequence of extensions of shifts of its homology sheaves, (CP)R is equivalent to the condition
$F \in \operatorname {DCoh}(\mathscr {X})$ is a finite sequence of extensions of shifts of its homology sheaves, (CP)R is equivalent to the condition ![]() $\pi _\ast ({\rm Coh} (\mathscr {X})) \subset \operatorname {{\mathbb {D}}APerf}(R)$, and using the right
$\pi _\ast ({\rm Coh} (\mathscr {X})) \subset \operatorname {{\mathbb {D}}APerf}(R)$, and using the right ![]() $t$-completeness of
$t$-completeness of ![]() $\operatorname {APerf}(\mathscr {X})$ and the left
$\operatorname {APerf}(\mathscr {X})$ and the left ![]() $t$-exactness of
$t$-exactness of ![]() $\pi _\ast$, one sees that it is also equivalent to
$\pi _\ast$, one sees that it is also equivalent to ![]() $\pi _\ast (\operatorname {{\mathbb {D}}APerf}(\mathscr {X}))\subset \operatorname {{\mathbb {D}}APerf}(R)$.
$\pi _\ast (\operatorname {{\mathbb {D}}APerf}(\mathscr {X}))\subset \operatorname {{\mathbb {D}}APerf}(R)$.
For a morphism ![]() $\pi : \mathscr {X} \to \mathscr {S}$ of noetherian stacks, we will sometimes abuse notation and write (CP)
$\pi : \mathscr {X} \to \mathscr {S}$ of noetherian stacks, we will sometimes abuse notation and write (CP)![]() ${}_{\mathscr {S}}$ to denote the property that
${}_{\mathscr {S}}$ to denote the property that ![]() $\pi _\ast (\operatorname {DCoh}(\mathscr {X})) \subset \operatorname {{\mathbb {D}}APerf}(\mathscr {S})$. It is an immediate consequence of fppf descent for
$\pi _\ast (\operatorname {DCoh}(\mathscr {X})) \subset \operatorname {{\mathbb {D}}APerf}(\mathscr {S})$. It is an immediate consequence of fppf descent for ![]() $\operatorname {{\mathbb {D}}APerf}$ that for a morphism
$\operatorname {{\mathbb {D}}APerf}$ that for a morphism ![]() $\pi : \mathscr {X} \to \mathscr {S}$ satisfying (CP),
$\pi : \mathscr {X} \to \mathscr {S}$ satisfying (CP), ![]() $\mathscr {X}_{\mathscr {S}'}$ satisfies (CP)
$\mathscr {X}_{\mathscr {S}'}$ satisfies (CP) ![]() ${}_{\mathscr {S}'}$ for any noetherian algebraic derived stack with a map
${}_{\mathscr {S}'}$ for any noetherian algebraic derived stack with a map ![]() $\mathscr {S}' \to \mathscr {S}$.
$\mathscr {S}' \to \mathscr {S}$.
Theorem 2.4.3 Let ![]() $\pi : \mathscr {X} \to \mathscr {S}$ be a relatively algebraic morphism of derived prestacks. Then the condition that
$\pi : \mathscr {X} \to \mathscr {S}$ be a relatively algebraic morphism of derived prestacks. Then the condition that ![]() $\pi$ satisfies (CP) is local over
$\pi$ satisfies (CP) is local over ![]() $\mathscr {S}$ with respect to the fppf topology. Furthermore, if
$\mathscr {S}$ with respect to the fppf topology. Furthermore, if ![]() $\pi$ is almost finitely presented, then (CP) is equivalent to the ‘fully faithful’ part of Definition 1.1.3 (formal properness):
$\pi$ is almost finitely presented, then (CP) is equivalent to the ‘fully faithful’ part of Definition 1.1.3 (formal properness):
For any noetherian algebraic derived stack
 $\mathscr {S}'$ which is complete along
$\mathscr {S}'$ which is complete along  $Z \subset |\mathscr {S}'|$, and any morphism
$Z \subset |\mathscr {S}'|$, and any morphism  $\mathscr {S}' \to \mathscr {S}$, if
$\mathscr {S}' \to \mathscr {S}$, if  $\mathscr {X}' := \mathscr {X} \times _\mathscr {S} \mathscr {S}'$ and
$\mathscr {X}' := \mathscr {X} \times _\mathscr {S} \mathscr {S}'$ and  $Z' \subset |\mathscr {X}'|$ is the preimage of
$Z' \subset |\mathscr {X}'|$ is the preimage of  $Z$, then the restriction map
$Z$, then the restriction map  $\operatorname {APerf}(\mathscr {X}') \to \operatorname {APerf}(\widehat {\mathscr {X}'})$ is fully faithful.
$\operatorname {APerf}(\mathscr {X}') \to \operatorname {APerf}(\widehat {\mathscr {X}'})$ is fully faithful.
In particular, every formally proper morphism satisfies (CP).
Lemma 2.4.4 Let ![]() $\pi : \mathscr {X} \to \operatorname {Spec}(R)$ be a morphism between noetherian algebraic derived stacks such that
$\pi : \mathscr {X} \to \operatorname {Spec}(R)$ be a morphism between noetherian algebraic derived stacks such that
is fully faithful, where ![]() $\widehat {\mathscr {X}}_{R[\![t]\!]}$ denotes the formal completion of
$\widehat {\mathscr {X}}_{R[\![t]\!]}$ denotes the formal completion of ![]() $\mathscr {X}_{R[\![t]\!]}$ along the preimage of the ideal
$\mathscr {X}_{R[\![t]\!]}$ along the preimage of the ideal ![]() $(t) \subset \pi _0(R[\![t]\!])$. Then
$(t) \subset \pi _0(R[\![t]\!])$. Then ![]() $\pi$ satisfies (CP)R.
$\pi$ satisfies (CP)R.
Proof. Let us denote ![]() $S = \operatorname {Spec}(R[\![t]\!])$ and
$S = \operatorname {Spec}(R[\![t]\!])$ and ![]() $R_n = R[\![t]\!]/(t^{n})$. Let
$R_n = R[\![t]\!]/(t^{n})$. Let ![]() $F \in \operatorname {DCoh}(\mathscr {X})$, and consider the
$F \in \operatorname {DCoh}(\mathscr {X})$, and consider the ![]() $R[\![t]\!]$-module
$R[\![t]\!]$-module ![]() $E:= (\pi _S)_\ast (F|_{\mathscr {X}_S}) \in \operatorname {QC}(S)_{\leqslant 0}$. Applying the base change Lemma A.1.3 to the finite Tor amplitude inclusions
$E:= (\pi _S)_\ast (F|_{\mathscr {X}_S}) \in \operatorname {QC}(S)_{\leqslant 0}$. Applying the base change Lemma A.1.3 to the finite Tor amplitude inclusions ![]() $\operatorname {Spec}(R_n) \hookrightarrow S$ and the full-faithfulness hypothesis of the lemma, we have
$\operatorname {Spec}(R_n) \hookrightarrow S$ and the full-faithfulness hypothesis of the lemma, we have
so ![]() $E$ is complete as an
$E$ is complete as an ![]() $R[\![t]\!]$-module, that is,
$R[\![t]\!]$-module, that is, ![]() $E \xrightarrow {\simeq } \widehat {E}$ is an equivalence. Applying base change to the flat map
$E \xrightarrow {\simeq } \widehat {E}$ is an equivalence. Applying base change to the flat map ![]() $S \to \operatorname {Spec}(R)$, we have
$S \to \operatorname {Spec}(R)$, we have ![]() $E \simeq R[\![t]\!] \otimes _R \pi _\ast (F)$.
$E \simeq R[\![t]\!] \otimes _R \pi _\ast (F)$.
It therefore suffices to show that a complex ![]() $M \in R {\rm {}\hbox{-}{\rm mod}}_{\leqslant 0}$ such that
$M \in R {\rm {}\hbox{-}{\rm mod}}_{\leqslant 0}$ such that ![]() $R[\![t]\!] \otimes _R M$ is complete must have coherent homology. By [Reference LurieLur3, Theorem 4.2.13] it suffices to prove this for
$R[\![t]\!] \otimes _R M$ is complete must have coherent homology. By [Reference LurieLur3, Theorem 4.2.13] it suffices to prove this for ![]() $M \in \operatorname {QC}(R)^{\heartsuit }$, for which we may assume that
$M \in \operatorname {QC}(R)^{\heartsuit }$, for which we may assume that ![]() $R$ is classical. Express
$R$ is classical. Express ![]() $M$ as a filtered union of coherent submodules
$M$ as a filtered union of coherent submodules ![]() $M = \bigcup M_\alpha$. If
$M = \bigcup M_\alpha$. If ![]() $M$ is not coherent, then this union does not stabilize, so we can find a sequence
$M$ is not coherent, then this union does not stabilize, so we can find a sequence ![]() $m_0,m_1,\ldots \in M$ which is not contained in any
$m_0,m_1,\ldots \in M$ which is not contained in any ![]() $M_\alpha$. Then
$M_\alpha$. Then ![]() $R[[t]] \otimes _R M = \bigcup R[[t]] \otimes _R M_\alpha$, but the element
$R[[t]] \otimes _R M = \bigcup R[[t]] \otimes _R M_\alpha$, but the element ![]() $\sum t^{i} m_i \in H_0( (R[[t]] \otimes _R M)^{\wedge })$ does not lie in the image of any of the
$\sum t^{i} m_i \in H_0( (R[[t]] \otimes _R M)^{\wedge })$ does not lie in the image of any of the ![]() $R[[t]]\otimes _R M_\alpha$, and so
$R[[t]]\otimes _R M_\alpha$, and so ![]() $R[[t]] \otimes _R M$ does not surject onto its completion. This contradicts the hypothesis that
$R[[t]] \otimes _R M$ does not surject onto its completion. This contradicts the hypothesis that ![]() $R[\![t]\!] \otimes M$ is complete.
$R[\![t]\!] \otimes M$ is complete.
Proof of Theorem 2.4.3 In order to show locality, consider an algebraic fppf morphism ![]() $\mathscr {S}' \to \mathscr {S}$, and let
$\mathscr {S}' \to \mathscr {S}$, and let ![]() $\pi ^{\prime } : \mathscr {X}^{\prime } := \mathscr {X} \times _\mathscr {S} \mathscr {S}^{\prime } \to \mathscr {S}^{\prime }$. We must show that
$\pi ^{\prime } : \mathscr {X}^{\prime } := \mathscr {X} \times _\mathscr {S} \mathscr {S}^{\prime } \to \mathscr {S}^{\prime }$. We must show that ![]() $\pi$ satisfies (CP) if
$\pi$ satisfies (CP) if ![]() $\pi ^{\prime }$ does – the other direction follows by definition. Note that the condition of being almost of finite presentation is local on the target for the fppf topology. For any map
$\pi ^{\prime }$ does – the other direction follows by definition. Note that the condition of being almost of finite presentation is local on the target for the fppf topology. For any map ![]() $\operatorname {Spec}(R) \to \mathscr {S}$ for a noetherian
$\operatorname {Spec}(R) \to \mathscr {S}$ for a noetherian ![]() $R\in \mathrm {SCR}$, there exists an fppf map
$R\in \mathrm {SCR}$, there exists an fppf map ![]() $\operatorname {Spec}(R^{\prime }) \to \operatorname {Spec}(R)$ such that
$\operatorname {Spec}(R^{\prime }) \to \operatorname {Spec}(R)$ such that ![]() $\operatorname {Spec}(R^{\prime }) \to \operatorname {Spec}(R) \to \mathscr {S}$ factors through
$\operatorname {Spec}(R^{\prime }) \to \operatorname {Spec}(R) \to \mathscr {S}$ factors through ![]() $\mathscr {S}^{\prime }$. Because
$\mathscr {S}^{\prime }$. Because ![]() $\pi ^{\prime } : \mathscr {X}^{\prime } \to \mathscr {S}^{\prime }$ satisfies (CP), we have that (CP)R' holds, and thus so does (CP)R by flat base change (Lemma A.1.3) and faithfully flat descent.
$\pi ^{\prime } : \mathscr {X}^{\prime } \to \mathscr {S}^{\prime }$ satisfies (CP), we have that (CP)R' holds, and thus so does (CP)R by flat base change (Lemma A.1.3) and faithfully flat descent.
The fact that the condition in the statement implies (CP) follows from Lemma 2.4.4, and the converse is Proposition 2.3.1.
Proposition 2.4.5 Let ![]() $\mathscr {S}$ be a noetherian derived stack. Then any morphism
$\mathscr {S}$ be a noetherian derived stack. Then any morphism ![]() $\pi \colon \mathscr {X} \to \mathscr {S}$ satisfying (CP), and in particular any formally proper morphism, is universally closed.
$\pi \colon \mathscr {X} \to \mathscr {S}$ satisfying (CP), and in particular any formally proper morphism, is universally closed.
Lemma 2.4.6 For a finitely presented morphism of classical algebraic stacks ![]() $\mathscr {X} \to \mathscr {Y}$, the following assertions are equivalent:
$\mathscr {X} \to \mathscr {Y}$, the following assertions are equivalent:
(i)
 $\mathscr {X} \to \mathscr {Y}$ is universally closed;
$\mathscr {X} \to \mathscr {Y}$ is universally closed;(ii)
 $\mathscr {X} \times _\mathscr {Y} \mathscr {Y}' \to \mathscr {Y}'$ is closed for any morphism
$\mathscr {X} \times _\mathscr {Y} \mathscr {Y}' \to \mathscr {Y}'$ is closed for any morphism  $\mathscr {Y}' \to \mathscr {Y}$ of finite type (and it suffices to assume
$\mathscr {Y}' \to \mathscr {Y}$ of finite type (and it suffices to assume  $\mathscr {Y}'$ is affine);
$\mathscr {Y}'$ is affine);(iii) for any
 $n$,
$n$,  $\mathscr {X} \times \mathbf {A}^{n} \to \mathscr {Y} \times \mathbf {A}^{n}$ is closed.
$\mathscr {X} \times \mathbf {A}^{n} \to \mathscr {Y} \times \mathbf {A}^{n}$ is closed.
Proof. The property of a morphism being closed is fppf local on the target, so it suffices to assume that ![]() $\mathscr {Y} = \operatorname {Spec}(R)$ is affine, and in (ii) it suffices to assume that
$\mathscr {Y} = \operatorname {Spec}(R)$ is affine, and in (ii) it suffices to assume that ![]() $\mathscr {Y}' = \operatorname {Spec}(A)$ is affine. We have immediate implications
$\mathscr {Y}' = \operatorname {Spec}(A)$ is affine. We have immediate implications ![]() $(\mathrm {i}) \Rightarrow (\mathrm {ii}) \Rightarrow (\mathrm {iii})$, and
$(\mathrm {i}) \Rightarrow (\mathrm {ii}) \Rightarrow (\mathrm {iii})$, and ![]() $(\mathrm {iii}) \Rightarrow (\mathrm {ii})$ because we can write
$(\mathrm {iii}) \Rightarrow (\mathrm {ii})$ because we can write ![]() $A' = A[x_1,\ldots,x_n] / I$ for some ideal
$A' = A[x_1,\ldots,x_n] / I$ for some ideal ![]() $I$ and thus realize
$I$ and thus realize ![]() $Y'$ as a closed subscheme of
$Y'$ as a closed subscheme of ![]() $Y \times \mathbf {A}^{n}$. So we must show that if
$Y \times \mathbf {A}^{n}$. So we must show that if ![]() $\mathscr {X}_{A} \to \operatorname {Spec}(A)$ is closed for any finitely generated
$\mathscr {X}_{A} \to \operatorname {Spec}(A)$ is closed for any finitely generated ![]() $R$-algebra
$R$-algebra ![]() $A$, then it is closed for any
$A$, then it is closed for any ![]() $R$-algebra.
$R$-algebra.
By relative noetherian approximation, ![]() $\mathscr {X}$ can be obtained by base change from a finitely presented algebraic stack over
$\mathscr {X}$ can be obtained by base change from a finitely presented algebraic stack over ![]() $\mathscr {X}'$ a noetherian subring
$\mathscr {X}'$ a noetherian subring ![]() $R' \subset R$. By Theorem A.2.1,
$R' \subset R$. By Theorem A.2.1, ![]() $\operatorname {QC}(\mathscr {X}')^{\heartsuit }$ is a locally noetherian
$\operatorname {QC}(\mathscr {X}')^{\heartsuit }$ is a locally noetherian ![]() $R'$-linear abelian category in the sense of [Reference PopescuPop73, § 5.8]. For any
$R'$-linear abelian category in the sense of [Reference PopescuPop73, § 5.8]. For any ![]() $R'$-algebra
$R'$-algebra ![]() $A$,
$A$, ![]() $\operatorname {QC}(\mathscr {X}_A)^{\heartsuit }$ is the category of
$\operatorname {QC}(\mathscr {X}_A)^{\heartsuit }$ is the category of ![]() $A$-module objects in
$A$-module objects in ![]() $\operatorname {QC}(\mathscr {X}')^{\heartsuit }$, and it is a locally finitely presentable (i.e. compactly generated) abelian category. In fact, it is generated by the pullbacks of coherent sheaves on
$\operatorname {QC}(\mathscr {X}')^{\heartsuit }$, and it is a locally finitely presentable (i.e. compactly generated) abelian category. In fact, it is generated by the pullbacks of coherent sheaves on ![]() $\mathscr {X}'$, which are finitely presented objects of
$\mathscr {X}'$, which are finitely presented objects of ![]() $\operatorname {QC}(\mathscr {X}_A)^{\heartsuit }$ [Reference Artin and ZhangAZ01, B3.17, B5.1i].
$\operatorname {QC}(\mathscr {X}_A)^{\heartsuit }$ [Reference Artin and ZhangAZ01, B3.17, B5.1i].
Now consider an ![]() $R$-algebra
$R$-algebra ![]() $A$, and write
$A$, and write ![]() $A = \bigcup _\alpha A_\alpha$ as a filtered union of finitely generated
$A = \bigcup _\alpha A_\alpha$ as a filtered union of finitely generated ![]() $R$-algebras
$R$-algebras ![]() $A_\alpha$. Then pullback induces an equivalence of categories of finitely presented objects
$A_\alpha$. Then pullback induces an equivalence of categories of finitely presented objects
If ![]() $\mathscr {Z} \hookrightarrow \mathscr {X}_A$ is a finitely presented closed immersion, then
$\mathscr {Z} \hookrightarrow \mathscr {X}_A$ is a finitely presented closed immersion, then ![]() $\mathcal {O}_\mathscr {Z} = \!\!\mathop {\rm ~coker}\nolimits (M \to \mathcal {O}_{\mathscr {X}_A})$ for some finitely presented quasi-coherent sheaf
$\mathcal {O}_\mathscr {Z} = \!\!\mathop {\rm ~coker}\nolimits (M \to \mathcal {O}_{\mathscr {X}_A})$ for some finitely presented quasi-coherent sheaf ![]() $M$. Then the map
$M$. Then the map ![]() $M \to \mathcal {O}_{\mathscr {X}_A}$ is the pullback of a map
$M \to \mathcal {O}_{\mathscr {X}_A}$ is the pullback of a map ![]() $M_\alpha \to \mathcal {O}_{\mathscr {X}_{A_\alpha }}$ in
$M_\alpha \to \mathcal {O}_{\mathscr {X}_{A_\alpha }}$ in ![]() $\operatorname {QC}(\mathscr {X}_{A_\alpha })^{\heartsuit }$ with
$\operatorname {QC}(\mathscr {X}_{A_\alpha })^{\heartsuit }$ with ![]() $M_\alpha$ finitely presented. In particular,
$M_\alpha$ finitely presented. In particular, ![]() $\mathscr {Z}$ is the preimage of a closed substack
$\mathscr {Z}$ is the preimage of a closed substack ![]() $\mathscr {Z}_\alpha \hookrightarrow \mathscr {X}_{A_\alpha }$. This gives a diagram of topological spaces, in which the square is cartesian:
$\mathscr {Z}_\alpha \hookrightarrow \mathscr {X}_{A_\alpha }$. This gives a diagram of topological spaces, in which the square is cartesian:

It follows that ![]() $\pi (|\mathscr {Z}|) = f^{-1}(\pi _\alpha (|\mathscr {Z}_\alpha |))$, and hence
$\pi (|\mathscr {Z}|) = f^{-1}(\pi _\alpha (|\mathscr {Z}_\alpha |))$, and hence ![]() $\pi (\mathscr {Z})$ is closed, because by hypothesis
$\pi (\mathscr {Z})$ is closed, because by hypothesis ![]() $\pi _\alpha$ is a closed map.
$\pi _\alpha$ is a closed map.
So we have shown that the image under ![]() $\pi$ of the underlying subset of a finitely presented closed immersion is closed in
$\pi$ of the underlying subset of a finitely presented closed immersion is closed in ![]() $|\!\operatorname {Spec}(A)|$, and we must show that the same is true for the subset underlying any closed immersion
$|\!\operatorname {Spec}(A)|$, and we must show that the same is true for the subset underlying any closed immersion ![]() $\mathscr {Z} \hookrightarrow \mathscr {X}_A$. We know that
$\mathscr {Z} \hookrightarrow \mathscr {X}_A$. We know that ![]() $\mathcal {O}_\mathscr {Z} = \!\!\mathop {\rm ~coker}\nolimits (M \to \mathcal {O}_{\mathscr {X}_A})$ for some
$\mathcal {O}_\mathscr {Z} = \!\!\mathop {\rm ~coker}\nolimits (M \to \mathcal {O}_{\mathscr {X}_A})$ for some ![]() $M \in \operatorname {QC}(\mathscr {X}_A)^{\heartsuit }$. Writing
$M \in \operatorname {QC}(\mathscr {X}_A)^{\heartsuit }$. Writing ![]() $M = \varinjlim _\alpha M_\alpha$ as a colimit of finitely presented quasi-coherent sheaves, we can write
$M = \varinjlim _\alpha M_\alpha$ as a colimit of finitely presented quasi-coherent sheaves, we can write ![]() $\mathscr {Z}$ as a cofiltered intersection of schemes
$\mathscr {Z}$ as a cofiltered intersection of schemes ![]() $\mathscr {Z} = \cap _\alpha \mathscr {Z}_\alpha$, where
$\mathscr {Z} = \cap _\alpha \mathscr {Z}_\alpha$, where ![]() $\mathcal {O}_{\mathscr {Z}_\alpha } = \!\!\mathop {\rm ~coker}\nolimits (M_\alpha \to \mathcal {O}_{\mathscr {X}_A})$, hence
$\mathcal {O}_{\mathscr {Z}_\alpha } = \!\!\mathop {\rm ~coker}\nolimits (M_\alpha \to \mathcal {O}_{\mathscr {X}_A})$, hence ![]() $\mathscr {Z}_\alpha \to \mathscr {X}_A$ is a finitely presented closed immersion.
$\mathscr {Z}_\alpha \to \mathscr {X}_A$ is a finitely presented closed immersion.
We claim that ![]() $\pi (|\mathscr {Z}|) = \cap _\alpha \pi (|\mathscr {Z}_\alpha |)$. The inclusion
$\pi (|\mathscr {Z}|) = \cap _\alpha \pi (|\mathscr {Z}_\alpha |)$. The inclusion ![]() $\pi (|\mathscr {Z}|) \subset \cap _\alpha \pi (|\mathscr {Z}_\alpha |)$ is clear. If
$\pi (|\mathscr {Z}|) \subset \cap _\alpha \pi (|\mathscr {Z}_\alpha |)$ is clear. If ![]() $p \in \pi (|\mathscr {Z}|) \subset |\!\operatorname {Spec}(A)|$ is a point, represented by a map
$p \in \pi (|\mathscr {Z}|) \subset |\!\operatorname {Spec}(A)|$ is a point, represented by a map ![]() $\operatorname {Spec}(K) \to \operatorname {Spec}(A)$ for some field
$\operatorname {Spec}(K) \to \operatorname {Spec}(A)$ for some field ![]() $K$, then
$K$, then ![]() $\mathscr {Z}_K \subset \mathscr {X}_K$ is non-empty. Because
$\mathscr {Z}_K \subset \mathscr {X}_K$ is non-empty. Because ![]() $\mathscr {X}_K$ is noetherian, the cofiltered system
$\mathscr {X}_K$ is noetherian, the cofiltered system ![]() $(\mathscr {Z}_\alpha )_K$ is eventually constant, that is,
$(\mathscr {Z}_\alpha )_K$ is eventually constant, that is, ![]() $\mathscr {Z}_K = (\mathscr {Z}_\alpha )_K$ for
$\mathscr {Z}_K = (\mathscr {Z}_\alpha )_K$ for ![]() $\alpha$ sufficiently large. It follows that
$\alpha$ sufficiently large. It follows that ![]() $p \in \cap _\alpha \pi (|\mathscr {Z}_\alpha |)$, hence
$p \in \cap _\alpha \pi (|\mathscr {Z}_\alpha |)$, hence ![]() $\pi (|\mathscr {Z}|) = \cap _\alpha \pi (|\mathscr {Z}_\alpha |)$. This shows that
$\pi (|\mathscr {Z}|) = \cap _\alpha \pi (|\mathscr {Z}_\alpha |)$. This shows that ![]() $\pi (|\mathscr {Z}|)$ is closed, because we have already shown that
$\pi (|\mathscr {Z}|)$ is closed, because we have already shown that ![]() $\pi (|\mathscr {Z}_\alpha |)$ is closed for all
$\pi (|\mathscr {Z}_\alpha |)$ is closed for all ![]() $\alpha$.
$\alpha$.
Proof of Proposition 2.4.5 Being universally closed is local for the smooth topology, so it suffices to assume ![]() $\mathscr {S} = \operatorname {Spec}(R)$ is an affine Noetherian derived scheme and show that for any
$\mathscr {S} = \operatorname {Spec}(R)$ is an affine Noetherian derived scheme and show that for any ![]() $R$-algebra
$R$-algebra ![]() $A$ the map
$A$ the map ![]() $|\mathscr {X}_A| \to |\!\operatorname {Spec}(A)|$ is closed. This is a statement about underlying classical stacks, so by Lemma 2.4.6 it suffices to consider only almost finitely presented discrete
$|\mathscr {X}_A| \to |\!\operatorname {Spec}(A)|$ is closed. This is a statement about underlying classical stacks, so by Lemma 2.4.6 it suffices to consider only almost finitely presented discrete ![]() $R$-algebras
$R$-algebras ![]() $A$. So it suffices to show that if
$A$. So it suffices to show that if ![]() $\pi : \mathscr {X} \to \operatorname {Spec}(A)$ is an almost finitely presented map of noetherian classical stacks which satisfies (CP), then it is closed.
$\pi : \mathscr {X} \to \operatorname {Spec}(A)$ is an almost finitely presented map of noetherian classical stacks which satisfies (CP), then it is closed.
By Chevalley's theorem the image of ![]() $\pi$ is constructible, so
$\pi$ is constructible, so ![]() $\pi$ factors through a closed subscheme of
$\pi$ factors through a closed subscheme of ![]() $\operatorname {Spec}(A)$ in which it has a dense image. We replace
$\operatorname {Spec}(A)$ in which it has a dense image. We replace ![]() $\operatorname {Spec}(A)$ with this closed subscheme, so that we may assume
$\operatorname {Spec}(A)$ with this closed subscheme, so that we may assume ![]() $\pi : \mathscr {X} \to \operatorname {Spec}(A)$ is dense, and we must show that it is surjective. We can choose any point
$\pi : \mathscr {X} \to \operatorname {Spec}(A)$ is dense, and we must show that it is surjective. We can choose any point ![]() $p \in |\!\operatorname {Spec}(A)|$, and consider the base change to the local ring
$p \in |\!\operatorname {Spec}(A)|$, and consider the base change to the local ring ![]() $A_p$.
$A_p$.
It suffices to show that ![]() $p$ lies in the image of
$p$ lies in the image of ![]() $\pi _{A_p} \colon \mathscr {X}_{A_{p}} \to \operatorname {Spec}(A_p)$ assuming the image of this map contains a dense open subscheme
$\pi _{A_p} \colon \mathscr {X}_{A_{p}} \to \operatorname {Spec}(A_p)$ assuming the image of this map contains a dense open subscheme ![]() $U \subset \operatorname {Spec}(A_p)$. We can choose a prime contained in
$U \subset \operatorname {Spec}(A_p)$. We can choose a prime contained in ![]() $U$ which has dimension
$U$ which has dimension ![]() $1$. Its closure defines a closed subscheme of dimension
$1$. Its closure defines a closed subscheme of dimension ![]() $1$,
$1$, ![]() $Z \subset \operatorname {Spec}(A_p)$, whose special point is
$Z \subset \operatorname {Spec}(A_p)$, whose special point is ![]() $p$, and whose generic point lies in
$p$, and whose generic point lies in ![]() $U$ and hence the image of
$U$ and hence the image of ![]() $\pi _{A_p}$. It suffices to consider the base change
$\pi _{A_p}$. It suffices to consider the base change ![]() $\pi _Z : \mathscr {X}_Z \to Z$, and to show that
$\pi _Z : \mathscr {X}_Z \to Z$, and to show that ![]() $p \in \operatorname {im}(\pi _Z)$.
$p \in \operatorname {im}(\pi _Z)$.
If the special point ![]() $p \in Z$ did not lie in the image of
$p \in Z$ did not lie in the image of ![]() $\pi _Z$, then
$\pi _Z$, then ![]() $\pi _Z$ would factor through the generic point
$\pi _Z$ would factor through the generic point ![]() $\mathscr {X}_Z \to Z \setminus \{p\} \to Z$. The latter morphism is affine, hence
$\mathscr {X}_Z \to Z \setminus \{p\} \to Z$. The latter morphism is affine, hence ![]() $t$-exact, and it is immediate that the pushforward of any non-zero coherent sheaf is no longer coherent. This contradicts the property (CP) for the map
$t$-exact, and it is immediate that the pushforward of any non-zero coherent sheaf is no longer coherent. This contradicts the property (CP) for the map ![]() $\pi _Z$, because
$\pi _Z$, because ![]() $(\pi _Z)_\ast (\mathcal {O}_{\mathscr {X}_Z}) \in \operatorname {{\mathbb {D}}APerf}(Z)$ is a non-zero object with coherent cohomology which we have argued is pushed forward from
$(\pi _Z)_\ast (\mathcal {O}_{\mathscr {X}_Z}) \in \operatorname {{\mathbb {D}}APerf}(Z)$ is a non-zero object with coherent cohomology which we have argued is pushed forward from ![]() $Z \setminus \{p\}$. It follows that we must have
$Z \setminus \{p\}$. It follows that we must have ![]() $p \in \operatorname {im}(\pi _Z)$.
$p \in \operatorname {im}(\pi _Z)$.
Theorem 2.4.3 shows that (CP) is ‘half’ of the condition of formal properness, so it is desirable to have a more direct criterion for (CP).
Proposition 2.4.7 Let ![]() $\pi : \mathscr {X} \to \mathscr {S}$ be an almost finitely presented morphism of algebraic derived (or spectral) stacks satisfying (CD), and assume
$\pi : \mathscr {X} \to \mathscr {S}$ be an almost finitely presented morphism of algebraic derived (or spectral) stacks satisfying (CD), and assume ![]() $\mathscr {S}$ is quasi-compact with affine diagonal. Then (CP) is equivalent to (CP)
$\mathscr {S}$ is quasi-compact with affine diagonal. Then (CP) is equivalent to (CP) ![]() ${}_{\mathscr {S}}$ for the morphism
${}_{\mathscr {S}}$ for the morphism ![]() $\pi$.
$\pi$.
Proof. Let ![]() $S \to \mathscr {S}$ be a morphism from a noetherian affine derived scheme, and let
$S \to \mathscr {S}$ be a morphism from a noetherian affine derived scheme, and let ![]() $\mathscr {X}^{\prime } := \mathscr {X} \times _\mathscr {S} S$. By taking shifts it suffices to show that (CP)
$\mathscr {X}^{\prime } := \mathscr {X} \times _\mathscr {S} S$. By taking shifts it suffices to show that (CP) ![]() ${}_{\mathscr {S}}$ implies that
${}_{\mathscr {S}}$ implies that ![]() $\pi ^{\prime }_\ast (\operatorname {APerf}(\mathscr {X}^{\prime })_{\geqslant d}) \subset \operatorname {APerf}(S)$ for any fixed
$\pi ^{\prime }_\ast (\operatorname {APerf}(\mathscr {X}^{\prime })_{\geqslant d}) \subset \operatorname {APerf}(S)$ for any fixed ![]() $d$. The base-change formula, Proposition A.1.5, shows that this holds on the full subcategory of
$d$. The base-change formula, Proposition A.1.5, shows that this holds on the full subcategory of ![]() $\operatorname {APerf}(\mathscr {X}')$ spanned by derived pullbacks from
$\operatorname {APerf}(\mathscr {X}')$ spanned by derived pullbacks from ![]() $\operatorname {APerf}(\mathscr {X})$. Since
$\operatorname {APerf}(\mathscr {X})$. Since ![]() $\mathscr {X}' \to \mathscr {X}$ is affine, any
$\mathscr {X}' \to \mathscr {X}$ is affine, any ![]() $F \in \operatorname {APerf}(\mathscr {X}^{\prime })_{\geqslant d}$ admits the cobar simplicial resolution by pullbacks of objects in
$F \in \operatorname {APerf}(\mathscr {X}^{\prime })_{\geqslant d}$ admits the cobar simplicial resolution by pullbacks of objects in ![]() $\operatorname {APerf}(\mathscr {X})_{\geqslant d}$. Let
$\operatorname {APerf}(\mathscr {X})_{\geqslant d}$. Let ![]() $d$ be bigger than the universal cohomological dimension of
$d$ be bigger than the universal cohomological dimension of ![]() $\pi$, so that each term in the pushforward simplicial resolution is connective. The result follows by noting that
$\pi$, so that each term in the pushforward simplicial resolution is connective. The result follows by noting that ![]() $\operatorname {APerf}(S)_{\geqslant 0}$ is preserved by geometric realizations [Reference LurieLur17, Proposition 7.2.4.11(4)].
$\operatorname {APerf}(S)_{\geqslant 0}$ is preserved by geometric realizations [Reference LurieLur17, Proposition 7.2.4.11(4)].
3.  $h$-descent theorems
$h$-descent theorems
In this section we establish a general ‘![]() $h$-descent’ theorem, Theorem 3.3.1, for
$h$-descent’ theorem, Theorem 3.3.1, for ![]() $\operatorname {APerf}$ and
$\operatorname {APerf}$ and ![]() $\operatorname {Perf}$ for later use, and we believe it is of independent interest. It is similar to – and can be deduced, in characteristic
$\operatorname {Perf}$ for later use, and we believe it is of independent interest. It is similar to – and can be deduced, in characteristic ![]() $0$ and in the presence of a dualizing complex, from – the
$0$ and in the presence of a dualizing complex, from – the ![]() $h$-descent theorem for
$h$-descent theorem for ![]() $\operatorname {Ind}\operatorname {DCoh}$ in [Reference PreygelPre11] and in [Reference GaitsgoryGai13]. Nevertheless, the proof is more elementary since it avoids use of the shriek pullback functors.
$\operatorname {Ind}\operatorname {DCoh}$ in [Reference PreygelPre11] and in [Reference GaitsgoryGai13]. Nevertheless, the proof is more elementary since it avoids use of the shriek pullback functors.
As an interesting consequence, we show in Proposition 3.3.7 that locally noetherian algebraic spectral stacks with quasi-affine diagonal are sheaves for the spectral ![]() $h$-topology. This is in contrast to the classical
$h$-topology. This is in contrast to the classical ![]() $h$-topology, for which the functor represented by an affine scheme is not a sheaf.
$h$-topology, for which the functor represented by an affine scheme is not a sheaf.
We state most of the results in this section for derived stacks, but all of the results hold in the spectral context as well (except for Proposition 3.3.7, which we only prove for spectral stacks). In the proofs, we indicate the modifications needed to prove the claim in both contexts. Throughout this section we fix a base noetherian simplicial commutative algebra ![]() $\mathbf {k} \in \mathrm {SCR}$, and in the spectral context we use the same symbol to denote a base
$\mathbf {k} \in \mathrm {SCR}$, and in the spectral context we use the same symbol to denote a base ![]() $E_\infty$-algebra
$E_\infty$-algebra ![]() $\mathbf {k} \in \mathrm {CAlg}^{\mathrm {cn}}$.
$\mathbf {k} \in \mathrm {CAlg}^{\mathrm {cn}}$.
3.1 Descent pattern for closed immersions
The aim for this subsection is to investigate a general descent pattern for what one might call the (derived) nil-immersion topology. This will be the Grothendieck topology on ![]() $\mathrm {SCR}_\mathbf {k}$ generated by surjective almost finitely presented closed immersions.
$\mathrm {SCR}_\mathbf {k}$ generated by surjective almost finitely presented closed immersions.
Lemma 3.1.1 Suppose that ![]() $\mathscr {F}$ is a presheaf on
$\mathscr {F}$ is a presheaf on ![]() $\mathrm {SCR}_\mathbf {k}$ that satisfies the following conditions.
$\mathrm {SCR}_\mathbf {k}$ that satisfies the following conditions.
(i) (nilcompleteness) The natural map
 $\mathscr {F}(R) \longrightarrow \mathop {\varprojlim }\limits _n \mathscr {F}(\tau _{\leqslant n} R)$ is an equivalence for all
$\mathscr {F}(R) \longrightarrow \mathop {\varprojlim }\limits _n \mathscr {F}(\tau _{\leqslant n} R)$ is an equivalence for all  $R \in \mathrm {SCR}_\mathbf {k}$.
$R \in \mathrm {SCR}_\mathbf {k}$.(ii) (infinitesimal cohesiveness) For every pullback diagram
in
 $\mathrm {SCR}_\mathbf {k}$ for which the maps
$\mathrm {SCR}_\mathbf {k}$ for which the maps  $\pi _0 A \to \pi _0 B$ and
$\pi _0 A \to \pi _0 B$ and  $\pi _0 B' \to \pi _0 B$ are surjections whose kernels are nilpotent ideals, the induced map
is an equivalence. (In fact, it is enough to require this only when the pullback diagram is a square-zero extension in the sense of [Reference LurieLur17, § 8.4].)
$\pi _0 B' \to \pi _0 B$ are surjections whose kernels are nilpotent ideals, the induced map
is an equivalence. (In fact, it is enough to require this only when the pullback diagram is a square-zero extension in the sense of [Reference LurieLur17, § 8.4].) \[ \mathscr{F}(A') \longrightarrow \mathscr{F}(A) \times_{\mathscr{F}(B)} \mathscr{F}(B') \]
\[ \mathscr{F}(A') \longrightarrow \mathscr{F}(A) \times_{\mathscr{F}(B)} \mathscr{F}(B') \]
Let ![]() $\pi \colon Z = \operatorname {Spec}(R') \to X = \operatorname {Spec}(R)$ be an almost finitely presented, surjective, closed immersion, and
$\pi \colon Z = \operatorname {Spec}(R') \to X = \operatorname {Spec}(R)$ be an almost finitely presented, surjective, closed immersion, and ![]() ${\rm Cech}(\pi )$ its Čech nerve. Then the natural pullback functor
${\rm Cech}(\pi )$ its Čech nerve. Then the natural pullback functor
is an equivalence. The analogous claim is true for spectral stacks as well.
Before giving the proof of this lemma, let us make some remarks and state a corollary.
Remark 3.1.2 There is a slight variant of the above where, rather than considering a single surjective closed immersion, we consider a finite family of closed immersions which are jointly surjective. To handle this one can, for instance, replace (ii) by an arbitrary pushout diagram along closed immersions. This is, in principle, convenient, but will be subsumed in our application by ![]() $h$-descent.
$h$-descent.
Remark 3.1.3 Note that in the derived context there is a difference between descent (i.e. for Čech covers) and hyperdescent (i.e. for hypercovers that are not ![]() $n$-coskeletal for any
$n$-coskeletal for any ![]() $n$). This difference is severe for surjective closed immersions. Indeed, the map from the constant simplicial diagram
$n$). This difference is severe for surjective closed immersions. Indeed, the map from the constant simplicial diagram ![]() $\left \{\operatorname {Spec}(\pi _0(R)^{\mathrm {red}}) \right \} \to \operatorname {Spec}(R)$ is a hypercover for the derived nil-immersion topology, and this shows that a presheaf
$\left \{\operatorname {Spec}(\pi _0(R)^{\mathrm {red}}) \right \} \to \operatorname {Spec}(R)$ is a hypercover for the derived nil-immersion topology, and this shows that a presheaf ![]() $\mathscr {F}$ is a hypersheaf for the derived nil-immersion topology if and only if
$\mathscr {F}$ is a hypersheaf for the derived nil-immersion topology if and only if ![]() $\mathscr {F}(R) \to \mathscr {F}(\pi _0(R)^{\mathrm {red}})$ is an equivalence for all
$\mathscr {F}(R) \to \mathscr {F}(\pi _0(R)^{\mathrm {red}})$ is an equivalence for all ![]() $R \in \mathrm {SCR}_{\mathbf {k}}$.
$R \in \mathrm {SCR}_{\mathbf {k}}$.
Corollary 3.1.4 Let ![]() $\mathscr {F}$ satisfy the conditions of Lemma 3.1.1, and suppose now only that
$\mathscr {F}$ satisfy the conditions of Lemma 3.1.1, and suppose now only that ![]() $\pi \colon Z \to X$ is an almost finitely presented closed immersion, but not necessarily surjective. Then the natural pullback functor gives an equivalence
$\pi \colon Z \to X$ is an almost finitely presented closed immersion, but not necessarily surjective. Then the natural pullback functor gives an equivalence
Proof. Recall that ![]() $\operatorname {Spf}(R) \simeq \mathop {\varinjlim }\limits \operatorname {Spec}(R_n)$ for
$\operatorname {Spf}(R) \simeq \mathop {\varinjlim }\limits \operatorname {Spec}(R_n)$ for ![]() $\{R_n\}$ as in Proposition 2.1.2 (we do not need the finite Tor amplitude assumption here, so this works in the spectral setting as well by Remark 2.1.3), so that
$\{R_n\}$ as in Proposition 2.1.2 (we do not need the finite Tor amplitude assumption here, so this works in the spectral setting as well by Remark 2.1.3), so that
and applying Lemma 3.1.1 to the base change of ![]() $\pi$ to each
$\pi$ to each ![]() $\operatorname {Spec}(R_n)$, we obtain that
$\operatorname {Spec}(R_n)$, we obtain that
Taking the inverse limit of these equivalences we complete the proof, since
as ![]() $\operatorname {Spec}(R'^{\otimes _R \bullet +1}) \to \operatorname {Spec}(R)$ factors through the monomorphism
$\operatorname {Spec}(R'^{\otimes _R \bullet +1}) \to \operatorname {Spec}(R)$ factors through the monomorphism ![]() $\operatorname {Spf}(R) \to \operatorname {Spec}(R)$.
$\operatorname {Spf}(R) \to \operatorname {Spec}(R)$.
We now give a proof of the lemma.
Proof of Lemma 3.1.1 Our plan of proof is as follows. Let ![]() $\mathcal {C}$ denote the class of all almost finitely presented nil-thickenings
$\mathcal {C}$ denote the class of all almost finitely presented nil-thickenings ![]() $i$ of affine derived
$i$ of affine derived ![]() $\mathbf {k}$-schemes, such that every base change of
$\mathbf {k}$-schemes, such that every base change of ![]() $i$ satisfies the conclusion of the lemma. We will show that
$i$ satisfies the conclusion of the lemma. We will show that ![]() $\mathcal {C}$ consists of all almost finitely presented nil-thickenings by showing it contains increasingly large classes of morphisms.
$\mathcal {C}$ consists of all almost finitely presented nil-thickenings by showing it contains increasingly large classes of morphisms.
Step 0: the case of ![]() $\pi$ with a section. In this case, the augmented cosimplicial diagram
$\pi$ with a section. In this case, the augmented cosimplicial diagram
extends to a split augmented cosimplicial diagram. And any split augmented cosimplicial diagram is a limit diagram.
Step 1: the case of square-zero extensions. Suppose that ![]() $\pi$ fits into a pushout square
$\pi$ fits into a pushout square

for some connective almost perfect ![]() $R'$-module
$R'$-module ![]() $M$ (i.e.
$M$ (i.e. ![]() $\pi$ is a square-zero extension). Then by hypothesis
$\pi$ is a square-zero extension). Then by hypothesis
Furthermore, square-zero extensions are stable under base change, so there are also equivalences
Taking totalizations, and commuting totalizations and inverse limits, we conclude that to show the conclusion for ![]() $\pi _R$ it suffices to know it for each of
$\pi _R$ it suffices to know it for each of ![]() $\pi _{R'}$ and
$\pi _{R'}$ and ![]() $\pi _{R' \oplus M[+1]}$. But each of these belong to
$\pi _{R' \oplus M[+1]}$. But each of these belong to ![]() $\mathcal {C}$ by Step 0. Thus, the conclusion holds for any square-zero extension
$\mathcal {C}$ by Step 0. Thus, the conclusion holds for any square-zero extension ![]() $\pi _R$. Thus, square-zero extensions lie in
$\pi _R$. Thus, square-zero extensions lie in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Step 2: composites, refinements, and locality. Note that ![]() $\mathcal {C}$ is closed under composites; this is a formal argument with computing a totalization of a bi-cosimplicial space along the diagonal.
$\mathcal {C}$ is closed under composites; this is a formal argument with computing a totalization of a bi-cosimplicial space along the diagonal.
It is also ‘local’ in the following sense. Suppose that ![]() $\pi \colon Z \to \operatorname {Spec}(R)$ is in
$\pi \colon Z \to \operatorname {Spec}(R)$ is in ![]() $\mathcal {C}$. Then a map
$\mathcal {C}$. Then a map ![]() $i \colon Z' \to \operatorname {Spec}(R)$ is in
$i \colon Z' \to \operatorname {Spec}(R)$ is in ![]() $\mathcal {C}$ if and only if its base extension
$\mathcal {C}$ if and only if its base extension ![]() $i_Z \colon Z' \times _{\operatorname {Spec}(R)} Z \to Z$ is in
$i_Z \colon Z' \times _{\operatorname {Spec}(R)} Z \to Z$ is in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Finally, if a composite ![]() $h = f \circ g$ is in
$h = f \circ g$ is in ![]() $\mathcal {C}$ (i.e.
$\mathcal {C}$ (i.e. ![]() $f$ is a ‘refinement’ of
$f$ is a ‘refinement’ of ![]() $h \in \mathcal {C}$) then
$h \in \mathcal {C}$) then ![]() $f \in \mathcal {C}$. A special case is the case of a morphism admitting a section (so that
$f \in \mathcal {C}$. A special case is the case of a morphism admitting a section (so that ![]() $h = \mathop {{\rm id}}\nolimits$). The general case reduces to this: to show that
$h = \mathop {{\rm id}}\nolimits$). The general case reduces to this: to show that ![]() $f \in \mathcal {C}$, it is enough to show that its base change along
$f \in \mathcal {C}$, it is enough to show that its base change along ![]() $h$ is so. But this base change has a section, induced from the diagonal of
$h$ is so. But this base change has a section, induced from the diagonal of ![]() $f$.
$f$.
Step 3: the case of ![]() $Z, X$ classical. Suppose that
$Z, X$ classical. Suppose that ![]() $\pi \colon Z \to X$ has both
$\pi \colon Z \to X$ has both ![]() $Z$ and
$Z$ and ![]() $X$ an ordinary classical scheme. In this case,
$X$ an ordinary classical scheme. In this case, ![]() $R \to R'$ is a nilpotent surjection of ordinary rings. Filtering by powers of the nilradical shows that it is a composite of (classical) square-zero extensions, which happen to also be derived square-zero extensions by [Reference LurieLur17, § 8.4]. Thus,
$R \to R'$ is a nilpotent surjection of ordinary rings. Filtering by powers of the nilradical shows that it is a composite of (classical) square-zero extensions, which happen to also be derived square-zero extensions by [Reference LurieLur17, § 8.4]. Thus, ![]() $\pi \in \mathcal {C}$. (Note that though such
$\pi \in \mathcal {C}$. (Note that though such ![]() $\pi$ are not preserved by base change, the base change will still be a composite of square-zero extensions.)
$\pi$ are not preserved by base change, the base change will still be a composite of square-zero extensions.)
Step 4: reduction to ![]() $X$ classical. Suppose that
$X$ classical. Suppose that ![]() $A \in \mathrm {SCR}_\mathbf {k}$ and that we write
$A \in \mathrm {SCR}_\mathbf {k}$ and that we write ![]() $A = \mathop {\varprojlim }\limits _n A_n$ as an inverse limit of almost perfect
$A = \mathop {\varprojlim }\limits _n A_n$ as an inverse limit of almost perfect ![]() $A$-algebras
$A$-algebras ![]() $\{A_n\}$ satisfying the conditions of Lemma 2.1.12. Then we claim that nilcompleteness implies that
$\{A_n\}$ satisfying the conditions of Lemma 2.1.12. Then we claim that nilcompleteness implies that
is an equivalence. Indeed, this follows by evaluating the inverse limit
in two ways (first ![]() $n$ then
$n$ then ![]() $m$, and vice versa) and applying nilcompleteness in each case.
$m$, and vice versa) and applying nilcompleteness in each case.
This hypothesis applies to the inverse systems ![]() $\{ \tau _{\leqslant n} R \}$ and any base change thereof, such as
$\{ \tau _{\leqslant n} R \}$ and any base change thereof, such as
This reduces proving that ![]() $\pi \in \mathcal {C}$ to proving that each base change
$\pi \in \mathcal {C}$ to proving that each base change ![]() $\pi _{\tau _{\leqslant n} R} \in \mathcal {C}$.
$\pi _{\tau _{\leqslant n} R} \in \mathcal {C}$.
Furthermore, note that for each ![]() $n$ the map
$n$ the map ![]() $\operatorname {Spec}(\pi _0(R)) \to \operatorname {Spec}(\tau _{\leqslant n} R)$ is a composite of square-zero extensions; thus it is in
$\operatorname {Spec}(\pi _0(R)) \to \operatorname {Spec}(\tau _{\leqslant n} R)$ is a composite of square-zero extensions; thus it is in ![]() $\mathcal {C}$. Using locality, we reduce proving
$\mathcal {C}$. Using locality, we reduce proving ![]() $\pi _{\tau _{\leqslant n} R} \in \mathcal {C}$ to proving
$\pi _{\tau _{\leqslant n} R} \in \mathcal {C}$ to proving ![]() $\pi _{\pi _0(R)} \in \mathcal {C}$.
$\pi _{\pi _0(R)} \in \mathcal {C}$.
Step 5: completing the proof. Suppose now that ![]() $\pi \colon Z = \operatorname {Spec}(R') \to X = \operatorname {Spec}(R)$ is a nil-thickening with
$\pi \colon Z = \operatorname {Spec}(R') \to X = \operatorname {Spec}(R)$ is a nil-thickening with ![]() $X$ classical. Let
$X$ classical. Let ![]() $i_0 \colon Z^{\mathrm {cl}} \to Z$ be the inclusion of the classical part of
$i_0 \colon Z^{\mathrm {cl}} \to Z$ be the inclusion of the classical part of ![]() $Z$. By Step 3, the composite
$Z$. By Step 3, the composite ![]() $\pi \circ i_0$ is in
$\pi \circ i_0$ is in ![]() $\mathcal {C}$. By Step 2 (‘refinements’) this proves that
$\mathcal {C}$. By Step 2 (‘refinements’) this proves that ![]() $\pi \in \mathcal {C}$.
$\pi \in \mathcal {C}$.
3.1.1 Closed descent for  $\operatorname {QC}^{\mathrm {cn}}$ and variants
$\operatorname {QC}^{\mathrm {cn}}$ and variants
As an application of the above pattern, we have:
Proposition 3.1.5 Suppose that ![]() $\pi \colon \mathscr {Z} \to \mathscr {X}$ is an almost finitely presented, surjective, closed immersion of derived (or spectral)
$\pi \colon \mathscr {Z} \to \mathscr {X}$ is an almost finitely presented, surjective, closed immersion of derived (or spectral) ![]() $\mathbf {k}$-stacks. Then the pullback functor induces an equivalence of
$\mathbf {k}$-stacks. Then the pullback functor induces an equivalence of ![]() $\infty$-categories
$\infty$-categories
The same holds with ![]() $\operatorname {QC}^{\mathrm {cn}}(-)$ replaced by
$\operatorname {QC}^{\mathrm {cn}}(-)$ replaced by ![]() $\operatorname {QC}^{\mathrm {acn}}(-)$,
$\operatorname {QC}^{\mathrm {acn}}(-)$, ![]() $\operatorname {APerf}(-)$ or
$\operatorname {APerf}(-)$ or ![]() $\operatorname {Perf}(-)$.
$\operatorname {Perf}(-)$.
Proof. Note that by commuting limits we may suppose ![]() $\mathscr {X} = \operatorname {Spec}(R)$ is affine. Now we are in a position to apply Lemma 3.1.1. Let us check the hypotheses hold:
$\mathscr {X} = \operatorname {Spec}(R)$ is affine. Now we are in a position to apply Lemma 3.1.1. Let us check the hypotheses hold:
Note that (i) holds for ![]() $\operatorname {QC}^{\mathrm {cn}}$ because it is left
$\operatorname {QC}^{\mathrm {cn}}$ because it is left ![]() $t$-complete. Let us write
$t$-complete. Let us write ![]() $R_n$ for
$R_n$ for ![]() $\tau _{\leqslant n} R$. To see that the restriction map is fully faithful we must show that the map
$\tau _{\leqslant n} R$. To see that the restriction map is fully faithful we must show that the map
is an equivalence. Using left ![]() $t$-completeness on both sides, we may identify this with
$t$-completeness on both sides, we may identify this with
Next, note that the maps
are all equivalences; from this it follows that the previous map is an equivalence.
To see that it is essentially surjective, suppose that
then note that the pushforwards ![]() $\{M_n\} \in R {\rm {}\hbox{-}{\rm mod}}^{\mathrm {cn}}$ form an inverse system satisfying the hypotheses of Lemma 2.1.12. In particular, letting
$\{M_n\} \in R {\rm {}\hbox{-}{\rm mod}}^{\mathrm {cn}}$ form an inverse system satisfying the hypotheses of Lemma 2.1.12. In particular, letting ![]() $M = \mathop {\varprojlim }\limits M_n$, we see that
$M = \mathop {\varprojlim }\limits M_n$, we see that ![]() $M$ is connective.
$M$ is connective.
A similar argument shows that (i) holds for ![]() $\operatorname {APerf}^{\mathrm {cn}}$. Full faithfulness follows from the above, and to conclude it is enough to note that if the system
$\operatorname {APerf}^{\mathrm {cn}}$. Full faithfulness follows from the above, and to conclude it is enough to note that if the system ![]() $\{M_n\}$ consists of modules which are perfect to order
$\{M_n\}$ consists of modules which are perfect to order ![]() $k$, then the inverse limit
$k$, then the inverse limit ![]() $M$ is also perfect to order
$M$ is also perfect to order ![]() $k$. This is because
$k$. This is because ![]() $\tau _{\leqslant k} M = \tau _{\leqslant k} M_n$ for
$\tau _{\leqslant k} M = \tau _{\leqslant k} M_n$ for ![]() $n \geqslant k$ compatibly with the natural equivalences
$n \geqslant k$ compatibly with the natural equivalences
Thus, if ![]() $\tau _{\leqslant k} M_n$ is compact in
$\tau _{\leqslant k} M_n$ is compact in ![]() $(R_n {\rm {}\hbox{-}{\rm mod}})^{\mathrm {cn}}_{\leqslant k}$, then the same is true for
$(R_n {\rm {}\hbox{-}{\rm mod}})^{\mathrm {cn}}_{\leqslant k}$, then the same is true for ![]() $\tau _{\leqslant k} M$.
$\tau _{\leqslant k} M$.
The case of (i) for each of ![]() $\operatorname {QC}^{\mathrm {acn}}$ and
$\operatorname {QC}^{\mathrm {acn}}$ and ![]() $\operatorname {APerf}$ then follows by shifting the modules as needed until they are connective; notice that if we shift
$\operatorname {APerf}$ then follows by shifting the modules as needed until they are connective; notice that if we shift ![]() $M_0$ to be connective, the rest will be as well. The case of
$M_0$ to be connective, the rest will be as well. The case of ![]() $\operatorname {Perf}$ follows from
$\operatorname {Perf}$ follows from ![]() $\operatorname {APerf}$ upon noting that
$\operatorname {APerf}$ upon noting that ![]() $\operatorname {Perf} \subset \operatorname {APerf}$ may be recognized as the dualizable objects.
$\operatorname {Perf} \subset \operatorname {APerf}$ may be recognized as the dualizable objects.
Finally, notice that (ii) for each of our four categories follows from [Reference LurieLur1, Theorem 7.1, Proposition 7.7] (these results apply to simplicial commutative rings as well, because the forgetful functor ![]() $\mathrm {SCR} \to \mathrm {CAlg}^{\mathrm {cn}}$ preserves fiber products). Thus, the hypotheses of Lemma 3.1.1 hold and our result is proved.
$\mathrm {SCR} \to \mathrm {CAlg}^{\mathrm {cn}}$ preserves fiber products). Thus, the hypotheses of Lemma 3.1.1 hold and our result is proved.
Corollary 3.1.6 Suppose that ![]() $\pi \colon \mathscr {Z} \to \mathscr {X}$ is an almost finitely presented closed immersion of algebraic derived (or spectral)
$\pi \colon \mathscr {Z} \to \mathscr {X}$ is an almost finitely presented closed immersion of algebraic derived (or spectral) ![]() $\mathbf {k}$-stacks. Let
$\mathbf {k}$-stacks. Let ![]() $\widehat {\mathscr {X}}$ denote the formal completion of
$\widehat {\mathscr {X}}$ denote the formal completion of ![]() $\mathscr {X}$ along the image of
$\mathscr {X}$ along the image of ![]() $\mathscr {Z}$. Then the pullback functor
$\mathscr {Z}$. Then the pullback functor
is an equivalence of ![]() $\infty$-categories. The same holds with
$\infty$-categories. The same holds with ![]() $\operatorname {QC}^{\mathrm {cn}}(-)$ replaced by
$\operatorname {QC}^{\mathrm {cn}}(-)$ replaced by ![]() $\operatorname {QC}^{\mathrm {acn}}(-)$,
$\operatorname {QC}^{\mathrm {acn}}(-)$, ![]() $\operatorname {APerf}(-)$, or
$\operatorname {APerf}(-)$, or ![]() $\operatorname {Perf}(-)$.
$\operatorname {Perf}(-)$.
Proof. Combine the argument of the previous proposition with Corollary 3.1.4.
3.2 Descent pattern for the  $h$-topology
$h$-topology
By a derived ![]() $h$-cover we will mean a morphism
$h$-cover we will mean a morphism ![]() $\pi \colon \mathscr {X}' \to \mathscr {X}$ which is representable by algebraic derived stacks almost of finite presentation, and which is a universal topological submersion, and we use the same definition for spectral stacks. Examples include fppf surjections (since they are universally open), proper surjections (since they are universally closed), and more generally formally proper surjections (which are also universally closed by Proposition 2.4.5).
$\pi \colon \mathscr {X}' \to \mathscr {X}$ which is representable by algebraic derived stacks almost of finite presentation, and which is a universal topological submersion, and we use the same definition for spectral stacks. Examples include fppf surjections (since they are universally open), proper surjections (since they are universally closed), and more generally formally proper surjections (which are also universally closed by Proposition 2.4.5).
Our descent pattern is based on the idea that the ![]() $h$-topology is generated by surjective closed immersions, fppf covers, and ‘abstract blowup squares’. In the derived context, closed immersions are no longer monomorphisms – this necessitates modifying the abstract blowup square condition by taking suitable formal completions. We say that a cartesian diagram of prestacks
$h$-topology is generated by surjective closed immersions, fppf covers, and ‘abstract blowup squares’. In the derived context, closed immersions are no longer monomorphisms – this necessitates modifying the abstract blowup square condition by taking suitable formal completions. We say that a cartesian diagram of prestacks

is an abstract blowup square (with affine base) if ![]() $\mathscr {X} = \operatorname {Spec}(R)$ for a noetherian
$\mathscr {X} = \operatorname {Spec}(R)$ for a noetherian ![]() $R \in \mathrm {SCR}_\mathbf {k}$,
$R \in \mathrm {SCR}_\mathbf {k}$, ![]() $\pi$ is a proper derived algebraic space,
$\pi$ is a proper derived algebraic space, ![]() $\widehat {\mathscr {X}}$ is the formal completion of
$\widehat {\mathscr {X}}$ is the formal completion of ![]() $\mathscr {X}$ along a closed subset
$\mathscr {X}$ along a closed subset ![]() $|\mathscr {Z}| \subset |\mathscr {X}|$, and
$|\mathscr {Z}| \subset |\mathscr {X}|$, and ![]() $\pi ^{-1}(\mathscr {X} \setminus \mathscr {Z}) \to \mathscr {X} \setminus \mathscr {Z}$ is an isomorphism.
$\pi ^{-1}(\mathscr {X} \setminus \mathscr {Z}) \to \mathscr {X} \setminus \mathscr {Z}$ is an isomorphism.
Proposition 3.2.1 Suppose that ![]() $\mathscr {F}$ is a presheaf on locally noetherian algebraic derived (or spectral)
$\mathscr {F}$ is a presheaf on locally noetherian algebraic derived (or spectral) ![]() $\mathbf {k}$-stacks satisfying the following conditions:
$\mathbf {k}$-stacks satisfying the following conditions:
(i)
 $\mathscr {F}$ has descent for surjective almost finitely presented closed immersions;
$\mathscr {F}$ has descent for surjective almost finitely presented closed immersions;(ii)
 $\mathscr {F}$ has fppf descent;
$\mathscr {F}$ has fppf descent;(iii) for any abstract blowup square (3) with affine base, the natural map
is an equivalence. \[ \mathscr{F}(\mathscr{X}) \longrightarrow \mathscr{F}(\widehat{\mathscr{X}}) \times_{\mathscr{F}(\widehat{\mathscr{Y}})} \mathscr{F}(\mathscr{Y}) \]
\[ \mathscr{F}(\mathscr{X}) \longrightarrow \mathscr{F}(\widehat{\mathscr{X}}) \times_{\mathscr{F}(\widehat{\mathscr{Y}})} \mathscr{F}(\mathscr{Y}) \]
Then ![]() $\mathscr {F}$ has descent for
$\mathscr {F}$ has descent for ![]() $h$-covers.
$h$-covers.
Proof. Let ![]() $\mathcal {D}$ denote the class of all almost finitely presented surjections
$\mathcal {D}$ denote the class of all almost finitely presented surjections ![]() $\pi \colon \mathscr {X}' \to \mathscr {X}$ with locally noetherian target. Let
$\pi \colon \mathscr {X}' \to \mathscr {X}$ with locally noetherian target. Let ![]() $\mathcal {C}\subset \mathcal {D}$ consist of those
$\mathcal {C}\subset \mathcal {D}$ consist of those ![]() $\pi$ satisfying, additionally, the condition that for every almost finitely presented affine map
$\pi$ satisfying, additionally, the condition that for every almost finitely presented affine map ![]() $\mathscr {Y} \to \mathscr {X}$,
$\mathscr {Y} \to \mathscr {X}$, ![]() $\mathscr {F}$ has descent for the base change
$\mathscr {F}$ has descent for the base change ![]() $\pi _\mathscr {Y}$, that is, restriction gives an equivalence
$\pi _\mathscr {Y}$, that is, restriction gives an equivalence ![]() $\mathscr {F}(\mathscr {Y}) \to \operatorname {Tot}\{\mathscr {F}({\rm Cech}(\pi _\mathscr {Y}))\}$. We wish to show that
$\mathscr {F}(\mathscr {Y}) \to \operatorname {Tot}\{\mathscr {F}({\rm Cech}(\pi _\mathscr {Y}))\}$. We wish to show that ![]() $\mathcal {C}$ contains all
$\mathcal {C}$ contains all ![]() $h$-covers.
$h$-covers.
Note that if ![]() $\pi \in \mathcal {C}$, then
$\pi \in \mathcal {C}$, then ![]() $\mathscr {F}$ has descent for
$\mathscr {F}$ has descent for ![]() $\pi _\mathscr {Y}$ for any almost finitely presented morphism
$\pi _\mathscr {Y}$ for any almost finitely presented morphism ![]() $\mathscr {Y} \to \mathscr {X}$: it suffices to consider
$\mathscr {Y} \to \mathscr {X}$: it suffices to consider ![]() $\mathscr {X}$ quasi-compact (i.e. noetherian). We can choose an étale surjection
$\mathscr {X}$ quasi-compact (i.e. noetherian). We can choose an étale surjection ![]() $p : \mathscr {V} \to \mathscr {Y}$ with
$p : \mathscr {V} \to \mathscr {Y}$ with ![]() $\mathscr {V}$ affine, and by étale descent and commuting limits it suffices to show that
$\mathscr {V}$ affine, and by étale descent and commuting limits it suffices to show that ![]() $\pi _{\mathscr {V}_n} \in \mathcal {C}$ for each level
$\pi _{\mathscr {V}_n} \in \mathcal {C}$ for each level ![]() $\mathscr {V}_n = \mathscr {V}^{\times _\mathscr {Y} n}$ in the Čech nerve of
$\mathscr {V}_n = \mathscr {V}^{\times _\mathscr {Y} n}$ in the Čech nerve of ![]() $p$. Thus, we can reduce to the case where
$p$. Thus, we can reduce to the case where ![]() $\mathscr {Y} \to \mathscr {X}$ is representable by derived algebraic spaces. Repeating this trick three more times, we reduce to the case where
$\mathscr {Y} \to \mathscr {X}$ is representable by derived algebraic spaces. Repeating this trick three more times, we reduce to the case where ![]() $\mathscr {Y} \to \mathscr {X}$ is representable by derived schemes, then by separated derived schemes, and finally to where
$\mathscr {Y} \to \mathscr {X}$ is representable by derived schemes, then by separated derived schemes, and finally to where ![]() $\mathscr {Y} \to \mathscr {X}$ is affine.
$\mathscr {Y} \to \mathscr {X}$ is affine.
The proof of Lemma 3.1.1, Step 2, applies verbatim to show that ![]() $\mathcal {C}$ is closed under composition and refinements, and to show locality along maps in
$\mathcal {C}$ is closed under composition and refinements, and to show locality along maps in ![]() $\mathcal {C}$.
$\mathcal {C}$.
Step 0: reduction to ![]() $\mathscr {X}$ an affine scheme. Since
$\mathscr {X}$ an affine scheme. Since ![]() $\mathscr {F}$ is an fppf sheaf, the assertion is fppf local on
$\mathscr {F}$ is an fppf sheaf, the assertion is fppf local on ![]() $\mathscr {X}$. Thus, we may suppose
$\mathscr {X}$. Thus, we may suppose ![]() $\mathscr {X}$ is affine.
$\mathscr {X}$ is affine.
Step 1: reduction to ![]() $\mathscr {X}$ classical and reduced,
$\mathscr {X}$ classical and reduced, ![]() $\mathscr {X}'$ classical. Since
$\mathscr {X}'$ classical. Since ![]() $\operatorname {Spec}(\pi _0(R)_{\mathrm {red}}) \to \operatorname {Spec}(R)$ is a surjective closed immersion, it is in
$\operatorname {Spec}(\pi _0(R)_{\mathrm {red}}) \to \operatorname {Spec}(R)$ is a surjective closed immersion, it is in ![]() $\mathcal {C}$. So by ‘locality’ to show that
$\mathcal {C}$. So by ‘locality’ to show that ![]() $\pi \in \mathcal {C}$ it is enough to show that the base change
$\pi \in \mathcal {C}$ it is enough to show that the base change ![]() $\pi _{\pi _0(R)_{\mathrm {red}}} \in \mathcal {C}$. That is, we may suppose that
$\pi _{\pi _0(R)_{\mathrm {red}}} \in \mathcal {C}$. That is, we may suppose that ![]() $\mathscr {X}$ is classical and reduced. Similarly, by ‘refinements’ we may suppose that
$\mathscr {X}$ is classical and reduced. Similarly, by ‘refinements’ we may suppose that ![]() $\mathscr {X}'$ is classical.
$\mathscr {X}'$ is classical.
Step 2: a general descent argument for (classical) ![]() $h$-covers. We will prove, by noetherian induction, that for every closed subscheme
$h$-covers. We will prove, by noetherian induction, that for every closed subscheme ![]() $Z \subset \mathscr {X}$ it is the case that all
$Z \subset \mathscr {X}$ it is the case that all ![]() $h$-coverings having target
$h$-coverings having target ![]() $Z$ belong to
$Z$ belong to ![]() $\mathcal {C}$. Thus, we may suppose that this holds for all (classical) proper closed subschemes of
$\mathcal {C}$. Thus, we may suppose that this holds for all (classical) proper closed subschemes of ![]() $\mathscr {X}$, and we must show that every
$\mathscr {X}$, and we must show that every ![]() $h$-cover
$h$-cover ![]() $\pi \colon \mathscr {X}' \to \mathscr {X}$ belongs to
$\pi \colon \mathscr {X}' \to \mathscr {X}$ belongs to ![]() $\mathcal {C}$. We can choose a smooth cover
$\mathcal {C}$. We can choose a smooth cover ![]() $\operatorname {Spec}(A) \to \mathscr {X}'$, and the composition
$\operatorname {Spec}(A) \to \mathscr {X}'$, and the composition ![]() $\operatorname {Spec}(A) \to \mathscr {X}$ is again an
$\operatorname {Spec}(A) \to \mathscr {X}$ is again an ![]() $h$-cover, so it suffices by refinement to consider the case where
$h$-cover, so it suffices by refinement to consider the case where ![]() $\pi$ is representable by derived algebraic spaces.
$\pi$ is representable by derived algebraic spaces.
Since ![]() $\mathscr {X}$ is reduced, we may apply ‘generic flatness’ to
$\mathscr {X}$ is reduced, we may apply ‘generic flatness’ to ![]() $\pi$ to deduce the existence of a dense open
$\pi$ to deduce the existence of a dense open ![]() $U \subset \mathscr {X}$ such that
$U \subset \mathscr {X}$ such that ![]() $\pi _U$ is flat. By ‘platification par éclatement’, there exists a closed subscheme
$\pi _U$ is flat. By ‘platification par éclatement’, there exists a closed subscheme ![]() $Z \subset \mathscr {X}$ disjoint from
$Z \subset \mathscr {X}$ disjoint from ![]() $U$ such that the strict transform
$U$ such that the strict transform ![]() $\widetilde {p_Z}(\mathscr {X}')$ is flat over
$\widetilde {p_Z}(\mathscr {X}')$ is flat over ![]() $\operatorname {Bl}_Z(\mathscr {Y}')$. More precisely, there is a commutative diagram
$\operatorname {Bl}_Z(\mathscr {Y}')$. More precisely, there is a commutative diagram

such that ![]() $\pi ' \colon \mathscr {Y}' \to \mathscr {Y}$ is flat. In order to show that
$\pi ' \colon \mathscr {Y}' \to \mathscr {Y}$ is flat. In order to show that ![]() $\pi \in \mathcal {C}$ it is enough, by refinement, to show that
$\pi \in \mathcal {C}$ it is enough, by refinement, to show that ![]() $p_Z \circ \pi ' \in \mathcal {C}$. Note that
$p_Z \circ \pi ' \in \mathcal {C}$. Note that ![]() $\pi '$ is surjective by the argument of [Reference VoevodskyVoe96, Proposition 3.1.3], so that it is a flat cover and thus in
$\pi '$ is surjective by the argument of [Reference VoevodskyVoe96, Proposition 3.1.3], so that it is a flat cover and thus in ![]() $\mathcal {C}$. It thus suffices to show that the blowup morphism
$\mathcal {C}$. It thus suffices to show that the blowup morphism ![]() $p_Z \in \mathcal {C}$.
$p_Z \in \mathcal {C}$.
We now simplify our notation by renaming ![]() $p_Z$ to just
$p_Z$ to just ![]() $\pi \colon \mathscr {X}' = \operatorname {Bl}_Z(\mathscr {X}) \longrightarrow \mathscr {X}$. We consider an almost finitely presented map
$\pi \colon \mathscr {X}' = \operatorname {Bl}_Z(\mathscr {X}) \longrightarrow \mathscr {X}$. We consider an almost finitely presented map ![]() $\mathscr {Y} = \operatorname {Spec}(R') \to \mathscr {X}$, and we wish to show that
$\mathscr {Y} = \operatorname {Spec}(R') \to \mathscr {X}$, and we wish to show that ![]() $\mathscr {F}$ has descent for the base change
$\mathscr {F}$ has descent for the base change ![]() $\pi _{\mathscr {Y}} : \mathscr {Y}' \to \mathscr {Y}$ of
$\pi _{\mathscr {Y}} : \mathscr {Y}' \to \mathscr {Y}$ of ![]() $\pi$.
$\pi$.
![]() $\pi _{Z} \in \mathcal {C}$ by our inductive hypothesis, so by Step 1,
$\pi _{Z} \in \mathcal {C}$ by our inductive hypothesis, so by Step 1, ![]() $\pi _{R/I^{n}} \in \mathcal {C}$ for all
$\pi _{R/I^{n}} \in \mathcal {C}$ for all ![]() $n \geqslant 1$, where
$n \geqslant 1$, where ![]() $I \subset R$ is the ideal defining
$I \subset R$ is the ideal defining ![]() $Z$. We may summarize this with the slight abuse of notation
$Z$. We may summarize this with the slight abuse of notation ![]() $\pi _{\operatorname {Spf}(R)} \in \mathcal {C}$. It follows that if
$\pi _{\operatorname {Spf}(R)} \in \mathcal {C}$. It follows that if ![]() $\widehat {\mathscr {Y}}$ is the formal completion of
$\widehat {\mathscr {Y}}$ is the formal completion of ![]() $\mathscr {Y}$ along the preimage of
$\mathscr {Y}$ along the preimage of ![]() $Z$, then
$Z$, then ![]() $\mathscr {F}(\widehat {\mathscr {Y}}) \to \operatorname {Tot}\{\mathscr {F}({\rm Cech}(\pi _{\widehat {\mathscr {Y}}}))\}$ is an equivalence. Now consider the cartesian diagram of simplicial derived schemes
$\mathscr {F}(\widehat {\mathscr {Y}}) \to \operatorname {Tot}\{\mathscr {F}({\rm Cech}(\pi _{\widehat {\mathscr {Y}}}))\}$ is an equivalence. Now consider the cartesian diagram of simplicial derived schemes

where the bottom row consists of constant simplicial schemes. This diagram is levelwise an abstract blowup square (3) with affine base, so applying our hypothesis (iii) and commuting limits, we see that
is an equivalence, and hence ![]() $\mathscr {F}(\mathscr {Y}) \to \operatorname {Tot}\{\mathscr {F}({\rm Cech}(\pi _\mathscr {Y}))\}$ is an equivalence.
$\mathscr {F}(\mathscr {Y}) \to \operatorname {Tot}\{\mathscr {F}({\rm Cech}(\pi _\mathscr {Y}))\}$ is an equivalence.
3.3  $h$-descent theorems for
$h$-descent theorems for  $\operatorname {APerf}$,
$\operatorname {APerf}$,  $\operatorname {Perf}$, and quasi-geometric stacks
$\operatorname {Perf}$, and quasi-geometric stacks
By a locally noetherian stack in the following theorem, we mean a stack which is a left Kan extension along the morphism ![]() $\mathrm {SCR}^{\mathrm {noeth}}_{\mathbf {k}} \hookrightarrow \mathrm {SCR}_{\mathbf {k}}$. Examples include locally noetherian algebraic derived
$\mathrm {SCR}^{\mathrm {noeth}}_{\mathbf {k}} \hookrightarrow \mathrm {SCR}_{\mathbf {k}}$. Examples include locally noetherian algebraic derived ![]() $\mathbf {k}$-stacks, as well as formal completions of such stacks along closed substacks.
$\mathbf {k}$-stacks, as well as formal completions of such stacks along closed substacks.
Theorem 3.3.1 Suppose that ![]() $\mathscr {X}$ is a locally noetherian derived (or spectral)
$\mathscr {X}$ is a locally noetherian derived (or spectral) ![]() $\mathbf {k}$-stack, and that
$\mathbf {k}$-stack, and that ![]() $\pi \colon \mathscr {X}' \to \mathscr {X}$ is an
$\pi \colon \mathscr {X}' \to \mathscr {X}$ is an ![]() $h$-covering. Then if
$h$-covering. Then if ![]() $\{\mathscr {X}'_\bullet \} := {\rm Cech}(\pi )$, the pullback functors determine equivalences of
$\{\mathscr {X}'_\bullet \} := {\rm Cech}(\pi )$, the pullback functors determine equivalences of ![]() $\infty$-categories
$\infty$-categories
The same is true with ![]() $\operatorname {APerf}(-)$ replaced by
$\operatorname {APerf}(-)$ replaced by ![]() $\operatorname {Perf}(-)$ or
$\operatorname {Perf}(-)$ or ![]() $\operatorname {APerf}(-)^{\mathrm {cn}}$.
$\operatorname {APerf}(-)^{\mathrm {cn}}$.
We will establish Theorem 3.3.1 after some preliminary lemmas.
Lemma 3.3.2 Let ![]() $p : \mathscr {X}' \to \mathscr {X}$ be a relatively algebraic qc.qs. map satisfying (CD) between derived (or spectral) stacks, and let
$p : \mathscr {X}' \to \mathscr {X}$ be a relatively algebraic qc.qs. map satisfying (CD) between derived (or spectral) stacks, and let ![]() $Z \subset |\mathscr {X}|$ be a cocompact closed subset such that
$Z \subset |\mathscr {X}|$ be a cocompact closed subset such that ![]() $\widehat {\mathscr {X}'}_{p^{-1}(Z)} \to \widehat {\mathscr {X}}_Z$ is an isomorphism. Then
$\widehat {\mathscr {X}'}_{p^{-1}(Z)} \to \widehat {\mathscr {X}}_Z$ is an isomorphism. Then ![]() $p^{\ast } : \operatorname {QC}_Z(\mathscr {X}) \to \operatorname {QC}_{p^{-1}(Z)}(\mathscr {X}')$ is a equivalence whose inverse is given by
$p^{\ast } : \operatorname {QC}_Z(\mathscr {X}) \to \operatorname {QC}_{p^{-1}(Z)}(\mathscr {X}')$ is a equivalence whose inverse is given by ![]() $p_\ast$.
$p_\ast$.
Proof. This follows from Theorem 2.2.3 in the derived setting, and from [Reference LurieLur3, Theorem 5.1.9] in the spectral setting for categories of almost connective modules. For the stronger statement in the spectral setting, note that the claim is local on ![]() $\mathscr {X}$, so we may assume
$\mathscr {X}$, so we may assume ![]() $\mathscr {X} = \operatorname {Spec}(R)$. The claim is equivalent to the canonical maps
$\mathscr {X} = \operatorname {Spec}(R)$. The claim is equivalent to the canonical maps ![]() $M \to p_\ast (p^{\ast }(M))$ and
$M \to p_\ast (p^{\ast }(M))$ and ![]() $p^{\ast } (p_\ast (F)) \to F$ being equivalences for all
$p^{\ast } (p_\ast (F)) \to F$ being equivalences for all ![]() $M \in \operatorname {QC}_Z(\mathscr {X})$ and
$M \in \operatorname {QC}_Z(\mathscr {X})$ and ![]() $F \in \operatorname {QC}_{p^{-1}(Z)}(\mathscr {X}')$. This follows from the case of almost connective objects, because the
$F \in \operatorname {QC}_{p^{-1}(Z)}(\mathscr {X}')$. This follows from the case of almost connective objects, because the ![]() $t$ structures on these categories are right
$t$ structures on these categories are right ![]() $t$-complete and
$t$-complete and ![]() $p_\ast$ and
$p_\ast$ and ![]() $p^{\ast }$ commute with filtered colimits by Proposition A.1.5.
$p^{\ast }$ commute with filtered colimits by Proposition A.1.5.
Lemma 3.3.3 (Excision for  $\operatorname {QC}$)
$\operatorname {QC}$)
Consider a cartesian diagram of derived (or spectral) stacks

such that both ![]() $p$ and
$p$ and ![]() $q$ are relatively algebraic, qc.qs. and satisfy (CD). Assume that there is a cocompact closed subset
$q$ are relatively algebraic, qc.qs. and satisfy (CD). Assume that there is a cocompact closed subset ![]() $Z \subset |\mathscr {X}|$ with complement
$Z \subset |\mathscr {X}|$ with complement ![]() $\mathscr {U} = \mathscr {X} \setminus Z$ such that
$\mathscr {U} = \mathscr {X} \setminus Z$ such that ![]() $\widehat {\mathscr {X}'}_{p^{-1}(Z)} \to \widehat {\mathscr {X}}_Z$ and
$\widehat {\mathscr {X}'}_{p^{-1}(Z)} \to \widehat {\mathscr {X}}_Z$ and ![]() $\mathscr {Y} \times _\mathscr {X} \mathscr {U} \to \mathscr {U}$ are isomorphisms. Then restriction induces an equivalence of categories
$\mathscr {Y} \times _\mathscr {X} \mathscr {U} \to \mathscr {U}$ are isomorphisms. Then restriction induces an equivalence of categories
If ![]() $p$ is flat at every point in
$p$ is flat at every point in ![]() $p^{-1}(Z) \subset |\mathscr {X}'|$, then the same holds with
$p^{-1}(Z) \subset |\mathscr {X}'|$, then the same holds with ![]() $\operatorname {QC}(-)$ replaced by
$\operatorname {QC}(-)$ replaced by ![]() $\operatorname {QC}(-)^{\mathrm {cn}}$,
$\operatorname {QC}(-)^{\mathrm {cn}}$, ![]() $\operatorname {QC}(-)^{\mathrm {acn}}$,
$\operatorname {QC}(-)^{\mathrm {acn}}$, ![]() $\operatorname {APerf}(-)$, or
$\operatorname {APerf}(-)$, or ![]() $\operatorname {Perf}(-)$.
$\operatorname {Perf}(-)$.
Proof. This assertion is local on ![]() $\mathscr {X}$, so we are free to assume that
$\mathscr {X}$, so we are free to assume that ![]() $\mathscr {X} = \operatorname {Spec}(R)$ is affine, and hence the other stacks are qc.qs. algebraic.
$\mathscr {X} = \operatorname {Spec}(R)$ is affine, and hence the other stacks are qc.qs. algebraic.
Let ![]() $g = p \circ q' \simeq q \circ p'$. Note that the pullback
$g = p \circ q' \simeq q \circ p'$. Note that the pullback ![]() $\operatorname {QC}(R) \to \operatorname {QC}(\mathscr {X}') \times _{\operatorname {QC}(\mathscr {Y}')} \operatorname {QC}(\mathscr {Y})$ has a right adjoint
$\operatorname {QC}(R) \to \operatorname {QC}(\mathscr {X}') \times _{\operatorname {QC}(\mathscr {Y}')} \operatorname {QC}(\mathscr {Y})$ has a right adjoint
For full faithfulness we must show that the unit of this adjunction is an isomorphism. By the base-change formula (Proposition A.1.5),
So for full faithfulness it suffices to show that for all ![]() $M \in \operatorname {QC}(R)$,
$M \in \operatorname {QC}(R)$,

is a pullback diagram. This follows from the fact that ![]() $\operatorname {cone}(M \to q_\ast q^{\ast }(M)) \in \operatorname {QC}_Z(\mathscr {X})$, and hence the unit of adjunction
$\operatorname {cone}(M \to q_\ast q^{\ast }(M)) \in \operatorname {QC}_Z(\mathscr {X})$, and hence the unit of adjunction ![]() $(-) \to p_\ast (p^{\ast }(-))$ is an isomorphism when applied to this object, by Lemma 3.3.2.
$(-) \to p_\ast (p^{\ast }(-))$ is an isomorphism when applied to this object, by Lemma 3.3.2.
For essential surjectivity, suppose given ![]() $F_\mathscr {Y}$,
$F_\mathscr {Y}$, ![]() $F_{\mathscr {Y}'}$, and
$F_{\mathscr {Y}'}$, and ![]() $F_{\mathscr {X}'}$, with an equivalence
$F_{\mathscr {X}'}$, with an equivalence ![]() $(q')^{*} F_{\mathscr {X}'} \simeq F_{\mathscr {Y}'} \simeq (p')^{*}(F_{\mathscr {Y}})$. We can tensor this triple with the fiber sequence
$(q')^{*} F_{\mathscr {X}'} \simeq F_{\mathscr {Y}'} \simeq (p')^{*}(F_{\mathscr {Y}})$. We can tensor this triple with the fiber sequence ![]() $R\Gamma _Z(R) \to R \to j_\ast (\mathcal {O}_\mathscr {U})$, where
$R\Gamma _Z(R) \to R \to j_\ast (\mathcal {O}_\mathscr {U})$, where ![]() $j : \mathscr {U} \hookrightarrow \operatorname {Spec}(R)$ is the open immersion. Making use of the projection formula, this shows that
$j : \mathscr {U} \hookrightarrow \operatorname {Spec}(R)$ is the open immersion. Making use of the projection formula, this shows that ![]() $(F_\mathscr {Y},F_{\mathscr {Y}'},F_{R'})$ is an extension of the two triples
$(F_\mathscr {Y},F_{\mathscr {Y}'},F_{R'})$ is an extension of the two triples
and
We have already shown full faithfulness, so it suffices to show that these two triples lie in the essential image of the restriction functor.
For the first triple, using the base-change and projection formulas, it suffices to show that restriction induces an equivalence
This follows from the hypothesis that ![]() $g^{-1}(\mathscr {U}) \to p^{-1}(\mathscr {U})$ and
$g^{-1}(\mathscr {U}) \to p^{-1}(\mathscr {U})$ and ![]() $q^{-1}(\mathscr {U}) \to \mathscr {U}$ are isomorphisms. For the second triple, it suffices to show that restriction induces an equivalence
$q^{-1}(\mathscr {U}) \to \mathscr {U}$ are isomorphisms. For the second triple, it suffices to show that restriction induces an equivalence
This follows from Lemma 3.3.2, which implies that ![]() $\operatorname {QC}_{q^{-1}(Z)}(\mathscr {Y}) \to \operatorname {QC}_{g^{-1}(Z)}(\mathscr {Y}')$ and
$\operatorname {QC}_{q^{-1}(Z)}(\mathscr {Y}) \to \operatorname {QC}_{g^{-1}(Z)}(\mathscr {Y}')$ and ![]() $\operatorname {QC}_Z(R) \to \operatorname {QC}_{p^{-1}(Z)}(\mathscr {X}')$ are equivalences.
$\operatorname {QC}_Z(R) \to \operatorname {QC}_{p^{-1}(Z)}(\mathscr {X}')$ are equivalences.
For the variants of the lemma, choose a smooth surjection ![]() $\operatorname {Spec}(R') \to \mathscr {X}'$, and let
$\operatorname {Spec}(R') \to \mathscr {X}'$, and let ![]() $S \subset \pi _0(R')$ be the multiplicative system consisting of all elements which do not vanish along the preimage of
$S \subset \pi _0(R')$ be the multiplicative system consisting of all elements which do not vanish along the preimage of ![]() $Z$. Then the map
$Z$. Then the map ![]() $\mathscr {U} \sqcup \operatorname {Spec}(S^{-1} R') \to \operatorname {Spec}(R)$ is an fpqc cover, so an
$\mathscr {U} \sqcup \operatorname {Spec}(S^{-1} R') \to \operatorname {Spec}(R)$ is an fpqc cover, so an ![]() $R$-module is connective/almost perfect/perfect if and only if its restrictions
$R$-module is connective/almost perfect/perfect if and only if its restrictions ![]() $p^{\ast }(M)$ and
$p^{\ast }(M)$ and ![]() $q^{\ast }(M)$ are. This allows us to deduce the claim for
$q^{\ast }(M)$ are. This allows us to deduce the claim for ![]() $\operatorname {QC}(-)^{\mathrm {cn}}$,
$\operatorname {QC}(-)^{\mathrm {cn}}$, ![]() $\operatorname {APerf}(-)$, and
$\operatorname {APerf}(-)$, and ![]() $\operatorname {Perf}(-)$ from the claim for
$\operatorname {Perf}(-)$ from the claim for ![]() $\operatorname {QC}(-)$.
$\operatorname {QC}(-)$.
Lemma 3.3.4 Given an abstract blowup square (3), the natural restriction map
is an equivalence. This is also true with ![]() $\operatorname {APerf}(-)$ replaced by
$\operatorname {APerf}(-)$ replaced by ![]() $\operatorname {Perf}(-)$ or
$\operatorname {Perf}(-)$ or ![]() $\operatorname {APerf}(-)^{\mathrm {cn}}$.
$\operatorname {APerf}(-)^{\mathrm {cn}}$.
Proof. Note that this assertion is flat local on ![]() $\mathscr {X}$, so we are free to assume that
$\mathscr {X}$, so we are free to assume that ![]() $\mathscr {X} = \operatorname {Spec}(R)$ is affine. Let
$\mathscr {X} = \operatorname {Spec}(R)$ is affine. Let ![]() $\widehat {R}$ be the
$\widehat {R}$ be the ![]() $I$-completion of
$I$-completion of ![]() $R$, where
$R$, where ![]() $I$ is the ideal defining
$I$ is the ideal defining ![]() $Z \hookrightarrow \mathscr {X}$. Restriction induces equivalences
$Z \hookrightarrow \mathscr {X}$. Restriction induces equivalences ![]() $\operatorname {APerf}(\mathscr {Y}') \simeq \operatorname {APerf}(\widehat {\mathscr {Y}})$, by the Grothendieck existence theorem, and
$\operatorname {APerf}(\mathscr {Y}') \simeq \operatorname {APerf}(\widehat {\mathscr {Y}})$, by the Grothendieck existence theorem, and ![]() $\operatorname {APerf}(\widehat {R}) \to \operatorname {APerf}(\operatorname {Spf}(R))$. It therefore suffices to show that restriction induces an equivalence
$\operatorname {APerf}(\widehat {R}) \to \operatorname {APerf}(\operatorname {Spf}(R))$. It therefore suffices to show that restriction induces an equivalence ![]() $\operatorname {APerf}(R) \to \operatorname {APerf}(\widehat {R}) \times _{\operatorname {APerf}(\mathscr {Y}')} \operatorname {APerf}(\mathscr {Y})$, which follows from Lemma 3.3.3.
$\operatorname {APerf}(R) \to \operatorname {APerf}(\widehat {R}) \times _{\operatorname {APerf}(\mathscr {Y}')} \operatorname {APerf}(\mathscr {Y})$, which follows from Lemma 3.3.3.
Proof of Theorem 3.3.1 The claim follows from applying Proposition 3.2.1 to the functors ![]() $\operatorname {APerf}(-)$,
$\operatorname {APerf}(-)$, ![]() $\operatorname {Perf}(-)$, and
$\operatorname {Perf}(-)$, and ![]() $\operatorname {APerf}(-)^{\mathrm {cn}}$. Condition (i) of Proposition 3.2.1 follows from Proposition 3.1.5, condition (ii) is fppf descent, which these functors have, and condition (iii) follows from Lemma 3.3.4.
$\operatorname {APerf}(-)^{\mathrm {cn}}$. Condition (i) of Proposition 3.2.1 follows from Proposition 3.1.5, condition (ii) is fppf descent, which these functors have, and condition (iii) follows from Lemma 3.3.4.
Corollary 3.3.5 Suppose that ![]() $\mathscr {X}$ is a locally noetherian algebraic derived (or spectral) stack, and that
$\mathscr {X}$ is a locally noetherian algebraic derived (or spectral) stack, and that ![]() $\pi \colon \mathscr {X}' \to \mathscr {X}$ is an almost finitely presented, universally closed morphism. Let
$\pi \colon \mathscr {X}' \to \mathscr {X}$ is an almost finitely presented, universally closed morphism. Let ![]() $\widehat {\mathscr {X}}$ denote the formal completion of
$\widehat {\mathscr {X}}$ denote the formal completion of ![]() $\mathscr {X}$ along the (closed) image of
$\mathscr {X}$ along the (closed) image of ![]() $\pi$. Then the pullback functors determine equivalences
$\pi$. Then the pullback functors determine equivalences
3.3.1 Complement to the work of Bhatt and Scholze
After the first version of this paper was released, Bhargav Bhatt and Peter Scholze proved that the functor ![]() $\operatorname {QC}(-)$ satisfies derived descent along
$\operatorname {QC}(-)$ satisfies derived descent along ![]() $h$-covers of classical noetherian schemes [Reference Bhatt and ScholzeBS17], using the methods of [Reference MathewMat16]. We thank Bhatt for explaining that this implies that
$h$-covers of classical noetherian schemes [Reference Bhatt and ScholzeBS17], using the methods of [Reference MathewMat16]. We thank Bhatt for explaining that this implies that ![]() $\operatorname {QC}(-)^{\mathrm {acn}}$, the category of almost connective complexes, satisfies derived descent along classical
$\operatorname {QC}(-)^{\mathrm {acn}}$, the category of almost connective complexes, satisfies derived descent along classical ![]() $h$-covers as well. Combined with our results, this implies the following proposition.
$h$-covers as well. Combined with our results, this implies the following proposition.
Proposition 3.3.6 ![]() $\operatorname {QC}(-)^{\mathrm {acn}}$ satisfies derived descent along arbitrary
$\operatorname {QC}(-)^{\mathrm {acn}}$ satisfies derived descent along arbitrary ![]() $h$-covers of locally noetherian derived (or spectral) algebraic stacks.
$h$-covers of locally noetherian derived (or spectral) algebraic stacks.
Proof. Let ![]() $\mathcal {C}$ denote the class of almost finitely presented surjections of locally noetherian algebraic derived stacks
$\mathcal {C}$ denote the class of almost finitely presented surjections of locally noetherian algebraic derived stacks ![]() $\pi \colon \mathscr {Y} \to \mathscr {X}$ for which
$\pi \colon \mathscr {Y} \to \mathscr {X}$ for which ![]() $\operatorname {QC}(-)^{\mathrm {acn}}$ satisfies descent after base change along an arbitrary affine morphism
$\operatorname {QC}(-)^{\mathrm {acn}}$ satisfies descent after base change along an arbitrary affine morphism ![]() $\mathscr {X}' \to \mathscr {X}$. We wish to show that any derived
$\mathscr {X}' \to \mathscr {X}$. We wish to show that any derived ![]() $h$-cover
$h$-cover ![]() $\pi \colon \mathscr {Y} \to \mathscr {X}$ is in
$\pi \colon \mathscr {Y} \to \mathscr {X}$ is in ![]() $\mathcal {C}$. One can reduce to the case where
$\mathcal {C}$. One can reduce to the case where ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $\mathscr {Y}$ are affine as in the proof of Proposition 3.2.1.
$\mathscr {Y}$ are affine as in the proof of Proposition 3.2.1.
We know that almost finitely presented closed immersions are in ![]() $\mathcal {C}$ by Proposition 3.1.5, so by ‘locality’ it suffices to show descent for the base change of
$\mathcal {C}$ by Proposition 3.1.5, so by ‘locality’ it suffices to show descent for the base change of ![]() $\pi$ along the inclusion of the underlying classical stack
$\pi$ along the inclusion of the underlying classical stack ![]() $i : \mathscr {X}^{\mathrm {cl}} \hookrightarrow \mathscr {X}$. Thus, we may assume
$i : \mathscr {X}^{\mathrm {cl}} \hookrightarrow \mathscr {X}$. Thus, we may assume ![]() $\mathscr {X}$ is classical. By ‘refinement’ it suffices to show that the composition
$\mathscr {X}$ is classical. By ‘refinement’ it suffices to show that the composition ![]() $\mathscr {Y}^{\mathrm {cl}} \to \mathscr {Y} \to \mathscr {X}$ is in
$\mathscr {Y}^{\mathrm {cl}} \to \mathscr {Y} \to \mathscr {X}$ is in ![]() $\mathcal {C}$, so it suffices to consider an
$\mathcal {C}$, so it suffices to consider an ![]() $h$-cover of classical affine schemes
$h$-cover of classical affine schemes ![]() $\operatorname {Spec}(B) \to \operatorname {Spec}(A)$.
$\operatorname {Spec}(B) \to \operatorname {Spec}(A)$.
Let ![]() $B^{\otimes _A \bullet +1}$ be the Čech nerve of
$B^{\otimes _A \bullet +1}$ be the Čech nerve of ![]() $\pi$. Then [Reference Bhatt and ScholzeBS17, Theorem 11.12] implies that the canonical map
$\pi$. Then [Reference Bhatt and ScholzeBS17, Theorem 11.12] implies that the canonical map ![]() $\operatorname {QC}(A) \to \operatorname {Tot}\{\operatorname {QC}(B^{\otimes _A \bullet +1})\}$ is an equivalence of symmetric monoidal
$\operatorname {QC}(A) \to \operatorname {Tot}\{\operatorname {QC}(B^{\otimes _A \bullet +1})\}$ is an equivalence of symmetric monoidal ![]() $\infty$-categories. It follows that for any simplicial commutative (or connective
$\infty$-categories. It follows that for any simplicial commutative (or connective ![]() $E_\infty$)
$E_\infty$) ![]() $A$-algebra
$A$-algebra ![]() $A'$, if we let
$A'$, if we let ![]() $B' = B \otimes _A A'$, then
$B' = B \otimes _A A'$, then ![]() $A' \otimes _A (B^{\otimes _A \bullet +1}) \simeq (B')^{\otimes _{A'} \bullet +1}$, and
$A' \otimes _A (B^{\otimes _A \bullet +1}) \simeq (B')^{\otimes _{A'} \bullet +1}$, and
is an equivalence of ![]() $\infty$ categories. Thus, to show that
$\infty$ categories. Thus, to show that ![]() $[\operatorname {Spec}(B) \to \operatorname {Spec}(A)] \in \mathcal {C}$ and complete the proof, it suffices to show that for any
$[\operatorname {Spec}(B) \to \operatorname {Spec}(A)] \in \mathcal {C}$ and complete the proof, it suffices to show that for any ![]() $A'$ as above, any
$A'$ as above, any ![]() $E \in A' {\rm {}\hbox{-}{\rm mod}}$ is almost connective if
$E \in A' {\rm {}\hbox{-}{\rm mod}}$ is almost connective if ![]() $B' \otimes _{A'} E$ is almost connective. But
$B' \otimes _{A'} E$ is almost connective. But ![]() $E \in A' {\rm {}\hbox{-}{\rm mod}}$ is almost connective if and only if its underlying
$E \in A' {\rm {}\hbox{-}{\rm mod}}$ is almost connective if and only if its underlying ![]() $A$-module is, and likewise for
$A$-module is, and likewise for ![]() $B'$-modules. The base-change formula implies
$B'$-modules. The base-change formula implies ![]() $B' \otimes _{A'} E \simeq B \otimes _A E$ as
$B' \otimes _{A'} E \simeq B \otimes _A E$ as ![]() $B$-modules, so it suffices to prove the claim when
$B$-modules, so it suffices to prove the claim when ![]() $A'=A$.
$A'=A$.
The classical ![]() $h$-cover
$h$-cover ![]() $\operatorname {Spec}(B) \to \operatorname {Spec}(A)$ can be refined by a fppf cover of a constructible stratification of
$\operatorname {Spec}(B) \to \operatorname {Spec}(A)$ can be refined by a fppf cover of a constructible stratification of ![]() $\operatorname {Spec}(A)$, and the claim is true for fppf covers because
$\operatorname {Spec}(A)$, and the claim is true for fppf covers because ![]() $\operatorname {QC}(-)$ and
$\operatorname {QC}(-)$ and ![]() $\operatorname {QC}(-)^{\mathrm {acn}}$ both satisfy fppf descent. Therefore, it suffices to show that for any discrete noetherian ring
$\operatorname {QC}(-)^{\mathrm {acn}}$ both satisfy fppf descent. Therefore, it suffices to show that for any discrete noetherian ring ![]() $A$, an object
$A$, an object ![]() $E \in \operatorname {QC}(A)$ is almost connective if and only if its restriction to a constructible stratification of
$E \in \operatorname {QC}(A)$ is almost connective if and only if its restriction to a constructible stratification of ![]() $\operatorname {Spec}(A)$ is almost connective. Working locally on
$\operatorname {Spec}(A)$ is almost connective. Working locally on ![]() $\operatorname {Spec}(A)$, one can reduce this to the following claim: if
$\operatorname {Spec}(A)$, one can reduce this to the following claim: if ![]() $f \in A$ is any element, then
$f \in A$ is any element, then ![]() $E \in A {\rm {}\hbox{-}{\rm mod}}$ is almost connective if and only if
$E \in A {\rm {}\hbox{-}{\rm mod}}$ is almost connective if and only if
are almost connective. The ‘only if’ direction is immediate. If ![]() $E[1/f]$ and
$E[1/f]$ and ![]() $E/f$ are almost connective, then we consider the fiber sequence
$E/f$ are almost connective, then we consider the fiber sequence ![]() $E \to E[1/f] \to E[1/f] / E$. The term
$E \to E[1/f] \to E[1/f] / E$. The term ![]() $E[1/f] / E$ has a bounded below exhaustive filtration whose associated graded pieces are isomorphic to
$E[1/f] / E$ has a bounded below exhaustive filtration whose associated graded pieces are isomorphic to ![]() $E/f$, so
$E/f$, so ![]() $E[1/f]/E$ and hence
$E[1/f]/E$ and hence ![]() $E$ are almost connective.
$E$ are almost connective.
3.3.2 Consequences for quasi-geometric stacks
Proposition 3.3.7 If ![]() $\mathscr {F}$ is a locally noetherian algebraic spectral stack with quasi-affine diagonal, then
$\mathscr {F}$ is a locally noetherian algebraic spectral stack with quasi-affine diagonal, then ![]() $\mathscr {F}$ has descent for spectral
$\mathscr {F}$ has descent for spectral ![]() $h$-covers.
$h$-covers.
Proof. It suffices, by Zariski descent, to prove this when ![]() $\mathscr {F}$ is quasi-compact (i.e. noetherian). Given an
$\mathscr {F}$ is quasi-compact (i.e. noetherian). Given an ![]() $h$-cover
$h$-cover ![]() $\pi \colon \mathscr {X}' \to \mathscr {X}$, let
$\pi \colon \mathscr {X}' \to \mathscr {X}$, let ![]() $\mathscr {X}'_\bullet = {\rm Cech}(\pi )$. By Theorem 3.3.1 restriction gives an equivalence
$\mathscr {X}'_\bullet = {\rm Cech}(\pi )$. By Theorem 3.3.1 restriction gives an equivalence ![]() $\operatorname {APerf}(\mathscr {X})^{\mathrm {cn}} \simeq \operatorname {Tot} \{ \operatorname {APerf}(\mathscr {X}'_\bullet )^{\mathrm {cn}} \}$. Note that
$\operatorname {APerf}(\mathscr {X})^{\mathrm {cn}} \simeq \operatorname {Tot} \{ \operatorname {APerf}(\mathscr {X}'_\bullet )^{\mathrm {cn}} \}$. Note that ![]() $\operatorname {Tot}$ is a limit, and colimits in the totalization are formed levelwise, so we have, for any symmetric monoidal
$\operatorname {Tot}$ is a limit, and colimits in the totalization are formed levelwise, so we have, for any symmetric monoidal ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$ which admits finite colimits.
$\mathcal {C}$ which admits finite colimits.
The result follows from the case where ![]() $\mathcal {C} = \operatorname {APerf}(\mathscr {F})^{\mathrm {cn}}$, by the Tannaka duality theorem Theorem 5.1.12.
$\mathcal {C} = \operatorname {APerf}(\mathscr {F})^{\mathrm {cn}}$, by the Tannaka duality theorem Theorem 5.1.12.
Corollary 3.3.8 In the ![]() $\infty$-category of noetherian algebraic spectral stacks with quasi-affine diagonal, any cartesian square which satisfies the conditions of Lemma 3.3.3, and in which
$\infty$-category of noetherian algebraic spectral stacks with quasi-affine diagonal, any cartesian square which satisfies the conditions of Lemma 3.3.3, and in which ![]() $p$ is flat along
$p$ is flat along ![]() $p^{-1}(Z)$, is a also a pushout square.
$p^{-1}(Z)$, is a also a pushout square.
4. Formally proper morphisms
In this section we establish many examples of formally proper morphisms. Theorem 4.2.1 states that ‘cohomologically projective’ morphisms are formally proper, and we give two examples of large classes of cohomologically projective morphisms in Propositions 4.2.3 and 4.2.5. We also develop a method of establishing formal properness using proper coverings in Theorem 4.3.1.
4.1 Cohomologically ample (CA) systems
We introduce a structure for a morphism of stacks which generalizes the notion of a relatively ample bundle for a proper morphism of schemes (Example 4.1.2).
We will say that a set ![]() $I$ is preordered by the non-negative integers if we have an assignment of an integer
$I$ is preordered by the non-negative integers if we have an assignment of an integer ![]() $\sharp (\alpha ) \geqslant 0$ to each
$\sharp (\alpha ) \geqslant 0$ to each ![]() $\alpha \in I$. In this case we say
$\alpha \in I$. In this case we say ![]() $\alpha \geqslant \beta$ (respectively,
$\alpha \geqslant \beta$ (respectively, ![]() $\alpha > \beta$) if
$\alpha > \beta$) if ![]() $\sharp (\alpha ) \geqslant \sharp (\beta )$ (respectively,
$\sharp (\alpha ) \geqslant \sharp (\beta )$ (respectively, ![]() $\sharp (\alpha ) > \sharp (\beta )$). For
$\sharp (\alpha ) > \sharp (\beta )$). For ![]() $E,F \in \operatorname {QC}(\mathscr {X})_{\geqslant 0}$ we say that a map
$E,F \in \operatorname {QC}(\mathscr {X})_{\geqslant 0}$ we say that a map ![]() $E \to F$ is surjective if it is
$E \to F$ is surjective if it is ![]() $0$-connective, or equivalently
$0$-connective, or equivalently ![]() $H_0(E) \to H_0(F)$ is surjective in
$H_0(E) \to H_0(F)$ is surjective in ![]() $\operatorname {QC}(\mathscr {X})^{\heartsuit }$.
$\operatorname {QC}(\mathscr {X})^{\heartsuit }$.
Definition 4.1.1 Let ![]() $\mathscr {X}$ be a noetherian algebraic derived (or spectral) stack, and let
$\mathscr {X}$ be a noetherian algebraic derived (or spectral) stack, and let ![]() $\{V_\alpha \}_{\alpha \in I}$ be a collection of locally free sheaves on
$\{V_\alpha \}_{\alpha \in I}$ be a collection of locally free sheaves on ![]() $\mathscr {X}$ indexed by a set preordered by the non-negative integers. We say that
$\mathscr {X}$ indexed by a set preordered by the non-negative integers. We say that ![]() $\{V_\alpha \}_{\alpha \in I}$ is a cohomologically ample (CA) system if for all
$\{V_\alpha \}_{\alpha \in I}$ is a cohomologically ample (CA) system if for all ![]() $F \in {\rm Coh} (\mathscr {X})$,
$F \in {\rm Coh} (\mathscr {X})$,
(CA1)
 $\forall N \geqslant 0$,
$\forall N \geqslant 0$,  $\operatorname {Hom}(V_\alpha,F) \neq 0$ from some
$\operatorname {Hom}(V_\alpha,F) \neq 0$ from some  $V_\alpha$ with
$V_\alpha$ with  $\sharp (\alpha ) \geqslant N$, and
$\sharp (\alpha ) \geqslant N$, and(CA2)
 $\forall i < 0$,
$\forall i < 0$,  $\exists N \geqslant 0$ such that
$\exists N \geqslant 0$ such that  $H_i \operatorname {RHom}(V_\alpha, F) = 0$ whenever
$H_i \operatorname {RHom}(V_\alpha, F) = 0$ whenever  $\sharp (\alpha ) \geqslant N$.
$\sharp (\alpha ) \geqslant N$.
If ![]() $\pi : \mathscr {X} \to \mathscr {S}$ is a qc.qs. morphism of locally noetherian algebraic derived stacks, we say that
$\pi : \mathscr {X} \to \mathscr {S}$ is a qc.qs. morphism of locally noetherian algebraic derived stacks, we say that ![]() $\{V_\alpha \}_{\alpha \in I}$ is a cohomologically ample system relative to
$\{V_\alpha \}_{\alpha \in I}$ is a cohomologically ample system relative to ![]() $\pi$ if, for any affine derived scheme
$\pi$ if, for any affine derived scheme ![]() $T$ which is flat and locally almost finitely presented over
$T$ which is flat and locally almost finitely presented over ![]() $\mathscr {S}$, the system
$\mathscr {S}$, the system ![]() $\{V_\alpha |_{\mathscr {X} \times _\mathscr {S} T} \}_{\alpha \in I}$ satisfies (CA1) and (CA2).
$\{V_\alpha |_{\mathscr {X} \times _\mathscr {S} T} \}_{\alpha \in I}$ satisfies (CA1) and (CA2).
We will often abbreviate by saying that ![]() $\{V_\alpha \}$ is a preordered system.
$\{V_\alpha \}$ is a preordered system.
Example 4.1.2 If ![]() $X$ is a projective classical scheme over an affine noetherian base
$X$ is a projective classical scheme over an affine noetherian base ![]() $S$, then
$S$, then ![]() $X$ admits a cohomologically ample system. We take
$X$ admits a cohomologically ample system. We take ![]() $I = \{n \geqslant 0\}$ with
$I = \{n \geqslant 0\}$ with ![]() $\sharp (n)=n$, and we let
$\sharp (n)=n$, and we let ![]() $V_n := L^{-n}$, where
$V_n := L^{-n}$, where ![]() $L$ is an ample invertible sheaf on
$L$ is an ample invertible sheaf on ![]() $X$.
$X$.
Definition 4.1.3 A morphism between locally noetherian algebraic derived stacks, ![]() $\pi : \mathscr {X} \to \mathscr {S}$, is cohomologically projective if it satisfies (CD) and (CP), and possesses a relatively (CA) system of locally free sheaves
$\pi : \mathscr {X} \to \mathscr {S}$, is cohomologically projective if it satisfies (CD) and (CP), and possesses a relatively (CA) system of locally free sheaves ![]() $\{V_\alpha \}_{\alpha \in I}$.
$\{V_\alpha \}_{\alpha \in I}$.
We will collect some useful (and familiar) properties of cohomologically ample systems over several lemmas.
Lemma 4.1.4 Let ![]() $\mathscr {X}$ be an algebraic derived (or spectral) stack and let
$\mathscr {X}$ be an algebraic derived (or spectral) stack and let ![]() $i\colon \mathscr {X}_{\mathrm {cl}} \to \mathscr {X}$ be the inclusion of the underlying classical stack. Then a preordered system
$i\colon \mathscr {X}_{\mathrm {cl}} \to \mathscr {X}$ be the inclusion of the underlying classical stack. Then a preordered system ![]() $\{V_\alpha \}$ is (CA) on
$\{V_\alpha \}$ is (CA) on ![]() $\mathscr {X}$ if and only if
$\mathscr {X}$ if and only if ![]() $\{i^{*} V_\alpha \}$ is (CA) on
$\{i^{*} V_\alpha \}$ is (CA) on ![]() $\mathscr {X}_{\mathrm {cl}}$.
$\mathscr {X}_{\mathrm {cl}}$.
Proof. This follows immediately from the ![]() $(i^{*}, i_*)$ adjunction and the fact that
$(i^{*}, i_*)$ adjunction and the fact that ![]() $i_* \colon {\rm Coh} (\mathscr {X}_{\mathrm {cl}}) \to {\rm Coh} (\mathscr {X})$ is an equivalence of categories.
$i_* \colon {\rm Coh} (\mathscr {X}_{\mathrm {cl}}) \to {\rm Coh} (\mathscr {X})$ is an equivalence of categories.
Lemma 4.1.5 Consider a cartesian square of locally noetherian algebraic derived (or spectral) stacks

such that ![]() $f$ is flat and locally almost finitely presented. Let
$f$ is flat and locally almost finitely presented. Let ![]() $\{V_\alpha \}_{\alpha \in I}$ be a preordered system of locally free sheaves on
$\{V_\alpha \}_{\alpha \in I}$ be a preordered system of locally free sheaves on ![]() $\mathscr {X}$, and let
$\mathscr {X}$, and let ![]() $V'_\alpha := (f')^{\ast }(V_\alpha )$. If
$V'_\alpha := (f')^{\ast }(V_\alpha )$. If ![]() $\{V_\alpha \}$ is (CA) relative to
$\{V_\alpha \}$ is (CA) relative to ![]() $\pi$, then
$\pi$, then ![]() $\{V'_\alpha \}$ is (CA) relative to
$\{V'_\alpha \}$ is (CA) relative to ![]() $\pi '$. The converse holds if
$\pi '$. The converse holds if ![]() $f$ is surjective.
$f$ is surjective.
Proof. The first claim follows immediately from the definition. For the converse, observe that for any flat and locally almost finitely presented map ![]() $\operatorname {Spec}(R) \to \mathscr {S}$, we can find a flat and locally almost finitely presented map
$\operatorname {Spec}(R) \to \mathscr {S}$, we can find a flat and locally almost finitely presented map ![]() $\operatorname {Spec}(R') \to \mathscr {S}'$ such that
$\operatorname {Spec}(R') \to \mathscr {S}'$ such that ![]() $\operatorname {Spec}(R^{\prime }) \to \mathscr {S}^{\prime } \to \mathscr {S}$ factors through
$\operatorname {Spec}(R^{\prime }) \to \mathscr {S}^{\prime } \to \mathscr {S}$ factors through ![]() $\operatorname {Spec}(R) \to \mathscr {S}$ via a faithfully flat map
$\operatorname {Spec}(R) \to \mathscr {S}$ via a faithfully flat map ![]() $\operatorname {Spec}(R^{\prime }) \to \operatorname {Spec}(R)$. For
$\operatorname {Spec}(R^{\prime }) \to \operatorname {Spec}(R)$. For ![]() $F \in {\rm Coh} (\mathscr {X}_R)$, conditions (CA1) and (CA2) can be checked after pullback along the faithfully flat map
$F \in {\rm Coh} (\mathscr {X}_R)$, conditions (CA1) and (CA2) can be checked after pullback along the faithfully flat map ![]() $\mathscr {X}_{R'} \to \mathscr {X}_{R}$, and thus they hold by the hypothesis that
$\mathscr {X}_{R'} \to \mathscr {X}_{R}$, and thus they hold by the hypothesis that ![]() $\{V'_\alpha \}$ is (CA) relative to
$\{V'_\alpha \}$ is (CA) relative to ![]() $\pi '$.
$\pi '$.
Lemma 4.1.6 Let ![]() $\pi : \mathscr {X} \to \mathscr {S}$ be a morphism of noetherian algebraic derived (or spectral) stacks, and let
$\pi : \mathscr {X} \to \mathscr {S}$ be a morphism of noetherian algebraic derived (or spectral) stacks, and let ![]() $\{V_\alpha \}_{\alpha \in I}$ be a (CA) system relative to
$\{V_\alpha \}_{\alpha \in I}$ be a (CA) system relative to ![]() $\pi$. Then, for all
$\pi$. Then, for all ![]() $F \in {\rm Coh} (\mathscr {X})$ and for all
$F \in {\rm Coh} (\mathscr {X})$ and for all ![]() $N\geqslant 0$, there is a locally free sheaf
$N\geqslant 0$, there is a locally free sheaf ![]() $W$ which is a finite direct sum of sheaves in the collection
$W$ which is a finite direct sum of sheaves in the collection ![]() $\{V_\alpha | \sharp (\alpha ) \geqslant N \}$ such that the canonical map obtained by composing
$\{V_\alpha | \sharp (\alpha ) \geqslant N \}$ such that the canonical map obtained by composing
is surjective. If ![]() $\pi$ satisfies (CD), then the map (4) is surjective for all
$\pi$ satisfies (CD), then the map (4) is surjective for all ![]() $F \in \operatorname {APerf}(\mathscr {X})_{\geqslant 0}$
$F \in \operatorname {APerf}(\mathscr {X})_{\geqslant 0}$
Note that the canonical map ![]() $H_0 \pi _\ast (W^{\ast } \otimes F) \to \pi _\ast (W^{\ast } \otimes F)$ used in this lemma exists because
$H_0 \pi _\ast (W^{\ast } \otimes F) \to \pi _\ast (W^{\ast } \otimes F)$ used in this lemma exists because ![]() $W^{\ast } \otimes F \in \operatorname {QC}(\mathscr {X})^{\heartsuit }$.
$W^{\ast } \otimes F \in \operatorname {QC}(\mathscr {X})^{\heartsuit }$.
Proof. The formation of (4) commutes with flat base change by Lemma A.1.3, so because ![]() $\mathscr {S}$ is quasi-compact we may reduce to the case where
$\mathscr {S}$ is quasi-compact we may reduce to the case where ![]() $\mathscr {S}$ is affine. Note that in this case if
$\mathscr {S}$ is affine. Note that in this case if ![]() $F$ admits a surjection
$F$ admits a surjection ![]() $W \to F$, then the canonical map (4) is surjective, so it suffices to find a
$W \to F$, then the canonical map (4) is surjective, so it suffices to find a ![]() $W$ as in the statement of the lemma which admits a surjection
$W$ as in the statement of the lemma which admits a surjection ![]() $W \to F$.
$W \to F$.
Let ![]() $W \to F$ be a non-zero homomorphism, with
$W \to F$ be a non-zero homomorphism, with ![]() $W$ locally free. Let
$W$ locally free. Let ![]() $Q = H_0(\operatorname {cone}(W \to F))$ be the cokernel of the map
$Q = H_0(\operatorname {cone}(W \to F))$ be the cokernel of the map ![]() $H_0(W) \to F$, and let
$H_0(W) \to F$, and let ![]() $K = \operatorname {fib}(F \to Q)$ be the kernel of the resulting quotient map. Condition (CA1) implies that we can find a non-zero homomorphism
$K = \operatorname {fib}(F \to Q)$ be the kernel of the resulting quotient map. Condition (CA1) implies that we can find a non-zero homomorphism ![]() $V_\alpha \to Q$ with
$V_\alpha \to Q$ with ![]() $\sharp (\alpha ) \geqslant N$, and, choosing
$\sharp (\alpha ) \geqslant N$, and, choosing ![]() $\alpha$ sufficiently large, we may suppose by (CA2) that
$\alpha$ sufficiently large, we may suppose by (CA2) that ![]() $\operatorname {Hom}(V_\alpha,K[1])=0$, so the map
$\operatorname {Hom}(V_\alpha,K[1])=0$, so the map ![]() $V_\alpha \to Q$ lifts to a map
$V_\alpha \to Q$ lifts to a map ![]() $V_\alpha \to F$. Note that the image of the resulting map
$V_\alpha \to F$. Note that the image of the resulting map ![]() $W \oplus V_\alpha \to F$ is strictly larger than
$W \oplus V_\alpha \to F$ is strictly larger than ![]() $\operatorname {im}(W \to F)$. We can thus replace
$\operatorname {im}(W \to F)$. We can thus replace ![]() $W$ with
$W$ with ![]() $W \oplus V_\alpha$ and repeat this process as long as
$W \oplus V_\alpha$ and repeat this process as long as ![]() $W \to F$ is not surjective, and this process must terminate after finitely many steps because
$W \to F$ is not surjective, and this process must terminate after finitely many steps because ![]() $\mathscr {X}$ is noetherian.
$\mathscr {X}$ is noetherian.
Now assume ![]() $\pi$ satisfies (CD), and
$\pi$ satisfies (CD), and ![]() $F \in \operatorname {APerf}(\mathscr {X})_{\geqslant 0}$. If
$F \in \operatorname {APerf}(\mathscr {X})_{\geqslant 0}$. If ![]() $\pi _\ast$ has cohomological dimension
$\pi _\ast$ has cohomological dimension ![]() $d$, then
$d$, then ![]() $H_0 \pi _\ast (\tau _{> d}(F)) = 0$. Condition (CA2) implies that, for
$H_0 \pi _\ast (\tau _{> d}(F)) = 0$. Condition (CA2) implies that, for ![]() $\alpha$ large enough, we can assume that
$\alpha$ large enough, we can assume that ![]() $H_0(\pi _\ast (H_i(F)[-i]))$ for
$H_0(\pi _\ast (H_i(F)[-i]))$ for ![]() $i=1,\ldots,d$. Because
$i=1,\ldots,d$. Because ![]() $F$ can be constructed as a finite sequence of extensions of the objects
$F$ can be constructed as a finite sequence of extensions of the objects ![]() $\tau _{>d}(F)$ and
$\tau _{>d}(F)$ and ![]() $H_i(F)[-i]$ for
$H_i(F)[-i]$ for ![]() $i=0,\ldots,d$, this reduces the claim to showing that
$i=0,\ldots,d$, this reduces the claim to showing that ![]() $W \otimes \pi ^{\ast }(H_0 \pi _\ast (H_0(F))) \to H_0(F)$ is surjective, which we have already done.
$W \otimes \pi ^{\ast }(H_0 \pi _\ast (H_0(F))) \to H_0(F)$ is surjective, which we have already done.
Under an additional cohomological dimension hypothesis, we can weaken the definition of (CA).
Lemma 4.1.7 Let ![]() $\mathscr {X}$ be a noetherian stack of finite cohomological dimension, and let
$\mathscr {X}$ be a noetherian stack of finite cohomological dimension, and let ![]() $\{V_\alpha \}_{\alpha \in I}$ be a preordered system of locally free sheaves on
$\{V_\alpha \}_{\alpha \in I}$ be a preordered system of locally free sheaves on ![]() $\mathscr {X}$ which satisfies (CA1). Then (CA2) is equivalent to either of the following conditions.
$\mathscr {X}$ which satisfies (CA1). Then (CA2) is equivalent to either of the following conditions.
(CA2
 $'$)
$'$)  $\forall \beta \in I$,
$\forall \beta \in I$,  $\exists N \geqslant 0$ such that
$\exists N \geqslant 0$ such that  $R\Gamma (V_\beta \otimes V_\alpha ^{\ast })$ is connective whenever
$R\Gamma (V_\beta \otimes V_\alpha ^{\ast })$ is connective whenever  $\sharp (\alpha ) \geqslant N$.
$\sharp (\alpha ) \geqslant N$.(CA2
 $''$)
$''$)  $\forall F \in \operatorname {APerf}(\mathscr {X})$,
$\forall F \in \operatorname {APerf}(\mathscr {X})$,  $\exists N \geqslant 0$ such that
$\exists N \geqslant 0$ such that  $\operatorname {RHom}(V_\alpha,F)$ is connective whenever
$\operatorname {RHom}(V_\alpha,F)$ is connective whenever  $\sharp (\alpha ) \geqslant N$.
$\sharp (\alpha ) \geqslant N$.
Proof. It is clear that (CA2![]() $''$) implies both (CA2) and (CA2
$''$) implies both (CA2) and (CA2![]() $'$), and an argument similar to the last paragraph in the proof of Lemma 4.1.6 shows that (CA2) implies (CA2
$'$), and an argument similar to the last paragraph in the proof of Lemma 4.1.6 shows that (CA2) implies (CA2![]() $''$) when
$''$) when ![]() $\mathscr {X}$ has finite cohomological dimension. We will thus show that (CA2
$\mathscr {X}$ has finite cohomological dimension. We will thus show that (CA2![]() $'$) implies (CA2
$'$) implies (CA2![]() $''$).
$''$).
We introduce the following condition for ![]() $p\geqslant 0$.
$p\geqslant 0$.
(CA2)
 $_p$ For all
$_p$ For all  $F \in \operatorname {APerf}(\mathscr {X})_{\geqslant 0}$, there exists an integer
$F \in \operatorname {APerf}(\mathscr {X})_{\geqslant 0}$, there exists an integer  $N$ such that
$N$ such that  $R\Gamma (F \otimes V_\alpha ^{*}) \in ({\mathbb {Z}} -Mod)_{> -p}$ for all
$R\Gamma (F \otimes V_\alpha ^{*}) \in ({\mathbb {Z}} -Mod)_{> -p}$ for all  $\sharp (\alpha ) \geqslant N$.
$\sharp (\alpha ) \geqslant N$.
Our goal is to prove that (CA2)![]() $_1$ holds, and we will show this by descending induction on
$_1$ holds, and we will show this by descending induction on ![]() $p > 0$. Note that (CD) implies that this holds for some sufficiently large
$p > 0$. Note that (CD) implies that this holds for some sufficiently large ![]() $p$, providing the base case.
$p$, providing the base case.
Assume (CA2)![]() $_p$, and note that by considering the long exact homology sequence associated to the exact triangle
$_p$, and note that by considering the long exact homology sequence associated to the exact triangle ![]() $(\tau _{>0} F) \otimes V_\alpha ^{\ast } \to F \otimes V_\alpha ^{\ast } \to (H_0 F)\otimes V_\alpha ^{\ast } \to$, it suffices to consider
$(\tau _{>0} F) \otimes V_\alpha ^{\ast } \to F \otimes V_\alpha ^{\ast } \to (H_0 F)\otimes V_\alpha ^{\ast } \to$, it suffices to consider ![]() $F \in {\rm Coh} (\mathscr {X})$ in order to show (CA2)
$F \in {\rm Coh} (\mathscr {X})$ in order to show (CA2)![]() $_{p-1}$. Let
$_{p-1}$. Let ![]() $F \in {\rm Coh} (\mathscr {X})$. By condition (CA1
$F \in {\rm Coh} (\mathscr {X})$. By condition (CA1![]() $'$) we have a non-zero homomorphism
$'$) we have a non-zero homomorphism ![]() $\phi : V_\beta \to F$. This leads to two exact triangles
$\phi : V_\beta \to F$. This leads to two exact triangles
We want to show that ![]() $H_{-p+1} R\Gamma (F \otimes V_\alpha ^{\ast }) = 0$ for
$H_{-p+1} R\Gamma (F \otimes V_\alpha ^{\ast }) = 0$ for ![]() $\sharp (\alpha ) \gg 0$. For
$\sharp (\alpha ) \gg 0$. For ![]() $\sharp (\alpha ) \gg 0$ we have
$\sharp (\alpha ) \gg 0$ we have ![]() $R\Gamma (V_\beta \otimes V_\alpha ^{\ast }) \in ({\mathbb {Z}}-Mod)_{\geqslant 0}$ by (CA2
$R\Gamma (V_\beta \otimes V_\alpha ^{\ast }) \in ({\mathbb {Z}}-Mod)_{\geqslant 0}$ by (CA2![]() $'$) and
$'$) and ![]() $H_{-p+1} R\Gamma (V_\alpha ^{\ast } \otimes \tau _{>0} \operatorname {cone}(\phi )) = 0$ by hypothesis (CA2)
$H_{-p+1} R\Gamma (V_\alpha ^{\ast } \otimes \tau _{>0} \operatorname {cone}(\phi )) = 0$ by hypothesis (CA2)![]() $_p$. Thus, from the long exact sequence in homology applied to the exact triangles above, we have
$_p$. Thus, from the long exact sequence in homology applied to the exact triangles above, we have
whenever ![]() $\sharp (\alpha ) \gg 0$.
$\sharp (\alpha ) \gg 0$.
Iterating this argument, we get a strictly descending sequence ![]() $F \twoheadrightarrow F_1 \twoheadrightarrow F_2 \twoheadrightarrow \cdots$ in
$F \twoheadrightarrow F_1 \twoheadrightarrow F_2 \twoheadrightarrow \cdots$ in ![]() ${\rm Coh} (\mathscr {X})$ such that
${\rm Coh} (\mathscr {X})$ such that ![]() $H_{-p+1} R\Gamma (F \otimes V_\alpha ^{\ast }) \simeq H_{-p+1} R\Gamma (F_i \otimes V_\alpha ^{\ast })$ for
$H_{-p+1} R\Gamma (F \otimes V_\alpha ^{\ast }) \simeq H_{-p+1} R\Gamma (F_i \otimes V_\alpha ^{\ast })$ for ![]() $\sharp (\alpha ) \gg 0$. Because
$\sharp (\alpha ) \gg 0$. Because ![]() $\mathscr {X}$ is noetherian, we must have
$\mathscr {X}$ is noetherian, we must have ![]() $F_n = 0$ for some
$F_n = 0$ for some ![]() $n$, hence
$n$, hence ![]() $H^{p} R\Gamma (F \otimes V_\alpha ^{\ast }) = 0$.
$H^{p} R\Gamma (F \otimes V_\alpha ^{\ast }) = 0$.
Using this alternate characterization of (CA) systems, we can establish that relatively (CA) systems are stable under base change.
Lemma 4.1.8 Consider a cartesian square of noetherian algebraic derived (or spectral) stacks

such that ![]() $\pi$ satisfies (CD). If a preordered system
$\pi$ satisfies (CD). If a preordered system ![]() $\{V_\alpha \}$ on
$\{V_\alpha \}$ on ![]() $\mathscr {X}$ is (CA), then its restriction
$\mathscr {X}$ is (CA), then its restriction ![]() $\{V_\alpha |_{\mathscr {X}^{\prime }}\}$ is (CA).
$\{V_\alpha |_{\mathscr {X}^{\prime }}\}$ is (CA).
Proof. By Lemma 4.1.7 it suffices to check that ![]() $\{V_\alpha |_{\mathscr {X}^{\prime }}\}$ satisfies (CA1) and (CA2
$\{V_\alpha |_{\mathscr {X}^{\prime }}\}$ satisfies (CA1) and (CA2![]() $'$). (CA1) is immediate: for any non-zero
$'$). (CA1) is immediate: for any non-zero ![]() $F \in {\rm Coh} (\mathscr {X}')$ we can choose a non-zero coherent subsheaf of
$F \in {\rm Coh} (\mathscr {X}')$ we can choose a non-zero coherent subsheaf of ![]() $F' \subset f_\ast (F)$, and if
$F' \subset f_\ast (F)$, and if ![]() $\operatorname {Hom}(V_\alpha,F') \neq 0$ then
$\operatorname {Hom}(V_\alpha,F') \neq 0$ then ![]() $\operatorname {Hom}(V_\alpha,f_\ast (F)) \simeq \operatorname {Hom}(V_\alpha |_{\mathscr {X}'},F) \neq 0$.
$\operatorname {Hom}(V_\alpha,f_\ast (F)) \simeq \operatorname {Hom}(V_\alpha |_{\mathscr {X}'},F) \neq 0$.
To check property (CA2![]() $'$), first note that when
$'$), first note that when ![]() $\mathscr {X}$ is defined over an affine base, the vanishing of higher global sections in property (CA2
$\mathscr {X}$ is defined over an affine base, the vanishing of higher global sections in property (CA2![]() $'$) is equivalent to
$'$) is equivalent to ![]() $\pi _\ast (V_\beta \otimes V_\alpha ^{\ast }) \in \operatorname {QC}(\operatorname {Spec}(R))_{\geqslant 0}$. By the base-change formula (Proposition A.1.5)
$\pi _\ast (V_\beta \otimes V_\alpha ^{\ast }) \in \operatorname {QC}(\operatorname {Spec}(R))_{\geqslant 0}$. By the base-change formula (Proposition A.1.5)
So it suffices to show that for each ![]() $\beta \in I$ there is an
$\beta \in I$ there is an ![]() $N$ such that
$N$ such that ![]() $\pi _* \big (V_\beta \otimes V_\alpha ^{*} \big ) \in \operatorname {QC}(\operatorname {Spec}(R))_{\geqslant 0}$ for
$\pi _* \big (V_\beta \otimes V_\alpha ^{*} \big ) \in \operatorname {QC}(\operatorname {Spec}(R))_{\geqslant 0}$ for ![]() $\sharp (\alpha ) \geqslant N$, but this holds by the hypothesis that
$\sharp (\alpha ) \geqslant N$, but this holds by the hypothesis that ![]() $\{V_\alpha \}$ is (CA) by Lemma 4.1.7.
$\{V_\alpha \}$ is (CA) by Lemma 4.1.7.
Corollary 4.1.9 Let ![]() $\pi : \mathscr {X} \to \operatorname {Spec}(R)$ be a morphism of noetherian algebraic derived (or spectral) stacks which satisfies (CD). A preordered system of locally free sheaves on
$\pi : \mathscr {X} \to \operatorname {Spec}(R)$ be a morphism of noetherian algebraic derived (or spectral) stacks which satisfies (CD). A preordered system of locally free sheaves on ![]() $\mathscr {X}$ is (CA) relative to
$\mathscr {X}$ is (CA) relative to ![]() $\pi$ if and only if it is (CA).
$\pi$ if and only if it is (CA).
Proof. The ‘only if’ direction is tautological, so we must show that if ![]() $\{V_\alpha \}$ is (CA), then for any flat finitely presented morphism
$\{V_\alpha \}$ is (CA), then for any flat finitely presented morphism ![]() $\operatorname {Spec}(R^{\prime }) \to \operatorname {Spec}(R)$, the preordered system
$\operatorname {Spec}(R^{\prime }) \to \operatorname {Spec}(R)$, the preordered system ![]() $\{V_\alpha |_{\mathscr {X}_{R^{\prime }}}\}$ is (CA). This follows from Lemma 4.1.8.
$\{V_\alpha |_{\mathscr {X}_{R^{\prime }}}\}$ is (CA). This follows from Lemma 4.1.8.
Corollary 4.1.10 Let ![]() $\pi : \mathscr {X} \to \mathscr {S}$ be a morphism of noetherian algebraic derived (or spectral) stacks which satisfies (CD). Let
$\pi : \mathscr {X} \to \mathscr {S}$ be a morphism of noetherian algebraic derived (or spectral) stacks which satisfies (CD). Let ![]() $S \to \mathscr {S}$ be an fppf morphism from an affine derived scheme. Then a preordered system
$S \to \mathscr {S}$ be an fppf morphism from an affine derived scheme. Then a preordered system ![]() $\{V_\alpha \}$ on
$\{V_\alpha \}$ on ![]() $\mathscr {X}$ is (CA) relative to
$\mathscr {X}$ is (CA) relative to ![]() $\pi$ if and only if
$\pi$ if and only if ![]() $\{V_\alpha |_{\mathscr {X} \times _\mathscr {S} S}\}$ is (CA).
$\{V_\alpha |_{\mathscr {X} \times _\mathscr {S} S}\}$ is (CA).
Corollary 4.1.11 Consider a cartesian square of locally noetherian algebraic derived (or spectral) stacks

such that ![]() $\pi$ is qc.qs. and satisfies (CD). If a preordered system
$\pi$ is qc.qs. and satisfies (CD). If a preordered system ![]() $\{V_\alpha \}$ is (CA) relative to
$\{V_\alpha \}$ is (CA) relative to ![]() $\pi$, then
$\pi$, then ![]() $\{V_\alpha |_{\mathscr {X}^{\prime }}\}$ is (CA) relative to
$\{V_\alpha |_{\mathscr {X}^{\prime }}\}$ is (CA) relative to ![]() $\pi ^{\prime }$.
$\pi ^{\prime }$.
Proof. By Lemma 4.1.5 we can reduce to the case where ![]() $\mathscr {S}'$ and
$\mathscr {S}'$ and ![]() $\mathscr {S}$ are affine, in which case the claim follows immediately from Corollary 4.1.9 and Lemma 4.1.8.
$\mathscr {S}$ are affine, in which case the claim follows immediately from Corollary 4.1.9 and Lemma 4.1.8.
Proposition 4.1.12 Let ![]() $\pi \colon \mathscr {X} \to \mathscr {S}$ be a morphism of noetherian algebraic derived (or spectral) stacks which satisfies (CD), and assume that
$\pi \colon \mathscr {X} \to \mathscr {S}$ be a morphism of noetherian algebraic derived (or spectral) stacks which satisfies (CD), and assume that ![]() $\mathscr {S}$ has affine diagonal. Then a preordered system
$\mathscr {S}$ has affine diagonal. Then a preordered system ![]() $\{V_\alpha \}_{\alpha \in I}$ on
$\{V_\alpha \}_{\alpha \in I}$ on ![]() $\mathscr {X}$ is relatively (CA) if and only if
$\mathscr {X}$ is relatively (CA) if and only if
(i)
 $\forall F \in {\rm Coh} (\mathscr {X})$,
$\forall F \in {\rm Coh} (\mathscr {X})$,  $\forall N \geqslant 0$, there is an
$\forall N \geqslant 0$, there is an  $\alpha$ with
$\alpha$ with  $\sharp (\alpha ) \geqslant N$ and
$\sharp (\alpha ) \geqslant N$ and  $H_0 \pi _\ast (F \otimes V_\alpha ^{\ast }) \neq 0$, and
$H_0 \pi _\ast (F \otimes V_\alpha ^{\ast }) \neq 0$, and(ii) for all
 $\beta \in I$,
$\beta \in I$,  $\exists N$ such that
$\exists N$ such that  $\pi _\ast (V_\beta \otimes V_\alpha ^{\ast }) \in \operatorname {QC}(\mathscr {S})_{\geqslant 0}$ whenever
$\pi _\ast (V_\beta \otimes V_\alpha ^{\ast }) \in \operatorname {QC}(\mathscr {S})_{\geqslant 0}$ whenever  $\sharp (\alpha ) \geqslant N$.
$\sharp (\alpha ) \geqslant N$.
Proof. Note that conditions (i) and (ii) can be checked after base change along an fppf map ![]() $\operatorname {Spec}(R) \to \mathscr {S}$, and so they hold if
$\operatorname {Spec}(R) \to \mathscr {S}$, and so they hold if ![]() $\{V_\alpha \}$ is relatively (CA).
$\{V_\alpha \}$ is relatively (CA).
To prove the converse, fix an fppf morphism from an affine scheme ![]() $S \to \mathscr {S}$ and let
$S \to \mathscr {S}$ and let ![]() $\mathscr {X}^{\prime } = \mathscr {X} \times _\mathscr {S} S$. By Corollary 4.1.10 it suffices to prove that
$\mathscr {X}^{\prime } = \mathscr {X} \times _\mathscr {S} S$. By Corollary 4.1.10 it suffices to prove that ![]() $\{V_\alpha |_{\mathscr {X}^{\prime }}\}$ is (CA).
$\{V_\alpha |_{\mathscr {X}^{\prime }}\}$ is (CA). ![]() $\mathscr {X}^{\prime } \to \mathscr {X}$ is an affine morphism of noetherian stacks, so the proof of (CA1) from Lemma 4.1.8 applies verbatim. By Lemma 4.1.7 it remains to verify (CA2
$\mathscr {X}^{\prime } \to \mathscr {X}$ is an affine morphism of noetherian stacks, so the proof of (CA1) from Lemma 4.1.8 applies verbatim. By Lemma 4.1.7 it remains to verify (CA2![]() $'$) for
$'$) for ![]() $\{V_\alpha |_{\mathscr {X}^{\prime }}\}$, and this follows from the base-change formula.
$\{V_\alpha |_{\mathscr {X}^{\prime }}\}$, and this follows from the base-change formula.
4.2 Cohomologically projective morphisms are formally proper
In this section we generalize the proof of the Grothendieck existence theorem for projective morphisms of schemes.
Theorem 4.2.1 (Strong Grothendieck existence)
Let ![]() $\mathscr {S}$ be a noetherian algebraic spectral (or derived) stack which is complete along a closed subset
$\mathscr {S}$ be a noetherian algebraic spectral (or derived) stack which is complete along a closed subset ![]() $Z \subset |\mathscr {S}|$. Then, for any cohomologically projective morphism
$Z \subset |\mathscr {S}|$. Then, for any cohomologically projective morphism ![]() $\pi :\mathscr {X} \to \mathscr {S}$,
$\pi :\mathscr {X} \to \mathscr {S}$, ![]() $\mathscr {X}$ is complete along
$\mathscr {X}$ is complete along ![]() $\pi ^{-1}(Z)$.
$\pi ^{-1}(Z)$.
The key idea of the proof is contained in the following lemma, which states that the formal completion of a (CA) system of locally free sheaves is again (CA) in a suitable sense.
Lemma 4.2.2 Let ![]() $\pi \colon \mathscr {X} \to \mathscr {S}$ be a cohomologically projective morphism of noetherian algebraic derived (or spectral) stacks, let
$\pi \colon \mathscr {X} \to \mathscr {S}$ be a cohomologically projective morphism of noetherian algebraic derived (or spectral) stacks, let ![]() $\{V_\alpha \}$ be a relatively (CA) system, and let
$\{V_\alpha \}$ be a relatively (CA) system, and let ![]() $Z \subset |\mathscr {S}|$ be a closed subset. Let
$Z \subset |\mathscr {S}|$ be a closed subset. Let ![]() $i : \widehat {\mathscr {X}} \to \mathscr {X}$ be the formal completion of
$i : \widehat {\mathscr {X}} \to \mathscr {X}$ be the formal completion of ![]() $\mathscr {X}$ along
$\mathscr {X}$ along ![]() $\pi ^{-1}(Z)$, and
$\pi ^{-1}(Z)$, and ![]() $\widehat {\pi } \colon \widehat {\mathscr {X}} \to \widehat {\mathscr {S}}$ the corresponding projection. Then, for all
$\widehat {\pi } \colon \widehat {\mathscr {X}} \to \widehat {\mathscr {S}}$ the corresponding projection. Then, for all ![]() $\widehat {F} \in {\rm Coh} (\widehat {\mathscr {X}})$:
$\widehat {F} \in {\rm Coh} (\widehat {\mathscr {X}})$:
(i)
 $\forall N \geqslant 0$, one can find
$\forall N \geqslant 0$, one can find  $W \in {\rm Coh} (\mathscr {X})$ which is a finite direct sum of locally free sheaves in the collection
$W \in {\rm Coh} (\mathscr {X})$ which is a finite direct sum of locally free sheaves in the collection  $\{V_\alpha | \sharp (\alpha ) \geqslant N \}$ such that
is surjective, meaning that its mapping cone is
$\{V_\alpha | \sharp (\alpha ) \geqslant N \}$ such that
is surjective, meaning that its mapping cone is \[ i^{\ast} (W) \otimes \widehat{\pi}^{\ast} \widehat{\pi}_\ast (i^{\ast} (W) \otimes \widehat{F}) \to \widehat{F} \]
\[ i^{\ast} (W) \otimes \widehat{\pi}^{\ast} \widehat{\pi}_\ast (i^{\ast} (W) \otimes \widehat{F}) \to \widehat{F} \]
 $1$-connective; and
$1$-connective; and(ii)
 $\exists N \geqslant 0$ such that
$\exists N \geqslant 0$ such that  $\widehat {\pi }_\ast (i^{\ast } (V_\alpha )^{\ast } \otimes \widehat {F}) \in \operatorname {APerf}(\widehat {\mathscr {S}})^{\mathrm {cn}}$ for
$\widehat {\pi }_\ast (i^{\ast } (V_\alpha )^{\ast } \otimes \widehat {F}) \in \operatorname {APerf}(\widehat {\mathscr {S}})^{\mathrm {cn}}$ for  $\sharp (\alpha ) \geqslant N$.
$\sharp (\alpha ) \geqslant N$.
Proof. The claim is fppf local, so by the base-change formula (Proposition A.1.5), it suffices to assume ![]() $\mathscr {S} = \operatorname {Spec}(R)$ is affine. First observe that, for
$\mathscr {S} = \operatorname {Spec}(R)$ is affine. First observe that, for ![]() $\widehat {F} \in \operatorname {APerf}(\widehat {\mathscr {X}})$,
$\widehat {F} \in \operatorname {APerf}(\widehat {\mathscr {X}})$, ![]() $\widehat {\pi }_\ast (\widehat {F}) \in \operatorname {APerf}(\operatorname {Spf}(R))$: this is equivalent to showing
$\widehat {\pi }_\ast (\widehat {F}) \in \operatorname {APerf}(\operatorname {Spf}(R))$: this is equivalent to showing ![]() $\widehat {\pi }_\ast (\widehat {F})|_{\operatorname {Spec}(R')} \in \operatorname {APerf}(R')$ for any map
$\widehat {\pi }_\ast (\widehat {F})|_{\operatorname {Spec}(R')} \in \operatorname {APerf}(R')$ for any map ![]() $\operatorname {Spec}(R') \to \mathscr {S}$ whose image lies in
$\operatorname {Spec}(R') \to \mathscr {S}$ whose image lies in ![]() $Z$. It thus suffices to show
$Z$. It thus suffices to show ![]() $\pi _{R'}$ maps
$\pi _{R'}$ maps ![]() $\operatorname {APerf}(\mathscr {X}_{R'})$ to
$\operatorname {APerf}(\mathscr {X}_{R'})$ to ![]() $\operatorname {APerf}(\operatorname {Spec}(R'))$, and this follows from (CD) and (CP).
$\operatorname {APerf}(\operatorname {Spec}(R'))$, and this follows from (CD) and (CP).
Let ![]() $\phi : \mathscr {Z} \to \mathscr {S}$ be the classical reduced closed substack whose support is
$\phi : \mathscr {Z} \to \mathscr {S}$ be the classical reduced closed substack whose support is ![]() $Z$. Note that
$Z$. Note that ![]() $\widehat {G} \in \operatorname {APerf}(\widehat {\mathscr {S}})$ is connective if and only if
$\widehat {G} \in \operatorname {APerf}(\widehat {\mathscr {S}})$ is connective if and only if ![]() $\phi ^{\ast }(\widehat {G}) \in \operatorname {APerf}(\mathscr {Z})$ is connective. Indeed, writing
$\phi ^{\ast }(\widehat {G}) \in \operatorname {APerf}(\mathscr {Z})$ is connective. Indeed, writing ![]() $\operatorname {Spf}(R) = \varinjlim \operatorname {Spec}(R_n)$ as in Proposition 2.1.2 (we do not need finite Tor amplitude, so this works in both the spectral and derived context), we see that
$\operatorname {Spf}(R) = \varinjlim \operatorname {Spec}(R_n)$ as in Proposition 2.1.2 (we do not need finite Tor amplitude, so this works in both the spectral and derived context), we see that ![]() $\widehat {G}$ is connective if and only if
$\widehat {G}$ is connective if and only if ![]() $G_n \in \operatorname {APerf}(\operatorname {Spec}(R_n))$ is connective for all
$G_n \in \operatorname {APerf}(\operatorname {Spec}(R_n))$ is connective for all ![]() $n$, and by Nakayama's lemma this is equivalent to the restriction to
$n$, and by Nakayama's lemma this is equivalent to the restriction to ![]() $\operatorname {Spec}(\pi _0(R_n)^{\mathrm {red}}) \simeq \mathscr {Z}$ being connective.
$\operatorname {Spec}(\pi _0(R_n)^{\mathrm {red}}) \simeq \mathscr {Z}$ being connective.
Now consider the base change ![]() $\pi ' \colon \mathscr {X}' := \mathscr {X} \times _\mathscr {S} \mathscr {Z} \to \mathscr {Z}$. By the base-change formula (Proposition A.1.5) and Lemma 4.1.7 applied to system
$\pi ' \colon \mathscr {X}' := \mathscr {X} \times _\mathscr {S} \mathscr {Z} \to \mathscr {Z}$. By the base-change formula (Proposition A.1.5) and Lemma 4.1.7 applied to system ![]() $\{V_\alpha |_{\mathscr {X}'}\}$, which is (CA) by Corollary 4.1.11, we have that
$\{V_\alpha |_{\mathscr {X}'}\}$, which is (CA) by Corollary 4.1.11, we have that ![]() $\phi ^{\ast }(\widehat {\pi }_\ast (\widehat {F} \otimes i^{\ast } V_\alpha ^{\ast })) \simeq \pi '_\ast (\widehat {F} \otimes i^{\ast } V_\alpha ^{\ast }|_{\mathscr {X}'})$ is connective for
$\phi ^{\ast }(\widehat {\pi }_\ast (\widehat {F} \otimes i^{\ast } V_\alpha ^{\ast })) \simeq \pi '_\ast (\widehat {F} \otimes i^{\ast } V_\alpha ^{\ast }|_{\mathscr {X}'})$ is connective for ![]() $\sharp (\alpha ) \gg 0$ and hence we have property (ii) above.
$\sharp (\alpha ) \gg 0$ and hence we have property (ii) above.
In order to prove (i), it suffices to consider only direct sums of ![]() $V_\alpha$ with
$V_\alpha$ with ![]() $\sharp (\alpha )$ sufficiently large so that (ii) holds. We must show that the cone of the canonical morphism in (i) lies in
$\sharp (\alpha )$ sufficiently large so that (ii) holds. We must show that the cone of the canonical morphism in (i) lies in ![]() $\operatorname {APerf}(\mathscr {X})_{\geqslant 1}$, and because both objects are almost perfect, it suffices by Nakayama's lemma to show this after restricting to
$\operatorname {APerf}(\mathscr {X})_{\geqslant 1}$, and because both objects are almost perfect, it suffices by Nakayama's lemma to show this after restricting to ![]() $\mathscr {X}'$. The base-change formula identifies the restriction of the canonical map in (i) with the canonical map
$\mathscr {X}'$. The base-change formula identifies the restriction of the canonical map in (i) with the canonical map
So again because ![]() $\{V_\alpha |_{\mathscr {X}'}\}$ is a (CA) system and
$\{V_\alpha |_{\mathscr {X}'}\}$ is a (CA) system and ![]() $\pi '$ is (CD), the fact that the cone of this morphism lies in
$\pi '$ is (CD), the fact that the cone of this morphism lies in ![]() $\operatorname {APerf}(\mathscr {X}')_{\geqslant 1}$ follows from Lemma 4.1.6.
$\operatorname {APerf}(\mathscr {X}')_{\geqslant 1}$ follows from Lemma 4.1.6.
Proof of Theorem 4.2.1 Let ![]() $i : \widehat {\mathscr {X}} \to \mathscr {X}$ be the inclusion, and
$i : \widehat {\mathscr {X}} \to \mathscr {X}$ be the inclusion, and ![]() $\pi \colon \widehat {\mathscr {X}} \to \widehat {\mathscr {S}}$ the projection. Theorem 2.4.3 implies that
$\pi \colon \widehat {\mathscr {X}} \to \widehat {\mathscr {S}}$ the projection. Theorem 2.4.3 implies that ![]() $i^{\ast } \colon \operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is fully faithful.
$i^{\ast } \colon \operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is fully faithful.
Lemma 4.2.2 implies that for any ![]() $\widehat {F} \in {\rm Coh} (\widehat {\mathscr {X}})$, we can find a locally free sheaf
$\widehat {F} \in {\rm Coh} (\widehat {\mathscr {X}})$, we can find a locally free sheaf ![]() $W$ on
$W$ on ![]() $\mathscr {X}$ such that
$\mathscr {X}$ such that ![]() $\widehat {\pi }_\ast (i^{\ast }(W)^{\ast } \otimes \widehat {F}) \in \operatorname {APerf}(\widehat {\mathscr {S}})^{\mathrm {cn}}$ and
$\widehat {\pi }_\ast (i^{\ast }(W)^{\ast } \otimes \widehat {F}) \in \operatorname {APerf}(\widehat {\mathscr {S}})^{\mathrm {cn}}$ and ![]() $i^{\ast }(W) \otimes \widehat {\pi }^{\ast } \widehat {\pi }_\ast (i^{\ast }(W)^{\ast } \otimes \widehat {F}) \to \widehat {F}$ is surjective. Because
$i^{\ast }(W) \otimes \widehat {\pi }^{\ast } \widehat {\pi }_\ast (i^{\ast }(W)^{\ast } \otimes \widehat {F}) \to \widehat {F}$ is surjective. Because ![]() $\mathscr {S}$ is complete, there is a unique
$\mathscr {S}$ is complete, there is a unique ![]() $G \in \operatorname {APerf}(\mathscr {S})^{\mathrm {cn}}$ such that
$G \in \operatorname {APerf}(\mathscr {S})^{\mathrm {cn}}$ such that ![]() $\widehat {G} \simeq \widehat {\pi }_\ast (i^{\ast }(W)^{\ast } \otimes \widehat {F})$. Note that
$\widehat {G} \simeq \widehat {\pi }_\ast (i^{\ast }(W)^{\ast } \otimes \widehat {F})$. Note that ![]() $i^{\ast }(W) \otimes (\widehat {\pi })^{\ast }( \widehat {G}) \simeq i^{\ast } (W \otimes \pi ^{\ast } G)$, and it follows that we have a surjection
$i^{\ast }(W) \otimes (\widehat {\pi })^{\ast }( \widehat {G}) \simeq i^{\ast } (W \otimes \pi ^{\ast } G)$, and it follows that we have a surjection ![]() $i^{\ast }(H_0(W \otimes \pi ^{\ast }(G))) \to \widehat {F}$. This verifies the criterion in Proposition 2.3.3 for
$i^{\ast }(H_0(W \otimes \pi ^{\ast }(G))) \to \widehat {F}$. This verifies the criterion in Proposition 2.3.3 for ![]() $i^{\ast } : \operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ to be essentially surjective.
$i^{\ast } : \operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ to be essentially surjective.
4.2.1 Examples of formally proper morphisms
Proposition 4.2.3 Let ![]() $\pi : X \to Y$ be a finite type projective-over-affine morphism of noetherian schemes over a field,
$\pi : X \to Y$ be a finite type projective-over-affine morphism of noetherian schemes over a field, ![]() $k$, and let
$k$, and let ![]() $G$ be a linearly reductive
$G$ be a linearly reductive ![]() $k$-group acting on
$k$-group acting on ![]() $X$ such that
$X$ such that ![]() $\pi$ is
$\pi$ is ![]() $G$-invariant and
$G$-invariant and ![]() $X$ admits a
$X$ admits a ![]() $G$-linearized ample invertible sheaf over
$G$-linearized ample invertible sheaf over ![]() $Y$. Suppose, furthermore, that
$Y$. Suppose, furthermore, that ![]() $H_0 \pi _\ast (X, \mathscr {O}_X)^{G} \in \operatorname {QC}(Y)^{\heartsuit }$ is coherent. Then
$H_0 \pi _\ast (X, \mathscr {O}_X)^{G} \in \operatorname {QC}(Y)^{\heartsuit }$ is coherent. Then ![]() $\mathscr {X} = X/G \to Y$ is cohomologically projective.
$\mathscr {X} = X/G \to Y$ is cohomologically projective.
Proof. Property (CD) is immediate, since ![]() $X/G \to BG \times Y$ is representable, and
$X/G \to BG \times Y$ is representable, and ![]() $G$ is linearly reductive.
$G$ is linearly reductive.
Verification of (CA). We abuse notation and denote ![]() $\pi : X/G \to BG \times Y$, and we let
$\pi : X/G \to BG \times Y$, and we let ![]() $L = \mathscr {O}_X(1)$ be the
$L = \mathscr {O}_X(1)$ be the ![]() $G$-linearized ample invertible sheaf on
$G$-linearized ample invertible sheaf on ![]() $X$, regarded as an invertible sheaf on
$X$, regarded as an invertible sheaf on ![]() $X/G$. Let
$X/G$. Let ![]() $I = {\mathbb {Z}}_{\geqslant 0} \times J$, where
$I = {\mathbb {Z}}_{\geqslant 0} \times J$, where ![]() $J$ indexes the set of irreducible representations
$J$ indexes the set of irreducible representations ![]() $\rho$ of
$\rho$ of ![]() $G$, and let
$G$, and let ![]() $V_{n,\rho } := L^{-n}(\rho )$, where we use the notation
$V_{n,\rho } := L^{-n}(\rho )$, where we use the notation ![]() $F(\rho )$ to denote the tensor product of
$F(\rho )$ to denote the tensor product of ![]() $F \in \operatorname {QC}(X/G)$ with the pullback of
$F \in \operatorname {QC}(X/G)$ with the pullback of ![]() $\rho \in \!\!\mathop {\rm ~Irrep}\nolimits (G)$ regarded as locally free sheaf on
$\rho \in \!\!\mathop {\rm ~Irrep}\nolimits (G)$ regarded as locally free sheaf on ![]() $BG$.
$BG$.
We will show that the preordered system ![]() $\{V_{n,\rho }\}$ satisfies (CA1) and (CA2) after base change along any map
$\{V_{n,\rho }\}$ satisfies (CA1) and (CA2) after base change along any map ![]() $\operatorname {Spec}(R) \to Y$. Equivalently, we may assume that
$\operatorname {Spec}(R) \to Y$. Equivalently, we may assume that ![]() $Y = \operatorname {Spec}(R)$, because the formation of
$Y = \operatorname {Spec}(R)$, because the formation of ![]() $\{V_{n,\rho }\}$ commutes with base change. For
$\{V_{n,\rho }\}$ commutes with base change. For ![]() $F \in {\rm Coh} (X/G)$,
$F \in {\rm Coh} (X/G)$, ![]() $\pi _\ast (F \otimes L^{n}) \in \operatorname {QC}(BG \times Y)_{\geqslant 0}$ for all
$\pi _\ast (F \otimes L^{n}) \in \operatorname {QC}(BG \times Y)_{\geqslant 0}$ for all ![]() $n \gg 0$ because
$n \gg 0$ because ![]() $L$ is ample relative to
$L$ is ample relative to ![]() $\pi$. Because
$\pi$. Because ![]() $G$ is linearly reductive this implies that
$G$ is linearly reductive this implies that ![]() $R\Gamma (X/G,F \otimes V_{n,\rho }^{\ast }) \in \operatorname {QC}(\operatorname {Spec}(R))_{\geqslant 0}$ for all
$R\Gamma (X/G,F \otimes V_{n,\rho }^{\ast }) \in \operatorname {QC}(\operatorname {Spec}(R))_{\geqslant 0}$ for all ![]() $\rho$ and
$\rho$ and ![]() $n \gg 0$. Furthermore, if
$n \gg 0$. Furthermore, if ![]() $F \neq 0$ then, for any
$F \neq 0$ then, for any ![]() $n$ sufficiently large,
$n$ sufficiently large, ![]() $H_0 R\Gamma (X,F\otimes L^{n}) \neq 0$. Therefore, for any
$H_0 R\Gamma (X,F\otimes L^{n}) \neq 0$. Therefore, for any ![]() $N$, we can find an
$N$, we can find an ![]() $n \geqslant N$ and a non-zero morphism
$n \geqslant N$ and a non-zero morphism ![]() $\rho \otimes _k R \to R\Gamma (X,F \otimes L^{n})$ in
$\rho \otimes _k R \to R\Gamma (X,F \otimes L^{n})$ in ![]() $\operatorname {QC}(BG \times Y)$. It follows that
$\operatorname {QC}(BG \times Y)$. It follows that ![]() $R\Gamma (X/G,F \otimes V_{n,\rho }^{\ast }) \neq 0$.
$R\Gamma (X/G,F \otimes V_{n,\rho }^{\ast }) \neq 0$.
Verification of (CP). We may assume ![]() $Y = \operatorname {Spec}(R)$ is affine and verify (CP)R. Let
$Y = \operatorname {Spec}(R)$ is affine and verify (CP)R. Let ![]() $X' = \operatorname {Spec}_Y(H_0 \pi _\ast (X, \mathscr {O}_X))$, so that
$X' = \operatorname {Spec}_Y(H_0 \pi _\ast (X, \mathscr {O}_X))$, so that ![]() $q : X \to X'$ is a projective
$q : X \to X'$ is a projective ![]() $G$-equivariant map by hypothesis. Suppose
$G$-equivariant map by hypothesis. Suppose ![]() $F$ is a
$F$ is a ![]() $G$-equivariant coherent sheaf on
$G$-equivariant coherent sheaf on ![]() $X$. We must show that
$X$. We must show that
is coherent over ![]() $R$ for each
$R$ for each ![]() $i$. By the usual coherent pushforward theorem for projective morphisms,
$i$. By the usual coherent pushforward theorem for projective morphisms, ![]() $H_{-i} \circ q_* F$ is coherent, and by functoriality it is
$H_{-i} \circ q_* F$ is coherent, and by functoriality it is ![]() $G$-equivariant. It is thus enough to show that, for any
$G$-equivariant. It is thus enough to show that, for any ![]() $G$-equivariant coherent
$G$-equivariant coherent ![]() $A = H^{0}(X, \mathscr {O}_X)$-module
$A = H^{0}(X, \mathscr {O}_X)$-module ![]() $M$,
$M$, ![]() $M^{G}$ is coherent over
$M^{G}$ is coherent over ![]() $A^{G}$ (and thus, by our hypotheses, over
$A^{G}$ (and thus, by our hypotheses, over ![]() $R$). This is a classical fact: one uses the existence of a Reynolds operator to show that, for any
$R$). This is a classical fact: one uses the existence of a Reynolds operator to show that, for any ![]() $A^{G}$-submodule
$A^{G}$-submodule ![]() $N \subset M^{G}$, we have
$N \subset M^{G}$, we have ![]() $(A \cdot N)^{G} = N$, and thus
$(A \cdot N)^{G} = N$, and thus ![]() $M^{G}$ must satisfy the ascending chain condition if
$M^{G}$ must satisfy the ascending chain condition if ![]() $M$ does.
$M$ does.
Next we show that any quotient stack which admits a projective good quotient is cohomologically projective. Recall that if ![]() $G$ is a smooth group scheme over a scheme
$G$ is a smooth group scheme over a scheme ![]() $S$, and
$S$, and ![]() $X$ is a
$X$ is a ![]() $G$-scheme over
$G$-scheme over ![]() $S$, then a good quotient [Reference SeshadriSes72] is a
$S$, then a good quotient [Reference SeshadriSes72] is a ![]() $G$-invariant map to an algebraic space
$G$-invariant map to an algebraic space ![]() $q : X \to Y$ such that
$q : X \to Y$ such that ![]() $q_\ast : \operatorname {QC}(X/G) \to \operatorname {QC}(Y)$ is
$q_\ast : \operatorname {QC}(X/G) \to \operatorname {QC}(Y)$ is ![]() $t$-exact, and
$t$-exact, and ![]() $q_\ast (\mathcal {O}_X)^{G} = \mathcal {O}_Y$. This is a special case of the notion of a good moduli space [Reference AlperAlp13].
$q_\ast (\mathcal {O}_X)^{G} = \mathcal {O}_Y$. This is a special case of the notion of a good moduli space [Reference AlperAlp13].
Example 4.2.4 Let ![]() $X$ be a projective variety over a field of characteristic 0. Let
$X$ be a projective variety over a field of characteristic 0. Let ![]() $G$ be a reductive group acting on
$G$ be a reductive group acting on ![]() $X$ linearized by an equivariant ample invertible sheaf
$X$ linearized by an equivariant ample invertible sheaf ![]() $L$. Then the morphism from the stacky GIT quotient to the scheme-theoretic GIT quotient,
$L$. Then the morphism from the stacky GIT quotient to the scheme-theoretic GIT quotient, ![]() $X^{ss}(L) / G \to X/\!\!/\!_{L} G$, is a good quotient.
$X^{ss}(L) / G \to X/\!\!/\!_{L} G$, is a good quotient.
We will need the technical hypothesis on a group scheme ![]() $G$ over
$G$ over ![]() $S$ that
$S$ that ![]() $B_S G$ has enough vector bundles (i.e. every coherent
$B_S G$ has enough vector bundles (i.e. every coherent ![]() $G$-representation is a quotient of a locally free
$G$-representation is a quotient of a locally free ![]() $G$-representation). This holds for
$G$-representation). This holds for ![]() $G = (\!\!\mathop {\rm ~GL}\nolimits _N)_S$, or any reductive closed subgroup
$G = (\!\!\mathop {\rm ~GL}\nolimits _N)_S$, or any reductive closed subgroup ![]() $G \subset (\!\!\mathop {\rm ~GL}\nolimits _N)_S$.
$G \subset (\!\!\mathop {\rm ~GL}\nolimits _N)_S$.
Proposition 4.2.5 Let ![]() $S$ be a scheme, and let
$S$ be a scheme, and let ![]() $G$ be a smooth group scheme over
$G$ be a smooth group scheme over ![]() $S$ such that
$S$ such that ![]() $B_S G$ has enough vector bundles. Let
$B_S G$ has enough vector bundles. Let ![]() $X$ be a finitely presented
$X$ be a finitely presented ![]() $G$-scheme over
$G$-scheme over ![]() $S$. If
$S$. If ![]() $X$ admits a good quotient
$X$ admits a good quotient ![]() $q : X \to Y$ such that
$q : X \to Y$ such that ![]() $Y$ is projective over
$Y$ is projective over ![]() $S$, then
$S$, then ![]() $\pi \colon X/G \to S$ is cohomologically projective.
$\pi \colon X/G \to S$ is cohomologically projective.
Lemma 4.2.6 Let ![]() $\mathscr {X} \xrightarrow {f} \mathscr {Y} \xrightarrow {g} \mathscr {Z}$ be morphisms of noetherian algebraic derived (or spectral) stacks which satisfy (CD). Assume that
$\mathscr {X} \xrightarrow {f} \mathscr {Y} \xrightarrow {g} \mathscr {Z}$ be morphisms of noetherian algebraic derived (or spectral) stacks which satisfy (CD). Assume that ![]() $f$ satisfies (CP). If
$f$ satisfies (CP). If ![]() $\{V_\alpha \}_{\alpha \in I}$ is a (CA) system relative to
$\{V_\alpha \}_{\alpha \in I}$ is a (CA) system relative to ![]() $f$, and
$f$, and ![]() $\{W_\beta \}_{\beta \in J}$ is a (CA) system relative to
$\{W_\beta \}_{\beta \in J}$ is a (CA) system relative to ![]() $g$, then
$g$, then
is a (CA) system relative to ![]() $g \circ f$.
$g \circ f$.
Proof. By Lemma 4.1.5, it suffices to assume ![]() $\mathscr {Z}$ is affine. We apply Proposition 4.1.12, which asks us to consider, for each
$\mathscr {Z}$ is affine. We apply Proposition 4.1.12, which asks us to consider, for each ![]() $F \in {\rm Coh} (\mathscr {X})$, the pushforward
$F \in {\rm Coh} (\mathscr {X})$, the pushforward
First we must show that there is an ![]() $N$ such that
$N$ such that ![]() $\sharp (\alpha,\beta ) \geqslant N$ implies
$\sharp (\alpha,\beta ) \geqslant N$ implies ![]() $E_{\alpha,\beta } \in \operatorname {QC}(\mathscr {Z})_{\geqslant 0}$. We can choose an
$E_{\alpha,\beta } \in \operatorname {QC}(\mathscr {Z})_{\geqslant 0}$. We can choose an ![]() $N$ such that
$N$ such that ![]() $\sharp (\alpha ) \geqslant N$ implies that
$\sharp (\alpha ) \geqslant N$ implies that ![]() $f_\ast (F \otimes V_\alpha ^{\ast })$ is connective. Furthermore, it lies in
$f_\ast (F \otimes V_\alpha ^{\ast })$ is connective. Furthermore, it lies in ![]() ${\rm Coh} (\mathscr {Y})$ because
${\rm Coh} (\mathscr {Y})$ because ![]() $f$ satisfies (CP). Thus, because
$f$ satisfies (CP). Thus, because ![]() $\{W_\beta \}$ is (CA) for
$\{W_\beta \}$ is (CA) for ![]() $g$, we can increase our choice of
$g$, we can increase our choice of ![]() $N$ such that
$N$ such that ![]() $\sharp (\beta ) \geqslant N$ implies that
$\sharp (\beta ) \geqslant N$ implies that ![]() $E_{\alpha,\beta }$ is connective, by Lemma 4.1.7. Clearly both inequalities hold if
$E_{\alpha,\beta }$ is connective, by Lemma 4.1.7. Clearly both inequalities hold if ![]() $\sharp (\alpha,\beta ) = \min (\sharp (\alpha ),\sharp (\beta )) \geqslant N$.
$\sharp (\alpha,\beta ) = \min (\sharp (\alpha ),\sharp (\beta )) \geqslant N$.
To complete the verification that ![]() $\{V_\alpha \otimes f^{\ast } V_\beta \}$ is (CA), one must show that, for any
$\{V_\alpha \otimes f^{\ast } V_\beta \}$ is (CA), one must show that, for any ![]() $N$, there is some
$N$, there is some ![]() $\sharp (\alpha,\beta ) \geqslant N$ with
$\sharp (\alpha,\beta ) \geqslant N$ with ![]() $H_0 (E_{\alpha,\beta }) \neq 0$. The argument is the same as that of the previous paragraph.
$H_0 (E_{\alpha,\beta }) \neq 0$. The argument is the same as that of the previous paragraph.
Proof of Proposition 4.2.5 The map ![]() $\pi$ is the composition
$\pi$ is the composition ![]() $X/G \to Y \to S$, so
$X/G \to Y \to S$, so ![]() $\pi$ satisfies (CD) because each of these morphisms do. Property (CP) follows from the fact that
$\pi$ satisfies (CD) because each of these morphisms do. Property (CP) follows from the fact that ![]() $q_\ast : \operatorname {QC}(X/G) \to \operatorname {QC}(Y)$ preserves coherence [Reference AlperAlp13, Theorem 4.16]. Thus, we focus on property (CA).
$q_\ast : \operatorname {QC}(X/G) \to \operatorname {QC}(Y)$ preserves coherence [Reference AlperAlp13, Theorem 4.16]. Thus, we focus on property (CA).
Choose a set of vector bundles ![]() $\{W_i\}_{i\in J}$ on
$\{W_i\}_{i\in J}$ on ![]() $B_S G$ which generate
$B_S G$ which generate ![]() $\operatorname {QC}(B_S G)$. If we define
$\operatorname {QC}(B_S G)$. If we define ![]() $I = J \times {\mathbb {Z}}_{\geqslant 0}$ and let
$I = J \times {\mathbb {Z}}_{\geqslant 0}$ and let ![]() $V_{i,n} = \mathcal {O}_X \otimes _S W_i$, then one can check that
$V_{i,n} = \mathcal {O}_X \otimes _S W_i$, then one can check that ![]() $\{V_{i,n}\}$ is a (CA) system relative to
$\{V_{i,n}\}$ is a (CA) system relative to ![]() $q \colon X/G \to Y$. Indeed, being a good quotient is local over
$q \colon X/G \to Y$. Indeed, being a good quotient is local over ![]() $Y$, so we may consider
$Y$, so we may consider ![]() $Y = \operatorname {Spec}(R)$. In this case (CA2) is immediate from the exactness of
$Y = \operatorname {Spec}(R)$. In this case (CA2) is immediate from the exactness of ![]() $q_\ast$, and (CA1) follows from the fact that
$q_\ast$, and (CA1) follows from the fact that ![]() $X \to Y$ is affine.
$X \to Y$ is affine.
Define ![]() $\pi ^{\prime } \colon Y \to S$, and let
$\pi ^{\prime } \colon Y \to S$, and let ![]() $L$ be a relatively ample invertible sheaf for
$L$ be a relatively ample invertible sheaf for ![]() $\pi ^{\prime }$. Then
$\pi ^{\prime }$. Then ![]() $\{L^{-n} | n \geqslant 0\}$ is a (CA) system for
$\{L^{-n} | n \geqslant 0\}$ is a (CA) system for ![]() $\pi ^{\prime }$. By Lemma 4.2.6 the composition
$\pi ^{\prime }$. By Lemma 4.2.6 the composition ![]() $\pi = \pi ^{\prime } \circ \phi$ admits a (CA) system.
$\pi = \pi ^{\prime } \circ \phi$ admits a (CA) system.
4.3 Formal properness via proper covers and  $h$-descent
$h$-descent
Our main application for the descent result Theorem 3.3.1 is the following ‘two-out-of-three’ result for formally proper morphisms.
Theorem 4.3.1 Consider relatively algebraic maps of derived (or spectral) stacks
If ![]() $f$ is surjective and satisfies (CP),
$f$ is surjective and satisfies (CP), ![]() $g$ is almost finitely presented, and
$g$ is almost finitely presented, and ![]() $g\circ f$ is formally proper (respectively, satisfies (CP)), then
$g\circ f$ is formally proper (respectively, satisfies (CP)), then ![]() $g$ is formally proper (respectively, satisfies (CP)).
$g$ is formally proper (respectively, satisfies (CP)).
Proof. Note that the hypotheses of the proposition are stable under base change over ![]() $\mathscr {S}$, so we may assume that
$\mathscr {S}$, so we may assume that ![]() $\mathscr {S}$ is algebraic, noetherian, and complete along a closed subset
$\mathscr {S}$ is algebraic, noetherian, and complete along a closed subset ![]() $Z \subset |\mathscr {S}|$, and it suffices to show that if
$Z \subset |\mathscr {S}|$, and it suffices to show that if ![]() $\mathscr {X}'$ is complete along the preimage of
$\mathscr {X}'$ is complete along the preimage of ![]() $Z$, then so is
$Z$, then so is ![]() $\mathscr {X}$.
$\mathscr {X}$.
Let ![]() $\mathscr {X}'_\bullet := \mathscr {X}'^{\times _\mathscr {X} (\bullet +1)}$ be the Čech nerve of
$\mathscr {X}'_\bullet := \mathscr {X}'^{\times _\mathscr {X} (\bullet +1)}$ be the Čech nerve of ![]() $f$, and let
$f$, and let ![]() $\widehat {\mathscr {X}}$ (respectively,
$\widehat {\mathscr {X}}$ (respectively, ![]() $\widehat {\mathscr {X}'}_\bullet$) denote the formal completion of
$\widehat {\mathscr {X}'}_\bullet$) denote the formal completion of ![]() $\mathscr {X}$ (respectively,
$\mathscr {X}$ (respectively, ![]() $\mathscr {X}'_\bullet$) along the preimage of
$\mathscr {X}'_\bullet$) along the preimage of ![]() $Z$. By Proposition 2.4.5,
$Z$. By Proposition 2.4.5, ![]() $f$ is an
$f$ is an ![]() $h$-cover of locally noetherian derived stacks, so Theorem 3.3.1 implies that restriction induces equivalences
$h$-cover of locally noetherian derived stacks, so Theorem 3.3.1 implies that restriction induces equivalences
Every map ![]() $\mathscr {X}_n' \to \mathscr {X}_0'=\mathscr {X}'$ satisfies (CP), and
$\mathscr {X}_n' \to \mathscr {X}_0'=\mathscr {X}'$ satisfies (CP), and ![]() $\mathscr {X}' \to \mathscr {S}$ satisfies (CP) by Theorem 2.4.3, so each
$\mathscr {X}' \to \mathscr {S}$ satisfies (CP) by Theorem 2.4.3, so each ![]() $\mathscr {X}_n' \to \mathscr {S}$ satisfies (CP). Proposition 2.3.1 thus implies that
$\mathscr {X}_n' \to \mathscr {S}$ satisfies (CP). Proposition 2.3.1 thus implies that ![]() $\operatorname {APerf}(\mathscr {X}'_n) \to \operatorname {APerf}(\widehat {\mathscr {X}}'_n)$ is fully faithful for all
$\operatorname {APerf}(\mathscr {X}'_n) \to \operatorname {APerf}(\widehat {\mathscr {X}}'_n)$ is fully faithful for all ![]() $n$. Furthermore, this map is an equivalence when
$n$. Furthermore, this map is an equivalence when ![]() $n=0$ because
$n=0$ because ![]() $\mathscr {X}'$ is complete along the preimage of
$\mathscr {X}'$ is complete along the preimage of ![]() $Z$. It follows that
$Z$. It follows that ![]() $\operatorname {Tot} \{ \operatorname {APerf}(\mathscr {X}'_\bullet ) \} \to \operatorname {Tot} \{ \operatorname {APerf}(\widehat {\mathscr {X}}'_\bullet ) \}$ is an equivalence as well.Footnote 5
$\operatorname {Tot} \{ \operatorname {APerf}(\mathscr {X}'_\bullet ) \} \to \operatorname {Tot} \{ \operatorname {APerf}(\widehat {\mathscr {X}}'_\bullet ) \}$ is an equivalence as well.Footnote 5
The argument that ![]() $g$ satisfies (CP) if
$g$ satisfies (CP) if ![]() $g \circ f$ does is similar. Theorem 2.4.3 says that (CP) is equivalent to universally satisfying the fully faithful part of the definition of formal properness. This amounts to showing in the setup above that
$g \circ f$ does is similar. Theorem 2.4.3 says that (CP) is equivalent to universally satisfying the fully faithful part of the definition of formal properness. This amounts to showing in the setup above that ![]() $\operatorname {Tot}\{\operatorname {APerf}(\mathscr {X}'_\bullet )\} \to \operatorname {Tot}\{\operatorname {APerf}(\widehat {\mathscr {X}'}_\bullet )\}$ is fully faithful, which follows from the levelwise full faithfulness.
$\operatorname {Tot}\{\operatorname {APerf}(\mathscr {X}'_\bullet )\} \to \operatorname {Tot}\{\operatorname {APerf}(\widehat {\mathscr {X}'}_\bullet )\}$ is fully faithful, which follows from the levelwise full faithfulness.
As an immediate consequence of this and Theorem 4.2.1, we have the following corollary.
Corollary 4.3.2 (Chow's lemma implies formal properness)
Let ![]() $\mathscr {S}$ be an algebraic derived stack, and let
$\mathscr {S}$ be an algebraic derived stack, and let ![]() $\mathscr {X} \to \mathscr {S}$ be an almost finitely presented map. If
$\mathscr {X} \to \mathscr {S}$ be an almost finitely presented map. If ![]() $\mathscr {X}$ admits a map
$\mathscr {X}$ admits a map ![]() $\mathscr {X}' \to \mathscr {X}$ which is surjective and representable by proper derived schemes, and
$\mathscr {X}' \to \mathscr {X}$ which is surjective and representable by proper derived schemes, and ![]() $\mathscr {X}'$ is a cohomologically projective
$\mathscr {X}'$ is a cohomologically projective ![]() $\mathscr {S}$-stack, then
$\mathscr {S}$-stack, then ![]() $\mathscr {X} \to \mathscr {S}$ is formally proper.
$\mathscr {X} \to \mathscr {S}$ is formally proper.
Example 4.3.3 Corollary 4.3.2 provides many examples of formally proper maps which are not cohomologically projective.
(i) Olsson proves in [Reference OlssonOls05] that if
 $S$ is a noetherian scheme and
$S$ is a noetherian scheme and  $\pi : \mathscr {X} \to S$ is a proper morphism (in the usual sense), then
$\pi : \mathscr {X} \to S$ is a proper morphism (in the usual sense), then  $\mathscr {X}$ admits a proper covering by a projective
$\mathscr {X}$ admits a proper covering by a projective  $S$-scheme, so
$S$-scheme, so  $\pi$ is formally proper.
$\pi$ is formally proper.(ii) If
 $X$ is a non-normal projective scheme over a field
$X$ is a non-normal projective scheme over a field  $k$, and
$k$, and  $G$ is a linearly reductive
$G$ is a linearly reductive  $k$-group, then
$k$-group, then  $X$ need not admit a
$X$ need not admit a  $G$-equivariant embedding into some
$G$-equivariant embedding into some  $\mathbf {P}^{n}$, but its normalization
$\mathbf {P}^{n}$, but its normalization  $X'$ will. Thus,
$X'$ will. Thus,  $X' / G$ is cohomologically projective, and
$X' / G$ is cohomologically projective, and  $X' / G \to X/G$ is finite and surjective, so
$X' / G \to X/G$ is finite and surjective, so  $X / G$ is formally proper. The simplest example of this is where
$X / G$ is formally proper. The simplest example of this is where  $G = {\mathbb {G}_m}$ and
$G = {\mathbb {G}_m}$ and  $X$ is the nodal curve obtained by identifying the two fixed points of the action on
$X$ is the nodal curve obtained by identifying the two fixed points of the action on  $\mathbf {P}^{1}$.
$\mathbf {P}^{1}$.(iii) Let
 $G$ be a smooth group scheme over a perfect field
$G$ be a smooth group scheme over a perfect field  $k$ and
$k$ and  $1 \to N \to G \to A \to 1$ be the factorization given by Chevalley's theorem, that is,
$1 \to N \to G \to A \to 1$ be the factorization given by Chevalley's theorem, that is,  $N$ is a connected affine group and
$N$ is a connected affine group and  $A$ is a finite extension of an Abelian variety. The fiber of
$A$ is a finite extension of an Abelian variety. The fiber of  $BN \to BG$ is
$BN \to BG$ is  $A$, so if
$A$, so if  $N$ is linearly reductive (or reductive by Proposition 4.3.4 below), then
$N$ is linearly reductive (or reductive by Proposition 4.3.4 below), then  $BG$ is formally proper.
$BG$ is formally proper.(iv) If
 $G$ is an algebraic
$G$ is an algebraic  $k$-group,
$k$-group,  $S$ is a noetherian
$S$ is a noetherian  $k$-scheme, and
$k$-scheme, and  $X$ is a
$X$ is a  $G$-scheme which admits a good quotient
$G$-scheme which admits a good quotient  $Y$ which is proper over
$Y$ which is proper over  $S$, then
$S$, then  $X/G$ is formally proper over
$X/G$ is formally proper over  $S$ by combining Corollary 4.3.2 with Chow's lemma for
$S$ by combining Corollary 4.3.2 with Chow's lemma for  $Y$ and Proposition 4.2.5.
$Y$ and Proposition 4.2.5.
4.3.1 Example: classifying stack of a reductive group scheme
Proposition 4.3.4 If ![]() $S$ is a Nagata scheme and
$S$ is a Nagata scheme and ![]() $G \to S$ is a reductive group scheme which admits a dominant cocharacter
$G \to S$ is a reductive group scheme which admits a dominant cocharacter ![]() $\lambda \colon (\mathbf {G}_m)_S \to G$, then
$\lambda \colon (\mathbf {G}_m)_S \to G$, then ![]() $B_S G \to S$ is formally proper.
$B_S G \to S$ is formally proper.
Example 4.3.5 Every reductive group ![]() $G$ over a field
$G$ over a field ![]() $k$ is split after a finite extension
$k$ is split after a finite extension ![]() $k \subset k'$, so Proposition 4.3.4 implies that
$k \subset k'$, so Proposition 4.3.4 implies that ![]() $(BG)_{k'} \to \operatorname {Spec}(k')$ is formally proper. Applying Theorem 4.3.1 to the finite morphism
$(BG)_{k'} \to \operatorname {Spec}(k')$ is formally proper. Applying Theorem 4.3.1 to the finite morphism ![]() $(BG)_{k'} \to BG$ implies that
$(BG)_{k'} \to BG$ implies that ![]() $BG \to \operatorname {Spec}(k)$ is formally proper.
$BG \to \operatorname {Spec}(k)$ is formally proper.
We will prove the proposition after establishing some preliminary results. The dominant cocharacter ![]() $\lambda$ defines a maximal torus
$\lambda$ defines a maximal torus ![]() $T \subset G$, the centralizer of
$T \subset G$, the centralizer of ![]() $\lambda$, and a Borel subgroup
$\lambda$, and a Borel subgroup ![]() $B \subset G$, the subgroup attracted to
$B \subset G$, the subgroup attracted to ![]() $T$ under conjugation by
$T$ under conjugation by ![]() $\lambda (t)$ as
$\lambda (t)$ as ![]() $t \to 0$. If we let
$t \to 0$. If we let ![]() $U = \ker (B \to T)$ be the subgroup attracted to the identity section under this conjugation action, then
$U = \ker (B \to T)$ be the subgroup attracted to the identity section under this conjugation action, then ![]() $U = \operatorname {Spec}_S(A)$ for some smooth quasi-coherent sheaf of algebras
$U = \operatorname {Spec}_S(A)$ for some smooth quasi-coherent sheaf of algebras ![]() $A$ which is a
$A$ which is a ![]() $T$-equivariant coalgebra, non-positively graded by the action of
$T$-equivariant coalgebra, non-positively graded by the action of ![]() $\lambda (\mathbf {G}_m)$, and with
$\lambda (\mathbf {G}_m)$, and with ![]() $A_0 = \mathcal {O}_S$.
$A_0 = \mathcal {O}_S$.
Lemma 4.3.6 Let ![]() $\mathscr {S}$ be a noetherian algebraic derived
$\mathscr {S}$ be a noetherian algebraic derived ![]() $S$-stack, and let
$S$-stack, and let ![]() $F \in \operatorname {QC}(BB_\mathscr {S})^{\heartsuit }$. Then, regarding
$F \in \operatorname {QC}(BB_\mathscr {S})^{\heartsuit }$. Then, regarding ![]() $F$ as a graded (with respect to
$F$ as a graded (with respect to ![]() $\lambda$) element of
$\lambda$) element of ![]() $\operatorname {QC}(\mathscr {S})^{\heartsuit }$, the submodule
$\operatorname {QC}(\mathscr {S})^{\heartsuit }$, the submodule ![]() $F_{\geqslant w}$ spanned by summands with
$F_{\geqslant w}$ spanned by summands with ![]() $\lambda$-weight greater than or equal to
$\lambda$-weight greater than or equal to ![]() $w$ is naturally a
$w$ is naturally a ![]() $B_\mathscr {S}$-equivariant submodule. If
$B_\mathscr {S}$-equivariant submodule. If ![]() $F$ is coherent, then so is
$F$ is coherent, then so is ![]() $F_{\geqslant w}$.
$F_{\geqslant w}$.
Proof. Note that it suffices to consider classical ![]() $\mathscr {S}$. The projection
$\mathscr {S}$. The projection ![]() $B B_\mathscr {S} \to B T_\mathscr {S}$ is a trivial
$B B_\mathscr {S} \to B T_\mathscr {S}$ is a trivial ![]() $B U_\mathscr {S}$ gerbe, and we can identify it with the classifying stack for the smooth affine relative group scheme
$B U_\mathscr {S}$ gerbe, and we can identify it with the classifying stack for the smooth affine relative group scheme ![]() $U_\S /T_\mathscr {S} \to BT_\mathscr {S}$, where
$U_\S /T_\mathscr {S} \to BT_\mathscr {S}$, where ![]() $T$ acts on
$T$ acts on ![]() $U$ by conjugation. We identify
$U$ by conjugation. We identify ![]() $\operatorname {QC}(BB_\mathscr {S})^{\heartsuit }$ with the category of
$\operatorname {QC}(BB_\mathscr {S})^{\heartsuit }$ with the category of ![]() $A_\mathscr {S}$-comodules in
$A_\mathscr {S}$-comodules in ![]() $\operatorname {QC}(BT_\mathscr {S})^{\heartsuit }$. Because
$\operatorname {QC}(BT_\mathscr {S})^{\heartsuit }$. Because ![]() $A$ is non-positively graded with respect to
$A$ is non-positively graded with respect to ![]() $\lambda$, and
$\lambda$, and ![]() $A_0=\mathcal {O}_S$, the image of the comultiplication map
$A_0=\mathcal {O}_S$, the image of the comultiplication map ![]() $F_{\geqslant w} \to A_\mathscr {S} \otimes _\mathscr {S} F$ must land in the subsheaf
$F_{\geqslant w} \to A_\mathscr {S} \otimes _\mathscr {S} F$ must land in the subsheaf ![]() $A_\mathscr {S} \otimes _\mathscr {S} F_{\geqslant w}$.
$A_\mathscr {S} \otimes _\mathscr {S} F_{\geqslant w}$.
Lemma 4.3.7 The map ![]() $\pi \colon BB \to S$ satisfies (CP).
$\pi \colon BB \to S$ satisfies (CP).
Proof. It suffices to assume that ![]() $S = \operatorname {Spec}(R)$ is affine, and to show that
$S = \operatorname {Spec}(R)$ is affine, and to show that ![]() $\pi _\ast ({\rm Coh} (BB)) \subset \operatorname {DCoh}(\operatorname {Spec}(R))$. For this, we may also assume that
$\pi _\ast ({\rm Coh} (BB)) \subset \operatorname {DCoh}(\operatorname {Spec}(R))$. For this, we may also assume that ![]() $R$ is discrete, because pushforward induces an equivalence
$R$ is discrete, because pushforward induces an equivalence ![]() ${\rm Coh} ((BB)^{\rm cl}) \simeq {\rm Coh} (BB)$.
${\rm Coh} ((BB)^{\rm cl}) \simeq {\rm Coh} (BB)$.
Let ![]() $p_\bullet \colon \mathscr {Z}_\bullet \to B_S B$ denote the Čech nerve of the smooth cover
$p_\bullet \colon \mathscr {Z}_\bullet \to B_S B$ denote the Čech nerve of the smooth cover ![]() $B_S T \to B_S B$, so we have
$B_S T \to B_S B$, so we have ![]() $\mathscr {Z}_n \simeq U^{n} / T$. By faithfully flat descent
$\mathscr {Z}_n \simeq U^{n} / T$. By faithfully flat descent ![]() $F \simeq \operatorname {Tot} \{(p_\bullet )_\ast F_\bullet \}$, where
$F \simeq \operatorname {Tot} \{(p_\bullet )_\ast F_\bullet \}$, where ![]() $F_n \simeq p_n^{\ast } F$, and thus
$F_n \simeq p_n^{\ast } F$, and thus ![]() $\pi _\ast F \simeq \operatorname {Tot} \{(\pi _\bullet )_\ast F_\bullet \}$ where
$\pi _\ast F \simeq \operatorname {Tot} \{(\pi _\bullet )_\ast F_\bullet \}$ where ![]() $\pi _n : \mathscr {Z}_n \to \operatorname {Spec}(R)$ is the projection. We may use the Dold–Kan correspondence to write the totalization as a complex
$\pi _n : \mathscr {Z}_n \to \operatorname {Spec}(R)$ is the projection. We may use the Dold–Kan correspondence to write the totalization as a complex
where
 \[ M^{n} = \!\!\mathop{\rm ~coker}\nolimits \bigg( \bigoplus_{i=1}^{n} (\pi_{n-1})_\ast F_{n-1} \xrightarrow{\delta^{n}_i} (\pi_n)_\ast F_n \bigg) \]
\[ M^{n} = \!\!\mathop{\rm ~coker}\nolimits \bigg( \bigoplus_{i=1}^{n} (\pi_{n-1})_\ast F_{n-1} \xrightarrow{\delta^{n}_i} (\pi_n)_\ast F_n \bigg) \]
and the differential ![]() $\delta ^{n} : M^{n-1} \to M^{n}$ is induced by
$\delta ^{n} : M^{n-1} \to M^{n}$ is induced by ![]() $\delta _0^{n}$.
$\delta _0^{n}$.
Because ![]() $T$ is linearly reductive, we have
$T$ is linearly reductive, we have ![]() $(\pi _n)_\ast F_n \simeq (A^{\otimes _R n} \otimes F_0)^{T} \in \operatorname {QC}(R)^{\heartsuit }$. If
$(\pi _n)_\ast F_n \simeq (A^{\otimes _R n} \otimes F_0)^{T} \in \operatorname {QC}(R)^{\heartsuit }$. If ![]() $F_0$ has highest
$F_0$ has highest ![]() $\lambda$-weight less than
$\lambda$-weight less than ![]() $h$, then the fact that
$h$, then the fact that ![]() $A_0 \simeq R$ and
$A_0 \simeq R$ and ![]() $A$ is non-positively graded implies that
$A$ is non-positively graded implies that ![]() $(A^{\otimes _R n} \otimes F_0)^{T}$ is spanned by simple tensors
$(A^{\otimes _R n} \otimes F_0)^{T}$ is spanned by simple tensors ![]() $a_1 \otimes \cdots \otimes a_n \otimes f$ with
$a_1 \otimes \cdots \otimes a_n \otimes f$ with ![]() $a_i = 1$ for all but at most
$a_i = 1$ for all but at most ![]() $h-1$ factors. If
$h-1$ factors. If ![]() $n>2h$, then there must be an
$n>2h$, then there must be an ![]() $i>0$ with
$i>0$ with ![]() $a_i = a_{i+1} = 1$. It follows from this and the fact that the boundary maps are induced by the comultiplication on
$a_i = a_{i+1} = 1$. It follows from this and the fact that the boundary maps are induced by the comultiplication on ![]() $A$ that this element is in the image of a boundary map. Hence,
$A$ that this element is in the image of a boundary map. Hence, ![]() $M^{n} = 0$.
$M^{n} = 0$.
We have thus shown that, assuming ![]() $F_0$ has a highest
$F_0$ has a highest ![]() $\lambda$-weight, which is always the case if
$\lambda$-weight, which is always the case if ![]() $F_0$ is coherent,
$F_0$ is coherent, ![]() $\pi _\ast (F)$ is computed by a complex involving finitely many
$\pi _\ast (F)$ is computed by a complex involving finitely many ![]() $M^{n}$. Furthermore,
$M^{n}$. Furthermore, ![]() $(A^{\otimes n} \otimes F_0)^{T}$ is coherent for every
$(A^{\otimes n} \otimes F_0)^{T}$ is coherent for every ![]() $n$, because
$n$, because ![]() $A$ is a finitely generated
$A$ is a finitely generated ![]() $R$-algebra and
$R$-algebra and ![]() $T$ is linearly reductive. It follows that
$T$ is linearly reductive. It follows that ![]() $M^{n} \in {\rm Coh} (\operatorname {Spec}(R))$ and hence
$M^{n} \in {\rm Coh} (\operatorname {Spec}(R))$ and hence ![]() $\pi _\ast (F) \in \operatorname {DCoh}(\operatorname {Spec}(R))$.
$\pi _\ast (F) \in \operatorname {DCoh}(\operatorname {Spec}(R))$.
Lemma 4.3.8 Let ![]() $\mathscr {S}$ be a noetherian algebraic derived
$\mathscr {S}$ be a noetherian algebraic derived ![]() $S$-stack. Then the pullback functor
$S$-stack. Then the pullback functor ![]() $\operatorname {QC}(BT_\mathscr {S})^{\heartsuit } \to \operatorname {QC}(BB_\mathscr {S})^{\heartsuit }$ for the morphism
$\operatorname {QC}(BT_\mathscr {S})^{\heartsuit } \to \operatorname {QC}(BB_\mathscr {S})^{\heartsuit }$ for the morphism ![]() $BB_\mathscr {S} \to BT_\mathscr {S}$ induces an equivalence between the full subcategories of objects concentrated in a single
$BB_\mathscr {S} \to BT_\mathscr {S}$ induces an equivalence between the full subcategories of objects concentrated in a single ![]() $\lambda$-weight.
$\lambda$-weight.
Proof. The argument for essential surjectivity is similar to the proof of Lemma 4.3.6, except now because ![]() $F$ is concentrated in a single
$F$ is concentrated in a single ![]() $\lambda$-weight and
$\lambda$-weight and ![]() $A$ is non-positively graded, the comultiplication map
$A$ is non-positively graded, the comultiplication map ![]() $F \to A_\mathscr {S} \otimes _\mathscr {S} F$ must agree with the canonical map induced by
$F \to A_\mathscr {S} \otimes _\mathscr {S} F$ must agree with the canonical map induced by ![]() $\mathcal {O}_S = A_0 \to A$. Hence, the
$\mathcal {O}_S = A_0 \to A$. Hence, the ![]() $A$-comodule structure on
$A$-comodule structure on ![]() $F$ is trivial.
$F$ is trivial.
The argument for full faithfulness is similar to the proof of Lemma 4.3.7. By faithfully flat descent for the smooth cover ![]() $BT_\mathscr {S} \to BB_\mathscr {S}$, we have
$BT_\mathscr {S} \to BB_\mathscr {S}$, we have
where ![]() $F_0$ and
$F_0$ and ![]() $G_0$ respectively denote the restrictions of
$G_0$ respectively denote the restrictions of ![]() $F$ and
$F$ and ![]() $G$ to
$G$ to ![]() $BT_\mathscr {S}$. If
$BT_\mathscr {S}$. If ![]() $F_0$ and
$F_0$ and ![]() $G_0$ are both concentrated in
$G_0$ are both concentrated in ![]() $\lambda$-weight
$\lambda$-weight ![]() $w$, then the restriction map
$w$, then the restriction map ![]() $\operatorname {RHom}_\mathscr {S}(F_0,G_0)^{T} \to \operatorname {RHom}_\mathscr {S} (F_0,A^{\otimes n} \otimes _\mathscr {S} G_0)^{T}$ is an equivalence for all
$\operatorname {RHom}_\mathscr {S}(F_0,G_0)^{T} \to \operatorname {RHom}_\mathscr {S} (F_0,A^{\otimes n} \otimes _\mathscr {S} G_0)^{T}$ is an equivalence for all ![]() $n$, and the result follows.
$n$, and the result follows.
Proof of Proposition 4.3.4 The morphism ![]() $B_S B \to B_S G$ is surjective, proper, and representable, hence satisfies (CP). By Theorem 4.3.1 it thus suffices to show that
$B_S B \to B_S G$ is surjective, proper, and representable, hence satisfies (CP). By Theorem 4.3.1 it thus suffices to show that ![]() $B_S B \to S$ is formally proper. Let
$B_S B \to S$ is formally proper. Let ![]() $\mathscr {S}$ be a noetherian derived algebraic
$\mathscr {S}$ be a noetherian derived algebraic ![]() $S$-stack which is complete along a closed subset
$S$-stack which is complete along a closed subset ![]() $Z \subset |\mathscr {S}|$, and let
$Z \subset |\mathscr {S}|$, and let ![]() $i : \widehat {BB_\mathscr {S}} \to BB_\mathscr {S}$ be the formal completion along the preimage of
$i : \widehat {BB_\mathscr {S}} \to BB_\mathscr {S}$ be the formal completion along the preimage of ![]() $Z$. We must show that
$Z$. We must show that ![]() $i^{\ast } \colon \operatorname {APerf}(BB_\mathscr {S}) \to \operatorname {APerf}(\widehat {BB_\mathscr {S}})$ is an equivalence.
$i^{\ast } \colon \operatorname {APerf}(BB_\mathscr {S}) \to \operatorname {APerf}(\widehat {BB_\mathscr {S}})$ is an equivalence.
Lemma 4.3.7 and Proposition 2.3.1 imply ![]() $i^{\ast }$ is fully faithful, so by Proposition 2.3.3 it suffices to show that
$i^{\ast }$ is fully faithful, so by Proposition 2.3.3 it suffices to show that ![]() ${\rm Coh} (BB_\mathscr {S}) \to {\rm Coh} (\widehat {BB_\mathscr {S}})$ is essentially surjective. Note that full faithfulness of
${\rm Coh} (BB_\mathscr {S}) \to {\rm Coh} (\widehat {BB_\mathscr {S}})$ is essentially surjective. Note that full faithfulness of ![]() $i^{\ast }$, combined with the fact that the natural truncation map is an equivalence
$i^{\ast }$, combined with the fact that the natural truncation map is an equivalence ![]() $\operatorname {APerf}(\widehat {BB_\mathscr {S}})^{\heartsuit } \simeq {\rm Coh} (\widehat {BB_\mathscr {S}})$, implies that the essential image of
$\operatorname {APerf}(\widehat {BB_\mathscr {S}})^{\heartsuit } \simeq {\rm Coh} (\widehat {BB_\mathscr {S}})$, implies that the essential image of ![]() ${\rm Coh} (BB_\mathscr {S}) \to {\rm Coh} (\widehat {BB_\mathscr {S}})$ is closed under extensions.
${\rm Coh} (BB_\mathscr {S}) \to {\rm Coh} (\widehat {BB_\mathscr {S}})$ is closed under extensions.
![]() ${\rm Coh} (\widehat {BB_\mathscr {S}})$ is the limit of the categories
${\rm Coh} (\widehat {BB_\mathscr {S}})$ is the limit of the categories ![]() ${\rm Coh} (BB_R)$ over all maps
${\rm Coh} (BB_R)$ over all maps ![]() $\operatorname {Spec}(R) \to \widehat {\mathscr {S}}$. Note that for any
$\operatorname {Spec}(R) \to \widehat {\mathscr {S}}$. Note that for any ![]() $F \in {\rm Coh} (BB_R)$ the canonical filtration
$F \in {\rm Coh} (BB_R)$ the canonical filtration ![]() $\cdots \subset F_{\geqslant w+1} \subset F_{\geqslant w} \subset \cdots \subset F$ of Lemma 4.3.6 is compatible with pullback along any map
$\cdots \subset F_{\geqslant w+1} \subset F_{\geqslant w} \subset \cdots \subset F$ of Lemma 4.3.6 is compatible with pullback along any map ![]() $\phi \colon \operatorname {Spec}(R') \to \operatorname {Spec}(R)$ in the sense that
$\phi \colon \operatorname {Spec}(R') \to \operatorname {Spec}(R)$ in the sense that
because the inclusion ![]() $F_{\geqslant w} \subset F$ is a summand once we forget the
$F_{\geqslant w} \subset F$ is a summand once we forget the ![]() $B$-action. It follows that any
$B$-action. It follows that any ![]() $\widehat {F} \in {\rm Coh} (\widehat {BB_\mathscr {S}})$ admits a canonical filtration
$\widehat {F} \in {\rm Coh} (\widehat {BB_\mathscr {S}})$ admits a canonical filtration ![]() $\cdots \subset \widehat {F}_{\geqslant w+1} \subset \widehat {F}_{\geqslant w} \subset \cdots \subset \widehat {F}$ which restricts to the filtration of Lemma 4.3.6 along any map
$\cdots \subset \widehat {F}_{\geqslant w+1} \subset \widehat {F}_{\geqslant w} \subset \cdots \subset \widehat {F}$ which restricts to the filtration of Lemma 4.3.6 along any map ![]() $\operatorname {Spec}(R) \to \widehat {\mathscr {S}}$. Furthermore, by restricting to the reduced classical closed substack of
$\operatorname {Spec}(R) \to \widehat {\mathscr {S}}$. Furthermore, by restricting to the reduced classical closed substack of ![]() $\mathscr {S}$ whose underlying subset is
$\mathscr {S}$ whose underlying subset is ![]() $Z$, one can see that this filtration is finite.
$Z$, one can see that this filtration is finite.
We have therefore reduced the claim to showing that ![]() $\widehat {F}_w / \widehat {F}_{w+1}$ lies in the essential image of
$\widehat {F}_w / \widehat {F}_{w+1}$ lies in the essential image of ![]() ${\rm Coh} (BB_\mathscr {S}) \to {\rm Coh} (\widehat {BB_\mathscr {S}})$. For any
${\rm Coh} (BB_\mathscr {S}) \to {\rm Coh} (\widehat {BB_\mathscr {S}})$. For any ![]() $\eta : \operatorname {Spec}(R) \to \widehat {\mathscr {S}}$, the object
$\eta : \operatorname {Spec}(R) \to \widehat {\mathscr {S}}$, the object ![]() $(\widehat {F}_w / \widehat {F}_{w+1})_\eta \in {\rm Coh} (BB_R)$ lies in the full subcategory concentrated in
$(\widehat {F}_w / \widehat {F}_{w+1})_\eta \in {\rm Coh} (BB_R)$ lies in the full subcategory concentrated in ![]() $\lambda$-weight
$\lambda$-weight ![]() $w$, so Lemma 4.3.8 implies that
$w$, so Lemma 4.3.8 implies that ![]() $\widehat {F}_w / \widehat {F}_{w+1}$ lies in the essential image of the pullback functor
$\widehat {F}_w / \widehat {F}_{w+1}$ lies in the essential image of the pullback functor ![]() ${\rm Coh} (\widehat {BT_\mathscr {S}}) \to {\rm Coh} (\widehat {BB_\mathscr {S}})$ along the map
${\rm Coh} (\widehat {BT_\mathscr {S}}) \to {\rm Coh} (\widehat {BB_\mathscr {S}})$ along the map ![]() $BB_\mathscr {S} \to BT_\mathscr {S}$. It therefore suffices to show that
$BB_\mathscr {S} \to BT_\mathscr {S}$. It therefore suffices to show that ![]() $BT \to S$ is formally proper, so that
$BT \to S$ is formally proper, so that ![]() ${\rm Coh} (BT_\mathscr {S}) \to {\rm Coh} (\widehat {BT_\mathscr {S}})$ is essentially surjective.
${\rm Coh} (BT_\mathscr {S}) \to {\rm Coh} (\widehat {BT_\mathscr {S}})$ is essentially surjective.
![]() $T$ becomes isotrivial (i.e. split after a finite étale cover) after pulling back to the normalization of
$T$ becomes isotrivial (i.e. split after a finite étale cover) after pulling back to the normalization of ![]() $S$ [Reference ConradCon14, Corollary B.3.6]. Thus,
$S$ [Reference ConradCon14, Corollary B.3.6]. Thus, ![]() $T$ is split after pullback to a finite (because
$T$ is split after pullback to a finite (because ![]() $S$ is Nagata) cover
$S$ is Nagata) cover ![]() $S' \to S$. Then
$S' \to S$. Then ![]() $(BT)_{S'} \to S'$ is cohomologically projective by Proposition 4.2.5 and hence formally proper by Theorem 4.2.1. We then apply Theorem 4.3.1 to the proper cover
$(BT)_{S'} \to S'$ is cohomologically projective by Proposition 4.2.5 and hence formally proper by Theorem 4.2.1. We then apply Theorem 4.3.1 to the proper cover ![]() $BT_{S'} \to BT_S$ to deduce that
$BT_{S'} \to BT_S$ to deduce that ![]() $BT_S \to S$ is formally proper.
$BT_S \to S$ is formally proper.
5. Applications
5.1 Algebraicity of mapping stacks
Recall that, for derived ![]() $\mathscr {S}$-stacks
$\mathscr {S}$-stacks ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $\mathscr {Y}$, the mapping prestack is defined by the functor of points
$\mathscr {Y}$, the mapping prestack is defined by the functor of points
where ![]() $T$ is a derived affine scheme over
$T$ is a derived affine scheme over ![]() $\mathscr {S}$.Footnote 6
$\mathscr {S}$.Footnote 6
For our main result of this section, we will fix a base algebraic stack ![]() $\mathscr {S}$ which admits a smooth surjection from a disjoint union of derived schemes of the form
$\mathscr {S}$ which admits a smooth surjection from a disjoint union of derived schemes of the form ![]() $\operatorname {Spec}(A)$, where
$\operatorname {Spec}(A)$, where ![]() $A$ is a derived
$A$ is a derived ![]() $G$-ring which admits a dualizing module (i.e.
$G$-ring which admits a dualizing module (i.e. ![]() $A$ is noetherian and
$A$ is noetherian and ![]() $\pi _0(A)$ is a
$\pi _0(A)$ is a ![]() $G$-ring which admits a dualizing complex [Reference LurieLur4, Theorem 4.3.5]). We will say that a map of derived stacks is quasi-affine if it is representable by derived algebraic spaces and its restriction to discrete simplicial commutative rings is quasi-affine.Footnote 7
$G$-ring which admits a dualizing complex [Reference LurieLur4, Theorem 4.3.5]). We will say that a map of derived stacks is quasi-affine if it is representable by derived algebraic spaces and its restriction to discrete simplicial commutative rings is quasi-affine.Footnote 7
Theorem 5.1.1 Let ![]() $\mathscr {S}$ be an algebraic derived stack as above, and let
$\mathscr {S}$ be an algebraic derived stack as above, and let ![]() $\mathscr {Y}$ be a locally almost finitely presented algebraic derived stack over
$\mathscr {Y}$ be a locally almost finitely presented algebraic derived stack over ![]() $\mathscr {S}$ whose diagonal
$\mathscr {S}$ whose diagonal ![]() $\mathscr {Y} \to \mathscr {Y} \times _\mathscr {S} \mathscr {Y}$ is quasi-affine. Let
$\mathscr {Y} \to \mathscr {Y} \times _\mathscr {S} \mathscr {Y}$ is quasi-affine. Let ![]() $\pi : \mathscr {X} \to \mathscr {S}$ be a formally proper morphism of Tor amplitude
$\pi : \mathscr {X} \to \mathscr {S}$ be a formally proper morphism of Tor amplitude ![]() $n$. Then the mapping stack
$n$. Then the mapping stack ![]() $\underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X},\mathscr {Y})$ is a locally almost finitely presented algebraic (
$\underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X},\mathscr {Y})$ is a locally almost finitely presented algebraic (![]() $n+1$)-stack over
$n+1$)-stack over ![]() $\mathscr {S}$, in the sense of [Reference LurieLur04, Definition 5.1.3]. Furthermore, if
$\mathscr {S}$, in the sense of [Reference LurieLur04, Definition 5.1.3]. Furthermore, if ![]() $\pi$ is flat, so that
$\pi$ is flat, so that ![]() $\underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X},\mathscr {Y})$ is an algebraic stack, then
$\underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X},\mathscr {Y})$ is an algebraic stack, then ![]() $\underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X},\mathscr {Y}) \to \mathscr {S}$ has quasi-affine diagonal, and it has affine diagonal if
$\underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X},\mathscr {Y}) \to \mathscr {S}$ has quasi-affine diagonal, and it has affine diagonal if ![]() $\mathscr {Y} \to \mathscr {S}$ has affine diagonal.
$\mathscr {Y} \to \mathscr {S}$ has affine diagonal.
Remark 5.1.2 In fact our proof uses only the two apparently weaker properties: ![]() $\pi$ satisfies property (L) below, and for any complete local noetherian classical ring
$\pi$ satisfies property (L) below, and for any complete local noetherian classical ring ![]() $R$ over
$R$ over ![]() $\mathscr {S}$, the stack
$\mathscr {S}$, the stack ![]() $\mathscr {X} \times _\mathscr {S} \operatorname {Spec}(R)$ is complete along the closed substack defined by the maximal ideal of
$\mathscr {X} \times _\mathscr {S} \operatorname {Spec}(R)$ is complete along the closed substack defined by the maximal ideal of ![]() $R$.
$R$.
Remark 5.1.3 (Classical versus derived mapping stacks)
There is a slightly stronger form of Tannaka duality available in the classical setting [Reference Hall and RydhHR19], which allows one to deduce the algebraicity of ![]() $\operatorname {Map}_\mathscr {S}(\mathscr {X},\mathscr {Y})$ when
$\operatorname {Map}_\mathscr {S}(\mathscr {X},\mathscr {Y})$ when ![]() $\pi : \mathscr {X} \to \mathscr {S}$ is a flat map of classical stacks satisfying the hypotheses of Theorem 5.1.1 and when
$\pi : \mathscr {X} \to \mathscr {S}$ is a flat map of classical stacks satisfying the hypotheses of Theorem 5.1.1 and when ![]() $\mathscr {Y}$ merely has affine stabilizers over
$\mathscr {Y}$ merely has affine stabilizers over ![]() $\mathscr {S}$ as in [Reference Hall and RydhHR19]. In addition, when
$\mathscr {S}$ as in [Reference Hall and RydhHR19]. In addition, when ![]() $\pi$ is flat, the algebraicity of the classical mapping stack is equivalent to the algebraicity of the derived mapping stack by [Reference Toën and VezzosiTV08, Theorem C.0.9] and Proposition 5.1.10 below, because
$\pi$ is flat, the algebraicity of the classical mapping stack is equivalent to the algebraicity of the derived mapping stack by [Reference Toën and VezzosiTV08, Theorem C.0.9] and Proposition 5.1.10 below, because ![]() $\operatorname {Map}_\mathscr {S}(\mathscr {X},\mathscr {Y})^{\rm cl} \simeq \operatorname {Map}_{\mathscr {S}^{\rm cl}}(\mathscr {X}^{\rm cl},\mathscr {Y}^{\rm cl})$. So by using classical Artin's criteria instead of the derived criteria, one could analogously strengthen Theorem 5.1.1 when
$\operatorname {Map}_\mathscr {S}(\mathscr {X},\mathscr {Y})^{\rm cl} \simeq \operatorname {Map}_{\mathscr {S}^{\rm cl}}(\mathscr {X}^{\rm cl},\mathscr {Y}^{\rm cl})$. So by using classical Artin's criteria instead of the derived criteria, one could analogously strengthen Theorem 5.1.1 when ![]() $\pi$ is flat.
$\pi$ is flat.
Remark 5.1.4 (Noetherian hypotheses)
Also in the classical setting, when ![]() $\mathscr {X} \to \mathscr {S}$ is proper one can remove the noetherian hypotheses on
$\mathscr {X} \to \mathscr {S}$ is proper one can remove the noetherian hypotheses on ![]() $\mathscr {S}$ using relative noetherian approximation. We do not carry this out here, because we do not know that a general formally proper map
$\mathscr {S}$ using relative noetherian approximation. We do not carry this out here, because we do not know that a general formally proper map ![]() $\mathscr {X} \to \operatorname {Spec}(A)$ admits a formally proper model over a finitely generated
$\mathscr {X} \to \operatorname {Spec}(A)$ admits a formally proper model over a finitely generated ![]() ${\mathbb {Z}}$-algebra (even in the classical context). However, if
${\mathbb {Z}}$-algebra (even in the classical context). However, if ![]() $\mathscr {S}$ is a stack satisfying the assumptions of Theorem 5.1.1 and
$\mathscr {S}$ is a stack satisfying the assumptions of Theorem 5.1.1 and ![]() $\pi : \mathscr {X} \to \mathscr {S}$ is a flat and formally proper morphism, then for any derived stack
$\pi : \mathscr {X} \to \mathscr {S}$ is a flat and formally proper morphism, then for any derived stack ![]() $\mathscr {S}'$ with a map
$\mathscr {S}'$ with a map ![]() $\mathscr {S}' \to \mathscr {S}$ and a map of derived stacks
$\mathscr {S}' \to \mathscr {S}$ and a map of derived stacks ![]() $\mathscr {Y} \to \mathscr {S}'$ which is relatively algebraic and locally almost of finite presentation with quasi-affine diagonal, one can apply Noetherian approximation to the underlying classical stack of
$\mathscr {Y} \to \mathscr {S}'$ which is relatively algebraic and locally almost of finite presentation with quasi-affine diagonal, one can apply Noetherian approximation to the underlying classical stack of ![]() $\mathscr {Y}$ to deduce that
$\mathscr {Y}$ to deduce that ![]() $\operatorname {Map}_{\mathscr {S}'}(\mathscr {X}\times _\mathscr {S} \mathscr {S}', \mathscr {Y})$ is algebraic and locally almost of finite presentation with quasi-affine diagonal over
$\operatorname {Map}_{\mathscr {S}'}(\mathscr {X}\times _\mathscr {S} \mathscr {S}', \mathscr {Y})$ is algebraic and locally almost of finite presentation with quasi-affine diagonal over ![]() $\mathscr {S}'$.
$\mathscr {S}'$.
Let us recall the derived version of Artin's representability criteria introduced by Lurie [Reference LurieLur04] (see also [Reference PridhamPri12b]). For a functor ![]() $\mathscr {F} : \mathrm {SCR}_A \to \mathcal {S}$ which satisfies étale descent, the Artin–Lurie criteria are as follows.
$\mathscr {F} : \mathrm {SCR}_A \to \mathcal {S}$ which satisfies étale descent, the Artin–Lurie criteria are as follows.
(i) Locally almost of finite presentation.
 $\mathscr {F}$ commutes with filtered colimits of
$\mathscr {F}$ commutes with filtered colimits of  $k$-truncated objects in
$k$-truncated objects in  $\mathrm {SCR}_A$, for any
$\mathrm {SCR}_A$, for any  $k$.
$k$.(ii)
 $n$-truncated.
$n$-truncated.  $\mathscr {F}(R)$ is
$\mathscr {F}(R)$ is  $n$-truncated for any discrete
$n$-truncated for any discrete  $R\in \mathrm {SCR}_A$.
$R\in \mathrm {SCR}_A$.(iii) Admits a corepresentable deformation theory.
(a) Admits a
 $(-n)$-connective cotangent complex. There is an
$(-n)$-connective cotangent complex. There is an  $L_\mathscr {F} \in \operatorname {QC}(\mathscr {F})_{\geqslant -n}$ such that, for any
$L_\mathscr {F} \in \operatorname {QC}(\mathscr {F})_{\geqslant -n}$ such that, for any  $R \in \mathrm {SCR}_A$ and
$R \in \mathrm {SCR}_A$ and  $\eta : \operatorname {Spec}(R) \to \mathscr {F}$ corresponding to a point in
$\eta : \operatorname {Spec}(R) \to \mathscr {F}$ corresponding to a point in  $\mathscr {F}(R)$,
The existence of
$\mathscr {F}(R)$,
The existence of \[ \mathscr{F}(R \oplus M) \times_{\mathscr{F}(R)} \{\eta\} \simeq \Omega^{\infty} R\operatorname{Hom}_R (\eta^{\ast} L_\mathscr{F}, M). \]
\[ \mathscr{F}(R \oplus M) \times_{\mathscr{F}(R)} \{\eta\} \simeq \Omega^{\infty} R\operatorname{Hom}_R (\eta^{\ast} L_\mathscr{F}, M). \]
 $L_\mathscr {F}$ is not automatic, but it is defined up to canonical isomorphism when it exists.
$L_\mathscr {F}$ is not automatic, but it is defined up to canonical isomorphism when it exists.(b) Infinitesimally cohesive and nilcomplete. See Lemma 3.1.1 conditions (i) and (ii).
(iv) Integrable. For any discrete complete local noetherian
 $R$ over
$R$ over  $A$,
$A$,  $\mathscr {F}(R) \to \operatorname {Map}(\operatorname {Spf}(R),\mathscr {F})$ is an equivalence.
$\mathscr {F}(R) \to \operatorname {Map}(\operatorname {Spf}(R),\mathscr {F})$ is an equivalence.
The main result of [Reference LurieLur04] is the following theorem.Footnote 8
Theorem 5.1.5 Let ![]() $A$ be a derived
$A$ be a derived ![]() $G$-ring and let
$G$-ring and let ![]() $\mathscr {F} \in \operatorname {Fun}(\mathrm {SCR}_A,\mathscr {S})$ be a functor which satisfies étale descent. Then
$\mathscr {F} \in \operatorname {Fun}(\mathrm {SCR}_A,\mathscr {S})$ be a functor which satisfies étale descent. Then ![]() $\mathscr {F}$ is a derived algebraic
$\mathscr {F}$ is a derived algebraic ![]() $n$-stack locally almost of finite presentation over
$n$-stack locally almost of finite presentation over ![]() $\operatorname {Spec}(A)$ if and only if the Artin–Lurie criteria (i)–(iv) above hold.
$\operatorname {Spec}(A)$ if and only if the Artin–Lurie criteria (i)–(iv) above hold.
Our proof of Theorem 5.1.1 closely follows the proof of the analogous result in the case where ![]() $\mathscr {X}$ is a flat and proper algebraic space in [Reference LurieLur04, Reference LurieLur4]. Namely, we will apply Theorem 5.1.5 after first establishing (iii) and (iv), whose proofs require some elaboration.
$\mathscr {X}$ is a flat and proper algebraic space in [Reference LurieLur04, Reference LurieLur4]. Namely, we will apply Theorem 5.1.5 after first establishing (iii) and (iv), whose proofs require some elaboration.
5.1.1 Left adjoint for the pullback functor
For a flat, proper, and finitely presented morphism of schemes ![]() $\pi :X \to S$, the pullback functor
$\pi :X \to S$, the pullback functor ![]() $\pi ^{\ast }:D_{\mathrm {qc}}(S) \to D_{\mathrm {qc}}(X)$ admits a left adjoint
$\pi ^{\ast }:D_{\mathrm {qc}}(S) \to D_{\mathrm {qc}}(X)$ admits a left adjoint ![]() $\pi _+$ with
$\pi _+$ with ![]() $\pi _+(F) \simeq (\pi _\ast (F^{\vee }))^{\vee }$ for perfect complexes, and defined in general by writing any
$\pi _+(F) \simeq (\pi _\ast (F^{\vee }))^{\vee }$ for perfect complexes, and defined in general by writing any ![]() $F$ as a filtered colimit of perfect complexes. In fact, for a morphism of perfect stacks (in the sense of [Reference Ben-Zvi, Francis and NadlerBZFN10]), the existence of
$F$ as a filtered colimit of perfect complexes. In fact, for a morphism of perfect stacks (in the sense of [Reference Ben-Zvi, Francis and NadlerBZFN10]), the existence of ![]() $f_+$ is equivalent to the property that
$f_+$ is equivalent to the property that ![]() $f_\ast$ preserves perfect complexes, and the same formula for
$f_\ast$ preserves perfect complexes, and the same formula for ![]() $f_+$ applies. More generally we have the following proposition.
$f_+$ applies. More generally we have the following proposition.
Proposition 5.1.6 Let ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $\mathscr {S}$ be locally noetherian algebraic derived stacks, and let
$\mathscr {S}$ be locally noetherian algebraic derived stacks, and let ![]() $\pi : \mathscr {X} \to \mathscr {S}$ be a qc.qs. morphism of Tor amplitude
$\pi : \mathscr {X} \to \mathscr {S}$ be a qc.qs. morphism of Tor amplitude ![]() $d < \infty$ satisfying (CP). Assume that locally
$d < \infty$ satisfying (CP). Assume that locally ![]() $\mathscr {S}$ admits a dualizing complex. Then
$\mathscr {S}$ admits a dualizing complex. Then ![]() $\pi ^{\ast } : \operatorname {QC}(\mathscr {S}) \to \operatorname {QC}(\mathscr {X})$ admits a left adjoint,
$\pi ^{\ast } : \operatorname {QC}(\mathscr {S}) \to \operatorname {QC}(\mathscr {X})$ admits a left adjoint, ![]() $\pi _+$, which maps
$\pi _+$, which maps ![]() $\operatorname {QC}(\mathscr {X})_{\geqslant 0}$ to
$\operatorname {QC}(\mathscr {X})_{\geqslant 0}$ to ![]() $\operatorname {QC}(\mathscr {X})_{\geqslant -d}$ and preserves almost perfect complexes.
$\operatorname {QC}(\mathscr {X})_{\geqslant -d}$ and preserves almost perfect complexes.
The key is to reduce the claim to the existence of an adjoint on small categories.
Lemma 5.1.7 Let ![]() $\pi : \mathscr {X} \to \mathscr {S}$ be a morphism of Tor amplitude
$\pi : \mathscr {X} \to \mathscr {S}$ be a morphism of Tor amplitude ![]() $d$ between noetherian algebraic derived stacks. Then
$d$ between noetherian algebraic derived stacks. Then ![]() $\pi ^{\ast } : \operatorname {QC}(\mathscr {S}) \to \operatorname {QC}(\mathscr {X})$ admits a left adjoint if and only if
$\pi ^{\ast } : \operatorname {QC}(\mathscr {S}) \to \operatorname {QC}(\mathscr {X})$ admits a left adjoint if and only if ![]() $\pi ^{\ast } : \operatorname {APerf}(\mathscr {S}) \to \operatorname {APerf}(\mathscr {X})$ admits a left adjoint.
$\pi ^{\ast } : \operatorname {APerf}(\mathscr {S}) \to \operatorname {APerf}(\mathscr {X})$ admits a left adjoint.
Proof. If ![]() $\pi _+$ exists, then for any
$\pi _+$ exists, then for any ![]() $F \in \operatorname {APerf}(\mathscr {X})$,
$F \in \operatorname {APerf}(\mathscr {X})$, ![]() $\operatorname {RHom}_\mathscr {S}(\pi _+(F),-) \simeq \operatorname {RHom}_\mathscr {X}(F,\pi ^{\ast } (-))$ commutes with filtered colimits in
$\operatorname {RHom}_\mathscr {S}(\pi _+(F),-) \simeq \operatorname {RHom}_\mathscr {X}(F,\pi ^{\ast } (-))$ commutes with filtered colimits in ![]() $\operatorname {QC}(\mathscr {S})_{\leqslant n}$, because
$\operatorname {QC}(\mathscr {S})_{\leqslant n}$, because ![]() $\pi ^{\ast } : \operatorname {QC}(\mathscr {S})_{\leqslant n} \to \operatorname {QC}(\mathscr {X})_{\leqslant d+n}$ commutes with filtered colimits. It follows that
$\pi ^{\ast } : \operatorname {QC}(\mathscr {S})_{\leqslant n} \to \operatorname {QC}(\mathscr {X})_{\leqslant d+n}$ commutes with filtered colimits. It follows that ![]() $\pi _+(F) \in \operatorname {APerf}(\mathscr {S})$, and thus
$\pi _+(F) \in \operatorname {APerf}(\mathscr {S})$, and thus ![]() $\pi _+$ is a left adjoint to
$\pi _+$ is a left adjoint to ![]() $\pi ^{\ast } : \operatorname {APerf}(\mathscr {S}) \to \operatorname {APerf}(\mathscr {X})$.
$\pi ^{\ast } : \operatorname {APerf}(\mathscr {S}) \to \operatorname {APerf}(\mathscr {X})$.
Conversely, assume that ![]() $\pi ^{\ast } : \operatorname {APerf}(\mathscr {S}) \to \operatorname {APerf}(\mathscr {X})$ admits a left adjoint. Let
$\pi ^{\ast } : \operatorname {APerf}(\mathscr {S}) \to \operatorname {APerf}(\mathscr {X})$ admits a left adjoint. Let ![]() $\mathcal {C} \subset \operatorname {QC}(\mathscr {X})$ be the full subcategory of objects such that
$\mathcal {C} \subset \operatorname {QC}(\mathscr {X})$ be the full subcategory of objects such that ![]() $\operatorname {Map}(F,\pi ^{\ast }(-))$ is corepresentable in
$\operatorname {Map}(F,\pi ^{\ast }(-))$ is corepresentable in ![]() $\operatorname {QC}(\mathscr {S})$. Because
$\operatorname {QC}(\mathscr {S})$. Because ![]() $\pi$ has finite Tor amplitude,
$\pi$ has finite Tor amplitude, ![]() $\operatorname {Map}(F,\pi ^{\ast }(-))$ commutes with the limit
$\operatorname {Map}(F,\pi ^{\ast }(-))$ commutes with the limit ![]() $M = \mathop {\varprojlim }\limits \tau _{\leqslant n} M$ for any
$M = \mathop {\varprojlim }\limits \tau _{\leqslant n} M$ for any ![]() $M\in \operatorname {QC}(\mathscr {S})$. It follows that
$M\in \operatorname {QC}(\mathscr {S})$. It follows that ![]() $F \in \mathcal {C}$ if and only if there exists
$F \in \mathcal {C}$ if and only if there exists ![]() $G \in \operatorname {QC}(\mathscr {S})$ such that for all
$G \in \operatorname {QC}(\mathscr {S})$ such that for all ![]() $n$,
$n$,
For any ![]() $F \in \operatorname {APerf}(\mathscr {X})$ and
$F \in \operatorname {APerf}(\mathscr {X})$ and ![]() $n \in {\mathbb {Z}}$, Theorem A.2.1 implies that
$n \in {\mathbb {Z}}$, Theorem A.2.1 implies that ![]() $\operatorname {Map}(F,\pi ^{\ast }(-)) \simeq \operatorname {Map}(\pi _+(F),-)$ as functors on
$\operatorname {Map}(F,\pi ^{\ast }(-)) \simeq \operatorname {Map}(\pi _+(F),-)$ as functors on ![]() $\operatorname {QC}(\mathscr {S})_{\leqslant n}$, because they agree on
$\operatorname {QC}(\mathscr {S})_{\leqslant n}$, because they agree on ![]() $\operatorname {DCoh}(\mathscr {S})_{\leqslant n}$ and both commute with filtered colimits. So the criterion (5) implies that
$\operatorname {DCoh}(\mathscr {S})_{\leqslant n}$ and both commute with filtered colimits. So the criterion (5) implies that ![]() $\operatorname {APerf}(F) \subset \mathcal {C}$.
$\operatorname {APerf}(F) \subset \mathcal {C}$. ![]() $\mathcal {C}$ is closed under colimits and contains
$\mathcal {C}$ is closed under colimits and contains ![]() $\operatorname {DCoh}(\mathscr {X})_{\leqslant n}$ for all
$\operatorname {DCoh}(\mathscr {X})_{\leqslant n}$ for all ![]() $n$, so Theorem A.2.1 implies that
$n$, so Theorem A.2.1 implies that ![]() $\operatorname {QC}(\mathscr {X})_{\leqslant n} \subset \mathcal {C}$ for all
$\operatorname {QC}(\mathscr {X})_{\leqslant n} \subset \mathcal {C}$ for all ![]() $n$.
$n$.
Finally, given a tower ![]() $\cdots \to F_2 \to F_1 \to F_0$ in
$\cdots \to F_2 \to F_1 \to F_0$ in ![]() $\mathcal {C}$ such that
$\mathcal {C}$ such that ![]() $\tau _{\leqslant k}(F_i)$ is eventually constant for any
$\tau _{\leqslant k}(F_i)$ is eventually constant for any ![]() $k$ as
$k$ as ![]() $i \to \infty$, the corresponding tower
$i \to \infty$, the corresponding tower ![]() $\cdots \to G_2 \to G_1 \to G_0$ of corepresenting objects
$\cdots \to G_2 \to G_1 \to G_0$ of corepresenting objects ![]() $G_i = \pi _+(F_i)$ has the same property because
$G_i = \pi _+(F_i)$ has the same property because ![]() $\pi ^{\ast }$ has finite Tor amplitude. Then
$\pi ^{\ast }$ has finite Tor amplitude. Then ![]() $G:= \lim _n G_n \in \operatorname {QC}(\mathscr {S})$ satisfies the criterion (5) for
$G:= \lim _n G_n \in \operatorname {QC}(\mathscr {S})$ satisfies the criterion (5) for ![]() $F = \lim _n F_n$. Writing any
$F = \lim _n F_n$. Writing any ![]() $F\in \operatorname {QC}(\mathscr {S})$ as
$F\in \operatorname {QC}(\mathscr {S})$ as ![]() $F \simeq \lim _n \tau _{\leqslant n}(F)$ shows that
$F \simeq \lim _n \tau _{\leqslant n}(F)$ shows that ![]() $\mathcal {C} = \operatorname {QC}(\mathscr {S})$.
$\mathcal {C} = \operatorname {QC}(\mathscr {S})$.
Lemma 5.1.8 (Base change for  $p_+$)
$p_+$)
Suppose we are given a cartesian square of prestacks

such that ![]() $q$ is relatively representable by qc.qs. algebraic derived stacks satisfying (CD). Assume that
$q$ is relatively representable by qc.qs. algebraic derived stacks satisfying (CD). Assume that ![]() $p^{\ast } : \operatorname {QC}(\mathscr {S}) \to \operatorname {QC}(\mathscr {X})$ admits a left adjoint
$p^{\ast } : \operatorname {QC}(\mathscr {S}) \to \operatorname {QC}(\mathscr {X})$ admits a left adjoint ![]() $p_+$ and likewise for
$p_+$ and likewise for ![]() $(p^{\prime })^{\ast }$. Then the canonical base-change morphism is an isomorphism of functors
$(p^{\prime })^{\ast }$. Then the canonical base-change morphism is an isomorphism of functors
Proof. The base-change isomorphism between these functors is induced by the base-change isomorphism of their right adjoints, ![]() $p^{*} q_* \xrightarrow {\simeq } (q')_* (p')^{*}$ provided by Proposition A.1.5.
$p^{*} q_* \xrightarrow {\simeq } (q')_* (p')^{*}$ provided by Proposition A.1.5.
Proof of Proposition 5.1.6 Let ![]() $U_\bullet \to \mathscr {S}$ be an fppf hypercover of
$U_\bullet \to \mathscr {S}$ be an fppf hypercover of ![]() $\mathscr {S}$ by derived schemes, and let
$\mathscr {S}$ by derived schemes, and let ![]() $\mathscr {X}_\bullet \to \mathscr {X}$ be the base change along
$\mathscr {X}_\bullet \to \mathscr {X}$ be the base change along ![]() $\pi : \mathscr {X} \to \mathscr {S}$. If, for each
$\pi : \mathscr {X} \to \mathscr {S}$. If, for each ![]() $n$, the functor
$n$, the functor ![]() $\pi _n^{\ast } : \operatorname {QC}(U_n) \to \operatorname {QC}(\mathscr {X}_n)$ admits a left adjoint
$\pi _n^{\ast } : \operatorname {QC}(U_n) \to \operatorname {QC}(\mathscr {X}_n)$ admits a left adjoint ![]() $(\pi _n)_+$, then Lemma 5.1.8 implies that applying the functors
$(\pi _n)_+$, then Lemma 5.1.8 implies that applying the functors ![]() $(\pi _n)_+$ levelwise defines a functor
$(\pi _n)_+$ levelwise defines a functor ![]() $(\pi _\bullet )_+ : \operatorname {Tot} \{\operatorname {QC}(\mathscr {X}_\bullet )\} \to \operatorname {Tot}\{ \operatorname {QC}(U_\bullet )\}$. It is straightforward to check that
$(\pi _\bullet )_+ : \operatorname {Tot} \{\operatorname {QC}(\mathscr {X}_\bullet )\} \to \operatorname {Tot}\{ \operatorname {QC}(U_\bullet )\}$. It is straightforward to check that ![]() $(\pi _\bullet )_+$ is left adjoint to
$(\pi _\bullet )_+$ is left adjoint to ![]() $(\pi _\bullet )^{\ast }$, which corresponds to
$(\pi _\bullet )^{\ast }$, which corresponds to ![]() $\pi ^{\ast }$ under the equivalences
$\pi ^{\ast }$ under the equivalences ![]() $\operatorname {QC}(\mathscr {X}) \simeq \operatorname {Tot}\{ \operatorname {QC}(\mathscr {X}_\bullet )\}$ and
$\operatorname {QC}(\mathscr {X}) \simeq \operatorname {Tot}\{ \operatorname {QC}(\mathscr {X}_\bullet )\}$ and ![]() $\operatorname {QC}(\mathscr {S}) \simeq \operatorname {Tot} \{\operatorname {QC}(U_\bullet )\}$. We may assume that
$\operatorname {QC}(\mathscr {S}) \simeq \operatorname {Tot} \{\operatorname {QC}(U_\bullet )\}$. We may assume that ![]() $U_n$ is a union of affine schemes, for which the existence of a left adjoint
$U_n$ is a union of affine schemes, for which the existence of a left adjoint ![]() $(\pi _n)_+$ is equivalent to the existence of a left adjoint for
$(\pi _n)_+$ is equivalent to the existence of a left adjoint for ![]() $(\pi _n)^{\ast }$ over each of the affine schemes comprising
$(\pi _n)^{\ast }$ over each of the affine schemes comprising ![]() $U_n$. Furthermore, if
$U_n$. Furthermore, if ![]() $\mathscr {S}$ locally admits a dualizing complex, then we can arrange that each affine scheme appearing in
$\mathscr {S}$ locally admits a dualizing complex, then we can arrange that each affine scheme appearing in ![]() $U_n$ admits a dualizing complex by [Reference LurieLur04, Theorem 3.6.8] (see also [Reference LurieLur4, Theorem 4.3.14]). Thus, we have reduced to the case where
$U_n$ admits a dualizing complex by [Reference LurieLur04, Theorem 3.6.8] (see also [Reference LurieLur4, Theorem 4.3.14]). Thus, we have reduced to the case where ![]() $\mathscr {S} = \operatorname {Spec}(R)$ for some noetherian simplicial commutative ring
$\mathscr {S} = \operatorname {Spec}(R)$ for some noetherian simplicial commutative ring ![]() $R$ which admits a dualizing complex.
$R$ which admits a dualizing complex.
By Lemma 5.1.7 it suffices to show that the functor ![]() $h(\bullet ) = \Omega ^{\infty } \operatorname {RHom}_\mathscr {X}(F, \pi ^{\ast } (-))$ is corepresentable for any
$h(\bullet ) = \Omega ^{\infty } \operatorname {RHom}_\mathscr {X}(F, \pi ^{\ast } (-))$ is corepresentable for any ![]() $F \in \operatorname {APerf}(\mathscr {X})$. We use [Reference LurieLur4, Theorem 4.4.2] which gives five conditions which guarantee that
$F \in \operatorname {APerf}(\mathscr {X})$. We use [Reference LurieLur4, Theorem 4.4.2] which gives five conditions which guarantee that ![]() $h(\bullet )$ is corepresentable by an almost perfect complex.
$h(\bullet )$ is corepresentable by an almost perfect complex.
(i) That
 $h(0)$ is contractible, which is immediate, and
$h(0)$ is contractible, which is immediate, and  $h$ maps pushout squares to pullback squares as
$h$ maps pushout squares to pullback squares as  $\pi ^{\ast }$ is an exact functor of stable
$\pi ^{\ast }$ is an exact functor of stable  $\infty$-categories and
$\infty$-categories and  $\operatorname {RHom}_\mathscr {X}(F,\bullet )$ takes pushout squares to pullback squares.
$\operatorname {RHom}_\mathscr {X}(F,\bullet )$ takes pushout squares to pullback squares.(ii) The canonical map
 $h(M) \mapsto \mathop {\varprojlim }\limits h(\tau _{\leqslant n} M)$ is an equivalence – because
$h(M) \mapsto \mathop {\varprojlim }\limits h(\tau _{\leqslant n} M)$ is an equivalence – because  $\pi$ has finite Tor dimension,
$\pi$ has finite Tor dimension,  $\pi ^{\ast } \mathop {\varprojlim }\limits \tau _{\leqslant n} M \simeq \mathop {\varprojlim }\limits \pi ^{\ast } \tau _{\leqslant n} M$, and
$\pi ^{\ast } \mathop {\varprojlim }\limits \tau _{\leqslant n} M \simeq \mathop {\varprojlim }\limits \pi ^{\ast } \tau _{\leqslant n} M$, and  $\operatorname {RHom}(F,\bullet )$ preserves limits.
$\operatorname {RHom}(F,\bullet )$ preserves limits.(iii)
 $h$ commutes with filtered colimits in
$h$ commutes with filtered colimits in  $\operatorname {QC}(R)^{\mathrm {cn}}_{\leqslant n}$ – the functor
$\operatorname {QC}(R)^{\mathrm {cn}}_{\leqslant n}$ – the functor  $\pi ^{\ast }$ commutes with colimits and maps
$\pi ^{\ast }$ commutes with colimits and maps  $\operatorname {QC}(R)^{\mathrm {cn}}_{\leqslant n}$ to
$\operatorname {QC}(R)^{\mathrm {cn}}_{\leqslant n}$ to  $\operatorname {QC}(\mathscr {X})^{\mathrm {cn}}_{\leqslant n+d}$ for some
$\operatorname {QC}(\mathscr {X})^{\mathrm {cn}}_{\leqslant n+d}$ for some  $d$, and
$d$, and  $\operatorname {RHom}(F,\bullet )$ commutes with filtered colimits in
$\operatorname {RHom}(F,\bullet )$ commutes with filtered colimits in  $\operatorname {QC}(\mathscr {X})^{\mathrm {cn}}_{\leqslant n+d}$ because
$\operatorname {QC}(\mathscr {X})^{\mathrm {cn}}_{\leqslant n+d}$ because  $F$ is almost perfect.
$F$ is almost perfect.(iv) There exists an integer
 $n\geqslant 0$ such that
$n\geqslant 0$ such that  $h(M)$ is
$h(M)$ is  $n$-truncated for every discrete
$n$-truncated for every discrete  $R$-module,
$R$-module,  $M$ –
$M$ –  $\pi ^{\ast } (\operatorname {QC}(R)^{\heartsuit }) \subset \operatorname {QC}(\mathscr {X})^{\mathrm {cn}}_{\leqslant d}$, so
$\pi ^{\ast } (\operatorname {QC}(R)^{\heartsuit }) \subset \operatorname {QC}(\mathscr {X})^{\mathrm {cn}}_{\leqslant d}$, so  $H_i(\operatorname {RHom}(F,\pi ^{\ast }(M))) = 0$ for
$H_i(\operatorname {RHom}(F,\pi ^{\ast }(M))) = 0$ for  $i>d-\min \{j | H_j(F) \neq 0\}$.
$i>d-\min \{j | H_j(F) \neq 0\}$.
The fifth condition requires that, for any coherent ![]() $R$-module,
$R$-module, ![]() $M$, the module
$M$, the module ![]() $\pi _0 h(M)$ is finitely generated as a module over
$\pi _0 h(M)$ is finitely generated as a module over ![]() $\pi _0 R$. We rewrite
$\pi _0 R$. We rewrite ![]() $h(M) \simeq \Omega ^{\infty } \pi _\ast H$, where
$h(M) \simeq \Omega ^{\infty } \pi _\ast H$, where ![]() $H:= \operatorname {RHom}^{\otimes _{\operatorname {QC}(\mathscr {X})}}_\mathscr {X}(F,\pi ^{\ast } M) \in \operatorname {{\mathbb {D}}APerf}(\mathscr {X})$ by Lemma 2.3.2. In particular,
$H:= \operatorname {RHom}^{\otimes _{\operatorname {QC}(\mathscr {X})}}_\mathscr {X}(F,\pi ^{\ast } M) \in \operatorname {{\mathbb {D}}APerf}(\mathscr {X})$ by Lemma 2.3.2. In particular, ![]() $\pi _\ast H \in \operatorname {{\mathbb {D}}APerf}(R)$ by property (CP), and
$\pi _\ast H \in \operatorname {{\mathbb {D}}APerf}(R)$ by property (CP), and ![]() $H_i \pi _\ast H$ is a coherent
$H_i \pi _\ast H$ is a coherent ![]() $\pi _0 R$-module for all
$\pi _0 R$-module for all ![]() $i$.
$i$.
5.1.2 Cotangent complex of the mapping stack
Definition 5.1.9 Let ![]() $\mathscr {X}$ be a stack over a noetherian affine derived scheme,
$\mathscr {X}$ be a stack over a noetherian affine derived scheme, ![]() $\operatorname {Spec}(R)$. We introduce the following property.
$\operatorname {Spec}(R)$. We introduce the following property.
 $(L)_R$: The pullback functor
$(L)_R$: The pullback functor  $f^{\ast } : \operatorname {QC}(\operatorname {Spec}(R)) \to \operatorname {QC}(\mathscr {X})$ admits a left adjoint
$f^{\ast } : \operatorname {QC}(\operatorname {Spec}(R)) \to \operatorname {QC}(\mathscr {X})$ admits a left adjoint  $f_+$.
$f_+$.
We say that a morphism of stacks ![]() $f : \mathscr {X} \to \mathscr {S}$ satisfies (L) if, for any noetherian affine derived scheme
$f : \mathscr {X} \to \mathscr {S}$ satisfies (L) if, for any noetherian affine derived scheme ![]() $\operatorname {Spec}(R) \to \mathscr {S}$, the base change
$\operatorname {Spec}(R) \to \mathscr {S}$, the base change ![]() $\mathscr {X} \times _\mathscr {S} \operatorname {Spec}(R) \to \operatorname {Spec}(R)$ satisfies (L)R.
$\mathscr {X} \times _\mathscr {S} \operatorname {Spec}(R) \to \operatorname {Spec}(R)$ satisfies (L)R.
Proposition 5.1.10 Let ![]() $S$ be an affine derived scheme, and let
$S$ be an affine derived scheme, and let ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $\mathscr {Y}$ be derived
$\mathscr {Y}$ be derived ![]() $S$-stacks such that
$S$-stacks such that ![]() $\pi : \mathscr {X} \to S$ satisfies (L) and has finite Tor amplitude. If
$\pi : \mathscr {X} \to S$ satisfies (L) and has finite Tor amplitude. If ![]() $\mathscr {Y}$ admits a cotangent complex then so does
$\mathscr {Y}$ admits a cotangent complex then so does ![]() $\underline {\operatorname {Map}}_S( \mathscr {X},\mathscr {Y})$. For any map
$\underline {\operatorname {Map}}_S( \mathscr {X},\mathscr {Y})$. For any map ![]() $\eta : \operatorname {Spec}(A) \to \underline {\operatorname {Map}}_S(\mathscr {X},\mathscr {Y})$ classifying a map
$\eta : \operatorname {Spec}(A) \to \underline {\operatorname {Map}}_S(\mathscr {X},\mathscr {Y})$ classifying a map ![]() $f : \mathscr {X}_A \to \mathscr {Y}$ over
$f : \mathscr {X}_A \to \mathscr {Y}$ over ![]() $S$, we have
$S$, we have
First we observe that the formation of the split square-zero extension ![]() $A \oplus M$ is compatible with pullback in the sense that for any map of rings
$A \oplus M$ is compatible with pullback in the sense that for any map of rings ![]() $A \to B$, corresponding to a map
$A \to B$, corresponding to a map ![]() $\operatorname {Spec}(B) \to \operatorname {Spec}(A)$, we have
$\operatorname {Spec}(B) \to \operatorname {Spec}(A)$, we have ![]() $B \otimes _A (A \oplus M) \simeq B \oplus (B \otimes _A M)$. This motivates the definition of the trivial square-zero extension
$B \otimes _A (A \oplus M) \simeq B \oplus (B \otimes _A M)$. This motivates the definition of the trivial square-zero extension ![]() $\mathscr {X}[F]$ for any functor
$\mathscr {X}[F]$ for any functor ![]() $\mathscr {X}$ and any
$\mathscr {X}$ and any ![]() $F \in \operatorname {QC}(\mathscr {X})^{\mathrm {cn}}$ by the fiber square
$F \in \operatorname {QC}(\mathscr {X})^{\mathrm {cn}}$ by the fiber square

In other words,
where the space of sections of ![]() $\operatorname {Spec}(A \oplus a^{\ast } F) \to \operatorname {Spec}(A)$ can further be identified with
$\operatorname {Spec}(A \oplus a^{\ast } F) \to \operatorname {Spec}(A)$ can further be identified with ![]() $\Omega ^{\infty } R \operatorname {Hom}_A (L_A, a^{\ast } F)$.
$\Omega ^{\infty } R \operatorname {Hom}_A (L_A, a^{\ast } F)$.
Lemma 5.1.11 Let ![]() $S = \operatorname {Spec}(A)$, and let
$S = \operatorname {Spec}(A)$, and let ![]() $\mathscr {X},\mathscr {Y} : \mathrm {SCR}_{A} \to \mathcal {S}$ be functors such that
$\mathscr {X},\mathscr {Y} : \mathrm {SCR}_{A} \to \mathcal {S}$ be functors such that ![]() $\mathscr {Y}$ admits a cotangent complex. Then, for any map
$\mathscr {Y}$ admits a cotangent complex. Then, for any map ![]() $f : \mathscr {X} \to \mathscr {Y}$ over
$f : \mathscr {X} \to \mathscr {Y}$ over ![]() $S$, there is a canonical isomorphism
$S$, there is a canonical isomorphism
as functors ![]() $\operatorname {QC}(\mathscr {X})^{\mathrm {cn}} \to \mathcal {S}$.
$\operatorname {QC}(\mathscr {X})^{\mathrm {cn}} \to \mathcal {S}$.
Proof. Let ![]() $\!\!\mathop {\rm ~Aff}\nolimits / \mathscr {X}[F]$ denote the
$\!\!\mathop {\rm ~Aff}\nolimits / \mathscr {X}[F]$ denote the ![]() $\infty$-category of affine schemes along with a morphism to
$\infty$-category of affine schemes along with a morphism to ![]() $\mathscr {X}[F]$. By the
$\mathscr {X}[F]$. By the ![]() $\infty$-categorical Yoneda lemma, we have
$\infty$-categorical Yoneda lemma, we have
By the canonical fiber square (6), we have a functor ![]() $\!\!\mathop {\rm ~Aff}\nolimits / \mathscr {X} \to \!\!\mathop {\rm ~Aff}\nolimits / \mathscr {X}[F]$ mapping
$\!\!\mathop {\rm ~Aff}\nolimits / \mathscr {X} \to \!\!\mathop {\rm ~Aff}\nolimits / \mathscr {X}[F]$ mapping ![]() $T \mapsto T \times _{\mathscr {X}} \mathscr {X}[F] \simeq T[F|_T]$. This functor is cofinal because any morphism
$T \mapsto T \times _{\mathscr {X}} \mathscr {X}[F] \simeq T[F|_T]$. This functor is cofinal because any morphism ![]() $T \to \mathscr {X}[F]$ factors canonically through
$T \to \mathscr {X}[F]$ factors canonically through ![]() $T \times _\mathscr {X} \mathscr {X}[F] \to \mathscr {X}[F]$, and this factorization is initial in the category of factorizations
$T \times _\mathscr {X} \mathscr {X}[F] \to \mathscr {X}[F]$, and this factorization is initial in the category of factorizations ![]() $T \to T^{\prime } [F|_{T^{\prime }}] \to \mathscr {X}[F]$ for varying
$T \to T^{\prime } [F|_{T^{\prime }}] \to \mathscr {X}[F]$ for varying ![]() $T^{\prime }$. Thus, we can write
$T^{\prime }$. Thus, we can write ![]() $\mathscr {X}[F]$ as a colimit over
$\mathscr {X}[F]$ as a colimit over ![]() $\!\!\mathop {\rm ~Aff}\nolimits / \mathscr {X}$:
$\!\!\mathop {\rm ~Aff}\nolimits / \mathscr {X}$:
Hence, on mapping spaces of presheaves we have
whereas
Taking fibers commutes with limits,
where we have used the defining property of ![]() $L_{\mathscr {Y} / S}$ as corepresenting the fiber of the map
$L_{\mathscr {Y} / S}$ as corepresenting the fiber of the map ![]() $\mathscr {Y}(T[-]) \to \mathscr {Y}(T)$ for affine schemes
$\mathscr {Y}(T[-]) \to \mathscr {Y}(T)$ for affine schemes ![]() $T$. This last expression is essentially the definition of
$T$. This last expression is essentially the definition of ![]() $\Omega ^{\infty } R\operatorname {Hom}_{\operatorname {QC}(\mathscr {X})}(f^{\ast } L_{\mathscr {Y} / S},F)$.
$\Omega ^{\infty } R\operatorname {Hom}_{\operatorname {QC}(\mathscr {X})}(f^{\ast } L_{\mathscr {Y} / S},F)$.
Proof of Proposition 5.1.10 Let ![]() $\eta \in \mathfrak {M}(A)$ correspond to an affine derived scheme
$\eta \in \mathfrak {M}(A)$ correspond to an affine derived scheme ![]() $\operatorname {Spec}(A)$ over
$\operatorname {Spec}(A)$ over ![]() $S$, together with a map
$S$, together with a map ![]() $f : \mathscr {X}_A \to \mathscr {Y}$ over
$f : \mathscr {X}_A \to \mathscr {Y}$ over ![]() $S$. Let
$S$. Let ![]() $M \in \operatorname {QC}(A)^{\mathrm {cn}}$. Then by definition
$M \in \operatorname {QC}(A)^{\mathrm {cn}}$. Then by definition ![]() $\mathfrak {M}(A \oplus M) = \operatorname {Map}_S(\mathscr {X}_{A \oplus M}, \mathscr {Y})$. If
$\mathfrak {M}(A \oplus M) = \operatorname {Map}_S(\mathscr {X}_{A \oplus M}, \mathscr {Y})$. If ![]() $\pi _A : \mathscr {X}_A \to \operatorname {Spec}(A)$ is the structure morphism, then
$\pi _A : \mathscr {X}_A \to \operatorname {Spec}(A)$ is the structure morphism, then ![]() $\mathscr {X}_{A \oplus M} \simeq \mathscr {X}_A[\pi _A^{\ast } M]$ over
$\mathscr {X}_{A \oplus M} \simeq \mathscr {X}_A[\pi _A^{\ast } M]$ over ![]() $\operatorname {Spec}(A)$, by the construction of the trivial square-zero extension of functors. Hence, by Lemma 5.1.11 we have a canonical isomorphism
$\operatorname {Spec}(A)$, by the construction of the trivial square-zero extension of functors. Hence, by Lemma 5.1.11 we have a canonical isomorphism
By hypothesis (L), the functor ![]() $\pi _A^{\ast }$ has a left adjoint
$\pi _A^{\ast }$ has a left adjoint ![]() $(\pi _A)_+$, hence we can define
$(\pi _A)_+$, hence we can define ![]() $L_{\mathfrak {M}/S}|_{\operatorname {Spec}(A)} := (\pi _A)_+ f^{\ast } L_{\mathscr {Y}/S}$. For any map of rings
$L_{\mathfrak {M}/S}|_{\operatorname {Spec}(A)} := (\pi _A)_+ f^{\ast } L_{\mathscr {Y}/S}$. For any map of rings ![]() $\phi : A \to B$, we have the pullback square
$\phi : A \to B$, we have the pullback square

By Lemma 5.1.8, we have a natural isomorphism ![]() $\phi ^{\ast } (\pi _A)_+ f^{\ast } L_{\mathscr {Y}/S} \simeq (\pi _B)_+ (\phi ^{\prime } \circ f)^{\ast } L_{\mathscr {Y}/S}$. Hence, the assignment
$\phi ^{\ast } (\pi _A)_+ f^{\ast } L_{\mathscr {Y}/S} \simeq (\pi _B)_+ (\phi ^{\prime } \circ f)^{\ast } L_{\mathscr {Y}/S}$. Hence, the assignment ![]() $\operatorname {Spec}(A) / \mathfrak {M} \mapsto (\pi _A)_+ f^{\ast } L_{\mathscr {Y}/S}$ determines an object of
$\operatorname {Spec}(A) / \mathfrak {M} \mapsto (\pi _A)_+ f^{\ast } L_{\mathscr {Y}/S}$ determines an object of ![]() $L_{\mathfrak {M} / S} \in QC(\mathfrak {M})$.
$L_{\mathfrak {M} / S} \in QC(\mathfrak {M})$.
5.1.3 Integrability via the Tannakian formalism
We recall the following version of Tannaka duality in the setting of spectral algebraic geometry, which is a refinement of Lurie's Tannaka duality theorem [Reference LurieLur2, Theorem 3.4.2]:
Theorem 5.1.12 (Theorem 5.1 and Lemma 3.13 of [Reference Bhatt and Halpern-LeistnerBHL17])
Let ![]() $\mathscr {Y}$ be a noetherian algebraic spectral stack with quasi-affine diagonal. Then, for any prestack
$\mathscr {Y}$ be a noetherian algebraic spectral stack with quasi-affine diagonal. Then, for any prestack ![]() $\mathscr {S}$ over
$\mathscr {S}$ over ![]() $\mathrm {CAlg}^{\mathrm {cn}}$, the association
$\mathrm {CAlg}^{\mathrm {cn}}$, the association ![]() $f \mapsto f^{\ast }$ gives an equivalence of
$f \mapsto f^{\ast }$ gives an equivalence of ![]() $\infty$-categories
$\infty$-categories
where the latter denotes symmetric monoidal functors of symmetric monoidal ![]() $\infty$-categories which preserve finite colimits.
$\infty$-categories which preserve finite colimits.
Integrability of the mapping stack functor will follow from the following slightly more general fact.
Proposition 5.1.13 Let ![]() $\mathscr {X}$ be a noetherian algebraic derived stack over a noetherian affine derived scheme
$\mathscr {X}$ be a noetherian algebraic derived stack over a noetherian affine derived scheme ![]() $S$, and let
$S$, and let ![]() $\widehat {\mathscr {X}}$ be the formal completion of
$\widehat {\mathscr {X}}$ be the formal completion of ![]() $\mathscr {X}$ along a closed substack. If
$\mathscr {X}$ along a closed substack. If ![]() $\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is an equivalence of
$\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is an equivalence of ![]() $\infty$-categories, then for any locally noetherian algebraic derived
$\infty$-categories, then for any locally noetherian algebraic derived ![]() $S$-stack
$S$-stack ![]() $\mathscr {Y}$ with quasi-affine diagonal, the canonical functor
$\mathscr {Y}$ with quasi-affine diagonal, the canonical functor
is an equivalence of ![]() $\infty$-groupoids.
$\infty$-groupoids.
Proof. If we write ![]() $\mathscr {Y}$ as a union of quasi-compact open substacks
$\mathscr {Y}$ as a union of quasi-compact open substacks ![]() $\mathscr {Y} = \bigcup _\alpha \mathscr {Y}_\alpha$, then both mapping
$\mathscr {Y} = \bigcup _\alpha \mathscr {Y}_\alpha$, then both mapping ![]() $\infty$-groupoids are filtered unions of the mapping groupoids into
$\infty$-groupoids are filtered unions of the mapping groupoids into ![]() $\mathscr {Y}_\alpha$, so it suffices to replace
$\mathscr {Y}_\alpha$, so it suffices to replace ![]() $\mathscr {Y}$ with
$\mathscr {Y}$ with ![]() $\mathscr {Y}_\alpha$ and assume that
$\mathscr {Y}_\alpha$ and assume that ![]() $\mathscr {Y}$ is noetherian. Also note that it suffices to prove the claim for both
$\mathscr {Y}$ is noetherian. Also note that it suffices to prove the claim for both ![]() $\operatorname {Map}(\mathscr {X},\mathscr {Y})$ and
$\operatorname {Map}(\mathscr {X},\mathscr {Y})$ and ![]() $\operatorname {Map}(\mathscr {X},S)$, so we may restrict to the absolute case.
$\operatorname {Map}(\mathscr {X},S)$, so we may restrict to the absolute case.
Step 1: the spectral version. Consider the variant of the statement of Proposition 5.1.13 in which the phrase ‘derived stack’ is replaced with ‘spectral stack’. Then the restriction functor ![]() $\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is a
$\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is a ![]() $t$-exact equivalence and therefore induces an equivalence of symmetric monoidal
$t$-exact equivalence and therefore induces an equivalence of symmetric monoidal ![]() $\infty$-categories
$\infty$-categories ![]() $\operatorname {APerf}(\mathscr {X})^{\mathrm {cn}} \simeq \operatorname {APerf}(\widehat {\mathscr {X}})^{\mathrm {cn}}$. So Theorem 5.1.12 immediately implies that
$\operatorname {APerf}(\mathscr {X})^{\mathrm {cn}} \simeq \operatorname {APerf}(\widehat {\mathscr {X}})^{\mathrm {cn}}$. So Theorem 5.1.12 immediately implies that ![]() $\operatorname {Map}(\mathscr {X},\mathscr {Y}) \to \operatorname {Map}(\widehat {\mathscr {X}},\mathscr {Y})$ is an equivalence of
$\operatorname {Map}(\mathscr {X},\mathscr {Y}) \to \operatorname {Map}(\widehat {\mathscr {X}},\mathscr {Y})$ is an equivalence of ![]() $\infty$-categories.
$\infty$-categories.
Step 2: the classical version. The ![]() $\infty$-category
$\infty$-category ![]() $\!\!\mathop {\rm ~Shv}\nolimits (\mathrm {Ring}^{\mathrm {op}})$ of étale sheaves on the category of classical affine schemes admits two fully faithful left Kan extension functors
$\!\!\mathop {\rm ~Shv}\nolimits (\mathrm {Ring}^{\mathrm {op}})$ of étale sheaves on the category of classical affine schemes admits two fully faithful left Kan extension functors
These functors commute with the formation of ![]() $\operatorname {APerf}(-)$, the underlying topological space, and formal completions; indeed, these claims reduce immediately to the case of representable functors (i.e. affine schemes) where they are evident. The left Kan extension functors also preserve Noetherian algebraic stacks. Finally, a derived stack or spectral stack is quasi-affine if and only if its underlying classical stack is quasi-affine, and it follows that a stack has quasi-affine diagonal if and only if its left Kan extension does.
$\operatorname {APerf}(-)$, the underlying topological space, and formal completions; indeed, these claims reduce immediately to the case of representable functors (i.e. affine schemes) where they are evident. The left Kan extension functors also preserve Noetherian algebraic stacks. Finally, a derived stack or spectral stack is quasi-affine if and only if its underlying classical stack is quasi-affine, and it follows that a stack has quasi-affine diagonal if and only if its left Kan extension does.
In particular, if ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $\mathscr {Y}$ are classical stacks, and
$\mathscr {Y}$ are classical stacks, and ![]() $\mathscr {X}^{\rm sp}$ and
$\mathscr {X}^{\rm sp}$ and ![]() $\mathscr {Y}^{\rm sp}$ the associated spectral stacks, then the condition that
$\mathscr {Y}^{\rm sp}$ the associated spectral stacks, then the condition that ![]() $\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is an equivalence implies that
$\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is an equivalence implies that ![]() $\operatorname {APerf}(\mathscr {X}^{\rm sp}) \to \operatorname {APerf}(\widehat {\mathscr {X}^{\rm sp}})$ is an equivalence, so the fact that
$\operatorname {APerf}(\mathscr {X}^{\rm sp}) \to \operatorname {APerf}(\widehat {\mathscr {X}^{\rm sp}})$ is an equivalence, so the fact that
is an equivalence follows from the full faithfulness of the left Kan extension.
Step 3: the derived version. Now let ![]() $\mathscr {X}^{\circ }$ and
$\mathscr {X}^{\circ }$ and ![]() $\mathscr {Y}$ be noetherian algebraic derived stacks, and assume
$\mathscr {Y}$ be noetherian algebraic derived stacks, and assume ![]() $\mathscr {Y}$ has quasi-affine diagonal,
$\mathscr {Y}$ has quasi-affine diagonal, ![]() $\mathscr {X}^{\circ }$ is the left Kan extension
$\mathscr {X}^{\circ }$ is the left Kan extension ![]() $LK_{\mathrm {SCR}}$ of a classical algebraic stack, and
$LK_{\mathrm {SCR}}$ of a classical algebraic stack, and ![]() $\operatorname {APerf}(\mathscr {X}^{\circ }) \to \operatorname {APerf}(\widehat {\mathscr {X}^{\circ }})$ is an equivalence. We will show that for any algebraic derived stack
$\operatorname {APerf}(\mathscr {X}^{\circ }) \to \operatorname {APerf}(\widehat {\mathscr {X}^{\circ }})$ is an equivalence. We will show that for any algebraic derived stack ![]() $\mathscr {X}$ admitting a surjective closed immersion
$\mathscr {X}$ admitting a surjective closed immersion ![]() $\mathscr {X}^{\circ } \to \mathscr {X}$,
$\mathscr {X}^{\circ } \to \mathscr {X}$, ![]() $\operatorname {Map}(\mathscr {X},\mathscr {Y}) \to \operatorname {Map}(\widehat {\mathscr {X}},\mathscr {Y})$ is an equivalence. This will complete the proof, because any
$\operatorname {Map}(\mathscr {X},\mathscr {Y}) \to \operatorname {Map}(\widehat {\mathscr {X}},\mathscr {Y})$ is an equivalence. This will complete the proof, because any ![]() $\mathscr {X}$ satisfying the hypotheses of the proposition admits a canonical surjective closed immersion from
$\mathscr {X}$ satisfying the hypotheses of the proposition admits a canonical surjective closed immersion from ![]() $\mathscr {X}^{\circ } = \mathscr {X}^{\rm cl}$, and
$\mathscr {X}^{\circ } = \mathscr {X}^{\rm cl}$, and ![]() $\operatorname {APerf}(\mathscr {X}^{\circ }) \to \operatorname {APerf}(\widehat {\mathscr {X}^{\circ }})$ is an equivalence by Lemma 2.3.4.
$\operatorname {APerf}(\mathscr {X}^{\circ }) \to \operatorname {APerf}(\widehat {\mathscr {X}^{\circ }})$ is an equivalence by Lemma 2.3.4.
Let ![]() $\mathcal {C} \subset \!\!\mathop {\rm ~Shv}\nolimits (\mathrm {SCR}^{\mathrm {op}})_{\mathscr {X}^{\circ }/}$ be the largest full subcategory consisting of algebraic derived stacks
$\mathcal {C} \subset \!\!\mathop {\rm ~Shv}\nolimits (\mathrm {SCR}^{\mathrm {op}})_{\mathscr {X}^{\circ }/}$ be the largest full subcategory consisting of algebraic derived stacks ![]() $\mathscr {X}$ admitting a surjective closed immersion
$\mathscr {X}$ admitting a surjective closed immersion ![]() $\mathscr {X}^{\circ } \to \mathscr {X}$, and let
$\mathscr {X}^{\circ } \to \mathscr {X}$, and let ![]() $\mathcal {C}' \subset \mathcal {C}$ be the full subcategory of stacks such that
$\mathcal {C}' \subset \mathcal {C}$ be the full subcategory of stacks such that ![]() $\operatorname {Map}(\mathscr {X},\mathscr {Y}) \to \operatorname {Map}(\widehat {\mathscr {X}},\mathscr {Y})$ is an equivalence. Note that Lemma 2.3.4 implies that
$\operatorname {Map}(\mathscr {X},\mathscr {Y}) \to \operatorname {Map}(\widehat {\mathscr {X}},\mathscr {Y})$ is an equivalence. Note that Lemma 2.3.4 implies that ![]() $\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is an equivalence for any
$\operatorname {APerf}(\mathscr {X}) \to \operatorname {APerf}(\widehat {\mathscr {X}})$ is an equivalence for any ![]() $\mathscr {X} \in \mathcal {C}$.
$\mathscr {X} \in \mathcal {C}$.
For the initial object ![]() $\mathscr {X}^{\circ } \in \mathcal {C}$,
$\mathscr {X}^{\circ } \in \mathcal {C}$, ![]() $\widehat {\mathscr {X}^{\circ }}$ is the left Kan extension of the formal completion of the underlying classical stack
$\widehat {\mathscr {X}^{\circ }}$ is the left Kan extension of the formal completion of the underlying classical stack ![]() $\mathscr {X}^{\circ }|_{\mathrm {Ring}^{\mathrm {op}}}$, so it suffices by adjunction to replace
$\mathscr {X}^{\circ }|_{\mathrm {Ring}^{\mathrm {op}}}$, so it suffices by adjunction to replace ![]() $\mathscr {Y}$ with
$\mathscr {Y}$ with ![]() $\mathscr {Y}^{\rm cl}$. Note also that we have
$\mathscr {Y}^{\rm cl}$. Note also that we have ![]() $\operatorname {APerf}(\mathscr {X}^{\circ }|_{\mathrm {Ring}^{\mathrm {op}}}) \to \operatorname {APerf}(\widehat {\mathscr {X}^{\circ }|_{\mathrm {Ring}^{\mathrm {op}}}})$ is an equivalence of
$\operatorname {APerf}(\mathscr {X}^{\circ }|_{\mathrm {Ring}^{\mathrm {op}}}) \to \operatorname {APerf}(\widehat {\mathscr {X}^{\circ }|_{\mathrm {Ring}^{\mathrm {op}}}})$ is an equivalence of ![]() $\infty$-categories, so
$\infty$-categories, so ![]() $\mathscr {X}^{\circ } \in \mathcal {C}'$ by Step 2.
$\mathscr {X}^{\circ } \in \mathcal {C}'$ by Step 2.
If ![]() $\mathscr {X} \in \mathcal {C}'$ and
$\mathscr {X} \in \mathcal {C}'$ and ![]() $F \in \operatorname {APerf}(\mathscr {X})^{\mathrm {cn}}$, then we claim that
$F \in \operatorname {APerf}(\mathscr {X})^{\mathrm {cn}}$, then we claim that ![]() $\mathscr {X}[F] \in \mathcal {C}'$ as well. Indeed, it suffices to show that the map
$\mathscr {X}[F] \in \mathcal {C}'$ as well. Indeed, it suffices to show that the map ![]() $\operatorname {Map}(\mathscr {X}[F],\mathscr {Y}) \to \operatorname {Map}(\widehat {\mathscr {X}[F]},\mathscr {Y})$ induces an equivalence on the fibers over each point
$\operatorname {Map}(\mathscr {X}[F],\mathscr {Y}) \to \operatorname {Map}(\widehat {\mathscr {X}[F]},\mathscr {Y})$ induces an equivalence on the fibers over each point ![]() $\{f\} \in \operatorname {Map}(\mathscr {X},\mathscr {Y}) \simeq \operatorname {Map}(\widehat {\mathscr {X}},\mathscr {Y})$. Given a map
$\{f\} \in \operatorname {Map}(\mathscr {X},\mathscr {Y}) \simeq \operatorname {Map}(\widehat {\mathscr {X}},\mathscr {Y})$. Given a map ![]() $f:\mathscr {X} \to \mathscr {Y}$, Lemma 5.1.11 identifies the map of fibers over
$f:\mathscr {X} \to \mathscr {Y}$, Lemma 5.1.11 identifies the map of fibers over ![]() $\{f\}$ with the restriction map
$\{f\}$ with the restriction map
where ![]() $\widehat {f}$ denotes the composition of
$\widehat {f}$ denotes the composition of ![]() $f$ with the inclusion
$f$ with the inclusion ![]() $\widehat {\mathscr {X}} \to \mathscr {X}$. This restriction map is an equivalence because
$\widehat {\mathscr {X}} \to \mathscr {X}$. This restriction map is an equivalence because ![]() $\mathscr {X} \in \mathcal {C}'$.
$\mathscr {X} \in \mathcal {C}'$.
Now let ![]() $\mathscr {X} \in \mathcal {C}$ be a
$\mathscr {X} \in \mathcal {C}$ be a ![]() $k$-truncated derived stack, and let
$k$-truncated derived stack, and let ![]() $\mathscr {X}' = \tau _{\leqslant k-1}(\mathcal {X})$ be the (
$\mathscr {X}' = \tau _{\leqslant k-1}(\mathcal {X})$ be the (![]() $k-1$)-truncation of
$k-1$)-truncation of ![]() $\mathscr {X}$. Recall that in the affine case, if
$\mathscr {X}$. Recall that in the affine case, if ![]() $A \in \mathrm {SCR}$ is
$A \in \mathrm {SCR}$ is ![]() $k$-truncated,
$k$-truncated, ![]() $A' = \tau _{\leqslant k-1}(A)$, and
$A' = \tau _{\leqslant k-1}(A)$, and ![]() $M = \pi _k(A)[k+1]$, then we have a canonical identification
$M = \pi _k(A)[k+1]$, then we have a canonical identification
where ![]() $\eta : A' \to A' \oplus M$ is induced by the fiber sequence of
$\eta : A' \to A' \oplus M$ is induced by the fiber sequence of ![]() $A$-modules
$A$-modules ![]() $\pi _k(A)[k] \to A \to A'$. The formation of this fiber square commutes with smooth extensions of
$\pi _k(A)[k] \to A \to A'$. The formation of this fiber square commutes with smooth extensions of ![]() $A$, so applying it to a smooth hypercover of
$A$, so applying it to a smooth hypercover of ![]() $\mathscr {X}$ by affine derived schemes gives a canonical commutative diagram of derived stacks realizing
$\mathscr {X}$ by affine derived schemes gives a canonical commutative diagram of derived stacks realizing ![]() $\mathscr {X}$ as a square-zero extension of
$\mathscr {X}$ as a square-zero extension of ![]() $\mathscr {X}'$:
$\mathscr {X}'$:

We claim that this diagram, as well as its formal completion, is a pushout square in the ![]() $\infty$-category of stacks which are hypersheaves for the smooth topology and are infinitesimally cohesive. Indeed, by hyperdescent it suffices to prove this claim after base change along a smooth map
$\infty$-category of stacks which are hypersheaves for the smooth topology and are infinitesimally cohesive. Indeed, by hyperdescent it suffices to prove this claim after base change along a smooth map ![]() $\operatorname {Spec}(A) \to \mathscr {X}$ (or
$\operatorname {Spec}(A) \to \mathscr {X}$ (or ![]() $\operatorname {Spec}(A) \to \widehat {\mathscr {X}}$), at which point this follows immediately from the definition of infinitesimally cohesive. Therefore, if
$\operatorname {Spec}(A) \to \widehat {\mathscr {X}}$), at which point this follows immediately from the definition of infinitesimally cohesive. Therefore, if ![]() $\mathscr {X}' \in \mathcal {C}'$, we have already shown
$\mathscr {X}' \in \mathcal {C}'$, we have already shown ![]() $\mathscr {X}'[\pi _k(\mathcal {O}_\mathscr {X})[k+1]] \in \mathcal {C}'$, and hence
$\mathscr {X}'[\pi _k(\mathcal {O}_\mathscr {X})[k+1]] \in \mathcal {C}'$, and hence ![]() $\mathscr {X} \in \mathcal {C}'$ by the above pushout square.
$\mathscr {X} \in \mathcal {C}'$ by the above pushout square.
By induction we now see that any ![]() $k$-truncated
$k$-truncated ![]() $\mathscr {X} \in \mathcal {C}$ also lies in
$\mathscr {X} \in \mathcal {C}$ also lies in ![]() $\mathcal {C}'$. Finally, an arbitrary
$\mathcal {C}'$. Finally, an arbitrary ![]() $\mathscr {X} \in \mathcal {C}$ is the colimit of the truncations
$\mathscr {X} \in \mathcal {C}$ is the colimit of the truncations ![]() $\mathscr {X}^{\circ } \to \tau _{\leqslant 1}(\mathscr {X}) \to \tau _{\leqslant 2}(\mathscr {X}) \to \cdots$ in the category of hypersheaves for the smooth topology which are nilcomplete, and the same is true for the formal completions. It follows that any
$\mathscr {X}^{\circ } \to \tau _{\leqslant 1}(\mathscr {X}) \to \tau _{\leqslant 2}(\mathscr {X}) \to \cdots$ in the category of hypersheaves for the smooth topology which are nilcomplete, and the same is true for the formal completions. It follows that any ![]() $\mathscr {X} \in \mathcal {C}$ lies in
$\mathscr {X} \in \mathcal {C}$ lies in ![]() $\mathcal {C}'$.
$\mathcal {C}'$.
5.1.4 Analysis of the Weil restriction
Proposition 5.1.14 Let ![]() $\pi : \mathscr {X} \to \mathscr {S}$ be a flat morphism of algebraic derived stacks satisfying property (L), with
$\pi : \mathscr {X} \to \mathscr {S}$ be a flat morphism of algebraic derived stacks satisfying property (L), with ![]() $\mathscr {S}$ noetherian, and let
$\mathscr {S}$ noetherian, and let ![]() $\mathscr {F} \to \mathscr {X}$ be a quasi-affine (respectively, affine) morphism. Then the Weil restriction
$\mathscr {F} \to \mathscr {X}$ be a quasi-affine (respectively, affine) morphism. Then the Weil restriction
is a quasi-affine (respectively, affine) stack over ![]() $\mathscr {S}$.
$\mathscr {S}$.
Before establishing this, let us note the following proposition.
Proposition 5.1.15 Let ![]() $\pi : \mathscr {X} \to \mathscr {S}$ be a flat morphism satisfying property (L) between qc.qs. algebraic derived stacks. Then the pullback functor
$\pi : \mathscr {X} \to \mathscr {S}$ be a flat morphism satisfying property (L) between qc.qs. algebraic derived stacks. Then the pullback functor ![]() $\pi ^{\ast } : \mathrm {CAlg}(\operatorname {QC}(\mathscr {S})^{\heartsuit }) \to \mathrm {CAlg}(\operatorname {QC}(\mathscr {X})^{\heartsuit })$ admits a left adjoint
$\pi ^{\ast } : \mathrm {CAlg}(\operatorname {QC}(\mathscr {S})^{\heartsuit }) \to \mathrm {CAlg}(\operatorname {QC}(\mathscr {X})^{\heartsuit })$ admits a left adjoint ![]() $\pi _{\dagger}$.
$\pi _{\dagger}$.
Proof. The proof of [Reference LurieLur4, Proposition 3.3.2] can be modified to this context: any quasi-coherent sheaf of algebras ![]() $\mathcal {A} \in \mathrm {CAlg}(\operatorname {QC}(\mathscr {X})^{\heartsuit })$ is a colimit (in fact a coequalizer) of free algebras
$\mathcal {A} \in \mathrm {CAlg}(\operatorname {QC}(\mathscr {X})^{\heartsuit })$ is a colimit (in fact a coequalizer) of free algebras ![]() $\!\!\mathop {\rm ~Sym}\nolimits _\mathscr {X}(E)$ for some
$\!\!\mathop {\rm ~Sym}\nolimits _\mathscr {X}(E)$ for some ![]() $E \in \operatorname {QC}(\mathscr {X})^{\heartsuit }$, so it suffices to show that
$E \in \operatorname {QC}(\mathscr {X})^{\heartsuit }$, so it suffices to show that ![]() $\pi _{\dagger} (\!\!\mathop {\rm ~Sym}\nolimits _\mathscr {X}(E)$ exists. Note that
$\pi _{\dagger} (\!\!\mathop {\rm ~Sym}\nolimits _\mathscr {X}(E)$ exists. Note that ![]() $\pi ^{\ast }$ admits a left adjoint
$\pi ^{\ast }$ admits a left adjoint ![]() $\pi _+ : \operatorname {QC}(\mathscr {X}) \to \operatorname {QC}(\mathscr {S})$ which preserves connective complexes because
$\pi _+ : \operatorname {QC}(\mathscr {X}) \to \operatorname {QC}(\mathscr {S})$ which preserves connective complexes because ![]() $\pi$ is flat; this follows from the case where
$\pi$ is flat; this follows from the case where ![]() $\mathscr {S}$ is affine using Lemma 5.1.8 as in the first paragraph of the proof of Proposition 5.1.6. Then the pullback functor
$\mathscr {S}$ is affine using Lemma 5.1.8 as in the first paragraph of the proof of Proposition 5.1.6. Then the pullback functor ![]() $\pi ^{\ast } : \operatorname {QC}(\mathscr {S})^{\heartsuit } \to \operatorname {QC}(\mathscr {X})^{\heartsuit }$ admits a left adjoint
$\pi ^{\ast } : \operatorname {QC}(\mathscr {S})^{\heartsuit } \to \operatorname {QC}(\mathscr {X})^{\heartsuit }$ admits a left adjoint ![]() $H_0(\pi _+(-))$, and one can check that
$H_0(\pi _+(-))$, and one can check that ![]() $\pi _{\dagger} (\!\!\mathop {\rm ~Sym}\nolimits _\mathscr {X}(E)) \simeq \!\!\mathop {\rm ~Sym}\nolimits _\mathscr {S}(H_0(\pi _+(E)))$ using the universal property of a free algebra.
$\pi _{\dagger} (\!\!\mathop {\rm ~Sym}\nolimits _\mathscr {X}(E)) \simeq \!\!\mathop {\rm ~Sym}\nolimits _\mathscr {S}(H_0(\pi _+(E)))$ using the universal property of a free algebra.
Proof of Proposition 5.1.14 The claim is local for the smooth topology, so we may assume that ![]() $\mathscr {S} = \operatorname {Spec}(A)$ is affine. As we will see in the proof of Theorem 5.1.1 below, the functor
$\mathscr {S} = \operatorname {Spec}(A)$ is affine. As we will see in the proof of Theorem 5.1.1 below, the functor ![]() $\pi _\ast (\mathscr {F}/\mathscr {X})$ is infinitesimally cohesive, nilcomplete, and admits a cotangent complex, so by [Reference Toën and VezzosiTV08, Theorem C.0.9] it suffices to check algebraicity of its restriction to the full subcategory
$\pi _\ast (\mathscr {F}/\mathscr {X})$ is infinitesimally cohesive, nilcomplete, and admits a cotangent complex, so by [Reference Toën and VezzosiTV08, Theorem C.0.9] it suffices to check algebraicity of its restriction to the full subcategory ![]() $\mathrm {Ring}_{\pi _0(A)} \subset \mathrm {SCR}_A$ of discrete objects, and restricting to
$\mathrm {Ring}_{\pi _0(A)} \subset \mathrm {SCR}_A$ of discrete objects, and restricting to ![]() $\mathrm {Ring}_{\pi _0(A)}$ also suffices to check that it is affine or quasi-affine. For any
$\mathrm {Ring}_{\pi _0(A)}$ also suffices to check that it is affine or quasi-affine. For any ![]() $R \in \mathrm {SCR}_A$, we have
$R \in \mathrm {SCR}_A$, we have
Because ![]() $\pi$ is flat,
$\pi$ is flat, ![]() $\mathscr {X} \times _S \operatorname {Spec}(R)$ is classical for any discrete
$\mathscr {X} \times _S \operatorname {Spec}(R)$ is classical for any discrete ![]() $R$, so the canonical map of functors
$R$, so the canonical map of functors ![]() $\pi _\ast (\mathscr {F}^{\rm cl}/\mathcal {X}) \to \pi _\ast (\mathcal {F}/\mathcal {X})$ is an isomorphism after restricting to
$\pi _\ast (\mathscr {F}^{\rm cl}/\mathcal {X}) \to \pi _\ast (\mathcal {F}/\mathcal {X})$ is an isomorphism after restricting to ![]() $\mathrm {Ring}_{\pi _0(A)}$.
$\mathrm {Ring}_{\pi _0(A)}$.
So we have reduced to the analogous claim when ![]() $\mathscr {X},S,$ and
$\mathscr {X},S,$ and ![]() $\mathscr {F}$ are classical stacks, and we work in the category of classical stacks for the remainder of the proof. If
$\mathscr {F}$ are classical stacks, and we work in the category of classical stacks for the remainder of the proof. If ![]() $\mathscr {F} \simeq \operatorname {Spec}_\mathscr {X}(\mathcal {A})$ for some quasi-coherent sheaf of algebras over
$\mathscr {F} \simeq \operatorname {Spec}_\mathscr {X}(\mathcal {A})$ for some quasi-coherent sheaf of algebras over ![]() $\mathscr {X}$, then one can check directly from the functor of points that
$\mathscr {X}$, then one can check directly from the functor of points that ![]() $\pi _\ast (\mathscr {F}/\mathscr {X}) \simeq \operatorname {Spec}_S(\pi _{\dagger} (\mathcal {A}))$, where
$\pi _\ast (\mathscr {F}/\mathscr {X}) \simeq \operatorname {Spec}_S(\pi _{\dagger} (\mathcal {A}))$, where ![]() $\pi _{\dagger} : \mathrm {CAlg}(\operatorname {QC}(\mathscr {X})^{\heartsuit }) \to \mathrm {CAlg}(\operatorname {QC}(\mathscr {S})^{\heartsuit })$ is the left adjoint to
$\pi _{\dagger} : \mathrm {CAlg}(\operatorname {QC}(\mathscr {X})^{\heartsuit }) \to \mathrm {CAlg}(\operatorname {QC}(\mathscr {S})^{\heartsuit })$ is the left adjoint to ![]() $\pi ^{\ast }$ provided by Proposition 5.1.15.
$\pi ^{\ast }$ provided by Proposition 5.1.15.
If ![]() $\mathscr {F}$ is quasi-affine, we have an open immersion
$\mathscr {F}$ is quasi-affine, we have an open immersion ![]() $\mathscr {F} \subset \mathscr {Y} = \operatorname {Spec}_\mathscr {X}(\mathcal {A})$, and the resulting map
$\mathscr {F} \subset \mathscr {Y} = \operatorname {Spec}_\mathscr {X}(\mathcal {A})$, and the resulting map ![]() $\pi _\ast (\mathscr {F}/\mathscr {X}) \to \pi _\ast (\mathscr {Y}/\mathscr {X})$ is a monomorphism. Given a map
$\pi _\ast (\mathscr {F}/\mathscr {X}) \to \pi _\ast (\mathscr {Y}/\mathscr {X})$ is a monomorphism. Given a map ![]() $\operatorname {Spec}(R) \to \pi _\ast (\mathscr {Y}/\mathscr {X})$, classifying a map
$\operatorname {Spec}(R) \to \pi _\ast (\mathscr {Y}/\mathscr {X})$, classifying a map ![]() $f : \mathscr {X}_R \to \mathscr {Y}$ over
$f : \mathscr {X}_R \to \mathscr {Y}$ over ![]() $\mathscr {X}$, a composition
$\mathscr {X}$, a composition ![]() $\operatorname {Spec}(R') \to \operatorname {Spec}(R) \to \pi _\ast (\mathscr {Y}/\mathscr {X})$ lifts (uniquely) to
$\operatorname {Spec}(R') \to \operatorname {Spec}(R) \to \pi _\ast (\mathscr {Y}/\mathscr {X})$ lifts (uniquely) to ![]() $\pi _\ast (\mathscr {F}/\mathscr {X})$ if and only if the canonical map
$\pi _\ast (\mathscr {F}/\mathscr {X})$ if and only if the canonical map ![]() $\mathscr {X}_{R'} \to \mathscr {X}_{R}$ factors through the open substack
$\mathscr {X}_{R'} \to \mathscr {X}_{R}$ factors through the open substack ![]() $f^{-1}(\mathscr {F}) \subset \mathscr {X}_R$. Thus,
$f^{-1}(\mathscr {F}) \subset \mathscr {X}_R$. Thus, ![]() $\operatorname {Spec}(R) \times _{\pi _\ast (\mathscr {Y}/\mathscr {X})} \pi _\ast (\mathscr {F}/\mathscr {X})$ is the subfunctor classified by the complement of the image of
$\operatorname {Spec}(R) \times _{\pi _\ast (\mathscr {Y}/\mathscr {X})} \pi _\ast (\mathscr {F}/\mathscr {X})$ is the subfunctor classified by the complement of the image of ![]() $\mathscr {X}_R \setminus f^{-1}(\mathscr {F})$ under
$\mathscr {X}_R \setminus f^{-1}(\mathscr {F})$ under ![]() $\mathscr {X}_R \to \operatorname {Spec}(R)$, which is an open subscheme by Proposition 2.4.5.
$\mathscr {X}_R \to \operatorname {Spec}(R)$, which is an open subscheme by Proposition 2.4.5.
5.1.5 Proof of Theorem 5.1.1
By Theorem 5.1.5 it suffices to check that ![]() $\mathscr {M} := \underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X}, \mathscr {Y})$ in the slice category
$\mathscr {M} := \underline {\operatorname {Map}}_\mathscr {S}(\mathscr {X}, \mathscr {Y})$ in the slice category ![]() $\operatorname {Fun}(\mathrm {SCR},\widehat {\mathcal {S}})/\mathscr {S}$ is a derived stack which satisfies the Artin–Lurie criteria. The proof of the second claim in [Reference LurieLur4, Proposition 3.3.5] applies verbatim in the context of simplicial commutative algebras to show that
$\operatorname {Fun}(\mathrm {SCR},\widehat {\mathcal {S}})/\mathscr {S}$ is a derived stack which satisfies the Artin–Lurie criteria. The proof of the second claim in [Reference LurieLur4, Proposition 3.3.5] applies verbatim in the context of simplicial commutative algebras to show that ![]() $\mathscr {M}$ is a sheaf for the smooth topology. So to verify that
$\mathscr {M}$ is a sheaf for the smooth topology. So to verify that ![]() $\mathscr {M} \to \mathscr {S}$ is representable by derived algebraic stacks, we may restrict to the situation where
$\mathscr {M} \to \mathscr {S}$ is representable by derived algebraic stacks, we may restrict to the situation where ![]() $\mathscr {S} = S = \operatorname {Spec}(A)$ for a derived
$\mathscr {S} = S = \operatorname {Spec}(A)$ for a derived ![]() $G$-ring
$G$-ring ![]() $A$ which admits a dualizing complex.
$A$ which admits a dualizing complex.
Realize ![]() $\mathscr {X}$ as a colimit of a simplicial diagram
$\mathscr {X}$ as a colimit of a simplicial diagram ![]() $X_\bullet$, where each
$X_\bullet$, where each ![]() $X_i = \operatorname {Spec}(R_i)$ is an affine derived scheme which is smooth over
$X_i = \operatorname {Spec}(R_i)$ is an affine derived scheme which is smooth over ![]() $\mathscr {X}$. Because
$\mathscr {X}$. Because ![]() $\mathscr {Y}$ satisfies smooth descent,
$\mathscr {Y}$ satisfies smooth descent, ![]() $\underline {\operatorname {Map}}_S(\mathscr {X},\mathscr {Y}) = \operatorname {Tot} \{\underline {\operatorname {Map}}_S(X_\bullet,\mathscr {Y}) \}$ in the
$\underline {\operatorname {Map}}_S(\mathscr {X},\mathscr {Y}) = \operatorname {Tot} \{\underline {\operatorname {Map}}_S(X_\bullet,\mathscr {Y}) \}$ in the ![]() $\infty$-category
$\infty$-category ![]() $\operatorname {Fun}(\mathrm {SCR}_A, \mathcal {S})$. The subcategory of infinitesimally cohesive and nilcomplete functors is closed under small limits [Reference LurieLur4, Remark 2.1.11], so it suffices to prove the claim for
$\operatorname {Fun}(\mathrm {SCR}_A, \mathcal {S})$. The subcategory of infinitesimally cohesive and nilcomplete functors is closed under small limits [Reference LurieLur4, Remark 2.1.11], so it suffices to prove the claim for ![]() $X_i$ which is [Reference LurieLur4, Proposition 3.3.6(2,3)], whose proof applies verbatim for stacks over
$X_i$ which is [Reference LurieLur4, Proposition 3.3.6(2,3)], whose proof applies verbatim for stacks over ![]() $\mathrm {SCR}$.
$\mathrm {SCR}$.
For a cosimplicial space ![]() $X^{\bullet }$ which is levelwise
$X^{\bullet }$ which is levelwise ![]() $k$-truncated, the map
$k$-truncated, the map ![]() $\operatorname {Tot} \{X^{\bullet }\} \to \operatorname {Tot}_{k+1} \{X^{\bullet }\}$ is
$\operatorname {Tot} \{X^{\bullet }\} \to \operatorname {Tot}_{k+1} \{X^{\bullet }\}$ is ![]() $(-1)$-truncated, which implies that
$(-1)$-truncated, which implies that ![]() $\operatorname {Tot} \{ - \}$ commutes with filtered colimits of cosimplicial spaces which are levelwise
$\operatorname {Tot} \{ - \}$ commutes with filtered colimits of cosimplicial spaces which are levelwise ![]() $k$-truncated for some fixed
$k$-truncated for some fixed ![]() $k$. For any
$k$. For any ![]() $A' \in \mathrm {SCR}_A$, we have
$A' \in \mathrm {SCR}_A$, we have
If ![]() $A'$ is
$A'$ is ![]() $k$-truncated, then
$k$-truncated, then ![]() $A' \otimes _A R_i$ is levelwise (
$A' \otimes _A R_i$ is levelwise (![]() $k+d$)-truncated, where
$k+d$)-truncated, where ![]() $d$ is the Tor amplitude of the maps
$d$ is the Tor amplitude of the maps ![]() $A \to R_i$, and
$A \to R_i$, and ![]() $\mathscr {Y}(A' \otimes _A R_i)$ is (
$\mathscr {Y}(A' \otimes _A R_i)$ is (![]() $n+d+k$)-truncated by [Reference LurieLur04, Corollary 5.3.8]. It follows that if
$n+d+k$)-truncated by [Reference LurieLur04, Corollary 5.3.8]. It follows that if ![]() $\mathscr {Y}(-)$ commutes with filtered colimits of
$\mathscr {Y}(-)$ commutes with filtered colimits of ![]() $k$-truncated objects for any
$k$-truncated objects for any ![]() $k$, then so does
$k$, then so does ![]() $\mathscr {M}(A')$. These observations also show that
$\mathscr {M}(A')$. These observations also show that ![]() $\mathscr {M}(A')$ is (
$\mathscr {M}(A')$ is (![]() $n+d$)-truncated when
$n+d$)-truncated when ![]() $A'$ is discrete.
$A'$ is discrete.
We have verified the Artin–Lurie criteria (i), (ii), (iii)(b), so it remains to show (iii)(a) and (iv), but we have verified these above: Propositions 5.1.10 and 5.1.6 imply that ![]() $\mathscr {M}$ admits a
$\mathscr {M}$ admits a ![]() $(-1-n)$-connective almost perfect cotangent complex. For integrability, consider a discrete complete local noetherian ring
$(-1-n)$-connective almost perfect cotangent complex. For integrability, consider a discrete complete local noetherian ring ![]() $R$ over
$R$ over ![]() $A$, and let
$A$, and let ![]() $\widehat {\mathscr {X}}_R$ be the formal completion of
$\widehat {\mathscr {X}}_R$ be the formal completion of ![]() $\mathscr {X}_R$ along the closed subset defined by the maximal ideal of
$\mathscr {X}_R$ along the closed subset defined by the maximal ideal of ![]() $R$. Proposition 5.1.13 applied to the formal completion of
$R$. Proposition 5.1.13 applied to the formal completion of ![]() $\mathscr {X} \times _S \operatorname {Spec}(R)$ along the closed substack defined by the maximal ideal
$\mathscr {X} \times _S \operatorname {Spec}(R)$ along the closed substack defined by the maximal ideal ![]() $\mathfrak {m} \subset R$ implies the integrability of
$\mathfrak {m} \subset R$ implies the integrability of ![]() $\mathscr {M}$.
$\mathscr {M}$.
5.2 Algebraicity of the stack of coherent sheaves
Pridham [Reference PridhamPri12a] uses a modified version of the Artin–Lurie criteria above [Reference PridhamPri12b] to give a simplified algebraicity criterion for substacks of the stack of quasi-coherent complexes on a derived algebraic stack. We apply this criterion below.
Given an ![]() $\infty$-category
$\infty$-category ![]() $\mathcal {C}$, we let
$\mathcal {C}$, we let ![]() $\mathcal {C}^{\cong }$ denote the largest
$\mathcal {C}^{\cong }$ denote the largest ![]() $\infty$-subcategory whose homomorphisms are invertible, that is, the largest Kan subcomplex of the quasi-category
$\infty$-subcategory whose homomorphisms are invertible, that is, the largest Kan subcomplex of the quasi-category ![]() $\mathcal {C}$. This is referred to as the ‘core’ and denoted by
$\mathcal {C}$. This is referred to as the ‘core’ and denoted by ![]() $\mathcal {W}(-)$ in [Reference PridhamPri12a].
$\mathcal {W}(-)$ in [Reference PridhamPri12a].
Definition 5.2.1 For a flat and almost finitely presented morphism of algebraic derived stacks ![]() $\mathscr {X} \to \operatorname {Spec}(R)$, let
$\mathscr {X} \to \operatorname {Spec}(R)$, let ![]() $\underline {{\rm Coh} }_{\mathscr {X}/R} \colon \mathrm {SCR}_R \to \mathcal {S}$ be the functor which maps
$\underline {{\rm Coh} }_{\mathscr {X}/R} \colon \mathrm {SCR}_R \to \mathcal {S}$ be the functor which maps ![]() $A \in \mathrm {SCR}_R$ to the full
$A \in \mathrm {SCR}_R$ to the full ![]() $\infty$-subgroupoid of
$\infty$-subgroupoid of ![]() $(\operatorname {APerf}(\mathscr {X}_A)^{\mathrm {cn}})^{\cong }$ whose objects are flat over
$(\operatorname {APerf}(\mathscr {X}_A)^{\mathrm {cn}})^{\cong }$ whose objects are flat over ![]() $A$.
$A$.
Theorem 5.2.2 Let ![]() $R$ be a derived
$R$ be a derived ![]() $G$-ring which admits a dualizing complex, and let
$G$-ring which admits a dualizing complex, and let ![]() $\pi \colon \mathscr {X} \to \operatorname {Spec}(R)$ be a flat and formally proper morphism of derived algebraic stacks. Then
$\pi \colon \mathscr {X} \to \operatorname {Spec}(R)$ be a flat and formally proper morphism of derived algebraic stacks. Then ![]() $\underline {{\rm Coh} }_{\mathscr {X}/R}$ is a derived algebraic stack with affine diagonal.
$\underline {{\rm Coh} }_{\mathscr {X}/R}$ is a derived algebraic stack with affine diagonal.
We first note the following lemma, which identifies ![]() $\underline {{\rm Coh} }_{\mathscr {X}/R}(A)$ with the full
$\underline {{\rm Coh} }_{\mathscr {X}/R}(A)$ with the full ![]() $\infty$-subgroupoid of
$\infty$-subgroupoid of ![]() $(\operatorname {QC}(\mathscr {X}_A)^{\mathrm {cn}})^{\cong }$ consisting of complexes whose restriction to
$(\operatorname {QC}(\mathscr {X}_A)^{\mathrm {cn}})^{\cong }$ consisting of complexes whose restriction to ![]() $\mathscr {X}_{\pi _0(A)}$ is flat and finitely presented (in the classical sense).
$\mathscr {X}_{\pi _0(A)}$ is flat and finitely presented (in the classical sense).
Lemma 5.2.3 Let ![]() $\pi \colon \mathscr {X} \to \operatorname {Spec}(A)$ be a flat morphism of algebraic spectral stacks which is finitely presented on underlying classical stacks, and let
$\pi \colon \mathscr {X} \to \operatorname {Spec}(A)$ be a flat morphism of algebraic spectral stacks which is finitely presented on underlying classical stacks, and let ![]() $\pi _0(A) \to A'$ be a surjection of (discrete) rings with nilpotent kernel. Then
$\pi _0(A) \to A'$ be a surjection of (discrete) rings with nilpotent kernel. Then ![]() $E \in \operatorname {QC}(\mathscr {X})^{\mathrm {cn}}$ is flat over
$E \in \operatorname {QC}(\mathscr {X})^{\mathrm {cn}}$ is flat over ![]() $A$ and almost perfect if and only if
$A$ and almost perfect if and only if ![]() $E \otimes _{A} A' \in \operatorname {QC}(\mathscr {X}\times _{\operatorname {Spec}(A)} \operatorname {Spec}(A'))^{\mathrm {cn}}$ is flat over
$E \otimes _{A} A' \in \operatorname {QC}(\mathscr {X}\times _{\operatorname {Spec}(A)} \operatorname {Spec}(A'))^{\mathrm {cn}}$ is flat over ![]() $A'$ (hence discrete) and classically finitely presented.
$A'$ (hence discrete) and classically finitely presented.
Proof. The claim is local, so we may assume ![]() $\mathscr {X} = \operatorname {Spec}(B)$ for some
$\mathscr {X} = \operatorname {Spec}(B)$ for some ![]() $E_\infty$-algebra
$E_\infty$-algebra ![]() $B$ over
$B$ over ![]() $A$, and let
$A$, and let ![]() $B' := B \otimes _A A'$. By [Reference LurieLur17, Theorem 7.2.2.15],
$B' := B \otimes _A A'$. By [Reference LurieLur17, Theorem 7.2.2.15], ![]() $E$ is flat as an
$E$ is flat as an ![]() $A$-module if and only if
$A$-module if and only if ![]() $E \otimes _A N$ is discrete whenever
$E \otimes _A N$ is discrete whenever ![]() $N \in (A {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$. The hypotheses imply
$N \in (A {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$. The hypotheses imply ![]() $(A {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$ is generated under extensions by objects of the form
$(A {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$ is generated under extensions by objects of the form ![]() $i_\ast (M)$ where
$i_\ast (M)$ where ![]() $i : \operatorname {Spec}(A') \to \operatorname {Spec}(A)$, and the projection formula implies
$i : \operatorname {Spec}(A') \to \operatorname {Spec}(A)$, and the projection formula implies ![]() $M \otimes _A i_\ast (-) \simeq i_\ast (i^{\ast }(M) \otimes _{A'} (-))$, so
$M \otimes _A i_\ast (-) \simeq i_\ast (i^{\ast }(M) \otimes _{A'} (-))$, so ![]() $M$ is flat if and only if
$M$ is flat if and only if ![]() $i^{\ast }(M) = M \otimes _B B'$ is flat.
$i^{\ast }(M) = M \otimes _B B'$ is flat.
Now assume ![]() $E \in B {\rm {}\hbox{-}{\rm mod}}$ is flat over
$E \in B {\rm {}\hbox{-}{\rm mod}}$ is flat over ![]() $A$, the map of (discrete) rings
$A$, the map of (discrete) rings ![]() $A' \to B'$ is finitely presented, and
$A' \to B'$ is finitely presented, and ![]() $E \otimes _B B'$ is a flat and finitely presented discrete
$E \otimes _B B'$ is a flat and finitely presented discrete ![]() $B'$-module. By classical noetherian approximation [Sta19, Tag 02JO], both
$B'$-module. By classical noetherian approximation [Sta19, Tag 02JO], both ![]() $B'$ and
$B'$ and ![]() $E \otimes _B B'$ arise via base change from the same data over a finitely generated subring
$E \otimes _B B'$ arise via base change from the same data over a finitely generated subring ![]() $A'' \subset A'$, so
$A'' \subset A'$, so ![]() $E \otimes _B B'$ is almost perfect.
$E \otimes _B B'$ is almost perfect.
We have already shown in the proof of Proposition 3.1.5 that the functor ![]() $\operatorname {APerf}(-)$ is nilcomplete (without noetherian hypotheses), so it suffices to assume that
$\operatorname {APerf}(-)$ is nilcomplete (without noetherian hypotheses), so it suffices to assume that ![]() $\pi _i(A)=0$ and hence
$\pi _i(A)=0$ and hence ![]() $\pi _i(B)=0$ for
$\pi _i(B)=0$ for ![]() $i\gg 0$. Then
$i\gg 0$. Then ![]() $B$ can be obtained from
$B$ can be obtained from ![]() $B'$ from a finite sequence of square-zero extensions, so it suffices to assume
$B'$ from a finite sequence of square-zero extensions, so it suffices to assume ![]() $B \to B'$ is a square-zero extension. In this case
$B \to B'$ is a square-zero extension. In this case ![]() $\operatorname {Spec}(B)$ is obtained as a pushout along two maps
$\operatorname {Spec}(B)$ is obtained as a pushout along two maps ![]() $\operatorname {Spec}(B' \oplus M) \to \operatorname {Spec}(B')$ (see [Reference LurieLur17, Remark 7.4.1.7]). It follows from [Reference LurieLur1, Proposition 7.7] that
$\operatorname {Spec}(B' \oplus M) \to \operatorname {Spec}(B')$ (see [Reference LurieLur17, Remark 7.4.1.7]). It follows from [Reference LurieLur1, Proposition 7.7] that ![]() $E$ is almost perfect if and only if
$E$ is almost perfect if and only if ![]() $E \otimes _B B'$ is almost perfect, which completes the proof.
$E \otimes _B B'$ is almost perfect, which completes the proof.
Proof of Theorem 5.2.2 Consider the functor ![]() $\mathscr {F} \colon \mathrm {SCR}_R \to \widehat {\mathcal {S}}$ which assigns
$\mathscr {F} \colon \mathrm {SCR}_R \to \widehat {\mathcal {S}}$ which assigns ![]() $A \mapsto \operatorname {QC}(\mathscr {X}_A)^{\cong }$, and the functor
$A \mapsto \operatorname {QC}(\mathscr {X}_A)^{\cong }$, and the functor ![]() $\mathcal {M} : \mathrm {Ring}_{\pi _0(R)} \to \!\!\mathop {\rm ~Cat}\nolimits _\infty$ which assigns
$\mathcal {M} : \mathrm {Ring}_{\pi _0(R)} \to \!\!\mathop {\rm ~Cat}\nolimits _\infty$ which assigns
We note that Lemma 5.2.3 implies that ![]() $\mathcal {M}$ is open in the functor
$\mathcal {M}$ is open in the functor ![]() $\mathscr {F}$ in the sense of [Reference PridhamPri12a, Definition 3.8]. Also by Lemma 5.2.3, the functor
$\mathscr {F}$ in the sense of [Reference PridhamPri12a, Definition 3.8]. Also by Lemma 5.2.3, the functor ![]() $\underline {{\rm Coh} }_{\mathscr {X}/R}$ defined above is the full subfunctor of
$\underline {{\rm Coh} }_{\mathscr {X}/R}$ defined above is the full subfunctor of ![]() $\mathscr {F}$ consisting of objects in
$\mathscr {F}$ consisting of objects in ![]() $\mathscr {F}(A)$ whose restriction to
$\mathscr {F}(A)$ whose restriction to ![]() $\mathscr {F}(\pi _0(A))$ is weakly equivalent in
$\mathscr {F}(\pi _0(A))$ is weakly equivalent in ![]() $\operatorname {QC}(\mathscr {X}_{\pi _0(A)})$ to an object of
$\operatorname {QC}(\mathscr {X}_{\pi _0(A)})$ to an object of ![]() $\mathcal {M}(\pi _0(A))$. [Reference PridhamPri12a, Theorem 4.12] gives criteria for the resulting functor to be an algebraic derived
$\mathcal {M}(\pi _0(A))$. [Reference PridhamPri12a, Theorem 4.12] gives criteria for the resulting functor to be an algebraic derived ![]() $1$-stack, which we now verify.
$1$-stack, which we now verify.
Condition (0) is the fact that one can check whether a complex in ![]() $\operatorname {QC}(\mathscr {X}_A)^{\mathrm {cn}}$ is flat and almost perfect étale locally over
$\operatorname {QC}(\mathscr {X}_A)^{\mathrm {cn}}$ is flat and almost perfect étale locally over ![]() $A$.
$A$.
Condition (1), that for any ![]() $A \in \mathrm {Ring}_{\pi _0(R)}$ and
$A \in \mathrm {Ring}_{\pi _0(R)}$ and ![]() $E \in \mathcal {M}(A)$ the functor
$E \in \mathcal {M}(A)$ the functor ![]() $H_i \operatorname {RHom}_{\mathscr {X}_A}(E,E\otimes _A (-))$ commutes with filtered colimits in
$H_i \operatorname {RHom}_{\mathscr {X}_A}(E,E\otimes _A (-))$ commutes with filtered colimits in ![]() $(A {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$, is immediate from the fact that
$(A {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$, is immediate from the fact that ![]() $E$ is
$E$ is ![]() $A$-flat and almost perfect.
$A$-flat and almost perfect.
Condition (2), that for all finitely generated ![]() $A \in \mathrm {Ring}_{\pi _0(R)}$ and all
$A \in \mathrm {Ring}_{\pi _0(R)}$ and all ![]() $E \in \mathcal {M}(A)$,
$E \in \mathcal {M}(A)$, ![]() $H_i \operatorname {RHom}_{\mathscr {X}_A}(E,E)$ are finitely generated
$H_i \operatorname {RHom}_{\mathscr {X}_A}(E,E)$ are finitely generated ![]() $A$-modules for all
$A$-modules for all ![]() $i$, follows from the fact that
$i$, follows from the fact that ![]() $\operatorname {RHom}_{\mathscr {X}_A}^{\otimes _{\operatorname {QC}(\mathscr {X}_A)}}(E,E) \in \operatorname {{\mathbb {D}}APerf}(\mathscr {X}_A)$ by Lemma 2.3.2 and from property (CP)A, which holds by Theorem 2.4.3.
$\operatorname {RHom}_{\mathscr {X}_A}^{\otimes _{\operatorname {QC}(\mathscr {X}_A)}}(E,E) \in \operatorname {{\mathbb {D}}APerf}(\mathscr {X}_A)$ by Lemma 2.3.2 and from property (CP)A, which holds by Theorem 2.4.3.
Condition (3) states that the functor of components of ![]() $\mathcal {M}$ preserves filtered colimits in
$\mathcal {M}$ preserves filtered colimits in ![]() $\mathrm {Ring}_{\pi _0(R)}$. This holds because by classical noetherian approximation if
$\mathrm {Ring}_{\pi _0(R)}$. This holds because by classical noetherian approximation if ![]() $A = \varinjlim _\alpha A_\alpha$ is a filtered colimit, then any flat and finitely presented object in
$A = \varinjlim _\alpha A_\alpha$ is a filtered colimit, then any flat and finitely presented object in ![]() $\operatorname {QC}(\mathscr {X}_A)^{\heartsuit }$ is the pullback of a finitely presented object in some
$\operatorname {QC}(\mathscr {X}_A)^{\heartsuit }$ is the pullback of a finitely presented object in some ![]() $\operatorname {QC}(\mathscr {X}_{A_\alpha })^{\heartsuit }$, and by [Sta19, Tag 02JO] one can increase
$\operatorname {QC}(\mathscr {X}_{A_\alpha })^{\heartsuit }$, and by [Sta19, Tag 02JO] one can increase ![]() $\alpha$ so that the object in
$\alpha$ so that the object in ![]() $\operatorname {QC}(\mathscr {X}_{A_\alpha })^{\heartsuit }$ is flat and finitely presented.
$\operatorname {QC}(\mathscr {X}_{A_\alpha })^{\heartsuit }$ is flat and finitely presented.
Finally, because ![]() $\mathcal {M}(A)$ is a
$\mathcal {M}(A)$ is a ![]() $1$-category for any
$1$-category for any ![]() $A \in \mathrm {Ring}_{\pi _0(R)}$, that is, flat and almost perfect objects in
$A \in \mathrm {Ring}_{\pi _0(R)}$, that is, flat and almost perfect objects in ![]() $\operatorname {QC}(\mathscr {X}_A)$ have no negative Exts, condition (4) amounts to the claim that for any complete local discrete noetherian
$\operatorname {QC}(\mathscr {X}_A)$ have no negative Exts, condition (4) amounts to the claim that for any complete local discrete noetherian ![]() $\pi _0(R)$-algebra
$\pi _0(R)$-algebra ![]() $A$ with maximal ideal
$A$ with maximal ideal ![]() $\mathfrak {m}$,
$\mathfrak {m}$, ![]() $\mathcal {M}(A)$ is the homotopy inverse limit of the categories
$\mathcal {M}(A)$ is the homotopy inverse limit of the categories ![]() $\mathcal {M}(A/\mathfrak {m}^{k})$. This follows from the definition of a formally proper morphism (Definition 1.1.3) and the fact that if
$\mathcal {M}(A/\mathfrak {m}^{k})$. This follows from the definition of a formally proper morphism (Definition 1.1.3) and the fact that if ![]() $E \in \operatorname {QC}(\mathscr {X}_A)^{\heartsuit }$ is such that
$E \in \operatorname {QC}(\mathscr {X}_A)^{\heartsuit }$ is such that ![]() $E \otimes _A (A/\mathfrak {m}^{k})$ is
$E \otimes _A (A/\mathfrak {m}^{k})$ is ![]() $(A/\mathfrak {m}^{k})$-flat for all
$(A/\mathfrak {m}^{k})$-flat for all ![]() $k\geqslant 1$, then
$k\geqslant 1$, then ![]() $E$ is flat over
$E$ is flat over ![]() $A$.
$A$.
This completes the proof that ![]() $\underline {{\rm Coh} }_{\mathscr {X}/R}$ is an algebraic derived
$\underline {{\rm Coh} }_{\mathscr {X}/R}$ is an algebraic derived ![]() $1$-stack locally almost of finite presentation over
$1$-stack locally almost of finite presentation over ![]() $R$. To show that
$R$. To show that ![]() $\underline {{\rm Coh}}_{\mathscr {X}/R}$ has affine diagonal, it suffices to show this for the underlying classical stack on
$\underline {{\rm Coh}}_{\mathscr {X}/R}$ has affine diagonal, it suffices to show this for the underlying classical stack on ![]() $\mathrm {Ring}_{\pi _0(R)}$. This stack agrees with the moduli functor
$\mathrm {Ring}_{\pi _0(R)}$. This stack agrees with the moduli functor ![]() $\mathcal {M}_\mathscr {A}$ of [Reference Alper, Halpern-Leistner and HeinlothAHH18, Definition 7.8] associated to the locally noetherian
$\mathcal {M}_\mathscr {A}$ of [Reference Alper, Halpern-Leistner and HeinlothAHH18, Definition 7.8] associated to the locally noetherian ![]() $\pi _0(R)$-linear abelian category
$\pi _0(R)$-linear abelian category ![]() $\mathscr {A} = \operatorname {QC}(\mathscr {X}_{\pi _0(R)})^{\heartsuit }$. By definition
$\mathscr {A} = \operatorname {QC}(\mathscr {X}_{\pi _0(R)})^{\heartsuit }$. By definition ![]() $\mathcal {M}_\mathscr {A}(A)$ is the groupoid of
$\mathcal {M}_\mathscr {A}(A)$ is the groupoid of ![]() $A$-flat and finitely presented
$A$-flat and finitely presented ![]() $A$-module objects in
$A$-module objects in ![]() $\mathscr {A}$. By [Reference Alper, Halpern-Leistner and HeinlothAHH18, Lemma 7.19], if
$\mathscr {A}$. By [Reference Alper, Halpern-Leistner and HeinlothAHH18, Lemma 7.19], if ![]() $\mathcal {M}_\mathscr {A}$ is algebraic and locally of finite presentation over
$\mathcal {M}_\mathscr {A}$ is algebraic and locally of finite presentation over ![]() $\pi _0(R)$, then it must have affine diagonal.
$\pi _0(R)$, then it must have affine diagonal.
Remark 5.2.4 Theorem 5.2.2 shows the algebraicity of ![]() $\underline {{\rm Coh} }_{\mathscr {X}/R}$ for certain algebraic stacks
$\underline {{\rm Coh} }_{\mathscr {X}/R}$ for certain algebraic stacks ![]() $\mathscr {X}$. The algebraicity of
$\mathscr {X}$. The algebraicity of ![]() $\underline {{\rm Coh} }_{\mathscr {X}/R}$ has also been shown for certain non-algebraic stacks
$\underline {{\rm Coh} }_{\mathscr {X}/R}$ has also been shown for certain non-algebraic stacks ![]() $\mathscr {X}$ in [Reference Porta and SalaPS21, Propositions 2.33,2.34], where
$\mathscr {X}$ in [Reference Porta and SalaPS21, Propositions 2.33,2.34], where ![]() $\mathscr {X}$ is either the de Rham or Dolbeault stack for a smooth and proper scheme over
$\mathscr {X}$ is either the de Rham or Dolbeault stack for a smooth and proper scheme over ![]() ${\mathbb {C}}$.
${\mathbb {C}}$.
Acknowledgements
We would like to thank Jacob Lurie for some helpful conversations in the early stages of this project. We would also like to thank Jarod Alper, Bhargav Bhatt, Brian Conrad, Jack Hall, Johan de Jong, Dmitry Kubrak, Jon Pridham, and David Rydh for helpful conversations and comments. Shortly after the first version of this paper was made public, Jack Hall, David Rydh, and Jarod Alper released a paper proving similar results on algebraicity of mapping stacks, and these results are strengthened in their followup work [Reference Alper, Hall and RydhAHR21]. Their work was developed independently and concurrently, and we have benefited from very helpful conversations with them as well as an early draft of [Reference Alper, Hall and RydhAHR21] while revising this paper. We would also like to thank the anonymous referee for helpful suggestions. A. Preygel was supported by an NSF Postdoctoral Fellowship, and D. Halpern-Leistner was supported by NSF postdoctoral fellowship DMS-1303960 and NSF grant DMS-1601976.
Appendix A. Quasi-coherent complexes on prestacks
Suppose that ![]() $R_\bullet$ is a simplicial commutative ring. The normalized chain complex
$R_\bullet$ is a simplicial commutative ring. The normalized chain complex ![]() $N(R_\bullet )$ obtains the structure of a differential graded algebra via the Eilenberg–Zilber product, and the category of
$N(R_\bullet )$ obtains the structure of a differential graded algebra via the Eilenberg–Zilber product, and the category of ![]() $R_\bullet$-modules,
$R_\bullet$-modules, ![]() $\mathcal {C} = R_\bullet {\rm {}\hbox{-}{\rm mod}}$, is the stable symmetric monoidal
$\mathcal {C} = R_\bullet {\rm {}\hbox{-}{\rm mod}}$, is the stable symmetric monoidal ![]() $\infty$-category of left
$\infty$-category of left ![]() $N(R_\bullet )$-modules in chain complexes (see [Reference Toën and VezzosiTV08, § 2.2.1]). Furthermore,
$N(R_\bullet )$-modules in chain complexes (see [Reference Toën and VezzosiTV08, § 2.2.1]). Furthermore,
(i)
 $\mathcal {C}_{\geqslant 0}$ is the unstable
$\mathcal {C}_{\geqslant 0}$ is the unstable  $\infty$-category of
$\infty$-category of  $N(R_\bullet )$-modules in homologically non-negative degrees – that is, the Dold–Kan correspondence provides an equivalence of
$N(R_\bullet )$-modules in homologically non-negative degrees – that is, the Dold–Kan correspondence provides an equivalence of  $\mathcal {C}_{\geqslant 0}$ with the
$\mathcal {C}_{\geqslant 0}$ with the  $\infty$-category of simplicial
$\infty$-category of simplicial  $R$-modules;
$R$-modules;(ii)
 $\mathcal {C}$ is equivalent to the
$\mathcal {C}$ is equivalent to the  $\infty$-category of modules over the
$\infty$-category of modules over the  $E_\infty$-algebra
$E_\infty$-algebra  $\!\!\mathop {\rm ~End}\nolimits _{\mathcal {C}}(R_\bullet )$ associated to
$\!\!\mathop {\rm ~End}\nolimits _{\mathcal {C}}(R_\bullet )$ associated to  $R_\bullet$;
$R_\bullet$;(iii) if
 $E,F \in R_\bullet {\rm {}\hbox{-}{\rm mod}}$, then, in our notation,
$E,F \in R_\bullet {\rm {}\hbox{-}{\rm mod}}$, then, in our notation,  $\operatorname {Map}_R(E,F)$ is the simplicial set of maps from a (cofibrant replacement of)
$\operatorname {Map}_R(E,F)$ is the simplicial set of maps from a (cofibrant replacement of)  $E$ to a (fibrant replacement) of
$E$ to a (fibrant replacement) of  $F$,
$F$,  $\operatorname {RHom}_R(E,F)$ is the
$\operatorname {RHom}_R(E,F)$ is the  $N(R_\bullet )$-module with
$N(R_\bullet )$-module with  $(\operatorname {RHom}_R(E,F))_i$ the degree
$(\operatorname {RHom}_R(E,F))_i$ the degree  $i$ morphisms from (a replacement of)
$i$ morphisms from (a replacement of)  $N(E)$ to (a replacement of)
$N(E)$ to (a replacement of)  $N(F)$, and
$N(F)$, and  $\operatorname {Hom}_R(E,F) = \operatorname {Ext}^{0}_R(E,F)$ denotes maps in the derived category of
$\operatorname {Hom}_R(E,F) = \operatorname {Ext}^{0}_R(E,F)$ denotes maps in the derived category of  $N(R_\bullet )$-modules.
$N(R_\bullet )$-modules.
For any functor ![]() $\mathcal {F} : \mathrm {SCR} \to \mathrm {CAlg}(\widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty )$, where the latter denotes the
$\mathcal {F} : \mathrm {SCR} \to \mathrm {CAlg}(\widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty )$, where the latter denotes the ![]() $\infty$-category of (not necessarily small) symmetric monoidal
$\infty$-category of (not necessarily small) symmetric monoidal ![]() $\infty$-categories, and any prestack
$\infty$-categories, and any prestack ![]() $\mathscr {X} \in \operatorname {Fun}(\mathrm {SCR},\widehat {\mathcal {S}})$, one can define
$\mathscr {X} \in \operatorname {Fun}(\mathrm {SCR},\widehat {\mathcal {S}})$, one can define ![]() $\mathcal {F}(\mathscr {X})$ as the right Kan extension of
$\mathcal {F}(\mathscr {X})$ as the right Kan extension of ![]() $\mathcal {F}$ along the Yoneda embedding
$\mathcal {F}$ along the Yoneda embedding ![]() $\mathrm {SCR} \hookrightarrow \operatorname {Fun}(\mathrm {SCR},\widehat {\mathcal {S}})^{\mathrm {op}}$ (see [Reference LurieLur2, § 2.7] for a detailed discussion). This means that
$\mathrm {SCR} \hookrightarrow \operatorname {Fun}(\mathrm {SCR},\widehat {\mathcal {S}})^{\mathrm {op}}$ (see [Reference LurieLur2, § 2.7] for a detailed discussion). This means that
that is, an object ![]() $E \in \mathcal {F}(\mathscr {X})$ is the coherent assignment to each pair of an
$E \in \mathcal {F}(\mathscr {X})$ is the coherent assignment to each pair of an ![]() $R \in \mathrm {SCR}$ and an
$R \in \mathrm {SCR}$ and an ![]() $R$-point
$R$-point ![]() $\eta \colon \operatorname {Spec}(R) \to \mathscr {X}$ of an object
$\eta \colon \operatorname {Spec}(R) \to \mathscr {X}$ of an object ![]() $E_\eta \in \mathcal {F}(R)$. Because the forgetful functor
$E_\eta \in \mathcal {F}(R)$. Because the forgetful functor ![]() $\mathrm {CAlg}(\widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty ) \to \widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty$ preserves limits, the
$\mathrm {CAlg}(\widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty ) \to \widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty$ preserves limits, the ![]() $\infty$-category underlying
$\infty$-category underlying ![]() $\mathcal {F}(\mathscr {X})$ is the limit of the
$\mathcal {F}(\mathscr {X})$ is the limit of the ![]() $\infty$-categories underlying
$\infty$-categories underlying ![]() $\mathcal {F}(R)$ above.
$\mathcal {F}(R)$ above.
Applying this to the functor ![]() $\mathcal {F} \colon R_\bullet \mapsto R_\bullet {\rm {}\hbox{-}{\rm mod}}$ defines the symmetric monoidal stable
$\mathcal {F} \colon R_\bullet \mapsto R_\bullet {\rm {}\hbox{-}{\rm mod}}$ defines the symmetric monoidal stable ![]() $\infty$-category
$\infty$-category ![]() $\operatorname {QC}(\mathscr {X})$ of quasi-coherent complexes on
$\operatorname {QC}(\mathscr {X})$ of quasi-coherent complexes on ![]() $\mathscr {X}$ [Reference LurieLur2, Definition 2.7.8], that is, a quasi-coherent complex
$\mathscr {X}$ [Reference LurieLur2, Definition 2.7.8], that is, a quasi-coherent complex ![]() $F \in \operatorname {QC}(\mathscr {X})$ is the coherent assignment to each pair
$F \in \operatorname {QC}(\mathscr {X})$ is the coherent assignment to each pair ![]() $(R, \eta \in \mathscr {X}(R))$ of an
$(R, \eta \in \mathscr {X}(R))$ of an ![]() $R$-module
$R$-module ![]() $F_\eta \in R {\rm {}\hbox{-}{\rm mod}}$. We also define several other categories associated to functors
$F_\eta \in R {\rm {}\hbox{-}{\rm mod}}$. We also define several other categories associated to functors ![]() $\mathrm {SCR} \to \mathrm {CAlg}(\widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty )$ or
$\mathrm {SCR} \to \mathrm {CAlg}(\widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty )$ or ![]() $\mathrm {SCR} \to \widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty$:
$\mathrm {SCR} \to \widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty$:
–
 ${\rm Coh}^{n} (\mathscr {X})$, associated to the
${\rm Coh}^{n} (\mathscr {X})$, associated to the  $\infty$-category of compact objects in the
$\infty$-category of compact objects in the  $\infty$-category of connective,
$\infty$-category of connective,  $n$-truncated
$n$-truncated  $R$-modules.
$R$-modules.–
 ${\rm Coh} (\mathscr {X})$, special notation for
${\rm Coh} (\mathscr {X})$, special notation for  ${\rm Coh}^{0} (\mathscr {X})$, associated to the compact objects of the abelian category
${\rm Coh}^{0} (\mathscr {X})$, associated to the compact objects of the abelian category  $(R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit } = (\pi _0(R) {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$, that is, the ordinary category of finitely presented
$(R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit } = (\pi _0(R) {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$, that is, the ordinary category of finitely presented  $\pi _0(R)$-modules.
$\pi _0(R)$-modules.–
 $\operatorname {APerf}(\mathscr {X}) \subset \operatorname {QC}(\mathscr {X})$, associated to the symmetric monoidal stable
$\operatorname {APerf}(\mathscr {X}) \subset \operatorname {QC}(\mathscr {X})$, associated to the symmetric monoidal stable  $\infty$-category
$\infty$-category  $\operatorname {APerf}(R) \subset R {\rm {}\hbox{-}{\rm mod}}$ of almost perfect complexes.
$\operatorname {APerf}(R) \subset R {\rm {}\hbox{-}{\rm mod}}$ of almost perfect complexes.  $\operatorname {APerf}(R)$ consists precisely of those
$\operatorname {APerf}(R)$ consists precisely of those  $R$-modules
$R$-modules  $M$ such that
$M$ such that  $\tau _{<\ell } M \in (R {\rm {}\hbox{-}{\rm mod}})_{<\ell }$ is compact for each
$\tau _{<\ell } M \in (R {\rm {}\hbox{-}{\rm mod}})_{<\ell }$ is compact for each  $\ell \in \mathbb {Z}$.
$\ell \in \mathbb {Z}$.–
 $\operatorname {Perf}(\mathscr {X}) \subset \operatorname {QC}(\mathscr {X})$, associated to the symmetric monoidal stable
$\operatorname {Perf}(\mathscr {X}) \subset \operatorname {QC}(\mathscr {X})$, associated to the symmetric monoidal stable  $\infty$-subcategory
$\infty$-subcategory  $\operatorname {Perf}(R) \subset R {\rm {}\hbox{-}{\rm mod}}$ of perfect complexes.
$\operatorname {Perf}(R) \subset R {\rm {}\hbox{-}{\rm mod}}$ of perfect complexes.  $\operatorname {Perf}(R)$ is the smallest subcategory of
$\operatorname {Perf}(R)$ is the smallest subcategory of  $R {\rm {}\hbox{-}{\rm mod}}$ closed under cones, shifts, and retracts and containing
$R {\rm {}\hbox{-}{\rm mod}}$ closed under cones, shifts, and retracts and containing  $R$. By [Reference LurieLur2, Proposition 2.7.28],
$R$. By [Reference LurieLur2, Proposition 2.7.28],  $\operatorname {Perf}(\mathscr {X}) \subset \operatorname {QC}(\mathscr {X})$ consists precisely of the dualizable objects with respect to the symmetric monoidal structure on
$\operatorname {Perf}(\mathscr {X}) \subset \operatorname {QC}(\mathscr {X})$ consists precisely of the dualizable objects with respect to the symmetric monoidal structure on  $\operatorname {QC}(\mathscr {X})$.
$\operatorname {QC}(\mathscr {X})$.
The functor ![]() $\mathrm {SCR} \to \mathrm {CAlg}(\widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty )$ which maps
$\mathrm {SCR} \to \mathrm {CAlg}(\widehat {\!\!\mathop {\rm ~Cat}\nolimits }_\infty )$ which maps ![]() $R \mapsto R {\rm {}\hbox{-}{\rm mod}}$ factors through the canonical functor
$R \mapsto R {\rm {}\hbox{-}{\rm mod}}$ factors through the canonical functor ![]() $\mathrm {SCR} \to \mathrm {CAlg}^{\mathrm {cn}}$ which maps
$\mathrm {SCR} \to \mathrm {CAlg}^{\mathrm {cn}}$ which maps ![]() $R \mapsto \!\!\mathop {\rm ~End}\nolimits _{R {\rm {}\hbox{-}{\rm mod}}}(R)$. It follows that if
$R \mapsto \!\!\mathop {\rm ~End}\nolimits _{R {\rm {}\hbox{-}{\rm mod}}}(R)$. It follows that if ![]() $\mathscr {X} : \mathrm {SCR} \to \widehat {\mathcal {S}}$ is a derived prestack, and
$\mathscr {X} : \mathrm {SCR} \to \widehat {\mathcal {S}}$ is a derived prestack, and ![]() $\mathscr {X}^{\rm sp}$ is the spectral algebraic stack obtained by left Kan extension along the functor
$\mathscr {X}^{\rm sp}$ is the spectral algebraic stack obtained by left Kan extension along the functor ![]() $\mathrm {SCR} \to \mathrm {CAlg}^{\mathrm {cn}}$, then
$\mathrm {SCR} \to \mathrm {CAlg}^{\mathrm {cn}}$, then ![]() $\operatorname {QC}(\mathscr {X}^{\rm sp}) \simeq \operatorname {QC}(\mathscr {X})$, where the former denotes the construction of
$\operatorname {QC}(\mathscr {X}^{\rm sp}) \simeq \operatorname {QC}(\mathscr {X})$, where the former denotes the construction of ![]() $\operatorname {QC}(-)$ for spectral prestacks. The same is true for all of the categories discussed above.
$\operatorname {QC}(-)$ for spectral prestacks. The same is true for all of the categories discussed above.
Definition A.0.1 We say that ![]() $\mathscr {X} \in \operatorname {Fun}(\mathrm {SCR}, \widehat {\mathcal {S}})$ is a locally noetherian prestack if it is left Kan extended, up to sheafification, from a functor on noetherian [Reference LurieLur04, Definition 2.5.9] simplicial commutative algebras
$\mathscr {X} \in \operatorname {Fun}(\mathrm {SCR}, \widehat {\mathcal {S}})$ is a locally noetherian prestack if it is left Kan extended, up to sheafification, from a functor on noetherian [Reference LurieLur04, Definition 2.5.9] simplicial commutative algebras ![]() $\mathscr {X}^{N} \in \operatorname {Fun}(\mathrm {SCR}^{\mathrm {noeth}}, \mathcal {S})$. In this case
$\mathscr {X}^{N} \in \operatorname {Fun}(\mathrm {SCR}^{\mathrm {noeth}}, \mathcal {S})$. In this case ![]() $\operatorname {QC}(\mathscr {X}) \simeq \operatorname {QC}(\mathscr {X}^{N})$, where the latter denotes the right Kan extension of
$\operatorname {QC}(\mathscr {X}) \simeq \operatorname {QC}(\mathscr {X}^{N})$, where the latter denotes the right Kan extension of ![]() $R {\rm {}\hbox{-}{\rm mod}}$ along the Yoneda embedding
$R {\rm {}\hbox{-}{\rm mod}}$ along the Yoneda embedding ![]() $\mathrm {SCR}^{\mathrm {noeth}} \hookrightarrow \operatorname {Fun}(\mathrm {SCR}^{\mathrm {noeth}},\widehat {\mathcal {S}})^{\mathrm {op}}$, and the same holds for all of the other categories considered above.
$\mathrm {SCR}^{\mathrm {noeth}} \hookrightarrow \operatorname {Fun}(\mathrm {SCR}^{\mathrm {noeth}},\widehat {\mathcal {S}})^{\mathrm {op}}$, and the same holds for all of the other categories considered above.
In particular, for a noetherian ring ![]() $R \in \mathrm {SCR}^{\mathrm {noeth}}$,
$R \in \mathrm {SCR}^{\mathrm {noeth}}$, ![]() $E \in R {\rm {}\hbox{-}{\rm mod}}$ is almost perfect if and only if
$E \in R {\rm {}\hbox{-}{\rm mod}}$ is almost perfect if and only if ![]() $H_i(E) \in \operatorname {QC}(R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$ is coherent for all
$H_i(E) \in \operatorname {QC}(R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$ is coherent for all ![]() $i$ and
$i$ and ![]() $H_i(E) = 0$ for
$H_i(E) = 0$ for ![]() $i \ll 0$ [Reference LurieLur17, Proposition 7.2.4.17]. So we could alternatively define
$i \ll 0$ [Reference LurieLur17, Proposition 7.2.4.17]. So we could alternatively define ![]() $\operatorname {APerf}(\mathscr {X}) = \operatorname {APerf}(\mathscr {X}^{N})$ as the right Kan extension of this functor
$\operatorname {APerf}(\mathscr {X}) = \operatorname {APerf}(\mathscr {X}^{N})$ as the right Kan extension of this functor ![]() $\mathrm {SCR}^{\mathrm {noeth}} \to \mathrm {CAlg}(\!\!\mathop {\rm ~Cat}\nolimits _\infty )$ for a locally noetherian
$\mathrm {SCR}^{\mathrm {noeth}} \to \mathrm {CAlg}(\!\!\mathop {\rm ~Cat}\nolimits _\infty )$ for a locally noetherian ![]() $\mathscr {X}$. This motivates the definition of the full stable subcategories of
$\mathscr {X}$. This motivates the definition of the full stable subcategories of ![]() $\operatorname {QC}(\mathscr {X}^{N})$:
$\operatorname {QC}(\mathscr {X}^{N})$:
–
 $\operatorname {{\mathbb {D}}APerf}(\mathscr {X}) \subset \operatorname {QC}(\mathscr {X}^{N})$, consisting of objects such that, for any pair
$\operatorname {{\mathbb {D}}APerf}(\mathscr {X}) \subset \operatorname {QC}(\mathscr {X}^{N})$, consisting of objects such that, for any pair  $(R,\eta \in \mathscr {X}^{N}(R))$,
$(R,\eta \in \mathscr {X}^{N}(R))$,  $H_i(F_\eta ) \in \operatorname {QC}(R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$ is coherent for all
$H_i(F_\eta ) \in \operatorname {QC}(R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$ is coherent for all  $i$ and
$i$ and  $H_i(F) = 0$ for
$H_i(F) = 0$ for  $i \gg 0$.
$i \gg 0$.–
 $\operatorname {DCoh}(\mathscr {X}) \subset \operatorname {QC}(\mathscr {X}^{N})$, consisting of objects such that, for any pair
$\operatorname {DCoh}(\mathscr {X}) \subset \operatorname {QC}(\mathscr {X}^{N})$, consisting of objects such that, for any pair  $(R,\eta \in \mathscr {X}^{N}(R))$,
$(R,\eta \in \mathscr {X}^{N}(R))$,  $H_i(F_\eta ) \in \operatorname {QC}(R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$ is coherent for all
$H_i(F_\eta ) \in \operatorname {QC}(R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$ is coherent for all  $i$ and
$i$ and  $H_i(F) = 0$ for
$H_i(F) = 0$ for  $i \gg 0$ and
$i \gg 0$ and  $i \ll 0$.
$i \ll 0$.
The notation ![]() $\operatorname {{\mathbb {D}}APerf}$ is motivated by the fact that when
$\operatorname {{\mathbb {D}}APerf}$ is motivated by the fact that when ![]() $\mathscr {X}$ admits a Grothendieck dualizing complex, Grothendieck duality provides an anti-equivalence
$\mathscr {X}$ admits a Grothendieck dualizing complex, Grothendieck duality provides an anti-equivalence ![]() $\operatorname {{\mathbb {D}}APerf}(\mathscr {X}) \simeq \operatorname {APerf}(\mathscr {X})^{\mathrm {op}}$.
$\operatorname {{\mathbb {D}}APerf}(\mathscr {X}) \simeq \operatorname {APerf}(\mathscr {X})^{\mathrm {op}}$. ![]() $\operatorname {DCoh}(\mathscr {X})$ is a version of the ‘bounded derived category of coherent sheaves’ for derived stacks. Note that in contrast to
$\operatorname {DCoh}(\mathscr {X})$ is a version of the ‘bounded derived category of coherent sheaves’ for derived stacks. Note that in contrast to ![]() $\operatorname {APerf}$,
$\operatorname {APerf}$, ![]() $\operatorname {DCoh}$ and
$\operatorname {DCoh}$ and ![]() $\operatorname {{\mathbb {D}}APerf}$ do not inherit pullback functors and symmetric monoidal structures from
$\operatorname {{\mathbb {D}}APerf}$ do not inherit pullback functors and symmetric monoidal structures from ![]() $\operatorname {QC}$.
$\operatorname {QC}$.
![]() $t$-structures. When
$t$-structures. When ![]() $\operatorname {QC}(\mathscr {X})$ is presentable, which is always the case for algebraic derived stacks and their formal completions, because presentable categories are closed under small limits,
$\operatorname {QC}(\mathscr {X})$ is presentable, which is always the case for algebraic derived stacks and their formal completions, because presentable categories are closed under small limits, ![]() $\operatorname {QC}(\mathscr {X})$ carries a
$\operatorname {QC}(\mathscr {X})$ carries a ![]() $t$-structure whose subcategory of connective objects
$t$-structure whose subcategory of connective objects ![]() $\operatorname {QC}(\mathscr {X})_{\geqslant 0} = \operatorname {QC}(\mathscr {X})^{\mathrm {cn}}$ consists of those
$\operatorname {QC}(\mathscr {X})_{\geqslant 0} = \operatorname {QC}(\mathscr {X})^{\mathrm {cn}}$ consists of those ![]() $F$ such that
$F$ such that ![]() $F_{\eta } \in (R {\rm {}\hbox{-}{\rm mod}})_{\geqslant 0}$ is connective for all pairs
$F_{\eta } \in (R {\rm {}\hbox{-}{\rm mod}})_{\geqslant 0}$ is connective for all pairs ![]() $(R, \eta \in \mathscr {X}(R))$. Although this definition is formally convenient, using the
$(R, \eta \in \mathscr {X}(R))$. Although this definition is formally convenient, using the ![]() $t$-structure is usually only practical when
$t$-structure is usually only practical when ![]() $\mathscr {X}$ is an algebraic stack. If
$\mathscr {X}$ is an algebraic stack. If ![]() $\pi \colon U = \operatorname {Spec}(R)\to \mathscr {X}$ is an fppf atlas then
$\pi \colon U = \operatorname {Spec}(R)\to \mathscr {X}$ is an fppf atlas then ![]() $\pi ^{*}$ is
$\pi ^{*}$ is ![]() $t$-exact; in particular,
$t$-exact; in particular, ![]() $F \in \operatorname {QC}(\mathscr {X})$ is connective (respectively, coconnective) if and only if
$F \in \operatorname {QC}(\mathscr {X})$ is connective (respectively, coconnective) if and only if ![]() $\pi ^{*} F$ is so. Note also that when
$\pi ^{*} F$ is so. Note also that when ![]() $\mathscr {X}$ is a locally noetherian prestack,
$\mathscr {X}$ is a locally noetherian prestack, ![]() $\operatorname {APerf}(\mathscr {X})$ and
$\operatorname {APerf}(\mathscr {X})$ and ![]() $\operatorname {DCoh}(\mathscr {X})$ carry unique
$\operatorname {DCoh}(\mathscr {X})$ carry unique ![]() $t$-structures for which the inclusion into
$t$-structures for which the inclusion into ![]() $\operatorname {QC}(\mathscr {X})$ is
$\operatorname {QC}(\mathscr {X})$ is ![]() $t$-exact.
$t$-exact.
One can also consider the Kan extension of ![]() $R \mapsto (R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$, the usual abelian category of quasi-coherent sheaves, which we denote by
$R \mapsto (R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$, the usual abelian category of quasi-coherent sheaves, which we denote by ![]() $\operatorname {QC}^{\heartsuit }(\mathscr {X})$. In contrast, let
$\operatorname {QC}^{\heartsuit }(\mathscr {X})$. In contrast, let ![]() $\operatorname {QC}(\mathscr {X})^{\heartsuit }$ denote the symmetric monoidal abelian category given by the heart of the
$\operatorname {QC}(\mathscr {X})^{\heartsuit }$ denote the symmetric monoidal abelian category given by the heart of the ![]() $t$-structure. Since pullback is right
$t$-structure. Since pullback is right ![]() $t$-exact, there is a truncation functor
$t$-exact, there is a truncation functor
 \[ \bigg(\mathop{\varprojlim}\limits_{\eta \in \mathscr{X}(R)} R\text{-mod}\bigg)^{\heartsuit} \longrightarrow \mathop{\varprojlim}\limits_{\eta \in \mathscr{X}(R)}\big((R\text{-mod})^{\heartsuit}\big) \quad F_{\eta} \mapsto H_0(F_{\eta}) \]
\[ \bigg(\mathop{\varprojlim}\limits_{\eta \in \mathscr{X}(R)} R\text{-mod}\bigg)^{\heartsuit} \longrightarrow \mathop{\varprojlim}\limits_{\eta \in \mathscr{X}(R)}\big((R\text{-mod})^{\heartsuit}\big) \quad F_{\eta} \mapsto H_0(F_{\eta}) \]
and one can check that this is a fully faithful embedding. When ![]() $\mathscr {X}$ is algebraic, it in fact gives an equivalence
$\mathscr {X}$ is algebraic, it in fact gives an equivalence ![]() $\operatorname {QC}(\mathscr {X})^{\heartsuit } \to \operatorname {QC}^{\heartsuit }(\mathscr {X})$. Note that because
$\operatorname {QC}(\mathscr {X})^{\heartsuit } \to \operatorname {QC}^{\heartsuit }(\mathscr {X})$. Note that because ![]() $(R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit } \simeq (\pi _0(R) {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$, one can further identify
$(R {\rm {}\hbox{-}{\rm mod}})^{\heartsuit } \simeq (\pi _0(R) {\rm {}\hbox{-}{\rm mod}})^{\heartsuit }$, one can further identify ![]() $\operatorname {QC}^{\heartsuit }(\mathscr {X})$ with the category of quasi-coherent sheaves on the classical stack obtained by restricting
$\operatorname {QC}^{\heartsuit }(\mathscr {X})$ with the category of quasi-coherent sheaves on the classical stack obtained by restricting ![]() $\mathscr {X}$ to the category of discrete simplicial commutative rings
$\mathscr {X}$ to the category of discrete simplicial commutative rings ![]() $\mathrm {Ring} \subset \mathrm {SCR}$. Likewise in the locally noetherian case,
$\mathrm {Ring} \subset \mathrm {SCR}$. Likewise in the locally noetherian case, ![]() $\operatorname {DCoh}(\mathscr {X})^{\heartsuit } \simeq \operatorname {APerf}(\mathscr {X})^{\heartsuit }$ coincides with the ordinary abelian category of coherent sheaves on underlying classical prestack.
$\operatorname {DCoh}(\mathscr {X})^{\heartsuit } \simeq \operatorname {APerf}(\mathscr {X})^{\heartsuit }$ coincides with the ordinary abelian category of coherent sheaves on underlying classical prestack.
A.1 Quasi-coherent pushforwards and base change
We recall the definition of the pushforward of quasi-coherent sheaves in our context.
Definition A.1.1 Suppose that ![]() $f \colon \mathscr {X} \to \mathscr {Y}$ is an arbitrary map of prestacks such that
$f \colon \mathscr {X} \to \mathscr {Y}$ is an arbitrary map of prestacks such that ![]() $\operatorname {QC}(\mathscr {X})$ and
$\operatorname {QC}(\mathscr {X})$ and ![]() $\operatorname {QC}(\mathscr {Y})$ are presentable. Then
$\operatorname {QC}(\mathscr {Y})$ are presentable. Then ![]() $f^{*} \colon \operatorname {QC}(\mathscr {Y}) \to \operatorname {QC}(\mathscr {X})$ is a colimit-preserving functor between presentable
$f^{*} \colon \operatorname {QC}(\mathscr {Y}) \to \operatorname {QC}(\mathscr {X})$ is a colimit-preserving functor between presentable ![]() $\infty$-categories and thus admits a right adjoint [Reference LurieLur09, Corollary 5.5.2.9], which we denote by
$\infty$-categories and thus admits a right adjoint [Reference LurieLur09, Corollary 5.5.2.9], which we denote by ![]() $f_*$.
$f_*$.
Remark A.1.2 It is a priori non-obvious that ![]() $\operatorname {QC}(\mathscr {X})$ has anything to do with sheaves of modules in some
$\operatorname {QC}(\mathscr {X})$ has anything to do with sheaves of modules in some ![]() $\infty$-topos, or that the pushforward defined above has anything to do with a pushforward of sheaves. Nevertheless, this is true if
$\infty$-topos, or that the pushforward defined above has anything to do with a pushforward of sheaves. Nevertheless, this is true if ![]() $\mathscr {X}$ (respectively,
$\mathscr {X}$ (respectively, ![]() $\mathscr {X} \to \mathscr {Y}$) is nice enough. We do not dwell on this point, but the interested reader may consult [Reference LurieLur2, Proposition 2.7.18] for the case of
$\mathscr {X} \to \mathscr {Y}$) is nice enough. We do not dwell on this point, but the interested reader may consult [Reference LurieLur2, Proposition 2.7.18] for the case of ![]() $\mathscr {X}$ a Deligne–Mumford stack and the étale
$\mathscr {X}$ a Deligne–Mumford stack and the étale ![]() $\infty$-topos.
$\infty$-topos.
One might expect that ![]() $f_\ast$ as defined above is well behaved for stacks which arise ‘in nature’, but in general this is quite false. Take
$f_\ast$ as defined above is well behaved for stacks which arise ‘in nature’, but in general this is quite false. Take
Then the functor ![]() $f_*$ will not preserve filtered colimits, will not be compatible with arbitrary base change, and will generally not be pleasant. Nevertheless, one has the following positive result.
$f_*$ will not preserve filtered colimits, will not be compatible with arbitrary base change, and will generally not be pleasant. Nevertheless, one has the following positive result.
Lemma A.1.3 Suppose that ![]() $f\colon \mathscr {X} \to \mathscr {Y}$ is a morphism of spectral (or derived) prestacks which is a relative qc.qs. algebraic stack.
$f\colon \mathscr {X} \to \mathscr {Y}$ is a morphism of spectral (or derived) prestacks which is a relative qc.qs. algebraic stack.
– Let
 $i : \mathscr {Y}' \to \mathscr {Y}$ be a relatively algebraic morphism of finite Tor amplitude (e.g. a flat morphism), and let
$i : \mathscr {Y}' \to \mathscr {Y}$ be a relatively algebraic morphism of finite Tor amplitude (e.g. a flat morphism), and let  $f' \colon \mathscr {X}' \to \mathscr {Y}'$ and
$f' \colon \mathscr {X}' \to \mathscr {Y}'$ and  $i' : \mathscr {X}' \to \mathscr {X}$ be the base change of
$i' : \mathscr {X}' \to \mathscr {X}$ be the base change of  $f$ and
$f$ and  $i$, respectively. For
$i$, respectively. For  $F \in \operatorname {QC}(\mathscr {X})$, the canonical base-change map
is an isomorphism if either
$F \in \operatorname {QC}(\mathscr {X})$, the canonical base-change map
is an isomorphism if either \[ i^{*}(f_*(F)) \to (f')_*( (i')^{*}(F)) \]
\[ i^{*}(f_*(F)) \to (f')_*( (i')^{*}(F)) \]
 $F$ is homologically bounded above (i.e.
$F$ is homologically bounded above (i.e.  $F \in \operatorname {QC}(\mathscr {X})_{<\infty }$) or if
$F \in \operatorname {QC}(\mathscr {X})_{<\infty }$) or if  $i$ is finite and
$i$ is finite and  $F$ is arbitrary.
$F$ is arbitrary.–
 $f_*$ preserves filtered colimits (equivalently, infinite sums) in
$f_*$ preserves filtered colimits (equivalently, infinite sums) in  $\operatorname {QC}(\mathscr {X})_{< n}$ for each
$\operatorname {QC}(\mathscr {X})_{< n}$ for each  $n$ (i.e. for uniformly bounded above colimits).
$n$ (i.e. for uniformly bounded above colimits).
Proof. Sketch
It is enough, by the definition of ![]() $\operatorname {QC}$ as extended from affines and smooth hyperdescent for
$\operatorname {QC}$ as extended from affines and smooth hyperdescent for ![]() $\operatorname {QC}$, to verify this in case where
$\operatorname {QC}$, to verify this in case where ![]() $\mathscr {Y} = \operatorname {Spec}(R)$ and
$\mathscr {Y} = \operatorname {Spec}(R)$ and ![]() $\mathscr {Y}' = \operatorname {Spec}(R')$ are affine. Let
$\mathscr {Y}' = \operatorname {Spec}(R')$ are affine. Let ![]() $p_\bullet \colon U_\bullet = \operatorname {Spec}(A_\bullet ) \to \mathscr {X}$ be a presentation of
$p_\bullet \colon U_\bullet = \operatorname {Spec}(A_\bullet ) \to \mathscr {X}$ be a presentation of ![]() $\mathscr {X}$ as the geometric realization, in smooth sheaves, of a simplicial diagram of affine schemes along smooth morphisms; such a diagram exists because
$\mathscr {X}$ as the geometric realization, in smooth sheaves, of a simplicial diagram of affine schemes along smooth morphisms; such a diagram exists because ![]() $\mathscr {X}$ is
$\mathscr {X}$ is ![]() $\infty$-quasi-compact.
$\infty$-quasi-compact.
By smooth hyperdescent for ![]() $\operatorname {QC}$, we thus have an equivalence
$\operatorname {QC}$, we thus have an equivalence
Under this equivalence ![]() $f^{*}$ identifies with the cosimplicial diagram of pullbacks
$f^{*}$ identifies with the cosimplicial diagram of pullbacks ![]() $(p_\bullet \circ f)^{*}$ mapping
$(p_\bullet \circ f)^{*}$ mapping ![]() $M \mapsto A_\bullet \otimes _R M$. Thus, we can compute the right adjoint
$M \mapsto A_\bullet \otimes _R M$. Thus, we can compute the right adjoint ![]() $f_*$ in terms of this Čech diagram, namely
$f_*$ in terms of this Čech diagram, namely
So if ![]() $p_\bullet ^{\ast }(\mathscr {F}) \simeq M_\bullet \in \operatorname {Tot}\{A_\bullet {\rm {}\hbox{-}{\rm mod}}\}$, then
$p_\bullet ^{\ast }(\mathscr {F}) \simeq M_\bullet \in \operatorname {Tot}\{A_\bullet {\rm {}\hbox{-}{\rm mod}}\}$, then ![]() $f_\ast (\mathscr {F}) \simeq \operatorname {Tot}\{M_\bullet \} \in R {\rm {}\hbox{-}{\rm mod}}$, where in the latter
$f_\ast (\mathscr {F}) \simeq \operatorname {Tot}\{M_\bullet \} \in R {\rm {}\hbox{-}{\rm mod}}$, where in the latter ![]() $M_\bullet$ is regarded as a cosimplicial
$M_\bullet$ is regarded as a cosimplicial ![]() $R$-module.
$R$-module.
If ![]() $i$ is finite and has finite Tor amplitude, we conclude that
$i$ is finite and has finite Tor amplitude, we conclude that ![]() $R'$ is perfect as
$R'$ is perfect as ![]() $R$-module (because it is almost perfect of finite Tor amplitude). Thus,
$R$-module (because it is almost perfect of finite Tor amplitude). Thus, ![]() $i^{*}$ commutes with arbitrary homotopy limits and in particular with the formation of the totalization, so the base-change statement follows from the case where
$i^{*}$ commutes with arbitrary homotopy limits and in particular with the formation of the totalization, so the base-change statement follows from the case where ![]() $\mathscr {X}$ is affine.
$\mathscr {X}$ is affine.
More generally, note that ![]() $\mathscr {F} \in \operatorname {QC}(\mathscr {X})_{<0}$ if and only if
$\mathscr {F} \in \operatorname {QC}(\mathscr {X})_{<0}$ if and only if ![]() $M_\bullet \in (R {\rm {}\hbox{-}{\rm mod}})_{<0}$ for all
$M_\bullet \in (R {\rm {}\hbox{-}{\rm mod}})_{<0}$ for all ![]() $\bullet$. For such objects, the resulting spectral sequence of a totalization is a (convergent) third-quadrant spectral sequence. The formation of this spectral sequence is evidently compatible with filtered colimits and flat base change; a slight elaboration gives the case of finite Tor dimension base change.
$\bullet$. For such objects, the resulting spectral sequence of a totalization is a (convergent) third-quadrant spectral sequence. The formation of this spectral sequence is evidently compatible with filtered colimits and flat base change; a slight elaboration gives the case of finite Tor dimension base change.
In order to obtain stronger base-change results, one must consider a restricted class of morphisms.
Definition A.1.4 We say that a morphism ![]() $f \colon \mathscr {X} \to \mathscr {Y}$ of spectral (or derived) prestacks is of cohomological dimension at most
$f \colon \mathscr {X} \to \mathscr {Y}$ of spectral (or derived) prestacks is of cohomological dimension at most ![]() $d$ if, for any
$d$ if, for any ![]() $F \in \operatorname {QC}(\mathscr {X})^{\heartsuit }$, we have
$F \in \operatorname {QC}(\mathscr {X})^{\heartsuit }$, we have ![]() $f_* F \in \operatorname {QC}(\mathscr {X})_{\geqslant -d}$. (Note that if
$f_* F \in \operatorname {QC}(\mathscr {X})_{\geqslant -d}$. (Note that if ![]() $\mathscr {X}$ is algebraic this depends only on the induced morphism of underlying classical stacks.)
$\mathscr {X}$ is algebraic this depends only on the induced morphism of underlying classical stacks.)
We say that a morphism ![]() $f \colon \mathscr {X} \to \mathscr {Y}$ of spectral (or derived) prestacks is universally of finite cohomological dimension (or, satisfies (CD) for short) if there is some
$f \colon \mathscr {X} \to \mathscr {Y}$ of spectral (or derived) prestacks is universally of finite cohomological dimension (or, satisfies (CD) for short) if there is some ![]() $d$ for which this condition is satisfied for the base change of
$d$ for which this condition is satisfied for the base change of ![]() $f$ along any morphism from an affine
$f$ along any morphism from an affine ![]() $\operatorname {Spec}(A) \to \mathscr {Y}$.
$\operatorname {Spec}(A) \to \mathscr {Y}$.
Proposition A.1.5 Suppose that ![]() $f \colon \mathscr {X} \to \mathscr {Y}$ is a morphism of prestacks which is relatively representable by qc.qs. algebraic spectral (or derived) stacks satisfying (CD). Then:
$f \colon \mathscr {X} \to \mathscr {Y}$ is a morphism of prestacks which is relatively representable by qc.qs. algebraic spectral (or derived) stacks satisfying (CD). Then:
(i)
 $f_*\colon \operatorname {QC}(\mathscr {X}) \to \operatorname {QC}(\mathscr {Y})$ preserves filtered colimits;
$f_*\colon \operatorname {QC}(\mathscr {X}) \to \operatorname {QC}(\mathscr {Y})$ preserves filtered colimits;(ii)
 $f_*$ and
$f_*$ and  $f^{*}$ satisfy the projection formula, that is, the natural morphism
$f^{*}$ satisfy the projection formula, that is, the natural morphism  $f_*(F) \otimes G \to f_*(F \otimes f^{*} G)$ is an equivalence for all
$f_*(F) \otimes G \to f_*(F \otimes f^{*} G)$ is an equivalence for all  $F, G$;
$F, G$;(iii) the formation of
 $f_*$ is compatible with arbitrary base change.
$f_*$ is compatible with arbitrary base change.
First we note an alternative definition of cohomological dimension which is often equivalent to the one above.
Lemma A.1.6 Let ![]() $f : \mathscr {X} \to \mathscr {Y}$ be a morphism of qc.qs. spectral (or derived) algebraic stacks. Then
$f : \mathscr {X} \to \mathscr {Y}$ be a morphism of qc.qs. spectral (or derived) algebraic stacks. Then ![]() $f$ is of cohomological dimension at most
$f$ is of cohomological dimension at most ![]() $d$ if and only if
$d$ if and only if ![]() $f_\ast (\operatorname {QC}(\mathscr {X})_{\geqslant 0}) \subset \operatorname {QC}(\mathscr {Y})_{\geqslant -d}$.
$f_\ast (\operatorname {QC}(\mathscr {X})_{\geqslant 0}) \subset \operatorname {QC}(\mathscr {Y})_{\geqslant -d}$.
Proof. This follows from part (ii) of Lemma 2.1.12 and the fact that ![]() $\operatorname {QC}(\mathscr {X})$ and
$\operatorname {QC}(\mathscr {X})$ and ![]() $\operatorname {QC}(\mathscr {Y})$ are
$\operatorname {QC}(\mathscr {Y})$ are ![]() $t$-complete: for any
$t$-complete: for any ![]() $F \in \operatorname {QC}(\mathscr {X})_{\geqslant 0}$,
$F \in \operatorname {QC}(\mathscr {X})_{\geqslant 0}$, ![]() $F = \varprojlim \tau _{\leqslant n} F$ and
$F = \varprojlim \tau _{\leqslant n} F$ and ![]() $f_\ast (F) \simeq \varprojlim f_\ast (\tau _{\leqslant n}(F))$, and finite cohomological dimension implies that
$f_\ast (F) \simeq \varprojlim f_\ast (\tau _{\leqslant n}(F))$, and finite cohomological dimension implies that ![]() $\tau _{\leqslant k}(f_\ast (\tau _{\leqslant n}(F)))$ is eventually constant in
$\tau _{\leqslant k}(f_\ast (\tau _{\leqslant n}(F)))$ is eventually constant in ![]() $n$, for any
$n$, for any ![]() $k$.
$k$.
Proof of Proposition A.1.6 First let us prove the proposition when ![]() $\mathscr {Y} = \operatorname {Spec}(A)$ is affine. The claims that
$\mathscr {Y} = \operatorname {Spec}(A)$ is affine. The claims that ![]() $f_\ast$ preserves filtered colimits and is compatible with flat base change on
$f_\ast$ preserves filtered colimits and is compatible with flat base change on ![]() $\operatorname {Spec}(A)$ can be checked at the level of homology groups, and the fact that
$\operatorname {Spec}(A)$ can be checked at the level of homology groups, and the fact that ![]() $f_\ast (\operatorname {QC}(\mathscr {X})_{\geqslant 0}) \subset A {\rm {}\hbox{-}{\rm mod}}_{\geqslant -d}$ by Lemma A.1.6 implies that
$f_\ast (\operatorname {QC}(\mathscr {X})_{\geqslant 0}) \subset A {\rm {}\hbox{-}{\rm mod}}_{\geqslant -d}$ by Lemma A.1.6 implies that
This reduces us to showing these claims for ![]() $f_\ast$ applied to
$f_\ast$ applied to ![]() $\operatorname {QC}(\mathscr {X})_{< n}$ for any fixed
$\operatorname {QC}(\mathscr {X})_{< n}$ for any fixed ![]() $n$, which is Lemma A.1.3.
$n$, which is Lemma A.1.3.
Next let us verify (ii). Pick a hypercover ![]() $U_\bullet = \operatorname {Spec}(B_\bullet ) \to \mathscr {X}$, let
$U_\bullet = \operatorname {Spec}(B_\bullet ) \to \mathscr {X}$, let ![]() $M_\bullet \in \operatorname {Tot}\{B_\bullet {\rm {}\hbox{-}{\rm mod}}\} \simeq \operatorname {QC}(\mathscr {X})$, and let
$M_\bullet \in \operatorname {Tot}\{B_\bullet {\rm {}\hbox{-}{\rm mod}}\} \simeq \operatorname {QC}(\mathscr {X})$, and let ![]() $N \in \operatorname {QC}(\mathscr {Y}) = A {\rm {}\hbox{-}{\rm mod}}$. We must verify that the natural map
$N \in \operatorname {QC}(\mathscr {Y}) = A {\rm {}\hbox{-}{\rm mod}}$. We must verify that the natural map
is a quasi-isomorphism.
Let ![]() $\mathcal {C} \subset A {\rm {}\hbox{-}{\rm mod}}$ denote the full subcategory consisting of those
$\mathcal {C} \subset A {\rm {}\hbox{-}{\rm mod}}$ denote the full subcategory consisting of those ![]() $N \in A {\rm {}\hbox{-}{\rm mod}}$ for which the preceding map is a quasi-isomorphism for all
$N \in A {\rm {}\hbox{-}{\rm mod}}$ for which the preceding map is a quasi-isomorphism for all ![]() $M_\bullet$. Note that
$M_\bullet$. Note that ![]() $\mathcal {C}$ is closed under cones, shifts, and retracts since
$\mathcal {C}$ is closed under cones, shifts, and retracts since ![]() $f_*$,
$f_*$, ![]() $f^{*}$, and
$f^{*}$, and ![]() $\otimes$ all preserve these operations up to quasi-isomorphism. Next, note that
$\otimes$ all preserve these operations up to quasi-isomorphism. Next, note that ![]() $\mathcal {C}$ is closed under filtered colimits, because all three operations preserve filtered colimits by (i). Finally, observe that
$\mathcal {C}$ is closed under filtered colimits, because all three operations preserve filtered colimits by (i). Finally, observe that ![]() $A \in \mathcal {C}$. But the smallest subcategory
$A \in \mathcal {C}$. But the smallest subcategory ![]() $A {\rm {}\hbox{-}{\rm mod}}$ containing
$A {\rm {}\hbox{-}{\rm mod}}$ containing ![]() $A$ and closed under cones, shifts, and filtered colimits is all of
$A$ and closed under cones, shifts, and filtered colimits is all of ![]() $A {\rm {}\hbox{-}{\rm mod}}$.
$A {\rm {}\hbox{-}{\rm mod}}$.
For (iii), it is enough to consider the case of an affine base change (See [Reference Drinfeld and GaitsgoryDG13, Proposition 1.3.6] for an argument in the setting of dg algebras which applies verbatim to ![]() $E_\infty$-algebras). Suppose that
$E_\infty$-algebras). Suppose that ![]() $S' = \operatorname {Spec}(A') \to \operatorname {Spec}(A)$ is arbitrary, and let
$S' = \operatorname {Spec}(A') \to \operatorname {Spec}(A)$ is arbitrary, and let ![]() $f' \colon \mathscr {X}' = \mathscr {X} \times _{\operatorname {Spec}(A)} S' \to S'$ be the base change of
$f' \colon \mathscr {X}' = \mathscr {X} \times _{\operatorname {Spec}(A)} S' \to S'$ be the base change of ![]() $S$. We must show that the natural map
$S$. We must show that the natural map
is an equivalence of ![]() $A'$-modules. Note, however, that regarding this as a morphism of
$A'$-modules. Note, however, that regarding this as a morphism of ![]() $A$-modules, this is precisely the equivalence of the projection formula.
$A$-modules, this is precisely the equivalence of the projection formula.
Extending to arbitrary bases. We have shown that after base change to an affine ![]() $\operatorname {Spec}(A) \times _\mathscr {Y} \mathscr {X}$, the base-change formula holds for
$\operatorname {Spec}(A) \times _\mathscr {Y} \mathscr {X}$, the base-change formula holds for ![]() $f$, and this implies the base-change formula holds for
$f$, and this implies the base-change formula holds for ![]() $f$ itself and arbitrary prestacks
$f$ itself and arbitrary prestacks ![]() $\mathscr {Y}' \to \mathscr {Y}$ (again by [Reference Drinfeld and GaitsgoryDG13, Proposition 1.3.6]). Once we have base change, (i) follows, because colimits in
$\mathscr {Y}' \to \mathscr {Y}$ (again by [Reference Drinfeld and GaitsgoryDG13, Proposition 1.3.6]). Once we have base change, (i) follows, because colimits in ![]() $QC(\mathscr {Y})$ can be identified by their restriction to affine derived schemes over
$QC(\mathscr {Y})$ can be identified by their restriction to affine derived schemes over ![]() $\mathscr {Y}$. Likewise, the base-change formula for
$\mathscr {Y}$. Likewise, the base-change formula for ![]() $f$ can be checked after base change to an arbitrary affine.
$f$ can be checked after base change to an arbitrary affine.
Example A.1.7 We have occasion to apply Proposition A.1.5 to stacks which are not algebraic when we prove a strong version of the Grothendieck existence theorem, Theorem 4.2.1. There we consider a fiber square of stacks which is the formal completion of a fiber square of algebraic stacks along a cocompact closed subset of the base.
In characteristic ![]() $0$, it turns out that (CD) is very often satisfied.
$0$, it turns out that (CD) is very often satisfied.
Proposition A.1.8 Suppose that ![]() $S$ is a noetherian characteristic
$S$ is a noetherian characteristic ![]() $0$ derived scheme, and that
$0$ derived scheme, and that ![]() $\mathscr {X}$ is a finite type algebraic derived
$\mathscr {X}$ is a finite type algebraic derived ![]() $S$-stack such that the automorphisms of its geometric points are affine. Then
$S$-stack such that the automorphisms of its geometric points are affine. Then ![]() $\mathscr {X}$ satisfies (CD) over
$\mathscr {X}$ satisfies (CD) over ![]() $S$.
$S$.
Proof. This is proven in slightly more generality in [Reference Drinfeld and GaitsgoryDG13, Theorem 1.4.2]: One can show that ![]() $\mathscr {X}$ has a finite stratification by global quotient stacks, and a straightforward argument shows that having finite cohomological dimension is stable under open-closed decompositions. It thus suffices to prove the result for global quotient stacks. This follows by noting that qc.qs. algebraic spaces have finite cohomological dimension, and that reductive groups (e.g.
$\mathscr {X}$ has a finite stratification by global quotient stacks, and a straightforward argument shows that having finite cohomological dimension is stable under open-closed decompositions. It thus suffices to prove the result for global quotient stacks. This follows by noting that qc.qs. algebraic spaces have finite cohomological dimension, and that reductive groups (e.g. ![]() $GL_n$) are linearly reductive in characteristic
$GL_n$) are linearly reductive in characteristic ![]() $0$.
$0$.
In addition, for many morphisms between algebraic derived stacks, satisfying (CD) is equivalent to having finite cohomological dimension.
Proposition A.1.9 If ![]() $f\colon \mathscr {X} \to \mathscr {Y}$ is a morphism of qc.qs. algebraic derived (or spectral) stacks and
$f\colon \mathscr {X} \to \mathscr {Y}$ is a morphism of qc.qs. algebraic derived (or spectral) stacks and ![]() $\mathscr {Y}$ has affine diagonal, then the following assertions are equivalent:
$\mathscr {Y}$ has affine diagonal, then the following assertions are equivalent:
(i)
 $f$ is universally of cohomological dimension at most
$f$ is universally of cohomological dimension at most  $d$;
$d$;(ii) for any flat morphism
 $S = \operatorname {Spec}(R) \to \mathscr {Y}$, the base change
$S = \operatorname {Spec}(R) \to \mathscr {Y}$, the base change  $f_S \colon \mathscr {X}_S \to S$ is of cohomological dimension at most
$f_S \colon \mathscr {X}_S \to S$ is of cohomological dimension at most  $d$;
$d$;(iii)
 $f$ is of cohomological dimension at most
$f$ is of cohomological dimension at most  $d$;
$d$;(iv)
 $f_*$ takes
$f_*$ takes  $\operatorname {QC}(\mathscr {X})_{>0}$ into
$\operatorname {QC}(\mathscr {X})_{>0}$ into  $\operatorname {QC}(\mathscr {Y})_{>-d}$.
$\operatorname {QC}(\mathscr {Y})_{>-d}$.
Proof. Lemma A.1.6 implies that (iii) and (iv) are equivalent. (i) implies (ii) by definition, and (ii) implies (iii) by flat base change and faithfully flat descent. Finally, the property of being of cohomological dimension at most ![]() $d$ is stable under affine base change, because affine maps are conservative and
$d$ is stable under affine base change, because affine maps are conservative and ![]() $t$-exact. Thus, because
$t$-exact. Thus, because ![]() $\mathscr {Y}$ is has affine diagonal, (iii) implies that
$\mathscr {Y}$ is has affine diagonal, (iii) implies that ![]() $f$ is of cohomological dimension at most
$f$ is of cohomological dimension at most ![]() $d$ after base change to any affine test scheme, which is (i).
$d$ after base change to any affine test scheme, which is (i).
Finally, we note the following proposition.
Proposition A.1.10 Given a morphism ![]() $f : \mathscr {X} \to \mathscr {Y}$ of derived (or spectral) stacks, property (CD) is fppf local over
$f : \mathscr {X} \to \mathscr {Y}$ of derived (or spectral) stacks, property (CD) is fppf local over ![]() $\mathscr {Y}$.
$\mathscr {Y}$.
Proof. (CD) is clearly stable under base change. Conversely, if ![]() $\mathscr {Y}' \to \mathscr {Y}$ is an fppf algebraic morphism such that
$\mathscr {Y}' \to \mathscr {Y}$ is an fppf algebraic morphism such that ![]() $\mathscr {X} \times _\mathscr {Y} \mathscr {Y}' \to \mathscr {Y}$ satisfies (CD), then for any morphism
$\mathscr {X} \times _\mathscr {Y} \mathscr {Y}' \to \mathscr {Y}$ satisfies (CD), then for any morphism ![]() $\operatorname {Spec}(R) \to \mathscr {Y}$, one can find an fppf morphism
$\operatorname {Spec}(R) \to \mathscr {Y}$, one can find an fppf morphism ![]() $\operatorname {Spec}(R') \to \operatorname {Spec}(R)$ such that the composition
$\operatorname {Spec}(R') \to \operatorname {Spec}(R)$ such that the composition ![]() $\operatorname {Spec}(R') \to \mathscr {Y}$ lifts to
$\operatorname {Spec}(R') \to \mathscr {Y}$ lifts to ![]() $\mathscr {Y}'$. It follows that
$\mathscr {Y}'$. It follows that ![]() $\mathscr {X}_{R'} \to \operatorname {Spec}(R')$ has cohomological dimension
$\mathscr {X}_{R'} \to \operatorname {Spec}(R')$ has cohomological dimension ![]() $d$ and thus so does
$d$ and thus so does ![]() $\mathscr {X}_R \to \operatorname {Spec}(R)$ by fppf descent and flat base change.
$\mathscr {X}_R \to \operatorname {Spec}(R)$ by fppf descent and flat base change.
A.2 Enough coherent complexes
We will often use the following compact generation statement.
Theorem A.2.1 If ![]() $\mathscr {X}$ is a noetherian algebraic derived (or spectral) stack, then the following assertions hold:
$\mathscr {X}$ is a noetherian algebraic derived (or spectral) stack, then the following assertions hold:
(i) [Reference Laumon and Moret-BaillyLMB00]
 $\operatorname {QC}(\mathscr {X})^{\heartsuit }$ is compactly-generated by
$\operatorname {QC}(\mathscr {X})^{\heartsuit }$ is compactly-generated by  $\operatorname {DCoh}(\mathscr {X})^{\heartsuit }$;
$\operatorname {DCoh}(\mathscr {X})^{\heartsuit }$;(ii) [Reference Drinfeld and GaitsgoryDG13] the subcategory
 $\operatorname {QC}(\mathscr {X})_{<0} \subset \operatorname {QC}(\mathscr {X})$ is compactly generated, with compact objects precisely
$\operatorname {QC}(\mathscr {X})_{<0} \subset \operatorname {QC}(\mathscr {X})$ is compactly generated, with compact objects precisely  $\operatorname {DCoh}(\mathscr {X})_{<0}$;
$\operatorname {DCoh}(\mathscr {X})_{<0}$;(iii) for each
 $d \geqslant 0$, the subcategory
$d \geqslant 0$, the subcategory  $\operatorname {QC}(\mathscr {X})_{\geqslant 0, < d} \subset \operatorname {QC}(\mathscr {X})$ is compactly generated, with compact objects precisely
$\operatorname {QC}(\mathscr {X})_{\geqslant 0, < d} \subset \operatorname {QC}(\mathscr {X})$ is compactly generated, with compact objects precisely  $\operatorname {DCoh}(\mathscr {X})_{\geqslant 0, < d}$.
$\operatorname {DCoh}(\mathscr {X})_{\geqslant 0, < d}$.
Proof. See [Reference Laumon and Moret-BaillyLMB00, Proposition 15.4] for (i). Since the ![]() $t$-structure on
$t$-structure on ![]() $\operatorname {QC}(\mathscr {X})$ is right
$\operatorname {QC}(\mathscr {X})$ is right ![]() $t$-complete and compatible with filtered colimits (these properties being flat-local and true for affines) both (ii) and (iii) reduce to (i) along with the assertion that, for any
$t$-complete and compatible with filtered colimits (these properties being flat-local and true for affines) both (ii) and (iii) reduce to (i) along with the assertion that, for any ![]() $K \in \operatorname {DCoh}(\mathscr {X})$, the functor
$K \in \operatorname {DCoh}(\mathscr {X})$, the functor ![]() $\operatorname {Map}(K,\bullet )$ preserves uniformly left
$\operatorname {Map}(K,\bullet )$ preserves uniformly left ![]() $t$-bounded filtered colimits. Because any such
$t$-bounded filtered colimits. Because any such ![]() $K$ is bounded, we can reduce to showing that for all
$K$ is bounded, we can reduce to showing that for all ![]() $K \in \operatorname {DCoh}(\mathscr {X})^{\heartsuit }$ and all
$K \in \operatorname {DCoh}(\mathscr {X})^{\heartsuit }$ and all ![]() $i \geqslant 0$,
$i \geqslant 0$, ![]() $\operatorname {Ext}^{i}(K,\bullet )$ preserves filtered colimits in
$\operatorname {Ext}^{i}(K,\bullet )$ preserves filtered colimits in ![]() $\operatorname {QC}(\mathscr {X})^{\heartsuit }$. This can be verified in the affine case by approximating
$\operatorname {QC}(\mathscr {X})^{\heartsuit }$. This can be verified in the affine case by approximating ![]() $K$ by perfect complexes, and the general case reduces to the affine case via the argument in the proof of Lemma A.1.3, where we only need to use the first
$K$ by perfect complexes, and the general case reduces to the affine case via the argument in the proof of Lemma A.1.3, where we only need to use the first ![]() $i$ levels of the hypercover of
$i$ levels of the hypercover of ![]() $\mathscr {X}$.
$\mathscr {X}$.