1. Introduction
Ice-core samples taken from depth in an ice sheet reveal strong fabrics, shown by significant alignment of initially randomly distributed c axes of individual crystals, and consequent substantial differences in shear viscosities in different planes. Macroscopic laws have been constructed from the properties of individual crystals and assumptions on how they interact (e.g. by Reference Van der Veen and WhillansVan der Veen and Whillans, 1994; Reference Azuma and Goto-AzumaAzuma and Goto-Azuma, 1996). Visco-plastic self-consistent theory has been applied (e.g. by Reference Castelnau, Duval, Lebensohn and CanovaCastelnau and others, 1996; Reference Meyssonnier and PhilipMeyssonnier and Philip, 1996) to derive average properties. Reference Meyssonnier and PhilipMeyssonnier and Philip (1996) also introduced an orientation distribution function to measure weightings of a continuous spectrum of c-axis orientations, and this approach has been used to construct direct macroscopic laws (e.g. by Reference Svendsen and HutterSvendsen and Hutter, 1996; Reference Gödert and HutterGödert and Hutter, 1998; Reference Gagliardini and MeyssonnierGagliardini and Meyssonnier, 1999).
An alternative macroscopic viscous law for the shear stress motivated by a simple picture of lattice rotation in which individual crystal-glide planes, material planes, are rotated towards planes normal to principal axes of compression, and away from planes normalto principal axes of extension, has been developed by Reference Morland and StaroszczykMorland and Staroszczyk (1998, Reference Morland and Staroszczyk2003) and Reference Staroszczyk and MorlandStaroszczyk and Morland (2000, Reference Staroszczyk and Morland2001). Instantaneous directional viscosities were introduced to define the induced anisotropy in any given fabric state, and a set of equalities and inequalities which must be satisfied by the instantaneous directional viscosities was derived from the above rotation concepts, designated by one author (L.W.M.) as the “Staroszczyk inequalities”. It was inferred that the instantaneous viscous response is orthotropic with respect to the current principal stretch planes, so that the base planes of the orthotropy are evolving, and that the directional strengths of the response depend on the current deformation. The orthotropic viscous law is then a frame-indifferent relation between stress, strain rate, deformation and the three structure tensors defined by the outer products of the three orthogonal vectors along the principal stretch axes.
Reference Morland and StaroszczykMorland and Staroszczyk (2003) analyzed the simplest forms of both stress and strain-rate formulations, relations for the deviatoric stress and for the strain rate, respectively, consistent with the Staroszczyk inequalities, which each involve two sets of tensor generators but only one independent fabric response coefficient depending on one invariant argument. The stress formulation yielded explicit relations between the primary stress and strain-rate components in both uniaxial compression and simple shear responses, and correlations between the predicted and assumed idealized responses were made to determine the corresponding fabric response function. For the strain-rate formulation, an explicit relation between the axial strain rate and stress was again obtained in uniaxial compression; in simple shear, however, the shear strain rate is governed by three coupled relations in terms of the shear stress and two axial deviatoric stresses, and involves the fabric response function in a complicated, non-linear manner. Correlations with the idealized responses did not appear feasible. We now re-examine the Reference Morland and StaroszczykMorland and Staroszczyk (2003) strain-rate formulation, and determine a crucial new result: the solution of this coupled system to derive an explicit relation for the shear strain rate in terms of the shear stress. We then determine the fabric response function for the strain-rate formulation by correlation with the same idealized uniaxial and shear responses adopted by Reference Morland and StaroszczykMorland and Staroszczyk (2003) for the stress formulation. Only relations necessary to describe the model and responses, and the new solution, are repeated.
2. Orthotropic Viscous Model
We adopt the orthotropic viscous law for the strain rate D presented by Reference Morland and StaroszczykMorland and Staroszczyk (2003),

where I is the unit tensor, T is temperature, D is an effective strain rate incorporating a temperature-dependent rate factor a(T), and B is the left Cauchy–Green strain tensor. & is the deviatoric-stress tensor with a dimensionless invariant J relative to a typical ice-sheet flow shear stress magnitude σ0:
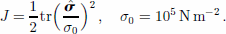
μ (J) is the isotropic viscosity function. ![]() are fabric response coefficients, functions of single deformation invariant arguments ξr and η, respectively, given by
are fabric response coefficients, functions of single deformation invariant arguments ξr and η, respectively, given by

where br (r = 1; 2; 3) are the ordered principal values (principal stretches squared) of B. ![]() and
and ![]() are supposed differentiable functions of their arguments. The three structure tensors M (r) are defined by the outer products of the unit vectors e (r) (r = 1; 2; 3) along the current principal stretch axes:
are supposed differentiable functions of their arguments. The three structure tensors M (r) are defined by the outer products of the unit vectors e (r) (r = 1; 2; 3) along the current principal stretch axes:

Isotropy in the undeformed state B = I gives the normalization condition

The non-trivial equality of the general Staroszczyk inequalities requires

for η ≥ 0, where f (ξ) has the decomposition into even, ![]() and odd ,
and odd , ![]() parts defined by
parts defined by

and the alternative fabric response function , defined by Equation (2.6), is finite and non-zero as .The limit of Equation (2.6) as , noting that , together with Equation (2.5), shows that

which is a restriction on ![]() at ξ = 0. Thus
at ξ = 0. Thus ![]() and
and ![]() are expressed explicitly in terms of
are expressed explicitly in terms of ![]() and the constitutive law given by Equation (2.1) can be expressed in terms of a single independent fabric response function
and the constitutive law given by Equation (2.1) can be expressed in terms of a single independent fabric response function ![]() Define, for
Define, for

then the remaining non-trivial Staroszczyk inequalities require

which must be verified for any adopted ![]() over the complete range of ordered br
(r = 1, 2, 3).
over the complete range of ordered br
(r = 1, 2, 3).
3. Uniaxial and Shear Responses
In uniaxial compression at constant temperature T along the Ox3
axis there are equal lateral stretches λ1 = λ2 > 1, and the axial stretch (a compression) is ![]() . The model viscous law (Equation (2.1)) gives the non-zero diagonal relations
. The model viscous law (Equation (2.1)) gives the non-zero diagonal relations

where u(0) = 1 and

As ![]() and u(ξ1) → A; A - 1 is the enhancement factor in uniaxial compression. Eliminating g(η) by Equation(2.6),
and u(ξ1) → A; A - 1 is the enhancement factor in uniaxial compression. Eliminating g(η) by Equation(2.6),

In a simple shear strain κ ≥ 0 at constant temperature and constant strain rate ![]() other Dij = 0, the strain tensor B has the non-zero components B11 = 1 + κ
2
, B22 = B33 = 1 and B13 = B31 = κ, and the deviatoric-stress tensor has axial components
other Dij = 0, the strain tensor B has the non-zero components B11 = 1 + κ
2
, B22 = B33 = 1 and B13 = B31 = κ, and the deviatoric-stress tensor has axial components ![]() where
where ![]() in addition to the direct shear components
in addition to the direct shear components ![]() The principal values of B, br
(r = 1; 2; 3), the associated principal vectors e (r) , and the invariants ξr , η = ηs , are given by
The principal values of B, br
(r = 1; 2; 3), the associated principal vectors e (r) , and the invariants ξr , η = ηs , are given by



The model law (Equation (2.1)) then has the three independent relations



where





and for (s = 1, 3):




Setting ![]() provides two linear relations to eliminate
provides two linear relations to eliminate ![]() and
and ![]() and in turn
and in turn ![]() in terms of
in terms of ![]() Then Equation (3.9) can be expressed as a linear relation between
Then Equation (3.9) can be expressed as a linear relation between ![]() and
and ![]() but involving
but involving ![]() and
and ![]() in a complicated manner; the derivation was not pursued by Reference Morland and StaroszczykMorland and Staroszczyk (2003).
in a complicated manner; the derivation was not pursued by Reference Morland and StaroszczykMorland and Staroszczyk (2003).
We now show that this coupled system does lead to a simple explicit relation between ![]() and
and ![]() which can then be combined with the uniaxial relation (3.1) to relate the fabric function to the uniaxial and shear responses, as done for the stress formulation by Reference Morland and StaroszczykMorland and Staroszczyk (2003). Ignoring the systematic procedure described above, we first determine the coefficients of a–13 in Equations (3.7) and (3.8) for
which can then be combined with the uniaxial relation (3.1) to relate the fabric function to the uniaxial and shear responses, as done for the stress formulation by Reference Morland and StaroszczykMorland and Staroszczyk (2003). Ignoring the systematic procedure described above, we first determine the coefficients of a–13 in Equations (3.7) and (3.8) for ![]() and
and ![]() Collecting the relevant terms from Equations (3.10–3.18), it is found that both coefficients are
Collecting the relevant terms from Equations (3.10–3.18), it is found that both coefficients are

Now, from Equations (3.4–3.6), it follows that

so that the coefficient (3.19) is a multiple of ![]() and is identically zero. Thus, setting
and is identically zero. Thus, setting ![]() yields two non-singular, homogeneous, linear equations for
yields two non-singular, homogeneous, linear equations for ![]() and
and ![]() which implies that
which implies that ![]() and hence Equation (3.9) reduces to
and hence Equation (3.9) reduces to

As ![]() is the enhancement factor in simple shear, and the shear relation (3.21) has the limit
is the enhancement factor in simple shear, and the shear relation (3.21) has the limit

Combining Equation (3.22) with the axial limit relation (3.3) then determines the fabric response function limit values

4. Correlations
We adopt the Reference Morland and StaroszczykMorland and Staroszczyk (2003) idealized monotonic responses for the uniaxial and shear responses which prescribe u (ξ1) and s(K), respectively, by

where b* and k* are the scales of b1 and K 2 , respectively, over which up(b1) and sp (K2 ) make a significant change. These prescriptions satisfy the limits at b1 = 1 and K = 0, and as b1 and K → ∞, and have zero and non-zero derivatives, respectively, with respect to their arguments at b1 = 1 and K 2 = 0 as required by Equations (3.1) and (3.21). Now s(K) given by Equation (3.21) can be matched exactly with the prescribed sp(K2) by setting

for ηs ≥ 0, which in turn expresses ![]() in terms of
in terms of ![]() and
and ![]() for all ξ, where
for all ξ, where

The required derivative condition (2.8), ![]() is automatically satisfied by Equation (4.2). While there is still a controversy whether the limit value A is greater or less than unity, we consider both the “warm-” and “cold-ice” parameters adopted by Reference Morland and StaroszczykMorland and Staroszczyk (2003), based respectively on laboratory tests by Reference Budd and JackaBudd and Jacka (1989), and modifications of estimates by Reference Mangeney, Califano and CastelnauMangeney and others (1996) from Greenland Icecore Project (GRIP) and Greenland Ice Sheet Project 2 (GISP2) ice-core data:
is automatically satisfied by Equation (4.2). While there is still a controversy whether the limit value A is greater or less than unity, we consider both the “warm-” and “cold-ice” parameters adopted by Reference Morland and StaroszczykMorland and Staroszczyk (2003), based respectively on laboratory tests by Reference Budd and JackaBudd and Jacka (1989), and modifications of estimates by Reference Mangeney, Califano and CastelnauMangeney and others (1996) from Greenland Icecore Project (GRIP) and Greenland Ice Sheet Project 2 (GISP2) ice-core data:
warm ice: ![]()

cold ice: ![]()

The fabric function limits are given by Equations (3.23) and (2.7).
Correlation of the predicted uniaxial and shear responses u(ξ1) and s(K) with the prescribed responses up(b1) and sp (K2) , respectively, determines the corresponding fabric response function ![]() in the assumed model. We apply the weighted least-squares difference minimization used by Reference Morland and StaroszczykMorland and Staroszczyk (2003) in the stress formulation. As there, the best correlation for “warm ice” was obtained by the combined uniaxial and shear response minimization, and for “cold ice” by the uniaxial minimization with s(K) matched exactly, adopting the same fabric response function representations. Since there is no apparent critical value of ξ(b) during the fabric evolution, it is expected that the function
in the assumed model. We apply the weighted least-squares difference minimization used by Reference Morland and StaroszczykMorland and Staroszczyk (2003) in the stress formulation. As there, the best correlation for “warm ice” was obtained by the combined uniaxial and shear response minimization, and for “cold ice” by the uniaxial minimization with s(K) matched exactly, adopting the same fabric response function representations. Since there is no apparent critical value of ξ(b) during the fabric evolution, it is expected that the function ![]() should be monotonic, satisfying the limit values given by Equations (4.4) and (4.5). Monotonicity of
should be monotonic, satisfying the limit values given by Equations (4.4) and (4.5). Monotonicity of ![]() ensures monotonicity of
ensures monotonicity of ![]() and
and ![]() but not of
but not of ![]() For the combined correlation, the representation is
For the combined correlation, the representation is

which is necessarily monotonic. The derivative condition (2.8) at ξ = 0, b = 1 becomes

which has a unique positive root α, leaving 2N free parameters an and cn
in the representation (4.6). For the uniaxial correlation, with the shear response matched identically, the representation for the even part ![]() is
is

with cn > 0, but allowing some of the coefficients an to be negative, so monotonicity of ~ e (ξ ) ![]() in ξ ≥ 0 is not ensured, nor, in general, is that of
in ξ ≥ 0 is not ensured, nor, in general, is that of ![]() The representation (4.8) also has two N-free parameters an
and cn.
The representation (4.8) also has two N-free parameters an
and cn.
The best correlations obtained with moderate N are as follows. For “warm ice”, the coefficients in Equation (4.6) are

Figure 1 shows the corresponding fabric response functions, all monotonic, and Figures 2 and 3 show the prescribed and predicted uniaxial and shear responses, respectively. The maximum uniaxial and shear differences are, respectively, 0.057 compared to A = 0.333, and 0.045 compared to S = 0.2. For “cold ice”, the coefficients in Equation (4.8) are

Fig. 1. Fabric functions f(ξ), g(ξ) and G(ξ) for warm ice.

Fig. 2. Calculated normalized axial viscosity u(ξ1) (Equation (3.1)) vs lateral stretch λ1 (dashed line) compared to prescribed response (solid line) for warm ice.

Fig. 3. Calculated normalized shear viscosity s(К) (Equation (3.21)) vs shear strain К (dashed line) compared to prescribed response (solid line) for warm ice.


Figure 4 shows the corresponding fabric response functions, all monotonic, Figure 5 shows the prescribed and predicted uniaxial response, and Figure 6 the identically matched prescribed shear response. The maximum uniaxial difference is 0.15 compared to A = 3. In both cases, the validity inequalities (2.10) were verified numerically over the wide range

Fig. 4. Fabric functions f(ξ), g(ξ) and G(ξ)for cold ice.

Fig. 5. Calculated normalized axial viscosity u(ξ1) (Equation (3.1)) vs lateral stretch λ1 (dashed line) compared to prescribed response (solid line) for cold ice.

Fig. 6. Calculated normalized shear viscosity s(κ) (Equation (3.21)) vs shear strain κ (dots) identical to prescribed response (solid line) for cold ice.

Conclusions
We have presented a strain-rate formulation of an orthotropic viscous law for evolving fabric in polar ice, and shown that explicit relations between the primary strain rate and stress can be obtained for both uniaxial compression and simple shear responses. These allow correlation with idealized uniaxial compression and simple shear responses, for both “warm-” and “cold-ice” properties, to determine the fabric response coefficient functions which yield good approximations to those prescribed responses. We therefore now have models for both stress and strain-rate formulations which determine, to a close approximation, the same uniaxial compression and simple shear responses.
Acknowledgement
This research was supported by a U.K. Engineering and Physical Sciences Research Council grant, “Evolving Anisotropy of Ice Sheet Flows”.










