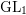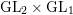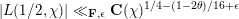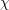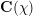1 Introduction
1.1 Statement of main result
If
![]() $\unicode[STIX]{x1D70B}$
is a (cuspidal) automorphic representation of
$\unicode[STIX]{x1D70B}$
is a (cuspidal) automorphic representation of
![]() $\text{GL}_{d}$
over a number field
$\text{GL}_{d}$
over a number field
![]() $\mathbf{F}$
with (usual) conductor
$\mathbf{F}$
with (usual) conductor
![]() $\mathbf{C}(\unicode[STIX]{x1D70B}_{\text{fin}})$
, archimedean analytic conductor
$\mathbf{C}(\unicode[STIX]{x1D70B}_{\text{fin}})$
, archimedean analytic conductor
![]() $\mathbf{C}(\unicode[STIX]{x1D70B}_{\infty })$
, and analytic conductor
$\mathbf{C}(\unicode[STIX]{x1D70B}_{\infty })$
, and analytic conductor
![]() $\mathbf{C}(\unicode[STIX]{x1D70B})=\mathbf{C}(\unicode[STIX]{x1D70B}_{\infty })\mathbf{C}(\unicode[STIX]{x1D70B}_{\text{fin}})$
, the absolute convergence for
$\mathbf{C}(\unicode[STIX]{x1D70B})=\mathbf{C}(\unicode[STIX]{x1D70B}_{\infty })\mathbf{C}(\unicode[STIX]{x1D70B}_{\text{fin}})$
, the absolute convergence for
![]() $\Re s>1$
of the associated
$\Re s>1$
of the associated
![]() $L$
-function
$L$
-function
![]() $L(s,\unicode[STIX]{x1D70B})$
and the functional equation implies for any
$L(s,\unicode[STIX]{x1D70B})$
and the functional equation implies for any
![]() $\unicode[STIX]{x1D716}>0$
, via the Phragmén–Lindelöf principle together with Iwaniec’s method [Reference Duke, Friedlander and IwaniecDFI02, (19.16)]Footnote
1
to establish the necessary bound on the vertical line with
$\unicode[STIX]{x1D716}>0$
, via the Phragmén–Lindelöf principle together with Iwaniec’s method [Reference Duke, Friedlander and IwaniecDFI02, (19.16)]Footnote
1
to establish the necessary bound on the vertical line with
![]() $\Re s=1+\unicode[STIX]{x1D716}$
with small
$\Re s=1+\unicode[STIX]{x1D716}$
with small
![]() $\unicode[STIX]{x1D716}>0$
, the estimation at the central point
$\unicode[STIX]{x1D716}>0$
, the estimation at the central point
called the convex bound or the convexity. If the Riemann hypothesis holds for
![]() $L(s,\unicode[STIX]{x1D70B})$
, then we have the optimal bound
$L(s,\unicode[STIX]{x1D70B})$
, then we have the optimal bound
called the Lindelöf hypothesis. Reducing the exponent of
![]() $\mathbf{C}(\unicode[STIX]{x1D70B})$
from
$\mathbf{C}(\unicode[STIX]{x1D70B})$
from
![]() $1/4+\unicode[STIX]{x1D716}$
to
$1/4+\unicode[STIX]{x1D716}$
to
![]() $1/4-\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D716}$
for some positive constant
$1/4-\unicode[STIX]{x1D6FF}+\unicode[STIX]{x1D716}$
for some positive constant
![]() $0<\unicode[STIX]{x1D6FF}<1/4$
is called the subconvexity problem. More generally, for
$0<\unicode[STIX]{x1D6FF}<1/4$
is called the subconvexity problem. More generally, for
![]() $Q=\mathbf{C}(\unicode[STIX]{x1D70B})$
(respectively,
$Q=\mathbf{C}(\unicode[STIX]{x1D70B})$
(respectively,
![]() $\mathbf{C}(\unicode[STIX]{x1D70B}_{\text{fin}})$
,
$\mathbf{C}(\unicode[STIX]{x1D70B}_{\text{fin}})$
,
![]() $\mathbf{C}(\unicode[STIX]{x1D70B}_{\infty })$
), an estimation
$\mathbf{C}(\unicode[STIX]{x1D70B}_{\infty })$
), an estimation
is called a (hybrid) subconvex bound (respectively, subconvex bound in the level aspect, subconvex bound in the archimedean aspect).
In the simplest case, the first and most famous subconvex bound was obtained for the Riemann zeta function by Weyl [Reference WeylWey21] (see, for example, [Reference PattersonPat88, § 6.6]),
which can be considered as (a special case of) a subconvex bound in the archimedean aspect for the Dirichlet
![]() $L$
-functions. If
$L$
-functions. If
![]() $\unicode[STIX]{x1D712}$
is a Dirichlet character of modulus
$\unicode[STIX]{x1D712}$
is a Dirichlet character of modulus
![]() $q=\mathbf{C}(\unicode[STIX]{x1D712}_{\text{fin}})\in \mathbb{N}$
, Burgess [Reference BurgessBur63] established his famous subconvex bound
$q=\mathbf{C}(\unicode[STIX]{x1D712}_{\text{fin}})\in \mathbb{N}$
, Burgess [Reference BurgessBur63] established his famous subconvex bound
Later, Heath-Brown [Reference Heath-BrownHea78, Reference Heath-BrownHea80] generalized the Burgess bound to include the
![]() $t$
-aspect as the hybrid bound
$t$
-aspect as the hybrid bound
Ever since, the subconvexity problem has become a venerable problem in analytic number theory, in which both the optimal subconvex saving
![]() $\unicode[STIX]{x1D6FF}$
and the largest class of
$\unicode[STIX]{x1D6FF}$
and the largest class of
![]() $L$
-function mark the limit of techniques of analytic number theory. The savings
$L$
-function mark the limit of techniques of analytic number theory. The savings
![]() $\unicode[STIX]{x1D6FF}=1/12$
and
$\unicode[STIX]{x1D6FF}=1/12$
and
![]() $1/16$
seem to be two natural barriers in the literature. They are called the Weyl-type (respectively, Burgess-type) subconvex bound for this historic reason. Moreover, it was discovered that for
$1/16$
seem to be two natural barriers in the literature. They are called the Weyl-type (respectively, Burgess-type) subconvex bound for this historic reason. Moreover, it was discovered that for
![]() $d>1$
the subconvexity problem of
$d>1$
the subconvexity problem of
![]() $L(s,\unicode[STIX]{x1D70B})$
is intimately related with various equidistribution problems [Reference DukeDuk88, Reference SarnakSar01]. More such relations can be found in [Reference MichelMic07, Lecture 5], as well as an application of the subconvexity problem in the level aspect for
$L(s,\unicode[STIX]{x1D70B})$
is intimately related with various equidistribution problems [Reference DukeDuk88, Reference SarnakSar01]. More such relations can be found in [Reference MichelMic07, Lecture 5], as well as an application of the subconvexity problem in the level aspect for
![]() $d=1$
and
$d=1$
and
![]() $\mathbf{F}$
imaginary quadratic.
$\mathbf{F}$
imaginary quadratic.
In this paper, we restrict to the case
![]() $d=1$
, that is, when
$d=1$
, that is, when
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D712}$
is a Hecke character. In the case
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D712}$
is a Hecke character. In the case
![]() $\mathbf{F}=\mathbb{Q}$
, many strong results are known besides the above bounds due to Weyl, Burgess and Heath-Brown (for example, [Reference Huxley and WattHW00]), especially in some special cases. For example, in [Reference Huxley and WattHW00] the case of
$\mathbf{F}=\mathbb{Q}$
, many strong results are known besides the above bounds due to Weyl, Burgess and Heath-Brown (for example, [Reference Huxley and WattHW00]), especially in some special cases. For example, in [Reference Huxley and WattHW00] the case of
![]() $q$
prime and of hybrid type is considered; in [Reference MilićevićMil16] with a very strong result of sub-Weyl-type, the case of
$q$
prime and of hybrid type is considered; in [Reference MilićevićMil16] with a very strong result of sub-Weyl-type, the case of
![]() $q=p^{n}$
a prime power and for the
$q=p^{n}$
a prime power and for the
![]() $q$
-aspect is treated. Another interesting special case is when we restrict to
$q$
-aspect is treated. Another interesting special case is when we restrict to
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{q}$
the quadratic character (and for
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{q}$
the quadratic character (and for
![]() $q$
special, say square-free). Bounds better than the Burgess one are known to hold for the Weyl-type. For example, among many other good results, Conrey and Iwaniec [Reference Conrey and IwaniecCI00, Corollary 1.5] obtained
$q$
special, say square-free). Bounds better than the Burgess one are known to hold for the Weyl-type. For example, among many other good results, Conrey and Iwaniec [Reference Conrey and IwaniecCI00, Corollary 1.5] obtained
which was recently generalized by Young [Reference YoungYou17, (1.5)] as
The above bound was further generalized for cube-free
![]() $q$
by Petrow and Young [Reference Petrow and YoungPY18]. Over a general number field, the best result known is the main theorem of Soehne [Reference SoehneSoe97, p. 227], which follows the method of Heath-Brown [Reference Heath-BrownHea78, Reference Heath-BrownHea80] (it attains the Weyl-type bound if the usual conductor
$q$
by Petrow and Young [Reference Petrow and YoungPY18]. Over a general number field, the best result known is the main theorem of Soehne [Reference SoehneSoe97, p. 227], which follows the method of Heath-Brown [Reference Heath-BrownHea78, Reference Heath-BrownHea80] (it attains the Weyl-type bound if the usual conductor
![]() $\mathfrak{f}=\mathfrak{f}_{0}^{3}$
is a cube):
$\mathfrak{f}=\mathfrak{f}_{0}^{3}$
is a cube):
where
![]() $\mathfrak{f}_{0}$
is any ideal dividing
$\mathfrak{f}_{0}$
is any ideal dividing
![]() $\mathfrak{f}$
, the usual conductor of
$\mathfrak{f}$
, the usual conductor of
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
In the work of Michel and Venkatesh [Reference Michel and VenkateshMV10, Theorem 5.1 and § 5.1.7], a subconvex bound for Hecke characters
![]() $\unicode[STIX]{x1D712}$
was obtained with the subconvex exponent unspecified. We shall modify their approach and obtain a hybrid subconvex bound of Burgess-type for
$\unicode[STIX]{x1D712}$
was obtained with the subconvex exponent unspecified. We shall modify their approach and obtain a hybrid subconvex bound of Burgess-type for
![]() $L$
-functions associated with Hecke characters over general number fields.
$L$
-functions associated with Hecke characters over general number fields.
Theorem 1.1. Let
![]() $\unicode[STIX]{x1D712}$
be a Hecke character of
$\unicode[STIX]{x1D712}$
be a Hecke character of
![]() $\mathbf{F}$
with analytic conductor
$\mathbf{F}$
with analytic conductor
![]() $\mathbf{C}(\unicode[STIX]{x1D712})$
. We have
$\mathbf{C}(\unicode[STIX]{x1D712})$
. We have
where
![]() $\unicode[STIX]{x1D703}$
is any constant towards the Ramanujan–Petersson conjecture.
$\unicode[STIX]{x1D703}$
is any constant towards the Ramanujan–Petersson conjecture.
Combining with Soehne’s bound, we deduce the following result.
Corollary 1.2. Let
![]() $\unicode[STIX]{x1D712}$
be a Hecke character of
$\unicode[STIX]{x1D712}$
be a Hecke character of
![]() $\mathbf{F}$
and
$\mathbf{F}$
and
![]() $t\in \mathbb{R}$
. Write
$t\in \mathbb{R}$
. Write
Then we have, for any
![]() $\unicode[STIX]{x1D716}>0$
,
$\unicode[STIX]{x1D716}>0$
,
 $$\begin{eqnarray}|L({\textstyle \frac{1}{2}}+it,\unicode[STIX]{x1D712})|\ll _{\unicode[STIX]{x1D716},\mathbf{F}}(Tq)^{\unicode[STIX]{x1D716}}\cdot \left\{\begin{array}{@{}ll@{}}(Tq)^{1/6} & \text{if}~T\geqslant q^{1/2},\\ q^{1/4} & \text{if}~q^{(1-2\unicode[STIX]{x1D703})/(3+2\unicode[STIX]{x1D703})}\leqslant T<q^{1/2},\\ (Tq)^{(3+2\unicode[STIX]{x1D703})/16} & \text{if}~T\leqslant q^{(1-2\unicode[STIX]{x1D703})/(3+2\unicode[STIX]{x1D703})},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}|L({\textstyle \frac{1}{2}}+it,\unicode[STIX]{x1D712})|\ll _{\unicode[STIX]{x1D716},\mathbf{F}}(Tq)^{\unicode[STIX]{x1D716}}\cdot \left\{\begin{array}{@{}ll@{}}(Tq)^{1/6} & \text{if}~T\geqslant q^{1/2},\\ q^{1/4} & \text{if}~q^{(1-2\unicode[STIX]{x1D703})/(3+2\unicode[STIX]{x1D703})}\leqslant T<q^{1/2},\\ (Tq)^{(3+2\unicode[STIX]{x1D703})/16} & \text{if}~T\leqslant q^{(1-2\unicode[STIX]{x1D703})/(3+2\unicode[STIX]{x1D703})},\end{array}\right.\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D703}$
is any constant towards the Ramanujan–Petersson conjecture.
$\unicode[STIX]{x1D703}$
is any constant towards the Ramanujan–Petersson conjecture.
Proof. We apply Soehne’s bound with
![]() $\mathfrak{f}_{0}=\mathfrak{o}$
the ring of integers of
$\mathfrak{f}_{0}=\mathfrak{o}$
the ring of integers of
![]() $\mathbf{F}$
, compare it with Theorem 1.1 and distinguish cases according to the relative size of
$\mathbf{F}$
, compare it with Theorem 1.1 and distinguish cases according to the relative size of
![]() $T$
and
$T$
and
![]() $q$
.◻
$q$
.◻
1.2 Discussion on method
The proof is inspired by the method of our earlier work [Reference WuWu14] where we established a Burgess-type subconvext bound for
![]() $\text{GL}_{1}$
twists of a
$\text{GL}_{1}$
twists of a
![]() $\text{GL}_{2}$
cuspidal representation
$\text{GL}_{2}$
cuspidal representation
![]() $\unicode[STIX]{x1D70B}$
:
$\unicode[STIX]{x1D70B}$
:
In this paper we show that it is possible to replace the cuspidal representation
![]() $\unicode[STIX]{x1D70B}$
by the Eisenstein series representation
$\unicode[STIX]{x1D70B}$
by the Eisenstein series representation
![]() $\unicode[STIX]{x1D70B}(1,1)$
and obtain the same bound. Theorem 1.1 then follows from the identity
$\unicode[STIX]{x1D70B}(1,1)$
and obtain the same bound. Theorem 1.1 then follows from the identity
The main hurdle is to address the non-square-integrability of Eisenstein series. For this we use a regularization process which we show does not harm the quality of the final outcome. By contrast, the original approach with truncation on Eisenstein series [Reference Michel and VenkateshMV10, § 5.1.7] does destroy the Burgess-like quality (see § 4.3 below for more details).
It is worthwhile to make some comments on our method, which is quite different from the methods applied in the case
![]() $\mathbf{F}=\mathbb{Q}$
by Burgess or by Conrey and Iwaniec. The Burgess method is based on the study of character sums of the shape
$\mathbf{F}=\mathbb{Q}$
by Burgess or by Conrey and Iwaniec. The Burgess method is based on the study of character sums of the shape
which makes use of Weil’s bound and hence makes extensive use of the periodicity of the summand function
![]() $n\mapsto \unicode[STIX]{x1D712}(n)$
. Its direct generalization,
$n\mapsto \unicode[STIX]{x1D712}(n)$
. Its direct generalization,
where
![]() $\mathfrak{A}$
runs over integral ideals, loses the periodicity for the summand function. Our method can be viewed as a variant of Conrey and Iwaniec’s method (see [Reference WuWu17a, § 1.1]). The main common feature is to bring a problem for
$\mathfrak{A}$
runs over integral ideals, loses the periodicity for the summand function. Our method can be viewed as a variant of Conrey and Iwaniec’s method (see [Reference WuWu17a, § 1.1]). The main common feature is to bring a problem for
![]() $\text{GL}_{1}$
into the setting for
$\text{GL}_{1}$
into the setting for
![]() $\text{GL}_{2}$
, and to use the available knowledge on the spectral theory of automorphic representations for
$\text{GL}_{2}$
, and to use the available knowledge on the spectral theory of automorphic representations for
![]() $\text{GL}_{2}$
. According to the comparison between [Reference Blomer and HarcosBH10] and [Reference WuWu14], this method virtually consists of taking (1.3) to the fourth power and studying the cancelation of the resulting character sums by means of the ‘spectral decomposition of the shifted convolution sums’ [Reference Blomer and HarcosBH08] instead of Weil’s bounds on character sums, hence it is also a variant of the original method of Burgess, ‘disguised’ in the language of periods, which treats the archimedean aspect equally well.
$\text{GL}_{2}$
. According to the comparison between [Reference Blomer and HarcosBH10] and [Reference WuWu14], this method virtually consists of taking (1.3) to the fourth power and studying the cancelation of the resulting character sums by means of the ‘spectral decomposition of the shifted convolution sums’ [Reference Blomer and HarcosBH08] instead of Weil’s bounds on character sums, hence it is also a variant of the original method of Burgess, ‘disguised’ in the language of periods, which treats the archimedean aspect equally well.
It would also be enlightening to point out the following explanation of identity (1.2) in terms of an identity of periods. Any function in the induced model of
![]() $\unicode[STIX]{x1D70B}(1,1)$
can be constructed from a Schwartz function
$\unicode[STIX]{x1D70B}(1,1)$
can be constructed from a Schwartz function
![]() $\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\mathbb{A}^{2})$
as
$\unicode[STIX]{x1D6F7}\in {\mathcal{S}}(\mathbb{A}^{2})$
as
whose Whittaker function is equal to
where
![]() $\mathfrak{F}_{2}(\unicode[STIX]{x1D6F7})$
is the Fourier transform of
$\mathfrak{F}_{2}(\unicode[STIX]{x1D6F7})$
is the Fourier transform of
![]() $\unicode[STIX]{x1D6F7}$
with respect to the second variable. Hence the period representing the left-hand side of (1.2) can be rewritten, with the change of variables
$\unicode[STIX]{x1D6F7}$
with respect to the second variable. Hence the period representing the left-hand side of (1.2) can be rewritten, with the change of variables
![]() $y\mapsto yt$
, as
$y\mapsto yt$
, as
The right-hand side of the above equation is exactly the integral representation of that of (1.2) if
![]() $\mathfrak{F}_{2}(\unicode[STIX]{x1D6F7})$
is decomposable as the tensor product of two functions in
$\mathfrak{F}_{2}(\unicode[STIX]{x1D6F7})$
is decomposable as the tensor product of two functions in
![]() ${\mathcal{S}}(\mathbb{A})$
. In other words, if we read the above discussion inversely, we see that our method makes use of the ‘two-dimensional Tate integral’, which brings in the structure of
${\mathcal{S}}(\mathbb{A})$
. In other words, if we read the above discussion inversely, we see that our method makes use of the ‘two-dimensional Tate integral’, which brings in the structure of
![]() $\text{GL}_{2}$
not present in the usual integral representation à la Tate of
$\text{GL}_{2}$
not present in the usual integral representation à la Tate of
![]() $L(s,\unicode[STIX]{x1D712})$
.
$L(s,\unicode[STIX]{x1D712})$
.
Remark 1.3. We also remark that the (global) factorizability
![]() $\unicode[STIX]{x1D712}(ty)=\unicode[STIX]{x1D712}(t)\unicode[STIX]{x1D712}(y)$
is responsible for such a link. For example, even though we have a similar identity of
$\unicode[STIX]{x1D712}(ty)=\unicode[STIX]{x1D712}(t)\unicode[STIX]{x1D712}(y)$
is responsible for such a link. For example, even though we have a similar identity of
![]() $L$
-functions,
$L$
-functions,
where
![]() $\unicode[STIX]{x1D70B}$
is a cuspidal representation of
$\unicode[STIX]{x1D70B}$
is a cuspidal representation of
![]() $\text{GL}_{2}$
, an identity of the integral representations of the two sides does not seem to exist: the left-hand side is represented by the Rankin–Selberg integral for
$\text{GL}_{2}$
, an identity of the integral representations of the two sides does not seem to exist: the left-hand side is represented by the Rankin–Selberg integral for
![]() $\text{GL}_{2}\times \text{GL}_{2}$
; the right-hand side is represented by twice or the square of the integral representation for the standard
$\text{GL}_{2}\times \text{GL}_{2}$
; the right-hand side is represented by twice or the square of the integral representation for the standard
![]() $L$
-function for
$L$
-function for
![]() $\text{GL}_{2}$
.
$\text{GL}_{2}$
.
1.3 Notation and conventions
![]() $\mathbb{N}$
is the set of natural numbers containing 0. All characters including Hecke characters are unitary. Non-unitary ones will be called quasi-characters.
$\mathbb{N}$
is the set of natural numbers containing 0. All characters including Hecke characters are unitary. Non-unitary ones will be called quasi-characters.
If
![]() $f$
is a meromorphic function around
$f$
is a meromorphic function around
![]() $s=s_{0}$
, we introduce the coefficients into its Laurent expansion,
$s=s_{0}$
, we introduce the coefficients into its Laurent expansion,
The terms for
![]() $k<0$
form the principal part [Reference RudinRud86, p. 211] of
$k<0$
form the principal part [Reference RudinRud86, p. 211] of
![]() $f$
at
$f$
at
![]() $s_{0}$
. We write
$s_{0}$
. We write
In particular, if
![]() $f$
has a pole of order
$f$
has a pole of order
![]() $k_{0}$
at
$k_{0}$
at
![]() $s_{0}$
, we have
$s_{0}$
, we have
Remark 1.4. The value
![]() $f^{\text{hol}}(s_{0})$
with notation as given above is intimately related with the finite part functional, denoted by f.p. in [Reference Gelbart and JacquetGJ79, Theorem (6.33)].
$f^{\text{hol}}(s_{0})$
with notation as given above is intimately related with the finite part functional, denoted by f.p. in [Reference Gelbart and JacquetGJ79, Theorem (6.33)].
In addition to the notation given above, we import [Reference WuWu14, § 2.1], in which most of the notation is in fact standard. (For example, our normalization of measures is just the Tamagawa measure with the standard convergence factors.) We simply address the following points/differences.
(i) The number field is written in bold character
 $\mathbf{F}$
, with ring of algebraic integers
$\mathbf{F}$
, with ring of algebraic integers
 $\mathfrak{o}$
and ring of adeles
$\mathfrak{o}$
and ring of adeles
 $\mathbb{A}$
.
$\mathbb{A}$
.
 $v$
denotes a place of
$v$
denotes a place of
 $\mathbf{F}$
. If
$\mathbf{F}$
. If
 $v<\infty$
is finite, we usually write
$v<\infty$
is finite, we usually write
 $v=\mathfrak{p}$
, which is identified with a prime ideal
$v=\mathfrak{p}$
, which is identified with a prime ideal
 $\mathfrak{p}$
of
$\mathfrak{p}$
of
 $\mathfrak{o}$
.
$\mathfrak{o}$
.(ii) We write the algebraic groups defined over
 $\mathbf{F}$
in bold characters such as
$\mathbf{F}$
in bold characters such as
 $\mathbf{G},\mathbf{N},\mathbf{B},\mathbf{Z}$
, where
$\mathbf{G},\mathbf{N},\mathbf{B},\mathbf{Z}$
, where
 $\mathbf{G}=\text{GL}_{2}$
,
$\mathbf{G}=\text{GL}_{2}$
,
 $\mathbf{B}$
is the upper triangular subgroup of
$\mathbf{B}$
is the upper triangular subgroup of
 $\mathbf{G}$
,
$\mathbf{G}$
,
 $\mathbf{N}{\vartriangleleft}\mathbf{B}$
is the unipotent upper triangular subgroup, and
$\mathbf{N}{\vartriangleleft}\mathbf{B}$
is the unipotent upper triangular subgroup, and
 $\mathbf{Z}$
is the center of
$\mathbf{Z}$
is the center of
 $\mathbf{G}$
.
$\mathbf{G}$
.(iii)
 $\mathbf{K}=\prod _{v}\mathbf{K}_{v}$
is the standard maximal compact subgroup of
$\mathbf{K}=\prod _{v}\mathbf{K}_{v}$
is the standard maximal compact subgroup of
 $\text{GL}_{2}(\mathbb{A})$
, where
$\text{GL}_{2}(\mathbb{A})$
, where  $$\begin{eqnarray}\mathbf{K}_{v}=\left\{\begin{array}{@{}ll@{}}\text{SO}_{2}(\mathbb{R}) & \text{if}~\mathbf{F}_{v}=\mathbb{R},\\ \text{SU}_{2}(\mathbb{C}) & \text{if}~\mathbf{F}_{v}=\mathbb{C},\\ \text{GL}_{2}(\mathfrak{o}_{\mathfrak{p}}) & \text{if}~v=\mathfrak{p}<\infty .\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{K}_{v}=\left\{\begin{array}{@{}ll@{}}\text{SO}_{2}(\mathbb{R}) & \text{if}~\mathbf{F}_{v}=\mathbb{R},\\ \text{SU}_{2}(\mathbb{C}) & \text{if}~\mathbf{F}_{v}=\mathbb{C},\\ \text{GL}_{2}(\mathfrak{o}_{\mathfrak{p}}) & \text{if}~v=\mathfrak{p}<\infty .\end{array}\right.\end{eqnarray}$$
(iv) In
 $\text{GL}_{2}$
, for local or global variables
$\text{GL}_{2}$
, for local or global variables
 $x\in \mathbf{F}_{v}$
or
$x\in \mathbf{F}_{v}$
or
 $\mathbb{A}$
,
$\mathbb{A}$
,
 $y\in \mathbf{F}_{v}^{\times }$
or
$y\in \mathbf{F}_{v}^{\times }$
or
 $\mathbb{A}^{\times }$
, we write
$\mathbb{A}^{\times }$
, we write  $$\begin{eqnarray}n(x)=\left(\begin{array}{@{}cc@{}}1 & x\\ & 1\end{array}\right),\quad a(y)=\left(\begin{array}{@{}cc@{}}y & \\ & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}n(x)=\left(\begin{array}{@{}cc@{}}1 & x\\ & 1\end{array}\right),\quad a(y)=\left(\begin{array}{@{}cc@{}}y & \\ & 1\end{array}\right).\end{eqnarray}$$
(v) We use the abbreviation
 $$\begin{eqnarray}[\text{GL}_{2}]=\text{GL}_{2}(\mathbf{F})\mathbf{Z}(\mathbb{A})\backslash \text{GL}_{2}(\mathbb{A})=[\text{PGL}_{2}].\end{eqnarray}$$
$$\begin{eqnarray}[\text{GL}_{2}]=\text{GL}_{2}(\mathbf{F})\mathbf{Z}(\mathbb{A})\backslash \text{GL}_{2}(\mathbb{A})=[\text{PGL}_{2}].\end{eqnarray}$$
(vi) If
 $f_{0}\in \unicode[STIX]{x1D70B}(1,1)$
, the global principal series representation induced from trivial characters, which defines a flat section
$f_{0}\in \unicode[STIX]{x1D70B}(1,1)$
, the global principal series representation induced from trivial characters, which defines a flat section
 $f_{s}\in \unicode[STIX]{x1D70B}(|\cdot |_{\mathbb{A}}^{s},|\cdot |_{\mathbb{A}}^{-s})$
, we normalize the usual Eisenstein series
$f_{s}\in \unicode[STIX]{x1D70B}(|\cdot |_{\mathbb{A}}^{s},|\cdot |_{\mathbb{A}}^{-s})$
, we normalize the usual Eisenstein series
 $\text{E}(s,f_{0})=\text{E}(f_{s})$
by
$\text{E}(s,f_{0})=\text{E}(f_{s})$
by  $$\begin{eqnarray}\text{E}^{\ast }(s,f_{0}):=\unicode[STIX]{x1D6EC}_{\mathbf{F}}(1+2s)\text{E}(s,f_{0}).\end{eqnarray}$$
$$\begin{eqnarray}\text{E}^{\ast }(s,f_{0}):=\unicode[STIX]{x1D6EC}_{\mathbf{F}}(1+2s)\text{E}(s,f_{0}).\end{eqnarray}$$
(vii) In the above equation,
 $\unicode[STIX]{x1D6EC}_{\mathbf{F}}(s)$
is the complete Dedekind zeta function of
$\unicode[STIX]{x1D6EC}_{\mathbf{F}}(s)$
is the complete Dedekind zeta function of
 $\unicode[STIX]{x1D701}_{\mathbf{F}}(s)$
. More generally,
$\unicode[STIX]{x1D701}_{\mathbf{F}}(s)$
. More generally,
 $L(\cdot )$
denotes
$L(\cdot )$
denotes
 $L$
-functions without factors at infinity.
$L$
-functions without factors at infinity.
 $\unicode[STIX]{x1D6EC}(\cdot )$
denotes the complete
$\unicode[STIX]{x1D6EC}(\cdot )$
denotes the complete
 $L$
-functions. We write
$L$
-functions. We write
 $\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }$
for the residue of
$\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }$
for the residue of
 $\unicode[STIX]{x1D701}_{\mathbf{F}}(s)$
at
$\unicode[STIX]{x1D701}_{\mathbf{F}}(s)$
at
 $s=1$
. We also introduce
$s=1$
. We also introduce  $$\begin{eqnarray}\unicode[STIX]{x1D706}_{\mathbf{F}}(s)=\frac{\unicode[STIX]{x1D6EC}_{\mathbf{F}}(-2s)}{\unicode[STIX]{x1D6EC}_{\mathbf{F}}(2+2s)}=\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}{s}+O(1).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{\mathbf{F}}(s)=\frac{\unicode[STIX]{x1D6EC}_{\mathbf{F}}(-2s)}{\unicode[STIX]{x1D6EC}_{\mathbf{F}}(2+2s)}=\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}{s}+O(1).\end{eqnarray}$$
Additional notation will be given in the course of proofs.
2 Miscellaneous preliminaries
2.1 Extension of Zagier’s regularized integrals
In this subsection we recall and summarize our extension of the theory of regularized integrals in [Reference WuWu18, §§ 2 and 3] without proofs. This extension fits well in the context of the Rankin–Selberg trace formula. It could not be well understood in the framework of the subconvexity problem. Hence we encourage the interested reader to read [Reference WuWu18, §§ 2 and 3] for a better understanding.
We begin by recalling the following space of functions on the automorphic quotient of
![]() $\text{GL}_{2}$
over a general number field
$\text{GL}_{2}$
over a general number field
![]() $\mathbf{F}$
with the ring of adeles
$\mathbf{F}$
with the ring of adeles
![]() $\mathbb{A}$
.
$\mathbb{A}$
.
Definition 2.1 [Reference WuWu18, Definition 2.14].
Let
![]() $\unicode[STIX]{x1D714}$
be a unitary character of
$\unicode[STIX]{x1D714}$
be a unitary character of
![]() $\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }$
. Let
$\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }$
. Let
![]() $\unicode[STIX]{x1D711}$
be a smooth function on
$\unicode[STIX]{x1D711}$
be a smooth function on
![]() $\text{GL}_{2}(\mathbf{F})\backslash \text{GL}_{2}(\mathbb{A})$
with central character
$\text{GL}_{2}(\mathbf{F})\backslash \text{GL}_{2}(\mathbb{A})$
with central character
![]() $\unicode[STIX]{x1D714}$
. We call
$\unicode[STIX]{x1D714}$
. We call
![]() $\unicode[STIX]{x1D711}$
finitely regularizable if there exist unitary characters
$\unicode[STIX]{x1D711}$
finitely regularizable if there exist unitary characters
![]() $\unicode[STIX]{x1D712}_{i}:\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }\rightarrow \mathbb{C}^{(1)}$
,
$\unicode[STIX]{x1D712}_{i}:\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }\rightarrow \mathbb{C}^{(1)}$
,
![]() $\unicode[STIX]{x1D6FC}_{i}\in \mathbb{C}$
,
$\unicode[STIX]{x1D6FC}_{i}\in \mathbb{C}$
,
![]() $n_{i}\in \mathbb{N}$
, and smooth functions
$n_{i}\in \mathbb{N}$
, and smooth functions
![]() $f_{i}\in \text{Ind}_{\mathbf{B}(\mathbb{A})\cap \mathbf{K}}^{\mathbf{K}}(\unicode[STIX]{x1D712}_{i},\unicode[STIX]{x1D714}\unicode[STIX]{x1D712}_{i}^{-1})$
for
$f_{i}\in \text{Ind}_{\mathbf{B}(\mathbb{A})\cap \mathbf{K}}^{\mathbf{K}}(\unicode[STIX]{x1D712}_{i},\unicode[STIX]{x1D714}\unicode[STIX]{x1D712}_{i}^{-1})$
for
![]() $1\leqslant i\leqslant l$
, such that:
$1\leqslant i\leqslant l$
, such that:
(i) for any
 $M\gg 1$
,
$M\gg 1$
,  $$\begin{eqnarray}\unicode[STIX]{x1D711}(n(x)a(y)k)=\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(n(x)a(y)k)+O(|y|_{\mathbb{ A}}^{-M})\quad \text{as}~|y|_{\mathbb{ A}}\rightarrow \infty ;\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(n(x)a(y)k)=\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(n(x)a(y)k)+O(|y|_{\mathbb{ A}}^{-M})\quad \text{as}~|y|_{\mathbb{ A}}\rightarrow \infty ;\end{eqnarray}$$
(ii) we can differentiate the above equality with respect to the universal enveloping algebra of the Lie algebra of
 $\text{GL}_{2}(\mathbb{A}_{\infty })$
.
$\text{GL}_{2}(\mathbb{A}_{\infty })$
.
Here we have written/defined the essential constant term
In this case, we call
![]() ${\mathcal{E}}\text{x}(\unicode[STIX]{x1D711})=\{\unicode[STIX]{x1D712}_{i}|\cdot |^{1/2+\unicode[STIX]{x1D6FC}_{i}}:1\leqslant i\leqslant l\}$
the exponent set of
${\mathcal{E}}\text{x}(\unicode[STIX]{x1D711})=\{\unicode[STIX]{x1D712}_{i}|\cdot |^{1/2+\unicode[STIX]{x1D6FC}_{i}}:1\leqslant i\leqslant l\}$
the exponent set of
![]() $\unicode[STIX]{x1D711}$
, and define
$\unicode[STIX]{x1D711}$
, and define
The space of finitely regularizable functions with central character
![]() $\unicode[STIX]{x1D714}$
is denoted by
$\unicode[STIX]{x1D714}$
is denoted by
![]() ${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
.
${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
.
Obviously
![]() ${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
is stable under the right regular translation of
${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
is stable under the right regular translation of
![]() $\text{GL}_{2}(\mathbb{A})$
and contains the Schwartz space with central character
$\text{GL}_{2}(\mathbb{A})$
and contains the Schwartz space with central character
![]() $\unicode[STIX]{x1D714}$
, hence the space of smooth cusp forms. It also contains any finite product of Eisenstein series [Reference WuWu18, Remark 2.19]. In the case
$\unicode[STIX]{x1D714}$
, hence the space of smooth cusp forms. It also contains any finite product of Eisenstein series [Reference WuWu18, Remark 2.19]. In the case
![]() $\unicode[STIX]{x1D714}=1$
and for any
$\unicode[STIX]{x1D714}=1$
and for any
![]() $\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\text{fr}}(\text{GL}_{2},1)$
, the integral
$\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\text{fr}}(\text{GL}_{2},1)$
, the integral
is convergent for any
![]() $\Re s\gg 1$
and admits meromorphic continuation. We use it to define the regularized integral as
$\Re s\gg 1$
and admits meromorphic continuation. We use it to define the regularized integral as
 $$\begin{eqnarray}\displaystyle & {\mathcal{A}}^{\text{fr}}(\text{GL}_{2},1)\rightarrow \mathbb{C}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D711}\mapsto \int _{[\text{PGL}_{2}]}^{\text{reg}}\unicode[STIX]{x1D711}(g)\,dg:=\frac{1}{\text{Vol}([\text{PGL}_{2}])}\biggl(\text{Res}_{s=1/2}R(s,\unicode[STIX]{x1D711})+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}_{i}=-1 \\ n_{i}=0 \\ \unicode[STIX]{x1D712}_{1}(\mathbb{A}^{(1)})=1}}\int _{\mathbf{K}}f_{i}(\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}\biggr). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & {\mathcal{A}}^{\text{fr}}(\text{GL}_{2},1)\rightarrow \mathbb{C}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D711}\mapsto \int _{[\text{PGL}_{2}]}^{\text{reg}}\unicode[STIX]{x1D711}(g)\,dg:=\frac{1}{\text{Vol}([\text{PGL}_{2}])}\biggl(\text{Res}_{s=1/2}R(s,\unicode[STIX]{x1D711})+\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}_{i}=-1 \\ n_{i}=0 \\ \unicode[STIX]{x1D712}_{1}(\mathbb{A}^{(1)})=1}}\int _{\mathbf{K}}f_{i}(\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}\biggr). & \displaystyle \nonumber\end{eqnarray}$$
If
![]() $f\in \text{Ind}_{\mathbf{B}(\mathbb{A})}^{\text{GL}_{2}(\mathbb{A})}(\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2})$
such that
$f\in \text{Ind}_{\mathbf{B}(\mathbb{A})}^{\text{GL}_{2}(\mathbb{A})}(\unicode[STIX]{x1D712}_{1},\unicode[STIX]{x1D712}_{2})$
such that
![]() $\unicode[STIX]{x1D712}_{1}\unicode[STIX]{x1D712}_{2}^{-1}=|\cdot |_{\mathbb{A}}^{i\unicode[STIX]{x1D707}}$
for some
$\unicode[STIX]{x1D712}_{1}\unicode[STIX]{x1D712}_{2}^{-1}=|\cdot |_{\mathbb{A}}^{i\unicode[STIX]{x1D707}}$
for some
![]() $\unicode[STIX]{x1D707}\in \mathbb{R}$
, we introduce the regularizing Eisenstein series as [Reference WuWu18, Definition 2.16]
$\unicode[STIX]{x1D707}\in \mathbb{R}$
, we introduce the regularizing Eisenstein series as [Reference WuWu18, Definition 2.16]
For any
![]() $\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
with auxiliary data given in Definition 2.1 we define [Reference WuWu18, (2.3)]
$\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
with auxiliary data given in Definition 2.1 we define [Reference WuWu18, (2.3)]
 $$\begin{eqnarray}{\mathcal{E}}(\unicode[STIX]{x1D711})=\mathop{\sum }_{\substack{ \Re \unicode[STIX]{x1D6FC}_{j}>0 \\ \unicode[STIX]{x1D6FC}_{j}\neq 1/2+i\unicode[STIX]{x1D707}_{j}}}\frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}\text{E}(\unicode[STIX]{x1D6FC}_{j},f_{j})+\mathop{\sum }_{\substack{ \Re \unicode[STIX]{x1D6FC}_{j}>0 \\ \unicode[STIX]{x1D6FC}_{j}=1/2+i\unicode[STIX]{x1D707}_{j}}}\frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}\text{E}^{\text{reg}}(\unicode[STIX]{x1D6FC}_{j},f_{j}),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}(\unicode[STIX]{x1D711})=\mathop{\sum }_{\substack{ \Re \unicode[STIX]{x1D6FC}_{j}>0 \\ \unicode[STIX]{x1D6FC}_{j}\neq 1/2+i\unicode[STIX]{x1D707}_{j}}}\frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}\text{E}(\unicode[STIX]{x1D6FC}_{j},f_{j})+\mathop{\sum }_{\substack{ \Re \unicode[STIX]{x1D6FC}_{j}>0 \\ \unicode[STIX]{x1D6FC}_{j}=1/2+i\unicode[STIX]{x1D707}_{j}}}\frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}\text{E}^{\text{reg}}(\unicode[STIX]{x1D6FC}_{j},f_{j}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D707}_{j}\in \mathbb{R}$
is defined only if
$\unicode[STIX]{x1D707}_{j}\in \mathbb{R}$
is defined only if
![]() $\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}_{j}^{2}(y)=|y|_{\mathbb{A}}^{-2i\unicode[STIX]{x1D707}_{j}}$
. This defines a linear map
$\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}_{j}^{2}(y)=|y|_{\mathbb{A}}^{-2i\unicode[STIX]{x1D707}_{j}}$
. This defines a linear map
such that
![]() $\unicode[STIX]{x1D711}-{\mathcal{E}}(\unicode[STIX]{x1D711})\in \text{L}^{1}(\text{GL}_{2},\unicode[STIX]{x1D714})$
, which is
$\unicode[STIX]{x1D711}-{\mathcal{E}}(\unicode[STIX]{x1D711})\in \text{L}^{1}(\text{GL}_{2},\unicode[STIX]{x1D714})$
, which is
![]() $\text{GL}_{2}(\mathbb{A})$
-intertwining when
$\text{GL}_{2}(\mathbb{A})$
-intertwining when
![]() ${\mathcal{E}}\text{x}(\unicode[STIX]{x1D711})$
does not contain
${\mathcal{E}}\text{x}(\unicode[STIX]{x1D711})$
does not contain
![]() $|\cdot |_{\mathbb{A}}$
. We denote the image by
$|\cdot |_{\mathbb{A}}$
. We denote the image by
![]() ${\mathcal{E}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
. Moreover, if
${\mathcal{E}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
. Moreover, if
![]() ${\mathcal{E}}\text{x}^{+}(\unicode[STIX]{x1D711})\cap {\mathcal{E}}\text{x}^{-}(\unicode[STIX]{x1D711})=\emptyset$
then
${\mathcal{E}}\text{x}^{+}(\unicode[STIX]{x1D711})\cap {\mathcal{E}}\text{x}^{-}(\unicode[STIX]{x1D711})=\emptyset$
then
![]() ${\mathcal{E}}(\unicode[STIX]{x1D711})$
is the unique element in
${\mathcal{E}}(\unicode[STIX]{x1D711})$
is the unique element in
![]() ${\mathcal{E}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
such that
${\mathcal{E}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
such that
![]() $\unicode[STIX]{x1D711}-{\mathcal{E}}(\unicode[STIX]{x1D711})\in \text{L}^{2}(\text{GL}_{2},\unicode[STIX]{x1D714})$
[Reference WuWu18, Proposition 2.25], and we call it the
$\unicode[STIX]{x1D711}-{\mathcal{E}}(\unicode[STIX]{x1D711})\in \text{L}^{2}(\text{GL}_{2},\unicode[STIX]{x1D714})$
[Reference WuWu18, Proposition 2.25], and we call it the
![]() $\text{L}^{2}$
-residue of
$\text{L}^{2}$
-residue of
![]() $\unicode[STIX]{x1D711}$
[Reference WuWu18, Definition 2.26]. In the case
$\unicode[STIX]{x1D711}$
[Reference WuWu18, Definition 2.26]. In the case
![]() $\unicode[STIX]{x1D714}=1$
,
$\unicode[STIX]{x1D714}=1$
,
![]() ${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},1)$
is in the range of applicability of the regularized integral and [Reference WuWu18, Proposition 2.27]
${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},1)$
is in the range of applicability of the regularized integral and [Reference WuWu18, Proposition 2.27]
In particular, the above equation proves the
![]() $\text{GL}_{2}(\mathbb{A})$
-invariance of the regularized integral as a functional on
$\text{GL}_{2}(\mathbb{A})$
-invariance of the regularized integral as a functional on
![]() ${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},1)$
, when
${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},1)$
, when
![]() ${\mathcal{E}}\text{x}(\unicode[STIX]{x1D711})$
does not contain
${\mathcal{E}}\text{x}(\unicode[STIX]{x1D711})$
does not contain
![]() $|\cdot |_{\mathbb{A}}$
. In this case the above equality was originally due to Zagier [Reference ZagierZag82]. In [Reference WuWu18, Theorem 2.12 and Definition 2.13] we carefully generalized this theory into the adelic setting and proved the above equality without constraint on
$|\cdot |_{\mathbb{A}}$
. In this case the above equality was originally due to Zagier [Reference ZagierZag82]. In [Reference WuWu18, Theorem 2.12 and Definition 2.13] we carefully generalized this theory into the adelic setting and proved the above equality without constraint on
![]() ${\mathcal{E}}\text{x}(\unicode[STIX]{x1D711})$
.
${\mathcal{E}}\text{x}(\unicode[STIX]{x1D711})$
.
In view of the inclusion [Reference WuWu18, Remark 2.19]
we can consider the following bilinear form. Let
![]() $\unicode[STIX]{x1D70B}_{j}$
,
$\unicode[STIX]{x1D70B}_{j}$
,
![]() $j=1,2$
, be two principal series representations with central character
$j=1,2$
, be two principal series representations with central character
![]() $\unicode[STIX]{x1D714}_{j}$
satisfying
$\unicode[STIX]{x1D714}_{j}$
satisfying
![]() $\unicode[STIX]{x1D714}_{1}\unicode[STIX]{x1D714}_{2}=1$
. Let
$\unicode[STIX]{x1D714}_{1}\unicode[STIX]{x1D714}_{2}=1$
. Let
![]() $V_{j}$
be the vector space of
$V_{j}$
be the vector space of
![]() $\unicode[STIX]{x1D70B}_{j}$
realized in the induced model from
$\unicode[STIX]{x1D70B}_{j}$
realized in the induced model from
![]() $\mathbf{B}(\mathbb{A})$
with subspace of smooth vectors
$\mathbf{B}(\mathbb{A})$
with subspace of smooth vectors
![]() $V_{j}^{\infty }$
. We then get a
$V_{j}^{\infty }$
. We then get a
![]() $\text{GL}_{2}(\mathbb{A})$
-invariant bilinear form
$\text{GL}_{2}(\mathbb{A})$
-invariant bilinear form
where
![]() $\text{E}(f_{j})$
should be suitably regularized if
$\text{E}(f_{j})$
should be suitably regularized if
![]() $\unicode[STIX]{x1D70B}_{j}$
is at a position which creates a pole/zero for the relevant Eisenstein series. In [Reference WuWu18, Theorem 3.5] we succeeded in identifying this bilinear form in the induced model. In order to present the result, we need to introduce some extra notation. If we identify for any
$\unicode[STIX]{x1D70B}_{j}$
is at a position which creates a pole/zero for the relevant Eisenstein series. In [Reference WuWu18, Theorem 3.5] we succeeded in identifying this bilinear form in the induced model. In order to present the result, we need to introduce some extra notation. If we identify for any
![]() $s\in \mathbb{C}$
the space of functions
$s\in \mathbb{C}$
the space of functions
![]() $\unicode[STIX]{x1D70B}_{s}$
with
$\unicode[STIX]{x1D70B}_{s}$
with
![]() $H$
, where
$H$
, where
then we can regard the intertwining operator
![]() ${\mathcal{M}}_{s}:\unicode[STIX]{x1D70B}_{s}\rightarrow \unicode[STIX]{x1D70B}_{-s}$
as a map from
${\mathcal{M}}_{s}:\unicode[STIX]{x1D70B}_{s}\rightarrow \unicode[STIX]{x1D70B}_{-s}$
as a map from
![]() $H$
to itself. Using the flat section map
$H$
to itself. Using the flat section map
![]() $H\rightarrow \unicode[STIX]{x1D70B}_{s}$
,
$H\rightarrow \unicode[STIX]{x1D70B}_{s}$
,
![]() $f\mapsto f_{s}$
, we mean
$f\mapsto f_{s}$
, we mean
Let
![]() $e_{0}\in H$
be the constant function taking value 1. Define
$e_{0}\in H$
be the constant function taking value 1. Define
where
![]() $d\unicode[STIX]{x1D705}$
is the probability Haar measure on
$d\unicode[STIX]{x1D705}$
is the probability Haar measure on
![]() $\mathbf{K}$
. We obtain a map from
$\mathbf{K}$
. We obtain a map from
![]() $H$
to itself,
$H$
to itself,
where
![]() $I$
is the identity map. Since
$I$
is the identity map. Since
![]() ${\mathcal{M}}_{s}$
is ‘diagonalizable’, we obtain the Taylor expansion as operators
${\mathcal{M}}_{s}$
is ‘diagonalizable’, we obtain the Taylor expansion as operators
Theorem 2.2 [Reference WuWu18, Theorem 3.5].
The regularized integral of the product of two unitary Eisenstein series is computed as follows.
(i) Suppose
 $\unicode[STIX]{x1D709}_{1}\neq \unicode[STIX]{x1D709}_{2}$
. If
$\unicode[STIX]{x1D709}_{1}\neq \unicode[STIX]{x1D709}_{2}$
. If
 $\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}),\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1}^{-1},\unicode[STIX]{x1D709}_{2}^{-1})$
(respectively,
$\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}),\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1}^{-1},\unicode[STIX]{x1D709}_{2}^{-1})$
(respectively,
 $\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{2}^{-1},\unicode[STIX]{x1D709}_{1}^{-1})$
), then
$\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{2}^{-1},\unicode[STIX]{x1D709}_{1}^{-1})$
), then  $$\begin{eqnarray}\displaystyle & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}(0,f_{1})\text{E}(0,f_{2})=\frac{2\unicode[STIX]{x1D706}_{\mathbf{F}}^{(0)}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\text{P}_{\mathbf{K}}(f_{1}f_{2})-\text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(1)}f_{1}\cdot {\mathcal{M}}_{0}f_{2}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \biggl(\text{respectively}~\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(0)}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}(\text{P}_{\mathbf{K}}(f_{1}{\mathcal{M}}_{0}f_{2})+\text{P}_{\mathbf{K}}(f_{2}{\mathcal{M}}_{0}f_{1}))-\text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(1)}f_{1}\cdot f_{2})\biggr). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}(0,f_{1})\text{E}(0,f_{2})=\frac{2\unicode[STIX]{x1D706}_{\mathbf{F}}^{(0)}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\text{P}_{\mathbf{K}}(f_{1}f_{2})-\text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(1)}f_{1}\cdot {\mathcal{M}}_{0}f_{2}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \biggl(\text{respectively}~\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(0)}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}(\text{P}_{\mathbf{K}}(f_{1}{\mathcal{M}}_{0}f_{2})+\text{P}_{\mathbf{K}}(f_{2}{\mathcal{M}}_{0}f_{1}))-\text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(1)}f_{1}\cdot f_{2})\biggr). & \displaystyle \nonumber\end{eqnarray}$$
(ii) If
 $\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}),\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D709}^{-1})$
, then
$\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}),\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D709}^{-1})$
, then  $$\begin{eqnarray}\displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{(1)}(0,f_{1})\text{E}^{(1)}(0,f_{2}) & = & \displaystyle \frac{4\unicode[STIX]{x1D706}_{\mathbf{F}}^{(2)}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{-1}(0)}\text{P}_{\mathbf{K}}(f_{1}f_{2})+\frac{4\unicode[STIX]{x1D706}_{\mathbf{F}}^{(2)}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{-1}(0)}\text{P}_{\mathbf{K}}(f_{1}\cdot {\mathcal{M}}_{0}^{(1)}f_{2})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(0)}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{-1}(0)}\text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(1)}f_{1}\cdot {\mathcal{M}}_{0}^{(1)}f_{2})-\frac{1}{3}\text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(3)}f_{1}\cdot f_{2})\nonumber\\ \displaystyle & & \displaystyle -\,\text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(2)}f_{1}\cdot {\mathcal{M}}_{0}^{(1)}f_{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{(1)}(0,f_{1})\text{E}^{(1)}(0,f_{2}) & = & \displaystyle \frac{4\unicode[STIX]{x1D706}_{\mathbf{F}}^{(2)}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{-1}(0)}\text{P}_{\mathbf{K}}(f_{1}f_{2})+\frac{4\unicode[STIX]{x1D706}_{\mathbf{F}}^{(2)}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{-1}(0)}\text{P}_{\mathbf{K}}(f_{1}\cdot {\mathcal{M}}_{0}^{(1)}f_{2})\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(0)}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{-1}(0)}\text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(1)}f_{1}\cdot {\mathcal{M}}_{0}^{(1)}f_{2})-\frac{1}{3}\text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(3)}f_{1}\cdot f_{2})\nonumber\\ \displaystyle & & \displaystyle -\,\text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(2)}f_{1}\cdot {\mathcal{M}}_{0}^{(1)}f_{2}).\nonumber\end{eqnarray}$$
Here we have written [Reference WuWu18, (2.2)]
2.2 Regularized triple product formula
Let us first complete the analysis for products of two Eisenstein series. We recall a lemma.
Lemma 2.3 [Reference WuWu18, Lemma 3.4].
Let
![]() $f,f_{1},f_{2}\in \text{Res}_{\mathbf{K}}^{\text{GL}_{2}(\mathbb{A})}\unicode[STIX]{x1D70B}(1,1)$
. For
$f,f_{1},f_{2}\in \text{Res}_{\mathbf{K}}^{\text{GL}_{2}(\mathbb{A})}\unicode[STIX]{x1D70B}(1,1)$
. For
![]() $0\neq s\in \mathbb{C}$
small, we have, for any
$0\neq s\in \mathbb{C}$
small, we have, for any
![]() $n,n_{1},n_{2}\in \mathbb{N}$
,
$n,n_{1},n_{2}\in \mathbb{N}$
,
 $$\begin{eqnarray}\displaystyle & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(n)}\biggl(\frac{1}{2}+s,f\biggr)=-\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n)}(s)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\text{P}_{\mathbf{K}}(f); & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(n_{1})}\biggl(\frac{1}{2}+s,f_{1}\biggr)\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(n)}\biggl(\frac{1}{2}+s,f\biggr)=-\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n)}(s)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\text{P}_{\mathbf{K}}(f); & \displaystyle \nonumber\\ \displaystyle & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(n_{1})}\biggl(\frac{1}{2}+s,f_{1}\biggr)\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0. & \displaystyle \nonumber\end{eqnarray}$$
We also recall the technique of deformation [Reference WuWu18, (3.1)], inspired by the work of Michel and Venkatesh. In general, if
![]() $\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\text{fr}}(\text{PGL}_{2})$
,
$\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\text{fr}}(\text{PGL}_{2})$
,
![]() ${\mathcal{E}}\in {\mathcal{E}}(\text{PGL}_{2})$
are given, so that
${\mathcal{E}}\in {\mathcal{E}}(\text{PGL}_{2})$
are given, so that
![]() $\unicode[STIX]{x1D711}-{\mathcal{E}}\in \text{L}^{1}([\text{PGL}_{2}])$
, and if we can find continuous families
$\unicode[STIX]{x1D711}-{\mathcal{E}}\in \text{L}^{1}([\text{PGL}_{2}])$
, and if we can find continuous families
![]() $\unicode[STIX]{x1D711}_{s}\in {\mathcal{A}}^{\text{fr}}(\text{PGL}_{2})$
,
$\unicode[STIX]{x1D711}_{s}\in {\mathcal{A}}^{\text{fr}}(\text{PGL}_{2})$
,
![]() ${\mathcal{E}}_{s}\in {\mathcal{E}}(\text{PGL}_{2})$
which coincide with
${\mathcal{E}}_{s}\in {\mathcal{E}}(\text{PGL}_{2})$
which coincide with
![]() $\unicode[STIX]{x1D711}$
,
$\unicode[STIX]{x1D711}$
,
![]() ${\mathcal{E}}$
at
${\mathcal{E}}$
at
![]() $s=0$
, then we have
$s=0$
, then we have
We turn to the study of regularized integrals of the form
Denote
![]() $e=e_{1}$
. We can write
$e=e_{1}$
. We can write
 $$\begin{eqnarray}\displaystyle \text{E}_{\mathbf{N}}^{\text{reg}}(s,f) & = & \displaystyle f_{s}+(\widetilde{{\mathcal{M}}}_{s}f)_{-s}+\unicode[STIX]{x1D706}_{\mathbf{F}}\biggl(s-\frac{1}{2}\biggr)\text{P}_{\mathbf{K}}(f)(e_{-s}-e_{-1/2});\nonumber\\ \displaystyle \text{E}_{\mathbf{N}}^{\text{reg},(n)}\biggl(\frac{1}{2},f\biggr) & = & \displaystyle f_{1/2}^{(n)}+\mathop{\sum }_{k=0}^{n}\binom{n}{k}(-1)^{k}(\widetilde{{\mathcal{M}}}_{1/2}^{(n-k)}f)_{-1/2}^{(k)}\nonumber\\ \displaystyle & & \displaystyle +\,\text{P}_{\mathbf{K}}(f)\cdot \bigg\{\frac{(-1)^{n+1}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}{n+1}e_{-1/2}^{(n+1)}+\mathop{\sum }_{k=1}^{n}\binom{n}{k}(-1)^{k}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n-k)}(0)e_{-1/2}^{k}\bigg\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{E}_{\mathbf{N}}^{\text{reg}}(s,f) & = & \displaystyle f_{s}+(\widetilde{{\mathcal{M}}}_{s}f)_{-s}+\unicode[STIX]{x1D706}_{\mathbf{F}}\biggl(s-\frac{1}{2}\biggr)\text{P}_{\mathbf{K}}(f)(e_{-s}-e_{-1/2});\nonumber\\ \displaystyle \text{E}_{\mathbf{N}}^{\text{reg},(n)}\biggl(\frac{1}{2},f\biggr) & = & \displaystyle f_{1/2}^{(n)}+\mathop{\sum }_{k=0}^{n}\binom{n}{k}(-1)^{k}(\widetilde{{\mathcal{M}}}_{1/2}^{(n-k)}f)_{-1/2}^{(k)}\nonumber\\ \displaystyle & & \displaystyle +\,\text{P}_{\mathbf{K}}(f)\cdot \bigg\{\frac{(-1)^{n+1}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}{n+1}e_{-1/2}^{(n+1)}+\mathop{\sum }_{k=1}^{n}\binom{n}{k}(-1)^{k}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n-k)}(0)e_{-1/2}^{k}\bigg\},\nonumber\end{eqnarray}$$
from which one can easily deduce
![]() $\text{E}_{\mathbf{N}}^{\text{reg}}(1/2+s,f_{1})\text{E}_{\mathbf{N}}^{\text{reg},(n_{2})}(1/2,f_{2})$
. We tentatively define
$\text{E}_{\mathbf{N}}^{\text{reg}}(1/2+s,f_{1})\text{E}_{\mathbf{N}}^{\text{reg},(n_{2})}(1/2,f_{2})$
. We tentatively define
 $$\begin{eqnarray}\displaystyle {\mathcal{E}}^{\text{reg}}(s) & := & \displaystyle \text{E}^{(n_{2})}\biggl(\frac{3}{2}+s,f_{1}f_{2}\biggr)+\mathop{\sum }_{k=0}^{n_{2}}\binom{n_{2}}{k}(-1)^{k}\text{E}^{\text{reg},(k)}\biggl(\frac{1}{2}+s,f_{1}\widetilde{{\mathcal{M}}}_{1/2}^{(n_{2}-k)}f_{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\text{P}_{\mathbf{K}}(f_{2})\cdot \bigg\{\frac{(-1)^{n_{2}+1}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}{n_{2}+1}\text{E}^{\text{reg},(n_{2}+1)}\biggl(\frac{1}{2}+s,f_{1}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{k=1}^{n_{2}}\binom{n_{2}}{k}(-1)^{k}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n_{2}-k)}(0)\text{E}^{\text{reg},(k)}\biggl(\frac{1}{2}+s,f_{1}\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle +\,\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2}-s,f_{2}\widetilde{{\mathcal{M}}}_{1/2+s}f_{1}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D706}_{\mathbf{F}}(s)\text{P}_{\mathbf{K}}(f_{1})\cdot \bigg\{\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2}-s,f_{2}\biggr)-\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)\bigg\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{E}}^{\text{reg}}(s) & := & \displaystyle \text{E}^{(n_{2})}\biggl(\frac{3}{2}+s,f_{1}f_{2}\biggr)+\mathop{\sum }_{k=0}^{n_{2}}\binom{n_{2}}{k}(-1)^{k}\text{E}^{\text{reg},(k)}\biggl(\frac{1}{2}+s,f_{1}\widetilde{{\mathcal{M}}}_{1/2}^{(n_{2}-k)}f_{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\text{P}_{\mathbf{K}}(f_{2})\cdot \bigg\{\frac{(-1)^{n_{2}+1}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}{n_{2}+1}\text{E}^{\text{reg},(n_{2}+1)}\biggl(\frac{1}{2}+s,f_{1}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{k=1}^{n_{2}}\binom{n_{2}}{k}(-1)^{k}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n_{2}-k)}(0)\text{E}^{\text{reg},(k)}\biggl(\frac{1}{2}+s,f_{1}\biggr)\bigg\}\nonumber\\ \displaystyle & & \displaystyle +\,\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2}-s,f_{2}\widetilde{{\mathcal{M}}}_{1/2+s}f_{1}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D706}_{\mathbf{F}}(s)\text{P}_{\mathbf{K}}(f_{1})\cdot \bigg\{\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2}-s,f_{2}\biggr)-\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)\bigg\}.\nonumber\end{eqnarray}$$
Applying Lemma 2.3 with
![]() $n_{1}=0$
together with (2.3), we get
$n_{1}=0$
together with (2.3), we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg}}\biggl(\frac{1}{2},f_{1}\biggr)\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{s\rightarrow 0}\int _{[\text{PGL}_{2}]}\text{E}^{\text{reg}}\biggl(\frac{1}{2}+s,f_{1}\biggr)\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)-{\mathcal{E}}^{\text{reg}}(s)\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{s\rightarrow 0}\mathop{\sum }_{k=0}^{n_{2}}\binom{n_{2}}{k}\frac{(-1)^{k}}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(k)}(s)\text{P}_{\mathbf{K}}(f_{1}\widetilde{{\mathcal{M}}}_{1/2}^{(n_{2}-k)}f_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n_{2})}(-s)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\text{P}_{\mathbf{K}}(f_{2}\widetilde{{\mathcal{M}}}_{1/2+s}f_{1})+\text{P}_{\mathbf{K}}(f_{1})\text{P}_{\mathbf{K}}(f_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\bigg\{\frac{(-1)^{n_{2}+1}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n_{2}+1)}(s)}{n_{2}+1}+\mathop{\sum }_{k=1}^{n_{2}}\binom{n_{2}}{k}(-1)^{k}\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n_{2}-k)}(0)\unicode[STIX]{x1D706}_{\boldsymbol{ F}}^{(k)}(s)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}+\unicode[STIX]{x1D706}_{\mathbf{F}}(s)\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n_{2})}(-s)\bigg\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg}}\biggl(\frac{1}{2},f_{1}\biggr)\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{s\rightarrow 0}\int _{[\text{PGL}_{2}]}\text{E}^{\text{reg}}\biggl(\frac{1}{2}+s,f_{1}\biggr)\text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)-{\mathcal{E}}^{\text{reg}}(s)\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{s\rightarrow 0}\mathop{\sum }_{k=0}^{n_{2}}\binom{n_{2}}{k}\frac{(-1)^{k}}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(k)}(s)\text{P}_{\mathbf{K}}(f_{1}\widetilde{{\mathcal{M}}}_{1/2}^{(n_{2}-k)}f_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n_{2})}(-s)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\text{P}_{\mathbf{K}}(f_{2}\widetilde{{\mathcal{M}}}_{1/2+s}f_{1})+\text{P}_{\mathbf{K}}(f_{1})\text{P}_{\mathbf{K}}(f_{2})\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\bigg\{\frac{(-1)^{n_{2}+1}\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n_{2}+1)}(s)}{n_{2}+1}+\mathop{\sum }_{k=1}^{n_{2}}\binom{n_{2}}{k}(-1)^{k}\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n_{2}-k)}(0)\unicode[STIX]{x1D706}_{\boldsymbol{ F}}^{(k)}(s)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}+\unicode[STIX]{x1D706}_{\mathbf{F}}(s)\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n_{2})}(-s)\bigg\}.\nonumber\end{eqnarray}$$
Taking Laurent expansions, we verify that the function in
![]() $s$
in the range of the above limit is regular at
$s$
in the range of the above limit is regular at
![]() $s=0$
, contrary to appearances. The symmetry
$s=0$
, contrary to appearances. The symmetry
must be used. Moreover, it can be differentiated
![]() $n_{1}$
times to deduce (iii) in the following theorem.
$n_{1}$
times to deduce (iii) in the following theorem.
Theorem 2.4. Consider two (global) principal series representations
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\unicode[STIX]{x1D70B}_{2}$
of
$\unicode[STIX]{x1D70B}_{2}$
of
![]() $\text{GL}_{2}(\mathbb{A})$
.
$\text{GL}_{2}(\mathbb{A})$
.
(i) Write
 $\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{1}^{\prime })$
and
$\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{1}^{\prime })$
and
 $\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{2}^{\prime })$
. Suppose
$\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{2}^{\prime })$
. Suppose
 $\unicode[STIX]{x1D70B}_{1}\not \simeq \tilde{\unicode[STIX]{x1D70B}}_{2}$
. This case is subdivided into four cases according to:
$\unicode[STIX]{x1D70B}_{1}\not \simeq \tilde{\unicode[STIX]{x1D70B}}_{2}$
. This case is subdivided into four cases according to:∙
 $\unicode[STIX]{x1D709}_{1}\neq \unicode[STIX]{x1D709}_{1}^{\prime }$
and
$\unicode[STIX]{x1D709}_{1}\neq \unicode[STIX]{x1D709}_{1}^{\prime }$
and
 $\unicode[STIX]{x1D709}_{2}\neq \unicode[STIX]{x1D709}_{2}^{\prime }$
;
$\unicode[STIX]{x1D709}_{2}\neq \unicode[STIX]{x1D709}_{2}^{\prime }$
;∙ respectively
 $\unicode[STIX]{x1D709}_{1}=\unicode[STIX]{x1D709}_{1}^{\prime }$
and
$\unicode[STIX]{x1D709}_{1}=\unicode[STIX]{x1D709}_{1}^{\prime }$
and
 $\unicode[STIX]{x1D709}_{2}\neq \unicode[STIX]{x1D709}_{2}^{\prime }$
;
$\unicode[STIX]{x1D709}_{2}\neq \unicode[STIX]{x1D709}_{2}^{\prime }$
;∙ respectively
 $\unicode[STIX]{x1D709}_{1}\neq \unicode[STIX]{x1D709}_{1}^{\prime }$
and
$\unicode[STIX]{x1D709}_{1}\neq \unicode[STIX]{x1D709}_{1}^{\prime }$
and
 $\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}_{2}^{\prime }$
;
$\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}_{2}^{\prime }$
;∙ respectively
 $\unicode[STIX]{x1D709}_{1}=\unicode[STIX]{x1D709}_{1}^{\prime }$
,
$\unicode[STIX]{x1D709}_{1}=\unicode[STIX]{x1D709}_{1}^{\prime }$
,
 $\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}_{2}^{\prime }$
,
$\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}_{2}^{\prime }$
,
 $\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}\neq 1$
and
$\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}\neq 1$
and
 $\unicode[STIX]{x1D709}_{1}^{2}\unicode[STIX]{x1D709}_{2}^{2}=1$
.
$\unicode[STIX]{x1D709}_{1}^{2}\unicode[STIX]{x1D709}_{2}^{2}=1$
.
Then, for any
 $n_{1},n_{2}\in \mathbb{N}$
, we have
$n_{1},n_{2}\in \mathbb{N}$
, we have  $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0;\nonumber\\ \displaystyle \text{respectively}\quad & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0;\nonumber\\ \displaystyle \text{respectively}\quad & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0;\nonumber\\ \displaystyle \text{respectively}\quad & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0;\nonumber\\ \displaystyle \text{respectively}\quad & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0;\nonumber\\ \displaystyle \text{respectively}\quad & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0;\nonumber\\ \displaystyle \text{respectively}\quad & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0.\nonumber\end{eqnarray}$$
(ii) Let
 $\unicode[STIX]{x1D709}_{1}\neq \unicode[STIX]{x1D709}_{2}$
. If
$\unicode[STIX]{x1D709}_{1}\neq \unicode[STIX]{x1D709}_{2}$
. If
 $\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})$
,
$\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})$
,
 $\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1}^{-1},\unicode[STIX]{x1D709}_{2}^{-1})$
, respectively
$\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1}^{-1},\unicode[STIX]{x1D709}_{2}^{-1})$
, respectively
 $\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{2}^{-1},\unicode[STIX]{x1D709}_{1}^{-1})$
, then, for any
$\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{2}^{-1},\unicode[STIX]{x1D709}_{1}^{-1})$
, then, for any
 $n_{1},n_{2}\in \mathbb{N}$
, we have is a linear combination with coefficients depending only on
$n_{1},n_{2}\in \mathbb{N}$
, we have is a linear combination with coefficients depending only on $$\begin{eqnarray}\int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0,\quad \text{respectively}\end{eqnarray}$$
$$\begin{eqnarray}\int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)=0,\quad \text{respectively}\end{eqnarray}$$
 $n_{1},n_{2}$
and
$n_{1},n_{2}$
and
 $\unicode[STIX]{x1D706}_{\mathbf{F}}(s)$
of
$\unicode[STIX]{x1D706}_{\mathbf{F}}(s)$
of  $$\begin{eqnarray}\text{P}_{\mathbf{K}}({\mathcal{M}}_{1/2}^{(n_{1}+n_{2}+1)}f_{1}\cdot f_{2});\quad \text{P}_{\mathbf{K}}({\mathcal{M}}_{1/2}^{(l)}f_{1}\cdot f_{2})=\text{P}_{\mathbf{K}}(f_{1}\cdot {\mathcal{M}}_{1/2}^{(l)}f_{2}),0\leqslant l\leqslant \max (n_{1},n_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\text{P}_{\mathbf{K}}({\mathcal{M}}_{1/2}^{(n_{1}+n_{2}+1)}f_{1}\cdot f_{2});\quad \text{P}_{\mathbf{K}}({\mathcal{M}}_{1/2}^{(l)}f_{1}\cdot f_{2})=\text{P}_{\mathbf{K}}(f_{1}\cdot {\mathcal{M}}_{1/2}^{(l)}f_{2}),0\leqslant l\leqslant \max (n_{1},n_{2}).\end{eqnarray}$$
(iii) If
 $\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}),\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D709}^{-1})$
, then for any
$\unicode[STIX]{x1D70B}_{1}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}),\unicode[STIX]{x1D70B}_{2}=\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}^{-1},\unicode[STIX]{x1D709}^{-1})$
, then for any
 $n_{1},n_{2}\in \mathbb{N}$
is a linear combination with coefficients depending only on
$n_{1},n_{2}\in \mathbb{N}$
is a linear combination with coefficients depending only on $$\begin{eqnarray}\int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(n_{1})}\biggl(\frac{1}{2},f_{1}\biggr)\cdot \text{E}^{\text{reg},(n_{2})}\biggl(\frac{1}{2},f_{2}\biggr)\end{eqnarray}$$
 $n_{1},n_{2}$
and
$n_{1},n_{2}$
and
 $\unicode[STIX]{x1D706}_{\mathbf{F}}(s)$
of
$\unicode[STIX]{x1D706}_{\mathbf{F}}(s)$
of  $$\begin{eqnarray}\displaystyle & \displaystyle \text{P}_{\mathbf{K}}(\widetilde{{\mathcal{M}}}_{1/2}^{(l)}f_{1}\cdot f_{2})=\text{P}_{\mathbf{K}}(f_{1}\cdot \widetilde{{\mathcal{M}}}_{1/2}^{(l)}f_{2}),0\leqslant l\leqslant \max (n_{1},n_{2}); & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{P}_{\mathbf{K}}(\widetilde{{\mathcal{M}}}_{1/2}^{(n_{1}+n_{2}+1)}f_{1}\cdot f_{2});\quad \text{P}_{\mathbf{K}}(f_{1})\text{P}_{\mathbf{K}}(f_{2}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{P}_{\mathbf{K}}(\widetilde{{\mathcal{M}}}_{1/2}^{(l)}f_{1}\cdot f_{2})=\text{P}_{\mathbf{K}}(f_{1}\cdot \widetilde{{\mathcal{M}}}_{1/2}^{(l)}f_{2}),0\leqslant l\leqslant \max (n_{1},n_{2}); & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{P}_{\mathbf{K}}(\widetilde{{\mathcal{M}}}_{1/2}^{(n_{1}+n_{2}+1)}f_{1}\cdot f_{2});\quad \text{P}_{\mathbf{K}}(f_{1})\text{P}_{\mathbf{K}}(f_{2}). & \displaystyle \nonumber\end{eqnarray}$$
Next, we give a complement of the main theorem of regularized integrals [Reference WuWu18, Theorem 2.12]. Let
![]() $\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D714}$
be Hecke characters with
$\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D714}$
be Hecke characters with
![]() $\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}\unicode[STIX]{x1D714}=1$
. Let
$\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}\unicode[STIX]{x1D714}=1$
. Let
![]() $f\in \unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})$
and
$f\in \unicode[STIX]{x1D70B}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})$
and
![]() $\unicode[STIX]{x1D711}\in \text{C}^{\infty }(\text{GL}_{2},\unicode[STIX]{x1D714})$
, that is, a smooth function on
$\unicode[STIX]{x1D711}\in \text{C}^{\infty }(\text{GL}_{2},\unicode[STIX]{x1D714})$
, that is, a smooth function on
![]() $\text{GL}_{2}(\mathbf{F})\backslash \text{GL}_{2}(\mathbb{A})$
with central character
$\text{GL}_{2}(\mathbf{F})\backslash \text{GL}_{2}(\mathbb{A})$
with central character
![]() $\unicode[STIX]{x1D714}$
. Suppose
$\unicode[STIX]{x1D714}$
. Suppose
![]() $\unicode[STIX]{x1D711}$
is finitely regularizable, as defined in Definition 2.1.
$\unicode[STIX]{x1D711}$
is finitely regularizable, as defined in Definition 2.1.
Proposition 2.5. For
![]() $\Re s\gg 1$
sufficiently large,
$\Re s\gg 1$
sufficiently large,
is absolutely convergent. It has a meromorphic continuation to
![]() $s\in \mathbb{C}$
. If, in addition,
$s\in \mathbb{C}$
. If, in addition,
then we have, with the right-hand side absolutely converging,
In the above region, the possible poles of
![]() $R(s,\unicode[STIX]{x1D711};f)$
are:
$R(s,\unicode[STIX]{x1D711};f)$
are:
∙
 $1/2+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}^{-1})$
if
$1/2+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}^{-1})$
if
 $\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}^{-1}$
is trivial on
$\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}^{-1}$
is trivial on
 $\mathbb{A}^{(1)}$
;
$\mathbb{A}^{(1)}$
;∙
 $(\unicode[STIX]{x1D70C}-1)/2$
where
$(\unicode[STIX]{x1D70C}-1)/2$
where
 $\unicode[STIX]{x1D70C}$
runs over the non-trivial zeros of
$\unicode[STIX]{x1D70C}$
runs over the non-trivial zeros of
 $L(s,\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}^{-1})$
.
$L(s,\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}^{-1})$
.
In particular,
![]() $R(s,\unicode[STIX]{x1D711};f)$
is holomorphic for
$R(s,\unicode[STIX]{x1D711};f)$
is holomorphic for
![]() $0\leqslant \Re s<\min (-\unicode[STIX]{x1D6E9},1/2)$
.
$0\leqslant \Re s<\min (-\unicode[STIX]{x1D6E9},1/2)$
.
Proof. The proof is quite similar to that of [Reference WuWu18, Theorem 2.12(3)], except that
![]() ${\mathcal{M}}f_{s}$
is no longer explicitly computable. In fact, we have, for
${\mathcal{M}}f_{s}$
is no longer explicitly computable. In fact, we have, for
![]() $T>1$
,
$T>1$
,
![]() $\Re s\gg 1$
, using the standard Rankin–Selberg unfolding,
$\Re s\gg 1$
, using the standard Rankin–Selberg unfolding,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}\cdot \unicode[STIX]{x1D6EC}^{T}\text{E}(s,f)\nonumber\\ \displaystyle & & \displaystyle \quad =R(s,\unicode[STIX]{x1D711};f)-\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}\biggl(\int _{\mathbf{K}}(\unicode[STIX]{x1D711}_{\mathbf{N}}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y)\unicode[STIX]{x1D705})f(\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}\biggr)\unicode[STIX]{x1D709}_{1}(y)|y|_{\mathbb{A}}^{s-1/2}1_{|y|_{\mathbb{A}}>T}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}\biggl(\int _{\mathbf{K}}(\unicode[STIX]{x1D711}_{\mathbf{N}}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y)\unicode[STIX]{x1D705}){\mathcal{M}}f_{s}(\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}\biggr)\unicode[STIX]{x1D709}_{2}(y)|y|_{\mathbb{A}}^{-s-1/2}1_{|y|_{\mathbb{A}}>T}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\text{Vol}(\mathbf{F}^{\times }\backslash \mathbb{A}^{(1)})\biggl(\mathop{\sum }_{j=1}^{l}\int _{\mathbf{K}}f_{j}(\unicode[STIX]{x1D705})f(\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}\cdot 1_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D709}_{1}(\mathbb{A}^{(1)})=1}\cdot \frac{1}{n_{j}!}\frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}\biggl(\frac{T^{s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}_{j}}}{s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}_{j}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\mathop{\sum }_{j=1}^{l}\int _{\mathbf{K}}f_{j}(\unicode[STIX]{x1D705}){\mathcal{M}}f_{s}(\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}\cdot 1_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D709}_{2}(\mathbb{A}^{(1)})=1}\cdot \frac{(-1)^{n_{j}}}{n_{j}!}\frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}\biggl(\frac{T^{-s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}_{j}^{\prime }}}{-s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}_{j}^{\prime }}\biggr)\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}\cdot \unicode[STIX]{x1D6EC}^{T}\text{E}(s,f)\nonumber\\ \displaystyle & & \displaystyle \quad =R(s,\unicode[STIX]{x1D711};f)-\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}\biggl(\int _{\mathbf{K}}(\unicode[STIX]{x1D711}_{\mathbf{N}}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y)\unicode[STIX]{x1D705})f(\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}\biggr)\unicode[STIX]{x1D709}_{1}(y)|y|_{\mathbb{A}}^{s-1/2}1_{|y|_{\mathbb{A}}>T}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}\biggl(\int _{\mathbf{K}}(\unicode[STIX]{x1D711}_{\mathbf{N}}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y)\unicode[STIX]{x1D705}){\mathcal{M}}f_{s}(\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}\biggr)\unicode[STIX]{x1D709}_{2}(y)|y|_{\mathbb{A}}^{-s-1/2}1_{|y|_{\mathbb{A}}>T}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\text{Vol}(\mathbf{F}^{\times }\backslash \mathbb{A}^{(1)})\biggl(\mathop{\sum }_{j=1}^{l}\int _{\mathbf{K}}f_{j}(\unicode[STIX]{x1D705})f(\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}\cdot 1_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D709}_{1}(\mathbb{A}^{(1)})=1}\cdot \frac{1}{n_{j}!}\frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}\biggl(\frac{T^{s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}_{j}}}{s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}_{j}}\biggr)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\mathop{\sum }_{j=1}^{l}\int _{\mathbf{K}}f_{j}(\unicode[STIX]{x1D705}){\mathcal{M}}f_{s}(\unicode[STIX]{x1D705})\,d\unicode[STIX]{x1D705}\cdot 1_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D709}_{2}(\mathbb{A}^{(1)})=1}\cdot \frac{(-1)^{n_{j}}}{n_{j}!}\frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}\biggl(\frac{T^{-s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}_{j}^{\prime }}}{-s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}_{j}^{\prime }}\biggr)\biggr),\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D707}_{j}$
(respectively,
$\unicode[STIX]{x1D707}_{j}$
(respectively,
![]() $\unicode[STIX]{x1D707}_{j}^{\prime }$
) is such that
$\unicode[STIX]{x1D707}_{j}^{\prime }$
) is such that
We conclude by first shifting
![]() $s$
to the desired region, then letting
$s$
to the desired region, then letting
![]() $T\rightarrow \infty$
. The possible poles are encoded in the possible poles of
$T\rightarrow \infty$
. The possible poles are encoded in the possible poles of
![]() ${\mathcal{M}}f_{s}$
, which are included in those of
${\mathcal{M}}f_{s}$
, which are included in those of
![]() $L(1+2s,\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}^{-1})^{-1}$
in the above region (cf., for example, [Reference WuWu17b, Corollaries 3.7, 3.10 and Lemma 3.18]).◻
$L(1+2s,\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}^{-1})^{-1}$
in the above region (cf., for example, [Reference WuWu17b, Corollaries 3.7, 3.10 and Lemma 3.18]).◻
Proposition 2.6. Retain the notation of the previous proposition, with
![]() $\unicode[STIX]{x1D6E9}\leqslant -1/2$
. Recall
$\unicode[STIX]{x1D6E9}\leqslant -1/2$
. Recall
(i) If
 $\unicode[STIX]{x1D709}_{1}\neq \unicode[STIX]{x1D709}_{2}$
, then where the summation is over
$\unicode[STIX]{x1D709}_{1}\neq \unicode[STIX]{x1D709}_{2}$
, then where the summation is over $$\begin{eqnarray}\biggl(\frac{\unicode[STIX]{x2202}^{n}R}{\unicode[STIX]{x2202}s^{n}}\biggr)^{\text{hol}}\biggl(\frac{1}{2},\unicode[STIX]{x1D711};f\biggr)=\int _{[\text{PGL}_{2}]}^{\text{reg}}\unicode[STIX]{x1D711}\cdot \text{E}^{(n)}\biggl(\frac{1}{2},f\biggr)-\mathop{\sum }_{j}^{\prime }\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n+n_{j})}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\text{P}_{\mathbf{K}}(f_{j}f),\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\frac{\unicode[STIX]{x2202}^{n}R}{\unicode[STIX]{x2202}s^{n}}\biggr)^{\text{hol}}\biggl(\frac{1}{2},\unicode[STIX]{x1D711};f\biggr)=\int _{[\text{PGL}_{2}]}^{\text{reg}}\unicode[STIX]{x1D711}\cdot \text{E}^{(n)}\biggl(\frac{1}{2},f\biggr)-\mathop{\sum }_{j}^{\prime }\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n+n_{j})}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\text{P}_{\mathbf{K}}(f_{j}f),\end{eqnarray}$$
 $j$
such that
$j$
such that
 $\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D712}_{j}(\mathbb{A}^{(1)})=1$
,
$\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D712}_{j}(\mathbb{A}^{(1)})=1$
,
 $\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D712}_{j})=-1/2$
.
$\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D712}_{j})=-1/2$
.(ii) If
 $\unicode[STIX]{x1D709}_{1}=\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}$
, then where the summation over
$\unicode[STIX]{x1D709}_{1}=\unicode[STIX]{x1D709}_{2}=\unicode[STIX]{x1D709}$
, then where the summation over $$\begin{eqnarray}\displaystyle \biggl(\frac{\unicode[STIX]{x2202}^{n}R}{\unicode[STIX]{x2202}s^{n}}\biggr)^{\text{hol}}\biggl(\frac{1}{2},\unicode[STIX]{x1D711};f\biggr) & = & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\unicode[STIX]{x1D711}\cdot \text{E}^{\text{reg},(n)}\biggl(\frac{1}{2},f\biggr)-\mathop{\sum }_{j}^{\prime }\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n+n_{j})}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\text{P}_{\mathbf{K}}(f_{j}f)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n)}(0)\cdot \text{P}_{\mathbf{K}}(f\cdot (\unicode[STIX]{x1D709}^{-1}\circ \det ))\cdot \int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}\cdot (\unicode[STIX]{x1D709}\circ \det ),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl(\frac{\unicode[STIX]{x2202}^{n}R}{\unicode[STIX]{x2202}s^{n}}\biggr)^{\text{hol}}\biggl(\frac{1}{2},\unicode[STIX]{x1D711};f\biggr) & = & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}\unicode[STIX]{x1D711}\cdot \text{E}^{\text{reg},(n)}\biggl(\frac{1}{2},f\biggr)-\mathop{\sum }_{j}^{\prime }\frac{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n+n_{j})}(0)}{\unicode[STIX]{x1D706}_{\mathbf{F}}^{(-1)}(0)}\text{P}_{\mathbf{K}}(f_{j}f)\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D706}_{\mathbf{F}}^{(n)}(0)\cdot \text{P}_{\mathbf{K}}(f\cdot (\unicode[STIX]{x1D709}^{-1}\circ \det ))\cdot \int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}\cdot (\unicode[STIX]{x1D709}\circ \det ),\nonumber\end{eqnarray}$$
 $j$
is as in the previous case.
$j$
is as in the previous case.
Proof. The case (i) being simpler, we only give details for (ii). By twisting, we may assume
![]() $\unicode[STIX]{x1D709}=1$
. Let
$\unicode[STIX]{x1D709}=1$
. Let
![]() $s$
be small with
$s$
be small with
![]() $\Re s<0$
. The
$\Re s<0$
. The
![]() $\text{L}^{2}$
-residue of
$\text{L}^{2}$
-residue of
![]() $\unicode[STIX]{x1D711}\cdot \text{E}(1/2+s,f)$
is given by
$\unicode[STIX]{x1D711}\cdot \text{E}(1/2+s,f)$
is given by
where the summation is over
![]() $j$
such that
$j$
such that
![]() $\Re \unicode[STIX]{x1D6FC}_{j}>-1$
. Define
$\Re \unicode[STIX]{x1D6FC}_{j}>-1$
. Define
where
![]() $\sum _{j}^{\prime }$
is the summation as in the statement and
$\sum _{j}^{\prime }$
is the summation as in the statement and
![]() $\sum _{j}^{\ast }$
is the rest. By the previous proposition, we have
$\sum _{j}^{\ast }$
is the rest. By the previous proposition, we have
 $$\begin{eqnarray}\displaystyle R\biggl(\frac{1}{2}+s,\unicode[STIX]{x1D711};f\biggr) & = & \displaystyle \!\int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}\cdot \text{E}\biggl(\frac{1}{2}+s,f\biggr)=\!\int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}\cdot \text{E}^{\text{reg}}\biggl(\frac{1}{2}+s,f\biggr)+\unicode[STIX]{x1D706}_{\mathbf{F}}(s)\text{P}_{\mathbf{K}}(f)\cdot \!\int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}\nonumber\\ \displaystyle & = & \displaystyle \!\int _{[\text{PGL}_{2}]}\biggl(\unicode[STIX]{x1D711}\cdot \text{E}^{\text{reg}}\biggl(\frac{1}{2}+s,f\biggr)-{\mathcal{E}}^{\text{reg}}(s)\biggr)-\int _{[\text{PGL}_{2}]}({\mathcal{E}}(s)-{\mathcal{E}}^{\text{reg}}(s))\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D706}_{\mathbf{F}}(s)\text{P}_{\mathbf{K}}(f)\cdot \!\int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R\biggl(\frac{1}{2}+s,\unicode[STIX]{x1D711};f\biggr) & = & \displaystyle \!\int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}\cdot \text{E}\biggl(\frac{1}{2}+s,f\biggr)=\!\int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}\cdot \text{E}^{\text{reg}}\biggl(\frac{1}{2}+s,f\biggr)+\unicode[STIX]{x1D706}_{\mathbf{F}}(s)\text{P}_{\mathbf{K}}(f)\cdot \!\int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}\nonumber\\ \displaystyle & = & \displaystyle \!\int _{[\text{PGL}_{2}]}\biggl(\unicode[STIX]{x1D711}\cdot \text{E}^{\text{reg}}\biggl(\frac{1}{2}+s,f\biggr)-{\mathcal{E}}^{\text{reg}}(s)\biggr)-\int _{[\text{PGL}_{2}]}({\mathcal{E}}(s)-{\mathcal{E}}^{\text{reg}}(s))\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D706}_{\mathbf{F}}(s)\text{P}_{\mathbf{K}}(f)\cdot \!\int _{[\text{PGL}_{2}]}\unicode[STIX]{x1D711}.\nonumber\end{eqnarray}$$
Since
![]() ${\mathcal{E}}^{\text{reg},(n)}(s)$
is the
${\mathcal{E}}^{\text{reg},(n)}(s)$
is the
![]() $\text{L}^{2}$
-residue of
$\text{L}^{2}$
-residue of
![]() $\unicode[STIX]{x1D711}\cdot \text{E}^{\text{reg},(n)}(1/2+s,f)$
, we can compare the finite parts of both sides and conclude by
$\unicode[STIX]{x1D711}\cdot \text{E}^{\text{reg},(n)}(1/2+s,f)$
, we can compare the finite parts of both sides and conclude by
Finally, we state and prove a special case of regularized triple product formulas. The method used in the proof is applicable in any general case but only the one treated in the following theorem is used in the current paper.
Theorem 2.7. Let
![]() $f_{j}\in \unicode[STIX]{x1D70B}(1,1),j=1,2,3$
. Then, for any
$f_{j}\in \unicode[STIX]{x1D70B}(1,1),j=1,2,3$
. Then, for any
![]() $n\in \mathbb{N}$
,
$n\in \mathbb{N}$
,
is the sum of
and a weighted sum with coefficients depending only on
![]() $\unicode[STIX]{x1D706}_{\mathbf{F}}(s)$
of
$\unicode[STIX]{x1D706}_{\mathbf{F}}(s)$
of
 $$\begin{eqnarray}\displaystyle & \text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(l)}f_{1}\cdot f_{2})\text{P}_{\mathbf{K}}(f_{3}),\quad 0\leqslant l\leqslant 3; & \displaystyle \nonumber\\ \displaystyle & \text{P}_{\mathbf{K}}(f_{1}\cdot f_{2}\cdot \widetilde{{\mathcal{M}}}_{1/2}^{(l)}f_{3}),\quad 0\leqslant l\leqslant \max (2,n),~l=n+3; & \displaystyle \nonumber\\ \displaystyle & \text{P}_{\mathbf{K}}((f_{1}{\mathcal{M}}_{0}f_{2}+f_{2}{\mathcal{M}}_{0}f_{1})\cdot \widetilde{{\mathcal{M}}}_{1/2}^{(l)}f_{3}),\quad 0\leqslant l\leqslant \max (1,n),~l=n+2; & \displaystyle \nonumber\\ \displaystyle & \text{P}_{\mathbf{K}}({\mathcal{M}}_{0}f_{1}\cdot {\mathcal{M}}_{0}f_{2}\cdot \widetilde{{\mathcal{M}}}_{1/2}^{(l)}f_{3}),\quad 0\leqslant l\leqslant n,~l=n+1. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \text{P}_{\mathbf{K}}({\mathcal{M}}_{0}^{(l)}f_{1}\cdot f_{2})\text{P}_{\mathbf{K}}(f_{3}),\quad 0\leqslant l\leqslant 3; & \displaystyle \nonumber\\ \displaystyle & \text{P}_{\mathbf{K}}(f_{1}\cdot f_{2}\cdot \widetilde{{\mathcal{M}}}_{1/2}^{(l)}f_{3}),\quad 0\leqslant l\leqslant \max (2,n),~l=n+3; & \displaystyle \nonumber\\ \displaystyle & \text{P}_{\mathbf{K}}((f_{1}{\mathcal{M}}_{0}f_{2}+f_{2}{\mathcal{M}}_{0}f_{1})\cdot \widetilde{{\mathcal{M}}}_{1/2}^{(l)}f_{3}),\quad 0\leqslant l\leqslant \max (1,n),~l=n+2; & \displaystyle \nonumber\\ \displaystyle & \text{P}_{\mathbf{K}}({\mathcal{M}}_{0}f_{1}\cdot {\mathcal{M}}_{0}f_{2}\cdot \widetilde{{\mathcal{M}}}_{1/2}^{(l)}f_{3}),\quad 0\leqslant l\leqslant n,~l=n+1. & \displaystyle \nonumber\end{eqnarray}$$
Proof. We shall only point out how the computation is effectuated, since the precise formulas are quite long, of no interest for the purpose of the current paper, and would only obscure matters.
is the
![]() $\text{L}^{2}$
-residue of
$\text{L}^{2}$
-residue of
![]() $\text{E}^{\ast }(0,f_{1})\cdot \text{E}^{\ast }(0,f_{2})$
. Let
$\text{E}^{\ast }(0,f_{1})\cdot \text{E}^{\ast }(0,f_{2})$
. Let
![]() $\unicode[STIX]{x1D711}:=\text{E}^{\ast }(0,f_{1})\cdot \text{E}^{\ast }(0,f_{2})-{\mathcal{E}}(f_{1},f_{2})$
. Then we need to compute
$\unicode[STIX]{x1D711}:=\text{E}^{\ast }(0,f_{1})\cdot \text{E}^{\ast }(0,f_{2})-{\mathcal{E}}(f_{1},f_{2})$
. Then we need to compute
The first term is computed by Proposition 2.6(ii), involving
which is treated in Theorem 2.2(ii). The second term is treated in Theorem 2.4(iii). ◻
2.3 Extension of global zeta integral
Fixing a central Hecke character
![]() $\unicode[STIX]{x1D714}$
over a number field
$\unicode[STIX]{x1D714}$
over a number field
![]() $\mathbf{F}$
, we extend the global part of the Hecke–Jacquet–Langlands theory to
$\mathbf{F}$
, we extend the global part of the Hecke–Jacquet–Langlands theory to
![]() ${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
(Definition 2.1), as well as an analogue of the ‘approximate functional equation’. Note that Eisenstein series are in
${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
(Definition 2.1), as well as an analogue of the ‘approximate functional equation’. Note that Eisenstein series are in
![]() ${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
.
${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
.
Definition 2.8. Let
![]() $\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
for some Hecke character
$\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
for some Hecke character
![]() $\unicode[STIX]{x1D714}$
. For a Hecke character
$\unicode[STIX]{x1D714}$
. For a Hecke character
![]() $\unicode[STIX]{x1D712}$
and
$\unicode[STIX]{x1D712}$
and
![]() $s\in \mathbb{C}$
,
$s\in \mathbb{C}$
,
![]() $\Re s\gg 1$
, we define the zeta functional by
$\Re s\gg 1$
, we define the zeta functional by
where we recall the essential constant term
Proposition 2.9.
![]() $\unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})$
has a meromorphic continuation to
$\unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})$
has a meromorphic continuation to
![]() $s\in \mathbb{C}$
with functional equation
$s\in \mathbb{C}$
with functional equation
It has possible poles at
![]() $s=-\unicode[STIX]{x1D6FC}_{j}-i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712})$
with
$s=-\unicode[STIX]{x1D6FC}_{j}-i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712})$
with
![]() $\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}(\mathbb{A}^{(1)})=1$
(respectively,
$\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}(\mathbb{A}^{(1)})=1$
(respectively,
![]() $s=1+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1})$
with
$s=1+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1})$
with
![]() $\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}(\mathbb{A}^{(1)})=1$
), with pure order
$\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}(\mathbb{A}^{(1)})=1$
), with pure order
![]() $n_{j}+1$
. Here
$n_{j}+1$
. Here
![]() $\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712})\in \mathbb{R}$
is defined for
$\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712})\in \mathbb{R}$
is defined for
![]() $\unicode[STIX]{x1D712}(\mathbb{A}^{(1)})=1$
as
$\unicode[STIX]{x1D712}(\mathbb{A}^{(1)})=1$
as
![]() $\unicode[STIX]{x1D712}(t)=|t|_{\mathbb{A}}^{i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712})}$
.
$\unicode[STIX]{x1D712}(t)=|t|_{\mathbb{A}}^{i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712})}$
.
Proof. By the invariance of
![]() $\unicode[STIX]{x1D711}$
at left by
$\unicode[STIX]{x1D711}$
at left by
![]() $w$
, we can rewrite the zeta integral as
$w$
, we can rewrite the zeta integral as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}) & = & \displaystyle \int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\geqslant 1}}(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s-1/2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\leqslant 1}}(w.\unicode[STIX]{x1D711}-w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y^{-1}))\unicode[STIX]{x1D714}\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s-1/2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle -\,\int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\leqslant 1}}\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(a(y))\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s-1/2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\leqslant 1}}w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(a(y^{-1}))\unicode[STIX]{x1D714}\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s-1/2}\,d^{\times }y.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}) & = & \displaystyle \int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\geqslant 1}}(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s-1/2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\leqslant 1}}(w.\unicode[STIX]{x1D711}-w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y^{-1}))\unicode[STIX]{x1D714}\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s-1/2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle -\,\int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\leqslant 1}}\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(a(y))\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s-1/2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\leqslant 1}}w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(a(y^{-1}))\unicode[STIX]{x1D714}\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s-1/2}\,d^{\times }y.\nonumber\end{eqnarray}$$
We can calculate the integral concerning
![]() $\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }$
and get
$\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }$
and get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\geqslant 1}}(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s-1/2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\geqslant 1}}(w.\unicode[STIX]{x1D711}-w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}(y)|y|_{\mathbb{A}}^{1/2-s}\,d^{\times }y+\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl(\mathop{\sum }_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}|_{\mathbb{ A}^{(1)}}=1}\frac{(-1)^{n_{j}+1}f_{j}(1)}{(s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}))^{n_{j}+1}}+\mathop{\sum }_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}|_{\mathbb{ A}^{(1)}}=1}\frac{(-1)^{n_{j}+1}f_{j}(w)}{(1-s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}))^{n_{j}+1}}\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\geqslant 1}}(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s-1/2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\int _{\substack{ y\in \mathbf{F}^{\times }\backslash \mathbb{A}^{\times } \\ |y|_{\mathbb{A}}\geqslant 1}}(w.\unicode[STIX]{x1D711}-w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}(y)|y|_{\mathbb{A}}^{1/2-s}\,d^{\times }y+\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\biggl(\mathop{\sum }_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}|_{\mathbb{ A}^{(1)}}=1}\frac{(-1)^{n_{j}+1}f_{j}(1)}{(s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}))^{n_{j}+1}}+\mathop{\sum }_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}|_{\mathbb{ A}^{(1)}}=1}\frac{(-1)^{n_{j}+1}f_{j}(w)}{(1-s+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}))^{n_{j}+1}}\biggr),\nonumber\end{eqnarray}$$
from which we easily deduce all the assertions. ◻
We turn to the special case
![]() $\unicode[STIX]{x1D711}(g)=\text{E}^{\ast }(s_{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1};f)(g)$
the usual completed Eisenstein series (respectively,
$\unicode[STIX]{x1D711}(g)=\text{E}^{\ast }(s_{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1};f)(g)$
the usual completed Eisenstein series (respectively,
![]() $\text{E}^{\text{reg}}(s_{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1};f)(g)$
defined in equation (2.1)), for which the local computation is the same as for a cusp form. Note that in this case
$\text{E}^{\text{reg}}(s_{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1};f)(g)$
defined in equation (2.1)), for which the local computation is the same as for a cusp form. Note that in this case
![]() $\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }=\unicode[STIX]{x1D711}_{\mathbf{N}}$
, hence
$\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }=\unicode[STIX]{x1D711}_{\mathbf{N}}$
, hence
![]() $\unicode[STIX]{x1D711}(a(y))-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(a(y))=\sum _{\unicode[STIX]{x1D6FC}\in \mathbf{F}^{\times }}W_{\unicode[STIX]{x1D711}}(a(\unicode[STIX]{x1D6FC}y))$
.
$\unicode[STIX]{x1D711}(a(y))-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(a(y))=\sum _{\unicode[STIX]{x1D6FC}\in \mathbf{F}^{\times }}W_{\unicode[STIX]{x1D711}}(a(\unicode[STIX]{x1D6FC}y))$
.
Proposition 2.10. Let
![]() $\unicode[STIX]{x1D711}(g)=\text{E}^{\ast }(s_{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1};f)(g)$
(respectively,
$\unicode[STIX]{x1D711}(g)=\text{E}^{\ast }(s_{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1};f)(g)$
(respectively,
![]() $\text{E}^{\text{reg}}(s_{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1};f)(g)$
) where
$\text{E}^{\text{reg}}(s_{0},\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1};f)(g)$
) where
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}$
are Hecke characters and
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}$
are Hecke characters and
![]() $f\in \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1}}$
. The zeta functional has a decomposition as an Euler product in which only a finite number of terms are not equal to
$f\in \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1}}$
. The zeta functional has a decomposition as an Euler product in which only a finite number of terms are not equal to
![]() $1$
:
$1$
:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}) & = & \displaystyle \unicode[STIX]{x1D6EC}(s+s_{0},\unicode[STIX]{x1D709}\unicode[STIX]{x1D712})\unicode[STIX]{x1D6EC}(s-s_{0},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1}\unicode[STIX]{x1D712})\cdot \mathop{\prod }_{v}\frac{L_{v}(1+2s_{0},\unicode[STIX]{x1D714}_{v}^{-1}\unicode[STIX]{x1D709}_{v}^{2})}{L_{v}(s+s_{0},\unicode[STIX]{x1D709}_{v}\unicode[STIX]{x1D712}_{v})L_{v}(s-s_{0},\unicode[STIX]{x1D714}_{v}\unicode[STIX]{x1D709}_{v}^{-1}\unicode[STIX]{x1D712}_{v})}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\int _{\mathbf{F}_{v}^{\times }}W_{f_{v}}^{(s_{0})}(a(y_{v}))|y_{v}|_{v}^{s-1/2}\,d^{\times }y_{v},\quad \biggl(\text{respectively}\nonumber\\ \displaystyle \unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}) & = & \displaystyle \frac{\unicode[STIX]{x1D6EC}(s+s_{0},\unicode[STIX]{x1D709}\unicode[STIX]{x1D712})\unicode[STIX]{x1D6EC}(s-s_{0},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1}\unicode[STIX]{x1D712})}{\unicode[STIX]{x1D6EC}(1+2s_{0},\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D709}^{2})}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\mathop{\prod }_{v}\frac{L_{v}(1+2s_{0},\unicode[STIX]{x1D714}_{v}^{-1}\unicode[STIX]{x1D709}_{v}^{2})}{L_{v}(s+s_{0},\unicode[STIX]{x1D709}_{v}\unicode[STIX]{x1D712}_{v})L_{v}(s-s_{0},\unicode[STIX]{x1D714}_{v}\unicode[STIX]{x1D709}_{v}^{-1}\unicode[STIX]{x1D712}_{v})}\int _{\mathbf{F}_{v}^{\times }}W_{f_{v}}^{(s_{0})}(a(y_{v}))|y_{v}|_{v}^{s-1/2}\,d^{\times }y_{v}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}) & = & \displaystyle \unicode[STIX]{x1D6EC}(s+s_{0},\unicode[STIX]{x1D709}\unicode[STIX]{x1D712})\unicode[STIX]{x1D6EC}(s-s_{0},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1}\unicode[STIX]{x1D712})\cdot \mathop{\prod }_{v}\frac{L_{v}(1+2s_{0},\unicode[STIX]{x1D714}_{v}^{-1}\unicode[STIX]{x1D709}_{v}^{2})}{L_{v}(s+s_{0},\unicode[STIX]{x1D709}_{v}\unicode[STIX]{x1D712}_{v})L_{v}(s-s_{0},\unicode[STIX]{x1D714}_{v}\unicode[STIX]{x1D709}_{v}^{-1}\unicode[STIX]{x1D712}_{v})}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\int _{\mathbf{F}_{v}^{\times }}W_{f_{v}}^{(s_{0})}(a(y_{v}))|y_{v}|_{v}^{s-1/2}\,d^{\times }y_{v},\quad \biggl(\text{respectively}\nonumber\\ \displaystyle \unicode[STIX]{x1D701}(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}) & = & \displaystyle \frac{\unicode[STIX]{x1D6EC}(s+s_{0},\unicode[STIX]{x1D709}\unicode[STIX]{x1D712})\unicode[STIX]{x1D6EC}(s-s_{0},\unicode[STIX]{x1D714}\unicode[STIX]{x1D709}^{-1}\unicode[STIX]{x1D712})}{\unicode[STIX]{x1D6EC}(1+2s_{0},\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D709}^{2})}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\mathop{\prod }_{v}\frac{L_{v}(1+2s_{0},\unicode[STIX]{x1D714}_{v}^{-1}\unicode[STIX]{x1D709}_{v}^{2})}{L_{v}(s+s_{0},\unicode[STIX]{x1D709}_{v}\unicode[STIX]{x1D712}_{v})L_{v}(s-s_{0},\unicode[STIX]{x1D714}_{v}\unicode[STIX]{x1D709}_{v}^{-1}\unicode[STIX]{x1D712}_{v})}\int _{\mathbf{F}_{v}^{\times }}W_{f_{v}}^{(s_{0})}(a(y_{v}))|y_{v}|_{v}^{s-1/2}\,d^{\times }y_{v}\biggr).\nonumber\end{eqnarray}$$
The method of truncation used in the proof of Proposition 2.9 for the analytic continuation of the global zeta functional is not the only possible one. Another version of truncation on the integral is closely related to the classical approximate functional equation. Let
![]() $h_{0}$
be a smooth function supported in the inteval
$h_{0}$
be a smooth function supported in the inteval
![]() $[0,2)$
, being equal to 1 on
$[0,2)$
, being equal to 1 on
![]() $[0,1]$
. For any
$[0,1]$
. For any
![]() $A>0$
, we denote by
$A>0$
, we denote by
![]() $h_{0,A}$
the function
$h_{0,A}$
the function
![]() $t\mapsto h_{0}(t/A)$
. We then have, for
$t\mapsto h_{0}(t/A)$
. We then have, for
![]() $\Re s\gg 1$
,
$\Re s\gg 1$
,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}\biggr) & = & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s}(1-h_{0,A}(|y|_{\mathbb{A}}))\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}(w.\unicode[STIX]{x1D711}-w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}(y)|y|_{\mathbb{A}}^{-s}h_{0,A}(|y|_{\mathbb{A}}^{-1})\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle -\,\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(a(y))\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s}h_{0,A}(|y|_{\mathbb{A}})\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(a(y))\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}(y)|y|_{\mathbb{A}}^{-s}h_{0,A}(|y|_{\mathbb{A}}^{-1})\,d^{\times }y.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}\biggr) & = & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s}(1-h_{0,A}(|y|_{\mathbb{A}}))\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}(w.\unicode[STIX]{x1D711}-w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}(y)|y|_{\mathbb{A}}^{-s}h_{0,A}(|y|_{\mathbb{A}}^{-1})\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle -\,\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(a(y))\unicode[STIX]{x1D712}(y)|y|_{\mathbb{A}}^{s}h_{0,A}(|y|_{\mathbb{A}})\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }(a(y))\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}(y)|y|_{\mathbb{A}}^{-s}h_{0,A}(|y|_{\mathbb{A}}^{-1})\,d^{\times }y.\end{eqnarray}$$
For the last two lines, it is not hard to compute their analytic continuation using the form of
![]() $\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }$
and the analytic continuation of the Mellin transform of
$\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }$
and the analytic continuation of the Mellin transform of
![]() $h_{0}$
as (since
$h_{0}$
as (since
![]() $h_{0}^{\prime }$
is of compact support contained in
$h_{0}^{\prime }$
is of compact support contained in
![]() $(1,2)$
)
$(1,2)$
)
 $$\begin{eqnarray}\displaystyle \mathfrak{M}(h_{0})(s) & = & \displaystyle \int _{0}^{\infty }h_{0}(t)t^{s}\frac{dt}{t}=\frac{1}{s}-\frac{\mathfrak{M}(h_{0}^{\prime })(s+1)+1}{s}\nonumber\\ \displaystyle & = & \displaystyle (-1)^{N}\mathop{\prod }_{j=0}^{N-1}(s+j)^{-1}\mathfrak{M}(h_{0}^{(N)})(s+N),\quad \forall N\in \mathbb{N},s\in \mathbb{C}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{M}(h_{0})(s) & = & \displaystyle \int _{0}^{\infty }h_{0}(t)t^{s}\frac{dt}{t}=\frac{1}{s}-\frac{\mathfrak{M}(h_{0}^{\prime })(s+1)+1}{s}\nonumber\\ \displaystyle & = & \displaystyle (-1)^{N}\mathop{\prod }_{j=0}^{N-1}(s+j)^{-1}\mathfrak{M}(h_{0}^{(N)})(s+N),\quad \forall N\in \mathbb{N},s\in \mathbb{C}.\nonumber\end{eqnarray}$$
Remark 2.11. We also have, first for
![]() $\Re s\ll -1$
then for
$\Re s\ll -1$
then for
![]() $s\in \mathbb{C}$
,
$s\in \mathbb{C}$
,
Then, writing
![]() $s_{j}=1/2+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712})$
, the last two lines of (2.4) are defined for
$s_{j}=1/2+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712})$
, the last two lines of (2.4) are defined for
![]() $s\in \mathbb{C}$
as
$s\in \mathbb{C}$
as
 $$\begin{eqnarray}\displaystyle & & \displaystyle -\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(1)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}\frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}(A^{s+s_{j}}\mathfrak{M}(h_{0})(s+s_{j}))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(1)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}\frac{(-1)^{n_{j}+1}}{(s+s_{j})^{n_{j}+1}}-\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(1)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{k=0}^{n_{j}}\binom{n_{j}}{k}(\log A)^{n_{j}-k+1}\int _{0}^{\infty }h_{0}^{\prime }(t)t^{s+s_{j}}\log ^{k}t\,dt\cdot \int _{0}^{1}A^{\unicode[STIX]{x1D6FF}(s+s_{j})}\unicode[STIX]{x1D6FF}^{n_{j}-k}\,d\unicode[STIX]{x1D6FF}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(1)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}\int _{0}^{\infty }h_{0}^{\prime }(t)\biggl(\int _{0}^{1}\unicode[STIX]{x1D6FF}^{n_{j}}t^{\unicode[STIX]{x1D6FF}(s+s_{j})}\,d\unicode[STIX]{x1D6FF}\biggr)\log ^{n_{j}+1}t\,dt,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle -\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(1)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}\frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}(A^{s+s_{j}}\mathfrak{M}(h_{0})(s+s_{j}))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(1)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}\frac{(-1)^{n_{j}+1}}{(s+s_{j})^{n_{j}+1}}-\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(1)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{k=0}^{n_{j}}\binom{n_{j}}{k}(\log A)^{n_{j}-k+1}\int _{0}^{\infty }h_{0}^{\prime }(t)t^{s+s_{j}}\log ^{k}t\,dt\cdot \int _{0}^{1}A^{\unicode[STIX]{x1D6FF}(s+s_{j})}\unicode[STIX]{x1D6FF}^{n_{j}-k}\,d\unicode[STIX]{x1D6FF}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(1)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}\int _{0}^{\infty }h_{0}^{\prime }(t)\biggl(\int _{0}^{1}\unicode[STIX]{x1D6FF}^{n_{j}}t^{\unicode[STIX]{x1D6FF}(s+s_{j})}\,d\unicode[STIX]{x1D6FF}\biggr)\log ^{n_{j}+1}t\,dt,\nonumber\end{eqnarray}$$
and, writing
![]() $s_{j}^{\prime }=1/2+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1})$
,
$s_{j}^{\prime }=1/2+\unicode[STIX]{x1D6FC}_{j}+i\unicode[STIX]{x1D707}(\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1})$
,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(w)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}(-1)^{n_{j}}\cdot \frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}(A^{s-s_{j}^{\prime }}\mathfrak{M}(h_{0})(s-s_{j}^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(w)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}\frac{(-1)^{n_{j}+1}}{(s_{j}^{\prime }-s)^{n_{j}+1}}+\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(w)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}(-1)^{n_{j}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{k=0}^{n_{j}}\binom{n_{j}}{k}(\log A)^{n_{j}-k+1}\int _{0}^{\infty }h_{0}^{\prime }(t)t^{s-s_{j}^{\prime }}\log ^{k}t\,dt\cdot \int _{0}^{1}A^{\unicode[STIX]{x1D6FF}(s-s_{j}^{\prime })}\unicode[STIX]{x1D6FF}^{n_{j}-k}\,d\unicode[STIX]{x1D6FF}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(w)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}(-1)^{n_{j}}\int _{0}^{\infty }h_{0}^{\prime }(t)\biggl(\int _{0}^{1}\unicode[STIX]{x1D6FF}^{n_{j}}t^{\unicode[STIX]{x1D6FF}(s-s_{j}^{\prime })}\,d\unicode[STIX]{x1D6FF}\biggr)\log ^{n_{j}+1}t\,dt.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(w)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}(-1)^{n_{j}}\cdot \frac{\unicode[STIX]{x2202}^{n_{j}}}{\unicode[STIX]{x2202}s^{n_{j}}}(A^{s-s_{j}^{\prime }}\mathfrak{M}(h_{0})(s-s_{j}^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(w)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}\frac{(-1)^{n_{j}+1}}{(s_{j}^{\prime }-s)^{n_{j}+1}}+\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(w)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}(-1)^{n_{j}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\sum }_{k=0}^{n_{j}}\binom{n_{j}}{k}(\log A)^{n_{j}-k+1}\int _{0}^{\infty }h_{0}^{\prime }(t)t^{s-s_{j}^{\prime }}\log ^{k}t\,dt\cdot \int _{0}^{1}A^{\unicode[STIX]{x1D6FF}(s-s_{j}^{\prime })}\unicode[STIX]{x1D6FF}^{n_{j}-k}\,d\unicode[STIX]{x1D6FF}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\mathop{\sum }_{j=1}^{l}f_{j}(w)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}(-1)^{n_{j}}\int _{0}^{\infty }h_{0}^{\prime }(t)\biggl(\int _{0}^{1}\unicode[STIX]{x1D6FF}^{n_{j}}t^{\unicode[STIX]{x1D6FF}(s-s_{j}^{\prime })}\,d\unicode[STIX]{x1D6FF}\biggr)\log ^{n_{j}+1}t\,dt.\nonumber\end{eqnarray}$$
We separate the terms in the sum
![]() $\sum _{j=1}^{l}$
according as
$\sum _{j=1}^{l}$
according as
![]() $s_{j}=0$
and
$s_{j}=0$
and
![]() $s_{j}\neq 0$
(respectively,
$s_{j}\neq 0$
(respectively,
![]() $s_{j}^{\prime }=0$
and
$s_{j}^{\prime }=0$
and
![]() $s_{j}^{\prime }\neq 0$
). For
$s_{j}^{\prime }\neq 0$
). For
![]() $s_{j}=0$
(respectively,
$s_{j}=0$
(respectively,
![]() $s_{j}^{\prime }=0$
), the finite part at
$s_{j}^{\prime }=0$
), the finite part at
![]() $s=0$
is bounded, with implied constants depending only on
$s=0$
is bounded, with implied constants depending only on
![]() $\mathbf{F},n_{j},h_{0}$
, by
$\mathbf{F},n_{j},h_{0}$
, by
For
![]() $s_{j}\neq 0$
(respectively,
$s_{j}\neq 0$
(respectively,
![]() $s_{j}^{\prime }\neq 0$
), they are of size at
$s_{j}^{\prime }\neq 0$
), they are of size at
![]() $s=0$
, with implied constants depending only on
$s=0$
, with implied constants depending only on
![]() $\mathbf{F},\unicode[STIX]{x1D6FC}_{j},n_{j},h_{0}$
and an arbitrary
$\mathbf{F},\unicode[STIX]{x1D6FC}_{j},n_{j},h_{0}$
and an arbitrary
![]() $N\in \mathbb{N}$
,
$N\in \mathbb{N}$
,
 $$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}1_{s_{j}\neq 0}O\biggl(\!\frac{A^{\Re s_{j}}|f_{j}(1)\log ^{n_{j}}A|}{|s_{j}|^{N}}\!\biggr), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \biggl(\text{respectively}~\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}1_{s_{j}^{\prime }\neq 0}O\biggl(\!\frac{A^{-\Re s_{j}^{\prime }}|f_{j}(w)\log ^{n_{j}}A|}{|s_{j}^{\prime }|^{N}}\!\biggr)\biggr). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}1_{s_{j}\neq 0}O\biggl(\!\frac{A^{\Re s_{j}}|f_{j}(1)\log ^{n_{j}}A|}{|s_{j}|^{N}}\!\biggr), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \biggl(\text{respectively}~\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}1_{s_{j}^{\prime }\neq 0}O\biggl(\!\frac{A^{-\Re s_{j}^{\prime }}|f_{j}(w)\log ^{n_{j}}A|}{|s_{j}^{\prime }|^{N}}\!\biggr)\biggr). & \displaystyle \nonumber\end{eqnarray}$$
The first (respectively, second) line of (2.4) is supported in
![]() $|y|_{\mathbb{A}}\in [A,\infty )$
(respectively,
$|y|_{\mathbb{A}}\in [A,\infty )$
(respectively,
![]() $[(2A)^{-1},\infty )$
), hence is well defined for all
$[(2A)^{-1},\infty )$
), hence is well defined for all
![]() $s\in \mathbb{C}$
by the rapid decay of
$s\in \mathbb{C}$
by the rapid decay of
![]() $\unicode[STIX]{x1D711}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }$
. For the second line at
$\unicode[STIX]{x1D711}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast }$
. For the second line at
![]() $s=0$
, we can apply Mellin inversion to see
$s=0$
, we can apply Mellin inversion to see
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}(w.\unicode[STIX]{x1D711}-w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}(y)h_{0,A}(|y|_{\mathbb{A}}^{-1})\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\int _{\Re s_{1}=c_{1}\gg 1}A^{s_{1}}\unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s_{1},\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1},w.\unicode[STIX]{x1D711}\biggr)\mathfrak{M}(h_{0})(s_{1})\frac{ds_{1}}{2\unicode[STIX]{x1D70B}i},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}(w.\unicode[STIX]{x1D711}-w.\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}(y)h_{0,A}(|y|_{\mathbb{A}}^{-1})\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D701}_{\mathbf{F}}^{\ast }(1)\int _{\Re s_{1}=c_{1}\gg 1}A^{s_{1}}\unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s_{1},\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1},w.\unicode[STIX]{x1D711}\biggr)\mathfrak{M}(h_{0})(s_{1})\frac{ds_{1}}{2\unicode[STIX]{x1D70B}i},\nonumber\end{eqnarray}$$
which is bounded, with implied constant depending only on
![]() $\mathbf{F},h_{0}$
and an arbitrary
$\mathbf{F},h_{0}$
and an arbitrary
![]() $N\in \mathbb{N}$
, as
$N\in \mathbb{N}$
, as
where
![]() $c_{1}$
can be chosen as any real number such that the integral defining
$c_{1}$
can be chosen as any real number such that the integral defining
![]() $\unicode[STIX]{x1D701}(1/2+s_{1},\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1},w.\unicode[STIX]{x1D711})$
is absolutely convergent for
$\unicode[STIX]{x1D701}(1/2+s_{1},\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1},w.\unicode[STIX]{x1D711})$
is absolutely convergent for
![]() $\Re s_{1}\geqslant c_{1}$
. Similarly, we have, for any
$\Re s_{1}\geqslant c_{1}$
. Similarly, we have, for any
![]() $B>0$
, that
$B>0$
, that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D712}(y)(1-h_{0,B})(|y|_{\mathbb{A}})\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \quad =-\int _{\Re s_{2}=c_{2}\gg 1}B^{-s_{2}}\unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s_{2},\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}\biggr)\mathfrak{M}(h_{0})(-s_{2})\frac{ds_{2}}{2\unicode[STIX]{x1D70B}i}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D711}_{\mathbf{N}}^{\ast })(a(y))\unicode[STIX]{x1D712}(y)(1-h_{0,B})(|y|_{\mathbb{A}})\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \quad =-\int _{\Re s_{2}=c_{2}\gg 1}B^{-s_{2}}\unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s_{2},\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}\biggr)\mathfrak{M}(h_{0})(-s_{2})\frac{ds_{2}}{2\unicode[STIX]{x1D70B}i}\nonumber\end{eqnarray}$$
is bounded, with implied constant depending only on
![]() $\mathbf{F},h_{0}$
and an arbitrary
$\mathbf{F},h_{0}$
and an arbitrary
![]() $N\in \mathbb{N}$
as
$N\in \mathbb{N}$
as
where
![]() $c_{2}$
can be chosen as any real number such that the integral defining
$c_{2}$
can be chosen as any real number such that the integral defining
![]() $\unicode[STIX]{x1D701}(1/2+s_{2},\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})$
is absolutely convergent for
$\unicode[STIX]{x1D701}(1/2+s_{2},\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})$
is absolutely convergent for
![]() $\Re s_{2}\geqslant c_{2}$
.
$\Re s_{2}\geqslant c_{2}$
.
Definition 2.12. For any function
![]() $h:\mathbb{R}_{+}\rightarrow \mathbb{C}$
and any Hecke character
$h:\mathbb{R}_{+}\rightarrow \mathbb{C}$
and any Hecke character
![]() $\unicode[STIX]{x1D712}$
, we define the
$\unicode[STIX]{x1D712}$
, we define the
![]() $h$
-truncated (zeta) integral on
$h$
-truncated (zeta) integral on
![]() ${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
as
${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
as
In summary, we have obtained the following proposition.
Proposition 2.13. Take
![]() $h_{0}$
as indicated at the beginning, some positive constants
$h_{0}$
as indicated at the beginning, some positive constants
![]() $0<A<B$
, and define
$0<A<B$
, and define
![]() $h(t)=h_{0,B}(t)-h_{0,A}(t)$
,
$h(t)=h_{0,B}(t)-h_{0,A}(t)$
,
![]() $t>0$
. For any
$t>0$
. For any
![]() $\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
with
$\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\text{fr}}(\text{GL}_{2},\unicode[STIX]{x1D714})$
with
![]() $\unicode[STIX]{x1D712}_{i},\unicode[STIX]{x1D6FC}_{i},n_{i}$
given in Definition 2.8, we write
$\unicode[STIX]{x1D712}_{i},\unicode[STIX]{x1D6FC}_{i},n_{i}$
given in Definition 2.8, we write
if
![]() $\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}$
(respectively,
$\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}$
(respectively,
![]() $\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}$
) is trivial on
$\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}$
) is trivial on
![]() $\mathbb{A}^{(1)}$
, and
$\mathbb{A}^{(1)}$
, and
![]() $\unicode[STIX]{x1D707}$
defined in Proposition 2.9. Then the difference
$\unicode[STIX]{x1D707}$
defined in Proposition 2.9. Then the difference
is bounded, with implied constants depending only on
![]() $\mathbf{F},\unicode[STIX]{x1D6FC}_{j},n_{j},h_{0}$
and an arbitrary
$\mathbf{F},\unicode[STIX]{x1D6FC}_{j},n_{j},h_{0}$
and an arbitrary
![]() $N\in \mathbb{N}$
, as the sum of:
$N\in \mathbb{N}$
, as the sum of:
(i) degenerate polar part,
 $$\begin{eqnarray}\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}1_{s_{j}=0}O(|f_{j}(1)\log ^{n_{j}+1}A|)+\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}1_{s_{j}^{\prime }=0}O(|f_{j}(w)\log ^{n_{j}+1}A|);\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}1_{s_{j}=0}O(|f_{j}(1)\log ^{n_{j}+1}A|)+\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}1_{s_{j}^{\prime }=0}O(|f_{j}(w)\log ^{n_{j}+1}A|);\end{eqnarray}$$
(ii) normal polar part,
 $$\begin{eqnarray}\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}1_{s_{j}\neq 0}O\biggl(\frac{A^{\Re s_{j}}|f_{j}(1)\log ^{n_{j}}A|}{|s_{j}|^{N}}\biggr)+\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}1_{s_{j}^{\prime }\neq 0}O\biggl(\frac{A^{-\Re s_{j}^{\prime }}|f_{j}(w)\log ^{n_{j}}A|}{|s_{j}^{\prime }|^{N}}\biggr);\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D712}}1_{s_{j}\neq 0}O\biggl(\frac{A^{\Re s_{j}}|f_{j}(1)\log ^{n_{j}}A|}{|s_{j}|^{N}}\biggr)+\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{j}\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1}}1_{s_{j}^{\prime }\neq 0}O\biggl(\frac{A^{-\Re s_{j}^{\prime }}|f_{j}(w)\log ^{n_{j}}A|}{|s_{j}^{\prime }|^{N}}\biggr);\end{eqnarray}$$
(iii) lower part,
 $$\begin{eqnarray}A^{c_{1}}O\biggl(\int _{\Re s=c_{1}\gg 1}\frac{|\unicode[STIX]{x1D701}(1/2+s,\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1},w.\unicode[STIX]{x1D711})|}{\mathop{\prod }_{m=0}^{N-1}|s+m|}\frac{|ds|}{2\unicode[STIX]{x1D70B}}\biggr);\end{eqnarray}$$
$$\begin{eqnarray}A^{c_{1}}O\biggl(\int _{\Re s=c_{1}\gg 1}\frac{|\unicode[STIX]{x1D701}(1/2+s,\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1},w.\unicode[STIX]{x1D711})|}{\mathop{\prod }_{m=0}^{N-1}|s+m|}\frac{|ds|}{2\unicode[STIX]{x1D70B}}\biggr);\end{eqnarray}$$
(iv) upper part,
 $$\begin{eqnarray}B^{-c_{2}}O\biggl(\int _{\Re s=c_{2}\gg 1}\frac{|\unicode[STIX]{x1D701}(1/2+s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})|}{\mathop{\prod }_{m=0}^{N-1}|s+m|}\frac{|ds|}{2\unicode[STIX]{x1D70B}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}B^{-c_{2}}O\biggl(\int _{\Re s=c_{2}\gg 1}\frac{|\unicode[STIX]{x1D701}(1/2+s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})|}{\mathop{\prod }_{m=0}^{N-1}|s+m|}\frac{|ds|}{2\unicode[STIX]{x1D70B}}\biggr).\end{eqnarray}$$
In (iii) (respectively, (iv)),
![]() $c_{1}>0$
(respectively,
$c_{1}>0$
(respectively,
![]() $c_{2}>0$
) is any real number such that the integral defining
$c_{2}>0$
) is any real number such that the integral defining
![]() $\unicode[STIX]{x1D701}(1/2+s,\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1},w.\unicode[STIX]{x1D711})$
(respectively,
$\unicode[STIX]{x1D701}(1/2+s,\unicode[STIX]{x1D714}^{-1}\unicode[STIX]{x1D712}^{-1},w.\unicode[STIX]{x1D711})$
(respectively,
![]() $\unicode[STIX]{x1D701}(1/2+s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})$
) is absolutely convergent for
$\unicode[STIX]{x1D701}(1/2+s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})$
) is absolutely convergent for
![]() $\Re s\geqslant c_{1}$
(respectively,
$\Re s\geqslant c_{1}$
(respectively,
![]() $\Re s\geqslant c_{2}$
).
$\Re s\geqslant c_{2}$
).
Remark 2.14. We will use the bound for the normal polar part in the case where
![]() $s_{j}$
is bounded away from 0.
$s_{j}$
is bounded away from 0.
2.4 Classical vectors in spherical series
Let
![]() $\mathbf{F}$
be a non-archimedean local field with uniformizer
$\mathbf{F}$
be a non-archimedean local field with uniformizer
![]() $\unicode[STIX]{x1D71B}$
, absolute valuation
$\unicode[STIX]{x1D71B}$
, absolute valuation
![]() $|\cdot |$
, valuation ring
$|\cdot |$
, valuation ring
![]() $\mathfrak{o}$
, ideal
$\mathfrak{o}$
, ideal
![]() $\mathfrak{p}$
and cardinality of the residue class field
$\mathfrak{p}$
and cardinality of the residue class field
![]() $q$
. Denote by
$q$
. Denote by
![]() $\unicode[STIX]{x1D70B}_{s}=\text{Ind}_{\mathbf{B}(\mathbf{F})}^{\text{GL}_{2}(\mathbf{F})}(|\cdot |^{s},|\cdot |^{-s})$
the principal series representation of
$\unicode[STIX]{x1D70B}_{s}=\text{Ind}_{\mathbf{B}(\mathbf{F})}^{\text{GL}_{2}(\mathbf{F})}(|\cdot |^{s},|\cdot |^{-s})$
the principal series representation of
![]() $\text{PGL}_{2}(\mathbf{F})$
, where
$\text{PGL}_{2}(\mathbf{F})$
, where
![]() $s\in \mathbb{C}$
. For
$s\in \mathbb{C}$
. For
![]() $s\in i\mathbb{R}$
, the underlying Hilbert spaces for the unitary representation
$s\in i\mathbb{R}$
, the underlying Hilbert spaces for the unitary representation
![]() $\unicode[STIX]{x1D70B}_{s}$
can be identified with each other. We denote this common Hilbert space by
$\unicode[STIX]{x1D70B}_{s}$
can be identified with each other. We denote this common Hilbert space by
![]() $H$
, that is,
$H$
, that is,
We regard
![]() $\unicode[STIX]{x1D70B}_{s},s\in \mathbb{C}$
as a family of representations of
$\unicode[STIX]{x1D70B}_{s},s\in \mathbb{C}$
as a family of representations of
![]() $\text{GL}_{2}(\mathbf{F})$
on
$\text{GL}_{2}(\mathbf{F})$
on
![]() $H$
. By the branching law, there is a canonical decomposition as
$H$
. By the branching law, there is a canonical decomposition as
![]() $\mathbf{K}$
-representations,
$\mathbf{K}$
-representations,
where
![]() $H_{n}$
is an irreducible
$H_{n}$
is an irreducible
![]() $\mathbf{K}$
-subspace of
$\mathbf{K}$
-subspace of
![]() $H$
generated by a unitary vector
$H$
generated by a unitary vector
![]() $e_{n}$
, such that
$e_{n}$
, such that
![]() $\{e_{0},\ldots ,e_{m}\}$
form an orthonormal basis of the
$\{e_{0},\ldots ,e_{m}\}$
form an orthonormal basis of the
![]() $\mathbf{K}_{0}[\mathfrak{p}^{m}]$
-invariant subspace of
$\mathbf{K}_{0}[\mathfrak{p}^{m}]$
-invariant subspace of
![]() $H$
for any
$H$
for any
![]() $m\in \mathbb{N}$
. These vectors
$m\in \mathbb{N}$
. These vectors
![]() $e_{n}$
, called ‘classical vectors’Footnote
2
in [Reference WuWu14, Definition 5.4], are defined up to a factor of modulus 1. We determine/choose them as follows. First of all, we impose
$e_{n}$
, called ‘classical vectors’Footnote
2
in [Reference WuWu14, Definition 5.4], are defined up to a factor of modulus 1. We determine/choose them as follows. First of all, we impose
Lemma 2.15. Let
![]() $e_{n}^{\prime }\in \unicode[STIX]{x1D70B}_{s}$
be defined by
$e_{n}^{\prime }\in \unicode[STIX]{x1D70B}_{s}$
be defined by
 $$\begin{eqnarray}\displaystyle & \displaystyle e_{1}^{\prime }=\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0}-\frac{q^{s}+q^{-s}}{q^{1/2}+q^{-1/2}}e_{0}, & \displaystyle \nonumber\\ \displaystyle & e_{n}^{\prime }=\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}-q^{-1/2}(q^{s}+q^{-s})\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n+1})).e_{0}+q^{-1}\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n+2})).e_{0},\quad \forall n\geqslant 2. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle e_{1}^{\prime }=\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0}-\frac{q^{s}+q^{-s}}{q^{1/2}+q^{-1/2}}e_{0}, & \displaystyle \nonumber\\ \displaystyle & e_{n}^{\prime }=\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}-q^{-1/2}(q^{s}+q^{-s})\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n+1})).e_{0}+q^{-1}\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n+2})).e_{0},\quad \forall n\geqslant 2. & \displaystyle \nonumber\end{eqnarray}$$
Then if
![]() $s\in i\mathbb{R}$
,
$s\in i\mathbb{R}$
,
![]() $\{e_{0},e_{1}^{\prime },\ldots ,e_{m}^{\prime }\}$
is an orthogonal basis of the
$\{e_{0},e_{1}^{\prime },\ldots ,e_{m}^{\prime }\}$
is an orthogonal basis of the
![]() $\mathbf{K}_{0}[\mathfrak{p}^{m}]$
-invariant subspace of
$\mathbf{K}_{0}[\mathfrak{p}^{m}]$
-invariant subspace of
![]() $H$
for any
$H$
for any
![]() $m\in \mathbb{N}$
.
$m\in \mathbb{N}$
.
Proof. If
![]() $s\in i\mathbb{R}$
,
$s\in i\mathbb{R}$
,
![]() $\{e_{0},\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0},\ldots ,\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-m})).e_{0}\}$
is a basis of the
$\{e_{0},\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0},\ldots ,\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-m})).e_{0}\}$
is a basis of the
![]() $\mathbf{K}_{0}[\mathfrak{p}^{m}]$
-invariant subspace of
$\mathbf{K}_{0}[\mathfrak{p}^{m}]$
-invariant subspace of
![]() $H$
for any
$H$
for any
![]() $m\in \mathbb{N}$
. Then use the Macdonald formula [Reference BumpBum98, Theorem 4.6.6] to verify that
$m\in \mathbb{N}$
. Then use the Macdonald formula [Reference BumpBum98, Theorem 4.6.6] to verify that
![]() $e_{n}^{\prime }$
is orthogonal to
$e_{n}^{\prime }$
is orthogonal to
![]() $\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-m})).e_{0}$
for
$\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-m})).e_{0}$
for
![]() $0\leqslant m\leqslant n-1$
.◻
$0\leqslant m\leqslant n-1$
.◻
Lemma 2.16. If we define
then
![]() $e_{n}$
is independent of
$e_{n}$
is independent of
![]() $s$
and
$s$
and
![]() $\{e_{0},\ldots ,e_{m}\}$
form an orthonormal basis of the
$\{e_{0},\ldots ,e_{m}\}$
form an orthonormal basis of the
![]() $\mathbf{K}_{0}[\mathfrak{p}^{m}]$
-invariant subspace of
$\mathbf{K}_{0}[\mathfrak{p}^{m}]$
-invariant subspace of
![]() $H$
for any
$H$
for any
![]() $m\in \mathbb{N}$
. Moreover, the dimension
$m\in \mathbb{N}$
. Moreover, the dimension
![]() $d_{n}$
of
$d_{n}$
of
![]() $H_{n}$
is given by
$H_{n}$
is given by
Proof. If we write
![]() $\mathfrak{o}_{n}=\unicode[STIX]{x1D71B}^{n}\mathfrak{o}-\unicode[STIX]{x1D71B}^{n+1}\mathfrak{o}$
,
$\mathfrak{o}_{n}=\unicode[STIX]{x1D71B}^{n}\mathfrak{o}-\unicode[STIX]{x1D71B}^{n+1}\mathfrak{o}$
,
![]() $n\geqslant 1$
, then
$n\geqslant 1$
, then
 $$\begin{eqnarray}\displaystyle & \displaystyle D_{0}=\mathbf{B}(\mathfrak{o})w\mathbf{N}(\mathfrak{o})=\left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \mathbf{K}:c\in \mathfrak{o}^{\times }\right\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle D_{n}=\mathbf{B}(\mathfrak{o})\mathbf{N}_{-}(\mathfrak{o}_{n})=\left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \mathbf{K}:c\in \mathfrak{o}_{n}\right\},\quad 1\leqslant n\leqslant m, & \displaystyle \nonumber\\ \displaystyle & D_{m}^{\prime }=\mathbf{K}_{0}[m]=\mathop{\bigcup }_{n=m}^{\infty }D_{n} & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle D_{0}=\mathbf{B}(\mathfrak{o})w\mathbf{N}(\mathfrak{o})=\left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \mathbf{K}:c\in \mathfrak{o}^{\times }\right\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle D_{n}=\mathbf{B}(\mathfrak{o})\mathbf{N}_{-}(\mathfrak{o}_{n})=\left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in \mathbf{K}:c\in \mathfrak{o}_{n}\right\},\quad 1\leqslant n\leqslant m, & \displaystyle \nonumber\\ \displaystyle & D_{m}^{\prime }=\mathbf{K}_{0}[m]=\mathop{\bigcup }_{n=m}^{\infty }D_{n} & \displaystyle \nonumber\end{eqnarray}$$
are the double cosets of
![]() $\mathbf{K}$
with respect to
$\mathbf{K}$
with respect to
![]() $\mathbf{B}(\mathfrak{o})$
and
$\mathbf{B}(\mathfrak{o})$
and
![]() $\mathbf{K}_{0}[m]$
. From the computation
$\mathbf{K}_{0}[m]$
. From the computation
 $$\begin{eqnarray}\displaystyle & \displaystyle \left(\begin{array}{@{}cc@{}}a\unicode[STIX]{x1D71B}^{-n} & b\\ c\unicode[STIX]{x1D71B}^{-n} & d\end{array}\right)\left(\begin{array}{@{}cc@{}}c^{-1}d\unicode[STIX]{x1D71B}^{n} & 1\\ -1 & 0\end{array}\right)=\left(\begin{array}{@{}cc@{}}c^{-1}(ad-bc) & \ast \\ 0 & c\unicode[STIX]{x1D71B}^{-n}\end{array}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(\begin{array}{@{}cc@{}}a\unicode[STIX]{x1D71B}^{-n} & b\\ c\unicode[STIX]{x1D71B}^{-n} & d\end{array}\right)\left(\begin{array}{@{}cc@{}}1 & 0\\ -d^{-1}c\unicode[STIX]{x1D71B}^{-n} & 1\end{array}\right)=\left(\begin{array}{@{}cc@{}}d^{-1}\unicode[STIX]{x1D71B}^{-n}(ad-bc) & \ast \\ 0 & d\end{array}\right), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left(\begin{array}{@{}cc@{}}a\unicode[STIX]{x1D71B}^{-n} & b\\ c\unicode[STIX]{x1D71B}^{-n} & d\end{array}\right)\left(\begin{array}{@{}cc@{}}c^{-1}d\unicode[STIX]{x1D71B}^{n} & 1\\ -1 & 0\end{array}\right)=\left(\begin{array}{@{}cc@{}}c^{-1}(ad-bc) & \ast \\ 0 & c\unicode[STIX]{x1D71B}^{-n}\end{array}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(\begin{array}{@{}cc@{}}a\unicode[STIX]{x1D71B}^{-n} & b\\ c\unicode[STIX]{x1D71B}^{-n} & d\end{array}\right)\left(\begin{array}{@{}cc@{}}1 & 0\\ -d^{-1}c\unicode[STIX]{x1D71B}^{-n} & 1\end{array}\right)=\left(\begin{array}{@{}cc@{}}d^{-1}\unicode[STIX]{x1D71B}^{-n}(ad-bc) & \ast \\ 0 & d\end{array}\right), & \displaystyle \nonumber\end{eqnarray}$$
one easily deduces that
 $$\begin{eqnarray}\displaystyle & \displaystyle e_{1}^{\prime }|_{D_{0}}=\frac{q^{s+1/2}-q^{-s-1/2}}{q^{1/2}+q^{-1/2}}\cdot (-q^{-1/2}),\quad e_{1}^{\prime }|_{D_{k}}=\frac{q^{s+1/2}-q^{-s-1/2}}{q^{1/2}+q^{-1/2}}\cdot q^{1/2},\quad k\geqslant 1; & \displaystyle \nonumber\\ \displaystyle & \displaystyle e_{n}^{\prime }|_{D_{k}}=0,\quad 0\leqslant k\leqslant n-2,\quad e_{n}^{\prime }|_{D_{n-1}}=(1-q^{-1-2s})q^{n(s+1/2)}(-q^{-1}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle e_{n}^{\prime }|_{D_{k}}=(1-q^{-1-2s})q^{n(s+1/2)}(1-q^{-1}),\quad k\geqslant n. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle e_{1}^{\prime }|_{D_{0}}=\frac{q^{s+1/2}-q^{-s-1/2}}{q^{1/2}+q^{-1/2}}\cdot (-q^{-1/2}),\quad e_{1}^{\prime }|_{D_{k}}=\frac{q^{s+1/2}-q^{-s-1/2}}{q^{1/2}+q^{-1/2}}\cdot q^{1/2},\quad k\geqslant 1; & \displaystyle \nonumber\\ \displaystyle & \displaystyle e_{n}^{\prime }|_{D_{k}}=0,\quad 0\leqslant k\leqslant n-2,\quad e_{n}^{\prime }|_{D_{n-1}}=(1-q^{-1-2s})q^{n(s+1/2)}(-q^{-1}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle e_{n}^{\prime }|_{D_{k}}=(1-q^{-1-2s})q^{n(s+1/2)}(1-q^{-1}),\quad k\geqslant n. & \displaystyle \nonumber\end{eqnarray}$$
The assertion follows since the mass
![]() $w_{n}$
of
$w_{n}$
of
![]() $D_{n}$
, assuming the mass of
$D_{n}$
, assuming the mass of
![]() $\mathbf{K}$
is 1, is given by
$\mathbf{K}$
is 1, is given by
For the ‘moreover’ part, it suffices to notice
and to evaluate the above equation at
![]() $\unicode[STIX]{x1D705}=1$
.◻
$\unicode[STIX]{x1D705}=1$
.◻
Corollary 2.17. We record some special values of
![]() $e_{n}$
:
$e_{n}$
:
 $$\begin{eqnarray}e_{n}(1)=\left\{\begin{array}{@{}ll@{}}1 & n=0,\\ q^{1/2} & n=1,\\ (q^{n}-q^{n-2})^{1/2} & n\geqslant 2,\end{array}\right.\quad e_{n}(w)=\left\{\begin{array}{@{}ll@{}}1 & n=0,\\ -q^{-1/2} & n=1,\\ 0 & n\geqslant 2.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}e_{n}(1)=\left\{\begin{array}{@{}ll@{}}1 & n=0,\\ q^{1/2} & n=1,\\ (q^{n}-q^{n-2})^{1/2} & n\geqslant 2,\end{array}\right.\quad e_{n}(w)=\left\{\begin{array}{@{}ll@{}}1 & n=0,\\ -q^{-1/2} & n=1,\\ 0 & n\geqslant 2.\end{array}\right.\end{eqnarray}$$
Lemma 2.18. The two bases
![]() $\{e_{0},e_{1},\ldots \,\}$
and
$\{e_{0},e_{1},\ldots \,\}$
and
![]() $\{e_{0},\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0},\ldots \,\}$
of the subspace of classical vectors in
$\{e_{0},\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0},\ldots \,\}$
of the subspace of classical vectors in
![]() $H$
are related as follows.
$H$
are related as follows.
(i) For
 $n\geqslant 2$
, we have
$n\geqslant 2$
, we have  $$\begin{eqnarray}\displaystyle \displaystyle e_{1} & = & \displaystyle \frac{q^{1/2}+q^{-1/2}}{q^{s+1/2}-q^{-s-1/2}}\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0}-\frac{q^{s}+q^{-s}}{q^{s+1/2}-q^{-s-1/2}}e_{0},\nonumber\\ \displaystyle \displaystyle e_{n} & = & \displaystyle \sqrt{\frac{q+1}{q-1}}\frac{q^{-ns}}{1-q^{-1-2s}}\nonumber\\ \displaystyle & & \displaystyle \times \,(\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}-q^{-1/2}(q^{s}+q^{-s})\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n+1})).e_{0}+q^{-1}\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n+2})).e_{0}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle e_{1} & = & \displaystyle \frac{q^{1/2}+q^{-1/2}}{q^{s+1/2}-q^{-s-1/2}}\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0}-\frac{q^{s}+q^{-s}}{q^{s+1/2}-q^{-s-1/2}}e_{0},\nonumber\\ \displaystyle \displaystyle e_{n} & = & \displaystyle \sqrt{\frac{q+1}{q-1}}\frac{q^{-ns}}{1-q^{-1-2s}}\nonumber\\ \displaystyle & & \displaystyle \times \,(\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}-q^{-1/2}(q^{s}+q^{-s})\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n+1})).e_{0}+q^{-1}\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n+2})).e_{0}).\nonumber\end{eqnarray}$$
(ii) For
 $n\geqslant 2$
, we have where the coefficients
$n\geqslant 2$
, we have where the coefficients $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0}=\frac{q^{s+1/2}-q^{-s-1/2}}{q^{1/2}+q^{-1/2}}e_{1}+\frac{q^{s}+q^{-s}}{q^{1/2}+q^{-1/2}}e_{0},\quad \unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}=\mathop{\sum }_{l=0}^{n}c(n,l;s)e_{l},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0}=\frac{q^{s+1/2}-q^{-s-1/2}}{q^{1/2}+q^{-1/2}}e_{1}+\frac{q^{s}+q^{-s}}{q^{1/2}+q^{-1/2}}e_{0},\quad \unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}=\mathop{\sum }_{l=0}^{n}c(n,l;s)e_{l},\end{eqnarray}$$
 $c(n,l;s)=c_{\mathfrak{p}}(n,l;s)$
are given by
$c(n,l;s)=c_{\mathfrak{p}}(n,l;s)$
are given by  $$\begin{eqnarray}\displaystyle & \displaystyle c(n,0;s)=\frac{q^{-n/2}}{1+q^{-1}}\bigg\{\frac{q^{(n+1)s}-q^{-(n+1)s}}{q^{s}-q^{-s}}-q^{-1}\frac{q^{(n-1)s}-q^{-(n-1)s}}{q^{s}-q^{-s}}\bigg\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle c(n,1;s)=\frac{q^{-(n-1)/2}}{1+q^{-1}}(q^{ns}-q^{-ns})\frac{1-q^{-1-2s}}{1-q^{-2s}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle c(n,l;s)=q^{-(n-l)/2}(q^{ns}-q^{(2l-2-n)s})\frac{1-q^{-1-2s}}{1-q^{-2s}}\sqrt{\frac{q-1}{q+1}},\quad 2\leqslant l\leqslant n. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle c(n,0;s)=\frac{q^{-n/2}}{1+q^{-1}}\bigg\{\frac{q^{(n+1)s}-q^{-(n+1)s}}{q^{s}-q^{-s}}-q^{-1}\frac{q^{(n-1)s}-q^{-(n-1)s}}{q^{s}-q^{-s}}\bigg\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle c(n,1;s)=\frac{q^{-(n-1)/2}}{1+q^{-1}}(q^{ns}-q^{-ns})\frac{1-q^{-1-2s}}{1-q^{-2s}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle c(n,l;s)=q^{-(n-l)/2}(q^{ns}-q^{(2l-2-n)s})\frac{1-q^{-1-2s}}{1-q^{-2s}}\sqrt{\frac{q-1}{q+1}},\quad 2\leqslant l\leqslant n. & \displaystyle \nonumber\end{eqnarray}$$
(iii) For
 $n\geqslant 2$
, we have where
$n\geqslant 2$
, we have where $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B})).e_{0}=\frac{q^{s+1/2}-q^{-s-1/2}}{q^{1/2}+q^{-1/2}}w.e_{1}+\frac{q^{s}+q^{-s}}{q^{1/2}+q^{-1/2}}e_{0},\quad \unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{n})).e_{0}=\mathop{\sum }_{l=0}^{n}c(n,l;s)w.e_{l},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B})).e_{0}=\frac{q^{s+1/2}-q^{-s-1/2}}{q^{1/2}+q^{-1/2}}w.e_{1}+\frac{q^{s}+q^{-s}}{q^{1/2}+q^{-1/2}}e_{0},\quad \unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{n})).e_{0}=\mathop{\sum }_{l=0}^{n}c(n,l;s)w.e_{l},\end{eqnarray}$$
 $w\in \mathbf{K}$
is the Weyl element and the coefficients
$w\in \mathbf{K}$
is the Weyl element and the coefficients
 $c(n,l;s)$
are the same as in (ii).
$c(n,l;s)$
are the same as in (ii).
Proof. (i) is merely a restatement of Lemmas 2.15 and 2.16. For (ii), we first use Lemma 2.15 to deduce a relation of two formal power series
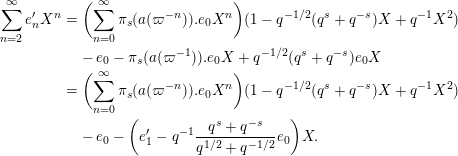 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=2}^{\infty }e_{n}^{\prime }X^{n} & = & \displaystyle \biggl(\mathop{\sum }_{n=0}^{\infty }\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}X^{n}\biggr)(1-q^{-1/2}(q^{s}+q^{-s})X+q^{-1}X^{2})\nonumber\\ \displaystyle & & \displaystyle -\,e_{0}-\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0}X+q^{-1/2}(q^{s}+q^{-s})e_{0}X\nonumber\\ \displaystyle & = & \displaystyle \biggl(\mathop{\sum }_{n=0}^{\infty }\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}X^{n}\biggr)(1-q^{-1/2}(q^{s}+q^{-s})X+q^{-1}X^{2})\nonumber\\ \displaystyle & & \displaystyle -\,e_{0}-\biggl(e_{1}^{\prime }-q^{-1}\frac{q^{s}+q^{-s}}{q^{1/2}+q^{-1/2}}e_{0}\biggr)X.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=2}^{\infty }e_{n}^{\prime }X^{n} & = & \displaystyle \biggl(\mathop{\sum }_{n=0}^{\infty }\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}X^{n}\biggr)(1-q^{-1/2}(q^{s}+q^{-s})X+q^{-1}X^{2})\nonumber\\ \displaystyle & & \displaystyle -\,e_{0}-\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-1})).e_{0}X+q^{-1/2}(q^{s}+q^{-s})e_{0}X\nonumber\\ \displaystyle & = & \displaystyle \biggl(\mathop{\sum }_{n=0}^{\infty }\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}X^{n}\biggr)(1-q^{-1/2}(q^{s}+q^{-s})X+q^{-1}X^{2})\nonumber\\ \displaystyle & & \displaystyle -\,e_{0}-\biggl(e_{1}^{\prime }-q^{-1}\frac{q^{s}+q^{-s}}{q^{1/2}+q^{-1/2}}e_{0}\biggr)X.\nonumber\end{eqnarray}$$
Reverting this relation, we obtain
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=0}^{\infty }\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}X^{n} & = & \displaystyle \biggl(\mathop{\sum }_{n=0}^{\infty }q^{-n/2}\frac{q^{(n+1)s}-q^{-(n+1)s}}{q^{s}-q^{-s}}X^{n}\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(e_{0}+\biggl(e_{1}^{\prime }-q^{-1}\frac{q^{s}+q^{-s}}{q^{1/2}+q^{-1/2}}e_{0}\biggr)X+\mathop{\sum }_{n=2}^{\infty }e_{n}^{\prime }X^{n}\biggr)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{n=0}^{\infty }\unicode[STIX]{x1D70B}_{s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}X^{n} & = & \displaystyle \biggl(\mathop{\sum }_{n=0}^{\infty }q^{-n/2}\frac{q^{(n+1)s}-q^{-(n+1)s}}{q^{s}-q^{-s}}X^{n}\biggr)\nonumber\\ \displaystyle & & \displaystyle \cdot \,\biggl(e_{0}+\biggl(e_{1}^{\prime }-q^{-1}\frac{q^{s}+q^{-s}}{q^{1/2}+q^{-1/2}}e_{0}\biggr)X+\mathop{\sum }_{n=2}^{\infty }e_{n}^{\prime }X^{n}\biggr)\nonumber\end{eqnarray}$$
and conclude by inserting Lemma 2.16. (iii) follows from (ii) by noting
Corollary 2.19. If
![]() ${\mathcal{R}}(s):\unicode[STIX]{x1D70B}_{s}\rightarrow \unicode[STIX]{x1D70B}_{-s}$
is the normalized intertwining operator sending
${\mathcal{R}}(s):\unicode[STIX]{x1D70B}_{s}\rightarrow \unicode[STIX]{x1D70B}_{-s}$
is the normalized intertwining operator sending
![]() $e_{0}$
to
$e_{0}$
to
![]() $e_{0}$
, then
$e_{0}$
, then
![]() ${\mathcal{R}}(s)$
acts on
${\mathcal{R}}(s)$
acts on
![]() $H_{n}$
by multiplication by
$H_{n}$
by multiplication by
Proof. This is a special case of the computation in [Reference WuWu17b, § 3.4.3]. Here is another proof.
![]() ${\mathcal{R}}(s)e_{n}$
is equal to
${\mathcal{R}}(s)e_{n}$
is equal to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \sqrt{\frac{q+1}{q-1}}\frac{q^{-ns}}{1-q^{-1-2s}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}-q^{-1/2}(q^{s}+q^{-s})\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n+1})).e_{0}+q^{-1}\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n+2})).e_{0})\nonumber\\ \displaystyle & & \displaystyle \quad =q^{-2ns}\frac{1-q^{-(1-2s)}}{1-q^{-(1+2s)}}\sqrt{\frac{q+1}{q-1}}\frac{q^{ns}}{1-q^{-1+2s}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}-q^{-1/2}(q^{s}+q^{-s})\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n+1})).e_{0}+q^{-1}\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n+2})).e_{0}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \sqrt{\frac{q+1}{q-1}}\frac{q^{-ns}}{1-q^{-1-2s}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}-q^{-1/2}(q^{s}+q^{-s})\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n+1})).e_{0}+q^{-1}\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n+2})).e_{0})\nonumber\\ \displaystyle & & \displaystyle \quad =q^{-2ns}\frac{1-q^{-(1-2s)}}{1-q^{-(1+2s)}}\sqrt{\frac{q+1}{q-1}}\frac{q^{ns}}{1-q^{-1+2s}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n})).e_{0}-q^{-1/2}(q^{s}+q^{-s})\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n+1})).e_{0}+q^{-1}\unicode[STIX]{x1D70B}_{-s}(a(\unicode[STIX]{x1D71B}^{-n+2})).e_{0}),\nonumber\end{eqnarray}$$
the last line being equal to
![]() $e_{n}$
since it is independent of
$e_{n}$
since it is independent of
![]() $s$
.◻
$s$
.◻
Remark 2.20. For
![]() $\mathbf{F}$
archimedean, we have similar computations already available in [Reference BumpBum98, Proposition 2.6.3] and [Reference WuWu14, § 2.7]. We recall them without proof.
$\mathbf{F}$
archimedean, we have similar computations already available in [Reference BumpBum98, Proposition 2.6.3] and [Reference WuWu14, § 2.7]. We recall them without proof.
∙
 $\mathbf{F}=\mathbb{R}$
.
$\mathbf{F}=\mathbb{R}$
.
 $H_{n}$
is the subspace of vectors
$H_{n}$
is the subspace of vectors
 $v$
such that and
$v$
such that and $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\cos \unicode[STIX]{x1D6FC} & \sin \unicode[STIX]{x1D6FC}\\ -\text{sin}\,\unicode[STIX]{x1D6FC} & \cos \unicode[STIX]{x1D6FC}\end{array}\right).v=e^{in\unicode[STIX]{x1D6FC}}v\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\cos \unicode[STIX]{x1D6FC} & \sin \unicode[STIX]{x1D6FC}\\ -\text{sin}\,\unicode[STIX]{x1D6FC} & \cos \unicode[STIX]{x1D6FC}\end{array}\right).v=e^{in\unicode[STIX]{x1D6FC}}v\end{eqnarray}$$
 $H_{n}\neq \{0\}$
only if
$H_{n}\neq \{0\}$
only if
 $2\mid n\in \mathbb{Z}$
. We have
$2\mid n\in \mathbb{Z}$
. We have  $$\begin{eqnarray}\unicode[STIX]{x1D707}(n;s)=\unicode[STIX]{x1D707}_{v}(n,s)=\mathop{\prod }_{2\mid k=0}^{|n|-2}\frac{k+1-2s}{k+1+2s}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(n;s)=\unicode[STIX]{x1D707}_{v}(n,s)=\mathop{\prod }_{2\mid k=0}^{|n|-2}\frac{k+1-2s}{k+1+2s}.\end{eqnarray}$$
∙
 $\mathbf{F}=\mathbb{C}$
.
$\mathbf{F}=\mathbb{C}$
.
 $H_{n}$
is the subspace on which
$H_{n}$
is the subspace on which
 $\text{SU}_{2}(\mathbb{C})$
acts as the unitary irreducible representation of dimension
$\text{SU}_{2}(\mathbb{C})$
acts as the unitary irreducible representation of dimension
 $n+1$
and
$n+1$
and
 $H_{n}\neq \{0\}$
only if
$H_{n}\neq \{0\}$
only if
 $2\mid n\in \mathbb{N}$
. We have
$2\mid n\in \mathbb{N}$
. We have  $$\begin{eqnarray}\unicode[STIX]{x1D707}(n;s)=\unicode[STIX]{x1D707}_{v}(n,s)=\mathop{\prod }_{2\mid k=1}^{n/2}\frac{k-2s}{k+2s}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}(n;s)=\unicode[STIX]{x1D707}_{v}(n,s)=\mathop{\prod }_{2\mid k=1}^{n/2}\frac{k-2s}{k+2s}.\end{eqnarray}$$
We write
![]() $e_{0}\in H_{0}$
for the spherical function taking value 1 on
$e_{0}\in H_{0}$
for the spherical function taking value 1 on
![]() $\mathbf{K}=\text{SO}_{2}(\mathbb{R})$
or
$\mathbf{K}=\text{SO}_{2}(\mathbb{R})$
or
![]() $\text{SU}_{2}(\mathbb{C})$
.
$\text{SU}_{2}(\mathbb{C})$
.
Definition 2.21. For
![]() $n,l\in \mathbb{Z}$
, we write
$n,l\in \mathbb{Z}$
, we write
![]() $l\preccurlyeq n$
to mean either
$l\preccurlyeq n$
to mean either
![]() $0\leqslant l\leqslant n$
or
$0\leqslant l\leqslant n$
or
![]() $n\leqslant l\leqslant 0$
. We extend the definition of
$n\leqslant l\leqslant 0$
. We extend the definition of
![]() $e_{n}$
,
$e_{n}$
,
![]() $\unicode[STIX]{x1D707}(n;s)$
and
$\unicode[STIX]{x1D707}(n;s)$
and
![]() $c(n,l;s)$
for
$c(n,l;s)$
for
![]() $n,l\in \mathbb{N}$
to
$n,l\in \mathbb{N}$
to
![]() $n,l\in \mathbb{Z},l\preccurlyeq n$
by requiring
$n,l\in \mathbb{Z},l\preccurlyeq n$
by requiring
3 Local estimations
3.1 Non-archimedean places for exceptional part
We work on a non-archimedean place
![]() $\mathfrak{p}$
and omit the subscript
$\mathfrak{p}$
and omit the subscript
![]() $\mathfrak{p}$
for simplicity of notation. Recall
$\mathfrak{p}$
for simplicity of notation. Recall
![]() $e_{n}$
defined in Lemma 2.16 and Definition 2.21, but change
$e_{n}$
defined in Lemma 2.16 and Definition 2.21, but change
![]() $s$
to
$s$
to
![]() $s_{0}$
. To emphasize the dependence on
$s_{0}$
. To emphasize the dependence on
![]() $s_{0}$
, we write
$s_{0}$
, we write
![]() $e_{n,s_{0}}\in \unicode[STIX]{x1D70B}_{s_{0}}$
for the flat section associated with
$e_{n,s_{0}}\in \unicode[STIX]{x1D70B}_{s_{0}}$
for the flat section associated with
![]() $e_{n}$
, and
$e_{n}$
, and
![]() $W_{n}(s_{0},\cdot )$
the associated Kirillov function in the Kirillov model
$W_{n}(s_{0},\cdot )$
the associated Kirillov function in the Kirillov model
![]() ${\mathcal{K}}(\unicode[STIX]{x1D70B}_{s_{0}},\unicode[STIX]{x1D713})$
of
${\mathcal{K}}(\unicode[STIX]{x1D70B}_{s_{0}},\unicode[STIX]{x1D713})$
of
![]() $\unicode[STIX]{x1D70B}_{s_{0}}$
, with respect to an unramified additive character
$\unicode[STIX]{x1D70B}_{s_{0}}$
, with respect to an unramified additive character
![]() $\unicode[STIX]{x1D713}$
of
$\unicode[STIX]{x1D713}$
of
![]() $\mathbf{F}$
. Recall the local zeta functional
$\mathbf{F}$
. Recall the local zeta functional
Lemma 3.1. The ratios of zeta functions
are determined by:
∙
 $\unicode[STIX]{x1D701}_{0}(s,s_{0})=1$
and
$\unicode[STIX]{x1D701}_{0}(s,s_{0})=1$
and  $$\begin{eqnarray}\unicode[STIX]{x1D701}_{1}(s,s_{0})=\frac{q^{1/2}+q^{-1/2}}{q^{s_{0}+1/2}-q^{-(s_{0}+1/2)}}q^{-s}-\frac{q^{s_{0}}+q^{-s_{0}}}{q^{s_{0}+1/2}-q^{-(s_{0}+1/2)}};\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{1}(s,s_{0})=\frac{q^{1/2}+q^{-1/2}}{q^{s_{0}+1/2}-q^{-(s_{0}+1/2)}}q^{-s}-\frac{q^{s_{0}}+q^{-s_{0}}}{q^{s_{0}+1/2}-q^{-(s_{0}+1/2)}};\end{eqnarray}$$
∙ if
 $n\geqslant 2$
, then
$n\geqslant 2$
, then  $$\begin{eqnarray}\unicode[STIX]{x1D701}_{n}(s,s_{0})=\sqrt{\frac{q+1}{q-1}}\frac{q^{-ns_{0}}}{1-q^{-1-2s_{0}}}(q^{-ns}-q^{-1/2}(q^{s_{0}}+q^{-s_{0}})q^{-(n-1)s}+q^{-1-(n-2)s});\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{n}(s,s_{0})=\sqrt{\frac{q+1}{q-1}}\frac{q^{-ns_{0}}}{1-q^{-1-2s_{0}}}(q^{-ns}-q^{-1/2}(q^{s_{0}}+q^{-s_{0}})q^{-(n-1)s}+q^{-1-(n-2)s});\end{eqnarray}$$
∙ if
 $n<0$
, then
$n<0$
, then
 $\unicode[STIX]{x1D701}_{n}(s,s_{0})=\unicode[STIX]{x1D701}_{-n}(-s,s_{0})$
.
$\unicode[STIX]{x1D701}_{n}(s,s_{0})=\unicode[STIX]{x1D701}_{-n}(-s,s_{0})$
.
Proof. From the relation of zeta functions
the desired formulas are simple consequences of those in Lemma 2.18(i) and (iii). ◻
Corollary 3.2. Assume
![]() $\Re s=\unicode[STIX]{x1D716}>0$
small,
$\Re s=\unicode[STIX]{x1D716}>0$
small,
![]() $|n|$
is bounded by a constant and
$|n|$
is bounded by a constant and
![]() $0\leqslant k\leqslant 2$
. Then we have
$0\leqslant k\leqslant 2$
. Then we have
3.2 Non-archimedean places for
 $\text{L}^{4}$
-norms
$\text{L}^{4}$
-norms
Using the notation of the previous subsection, we define the Rankin–Selberg local zeta ratios for
![]() $n_{1},n_{2},n\in \mathbb{Z}$
and
$n_{1},n_{2},n\in \mathbb{Z}$
and
![]() $s_{1},s_{2},s\in \mathbb{C}$
,
$s_{1},s_{2},s\in \mathbb{C}$
,

Lemma 3.3.
(i) We have

(ii) Let
 $n_{2}=0=s_{2}$
. The ratio is non-vanishing only if
$n_{2}=0=s_{2}$
. The ratio is non-vanishing only if
 $|n_{1}|=|n|$
.
$|n_{1}|=|n|$
.(iii) Recall the dimension
 $d_{n}$
of
$d_{n}$
of
 $H_{n}$
computed in Lemma 2.16. We have, for
$H_{n}$
computed in Lemma 2.16. We have, for
 $n\geqslant 2$
,while for
$n\geqslant 2$
,while for
 $n=1$
,
$n=1$
,
Proof. (i) is a consequence of the
![]() $w$
-invariance of the Rankin–Selberg local zeta functional. For (ii), we may assume
$w$
-invariance of the Rankin–Selberg local zeta functional. For (ii), we may assume
![]() $n\geqslant 0$
by (i). It suffices to notice that
$n\geqslant 0$
by (i). It suffices to notice that
is non-vanishing only if
![]() $|n_{1}|=|n|$
, since by (2.5),
$|n_{1}|=|n|$
, since by (2.5),
![]() $\int _{\mathbf{K}}\overline{e_{n}(\unicode[STIX]{x1D705})}\unicode[STIX]{x1D705}\,d\unicode[STIX]{x1D705}$
is
$\int _{\mathbf{K}}\overline{e_{n}(\unicode[STIX]{x1D705})}\unicode[STIX]{x1D705}\,d\unicode[STIX]{x1D705}$
is
![]() $d_{n}^{-1/2}$
times the orthogonal projection onto the
$d_{n}^{-1/2}$
times the orthogonal projection onto the
![]() $e_{n}$
-vector of
$e_{n}$
-vector of
![]() $H_{n}$
. In particular, we deduce, for
$H_{n}$
. In particular, we deduce, for
![]() $n\geqslant 0$
,
$n\geqslant 0$
,
Hence for (iii), we are reduced to computing
By Lemma 2.18(i), we are again reduced to computing
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbf{F}^{\times }}\overline{W_{0}(0,a(y\unicode[STIX]{x1D71B}^{-n}))}W_{0}(0,a(y))|y|^{s-1/2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{m=0}^{\infty }q^{-m/2}(m+1)\cdot q^{-(n+m)/2}(n+m+1)\cdot q^{-(n+m)(s-1/2)}\nonumber\\ \displaystyle & & \displaystyle \quad =q^{-ns}\cdot \frac{2+(n-1)(1-q^{-(s+1/2)})}{(1-q^{-(s+1/2)})^{3}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbf{F}^{\times }}\overline{W_{0}(0,a(y\unicode[STIX]{x1D71B}^{-n}))}W_{0}(0,a(y))|y|^{s-1/2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{m=0}^{\infty }q^{-m/2}(m+1)\cdot q^{-(n+m)/2}(n+m+1)\cdot q^{-(n+m)(s-1/2)}\nonumber\\ \displaystyle & & \displaystyle \quad =q^{-ns}\cdot \frac{2+(n-1)(1-q^{-(s+1/2)})}{(1-q^{-(s+1/2)})^{3}},\nonumber\end{eqnarray}$$
and conclude from it. ◻
Corollary 3.4. For any integer
![]() $k\geqslant 0$
, we have
$k\geqslant 0$
, we have
4 Proof of main result
The main structure of the proof is similar to our former work [Reference WuWu14]. We shall only emphasize the differences and the extra difficulties. We shall not recall the intuition of the method in terms of the equidistribution of certain lines approaching the low-lying horocycles, but refer the reader to the first two pages of [Reference WuWu14, § 3].
4.1 Reduction to global period bound
The fixed
![]() $\text{GL}_{2}$
automorphic representation
$\text{GL}_{2}$
automorphic representation
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}(1,1)$
is realized as the completed Eisenstein series
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}(1,1)$
is realized as the completed Eisenstein series
![]() $\text{E}^{\ast }(0,\cdot )$
. We imitate the cuspidal case by choosing
$\text{E}^{\ast }(0,\cdot )$
. We imitate the cuspidal case by choosing
where
![]() $f_{0}$
is the spherical function taking value 1 on
$f_{0}$
is the spherical function taking value 1 on
![]() $\mathbf{K}$
in the induced model of
$\mathbf{K}$
in the induced model of
![]() $\unicode[STIX]{x1D70B}(1,1)$
. Writing the normalized Whittaker functions as
$\unicode[STIX]{x1D70B}(1,1)$
. Writing the normalized Whittaker functions as
we get by Proposition 2.10 an expression for the relevant
![]() $L$
-function.
$L$
-function.
where the global zeta integral is defined in Definition 2.8 and reduces in our case to
whose value at
![]() $s=1/2$
must be interpreted via analytic continuation, unlike the cuspidal case.
$s=1/2$
must be interpreted via analytic continuation, unlike the cuspidal case.
Proposition 4.1. We can choose
![]() $T_{v}$
with
$T_{v}$
with
![]() $|T_{v}|_{v}\in [\mathbf{C}(\unicode[STIX]{x1D712}_{v}),2\mathbf{C}(\unicode[STIX]{x1D712}_{v})]$
such that
$|T_{v}|_{v}\in [\mathbf{C}(\unicode[STIX]{x1D712}_{v}),2\mathbf{C}(\unicode[STIX]{x1D712}_{v})]$
such that
where
![]() $Q=\mathbf{C}(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D6F1}_{v}\mathbf{C}(\unicode[STIX]{x1D712}_{v})$
is the analytic conductor of
$Q=\mathbf{C}(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D6F1}_{v}\mathbf{C}(\unicode[STIX]{x1D712}_{v})$
is the analytic conductor of
![]() $\unicode[STIX]{x1D712}$
(we keep this notation in what follows).
$\unicode[STIX]{x1D712}$
(we keep this notation in what follows).
Proof. This is a special case of [Reference WuWu17a, Proposition 2.4] for ‘option (B)’. ◻
4.2 Reduction to bound of truncated integral
We are reduced to bounding
![]() $\unicode[STIX]{x1D701}(1/2,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})$
. This can be defined only via analytic continuation. However, we can still approximate it with a truncated integral, just as the classical approximate functional equation does. The outcome is that we essentially only need to estimate a compact domain integral, which is equivalent to a finite sum in the classical setting. Recall Definition 2.12. We shall apply Proposition 2.13 with
$\unicode[STIX]{x1D701}(1/2,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})$
. This can be defined only via analytic continuation. However, we can still approximate it with a truncated integral, just as the classical approximate functional equation does. The outcome is that we essentially only need to estimate a compact domain integral, which is equivalent to a finite sum in the classical setting. Recall Definition 2.12. We shall apply Proposition 2.13 with
![]() $A=Q^{-\unicode[STIX]{x1D705}-1}$
,
$A=Q^{-\unicode[STIX]{x1D705}-1}$
,
![]() $B=Q^{\unicode[STIX]{x1D705}-1}$
for some
$B=Q^{\unicode[STIX]{x1D705}-1}$
for some
![]() $\unicode[STIX]{x1D705}\in (0,1)$
to be chosen later, with
$\unicode[STIX]{x1D705}\in (0,1)$
to be chosen later, with
![]() $c_{1}=c_{2}=1/2+\unicode[STIX]{x1D716}$
and with
$c_{1}=c_{2}=1/2+\unicode[STIX]{x1D716}$
and with
![]() $h_{0}$
and
$h_{0}$
and
![]() $h$
specified there.
$h$
specified there.
Lemma 4.2. Assume
![]() $Q$
is bounded away from
$Q$
is bounded away from
![]() $0$
. Then we have, for any small
$0$
. Then we have, for any small
![]() $\unicode[STIX]{x1D716}>0$
,
$\unicode[STIX]{x1D716}>0$
,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(\frac{1}{2},\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}\biggr) & = & \displaystyle \unicode[STIX]{x1D701}(\unicode[STIX]{x1D70E}\ast h,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})+O_{\mathbf{F},h_{0},\unicode[STIX]{x1D716}}(Q^{-\unicode[STIX]{x1D705}/2+\unicode[STIX]{x1D716}})\nonumber\\ \displaystyle & = & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}\unicode[STIX]{x1D70E}\ast h(|y|_{\mathbb{A}})\unicode[STIX]{x1D711}(a(y))\unicode[STIX]{x1D712}(y)\,d^{\times }y+O_{\mathbf{F},h_{0},\unicode[STIX]{x1D716}}(Q^{-\unicode[STIX]{x1D705}/2+\unicode[STIX]{x1D716}}+Q^{(\unicode[STIX]{x1D705}-1)/2+\unicode[STIX]{x1D716}}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(\frac{1}{2},\unicode[STIX]{x1D712},\unicode[STIX]{x1D711}\biggr) & = & \displaystyle \unicode[STIX]{x1D701}(\unicode[STIX]{x1D70E}\ast h,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})+O_{\mathbf{F},h_{0},\unicode[STIX]{x1D716}}(Q^{-\unicode[STIX]{x1D705}/2+\unicode[STIX]{x1D716}})\nonumber\\ \displaystyle & = & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}\unicode[STIX]{x1D70E}\ast h(|y|_{\mathbb{A}})\unicode[STIX]{x1D711}(a(y))\unicode[STIX]{x1D712}(y)\,d^{\times }y+O_{\mathbf{F},h_{0},\unicode[STIX]{x1D716}}(Q^{-\unicode[STIX]{x1D705}/2+\unicode[STIX]{x1D716}}+Q^{(\unicode[STIX]{x1D705}-1)/2+\unicode[STIX]{x1D716}}),\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70E}$
is the average of Dirac measures given by
$\unicode[STIX]{x1D70E}$
is the average of Dirac measures given by
with a parameter
![]() $E>0$
to be chosen later, and
$E>0$
to be chosen later, and
Proof. We only need to consider the case for
![]() $h$
since
$h$
since
![]() $\unicode[STIX]{x1D70E}\ast h$
gives bounded translations. Compared to [Reference WuWu14, Lemma 3.2], the new situation is as follows.
$\unicode[STIX]{x1D70E}\ast h$
gives bounded translations. Compared to [Reference WuWu14, Lemma 3.2], the new situation is as follows.
∙ The normal polar part is non-vanishing.
∙ At
 $v\mid \infty$
,
$v\mid \infty$
,
 $W_{0,v}^{\ast }$
is no longer of compact support in
$W_{0,v}^{\ast }$
is no longer of compact support in
 $\mathbf{F}_{v}^{\times }$
, hence [Reference WuWu14, Corollary 4.3] used in [Reference WuWu14, § 6.1] for local archimedean bounds on the vertical line
$\mathbf{F}_{v}^{\times }$
, hence [Reference WuWu14, Corollary 4.3] used in [Reference WuWu14, § 6.1] for local archimedean bounds on the vertical line
 $\Re s=-1/2-\unicode[STIX]{x1D716}$
needs to be reconsidered.
$\Re s=-1/2-\unicode[STIX]{x1D716}$
needs to be reconsidered.∙ There is a new passage from the first line to the second line, for which the estimation of an integral of the constant term
 $\unicode[STIX]{x1D711}_{\mathbf{N}}$
needs to be done.
$\unicode[STIX]{x1D711}_{\mathbf{N}}$
needs to be done.
We proceed to bound each part appearing in Proposition 2.13.
(0) The degenerate polar part is vanishing.
(1) The normal polar part and the integral of
![]() $\unicode[STIX]{x1D711}_{\mathbf{N}}$
are non-vanishing only if
$\unicode[STIX]{x1D711}_{\mathbf{N}}$
are non-vanishing only if
![]() $\unicode[STIX]{x1D712}=|\cdot |^{i\unicode[STIX]{x1D707}}$
for some
$\unicode[STIX]{x1D712}=|\cdot |^{i\unicode[STIX]{x1D707}}$
for some
![]() $\unicode[STIX]{x1D707}\in \mathbb{R}$
, in which case
$\unicode[STIX]{x1D707}\in \mathbb{R}$
, in which case
![]() $\mathbf{C}(\unicode[STIX]{x1D712}_{v})=1$
for all
$\mathbf{C}(\unicode[STIX]{x1D712}_{v})=1$
for all
![]() $v<\infty$
and
$v<\infty$
and
![]() $\mathbf{C}(\unicode[STIX]{x1D712}_{v})\asymp |\unicode[STIX]{x1D707}|^{[\mathbf{F}_{v}:\mathbb{R}]}$
for all
$\mathbf{C}(\unicode[STIX]{x1D712}_{v})\asymp |\unicode[STIX]{x1D707}|^{[\mathbf{F}_{v}:\mathbb{R}]}$
for all
![]() $v\mid \infty$
. Hence
$v\mid \infty$
. Hence
![]() $Q\asymp |\unicode[STIX]{x1D707}|^{[\mathbf{F}:\mathbb{Q}]}$
. Note that by [Reference WuWu18, Proposition 5.33], there are
$Q\asymp |\unicode[STIX]{x1D707}|^{[\mathbf{F}:\mathbb{Q}]}$
. Note that by [Reference WuWu18, Proposition 5.33], there are
![]() $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in \mathbb{C}$
depending only on
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in \mathbb{C}$
depending only on
![]() $\mathbf{F}$
such that
$\mathbf{F}$
such that
If we write
then we can easily calculate
 $$\begin{eqnarray}\displaystyle & \displaystyle f_{1}(1)=\unicode[STIX]{x1D707}_{1},\quad f_{2}(1)=\unicode[STIX]{x1D707}_{2},\quad f_{1}(w)=\unicode[STIX]{x1D707}_{1}\mathop{\prod }_{v\mid \infty }(1+|T_{v}|^{2})^{-[\mathbf{F}_{v}:\mathbb{R}]/2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f_{2}(w)=\unicode[STIX]{x1D707}_{2}\mathop{\prod }_{v\mid \infty }(1+|T_{v}|^{2})^{-[\mathbf{F}_{v}:\mathbb{R}]/2}\log \biggl(\mathop{\prod }_{v\mid \infty }(1+|T_{v}|^{2})^{-[\mathbf{F}_{v}:\mathbb{R}]/2}\biggr). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f_{1}(1)=\unicode[STIX]{x1D707}_{1},\quad f_{2}(1)=\unicode[STIX]{x1D707}_{2},\quad f_{1}(w)=\unicode[STIX]{x1D707}_{1}\mathop{\prod }_{v\mid \infty }(1+|T_{v}|^{2})^{-[\mathbf{F}_{v}:\mathbb{R}]/2}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f_{2}(w)=\unicode[STIX]{x1D707}_{2}\mathop{\prod }_{v\mid \infty }(1+|T_{v}|^{2})^{-[\mathbf{F}_{v}:\mathbb{R}]/2}\log \biggl(\mathop{\prod }_{v\mid \infty }(1+|T_{v}|^{2})^{-[\mathbf{F}_{v}:\mathbb{R}]/2}\biggr). & \displaystyle \nonumber\end{eqnarray}$$
We thus find that the normal polar part, which is of the form
can be bounded as
![]() $O(Q^{-N})$
for any
$O(Q^{-N})$
for any
![]() $N\in \mathbb{N}$
, due to the arbitrarily large denominators. For the integral of
$N\in \mathbb{N}$
, due to the arbitrarily large denominators. For the integral of
![]() $\unicode[STIX]{x1D711}_{\mathbf{N}}$
, since
$\unicode[STIX]{x1D711}_{\mathbf{N}}$
, since
![]() $h(t)$
has support contained in
$h(t)$
has support contained in
![]() $[Q^{-\unicode[STIX]{x1D705}-1},Q^{\unicode[STIX]{x1D705}-1}]$
with
$[Q^{-\unicode[STIX]{x1D705}-1},Q^{\unicode[STIX]{x1D705}-1}]$
with
![]() $|h(t)|\leqslant 1$
, we find that (note that
$|h(t)|\leqslant 1$
, we find that (note that
![]() $n(T).\unicode[STIX]{x1D711}_{\mathbf{N}}(a(y))=\unicode[STIX]{x1D711}_{\mathbf{N}}(a(y))$
)
$n(T).\unicode[STIX]{x1D711}_{\mathbf{N}}(a(y))=\unicode[STIX]{x1D711}_{\mathbf{N}}(a(y))$
)
(2) We turn to the lower part. Recall the choice
![]() $c_{1}=1/2+\unicode[STIX]{x1D716}$
. The relevant zeta function has a decomposition as a finite product
$c_{1}=1/2+\unicode[STIX]{x1D716}$
. The relevant zeta function has a decomposition as a finite product
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s,\unicode[STIX]{x1D712}^{-1},w.\unicode[STIX]{x1D711}\biggr) & = & \displaystyle L\biggl(\frac{1}{2}+s,\unicode[STIX]{x1D712}^{-1}\biggr)^{2}\cdot \mathop{\prod }_{v\mid \infty }\int _{\mathbf{F}_{v}^{\times }}wn(T_{v}).W_{0,v}^{\ast }(a(y_{v}))\unicode[STIX]{x1D712}_{v}^{-1}(y_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\mathop{\prod }_{v<\infty }\frac{\int _{\mathbf{F}_{v}^{\times }}wn(T_{v}).W_{0,v}^{\ast }(a(y_{v}))\unicode[STIX]{x1D712}_{v}^{-1}(y_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}}{L_{v}(1/2+s,\unicode[STIX]{x1D712}_{v}^{-1})^{2}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s,\unicode[STIX]{x1D712}^{-1},w.\unicode[STIX]{x1D711}\biggr) & = & \displaystyle L\biggl(\frac{1}{2}+s,\unicode[STIX]{x1D712}^{-1}\biggr)^{2}\cdot \mathop{\prod }_{v\mid \infty }\int _{\mathbf{F}_{v}^{\times }}wn(T_{v}).W_{0,v}^{\ast }(a(y_{v}))\unicode[STIX]{x1D712}_{v}^{-1}(y_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\mathop{\prod }_{v<\infty }\frac{\int _{\mathbf{F}_{v}^{\times }}wn(T_{v}).W_{0,v}^{\ast }(a(y_{v}))\unicode[STIX]{x1D712}_{v}^{-1}(y_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}}{L_{v}(1/2+s,\unicode[STIX]{x1D712}_{v}^{-1})^{2}}\nonumber\end{eqnarray}$$
At an archimedean place
![]() $v$
, say
$v$
, say
![]() $\mathbf{F}_{v}=\mathbb{R}$
, [Reference WuWu17a, Lemma 3.12(2)] gives the relevant local integral
$\mathbf{F}_{v}=\mathbb{R}$
, [Reference WuWu17a, Lemma 3.12(2)] gives the relevant local integral
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{R}^{\times }}wn(T_{v}).W_{0,v}^{\ast }(a(y_{v}))\unicode[STIX]{x1D712}_{v}^{-1}(y_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D712}_{v}(1+T_{v}^{2})^{-1}(1+T_{v}^{2})^{s}\int _{\mathbb{R}^{\times }}W_{0,v}^{\ast }(a(y))\unicode[STIX]{x1D713}_{v}(yT_{v})\unicode[STIX]{x1D712}_{v}^{-1}(y_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{R}^{\times }}wn(T_{v}).W_{0,v}^{\ast }(a(y_{v}))\unicode[STIX]{x1D712}_{v}^{-1}(y_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D712}_{v}(1+T_{v}^{2})^{-1}(1+T_{v}^{2})^{s}\int _{\mathbb{R}^{\times }}W_{0,v}^{\ast }(a(y))\unicode[STIX]{x1D713}_{v}(yT_{v})\unicode[STIX]{x1D712}_{v}^{-1}(y_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}.\nonumber\end{eqnarray}$$
a bound
![]() $O(|T_{v}|_{v}^{1/2+\unicode[STIX]{x1D716}})$
. For
$O(|T_{v}|_{v}^{1/2+\unicode[STIX]{x1D716}})$
. For
![]() $\mathbf{F}_{v}=\mathbb{C}$
the argument is similar, using [Reference WuWu17a, Lemma 3.13(2)]. At
$\mathbf{F}_{v}=\mathbb{C}$
the argument is similar, using [Reference WuWu17a, Lemma 3.13(2)]. At
![]() $v<\infty$
, [Reference WuWu14, Corollary 4.8] is still applicable. We thus deduce that, using the convex bound of
$v<\infty$
, [Reference WuWu14, Corollary 4.8] is still applicable. We thus deduce that, using the convex bound of
![]() $L(1/2+s,\unicode[STIX]{x1D712}^{-1})$
,
$L(1/2+s,\unicode[STIX]{x1D712}^{-1})$
,
The desired bound is thus
![]() $O(Q^{-(\unicode[STIX]{x1D705}+1)/2}Q^{1/2+\unicode[STIX]{x1D716}})=O(Q^{-\unicode[STIX]{x1D705}/2+\unicode[STIX]{x1D716}})$
.
$O(Q^{-(\unicode[STIX]{x1D705}+1)/2}Q^{1/2+\unicode[STIX]{x1D716}})=O(Q^{-\unicode[STIX]{x1D705}/2+\unicode[STIX]{x1D716}})$
.
(3) The treatment of the upper part is similar and simpler. It gives the desired bound
![]() $O(Q^{-\unicode[STIX]{x1D705}/2+\unicode[STIX]{x1D716}})$
.◻
$O(Q^{-\unicode[STIX]{x1D705}/2+\unicode[STIX]{x1D716}})$
.◻
4.3 Interlude: failure of truncation on Eisenstein series
We have approximated
![]() $\unicode[STIX]{x1D701}(1/2,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})$
by some smoothly truncated integral
$\unicode[STIX]{x1D701}(1/2,\unicode[STIX]{x1D712},\unicode[STIX]{x1D711})$
by some smoothly truncated integral
as in the cuspidal case. We then would like to apply the Cauchy–Schwarz inequality
and apply Fourier inversion to
![]() $|\unicode[STIX]{x1D711}_{0}|^{2}$
, interchange the order of summation and estimate each component as in the cuspidal case. This is not possible because
$|\unicode[STIX]{x1D711}_{0}|^{2}$
, interchange the order of summation and estimate each component as in the cuspidal case. This is not possible because
![]() $\unicode[STIX]{x1D711}_{0}$
is no longer of rapid decay hence
$\unicode[STIX]{x1D711}_{0}$
is no longer of rapid decay hence
![]() $|\unicode[STIX]{x1D711}_{0}|^{2}$
is not square-integrable any more. A first idea, already employed in [Reference Michel and VenkateshMV10, § 5.1.7], is to (smoothly) truncate the Eisenstein series
$|\unicode[STIX]{x1D711}_{0}|^{2}$
is not square-integrable any more. A first idea, already employed in [Reference Michel and VenkateshMV10, § 5.1.7], is to (smoothly) truncate the Eisenstein series
![]() $\unicode[STIX]{x1D711}_{0}$
up to some height
$\unicode[STIX]{x1D711}_{0}$
up to some height
![]() $X$
, denoted by
$X$
, denoted by
![]() $\unicode[STIX]{x1D6EC}^{X}\unicode[STIX]{x1D711}_{0}$
. For example, if we naively choose
$\unicode[STIX]{x1D6EC}^{X}\unicode[STIX]{x1D711}_{0}$
. For example, if we naively choose
![]() $X$
no less than the height of the truncation on the integral (namely,
$X$
no less than the height of the truncation on the integral (namely,
![]() $Q^{\unicode[STIX]{x1D705}+1}$
in the notation of [Reference WuWu14]), we find
$Q^{\unicode[STIX]{x1D705}+1}$
in the notation of [Reference WuWu14]), we find
We could continue the argument by replacing
![]() $\unicode[STIX]{x1D711}_{0}$
with
$\unicode[STIX]{x1D711}_{0}$
with
![]() $\unicode[STIX]{x1D6EC}^{X}\unicode[STIX]{x1D711}_{0}$
. But then some
$\unicode[STIX]{x1D6EC}^{X}\unicode[STIX]{x1D711}_{0}$
. But then some
![]() $\text{L}^{2}$
-Sobolev norm of
$\text{L}^{2}$
-Sobolev norm of
![]() $|\unicode[STIX]{x1D6EC}^{X}\unicode[STIX]{x1D711}_{0}|^{2}$
would come in as a multiplicative factor of the final estimation of the above integral. This causes no problem in the cuspidal case since the relevant norm is bounded by some
$|\unicode[STIX]{x1D6EC}^{X}\unicode[STIX]{x1D711}_{0}|^{2}$
would come in as a multiplicative factor of the final estimation of the above integral. This causes no problem in the cuspidal case since the relevant norm is bounded by some
![]() $\text{L}^{4}$
-Sobolev norms of
$\text{L}^{4}$
-Sobolev norms of
![]() $\unicode[STIX]{x1D711}_{0}$
, which depend only on
$\unicode[STIX]{x1D711}_{0}$
, which depend only on
![]() $\unicode[STIX]{x1D70B}$
. This is no longer the case for
$\unicode[STIX]{x1D70B}$
. This is no longer the case for
![]() $\unicode[STIX]{x1D6EC}^{X}\unicode[STIX]{x1D711}_{0}$
since its norms all depend on
$\unicode[STIX]{x1D6EC}^{X}\unicode[STIX]{x1D711}_{0}$
since its norms all depend on
![]() $X$
, hence some positive power of
$X$
, hence some positive power of
![]() $Q=\mathbf{C}(\unicode[STIX]{x1D712})$
. This means that in the final optimization just before [Reference WuWu14, Remark 3.11], we would have to replace
$Q=\mathbf{C}(\unicode[STIX]{x1D712})$
. This means that in the final optimization just before [Reference WuWu14, Remark 3.11], we would have to replace
![]() $EQ^{-1/4+\unicode[STIX]{x1D703}/2}$
by something like
$EQ^{-1/4+\unicode[STIX]{x1D703}/2}$
by something like
![]() $XEQ^{-1/4+\unicode[STIX]{x1D703}/2}$
, which completely destroys the Burgess-like quality. Indeed, in the thesis version of [Reference WuWu14] we have pursued this idea and were only able to obtain a saving
$XEQ^{-1/4+\unicode[STIX]{x1D703}/2}$
, which completely destroys the Burgess-like quality. Indeed, in the thesis version of [Reference WuWu14] we have pursued this idea and were only able to obtain a saving
![]() $(1-2\unicode[STIX]{x1D703})/12$
instead of the Burgess-like saving
$(1-2\unicode[STIX]{x1D703})/12$
instead of the Burgess-like saving
![]() $(1-2\unicode[STIX]{x1D703})/8$
.
$(1-2\unicode[STIX]{x1D703})/8$
.
A better way, which is also the main innovation of this paper, is to generalize the spectral decomposition/Fourier inversion into a space of functions suitably larger than the square-integrable ones. As we have seen in § 2.2,
![]() ${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},1)$
is a good candidate: it contains
${\mathcal{A}}^{\text{fr}}(\text{GL}_{2},1)$
is a good candidate: it contains
![]() $|\unicode[STIX]{x1D711}_{0}|^{2}$
and differs from smooth vectors in the
$|\unicode[STIX]{x1D711}_{0}|^{2}$
and differs from smooth vectors in the
![]() $\text{L}^{2}$
-space only by (non-unitary) Eisenstein series. Specifically, we shall decompose
$\text{L}^{2}$
-space only by (non-unitary) Eisenstein series. Specifically, we shall decompose
where we have written
![]() ${\mathcal{E}}={\mathcal{E}}(|\unicode[STIX]{x1D711}_{0}|^{2})$
for simplicity. Without amplification, the norms of
${\mathcal{E}}={\mathcal{E}}(|\unicode[STIX]{x1D711}_{0}|^{2})$
for simplicity. Without amplification, the norms of
![]() $|\unicode[STIX]{x1D711}_{0}|^{2}-{\mathcal{E}}$
depend only on
$|\unicode[STIX]{x1D711}_{0}|^{2}-{\mathcal{E}}$
depend only on
![]() $\unicode[STIX]{x1D711}_{0}$
, hence
$\unicode[STIX]{x1D711}_{0}$
, hence
![]() $\unicode[STIX]{x1D70B}$
; with amplification the relevant norms have contributions as small as
$\unicode[STIX]{x1D70B}$
; with amplification the relevant norms have contributions as small as
![]() $(\log E)^{3}$
(see Theorem 5.4) where
$(\log E)^{3}$
(see Theorem 5.4) where
![]() $E$
denotes the length of the amplifiers, which is negligible. Hence we can treat the term related to
$E$
denotes the length of the amplifiers, which is negligible. Hence we can treat the term related to
![]() $|\unicode[STIX]{x1D711}_{0}|^{2}-{\mathcal{E}}$
in the same way as in the cuspidal case without harming the quality of the bound. Since
$|\unicode[STIX]{x1D711}_{0}|^{2}-{\mathcal{E}}$
in the same way as in the cuspidal case without harming the quality of the bound. Since
![]() ${\mathcal{E}}$
is determined explicitly by
${\mathcal{E}}$
is determined explicitly by
![]() $\unicode[STIX]{x1D711}_{0}$
, the term related to it is explicitly estimable. We will treat the estimation and see that its contribution does not harm the quality of the final bound either. Namely, the generalized spectral decomposition fits as well with the estimation of the integrals as the ordinary one in the cuspidal case. Note that the simpler
$\unicode[STIX]{x1D711}_{0}$
, the term related to it is explicitly estimable. We will treat the estimation and see that its contribution does not harm the quality of the final bound either. Namely, the generalized spectral decomposition fits as well with the estimation of the integrals as the ordinary one in the cuspidal case. Note that the simpler
![]() $\unicode[STIX]{x1D711}_{0}$
is, the simpler
$\unicode[STIX]{x1D711}_{0}$
is, the simpler
![]() ${\mathcal{E}}$
is.
${\mathcal{E}}$
is.
4.4 Regroupment of generalized Fourier inversion
We make the strategy described in the above remark more precise. Introducing
we can apply the Cauchy–Schwarz inequality
 $$\begin{eqnarray}\displaystyle \biggl|\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}\unicode[STIX]{x1D70E}\ast h(|y|_{\mathbb{A}})\unicode[STIX]{x1D711}(a(y))\unicode[STIX]{x1D712}(y)\,d^{\times }y\biggr|^{2} & = & \displaystyle \biggl|\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}^{\prime }\ast \unicode[STIX]{x1D711}(a(y))\unicode[STIX]{x1D712}(y)\,d^{\times }y\biggr|^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})\,d^{\times }y\cdot \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})|\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}^{\prime }\ast \unicode[STIX]{x1D711}(a(y))|^{2}\,d^{\times }y.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl|\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}\unicode[STIX]{x1D70E}\ast h(|y|_{\mathbb{A}})\unicode[STIX]{x1D711}(a(y))\unicode[STIX]{x1D712}(y)\,d^{\times }y\biggr|^{2} & = & \displaystyle \biggl|\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}^{\prime }\ast \unicode[STIX]{x1D711}(a(y))\unicode[STIX]{x1D712}(y)\,d^{\times }y\biggr|^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})\,d^{\times }y\cdot \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})|\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}^{\prime }\ast \unicode[STIX]{x1D711}(a(y))|^{2}\,d^{\times }y.\nonumber\end{eqnarray}$$
The first integral in the last line is of size
![]() $O_{\mathbf{F}}(\log Q)$
, hence negligible. Opening the square, we get
$O_{\mathbf{F}}(\log Q)$
, hence negligible. Opening the square, we get
 $$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}^{\prime }\ast \unicode[STIX]{x1D711}(a(y))|^{2} & = & \displaystyle \frac{1}{M_{E}^{4}}\mathop{\sum }_{\mathfrak{p}_{1},\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2},\mathfrak{p}_{2}^{\prime }\in I_{E}}\unicode[STIX]{x1D712}\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr)\unicode[STIX]{x1D712}^{-1}\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr)\biggl(a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr).\unicode[STIX]{x1D711}\cdot \overline{a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr).\unicode[STIX]{x1D711}}\biggr)(a(y))\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{M_{E}^{4}}\mathop{\sum }_{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr)n(T).\biggl(a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}\biggr).\unicode[STIX]{x1D711}_{0}\cdot \overline{\unicode[STIX]{x1D711}_{0}}\biggr)(a(y)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}^{\prime }\ast \unicode[STIX]{x1D711}(a(y))|^{2} & = & \displaystyle \frac{1}{M_{E}^{4}}\mathop{\sum }_{\mathfrak{p}_{1},\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2},\mathfrak{p}_{2}^{\prime }\in I_{E}}\unicode[STIX]{x1D712}\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr)\unicode[STIX]{x1D712}^{-1}\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr)\biggl(a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr).\unicode[STIX]{x1D711}\cdot \overline{a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr).\unicode[STIX]{x1D711}}\biggr)(a(y))\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{M_{E}^{4}}\mathop{\sum }_{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr)n(T).\biggl(a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}\biggr).\unicode[STIX]{x1D711}_{0}\cdot \overline{\unicode[STIX]{x1D711}_{0}}\biggr)(a(y)),\nonumber\end{eqnarray}$$
where we have abbreviated
Decomposing the non-square-integrable function as
where the
![]() $\text{L}^{2}$
-residual part (2.2) or [Reference WuWu18, Definition 2.26] is given an abbreviated notation
$\text{L}^{2}$
-residual part (2.2) or [Reference WuWu18, Definition 2.26] is given an abbreviated notation
applying to
![]() $\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})=\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\mathbf{N}}+\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{cusp}}+\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{Eis}}$
the Fourier inversion decomposition in the sense of [Reference WuWu14, Theorem 2.18] and regrouping the two constant terms, we can rewrite the second integral as
$\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})=\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\mathbf{N}}+\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{cusp}}+\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{Eis}}$
the Fourier inversion decomposition in the sense of [Reference WuWu14, Theorem 2.18] and regrouping the two constant terms, we can rewrite the second integral as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})|\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}^{\prime }\ast \unicode[STIX]{x1D711}(a(y))|^{2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{M_{E}^{4}}\mathop{\sum }_{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})\biggl(a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{0}\cdot \overline{a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{0}}\biggr)_{\mathbf{N}}(a(y))\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{M_{E}^{4}}\mathop{\sum }_{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\unicode[STIX]{x1D701}(h,1,n(T).\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{cusp}})+\frac{1}{M_{E}^{4}}\mathop{\sum }_{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\unicode[STIX]{x1D701}(h,1,n(T).\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{Eis}})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{M_{E}^{4}}\mathop{\sum }_{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\unicode[STIX]{x1D701}(h_{|\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}/\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}|_{\mathbb{A}}},1,n(T).{\mathcal{E}}_{0}(\vec{\mathfrak{p}})),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})|\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D712}}^{\prime }\ast \unicode[STIX]{x1D711}(a(y))|^{2}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{M_{E}^{4}}\mathop{\sum }_{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})\biggl(a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{0}\cdot \overline{a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{0}}\biggr)_{\mathbf{N}}(a(y))\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{M_{E}^{4}}\mathop{\sum }_{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\unicode[STIX]{x1D701}(h,1,n(T).\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{cusp}})+\frac{1}{M_{E}^{4}}\mathop{\sum }_{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\unicode[STIX]{x1D701}(h,1,n(T).\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{Eis}})\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{M_{E}^{4}}\mathop{\sum }_{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\unicode[STIX]{x1D701}(h_{|\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}/\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}|_{\mathbb{A}}},1,n(T).{\mathcal{E}}_{0}(\vec{\mathfrak{p}})),\nonumber\end{eqnarray}$$
where we have used the
![]() $h$
-truncated zeta integral in Definition 2.12. Note that we can drop
$h$
-truncated zeta integral in Definition 2.12. Note that we can drop
![]() $\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}/\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}$
in the second integrand, since its adelic norm is contained in
$\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}/\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}$
in the second integrand, since its adelic norm is contained in
![]() $[1/2,2]$
.
$[1/2,2]$
.
4.5 Bounds for each part
Lemma 4.3. We have, for any
![]() $\unicode[STIX]{x1D716}>0$
,
$\unicode[STIX]{x1D716}>0$
,
Proof. We write and decompose
 $$\begin{eqnarray}\displaystyle \displaystyle S_{\mathbf{N}}(\vec{\mathfrak{p}};h) & := & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})\biggl(a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{0}\cdot \overline{a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{0}}\biggr)_{\mathbf{N}}(a(y))\,d^{\times }y,\nonumber\\ \displaystyle \displaystyle S_{\mathbf{N}}(\vec{\mathfrak{p}};h) & = & \displaystyle S_{\mathbf{N}}^{{\mathcal{W}}}(\vec{\mathfrak{p}};h)+S_{\mathbf{N}}^{\ast }(\vec{\mathfrak{p}};h),\nonumber\\ \displaystyle \displaystyle S_{\mathbf{N}}^{\ast }(\vec{\mathfrak{p}};h) & = & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{\mathbf{N}}(a(y))\cdot \overline{a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{\mathbf{N}}(a(y))}\,d^{\times }y.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle S_{\mathbf{N}}(\vec{\mathfrak{p}};h) & := & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})\biggl(a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{0}\cdot \overline{a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{0}}\biggr)_{\mathbf{N}}(a(y))\,d^{\times }y,\nonumber\\ \displaystyle \displaystyle S_{\mathbf{N}}(\vec{\mathfrak{p}};h) & = & \displaystyle S_{\mathbf{N}}^{{\mathcal{W}}}(\vec{\mathfrak{p}};h)+S_{\mathbf{N}}^{\ast }(\vec{\mathfrak{p}};h),\nonumber\\ \displaystyle \displaystyle S_{\mathbf{N}}^{\ast }(\vec{\mathfrak{p}};h) & = & \displaystyle \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{\mathbf{N}}(a(y))\cdot \overline{a\biggl(\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr).\unicode[STIX]{x1D711}_{\mathbf{N}}(a(y))}\,d^{\times }y.\nonumber\end{eqnarray}$$
The treatment of
is the same as [Reference WuWu14, Lemma 3.4], which gives a term
![]() $\ll _{\mathbf{F},\unicode[STIX]{x1D716}}E^{-2+\unicode[STIX]{x1D716}}Q^{\unicode[STIX]{x1D716}}$
. Using (4.1), we find
$\ll _{\mathbf{F},\unicode[STIX]{x1D716}}E^{-2+\unicode[STIX]{x1D716}}Q^{\unicode[STIX]{x1D716}}$
. Using (4.1), we find
 $$\begin{eqnarray}\displaystyle S_{\mathbf{N}}^{\ast }(\vec{\mathfrak{p}};h) & = & \displaystyle \biggl(|\unicode[STIX]{x1D707}_{1}|^{2}+\unicode[STIX]{x1D707}_{1}\overline{\unicode[STIX]{x1D707}_{2}}\log \biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr|_{\mathbb{A}}+\unicode[STIX]{x1D707}_{2}\overline{\unicode[STIX]{x1D707}_{1}}\log \biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr|_{\mathbb{A}}\biggr)\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})|y|_{\mathbb{A}}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D707}_{1}\overline{\unicode[STIX]{x1D707}_{2}}+\unicode[STIX]{x1D707}_{2}\overline{\unicode[STIX]{x1D707}_{1}})\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\cdot \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})|y|_{\mathbb{A}}\log |y|_{\mathbb{A}}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,|\unicode[STIX]{x1D707}_{2}|^{2}\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\cdot \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})|y|_{\mathbb{A}}\log ^{2}|y|_{\mathbb{A}}\,d^{\times }y,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S_{\mathbf{N}}^{\ast }(\vec{\mathfrak{p}};h) & = & \displaystyle \biggl(|\unicode[STIX]{x1D707}_{1}|^{2}+\unicode[STIX]{x1D707}_{1}\overline{\unicode[STIX]{x1D707}_{2}}\log \biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr|_{\mathbb{A}}+\unicode[STIX]{x1D707}_{2}\overline{\unicode[STIX]{x1D707}_{1}}\log \biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr|_{\mathbb{A}}\biggr)\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})|y|_{\mathbb{A}}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,(\unicode[STIX]{x1D707}_{1}\overline{\unicode[STIX]{x1D707}_{2}}+\unicode[STIX]{x1D707}_{2}\overline{\unicode[STIX]{x1D707}_{1}})\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\cdot \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})|y|_{\mathbb{A}}\log |y|_{\mathbb{A}}\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,|\unicode[STIX]{x1D707}_{2}|^{2}\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{1}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\biggl|\frac{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}}}{\unicode[STIX]{x1D71B}_{\mathfrak{p}_{2}^{\prime }}}\biggr|_{\mathbb{A}}^{1/2}\cdot \int _{\mathbf{F}^{\times }\backslash \mathbb{A}^{\times }}h(|y|_{\mathbb{A}})|y|_{\mathbb{A}}\log ^{2}|y|_{\mathbb{A}}\,d^{\times }y,\nonumber\end{eqnarray}$$
from which we easily see, by the same consideration of (4.2),
Remark 4.4. There are nine different patterns of the positions of
![]() $\mathfrak{p}_{1},\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2},\mathfrak{p}_{2}^{\prime }$
, listed in [Reference WuWu14, Proposition 3.5]. The estimation of the remaining three terms depends on the pattern. For simplicity, we only treat the typical pattern in detail in what follows, that is, when
$\mathfrak{p}_{1},\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2},\mathfrak{p}_{2}^{\prime }$
, listed in [Reference WuWu14, Proposition 3.5]. The estimation of the remaining three terms depends on the pattern. For simplicity, we only treat the typical pattern in detail in what follows, that is, when
![]() $\mathfrak{p}_{1},\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2},\mathfrak{p}_{2}^{\prime }$
are distinct. The treatment of the other patterns is quite similar.
$\mathfrak{p}_{1},\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2},\mathfrak{p}_{2}^{\prime }$
are distinct. The treatment of the other patterns is quite similar.
Lemma 4.5. For any
![]() $\unicode[STIX]{x1D716}>0$
, we have
$\unicode[STIX]{x1D716}>0$
, we have
Proof. This follows from Corollary 5.3 and the omitted calculation for other patterns. The situation is quite similar to that of [Reference WuWu14, §§ 6.2–6.4]. ◻
The estimation of
![]() $(1/M_{E}^{4})\sum _{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\unicode[STIX]{x1D701}(h,1,n(T).\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{cusp}})$
and
$(1/M_{E}^{4})\sum _{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\unicode[STIX]{x1D701}(h,1,n(T).\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{cusp}})$
and
![]() $(1/M_{E}^{4})\sum _{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\unicode[STIX]{x1D701}(h,1,n(T).\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{Eis}})$
is essentially the same as the cuspidal case given in [Reference WuWu14, §§ 6.3 and 6.4]. In fact, the only difference appears in [Reference WuWu14, (6.16)], where we could bound
$(1/M_{E}^{4})\sum _{\vec{\mathfrak{p}}\in I_{E}^{4}}\unicode[STIX]{x1D712}_{\vec{\mathfrak{p}}}\unicode[STIX]{x1D701}(h,1,n(T).\unicode[STIX]{x1D711}_{0}(\vec{\mathfrak{p}})_{\text{Eis}})$
is essentially the same as the cuspidal case given in [Reference WuWu14, §§ 6.3 and 6.4]. In fact, the only difference appears in [Reference WuWu14, (6.16)], where we could bound
![]() $\Vert \unicode[STIX]{x1D6E5}_{\infty }^{A^{\prime }}a(\unicode[STIX]{x1D71B}_{v_{1}}/\unicode[STIX]{x1D71B}_{v_{1}^{\prime }}).\unicode[STIX]{x1D711}_{0}\cdot \overline{a(\unicode[STIX]{x1D71B}_{v_{2}}/\unicode[STIX]{x1D71B}_{v_{2}^{\prime }}).\unicode[STIX]{x1D711}_{0}}\Vert$
easily by
$\Vert \unicode[STIX]{x1D6E5}_{\infty }^{A^{\prime }}a(\unicode[STIX]{x1D71B}_{v_{1}}/\unicode[STIX]{x1D71B}_{v_{1}^{\prime }}).\unicode[STIX]{x1D711}_{0}\cdot \overline{a(\unicode[STIX]{x1D71B}_{v_{2}}/\unicode[STIX]{x1D71B}_{v_{2}^{\prime }}).\unicode[STIX]{x1D711}_{0}}\Vert$
easily by
![]() $\text{L}^{4}$
-norm of
$\text{L}^{4}$
-norm of
![]() $\unicode[STIX]{x1D711}_{0}$
. For the current case, we need to bound
$\unicode[STIX]{x1D711}_{0}$
. For the current case, we need to bound
![]() $\Vert \unicode[STIX]{x1D6E5}_{\infty }^{A^{\prime }}\unicode[STIX]{x1D711}_{0}(v_{1},v_{1}^{\prime },v_{2},v_{2}^{\prime })\Vert$
defined in (4.3). Decomposing the relevant function into
$\Vert \unicode[STIX]{x1D6E5}_{\infty }^{A^{\prime }}\unicode[STIX]{x1D711}_{0}(v_{1},v_{1}^{\prime },v_{2},v_{2}^{\prime })\Vert$
defined in (4.3). Decomposing the relevant function into
![]() $\mathbf{K}_{\infty }$
-isotypic parts, we can apply Theorem 5.4. Thus unlike the cuspidal case, we get an extra
$\mathbf{K}_{\infty }$
-isotypic parts, we can apply Theorem 5.4. Thus unlike the cuspidal case, we get an extra
![]() $(\log E)^{3}$
in our estimation, which is harmless. Hence [Reference WuWu14, Lemmas 3.6 and 3.7] remain valid in the current case, giving the following results.
$(\log E)^{3}$
in our estimation, which is harmless. Hence [Reference WuWu14, Lemmas 3.6 and 3.7] remain valid in the current case, giving the following results.
Lemma 4.6. For any
![]() $\unicode[STIX]{x1D716}>0$
, we have
$\unicode[STIX]{x1D716}>0$
, we have
Lemma 4.7. For any
![]() $\unicode[STIX]{x1D716}>0$
, we have
$\unicode[STIX]{x1D716}>0$
, we have
We are finally led to establishing (1.1) by
with an optimal choice given by
5 Complements of global estimations
5.1 Estimation for exceptional part
Recall
![]() ${\mathcal{E}}_{0}(\vec{\mathfrak{p}})$
defined in (4.4).
${\mathcal{E}}_{0}(\vec{\mathfrak{p}})$
defined in (4.4).
Definition 5.1. For
![]() $\vec{\mathfrak{p}}$
, we define
$\vec{\mathfrak{p}}$
, we define
![]() $\vec{n}(\vec{\mathfrak{p}})=(n_{v})_{v}$
for
$\vec{n}(\vec{\mathfrak{p}})=(n_{v})_{v}$
for
![]() $v$
running over the set of places of
$v$
running over the set of places of
![]() $\mathbf{F}$
such that:
$\mathbf{F}$
such that:
∙
 $n_{v}=0$
for
$n_{v}=0$
for
 $v\mid \infty$
and
$v\mid \infty$
and
 $v\notin \{\mathfrak{p}_{1},\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2},\mathfrak{p}_{2}^{\prime }\}$
;
$v\notin \{\mathfrak{p}_{1},\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2},\mathfrak{p}_{2}^{\prime }\}$
;∙
 $n_{\mathfrak{p}}=1$
if
$n_{\mathfrak{p}}=1$
if
 $\mathfrak{p}\in \{\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2}\}$
,
$\mathfrak{p}\in \{\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2}\}$
,
 $n_{\mathfrak{p}}=-1$
if
$n_{\mathfrak{p}}=-1$
if
 $\mathfrak{p}\in \{\mathfrak{p}_{1},\mathfrak{p}_{2}^{\prime }\}$
.
$\mathfrak{p}\in \{\mathfrak{p}_{1},\mathfrak{p}_{2}^{\prime }\}$
.
For
![]() $\vec{n}=(n_{v})_{v},\vec{l}=(l_{v})_{v}$
with components in
$\vec{n}=(n_{v})_{v},\vec{l}=(l_{v})_{v}$
with components in
![]() $\mathbb{Z}$
, we write
$\mathbb{Z}$
, we write
![]() $\vec{l}\preccurlyeq \vec{n}$
to mean
$\vec{l}\preccurlyeq \vec{n}$
to mean
![]() $l_{v}\preccurlyeq n_{v}$
at each
$l_{v}\preccurlyeq n_{v}$
at each
![]() $v$
, defined in Definition 2.21. We define, for
$v$
, defined in Definition 2.21. We define, for
![]() $\vec{l},\preccurlyeq \vec{n}$
$\vec{l},\preccurlyeq \vec{n}$
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}(\vec{l})=\mathop{\sum }_{v}l_{v},\quad \Vert \vec{l}\Vert =\mathop{\sum }_{v}|l_{v}|,\quad e_{\vec{n}}=\bigotimes _{v}^{\prime }e_{n_{v}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D707}(\vec{n};s)=\mathop{\prod }_{v}\unicode[STIX]{x1D707}_{v}(n_{v};s),\quad c(\vec{n},\vec{l};s):=\mathop{\prod }_{\mathfrak{p}<\infty }c_{\mathfrak{p}}(n_{\mathfrak{p}},l_{\mathfrak{p}};s), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}(\vec{l})=\mathop{\sum }_{v}l_{v},\quad \Vert \vec{l}\Vert =\mathop{\sum }_{v}|l_{v}|,\quad e_{\vec{n}}=\bigotimes _{v}^{\prime }e_{n_{v}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D707}(\vec{n};s)=\mathop{\prod }_{v}\unicode[STIX]{x1D707}_{v}(n_{v};s),\quad c(\vec{n},\vec{l};s):=\mathop{\prod }_{\mathfrak{p}<\infty }c_{\mathfrak{p}}(n_{\mathfrak{p}},l_{\mathfrak{p}};s), & \displaystyle \nonumber\end{eqnarray}$$
where the local components are defined in Lemma 2.18(ii), Corollary 2.19, Remark 2.20 and Definition 2.21. We write the Laurent expansion at
![]() $s=1$
of the complete zeta function
$s=1$
of the complete zeta function
![]() $\unicode[STIX]{x1D6EC}_{\mathbf{F}}(s)$
as
$\unicode[STIX]{x1D6EC}_{\mathbf{F}}(s)$
as
We recall
![]() $\text{E}^{\text{reg}}(s,f)$
in (2.1) or [Reference WuWu18, Definition 2.16] as well as the abbreviation
$\text{E}^{\text{reg}}(s,f)$
in (2.1) or [Reference WuWu18, Definition 2.16] as well as the abbreviation
We compute
![]() ${\mathcal{E}}_{0}(\vec{\mathfrak{p}})$
explicitly as
${\mathcal{E}}_{0}(\vec{\mathfrak{p}})$
explicitly as
 $$\begin{eqnarray}\displaystyle {\mathcal{E}}_{0}(\vec{\mathfrak{p}}) & = & \displaystyle \mathop{\sum }_{\vec{l}\preccurlyeq \vec{n}(\vec{\mathfrak{p}})}c(\vec{n}(\vec{\mathfrak{p}}),\vec{l};0)\bigg\{|\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }|^{2}\text{E}^{\text{reg},(2)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)+\biggl(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-\frac{1}{2}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\unicode[STIX]{x1D707}^{\prime }(\vec{l};0)\biggr)\overline{2\unicode[STIX]{x1D6FE}_{\boldsymbol{ F}}}\text{E}^{\text{reg}}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(2\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\overline{\unicode[STIX]{x1D6FE}_{\mathbf{F}}}+\overline{\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }}\biggl(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-\frac{1}{2}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\unicode[STIX]{x1D707}^{\prime }(\vec{l};0)\biggr)\biggr)\text{E}^{\text{reg},(1)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\bigg\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{E}}_{0}(\vec{\mathfrak{p}}) & = & \displaystyle \mathop{\sum }_{\vec{l}\preccurlyeq \vec{n}(\vec{\mathfrak{p}})}c(\vec{n}(\vec{\mathfrak{p}}),\vec{l};0)\bigg\{|\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }|^{2}\text{E}^{\text{reg},(2)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)+\biggl(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-\frac{1}{2}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\unicode[STIX]{x1D707}^{\prime }(\vec{l};0)\biggr)\overline{2\unicode[STIX]{x1D6FE}_{\boldsymbol{ F}}}\text{E}^{\text{reg}}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(2\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\overline{\unicode[STIX]{x1D6FE}_{\mathbf{F}}}+\overline{\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }}\biggl(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-\frac{1}{2}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\unicode[STIX]{x1D707}^{\prime }(\vec{l};0)\biggr)\biggr)\text{E}^{\text{reg},(1)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\bigg\},\nonumber\end{eqnarray}$$
where the derivative
![]() $\unicode[STIX]{x1D707}^{\prime }(\vec{l};0)$
is taken with respect to
$\unicode[STIX]{x1D707}^{\prime }(\vec{l};0)$
is taken with respect to
![]() $s$
in
$s$
in
![]() $\unicode[STIX]{x1D707}(\vec{l};s)$
. Consequently, we obtain
$\unicode[STIX]{x1D707}(\vec{l};s)$
. Consequently, we obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(h,1,n(T).{\mathcal{E}}_{0}(\vec{\mathfrak{p}})) & = & \displaystyle \mathop{\sum }_{\vec{l}\preccurlyeq \vec{n}(\vec{\mathfrak{p}})}c(\vec{n}(\vec{\mathfrak{p}}),\vec{l};0)\bigg\{|\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }|^{2}\unicode[STIX]{x1D701}\biggl(h,1,n(T).\text{E}^{\text{reg},(2)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-\frac{1}{2}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\unicode[STIX]{x1D707}^{\prime }(\vec{l};0)\biggr)\overline{2\unicode[STIX]{x1D6FE}_{\boldsymbol{ F}}}\unicode[STIX]{x1D701}\biggl(h,1,n(T).\text{E}^{\text{reg}}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(2\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\overline{\unicode[STIX]{x1D6FE}_{\mathbf{F}}}+\overline{\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }}\biggl(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-\frac{1}{2}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\unicode[STIX]{x1D707}^{\prime }(\vec{l};0)\biggr)\biggr)\unicode[STIX]{x1D701}\biggl(h,1,n(T).\text{E}^{\text{reg},(1)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr)\bigg\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(h,1,n(T).{\mathcal{E}}_{0}(\vec{\mathfrak{p}})) & = & \displaystyle \mathop{\sum }_{\vec{l}\preccurlyeq \vec{n}(\vec{\mathfrak{p}})}c(\vec{n}(\vec{\mathfrak{p}}),\vec{l};0)\bigg\{|\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }|^{2}\unicode[STIX]{x1D701}\biggl(h,1,n(T).\text{E}^{\text{reg},(2)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-\frac{1}{2}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\unicode[STIX]{x1D707}^{\prime }(\vec{l};0)\biggr)\overline{2\unicode[STIX]{x1D6FE}_{\boldsymbol{ F}}}\unicode[STIX]{x1D701}\biggl(h,1,n(T).\text{E}^{\text{reg}}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(2\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\overline{\unicode[STIX]{x1D6FE}_{\mathbf{F}}}+\overline{\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }}\biggl(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-\frac{1}{2}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }\unicode[STIX]{x1D707}^{\prime }(\vec{l};0)\biggr)\biggr)\unicode[STIX]{x1D701}\biggl(h,1,n(T).\text{E}^{\text{reg},(1)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr)\bigg\}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Thus we are reduced to bounding, for
![]() $n=0,1,2$
,
$n=0,1,2$
,
Lemma 5.2. For
![]() $n=0,1,2$
and any
$n=0,1,2$
and any
![]() $\unicode[STIX]{x1D716}>0$
sufficiently small, we have
$\unicode[STIX]{x1D716}>0$
sufficiently small, we have
Proof. At the left-hand side, the Mellin transform of the integrand is related to
![]() $L$
-functions. We make use of this fact by applying the Mellin inversion formula to get
$L$
-functions. We make use of this fact by applying the Mellin inversion formula to get
and then shift the vertical line of integration to the left. There are poles of the integrand determined by Proposition 2.9. We calculate the constant terms in order to analyze the poles. We have
 $$\begin{eqnarray}\displaystyle & \displaystyle \text{E}_{\mathbf{N}}^{\text{reg}}\biggl(\frac{1}{2}+s,e_{\vec{l}}\biggr)(a(y)k)=|y|_{\mathbb{A}}^{1+s}e_{\vec{l}}(k)+\frac{2s\unicode[STIX]{x1D6EC}_{\mathbf{F}}(-2s)}{\unicode[STIX]{x1D6EC}_{\mathbf{F}}(2+2s)}\frac{\unicode[STIX]{x1D707}(\vec{l};1/2+s)}{2s}|y|_{\mathbb{A}}^{-s}e_{\vec{l}}(k),\quad \vec{l}\neq 0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{E}_{\mathbf{N}}^{\text{reg}}\biggl(\frac{1}{2}+s\biggr)(a(y)k,e_{\vec{0}})=|y|_{\mathbb{A}}^{1+s}e_{\vec{0}}(1)+\frac{2s\unicode[STIX]{x1D6EC}_{\mathbf{F}}(-2s)}{\unicode[STIX]{x1D6EC}_{\mathbf{F}}(2+2s)}\frac{|y|_{\mathbb{A}}^{-s}-1}{2s}e_{\vec{0}}(1). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{E}_{\mathbf{N}}^{\text{reg}}\biggl(\frac{1}{2}+s,e_{\vec{l}}\biggr)(a(y)k)=|y|_{\mathbb{A}}^{1+s}e_{\vec{l}}(k)+\frac{2s\unicode[STIX]{x1D6EC}_{\mathbf{F}}(-2s)}{\unicode[STIX]{x1D6EC}_{\mathbf{F}}(2+2s)}\frac{\unicode[STIX]{x1D707}(\vec{l};1/2+s)}{2s}|y|_{\mathbb{A}}^{-s}e_{\vec{l}}(k),\quad \vec{l}\neq 0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{E}_{\mathbf{N}}^{\text{reg}}\biggl(\frac{1}{2}+s\biggr)(a(y)k,e_{\vec{0}})=|y|_{\mathbb{A}}^{1+s}e_{\vec{0}}(1)+\frac{2s\unicode[STIX]{x1D6EC}_{\mathbf{F}}(-2s)}{\unicode[STIX]{x1D6EC}_{\mathbf{F}}(2+2s)}\frac{|y|_{\mathbb{A}}^{-s}-1}{2s}e_{\vec{0}}(1). & \displaystyle \nonumber\end{eqnarray}$$
Hence we get, for
![]() $n=0,1,2$
,
$n=0,1,2$
,
![]() $\vec{l}\neq \vec{0}$
and with constants
$\vec{l}\neq \vec{0}$
and with constants
![]() $c_{k}$
depending only on
$c_{k}$
depending only on
![]() $\mathbf{F}$
,
$\mathbf{F}$
,
 $$\begin{eqnarray}\displaystyle n(T).\text{E}_{\mathbf{N}}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)(a(y)w) & = & \displaystyle (\text{Ht}(wn(T))|y|_{\mathbb{A}})\log ^{n}(\text{Ht}(wn(T))|y|_{\mathbb{ A}})e_{\vec{l}}(w)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{k=\Vert \vec{l}\Vert -1}^{n}c_{k}E^{-\Vert \vec{l}\Vert }(\log E)^{k-\Vert \vec{l}\Vert +1}\log ^{n-k}(|y|_{\mathbb{A}}\text{Ht}(wn(T)))e_{\vec{l}}(w);\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n(T).\text{E}_{\mathbf{N}}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)(a(y)w) & = & \displaystyle (\text{Ht}(wn(T))|y|_{\mathbb{A}})\log ^{n}(\text{Ht}(wn(T))|y|_{\mathbb{ A}})e_{\vec{l}}(w)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{k=\Vert \vec{l}\Vert -1}^{n}c_{k}E^{-\Vert \vec{l}\Vert }(\log E)^{k-\Vert \vec{l}\Vert +1}\log ^{n-k}(|y|_{\mathbb{A}}\text{Ht}(wn(T)))e_{\vec{l}}(w);\nonumber\end{eqnarray}$$
while for
![]() $\vec{l}=\vec{0}$
,
$\vec{l}=\vec{0}$
,
 $$\begin{eqnarray}\displaystyle n(T).\text{E}_{\mathbf{N}}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{0}}\biggr)(a(y)) & = & \displaystyle |y|_{\mathbb{A}}\log ^{n}|y|_{\mathbb{ A}}e_{\vec{0}}(1)+\mathop{\sum }_{k=0}^{n}c_{k}\log ^{n-k+1}|y|_{\mathbb{A}}e_{\vec{0}}(1),\nonumber\\ \displaystyle n(T).\text{E}_{\mathbf{N}}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{0}}\biggr)(a(y)w) & = & \displaystyle (\text{Ht}(wn(T))|y|_{\mathbb{A}})(\log \text{Ht}(wn(T))|y|_{\mathbb{A}})^{n}e_{\vec{0}}(1)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{k=0}^{n}c_{k}(\log |y|_{\mathbb{A}}\text{Ht}(wn(T)))^{n-k+1}e_{\vec{0}}(1).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle n(T).\text{E}_{\mathbf{N}}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{0}}\biggr)(a(y)) & = & \displaystyle |y|_{\mathbb{A}}\log ^{n}|y|_{\mathbb{ A}}e_{\vec{0}}(1)+\mathop{\sum }_{k=0}^{n}c_{k}\log ^{n-k+1}|y|_{\mathbb{A}}e_{\vec{0}}(1),\nonumber\\ \displaystyle n(T).\text{E}_{\mathbf{N}}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{0}}\biggr)(a(y)w) & = & \displaystyle (\text{Ht}(wn(T))|y|_{\mathbb{A}})(\log \text{Ht}(wn(T))|y|_{\mathbb{A}})^{n}e_{\vec{0}}(1)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{k=0}^{n}c_{k}(\log |y|_{\mathbb{A}}\text{Ht}(wn(T)))^{n-k+1}e_{\vec{0}}(1).\nonumber\end{eqnarray}$$
By Proposition 2.9,
![]() $\unicode[STIX]{x1D701}(1/2+s,1,n(T).\text{E}^{\text{reg},(n)}(1/2,e_{\vec{l}}))$
has:
$\unicode[STIX]{x1D701}(1/2+s,1,n(T).\text{E}^{\text{reg},(n)}(1/2,e_{\vec{l}}))$
has:
∙ a pole at
 $s=1$
with residue equal to which is bounded, using Corollary 2.17, as
$s=1$
with residue equal to which is bounded, using Corollary 2.17, as $$\begin{eqnarray}\text{Ht}(wn(T))\log ^{n}\text{Ht}(wn(T))e_{\vec{l}}(w),\end{eqnarray}$$
$$\begin{eqnarray}\text{Ht}(wn(T))\log ^{n}\text{Ht}(wn(T))e_{\vec{l}}(w),\end{eqnarray}$$
 $$\begin{eqnarray}Q^{-2}\log ^{n}Q\cdot E^{-(1/2)\unicode[STIX]{x1D70E}(\vec{l})};\end{eqnarray}$$
$$\begin{eqnarray}Q^{-2}\log ^{n}Q\cdot E^{-(1/2)\unicode[STIX]{x1D70E}(\vec{l})};\end{eqnarray}$$
∙ a pole at
 $s=0$
;
$s=0$
;∙ a pole at
 $s=-1$
.
$s=-1$
.
We can thus write, for
![]() $0<\unicode[STIX]{x1D716}<1$
, using [Reference WuWu14, (6.1) and (6.2)] and Proposition 2.9,
$0<\unicode[STIX]{x1D716}<1$
, using [Reference WuWu14, (6.1) and (6.2)] and Proposition 2.9,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(h,1,n(T).\text{E}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr) & = & \displaystyle \int _{\Re s=\unicode[STIX]{x1D716}}\unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s,1,n(T).\text{E}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr)\mathfrak{M}(h)(-s)\frac{ds}{2\unicode[STIX]{x1D70B}i}\nonumber\\ \displaystyle & & \displaystyle +\,O_{\mathbf{F},h_{0},\unicode[STIX]{x1D716}}(Q^{\unicode[STIX]{x1D705}-1+\unicode[STIX]{x1D716}}E^{-(1/2)\unicode[STIX]{x1D70E}(\vec{l})}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}\biggl(h,1,n(T).\text{E}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr) & = & \displaystyle \int _{\Re s=\unicode[STIX]{x1D716}}\unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s,1,n(T).\text{E}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr)\mathfrak{M}(h)(-s)\frac{ds}{2\unicode[STIX]{x1D70B}i}\nonumber\\ \displaystyle & & \displaystyle +\,O_{\mathbf{F},h_{0},\unicode[STIX]{x1D716}}(Q^{\unicode[STIX]{x1D705}-1+\unicode[STIX]{x1D716}}E^{-(1/2)\unicode[STIX]{x1D70E}(\vec{l})}).\nonumber\end{eqnarray}$$
To bound the integral on the vertical line
![]() $\Re s=\unicode[STIX]{x1D716}$
, we have, by Proposition 2.10,
$\Re s=\unicode[STIX]{x1D716}$
, we have, by Proposition 2.10,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s,1,n(T).\text{E}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x2202}^{n}}{\unicode[STIX]{x2202}s_{0}^{n}}\,\biggr|_{s_{0}=1/2}\,\bigg\{\frac{\unicode[STIX]{x1D701}_{\mathbf{F}}(1/2+s+s_{0})\unicode[STIX]{x1D701}_{\mathbf{F}}(1/2+s-s_{0})}{\unicode[STIX]{x1D701}_{\mathbf{F}}(1+2s_{0})}\cdot \mathop{\prod }_{v\mid \infty }\int _{\mathbf{F}_{v}^{\times }}W_{0,v}(s_{0},a(y_{v}))\unicode[STIX]{x1D713}_{v}(y_{v}T_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\prod }_{\mathfrak{p}<\infty ,T_{\mathfrak{p}}\neq 0}\frac{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1+2s_{0})}{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s+s_{0})\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s-s_{0})}\int _{\mathbf{F}_{\mathfrak{p}}^{\times }}W_{0,\mathfrak{p}}(s_{0},a(y_{\mathfrak{p}}))\unicode[STIX]{x1D713}_{\mathfrak{p}}(y_{\mathfrak{p}}T_{\mathfrak{p}})|y_{\mathfrak{p}}|_{\mathfrak{p}}^{s}\,d^{\times }y_{\mathfrak{p}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\prod }_{\mathfrak{p}\in \{\mathfrak{p}_{1},\mathfrak{p}_{2},\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2}^{\prime }\}}\mathbf{C}(\unicode[STIX]{x1D713}_{\mathfrak{p}})^{s-s_{0}}\unicode[STIX]{x1D701}_{\mathfrak{p},l_{\mathfrak{p}}}(s,s_{0})\bigg\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D701}\biggl(\frac{1}{2}+s,1,n(T).\text{E}^{\text{reg},(n)}\biggl(\frac{1}{2},e_{\vec{l}}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x2202}^{n}}{\unicode[STIX]{x2202}s_{0}^{n}}\,\biggr|_{s_{0}=1/2}\,\bigg\{\frac{\unicode[STIX]{x1D701}_{\mathbf{F}}(1/2+s+s_{0})\unicode[STIX]{x1D701}_{\mathbf{F}}(1/2+s-s_{0})}{\unicode[STIX]{x1D701}_{\mathbf{F}}(1+2s_{0})}\cdot \mathop{\prod }_{v\mid \infty }\int _{\mathbf{F}_{v}^{\times }}W_{0,v}(s_{0},a(y_{v}))\unicode[STIX]{x1D713}_{v}(y_{v}T_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\prod }_{\mathfrak{p}<\infty ,T_{\mathfrak{p}}\neq 0}\frac{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1+2s_{0})}{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s+s_{0})\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s-s_{0})}\int _{\mathbf{F}_{\mathfrak{p}}^{\times }}W_{0,\mathfrak{p}}(s_{0},a(y_{\mathfrak{p}}))\unicode[STIX]{x1D713}_{\mathfrak{p}}(y_{\mathfrak{p}}T_{\mathfrak{p}})|y_{\mathfrak{p}}|_{\mathfrak{p}}^{s}\,d^{\times }y_{\mathfrak{p}}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,\mathop{\prod }_{\mathfrak{p}\in \{\mathfrak{p}_{1},\mathfrak{p}_{2},\mathfrak{p}_{1}^{\prime },\mathfrak{p}_{2}^{\prime }\}}\mathbf{C}(\unicode[STIX]{x1D713}_{\mathfrak{p}})^{s-s_{0}}\unicode[STIX]{x1D701}_{\mathfrak{p},l_{\mathfrak{p}}}(s,s_{0})\bigg\},\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D701}_{\mathfrak{p},l_{\mathfrak{p}}}(s,s_{0})$
is defined in Lemma 3.1. From Corollary 3.2 we deduce
$\unicode[STIX]{x1D701}_{\mathfrak{p},l_{\mathfrak{p}}}(s,s_{0})$
is defined in Lemma 3.1. From Corollary 3.2 we deduce
At
![]() $\mathfrak{p}<\infty$
,
$\mathfrak{p}<\infty$
,
![]() $T_{\mathfrak{p}}\neq 0$
, assuming
$T_{\mathfrak{p}}\neq 0$
, assuming
![]() $T_{\mathfrak{p}}=\unicode[STIX]{x1D71B}_{\mathfrak{p}}^{-k_{\mathfrak{p}}}$
, we can calculate explicitly (using, for example, [Reference WuWu14, Lemma 4.7])
$T_{\mathfrak{p}}=\unicode[STIX]{x1D71B}_{\mathfrak{p}}^{-k_{\mathfrak{p}}}$
, we can calculate explicitly (using, for example, [Reference WuWu14, Lemma 4.7])
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1+2s_{0})}{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s+s_{0})\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s-s_{0})}\int _{\mathbf{F}_{\mathfrak{p}}^{\times }}W_{0,\mathfrak{p}}(s_{0},a(y_{\mathfrak{p}}))\unicode[STIX]{x1D713}_{\mathfrak{p}}(y_{\mathfrak{p}}T_{\mathfrak{p}})|y_{\mathfrak{p}}|_{\mathfrak{p}}^{s}\,d^{\times }y_{\mathfrak{p}}\nonumber\\ \displaystyle & & \displaystyle \quad =q_{\mathfrak{p}}^{-k_{\mathfrak{p}}(1/2+s-s_{0})}\frac{1-q_{\mathfrak{p}}^{-1/2-s-s_{0}}}{1-q_{\mathfrak{p}}^{-2s_{0}}}-q_{\mathfrak{p}}^{-k_{\mathfrak{p}}(1/2+s+s_{0})-2s_{0}}\frac{1-q_{\mathfrak{p}}^{-1/2-s+s_{0}}}{1-q_{\mathfrak{p}}^{-2s_{0}}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,q_{\mathfrak{p}}^{-(k_{\mathfrak{p}}-1)(1/2+s-s_{0})}\frac{(1-q_{\mathfrak{p}}^{-1/2-s-s_{0}})(1-q_{\mathfrak{ p}}^{-1/2-s+s_{0}})}{q_{\mathfrak{p}}-1}\frac{1-q_{\mathfrak{p}}^{-2k_{\mathfrak{p}}s_{0}}}{1-q_{\mathfrak{p}}^{-2s_{0}}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1+2s_{0})}{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s+s_{0})\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s-s_{0})}\int _{\mathbf{F}_{\mathfrak{p}}^{\times }}W_{0,\mathfrak{p}}(s_{0},a(y_{\mathfrak{p}}))\unicode[STIX]{x1D713}_{\mathfrak{p}}(y_{\mathfrak{p}}T_{\mathfrak{p}})|y_{\mathfrak{p}}|_{\mathfrak{p}}^{s}\,d^{\times }y_{\mathfrak{p}}\nonumber\\ \displaystyle & & \displaystyle \quad =q_{\mathfrak{p}}^{-k_{\mathfrak{p}}(1/2+s-s_{0})}\frac{1-q_{\mathfrak{p}}^{-1/2-s-s_{0}}}{1-q_{\mathfrak{p}}^{-2s_{0}}}-q_{\mathfrak{p}}^{-k_{\mathfrak{p}}(1/2+s+s_{0})-2s_{0}}\frac{1-q_{\mathfrak{p}}^{-1/2-s+s_{0}}}{1-q_{\mathfrak{p}}^{-2s_{0}}}\nonumber\\ \displaystyle & & \displaystyle \qquad -\,q_{\mathfrak{p}}^{-(k_{\mathfrak{p}}-1)(1/2+s-s_{0})}\frac{(1-q_{\mathfrak{p}}^{-1/2-s-s_{0}})(1-q_{\mathfrak{ p}}^{-1/2-s+s_{0}})}{q_{\mathfrak{p}}-1}\frac{1-q_{\mathfrak{p}}^{-2k_{\mathfrak{p}}s_{0}}}{1-q_{\mathfrak{p}}^{-2s_{0}}}.\nonumber\end{eqnarray}$$
Thus we obtain the following bound
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\frac{\unicode[STIX]{x2202}^{k}}{\unicode[STIX]{x2202}s_{0}^{k}}\biggr|_{s_{0}=1/2}\,\frac{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1+2s_{0})}{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s+s_{0})\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s-s_{0})}\int _{\mathbf{F}_{\mathfrak{p}}^{\times }}W_{0,\mathfrak{p}}(s_{0},a(y_{\mathfrak{p}}))\unicode[STIX]{x1D713}_{\mathfrak{p}}(y_{\mathfrak{p}}T_{\mathfrak{p}})|y_{\mathfrak{p}}|_{\mathfrak{p}}^{s}\,d^{\times }y_{\mathfrak{p}}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \ll q_{\mathfrak{p}}^{-k_{\mathfrak{p}}\unicode[STIX]{x1D716}}(k_{\mathfrak{p}}\log q_{\mathfrak{p}})^{k}\ll _{k}\unicode[STIX]{x1D716}^{-k}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\frac{\unicode[STIX]{x2202}^{k}}{\unicode[STIX]{x2202}s_{0}^{k}}\biggr|_{s_{0}=1/2}\,\frac{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1+2s_{0})}{\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s+s_{0})\unicode[STIX]{x1D701}_{\mathfrak{p}}(1/2+s-s_{0})}\int _{\mathbf{F}_{\mathfrak{p}}^{\times }}W_{0,\mathfrak{p}}(s_{0},a(y_{\mathfrak{p}}))\unicode[STIX]{x1D713}_{\mathfrak{p}}(y_{\mathfrak{p}}T_{\mathfrak{p}})|y_{\mathfrak{p}}|_{\mathfrak{p}}^{s}\,d^{\times }y_{\mathfrak{p}}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \ll q_{\mathfrak{p}}^{-k_{\mathfrak{p}}\unicode[STIX]{x1D716}}(k_{\mathfrak{p}}\log q_{\mathfrak{p}})^{k}\ll _{k}\unicode[STIX]{x1D716}^{-k}.\nonumber\end{eqnarray}$$
At
![]() $v\mid \infty$
, we can trivially bound
$v\mid \infty$
, we can trivially bound
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\frac{\unicode[STIX]{x2202}^{k}}{\unicode[STIX]{x2202}s_{0}^{k}}\biggr|_{s_{0}=1/2}\,\int _{\mathbf{F}_{v}^{\times }}W_{0,v}(s_{0},a(y_{v}))\unicode[STIX]{x1D713}_{v}(y_{v}T_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\mathbf{F}_{v}^{\times }}\biggl|\frac{\unicode[STIX]{x2202}^{k}}{\unicode[STIX]{x2202}s_{0}^{k}}\biggr|_{s_{0}=1/2}\,W_{0,v}(s_{0},a(y_{v}))\biggr||y_{v}|_{v}^{\unicode[STIX]{x1D716}}\,d^{\times }{y_{v}\ll }_{\unicode[STIX]{x1D716}}1\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl|\frac{\unicode[STIX]{x2202}^{k}}{\unicode[STIX]{x2202}s_{0}^{k}}\biggr|_{s_{0}=1/2}\,\int _{\mathbf{F}_{v}^{\times }}W_{0,v}(s_{0},a(y_{v}))\unicode[STIX]{x1D713}_{v}(y_{v}T_{v})|y_{v}|_{v}^{s}\,d^{\times }y_{v}\biggr|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\mathbf{F}_{v}^{\times }}\biggl|\frac{\unicode[STIX]{x2202}^{k}}{\unicode[STIX]{x2202}s_{0}^{k}}\biggr|_{s_{0}=1/2}\,W_{0,v}(s_{0},a(y_{v}))\biggr||y_{v}|_{v}^{\unicode[STIX]{x1D716}}\,d^{\times }{y_{v}\ll }_{\unicode[STIX]{x1D716}}1\nonumber\end{eqnarray}$$
using classical asymptotic estimation for Whittaker functions (or [Reference Jacquet, Hida, Ramakrishnan and ShahidiJac04, Proposition 4.1]). Together with convex bounds for
![]() $\unicode[STIX]{x1D701}_{\mathbf{F}}$
, we see, for
$\unicode[STIX]{x1D701}_{\mathbf{F}}$
, we see, for
![]() $n=0,1,2$
,
$n=0,1,2$
,
We get the desired bound using [Reference WuWu14, (6.1) and (6.2)] again. ◻
Corollary 5.3. For a typical pattern, we have, for any
![]() $\unicode[STIX]{x1D716}>0$
,
$\unicode[STIX]{x1D716}>0$
,
Proof. This follows from (5.2) and the following bounds resulting from Lemma 2.18(ii), Corollary 2.19 and Remark 2.20:
5.2 Estimation for regularized
 $\text{L}^{4}$
-norms
$\text{L}^{4}$
-norms
Recall
![]() $E>0$
defined in Lemma 4.2. Choose a uniformizer
$E>0$
defined in Lemma 4.2. Choose a uniformizer
![]() $\unicode[STIX]{x1D71B}_{\mathfrak{p}}$
at every finite place
$\unicode[STIX]{x1D71B}_{\mathfrak{p}}$
at every finite place
![]() $\mathfrak{p}$
. Let
$\mathfrak{p}$
. Let
![]() $\vec{n}=(n_{\mathfrak{p}})_{\mathfrak{p}},n_{\mathfrak{p}}\in \mathbb{N}$
such that:
$\vec{n}=(n_{\mathfrak{p}})_{\mathfrak{p}},n_{\mathfrak{p}}\in \mathbb{N}$
such that:
∙
 $n_{\mathfrak{p}}=0$
unless
$n_{\mathfrak{p}}=0$
unless
 $E\leqslant q_{\mathfrak{p}}<2E$
;
$E\leqslant q_{\mathfrak{p}}<2E$
;∙ both the number of
 $\mathfrak{p}$
such that
$\mathfrak{p}$
such that
 $n_{\mathfrak{p}}\neq 0$
and
$n_{\mathfrak{p}}\neq 0$
and
 $|n_{\mathfrak{p}}|$
are bounded by some absolute constant.
$|n_{\mathfrak{p}}|$
are bounded by some absolute constant.
Associated to
![]() $\vec{n}$
we define
$\vec{n}$
we define
![]() $t=t(\vec{n})\in \mathbb{A}^{\times }$
such that
$t=t(\vec{n})\in \mathbb{A}^{\times }$
such that
![]() $t_{v}=1$
,
$t_{v}=1$
,
![]() $v\mid \infty$
and
$v\mid \infty$
and
![]() $t_{\mathfrak{p}}=\unicode[STIX]{x1D71B}_{\mathfrak{p}}^{-n_{\mathfrak{p}}}$
. Take
$t_{\mathfrak{p}}=\unicode[STIX]{x1D71B}_{\mathfrak{p}}^{-n_{\mathfrak{p}}}$
. Take
![]() $\unicode[STIX]{x1D711}_{j}=\text{E}^{\ast }(0,f_{j})$
, for
$\unicode[STIX]{x1D711}_{j}=\text{E}^{\ast }(0,f_{j})$
, for
![]() $j=1,2$
, where:
$j=1,2$
, where:
∙
 $f_{j,v}\in \unicode[STIX]{x1D70B}_{v}(1,1)$
is a unitary vector, spherical at each
$f_{j,v}\in \unicode[STIX]{x1D70B}_{v}(1,1)$
is a unitary vector, spherical at each
 $v=\mathfrak{p}<\infty$
;
$v=\mathfrak{p}<\infty$
;∙ at each
 $v\mid \infty$
,
$v\mid \infty$
,
 $f_{j,v}$
lies in some
$f_{j,v}$
lies in some
 $\mathbf{K}_{v}$
-isotypic
$\mathbf{K}_{v}$
-isotypic
 $H_{n_{j,v}}$
, whose definition is recalled in Remark 2.20;
$H_{n_{j,v}}$
, whose definition is recalled in Remark 2.20;∙ write
 $\vec{n}_{j}=(n_{j,v})_{v\mid \infty }$
or
$\vec{n}_{j}=(n_{j,v})_{v\mid \infty }$
or
 $(n_{j,v})_{v}$
with
$(n_{j,v})_{v}$
with
 $n_{j,\mathfrak{p}}=0$
for
$n_{j,\mathfrak{p}}=0$
for
 $\mathfrak{p}<\infty$
;
$\mathfrak{p}<\infty$
;∙
 $|n_{j,v}|,v\mid \infty$
are bounded by some absolute constant.
$|n_{j,v}|,v\mid \infty$
are bounded by some absolute constant.
Recall [Reference WuWu18, Definition 2.26] and write, for
![]() $j=1,2$
,
$j=1,2$
,
We are interested in the
![]() $\text{L}^{2}$
-norm of
$\text{L}^{2}$
-norm of
![]() $\unicode[STIX]{x1D711}_{t}$
in terms of
$\unicode[STIX]{x1D711}_{t}$
in terms of
![]() $E$
.
$E$
.
Theorem 5.4. With the above notation and conditions, we have
Proof. Note that
 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D711}_{t}\Vert ^{2} & = & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}(a(t)|\unicode[STIX]{x1D711}_{1}|^{2}-a(t){\mathcal{E}}_{1})(g)(|\unicode[STIX]{x1D711}_{2}|^{2}-{\mathcal{E}}_{2})(g)\,dg+\int _{[\text{PGL}_{2}]}^{\text{reg}}|\unicode[STIX]{x1D711}_{2}|^{2}(g)a(t){\mathcal{E}}_{1}(g)\,dg\nonumber\\ \displaystyle & & \displaystyle -\,\int _{[\text{PGL}_{2}]}^{\text{reg}}a(t){\mathcal{E}}_{1}(g){\mathcal{E}}_{2}(g)\,dg+\int _{[\text{PGL}_{2}]}^{\text{reg}}|{\mathcal{E}}_{t}(g)|^{2}\,dg\nonumber\\ \displaystyle & & \displaystyle -\,2\Re \int _{[\text{PGL}_{2}]}^{\text{reg}}a(t)\unicode[STIX]{x1D711}_{1}(g)\overline{\unicode[STIX]{x1D711}_{2}(g)}\overline{{\mathcal{E}}_{t}(g)}\,dg+\int _{[\text{PGL}_{2}]}^{\text{reg}}a(t)|\unicode[STIX]{x1D711}_{1}|^{2}(g){\mathcal{E}}_{2}(g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D711}_{t}\Vert ^{2} & = & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}(a(t)|\unicode[STIX]{x1D711}_{1}|^{2}-a(t){\mathcal{E}}_{1})(g)(|\unicode[STIX]{x1D711}_{2}|^{2}-{\mathcal{E}}_{2})(g)\,dg+\int _{[\text{PGL}_{2}]}^{\text{reg}}|\unicode[STIX]{x1D711}_{2}|^{2}(g)a(t){\mathcal{E}}_{1}(g)\,dg\nonumber\\ \displaystyle & & \displaystyle -\,\int _{[\text{PGL}_{2}]}^{\text{reg}}a(t){\mathcal{E}}_{1}(g){\mathcal{E}}_{2}(g)\,dg+\int _{[\text{PGL}_{2}]}^{\text{reg}}|{\mathcal{E}}_{t}(g)|^{2}\,dg\nonumber\\ \displaystyle & & \displaystyle -\,2\Re \int _{[\text{PGL}_{2}]}^{\text{reg}}a(t)\unicode[STIX]{x1D711}_{1}(g)\overline{\unicode[STIX]{x1D711}_{2}(g)}\overline{{\mathcal{E}}_{t}(g)}\,dg+\int _{[\text{PGL}_{2}]}^{\text{reg}}a(t)|\unicode[STIX]{x1D711}_{1}|^{2}(g){\mathcal{E}}_{2}(g)\,dg.\end{eqnarray}$$
We bound the right-hand side term by term, which will occupy the rest of this subsection. Note that only the fourth and sixth terms have growing contribution as
![]() $(\log E)^{3}$
and
$(\log E)^{3}$
and
![]() $(\log E)^{6}$
, respectively.◻
$(\log E)^{6}$
, respectively.◻
For the first term in (5.3), we use the Cauchy–Schwarz inequality to get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}(a(t)|\unicode[STIX]{x1D711}_{1}|^{2}-a(t){\mathcal{E}}_{1})(g)(|\unicode[STIX]{x1D711}_{2}|^{2}-{\mathcal{E}}_{2})(g)\,dg\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{[\text{PGL}_{2}]}a(t)(|\unicode[STIX]{x1D711}_{1}|^{2}-{\mathcal{E}}_{1})(g)(|\unicode[STIX]{x1D711}_{2}|^{2}-{\mathcal{E}}_{2})(g)\,dg\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \Vert a(t)(|\unicode[STIX]{x1D711}_{1}|^{2}-{\mathcal{E}}_{1})\Vert \cdot \Vert |\unicode[STIX]{x1D711}_{2}|^{2}-{\mathcal{E}}_{2}\Vert =\Vert |\unicode[STIX]{x1D711}_{1}|^{2}-{\mathcal{E}}_{1}\Vert \cdot \Vert |\unicode[STIX]{x1D711}_{2}|^{2}-{\mathcal{E}}_{2}\Vert ,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}(a(t)|\unicode[STIX]{x1D711}_{1}|^{2}-a(t){\mathcal{E}}_{1})(g)(|\unicode[STIX]{x1D711}_{2}|^{2}-{\mathcal{E}}_{2})(g)\,dg\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{[\text{PGL}_{2}]}a(t)(|\unicode[STIX]{x1D711}_{1}|^{2}-{\mathcal{E}}_{1})(g)(|\unicode[STIX]{x1D711}_{2}|^{2}-{\mathcal{E}}_{2})(g)\,dg\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \Vert a(t)(|\unicode[STIX]{x1D711}_{1}|^{2}-{\mathcal{E}}_{1})\Vert \cdot \Vert |\unicode[STIX]{x1D711}_{2}|^{2}-{\mathcal{E}}_{2}\Vert =\Vert |\unicode[STIX]{x1D711}_{1}|^{2}-{\mathcal{E}}_{1}\Vert \cdot \Vert |\unicode[STIX]{x1D711}_{2}|^{2}-{\mathcal{E}}_{2}\Vert ,\nonumber\end{eqnarray}$$
which is independent of
![]() $t$
, hence
$t$
, hence
![]() $E$
.
$E$
.
For the second and third terms in (5.3), first notice that we can write
where
![]() ${\mathcal{E}}_{1,k}(s)$
is a regularizing Eisenstein series (2.1) and the superscript
${\mathcal{E}}_{1,k}(s)$
is a regularizing Eisenstein series (2.1) and the superscript
![]() $(k)$
means taking derivative
$(k)$
means taking derivative
![]() $k$
times with respect to
$k$
times with respect to
![]() $s$
. Moreover,
$s$
. Moreover,
![]() ${\mathcal{E}}_{1,k}(s)$
are spherical at finite places. We notice further that although the regularized integral is not
${\mathcal{E}}_{1,k}(s)$
are spherical at finite places. We notice further that although the regularized integral is not
![]() $\text{GL}_{2}(\mathbb{A})$
-invariant, it is still
$\text{GL}_{2}(\mathbb{A})$
-invariant, it is still
![]() $\mathbf{K}$
-invariant [Reference WuWu18, Proposition 2.27(2)]. Hence if we write the Hecke operator associated with
$\mathbf{K}$
-invariant [Reference WuWu18, Proposition 2.27(2)]. Hence if we write the Hecke operator associated with
![]() $\vec{n}$
as
$\vec{n}$
as
where
![]() $\text{R}(\cdot )$
denotes the
$\text{R}(\cdot )$
denotes the
![]() $\text{GL}_{2}(\mathbb{A})$
-translation, we have
$\text{GL}_{2}(\mathbb{A})$
-translation, we have
 $$\begin{eqnarray}\displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}|\unicode[STIX]{x1D711}_{2}|^{2}(g)a(t){\mathcal{E}}_{1}(g)\,dg & = & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}|\unicode[STIX]{x1D711}_{2}|^{2}(g)(T(\vec{n}){\mathcal{E}}_{1}(g))\,dg,\nonumber\\ \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}a(t){\mathcal{E}}_{1}(g){\mathcal{E}}_{2}(g)\,dg & = & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}(T(\vec{n}){\mathcal{E}}_{1}(g)){\mathcal{E}}_{2}(g)\,dg.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}|\unicode[STIX]{x1D711}_{2}|^{2}(g)a(t){\mathcal{E}}_{1}(g)\,dg & = & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}|\unicode[STIX]{x1D711}_{2}|^{2}(g)(T(\vec{n}){\mathcal{E}}_{1}(g))\,dg,\nonumber\\ \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}a(t){\mathcal{E}}_{1}(g){\mathcal{E}}_{2}(g)\,dg & = & \displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}(T(\vec{n}){\mathcal{E}}_{1}(g)){\mathcal{E}}_{2}(g)\,dg.\nonumber\end{eqnarray}$$
![]() ${\mathcal{E}}_{1,k}(s)$
is a generalized eigenvector of
${\mathcal{E}}_{1,k}(s)$
is a generalized eigenvector of
![]() $T(\vec{n})$
with eigenvalue [Reference BumpBum98, Theorem 4.6.6]
$T(\vec{n})$
with eigenvalue [Reference BumpBum98, Theorem 4.6.6]
in the sense that (cf. [Reference WuWu18, Remark 2.17])
where
![]() $\unicode[STIX]{x1D706}_{\mathbf{F}}(s)$
is a ratio of zeta functions of
$\unicode[STIX]{x1D706}_{\mathbf{F}}(s)$
is a ratio of zeta functions of
![]() $\mathbf{F}$
(see, for example, Theorem 2.2) and
$\mathbf{F}$
(see, for example, Theorem 2.2) and
![]() $c_{k}\in \mathbb{C}$
is some constant depending on
$c_{k}\in \mathbb{C}$
is some constant depending on
![]() $\unicode[STIX]{x1D711}_{1}$
. Note that
$\unicode[STIX]{x1D711}_{1}$
. Note that
![]() $\unicode[STIX]{x1D706}(\vec{n};1/2)=1$
. Consequently, we get
$\unicode[STIX]{x1D706}(\vec{n};1/2)=1$
. Consequently, we get
 $$\begin{eqnarray}\displaystyle T(\vec{n}){\mathcal{E}}_{1,k}^{(k)}(1/2) & = & \displaystyle \mathop{\sum }_{l=0}^{k}\binom{k}{l}\unicode[STIX]{x1D706}^{(l)}(\vec{n};1/2){\mathcal{E}}_{1,k}^{(k-l)}(1/2)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k}\mathop{\sum }_{l=0}^{k-1}\binom{k}{l+1}\unicode[STIX]{x1D706}^{(l+1)}(\vec{n};1/2)\unicode[STIX]{x1D706}_{\boldsymbol{ F}}^{(k-l)}(0)+\frac{\unicode[STIX]{x1D706}^{(k+1)}(\vec{n};1/2)\unicode[STIX]{x1D706}_{\boldsymbol{ F}}^{(-1)}(0)}{k+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T(\vec{n}){\mathcal{E}}_{1,k}^{(k)}(1/2) & = & \displaystyle \mathop{\sum }_{l=0}^{k}\binom{k}{l}\unicode[STIX]{x1D706}^{(l)}(\vec{n};1/2){\mathcal{E}}_{1,k}^{(k-l)}(1/2)\nonumber\\ \displaystyle & & \displaystyle +\,c_{k}\mathop{\sum }_{l=0}^{k-1}\binom{k}{l+1}\unicode[STIX]{x1D706}^{(l+1)}(\vec{n};1/2)\unicode[STIX]{x1D706}_{\boldsymbol{ F}}^{(k-l)}(0)+\frac{\unicode[STIX]{x1D706}^{(k+1)}(\vec{n};1/2)\unicode[STIX]{x1D706}_{\boldsymbol{ F}}^{(-1)}(0)}{k+1}.\nonumber\end{eqnarray}$$
Inserting the obvious bound
![]() $\unicode[STIX]{x1D706}^{(l)}(\vec{n};1/2)\ll (\log E)^{l}$
, we see that the second and third term in (5.3) are bounded as
$\unicode[STIX]{x1D706}^{(l)}(\vec{n};1/2)\ll (\log E)^{l}$
, we see that the second and third term in (5.3) are bounded as
![]() $\ll (\log E)^{3}$
.
$\ll (\log E)^{3}$
.
Remark 5.5.
![]() $\unicode[STIX]{x1D706}_{\mathfrak{p}}(n;s)=c_{\mathfrak{p}}(n,0;s)$
defined in Lemma 2.18(ii).
$\unicode[STIX]{x1D706}_{\mathfrak{p}}(n;s)=c_{\mathfrak{p}}(n,0;s)$
defined in Lemma 2.18(ii).
For the fourth term in (5.3), we first make
![]() ${\mathcal{E}}_{t}$
explicit.
${\mathcal{E}}_{t}$
explicit.
Definition 5.6. We extend the definition of
![]() $\vec{l}\preccurlyeq \vec{n}$
in Definition 5.1 to the case
$\vec{l}\preccurlyeq \vec{n}$
in Definition 5.1 to the case
![]() $n_{v}\neq 0,v\mid \infty$
as follows:
$n_{v}\neq 0,v\mid \infty$
as follows:
∙
 $\mathbf{F}_{v}=\mathbb{R}$
:
$\mathbf{F}_{v}=\mathbb{R}$
:
 $l_{v}\preccurlyeq n_{v}$
means
$l_{v}\preccurlyeq n_{v}$
means
 $l_{v}=n_{v}$
;
$l_{v}=n_{v}$
;∙
 $\mathbf{F}_{v}=\mathbb{C}$
:
$\mathbf{F}_{v}=\mathbb{C}$
:
 $l_{v}\preccurlyeq n_{v}$
means
$l_{v}\preccurlyeq n_{v}$
means
 $0\leqslant l_{v}\leqslant n_{v}$
.
$0\leqslant l_{v}\leqslant n_{v}$
.
At
![]() $v\mid \infty$
, we write
$v\mid \infty$
, we write
![]() $e_{n_{v}}$
for some unitary vector in
$e_{n_{v}}$
for some unitary vector in
![]() $H_{n_{v}}$
recalled in Remark 2.20 without specification.
$H_{n_{v}}$
recalled in Remark 2.20 without specification.
We can thus write
Recall the tensor product formulas for representations of
![]() $\mathbf{K}_{v},v\mid \infty$
:
$\mathbf{K}_{v},v\mid \infty$
:
∙
 $\mathbf{F}_{v}=\mathbb{R}$
:
$\mathbf{F}_{v}=\mathbb{R}$
:
 $H_{n}\otimes H_{m}\simeq H_{n+m}$
;
$H_{n}\otimes H_{m}\simeq H_{n+m}$
;∙
 $\mathbf{F}_{v}=\mathbb{C}$
:
$\mathbf{F}_{v}=\mathbb{C}$
:
 $H_{n}\otimes H_{m}\simeq H_{n+m}\oplus H_{n+m-2}\oplus \cdots \oplus H_{|n-m|}$
.
$H_{n}\otimes H_{m}\simeq H_{n+m}\oplus H_{n+m-2}\oplus \cdots \oplus H_{|n-m|}$
.
Together with the explicit determination of constant terms
 $$\begin{eqnarray}\displaystyle & \displaystyle \text{E}_{\mathbf{N}}^{\ast }(0,e_{\vec{n}_{1}+\vec{l}})(a(y)\unicode[STIX]{x1D705})=\big\{\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }(1)|y|_{\mathbb{A}}^{1/2}\log |y|_{\mathbb{A}}+(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }(1)\unicode[STIX]{x1D707}^{\prime }(\vec{n}_{1}+\vec{l};0))|y|_{\mathbb{A}}^{1/2}\big\}e_{\vec{n}_{1}+\vec{l}}(\unicode[STIX]{x1D705}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D711}_{2,\mathbf{N}}(a(y)\unicode[STIX]{x1D705})=\big\{\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }(1)|y|_{\mathbb{A}}^{1/2}\log |y|_{\mathbb{A}}+(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }(1)\unicode[STIX]{x1D707}^{\prime }(\vec{n}_{2};0))|y|_{\mathbb{A}}^{1/2}\big\}f_{2}(\unicode[STIX]{x1D705}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \text{E}_{\mathbf{N}}^{\ast }(0,e_{\vec{n}_{1}+\vec{l}})(a(y)\unicode[STIX]{x1D705})=\big\{\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }(1)|y|_{\mathbb{A}}^{1/2}\log |y|_{\mathbb{A}}+(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }(1)\unicode[STIX]{x1D707}^{\prime }(\vec{n}_{1}+\vec{l};0))|y|_{\mathbb{A}}^{1/2}\big\}e_{\vec{n}_{1}+\vec{l}}(\unicode[STIX]{x1D705}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D711}_{2,\mathbf{N}}(a(y)\unicode[STIX]{x1D705})=\big\{\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }(1)|y|_{\mathbb{A}}^{1/2}\log |y|_{\mathbb{A}}+(2\unicode[STIX]{x1D6FE}_{\mathbf{F}}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6EC}_{\mathbf{F}}^{\ast }(1)\unicode[STIX]{x1D707}^{\prime }(\vec{n}_{2};0))|y|_{\mathbb{A}}^{1/2}\big\}f_{2}(\unicode[STIX]{x1D705}), & \displaystyle \nonumber\end{eqnarray}$$
we deduce the existence of
![]() $c_{\vec{m}}$
such that
$c_{\vec{m}}$
such that
where we have written
Lemma 5.7. For
![]() $k_{1},k_{2}\geqslant 0$
, the regularized integral
$k_{1},k_{2}\geqslant 0$
, the regularized integral
is non-vanishing only if
![]() $\vec{m}_{1}=\vec{m}_{2},\vec{l}_{1}=\vec{l}_{2}$
. We also have
$\vec{m}_{1}=\vec{m}_{2},\vec{l}_{1}=\vec{l}_{2}$
. We also have
Proof. This is a direct consequence of Theorem 2.4, together with
Applying the lemma and the estimations
we finally get
 $$\begin{eqnarray}\displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}|{\mathcal{E}}_{t}(g)|^{2}\,dg & = & \displaystyle \mathop{\sum }_{\vec{l}\preccurlyeq \vec{n}}\mathop{\sum }_{\vec{m}\preccurlyeq \vec{n}_{1}+\vec{n}_{2}}|c(\vec{n},\vec{l};0)c_{\vec{m}}|^{2}\mathop{\sum }_{k_{1},k_{2}=0}^{2}c_{k_{1}}(\vec{l})\overline{c_{k_{2}}(\vec{l})}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(k_{1})}\biggl(\frac{1}{2},e_{\vec{m}+\vec{l}}\biggr)(g)\overline{\text{E}^{\text{reg},(k_{2})}\biggl(\frac{1}{2},e_{\vec{m}+\vec{l}}\biggr)(g)}\,dg\nonumber\\ \displaystyle & \ll & \displaystyle E^{-\Vert \vec{n}\Vert }(\log E)^{6}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}|{\mathcal{E}}_{t}(g)|^{2}\,dg & = & \displaystyle \mathop{\sum }_{\vec{l}\preccurlyeq \vec{n}}\mathop{\sum }_{\vec{m}\preccurlyeq \vec{n}_{1}+\vec{n}_{2}}|c(\vec{n},\vec{l};0)c_{\vec{m}}|^{2}\mathop{\sum }_{k_{1},k_{2}=0}^{2}c_{k_{1}}(\vec{l})\overline{c_{k_{2}}(\vec{l})}\nonumber\\ \displaystyle & & \displaystyle \cdot \,\int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\text{reg},(k_{1})}\biggl(\frac{1}{2},e_{\vec{m}+\vec{l}}\biggr)(g)\overline{\text{E}^{\text{reg},(k_{2})}\biggl(\frac{1}{2},e_{\vec{m}+\vec{l}}\biggr)(g)}\,dg\nonumber\\ \displaystyle & \ll & \displaystyle E^{-\Vert \vec{n}\Vert }(\log E)^{6}.\nonumber\end{eqnarray}$$
For the fifth term in (5.3), note that we have computed/decomposed
![]() $a(t).\unicode[STIX]{x1D711}_{1}$
and
$a(t).\unicode[STIX]{x1D711}_{1}$
and
![]() ${\mathcal{E}}_{t}$
in (5.5) and (5.6).
${\mathcal{E}}_{t}$
in (5.5) and (5.6).
Lemma 5.8. For any
![]() $k\geqslant 0$
, the regularized integral
$k\geqslant 0$
, the regularized integral
is non-vanishing only if
![]() $\vec{l}_{1}=\vec{l}_{2}$
. We also have
$\vec{l}_{1}=\vec{l}_{2}$
. We also have
Proof. We apply Theorem 2.7. The ‘degenerate part’, that is, the weighted sum involving
![]() $\text{P}_{\mathbf{K}}$
, is easily seen to be non-vanishing only if
$\text{P}_{\mathbf{K}}$
, is easily seen to be non-vanishing only if
![]() $\vec{l}_{1}=\vec{l}_{2}$
, and in the case
$\vec{l}_{1}=\vec{l}_{2}$
, and in the case
![]() $\vec{l}_{1}=\vec{l}_{2}=\vec{l}$
it is bounded by
$\vec{l}_{1}=\vec{l}_{2}=\vec{l}$
it is bounded by
![]() $E^{-\Vert \vec{l}\Vert }(\log E)^{k+4}$
since
$E^{-\Vert \vec{l}\Vert }(\log E)^{k+4}$
since
![]() $\unicode[STIX]{x1D707}^{(n)}(\vec{l};1/2)\ll E^{-\Vert l\Vert }(\log E)^{n}$
. For the ‘main part’, we note that
$\unicode[STIX]{x1D707}^{(n)}(\vec{l};1/2)\ll E^{-\Vert l\Vert }(\log E)^{n}$
. For the ‘main part’, we note that
is the product of
![]() $\overline{\unicode[STIX]{x1D701}_{\mathbf{F}}(s+1)^{4}\unicode[STIX]{x1D701}_{\mathbf{F}}(2s+2)^{-1}}$
, some local components at
$\overline{\unicode[STIX]{x1D701}_{\mathbf{F}}(s+1)^{4}\unicode[STIX]{x1D701}_{\mathbf{F}}(2s+2)^{-1}}$
, some local components at
![]() $v\mid \infty$
irrelevant for estimation, and
$v\mid \infty$
irrelevant for estimation, and
defined in (3.1). Lemma 3.3(ii) implies the non-vanishing assertion. We need to estimate
Corollary 3.4 concludes the bound. ◻
We deduce that
 $$\begin{eqnarray}\displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}a(t)\unicode[STIX]{x1D711}_{1}(g)\overline{\unicode[STIX]{x1D711}_{2}(g)}\overline{{\mathcal{E}}_{t}(g)}\,dg & = & \displaystyle \mathop{\sum }_{\vec{m}\preccurlyeq \vec{n}_{1}\cdot \vec{n}_{2}}\mathop{\sum }_{\vec{l}\preccurlyeq \vec{n}}c_{\vec{m}}|c(\vec{n},\vec{l};0)|^{2}\cdot \mathop{\sum }_{k=0}^{2}c_{k}(\vec{l})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\ast }(0,e_{\vec{n}_{1}+\vec{l}})(g)\overline{\unicode[STIX]{x1D711}_{2}(g)}\overline{\text{E}^{\text{reg},(k)}\biggl(\frac{1}{2},e_{\vec{m}+\vec{l}}\biggr)(g)}\,dg\nonumber\\ \displaystyle & \ll & \displaystyle E^{-\Vert \vec{n}\Vert }(\log E)^{6}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{[\text{PGL}_{2}]}^{\text{reg}}a(t)\unicode[STIX]{x1D711}_{1}(g)\overline{\unicode[STIX]{x1D711}_{2}(g)}\overline{{\mathcal{E}}_{t}(g)}\,dg & = & \displaystyle \mathop{\sum }_{\vec{m}\preccurlyeq \vec{n}_{1}\cdot \vec{n}_{2}}\mathop{\sum }_{\vec{l}\preccurlyeq \vec{n}}c_{\vec{m}}|c(\vec{n},\vec{l};0)|^{2}\cdot \mathop{\sum }_{k=0}^{2}c_{k}(\vec{l})\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{[\text{PGL}_{2}]}^{\text{reg}}\text{E}^{\ast }(0,e_{\vec{n}_{1}+\vec{l}})(g)\overline{\unicode[STIX]{x1D711}_{2}(g)}\overline{\text{E}^{\text{reg},(k)}\biggl(\frac{1}{2},e_{\vec{m}+\vec{l}}\biggr)(g)}\,dg\nonumber\\ \displaystyle & \ll & \displaystyle E^{-\Vert \vec{n}\Vert }(\log E)^{6}.\nonumber\end{eqnarray}$$
For the last term in (5.3), first notice that we can write
where
![]() $h_{k}$
are spherical at
$h_{k}$
are spherical at
![]() $\mathfrak{p}$
for which
$\mathfrak{p}$
for which
![]() $n_{\mathfrak{p}}\neq 0$
. We are reduced to bounding
$n_{\mathfrak{p}}\neq 0$
. We are reduced to bounding
to which Theorem 2.7 applies directly.
The degenerate part contributes
![]() $(\log E)^{3}$
. In fact, only
$(\log E)^{3}$
. In fact, only
has non-constant contribution. For the main part, using the
![]() $\text{GL}_{2}(\mathbf{F}_{\mathfrak{p}})$
-invariance of the local Rankin–Selberg zeta functions, we easily deduce
$\text{GL}_{2}(\mathbf{F}_{\mathfrak{p}})$
-invariance of the local Rankin–Selberg zeta functions, we easily deduce
where only the term
![]() $\unicode[STIX]{x1D706}(\vec{n};1/2+s)$
defined in (5.4) depends on
$\unicode[STIX]{x1D706}(\vec{n};1/2+s)$
defined in (5.4) depends on
![]() $E$
. We bound
$E$
. We bound
from
![]() $\unicode[STIX]{x1D706}^{(l)}(\vec{n};1/2)\ll (\log E)^{l}$
, and conclude that the last term in (5.3) is bounded as
$\unicode[STIX]{x1D706}^{(l)}(\vec{n};1/2)\ll (\log E)^{l}$
, and conclude that the last term in (5.3) is bounded as
![]() $\ll (\log E)^{6}$
.
$\ll (\log E)^{6}$
.
Acknowledgements
This paper was prepared while staying at FIM at ETHZ, YMSC at Tsinghua University, Alfréd Renyi Institute in Hungary supported by the MTA Rényi Intézet Lendület Automorphic Research Group, and TAN at EPFL. The author would like to thank all four institutes for their hospitality. The author would like to thank Professor Paul Nelson for useful discussions. The author would also like to thank Professor Philippe Michel, his former thesis adviser, for his encouragement and enlightening strategic argument. The author would like to thank Dr. Bingrong Huang for bringing the paper of Soehne [Reference SoehneSoe97] to his attention. The author is grateful for the referees’ detailed check and suggestions.
Appendix A Disadelization in a special case
For the convenience of readers not familiar with adelic language, and also for those who want to see the computation in the classical setting, we provide part of the disadelized computation in the case
![]() $\mathbf{F}=\mathbb{Q}$
and
$\mathbf{F}=\mathbb{Q}$
and
![]() $\unicode[STIX]{x1D712}=|\cdot |_{\mathbb{A}}^{i\unicode[STIX]{x1D707}}$
, that is, the case for the Riemann zeta function.
$\unicode[STIX]{x1D712}=|\cdot |_{\mathbb{A}}^{i\unicode[STIX]{x1D707}}$
, that is, the case for the Riemann zeta function.
On the adelic side, we shall work in the framework of
![]() $\text{PGL}_{2}$
, hence all previous groups such as
$\text{PGL}_{2}$
, hence all previous groups such as
![]() $\mathbf{N},\mathbf{B},\mathbf{K}$
are considered as subgroups of
$\mathbf{N},\mathbf{B},\mathbf{K}$
are considered as subgroups of
![]() $\text{PGL}_{2}$
via the canonical projection.
$\text{PGL}_{2}$
via the canonical projection.
![]() $1_{\text{fin}}$
denotes the identity element in
$1_{\text{fin}}$
denotes the identity element in
![]() $\text{PGL}_{2}(\mathbb{A}_{\text{fin}})$
.
$\text{PGL}_{2}(\mathbb{A}_{\text{fin}})$
.
![]() $\unicode[STIX]{x1D711}$
is reserved for functions on
$\unicode[STIX]{x1D711}$
is reserved for functions on
![]() $[\text{PGL}_{2}]$
. We restrict ourselves to
$[\text{PGL}_{2}]$
. We restrict ourselves to
![]() $\text{SO}_{2}(\mathbb{R})$
-invariant functions. The finite places of
$\text{SO}_{2}(\mathbb{R})$
-invariant functions. The finite places of
![]() $\mathbb{Q}$
correspond to prime numbers
$\mathbb{Q}$
correspond to prime numbers
![]() $\mathfrak{p}=p\mathbb{Z}$
.
$\mathfrak{p}=p\mathbb{Z}$
.
On the classical side, we shall confuse
![]() $\text{SO}_{2}(\mathbb{R})$
-invariant modular forms on
$\text{SO}_{2}(\mathbb{R})$
-invariant modular forms on
![]() $\widetilde{\unicode[STIX]{x1D6E4}}\backslash \text{PGL}_{2}(\mathbb{R})$
with functions on
$\widetilde{\unicode[STIX]{x1D6E4}}\backslash \text{PGL}_{2}(\mathbb{R})$
with functions on
![]() $\unicode[STIX]{x1D6E4}\backslash \mathbb{H}$
, where
$\unicode[STIX]{x1D6E4}\backslash \mathbb{H}$
, where
![]() $\unicode[STIX]{x1D6E4}<\text{PSL}_{2}(\mathbb{R})$
is a lattice,
$\unicode[STIX]{x1D6E4}<\text{PSL}_{2}(\mathbb{R})$
is a lattice,
![]() $\widetilde{\unicode[STIX]{x1D6E4}}$
is the subgroup generated by
$\widetilde{\unicode[STIX]{x1D6E4}}$
is the subgroup generated by
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\text{diag}(1,-1)$
.
$\text{diag}(1,-1)$
.
![]() $f$
is reserved for functions on
$f$
is reserved for functions on
![]() $\widetilde{\unicode[STIX]{x1D6E4}}\backslash \text{PGL}_{2}(\mathbb{R})$
. Hence
$\widetilde{\unicode[STIX]{x1D6E4}}\backslash \text{PGL}_{2}(\mathbb{R})$
. Hence
We also write
![]() $e(x):=e^{2\unicode[STIX]{x1D70B}ix}$
for
$e(x):=e^{2\unicode[STIX]{x1D70B}ix}$
for
![]() $x\in \mathbb{R}$
.
$x\in \mathbb{R}$
.
We assume the existence of a compact subgroup
![]() $\mathbf{K}_{\unicode[STIX]{x1D6E4}}<\text{PGL}_{2}(\mathbb{A}_{\text{fin}})$
such that
$\mathbf{K}_{\unicode[STIX]{x1D6E4}}<\text{PGL}_{2}(\mathbb{A}_{\text{fin}})$
such that
Then the strong approximation theorem,
![]() $\text{PGL}_{2}(\mathbb{A}_{\text{fin}})=\text{PGL}_{2}(\mathbb{Q})\mathbf{K}_{\unicode[STIX]{x1D6E4}}$
, yields
$\text{PGL}_{2}(\mathbb{A}_{\text{fin}})=\text{PGL}_{2}(\mathbb{Q})\mathbf{K}_{\unicode[STIX]{x1D6E4}}$
, yields
![]() $\mathbf{K}_{\unicode[STIX]{x1D6E4}}$
-invariant functions
$\mathbf{K}_{\unicode[STIX]{x1D6E4}}$
-invariant functions
![]() $\unicode[STIX]{x1D711}$
are in bijective correspondence with functions
$\unicode[STIX]{x1D711}$
are in bijective correspondence with functions
![]() $f$
, determining each other by
$f$
, determining each other by
Consequently, if
![]() $p$
denotes the standard uniformizer at the place
$p$
denotes the standard uniformizer at the place
![]() $p$
, then since
$p$
, then since
![]() $p\in \mathbb{Z}_{q}^{\times }$
for any prime
$p\in \mathbb{Z}_{q}^{\times }$
for any prime
![]() $q\neq p$
and
$q\neq p$
and
![]() $\unicode[STIX]{x1D711}$
is invariant by
$\unicode[STIX]{x1D711}$
is invariant by
![]() $a(\widehat{\mathbb{Z}}^{\times })$
, we get
$a(\widehat{\mathbb{Z}}^{\times })$
, we get
or
![]() $(a(p^{-1})f)(z):=f(pz)$
. The constant term, defined by
$(a(p^{-1})f)(z):=f(pz)$
. The constant term, defined by
is left-
![]() $\mathbf{B}(\mathbb{Q})$
right-
$\mathbf{B}(\mathbb{Q})$
right-
![]() $\mathbf{K}_{\unicode[STIX]{x1D6E4}}$
invariant. From the strong approximation theorem, we deduce that
$\mathbf{K}_{\unicode[STIX]{x1D6E4}}$
invariant. From the strong approximation theorem, we deduce that
corresponds bijectively with the set of cusps of
![]() $\unicode[STIX]{x1D6E4}$
. (Look at the right action of
$\unicode[STIX]{x1D6E4}$
. (Look at the right action of
![]() $\text{PGL}_{2}(\mathbb{Q})$
on
$\text{PGL}_{2}(\mathbb{Q})$
on
![]() $\mathbb{P}^{1}(\mathbb{Q})$
!) We take a system of representatives
$\mathbb{P}^{1}(\mathbb{Q})$
!) We take a system of representatives
![]() $[\unicode[STIX]{x1D6E4}]\subset \text{PGL}_{2}(\mathbb{Q})$
for the above double coset decomposition. Hence
$[\unicode[STIX]{x1D6E4}]\subset \text{PGL}_{2}(\mathbb{Q})$
for the above double coset decomposition. Hence
![]() $\unicode[STIX]{x1D711}_{\mathbf{N}}$
and the following finite collection determine each other:
$\unicode[STIX]{x1D711}_{\mathbf{N}}$
and the following finite collection determine each other:
For every
![]() $\unicode[STIX]{x1D6FE}\in [\unicode[STIX]{x1D6E4}]$
,
$\unicode[STIX]{x1D6FE}\in [\unicode[STIX]{x1D6E4}]$
,
![]() $\mathbf{N}(\mathbb{A}_{\text{fin}})\cap \unicode[STIX]{x1D6FE}\mathbf{K}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D6FE}^{-1}$
is a compact subgroup of
$\mathbf{N}(\mathbb{A}_{\text{fin}})\cap \unicode[STIX]{x1D6FE}\mathbf{K}_{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D6FE}^{-1}$
is a compact subgroup of
![]() $\mathbf{N}(\mathbb{A}_{\text{fin}})$
, hence equal to
$\mathbf{N}(\mathbb{A}_{\text{fin}})$
, hence equal to
![]() $\mathbf{N}(d_{\unicode[STIX]{x1D6FE}}\widehat{\mathbb{Z}})$
for some
$\mathbf{N}(d_{\unicode[STIX]{x1D6FE}}\widehat{\mathbb{Z}})$
for some
![]() $d_{\unicode[STIX]{x1D6FE}}\in \mathbb{Q}^{\times }$
. The strong approximation theorem for
$d_{\unicode[STIX]{x1D6FE}}\in \mathbb{Q}^{\times }$
. The strong approximation theorem for
![]() $\mathbb{Q}$
implies
$\mathbb{Q}$
implies
where
![]() $\unicode[STIX]{x1D6FC}$
runs over a system of representatives for
$\unicode[STIX]{x1D6FC}$
runs over a system of representatives for
![]() $\mathbb{Q}/d_{\unicode[STIX]{x1D6FE}}\mathbb{Z}$
. Hence
$\mathbb{Q}/d_{\unicode[STIX]{x1D6FE}}\mathbb{Z}$
. Hence
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{\mathbf{N}}(g,\unicode[STIX]{x1D6FE}) & = & \displaystyle \int _{d_{\unicode[STIX]{x1D6FE}}\mathbb{Z}\backslash \mathbb{R}}\int _{d_{\unicode[STIX]{x1D6FE}}\widehat{\mathbb{Z}}}\unicode[STIX]{x1D711}(n(u)g,n(z)\unicode[STIX]{x1D6FE})\,dz\,du=|d_{\unicode[STIX]{x1D6FE}}|^{-1}\int _{d_{\unicode[STIX]{x1D6FE}}\mathbb{Z}\backslash \mathbb{R}}\unicode[STIX]{x1D711}(n(u)g,\unicode[STIX]{x1D6FE})\,du\nonumber\\ \displaystyle & = & \displaystyle |d_{\unicode[STIX]{x1D6FE}}|^{-1}\int _{d_{\unicode[STIX]{x1D6FE}}\mathbb{Z}\backslash \mathbb{R}}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FE}^{-1}n(u)g,1_{\text{fin}})\,du,\quad \forall g\in \text{PGL}_{2}(\mathbb{R}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{\mathbf{N}}(g,\unicode[STIX]{x1D6FE}) & = & \displaystyle \int _{d_{\unicode[STIX]{x1D6FE}}\mathbb{Z}\backslash \mathbb{R}}\int _{d_{\unicode[STIX]{x1D6FE}}\widehat{\mathbb{Z}}}\unicode[STIX]{x1D711}(n(u)g,n(z)\unicode[STIX]{x1D6FE})\,dz\,du=|d_{\unicode[STIX]{x1D6FE}}|^{-1}\int _{d_{\unicode[STIX]{x1D6FE}}\mathbb{Z}\backslash \mathbb{R}}\unicode[STIX]{x1D711}(n(u)g,\unicode[STIX]{x1D6FE})\,du\nonumber\\ \displaystyle & = & \displaystyle |d_{\unicode[STIX]{x1D6FE}}|^{-1}\int _{d_{\unicode[STIX]{x1D6FE}}\mathbb{Z}\backslash \mathbb{R}}\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FE}^{-1}n(u)g,1_{\text{fin}})\,du,\quad \forall g\in \text{PGL}_{2}(\mathbb{R}).\nonumber\end{eqnarray}$$
On the other hand, the function
is a modular form for the lattice
![]() $\unicode[STIX]{x1D6FE}\widetilde{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D6FE}^{-1}$
. Since
$\unicode[STIX]{x1D6FE}\widetilde{\unicode[STIX]{x1D6E4}}\unicode[STIX]{x1D6FE}^{-1}$
. Since
the normalized constant term at the cusp
![]() $\infty$
of
$\infty$
of
![]() $f_{\unicode[STIX]{x1D6FE}}$
is
$f_{\unicode[STIX]{x1D6FE}}$
is
Write
![]() $f_{\mathbf{N}}=f_{1,\mathbf{N}}$
. Since both functions
$f_{\mathbf{N}}=f_{1,\mathbf{N}}$
. Since both functions
are left-
![]() $\mathbb{Q}^{\times }$
right-
$\mathbb{Q}^{\times }$
right-
![]() $\widehat{\mathbb{Z}}^{\times }$
invariant, and since, by class number 1 of
$\widehat{\mathbb{Z}}^{\times }$
invariant, and since, by class number 1 of
![]() $\mathbb{Q}$
,
$\mathbb{Q}$
,
we can compute the zeta functional as
Write
![]() $e_{0}\in H:=\text{Ind}_{\mathbf{B}(\mathbb{A})\cap \mathbf{K}}^{\mathbf{K}}1$
for the constant function taking value 1 on
$e_{0}\in H:=\text{Ind}_{\mathbf{B}(\mathbb{A})\cap \mathbf{K}}^{\mathbf{K}}1$
for the constant function taking value 1 on
![]() $\mathbf{K}$
. The normalized Eisenstein series
$\mathbf{K}$
. The normalized Eisenstein series
![]() $\text{E}^{\ast }(s,e_{0})$
corresponds to the usual normalized real analytic Eisenstein series for the full modular group
$\text{E}^{\ast }(s,e_{0})$
corresponds to the usual normalized real analytic Eisenstein series for the full modular group
 $$\begin{eqnarray}\text{E}^{\ast }(s,z):=\unicode[STIX]{x1D6EC}(1+2s)\mathop{\sum }_{\substack{ (c,d)=1 \\ c,d\in \mathbb{Z}}}\frac{y^{1/2+s}}{|cz+d|^{1+2s}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{E}^{\ast }(s,z):=\unicode[STIX]{x1D6EC}(1+2s)\mathop{\sum }_{\substack{ (c,d)=1 \\ c,d\in \mathbb{Z}}}\frac{y^{1/2+s}}{|cz+d|^{1+2s}}.\end{eqnarray}$$
Introducing, first for
![]() $\Re s\gg 1$
then by analytic continuation using the second expression, the function
$\Re s\gg 1$
then by analytic continuation using the second expression, the function
one computes the Fourier expansion at
![]() $\infty$
as
$\infty$
as
 $$\begin{eqnarray}\displaystyle (\text{E}^{\ast }-\text{E}_{\mathbf{N}}^{\ast })(s,z) & = & \displaystyle (\text{E}^{\ast }-\text{E}_{\mathbf{N}}^{\ast })(s,e_{0})\left(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),1_{\text{fin}}\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{0\neq n\in \mathbb{Z}}e(nx){\mathcal{K}}_{\infty }(s,ny)\cdot |n|^{-1/2}\mathop{\prod }_{p^{e}\Vert n}\frac{p^{(e+1)s}-p^{-(e+1)s}}{p^{s}-p^{-s}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{0\neq n\in \mathbb{Z}}e(nx){\mathcal{K}}_{\infty }(s,ny)\cdot |n|^{s-1/2}\unicode[STIX]{x1D70E}_{-2s}(|n|),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\text{E}^{\ast }-\text{E}_{\mathbf{N}}^{\ast })(s,z) & = & \displaystyle (\text{E}^{\ast }-\text{E}_{\mathbf{N}}^{\ast })(s,e_{0})\left(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),1_{\text{fin}}\right)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{0\neq n\in \mathbb{Z}}e(nx){\mathcal{K}}_{\infty }(s,ny)\cdot |n|^{-1/2}\mathop{\prod }_{p^{e}\Vert n}\frac{p^{(e+1)s}-p^{-(e+1)s}}{p^{s}-p^{-s}}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{0\neq n\in \mathbb{Z}}e(nx){\mathcal{K}}_{\infty }(s,ny)\cdot |n|^{s-1/2}\unicode[STIX]{x1D70E}_{-2s}(|n|),\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70E}_{s}(m):=\sum _{d\mid m}\,d^{s}$
is the usual divisor sum function. Hence the zeta functional is equal to
$\unicode[STIX]{x1D70E}_{s}(m):=\sum _{d\mid m}\,d^{s}$
is the usual divisor sum function. Hence the zeta functional is equal to
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(s,1,\text{E}^{\ast }(s_{0},e_{0})) & = & \displaystyle \int _{0}^{\infty }\mathop{\sum }_{0\neq n\in \mathbb{Z}}{\mathcal{K}}_{\infty }(s_{0},ny)\cdot |n|^{s_{0}-1/2}\unicode[STIX]{x1D70E}_{-2s_{0}}(|n|)y^{s-1/2}\,d^{\times }t\nonumber\\ \displaystyle & = & \displaystyle 2\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D70E}_{-2s_{0}}(n)\int _{0}^{\infty }\int _{0}^{\infty }e^{-\unicode[STIX]{x1D70B}(t+n^{2}y^{2}/t)}t^{s_{0}}y^{s-s_{0}}\,d^{\times }t\,d^{\times }y\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D70E}_{-2s_{0}}(n)n^{s_{0}-s}\int _{0}^{\infty }\int _{0}^{\infty }e^{-\unicode[STIX]{x1D70B}(t+y)}t^{(s+s_{0})/2}y^{(s-s_{0})/2}\,d^{\times }t\,d^{\times }y\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E4}_{\mathbb{R}}(s-s_{0})\unicode[STIX]{x1D6E4}_{\mathbb{R}}(s+s_{0})\unicode[STIX]{x1D701}(s-s_{0})\unicode[STIX]{x1D701}(s+s_{0})=\unicode[STIX]{x1D6EC}(s-s_{0})\unicode[STIX]{x1D6EC}(s+s_{0}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(s,1,\text{E}^{\ast }(s_{0},e_{0})) & = & \displaystyle \int _{0}^{\infty }\mathop{\sum }_{0\neq n\in \mathbb{Z}}{\mathcal{K}}_{\infty }(s_{0},ny)\cdot |n|^{s_{0}-1/2}\unicode[STIX]{x1D70E}_{-2s_{0}}(|n|)y^{s-1/2}\,d^{\times }t\nonumber\\ \displaystyle & = & \displaystyle 2\mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D70E}_{-2s_{0}}(n)\int _{0}^{\infty }\int _{0}^{\infty }e^{-\unicode[STIX]{x1D70B}(t+n^{2}y^{2}/t)}t^{s_{0}}y^{s-s_{0}}\,d^{\times }t\,d^{\times }y\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{n=1}^{\infty }\unicode[STIX]{x1D70E}_{-2s_{0}}(n)n^{s_{0}-s}\int _{0}^{\infty }\int _{0}^{\infty }e^{-\unicode[STIX]{x1D70B}(t+y)}t^{(s+s_{0})/2}y^{(s-s_{0})/2}\,d^{\times }t\,d^{\times }y\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E4}_{\mathbb{R}}(s-s_{0})\unicode[STIX]{x1D6E4}_{\mathbb{R}}(s+s_{0})\unicode[STIX]{x1D701}(s-s_{0})\unicode[STIX]{x1D701}(s+s_{0})=\unicode[STIX]{x1D6EC}(s-s_{0})\unicode[STIX]{x1D6EC}(s+s_{0}).\nonumber\end{eqnarray}$$
Proposition 4.1 studies a variant of the above equality by replacing
![]() $s$
with
$s$
with
![]() $1/2+i\unicode[STIX]{x1D707}$
,
$1/2+i\unicode[STIX]{x1D707}$
,
![]() $\text{E}^{\ast }(s_{0},e_{0})$
with
$\text{E}^{\ast }(s_{0},e_{0})$
with
![]() $n(T).\text{E}^{\ast }(0,e_{0})$
for some
$n(T).\text{E}^{\ast }(0,e_{0})$
for some
![]() $T\in \mathbb{R},|T|\asymp |\unicode[STIX]{x1D707}|$
. Together with Lemma 4.2, we are reduced to bounding
$T\in \mathbb{R},|T|\asymp |\unicode[STIX]{x1D707}|$
. Together with Lemma 4.2, we are reduced to bounding
where
![]() $h$
is a positive function with support in
$h$
is a positive function with support in
![]() $[|\unicode[STIX]{x1D707}|^{-\unicode[STIX]{x1D705}-1},|\unicode[STIX]{x1D707}|^{\unicode[STIX]{x1D705}-1}]$
. We would like to apply the Cauchy–Schwarz inequality,
$[|\unicode[STIX]{x1D707}|^{-\unicode[STIX]{x1D705}-1},|\unicode[STIX]{x1D707}|^{\unicode[STIX]{x1D705}-1}]$
. We would like to apply the Cauchy–Schwarz inequality,
and Fourier inverse
![]() $|\text{E}^{\ast }(0,z)|^{2}$
, which is not square-integrable. Michel and Venkatesh’s idea is to Fourier invert the restriction of
$|\text{E}^{\ast }(0,z)|^{2}$
, which is not square-integrable. Michel and Venkatesh’s idea is to Fourier invert the restriction of
![]() $|\text{E}^{\ast }(0,z)|^{2}$
on a large compact region containing the domain of integration, which fails to give the Burgess-like quality because the
$|\text{E}^{\ast }(0,z)|^{2}$
on a large compact region containing the domain of integration, which fails to give the Burgess-like quality because the
![]() $\text{L}^{2}$
-norm of such restriction depends polynoimally on
$\text{L}^{2}$
-norm of such restriction depends polynoimally on
![]() $\unicode[STIX]{x1D707}$
. Our idea is to find
$\unicode[STIX]{x1D707}$
. Our idea is to find
![]() ${\mathcal{E}}$
, some linear combination of derivatives of Eisenstein series such that
${\mathcal{E}}$
, some linear combination of derivatives of Eisenstein series such that
![]() $|\text{E}^{\ast }(0,z)|^{2}-{\mathcal{E}}$
comes back to
$|\text{E}^{\ast }(0,z)|^{2}-{\mathcal{E}}$
comes back to
![]() $\text{L}^{2}$
. The existence of
$\text{L}^{2}$
. The existence of
![]() ${\mathcal{E}}$
is due to Zagier [Reference ZagierZag82] and our extension [Reference WuWu18, § 2]. Hence, for
${\mathcal{E}}$
is due to Zagier [Reference ZagierZag82] and our extension [Reference WuWu18, § 2]. Hence, for
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }h(y)\cdot (n(T).|\text{E}^{\ast }|^{2})(0,iy)\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{\infty }h(y)\cdot (n(T).(|\text{E}^{\ast }|^{2}-{\mathcal{E}}))(0,iy)\,d^{\times }y+\int _{0}^{\infty }h(y)\cdot (n(T).{\mathcal{E}})(iy)\,d^{\times }y,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{0}^{\infty }h(y)\cdot (n(T).|\text{E}^{\ast }|^{2})(0,iy)\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{\infty }h(y)\cdot (n(T).(|\text{E}^{\ast }|^{2}-{\mathcal{E}}))(0,iy)\,d^{\times }y+\int _{0}^{\infty }h(y)\cdot (n(T).{\mathcal{E}})(iy)\,d^{\times }y,\nonumber\end{eqnarray}$$
we can estimate the two terms on the right-hand side separately. To the first term we apply Fourier inversion to
![]() $|\text{E}^{\ast }|^{2}-{\mathcal{E}}$
. For the second, we compute directly. The advantage over Michel and Venkatesh’s approach is that the
$|\text{E}^{\ast }|^{2}-{\mathcal{E}}$
. For the second, we compute directly. The advantage over Michel and Venkatesh’s approach is that the
![]() $\text{L}^{2}$
-norm of
$\text{L}^{2}$
-norm of
![]() $|\text{E}^{\ast }|^{2}-{\mathcal{E}}$
is essentially constant, while the second term contributes no more than the constant part of the the first term.
$|\text{E}^{\ast }|^{2}-{\mathcal{E}}$
is essentially constant, while the second term contributes no more than the constant part of the the first term.
The truth is a little more complicated due to the large contribution of the one-dimensional part of
![]() $|\text{E}^{\ast }|^{2}-{\mathcal{E}}$
. Hence we need to use the method of amplification. We shall not be precise as to the exact form of amplification since the aim is to give an idea of how things look. If
$|\text{E}^{\ast }|^{2}-{\mathcal{E}}$
. Hence we need to use the method of amplification. We shall not be precise as to the exact form of amplification since the aim is to give an idea of how things look. If
![]() $p$
is a prime regarded as the uniformizer of
$p$
is a prime regarded as the uniformizer of
![]() $\mathbb{Q}_{p}^{\times }$
embedded in
$\mathbb{Q}_{p}^{\times }$
embedded in
![]() $\mathbb{A}_{\text{fin}}^{\times }$
, then
$\mathbb{A}_{\text{fin}}^{\times }$
, then
from which we deduce that
We can replace
![]() $\text{E}^{\ast }(0,e_{0})$
with some balanced average of
$\text{E}^{\ast }(0,e_{0})$
with some balanced average of
![]() $p^{i\unicode[STIX]{x1D707}}a(p^{-1}).\text{E}^{\ast }(0,e_{0})$
without affecting the integral representation and Lemma 4.2 given above, since
$p^{i\unicode[STIX]{x1D707}}a(p^{-1}).\text{E}^{\ast }(0,e_{0})$
without affecting the integral representation and Lemma 4.2 given above, since
![]() $a(p^{-1})$
commutes with the
$a(p^{-1})$
commutes with the
![]() $n(T),T\in \mathbb{R}$
. After applying Cauchy–Schwarz, we are led to Fourier inverting
$n(T),T\in \mathbb{R}$
. After applying Cauchy–Schwarz, we are led to Fourier inverting
In the classical setting, we should view all modular forms for
![]() $\text{PSL}_{2}(\mathbb{Z})$
as forms for
$\text{PSL}_{2}(\mathbb{Z})$
as forms for
![]() $\unicode[STIX]{x1D6E4}_{0}(p)$
at this step. Hence we need to find some linear combination
$\unicode[STIX]{x1D6E4}_{0}(p)$
at this step. Hence we need to find some linear combination
![]() ${\mathcal{E}}(p)$
of derivatives of Eisenstein series for
${\mathcal{E}}(p)$
of derivatives of Eisenstein series for
![]() $\unicode[STIX]{x1D6E4}_{0}(p)$
, such that
$\unicode[STIX]{x1D6E4}_{0}(p)$
, such that
has slow increase at every cusp of
![]() $\unicode[STIX]{x1D6E4}_{0}(p)$
. This is of course feasible in the classical setting, but with painful computations. The more convenient adelic computation goes as follows.
$\unicode[STIX]{x1D6E4}_{0}(p)$
. This is of course feasible in the classical setting, but with painful computations. The more convenient adelic computation goes as follows.
Definition A.1. For
![]() $e\in H:=\text{Ind}_{\mathbf{B}(\mathbb{A})\cap \mathbf{K}}^{\mathbf{K}}1$
, we write
$e\in H:=\text{Ind}_{\mathbf{B}(\mathbb{A})\cap \mathbf{K}}^{\mathbf{K}}1$
, we write
![]() $e_{s}\in \text{Ind}_{\mathbf{B}(\mathbb{A})}^{\text{GL}_{2}(\mathbb{A})}(|\cdot |_{\mathbb{A}}^{s},|\cdot |_{\mathbb{A}}^{-s})$
for the flat section associated with it. For any
$e_{s}\in \text{Ind}_{\mathbf{B}(\mathbb{A})}^{\text{GL}_{2}(\mathbb{A})}(|\cdot |_{\mathbb{A}}^{s},|\cdot |_{\mathbb{A}}^{-s})$
for the flat section associated with it. For any
![]() $s_{0}\in \mathbb{C}$
,
$s_{0}\in \mathbb{C}$
,
![]() $n\in \mathbb{N}$
we write
$n\in \mathbb{N}$
we write
It is easy to verify
Let
![]() $e_{1}\in H$
, admitting the same local component as
$e_{1}\in H$
, admitting the same local component as
![]() $e_{0}$
at places
$e_{0}$
at places
![]() $\infty$
and
$\infty$
and
![]() $q\neq p$
. At
$q\neq p$
. At
![]() $p$
we take its local component as the
$p$
we take its local component as the
![]() $e_{1}$
in Lemma 2.16. Specifically,
$e_{1}$
in Lemma 2.16. Specifically,
![]() $\text{E}(s,e_{1})$
corresponds to an Eisenstein series for
$\text{E}(s,e_{1})$
corresponds to an Eisenstein series for
![]() $\unicode[STIX]{x1D6E4}_{0}(p)$
given by
$\unicode[STIX]{x1D6E4}_{0}(p)$
given by
 $$\begin{eqnarray}\displaystyle \text{E}_{1}(s,z) & = & \displaystyle \text{E}(s,e_{1})\left(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),1_{\text{fin}}\right)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \mathbf{B}(\mathbb{Q})\backslash \text{PGL}_{2}(\mathbb{Q})}\sum e_{1,s}\biggl(\unicode[STIX]{x1D6FE}\biggl(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),1_{\text{fin}}\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \mathbf{N}(\mathbb{Z})\backslash \widetilde{\unicode[STIX]{x1D6E4}_{0}(p)}}e_{1,s}\biggl(\unicode[STIX]{x1D6FE}\biggl(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),1_{\text{fin}}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \mathbf{N}_{-}(p\mathbb{Z})\backslash \widetilde{\unicode[STIX]{x1D6E4}_{0}(p)}}e_{1,s}\biggl(\left(\begin{array}{@{}cc@{}} & 1\\ 1 & \end{array}\right)\unicode[STIX]{x1D6FE}\biggl(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),1_{\text{fin}}\biggr)\biggr)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{E}_{1}(s,z) & = & \displaystyle \text{E}(s,e_{1})\left(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),1_{\text{fin}}\right)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \mathbf{B}(\mathbb{Q})\backslash \text{PGL}_{2}(\mathbb{Q})}\sum e_{1,s}\biggl(\unicode[STIX]{x1D6FE}\biggl(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),1_{\text{fin}}\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \mathbf{N}(\mathbb{Z})\backslash \widetilde{\unicode[STIX]{x1D6E4}_{0}(p)}}e_{1,s}\biggl(\unicode[STIX]{x1D6FE}\biggl(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),1_{\text{fin}}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \mathbf{N}_{-}(p\mathbb{Z})\backslash \widetilde{\unicode[STIX]{x1D6E4}_{0}(p)}}e_{1,s}\biggl(\left(\begin{array}{@{}cc@{}} & 1\\ 1 & \end{array}\right)\unicode[STIX]{x1D6FE}\biggl(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),1_{\text{fin}}\biggr)\biggr)\nonumber\end{eqnarray}$$
since we know the set
![]() $\{0,\infty \}$
of cusps for
$\{0,\infty \}$
of cusps for
![]() $\widetilde{\unicode[STIX]{x1D6E4}_{0}(p)}$
as
$\widetilde{\unicode[STIX]{x1D6E4}_{0}(p)}$
as
We insert the value of
![]() $e_{1,s}$
to obtain
$e_{1,s}$
to obtain
 $$\begin{eqnarray}\displaystyle \text{E}_{1}(s,z)=p^{1/2}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \mathbf{N}(\mathbb{Z})\backslash \widetilde{\unicode[STIX]{x1D6E4}_{0}(p)}}\Im (\unicode[STIX]{x1D6FE}.z)^{1/2+s}-p^{-1/2}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \mathbf{N}_{-}(p\mathbb{Z})\backslash \widetilde{\unicode[STIX]{x1D6E4}_{0}(p)}}\Im \biggl(\left(\begin{array}{@{}cc@{}} & 1\\ 1 & \end{array}\right)\unicode[STIX]{x1D6FE}.z\biggr)^{1/2+s}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{E}_{1}(s,z)=p^{1/2}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \mathbf{N}(\mathbb{Z})\backslash \widetilde{\unicode[STIX]{x1D6E4}_{0}(p)}}\Im (\unicode[STIX]{x1D6FE}.z)^{1/2+s}-p^{-1/2}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \mathbf{N}_{-}(p\mathbb{Z})\backslash \widetilde{\unicode[STIX]{x1D6E4}_{0}(p)}}\Im \biggl(\left(\begin{array}{@{}cc@{}} & 1\\ 1 & \end{array}\right)\unicode[STIX]{x1D6FE}.z\biggr)^{1/2+s}. & & \displaystyle \nonumber\end{eqnarray}$$
Note that this is regular at
![]() $s=1/2$
. We now turn to the determination of
$s=1/2$
. We now turn to the determination of
![]() ${\mathcal{E}}(p)$
. Using the Laurent expansion of
${\mathcal{E}}(p)$
. Using the Laurent expansion of
![]() $\unicode[STIX]{x1D6EC}$
in (5.1), we can write the constant term as
$\unicode[STIX]{x1D6EC}$
in (5.1), we can write the constant term as
Computing the constant term of
![]() $a(p^{-1}).\text{E}^{\ast }(0,e_{0})$
is convenient only if we can express
$a(p^{-1}).\text{E}^{\ast }(0,e_{0})$
is convenient only if we can express
![]() $a(p^{-1})e_{0,s}$
as a linear combination of flat sections. This is done in Lemma 2.18, yielding
$a(p^{-1})e_{0,s}$
as a linear combination of flat sections. This is done in Lemma 2.18, yielding
 $$\begin{eqnarray}\displaystyle & \displaystyle a(p^{-1}).e_{0,s}=\frac{p^{s+1/2}-p^{-(s+1/2)}}{p^{1/2}+p^{-1/2}}e_{1,s}+\frac{p^{s}+p^{-s}}{p^{1/2}+p^{-1/2}}e_{0,s}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle a(p^{-1}).e_{0,0}^{(1)}=e_{0,0}^{(1)}+\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}e_{1,0}^{(1)}+\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}(\log p)e_{0,0}+(\log p)e_{1,0}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle a(p^{-1}).e_{0,s}=\frac{p^{s+1/2}-p^{-(s+1/2)}}{p^{1/2}+p^{-1/2}}e_{1,s}+\frac{p^{s}+p^{-s}}{p^{1/2}+p^{-1/2}}e_{0,s}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle a(p^{-1}).e_{0,0}^{(1)}=e_{0,0}^{(1)}+\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}e_{1,0}^{(1)}+\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}(\log p)e_{0,0}+(\log p)e_{1,0}. & \displaystyle \nonumber\end{eqnarray}$$
We thus obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle (a(p^{-1}).\text{E}^{\ast })_{\mathbf{N}}(0,e_{0})\cdot \overline{\text{E}_{\mathbf{N}}^{\ast }(0,e_{0})}\nonumber\\ \displaystyle & & \displaystyle \quad =|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}e_{0,1/2}^{(2)}+|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}e_{1,1/2}^{(2)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\biggl(|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}(\log p)+2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }+2\unicode[STIX]{x1D6FE}_{\mathbb{Q}}\overline{\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }}\biggr)e_{0,1/2}^{(1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\biggl(|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}(\log p)+2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}+2\unicode[STIX]{x1D6FE}_{\mathbb{Q}}\overline{\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}\biggr)e_{1,1/2}^{(1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\biggl(2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}(\log p)+4|\unicode[STIX]{x1D6FE}_{\mathbb{Q}}|^{2}\biggr)e_{0,1/2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\biggl(2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }(\log p)+4|\unicode[STIX]{x1D6FE}_{\mathbb{Q}}|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}}\biggr)e_{1,1/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (a(p^{-1}).\text{E}^{\ast })_{\mathbf{N}}(0,e_{0})\cdot \overline{\text{E}_{\mathbf{N}}^{\ast }(0,e_{0})}\nonumber\\ \displaystyle & & \displaystyle \quad =|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}e_{0,1/2}^{(2)}+|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}e_{1,1/2}^{(2)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\biggl(|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}(\log p)+2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }+2\unicode[STIX]{x1D6FE}_{\mathbb{Q}}\overline{\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }}\biggr)e_{0,1/2}^{(1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\biggl(|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}(\log p)+2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}+2\unicode[STIX]{x1D6FE}_{\mathbb{Q}}\overline{\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}\biggr)e_{1,1/2}^{(1)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\biggl(2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}(\log p)+4|\unicode[STIX]{x1D6FE}_{\mathbb{Q}}|^{2}\biggr)e_{0,1/2}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\biggl(2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }(\log p)+4|\unicode[STIX]{x1D6FE}_{\mathbb{Q}}|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}}\biggr)e_{1,1/2}.\nonumber\end{eqnarray}$$
Writing for
![]() $\text{E}(s,z)$
the usual (non-completed) real analytic Eisenstein series and, for
$\text{E}(s,z)$
the usual (non-completed) real analytic Eisenstein series and, for
![]() $n\in \mathbb{N}$
,
$n\in \mathbb{N}$
,
we deduce via the adelic classical correspondence of constant terms that
 $$\begin{eqnarray}\displaystyle {\mathcal{E}}(p)(z) & := & \displaystyle |\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}\text{E}^{\text{reg},(2)}(1/2,z)+|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}\text{E}_{1}^{(2)}(1/2,z)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}(\log p)+2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }+2\unicode[STIX]{x1D6FE}_{\mathbb{Q}}\overline{\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }}\biggr)\text{E}^{\text{reg},(1)}(1/2,z)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}(\log p)+2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}+2\unicode[STIX]{x1D6FE}_{\mathbb{Q}}\overline{\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}\biggr)\text{E}_{1}^{(1)}(1/2,z)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}(\log p)+4|\unicode[STIX]{x1D6FE}_{\mathbb{Q}}|^{2}\biggr)\text{E}^{\text{reg}}(1/2,z)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }(\log p)+4|\unicode[STIX]{x1D6FE}_{\mathbb{Q}}|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}}\biggr)\text{E}_{1}(1/2,z)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{E}}(p)(z) & := & \displaystyle |\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}\text{E}^{\text{reg},(2)}(1/2,z)+|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}\text{E}_{1}^{(2)}(1/2,z)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}(\log p)+2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }+2\unicode[STIX]{x1D6FE}_{\mathbb{Q}}\overline{\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }}\biggr)\text{E}^{\text{reg},(1)}(1/2,z)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(|\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }|^{2}(\log p)+2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}+2\unicode[STIX]{x1D6FE}_{\mathbb{Q}}\overline{\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}\biggr)\text{E}_{1}^{(1)}(1/2,z)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }\frac{p^{1/2}-p^{-1/2}}{p^{1/2}+p^{-1/2}}(\log p)+4|\unicode[STIX]{x1D6FE}_{\mathbb{Q}}|^{2}\biggr)\text{E}^{\text{reg}}(1/2,z)\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(2\overline{\unicode[STIX]{x1D6FE}_{\mathbb{Q}}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}}^{\ast }(\log p)+4|\unicode[STIX]{x1D6FE}_{\mathbb{Q}}|^{2}\frac{p^{1/2}-p^{-1/2}}{p^{1/2}}\biggr)\text{E}_{1}(1/2,z)\nonumber\end{eqnarray}$$
does the job.
With the above construction, we then showed that the (renormalized)
![]() $\text{L}^{2}$
-norm of
$\text{L}^{2}$
-norm of
![]() $\unicode[STIX]{x1D711}_{0}(p)$
on
$\unicode[STIX]{x1D711}_{0}(p)$
on
![]() $\unicode[STIX]{x1D6E4}_{0}(p)\backslash \mathbb{H}$
is
$\unicode[STIX]{x1D6E4}_{0}(p)\backslash \mathbb{H}$
is
![]() $\ll (\log p)^{3}$
, as well as its derivatives with respect to the Lie algebra of
$\ll (\log p)^{3}$
, as well as its derivatives with respect to the Lie algebra of
![]() $\text{PGL}_{2}(\mathbb{R})$
. Its Fourier inversion,
$\text{PGL}_{2}(\mathbb{R})$
. Its Fourier inversion,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{0}(p)(z) & = & \displaystyle \frac{\langle \unicode[STIX]{x1D711}_{0}(p),1\rangle }{\text{Vol}(\unicode[STIX]{x1D6E4}_{0}(p)\backslash \mathbb{H})}\cdot 1+\mathop{\sum }_{f\,\,\text{cusp form for}\,\,\unicode[STIX]{x1D6E4}_{0}(p)}C_{p}(f)f(z)\nonumber\\ \displaystyle & & \displaystyle +\,\int _{-\infty }^{\infty }C_{p}(0,i\unicode[STIX]{x1D70F})\text{E}(i\unicode[STIX]{x1D70F},z)\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}}+\int _{-\infty }^{\infty }C_{p}(1,i\unicode[STIX]{x1D70F})\text{E}_{1}(i\unicode[STIX]{x1D70F},z)\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D711}_{0}(p)_{\mathbf{N}}(z)+\mathop{\sum }_{f\,\,\text{cusp form for}\,\,\unicode[STIX]{x1D6E4}_{0}(p)}C_{p}(f)f(z)\nonumber\\ \displaystyle & & \displaystyle +\,\int _{-\infty }^{\infty }C_{p}(0,i\unicode[STIX]{x1D70F})(\text{E}-\text{E}_{\mathbf{N}})(i\unicode[STIX]{x1D70F},z)\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}}+\int _{-\infty }^{\infty }C_{p}(1,i\unicode[STIX]{x1D70F})(\text{E}_{1}-\text{E}_{1,\mathbf{N}})(i\unicode[STIX]{x1D70F},z)\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}_{0}(p)(z) & = & \displaystyle \frac{\langle \unicode[STIX]{x1D711}_{0}(p),1\rangle }{\text{Vol}(\unicode[STIX]{x1D6E4}_{0}(p)\backslash \mathbb{H})}\cdot 1+\mathop{\sum }_{f\,\,\text{cusp form for}\,\,\unicode[STIX]{x1D6E4}_{0}(p)}C_{p}(f)f(z)\nonumber\\ \displaystyle & & \displaystyle +\,\int _{-\infty }^{\infty }C_{p}(0,i\unicode[STIX]{x1D70F})\text{E}(i\unicode[STIX]{x1D70F},z)\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}}+\int _{-\infty }^{\infty }C_{p}(1,i\unicode[STIX]{x1D70F})\text{E}_{1}(i\unicode[STIX]{x1D70F},z)\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D711}_{0}(p)_{\mathbf{N}}(z)+\mathop{\sum }_{f\,\,\text{cusp form for}\,\,\unicode[STIX]{x1D6E4}_{0}(p)}C_{p}(f)f(z)\nonumber\\ \displaystyle & & \displaystyle +\,\int _{-\infty }^{\infty }C_{p}(0,i\unicode[STIX]{x1D70F})(\text{E}-\text{E}_{\mathbf{N}})(i\unicode[STIX]{x1D70F},z)\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}}+\int _{-\infty }^{\infty }C_{p}(1,i\unicode[STIX]{x1D70F})(\text{E}_{1}-\text{E}_{1,\mathbf{N}})(i\unicode[STIX]{x1D70F},z)\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}},\nonumber\end{eqnarray}$$
with Fourier coefficients
![]() $C_{p}(f),C_{p}(0,i\unicode[STIX]{x1D70F}),C_{p}(1,i\unicode[STIX]{x1D70F})\in \mathbb{C}$
, converges uniformly in any compact (for the first version) or Siegel domain (for the second). Thus
$C_{p}(f),C_{p}(0,i\unicode[STIX]{x1D70F}),C_{p}(1,i\unicode[STIX]{x1D70F})\in \mathbb{C}$
, converges uniformly in any compact (for the first version) or Siegel domain (for the second). Thus
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(h,n(T).\unicode[STIX]{x1D711}_{0}(p)) & := & \displaystyle \int _{0}^{\infty }h(y)\cdot \unicode[STIX]{x1D711}_{0}(p)(iy)\,d^{\times }y\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }h(y)\cdot \unicode[STIX]{x1D711}_{0}(p)_{\mathbf{N}}(iy)\,d^{\times }y+\mathop{\sum }_{f}C_{p}(f)\int _{0}^{\infty }h(y)\cdot f(iy)\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,\int _{-\infty }^{\infty }C_{p}(0,i\unicode[STIX]{x1D70F})\int _{0}^{\infty }h(y)\cdot (\text{E}-\text{E}_{\mathbf{N}})(i\unicode[STIX]{x1D70F},iy)\,d^{\times }y\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{-\infty }^{\infty }C_{p}(1,i\unicode[STIX]{x1D70F})\int _{0}^{\infty }(\text{E}_{1}-\text{E}_{1,\mathbf{N}})(i\unicode[STIX]{x1D70F},iy)\,d^{\times }y\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D701}(h,n(T).\unicode[STIX]{x1D711}_{0}(p)) & := & \displaystyle \int _{0}^{\infty }h(y)\cdot \unicode[STIX]{x1D711}_{0}(p)(iy)\,d^{\times }y\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{\infty }h(y)\cdot \unicode[STIX]{x1D711}_{0}(p)_{\mathbf{N}}(iy)\,d^{\times }y+\mathop{\sum }_{f}C_{p}(f)\int _{0}^{\infty }h(y)\cdot f(iy)\,d^{\times }y\nonumber\\ \displaystyle & & \displaystyle +\,\int _{-\infty }^{\infty }C_{p}(0,i\unicode[STIX]{x1D70F})\int _{0}^{\infty }h(y)\cdot (\text{E}-\text{E}_{\mathbf{N}})(i\unicode[STIX]{x1D70F},iy)\,d^{\times }y\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{-\infty }^{\infty }C_{p}(1,i\unicode[STIX]{x1D70F})\int _{0}^{\infty }(\text{E}_{1}-\text{E}_{1,\mathbf{N}})(i\unicode[STIX]{x1D70F},iy)\,d^{\times }y\frac{d\unicode[STIX]{x1D70F}}{4\unicode[STIX]{x1D70B}}\nonumber\end{eqnarray}$$
and we estimate the right-hand side term by term.