1. Introduction
Recent decades have witnessed an explosion of interest in the development, utilization and optimization of superhydrophobic materials. Such materials enjoy wide-ranging applications, e.g. in the fabrication of surfaces that are self-cleaning (Nakajima et al. Reference Nakajima, Hashimoto, Watanabe, Takai, Yamauchi and Fujishima2000; Wang et al. Reference Wang, Zhu, Hu, Zhang, Wu, Wang and Zhu2016) or resistant to ice accretion (Varanasi et al. Reference Varanasi, Deng, Smith, Hsu and Bhute2010). In other respects, superhydrophobic materials are used in the more general context of water repellency, e.g. water-shedding fabrics (Zimmermann et al. Reference Zimmermann, Reifler, Fortunato, Gerhardt and Seeger2008), or in the development of materials classified as anti-reflection (Manca et al. Reference Manca, Cannavale, De Marco, Aricò, Cingolani and Gigli2009) or corrosion-resistant (Zhang et al. Reference Zhang, Zhao, Chen, Xu, Evans and Duan2008). In no small number of cases, engineering designs at the microscale are inspired by Nature, the lotus leaf representing the classical example (Reyssat Reference Reyssat2007). Elsewhere in Nature, the superhydrophobic character of the integument of many species of insects and arachnids allows these animals to carry integument-attached bubbles underwater (Thorpe Reference Thorpe1950; Gittelman Reference Gittelman1975; Hinton Reference Hinton1976; Flynn & Bush Reference Flynn and Bush2008). Although the function of such bubbles (or ‘plastrons’) is, for most species, to facilitate underwater breathing, insects such the intertidal midge Clunio use integument-attached bubbles to shield themselves from the violent surf of their natural habitat (Neumann & Woermann Reference Neumann and Woermann2009).
Further to the seminal studies of Fukuda et al. (Reference Fukuda, Tokunaga, Nobunaga, Nakatani, Iwasaki and Kunitake2000), Daniello, Waterhouse & Rothstein (Reference Daniello, Waterhouse and Rothstein2009), Vakarelski et al. (Reference Vakarelski, Marston, Chan and Thoroddsen2011) and many others, the last example of the previous paragraph highlights the important role that surface-attached air bubbles may play in drag reduction. This topic was the subject of the theoretical investigation of Busse et al. (Reference Busse, Sandham, McHale and Newton2013), who studied different manifestations of Couette and Poiseuille flow. They thereby characterized the impact of air layer thickness on drag reduction e.g. by defining, for different flow geometries and configurations, the optimal thickness ![]() $d^{opt}$ such that drag is minimized. As with the precursor investigation of McHale, Flynn & Newton (Reference McHale, Flynn and Newton2011), calculations were performed in the ‘perfect plastron’ limit and therefore considered a scenario in which the (continuous) air layer is maintained without reference to the ridges (Rosengarten, Stanley & Kwok Reference Rosengarten, Stanley and Kwok2008; Teo & Khoo Reference Teo and Khoo2009; Woolford et al. Reference Woolford, Prince, Maynes and Webb2009; Costantini, Mollicone & Battista Reference Costantini, Mollicone and Battista2018) or pillars (Kim & Rothstein Reference Kim and Rothstein2017; Nasser et al. Reference Nasser, Lin, Zhang and Sodano2020; Xia et al. Reference Xia, Zhao, Yang, Yang, Li, Wang and Wang2021) that characterize superhydrophobic surfaces at the microscale.
$d^{opt}$ such that drag is minimized. As with the precursor investigation of McHale, Flynn & Newton (Reference McHale, Flynn and Newton2011), calculations were performed in the ‘perfect plastron’ limit and therefore considered a scenario in which the (continuous) air layer is maintained without reference to the ridges (Rosengarten, Stanley & Kwok Reference Rosengarten, Stanley and Kwok2008; Teo & Khoo Reference Teo and Khoo2009; Woolford et al. Reference Woolford, Prince, Maynes and Webb2009; Costantini, Mollicone & Battista Reference Costantini, Mollicone and Battista2018) or pillars (Kim & Rothstein Reference Kim and Rothstein2017; Nasser et al. Reference Nasser, Lin, Zhang and Sodano2020; Xia et al. Reference Xia, Zhao, Yang, Yang, Li, Wang and Wang2021) that characterize superhydrophobic surfaces at the microscale.
Motivated by the elegance of the Busse et al. (Reference Busse, Sandham, McHale and Newton2013) analytical solutions, we wish to revisit their derivations but now in the context of a transfer of thermal energy rather than of momentum. To this end, and further to the laboratory experiments and numerical simulations reported in Rosengarten et al. (Reference Rosengarten, Stanley and Kwok2008), the current paper is devoted to addressing the following question: can surface-attached air bubbles serve as effective thermal insulators when considering pressure-driven internal flow? Despite the breadth of the application space (e.g. lab-on-a-chip devices) or its extrapolation to biological systems (e.g. Brock Reference Brock1970), this topic has garnered only modest attention, at least compared to the voluminous literature on drag reduction. Among available studies, some focus on phase change, e.g. the possibility that superhydrophobic surfaces might slow evaporation (Fernandes, Vainsten & Brito Reference Fernandes, Vainsten and Brito2015). A separate line of inquiry has focused on sensible heat transfer; however, among theoretical/numerical investigations, the flow that develops within the air bubbles is typically disregarded (e.g. Ng & Wang Reference Ng and Wang2014) or else the air–water interface is modelled as adiabatic (e.g. Maynes et al. Reference Maynes, Webb, Crockett and Solovjov2013; Enright et al. Reference Enright, Hodes, Salamon and Muzychka2014; Maynes & Crockett Reference Maynes and Crockett2014; Cheng, Xu & Sui Reference Cheng, Xu and Sui2015; Cowley, Maynes & Crockett Reference Cowley, Maynes and Crockett2016; Kirk, Hodes & Papageorgiou Reference Kirk, Hodes and Papageorgiou2017; Karamanis et al. Reference Karamanis, Hodes, Kirk and Papageorgiou2018; Game et al. Reference Game, Hodes, Kirk and Papageorgiou2018; Tomlinson et al. Reference Tomlinson, Mayer, Kirk, Hodes and Papageorgiou2024). Though certainly reasonable when air bubbles are interspersed within a dense, thermally conductive forest of roughness elements (e.g. micro-pillars or -ridges) that are good conductors of heat, it remains unclear whether such motions in the gas phase should be omitted when bubble volumes are comparatively large and/or the solid consists of material with a very low thermal conductivity. Therefore, following in the footsteps of Busse et al. (Reference Busse, Sandham, McHale and Newton2013), and motivated by a desire to derive analytical (if somewhat unwieldy) solutions, our exposition will likewise examine the ‘perfect plastron’ limit. In this way, our solutions represent an upper bound for the thermal insulation efficacy of surface-attached bubbles. Our solutions also represent an opposite bookend to those (as or more detailed) studies that prioritize heat transfer along roughness elements. In this way, we hope to provide helpful guidance as to when the adiabatic interface assumption is most applicable.
As with Busse et al. (Reference Busse, Sandham, McHale and Newton2013), roughly equal attention will be devoted to channel versus pipe flow – see figure 1. More specifically, and borrowing the nomenclature adopted in Busse et al. (Reference Busse, Sandham, McHale and Newton2013), we plan to investigate each of the flows enumerated in table 1. A review of the entries in this table reveals that not all scenarios are, in fact, amenable to an analytical solution. Thus we adopt a numerical approach when characterizing the behaviour of the flows labelled CHSYM3, PIPE3, CHSYM4 and PIPE4, or the relevance of these idealized flows to a real superhydrophobic surface. Numerical simulations are likewise deployed when studying the complementary cases CHSYM1, PIPE1, CHSYM2 and PIPE2; here, however, the primary purpose of the numerical output is to validate the accuracy of the associated theoretical solutions.

Figure 1. Schematics of the flow geometries: (a) rectilinear channel (CHSYM), (b) axisymmetric pipe (PIPE). The regions occupied by the water and air are indicated in blue and grey, respectively. For mathematical simplicity, our analysis will idealize the channel as being very wide (and very long) relative to the vertical distance ![]() $2H$.
$2H$.
Table 1. Classification of the flow/thermal forcing regimes considered in this study. When ![]() $\dot {m}_a > 0$, we assume that the horizontal/axial pressure gradients driving the water and air flows are identical. By contrast, when
$\dot {m}_a > 0$, we assume that the horizontal/axial pressure gradients driving the water and air flows are identical. By contrast, when ![]() $\dot {m}_a = 0$, there is no net flow of air in the streamwise direction. For future reference, note that uniform surface heat flux (uniform surface temperature) cases will be referred to as USF (UST).
$\dot {m}_a = 0$, there is no net flow of air in the streamwise direction. For future reference, note that uniform surface heat flux (uniform surface temperature) cases will be referred to as USF (UST).

The rest of the paper is organized as follows. In § 2, analytical solutions are derived for cases labelled in table 1 as CHSYM1, PIPE1, CHSYM2 and PIPE2. The theoretical exposition begins with a description of the velocity field, and progresses to a description of the energy field. In § 3, our complementary numerical simulations are described. Numerical output is compared against the theoretical predictions in §§ 4 and 5. The latter of these sections characterizes the thermal insulation efficacy of surface-attached air bubbles, e.g. by showing the variation of the Nusselt number with the thickness of the air layer. Numerical simulations are also performed for the purposes of contextualizing our results vis-à-vis real micro-channels; the output and discussion in question appears in § 6. Finally, in § 7, we present a series of conclusions for the work as a whole.
2. Theory
2.1. Assumptions
In order to make the mathematical treatment tractable, a series of simplifying assumptions must be applied, as follows. (i) The air bubble that appears along the inside boundary is a ‘perfect plastron’. Stated differently, and excepting the discussion of § 6, we suppose that the bubble is maintained in place without reference to micro-topological elements. In a related vein, we suppose that the bubble maintains a uniform depth. So as to provide a fulsome comparison with Busse et al. (Reference Busse, Sandham, McHale and Newton2013), we consider a range of bubble depths that spans the entire channel depth. In other words, and in the context of figure 1, we examine ![]() $0 < \delta /H, \delta /R < 1$. Note, however, that there are practical limitations associated with stabilizing a thick surface-attached bubble, particularly when the bubble thickness exceeds the capillary length. As such, our most significant results apply to the cases of relatively small
$0 < \delta /H, \delta /R < 1$. Note, however, that there are practical limitations associated with stabilizing a thick surface-attached bubble, particularly when the bubble thickness exceeds the capillary length. As such, our most significant results apply to the cases of relatively small ![]() $\delta /H$ or
$\delta /H$ or ![]() $\delta /R$. (ii) Insofar as the fluid flows interior and exterior to the bubble are concerned, we assume that these flows of air and of water are steady, laminar, parallel and therefore fully developed. Note that the assumption of a fully developed flow applies when considering both thermal as well as hydrodynamic effects. (iii) Air and water share the properties of incompressibility and immiscibility. Meanwhile, properties such as density, viscosity and gas solubility are supposed to exhibit negligible variations with temperature. Assumptions (i)–(iii) provide the robust foundation needed to study the eight different configurations of table 1.
$\delta /R$. (ii) Insofar as the fluid flows interior and exterior to the bubble are concerned, we assume that these flows of air and of water are steady, laminar, parallel and therefore fully developed. Note that the assumption of a fully developed flow applies when considering both thermal as well as hydrodynamic effects. (iii) Air and water share the properties of incompressibility and immiscibility. Meanwhile, properties such as density, viscosity and gas solubility are supposed to exhibit negligible variations with temperature. Assumptions (i)–(iii) provide the robust foundation needed to study the eight different configurations of table 1.
2.2. Velocity profile
The determination of the velocity profile using the Navier–Stokes equations is a crucial first step in characterizing the thermal insulation efficacy of surface-attached air bubbles via the energy equation. For this purpose, we borrow the analytical solutions of Busse et al. (Reference Busse, Sandham, McHale and Newton2013). The equations in question are extensions of the classical Poiseuille solution to two immiscible phases, and are derived by balancing the forces associated with the pressure gradient and viscous shear. As we document below, different formulations apply depending on the duct geometry and on whether or not the net mass flow rate of air, ![]() $\dot {m}_a$, vanishes. On the other hand, whether
$\dot {m}_a$, vanishes. On the other hand, whether ![]() $\dot {m}_a = 0$ or
$\dot {m}_a = 0$ or ![]() $\dot {m}_{a} > 0$ does not change the hydrodynamic boundary conditions. With reference to the schematics of figures 1–3 and the length scales defined therein, these boundary conditions read as follows. (i) Zero air velocity (
$\dot {m}_{a} > 0$ does not change the hydrodynamic boundary conditions. With reference to the schematics of figures 1–3 and the length scales defined therein, these boundary conditions read as follows. (i) Zero air velocity (![]() $u_a = 0$) along the wall, i.e. at
$u_a = 0$) along the wall, i.e. at ![]() $z=H$ for the channel of figure 2, and at
$z=H$ for the channel of figure 2, and at ![]() $r=R$ for the pipe of figure 3. (ii) Zero (water) vertical/radial velocity gradient along the centreline, i.e.
$r=R$ for the pipe of figure 3. (ii) Zero (water) vertical/radial velocity gradient along the centreline, i.e. ![]() $(\mathrm {d}u_w/\mathrm {d}z)_{z=0} = 0$ for the channel, and
$(\mathrm {d}u_w/\mathrm {d}z)_{z=0} = 0$ for the channel, and ![]() $(\mathrm {d}u_w/\mathrm {d}r)_{r=0} = 0$ for the pipe. (iii) Along the air–water interface, we require continuity of velocity and of shear stress. Expressed symbolically, we write
$(\mathrm {d}u_w/\mathrm {d}r)_{r=0} = 0$ for the pipe. (iii) Along the air–water interface, we require continuity of velocity and of shear stress. Expressed symbolically, we write ![]() $u_a(z=H-\delta ) = u_w(z=H-\delta )$ and
$u_a(z=H-\delta ) = u_w(z=H-\delta )$ and ![]() $\mu _a (\mathrm {d}u_a/\mathrm {d}z)_{H-\delta } = \mu _w (\mathrm {d}u_w/\mathrm {d}z)_{H-\delta }$ for the channel, and
$\mu _a (\mathrm {d}u_a/\mathrm {d}z)_{H-\delta } = \mu _w (\mathrm {d}u_w/\mathrm {d}z)_{H-\delta }$ for the channel, and ![]() $u_a(r=R-\delta ) = u_w(r=R-\delta )$ and
$u_a(r=R-\delta ) = u_w(r=R-\delta )$ and ![]() $\mu _a (\mathrm {d}u_a/\mathrm {d}r)_{R-\delta } = \mu _w (\mathrm {d}u_w/\mathrm {d}r)_{R-\delta }$ for the pipe. Here,
$\mu _a (\mathrm {d}u_a/\mathrm {d}r)_{R-\delta } = \mu _w (\mathrm {d}u_w/\mathrm {d}r)_{R-\delta }$ for the pipe. Here, ![]() $\mu _w$ and
$\mu _w$ and ![]() $\mu _a$ respectively denote the dynamic viscosities of water and air. In the material to follow, the above boundary conditions are combined with relevant governing equations to derive expressions for the velocity distribution and the average velocity of the water and air for the flow geometries depicted in figures 1–3.
$\mu _a$ respectively denote the dynamic viscosities of water and air. In the material to follow, the above boundary conditions are combined with relevant governing equations to derive expressions for the velocity distribution and the average velocity of the water and air for the flow geometries depicted in figures 1–3.

Figure 2. Schematic showing 2-D symmetric pressure-driven channel flow with air and water as the working fluids. (C.V. indicates control volume.)

Figure 3. Schematic showing 2-D axisymmetric pipe flow with air and water as the working fluids.
2.2.1. Equal pressure gradient ( $\dot {m}_a > 0$)
$\dot {m}_a > 0$)
The first problems of interest are ones where the pressure gradient forcing the flow of air matches the pressure gradient forcing the flow of water. In symbols, the pressure gradient of air is ![]() $-\partial P_a / \partial x\ (> 0)$, but for notational convenience, we will henceforth write this term as
$-\partial P_a / \partial x\ (> 0)$, but for notational convenience, we will henceforth write this term as ![]() $G_a$. Likewise, the pressure gradient of water is
$G_a$. Likewise, the pressure gradient of water is ![]() $-\partial P_w / \partial x$, but for notational convenience, we will henceforth write this term as
$-\partial P_w / \partial x$, but for notational convenience, we will henceforth write this term as ![]() $G_w$. In this equal pressure gradient scenario,
$G_w$. In this equal pressure gradient scenario, ![]() $G_a = G_w$ and
$G_a = G_w$ and ![]() $\dot {m}_a > 0$. Consistent with table 1, calculations are performed for two different geometries, namely rectilinear (corresponding to symmetric channel flow, CHSYM) and axisymmetric (corresponding to pipe flow, PIPE).
$\dot {m}_a > 0$. Consistent with table 1, calculations are performed for two different geometries, namely rectilinear (corresponding to symmetric channel flow, CHSYM) and axisymmetric (corresponding to pipe flow, PIPE).
We begin by considering symmetric pressure-driven channel flow (CHSYM1 and CHSYM3). A schematic of a two-dimensional (2-D) pressure-driven channel flow is shown in figure 2. The cargo fluid is water; however, a uniform layer of air appears along the top and bottom surfaces such that direct contact of the liquid with the solid boundary is avoided.
According to our assumptions, the simplified Navier–Stokes equation in rectilinear coordinates is given by
where the subscript ![]() $i$ may designate water (
$i$ may designate water (![]() $w$) or air (
$w$) or air (![]() $a$). Thus we find that
$a$). Thus we find that
and
where ![]() $c_1$,
$c_1$, ![]() $c_2$,
$c_2$, ![]() $c_3$ and
$c_3$ and ![]() $c_4$ are constants to be resolved by application of the aforementioned boundary conditions. Accordingly, it can be shown that
$c_4$ are constants to be resolved by application of the aforementioned boundary conditions. Accordingly, it can be shown that
and
where ![]() $\delta$ and
$\delta$ and ![]() $H$ are defined in figure 2. In the former equation,
$H$ are defined in figure 2. In the former equation, ![]() $d \equiv \delta /H$ and
$d \equiv \delta /H$ and ![]() $C_{\mu } \equiv \mu _{w}/\mu _{a}$. With
$C_{\mu } \equiv \mu _{w}/\mu _{a}$. With ![]() $u_w$ and
$u_w$ and ![]() $u_a$ to hand, it is straightforward to evaluate corresponding average velocities (
$u_a$ to hand, it is straightforward to evaluate corresponding average velocities (![]() $\bar {V}_w$ for water,
$\bar {V}_w$ for water, ![]() $\bar {V}_a$ for air):
$\bar {V}_a$ for air):
The analogue axisymmetric pipe flow (PIPE1 and PIPE3) is similar, so much so that the schematics of figures 2 and 3 are almost identical. In this spirit, a similar procedure may be applied for solving for the velocity distributions of water and air. In the interests of brevity, we omit derivational details and instead present the final solutions, which read as follows:
In the above equations, the parameter ![]() $d$ has been redefined as
$d$ has been redefined as ![]() $d \equiv \delta /R$.
$d \equiv \delta /R$.
2.2.2. Zero mass flow rate of air ( $\dot {m}_a = 0$)
$\dot {m}_a = 0$)
In contrast to the analysis of § 2.2.1, which assumed that the air and water layers were driven by the same pressure gradient, one may alternatively consider a case where the net mass flow rate of air, ![]() $\dot {m}_a$, vanishes. Such an assumption more closely mimics the trapped air bubbles that are affixed in place by the micro-structures of a superhydrophobic surface. Thus we find that the air layer exhibits an S-shaped velocity distribution where, close to the wall, the flow is directed opposite to that of the cargo fluid. Accordingly, the pressure gradient for the air layer is different from that of the water layer and must be calculated from the condition
$\dot {m}_a$, vanishes. Such an assumption more closely mimics the trapped air bubbles that are affixed in place by the micro-structures of a superhydrophobic surface. Thus we find that the air layer exhibits an S-shaped velocity distribution where, close to the wall, the flow is directed opposite to that of the cargo fluid. Accordingly, the pressure gradient for the air layer is different from that of the water layer and must be calculated from the condition ![]() $\dot {m}_a = 0$. All other assumptions remain the same as in § 2.2.1.
$\dot {m}_a = 0$. All other assumptions remain the same as in § 2.2.1.
By adopting the previous methodology to the CHSYM2 and CHSYM4 cases, it is straightforward to derive the following velocity distributions for the water and air layers, respectively:
 \begin{align} u_{w}(z) &= \frac{G_w H^2}{2\mu_{w}} \left [ 2C_{\mu}(d - d^2)+ (1-d)^2- \frac{z^2}{H^2} \right ] + \frac{G_a H^2 d^2}{2\mu_{a}},\nonumber\\ &\qquad {-H}+\delta \leq z \leq H-\delta , \end{align}
\begin{align} u_{w}(z) &= \frac{G_w H^2}{2\mu_{w}} \left [ 2C_{\mu}(d - d^2)+ (1-d)^2- \frac{z^2}{H^2} \right ] + \frac{G_a H^2 d^2}{2\mu_{a}},\nonumber\\ &\qquad {-H}+\delta \leq z \leq H-\delta , \end{align} \begin{align} u_{a}(z) &= \frac{H^2}{2\mu_{a}} \left( 1-\frac{z}{H}\right)\left [ 2G_w \left( 1-d \right) + G_a \left( 2d+\frac{z}{H} -1 \right) \right ],\nonumber\\ &\qquad \{-H \leq z \leq-H+\delta\} \cup \{H-\delta \leq z \leq H\}. \end{align}
\begin{align} u_{a}(z) &= \frac{H^2}{2\mu_{a}} \left( 1-\frac{z}{H}\right)\left [ 2G_w \left( 1-d \right) + G_a \left( 2d+\frac{z}{H} -1 \right) \right ],\nonumber\\ &\qquad \{-H \leq z \leq-H+\delta\} \cup \{H-\delta \leq z \leq H\}. \end{align}
Because ![]() $\dot {m}_a = 0$, the average velocity in the air layer is likewise zero, i.e.
$\dot {m}_a = 0$, the average velocity in the air layer is likewise zero, i.e.
By substituting (2.13) in the above integral, it can be shown that
Applying (2.15) in (2.12) and (2.13), these expressions for the velocity profiles can be correspondingly simplified, i.e.
 \begin{align} u_{a}(z) &= \frac{G_wH^2}{4d\mu_{a}} \left[(1 -d) \left(1-\frac{z}{H} \right) \left(3-2d-3\,\frac{z}{H}\right) \right ],\nonumber\\ &\qquad \{-H \leq z \leq-H+\delta\} \cup \{H-\delta \leq z \leq H\}. \end{align}
\begin{align} u_{a}(z) &= \frac{G_wH^2}{4d\mu_{a}} \left[(1 -d) \left(1-\frac{z}{H} \right) \left(3-2d-3\,\frac{z}{H}\right) \right ],\nonumber\\ &\qquad \{-H \leq z \leq-H+\delta\} \cup \{H-\delta \leq z \leq H\}. \end{align}
In turn, averaging (2.16) over the vertical distance ![]() $-H+\delta \leq z \leq H-\delta$ indicates that
$-H+\delta \leq z \leq H-\delta$ indicates that
As with the CHSYM2 case, we utilize the condition ![]() $\dot {m}_a = 0$ for axisymmetric pipe flow (PIPE2 and PIPE4) to solve for
$\dot {m}_a = 0$ for axisymmetric pipe flow (PIPE2 and PIPE4) to solve for ![]() $G_a$ in terms of
$G_a$ in terms of ![]() $G_w$. With this relationship to hand, simplified expressions for the velocity distributions in the water and air layers may be obtained. In particular,
$G_w$. With this relationship to hand, simplified expressions for the velocity distributions in the water and air layers may be obtained. In particular, ![]() $u_w$ is given by
$u_w$ is given by
 \begin{align} u_{w}(r)& = \frac{G_w R^2 }{4\mu_{a}} \left [ \frac{r^2}{R^2}-\sigma_1^2 -\frac{2C_{\mu } d \sigma_1^2 {(1+\sigma_1)} {[ \sigma_2+{(\sigma_1^2 +1)} \log \sigma_1]}}{\sigma_3}\right ],\nonumber\\ &\qquad 0 \leq r \leq R-\delta, \end{align}
\begin{align} u_{w}(r)& = \frac{G_w R^2 }{4\mu_{a}} \left [ \frac{r^2}{R^2}-\sigma_1^2 -\frac{2C_{\mu } d \sigma_1^2 {(1+\sigma_1)} {[ \sigma_2+{(\sigma_1^2 +1)} \log \sigma_1]}}{\sigma_3}\right ],\nonumber\\ &\qquad 0 \leq r \leq R-\delta, \end{align}where
Conversely, ![]() $u_a$ is given by
$u_a$ is given by
 \begin{align} u_{a}(r) & = \frac{G_w R^2 \sigma_1^2}{2\mu_{a}} \left\{ \frac{\left ( \dfrac{r^2}{R^2}-1 \right ) [ 2\sigma_1^2\log \sigma_1 + \sigma_2 ] + \sigma_2^2 \log \left(\dfrac{R}{r}\right) }{\sigma_3 }\right\} ,\nonumber\\ &\qquad R-\delta \leq r \leq R. \end{align}
\begin{align} u_{a}(r) & = \frac{G_w R^2 \sigma_1^2}{2\mu_{a}} \left\{ \frac{\left ( \dfrac{r^2}{R^2}-1 \right ) [ 2\sigma_1^2\log \sigma_1 + \sigma_2 ] + \sigma_2^2 \log \left(\dfrac{R}{r}\right) }{\sigma_3 }\right\} ,\nonumber\\ &\qquad R-\delta \leq r \leq R. \end{align}2.3. Thermal energy balance with USF
For either of the geometries considered in § 2.2, the heat fluxes associated with a (steady-state) thermal energy balance are as indicated schematically in figure 4. The control volume indicated in figure 4 is the same as that indicated by the red dashed lines in figures 2 and 3.
The rate of heat addition from the boundary is ![]() $\dot {q}_s A_s$, where
$\dot {q}_s A_s$, where ![]() $\dot {q}_s$ is surface heat flux, and
$\dot {q}_s$ is surface heat flux, and ![]() $A_s = p L$ represents the surface area. In this study, it is assumed that the perimeter of the control volume for rectilinear channel flow is
$A_s = p L$ represents the surface area. In this study, it is assumed that the perimeter of the control volume for rectilinear channel flow is ![]() $p = 1$, and for axisymmetric pipe flow is
$p = 1$, and for axisymmetric pipe flow is ![]() $p = 2{\rm \pi} R$. Also, the length of the control volume is
$p = 2{\rm \pi} R$. Also, the length of the control volume is ![]() $L = \mathrm {d}\kern 0.06em x$. For future reference, we note that the surface heat flux can be expressed via Newton's law of cooling as
$L = \mathrm {d}\kern 0.06em x$. For future reference, we note that the surface heat flux can be expressed via Newton's law of cooling as
where ![]() $T_{s}$ is the (
$T_{s}$ is the (![]() $x$-dependent) surface temperature, and
$x$-dependent) surface temperature, and ![]() $h_{s}$ is the (surface) convective heat transfer coefficient. Ultimately, we will show the variation of
$h_{s}$ is the (surface) convective heat transfer coefficient. Ultimately, we will show the variation of ![]() $h_s$, or its non-dimensional analogue, the Nusselt number, with the air layer thickness (among other variables).
$h_s$, or its non-dimensional analogue, the Nusselt number, with the air layer thickness (among other variables).
In figure 4, energy flows are represented generically as ![]() $\dot {E} = \dot {m} C_p T_m$, where
$\dot {E} = \dot {m} C_p T_m$, where ![]() $C_p$ is the specific heat capacity,
$C_p$ is the specific heat capacity, ![]() $T_m$ is the depth-integrated mean temperature (defined below), and the mass flow rate is
$T_m$ is the depth-integrated mean temperature (defined below), and the mass flow rate is ![]() $\dot {m} = \rho \bar {V} A_c$. Here,
$\dot {m} = \rho \bar {V} A_c$. Here, ![]() $\rho$ is the density, and
$\rho$ is the density, and ![]() $A_c$ is the cross-sectional area. (Note that the mass flow rate of air may be zero.) In figure 4, there is, by symmetry, no energy transfer along the bottom of the control volume. For the steady conditions of interest here, and considering the control volume as a whole, thermal energy inflows must balance thermal energy outflows. Alas, such a balance does not apply to the individual fluid layers because of the possibility of heat transfer along the air–water interface. We denote this interfacial heat flux by
$A_c$ is the cross-sectional area. (Note that the mass flow rate of air may be zero.) In figure 4, there is, by symmetry, no energy transfer along the bottom of the control volume. For the steady conditions of interest here, and considering the control volume as a whole, thermal energy inflows must balance thermal energy outflows. Alas, such a balance does not apply to the individual fluid layers because of the possibility of heat transfer along the air–water interface. We denote this interfacial heat flux by ![]() $\dot {q}_{in}$.
$\dot {q}_{in}$.
In the following subsubsections, the above thermal energy balance will be combined with heat transfer considerations for both the rectilinear and axisymmetric geometries. Calculations will be performed assuming an equal pressure gradient in the air and water, and also assuming zero air mass flow rate.
2.3.1. CHSYM1 and PIPE1
When the water and air flows are driven by an equal pressure gradient, ![]() $\dot {m}_a > 0$. Results pertinent to this case are listed below where we distinguish between the two fluid phases.
$\dot {m}_a > 0$. Results pertinent to this case are listed below where we distinguish between the two fluid phases.
Air layer. A balance of the thermal energy inflows and outflows for the air layer shows that
from which we conclude that
Adapting (2.22) yields
This last equality follows from the fact that ![]() $\dot {q}_s/h_s$ is constant by assumption. Also constant in the thermally fully developed region is, by definition, the following ratio of temperature differences:
$\dot {q}_s/h_s$ is constant by assumption. Also constant in the thermally fully developed region is, by definition, the following ratio of temperature differences: ![]() $(T_{s}-T_{a})/(T_{s}-T_{m_{a}})$. Symbolically, we write
$(T_{s}-T_{a})/(T_{s}-T_{m_{a}})$. Symbolically, we write
demonstrating that the streamwise temperature gradient is the same whether measured along the solid surface or at any depth through the air layer. From (2.24), (2.25) and (2.26b), we therefore conclude that
Water layer. In similar fashion to the air layer, the thermal energy balance for the water layer can be written as
implying that
Analogous to (2.27), it can be shown that
in which ![]() $T_{in}$ is the temperature measured along the air–water interface. Whereas this last result establishes the equality of the streamwise temperature gradients
$T_{in}$ is the temperature measured along the air–water interface. Whereas this last result establishes the equality of the streamwise temperature gradients ![]() $\partial T_{in}/\partial x$ and
$\partial T_{in}/\partial x$ and ![]() $\partial T_w/\partial x$, it must also be true that
$\partial T_w/\partial x$, it must also be true that ![]() $\partial T_{in}/\partial x = \partial T_a/\partial x$. Therefore, and by combining (2.27) and (2.30),
$\partial T_{in}/\partial x = \partial T_a/\partial x$. Therefore, and by combining (2.27) and (2.30),
Solving this last result for the interfacial heat flux indicates that
Finally, substitution of (2.32) into (2.27) and (2.30) gives
which shows that, relative to the streamwise coordinate ![]() $x$, the air and water temperatures change in an identical manner.
$x$, the air and water temperatures change in an identical manner.
2.3.2. CHSYM2 and PIPE2
As noted in § 2.2, the mass flow rate for air vanishes (![]() $\dot {m}_a=0$) for the cases labelled as CHSYM2 and PIPE2. This fact simplifies the process of balancing thermal energy inflows and outflows: we find that
$\dot {m}_a=0$) for the cases labelled as CHSYM2 and PIPE2. This fact simplifies the process of balancing thermal energy inflows and outflows: we find that
Furthermore, the streamwise temperature distribution in the air and water layers can be recovered from the derivatives
Unfortunately, (2.35) is incomplete (and likewise for the analogue expression 2.33): although the streamwise variation of e.g. ![]() $T_a$ or
$T_a$ or ![]() $T_w$ is well-characterized, we have no information concerning temperature variations in the cross-stream direction. In order to infer such information, we turn from the thermal energy balances of the present subsection to the energy equation of §§ 2.4 and 2.5. Consistent with figure 4, the former subsection considers USF; meanwhile, the latter subsection considers a case omitted in the current subsection, namely UST.
$T_w$ is well-characterized, we have no information concerning temperature variations in the cross-stream direction. In order to infer such information, we turn from the thermal energy balances of the present subsection to the energy equation of §§ 2.4 and 2.5. Consistent with figure 4, the former subsection considers USF; meanwhile, the latter subsection considers a case omitted in the current subsection, namely UST.
2.4. Energy equation (USF)
2.4.1. CHSYM1
Complementing (2.1), we write the (steady) thermal energy equations as
for the air and water phases, respectively. Thermal diffusivities are defined as ![]() $\alpha _i={k_i}/({\rho _i C_{p_i}})$, in which
$\alpha _i={k_i}/({\rho _i C_{p_i}})$, in which ![]() $k$ is the fluid thermal conductivity,
$k$ is the fluid thermal conductivity, ![]() $\rho$ is the fluid density, and
$\rho$ is the fluid density, and ![]() $i$ stands for
$i$ stands for ![]() $a$ or
$a$ or ![]() $w$. Boundary conditions corresponding to (2.36) are as follows: (i)
$w$. Boundary conditions corresponding to (2.36) are as follows: (i) ![]() $(\partial T_{w} / \partial z)_{z = 0} = 0$, which enforces symmetry across the channel centreline; (ii)
$(\partial T_{w} / \partial z)_{z = 0} = 0$, which enforces symmetry across the channel centreline; (ii) ![]() $T_w(z=H-\delta ) = T_a(z=H-\delta )$, which enforces temperature equality at the air–water interface; (iii)
$T_w(z=H-\delta ) = T_a(z=H-\delta )$, which enforces temperature equality at the air–water interface; (iii) ![]() $-k_{a} (\partial T_{a}/\partial z)_{z = H-\delta } = -k_w (\partial T_{w}/\partial z)_{z = H - \delta }$, which enforces continuity of conductive heat flux across the air–water interface; and (iv)
$-k_{a} (\partial T_{a}/\partial z)_{z = H-\delta } = -k_w (\partial T_{w}/\partial z)_{z = H - \delta }$, which enforces continuity of conductive heat flux across the air–water interface; and (iv) ![]() $T_{a}(z = H)=T_{s}$, which enforces temperature equality at the wall. As regards the latter boundary condition, recall that USF thermal forcing demands that
$T_{a}(z = H)=T_{s}$, which enforces temperature equality at the wall. As regards the latter boundary condition, recall that USF thermal forcing demands that ![]() $T_s = T_s(x)$. Thus the functional dependence of
$T_s = T_s(x)$. Thus the functional dependence of ![]() $T_s$ remains to be determined from
$T_s$ remains to be determined from ![]() $\dot {q}_s$; calculation details are given below.
$\dot {q}_s$; calculation details are given below.
The boundary conditions given in the previous paragraph are used to resolve the constants of integration that result from integrating (2.36) in ![]() $z$. Of course, before such integrations can be performed, it is first necessary to substitute into (2.36) the previously derived expressions for
$z$. Of course, before such integrations can be performed, it is first necessary to substitute into (2.36) the previously derived expressions for ![]() $u_w$ in (2.4),
$u_w$ in (2.4), ![]() $u_a$ in (2.5) and
$u_a$ in (2.5) and ![]() $\partial T_a/\partial x = \partial T_w/\partial x$ in (2.33), which in turn requires application of
$\partial T_a/\partial x = \partial T_w/\partial x$ in (2.33), which in turn requires application of ![]() $\dot {m}_{w}=\rho _{w} \bar {V}_w (H-\delta )$ and
$\dot {m}_{w}=\rho _{w} \bar {V}_w (H-\delta )$ and ![]() $\dot {m}_{a}=\rho _{a} \bar {V}_a \delta$. By applying the substitutions and boundary conditions in question, it can ultimately be shown that
$\dot {m}_{a}=\rho _{a} \bar {V}_a \delta$. By applying the substitutions and boundary conditions in question, it can ultimately be shown that
where
and
In similar fashion,
where
and
In interpreting (2.37) and (2.40), note that ![]() $T_a$ and
$T_a$ and ![]() $T_w$ inherit a dependence on
$T_w$ inherit a dependence on ![]() $x$ from the surface temperature
$x$ from the surface temperature ![]() $T_s$.
$T_s$.
From (2.37) and (2.40), it is useful to evaluate the mean temperatures of air (![]() ${T_m}_a$) and water (
${T_m}_a$) and water (![]() ${T_m}_w$), respectively. Although the mean temperature is independent of
${T_m}_w$), respectively. Although the mean temperature is independent of ![]() $z$ by construction,
$z$ by construction, ![]() ${T_m}_a$ and
${T_m}_a$ and ![]() ${T_m}_w$ must obviously vary with
${T_m}_w$ must obviously vary with ![]() $x$. With reference to the thermal energy equation of either air or water, mean temperatures can be calculated from
$x$. With reference to the thermal energy equation of either air or water, mean temperatures can be calculated from
 \begin{equation} T_{m} = \frac{\displaystyle\rho C_{p_i} \int_{z_1}^{z_2}T_i(z)\,u_i(z)\,\mathrm{d}z}{\rho \bar{V} C_{p_i} (z_2 - z_1)}=\frac{1}{\bar{V}(z_2 - z_1)} \int_{z_1}^{z_2}T_i(z)\,u_i(z)\,\mathrm{d}z, \end{equation}
\begin{equation} T_{m} = \frac{\displaystyle\rho C_{p_i} \int_{z_1}^{z_2}T_i(z)\,u_i(z)\,\mathrm{d}z}{\rho \bar{V} C_{p_i} (z_2 - z_1)}=\frac{1}{\bar{V}(z_2 - z_1)} \int_{z_1}^{z_2}T_i(z)\,u_i(z)\,\mathrm{d}z, \end{equation}
where ![]() $z_2 - z_1$ indicates the thickness of the layer in question. On the basis of (2.44), we conclude that
$z_2 - z_1$ indicates the thickness of the layer in question. On the basis of (2.44), we conclude that
and therefore
 \begin{equation} {T_m}_a= \frac{C_{\mu} C_{{p}_a} d^2 \rho_a \left[T_{s} k_a (3-d)^2 -H d q_s \left(\dfrac{9d^2 }{14}-\dfrac{7d}{2}+\dfrac{24}{5}\right)\right]+\dfrac{1}{4}(C_{{p}_w} \rho_w \beta_{1} \beta_{6})}{k_a (3-d) [C_{{p}_w} \rho_w (1-d) \beta_{1} + C_{\mu} C_{{p}_a} d^2 \rho_a (3-d) ]}. \end{equation}
\begin{equation} {T_m}_a= \frac{C_{\mu} C_{{p}_a} d^2 \rho_a \left[T_{s} k_a (3-d)^2 -H d q_s \left(\dfrac{9d^2 }{14}-\dfrac{7d}{2}+\dfrac{24}{5}\right)\right]+\dfrac{1}{4}(C_{{p}_w} \rho_w \beta_{1} \beta_{6})}{k_a (3-d) [C_{{p}_w} \rho_w (1-d) \beta_{1} + C_{\mu} C_{{p}_a} d^2 \rho_a (3-d) ]}. \end{equation}Here,
Similarly,
therefore
 \begin{align} {T_m}_w & = \frac{1}{\beta_{7}} \left\{ \left [ C_{{p}_w} \rho_w \left ( \frac{H \dot{q}_{s}(1-d)^2 \beta_{8}}{35 k_w \beta_{1}}- T_{s} (1-d) \beta_{1} \right ) \right ] -[ T_{s} C_{\mu} C_{{p}_a} d^2 \rho_a (3-d) ] \right.\nonumber\\ &\quad \left. {}+ \left [ \frac{H d \dot{q}_{s}}{4 k_a}\,( 4 C_{{p}_w}\rho_w \beta_{1} + C_{\mu} C_{{p}_a} \rho_a d^2 (8-3d) ) \right ]\right\}\!. \end{align}
\begin{align} {T_m}_w & = \frac{1}{\beta_{7}} \left\{ \left [ C_{{p}_w} \rho_w \left ( \frac{H \dot{q}_{s}(1-d)^2 \beta_{8}}{35 k_w \beta_{1}}- T_{s} (1-d) \beta_{1} \right ) \right ] -[ T_{s} C_{\mu} C_{{p}_a} d^2 \rho_a (3-d) ] \right.\nonumber\\ &\quad \left. {}+ \left [ \frac{H d \dot{q}_{s}}{4 k_a}\,( 4 C_{{p}_w}\rho_w \beta_{1} + C_{\mu} C_{{p}_a} \rho_a d^2 (8-3d) ) \right ]\right\}\!. \end{align}Here,
and
Equation (2.33) provides a second means of evaluating the mean water temperature, i.e.
where ![]() ${T_m}_{w0}$ is the upstream water temperature as measured at
${T_m}_{w0}$ is the upstream water temperature as measured at ![]() $x = 0$, the critical distance at which the flow becomes hydrodynamically and thermally fully developed.
$x = 0$, the critical distance at which the flow becomes hydrodynamically and thermally fully developed.
Because calculating the surface temperature as a function of ![]() $x$ is a prerequisite for estimating the temperature profile of either phase, the next step of the derivation consists of equating (2.48) and (2.52) then solving for
$x$ is a prerequisite for estimating the temperature profile of either phase, the next step of the derivation consists of equating (2.48) and (2.52) then solving for ![]() $T_s$ for a prescribed value of
$T_s$ for a prescribed value of ![]() ${T_m}_{w0}$. On this basis, and after considerable algebra, we find that
${T_m}_{w0}$. On this basis, and after considerable algebra, we find that
 \begin{align} &T_{s} = {T_m}_{w0} - \mu_w \dot{q}_{s} H \left\{ \left [\frac{6x}{H^{4}G_w \beta_{7}} \right ] + \left [ \frac{C_{{p}_w}\rho_w \beta_{8} (1-d)^2 }{35 k_w \mu_w \beta_{1} \beta_{7} } \right ] \right.\nonumber\\ &\quad +\left. \left [ \frac{C_{{p}_w}\rho_w d \{(2-2d)^3+12 C_\mu(1-d)[ 1-(1-d)^2 ]\} + C_{\mu} C_{{p}_a} \rho_a d^3 (8-3d) } {4k_a \mu_w \beta_{7}} \right ] \right\} . \end{align}
\begin{align} &T_{s} = {T_m}_{w0} - \mu_w \dot{q}_{s} H \left\{ \left [\frac{6x}{H^{4}G_w \beta_{7}} \right ] + \left [ \frac{C_{{p}_w}\rho_w \beta_{8} (1-d)^2 }{35 k_w \mu_w \beta_{1} \beta_{7} } \right ] \right.\nonumber\\ &\quad +\left. \left [ \frac{C_{{p}_w}\rho_w d \{(2-2d)^3+12 C_\mu(1-d)[ 1-(1-d)^2 ]\} + C_{\mu} C_{{p}_a} \rho_a d^3 (8-3d) } {4k_a \mu_w \beta_{7}} \right ] \right\} . \end{align} With ![]() $T_s$ and
$T_s$ and ![]() ${T_m}_w$ to hand, determination of the temperature difference
${T_m}_w$ to hand, determination of the temperature difference ![]() $T_s - {T_m}_w$ is now straightforward. Such a calculation is necessary for the evaluation of the (surface) convective heat transfer coefficient. By (2.22),
$T_s - {T_m}_w$ is now straightforward. Such a calculation is necessary for the evaluation of the (surface) convective heat transfer coefficient. By (2.22), ![]() $h_s$ is given by
$h_s$ is given by
(Note that ![]() $h_s$ is independent of
$h_s$ is independent of ![]() $x$.) In turn, and from
$x$.) In turn, and from ![]() $h_s$, we can make a theoretical estimate of the Nusselt number
$h_s$, we can make a theoretical estimate of the Nusselt number ![]() $Nu$, which is defined as the ratio of the convective to the conductive heat transfer across a boundary. Restricting attention to the water layer, we consider
$Nu$, which is defined as the ratio of the convective to the conductive heat transfer across a boundary. Restricting attention to the water layer, we consider ![]() $Nu_w$, which is expressed as
$Nu_w$, which is expressed as
The former factor of 2 from the numerator is included because heat is supposed to be added by both of the lower and upper solid surfaces. The latter factor of 2 is included because the total water depth measures ![]() $2(H - \delta )$ – cf. figure 2.
$2(H - \delta )$ – cf. figure 2.
2.4.2. PIPE1
Changing the flow geometry from rectilinear to axisymmetric modifies (slightly) the form of the equations to be solved but does not alter the overall solution methodology. For this reason, we provide only a concise summary below.
The reduced form of the thermal energy equation associated with the flow of figure 3 reads
where ![]() $x$ and
$x$ and ![]() $r$ represent the axial and radial directions, respectively. Therefore, heat transfers in the water and air phases are respectively governed by the equations
$r$ represent the axial and radial directions, respectively. Therefore, heat transfers in the water and air phases are respectively governed by the equations
These equations are solved by integrating in ![]() $r$, where the right-hand-side axial temperature gradients are given by (2.33), and the velocities
$r$, where the right-hand-side axial temperature gradients are given by (2.33), and the velocities ![]() $u_w$ and
$u_w$ and ![]() $u_a$ are given by (2.8) and (2.9), respectively. Boundary conditions are the same as those of § 2.4.1 (see the discussion following (2.36)) but with
$u_a$ are given by (2.8) and (2.9), respectively. Boundary conditions are the same as those of § 2.4.1 (see the discussion following (2.36)) but with ![]() $r$ replacing
$r$ replacing ![]() $z$, and
$z$, and ![]() $R$ replacing
$R$ replacing ![]() $H$. From the so-determined solutions for
$H$. From the so-determined solutions for ![]() $T_w$ and
$T_w$ and ![]() $T_a$, depth-integrated mean temperatures can be evaluated. Thereafter, we calculate, in order,
$T_a$, depth-integrated mean temperatures can be evaluated. Thereafter, we calculate, in order, ![]() $T_s$,
$T_s$, ![]() $T_s - {T_m}_w$,
$T_s - {T_m}_w$, ![]() $h_s$ and
$h_s$ and ![]() $Nu_w$. Details are omitted in the interests of brevity.
$Nu_w$. Details are omitted in the interests of brevity.
2.4.3. CHSYM2 and PIPE2
Similar to the discussion from the start of § 2.4.2, the theoretical analyses corresponding to the zero air mass flow rate cases CHSYM2 and PIPE2 are comparable to those outlined in the last two subsubsections. More specifically, we employ the same thermal energy equations and also the same boundary conditions. Now, however, axial temperature gradients are given by (2.35) rather than (2.33). Likewise, we consider as the analytical solution for ![]() $u_w$ either (2.16) or (2.19), and as the analytical solution for
$u_w$ either (2.16) or (2.19), and as the analytical solution for ![]() $u_a$ either (2.17) or (2.21). By combining the relevant equations, our goal is to again solve for the surface temperature
$u_a$ either (2.17) or (2.21). By combining the relevant equations, our goal is to again solve for the surface temperature ![]() $T_s$ in terms of
$T_s$ in terms of ![]() $x$ so that theoretical estimates may be made for
$x$ so that theoretical estimates may be made for ![]() $T_s - {T_m}_w$,
$T_s - {T_m}_w$, ![]() $h_s$ and ultimately
$h_s$ and ultimately ![]() $Nu_w$. Corresponding details are again omitted owing to the complexity of the resulting equations.
$Nu_w$. Corresponding details are again omitted owing to the complexity of the resulting equations.
2.5. Energy equation (UST)
In the formulation where the surface temperature is uniform and therefore not a function of the downstream coordinate, quantities such as ![]() $\partial T_w/\partial x$ and
$\partial T_w/\partial x$ and ![]() $\partial T_a/\partial x$ are no longer constant. To confirm this statement, we adopt the generic expression for the surface heat flux under UST conditions, i.e.
$\partial T_a/\partial x$ are no longer constant. To confirm this statement, we adopt the generic expression for the surface heat flux under UST conditions, i.e.
(Çengel & Ghajar Reference Çengel and Ghajar2021). Recall, however, that
Accordingly,
The implications of this last inequality can be understood with respect to the thermal energy equation as expressed for either phase in rectilinear coordinates, i.e.
If the right-hand-side derivative depends on ![]() $x$, then one must either (i) impose a temperature decay rate in the axial direction (see e.g. equation 5 of Sparrow, Baliga & Patankar Reference Sparrow, Baliga and Patankar1978), or (ii) solve a partial differential equation rather than the ordinary differential equations considered until this point. Given the added complications of deriving analytical solutions for
$x$, then one must either (i) impose a temperature decay rate in the axial direction (see e.g. equation 5 of Sparrow, Baliga & Patankar Reference Sparrow, Baliga and Patankar1978), or (ii) solve a partial differential equation rather than the ordinary differential equations considered until this point. Given the added complications of deriving analytical solutions for ![]() $T_w$ and
$T_w$ and ![]() $T_a$, we instead seek a numerical solution. Because
$T_a$, we instead seek a numerical solution. Because ![]() $u(z)$ is decoupled from
$u(z)$ is decoupled from ![]() $T(x,z)$, the simplest approach is to solve (2.61) subject to appropriate boundary/matching conditions on
$T(x,z)$, the simplest approach is to solve (2.61) subject to appropriate boundary/matching conditions on ![]() $T_w$ and
$T_w$ and ![]() $T_a$. On the other hand, we wish to run computational fluid dynamics (CFD) simulations so as to validate USF solutions such as those detailed in § 2.4.1. With this being the case, it needs relatively little additional effort to resolve CHSYM3, PIPE3, CHSYM4 and PIPE4 using the same CFD algorithm, and this is the approach that we prefer to follow here. Before showing the numerical solutions in question, however, it is first necessary to describe the numerical methodology. This is the topic of the next section.
$T_a$. On the other hand, we wish to run computational fluid dynamics (CFD) simulations so as to validate USF solutions such as those detailed in § 2.4.1. With this being the case, it needs relatively little additional effort to resolve CHSYM3, PIPE3, CHSYM4 and PIPE4 using the same CFD algorithm, and this is the approach that we prefer to follow here. Before showing the numerical solutions in question, however, it is first necessary to describe the numerical methodology. This is the topic of the next section.
3. Numerical simulations
Steady, incompressible, laminar CFD simulations are performed using the commercial software platform COMSOL. Our objectives are twofold: (i) to validate the accuracy of the analytical solutions presented and discussed in § 2; and (ii) to derive novel results for the UST cases, where no analytical solution is available. As regards (ii), not only do we consider the perfect plastron cases summarized in table 1, we also examine select superhydrophobic surfaces containing transverse micro-ridges. This latter category of numerical simulations, described in § 3.3, is meant to shed light on the connection between the solutions of § 2 and real microfluidic devices, e.g. from lab-on-a-chip devices.
3.1. Numerical set-up (flat superhydrophobic surface)
Figure 5 demonstrates the 2-D computational domain and boundary conditions used for simulations of type CHSYM and PIPE. So as to characterize the thermal insulation efficacy of the air layer, we vary the thickness ![]() $\delta$ of this layer. Moreover, to avoid a tangential discussion of shear-driven flow instabilities or a capillary-induced deflection of the air–water interface, we model this interface as a horizontal dividing line. Along the upper surface, we apply either a uniform heat flux or a uniform temperature boundary condition corresponding, respectively, to the states described in § 2 as USF and UST. When we model the upper boundary as USF, we consider a value for the surface heat flux of
$\delta$ of this layer. Moreover, to avoid a tangential discussion of shear-driven flow instabilities or a capillary-induced deflection of the air–water interface, we model this interface as a horizontal dividing line. Along the upper surface, we apply either a uniform heat flux or a uniform temperature boundary condition corresponding, respectively, to the states described in § 2 as USF and UST. When we model the upper boundary as USF, we consider a value for the surface heat flux of ![]() $\dot {q}_{s}= 10$ W m
$\dot {q}_{s}= 10$ W m![]() $^{-1}$. Meanwhile,
$^{-1}$. Meanwhile, ![]() $T_{s} = 330$ K when we model the upper boundary as UST. Moreover, we consider a horizontal/axial pressure gradient
$T_{s} = 330$ K when we model the upper boundary as UST. Moreover, we consider a horizontal/axial pressure gradient ![]() $-\partial p/\partial x = 6.4\times 10^{-6}$ Pa m
$-\partial p/\partial x = 6.4\times 10^{-6}$ Pa m![]() $^{-1}$, which is sufficiently small to avoid a transition to turbulent flow. For instance, and for CHSYM1 and CHSYM3, we estimate that the Reynolds numbers vary between approximately 30 and
$^{-1}$, which is sufficiently small to avoid a transition to turbulent flow. For instance, and for CHSYM1 and CHSYM3, we estimate that the Reynolds numbers vary between approximately 30 and ![]() $1.2 \times 10^3$, depending on the value for
$1.2 \times 10^3$, depending on the value for ![]() $d$. Corresponding ranges for CHSYM2/CHSYM4, PIPE1/PIPE3 and PIPE2/PIPE4 are
$d$. Corresponding ranges for CHSYM2/CHSYM4, PIPE1/PIPE3 and PIPE2/PIPE4 are ![]() $1 \lesssim Re \lesssim 2.4 \times 10^2$,
$1 \lesssim Re \lesssim 2.4 \times 10^2$, ![]() $15 \lesssim Re \lesssim 6.0 \times 10^2$ and
$15 \lesssim Re \lesssim 6.0 \times 10^2$ and ![]() $1 \lesssim Re \lesssim 1.2 \times 10^2$.
$1 \lesssim Re \lesssim 1.2 \times 10^2$.

Figure 5. Schematic of the 2-D numerical domain corresponding to a rectilinear channel or an axisymmetric pipe.
Average inlet and outlet pressures are specified such that (i) the same pressure gradient applies through both phases when ![]() $\dot {m}_a > 0$, or (ii) conditions within the air layer are adjusted such that the average velocity vanishes when
$\dot {m}_a > 0$, or (ii) conditions within the air layer are adjusted such that the average velocity vanishes when ![]() $\dot {m}_a = 0$. Furthermore, the inlet water and air temperatures are set at
$\dot {m}_a = 0$. Furthermore, the inlet water and air temperatures are set at ![]() $300$ K. We solve a Graetz-type problem where, with the benefit of the solutions for
$300$ K. We solve a Graetz-type problem where, with the benefit of the solutions for ![]() $u_a$ and
$u_a$ and ![]() $u_w$ given in § 2.2, the flow is hydrodynamically fully developed for all
$u_w$ given in § 2.2, the flow is hydrodynamically fully developed for all ![]() $x$. By contrast, realizing a thermally fully developed state requires long horizontal/axial distances, where the precise thermal entry length depends on
$x$. By contrast, realizing a thermally fully developed state requires long horizontal/axial distances, where the precise thermal entry length depends on ![]() $d$ and the nature of the thermal forcing, e.g. USF versus UST. For consistency's sake, the length of the numerical domain is set to
$d$ and the nature of the thermal forcing, e.g. USF versus UST. For consistency's sake, the length of the numerical domain is set to ![]() $L/H = L/R = 1000$, where the channel height (pipe radius) is set to
$L/H = L/R = 1000$, where the channel height (pipe radius) is set to ![]() $H=0.2$ m (
$H=0.2$ m (![]() $R=0.2$ m). Finally, and for simplicity, we assume constant thermophysical properties for water and air, the values of density, viscosity, and so on, being only modestly influenced by temperature over the range of temperatures germane to our simulations.
$R=0.2$ m). Finally, and for simplicity, we assume constant thermophysical properties for water and air, the values of density, viscosity, and so on, being only modestly influenced by temperature over the range of temperatures germane to our simulations.
Numerical simulations are performed using a non-uniform structured grid that is generated with local refinement in the vicinity of the wall and the air–water interface – see figure 6. The maximum size of the grid elements is ![]() $0.03$ m, with expansion ratio
$0.03$ m, with expansion ratio ![]() $1.01$.
$1.01$.

Figure 6. Section of the grid used for numerical simulations of type CHSYM and PIPE. Here, we consider ![]() $d=0.2$ though our numerical simulations span a large range of
$d=0.2$ though our numerical simulations span a large range of ![]() $d$ values as documented in figures 12 and 13 below.
$d$ values as documented in figures 12 and 13 below.
3.2. Grid independence
Grid independence tests were carried out by considering six different mesh sizes for various ![]() $d$. Representative results, which consider both the rectilinear and the axisymmetric geometries, and
$d$. Representative results, which consider both the rectilinear and the axisymmetric geometries, and ![]() $d=0.2$, are summarized in figure 7. We consider as the metric the horizontal (axial) temperature gradient as measured along the interface at downstream distance 995
$d=0.2$, are summarized in figure 7. We consider as the metric the horizontal (axial) temperature gradient as measured along the interface at downstream distance 995![]() $H$ (995
$H$ (995![]() $R$), by which point the flow is thermally fully developed. Figure 7 demonstrates that the largest divergence between the meshes labelled 4, 5 and 6 is less than 1 %. We conclude, therefore, that mesh 5 has sufficient resolution to capture the flow characteristics, all the while avoiding unreasonably long run times. Similar conclusions apply for other values of
$R$), by which point the flow is thermally fully developed. Figure 7 demonstrates that the largest divergence between the meshes labelled 4, 5 and 6 is less than 1 %. We conclude, therefore, that mesh 5 has sufficient resolution to capture the flow characteristics, all the while avoiding unreasonably long run times. Similar conclusions apply for other values of ![]() $d$, so we do not show the data in question.
$d$, so we do not show the data in question.

Figure 7. Mesh independence analysis: (a) rectilinear channel, and (b) axisymmetric pipe.
3.3. Numerical set-up (textured superhydrophobic surface)
Further to the smooth-solid surface numerical simulations described in the last two subsections, we additionally conducted a limited set of (2-D) channel flow simulations employing the domain illustrated in figures 8 and 9. Similar to Maynes, Webb & Davies (Reference Maynes, Webb and Davies2008), these are of the UST variety and include transverse ridges that span the channel breadth. Ridges are assumed to be made of PDMS such that the thermal conductivity ratio ![]() $k_{ridge}/k_a$ is approximately 6.274. As illustrated in figure 8, the ridge width measures
$k_{ridge}/k_a$ is approximately 6.274. As illustrated in figure 8, the ridge width measures ![]() $w$, and the centre-to-centre ridge spacing measures
$w$, and the centre-to-centre ridge spacing measures ![]() $\lambda$. Meanwhile, the ridge height matches the depth of the air pockets that are entrapped between adjacent ridges. Air pockets are assumed to be of uniform depth, i.e. we ignore the impact of meniscus curvature; cf. Game et al. (Reference Game, Hodes, Keaveny and Papageorgiou2017, Reference Game, Hodes, Kirk and Papageorgiou2018) and Tomlinson et al. (Reference Tomlinson, Mayer, Kirk, Hodes and Papageorgiou2024). Because air pockets are isolated one from the other, this new category of numerical simulations most closely resembles flow/thermal forcing regime CHSYM4 from table 1. To this end, and relative to the numerical simulations of § 3.1, we consider the same surface temperature, inlet/outlet boundary conditions and Reynolds number range, where, in the latter case, the value of
$\lambda$. Meanwhile, the ridge height matches the depth of the air pockets that are entrapped between adjacent ridges. Air pockets are assumed to be of uniform depth, i.e. we ignore the impact of meniscus curvature; cf. Game et al. (Reference Game, Hodes, Keaveny and Papageorgiou2017, Reference Game, Hodes, Kirk and Papageorgiou2018) and Tomlinson et al. (Reference Tomlinson, Mayer, Kirk, Hodes and Papageorgiou2024). Because air pockets are isolated one from the other, this new category of numerical simulations most closely resembles flow/thermal forcing regime CHSYM4 from table 1. To this end, and relative to the numerical simulations of § 3.1, we consider the same surface temperature, inlet/outlet boundary conditions and Reynolds number range, where, in the latter case, the value of ![]() $-\partial p/\partial x$ is adjusted accordingly. Importantly, however, the free-slip hydrodynamic boundary condition that we apply in studying flows relevant to figures 2 and 5 is now replaced with a mixed free-slip/no-slip boundary condition.
$-\partial p/\partial x$ is adjusted accordingly. Importantly, however, the free-slip hydrodynamic boundary condition that we apply in studying flows relevant to figures 2 and 5 is now replaced with a mixed free-slip/no-slip boundary condition.

Figure 8. Schematic of the 2-D numerical domain corresponding to a rectilinear channel containing transverse ridges.

Figure 9. Section of the grid used for numerical simulations of type CHSYM4, where the channel contains transverse ridges. Here, we consider ![]() $d = 0.2$ though our numerical simulations span a large range of
$d = 0.2$ though our numerical simulations span a large range of ![]() $d$ values as documented in figure 17 below.
$d$ values as documented in figure 17 below.
Another important difference compared with the earlier numerical simulations concerns the channel length. Just as we aspire to model more faithfully a real superhydrophobic surface by adding transverse ridges, so too is it necessary to limit the channel dimensions to values that are more typical of lab-on-a-chip devices. Thus we conduct two different studies. In the first, we fix ![]() $H = 0.2$ mm and
$H = 0.2$ mm and ![]() $L/H = 180$, then examine the impact of changing
$L/H = 180$, then examine the impact of changing ![]() $d$ and
$d$ and ![]() $w/\lambda$. In the second, we specifically model the influence of
$w/\lambda$. In the second, we specifically model the influence of ![]() $L$ by running numerical simulations in the range
$L$ by running numerical simulations in the range ![]() $30 \leq L/H \leq 1440$.
$30 \leq L/H \leq 1440$.
Owing to the aforementioned change of hydrodynamic boundary condition, a finer mesh is required, as evidenced by a visual comparison of figures 6 and 9. This change notwithstanding, a grid independency test was performed and results qualitatively similar to those exhibited in figure 7 were obtained. In § 6, we present numerical results derived from meshes containing approximately ![]() $1.6\times 10^{6}$ elements.
$1.6\times 10^{6}$ elements.
4. Validation of the theoretical solutions
Before presenting our results in the next section, it is first necessary to confirm the accuracy of the theoretical solutions. We do so by comparison with the numerical output. This comparison begins with an assessment of the vertical flow profiles and the velocities ![]() $u_w$ and
$u_w$ and ![]() $u_a$. Figures 10(a,b) show the non-dimensional velocity profiles associated with
$u_a$. Figures 10(a,b) show the non-dimensional velocity profiles associated with ![]() $\dot {m}_a > 0$ (CHSYM1/PIPE1) and
$\dot {m}_a > 0$ (CHSYM1/PIPE1) and ![]() $\dot {m}_a = 0$ (CHSYM2/PIPE2). The former figure corresponds to the rectilinear geometry, whereas the latter corresponds to the asymmetric geometry. Reassuringly, we observe very little difference between the theoretical predictions (indicated by the blue and black curves) as compared to their numerical counterparts (red and green curves). A separate analysis (not shown) confirms that our theoretical and numerical results likewise match the predictions made in the isothermal study of Busse et al. (Reference Busse, Sandham, McHale and Newton2013).
$\dot {m}_a = 0$ (CHSYM2/PIPE2). The former figure corresponds to the rectilinear geometry, whereas the latter corresponds to the asymmetric geometry. Reassuringly, we observe very little difference between the theoretical predictions (indicated by the blue and black curves) as compared to their numerical counterparts (red and green curves). A separate analysis (not shown) confirms that our theoretical and numerical results likewise match the predictions made in the isothermal study of Busse et al. (Reference Busse, Sandham, McHale and Newton2013).

Figure 10. Velocity profiles measured for (a) a rectilinear channel, and (b) an axisymmetric pipe. Here, ![]() $u_{0}$ is defined as the inlet velocity, and in both cases,
$u_{0}$ is defined as the inlet velocity, and in both cases, ![]() $d=0.2$.
$d=0.2$.
Expanding on the comparisons drawn in figure 10, figures 11(a,b) show the USF-derived temperature profiles for the CHSYM and PIPE cases. Temperature profiles are here specified with respect to ![]() $T_s$,
$T_s$, ![]() $T_i$ (defined as the inlet temperature for either fluid phase) and
$T_i$ (defined as the inlet temperature for either fluid phase) and ![]() $T_0$, defined as the temperature measured at a fixed location far downstream and along the plane or axis of symmetry, i.e.
$T_0$, defined as the temperature measured at a fixed location far downstream and along the plane or axis of symmetry, i.e. ![]() $z=0$ or
$z=0$ or ![]() $r=0$. In figure 11, theoretical data are shown with the black and blue curves, and numerical data are shown with the red and green curves; as with figure 10, excellent agreement is observed between the corresponding pairs of data sets.
$r=0$. In figure 11, theoretical data are shown with the black and blue curves, and numerical data are shown with the red and green curves; as with figure 10, excellent agreement is observed between the corresponding pairs of data sets.

Figure 11. As in figure 10, but considering the non-dimensional temperature profile rather than the non-dimensional velocity profile.
5. Results
5.1. Variation of water temperature with air layer thickness
A major objective of this study is to estimate the degree to which a surface-attached air layer can serve as a thermal insulator. To this end, it is helpful to categorize the percentage reduction of the cargo fluid (i.e. water) temperature as compared to a case where no air film exists such that the water is in direct contact with the (hot) solid boundary. Data of this type are summarized in figure 12 for the USF case, and in figure 13 for the UST case. In these figures, the vertical axis variable ![]() $\Delta T$ (%) is defined as
$\Delta T$ (%) is defined as
where ![]() $T_{d=0}$ is the water mean temperature for the case
$T_{d=0}$ is the water mean temperature for the case ![]() $d=0$. Note that in contrast to
$d=0$. Note that in contrast to ![]() ${T_m}_{w0}$,
${T_m}_{w0}$, ![]() ${T_m}_w$ and
${T_m}_w$ and ![]() $T_{d=0}$ are measured at the same location, situated sufficiently far downstream that fully developed flow conditions apply. Note also that
$T_{d=0}$ are measured at the same location, situated sufficiently far downstream that fully developed flow conditions apply. Note also that ![]() ${T_m}_{w0}$ is the same for all values of
${T_m}_{w0}$ is the same for all values of ![]() $d$, including
$d$, including ![]() $d = 0$. Thus the denominator of (5.1) measures the horizontal (axial) temperature change experienced by the water when air is absent from the channel (pipe). Meanwhile, the numerator compares the downstream temperature for cases where the air layer is versus is not present. Thus
$d = 0$. Thus the denominator of (5.1) measures the horizontal (axial) temperature change experienced by the water when air is absent from the channel (pipe). Meanwhile, the numerator compares the downstream temperature for cases where the air layer is versus is not present. Thus ![]() $\Delta T$ can be best interpreted by considering the following two limiting cases: (i) when the air layer contributes minimal thermal insulation,
$\Delta T$ can be best interpreted by considering the following two limiting cases: (i) when the air layer contributes minimal thermal insulation, ![]() ${T_m}_w \to T_{d=0}$ and thus
${T_m}_w \to T_{d=0}$ and thus ![]() $\Delta T \to 0\,\%$; (ii) when the air layer instead serves as a highly effective insulator,
$\Delta T \to 0\,\%$; (ii) when the air layer instead serves as a highly effective insulator, ![]() ${T_m}_w$ is little different from
${T_m}_w$ is little different from ![]() ${T_m}_{w=0}$ and therefore
${T_m}_{w=0}$ and therefore ![]() $\Delta T \to -100\,\%$.
$\Delta T \to -100\,\%$.

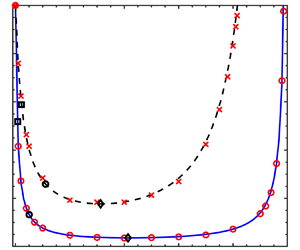
Figure 12. Change in the water temperature, ![]() $\Delta T$, with respect to the thickness of the air layer: (a) USF and rectilinear channel flow; (b) USF and axisymmetric pipe flow.
$\Delta T$, with respect to the thickness of the air layer: (a) USF and rectilinear channel flow; (b) USF and axisymmetric pipe flow.

Figure 13. As in figure 12, but considering UST rather than USF.
Because both theoretical and numerical solutions are possible for the USF cases, figures 12(a,b) include both categories of data. Consistent with the discussion of § 4, we find excellent agreement between the numerical results (red symbols) and the analogue theoretical predictions (blue solid and black dashed curves). From either of the theoretical or numerical data sets, therefore, figures 12(a,b) reveal that heat transfer can be substantially impeded by increasing the air layer thickness. Note, however, the limitations of increasing ![]() $d$ too much: beyond the critical values indicated by the open diamonds,
$d$ too much: beyond the critical values indicated by the open diamonds, ![]() $\Delta T$ increases rather than decreases. Such behaviour arises because of the impact of a thicker air layer within the channel or pipe. A thicker layer of air occupies more vertical space in the duct, resulting in a reduced cross-sectional area available for water flow. In turn, and for fixed pressure gradient in
$\Delta T$ increases rather than decreases. Such behaviour arises because of the impact of a thicker air layer within the channel or pipe. A thicker layer of air occupies more vertical space in the duct, resulting in a reduced cross-sectional area available for water flow. In turn, and for fixed pressure gradient in ![]() $x$, the water mass flow rate and average velocity both fall. The decrease of
$x$, the water mass flow rate and average velocity both fall. The decrease of ![]() $\bar {V}_w$ and
$\bar {V}_w$ and ![]() $H-\delta$ cause
$H-\delta$ cause ![]() ${T_m}_w$ to rise, as is evident from (2.48). Of course, precisely the opposite behaviour is noted for the air layer, i.e. increasing
${T_m}_w$ to rise, as is evident from (2.48). Of course, precisely the opposite behaviour is noted for the air layer, i.e. increasing ![]() $\delta$ causes
$\delta$ causes ![]() $\bar {V}_a$ to increase along with
$\bar {V}_a$ to increase along with ![]() ${T_m}_a$ – see (2.45).
${T_m}_a$ – see (2.45).
Upon comparing the solid blue and black dashed curves of figures 12(a,b), we find that the cases for which ![]() $\dot {m}_a > 0$ admit more thermal resistance than their
$\dot {m}_a > 0$ admit more thermal resistance than their ![]() $\dot {m}_a = 0$ counterparts. This observation is consistent with the velocity data shown in figure 10. The velocity profiles in question demonstrate that flow speeds are larger overall when
$\dot {m}_a = 0$ counterparts. This observation is consistent with the velocity data shown in figure 10. The velocity profiles in question demonstrate that flow speeds are larger overall when ![]() $\dot {m}_a > 0$ versus when
$\dot {m}_a > 0$ versus when ![]() $\dot {m}_a = 0$. As a consequence, and considering e.g. the air layer, the advection of thermal energy in
$\dot {m}_a = 0$. As a consequence, and considering e.g. the air layer, the advection of thermal energy in ![]() $x$ is more robust when the net mass flow rate is non-zero. In turn, thermal energy advected in
$x$ is more robust when the net mass flow rate is non-zero. In turn, thermal energy advected in ![]() $x$ is not conducted in
$x$ is not conducted in ![]() $z$ or
$z$ or ![]() $r$ into the underlying water layer, suggesting a more effective thermal insulator.
$r$ into the underlying water layer, suggesting a more effective thermal insulator.
The U-shape associated with the curves of figure 12 is reminiscent of the shapes of the curves in figure 6(a,c) of Busse et al. (Reference Busse, Sandham, McHale and Newton2013). Busse et al. (Reference Busse, Sandham, McHale and Newton2013) were interested in the drag reduction potential of surface-attached air bubbles, so plotted the change of drag force (![]() $\Delta D$) as a function of the air film thickness
$\Delta D$) as a function of the air film thickness ![]() $d$. However, beyond a mere qualitative comparison between our results versus those of Busse et al. (Reference Busse, Sandham, McHale and Newton2013), we prefer to make a quantitative comparison that juxtaposes predictions for
$d$. However, beyond a mere qualitative comparison between our results versus those of Busse et al. (Reference Busse, Sandham, McHale and Newton2013), we prefer to make a quantitative comparison that juxtaposes predictions for ![]() $\Delta T$ versus
$\Delta T$ versus ![]() $\Delta D$. To this end, a remarkable observation is made, namely that the curves of
$\Delta D$. To this end, a remarkable observation is made, namely that the curves of ![]() $\Delta T$ versus
$\Delta T$ versus ![]() $d$ exactly overlap with the curves of
$d$ exactly overlap with the curves of ![]() $\Delta D$ versus
$\Delta D$ versus ![]() $d$. The explanation is as follows. For pressure-driven flow,
$d$. The explanation is as follows. For pressure-driven flow, ![]() $\Delta D$ is defined based on the change in the mean streamwise pressure gradient,
$\Delta D$ is defined based on the change in the mean streamwise pressure gradient, ![]() $\mathrm {d}p/\mathrm {d}\kern 0.06em x$. Moreover, in the USF case, the mean water temperature measured at the duct outlet can be estimated from
$\mathrm {d}p/\mathrm {d}\kern 0.06em x$. Moreover, in the USF case, the mean water temperature measured at the duct outlet can be estimated from ![]() ${T_m}_{w,x=L} = {T_m}_{w0}+ (\dot {q}A_{s}/\dot {m}_w C_{p_w})$ (Çengel & Ghajar Reference Çengel and Ghajar2021). On the other hand, and for the Poiseuille flows of interest here,
${T_m}_{w,x=L} = {T_m}_{w0}+ (\dot {q}A_{s}/\dot {m}_w C_{p_w})$ (Çengel & Ghajar Reference Çengel and Ghajar2021). On the other hand, and for the Poiseuille flows of interest here, ![]() $\dot {m}_w$ is linearly related to the pressure gradient. As a result, any fractional reduction in the drag experienced by the cargo fluid must be matched exactly by a fractional reduction of the temperature change.
$\dot {m}_w$ is linearly related to the pressure gradient. As a result, any fractional reduction in the drag experienced by the cargo fluid must be matched exactly by a fractional reduction of the temperature change.
For the UST cases, one does not have the luxury of computing a theoretical solution. For this reason, figures 13(a,b) include only a single pair of curves, both of which are derived from numerical output. The curves in blue and black respectively consider ![]() $\dot {m}_a > 0$ and
$\dot {m}_a > 0$ and ![]() $\dot {m}_a = 0$. As compared to figure 12, the difference between the
$\dot {m}_a = 0$. As compared to figure 12, the difference between the ![]() $\dot {m}_a > 0$ and
$\dot {m}_a > 0$ and ![]() $\dot {m}_a = 0$ cases is relatively small, particularly for the rectilinear geometry. A more general comparison of figures 12 and 13 reveals two additional insights. First, although similar trends arise, the results of figures 12 and 13 are not identical. We conclude, therefore, that the UST case is not the direct analogue of the drag reduction scenario studied by Busse et al. (Reference Busse, Sandham, McHale and Newton2013). Elaborating on this point, graphical evidence suggests that less thermal energy is transferred from the solid surface to the cargo fluid when the thermal boundary condition is UST versus USF. This observation is consistent with the engineering principle that scalar transport is maximized when the driving force (here, the temperature difference
$\dot {m}_a = 0$ cases is relatively small, particularly for the rectilinear geometry. A more general comparison of figures 12 and 13 reveals two additional insights. First, although similar trends arise, the results of figures 12 and 13 are not identical. We conclude, therefore, that the UST case is not the direct analogue of the drag reduction scenario studied by Busse et al. (Reference Busse, Sandham, McHale and Newton2013). Elaborating on this point, graphical evidence suggests that less thermal energy is transferred from the solid surface to the cargo fluid when the thermal boundary condition is UST versus USF. This observation is consistent with the engineering principle that scalar transport is maximized when the driving force (here, the temperature difference ![]() $T_{s}- {T_m}_w$) is constant. By contrast, the UST boundary condition demands that
$T_{s}- {T_m}_w$) is constant. By contrast, the UST boundary condition demands that ![]() $T_{s}- {T_m}_w$ decrease monotonically with
$T_{s}- {T_m}_w$ decrease monotonically with ![]() $x$, leading to a reduction in the overall transfer of thermal energy.
$x$, leading to a reduction in the overall transfer of thermal energy.
The central conclusion of the paragraph above, namely that the UST case admits solutions different to those derived by Busse et al. (Reference Busse, Sandham, McHale and Newton2013), contrasts from the findings of Maynes et al. (Reference Maynes, Webb and Davies2008). Abandoning the adiabatic interface assumption, they performed numerical simulations of micro-channel flow featuring transverse ribs maintained at a fixed temperature. In the limit of vanishing rib thickness, their figure 11 suggests an equal impact on momentum versus heat transfer. It is important to recall, however, that the Maynes et al. (Reference Maynes, Webb and Davies2008) result is derived for particular values of rib height and Reynolds number, i.e. ![]() $Re = 1000$. For
$Re = 1000$. For ![]() $Re < 1000$, figure 10 of Maynes et al. (Reference Maynes, Webb and Davies2008) suggests that the aforementioned equivalence is likely to disappear.
$Re < 1000$, figure 10 of Maynes et al. (Reference Maynes, Webb and Davies2008) suggests that the aforementioned equivalence is likely to disappear.
5.2. Optimum air layer thickness
Recall that figures 12 and 13 include open diamonds that indicate those optimum ![]() $d$ values that minimize
$d$ values that minimize ![]() $\Delta T$. Motivated by the exposition of Busse et al. (Reference Busse, Sandham, McHale and Newton2013), figures 12 and 13 also demarcate those points where, for
$\Delta T$. Motivated by the exposition of Busse et al. (Reference Busse, Sandham, McHale and Newton2013), figures 12 and 13 also demarcate those points where, for ![]() $d < d_{optimum}$, the value of
$d < d_{optimum}$, the value of ![]() $\Delta T$ is either 50 % or 90 % of the value indicated by the open diamond. Expanding on this graphical information, table 2 quantifies the amount of the temperature decrease when
$\Delta T$ is either 50 % or 90 % of the value indicated by the open diamond. Expanding on this graphical information, table 2 quantifies the amount of the temperature decrease when ![]() $d = d_{optimum}$. For example, and considering CHSYM1, the minimum possible value of
$d = d_{optimum}$. For example, and considering CHSYM1, the minimum possible value of ![]() $\Delta T$ is
$\Delta T$ is ![]() $-$96.64 % and this minimum value is realized when
$-$96.64 % and this minimum value is realized when ![]() $d = 0.414$, i.e. when just over 40 % of the channel cross-section is occupied by a surface-attached air bubble. Recognizing the difficulty of stabilizing such a thick air layer outside of a microfluidics context, it is welcome news that still substantial
$d = 0.414$, i.e. when just over 40 % of the channel cross-section is occupied by a surface-attached air bubble. Recognizing the difficulty of stabilizing such a thick air layer outside of a microfluidics context, it is welcome news that still substantial ![]() $\Delta T$ values
$\Delta T$ values ![]() $-$86.97 % and
$-$86.97 % and ![]() $-$48.32 % can be realized for the much smaller
$-$48.32 % can be realized for the much smaller ![]() $d$ values 0.0502 and 0.0083, respectively. So although it may prove difficult to achieve the minimum possible value for
$d$ values 0.0502 and 0.0083, respectively. So although it may prove difficult to achieve the minimum possible value for ![]() $\Delta T$, the steep sides associated with the U-shaped curves of figures 12 and 13 suggest that close to optimal solutions may be realized with significantly thinner air layers. This conclusion applies not only to CHSYM1 but to the other cases considered in table 2 as well.
$\Delta T$, the steep sides associated with the U-shaped curves of figures 12 and 13 suggest that close to optimal solutions may be realized with significantly thinner air layers. This conclusion applies not only to CHSYM1 but to the other cases considered in table 2 as well.
Table 2. Values for the optimum temperature change and corresponding optimum air layer thickness. Also shown are the air layer thicknesses required to achieve either 90 % or 50 % of the optimum (i.e. minimum) value for ![]() $\Delta T$.
$\Delta T$.

5.3. Nusselt number
Nusselt numbers are important in this study because they provide the most direct measure of the thermal insulation efficacy of surface-attached air bubbles. In the limit ![]() $d \to 0$, we reproduce the classical Nusselt numbers relevant to single-phase flow, e.g. 4.36 in the case of laminar pipe flow subject to USF. On the other hand, our study admits a far richer behaviour because we allow
$d \to 0$, we reproduce the classical Nusselt numbers relevant to single-phase flow, e.g. 4.36 in the case of laminar pipe flow subject to USF. On the other hand, our study admits a far richer behaviour because we allow ![]() $d$ to assume values between zero and unity. To this end, figure 14 confirms that
$d$ to assume values between zero and unity. To this end, figure 14 confirms that ![]() $Nu_w$ is a strong function of
$Nu_w$ is a strong function of ![]() $d$ for all of the cases defined in tables 1 and 2. More specifically, and for each of the curves of figure 14, we observe a rapid initial decrease of
$d$ for all of the cases defined in tables 1 and 2. More specifically, and for each of the curves of figure 14, we observe a rapid initial decrease of ![]() $Nu_w$ followed by a gradual relaxation to the limiting value
$Nu_w$ followed by a gradual relaxation to the limiting value ![]() $Nu_w = 0$ when
$Nu_w = 0$ when ![]() $d \to 1$.
$d \to 1$.

Figure 14. Plots of ![]() $Nu_w$ versus
$Nu_w$ versus ![]() $d$ for (a) USF and rectilinear channel flow, (b) USF and axisymmetric pipe flow, (c) UST and rectilinear channel flow, and (d) UST and axisymmetric pipe flow. Note the variation of the
$d$ for (a) USF and rectilinear channel flow, (b) USF and axisymmetric pipe flow, (c) UST and rectilinear channel flow, and (d) UST and axisymmetric pipe flow. Note the variation of the ![]() $y$-axis limits.
$y$-axis limits.
The complicated mathematical form of equations such as (2.49) and (2.53) makes it difficult to predict, in purely mathematical terms, how ![]() $Nu_w$ should vary with
$Nu_w$ should vary with ![]() $d$. On the other hand, the monotone variations exhibited by the curves of figure 14 are straightforward to reconcile using physical intuition. We expect, and observe, that as the air bubble thickens, less thermal energy is transferred from the solid surface to the cargo fluid. Consistent with the trends observed in figures 12 and 13, even a relatively thin air bubble can non-trivially impede heat transfer; however, the law of diminishing returns manifests when
$d$. On the other hand, the monotone variations exhibited by the curves of figure 14 are straightforward to reconcile using physical intuition. We expect, and observe, that as the air bubble thickens, less thermal energy is transferred from the solid surface to the cargo fluid. Consistent with the trends observed in figures 12 and 13, even a relatively thin air bubble can non-trivially impede heat transfer; however, the law of diminishing returns manifests when ![]() $d \gtrsim 0.1$, regardless of the duct geometry and thermal forcing regime.
$d \gtrsim 0.1$, regardless of the duct geometry and thermal forcing regime.
Until now, we have deliberately avoided introducing slip lengths into the discussion. In the superhydrophobic surface context, however, Nusselt numbers are often plotted versus slip lengths. It is therefore appropriate to include similar kinds of figures here, at least for the USF cases, which offer the best opportunity for comparison with important earlier studies. To this end, we define the hydrodynamic slip length ![]() ${\mathcal {L}}_{slip}$ as
${\mathcal {L}}_{slip}$ as
 \begin{equation} {\mathcal{L}}_{slip} = \frac{u_{in}}{\left.\dfrac{\partial u}{\partial z}\right|_{in}}, \end{equation}
\begin{equation} {\mathcal{L}}_{slip} = \frac{u_{in}}{\left.\dfrac{\partial u}{\partial z}\right|_{in}}, \end{equation}
where velocities and velocity gradients are measured at the location of the interface. We also consider the thermal slip length ![]() ${\mathcal {L}}_{slip}^t$, which is expressed as
${\mathcal {L}}_{slip}^t$, which is expressed as
 \begin{equation} {\mathcal{L}}_{slip}^t = \frac{T_{in} - T_s}{\left.\dfrac{\partial T}{\partial z}\right|_{in}}; \end{equation}
\begin{equation} {\mathcal{L}}_{slip}^t = \frac{T_{in} - T_s}{\left.\dfrac{\partial T}{\partial z}\right|_{in}}; \end{equation}
cf. figure 1 of Maynes & Crockett (Reference Maynes and Crockett2014). With a view towards comparing our slip lengths with those estimated by Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014), we non-dimensionalize (5.2) and (5.3) by defining ![]() $\tilde {{\mathcal {L}}}_{slip} = {\mathcal {L}}_{slip}/2 (H - \delta )$ and
$\tilde {{\mathcal {L}}}_{slip} = {\mathcal {L}}_{slip}/2 (H - \delta )$ and ![]() $\tilde {{\mathcal {L}}^t}_{slip} = {\mathcal {L}}_{slip}^t/2 (H - \delta )$, respectively, for the CHSYM cases. For the corresponding PIPE cases, we instead write
$\tilde {{\mathcal {L}}^t}_{slip} = {\mathcal {L}}_{slip}^t/2 (H - \delta )$, respectively, for the CHSYM cases. For the corresponding PIPE cases, we instead write ![]() $\tilde {{\mathcal {L}}}_{slip} = {\mathcal {L}}_{slip}/2 (R - \delta )$ and
$\tilde {{\mathcal {L}}}_{slip} = {\mathcal {L}}_{slip}/2 (R - \delta )$ and ![]() $\widetilde {{\mathcal {L}}^t}_{slip} = {\mathcal {L}}_{slip}^t/2 (R - \delta )$, respectively.
$\widetilde {{\mathcal {L}}^t}_{slip} = {\mathcal {L}}_{slip}^t/2 (R - \delta )$, respectively.
Within the range ![]() $0 \leq \tilde {{\mathcal {L}}}_{slip} \leq 1$, figure 15 shows the connection between the thermal and hydrodynamic slip lengths for CHSYM1 and CHSYM2 (figure 15a), and for PIPE1 and PIPE2 (figure 15b). In both plots, we note that
$0 \leq \tilde {{\mathcal {L}}}_{slip} \leq 1$, figure 15 shows the connection between the thermal and hydrodynamic slip lengths for CHSYM1 and CHSYM2 (figure 15a), and for PIPE1 and PIPE2 (figure 15b). In both plots, we note that ![]() $\tilde {{\mathcal {L}}}_{slip}^t$ is larger when
$\tilde {{\mathcal {L}}}_{slip}^t$ is larger when ![]() $\dot {m}_a = 0$ as compared to when
$\dot {m}_a = 0$ as compared to when ![]() $\dot {m}_a > 0$. By contrast, figures 12(a,b) show that
$\dot {m}_a > 0$. By contrast, figures 12(a,b) show that ![]() $|\Delta T|$ is larger (and therefore the air layer acts as a more effective insulator) when
$|\Delta T|$ is larger (and therefore the air layer acts as a more effective insulator) when ![]() $\dot {m}_a >0$ versus
$\dot {m}_a >0$ versus ![]() $\dot {m}_a = 0$. The apparent contradiction is reconciled by superposing the influence of the hydrodynamic slip length:
$\dot {m}_a = 0$. The apparent contradiction is reconciled by superposing the influence of the hydrodynamic slip length: ![]() $\dot {m}_a = 0$ is associated with smaller
$\dot {m}_a = 0$ is associated with smaller ![]() $\tilde {{\mathcal {L}}}_{slip}$ and smaller interfacial flow velocities, and therefore longer residence times, for the water flowing along the channel or pipe – cf. Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) and Lam, Hodes & Enright (Reference Lam, Hodes and Enright2015).
$\tilde {{\mathcal {L}}}_{slip}$ and smaller interfacial flow velocities, and therefore longer residence times, for the water flowing along the channel or pipe – cf. Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) and Lam, Hodes & Enright (Reference Lam, Hodes and Enright2015).

Figure 15. Plots of ![]() $\tilde {{\mathcal {L}}}^t_{slip}$ versus
$\tilde {{\mathcal {L}}}^t_{slip}$ versus ![]() $\tilde {{\mathcal {L}}}_{slip}$ for USF and (a) rectilinear channel flow, and (b) axisymmetric pipe flow.
$\tilde {{\mathcal {L}}}_{slip}$ for USF and (a) rectilinear channel flow, and (b) axisymmetric pipe flow.
A further striking feature of figure 15 is that ![]() $\tilde {{\mathcal {L}}}_{slip}^t$ varies approximately linearly with
$\tilde {{\mathcal {L}}}_{slip}^t$ varies approximately linearly with ![]() $\tilde {{\mathcal {L}}}_{slip}$, particularly for the rectilinear geometry. This finding is consistent with that of Ng & Wang (Reference Ng and Wang2014) (see their figures 6a–d) and Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) (see their figure a). There, likewise, nearly linear relationships are observed; (modest) deviations from linearity arise owing to the different solids fractions for the superhydrophobic surfaces that entrap the air layer. (Considerations of the solids fraction are, of course, moot in the perfect plastron limit.)
$\tilde {{\mathcal {L}}}_{slip}$, particularly for the rectilinear geometry. This finding is consistent with that of Ng & Wang (Reference Ng and Wang2014) (see their figures 6a–d) and Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) (see their figure a). There, likewise, nearly linear relationships are observed; (modest) deviations from linearity arise owing to the different solids fractions for the superhydrophobic surfaces that entrap the air layer. (Considerations of the solids fraction are, of course, moot in the perfect plastron limit.)
Expanding on the comparison with Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014), we include data extracted from their figure 6(b) in figure 16, which shows the variation of the Nusselt number from figure 14 with the hydrodynamic slip length from figure 15. From figure 15(a), the approximate ratio ![]() $\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip}$ for CHSYM1 (CHSYM2) is 0.5 (2.0). Fortuitously, Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) include data with
$\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip}$ for CHSYM1 (CHSYM2) is 0.5 (2.0). Fortuitously, Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) include data with ![]() $\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} \simeq 0.5$ in their figure 6(b); extracting these data and including them in figure 16(a) shows a near perfect overlap with our own predictions. Although figure 6(b) of Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) does not include comparable results for
$\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} \simeq 0.5$ in their figure 6(b); extracting these data and including them in figure 16(a) shows a near perfect overlap with our own predictions. Although figure 6(b) of Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) does not include comparable results for ![]() $\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} = 2.0$, it does include data for
$\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} = 2.0$, it does include data for ![]() $\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} \simeq 1.5$ and
$\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} \simeq 1.5$ and ![]() $\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} \simeq 2.1$, and these results are likewise presented in figure 16(a). Here again, excellent agreement is observed, i.e. our results lie between the corresponding curves of Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014), and are much closer to the curve labelled
$\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} \simeq 2.1$, and these results are likewise presented in figure 16(a). Here again, excellent agreement is observed, i.e. our results lie between the corresponding curves of Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014), and are much closer to the curve labelled ![]() $\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} \simeq 2.1$ than they are to the curve labelled
$\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} \simeq 2.1$ than they are to the curve labelled ![]() $\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} \simeq 1.5$. These observations are important because they affirm that the relationship between the Nusselt number and the hydrodynamic slip length is, at least in some scenarios (e.g. USF, modest solids fraction), independent of the details of the superhydrophobic surface that defines
$\tilde {{\mathcal {L}}}_{slip}^t/\tilde {{\mathcal {L}}}_{slip} \simeq 1.5$. These observations are important because they affirm that the relationship between the Nusselt number and the hydrodynamic slip length is, at least in some scenarios (e.g. USF, modest solids fraction), independent of the details of the superhydrophobic surface that defines ![]() $\tilde {{\mathcal {L}}}_{slip}$. Correspondingly, one may consider an idealized superhydrophobic surface, e.g. one altogether devoid of pillars or ridges, and thereby sidestep some of the more intricate mathematical calculations needed when such topographical features are included. We return to the comparison between our approach and that of Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) and others in § 5.4.
$\tilde {{\mathcal {L}}}_{slip}$. Correspondingly, one may consider an idealized superhydrophobic surface, e.g. one altogether devoid of pillars or ridges, and thereby sidestep some of the more intricate mathematical calculations needed when such topographical features are included. We return to the comparison between our approach and that of Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) and others in § 5.4.

Figure 16. Plots of ![]() $Nu_w$ versus
$Nu_w$ versus ![]() $\tilde {{\mathcal {L}}}_{slip}$ for USF and (a) rectilinear channel flow, (b) axisymmetric pipe flow. In (a), results extracted from Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) are included.
$\tilde {{\mathcal {L}}}_{slip}$ for USF and (a) rectilinear channel flow, (b) axisymmetric pipe flow. In (a), results extracted from Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) are included.
For completeness, figure 16 also includes results relevant to PIPE1 and PIPE2. The trends on display are qualitatively very similar to CHSYM1 and CHSYM2 except that the Nusselt number exhibits a more rapid initial decrease with ![]() $\tilde {{\mathcal {L}}}_{slip}$. Unfortunately, no comparison with Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) is possible here because they do not consider the case of axisymmetric flow.
$\tilde {{\mathcal {L}}}_{slip}$. Unfortunately, no comparison with Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) is possible here because they do not consider the case of axisymmetric flow.
5.4. The perfect plastron limit and the adiabatic interface assumption
As suggested in the Introduction, our analysis takes a different approach to the seminal studies of Maynes & Crockett (Reference Maynes and Crockett2014), Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014), Kirk et al. (Reference Kirk, Hodes and Papageorgiou2017), Karamanis et al. (Reference Karamanis, Hodes, Kirk and Papageorgiou2018), Game et al. (Reference Game, Hodes, Kirk and Papageorgiou2018) and others, wherein the air–water interface is regarded as adiabatic such that heat transfer from the solid boundary to the cargo liquid occurs via roughness elements. Juxtaposing our approach versus theirs, the perfect plastron limit represents, in the words of Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014), ‘a flow completely insulated from the channel surfaces’. The justification for considering an adiabatic interface often references the small thermal conductivity of air or the relatively large solids fraction that is associated with at least some superhydrophobic surfaces – see e.g. figure 3(a) of Ng & Wang (Reference Ng and Wang2014). Elsewhere, attention has been drawn to the height versus spacing of roughness elements. For instance, and citing the numerical data of Maynes et al. (Reference Maynes, Webb and Davies2008), Game et al. (Reference Game, Hodes, Kirk and Papageorgiou2018) remark that ‘the rate of heat conducting into the liquid through the gas cavities is negligible in comparison to the rate entering through the solid ridges for cavity depths greater than about 25 % of the cavity width’.
The data of figure 14, derived as they are for a highly-idealized superhydrophobic surface devoid of roughness elements, offer a different perspective. More specifically, our results caution against always ignoring the air layer (or the depth ratio ![]() $d = \delta /H$) in assessing the relative importance of the interface as a vehicle for heat transfer. In other words – and although
$d = \delta /H$) in assessing the relative importance of the interface as a vehicle for heat transfer. In other words – and although ![]() $Nu_w$ is very small when
$Nu_w$ is very small when ![]() $d \gtrsim 0.4$ –
$d \gtrsim 0.4$ – ![]() $Nu_w \gtrsim 1$ when
$Nu_w \gtrsim 1$ when ![]() $d \lesssim 0.1$. For this range of non-dimensional roughness heights, we predict Nusselt numbers not dissimilar to those exhibited in figure 7 of Maynes et al. (Reference Maynes, Webb and Davies2008), figure 6(b) of Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) or figure 7 of Kirk et al. (Reference Kirk, Hodes and Papageorgiou2017). In our opinion, the adiabatic interface assumption should therefore be applied with some care in cases of relatively short roughness elements.
$d \lesssim 0.1$. For this range of non-dimensional roughness heights, we predict Nusselt numbers not dissimilar to those exhibited in figure 7 of Maynes et al. (Reference Maynes, Webb and Davies2008), figure 6(b) of Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) or figure 7 of Kirk et al. (Reference Kirk, Hodes and Papageorgiou2017). In our opinion, the adiabatic interface assumption should therefore be applied with some care in cases of relatively short roughness elements.
The conclusion of the last paragraph requires appropriate contextualization and should not be misconstrued as a critique of the aforementioned seminal papers. After all, these studies apply intricate theoretical and/or numerical techniques to solve for the velocity and temperature distributions given e.g. mixed free-slip and no-slip bottom boundary conditions. A non-trivial challenge, arguably tackled with the greatest theoretical rigour by Game et al. (Reference Game, Hodes, Keaveny and Papageorgiou2017, Reference Game, Hodes, Kirk and Papageorgiou2018), is to account for the deflection of the air–water interface and to remove the associated singularities that arise at the triple point. (The former topic is also considered in healthy detail by Lam et al. (Reference Lam, Hodes and Enright2015) and Kirk et al. (Reference Kirk, Hodes and Papageorgiou2017); meanwhile, a novel extension to the Game et al. (Reference Game, Hodes, Keaveny and Papageorgiou2017, Reference Game, Hodes, Kirk and Papageorgiou2018) model is to superpose thermocapillary stresses – see the recent study by Tomlinson et al. (Reference Tomlinson, Mayer, Kirk, Hodes and Papageorgiou2024).) Given the associated level of difficulty of these calculations, we suggest retaining the edifice erected by Game et al. (Reference Game, Hodes, Kirk and Papageorgiou2018) and others, but softening the (sometimes restrictive) assumption of an adiabatic interface. In practical terms, this could be achieved by replacing the requirement that ![]() $Nu = 0$ along the interface (see e.g. equation 2.18 of Kirk et al. (Reference Kirk, Hodes and Papageorgiou2017)) with a result more reflective of the trends exhibited in figure 14. In turn, and for each of Maynes & Crockett (Reference Maynes and Crockett2014), Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014), Kirk et al. (Reference Kirk, Hodes and Papageorgiou2017), Karamanis et al. (Reference Karamanis, Hodes, Kirk and Papageorgiou2018) and Game et al. (Reference Game, Hodes, Kirk and Papageorgiou2018), the suggested incorporation would require explicitly defining the depth of the air layer (as is done, for example, in the isothermal study of Game et al. (Reference Game, Hodes, Keaveny and Papageorgiou2017)). Stated differently, one should not automatically assume that ‘the depth of the ribs exerts no influence on the overall thermal transport’ (Maynes & Crockett Reference Maynes and Crockett2014).
$Nu = 0$ along the interface (see e.g. equation 2.18 of Kirk et al. (Reference Kirk, Hodes and Papageorgiou2017)) with a result more reflective of the trends exhibited in figure 14. In turn, and for each of Maynes & Crockett (Reference Maynes and Crockett2014), Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014), Kirk et al. (Reference Kirk, Hodes and Papageorgiou2017), Karamanis et al. (Reference Karamanis, Hodes, Kirk and Papageorgiou2018) and Game et al. (Reference Game, Hodes, Kirk and Papageorgiou2018), the suggested incorporation would require explicitly defining the depth of the air layer (as is done, for example, in the isothermal study of Game et al. (Reference Game, Hodes, Keaveny and Papageorgiou2017)). Stated differently, one should not automatically assume that ‘the depth of the ribs exerts no influence on the overall thermal transport’ (Maynes & Crockett Reference Maynes and Crockett2014).
6. Application to real micro-channels
Subsection 5.4 discusses the parallel pathways for heat transfer from a real superhydrophobic surface to the cargo liquid, namely along the axis of micro-topographical elements or via the air bubbles situated in between such elements. Here, we revisit this duality and thereby contextualize results pertinent to perfect plastrons versus results anticipated in real micro-channel flows. Consistent with the discussion of § 3.3, attention is focused on a CHSYM4-analogue case where the underlying solid includes micro-ridges that are oriented perpendicular to the flow direction – cf. Maynes et al. (Reference Maynes, Webb and Davies2008). In this respect, we intend to answer the question: is the dashed-curve solution of figure 13(a) relevant to real lab-on-a-chip-type flows?
Figure 17 reproduces figure 13(a), but eliminates the solid blue curve (![]() $\dot {m}_a > 0$) and adds
$\dot {m}_a > 0$) and adds ![]() $\dot {m}_a = 0$ results derived from the numerical simulations described in § 3.3. More specifically, we consider ridge geometries characterized by four different
$\dot {m}_a = 0$ results derived from the numerical simulations described in § 3.3. More specifically, we consider ridge geometries characterized by four different ![]() $w/\lambda$ ratios, namely 0, 0.1, 0.2 and 0.278. (The former value indicates no ridges and is included for comparison with the solution derived at much larger
$w/\lambda$ ratios, namely 0, 0.1, 0.2 and 0.278. (The former value indicates no ridges and is included for comparison with the solution derived at much larger ![]() $L/H$; the latter value is selected to approximately coincide with the figure considered by Rosengarten et al. (Reference Rosengarten, Stanley and Kwok2008).) In comparing the two curves labelled ‘
$L/H$; the latter value is selected to approximately coincide with the figure considered by Rosengarten et al. (Reference Rosengarten, Stanley and Kwok2008).) In comparing the two curves labelled ‘![]() $w/\lambda = 0$’, we find from their difference that the full insulation benefit of surface-attached air bubbles is realized only for sufficiently long channels. On the other hand, the difference in question remains relatively small except for relatively large values of
$w/\lambda = 0$’, we find from their difference that the full insulation benefit of surface-attached air bubbles is realized only for sufficiently long channels. On the other hand, the difference in question remains relatively small except for relatively large values of ![]() $d$, i.e.
$d$, i.e. ![]() $d \gtrsim 0.7$. Meanwhile, in comparing the curves labelled ‘
$d \gtrsim 0.7$. Meanwhile, in comparing the curves labelled ‘![]() $w/\lambda = 0.1$’, ‘
$w/\lambda = 0.1$’, ‘![]() $w/\lambda = 0.2$’ and ‘
$w/\lambda = 0.2$’ and ‘![]() $w/\lambda = 0.278$’, we find that as the transverse ridges are made wider, a greater proportion of the heat is conducted through these ridges, and a lesser proportion is transferred through the entrapped air bubbles. As such, the curve corresponding to
$w/\lambda = 0.278$’, we find that as the transverse ridges are made wider, a greater proportion of the heat is conducted through these ridges, and a lesser proportion is transferred through the entrapped air bubbles. As such, the curve corresponding to ![]() $w/\lambda = 0.278$ shows the greatest difference with the perfect plastron solution. Better agreement is noted when
$w/\lambda = 0.278$ shows the greatest difference with the perfect plastron solution. Better agreement is noted when ![]() $w/\lambda$ is reduced to 0.1, in which case
$w/\lambda$ is reduced to 0.1, in which case ![]() $\Delta T$ values as low as approximately
$\Delta T$ values as low as approximately ![]() $-$80 % can be realized, i.e. when
$-$80 % can be realized, i.e. when ![]() $d \simeq 0.3$. Up to and even slightly beyond this value for
$d \simeq 0.3$. Up to and even slightly beyond this value for ![]() $d$, the perfect plastron limiting solution from figure 13(a) represents an ambitious but still representative upper bound vis-à-vis bubble thermal insulation efficacy. As
$d$, the perfect plastron limiting solution from figure 13(a) represents an ambitious but still representative upper bound vis-à-vis bubble thermal insulation efficacy. As ![]() $d$ increases still further, however, a greater divergence is noted between the curves of figure 17. Within this latter range of
$d$ increases still further, however, a greater divergence is noted between the curves of figure 17. Within this latter range of ![]() $d$, therefore, the perfect plastron limit cannot be considered an especially meaningful descriptor of actual heat transfer processes. Most notably, the dashed curve extracted from figure 13(a) predicts that
$d$, therefore, the perfect plastron limit cannot be considered an especially meaningful descriptor of actual heat transfer processes. Most notably, the dashed curve extracted from figure 13(a) predicts that ![]() $\Delta T > 0$ only when
$\Delta T > 0$ only when ![]() $d \gtrsim 0.97$, whereas the numerical results suggest that
$d \gtrsim 0.97$, whereas the numerical results suggest that ![]() $\Delta T > 0$ for
$\Delta T > 0$ for ![]() $d$ as small as 0.68.
$d$ as small as 0.68.

Figure 17. Change in the water temperature, ![]() $\Delta T$, with respect to the thickness of the air layer. The black dashed curve is reproduced from figure 13(a), whereas the coloured curves show the output from the numerical simulations of § 3.3, where
$\Delta T$, with respect to the thickness of the air layer. The black dashed curve is reproduced from figure 13(a), whereas the coloured curves show the output from the numerical simulations of § 3.3, where ![]() $L/H = 180$. The variables
$L/H = 180$. The variables ![]() $w$ and
$w$ and ![]() $\lambda$ are as defined in figure 8.
$\lambda$ are as defined in figure 8.
The precise values for ![]() $d$ quoted at the end of the last paragraph must be interpreted with some care: the coloured curves of figure 17 assume the same channel length, i.e.
$d$ quoted at the end of the last paragraph must be interpreted with some care: the coloured curves of figure 17 assume the same channel length, i.e. ![]() $L/H = 180$. As the channel length is either increased or decreased, numerically determined values for
$L/H = 180$. As the channel length is either increased or decreased, numerically determined values for ![]() $\Delta T$ likewise adjust. This behaviour is exhibited in figure 18, which fixes the value of
$\Delta T$ likewise adjust. This behaviour is exhibited in figure 18, which fixes the value of ![]() $w/\lambda$ at 0.278, and plots
$w/\lambda$ at 0.278, and plots ![]() $\Delta T$ versus
$\Delta T$ versus ![]() $L/H$ for two different values of
$L/H$ for two different values of ![]() $d$. In both cases, we find that as the channel is elongated,
$d$. In both cases, we find that as the channel is elongated, ![]() $\Delta T$ increases until reaching a plateau. In the context of figure 17, this behaviour suggests a greater separation between the perfect plastron solution and its counterpart numerical curve. Synthesizing the results of both figures 17 and 18, caution is therefore recommended in applying the perfect plastron solution when
$\Delta T$ increases until reaching a plateau. In the context of figure 17, this behaviour suggests a greater separation between the perfect plastron solution and its counterpart numerical curve. Synthesizing the results of both figures 17 and 18, caution is therefore recommended in applying the perfect plastron solution when ![]() $L/H$ and
$L/H$ and ![]() $w/\lambda$ or
$w/\lambda$ or ![]() $d$ are too large. Although we expect this caution to apply equally to other scenarios (e.g. pipe flow versus channel flow, or pillar-type micro-topography versus ridge-type micro-topography), there obviously remain numerous quantitative details to resolve. Pursuit of the research in question is the topic of ongoing research.
$d$ are too large. Although we expect this caution to apply equally to other scenarios (e.g. pipe flow versus channel flow, or pillar-type micro-topography versus ridge-type micro-topography), there obviously remain numerous quantitative details to resolve. Pursuit of the research in question is the topic of ongoing research.

Figure 18. Change in the water temperature, ![]() $\Delta T$, with respect to the non-dimensional channel length
$\Delta T$, with respect to the non-dimensional channel length ![]() $L/H$, for two different air layer thicknesses
$L/H$, for two different air layer thicknesses ![]() $d = \delta /H$.
$d = \delta /H$.
7. Conclusions
This study is motivated by the simple question of whether surface-attached air bubbles, here modelled as a continuous air film, can serve as effective thermal insulators for pressure-driven internal flow. The basis for pursuing this topic comes from the long line of inquiry devoted to drag reduction and the influence of the hydrodynamic boundary condition (no-slip versus free-slip) on said drag reduction. Thus are we guided by the earlier theoretical investigation of Busse et al. (Reference Busse, Sandham, McHale and Newton2013), who meticulously characterized the degree of drag reduction realized for different internal flows with different air layer thicknesses ![]() $\delta$. Relative to this list of flows studied by Busse et al. (Reference Busse, Sandham, McHale and Newton2013), we restrict attention to those enumerated in tables 1 and 2, i.e. we focus on symmetric rectilinear channel flow and on axisymmetric pipe flow. However, and in a major extension to Busse et al. (Reference Busse, Sandham, McHale and Newton2013), we introduce temperature differences between the boundary (or solid surface) and the water and air flowing inside of the duct. In so doing, and by superposing a thermal energy balance and thermal energy equation onto the Busse et al. (Reference Busse, Sandham, McHale and Newton2013) analysis, we are able to characterize the effectiveness of bubbles as insulators for
$\delta$. Relative to this list of flows studied by Busse et al. (Reference Busse, Sandham, McHale and Newton2013), we restrict attention to those enumerated in tables 1 and 2, i.e. we focus on symmetric rectilinear channel flow and on axisymmetric pipe flow. However, and in a major extension to Busse et al. (Reference Busse, Sandham, McHale and Newton2013), we introduce temperature differences between the boundary (or solid surface) and the water and air flowing inside of the duct. In so doing, and by superposing a thermal energy balance and thermal energy equation onto the Busse et al. (Reference Busse, Sandham, McHale and Newton2013) analysis, we are able to characterize the effectiveness of bubbles as insulators for ![]() $0 < d < 1$, where
$0 < d < 1$, where ![]() $d = \delta /H$ (rectilinear geometry) or
$d = \delta /H$ (rectilinear geometry) or ![]() $d = \delta /R$ (axisymmetric geometry). The characterization in question employs as (interrelated) metrics the percentage temperature change relative to the no air bubble case (figures 12 and 13) and the Nusselt number
$d = \delta /R$ (axisymmetric geometry). The characterization in question employs as (interrelated) metrics the percentage temperature change relative to the no air bubble case (figures 12 and 13) and the Nusselt number ![]() $Nu_w$, which is plotted versus
$Nu_w$, which is plotted versus ![]() $d$ in figure 14, and versus the non-dimensional hydrodynamic slip length
$d$ in figure 14, and versus the non-dimensional hydrodynamic slip length ![]() $\tilde {{\mathcal {L}}}^t_{slip}$ in figure 16.
$\tilde {{\mathcal {L}}}^t_{slip}$ in figure 16.
A remarkable aspect of figure 12, which considers the case of USF, is the exact overlap of its curves of ![]() $\Delta T$ versus
$\Delta T$ versus ![]() $d$ with the corresponding drag reduction curves presented in figures 6(a,c) of Busse et al. (Reference Busse, Sandham, McHale and Newton2013). The reason for this coincidence is that both
$d$ with the corresponding drag reduction curves presented in figures 6(a,c) of Busse et al. (Reference Busse, Sandham, McHale and Newton2013). The reason for this coincidence is that both ![]() $\Delta T$ and
$\Delta T$ and ![]() $\Delta D$ are linked to the water mass flow rate, so a change in this quantity, due e.g. to an increase or decrease in the thickness of the air layer, will impact the cross-stream transport of momentum and of thermal energy in equal proportion. This point notwithstanding, the aforementioned coincidence is lost when the surface boundary condition is changed from uniform surface heat flux (figure 12) to uniform surface temperature (figure 13). In this latter case, which we explore only numerically and without the benefit of a complementary analytical solution, there is a comparatively smaller difference between solutions characterized as
$\Delta D$ are linked to the water mass flow rate, so a change in this quantity, due e.g. to an increase or decrease in the thickness of the air layer, will impact the cross-stream transport of momentum and of thermal energy in equal proportion. This point notwithstanding, the aforementioned coincidence is lost when the surface boundary condition is changed from uniform surface heat flux (figure 12) to uniform surface temperature (figure 13). In this latter case, which we explore only numerically and without the benefit of a complementary analytical solution, there is a comparatively smaller difference between solutions characterized as ![]() $\dot {m}_a > 0$ versus
$\dot {m}_a > 0$ versus ![]() $\dot {m}_a = 0$, where
$\dot {m}_a = 0$, where ![]() $\dot {m}_a$ represents the net mass flow rate of air.
$\dot {m}_a$ represents the net mass flow rate of air.
A limitation of our theoretical work, inherited from the precursor studies of McHale et al. (Reference McHale, Flynn and Newton2011) and Busse et al. (Reference Busse, Sandham, McHale and Newton2013), is that we consider the ‘perfect plastron’ limit and do not, therefore, make theoretical or numerical reference to the micro-pillars, -ridges or -posts that characterize real superhydrophobic surfaces. In other words, our hydrodynamic solutions of § 2 do not consider the protrusion of solid elements into the flow, or the loss of a purely no-slip boundary condition e.g. along the air–water interface. Although we can nonetheless reproduce important results from earlier studies, e.g. the ![]() $Nu_w-\tilde {{\mathcal {L}}}^t_{slip}$ relationship derived by Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) – see figure 16(a) – our study cannot thoroughly resolve broader questions of bubble stability and the possibility of air–solid detachment or ‘flushing’, the term applied by Cowley et al. (Reference Cowley, Maynes, Crockett and Iverson2018). With this limitation in mind, results from our analysis are likely more applicable to lab-on-a-chip technologies than they are to larger-scale engineering devices for which it may prove difficult to maintain an air layer with relative thickness
$Nu_w-\tilde {{\mathcal {L}}}^t_{slip}$ relationship derived by Enright et al. (Reference Enright, Hodes, Salamon and Muzychka2014) – see figure 16(a) – our study cannot thoroughly resolve broader questions of bubble stability and the possibility of air–solid detachment or ‘flushing’, the term applied by Cowley et al. (Reference Cowley, Maynes, Crockett and Iverson2018). With this limitation in mind, results from our analysis are likely more applicable to lab-on-a-chip technologies than they are to larger-scale engineering devices for which it may prove difficult to maintain an air layer with relative thickness ![]() $d \simeq 0.1$ (cf. table 2) and absolute thickness exceeding the capillary length. Of course, air (or some similar gas) may be added continually along the solid boundary e.g. by direct injection or, as examined by Panchanathan et al. (Reference Panchanathan, Rajappan, Varanasi and McKinley2018), as a byproduct of a chemical reaction. A further possibility, relevant to the case of a hot boundary, is that air dissolved into the cargo fluid effervesces out of solution and thereby regenerates those portions of the plastron lost due to shear stress (Cowley et al. Reference Cowley, Maynes, Crockett and Iverson2018; see also Lam et al. Reference Lam, Hodes and Enright2015). Unfortunately, it would be difficult to balance precisely the air lost versus regenerated by direct addition, chemical reaction and/or effervescence. If too little air is added relative to the volume lost, then the solid surface will eventually be wet. Conversely, if too much air is added, then one risks obstructing too large a fraction of the channel or pipe cross-sectional area. In this latter case, substantial increases to the drag force may result, as reported by Cowley et al. (Reference Cowley, Maynes, Crockett and Iverson2018) – see e.g. their figure 7.
$d \simeq 0.1$ (cf. table 2) and absolute thickness exceeding the capillary length. Of course, air (or some similar gas) may be added continually along the solid boundary e.g. by direct injection or, as examined by Panchanathan et al. (Reference Panchanathan, Rajappan, Varanasi and McKinley2018), as a byproduct of a chemical reaction. A further possibility, relevant to the case of a hot boundary, is that air dissolved into the cargo fluid effervesces out of solution and thereby regenerates those portions of the plastron lost due to shear stress (Cowley et al. Reference Cowley, Maynes, Crockett and Iverson2018; see also Lam et al. Reference Lam, Hodes and Enright2015). Unfortunately, it would be difficult to balance precisely the air lost versus regenerated by direct addition, chemical reaction and/or effervescence. If too little air is added relative to the volume lost, then the solid surface will eventually be wet. Conversely, if too much air is added, then one risks obstructing too large a fraction of the channel or pipe cross-sectional area. In this latter case, substantial increases to the drag force may result, as reported by Cowley et al. (Reference Cowley, Maynes, Crockett and Iverson2018) – see e.g. their figure 7.
Returning to the application of e.g. figures 12, 13, 14 and 16 to microfluidic devices, it is necessary to reiterate a further assumption applied in the development of our theoretical model, namely that the flow is fully developed. Even at small scales, such a state may not be fully realized except in the limit of small Reynolds number. For example, and considering single-phase pipe flow, the thermal entry length ![]() $L_t$ can be estimated from
$L_t$ can be estimated from
(Çengel & Ghajar Reference Çengel and Ghajar2021). Here, ![]() $L_h$ is the hydrodynamic entry length,
$L_h$ is the hydrodynamic entry length, ![]() $Pr$ is the Prandtl number,
$Pr$ is the Prandtl number, ![]() ${Re}$ is the Reynolds number, and
${Re}$ is the Reynolds number, and ![]() $D = 2R$ is the pipe diameter. The impact of entrance effects has been considered by a variety of authors, including Maynes et al. (Reference Maynes, Webb, Crockett and Solovjov2013) and Lam et al. (Reference Lam, Hodes and Enright2015). Although the related core annular flow analysis of Mukerjee & Davis (Reference Mukerjee and Davis1972) suggests that the Nusselt number ought to be larger throughout the developing regime, it remains to quantify this effect more precisely for the perfect plastron limit and the flow types summarized in table 1.
$D = 2R$ is the pipe diameter. The impact of entrance effects has been considered by a variety of authors, including Maynes et al. (Reference Maynes, Webb, Crockett and Solovjov2013) and Lam et al. (Reference Lam, Hodes and Enright2015). Although the related core annular flow analysis of Mukerjee & Davis (Reference Mukerjee and Davis1972) suggests that the Nusselt number ought to be larger throughout the developing regime, it remains to quantify this effect more precisely for the perfect plastron limit and the flow types summarized in table 1.
Whereas the restrictions described in the last two paragraphs may give the impression of a study of limited scope or applicability, the discussion of § 6 argues that the theoretical and numerical solutions presented in figures 12 and 13 are meaningful provided that the micro-topographical dimensions are modest and the micro-channel is not too long. Consider also that the theoretical solutions of § 2 can be adapted immediately to fluid pairs besides water and air. In other words, it is a trivial exercise to extend our ![]() $\dot {m}_a > 0$ solutions to other examples of core annular flows, e.g. the pipeline transport of heavy oils in the presence of a lubricating water layer (Joseph et al. Reference Joseph, Bai, Chen and Renardy1997). Indeed, heat transfer considerations may be especially important to this latter flow example given (i) the strong sensitivity of heavy oil viscosity to temperature, and (ii) the strong sensitivity of drag to viscosity.
$\dot {m}_a > 0$ solutions to other examples of core annular flows, e.g. the pipeline transport of heavy oils in the presence of a lubricating water layer (Joseph et al. Reference Joseph, Bai, Chen and Renardy1997). Indeed, heat transfer considerations may be especially important to this latter flow example given (i) the strong sensitivity of heavy oil viscosity to temperature, and (ii) the strong sensitivity of drag to viscosity.
Acknowledgements
The authors are grateful to S. Abraham, R. Meister, K. Rahnama, F. Sperling and F. Yeganehdoust for timely and insightful discussions. The thoughtful feedback provided by three anonymous referees helped to improve the quality and scope of the exposition.
Funding
This study was generously provided by the New Frontiers in Research Fund (Exploration).
Declaration of interests
The authors report no conflict of interest.