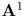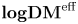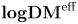Introduction
We fix once and for all a perfect base field ![]() $k$. The main purpose of this paper is to connect two developments that aim to extend Voevodsky's theory of motives over
$k$. The main purpose of this paper is to connect two developments that aim to extend Voevodsky's theory of motives over ![]() $k$ in such a way as to encompass non-
$k$ in such a way as to encompass non-![]() $\mathbf {A}^1$-invariant phenomena. One is the theory of reciprocity sheaves introduced by Kahn, Saito and Yamazaki [Reference Kahn, Saito and YamazakiKSY16, Reference Kahn, Saito and YamazakiKSY22] and developed in [Reference SaitoSai20, Reference Binda, Rülling and SaitoBRS22]. Voevodsky's theory is based on the category
$\mathbf {A}^1$-invariant phenomena. One is the theory of reciprocity sheaves introduced by Kahn, Saito and Yamazaki [Reference Kahn, Saito and YamazakiKSY16, Reference Kahn, Saito and YamazakiKSY22] and developed in [Reference SaitoSai20, Reference Binda, Rülling and SaitoBRS22]. Voevodsky's theory is based on the category ![]() ${\operatorname {\mathbf {PST}}}$ of presheaves with transfers, defined as the category of additive presheaves of abelian groups on the category
${\operatorname {\mathbf {PST}}}$ of presheaves with transfers, defined as the category of additive presheaves of abelian groups on the category ![]() $\operatorname {\mathbf {Cor}}$ of finite correspondences:
$\operatorname {\mathbf {Cor}}$ of finite correspondences: ![]() $\operatorname {\mathbf {Cor}}$ has the same objects as the category
$\operatorname {\mathbf {Cor}}$ has the same objects as the category ![]() $\operatorname {\mathbf {Sm}}$ of separated smooth schemes of finite type over
$\operatorname {\mathbf {Sm}}$ of separated smooth schemes of finite type over ![]() $k$, and morphisms in
$k$, and morphisms in ![]() $\operatorname {\mathbf {Cor}}$ are finite correspondences. Let
$\operatorname {\mathbf {Cor}}$ are finite correspondences. Let ![]() $\operatorname {\mathbf {NST}}\subset {\operatorname {\mathbf {PST}}}$ be the full subcategory of Nisnevich sheaves, that is, those objects
$\operatorname {\mathbf {NST}}\subset {\operatorname {\mathbf {PST}}}$ be the full subcategory of Nisnevich sheaves, that is, those objects ![]() $F\in {\operatorname {\mathbf {PST}}}$ whose restrictions
$F\in {\operatorname {\mathbf {PST}}}$ whose restrictions ![]() $F_X$ to the small étale site
$F_X$ to the small étale site ![]() $X_{{\operatorname {\acute {e}t}}}$ over
$X_{{\operatorname {\acute {e}t}}}$ over ![]() $X$ are Nisnevich sheaves for all
$X$ are Nisnevich sheaves for all ![]() $X\in \operatorname {\mathbf {Sm}}$. Voevodsky proved that
$X\in \operatorname {\mathbf {Sm}}$. Voevodsky proved that ![]() $\operatorname {\mathbf {NST}}$ is a Grothendieck abelian category and defined the triangulated category
$\operatorname {\mathbf {NST}}$ is a Grothendieck abelian category and defined the triangulated category ![]() $\operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$ of effective motives as the localization of the derived category
$\operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$ of effective motives as the localization of the derived category ![]() $D(\operatorname {\mathbf {NST}})$ of complexes in
$D(\operatorname {\mathbf {NST}})$ of complexes in ![]() $\operatorname {\mathbf {NST}}$ with respect to an
$\operatorname {\mathbf {NST}}$ with respect to an ![]() $\mathbf {A}^1$-weak equivalence (see [Reference Mazza, Voevodsky and WeibelMVW06, Definition 14.1]). It is equipped with a functor
$\mathbf {A}^1$-weak equivalence (see [Reference Mazza, Voevodsky and WeibelMVW06, Definition 14.1]). It is equipped with a functor ![]() $M: \operatorname {\mathbf {Sm}} \to \operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$ associating the motive
$M: \operatorname {\mathbf {Sm}} \to \operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$ associating the motive ![]() $M(X)$ of
$M(X)$ of ![]() $X\in \operatorname {\mathbf {Sm}}$.
$X\in \operatorname {\mathbf {Sm}}$.
Let ![]() $\operatorname {\mathbf {HI}}_{\operatorname {Nis}}\subset \operatorname {\mathbf {NST}}$ be the full subcategory consisting of
$\operatorname {\mathbf {HI}}_{\operatorname {Nis}}\subset \operatorname {\mathbf {NST}}$ be the full subcategory consisting of ![]() $\mathbf {A}^1$-invariant objects, namely such
$\mathbf {A}^1$-invariant objects, namely such ![]() $F\in \operatorname {\mathbf {NST}}$ that the projection
$F\in \operatorname {\mathbf {NST}}$ that the projection ![]() $\pi _X: X\times \mathbf {A}^1\to X$ induces an isomorphism
$\pi _X: X\times \mathbf {A}^1\to X$ induces an isomorphism ![]() $\pi _X^* :F(X)\simeq F(X\times \mathbf {A}^1)$ for any
$\pi _X^* :F(X)\simeq F(X\times \mathbf {A}^1)$ for any ![]() $X\in \operatorname {\mathbf {Sm}}$. We say that
$X\in \operatorname {\mathbf {Sm}}$. We say that ![]() $F\in \operatorname {\mathbf {HI}}_{\operatorname {Nis}}$ is strictly
$F\in \operatorname {\mathbf {HI}}_{\operatorname {Nis}}$ is strictly ![]() $\mathbf {A}^1$-invariant if
$\mathbf {A}^1$-invariant if ![]() $\pi _X$ induces isomorphisms
$\pi _X$ induces isomorphisms
The following theorem plays a fundamental role in Voevodsky's theory.
Theorem 0.1 (Voevodsky [Reference Voevodsky, Friedlander, Suslin and VoevodskyVoe00])
Any ![]() $F\in \operatorname {\mathbf {HI}}_{\operatorname {Nis}}$ is strictly
$F\in \operatorname {\mathbf {HI}}_{\operatorname {Nis}}$ is strictly ![]() $\mathbf {A}^1$-invariant and we have a natural isomorphism
$\mathbf {A}^1$-invariant and we have a natural isomorphism
where ![]() $L^{\mathbf {A}^1} : D(\operatorname {\mathbf {NST}})\to \operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$ is the localization functor.
$L^{\mathbf {A}^1} : D(\operatorname {\mathbf {NST}})\to \operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$ is the localization functor.
Notice that there are interesting and important objects of ![]() $\operatorname {\mathbf {NST}}$ which do not belong to
$\operatorname {\mathbf {NST}}$ which do not belong to ![]() $\operatorname {\mathbf {HI}}_{\operatorname {Nis}}$. Such examples are given by the sheaves
$\operatorname {\mathbf {HI}}_{\operatorname {Nis}}$. Such examples are given by the sheaves ![]() $\Omega ^i$ of (absolute or relative) differential forms; the
$\Omega ^i$ of (absolute or relative) differential forms; the ![]() $p$-typical de Rham–Witt sheaves
$p$-typical de Rham–Witt sheaves ![]() $W_m\Omega ^i$ of Bloch, Deligne and Illusie; smooth commutative
$W_m\Omega ^i$ of Bloch, Deligne and Illusie; smooth commutative ![]() $k$-group schemes with a unipotent part (seen as objects of
$k$-group schemes with a unipotent part (seen as objects of ![]() $\operatorname {\mathbf {NST}}$); and the complexes
$\operatorname {\mathbf {NST}}$); and the complexes ![]() $R\varepsilon _* \mathbb {Z}/p^r(n)$ with
$R\varepsilon _* \mathbb {Z}/p^r(n)$ with ![]() ${\operatorname {ch}}(k)=p>0$, where
${\operatorname {ch}}(k)=p>0$, where ![]() $\mathbb {Z}/p^r(n)$ is the étale motivic complex of weight
$\mathbb {Z}/p^r(n)$ is the étale motivic complex of weight ![]() $n$ with
$n$ with ![]() $\mathbb {Z}/p^r$ coefficients and
$\mathbb {Z}/p^r$ coefficients and ![]() $\varepsilon$ is the change of site functor from the étale to the Nisnevich topology. For such examples, (0.1.1) fails to hold since
$\varepsilon$ is the change of site functor from the étale to the Nisnevich topology. For such examples, (0.1.1) fails to hold since ![]() $\pi _X:X\times \mathbf {A}^1\to X$ induces an isomorphism
$\pi _X:X\times \mathbf {A}^1\to X$ induces an isomorphism ![]() $M(X\times \mathbf {A}^1)\simeq M(X)$ in
$M(X\times \mathbf {A}^1)\simeq M(X)$ in ![]() $\operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$ but the maps induced on the cohomology of those sheaves are not isomorphisms.
$\operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$ but the maps induced on the cohomology of those sheaves are not isomorphisms.
The category ![]() ${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ of reciprocity sheaves is a full abelian subcategory of
${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ of reciprocity sheaves is a full abelian subcategory of ![]() $\operatorname {\mathbf {NST}}$ that contains
$\operatorname {\mathbf {NST}}$ that contains ![]() $\operatorname {\mathbf {HI}}_{{\operatorname {Nis}}}$ as well as the non-
$\operatorname {\mathbf {HI}}_{{\operatorname {Nis}}}$ as well as the non-![]() $\mathbf {A}^1$-invariant objects mentioned above. Heuristically, its objects satisfy the property that for any
$\mathbf {A}^1$-invariant objects mentioned above. Heuristically, its objects satisfy the property that for any ![]() $X\in \operatorname {\mathbf {Sm}}$, each section
$X\in \operatorname {\mathbf {Sm}}$, each section ![]() $a\in F(X)$ ‘has bounded ramification at infinity’ and the objects of
$a\in F(X)$ ‘has bounded ramification at infinity’ and the objects of ![]() $\operatorname {\mathbf {HI}}_{\operatorname {Nis}}$ are special reciprocity sheaves with the property that every section
$\operatorname {\mathbf {HI}}_{\operatorname {Nis}}$ are special reciprocity sheaves with the property that every section ![]() $a\in F(X)$ has ‘tame’ ramification at infinity.Footnote 1 Slightly more exotic examples of reciprocity sheaves are given by the sheaves
$a\in F(X)$ has ‘tame’ ramification at infinity.Footnote 1 Slightly more exotic examples of reciprocity sheaves are given by the sheaves ![]() ${\rm Conn}^1$ (for
${\rm Conn}^1$ (for ![]() ${\operatorname {ch}}(k)=0$), whose sections over
${\operatorname {ch}}(k)=0$), whose sections over ![]() $X$ are rank
$X$ are rank ![]() $1$-connections, or
$1$-connections, or ![]() ${\rm Lisse}^1_\ell$ (in case
${\rm Lisse}^1_\ell$ (in case ![]() ${\operatorname {ch}}(k)=p>0$), whose sections on
${\operatorname {ch}}(k)=p>0$), whose sections on ![]() $X$ are the lisse
$X$ are the lisse ![]() $\overline {\mathbb {Q}}_\ell$-sheaves of rank
$\overline {\mathbb {Q}}_\ell$-sheaves of rank ![]() $1$. Since
$1$. Since ![]() ${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ is an abelian category equipped with a lax symmetric monoidal structure by [Reference Rülling, Sugiyama and YamazakiRSY22], many more interesting examples can be manufactured by taking kernels, quotients and tensor products (see [Reference Binda, Rülling and SaitoBRS22, § 11.1] for more examples).
${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ is an abelian category equipped with a lax symmetric monoidal structure by [Reference Rülling, Sugiyama and YamazakiRSY22], many more interesting examples can be manufactured by taking kernels, quotients and tensor products (see [Reference Binda, Rülling and SaitoBRS22, § 11.1] for more examples).
The main purpose of this paper is to establish formula (0.1.1) for all ![]() $F\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$ in a new category which enlarges
$F\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$ in a new category which enlarges ![]() $\operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$ (see (0.2)). It is the triangulated category
$\operatorname {\mathbf {DM}}^{{\operatorname {eff}}}$ (see (0.2)). It is the triangulated category ![]() $\operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ of logarithmic motives introduced by Binda, Park and Østvær in [Reference Binda, Park and ØstværBPØ22]. Let
$\operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ of logarithmic motives introduced by Binda, Park and Østvær in [Reference Binda, Park and ØstværBPØ22]. Let ![]() ${\operatorname {l\mathbf {Sm}}}$ be the category of log smooth and separated
${\operatorname {l\mathbf {Sm}}}$ be the category of log smooth and separated ![]() $\mathrm {fs}$ log schemes of finite type over
$\mathrm {fs}$ log schemes of finite type over ![]() $k$, and
$k$, and ![]() ${\operatorname {l\mathbf {Cor}}}$ be the category with the same objects as
${\operatorname {l\mathbf {Cor}}}$ be the category with the same objects as ![]() ${\operatorname {l\mathbf {Sm}}}$ and whose morphisms are log finite correspondences (see [Reference Binda, Park and ØstværBPØ22, Definition 2.1.1]). Let
${\operatorname {l\mathbf {Sm}}}$ and whose morphisms are log finite correspondences (see [Reference Binda, Park and ØstværBPØ22, Definition 2.1.1]). Let ![]() ${\operatorname {\mathbf {PSh}}^{\rm ltr}}$ be the category of additive presheaves of abelian groups on
${\operatorname {\mathbf {PSh}}^{\rm ltr}}$ be the category of additive presheaves of abelian groups on ![]() ${\operatorname {l\mathbf {Cor}}}$ and
${\operatorname {l\mathbf {Cor}}}$ and ![]() ${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}\subset {\operatorname {\mathbf {PSh}}^{\rm ltr}}$ be the full subcategory consisting of those
${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}\subset {\operatorname {\mathbf {PSh}}^{\rm ltr}}$ be the full subcategory consisting of those ![]() $\mathcal {F}$ whose restrictions to
$\mathcal {F}$ whose restrictions to ![]() ${\operatorname {l\mathbf {Sm}}}$ are dividing Nisnevich sheaves (see [Reference Binda, Park and ØstværBPØ22, Definition 3.1.4]). It is shown in [Reference Binda, Park and ØstværBPØ22, Theorem 1.2.1] that
${\operatorname {l\mathbf {Sm}}}$ are dividing Nisnevich sheaves (see [Reference Binda, Park and ØstværBPØ22, Definition 3.1.4]). It is shown in [Reference Binda, Park and ØstværBPØ22, Theorem 1.2.1] that ![]() ${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ is a Grothendieck abelian category, and
${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ is a Grothendieck abelian category, and ![]() $\operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ is defined as the localization of the derived category
$\operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ is defined as the localization of the derived category ![]() $D({\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}})$ of complexes in
$D({\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}})$ of complexes in ![]() ${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ with respect to a
${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ with respect to a ![]() ${\overline {\square }}$-weak equivalence, where
${\overline {\square }}$-weak equivalence, where ![]() ${\overline {\square }}$ is
${\overline {\square }}$ is ![]() $\mathbf {P}^1$ with the log structure associated to the effective divisor
$\mathbf {P}^1$ with the log structure associated to the effective divisor ![]() $\infty \hookrightarrow \mathbf {P}^1$ (see [Reference Binda, Park and ØstværBPØ22, Definition 5.2.1]).Footnote 2 It is equipped with a functor
$\infty \hookrightarrow \mathbf {P}^1$ (see [Reference Binda, Park and ØstværBPØ22, Definition 5.2.1]).Footnote 2 It is equipped with a functor ![]() $M: {\operatorname {l\mathbf {Sm}}} \to \operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ associating the logarithmic motive
$M: {\operatorname {l\mathbf {Sm}}} \to \operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ associating the logarithmic motive ![]() $M(\mathfrak {X})$ of
$M(\mathfrak {X})$ of ![]() $\mathfrak {X}\in {\operatorname {l\mathbf {Sm}}}$. Thanks to [Reference Binda and MericiBM12, Theorem 1,1], the standard
$\mathfrak {X}\in {\operatorname {l\mathbf {Sm}}}$. Thanks to [Reference Binda and MericiBM12, Theorem 1,1], the standard ![]() $t$-structure on
$t$-structure on ![]() $D({\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}})$ induces a
$D({\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}})$ induces a ![]() $t$-structure on
$t$-structure on ![]() $\operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ called the homotopy
$\operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ called the homotopy ![]() $t$-structure, and its heart is identified with the abelian full subcategory
$t$-structure, and its heart is identified with the abelian full subcategory ![]() $\operatorname {\mathbf {CI}}^{\rm ltr}_{\rm dNis}\subset {\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ consisting of strictly
$\operatorname {\mathbf {CI}}^{\rm ltr}_{\rm dNis}\subset {\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ consisting of strictly ![]() ${\overline {\square }}$-invariant objects in the sense of [Reference Binda, Park and ØstværBPØ22, Definition 5.2.2].Footnote 3 We can now state the main result of this paper.
${\overline {\square }}$-invariant objects in the sense of [Reference Binda, Park and ØstværBPØ22, Definition 5.2.2].Footnote 3 We can now state the main result of this paper.
Theorem 0.2 (Theorems 6.1 and 6.3)
There exists an exact and fully faithful functor
For ![]() $X\in \operatorname {\mathbf {Sm}}$ we have a natural isomorphism
$X\in \operatorname {\mathbf {Sm}}$ we have a natural isomorphism
where ![]() $L^{{\overline {\square }}} : D({\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}})\to \operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ is the localization functor and
$L^{{\overline {\square }}} : D({\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}})\to \operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ is the localization functor and ![]() $(X, \mathrm {triv})$ is the log scheme with the trivial log structure.
$(X, \mathrm {triv})$ is the log scheme with the trivial log structure.
We remark (see Remark 5.6) that, for ![]() $F=\Omega ^i$,
$F=\Omega ^i$, ![]() $F^{\log }(\mathfrak {X})$ for
$F^{\log }(\mathfrak {X})$ for ![]() $\mathfrak {X}\in {\operatorname {l\mathbf {Sm}}}$ whose underlying scheme is smooth agrees with the sheaf of logarithmic differential forms of
$\mathfrak {X}\in {\operatorname {l\mathbf {Sm}}}$ whose underlying scheme is smooth agrees with the sheaf of logarithmic differential forms of ![]() $\mathfrak {X}$ at least assuming
$\mathfrak {X}$ at least assuming ![]() ${\operatorname {ch}}(k)=0$.Footnote 4
${\operatorname {ch}}(k)=0$.Footnote 4
We now explain the organization of the paper.
In § 1 we discuss some preliminaries and fix notation. We recall the definitions and basic properties of modulus (pre)sheaves with transfers from [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Reference Kahn, Miyazaki, Saito and YamazakiKMSY21b, Reference Kahn, Saito and YamazakiKSY22, Reference SaitoSai20]. These are a generalization of Voevodsky's (pre)sheaves with transfers to a version with modulus. The category ![]() $\operatorname {\mathbf {\underline {M}Cor}}$ of modulus correspondences is introduced. Its objects are pairs
$\operatorname {\mathbf {\underline {M}Cor}}$ of modulus correspondences is introduced. Its objects are pairs ![]() $\mathcal {X} = (\overline {X}, D)$, where
$\mathcal {X} = (\overline {X}, D)$, where ![]() $\overline {X}$ is a separated scheme of finite type over
$\overline {X}$ is a separated scheme of finite type over ![]() $k$ equipped with an effective Cartier divisor
$k$ equipped with an effective Cartier divisor ![]() $D$ such that the interior
$D$ such that the interior ![]() $\overline {X}-D = X$ is smooth. The morphisms are finite correspondences on the interiors satisfying admissibility and a properness condition. Let
$\overline {X}-D = X$ is smooth. The morphisms are finite correspondences on the interiors satisfying admissibility and a properness condition. Let ![]() $\operatorname {\mathbf {\underline {M}PST}}$ be the category of additive presheaves of abelian groups on
$\operatorname {\mathbf {\underline {M}PST}}$ be the category of additive presheaves of abelian groups on ![]() $\operatorname {\mathbf {\underline {M}Cor}}$. A full subcategory
$\operatorname {\mathbf {\underline {M}Cor}}$. A full subcategory ![]() $\operatorname {\mathbf {\underline {M}NST}}\subset \operatorname {\mathbf {\underline {M}PST}}$ of Nisnevich sheaves is defined and there is a functor (see § 1(20))
$\operatorname {\mathbf {\underline {M}NST}}\subset \operatorname {\mathbf {\underline {M}PST}}$ of Nisnevich sheaves is defined and there is a functor (see § 1(20))
For every ![]() $F\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$ and
$F\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$ and ![]() $X\in \operatorname {\mathbf {Sm}}$, it provides an exhaustive filtration on the group
$X\in \operatorname {\mathbf {Sm}}$, it provides an exhaustive filtration on the group ![]() $F(X)$ of sections over
$F(X)$ of sections over ![]() $X$ which measures the depth of ramification along a boundary of a partial compactification of
$X$ which measures the depth of ramification along a boundary of a partial compactification of ![]() $X$: for
$X$: for ![]() $({\overline {X}},D)\in \operatorname {\mathbf {\underline {M}Cor}}$ with
$({\overline {X}},D)\in \operatorname {\mathbf {\underline {M}Cor}}$ with ![]() ${\overline {X}}-D=X$, we get the subgroups
${\overline {X}}-D=X$, we get the subgroups ![]() $\tilde {F}({\overline {X}},D)\subset F(X)$ with
$\tilde {F}({\overline {X}},D)\subset F(X)$ with ![]() $\tilde {F}=\underline {\omega }^{\operatorname {\mathbf {CI}}} F$ such that
$\tilde {F}=\underline {\omega }^{\operatorname {\mathbf {CI}}} F$ such that ![]() $\tilde {F}({\overline {X}},D_1)\subset \tilde {F}({\overline {X}},D_2)$ if
$\tilde {F}({\overline {X}},D_1)\subset \tilde {F}({\overline {X}},D_2)$ if ![]() $D_1\leq D_2$.
$D_1\leq D_2$.
In § 2 we prove as a key technical input an analogue of the Zariski–Nagata purity theorem [Reference GrothendieckSGA2, X 3.4] for ![]() $\tilde {F}({\overline {X}},D)$ as above. This asserts the exactness of the sequence
$\tilde {F}({\overline {X}},D)$ as above. This asserts the exactness of the sequence
 \[ 0\to \tilde{F}({\overline{X}},D) \to F(X) \to \underset{\xi\in {{D}^{(0)}}}\bigoplus \frac{F({{{\overline{X}}}^{h}_{|\xi}}-\xi)}{\tilde{F}({{{\overline{X}}}^{h}_{|\xi}},\xi)}, \]
\[ 0\to \tilde{F}({\overline{X}},D) \to F(X) \to \underset{\xi\in {{D}^{(0)}}}\bigoplus \frac{F({{{\overline{X}}}^{h}_{|\xi}}-\xi)}{\tilde{F}({{{\overline{X}}}^{h}_{|\xi}},\xi)}, \]
where ![]() ${\overline {X}}\in \operatorname {\mathbf {Sm}}$ and
${\overline {X}}\in \operatorname {\mathbf {Sm}}$ and ![]() $D$ is a reduced simple normal crossing divisor, and where
$D$ is a reduced simple normal crossing divisor, and where ![]() ${{D}^{(0)}}$ is the set of the irreducible components of
${{D}^{(0)}}$ is the set of the irreducible components of ![]() $D$ and
$D$ and ![]() ${{{\overline{X}}}^{h}_{|\xi}}$ is the henselization of
${{{\overline{X}}}^{h}_{|\xi}}$ is the henselization of ![]() ${\overline {X}}$ at
${\overline {X}}$ at ![]() $\xi$. In [Reference Rülling and SaitoRS21b] this result is generalized to the case where
$\xi$. In [Reference Rülling and SaitoRS21b] this result is generalized to the case where ![]() $D$ may not be reduced under the assumption that
$D$ may not be reduced under the assumption that ![]() ${\overline {X}}$ admits a smooth compactification.
${\overline {X}}$ admits a smooth compactification.
In § 3 we review higher local symbols for reciprocity sheaves constructed in [Reference Rülling and SaitoRS21c]. These are an effective tool with which one can decide when a given element of ![]() $F(X)$ with
$F(X)$ with ![]() $F\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$ and
$F\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$ and ![]() $X\in \operatorname {\mathbf {Sm}}$ belongs to
$X\in \operatorname {\mathbf {Sm}}$ belongs to ![]() $\tilde {F}({\overline {X}},D)$ as above. The construction of the pairing depends on pushforward maps for the cohomology of reciprocity sheaves constructed in [Reference Binda, Rülling and SaitoBRS22] (which means that Theorem 0.2 depends on the result of [Reference Binda, Rülling and SaitoBRS22]).
$\tilde {F}({\overline {X}},D)$ as above. The construction of the pairing depends on pushforward maps for the cohomology of reciprocity sheaves constructed in [Reference Binda, Rülling and SaitoBRS22] (which means that Theorem 0.2 depends on the result of [Reference Binda, Rülling and SaitoBRS22]).
In § 4 we prove the following result. Let ![]() $\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$ be the subcategory of
$\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$ be the subcategory of ![]() $\operatorname {\mathbf {\underline {M}Cor}}$ whose objects are pairs
$\operatorname {\mathbf {\underline {M}Cor}}$ whose objects are pairs ![]() $(X,D)$ such that
$(X,D)$ such that ![]() $X\in \operatorname {\mathbf {Sm}}$ and the reduced divisor
$X\in \operatorname {\mathbf {Sm}}$ and the reduced divisor ![]() $D_{{\operatorname {red}}}$ underlying
$D_{{\operatorname {red}}}$ underlying ![]() $D$ is a simple normal crossing divisor on
$D$ is a simple normal crossing divisor on ![]() $X$ and whose morphisms are modulus correspondences satisfying a finiteness conditions instead of the properness condition (see § 1(5)). Then, for
$X$ and whose morphisms are modulus correspondences satisfying a finiteness conditions instead of the properness condition (see § 1(5)). Then, for ![]() $F\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$, the association
$F\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$, the association
gives a presheaf on ![]() $\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$, which gives rise to a cohomology theory
$\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$, which gives rise to a cohomology theory ![]() $H^i_{\log }(-,\tilde {F}^{\log })$ on
$H^i_{\log }(-,\tilde {F}^{\log })$ on ![]() $\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$, called the
$\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$, called the ![]() $i$th logarithmic cohomology with coefficient
$i$th logarithmic cohomology with coefficient ![]() $F$ (see Definition 4.4). The higher local symbols for
$F$ (see Definition 4.4). The higher local symbols for ![]() $F$ play a fundamental role in the proof of the result.
$F$ play a fundamental role in the proof of the result.
In § 5 we prove the invariance of logarithmic cohomology under blowups. Let ![]() $\Lambda ^{{\operatorname {fin}}}_{\rm ls}$ be the subcategory of
$\Lambda ^{{\operatorname {fin}}}_{\rm ls}$ be the subcategory of ![]() $\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$ whose objects are the same as
$\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$ whose objects are the same as ![]() $\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$ and whose morphisms are those
$\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$ and whose morphisms are those ![]() $\rho : (Y,E) \to (X,D)$ where
$\rho : (Y,E) \to (X,D)$ where ![]() $E=\rho ^* D$ and
$E=\rho ^* D$ and ![]() $\rho$ are induced by blowups of
$\rho$ are induced by blowups of ![]() $X$ in smooth centers
$X$ in smooth centers ![]() $Z\subset D$ which are normal crossing to
$Z\subset D$ which are normal crossing to ![]() $D$ (see the beginning of the section). Then, for
$D$ (see the beginning of the section). Then, for ![]() $F\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$ and
$F\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$ and ![]() $\rho :\mathcal {Y}\to \mathcal {X}$ in
$\rho :\mathcal {Y}\to \mathcal {X}$ in ![]() $\Lambda ^{{\operatorname {fin}}}_{\rm ls}$, we have
$\Lambda ^{{\operatorname {fin}}}_{\rm ls}$, we have
In § 6 we prove Theorem 0.2, which is a formal consequence of the theorems in §§ 4 and 5.
1. Preliminaries
We fix once and for all a perfect base field ![]() $k$. In this section we recall the definitions and basic properties of modulus sheaves with transfers from [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Reference SaitoSai20].
$k$. In this section we recall the definitions and basic properties of modulus sheaves with transfers from [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Reference SaitoSai20].
(1) Denote by
 $\operatorname {\mathbf {Sch}}$ the category of separated schemes of finite type over
$\operatorname {\mathbf {Sch}}$ the category of separated schemes of finite type over  $k$ and by
$k$ and by  $\operatorname {\mathbf {Sm}}$ the full subcategory of smooth schemes. For
$\operatorname {\mathbf {Sm}}$ the full subcategory of smooth schemes. For  $X, Y \in \operatorname {\mathbf {Sm}}$, an integral closed subscheme of
$X, Y \in \operatorname {\mathbf {Sm}}$, an integral closed subscheme of  $X\times Y$ that is finite and surjective over a connected component of
$X\times Y$ that is finite and surjective over a connected component of  $X$ is called a prime correspondence from
$X$ is called a prime correspondence from  $X$ to
$X$ to  $Y$. The category
$Y$. The category  $\operatorname {\mathbf {Cor}}$ of finite correspondences has the same objects as
$\operatorname {\mathbf {Cor}}$ of finite correspondences has the same objects as  $\operatorname {\mathbf {Sm}}$, and for
$\operatorname {\mathbf {Sm}}$, and for  $X, Y \in \operatorname {\mathbf {Sm}}$,
$X, Y \in \operatorname {\mathbf {Sm}}$,  $\operatorname {\mathbf {Cor}}(X,Y)$ is the free abelian group on the set of all prime correspondences from
$\operatorname {\mathbf {Cor}}(X,Y)$ is the free abelian group on the set of all prime correspondences from  $X$ to
$X$ to  $Y$ (see [Reference Voevodsky, Friedlander, Suslin and VoevodskyVoe00]). We consider
$Y$ (see [Reference Voevodsky, Friedlander, Suslin and VoevodskyVoe00]). We consider  $\operatorname {\mathbf {Sm}}$ as a subcategory of
$\operatorname {\mathbf {Sm}}$ as a subcategory of  $\operatorname {\mathbf {Cor}}$ by regarding a morphism in
$\operatorname {\mathbf {Cor}}$ by regarding a morphism in  $\operatorname {\mathbf {Sm}}$ as its graph in
$\operatorname {\mathbf {Sm}}$ as its graph in  $\operatorname {\mathbf {Cor}}$.
$\operatorname {\mathbf {Cor}}$.Let
 ${\operatorname {\mathbf {PST}}}$ be the category of additive presheaves of abelian groups on
${\operatorname {\mathbf {PST}}}$ be the category of additive presheaves of abelian groups on  $\operatorname {\mathbf {Cor}}$ whose objects are called presheaves with transfers. Let
$\operatorname {\mathbf {Cor}}$ whose objects are called presheaves with transfers. Let  $\operatorname {\mathbf {NST}}\subseteq {\operatorname {\mathbf {PST}}}$ be the category of Nisnevich sheaves with transfers and let
be Voevodsky's Nisnevich sheafification functor, which is an exact left adjoint to the inclusion
$\operatorname {\mathbf {NST}}\subseteq {\operatorname {\mathbf {PST}}}$ be the category of Nisnevich sheaves with transfers and let
be Voevodsky's Nisnevich sheafification functor, which is an exact left adjoint to the inclusion \[ a^V_{\operatorname{Nis}} :{\operatorname{\mathbf{PST}}}\to \operatorname{\mathbf{NST}} \]
\[ a^V_{\operatorname{Nis}} :{\operatorname{\mathbf{PST}}}\to \operatorname{\mathbf{NST}} \]
 $\operatorname {\mathbf {NST}}\to {\operatorname {\mathbf {PST}}}$. Let
$\operatorname {\mathbf {NST}}\to {\operatorname {\mathbf {PST}}}$. Let  $\operatorname {\mathbf {HI}}\subseteq {\operatorname {\mathbf {PST}}}$ be the category of
$\operatorname {\mathbf {HI}}\subseteq {\operatorname {\mathbf {PST}}}$ be the category of  $\mathbf {A}^1$-invariant presheaves and put
$\mathbf {A}^1$-invariant presheaves and put  $\operatorname {\mathbf {HI}}_{\operatorname {Nis}}=\operatorname {\mathbf {HI}}\cap \operatorname {\mathbf {NST}}\subseteq \operatorname {\mathbf {NST}}$.
$\operatorname {\mathbf {HI}}_{\operatorname {Nis}}=\operatorname {\mathbf {HI}}\cap \operatorname {\mathbf {NST}}\subseteq \operatorname {\mathbf {NST}}$.(2) Let
 $\operatorname {\mathbf {Sm}}^{\rm pro}$ be the category of
$\operatorname {\mathbf {Sm}}^{\rm pro}$ be the category of  $k$-schemes
$k$-schemes  $X$ which are essentially smooth over
$X$ which are essentially smooth over  $k$, that is,
$k$, that is,  $X$ is a limit
$X$ is a limit  $\mathop {\varprojlim }_{i \in I} X_i$ over a filtered set
$\mathop {\varprojlim }_{i \in I} X_i$ over a filtered set  $I$, where
$I$, where  $X_i$ is smooth over
$X_i$ is smooth over  $k$ and all transition maps are étale. Note that
$k$ and all transition maps are étale. Note that  $\operatorname {Spec} K\in \operatorname {\mathbf {Sm}}^{\rm pro}$ for a function field
$\operatorname {Spec} K\in \operatorname {\mathbf {Sm}}^{\rm pro}$ for a function field  $K$ over
$K$ over  $k$ thanks to the assumption that
$k$ thanks to the assumption that  $k$ is perfect. We define
$k$ is perfect. We define  $\operatorname {\mathbf {Cor}}^{\rm pro}$ whose objects are the same as
$\operatorname {\mathbf {Cor}}^{\rm pro}$ whose objects are the same as  $\operatorname {\mathbf {Sm}}^{\rm pro}$ and whose morphisms are defined as [Reference Rülling and SaitoRS21a, Definition 2,2]. We extend
$\operatorname {\mathbf {Sm}}^{\rm pro}$ and whose morphisms are defined as [Reference Rülling and SaitoRS21a, Definition 2,2]. We extend  $F\in {\operatorname {\mathbf {PST}}}$ to a presheaf on
$F\in {\operatorname {\mathbf {PST}}}$ to a presheaf on  $\operatorname {\mathbf {Cor}}^{\rm pro}$ by
$\operatorname {\mathbf {Cor}}^{\rm pro}$ by  $F(X) := \mathop {\varinjlim }_{i \in I} F(X_i)$ for
$F(X) := \mathop {\varinjlim }_{i \in I} F(X_i)$ for  $X$ as above.
$X$ as above.(3) We recall the definition of the category
 $\operatorname {\mathbf {\underline {M}Cor}}$ from [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Definition 1.3.1]. A pair
$\operatorname {\mathbf {\underline {M}Cor}}$ from [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Definition 1.3.1]. A pair  $\mathcal {X} = (X,D)$ consisting of
$\mathcal {X} = (X,D)$ consisting of  $X \in \operatorname {\mathbf {Sch}}$ and an effective Cartier divisor
$X \in \operatorname {\mathbf {Sch}}$ and an effective Cartier divisor  $D$ on
$D$ on  $X$ is called a modulus pair if
$X$ is called a modulus pair if  $X - D \in \operatorname {\mathbf {Sm}}$. Let
$X - D \in \operatorname {\mathbf {Sm}}$. Let  $\mathcal {X}=(X,D_X)$,
$\mathcal {X}=(X,D_X)$,  $\mathcal {Y}=(Y,D_Y)$ be modulus pairs and
$\mathcal {Y}=(Y,D_Y)$ be modulus pairs and  $\Gamma \in \operatorname {\mathbf {Cor}}(X-D_X,Y-D_Y)$ be a prime correspondence. Let
$\Gamma \in \operatorname {\mathbf {Cor}}(X-D_X,Y-D_Y)$ be a prime correspondence. Let  $\overline {\Gamma } \subseteq X \times Y$ be the closure of
$\overline {\Gamma } \subseteq X \times Y$ be the closure of  $\Gamma$, and let
$\Gamma$, and let  $\overline {\Gamma }^N\to X\times Y$ be the normalization. We say that
$\overline {\Gamma }^N\to X\times Y$ be the normalization. We say that  $\Gamma$ is admissible (respectively, left proper) if
$\Gamma$ is admissible (respectively, left proper) if  $(D_X)_{\overline {\Gamma }^N}\geq (D_Y)_{\overline {\Gamma }^N}$ (respectively, if
$(D_X)_{\overline {\Gamma }^N}\geq (D_Y)_{\overline {\Gamma }^N}$ (respectively, if  $\overline {\Gamma }$ is proper over
$\overline {\Gamma }$ is proper over  $X$). Let
$X$). Let  $\operatorname {\mathbf {\underline {M}Cor}}(\mathcal {X}, \mathcal {Y})$ be the subgroup of
$\operatorname {\mathbf {\underline {M}Cor}}(\mathcal {X}, \mathcal {Y})$ be the subgroup of  $\operatorname {\mathbf {Cor}}(X-D_X,Y-D_Y)$ generated by all admissible left proper prime correspondences. The category
$\operatorname {\mathbf {Cor}}(X-D_X,Y-D_Y)$ generated by all admissible left proper prime correspondences. The category  $\operatorname {\mathbf {\underline {M}Cor}}$ has modulus pairs as objects and
$\operatorname {\mathbf {\underline {M}Cor}}$ has modulus pairs as objects and  $\operatorname {\mathbf {\underline {M}Cor}}(\mathcal {X}, \mathcal {Y})$ as the group of morphisms from
$\operatorname {\mathbf {\underline {M}Cor}}(\mathcal {X}, \mathcal {Y})$ as the group of morphisms from  $\mathcal {X}$ to
$\mathcal {X}$ to  $\mathcal {Y}$.
$\mathcal {Y}$.(4) Let
 $\operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}\subset \operatorname {\mathbf {\underline {M}Cor}}$ be the full subcategory of
$\operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}\subset \operatorname {\mathbf {\underline {M}Cor}}$ be the full subcategory of  $(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}$ with
$(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}$ with  $X\in \operatorname {\mathbf {Sm}}$ and
$X\in \operatorname {\mathbf {Sm}}$ and  $|D|$ a normal crossing divisor on
$|D|$ a normal crossing divisor on  $X$.
$X$.(5) Let
 $\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}\subset \operatorname {\mathbf {\underline {M}Cor}}$ be the full subcategory of the same objects such that
$\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}\subset \operatorname {\mathbf {\underline {M}Cor}}$ be the full subcategory of the same objects such that  $\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}(\mathcal {X}, \mathcal {Y})$ are generated by all admissible finite prime correspondences, where finite prime correspondences are defined by replacing the left properness in (3) by finiteness. We also define
$\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}(\mathcal {X}, \mathcal {Y})$ are generated by all admissible finite prime correspondences, where finite prime correspondences are defined by replacing the left properness in (3) by finiteness. We also define  $\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls} = \operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}\cap \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$.
$\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls} = \operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}\cap \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$.(6) There is a canonical pair of adjoint functors
 $\lambda \dashv \underline {\omega }$:
$\lambda \dashv \underline {\omega }$:
 \begin{gather*} \lambda: \operatorname{\mathbf{Cor}}\to \operatorname{\mathbf{\underline{M}Cor}}\quad X\mapsto (X,\emptyset),\end{gather*}
\begin{gather*} \lambda: \operatorname{\mathbf{Cor}}\to \operatorname{\mathbf{\underline{M}Cor}}\quad X\mapsto (X,\emptyset),\end{gather*}
 \begin{gather*} \underline{\omega}:
\operatorname{\mathbf{\underline{M}Cor}}\to\operatorname{\mathbf{Cor}}\quad
(X,D)\mapsto X-D.\end{gather*}
\begin{gather*} \underline{\omega}:
\operatorname{\mathbf{\underline{M}Cor}}\to\operatorname{\mathbf{Cor}}\quad
(X,D)\mapsto X-D.\end{gather*}
(7) There is a full subcategory
 $\mathbf {MCor}\subset \operatorname {\mathbf {\underline {M}Cor}}$ consisting of proper modulus pairs, where a modulus pair
$\mathbf {MCor}\subset \operatorname {\mathbf {\underline {M}Cor}}$ consisting of proper modulus pairs, where a modulus pair  $(X,D)$ is proper if
$(X,D)$ is proper if  $X$ is proper. Let
$X$ is proper. Let  $\tau :\operatorname {\mathbf {MCor}}\hookrightarrow \operatorname {\mathbf {\underline {M}Cor}}$ be the inclusion functor and
$\tau :\operatorname {\mathbf {MCor}}\hookrightarrow \operatorname {\mathbf {\underline {M}Cor}}$ be the inclusion functor and  $\omega =\underline {\omega }\tau$.
$\omega =\underline {\omega }\tau$.(8) Let
 $\operatorname {\mathbf {MPST}}$ (respectively,
$\operatorname {\mathbf {MPST}}$ (respectively,  $\operatorname {\mathbf {\underline {M}PST}}$) be the category of additive presheaves of abelian groups on
$\operatorname {\mathbf {\underline {M}PST}}$) be the category of additive presheaves of abelian groups on  $\operatorname {\mathbf {MCor}}$ (respectively,
$\operatorname {\mathbf {MCor}}$ (respectively,  $\operatorname {\mathbf {\underline {M}Cor}}$) whose objects are called modulus presheaves with transfers. For
$\operatorname {\mathbf {\underline {M}Cor}}$) whose objects are called modulus presheaves with transfers. For  $\mathcal {X} \in \operatorname {\mathbf {MCor}}$, let
$\mathcal {X} \in \operatorname {\mathbf {MCor}}$, let  ${\operatorname {\mathbb {Z}_{{\operatorname {tr}}}}}(\mathcal {X})=\operatorname {\mathbf {\underline {M}Cor}}(-,\mathcal {X})$ be the representable object of
${\operatorname {\mathbb {Z}_{{\operatorname {tr}}}}}(\mathcal {X})=\operatorname {\mathbf {\underline {M}Cor}}(-,\mathcal {X})$ be the representable object of  $\operatorname {\mathbf {\underline {M}PST}}$. We sometimes write
$\operatorname {\mathbf {\underline {M}PST}}$. We sometimes write  $\mathcal {X}$ for
$\mathcal {X}$ for  ${\operatorname {\mathbb {Z}_{{\operatorname {tr}}}}}(\mathcal {X})$ for simplicity.
${\operatorname {\mathbb {Z}_{{\operatorname {tr}}}}}(\mathcal {X})$ for simplicity.(9) In the same manner as (2), the category
 $\operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$ is defined and
$\operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$ is defined and  $F\in \operatorname {\mathbf {\underline {M}PST}}$ is extended to a presheaf on
$F\in \operatorname {\mathbf {\underline {M}PST}}$ is extended to a presheaf on  $\operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$ (see [Reference Rülling and SaitoRS21a, § 3.7]).
$\operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$ (see [Reference Rülling and SaitoRS21a, § 3.7]).(10) The adjunction
 $\lambda \dashv \underline {\omega }$ induces a string of four adjoint functors
$\lambda \dashv \underline {\omega }$ induces a string of four adjoint functors  $(\lambda _!=\underline {\omega }^!,\lambda ^*=\underline {\omega }_!,\lambda _*=\underline {\omega }^*,\underline {\omega }_*)$ (see [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Proposition 2.3.1]):
where
$(\lambda _!=\underline {\omega }^!,\lambda ^*=\underline {\omega }_!,\lambda _*=\underline {\omega }^*,\underline {\omega }_*)$ (see [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Proposition 2.3.1]):
where \[ \operatorname{\mathbf{\underline{M}PST}}\begin{smallmatrix}\underline{\omega}^!\\\longleftarrow\\\underline{\omega}_!\\\longrightarrow\\\underline{\omega}^*\\\longleftarrow\\\underline{\omega}_*\\ \longrightarrow\end{smallmatrix}{\operatorname{\mathbf{PST}}} \]
\[ \operatorname{\mathbf{\underline{M}PST}}\begin{smallmatrix}\underline{\omega}^!\\\longleftarrow\\\underline{\omega}_!\\\longrightarrow\\\underline{\omega}^*\\\longleftarrow\\\underline{\omega}_*\\ \longrightarrow\end{smallmatrix}{\operatorname{\mathbf{PST}}} \]
 $\underline {\omega }_!,\underline {\omega }_*$ are localizations and
$\underline {\omega }_!,\underline {\omega }_*$ are localizations and  $\underline {\omega }^!$ and
$\underline {\omega }^!$ and  $\underline {\omega }^*$ are fully faithful.
$\underline {\omega }^*$ are fully faithful.(11) The functor
 $\tau$ yields a string of three adjoint functors
$\tau$ yields a string of three adjoint functors  $(\tau _!,\tau ^*,\tau _*)$:
where
$(\tau _!,\tau ^*,\tau _*)$:
where \[ \operatorname{\mathbf{MPST}}\begin{smallmatrix}\tau_!\\\longrightarrow\\\tau^*\\\longleftarrow\\\tau_*\\ \longrightarrow\end{smallmatrix}\operatorname{\mathbf{\underline{M}PST}} \]
\[ \operatorname{\mathbf{MPST}}\begin{smallmatrix}\tau_!\\\longrightarrow\\\tau^*\\\longleftarrow\\\tau_*\\ \longrightarrow\end{smallmatrix}\operatorname{\mathbf{\underline{M}PST}} \]
 $\tau _!,\tau _*$ are fully faithful and
$\tau _!,\tau _*$ are fully faithful and  $\tau ^*$ is a localization;
$\tau ^*$ is a localization;  $\tau _!$ has a pro-left adjoint
$\tau _!$ has a pro-left adjoint  $\tau ^!$, hence is exact (see [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Proposition 2.4.1]). We will denote by
$\tau ^!$, hence is exact (see [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Proposition 2.4.1]). We will denote by  $\operatorname {\mathbf {\underline {M}PST}}^{\tau }$ the essential image of
$\operatorname {\mathbf {\underline {M}PST}}^{\tau }$ the essential image of  $\tau _!$ in
$\tau _!$ in  $\operatorname {\mathbf {\underline {M}PST}}$.
$\operatorname {\mathbf {\underline {M}PST}}$.(12) The modulus pair
 ${\overline {\square }}:=(\mathbf {P}^1,\infty )$ has an interval structure induced by that of
${\overline {\square }}:=(\mathbf {P}^1,\infty )$ has an interval structure induced by that of  $\mathbf {A}^1$ (see [Reference Kahn, Saito and YamazakiKSY22, Lemma 2.1.3]). We say that
$\mathbf {A}^1$ (see [Reference Kahn, Saito and YamazakiKSY22, Lemma 2.1.3]). We say that  $F \in \operatorname {\mathbf {MPST}}$ is
$F \in \operatorname {\mathbf {MPST}}$ is  ${\overline {\square }}$-invariant if
${\overline {\square }}$-invariant if  $p^* : F(\mathcal {X}) \to F(\mathcal {X} \otimes {\overline {\square }})$ is an isomorphism for any
$p^* : F(\mathcal {X}) \to F(\mathcal {X} \otimes {\overline {\square }})$ is an isomorphism for any  $\mathcal {X} \in \operatorname {\mathbf {MCor}}$, where
$\mathcal {X} \in \operatorname {\mathbf {MCor}}$, where  $p : \mathcal {X} \otimes {\overline {\square }} \to \mathcal {X}$ is the projection. Let
$p : \mathcal {X} \otimes {\overline {\square }} \to \mathcal {X}$ is the projection. Let  $\operatorname {\mathbf {CI}}$ be the full subcategory of
$\operatorname {\mathbf {CI}}$ be the full subcategory of  $\operatorname {\mathbf {MPST}}$ consisting of all
$\operatorname {\mathbf {MPST}}$ consisting of all  ${\overline {\square }}$-invariant objects and
${\overline {\square }}$-invariant objects and  $\operatorname {\mathbf {CI}}^{\tau }\subset \operatorname {\mathbf {\underline {M}PST}}$ be the essential image of
$\operatorname {\mathbf {CI}}^{\tau }\subset \operatorname {\mathbf {\underline {M}PST}}$ be the essential image of  $\operatorname {\mathbf {CI}}$ under
$\operatorname {\mathbf {CI}}$ under  $\tau _!$.
$\tau _!$.(13) Recall from [Reference Kahn, Saito and YamazakiKSY22, Theorem 2.1.8] that
 $\operatorname {\mathbf {CI}}$ is a Serre subcategory of
$\operatorname {\mathbf {CI}}$ is a Serre subcategory of  $\operatorname {\mathbf {MPST}}$, and that the inclusion functor
$\operatorname {\mathbf {MPST}}$, and that the inclusion functor  $i^{\overline {\square }} : \operatorname {\mathbf {CI}} \to \operatorname {\mathbf {MPST}}$ has a left adjoint
$i^{\overline {\square }} : \operatorname {\mathbf {CI}} \to \operatorname {\mathbf {MPST}}$ has a left adjoint  $h_0^{\overline {\square }}$ and a right adjoint
$h_0^{\overline {\square }}$ and a right adjoint  $h^0_{\overline {\square }}$ given for
$h^0_{\overline {\square }}$ given for  $F \in \operatorname {\mathbf {MPST}}$ and
$F \in \operatorname {\mathbf {MPST}}$ and  $\mathcal {X} \in \operatorname {\mathbf {MCor}}$ by
For
$\mathcal {X} \in \operatorname {\mathbf {MCor}}$ by
For \begin{align*} &h_0^{\overline{\square}}(F)(\mathcal{X})=\operatorname{Coker}(i_0^* - i_1^* : F(\mathcal{X} \otimes {\overline{\square}}) \to F(\mathcal{X})),\\ &h^0_{\overline{\square}}(F)(\mathcal{X})=\operatorname{Hom}(h_0^{\overline{\square}}(\mathcal{X}), F). \end{align*}
\begin{align*} &h_0^{\overline{\square}}(F)(\mathcal{X})=\operatorname{Coker}(i_0^* - i_1^* : F(\mathcal{X} \otimes {\overline{\square}}) \to F(\mathcal{X})),\\ &h^0_{\overline{\square}}(F)(\mathcal{X})=\operatorname{Hom}(h_0^{\overline{\square}}(\mathcal{X}), F). \end{align*}
 $\mathcal {X}\in \operatorname {\mathbf {MCor}}$, we write
$\mathcal {X}\in \operatorname {\mathbf {MCor}}$, we write  $h_0^{\overline {\square }}(\mathcal {X})=h_0^{\overline {\square }}({\operatorname {\mathbb {Z}_{{\operatorname {tr}}}}}(\mathcal {X}))\in \operatorname {\mathbf {CI}}$, and by abuse of notation we also write
$h_0^{\overline {\square }}(\mathcal {X})=h_0^{\overline {\square }}({\operatorname {\mathbb {Z}_{{\operatorname {tr}}}}}(\mathcal {X}))\in \operatorname {\mathbf {CI}}$, and by abuse of notation we also write  $h_0^{\overline {\square }}(\mathcal {X})$ for
$h_0^{\overline {\square }}(\mathcal {X})$ for  $\tau _!h_0^{\overline {\square }}(\mathcal {X})\in \operatorname {\mathbf {CI}}^{\tau }$.
$\tau _!h_0^{\overline {\square }}(\mathcal {X})\in \operatorname {\mathbf {CI}}^{\tau }$.(14) For
 $F\in \operatorname {\mathbf {\underline {M}PST}}$ and
$F\in \operatorname {\mathbf {\underline {M}PST}}$ and  $\mathcal {X}=(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}$, write
$\mathcal {X}=(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}$, write  $F_{\mathcal {X}}$ for the presheaf on the small étale site
$F_{\mathcal {X}}$ for the presheaf on the small étale site  $X_{{\operatorname {\acute {e}t}}}$ over
$X_{{\operatorname {\acute {e}t}}}$ over  $X$ given by
$X$ given by  $U\to F(\mathcal {X}_U)$ for
$U\to F(\mathcal {X}_U)$ for  $U\to X$ étale, where
$U\to X$ étale, where  $\mathcal {X}_U=(U,D_{|U})\in \operatorname {\mathbf {\underline {M}Cor}}$. We say that
$\mathcal {X}_U=(U,D_{|U})\in \operatorname {\mathbf {\underline {M}Cor}}$. We say that  $F$ is a Nisnevich sheaf if
$F$ is a Nisnevich sheaf if  $F_{\mathcal {X}}$ is also one for all
$F_{\mathcal {X}}$ is also one for all  $\mathcal {X}\in \operatorname {\mathbf {\underline {M}Cor}}$ (see [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, § 3]). We write
$\mathcal {X}\in \operatorname {\mathbf {\underline {M}Cor}}$ (see [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, § 3]). We write  $\operatorname {\mathbf {\underline {M}NST}}\subset \operatorname {\mathbf {\underline {M}PST}}$ for the full subcategory of Nisnevich sheaves and put
By [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Proposition 3.5.3] and [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21b, Theorem 2], the inclusion functor
$\operatorname {\mathbf {\underline {M}NST}}\subset \operatorname {\mathbf {\underline {M}PST}}$ for the full subcategory of Nisnevich sheaves and put
By [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Proposition 3.5.3] and [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21b, Theorem 2], the inclusion functor \[ \operatorname{\mathbf{MNST}}^\tau=\operatorname{\mathbf{\underline{M}NST}}\cap \operatorname{\mathbf{MPST}}^\tau,\quad \operatorname{\mathbf{CI}}^{\tau}_{\operatorname{Nis}} =\operatorname{\mathbf{CI}}^{\tau}\cap \operatorname{\mathbf{MNST}}^\tau. \]
\[ \operatorname{\mathbf{MNST}}^\tau=\operatorname{\mathbf{\underline{M}NST}}\cap \operatorname{\mathbf{MPST}}^\tau,\quad \operatorname{\mathbf{CI}}^{\tau}_{\operatorname{Nis}} =\operatorname{\mathbf{CI}}^{\tau}\cap \operatorname{\mathbf{MNST}}^\tau. \]
 $i_{\operatorname {Nis}}: \operatorname {\mathbf {\underline {M}NST}}\to \operatorname {\mathbf {\underline {M}PST}}$ has an exact left adjoint
$i_{\operatorname {Nis}}: \operatorname {\mathbf {\underline {M}NST}}\to \operatorname {\mathbf {\underline {M}PST}}$ has an exact left adjoint  ${\underline {a}}_{\operatorname {Nis}}$ such that
${\underline {a}}_{\operatorname {Nis}}$ such that  ${\underline {a}}_{\operatorname {Nis}}(\operatorname {\mathbf {MPST}}^\tau )\subset \operatorname {\mathbf {MNST}}^\tau$. The functor
${\underline {a}}_{\operatorname {Nis}}(\operatorname {\mathbf {MPST}}^\tau )\subset \operatorname {\mathbf {MNST}}^\tau$. The functor  ${\underline {a}}_{\operatorname {Nis}}$ has the following description. For
${\underline {a}}_{\operatorname {Nis}}$ has the following description. For  $F\in \operatorname {\mathbf {\underline {M}PST}}$ and
$F\in \operatorname {\mathbf {\underline {M}PST}}$ and  $\mathcal {Y}\in \operatorname {\mathbf {\underline {M}Cor}}$, let
$\mathcal {Y}\in \operatorname {\mathbf {\underline {M}Cor}}$, let  $F_{\mathcal {Y},{\operatorname {Nis}}}$ be the usual Nisnevich sheafification of
$F_{\mathcal {Y},{\operatorname {Nis}}}$ be the usual Nisnevich sheafification of  $F_{\mathcal {Y}}$. Then, for
$F_{\mathcal {Y}}$. Then, for  $(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}$, we have
where the colimit is taken over all proper maps
$(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}$, we have
where the colimit is taken over all proper maps \[ {\underline{a}}_{\operatorname{Nis}} F (X,D) = \mathop{\varinjlim}_{f:Y\to X} F_{(Y,f^*D),{\operatorname{Nis}}}(Y) \]
\[ {\underline{a}}_{\operatorname{Nis}} F (X,D) = \mathop{\varinjlim}_{f:Y\to X} F_{(Y,f^*D),{\operatorname{Nis}}}(Y) \]
 $f:Y\to X$ that induce isomorphisms
$f:Y\to X$ that induce isomorphisms  $Y-|f^*D|\xrightarrow {\sim }X-|D|$.
$Y-|f^*D|\xrightarrow {\sim }X-|D|$.(15) By [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21b, Proposition 6.2.1],
 $\underline {\omega }^*$ and
$\underline {\omega }^*$ and  $\underline {\omega }_!$ from (10) respect
$\underline {\omega }_!$ from (10) respect  $\operatorname {\mathbf {\underline {M}NST}}$ and
$\operatorname {\mathbf {\underline {M}NST}}$ and  $\operatorname {\mathbf {NST}}$ and induce a pair of adjoint functors (which for simplicity we write
$\operatorname {\mathbf {NST}}$ and induce a pair of adjoint functors (which for simplicity we write  $\underline {\omega }_!$ and
$\underline {\omega }_!$ and  $\underline {\omega }^*$). Moreover, we have
By [Reference Kahn, Saito and YamazakiKSY22, Lemma 2.3.1] and [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21b, Proposition 6.2.1a)], for
$\underline {\omega }^*$). Moreover, we have
By [Reference Kahn, Saito and YamazakiKSY22, Lemma 2.3.1] and [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21b, Proposition 6.2.1a)], for \[ \underline{\omega}_!{\underline{a}}_{\operatorname{Nis}}=a^V_{\operatorname{Nis}}\underline{\omega}_!. \]
\[ \underline{\omega}_!{\underline{a}}_{\operatorname{Nis}}=a^V_{\operatorname{Nis}}\underline{\omega}_!. \]
 $F\in {\operatorname {\mathbf {PST}}}$, we have
$F\in {\operatorname {\mathbf {PST}}}$, we have  $F\in \operatorname {\mathbf {HI}}$ (respectively,
$F\in \operatorname {\mathbf {HI}}$ (respectively,  $F\in \operatorname {\mathbf {HI}}_{\operatorname {Nis}}$) if and only if
$F\in \operatorname {\mathbf {HI}}_{\operatorname {Nis}}$) if and only if  $\underline {\omega }^*F\in \operatorname {\mathbf {CI}}^{\tau }$ (respectively,
$\underline {\omega }^*F\in \operatorname {\mathbf {CI}}^{\tau }$ (respectively,  $\underline {\omega }^*F\in \operatorname {\mathbf {CI}}^{\tau }_{\operatorname {Nis}}$).
$\underline {\omega }^*F\in \operatorname {\mathbf {CI}}^{\tau }_{\operatorname {Nis}}$).(16) We say that
 $F\in \operatorname {\mathbf {\underline {M}PST}}$ is semipure if the unit map
is injective. For
$F\in \operatorname {\mathbf {\underline {M}PST}}$ is semipure if the unit map
is injective. For \[ u: F\to \underline{\omega}^*\underline{\omega}_!F \]
\[ u: F\to \underline{\omega}^*\underline{\omega}_!F \]
 $F\in \operatorname {\mathbf {\underline {M}PST}}$ (respectively,
$F\in \operatorname {\mathbf {\underline {M}PST}}$ (respectively,  $F\in \operatorname {\mathbf {\underline {M}NST}}$), let
$F\in \operatorname {\mathbf {\underline {M}NST}}$), let  $F^{{\rm sp}}\in \operatorname {\mathbf {\underline {M}PST}}$ (respectively,
$F^{{\rm sp}}\in \operatorname {\mathbf {\underline {M}PST}}$ (respectively,  $F^{{\rm sp}}\in \operatorname {\mathbf {\underline {M}NST}}$) be the image of
$F^{{\rm sp}}\in \operatorname {\mathbf {\underline {M}NST}}$) be the image of  $F\to \underline {\omega }^*\underline {\omega }_! F$ (called the semipurification of
$F\to \underline {\omega }^*\underline {\omega }_! F$ (called the semipurification of  $F$. See [Reference SaitoSai20, Lemma 1.30]). For
$F$. See [Reference SaitoSai20, Lemma 1.30]). For  $F\in \operatorname {\mathbf {\underline {M}PST}}$ we have
This follows from the fact that
$F\in \operatorname {\mathbf {\underline {M}PST}}$ we have
This follows from the fact that \[ {\underline{a}}_{\operatorname{Nis}}(F^{{\rm sp}}) \simeq ({\underline{a}}_{\operatorname{Nis}} F)^{{\rm sp}}. \]
\[ {\underline{a}}_{\operatorname{Nis}}(F^{{\rm sp}}) \simeq ({\underline{a}}_{\operatorname{Nis}} F)^{{\rm sp}}. \]
 ${\underline {a}}_{\operatorname {Nis}}$ is exact and commutes with
${\underline {a}}_{\operatorname {Nis}}$ is exact and commutes with  $\underline {\omega }^*\underline {\omega }_!$. For
$\underline {\omega }^*\underline {\omega }_!$. For  $F\in \operatorname {\mathbf {MPST}}^{\tau }$ we have
$F\in \operatorname {\mathbf {MPST}}^{\tau }$ we have  $F^{{\rm sp}}\in \operatorname {\mathbf {MPST}}^{\tau }$ since
$F^{{\rm sp}}\in \operatorname {\mathbf {MPST}}^{\tau }$ since  $\tau$ is exact and
$\tau$ is exact and  $\underline {\omega }^*\underline {\omega }_!\tau _!=\tau _! \omega ^*\omega _!$.
$\underline {\omega }^*\underline {\omega }_!\tau _!=\tau _! \omega ^*\omega _!$.(17) Let
 $\operatorname {\mathbf {CI}}^{\tau,{\rm sp}}\subset \operatorname {\mathbf {CI}}^{\tau }$ be the full subcategory of semipure objects and consider the full subcategory
By [Reference SaitoSai20, Theorems 0.1 and 0.4], we have
$\operatorname {\mathbf {CI}}^{\tau,{\rm sp}}\subset \operatorname {\mathbf {CI}}^{\tau }$ be the full subcategory of semipure objects and consider the full subcategory
By [Reference SaitoSai20, Theorems 0.1 and 0.4], we have \[ \operatorname{\mathbf{CI}}^{\tau,{\rm sp}}_{\operatorname{Nis}} =\operatorname{\mathbf{CI}}^{\tau,{\rm sp}}\cap \operatorname{\mathbf{MNST}}^\tau \subset \operatorname{\mathbf{CI}}^{\tau}_{\operatorname{Nis}}. \]
\[ \operatorname{\mathbf{CI}}^{\tau,{\rm sp}}_{\operatorname{Nis}} =\operatorname{\mathbf{CI}}^{\tau,{\rm sp}}\cap \operatorname{\mathbf{MNST}}^\tau \subset \operatorname{\mathbf{CI}}^{\tau}_{\operatorname{Nis}}. \]
 ${\underline {a}}_{\operatorname {Nis}}(\operatorname {\mathbf {CI}}^{\tau,{\rm sp}})\subset \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{\operatorname {Nis}}$.
${\underline {a}}_{\operatorname {Nis}}(\operatorname {\mathbf {CI}}^{\tau,{\rm sp}})\subset \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{\operatorname {Nis}}$.(18) We write
 ${\operatorname {\mathbf {RSC}}}\subseteq {\operatorname {\mathbf {PST}}}$ for the essential image of
${\operatorname {\mathbf {RSC}}}\subseteq {\operatorname {\mathbf {PST}}}$ for the essential image of  $\operatorname {\mathbf {CI}}$ under
$\operatorname {\mathbf {CI}}$ under  $\omega _!$ (which is the same as the essential image of
$\omega _!$ (which is the same as the essential image of  $\operatorname {\mathbf {CI}}^{\tau,{\rm sp}}$ under
$\operatorname {\mathbf {CI}}^{\tau,{\rm sp}}$ under  $\underline {\omega }_!$ since
$\underline {\omega }_!$ since  $\omega _!=\underline {\omega }_!\tau _!$ and
$\omega _!=\underline {\omega }_!\tau _!$ and  $\underline {\omega }_!F=\underline {\omega }_!F^{{\rm sp}}$). Put
$\underline {\omega }_!F=\underline {\omega }_!F^{{\rm sp}}$). Put  ${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}={\operatorname {\mathbf {RSC}}}\cap \operatorname {\mathbf {NST}}$. The objects of
${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}={\operatorname {\mathbf {RSC}}}\cap \operatorname {\mathbf {NST}}$. The objects of  ${\operatorname {\mathbf {RSC}}}$ (respectively,
${\operatorname {\mathbf {RSC}}}$ (respectively,  ${\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$) are called reciprocity presheaves (respectively, sheaves). By [Reference SaitoSai20, Theorem 0.1], we have
(1.0.1)We have
${\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$) are called reciprocity presheaves (respectively, sheaves). By [Reference SaitoSai20, Theorem 0.1], we have
(1.0.1)We have \begin{equation} a^V_{\operatorname{Nis}}({\operatorname{\mathbf{RSC}}})\subset {\operatorname{\mathbf{RSC}}}_{\operatorname{Nis}}. \end{equation}
\begin{equation} a^V_{\operatorname{Nis}}({\operatorname{\mathbf{RSC}}})\subset {\operatorname{\mathbf{RSC}}}_{\operatorname{Nis}}. \end{equation} $\operatorname {\mathbf {HI}}\subseteq {\operatorname {\mathbf {RSC}}}$ which also contains smooth commutative group schemes (which may have non-trivial unipotent part), the sheaf
$\operatorname {\mathbf {HI}}\subseteq {\operatorname {\mathbf {RSC}}}$ which also contains smooth commutative group schemes (which may have non-trivial unipotent part), the sheaf  $\Omega ^i$ of Kähler differentials, and the de Rham–Witt sheaves
$\Omega ^i$ of Kähler differentials, and the de Rham–Witt sheaves  $W_n\Omega ^i$ (see [Reference Kahn, Saito and YamazakiKSY16, Reference Kahn, Saito and YamazakiKSY22]).
$W_n\Omega ^i$ (see [Reference Kahn, Saito and YamazakiKSY16, Reference Kahn, Saito and YamazakiKSY22]).(19)
 $\operatorname {\mathbf {NST}}$ is a Grothendieck abelian category by [Reference Voevodsky, Friedlander, Suslin and VoevodskyVoe00, Lemma 3.1.6] and we can make
$\operatorname {\mathbf {NST}}$ is a Grothendieck abelian category by [Reference Voevodsky, Friedlander, Suslin and VoevodskyVoe00, Lemma 3.1.6] and we can make  ${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ its full subabelian category as follows. We define the kernel (respectively, cokernel) of a map
${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ its full subabelian category as follows. We define the kernel (respectively, cokernel) of a map  $\phi : F\to G$ in
$\phi : F\to G$ in  ${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ to be that of
${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ to be that of  $\phi$ as a map in
$\phi$ as a map in  $\operatorname {\mathbf {NST}}$. Here we need (1.0.1) to ensure that the cokernel of
$\operatorname {\mathbf {NST}}$. Here we need (1.0.1) to ensure that the cokernel of  $\phi$ in
$\phi$ in  $\operatorname {\mathbf {NST}}$ stays in
$\operatorname {\mathbf {NST}}$ stays in  ${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$. By definition, a sequence
${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$. By definition, a sequence  $0\to F\to G\to H\to 0$ is exact in
$0\to F\to G\to H\to 0$ is exact in  ${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ if and only if it is exact in
${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ if and only if it is exact in  $\operatorname {\mathbf {NST}}$.
$\operatorname {\mathbf {NST}}$.(20) By [Reference Kahn, Saito and YamazakiKSY22, Proposition 2.3.7] we have a pair of adjoint functors
(1.0.2)where \begin{equation} \operatorname{\mathbf{CI}}\begin{smallmatrix}\omega^{\operatorname{\mathbf{CI}}}\\\longleftarrow\\\omega_!\\\longrightarrow \end{smallmatrix}{\operatorname{\mathbf{RSC}}}, \end{equation}
\begin{equation} \operatorname{\mathbf{CI}}\begin{smallmatrix}\omega^{\operatorname{\mathbf{CI}}}\\\longleftarrow\\\omega_!\\\longrightarrow \end{smallmatrix}{\operatorname{\mathbf{RSC}}}, \end{equation} $\omega ^{\operatorname {\mathbf {CI}}}=h^0_{\overline {\square }}\omega ^*$ and is fully faithful. It induces a pair of adjoint functors
(1.0.3)where
$\omega ^{\operatorname {\mathbf {CI}}}=h^0_{\overline {\square }}\omega ^*$ and is fully faithful. It induces a pair of adjoint functors
(1.0.3)where \begin{equation} \operatorname{\mathbf{CI}}^{\tau}\begin{smallmatrix}\underline{\omega}^{\operatorname{\mathbf{CI}}}\\\longleftarrow\\\underline{\omega}_!\\\longrightarrow \end{smallmatrix}{\operatorname{\mathbf{RSC}}}, \end{equation}
\begin{equation} \operatorname{\mathbf{CI}}^{\tau}\begin{smallmatrix}\underline{\omega}^{\operatorname{\mathbf{CI}}}\\\longleftarrow\\\underline{\omega}_!\\\longrightarrow \end{smallmatrix}{\operatorname{\mathbf{RSC}}}, \end{equation} $\underline {\omega }^{\operatorname {\mathbf {CI}}}=\tau _!h^0_{\overline {\square }}\omega ^*$ and is fully faithful. Indeed, let
$\underline {\omega }^{\operatorname {\mathbf {CI}}}=\tau _!h^0_{\overline {\square }}\omega ^*$ and is fully faithful. Indeed, let  $F=\tau _!\hat {F}$ for
$F=\tau _!\hat {F}$ for  $\hat {F}\in \operatorname {\mathbf {CI}}$ and
$\hat {F}\in \operatorname {\mathbf {CI}}$ and  $G \in {\operatorname {\mathbf {RSC}}}$. In view of (13) and the exactness and full faithfulness of
$G \in {\operatorname {\mathbf {RSC}}}$. In view of (13) and the exactness and full faithfulness of  $\tau _!$, we have
In view of (15), (1.0.3) induces a pair of adjoint functors
$\tau _!$, we have
In view of (15), (1.0.3) induces a pair of adjoint functors \begin{align*} \operatorname{Hom}_{\operatorname{\mathbf{CI}}^{\tau}}(F,\tau_!h^0_{\overline{\square}}\omega^* G) &\simeq\operatorname{Hom}_{\operatorname{\mathbf{CI}}}(\hat{F},h^0_{\overline{\square}}\omega^*G) \\ \simeq \operatorname{Hom}_{\operatorname{\mathbf{MPST}}}(\hat{F},\omega^*G) &\simeq\operatorname{Hom}_{\operatorname{\mathbf{\underline{M}PST}}}(\tau_! \hat{F},\underline{\omega}^*G) \simeq \operatorname{Hom}_{{\operatorname{\mathbf{RSC}}}}(\underline{\omega}_! F,G). \end{align*}
(1.0.4)
\begin{align*} \operatorname{Hom}_{\operatorname{\mathbf{CI}}^{\tau}}(F,\tau_!h^0_{\overline{\square}}\omega^* G) &\simeq\operatorname{Hom}_{\operatorname{\mathbf{CI}}}(\hat{F},h^0_{\overline{\square}}\omega^*G) \\ \simeq \operatorname{Hom}_{\operatorname{\mathbf{MPST}}}(\hat{F},\omega^*G) &\simeq\operatorname{Hom}_{\operatorname{\mathbf{\underline{M}PST}}}(\tau_! \hat{F},\underline{\omega}^*G) \simeq \operatorname{Hom}_{{\operatorname{\mathbf{RSC}}}}(\underline{\omega}_! F,G). \end{align*}
(1.0.4) \begin{equation} \operatorname{\mathbf{CI}}^{\tau,{\rm sp}}_{\operatorname{Nis}}\begin{smallmatrix}\underline{\omega}^{\operatorname{\mathbf{CI}}}\\\longleftarrow\\\underline{\omega}_!\\\longrightarrow \end{smallmatrix}{\operatorname{\mathbf{RSC}}}_{\operatorname{Nis}}. \end{equation}
\begin{equation} \operatorname{\mathbf{CI}}^{\tau,{\rm sp}}_{\operatorname{Nis}}\begin{smallmatrix}\underline{\omega}^{\operatorname{\mathbf{CI}}}\\\longleftarrow\\\underline{\omega}_!\\\longrightarrow \end{smallmatrix}{\operatorname{\mathbf{RSC}}}_{\operatorname{Nis}}. \end{equation}
2. Purity with reduced modulus
For ![]() $F\in \operatorname {\mathbf {\underline {M}PST}}$, we put
$F\in \operatorname {\mathbf {\underline {M}PST}}$, we put
Note that if ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$, then
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$, then ![]() $F_{-1},F_{-1}^{(1)}\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and
$F_{-1},F_{-1}^{(1)}\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and
 \begin{equation} \begin{aligned}F_{-1}^{(1)}(\mathcal{X}) & = \operatorname{Hom}_{\operatorname{\mathbf{\underline{M}PST}}}(h_{0,{\operatorname{Nis}}}^{{\overline{\square}},{\rm sp}}(\mathbf{P}^1,0+\infty)^0,\operatorname{\underline{Hom}}_{\operatorname{\mathbf{\underline{M}PST}}}({\operatorname{\mathbb{Z}_{{\operatorname{tr}}}}}(\mathcal{X}),F)),\\ F_{-1}(\mathcal{X}) & =\mathop{\varinjlim}_n \operatorname{Hom}_{\operatorname{\mathbf{\underline{M}PST}}}(h_{0,{\operatorname{Nis}}}^{{\overline{\square}},{\rm sp}}(\mathbf{P}^1,n\cdot 0+\infty)^0,\operatorname{\underline{Hom}}_{\operatorname{\mathbf{\underline{M}PST}}}({\operatorname{\mathbb{Z}_{{\operatorname{tr}}}}}(\mathcal{X}),F)) \end{aligned} \end{equation}
\begin{equation} \begin{aligned}F_{-1}^{(1)}(\mathcal{X}) & = \operatorname{Hom}_{\operatorname{\mathbf{\underline{M}PST}}}(h_{0,{\operatorname{Nis}}}^{{\overline{\square}},{\rm sp}}(\mathbf{P}^1,0+\infty)^0,\operatorname{\underline{Hom}}_{\operatorname{\mathbf{\underline{M}PST}}}({\operatorname{\mathbb{Z}_{{\operatorname{tr}}}}}(\mathcal{X}),F)),\\ F_{-1}(\mathcal{X}) & =\mathop{\varinjlim}_n \operatorname{Hom}_{\operatorname{\mathbf{\underline{M}PST}}}(h_{0,{\operatorname{Nis}}}^{{\overline{\square}},{\rm sp}}(\mathbf{P}^1,n\cdot 0+\infty)^0,\operatorname{\underline{Hom}}_{\operatorname{\mathbf{\underline{M}PST}}}({\operatorname{\mathbb{Z}_{{\operatorname{tr}}}}}(\mathcal{X}),F)) \end{aligned} \end{equation}
for ![]() $\mathcal {X}\in \operatorname {\mathbf {\underline {M}Cor}}$, where
$\mathcal {X}\in \operatorname {\mathbf {\underline {M}Cor}}$, where
Definition 2.1 For ![]() $e_1,\dots,e_r\in \{0,1\}$, put
$e_1,\dots,e_r\in \{0,1\}$, put
where
where the quotient is taken in ![]() $\operatorname {\mathbf {\underline {M}PST}}$.
$\operatorname {\mathbf {\underline {M}PST}}$.
The existence of retractions in the following lemma was suggested by A. Merici. It implies ![]() ${\tau^{(e_1,\dots,e_r)}}F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ if
${\tau^{(e_1,\dots,e_r)}}F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ if ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$.
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$.
Lemma 2.2 For ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$, the inclusion
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$, the inclusion ![]() $F_{-1}^{(1)} \to F_{-1}$ admits a retraction
$F_{-1}^{(1)} \to F_{-1}$ admits a retraction ![]() $s_F : F_{-1}\to F_{-1}^{(1)}$ such that for any map
$s_F : F_{-1}\to F_{-1}^{(1)}$ such that for any map ![]() $\phi : F\to G$ in
$\phi : F\to G$ in ![]() $\operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$, the following diagram is commutative:
$\operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$, the following diagram is commutative:

In particular, ![]() ${\tau^{(1)}} F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ if
${\tau^{(1)}} F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ if ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$.
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$.
Proof. In view of (2.0.1), this follows from [Reference Binda, Rülling and SaitoBRS22, Lemma 2.4].
Theorem 2.3 Let ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$. Let
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$. Let ![]() $K\{t_1,\dots,t_n\}$ be the henselization of
$K\{t_1,\dots,t_n\}$ be the henselization of ![]() $K[t_1,\dots,t_n]$ at
$K[t_1,\dots,t_n]$ at ![]() $(t_1,\dots,t_n)$ and
$(t_1,\dots,t_n)$ and ![]() $\mathcal {X}=\operatorname {Spec} K\{t_1,\dots,t_n\}$ and
$\mathcal {X}=\operatorname {Spec} K\{t_1,\dots,t_n\}$ and ![]() $D= \{t_1^{e_1}\cdots t_n^{e_n}=0\}\subset \mathcal {X}$ with
$D= \{t_1^{e_1}\cdots t_n^{e_n}=0\}\subset \mathcal {X}$ with ![]() $e_1,\dots,e_n\in \{0,1\}$. For a subset
$e_1,\dots,e_n\in \{0,1\}$. For a subset ![]() $I\subset [1,n]$ let
$I\subset [1,n]$ let ![]() $i_\mathcal {H} : \mathcal {H} \hookrightarrow \mathcal {X}$ be the closed immersion defined by
$i_\mathcal {H} : \mathcal {H} \hookrightarrow \mathcal {X}$ be the closed immersion defined by ![]() $\{t_i=0\}_{i\in I}$ and
$\{t_i=0\}_{i\in I}$ and ![]() $D_\mathcal {H}=\bigl \{ \prod _{j\in [1,n]-I}t_j^{e_j}=0\bigr \}\subset \mathcal {H}$. Then
$D_\mathcal {H}=\bigl \{ \prod _{j\in [1,n]-I}t_j^{e_j}=0\bigr \}\subset \mathcal {H}$. Then
and there is an isomorphism
Proof. The proof is divided into two steps.
Step 1: we prove (2.3.1) and (2.3.2) for ![]() $q=|I|=1$. For
$q=|I|=1$. For ![]() $\nu =0$, (2.3.1) follows from the semipurity of
$\nu =0$, (2.3.1) follows from the semipurity of ![]() $F$ and [Reference SaitoSai20, Theorem 3.1]. Thus, it suffices to show (2.3.1) only for
$F$ and [Reference SaitoSai20, Theorem 3.1]. Thus, it suffices to show (2.3.1) only for ![]() $\nu >1$. Let
$\nu >1$. Let ![]() $J=\{j\in [1,n]\;|\; e_j\not =0\}$ and
$J=\{j\in [1,n]\;|\; e_j\not =0\}$ and ![]() $r=|J|$. If
$r=|J|$. If ![]() $\dim (\mathcal {X})=0$, the assertion is trivial. If
$\dim (\mathcal {X})=0$, the assertion is trivial. If ![]() $r=0$, the assertion follows from [Reference SaitoSai20, Corollary 8.6(3)]. Assume
$r=0$, the assertion follows from [Reference SaitoSai20, Corollary 8.6(3)]. Assume ![]() $r>0$ and
$r>0$ and ![]() $\dim (\mathcal {X})\geq 1$, and proceed by the double induction on
$\dim (\mathcal {X})\geq 1$, and proceed by the double induction on ![]() $r$ and
$r$ and ![]() $\dim (\mathcal {X})$. Without loss of generality, we may assume
$\dim (\mathcal {X})$. Without loss of generality, we may assume
 $(\spadesuit )$
$(\spadesuit )$  $e_1\not =0$, and
$e_1\not =0$, and  $\mathcal {H}=\{t_1=0\}$ if
$\mathcal {H}=\{t_1=0\}$ if  $\mathcal {H}\subset |D|$.
$\mathcal {H}\subset |D|$.
Let ![]() $\iota :\mathcal {Z}\hookrightarrow \mathcal {X}$ be the closed immersion defined by
$\iota :\mathcal {Z}\hookrightarrow \mathcal {X}$ be the closed immersion defined by ![]() $\{t_1=0\}$ and
$\{t_1=0\}$ and ![]() $D_\mathcal {Z}=\{t_2^{e_2}\cdots t_r^{e_r}=0\}\subset \mathcal {Z}$ and
$D_\mathcal {Z}=\{t_2^{e_2}\cdots t_r^{e_r}=0\}\subset \mathcal {Z}$ and ![]() $D'=\{t_2^{e_2}\cdots t_r^{e_r}=0\}\subset \mathcal {X}$. By [Reference SaitoSai20, Lemma 7.1], we have an exact sequence sheaves on
$D'=\{t_2^{e_2}\cdots t_r^{e_r}=0\}\subset \mathcal {X}$. By [Reference SaitoSai20, Lemma 7.1], we have an exact sequence sheaves on ![]() $\mathcal {X}_{{\operatorname {Nis}}}$,
$\mathcal {X}_{{\operatorname {Nis}}}$,
which gives rise to a long exact sequence of sheaves on ![]() $\mathcal {H}_{{\operatorname {Nis}}}$,
$\mathcal {H}_{{\operatorname {Nis}}}$,
By the induction hypothesis, ![]() $R^\nu i_\mathcal {H}^!F_{(\mathcal {X},D')}=0$ for
$R^\nu i_\mathcal {H}^!F_{(\mathcal {X},D')}=0$ for ![]() $\nu >1$. If
$\nu >1$. If ![]() $\mathcal {H}\not =\mathcal {Z}$, we have a Cartesian diagram of closed immersions
$\mathcal {H}\not =\mathcal {Z}$, we have a Cartesian diagram of closed immersions

and we have an isomorphism
By the induction hypothesis, ![]() $R^\nu i_{\mathcal {H}\cap \mathcal {Z}}^!({F^{(e)}_{-1}})_{(\mathcal {Z},D_\mathcal {Z})}=0$ for
$R^\nu i_{\mathcal {H}\cap \mathcal {Z}}^!({F^{(e)}_{-1}})_{(\mathcal {Z},D_\mathcal {Z})}=0$ for ![]() $\nu >1$, noting that
$\nu >1$, noting that ![]() ${{F^{(e)}_{-1}}}\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ by Lemma 2.2. So the desired vanishing follows from (2.3.3). Moreover, the assumptions
${{F^{(e)}_{-1}}}\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ by Lemma 2.2. So the desired vanishing follows from (2.3.3). Moreover, the assumptions ![]() $(\spadesuit )$ and
$(\spadesuit )$ and ![]() $\mathcal {H}\not =\mathcal {Z}$ imply that
$\mathcal {H}\not =\mathcal {Z}$ imply that ![]() $\mathcal {H}\not \subset |D|$. Then (2.3.2) (with
$\mathcal {H}\not \subset |D|$. Then (2.3.2) (with ![]() $q=1$) follows from [Reference SaitoSai20, Lemma 7.1(2)].
$q=1$) follows from [Reference SaitoSai20, Lemma 7.1(2)].
If ![]() $\mathcal {Z}=\mathcal {H}$, we have
$\mathcal {Z}=\mathcal {H}$, we have
which vanishes for ![]() $\nu >0$. Hence, (2.3.3) gives the desired vanishing together with an exact sequence
$\nu >0$. Hence, (2.3.3) gives the desired vanishing together with an exact sequence
By [Reference SaitoSai20, Lemma 7.1(2)] we have an isomorphism
through which ![]() $\delta$ is identified with the map induced by the canonical map
$\delta$ is identified with the map induced by the canonical map ![]() ${F^{(e)}_{-1}} \to F_{-1}$. This proves the desired isomorphism (2.3.2) for
${F^{(e)}_{-1}} \to F_{-1}$. This proves the desired isomorphism (2.3.2) for ![]() $\mathcal {Z}=\mathcal {H}$ and completes step 1.
$\mathcal {Z}=\mathcal {H}$ and completes step 1.
Step 2: we prove the theorem by induction on ![]() $q$ assuming
$q$ assuming ![]() $q>0$. Let
$q>0$. Let ![]() $I=\{i_1,\dots,i_q\}\subset [1,n]$ and
$I=\{i_1,\dots,i_q\}\subset [1,n]$ and ![]() $\mathcal {Y}\subset \mathcal {X}$ be the closed subscheme defined by
$\mathcal {Y}\subset \mathcal {X}$ be the closed subscheme defined by ![]() $\{t_{i_1}=0\}$. Let
$\{t_{i_1}=0\}$. Let ![]() $i_\mathcal {Y}:\mathcal {Y}\hookrightarrow \mathcal {X}$ and
$i_\mathcal {Y}:\mathcal {Y}\hookrightarrow \mathcal {X}$ and ![]() $i_{\mathcal {H},\mathcal {Y}}:\mathcal {H}\to \mathcal {Y}$ be the induced closed immersions. By step 1 we have
$i_{\mathcal {H},\mathcal {Y}}:\mathcal {H}\to \mathcal {Y}$ be the induced closed immersions. By step 1 we have ![]() $R^\nu i_{\mathcal {Y}}^! F_{(\mathcal {X},D)} =0$ for
$R^\nu i_{\mathcal {Y}}^! F_{(\mathcal {X},D)} =0$ for ![]() $\nu \not =1$ and we have an isomorphism
$\nu \not =1$ and we have an isomorphism
Note ![]() ${\tau^{(e_{i_1})}} F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ by Lemma 2.2. Thus, by the induction hypothesis, we have
${\tau^{(e_{i_1})}} F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ by Lemma 2.2. Thus, by the induction hypothesis, we have ![]() $R^\nu i_{\mathcal {H},\mathcal {Y}}^! {\tau^{(e_{i_1})}} F_{(\mathcal {Y},D_\mathcal {Y})} =0$ for
$R^\nu i_{\mathcal {H},\mathcal {Y}}^! {\tau^{(e_{i_1})}} F_{(\mathcal {Y},D_\mathcal {Y})} =0$ for ![]() $\nu \not =q-1$. By the spectral sequence
$\nu \not =q-1$. By the spectral sequence
we get the desired vanishing (2.3.1) and an isomorphism
 \begin{align*} R^q i_{\mathcal{H}}^! F_{(\mathcal{X},D)} &\simeq R^{q-1} i_{\mathcal{H},\mathcal{Y}}^! R^1 i_{\mathcal{Y}}^! F_{(\mathcal{X},D)} \simeq R^{q-1} i_{\mathcal{H},\mathcal{Y}}^! ({\tau^{(e_{i_1})}} F)_{(\mathcal{Y},D_\mathcal{Y})}\\ &\simeq ({\tau^{(e_{i_2},\dots,e_{i_q})}}({\tau^{(e_{i_1})}} F))_{(\mathcal{H},D_\mathcal{H})}\simeq ({\tau^{(e_{i_1}, e_{i_2},\dots,e_{i_q})}} F)_{(\mathcal{H},D_\mathcal{H})}, \end{align*}
\begin{align*} R^q i_{\mathcal{H}}^! F_{(\mathcal{X},D)} &\simeq R^{q-1} i_{\mathcal{H},\mathcal{Y}}^! R^1 i_{\mathcal{Y}}^! F_{(\mathcal{X},D)} \simeq R^{q-1} i_{\mathcal{H},\mathcal{Y}}^! ({\tau^{(e_{i_1})}} F)_{(\mathcal{Y},D_\mathcal{Y})}\\ &\simeq ({\tau^{(e_{i_2},\dots,e_{i_q})}}({\tau^{(e_{i_1})}} F))_{(\mathcal{H},D_\mathcal{H})}\simeq ({\tau^{(e_{i_1}, e_{i_2},\dots,e_{i_q})}} F)_{(\mathcal{H},D_\mathcal{H})}, \end{align*}
where the third isomorphism holds by the induction hypothesis. This completes the proof of the theorem.
We say that ![]() $\mathcal {X}=(X,D) \in \operatorname {\mathbf {\underline {M}Cor}}$ is reduced if so is
$\mathcal {X}=(X,D) \in \operatorname {\mathbf {\underline {M}Cor}}$ is reduced if so is ![]() $D$. The following Corollaries 2.4 and 2.5 are immediate consequences of Theorem 2.3.
$D$. The following Corollaries 2.4 and 2.5 are immediate consequences of Theorem 2.3.
Corollary 2.4 Take ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and ![]() $(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ reduced. Let
$(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ reduced. Let ![]() $x\in {{X}^{(n)}}$ with
$x\in {{X}^{(n)}}$ with ![]() $K=k(x)$ and let
$K=k(x)$ and let ![]() $\mathcal {X}=X^{h}_{|x}$ be the henselization of
$\mathcal {X}=X^{h}_{|x}$ be the henselization of ![]() $X$ at
$X$ at ![]() $x$. Then
$x$. Then
Choosing an isomorphism
such that ![]() $D_{|\mathcal {X}} = \{t_1^{e_1}\cdots t_n^{e_n}=0\}\subset \mathcal {X}$ with
$D_{|\mathcal {X}} = \{t_1^{e_1}\cdots t_n^{e_n}=0\}\subset \mathcal {X}$ with ![]() $e_1,\dots,e_n\in \{0,1\}$, there exists an isomorphism depending on
$e_1,\dots,e_n\in \{0,1\}$, there exists an isomorphism depending on ![]() $\varepsilon$:
$\varepsilon$:
Corollary 2.5 For ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and ![]() $\mathcal {X}=(X,D) \in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ reduced, the following sequence is exact:
$\mathcal {X}=(X,D) \in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ reduced, the following sequence is exact:
 \[ 0\to F(X,D) \to F(X-D,\emptyset) \to \underset{\xi\in {{D}^{(0)}}}\bigoplus \frac{F({{{X}}^{h}_{|\xi}}-\xi,\emptyset)}{F({{{X}}^{h}_{|\xi}},\xi)}. \]
\[ 0\to F(X,D) \to F(X-D,\emptyset) \to \underset{\xi\in {{D}^{(0)}}}\bigoplus \frac{F({{{X}}^{h}_{|\xi}}-\xi,\emptyset)}{F({{{X}}^{h}_{|\xi}},\xi)}. \]
The idea of deducing the following corollary from the above is due to A. Merici.
Corollary 2.6 Let ![]() $\mathcal {X}=(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ be reduced.
$\mathcal {X}=(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ be reduced.
(1) Assume given an exact sequence in
 $\operatorname {\mathbf {\underline {M}NST}}$,
(2.6.1)such that
$\operatorname {\mathbf {\underline {M}NST}}$,
(2.6.1)such that \begin{equation} {0\to H \overset{\phi}{\longrightarrow} G \overset{\psi}{\longrightarrow} F}, \end{equation}
\begin{equation} {0\to H \overset{\phi}{\longrightarrow} G \overset{\psi}{\longrightarrow} F}, \end{equation} $F,G, H\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and that
$F,G, H\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and that  $\underline {\omega }_!\psi$ is surjective in
$\underline {\omega }_!\psi$ is surjective in  $\operatorname {\mathbf {NST}}$. If
$\operatorname {\mathbf {NST}}$. If  $X$ is henselian local, then
is exact.
$X$ is henselian local, then
is exact. \[ 0\to H(\mathcal{X}) \to G(\mathcal{X}) \to F(\mathcal{X}) \to 0 \]
\[ 0\to H(\mathcal{X}) \to G(\mathcal{X}) \to F(\mathcal{X}) \to 0 \]
(2) Let
 $\gamma : F\to G$ be a map in
$\gamma : F\to G$ be a map in  $\operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ such that
$\operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ such that  $\underline {\omega }_!\gamma$ is an isomorphism. Then
$\underline {\omega }_!\gamma$ is an isomorphism. Then  $F(\mathcal {X})\to G(\mathcal {X})$ is an isomorphism.
$F(\mathcal {X})\to G(\mathcal {X})$ is an isomorphism.(3) For
 $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$, the unit map
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$, the unit map  $u: F\to \underline {\omega }^{\operatorname {\mathbf {CI}}}\underline {\omega }_! F$ induces an isomorphism
$u: F\to \underline {\omega }^{\operatorname {\mathbf {CI}}}\underline {\omega }_! F$ induces an isomorphism  $F(\mathcal {X})\cong \underline {\omega }^{\operatorname {\mathbf {CI}}}\underline {\omega }_! F(\mathcal {X})$.
$F(\mathcal {X})\cong \underline {\omega }^{\operatorname {\mathbf {CI}}}\underline {\omega }_! F(\mathcal {X})$.
Proof. To show (1), it suffices to show the surjectivity of ![]() $G(\mathcal {X}) \to F(\mathcal {X})$. Let
$G(\mathcal {X}) \to F(\mathcal {X})$. Let ![]() $\eta \in X$ be the generic point and consider the following commutative diagram of the Cousin complexes:
$\eta \in X$ be the generic point and consider the following commutative diagram of the Cousin complexes:

By Corollary 2.4, the horizontal sequences are exact. By the assumption, ![]() $\psi (\eta )$ is surjective. By a diagram chase we are reduced to showing the following claim.
$\psi (\eta )$ is surjective. By a diagram chase we are reduced to showing the following claim.
Claim 2.6.1
(i) For
 $x\in {{X}^{(1)}}$, the sequence
is exact.
$x\in {{X}^{(1)}}$, the sequence
is exact. \[ H^1_x(X,H_\mathcal{X}) \to H^1_x(X,G_\mathcal{X}) \to H^1_x(X,F_\mathcal{X}) \]
\[ H^1_x(X,H_\mathcal{X}) \to H^1_x(X,G_\mathcal{X}) \to H^1_x(X,F_\mathcal{X}) \]
(ii) For
 $y\in {{X}^{(2)}}$,
$y\in {{X}^{(2)}}$,  $H^2_y(\phi )$ is injective.
$H^2_y(\phi )$ is injective.
To show (i), by Corollary 2.4, it suffices to show the exactness of ![]() ${\tau^{(e)}} H \to {\tau^{(e)}} G \to {\tau^{(e)}} F$ for
${\tau^{(e)}} H \to {\tau^{(e)}} G \to {\tau^{(e)}} F$ for ![]() $e\in \{0,1\}$. The case
$e\in \{0,1\}$. The case ![]() $e=0$ follows from the left exactness of the endofunctor
$e=0$ follows from the left exactness of the endofunctor ![]() $\operatorname {\underline {Hom}}_{\operatorname {\mathbf {\underline {M}PST}}}(\mathcal {X}, -)$ on
$\operatorname {\underline {Hom}}_{\operatorname {\mathbf {\underline {M}PST}}}(\mathcal {X}, -)$ on ![]() $\operatorname {\mathbf {\underline {M}NST}}$ for any
$\operatorname {\mathbf {\underline {M}NST}}$ for any ![]() $\mathcal {X}\in \operatorname {\mathbf {\underline {M}Cor}}$. We have a commutative diagram
$\mathcal {X}\in \operatorname {\mathbf {\underline {M}Cor}}$. We have a commutative diagram

where ![]() $p_*$ are the projections and
$p_*$ are the projections and ![]() $s_*$ is a right inverse of
$s_*$ is a right inverse of ![]() $p_*$ coming from the retractions from Lemma 2.2. We have
$p_*$ coming from the retractions from Lemma 2.2. We have
By a diagram chase, the case ![]() $e=1$ follows from the case
$e=1$ follows from the case ![]() $e=0$.
$e=0$.
To show (ii), by Corollary 2.4, it suffices to show the injectivity of ![]() ${\tau^{({{\underline {e}}})}} H \to {\tau^{({{\underline {e}}})}} G$ for
${\tau^{({{\underline {e}}})}} H \to {\tau^{({{\underline {e}}})}} G$ for ![]() ${\underline {e}}\in \{(0,0),(0,1),(1,0),(1.1)\}$. The case
${\underline {e}}\in \{(0,0),(0,1),(1,0),(1.1)\}$. The case ![]() ${\underline {e}}=(0,0)$ follows from the same left exactness as above, and the other cases from this case thanks to Lemma 2.2.
${\underline {e}}=(0,0)$ follows from the same left exactness as above, and the other cases from this case thanks to Lemma 2.2.
To show (2), we may assume ![]() $\mathcal {X}$ is henselian local. Then it follows from (1).
$\mathcal {X}$ is henselian local. Then it follows from (1).
Finally, (3) follows from (2) since ![]() $\underline {\omega }_! u$ is an isomorphism. This completes the proof of the corollary.
$\underline {\omega }_! u$ is an isomorphism. This completes the proof of the corollary.
3. Review of higher local symbols
In this section we recall from [Reference Rülling and SaitoRS21c] the higher local symbols for reciprocity sheaves, which are a fundamental tool to prove Theorem 4.2, one of the main theorems of this paper. First we introduce some basic notation. In this section ![]() $X$ is a reduced noetherian separated scheme of dimension
$X$ is a reduced noetherian separated scheme of dimension ![]() $d<\infty$ such that
$d<\infty$ such that ![]() $X_{(0)}=X^{(d)}$.
$X_{(0)}=X^{(d)}$.
Let ![]() $K$ be a field. For an integer
$K$ be a field. For an integer ![]() $r\geq 0$, let
$r\geq 0$, let ![]() $K^{\rm M}_r(K)$ be the Milnor
$K^{\rm M}_r(K)$ be the Milnor ![]() $K$-group of
$K$-group of ![]() $K$. Let
$K$. Let ![]() $A$ be a local domain with the function field
$A$ be a local domain with the function field ![]() $K$. For an ideal
$K$. For an ideal ![]() $I\subset A$, let
$I\subset A$, let ![]() $\overline {K}^{\rm M}_r(A,I)\subset K^{\rm M}_r(K)$ denote the subgroup generated by symbols
$\overline {K}^{\rm M}_r(A,I)\subset K^{\rm M}_r(K)$ denote the subgroup generated by symbols
Let ![]() $A$ be a noetherian excellent one-dimensional local domain with function field
$A$ be a noetherian excellent one-dimensional local domain with function field ![]() $K$ and residue field
$K$ and residue field ![]() $F$. Let
$F$. Let ![]() $\tilde {A}$ be the normalization of
$\tilde {A}$ be the normalization of ![]() $A$ and
$A$ and ![]() $S$ be the set of the maximal ideals of
$S$ be the set of the maximal ideals of ![]() $\tilde {A}$. For
$\tilde {A}$. For ![]() $\mathfrak {m}\in S$, denote
$\mathfrak {m}\in S$, denote ![]() $\kappa (\mathfrak {m})=\tilde {A}/\mathfrak {m}$. Then we define
$\kappa (\mathfrak {m})=\tilde {A}/\mathfrak {m}$. Then we define
where ![]() $\partial _{\mathfrak {m}} :K^{\rm M}_r(K)\to K^{\rm M}_{r-1}(\kappa (\mathfrak {m}))$ denotes the tame symbol for the discrete valuation ring
$\partial _{\mathfrak {m}} :K^{\rm M}_r(K)\to K^{\rm M}_{r-1}(\kappa (\mathfrak {m}))$ denotes the tame symbol for the discrete valuation ring ![]() $\tilde {A}_{\mathfrak {m}}$, the localization of
$\tilde {A}_{\mathfrak {m}}$, the localization of ![]() $\tilde {A}$ at
$\tilde {A}$ at ![]() $\mathfrak {m}$, and
$\mathfrak {m}$, and ![]() $\operatorname {Nm}_{\kappa (\mathfrak {m})/F}$ is the norm map.
$\operatorname {Nm}_{\kappa (\mathfrak {m})/F}$ is the norm map.
For ![]() $x, y\in X$, we write
$x, y\in X$, we write
A chain on ![]() $X$ is a sequence
$X$ is a sequence
The chain ![]() $\underline {x}$ is a maximal Paršin chain (or maximal chain) if
$\underline {x}$ is a maximal Paršin chain (or maximal chain) if ![]() $n=d$ and
$n=d$ and ![]() $x_i\in X_{(i)}$. Note that the assumptions on
$x_i\in X_{(i)}$. Note that the assumptions on ![]() $X$ imply
$X$ imply ![]() $x_{i}\in \overline {\{x_{i+1}\}}^{(1)}$. We denote
$x_{i}\in \overline {\{x_{i+1}\}}^{(1)}$. We denote
A maximal chain with break at ![]() $r\in \{0,\ldots, d\}$ is a chain (3.0.2) with
$r\in \{0,\ldots, d\}$ is a chain (3.0.2) with ![]() $n=d-1$ and
$n=d-1$ and ![]() $x_i\in X_{(i)}$, for
$x_i\in X_{(i)}$, for ![]() $i< r$, and
$i< r$, and ![]() $x_i\in X_{(i+1)}$, for
$x_i\in X_{(i+1)}$, for ![]() $i\ge r$. We denote
$i\ge r$. We denote
For ![]() $\underline {x}=(x_0,\ldots, x_{d-1})\in \mathrm {mc}_r(X)$, we denote by
$\underline {x}=(x_0,\ldots, x_{d-1})\in \mathrm {mc}_r(X)$, we denote by ![]() $b(\underline {x})$ the set of
$b(\underline {x})$ the set of ![]() $y\in X_{(r)}$ such that
$y\in X_{(r)}$ such that
In the rest of this section we fix ![]() $F=\underline {\omega }^{\operatorname {\mathbf {CI}}} G\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{\operatorname {Nis}}$ with
$F=\underline {\omega }^{\operatorname {\mathbf {CI}}} G\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{\operatorname {Nis}}$ with ![]() $G\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$ (cf. (1.0.4)). We also fix a function field
$G\in {\operatorname {\mathbf {RSC}}}_{\operatorname {Nis}}$ (cf. (1.0.4)). We also fix a function field ![]() $K$ over the base field
$K$ over the base field ![]() $k$. Let
$k$. Let ![]() $X$ be an integral scheme of finite type over
$X$ be an integral scheme of finite type over ![]() $K$ and assume
$K$ and assume ![]() $d=\dim (X)\geq 1$. Recall from [Reference Rülling and SaitoRS21c, § 5] that we have a collection of bilinear pairings (cf. the convention from § 1(9))
$d=\dim (X)\geq 1$. Recall from [Reference Rülling and SaitoRS21c, § 5] that we have a collection of bilinear pairings (cf. the convention from § 1(9))
The following properties hold for all ![]() $a\in F(K(X))$ (see Remark 3.1 below).
$a\in F(K(X))$ (see Remark 3.1 below).
(HS1) Let
 $X\hookrightarrow X'$ be an open immersion where
$X\hookrightarrow X'$ be an open immersion where  $X'$ is an integral
$X'$ is an integral  $K$-scheme of dimension
$K$-scheme of dimension  $d$. Then, for all
$d$. Then, for all  $\beta \in K^{\rm M}_d(K(X))$,
$\beta \in K^{\rm M}_d(K(X))$,
 \[ (a,\beta)_{X/K,\underline{x}}=(a,\beta)_{X'/K,\underline{x}}. \]
\[ (a,\beta)_{X/K,\underline{x}}=(a,\beta)_{X'/K,\underline{x}}. \]
(HS2) Let
 $\underline {x}=(x_0,\ldots,x_{d-1}, x_d)\in \mathrm {mc}(X)$ and
$\underline {x}=(x_0,\ldots,x_{d-1}, x_d)\in \mathrm {mc}(X)$ and  $Z\subset X$ be the closure of
$Z\subset X$ be the closure of  $z=x_{d-1}$, and set
$z=x_{d-1}$, and set  $\underline {x}'=(x_0,\ldots, x_{d-1})\in \mathrm {mc}(Z)$. Assume
$\underline {x}'=(x_0,\ldots, x_{d-1})\in \mathrm {mc}(Z)$. Assume  $a\in F(\mathcal {O}_{X, z})$ and let
$a\in F(\mathcal {O}_{X, z})$ and let  $a(z)\in F(K(Z))$ be the restriction of
$a(z)\in F(K(Z))$ be the restriction of  $a$. Then
where
$a$. Then
where \[ (a, \beta)_{X/K, \underline{x}} = (a(z), \partial_{z}\beta)_{Z/K, \underline{x}'}\quad \text{for $\beta\in K^{\rm M}_d(K(X))$}, \]
\[ (a, \beta)_{X/K, \underline{x}} = (a(z), \partial_{z}\beta)_{Z/K, \underline{x}'}\quad \text{for $\beta\in K^{\rm M}_d(K(X))$}, \]
 $\partial _{z}: K^{\rm M}_d(K(X)) \to K^{\rm M}_{d-1}(K(Z))$ is the map (3.0.1) for
$\partial _{z}: K^{\rm M}_d(K(X)) \to K^{\rm M}_{d-1}(K(Z))$ is the map (3.0.1) for  $A=\mathcal {O}_{X, z}$.
$A=\mathcal {O}_{X, z}$.(HS3) Let
 $D\subset X$ be an effective Cartier divisor with
$D\subset X$ be an effective Cartier divisor with  $I_D\subset \mathcal {O}_X$ its ideal sheaf. Assume that
$I_D\subset \mathcal {O}_X$ its ideal sheaf. Assume that  $X{\setminus} D$ is regular so that
$X{\setminus} D$ is regular so that  $(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$ and that
$(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$ and that  $a\in F(X,D)$. For
$a\in F(X,D)$. For  $\underline {x}=(x_0,\ldots, x_{d-1},x_d)\in \mathrm {mc}(X)$, we have
$\underline {x}=(x_0,\ldots, x_{d-1},x_d)\in \mathrm {mc}(X)$, we have
 \[ (a, \beta)_{X/K,\underline{x}}=0\quad \text{for $\beta\in \overline{K}^{\rm M}_d(\mathcal{O}_{X, x_{d-1}},I_D \mathcal{O}_{X, x_{d-1}})$.} \]
\[ (a, \beta)_{X/K,\underline{x}}=0\quad \text{for $\beta\in \overline{K}^{\rm M}_d(\mathcal{O}_{X, x_{d-1}},I_D \mathcal{O}_{X, x_{d-1}})$.} \]
(HS4) Let
 $\underline {x}'\in \mathrm {mc}_r(X)$ with
$\underline {x}'\in \mathrm {mc}_r(X)$ with  $0\leq r\leq d-1$. For
$0\leq r\leq d-1$. For  $\beta \in K^{\rm M}_d(K(X))$,
Assume that either
$\beta \in K^{\rm M}_d(K(X))$,
Assume that either \[ (a, \beta)_{X/K, \underline{x}'(y)}=0\quad \text{for almost all } y\in _{-}(\underline{x}'). \]
\[ (a, \beta)_{X/K, \underline{x}'(y)}=0\quad \text{for almost all } y\in _{-}(\underline{x}'). \]
 $r\ge 1$ or
$r\ge 1$ or  $r=0$,
$r=0$,  $X$ is quasi-projective, and the closure of
$X$ is quasi-projective, and the closure of  $x_1$ in
$x_1$ in  $X$ is projective over
$X$ is projective over  $K$, where
$K$, where  $\underline {x}'=(x_1,\ldots, x_d)$. Then
$\underline {x}'=(x_1,\ldots, x_d)$. Then
 \[ \sum_{y\in b(\underline{x}')} (a, \beta)_{X/K, \underline{x}'(y)}=0. \]
\[ \sum_{y\in b(\underline{x}')} (a, \beta)_{X/K, \underline{x}'(y)}=0. \]
Remark 3.1 Properties (HS1)–(HS4) are slight variants of the (stronger) properties (HS1)–(HS4) in [Reference Rülling and SaitoRS21c, Proposition 5.3], where the Milnor ![]() $K$-group
$K$-group ![]() $K^{\rm M}_{d}(K^h_{X,\underline {x}})$ of the iterated henselization
$K^{\rm M}_{d}(K^h_{X,\underline {x}})$ of the iterated henselization ![]() $K^h_{X,\underline {x}}$ of
$K^h_{X,\underline {x}}$ of ![]() $K(X)$ along the chain
$K(X)$ along the chain ![]() $\underline {x}$ is used instead of
$\underline {x}$ is used instead of ![]() $K^{\rm M}_{d}(K(X))$. The version stated here follows easily using the natural maps
$K^{\rm M}_{d}(K(X))$. The version stated here follows easily using the natural maps ![]() $\iota _{\underline {x}}: K(X) \to K^h_{X,\underline {x}}$ and the commutative diagram in the situation of (HS2),
$\iota _{\underline {x}}: K(X) \to K^h_{X,\underline {x}}$ and the commutative diagram in the situation of (HS2),

and the commutative diagram in the situation of (HS4),

where ![]() $\partial _{\underline {x}}$ (respectively,
$\partial _{\underline {x}}$ (respectively, ![]() $\iota _y$) is defined in [Reference Rülling and SaitoRS21c, (4.1.1)] (respectively, [Reference Rülling and SaitoRS21c, (3.2.3)]). We also note that
$\iota _y$) is defined in [Reference Rülling and SaitoRS21c, (4.1.1)] (respectively, [Reference Rülling and SaitoRS21c, (3.2.3)]). We also note that ![]() $\overline {K}^{\rm M}_d(\mathcal {O}_{X, x_{d-1}},I_D \mathcal {O}_{X, x_{d-1}})$ in (HS2) coincides with the Zariski stalk at
$\overline {K}^{\rm M}_d(\mathcal {O}_{X, x_{d-1}},I_D \mathcal {O}_{X, x_{d-1}})$ in (HS2) coincides with the Zariski stalk at ![]() $x_{d-1}$ of the sheaf
$x_{d-1}$ of the sheaf ![]() $\overline {V}_{d,X|D}$ defined in [Reference Rülling and SaitoRS21c, 4.4].
$\overline {V}_{d,X|D}$ defined in [Reference Rülling and SaitoRS21c, 4.4].
For a scheme ![]() $Z$ over
$Z$ over ![]() $k$, write
$k$, write ![]() $Z_K=Z\otimes _k K$. If
$Z_K=Z\otimes _k K$. If ![]() $Z_K$ is integral, we denote by
$Z_K$ is integral, we denote by ![]() $K(Z)$ the function field of
$K(Z)$ the function field of ![]() $Z_K$. We quote the following result from [Reference Rülling and SaitoRS21c, Proposition 7.3]. It is a key tool in the proof of Theorem 4.2.
$Z_K$. We quote the following result from [Reference Rülling and SaitoRS21c, Proposition 7.3]. It is a key tool in the proof of Theorem 4.2.
Proposition 3.2 Let ![]() $X\in \operatorname {\mathbf {Sm}}$ and assume
$X\in \operatorname {\mathbf {Sm}}$ and assume ![]() $D$ is a reduced simple normal crossing divisor on
$D$ is a reduced simple normal crossing divisor on ![]() $X$ with
$X$ with ![]() $I_D\subset \mathcal {O}_X$ its ideal sheaf. Let
$I_D\subset \mathcal {O}_X$ its ideal sheaf. Let ![]() $U\subset X$ be an open subset containing all the generic points of
$U\subset X$ be an open subset containing all the generic points of ![]() $D$. Let
$D$. Let ![]() $a\in F(X{\setminus} D)$. Assume that, for all function fields
$a\in F(X{\setminus} D)$. Assume that, for all function fields ![]() $K/k$ and for all
$K/k$ and for all ![]() $\underline {x}=(x_0,\ldots,x_{d-1}, x_d)\in \mathrm {mc}(U_K)$ with
$\underline {x}=(x_0,\ldots,x_{d-1}, x_d)\in \mathrm {mc}(U_K)$ with ![]() $x_{d-1}\in D_K^{(0)}$, we have
$x_{d-1}\in D_K^{(0)}$, we have
Then ![]() $a\in F(X,D)$.
$a\in F(X,D)$.
4. Logarithmic cohomology of reciprocity sheaves
For ![]() $\mathcal {X}=(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$, we write
$\mathcal {X}=(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$, we write ![]() $\mathcal {X}_{{\operatorname {red}}}=(X,D_{{\operatorname {red}}})\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$. We say that
$\mathcal {X}_{{\operatorname {red}}}=(X,D_{{\operatorname {red}}})\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$. We say that ![]() $\mathcal {X}=(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ is reduced if
$\mathcal {X}=(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ is reduced if ![]() $\mathcal {X}=\mathcal {X}_{{\operatorname {red}}}$.
$\mathcal {X}=\mathcal {X}_{{\operatorname {red}}}$.
Definition 4.1 Let ![]() $F\in \operatorname {\mathbf {\underline {M}PST}}$.
$F\in \operatorname {\mathbf {\underline {M}PST}}$.
(1) We say that
 $F$ is log-semipure if for any
$F$ is log-semipure if for any  $\mathcal {X}\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$, the map
$\mathcal {X}\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$, the map  $F(\mathcal {X}_{{\operatorname {red}}}) \to F(\mathcal {X})$ is injective. Note that if
$F(\mathcal {X}_{{\operatorname {red}}}) \to F(\mathcal {X})$ is injective. Note that if  $F$ is semipure,
$F$ is semipure,  $F$ is log-semipure (cf. § 1(16)).
$F$ is log-semipure (cf. § 1(16)).(2) We say that
 $F$ is logarithmic if it is log-semipure and satisfies the condition that for
$F$ is logarithmic if it is log-semipure and satisfies the condition that for  $\mathcal {X},\mathcal {Y}\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ with
$\mathcal {X},\mathcal {Y}\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ with  $\mathcal {X}$ reduced and
$\mathcal {X}$ reduced and  $\alpha \in \operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}(\mathcal {Y},\mathcal {X})$, the image of
$\alpha \in \operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}(\mathcal {Y},\mathcal {X})$, the image of  $\alpha ^*: F(\mathcal {X}) \to F(\mathcal {Y})$ is contained in
$\alpha ^*: F(\mathcal {X}) \to F(\mathcal {Y})$ is contained in  $F(\mathcal {Y}_{{\operatorname {red}}})\subset F(\mathcal {Y})$.
$F(\mathcal {Y}_{{\operatorname {red}}})\subset F(\mathcal {Y})$.
Let ![]() $\operatorname {\mathbf {\underline {M}PST}}_{\log }$ be the full subcategory of
$\operatorname {\mathbf {\underline {M}PST}}_{\log }$ be the full subcategory of ![]() $\operatorname {\mathbf {\underline {M}PST}}$ consisting of logarithmic objects and put
$\operatorname {\mathbf {\underline {M}PST}}$ consisting of logarithmic objects and put ![]() $\operatorname {\mathbf {\underline {M}NST}}_{\log }=\operatorname {\mathbf {\underline {M}NST}}\cap \operatorname {\mathbf {\underline {M}PST}}_{\log }$.
$\operatorname {\mathbf {\underline {M}NST}}_{\log }=\operatorname {\mathbf {\underline {M}NST}}\cap \operatorname {\mathbf {\underline {M}PST}}_{\log }$.
Theorem 4.2 Any ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ is logarithmic, that is,
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ is logarithmic, that is, ![]() $\operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}\subset \operatorname {\mathbf {\underline {M}NST}}_{\log }$.
$\operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}\subset \operatorname {\mathbf {\underline {M}NST}}_{\log }$.
We need a preliminary lemma for the proof of the theorem.
Lemma 4.3 Let ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$. Let
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$. Let ![]() $\mathbf {A}^n_K=\operatorname {Spec} K[x_1,\dots,x_n]$ be the affine space over a function field
$\mathbf {A}^n_K=\operatorname {Spec} K[x_1,\dots,x_n]$ be the affine space over a function field ![]() $K$ over
$K$ over ![]() $k$ and
$k$ and ![]() $V=\operatorname {Spec} K\{x_1,\dots,x_n\}$ be the henselization of
$V=\operatorname {Spec} K\{x_1,\dots,x_n\}$ be the henselization of ![]() $\mathbf {A}^n_K$ at the origin and
$\mathbf {A}^n_K$ at the origin and ![]() $\mathcal {L}_i=\{x_i=0\}\subset V$ for
$\mathcal {L}_i=\{x_i=0\}\subset V$ for ![]() $i\in [1,n]$. For an integer
$i\in [1,n]$. For an integer ![]() $0< r\leq n$, the natural map
$0< r\leq n$, the natural map
induces a map in ![]() $\operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$ (cf. § 1(9)):
$\operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$ (cf. § 1(9)):
where ![]() $S=\operatorname {Spec} K\{x_{r+1},\dots,x_{n}\}$. It induces
$S=\operatorname {Spec} K\{x_{r+1},\dots,x_{n}\}$. It induces
Then ![]() $F(V,\mathcal {L}_1+\cdots + \mathcal {L}_r)$ is generated by the image of
$F(V,\mathcal {L}_1+\cdots + \mathcal {L}_r)$ is generated by the image of ![]() $\rho _r^*$ and
$\rho _r^*$ and
Proof. For ![]() $\mathcal {Y}\in \operatorname {\mathbf {\underline {M}Cor}}$, let
$\mathcal {Y}\in \operatorname {\mathbf {\underline {M}Cor}}$, let ![]() $F^\mathcal {Y}\in \operatorname {\mathbf {\underline {M}PST}}$ be defined by
$F^\mathcal {Y}\in \operatorname {\mathbf {\underline {M}PST}}$ be defined by ![]() $F^\mathcal {Y}(\mathcal {Z})=F(\mathcal {Y}\otimes \mathcal {Z})$. Clearly, we have
$F^\mathcal {Y}(\mathcal {Z})=F(\mathcal {Y}\otimes \mathcal {Z})$. Clearly, we have ![]() $F^\mathcal {Y}\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ for
$F^\mathcal {Y}\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ for ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$. We prove the lemma by induction on
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$. We prove the lemma by induction on ![]() $r$. The case
$r$. The case ![]() $r=1$ holds since by [Reference SaitoSai20, Lemmas 7.1 and 5.9],
$r=1$ holds since by [Reference SaitoSai20, Lemmas 7.1 and 5.9], ![]() $\rho _1$ induces an isomorphism
$\rho _1$ induces an isomorphism
By definition ![]() $\mathcal {L}_1=\operatorname {Spec} K\{x_2,\dots,x_n\}$ and we have a map in
$\mathcal {L}_1=\operatorname {Spec} K\{x_2,\dots,x_n\}$ and we have a map in ![]() $\operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$,
$\operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$,
induced by the natural map ![]() $K\{x_2,\dots,x_{n}\} [x_1] \to K\{x_1,\dots,x_n\}$. By [Reference SaitoSai20, Lemmas 7.1 and 5.9], it induces an isomorphism
$K\{x_2,\dots,x_{n}\} [x_1] \to K\{x_1,\dots,x_n\}$. By [Reference SaitoSai20, Lemmas 7.1 and 5.9], it induces an isomorphism
with ![]() $E=\mathcal {L}_1\cap (\mathcal {L}_2+\cdots +\mathcal {L}_r)$. By the induction hypothesis,
$E=\mathcal {L}_1\cap (\mathcal {L}_2+\cdots +\mathcal {L}_r)$. By the induction hypothesis, ![]() $F^{(\mathbf {A}^1,0)}(\mathcal {L}_1,E)$ is generated by
$F^{(\mathbf {A}^1,0)}(\mathcal {L}_1,E)$ is generated by ![]() $F^{(\mathbf {A}^1,0)}(\mathcal {L}_1,E_j)$ with
$F^{(\mathbf {A}^1,0)}(\mathcal {L}_1,E_j)$ with ![]() $E_j=\mathcal {L}_1\cap (\mathcal {L}_2\cdots +\overset {\vee }{\mathcal {L}_j}+\cdots \mathcal {L}_{r})$ for
$E_j=\mathcal {L}_1\cap (\mathcal {L}_2\cdots +\overset {\vee }{\mathcal {L}_j}+\cdots \mathcal {L}_{r})$ for ![]() $j=2,\dots, r$ together with the image of the map
$j=2,\dots, r$ together with the image of the map
induced by
coming from the map ![]() $K\{x_{r+1},\dots,x_n\}[x_2,\dots,x_r] \to K\{x_2,\dots,x_d\}$. This proves the lemma.
$K\{x_{r+1},\dots,x_n\}[x_2,\dots,x_r] \to K\{x_2,\dots,x_d\}$. This proves the lemma.
Proof of Theorem 4.2 By Corollary 2.6(3), we may assume ![]() $F=\underline {\omega }^{\operatorname {\mathbf {CI}}} G$ for
$F=\underline {\omega }^{\operatorname {\mathbf {CI}}} G$ for ![]() $G\in {\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$. Take
$G\in {\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$. Take ![]() $\mathcal {X}=(X,D),\mathcal {Y}=(Y,E)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ with
$\mathcal {X}=(X,D),\mathcal {Y}=(Y,E)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ with ![]() $\mathcal {X}$ reduced, and let
$\mathcal {X}$ reduced, and let ![]() $\alpha \in \operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}(\mathcal {Y},\mathcal {X})$ be an elementary correspondence. We need to show that
$\alpha \in \operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}(\mathcal {Y},\mathcal {X})$ be an elementary correspondence. We need to show that ![]() $\alpha ^*(F(\mathcal {X}))\subset F(\mathcal {Y}_{{\operatorname {red}}})$. The question is Nisnevich local over
$\alpha ^*(F(\mathcal {X}))\subset F(\mathcal {Y}_{{\operatorname {red}}})$. The question is Nisnevich local over ![]() $X$ and
$X$ and ![]() $Y$. Hence, we may assume
$Y$. Hence, we may assume ![]() $(X,D)=(V,\mathcal {L}_1+\cdots +\mathcal {L}_r)\in \operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$ in the notation of Lemma 4.3. If
$(X,D)=(V,\mathcal {L}_1+\cdots +\mathcal {L}_r)\in \operatorname {\mathbf {\underline {M}Cor}}^{\rm pro}$ in the notation of Lemma 4.3. If ![]() $r=0$, we have
$r=0$, we have ![]() $\alpha \in \operatorname {\mathbf {\underline {M}Cor}}((Y,\emptyset ),(X,\emptyset ))$ by the assumption
$\alpha \in \operatorname {\mathbf {\underline {M}Cor}}((Y,\emptyset ),(X,\emptyset ))$ by the assumption ![]() $\alpha \in \operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}(\mathcal {Y},\mathcal {X})$ so that
$\alpha \in \operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}(\mathcal {Y},\mathcal {X})$ so that
Assume ![]() $r>0$ and proceed by induction on
$r>0$ and proceed by induction on ![]() $r$. By Lemma 4.3, we may then assume
$r$. By Lemma 4.3, we may then assume
On the other hand, by Corollary 2.5, we have an exact sequence
 \[ 0\to F(Y,E_{{\operatorname{red}}}) \to F(Y-E_{{\operatorname{red}}},\emptyset) \to \underset{\xi\in {{E}^{(0)}}}\bigoplus \frac{F({{{Y}}^{h}_{|\xi}}-\xi,\emptyset)}{F({{Y}^{h}_{|\xi}},\xi)}. \]
\[ 0\to F(Y,E_{{\operatorname{red}}}) \to F(Y-E_{{\operatorname{red}}},\emptyset) \to \underset{\xi\in {{E}^{(0)}}}\bigoplus \frac{F({{{Y}}^{h}_{|\xi}}-\xi,\emptyset)}{F({{Y}^{h}_{|\xi}},\xi)}. \]
Hence, we may replace ![]() $Y$ with its Nisnevich neighborhood of a generic point
$Y$ with its Nisnevich neighborhood of a generic point ![]() $\xi$ of
$\xi$ of ![]() $E$. Using the assumption that
$E$. Using the assumption that ![]() $k$ is perfect, we may then assume the following condition
$k$ is perfect, we may then assume the following condition ![]() $(\spadesuit )$. Recall that
$(\spadesuit )$. Recall that ![]() $\alpha$ is by definition an integral closed subscheme of
$\alpha$ is by definition an integral closed subscheme of ![]() $(Y-E)\times (X-D)$ finite surjective over
$(Y-E)\times (X-D)$ finite surjective over ![]() $Y-E$, and its closure
$Y-E$, and its closure ![]() $\overline {\alpha }$ in
$\overline {\alpha }$ in ![]() $Y\times X$ is finite surjective over
$Y\times X$ is finite surjective over ![]() $Y$.
$Y$.
 $(\spadesuit )$ Let
$(\spadesuit )$ Let  $Y'$ be the normalization of
$Y'$ be the normalization of  $\overline {\alpha }$ and
$\overline {\alpha }$ and  $E':=E\times _Y Y'$. Then
$E':=E\times _Y Y'$. Then  $X$,
$X$,  $Y$,
$Y$,  $E$ and
$E$ and  $E'$ are irreducible, and
$E'$ are irreducible, and  $\alpha$,
$\alpha$,  $Y'$,
$Y'$,  $E_{{\operatorname {red}}}$ and
$E_{{\operatorname {red}}}$ and  $E'_{{\operatorname {red}}}$ are essentially smooth over
$E'_{{\operatorname {red}}}$ are essentially smooth over  $k$.
$k$.
Let ![]() $g: Y'\to Y$ and
$g: Y'\to Y$ and ![]() $f: Y'\to X$ be the induced maps. We have
$f: Y'\to X$ be the induced maps. We have ![]() $E'=g^*E \geq f^*D$ as Cartier divisors on
$E'=g^*E \geq f^*D$ as Cartier divisors on ![]() $Y'$ by the modulus condition for
$Y'$ by the modulus condition for ![]() $\alpha$. Hence, these maps induce
$\alpha$. Hence, these maps induce
We claim that ![]() $\alpha ^*:F(X,D)\to F(Y,E)$ agrees with this map. Indeed, this follows from the equality
$\alpha ^*:F(X,D)\to F(Y,E)$ agrees with this map. Indeed, this follows from the equality
where ![]() $^t\Gamma _g\in \operatorname {\mathbf {Cor}}(Y-E,Y'-E')$ is the transpose of the graph of
$^t\Gamma _g\in \operatorname {\mathbf {Cor}}(Y-E,Y'-E')$ is the transpose of the graph of ![]() $g$ and
$g$ and ![]() $\Gamma _f\in \operatorname {\mathbf {Cor}}(Y'-E', X-D)$ is the graph of
$\Gamma _f\in \operatorname {\mathbf {Cor}}(Y'-E', X-D)$ is the graph of ![]() $f$. By definition this follows from the equality
$f$. By definition this follows from the equality
which one can check easily, noting that ![]() $Y'\to \overline {\alpha }$ is an isomorphism over
$Y'\to \overline {\alpha }$ is an isomorphism over ![]() $\alpha$ since
$\alpha$ since ![]() $\alpha$ is regular by
$\alpha$ is regular by ![]() $(\spadesuit )$. Then we get a commutative diagram
$(\spadesuit )$. Then we get a commutative diagram

where the top inclusion comes from the inequality ![]() $E_{{\operatorname {red}}} \times _Y Y'\geq E'_{{\operatorname {red}}}$ as Cartier divisors on
$E_{{\operatorname {red}}} \times _Y Y'\geq E'_{{\operatorname {red}}}$ as Cartier divisors on ![]() $Y'$ thanks to the semipurity of
$Y'$ thanks to the semipurity of ![]() $F$ (cf. § 1(16)). Hence, it suffices to show
$F$ (cf. § 1(16)). Hence, it suffices to show ![]() $f^*(F(X,D))\subset F(Y',E'_{{\operatorname {red}}})$. By replacing
$f^*(F(X,D))\subset F(Y',E'_{{\operatorname {red}}})$. By replacing ![]() $(Y,E)$ with
$(Y,E)$ with ![]() $(Y',E')$, we may now assume that
$(Y',E')$, we may now assume that ![]() $\alpha$ is induced by a morphism
$\alpha$ is induced by a morphism ![]() $f: Y\to X=\mathbf {A}^r\times S$. Then
$f: Y\to X=\mathbf {A}^r\times S$. Then ![]() $\alpha$ factors in
$\alpha$ factors in ![]() $\operatorname {\mathbf {\underline {M}Cor}}$ as
$\operatorname {\mathbf {\underline {M}Cor}}$ as
where the first map is induced by the map
and the second is induced by
Note that ![]() $i$ is a section of the projection
$i$ is a section of the projection ![]() $\mathbf {A}^r\times Y \to Y$. Thus, we are reduced to showing
$\mathbf {A}^r\times Y \to Y$. Thus, we are reduced to showing ![]() $i^*(F((\mathbf {A}^1,0)^{\otimes r}\otimes (Y,\emptyset )))\subset F(Y,E_{{\operatorname {red}}})$. By Proposition 3.2 this follows from the following claim.
$i^*(F((\mathbf {A}^1,0)^{\otimes r}\otimes (Y,\emptyset )))\subset F(Y,E_{{\operatorname {red}}})$. By Proposition 3.2 this follows from the following claim.
Claim 4.3.1 Take ![]() $a\in F((\mathbf {A}^1,0)^{\otimes r}\otimes (Y,\emptyset ))$. There exists an open neighborhood
$a\in F((\mathbf {A}^1,0)^{\otimes r}\otimes (Y,\emptyset ))$. There exists an open neighborhood ![]() $U\subset Y$ of the generic point of
$U\subset Y$ of the generic point of ![]() $E$ such that for every function field
$E$ such that for every function field ![]() $K$ over
$K$ over ![]() $k$ and every
$k$ and every ![]() $\delta =(\delta _0,\dots,\delta _{e-1},\delta _{e})\in \mathrm {mc}(U_K)$ with
$\delta =(\delta _0,\dots,\delta _{e-1},\delta _{e})\in \mathrm {mc}(U_K)$ with ![]() $\xi :=\delta _{e-1}\in E_K^{(0)}$ and
$\xi :=\delta _{e-1}\in E_K^{(0)}$ and ![]() $e=\dim (Y)$, we have
$e=\dim (Y)$, we have
for the pairing from (3.0.4):
Proof. After replacing ![]() $Y$ by an open neighborhood of the generic point of
$Y$ by an open neighborhood of the generic point of ![]() $E$, we may assume that
$E$, we may assume that ![]() $Y=\operatorname {Spec}(A)$ is affine and
$Y=\operatorname {Spec}(A)$ is affine and ![]() $E_{{\operatorname {red}}}=\operatorname {Spec}(A/(\pi ))$ for
$E_{{\operatorname {red}}}=\operatorname {Spec}(A/(\pi ))$ for ![]() $\pi \in A$ and, moreover, that writing
$\pi \in A$ and, moreover, that writing
we have
Let ![]() $\delta =(\delta _0,\dots,\delta _e)$ be as in the claim and put
$\delta =(\delta _0,\dots,\delta _e)$ be as in the claim and put ![]() $\delta '=(\delta _0,\dots,\delta _{e-1})\in \mathrm {mc}((E_{{\operatorname {red}}})_K)$. Put
$\delta '=(\delta _0,\dots,\delta _{e-1})\in \mathrm {mc}((E_{{\operatorname {red}}})_K)$. Put ![]() $\tilde {X}_K=\mathbf {A}^r\times Y_K$ and
$\tilde {X}_K=\mathbf {A}^r\times Y_K$ and ![]() $F=\{\pi =0\}\subset \tilde {X}_K$. Note
$F=\{\pi =0\}\subset \tilde {X}_K$. Note ![]() $d:=\dim (\tilde {X}_K)=e+r$. Let
$d:=\dim (\tilde {X}_K)=e+r$. Let ![]() $z_j$ for
$z_j$ for ![]() $e\leq j\leq d-1$ be the generic point of
$e\leq j\leq d-1$ be the generic point of
which lies over ![]() $\delta _e$,Footnote 5 and
$\delta _e$,Footnote 5 and ![]() $w_j$ for
$w_j$ for ![]() $e-1\leq j\leq d-2$ be the generic point of
$e-1\leq j\leq d-2$ be the generic point of
which is contained in the closure of ![]() $z_{j+1}$. Note
$z_{j+1}$. Note ![]() $\dim (Z_j)=\dim (W_j)=j$ and the section
$\dim (Z_j)=\dim (W_j)=j$ and the section ![]() $i$ induces isomorphisms
$i$ induces isomorphisms
Let ![]() $\sigma =(i(\delta '),w_e,\dots,w_{d-2},\eta _1,\nu )\in \mathrm {mc}(\tilde {X}_K)$, where
$\sigma =(i(\delta '),w_e,\dots,w_{d-2},\eta _1,\nu )\in \mathrm {mc}(\tilde {X}_K)$, where ![]() $\nu$ is the generic point of
$\nu$ is the generic point of ![]() $\tilde {X}_K$ lying over
$\tilde {X}_K$ lying over ![]() $\delta _e$,
$\delta _e$, ![]() $\eta _1$ is the generic point of
$\eta _1$ is the generic point of ![]() $D_1=\{x_1=0\}\subset \tilde {X}_K$ contained in the closure of
$D_1=\{x_1=0\}\subset \tilde {X}_K$ contained in the closure of ![]() $\nu$, and
$\nu$, and ![]() $i(\delta ')\in \mathrm {mc}(W_{e-1})$ is the image of
$i(\delta ')\in \mathrm {mc}(W_{e-1})$ is the image of ![]() $\delta '$ under (4.3.2). Take any
$\delta '$ under (4.3.2). Take any ![]() $\gamma \in \overline {K}^{\rm M}_e(\mathcal {O}_{Y_K,\xi },\mathfrak {m}_\xi )$ and put
$\gamma \in \overline {K}^{\rm M}_e(\mathcal {O}_{Y_K,\xi },\mathfrak {m}_\xi )$ and put
where ![]() $\iota : K^{\rm M}_e(\mathcal {O}_{Y_K,\delta _e}) \to K^{\rm M}_e(\mathcal {O}_{\tilde {X}_K,\nu })$ is induced by the projection
$\iota : K^{\rm M}_e(\mathcal {O}_{Y_K,\delta _e}) \to K^{\rm M}_e(\mathcal {O}_{\tilde {X}_K,\nu })$ is induced by the projection ![]() $\tilde {X}_K \to Y_K$. For
$\tilde {X}_K \to Y_K$. For ![]() $a\in F((\mathbf {A}^1,0)^{\otimes r}\otimes (Y,\emptyset ))$ and its restriction
$a\in F((\mathbf {A}^1,0)^{\otimes r}\otimes (Y,\emptyset ))$ and its restriction ![]() $a_K\in F((\mathbf {A}^1,0)^{\otimes r}\otimes (Y_K,\emptyset ))$, we have
$a_K\in F((\mathbf {A}^1,0)^{\otimes r}\otimes (Y_K,\emptyset ))$, we have
 \begin{align*} 0=(a_K,\beta)_{\tilde{X}_K/K,\sigma} &=-\underset{\substack{\tau\in \tilde{X}_K^{(1)}-\{\eta_1\}\\\tau>w_{d-2}}}{\sum} (a_K,\beta)_{\tilde{X}_K/K,(i(\delta'),w_e,\dots,w_{d-2},\tau,\nu)} \\ &=-(a_K,\beta)_{\tilde{X}_K/K,(i(\delta'),w_e,\dots,w_{d-2},z_{d-1},\nu)} \\ &=\pm ((a_K)_{|Z_{d-1}},\beta_1)_{Z_{d-1}/K,(i(\delta'),w_e,\dots,w_{d-2},z_{d-1})}, \end{align*}
\begin{align*} 0=(a_K,\beta)_{\tilde{X}_K/K,\sigma} &=-\underset{\substack{\tau\in \tilde{X}_K^{(1)}-\{\eta_1\}\\\tau>w_{d-2}}}{\sum} (a_K,\beta)_{\tilde{X}_K/K,(i(\delta'),w_e,\dots,w_{d-2},\tau,\nu)} \\ &=-(a_K,\beta)_{\tilde{X}_K/K,(i(\delta'),w_e,\dots,w_{d-2},z_{d-1},\nu)} \\ &=\pm ((a_K)_{|Z_{d-1}},\beta_1)_{Z_{d-1}/K,(i(\delta'),w_e,\dots,w_{d-2},z_{d-1})}, \end{align*}
where ![]() $\iota _1: K^{\rm M}_e(\mathcal {O}_{Y_K,\delta _e}) \to K^{\rm M}_e(\mathcal {O}_{Z_{d-1},z_{d-1}})$ is induced by the dominant map
$\iota _1: K^{\rm M}_e(\mathcal {O}_{Y_K,\delta _e}) \to K^{\rm M}_e(\mathcal {O}_{Z_{d-1},z_{d-1}})$ is induced by the dominant map ![]() $Z_{d-1}\to Y_K$ induced by the projection
$Z_{d-1}\to Y_K$ induced by the projection ![]() $\tilde {X}_K \to Y_K$. The first equality follows from § 3 (HS3) applied to
$\tilde {X}_K \to Y_K$. The first equality follows from § 3 (HS3) applied to ![]() $D_1\subset \tilde {X}_K$, noting that
$D_1\subset \tilde {X}_K$, noting that ![]() $\beta$ lies in
$\beta$ lies in ![]() $\overline {K}^{\rm M}_d(\mathcal {O}_{\tilde {X}_K, \eta _1},\mathfrak {m}_{\eta _1})$ since
$\overline {K}^{\rm M}_d(\mathcal {O}_{\tilde {X}_K, \eta _1},\mathfrak {m}_{\eta _1})$ since ![]() $(u_1\pi ^{m_1}-x_1)/u_1\pi ^{m_1} \in 1+ x_1 \mathcal {O}_{\tilde {X}_K,\eta _1}$. The second follows from (HS4). The third equality holds since
$(u_1\pi ^{m_1}-x_1)/u_1\pi ^{m_1} \in 1+ x_1 \mathcal {O}_{\tilde {X}_K,\eta _1}$. The second follows from (HS4). The third equality holds since ![]() $z_{d-1}$ is the unique
$z_{d-1}$ is the unique ![]() $\tau \in \tilde {X}_K^{(1)}-\{\eta _1\}$ such that
$\tau \in \tilde {X}_K^{(1)}-\{\eta _1\}$ such that ![]() $\tau >w_{d-2}$ and
$\tau >w_{d-2}$ and ![]() $(a_K,\beta )_{\tilde {X}_K/K,(i(\delta '),w_e,\dots,w_{d-2},\tau,\nu )}$ may not vanish, which follows from (HS2), noting that
$(a_K,\beta )_{\tilde {X}_K/K,(i(\delta '),w_e,\dots,w_{d-2},\tau,\nu )}$ may not vanish, which follows from (HS2), noting that ![]() $\iota (\gamma )_{|F}=0$. The final equality follows from (HS2). When
$\iota (\gamma )_{|F}=0$. The final equality follows from (HS2). When ![]() $r=1$, the last term in the above formula is equal to
$r=1$, the last term in the above formula is equal to ![]() $((a_K)_{|Y_K},\gamma )_{Y_K/K,\delta }$ by (4.3.2), so that the proof is complete. When
$((a_K)_{|Y_K},\gamma )_{Y_K/K,\delta }$ by (4.3.2), so that the proof is complete. When ![]() $r>1$, we further get
$r>1$, we further get
 \begin{align*} 0&=((a_K)_{|Z_{d-1}},\beta_1)_{Z_{d-1}/K,(i(\delta'),w_e,\dots,w_{d-2},z_{d-1})}\\ &=-\underset{\substack{\tau\in Z_{d-1}^{(1)}-\{w_{d-2}\}\\\tau>w_{d-3}}}{\sum} ((a_K)_{|Z_{d-1}},\beta_1)_{Z_{d-1}/K,(i(\delta'),w_e,\dots,w_{d-3},\tau,z_{d-1})} \\ &=-((a_K)_{|Z_{d-1}},\beta_1)_{Z_{d-1}/K,(i(\delta'),w_e,\dots,w_{d-3},z_{d-2},z_{d-1})} \\ &=\pm ((a_K)_{|Z_{d-2}},\beta_2)_{Z_{d-2}/K,(i(\delta'),w_e,\dots,w_{d-3},z_{d-2})} , \end{align*}
\begin{align*} 0&=((a_K)_{|Z_{d-1}},\beta_1)_{Z_{d-1}/K,(i(\delta'),w_e,\dots,w_{d-2},z_{d-1})}\\ &=-\underset{\substack{\tau\in Z_{d-1}^{(1)}-\{w_{d-2}\}\\\tau>w_{d-3}}}{\sum} ((a_K)_{|Z_{d-1}},\beta_1)_{Z_{d-1}/K,(i(\delta'),w_e,\dots,w_{d-3},\tau,z_{d-1})} \\ &=-((a_K)_{|Z_{d-1}},\beta_1)_{Z_{d-1}/K,(i(\delta'),w_e,\dots,w_{d-3},z_{d-2},z_{d-1})} \\ &=\pm ((a_K)_{|Z_{d-2}},\beta_2)_{Z_{d-2}/K,(i(\delta'),w_e,\dots,w_{d-3},z_{d-2})} , \end{align*}
where ![]() $\iota _2: K^{\rm M}_e(\mathcal {O}_{Y_K,\delta _e}) \to K^{\rm M}_e(\mathcal {O}_{Z_{d-2},z_{d-2}})$ is induced by the dominant map
$\iota _2: K^{\rm M}_e(\mathcal {O}_{Y_K,\delta _e}) \to K^{\rm M}_e(\mathcal {O}_{Z_{d-2},z_{d-2}})$ is induced by the dominant map ![]() $Z_{d-2}\to Y_K$ induced by the projection
$Z_{d-2}\to Y_K$ induced by the projection ![]() $\tilde {X}_K \to Y_K$. The above equalities hold by the same arguments as above, except that for the third equality there are a priori two
$\tilde {X}_K \to Y_K$. The above equalities hold by the same arguments as above, except that for the third equality there are a priori two ![]() $\tau \in Z_{d-1}^{(1)}-\{w_{d-2}\}$ with
$\tau \in Z_{d-1}^{(1)}-\{w_{d-2}\}$ with ![]() $\tau >w_{d-3}$ for which
$\tau >w_{d-3}$ for which ![]() $((a_K)_{|Z_{d-1}},\beta _1)_{Z_{d-1}/K,(i(\delta '),w_e,\dots,w_{d-3},\tau,z_{d-1})}$ may not vanish. One is
$((a_K)_{|Z_{d-1}},\beta _1)_{Z_{d-1}/K,(i(\delta '),w_e,\dots,w_{d-3},\tau,z_{d-1})}$ may not vanish. One is ![]() $z_{d-2}$ and the other is the generic point
$z_{d-2}$ and the other is the generic point ![]() $\eta _2$ of
$\eta _2$ of ![]() $Z_{d-1}\cap D_2$ with
$Z_{d-1}\cap D_2$ with ![]() $D_2= \{x_2=0\}\subset \tilde {X}_K$ which is contained in the closure of
$D_2= \{x_2=0\}\subset \tilde {X}_K$ which is contained in the closure of ![]() $z_{d-1}$. But
$z_{d-1}$. But ![]() $((a_K)_{|Z_{d-1}},\beta _1)_{Z_{d-1}/K,(i(\delta '),w_e,\dots,w_{d-3},\eta _2,z_{d-1})}=0$. Indeed,
$((a_K)_{|Z_{d-1}},\beta _1)_{Z_{d-1}/K,(i(\delta '),w_e,\dots,w_{d-3},\eta _2,z_{d-1})}=0$. Indeed, ![]() $(a_K)_{|Z_{d-1}}\in F(\operatorname {Spec}(\mathcal {O}_{Z_{d-1},\eta _2}),\eta _2)$ since
$(a_K)_{|Z_{d-1}}\in F(\operatorname {Spec}(\mathcal {O}_{Z_{d-1},\eta _2}),\eta _2)$ since ![]() $Z_{d-1}$ and
$Z_{d-1}$ and ![]() $D_2$ intersect transversally in
$D_2$ intersect transversally in ![]() $\tilde {X}_K$. Hence, the vanishing follows from (HS3) applied to
$\tilde {X}_K$. Hence, the vanishing follows from (HS3) applied to ![]() $Z_{d-1}\cap D_2\subset Z_{d-1}$, noting that
$Z_{d-1}\cap D_2\subset Z_{d-1}$, noting that ![]() $\big ((u_2\pi ^{m_2}-x_2)/u_2\pi ^{m_2}\big )_{|Z_{d-1}} \in 1+ x_2 \mathcal {O}_{Z_{d-1},\eta _2}$ so that
$\big ((u_2\pi ^{m_2}-x_2)/u_2\pi ^{m_2}\big )_{|Z_{d-1}} \in 1+ x_2 \mathcal {O}_{Z_{d-1},\eta _2}$ so that ![]() $\beta _1\in K^{\rm M}_d(\mathcal {O}_{Z_{d-1},\eta _2},\mathfrak {m}_{\eta _2})$. Repeating the same arguments, we finally get
$\beta _1\in K^{\rm M}_d(\mathcal {O}_{Z_{d-1},\eta _2},\mathfrak {m}_{\eta _2})$. Repeating the same arguments, we finally get
where ![]() $\iota _r: K^{\rm M}_e(\mathcal {O}_{Y_K,\delta _e}) \to K^{\rm M}_e(\mathcal {O}_{Z_e,z_e})$ is induced by the isomorphism
$\iota _r: K^{\rm M}_e(\mathcal {O}_{Y_K,\delta _e}) \to K^{\rm M}_e(\mathcal {O}_{Z_e,z_e})$ is induced by the isomorphism ![]() $Z_e\to Y_K$ induced by the projection
$Z_e\to Y_K$ induced by the projection ![]() $\tilde {X}_K \to Y_K$ and the second equality follows from (4.3.2). This completes the proof of the claim and Theorem 4.2.
$\tilde {X}_K \to Y_K$ and the second equality follows from (4.3.2). This completes the proof of the claim and Theorem 4.2.
Definition 4.4 For ![]() $F\in \operatorname {\mathbf {\underline {M}NST}}_{\log }$ and an integer
$F\in \operatorname {\mathbf {\underline {M}NST}}_{\log }$ and an integer ![]() $i\geq 0$, consider the association
$i\geq 0$, consider the association
By the definition this gives a presheaf on ![]() $\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$, which we call the
$\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$, which we call the ![]() $i$th logarithmic cohomology with coefficient
$i$th logarithmic cohomology with coefficient ![]() $F$.
$F$.
5. Invariance of logarithmic cohomology under blowups
Retain the notation of § 4.
Definition 5.1 Let ![]() $\Lambda ^{{\operatorname {fin}}}_{\rm ls}$ be the class of morphisms
$\Lambda ^{{\operatorname {fin}}}_{\rm ls}$ be the class of morphisms ![]() $\rho : (Y,E) \to (X,D)$ in
$\rho : (Y,E) \to (X,D)$ in ![]() $\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$ satisfying the following conditions.
$\operatorname {\mathbf {\underline {M}Cor}}^{{\operatorname {fin}}}_{\rm ls}$ satisfying the following conditions.
(a)
 $\rho$ is induced by a proper morphism
$\rho$ is induced by a proper morphism  $\rho : Y\to X$ inducing an isomorphism
$\rho : Y\to X$ inducing an isomorphism  $Y{\setminus} E\overset {\simeq }\longrightarrow X{\setminus} D$ and
$Y{\setminus} E\overset {\simeq }\longrightarrow X{\setminus} D$ and  $E=\rho ^* D$.
$E=\rho ^* D$.(b) Zariski locally on
 $X$,
$X$,  $\rho :Y \to X$ is the blowup of
$\rho :Y \to X$ is the blowup of  $X$ in a smooth center
$X$ in a smooth center  $Z\subset D$ which is normal crossing to
$Z\subset D$ which is normal crossing to  $D$.
$D$.
Here, a smooth ![]() $Z$ contained in
$Z$ contained in ![]() $D$ is normal crossing to
$D$ is normal crossing to ![]() $D$ if, letting
$D$ if, letting ![]() $D_1,\dots,D_n$ be the irreducible components of
$D_1,\dots,D_n$ be the irreducible components of ![]() $D$, there exists a subset
$D$, there exists a subset ![]() $I\subset \{1,\dots,n\}$ such that
$I\subset \{1,\dots,n\}$ such that ![]() $Z\subset {\bigcap }_{i\in I} D_i$ and
$Z\subset {\bigcap }_{i\in I} D_i$ and ![]() $Z$ is not contained in
$Z$ is not contained in ![]() $D_j$ for any
$D_j$ for any ![]() $j\not \in I$ and intersects
$j\not \in I$ and intersects ![]() $\sum _{{j\not \in I}} D_j$ transversally. Note that the condition is equivalent to that called strict normal crossing in [Reference Binda, Park and ØstværBPØ22, Definition 7.2.1].
$\sum _{{j\not \in I}} D_j$ transversally. Note that the condition is equivalent to that called strict normal crossing in [Reference Binda, Park and ØstværBPØ22, Definition 7.2.1].
Theorem 5.2 For ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and ![]() $\rho :\mathcal {Y}\to \mathcal {X}$ in
$\rho :\mathcal {Y}\to \mathcal {X}$ in ![]() $\Lambda ^{{\operatorname {fin}}}_{\rm ls}$, we have
$\Lambda ^{{\operatorname {fin}}}_{\rm ls}$, we have
Proof. Write ![]() $\mathcal {Y}=(Y,E)$ and
$\mathcal {Y}=(Y,E)$ and ![]() $\mathcal {X}=(X,D)$. First we prove the theorem for
$\mathcal {X}=(X,D)$. First we prove the theorem for ![]() $i=0$. We may assume that
$i=0$. We may assume that ![]() $D$ is reduced and
$D$ is reduced and ![]() $E=\rho ^*D$. By [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Proposition 1.9.2 b)],
$E=\rho ^*D$. By [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Proposition 1.9.2 b)], ![]() $\rho$ is invertible in
$\rho$ is invertible in ![]() $\operatorname {\mathbf {\underline {M}Cor}}$, so that
$\operatorname {\mathbf {\underline {M}Cor}}$, so that ![]() $\rho ^*:F(\mathcal {X})\cong F(\mathcal {Y})$. Since this factors through
$\rho ^*:F(\mathcal {X})\cong F(\mathcal {Y})$. Since this factors through ![]() $F(Y,E_{{\operatorname {red}}})$ by Theorem 4.2, we get (5.2.1) for
$F(Y,E_{{\operatorname {red}}})$ by Theorem 4.2, we get (5.2.1) for ![]() $i=0$.
$i=0$.
To show (5.2.1) for ![]() $i>0$, it suffices to prove
$i>0$, it suffices to prove ![]() $R^i\rho _* F_{(Y,E_{{\operatorname {red}}})} =0$. The problem is Nisnevich local, so we may assume that
$R^i\rho _* F_{(Y,E_{{\operatorname {red}}})} =0$. The problem is Nisnevich local, so we may assume that ![]() $\rho$ is induced by a blowup
$\rho$ is induced by a blowup ![]() $\rho :Y\to X$ in a smooth center
$\rho :Y\to X$ in a smooth center ![]() $Z\subset D$ normal crossing to
$Z\subset D$ normal crossing to ![]() $D$. By [Reference Kelly and SaitoKS21, Corollary 9], Nisnevich locally around a point of
$D$. By [Reference Kelly and SaitoKS21, Corollary 9], Nisnevich locally around a point of ![]() $Z$,
$Z$, ![]() $(X,D)$ is isomorphic to
$(X,D)$ is isomorphic to
where ![]() $\mathbf {A}^c=\operatorname {Spec} k[t_1,\dots,t_c]$ with
$\mathbf {A}^c=\operatorname {Spec} k[t_1,\dots,t_c]$ with ![]() $c={\operatorname {codim}}_z(Z,X)$ and
$c={\operatorname {codim}}_z(Z,X)$ and ![]() $L_i=V(t_i)$ for
$L_i=V(t_i)$ for ![]() $i=1,\dots,r$ with
$i=1,\dots,r$ with ![]() $1\leq r\leq c$, and
$1\leq r\leq c$, and ![]() $Z$ corresponds to
$Z$ corresponds to ![]() $0\times W$. Hence, the theorem follows from the following proposition.
$0\times W$. Hence, the theorem follows from the following proposition.
Proposition 5.3 Let ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$ and ![]() $\mathcal {W}=(W,W^\infty )\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$. Let
$\mathcal {W}=(W,W^\infty )\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$. Let ![]() $\mathbf {A}^n=\operatorname {Spec} k[t_1,\dots,t_n]$ and put
$\mathbf {A}^n=\operatorname {Spec} k[t_1,\dots,t_n]$ and put ![]() $L_i=V(t_i)$ for
$L_i=V(t_i)$ for ![]() $1\leq i\leq n$. Let
$1\leq i\leq n$. Let ![]() $\rho : Y\to \mathbf {A}^n$ be the blowup at the origin
$\rho : Y\to \mathbf {A}^n$ be the blowup at the origin ![]() $0\in \mathbf {A}^n$ and
$0\in \mathbf {A}^n$ and ![]() $\tilde {L}_i\subset Y$ be the strict transforms of
$\tilde {L}_i\subset Y$ be the strict transforms of ![]() $L_i$ for
$L_i$ for ![]() $1\leq i\leq n$ and
$1\leq i\leq n$ and ![]() $E=\rho ^{-1}(0)\subset Y$. For any
$E=\rho ^{-1}(0)\subset Y$. For any ![]() $1\leq r\leq n$, we have
$1\leq r\leq n$, we have
where ![]() $\rho _W:=\rho \times {\operatorname {id}}_W: Y\times W\to \mathbf {A}^2\times W$.
$\rho _W:=\rho \times {\operatorname {id}}_W: Y\times W\to \mathbf {A}^2\times W$.
Lemma 5.4 Proposition 5.3 holds for ![]() $n=2$.
$n=2$.
Proof. The case ![]() $r=1$ is proved in [Reference Binda, Rülling and SaitoBRS22, Lemma 2.13] and we show the case
$r=1$ is proved in [Reference Binda, Rülling and SaitoBRS22, Lemma 2.13] and we show the case ![]() $r=2$.Footnote 6 Put
$r=2$.Footnote 6 Put ![]() $D= L_1+ L_2$. By the case
$D= L_1+ L_2$. By the case ![]() $i=0$ of Theorem 5.2, we get
$i=0$ of Theorem 5.2, we get
Set
and ![]() $\mathbf {A}^2_W=\mathbf {A}^2\times W$ with the projection
$\mathbf {A}^2_W=\mathbf {A}^2\times W$ with the projection ![]() $p:A^2_W \to W$. Since
$p:A^2_W \to W$. Since ![]() $R^i\rho _{W*}\mathcal {F}$ for
$R^i\rho _{W*}\mathcal {F}$ for ![]() $i\ge 1$ is supported in
$i\ge 1$ is supported in ![]() $0\times W$, we have
$0\times W$, we have
 \begin{align*} R^i\rho_{W*}\mathcal{F}=0&\Longleftrightarrow p_*R^i\rho_{W*}\mathcal{F}=0\\ &\Longleftrightarrow (p_*R^i\rho_{W*}\mathcal{F})_w=0\quad\forall w\in W\\ &\Longleftrightarrow H^0(\mathbf{A}^2_{W_w}, R^i\rho_{W*}\mathcal{F})=0\quad\forall w\in W, \end{align*}
\begin{align*} R^i\rho_{W*}\mathcal{F}=0&\Longleftrightarrow p_*R^i\rho_{W*}\mathcal{F}=0\\ &\Longleftrightarrow (p_*R^i\rho_{W*}\mathcal{F})_w=0\quad\forall w\in W\\ &\Longleftrightarrow H^0(\mathbf{A}^2_{W_w}, R^i\rho_{W*}\mathcal{F})=0\quad\forall w\in W, \end{align*}
where ![]() $W_w$ is the henselization of
$W_w$ is the henselization of ![]() $W$ at
$W$ at ![]() $w$. Hence, it suffices to show
$w$. Hence, it suffices to show ![]() $H^0(\mathbf {A}^2_W, R^i\rho _{W*}\mathcal {F})=0$, assuming
$H^0(\mathbf {A}^2_W, R^i\rho _{W*}\mathcal {F})=0$, assuming ![]() $W$ is henselian local. Then we have
$W$ is henselian local. Then we have
By (5.4.1) and [Reference Binda, Rülling and SaitoBRS22, Lemma 2.10],
Thus, the Leray spectral sequence yields
and we have to show that this group vanishes for ![]() $i\ge 1$. We can write
$i\ge 1$. We can write
Then we have
Denote by
the morphism induced by projection, and let ![]() $\pi : Y\times W \to \mathbf {P}^1_W$ be its base change. Then
$\pi : Y\times W \to \mathbf {P}^1_W$ be its base change. Then ![]() $\pi _0$ induces an isomorphism
$\pi _0$ induces an isomorphism ![]() $E\simeq \mathbf {P}^1$, and we have
$E\simeq \mathbf {P}^1$, and we have
Set ![]() $s=S/T=x/y$ and write
$s=S/T=x/y$ and write
Set ![]() $U:=\mathbf {A}^1_s \times W$,
$U:=\mathbf {A}^1_s \times W$, ![]() $V:=(\mathbf {P}^1{\setminus} \{0\})\times W$ and
$V:=(\mathbf {P}^1{\setminus} \{0\})\times W$ and
We have
and the restriction of ![]() $\pi$ to these open subsets is given by projection. Furthermore,
$\pi$ to these open subsets is given by projection. Furthermore, ![]() $E\times W\subset Y$ is defined by
$E\times W\subset Y$ is defined by ![]() $y=0$ on
$y=0$ on ![]() $\pi ^{-1}(U)$ and by
$\pi ^{-1}(U)$ and by ![]() $x=0$ on
$x=0$ on ![]() $\pi ^{-1}(V)$. In view of (5.4.2), we have
$\pi ^{-1}(V)$. In view of (5.4.2), we have
Thus, [Reference Binda, Rülling and SaitoBRS22, Lemma 2.10] yields
and it remains to show
where ![]() $\mathbf {P}^1_W=\mathbf {P}^1\times W$. For this consider the map
$\mathbf {P}^1_W=\mathbf {P}^1\times W$. For this consider the map
which is the closed immersion ![]() $Y\hookrightarrow \mathbf {A}^2\times \mathbf {P}^1$ followed by the projection
$Y\hookrightarrow \mathbf {A}^2\times \mathbf {P}^1$ followed by the projection ![]() $\mathbf {A}^2\to \mathbf {A}^1_x$. Let
$\mathbf {A}^2\to \mathbf {A}^1_x$. Let ![]() $a: Y\times W\to \mathbf {A}^1_x\times \mathbf {P}^1\times W$ be its base change. In view of (5.4.2), the map
$a: Y\times W\to \mathbf {A}^1_x\times \mathbf {P}^1\times W$ be its base change. In view of (5.4.2), the map ![]() $a$ induces a morphism in
$a$ induces a morphism in ![]() $\operatorname {\mathbf {\underline {M}Cor}}$,
$\operatorname {\mathbf {\underline {M}Cor}}$,
which is an isomorphism over ![]() $(\mathbf {A}^1_x, 0)\otimes (\mathbf {P}^1\backslash \{0\},\infty )\otimes \mathcal {W}$. Setting
$(\mathbf {A}^1_x, 0)\otimes (\mathbf {P}^1\backslash \{0\},\infty )\otimes \mathcal {W}$. Setting
it induces a map of Nisnevich sheaves on ![]() $\mathbf {P}^1_W$,
$\mathbf {P}^1_W$,
which becomes an isomorphism over ![]() $(\mathbf {P}^1-\{0\})\times W$. Hence, (5.4.4) follows from
$(\mathbf {P}^1-\{0\})\times W$. Hence, (5.4.4) follows from
which follows from [Reference SaitoSai20, Theorem 0.6].
Lemma 5.5 Let ![]() $N>2$ be an integer and assume that Proposition 5.3 holds for
$N>2$ be an integer and assume that Proposition 5.3 holds for ![]() $n< N$. Let
$n< N$. Let ![]() $(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ and
$(X,D)\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$ and ![]() $Z\subset X$ be a smooth integral closed subscheme with
$Z\subset X$ be a smooth integral closed subscheme with ![]() $2\le {\operatorname {codim}}(Z,X)=:c < N$. Assume
$2\le {\operatorname {codim}}(Z,X)=:c < N$. Assume
where ![]() $D_1,\dots,D_r$ are distinct and reduced irreducible components of
$D_1,\dots,D_r$ are distinct and reduced irreducible components of ![]() $D$ containing
$D$ containing ![]() $Z$, and
$Z$, and ![]() $D'$ is an effective divisor on
$D'$ is an effective divisor on ![]() $X$ such that none of the component of
$X$ such that none of the component of ![]() $D'$ contains
$D'$ contains ![]() $Z$ and
$Z$ and ![]() $Z$ is transversal to
$Z$ is transversal to ![]() $|D'|$. Let
$|D'|$. Let ![]() $\rho : Y\to X$ be the blowup of
$\rho : Y\to X$ be the blowup of ![]() $X$ in
$X$ in ![]() $Z$, let
$Z$, let ![]() $\tilde {D}_i$ and
$\tilde {D}_i$ and ![]() $\tilde {D}'\subset Y$ be the strict transforms of
$\tilde {D}'\subset Y$ be the strict transforms of ![]() $D_i$ and
$D_i$ and ![]() $D'$ respectively, and let
$D'$ respectively, and let ![]() $E_Z=\rho ^{-1}(Z)$. Then, for all
$E_Z=\rho ^{-1}(Z)$. Then, for all ![]() $\mathcal {W}=(W,W^\infty )\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$,
$\mathcal {W}=(W,W^\infty )\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$,
where ![]() $\rho _W: Y\times W \to X\times W$ denotes the base change of
$\rho _W: Y\times W \to X\times W$ denotes the base change of ![]() $\rho$.
$\rho$.
Proof. This proof is adapted from [Reference Binda, Rülling and SaitoBRS22, Lemma 2.14]. The question is Nisnevich local around the points in ![]() $Z\times W$. Let
$Z\times W$. Let ![]() $z\in Z\times W$ be a point and set
$z\in Z\times W$ be a point and set ![]() $A:=\mathcal {O}_{X\times W,z}^h$. For
$A:=\mathcal {O}_{X\times W,z}^h$. For ![]() $V\subset Y\times W$, we denote
$V\subset Y\times W$, we denote ![]() $V_{(z)}:= V\times _{X\times W} \operatorname {Spec} A$. By assumption we find a regular system of local parameters
$V_{(z)}:= V\times _{X\times W} \operatorname {Spec} A$. By assumption we find a regular system of local parameters ![]() $t_1,\ldots, t_m$ of
$t_1,\ldots, t_m$ of ![]() $A$, such that
$A$, such that
Letting ![]() $K$ be the residue field of
$K$ be the residue field of ![]() $A$, we can choose a ring homomorphism
$A$, we can choose a ring homomorphism ![]() $K\hookrightarrow A$ which is a section of
$K\hookrightarrow A$ which is a section of ![]() $A \to K$. Then we obtain an isomorphism
$A \to K$. Then we obtain an isomorphism
Let ![]() $\rho _1:\widetilde {\mathbf {A}^c}\to \mathbf {A}^c$ be the blowup in
$\rho _1:\widetilde {\mathbf {A}^c}\to \mathbf {A}^c$ be the blowup in ![]() $0$. By the above,
$0$. By the above,
is Nisnevich locally around ![]() $z$ isomorphic over
$z$ isomorphic over ![]() $k$ to the morphism
$k$ to the morphism
 \[ \bigg(\mathcal{W}'=\bigg(\mathbf{A}_K^{m-c}, \bigg(\prod_{i=c+1}^{m_1} t_{i}^{e_{i}}\bigg)\bigg)\bigg) \]
\[ \bigg(\mathcal{W}'=\bigg(\mathbf{A}_K^{m-c}, \bigg(\prod_{i=c+1}^{m_1} t_{i}^{e_{i}}\bigg)\bigg)\bigg) \]
induced by a map ![]() $(\widetilde {\mathbf {A}^c},\tilde {L}_1+\cdots +\tilde {L}_r + E)\to (\mathbf {A}^c, L_1+\cdots + L_r)$ as in Proposition 5.3. Hence, the statement follows from the proposition for
$(\widetilde {\mathbf {A}^c},\tilde {L}_1+\cdots +\tilde {L}_r + E)\to (\mathbf {A}^c, L_1+\cdots + L_r)$ as in Proposition 5.3. Hence, the statement follows from the proposition for ![]() $n=c< N$.
$n=c< N$.
Proof of Proposition 5.3 The proof is by induction on ![]() $n\geq 2$. The case
$n\geq 2$. The case ![]() $n=2$ follows from Lemma 5.4. Assume that
$n=2$ follows from Lemma 5.4. Assume that ![]() $n>2$ and that the proposition is proven for
$n>2$ and that the proposition is proven for ![]() $\mathbf {A}^m$ with
$\mathbf {A}^m$ with ![]() $m< n$. For
$m< n$. For ![]() $r=1$, Proposition 5.3 is proved in [Reference Binda, Rülling and SaitoBRS22, Theorem 2.12]. Assume that
$r=1$, Proposition 5.3 is proved in [Reference Binda, Rülling and SaitoBRS22, Theorem 2.12]. Assume that ![]() $r\geq 2$. Let
$r\geq 2$. Let ![]() $Z:=L_1\cap L_2\subset \mathbf {A}^n$ and
$Z:=L_1\cap L_2\subset \mathbf {A}^n$ and ![]() $\tilde {Z}\subset Y$ be the strict transform of
$\tilde {Z}\subset Y$ be the strict transform of ![]() $Z$. Denote by
$Z$. Denote by ![]() $\rho ': Y'\to Y$ the blowup of
$\rho ': Y'\to Y$ the blowup of ![]() $Y$ in
$Y$ in ![]() $\tilde {Z}$, let
$\tilde {Z}$, let ![]() $\tilde {L}_i', E'\subset Y'$ be the strict transforms of
$\tilde {L}_i', E'\subset Y'$ be the strict transforms of ![]() $\tilde {L}, E$ respectively, and let
$\tilde {L}, E$ respectively, and let ![]() $E''=(\rho ')^{-1}(\tilde {Z})$. Note that
$E''=(\rho ')^{-1}(\tilde {Z})$. Note that ![]() $\tilde {Z}=\tilde {L}_1\cap \tilde {L}_2$ intersecting transversally with
$\tilde {Z}=\tilde {L}_1\cap \tilde {L}_2$ intersecting transversally with ![]() $\tilde {L}_3+\cdots +\tilde {L}_r+ E$ and
$\tilde {L}_3+\cdots +\tilde {L}_r+ E$ and ![]() ${\operatorname {codim}}(\tilde {Z}, Y)=2$. Hence, by Lemma 5.5,
${\operatorname {codim}}(\tilde {Z}, Y)=2$. Hence, by Lemma 5.5,
Since Theorem 5.2 has been proved for ![]() $i=0$, we have
$i=0$, we have
Hence, we obtain
Denote by ![]() $\sigma :\hat {Y} \to \mathbf {A}^n$ the blowup in
$\sigma :\hat {Y} \to \mathbf {A}^n$ the blowup in ![]() $Z$, let
$Z$, let ![]() $\hat {L}_i\subset \hat {Y}$ be the strict transform of
$\hat {L}_i\subset \hat {Y}$ be the strict transform of ![]() $L_i$, and let
$L_i$, and let ![]() $\Xi =\sigma ^{-1}(Z)$. By Lemma 5.5 we get
$\Xi =\sigma ^{-1}(Z)$. By Lemma 5.5 we get
Denote by ![]() $\sigma ':\hat {Y}'\to \hat {Y}$ the blowup in
$\sigma ':\hat {Y}'\to \hat {Y}$ the blowup in ![]() $\hat {Z}=\sigma ^{-1}(0)\subset \Xi$, let
$\hat {Z}=\sigma ^{-1}(0)\subset \Xi$, let ![]() $\hat {L}'_i,\; \Xi '\subset \hat {Y}'$ be the strict transforms of
$\hat {L}'_i,\; \Xi '\subset \hat {Y}'$ be the strict transforms of ![]() $\hat {L}_i,\; \Xi$ respectively, and let
$\hat {L}_i,\; \Xi$ respectively, and let ![]() $\Xi ''=\sigma '^{-1}(\hat {Z})$. Note that
$\Xi ''=\sigma '^{-1}(\hat {Z})$. Note that ![]() $\hat {Z}\subset \hat {L}_3\cap \cdots \cap \hat {L}_n\cap \Xi$ and
$\hat {Z}\subset \hat {L}_3\cap \cdots \cap \hat {L}_n\cap \Xi$ and ![]() ${\operatorname {codim}}(\hat {Z}, \hat {Y})= n-1$ and
${\operatorname {codim}}(\hat {Z}, \hat {Y})= n-1$ and ![]() $\hat {Z}$ intersects transversally with
$\hat {Z}$ intersects transversally with ![]() $\hat {L}_1+ \hat {L}_2$. Thus, by Lemma 5.5 and the case
$\hat {L}_1+ \hat {L}_2$. Thus, by Lemma 5.5 and the case ![]() $i=0$ of Theorem 5.2, we obtain
$i=0$ of Theorem 5.2, we obtain
Finally, by [Reference Binda, Rülling and SaitoBRS22, Lemma 2.15], there is an isomorphism of ![]() $\mathbf {A}^n\times W$-schemes
$\mathbf {A}^n\times W$-schemes
Altogether we obtain, for ![]() $i\ge 1$,
$i\ge 1$,
 \begin{align*} R^i\rho_{W*} F_{(Y, \tilde{L}_1+\cdots+\tilde{L}_r + E)\otimes \mathcal{W}} &= R^i(\rho\rho')_{W*} F_{(Y', \tilde{L}_1'+\cdots+\tilde{L}_r' + E' + E'')\otimes \mathcal{W}}, & & \text{by (5.5.1)},\\ & = R^i(\sigma\sigma')_{W*} F_{(\hat{Y}',\hat{L}_1'+\cdots+\hat{L}_r'+ \Xi'+\Xi'')\otimes \mathcal{W}}, & & \text{by (5.5.4)},\\ & = R^i\sigma_{W*} F_{(\hat{Y}, \hat{L}_1+\cdots+\hat{L}_r+ \Xi)\otimes \mathcal{W}}, & & \text{by (5.5.3)},\\ & = 0, & & \text{by (5.5.2)}. \end{align*}
\begin{align*} R^i\rho_{W*} F_{(Y, \tilde{L}_1+\cdots+\tilde{L}_r + E)\otimes \mathcal{W}} &= R^i(\rho\rho')_{W*} F_{(Y', \tilde{L}_1'+\cdots+\tilde{L}_r' + E' + E'')\otimes \mathcal{W}}, & & \text{by (5.5.1)},\\ & = R^i(\sigma\sigma')_{W*} F_{(\hat{Y}',\hat{L}_1'+\cdots+\hat{L}_r'+ \Xi'+\Xi'')\otimes \mathcal{W}}, & & \text{by (5.5.4)},\\ & = R^i\sigma_{W*} F_{(\hat{Y}, \hat{L}_1+\cdots+\hat{L}_r+ \Xi)\otimes \mathcal{W}}, & & \text{by (5.5.3)},\\ & = 0, & & \text{by (5.5.2)}. \end{align*}
This completes the proof of the proposition.
Remark 5.6 For simplicity, we write
By [Reference Rülling and SaitoRS21a, Corollary 6.8], if ![]() ${\operatorname {ch}}(k)=0$ and
${\operatorname {ch}}(k)=0$ and ![]() $F=\Omega ^i$, we have
$F=\Omega ^i$, we have
Hence, ![]() ${H_{\log}^{i}}(-,F)$ for
${H_{\log}^{i}}(-,F)$ for ![]() $F\in {\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ is a generalization of cohomology of sheaves of logarithmic differentials.
$F\in {\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ is a generalization of cohomology of sheaves of logarithmic differentials.
6. Relation with logarithmic sheaves with transfers
In this section we use the same notation as [Reference Binda, Park and ØstværBPØ22].
Let ![]() ${\operatorname {l\mathbf {Sm}}}$ be the category of log smooth and separated
${\operatorname {l\mathbf {Sm}}}$ be the category of log smooth and separated ![]() $\mathrm {fs}$ log schemes of finite type over the base field
$\mathrm {fs}$ log schemes of finite type over the base field ![]() $k$ and
$k$ and ![]() ${\operatorname {\mathbf {Sm}l\mathbf {Sm}}}\subset {\operatorname {l\mathbf {Sm}}}$ be the full subcategory consisting of objects whose underlying schemes are smooth over
${\operatorname {\mathbf {Sm}l\mathbf {Sm}}}\subset {\operatorname {l\mathbf {Sm}}}$ be the full subcategory consisting of objects whose underlying schemes are smooth over ![]() $k$. Let
$k$. Let ![]() ${\operatorname {l\mathbf {Cor}}}$ be the category with the same objects as
${\operatorname {l\mathbf {Cor}}}$ be the category with the same objects as ![]() ${\operatorname {l\mathbf {Sm}}}$ and whose morphisms are log correspondences defined in [Reference Binda, Park and ØstværBPØ22, Definition 2.1.1]. Let
${\operatorname {l\mathbf {Sm}}}$ and whose morphisms are log correspondences defined in [Reference Binda, Park and ØstværBPØ22, Definition 2.1.1]. Let ![]() ${\operatorname {l\mathbf {Cor}}}_{{\operatorname {\mathbf {Sm}l\mathbf {Sm}}}}\subset {\operatorname {l\mathbf {Cor}}}$ be the full subcategory consisting of all objects in
${\operatorname {l\mathbf {Cor}}}_{{\operatorname {\mathbf {Sm}l\mathbf {Sm}}}}\subset {\operatorname {l\mathbf {Cor}}}$ be the full subcategory consisting of all objects in ![]() ${\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$.
${\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$.
Let ![]() ${\operatorname {\mathbf {PSh}}^{\rm ltr}}$ be the category of additive presheaves of abelian groups on
${\operatorname {\mathbf {PSh}}^{\rm ltr}}$ be the category of additive presheaves of abelian groups on ![]() ${\operatorname {l\mathbf {Cor}}}$ and
${\operatorname {l\mathbf {Cor}}}$ and ![]() ${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}\subset {\operatorname {\mathbf {PSh}}^{\rm ltr}}$ be the full subcategory consisting of those
${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}\subset {\operatorname {\mathbf {PSh}}^{\rm ltr}}$ be the full subcategory consisting of those ![]() $\mathcal {F}$ whose restrictions to
$\mathcal {F}$ whose restrictions to ![]() ${\operatorname {l\mathbf {Sm}}}$ are dividing Nisnevich sheaves (see [Reference Binda, Park and ØstværBPØ22, Definition 3.1.4]). It is shown in [Reference Binda, Park and ØstværBPØ22, Theorem 1.2.1 and Proposition 4.7.5] that
${\operatorname {l\mathbf {Sm}}}$ are dividing Nisnevich sheaves (see [Reference Binda, Park and ØstværBPØ22, Definition 3.1.4]). It is shown in [Reference Binda, Park and ØstværBPØ22, Theorem 1.2.1 and Proposition 4.7.5] that ![]() ${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ is a Grothendieck abelian category and there is an equivalence of categories
${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ is a Grothendieck abelian category and there is an equivalence of categories
where the right-hand side denotes the full subcategory of the category ![]() ${\operatorname {\mathbf {PSh}}^{\rm ltr}}({\operatorname {\mathbf {Sm}l\mathbf {Sm}}})$ of additive presheaves of abelian groups on
${\operatorname {\mathbf {PSh}}^{\rm ltr}}({\operatorname {\mathbf {Sm}l\mathbf {Sm}}})$ of additive presheaves of abelian groups on ![]() ${\operatorname {l\mathbf {Cor}}}_{{\operatorname {\mathbf {Sm}l\mathbf {Sm}}}}$ consisting of those
${\operatorname {l\mathbf {Cor}}}_{{\operatorname {\mathbf {Sm}l\mathbf {Sm}}}}$ consisting of those ![]() $\mathcal {F}$ whose restrictions to
$\mathcal {F}$ whose restrictions to ![]() ${\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ are dividing Nisnevich sheaves.
${\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ are dividing Nisnevich sheaves.
We now construct a functor
For ![]() $\mathfrak {X}=(X,\mathcal {M})\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$, we put
$\mathfrak {X}=(X,\mathcal {M})\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$, we put ![]() $\mathfrak {X}^{\rm MP}=(X, \partial \mathfrak {X})$, where
$\mathfrak {X}^{\rm MP}=(X, \partial \mathfrak {X})$, where ![]() $\partial \mathfrak {X}\subset X$ is the closed subscheme consisting of the points where the log structure
$\partial \mathfrak {X}\subset X$ is the closed subscheme consisting of the points where the log structure ![]() $\mathcal {M}$ is not trivial. By [Reference Binda, Park and ØstværBPØ22, Lemma A.5.10],
$\mathcal {M}$ is not trivial. By [Reference Binda, Park and ØstværBPØ22, Lemma A.5.10], ![]() $\partial \mathfrak {X}$ with reduced structure is a normal crossing divisor on
$\partial \mathfrak {X}$ with reduced structure is a normal crossing divisor on ![]() $X$, so that we can view
$X$, so that we can view ![]() $\mathfrak {X}^{\rm MP}$ as an object of
$\mathfrak {X}^{\rm MP}$ as an object of ![]() $\operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$. For
$\operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$. For ![]() $F\in \operatorname {\mathbf {\underline {M}PST}}_{\log }$ and
$F\in \operatorname {\mathbf {\underline {M}PST}}_{\log }$ and ![]() $\mathfrak {X}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$, we put
$\mathfrak {X}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$, we put
Take ![]() $\mathfrak {Y} \in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ and
$\mathfrak {Y} \in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ and ![]() $\alpha \in {\operatorname {l\mathbf {Cor}}}(\mathfrak {Y},\mathfrak {X})$. By [Reference Binda, Park and ØstværBPØ22, Definition 2.1.1 and Remark 2.1.2(iii)], we have
$\alpha \in {\operatorname {l\mathbf {Cor}}}(\mathfrak {Y},\mathfrak {X})$. By [Reference Binda, Park and ØstværBPØ22, Definition 2.1.1 and Remark 2.1.2(iii)], we have
where ![]() $n\cdot \partial \mathfrak {Y}\hookrightarrow Y$ is the
$n\cdot \partial \mathfrak {Y}\hookrightarrow Y$ is the ![]() $n$th thickening of
$n$th thickening of ![]() $\partial \mathfrak {Y}\hookrightarrow Y$. By the assumption
$\partial \mathfrak {Y}\hookrightarrow Y$. By the assumption ![]() $F\in \operatorname {\mathbf {\underline {M}PST}}_{\log }$, the induced map
$F\in \operatorname {\mathbf {\underline {M}PST}}_{\log }$, the induced map
factors through ![]() $F^{\log }(\mathfrak {Y})=F(Y,\partial \mathfrak {Y})\subset F(Y,n\cdot \partial \mathfrak {Y})$ and we get a map
$F^{\log }(\mathfrak {Y})=F(Y,\partial \mathfrak {Y})\subset F(Y,n\cdot \partial \mathfrak {Y})$ and we get a map
Moreover, for a map ![]() $\gamma : F\to G$ in
$\gamma : F\to G$ in ![]() $\operatorname {\mathbf {\underline {M}PST}}_{\log }$, the diagram
$\operatorname {\mathbf {\underline {M}PST}}_{\log }$, the diagram

is obviously commutative. Hence, the assignment ![]() $\mathcal {X}\to F^{\log }(\mathcal {X})$ gives an object
$\mathcal {X}\to F^{\log }(\mathcal {X})$ gives an object ![]() $F^{\log }$ of
$F^{\log }$ of ![]() ${\operatorname {\mathbf {PSh}}^{\rm ltr}}({\operatorname {\mathbf {Sm}l\mathbf {Sm}}})$ and we get a functor
${\operatorname {\mathbf {PSh}}^{\rm ltr}}({\operatorname {\mathbf {Sm}l\mathbf {Sm}}})$ and we get a functor
By the definitions of sheaves ([Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Definition 1], [Reference Binda, Park and ØstværBPØ22, Definition 3.1.4] and [Reference Kahn, Miyazaki, Saito and YamazakiKMSY21a, Proposition 1.9.2]), this induces a functor
which induces the desired functor (6.0.2) using (6.0.1). By the construction, for ![]() $F\in \operatorname {\mathbf {\underline {M}NST}}_{\log }$ and
$F\in \operatorname {\mathbf {\underline {M}NST}}_{\log }$ and ![]() $\mathfrak {X}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ with
$\mathfrak {X}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ with ![]() $\mathcal {X}=\mathfrak {X}^{\rm MP}\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$, we have
$\mathcal {X}=\mathfrak {X}^{\rm MP}\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$, we have
where the right-hand side is the cohomology for the strict Nisnevich topology (see [Reference Binda, Park and ØstværBPØ22, Definition 4.3.1]).
Theorem 6.1 For ![]() $F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$,
$F\in \operatorname {\mathbf {CI}}^{\tau,{\rm sp}}_{{\operatorname {Nis}}}$, ![]() $F^{\log }=\mathcal {L}og(F)\in {\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ is strictly
$F^{\log }=\mathcal {L}og(F)\in {\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ is strictly ![]() ${\overline {\square }}$-invariant in the sense of [Reference Binda, Park and ØstværBPØ22, Definition 5.2.2]. For
${\overline {\square }}$-invariant in the sense of [Reference Binda, Park and ØstværBPØ22, Definition 5.2.2]. For ![]() $\mathfrak {X}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ with
$\mathfrak {X}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ with ![]() $\mathcal {X}=\mathfrak {X}^{\rm MP}\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$, we have a natural isomorphism
$\mathcal {X}=\mathfrak {X}^{\rm MP}\in \operatorname {\mathbf {\underline {M}Cor}}_{\rm ls}$, we have a natural isomorphism
where ![]() $\operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ is the triangulated category of logarithmic motives defined in [Reference Binda, Park and ØstværBPØ22, Definition 5.2.1].
$\operatorname {\mathbf {logDM}}^{{\operatorname {eff}}}$ is the triangulated category of logarithmic motives defined in [Reference Binda, Park and ØstværBPØ22, Definition 5.2.1].
Proof. Let ![]() $\mathfrak {X}_{\rm div}^{\rm Sm}$ be the category of log modifications
$\mathfrak {X}_{\rm div}^{\rm Sm}$ be the category of log modifications ![]() $\mathfrak {Y} \to \mathfrak {X}$ such that
$\mathfrak {Y} \to \mathfrak {X}$ such that ![]() $\mathfrak {Y}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ (see [Reference Binda, Park and ØstværBPØ22, Definition A.11.12]) and
$\mathfrak {Y}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ (see [Reference Binda, Park and ØstværBPØ22, Definition A.11.12]) and ![]() $\mathfrak {X}_{\rm divsc}^{\rm Sm}\subset \mathfrak {X}_{\rm div}^{\rm Sm}$ be the full subcategory given by those maps
$\mathfrak {X}_{\rm divsc}^{\rm Sm}\subset \mathfrak {X}_{\rm div}^{\rm Sm}$ be the full subcategory given by those maps ![]() $\mathfrak {Y}\to \mathfrak {X}$ that are isomorphic to compositions of log modifications along smooth centers (see [Reference Binda, Park and ØstværBPØ22, Definitions 4.4.4 and A.14.10]). We have isomorphisms
$\mathfrak {Y}\to \mathfrak {X}$ that are isomorphic to compositions of log modifications along smooth centers (see [Reference Binda, Park and ØstværBPØ22, Definitions 4.4.4 and A.14.10]). We have isomorphisms
 \begin{align*} H^i_{\operatorname{Nis}}(X,F_{\mathcal{X}}) &\overset{(6.0.5)}{\simeq} H^i_{s\mathrm{Nis}}(\mathfrak{X},F^{\log}) \overset{(*1)}{\simeq} \mathop {\varinjlim}_{\mathfrak{Y}\in \mathfrak{X}_{\rm divsc}^{\rm Sm}} H^i_{s\mathrm{Nis}}(\mathfrak{Y},F^{\log}) \\ &\overset{(*2)}{\simeq} \mathop {\varinjlim}_{\mathfrak{Y}\in \mathfrak{X}_{\rm div}^{\rm Sm}} H^i_{s\mathrm{Nis}}(\mathfrak{Y},F^{\log}) \overset{(*3)}{\simeq} H^i_{d\mathrm{Nis}}(\mathfrak{X},F^{\log}), \end{align*}
\begin{align*} H^i_{\operatorname{Nis}}(X,F_{\mathcal{X}}) &\overset{(6.0.5)}{\simeq} H^i_{s\mathrm{Nis}}(\mathfrak{X},F^{\log}) \overset{(*1)}{\simeq} \mathop {\varinjlim}_{\mathfrak{Y}\in \mathfrak{X}_{\rm divsc}^{\rm Sm}} H^i_{s\mathrm{Nis}}(\mathfrak{Y},F^{\log}) \\ &\overset{(*2)}{\simeq} \mathop {\varinjlim}_{\mathfrak{Y}\in \mathfrak{X}_{\rm div}^{\rm Sm}} H^i_{s\mathrm{Nis}}(\mathfrak{Y},F^{\log}) \overset{(*3)}{\simeq} H^i_{d\mathrm{Nis}}(\mathfrak{X},F^{\log}), \end{align*}
where ![]() $(*2)$ follows from [Reference Binda, Park and ØstværBPØ22, Corollary 4.4.5] and
$(*2)$ follows from [Reference Binda, Park and ØstværBPØ22, Corollary 4.4.5] and ![]() $(*3)$ from [Reference Binda, Park and ØstværBPØ22, Theorem 5.1.8], and
$(*3)$ from [Reference Binda, Park and ØstværBPØ22, Theorem 5.1.8], and ![]() $(*1)$ is a consequence of Theorem 5.2 in view of (6.0.5) and the fact that a log modification of
$(*1)$ is a consequence of Theorem 5.2 in view of (6.0.5) and the fact that a log modification of ![]() $\mathfrak {X}=(X,\mathcal {M})\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ along smooth center is induced Zariski locally by a blowup of
$\mathfrak {X}=(X,\mathcal {M})\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ along smooth center is induced Zariski locally by a blowup of ![]() $X$ in an intersection of irreducible components of
$X$ in an intersection of irreducible components of ![]() $\partial \mathfrak {X}$ so that it corresponds to a morphism in
$\partial \mathfrak {X}$ so that it corresponds to a morphism in ![]() $\Lambda ^{{\operatorname {fin}}}_{\rm ls}$ from Definition 5.1.
$\Lambda ^{{\operatorname {fin}}}_{\rm ls}$ from Definition 5.1.
Hence, the strict ![]() ${\overline {\square }}$-invariance of
${\overline {\square }}$-invariance of ![]() $F^{\log }$ follows from [Reference SaitoSai20, Theorem 0.6]. Finally, (6.1.1) follows from [Reference Binda, Park and ØstværBPØ22, Proposition 5.2.3].
$F^{\log }$ follows from [Reference SaitoSai20, Theorem 0.6]. Finally, (6.1.1) follows from [Reference Binda, Park and ØstværBPØ22, Proposition 5.2.3].
We now consider the composite functor
where ![]() $\operatorname {\mathbf {CI}}^{\rm ltr}_{\rm dNis}\subset {\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ is the full subcategory consisting of strictly
$\operatorname {\mathbf {CI}}^{\rm ltr}_{\rm dNis}\subset {\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$ is the full subcategory consisting of strictly ![]() ${\overline {\square }}$-invariant objects. By [Reference Binda and MericiBM12, Theorem 5.7],
${\overline {\square }}$-invariant objects. By [Reference Binda and MericiBM12, Theorem 5.7], ![]() $\operatorname {\mathbf {CI}}^{\rm ltr}_{\rm dNis}$ is a Grothendieck abelian category.
$\operatorname {\mathbf {CI}}^{\rm ltr}_{\rm dNis}$ is a Grothendieck abelian category.
Lemma 6.2 ![]() $\mathcal {L}og$ and
$\mathcal {L}og$ and ![]() $\mathcal {L}og'$ have the same essential image.
$\mathcal {L}og'$ have the same essential image.
Proof. This follows directly from the construction and Corollary 2.6(3).
In what follows, we let
denote ![]() $\mathcal {L}og'$ defined as above. By (6.0.3), we have
$\mathcal {L}og'$ defined as above. By (6.0.3), we have
where ![]() $(X,\mathrm {triv})$ denotes the log scheme with the trivial log structure.
$(X,\mathrm {triv})$ denotes the log scheme with the trivial log structure.
Theorem 6.3 ![]() $\mathcal {L}og$ is exact and fully faithful.
$\mathcal {L}og$ is exact and fully faithful.
Proof. First we prove the full faithfulness. Faithfulness follows from (6.2.2). Let ![]() $F,G\in {\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ and
$F,G\in {\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$ and ![]() $\gamma : F^{\log }\to G^{\log }$ be a map in
$\gamma : F^{\log }\to G^{\log }$ be a map in ![]() ${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$. By (6.2.2) it induces maps
${\operatorname {\mathbf {Shv}}^{\rm ltr}_{\rm dNis}}$. By (6.2.2) it induces maps ![]() $\gamma _X: F(X) \to G(X)$ for all
$\gamma _X: F(X) \to G(X)$ for all ![]() $X\in \operatorname {\mathbf {Sm}}$. They are compatible with the action of
$X\in \operatorname {\mathbf {Sm}}$. They are compatible with the action of ![]() $\operatorname {\mathbf {Cor}}$ since by [Reference Binda, Park and ØstværBPØ22, Example 2.1.3(3)],
$\operatorname {\mathbf {Cor}}$ since by [Reference Binda, Park and ØstværBPØ22, Example 2.1.3(3)],
Thus, ![]() $\gamma _X$ for
$\gamma _X$ for ![]() $X\in \operatorname {\mathbf {Sm}}$ give a map
$X\in \operatorname {\mathbf {Sm}}$ give a map ![]() $\gamma _{{\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}}:F\to G$ in
$\gamma _{{\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}}:F\to G$ in ![]() ${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$. To see
${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$. To see ![]() $\mathcal {L}og(\gamma _{{\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}})=\gamma$, it suffices by (6.0.1) to show that
$\mathcal {L}og(\gamma _{{\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}})=\gamma$, it suffices by (6.0.1) to show that ![]() $\mathcal {L}og(\gamma _{{\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}})$ and
$\mathcal {L}og(\gamma _{{\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}})$ and ![]() $\gamma$ induce the same map
$\gamma$ induce the same map ![]() $F^{\log }(\mathfrak {X}) \to G^{\log }(\mathfrak {X})$ for
$F^{\log }(\mathfrak {X}) \to G^{\log }(\mathfrak {X})$ for ![]() $\mathfrak {X}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$. If
$\mathfrak {X}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$. If ![]() $\mathfrak {X}$ has the trivial log structure, this follows immediately from the construction of
$\mathfrak {X}$ has the trivial log structure, this follows immediately from the construction of ![]() $\gamma _{{\operatorname {\mathbf {RSC}}}}$. The general case follows from this in view of the commutative diagram
$\gamma _{{\operatorname {\mathbf {RSC}}}}$. The general case follows from this in view of the commutative diagram

where ![]() $j^*$ are induced by the natural map
$j^*$ are induced by the natural map ![]() $(X\backslash \partial \mathfrak {X},\mathrm {triv})\to \mathfrak {X}$ of log schemes and are injective by the construction and the semipurity of
$(X\backslash \partial \mathfrak {X},\mathrm {triv})\to \mathfrak {X}$ of log schemes and are injective by the construction and the semipurity of ![]() $\underline {\omega }^{\operatorname {\mathbf {CI}}} F$. This completes the proof of the full faithfulness.
$\underline {\omega }^{\operatorname {\mathbf {CI}}} F$. This completes the proof of the full faithfulness.
Next we show the exactness of ![]() $\mathcal {L}og$. It suffices to show the following claim.
$\mathcal {L}og$. It suffices to show the following claim.
Claim 6.3.1 Given an exact sequence ![]() $0\to F\to G\to H\to 0$ in
$0\to F\to G\to H\to 0$ in ![]() ${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$, the induced sequence
${\operatorname {\mathbf {RSC}}}_{{\operatorname {Nis}}}$, the induced sequence
is exact for every ![]() $\mathfrak {X}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ with
$\mathfrak {X}\in {\operatorname {\mathbf {Sm}l\mathbf {Sm}}}$ with ![]() $X$ henselian local.
$X$ henselian local.
Indeed, by the definition of ![]() $\mathcal {L}og$, this is reduced to the exactness of
$\mathcal {L}og$, this is reduced to the exactness of
which follows from Corollary 2.6(2). This completes the proof of Theorem 6.3.
Acknowledgements
The author would like to thank Kay Rülling, F. Binda and A. Merici for many valuable discussions and comments. He is also grateful to A. Merici to whom he owes crucial ideas for § 2. The author also thanks the referee for a very careful reading and numerous suggestions improving this paper.