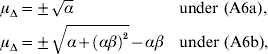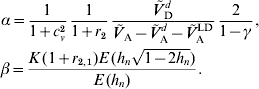1. Introduction
Quantitative traits can be controlled by many genes and environmental factors. One main concept to deal with these traits is the infinitesimal model (Fisher, Reference Fisher1918; Goddard, Reference Goddard2001) which assumes an infinite number of genes each with infinitesimal effects. But in fact, the number of genes is finite. Even though the assumptions of this model are violated, the use of this concept has yielded substantial genetic gain for many quantitative traits in livestock and plant breeding over the past few decades (Dekkers & Hospital, Reference Dekkers and Hospital2002). Research on the genetic architecture of quantitative traits and its deviation from the infinitesimal model has a long history, see e.g. Lynch & Walsh (Reference Lynch and Walsh1998), Mackay (Reference Mackay2001) or Hill (Reference Hill2010) and references therein. Many results are trait specific and controversial. Having knowledge about the number of quantitative trait loci (QTLs) as well as the distribution of their effects for a particular trait would contribute to a deeper understanding of its genetic architecture. Furthermore, in animal breeding, genetic evaluation methods that use massive genetic marker data have become common in practice (Hayes et al., Reference Hayes, Bowman, Chamberlain and Goddard2009). For the development of these models as well as for the assessment of long-term genetic progress using this technology it would be helpful to have knowledge about the number of QTLs and the distribution of QTL effects (Goddard, Reference Goddard2009; Daetwyler et al., Reference Daetwyler, Pong-Wong, Villanueva and Woolliams2010).
Estimators of the number of QTLs have been proposed by Hayes & Goddard (Reference Goddard2001) and Chamberlain et al. (Reference Chamberlain, McPartlan and Goddard2007). Hayes & Goddard (Reference Goddard2001) estimated 50–100 segregating QTLs per trait in dairy cattle. Chamberlain et al. (Reference Chamberlain, McPartlan and Goddard2007) concluded that at least 30 QTLs are segregating. However, both authors could not rule out the possibility that there are many more QTLs with small effects, because they used results from QTL mapping studies. It was frequently shown that mapped QTLs were separated into a series of additional QTLs by fine mapping experiments (e.g. Mackay & Anholt, Reference Mackay and Anholt2006), pointing towards larger numbers of QTLs. Support for a higher number of QTLs comes also from human height data (Visscher, Reference Visscher2008) and from genomic selection experiments. Luan et al. (Reference Luan, Woolliams, Lien, Kent, Svendsen and Meuwissen2009) using 20 k single nucleotide polymorphisms (SNPs) for genomic breeding value estimation in dairy cattle found that the method called G-BLUP for the estimation of genomic breeding values produced similar or better than Bayesian methods. This is usually only the case if many QTLs are segregating and the ratio of marker to QTL is low (Meuwissen & Goddard, Reference Meuwissen and Goddard2010). Several estimators are known that are not applicable to outbred populations, e.g. the Castle–Wright estimator or the estimator proposed by Otto & Jones (Reference Otto and Jones2000). Hill et al. (Reference Hill, Goddard and Visscher2008) noted that for a given rate of inbreeding depression, as the number of loci increases and the gene frequencies move towards 0 or 1, the dominance variance decreases towards zero. Consequently, the relationship between dominance variance and inbreeding depression, which is the mean decrease of the trait value when the inbreeding coefficient increases from 0 to 1, could be used to estimate the number of QTLs. Such an estimator would not rely on QTL mapping results but would need knowledge about inbreeding depression and dominance variance, which have been estimated for some populations and traits (Misztal, Reference Misztal1997).
A second main issue in the genetic architecture of quantitative traits is the distribution of QTL effects. In a meta-analysis of information from QTL mapping experiments, Hayes & Goddard (Reference Goddard2001) found the distribution to be moderately leptocurtic, consistent with many genes of small effect and few of large effect. Some studies have reported double exponential distributions (Eyre-Walker & Keightley, Reference Eyre-Walker and Keightley2007; Bennewitz & Meuwissen, Reference Bennewitz and Meuwissen2010). Traits are known with segregating QTLs of large effect (e.g. the pleiotropic DGAT1 in Holstein cattle, see Grisart et al., Reference Grisart, Farnir, Karim, Cambisano, Kim, Kvasz, Mni, Simon, Frère, Coppieters and Georges2004) even though the trait has been under selection for a long time. On the other hand, recent large-scale association studies conducted for human height revealed 54 variants which collectively explained only a few percent of the genetic variance of this highly heritable trait (Visscher, Reference Visscher2008), indicating that there are many QTLs with small effects and none with an exceptional large effect for this trait. This suggests that the distribution of QTL effects is trait specific. In QTL mapping studies, it is often estimated how many QTLs with a ‘large’ effect are segregating. Naturally, these ‘large’ QTLs determine the distribution of the effects and could therefore be used to derive parameters of the distribution. However, the true number of segregating large QTLs may be even smaller than reported by QTL mapping studies due to publication bias, as negative results tend not to be published.
The distribution of the dominance coefficient was derived by Bennewitz & Meuwissen (Reference Bennewitz and Meuwissen2010) for meat production traits in pigs. The dominance coefficient δn=d n/|a n| depends on the dominance effect d n and on the absolute additive effect |a n|, which is half the difference between the homozygous genotypic values. They postulated a normal distribution with a mean of μΔ=0·193 and a standard deviation of σΔ=0·312 for segregating alleles. Thus, overdominance is a rare but not negligible event for these traits. However, if dominance is more important, e.g. for fitness-related traits, these figures might not hold and overdominance might play a more important role. For example, Ishikawa (Reference Ishikawa2009) mapped an overdominant allele affecting body weight in mice at 6 weeks of age with a dominance coefficient of up to 6·6. Luo et al. (Reference Luo, Li, Mei, Shu, Tabien, Zhong, Ying, Stansel, Khush and Paterson2001) found that overdominance is an important property of most loci associated with heterosis in rice. Rocha et al. (Reference Rocha, Eisen, Siewerdt, Van Vleck and Pomp2004) found more directional dominance in fitness-related traits compared to growth or body composition traits in mice. García-Dorado et al. (Reference García-Dorado, López-Fanjul and Caballero1999) suggested in their review an average dominance coefficient of 0·94<![]() <0·98 (0·01<"
<0·98 (0·01<"![]() =(1−
=(1−![]() )/2<0·03) for new lethal mutants and argued that the typical value
)/2<0·03) for new lethal mutants and argued that the typical value ![]() =0·2 (
=0·2 (![]() =0·4) can be questioned for new non-severe deleterious mutations, but suggested
=0·4) can be questioned for new non-severe deleterious mutations, but suggested ![]() =0·8 (
=0·8 (![]() =0·1). However, even if dominance is common, it does not necessarily cause much dominance variance due to the U-shaped distribution of allele frequencies (Hill et al., Reference Hill, Goddard and Visscher2008).
=0·1). However, even if dominance is common, it does not necessarily cause much dominance variance due to the U-shaped distribution of allele frequencies (Hill et al., Reference Hill, Goddard and Visscher2008).
Also important is the joint distribution of the additive effects a n of the mutant alleles, the dominance coefficients δn and allele frequencies p n. Several studies assume that they are independent, e.g. Bennewitz & Meuwissen (Reference Bennewitz and Meuwissen2010). But this is likely not true. Kacser & Burns (Reference Kacser and Burns1981) argued that the relationship between enzyme activity and end-product is hyperbolic. Thus, if a high enzyme activity is needed to produce a large trait value, then it is expected that the allele that increases the trait value shows incomplete dominance (i.e. δn>0). Moreover, since a differentiable function is locally approximately linear, one would expect that alleles with small effect show little dominance (i.e. δn≈0), although this is not always confirmed empirically, e.g. Caballero & Keightley (Reference Caballero and Keightley1994), Bennewitz & Meuwissen (Reference Bennewitz and Meuwissen2010). Thus, |a n| and δn should be positively correlated. Not only arguments based on metabolic pathways (Keightley, Reference Keightley1996) but also arguments based on selection point into this direction. New mutations that affect a trait that was under selection are most often deleterious and recessive. Recessivity of mutants arises as a side effect of the margin of safety built into most metabolic pathways. But the extent to which this safety margin results from natural selection remains controversial (Bourguet, Reference Bourguet1999). Since selection on modifier alleles that act on heterozygote mutant alleles would be much stronger than that acting on homozygotes (Fisher, Reference Fisher1928) and since advantageous dominant alleles less likely become lost by random drift than recessive alleles with the same function, alleles that have been fixed are likely to be dominant over new mutant alleles. However, selection coefficients on modifier alleles would be extremely small (Wright, Reference Wright1934), so modifier alleles may be of little importance. More important for the joint distribution of allelic effects and allele frequencies is the change of an allele frequency by one generation of selection, as it depends on the current allele frequency (Falconer & Mackay, Reference Falconer and Mackay1996, p. 28). Since selection against a recessive deleterious allele becomes inefficient when the allele frequency p n is small, and since most mutant alleles are recessive and deleterious, one would expect that segregating deleterious alleles (a n<0) with small frequency (p n≈0) tend to be recessive (δn≈1). For the same reason, segregating advantageous alleles (a n>0) with high frequency (p n≈1) tend to be dominant (δn≈1). Due to the U-shaped distribution of allele frequencies, most allele frequencies are close to 0 or 1, so these arguments are valid for the majority of the alleles. Therefore, we have likely p n>0·5 if sign(a n)=sign(δn) and p n<0·5 if sign(a n)≠sign(δn). All these arguments also confirm that |a n| and δn are likely positively correlated.
Table 1. Table of symbols

Allelic effects and allele frequencies affect the additive variance, the dominance variance and the inbreeding depression of a trait. However, dominance variance is not only determined by these quantities, but may be increased quite substantially by linkage disequilibrium as shown by Avery & Hill (Reference Avery and Hill1979). Given that alleles are coded as 0 and 1, the coefficient of linkage disequilibrium D n,m between loci n and m equals the covariance of the alleles, if they are chosen at random from the infinite gametic pool.
The objective of this paper was to find parameter settings for the simulation of a particular trait that account for dominance realistically and are consistent with literature reports. A further concern is the identification of genetic architectures for a particular trait that are consistent with available estimates of variance components and inbreeding depression. First, formulae were developed that quantify the contributions of different sources that affect the phenotypic variance. The minimum number of QTLs is calculated that is needed such that inbreeding depression on average does not cause more dominance variance than the true dominance variance of the trait. This novel estimator predicts a lower bound for the number of QTLs. Using the developed formulae, it is shown how the number of ‘large’ QTLs can be used to derive parameters of the distribution of QTL effects. Finally, the role of overdominance for cases where the ratio of dominance variance to additive genetic variance is high is investigated. The developed formulae are based on the availability of additive genetic variance as well as dominance variance components. They were applied using published variance components estimates for milk yield and productive life (PL) in Holstein dairy cattle.
2. Theory
This section is divided into several parts. In (i), formulae for the variance components are derived that account for linkage disequilibrium. Their expectations under a wide range of assumptions are derived in (ii). Part (iii) discusses the distribution of allele frequencies and linkage disequilibrium of alleles. In (iv), parameters that describe the joint distribution of additive effect and dominance coefficients are derived for different scenarios. Parameters that are estimated in (iii) and (iv) are needed to evaluate the formulae that are derived in later parts. In (v), formulae are derived to estimate the contributions of different sources to the additive and dominance variance. Lower bounds for the number of QTLs are presented in (vi). Implications on the importance of overdominance can be found in (vii). Upper bounds for the number of large QTLs are given in (viii). Part (ix) shows how the formulae can be used to estimate the number of QTLs, the variance of the additive effects, and the mean and variance of the dominance coefficients. For a better readability, the proofs of the formulae are given in the electronic appendix (available at http://journals.cambridge.org/GRH). A list of symbols used in the paper is given in Table 1.
(i) Variance components and inbreeding depression
According to Falconer & Mackay (Reference Falconer and Mackay1996), the breeding value of an individual is the sum of all substitution effects that are carried by this individual, i.e. up to an additive constant the breeding value is
where v n∊{0, 1} is the paternal and m n∊{0, 1} is the maternal allele of the individual at QTL n and ![]() consists of all polymorphic QTLs. Here, it is assumed that all QTLs are biallelic with alleles 0 and 1. Moreover, we assume throughout the paper the absence of genetic interactions. The mutant allele at QTL n has frequency p n, additive effect a n and dominance effect d n. The other allele has frequency q n=1−p n. The dominance deviation of the individual is
consists of all polymorphic QTLs. Here, it is assumed that all QTLs are biallelic with alleles 0 and 1. Moreover, we assume throughout the paper the absence of genetic interactions. The mutant allele at QTL n has frequency p n, additive effect a n and dominance effect d n. The other allele has frequency q n=1−p n. The dominance deviation of the individual is
see Falconer & Mackay (Reference Falconer and Mackay1996, Table 7.3). The additive variance is the variance of the breeding value and the dominance variance is the variance of the dominance deviation of an individual whose parents are randomly chosen from the population. Thereby, the additive effects, the dominance effects and the allele frequencies are assumed to be fixed parameters and randomness arises from random sampling of the genotypes. That is, only the paternal and maternal alleles are random. Since maternal and paternal alleles are independent and identically distributed with Var(v n)=Var(m n)=p nq n and E (v n)=E (m n)=p n, we obtain (see the proofs in the electronic appendix)
where h n=2p nq n is the heterozygosity at locus n in the case of Hardy-Weinberg Equilibrium (HWE) and D n,m=Cov (v n, v m)=Cov (m n, m m) is the coefficient of linkage disequilibrium between locus n and m. For the dominance variance, we obtain
Note that V A+V D equals the genotypic variance within a line given by Avery & Hill (Reference Avery and Hill1979). If linkage disequilibrium is neglected, i.e. if D n,m=0 is assumed, then only the left summands in eqns (1) and (2) remain, which is equal to the well-known formulae given in Falconer & Mackay (Reference Falconer and Mackay1996). We assume that loci from different chromosomes are not in linkage disequilibrium, but loci from the same chromosome may be linked. Take ![]() to be the set of chromosomes and for c∊
to be the set of chromosomes and for c∊![]() let
let ![]() c denote the polymorphic QTL at chromosome c. Then we have
c denote the polymorphic QTL at chromosome c. Then we have
and
The first summand in eqn (3) equals

Therefore, we can write
where V Aa=∑n∊![]() h na n2 and V Ad=∑n∊
h na n2 and V Ad=∑n∊![]() h n (q n−p n)2d n2 are the contributions of single additive effects and dominance effects to V A, respectively. V Aad=∑n∊
h n (q n−p n)2d n2 are the contributions of single additive effects and dominance effects to V A, respectively. V Aad=∑n∊![]() 2×h n (q n−p n)a nd n is a correction term that can be negative. Finally,
2×h n (q n−p n)a nd n is a correction term that can be negative. Finally, ![]() is the contribution that comes from covariances between linked loci. Similarly, we can write
is the contribution that comes from covariances between linked loci. Similarly, we can write
where V Dd=∑n∊![]() h n2d n2 is the contribution of single dominance effects to V D and
h n2d n2 is the contribution of single dominance effects to V D and ![]() is the contribution that comes from covariances between linked loci.
is the contribution that comes from covariances between linked loci.
The expected genotypic value of an individual that is randomly chosen from the population in HWE is
Assume that an inbred line is established from two individuals that are randomly chosen from the population. Individuals from this line carry the genotype 00 at locus n with probability q n and the genotype 11 with probability p n. Thus, the expected genotypic value of a completely inbred individual is
The inbreeding depression, i.e. the expected decrease of the genotypic value when the inbreeding coefficient increases from 0 to 1 is therefore
(ii) Expectations of variance components and inbreeding depression
In this paper, we treat a population as if it would be a random outcome of a simulation study, i.e. a population is viewed as a realization from all hypothetical populations. Therefore, not only the genotypes are random but also the additive effects, the dominance effects, the allele frequencies and the coefficients of linkage disequilibrium for each pair of loci. Alternatively, randomness of the additive and dominance effects could be due to uncertainty about the true effects (Gianola et al., Reference Gianola, des los Campos, Hill, Manfredi and Fernando2009). In both cases, V A and V D are random variables. In our setting, V A and V D are treated as random since they would attain different values in each hypothetical replicated population. Their expectations are of interest in order to relate parameters of the distributions of additive effects and dominance coefficients to the expected variance components.
For n∊![]() , the additive effect a n of the mutant allele has mean μA and variance σA2, the dominance effect d n has mean μD and variance σD2. The dominance coefficient δn=d n/|a n| has mean μΔ and variance σΔ2. Take
, the additive effect a n of the mutant allele has mean μA and variance σA2, the dominance effect d n has mean μD and variance σD2. The dominance coefficient δn=d n/|a n| has mean μΔ and variance σΔ2. Take ![]() c to be the set of nucleotides at chromosome c. The probability that a nucleotide is a segregating QTL is equal for all nucleotides and nucleotides become QTL independent from each other. For simplicity, we assume that all chromosomes have equal length. The expected number of segregating QTLs at one chromosome is therefore Q/C, where Q=E (#
c to be the set of nucleotides at chromosome c. The probability that a nucleotide is a segregating QTL is equal for all nucleotides and nucleotides become QTL independent from each other. For simplicity, we assume that all chromosomes have equal length. The expected number of segregating QTLs at one chromosome is therefore Q/C, where Q=E (#![]() ) is the expected total number of segregating QTLs and C=#
) is the expected total number of segregating QTLs and C=#![]() is the number of chromosomes.
is the number of chromosomes.
We derive expectations of the variance components under a wide range of assumptions. That is, we first derive equations using only a small number of assumptions and successive include more of them. The assumptions are
(A1) (p n, a n, d n) and (p m, a m, d m) are identically distributed,
(A2) allelic effects are independent from the allelic effects and the allele frequencies at other loci and linkage disequilibrium does not depend on the allelic effects (see below),
(A3) D LD1,0,0=D LD1,0,1=D LD1,1,0=0 (see below),
(A4) dominance effect d n and heterozygosity h n are independent,
(A5) (|a n|, d n) and heterozygosity h n are independent,
(A6)
(a) a n|δn, p n has a symmetrical distribution with mean μA=0, or
(b) p n>0·5 if sign (a n)=sign (δn) and p n<0·5 if sign (a n)≠sign (δn), i.e. sign (a n)=−sign ((q n−p n)δn) (see the introduction),
given n≠m∊![]() . Note that additive effects and dominance coefficients may be dependent. By using only (A1) we obtain
. Note that additive effects and dominance coefficients may be dependent. By using only (A1) we obtain
where
and
In most of the following formulae, we suppress the condition that the SNPs are polymorphic QTLs in order to improve the readability.
Note that a n denotes the effect of the mutant allele. However, in real populations it is unknown which allele the mutant allele is. One would rather use an arbitrary coding of the alleles. Take a′n to be the additive effect of the arbitrarily coded allele. We have a′n=a n or a′n=−a n, each with probability 0·5. Although |a′n|=|a n|, the distributions of both random variables are different. Whereas the effect of the mutant allele may have a non-zero mean μA, the effect of the arbitrary coded allele a′n has a symmetrical distribution with mean μA′=0 and variance σA′2=E (a n2). Since a′n has mean 0, we can write E (|a n|)=E (|a′n|)=λσA′, where the parameter λ depends on the standardized distribution of a′n.
Let D n,mi,j,k =D n,mi (q n−p n)j (q m−p m)k, which is needed to simplify Ṽ ALD. Now we assume additionally that linkage disequilibrium does not depend on the allelic effects and that allelic effects at different loci are independent, i.e. a n is independent from (a m, d m, p m, D n,m) and d n is independent from (a m, d m, p m, D n,m, D n,m1,1,1), given n≠m∊![]() . With (A1) and (A2) we obtain
. With (A1) and (A2) we obtain
where
Roughly speaking, E (D n,m2,0,0|n, m∊![]() ) would be the mean D 2-value for loci n and m, averaged over many hypothetical populations for which n and m are polymorphic QTLs. If these expected D 2-values are averaged over all pairs of loci at one chromosome, then D LD2,0,0 is obtained. Simulations of neutral alleles showed that likely D LD1,0,0=D LD1,0,1=D LD1,1,0=0 but D LD1,1,1≠0 (A3), so this will be assumed in the rest of this paper. Thus, linkage disequilibrium not only contributes to the dominance variance but also to the additive variance. If there are many QTLs per chromosome that affect the trait, the contributions from single loci can in principle be much smaller than the contributions that arise from covariances of linked loci, since the latter increases quadratically with the number of QTLs. If additionally dominance effect and heterozygosity are independent (A4), then
) would be the mean D 2-value for loci n and m, averaged over many hypothetical populations for which n and m are polymorphic QTLs. If these expected D 2-values are averaged over all pairs of loci at one chromosome, then D LD2,0,0 is obtained. Simulations of neutral alleles showed that likely D LD1,0,0=D LD1,0,1=D LD1,1,0=0 but D LD1,1,1≠0 (A3), so this will be assumed in the rest of this paper. Thus, linkage disequilibrium not only contributes to the dominance variance but also to the additive variance. If there are many QTLs per chromosome that affect the trait, the contributions from single loci can in principle be much smaller than the contributions that arise from covariances of linked loci, since the latter increases quadratically with the number of QTLs. If additionally dominance effect and heterozygosity are independent (A4), then
where γ=E (h n(q n−p n)2)/E (h n)=1−2E (h n2)/E (h n). The last equation in (8) shows that inbreeding depression occurs only if dominance effects do not have mean zero. It may be more convenient to express the formulae for Ṽ Ad, Ṽ Dd and ![]() using moments of the dominance coefficients rather than moments of the dominance effects. These can be obtained from eqn (8) with
using moments of the dominance coefficients rather than moments of the dominance effects. These can be obtained from eqn (8) with
where
The scale invariant parameters r 1 and r 2 characterize the dependency between additive effects and dominance coefficients. Scale invariance means in particular that r 1 and r 2 do not depend on the variance of the additive effects. For biological reasons, we expect that r 1, r 2⩾0. If additive effects and dominance coefficients are independent, then r 1=r 2=0.
Now we assume additionally that the absolute additive effect and the heterozygosity are independent (A5). We have
In simulation studies, the additive effect a n often has a symmetrical distribution with mean 0 given δn and p n (A6a). In this case, we have
However, we believe that (A6a) is an unrealistic assumption for real populations for several reasons. Most important, selection acts mainly on the additive component of genotypic values. Therefore, one would expect that in a long-term selected population alleles with small contribution to the additive variance are overrepresented. The contribution of QTL n to the additive variance depends on |αn|=|a n+(q n−p n)d n| which is small if a n and (q n−p n)d n have opposite signs. Although this is violated in real populations as well for some alleles, it likely holds for the majority of the alleles as pointed out in the introduction and it provides not only more realistic results as (A6a), but it can also easily be accounted for in simulation studies by simply choosing the sign of a n as sign(a n)=−sign((q n−p n)δn). Under (A6b) we have
where
We can write E (|δn|)=μΔK, where K depends on the coefficient of variation c v=σΔ/μΔ.
Several parameters appeared in these equations that need to be estimated for the application of formulae. The next part provides estimates of parameters that are related to heterozygosity and linkage disequilibrium. In Part (iv), parameters that characterize the joint distribution of additive effect and dominance coefficient are calculated for different scenarios.
(iii) Heterozygosity and linkage disequilibrium
In accordance with the diffusion approximation (Crow & Kimura, Reference Crow and Kimura1970) and Hill et al. (Reference Hill, Goddard and Visscher2008), the density of a segregating neutral mutant allele is f(p)=1/(κp) on the interval [1/(2N), 1−(1/2N)] if mutations are rare and the population is in mutation drift equilibrium. Since f(p) is a density, we have κ=ln(2N−1), where N is the population size. Take p k=P (k<p n<1−k) to be the probability that a segregating allele has minor allele frequency (MAF) larger than k, where 1/(2N)⩽k⩽0·5. We have
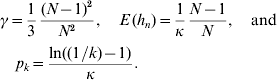
Note that the population size is usually so large that the factors (N−1)2/N 2 and (N−1)/N can be ignored. The effective population size is assumed to be constant. But for most livestock populations, the effective population size decreased in the past. In a small bottlenecked population, more alleles with extreme frequencies become lost than new mutations arise and the remaining alleles more likely have intermediate frequencies. Thus, the mean heterozygosity of segregating alleles would be larger. But on the other hand, the population size is usually much larger than the effective population size, so many new mutations arise each generation and these new mutations decrease the mean heterozygosity of segregating alleles. In order to get estimates of γ, E (h n) and p k for a bottlenecked population, we simulated a population for which the effective population size decreased from N e=1000 to N e=100 within 400 generations in accordance with the results of Villa-Angulo et al. (Reference Villa-Angulo, Matukumalli, Gill, Choi, Van Tassell and Grefenstette2009). The total population size remained constant with N=1000, which was achieved by an unequal number of males and females. We obtained the estimates ![]() ,
, ![]() ,
, ![]() , and
, and ![]() of the segregating alleles had an MAF larger than k=0·01. We also obtained estimates for the LD from the simulated population resulting in
of the segregating alleles had an MAF larger than k=0·01. We also obtained estimates for the LD from the simulated population resulting in ![]() and
and ![]() . These values are used in the examples. They are needed to apply the formulae that were derived in the previous section. For a population in mutation–selection equilibrium a more extreme L- or U-shaped distribution may be expected. The shape of this distribution would affect these parameters, but not the validity of the formulae.
. These values are used in the examples. They are needed to apply the formulae that were derived in the previous section. For a population in mutation–selection equilibrium a more extreme L- or U-shaped distribution may be expected. The shape of this distribution would affect these parameters, but not the validity of the formulae.
(iv) Dependency between additive effect and dominance coefficient
The formulae that are derived could be applied by assuming r 1=r 2=r 2,1=0 which holds if additive effect and dominance coefficient are independent. However, the literature suggests that they are not independent. Therefore, we consider different possibilities to model dependent effects and for these scenarios we give estimates for the scale invariant parameters c v, r 1, r 2, r 2,1, λ and K. In all scenarios, |a n| and δn are positively correlated.
Because of the scale invariance of all relevant parameters, the distributions of a′n and δn need to be specified only up to constant factors that will be estimated in the next sections. That is, we only need to specify the joint distribution of random variables ã n, ![]() n. These are multiplied by constant factors to obtain a′n and δn. The parameters c v, r 1, r 2, r 2,1, λ and K for (a n, δn) are exactly the same as for (ã n,
n. These are multiplied by constant factors to obtain a′n and δn. The parameters c v, r 1, r 2, r 2,1, λ and K for (a n, δn) are exactly the same as for (ã n, ![]() n). In scenarios (1), (3) and (4), mean and standard deviation of
n). In scenarios (1), (3) and (4), mean and standard deviation of ![]() n were chosen as 0·2 and 0·3, as suggested by Bennewitz & Meuwissen (Reference Bennewitz and Meuwissen2010).
n were chosen as 0·2 and 0·3, as suggested by Bennewitz & Meuwissen (Reference Bennewitz and Meuwissen2010).
Scenario (1) assumes that δn and a′n are independent with
where ![]() denotes the Laplace distribution with mean 0 and variance 1.
denotes the Laplace distribution with mean 0 and variance 1.
In all other scenarios there is a lack of segregating additive alleles with large effect. This could arise in real populations because these alleles have been fixed due to selection or because of a hyperbolic relationship between enzyme activity and flux (Kacser & Burns, Reference Kacser and Burns1981).
Scenario (2) reflects the conclusions drawn from the analysis of enzyme networks. Genes of large effect show directional dominance, but for genes of small effect the dominance coefficient is close to 0. That is,
Scenario (3) reflects the results reported by Caballero & Keightley (Reference Caballero and Keightley1994), i.e. alleles with large effect tend to be partially recessive or even overdominant and the heterozygous effect is above the average effect of the two homozygotes. But alleles of small effect show highly variable dominance coefficients. More precisely,
Scenario (4) is similar to scenario (3), but for alleles with large effect, the heterozygous effect could also be below the average effect of the two homozygotes. This may be more suitable for traits where mutant alleles with large effect could also be recessive and advantageous. We have
Scatter plots of the distributions are shown in Fig. 1. This figure was fitted for the trait PL in Holstein cattle (see Examples section). Table 2 shows the parameter values for all scenarios.
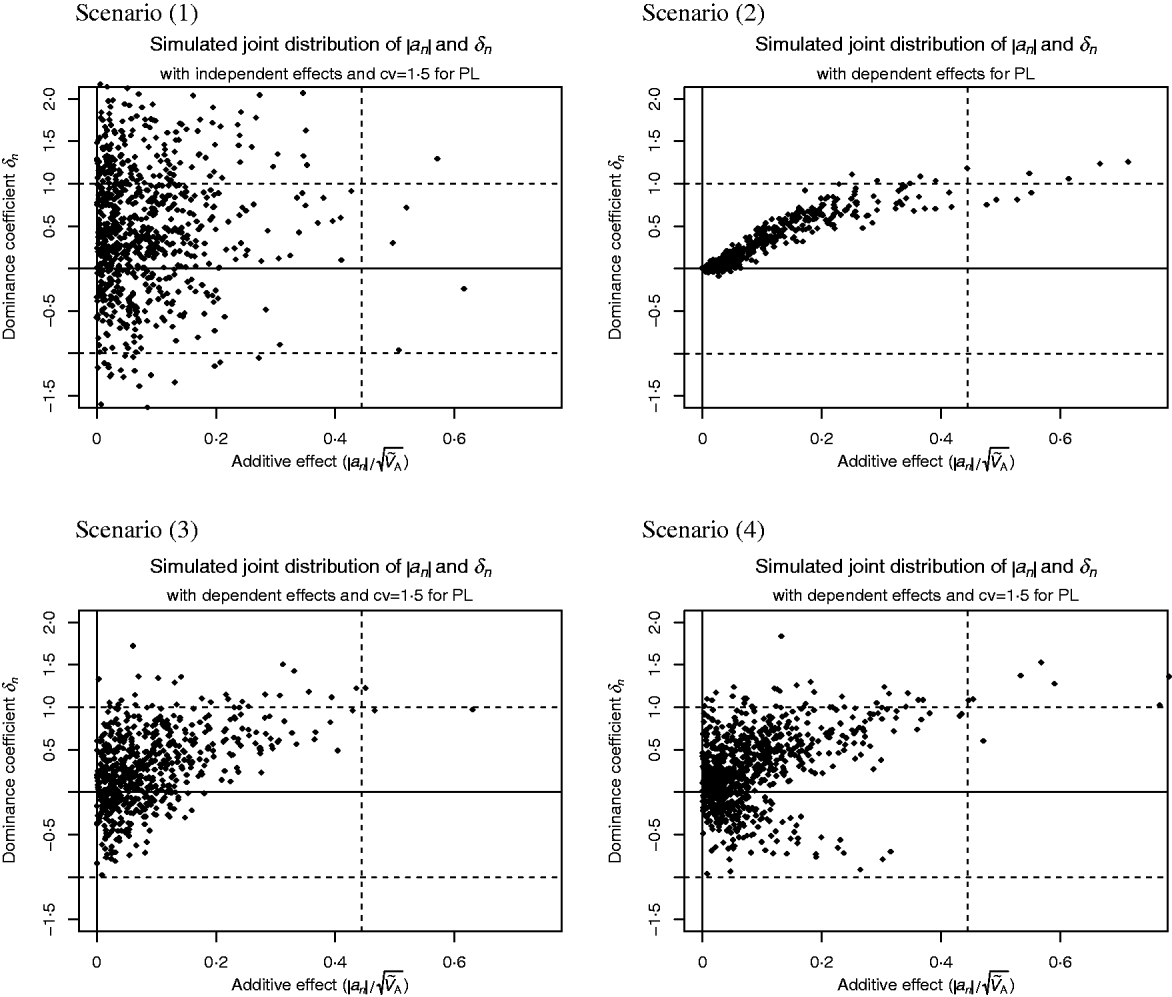
Fig. 1. Scatter plots of the considered joint distributions of |a n| and δn from Part (iv), fitted to the trait productive life (PL) under assumption (6b), so the signs of the additive effects are such that the alleles contribute little to the additive variance. (1) Absolute additive effect and dominance coefficient are independent. (2) Alleles with large effect show directional dominance, but alleles of small effect are additive. (3) Alleles with small effects show highly variable dominance coefficients, but for alleles with large effects, heterozygous effect is above the average effect of the two homozygotes. (4) Alleles with small effects show highly variable dominance coefficients, but alleles with large effect are incomplete recessive or dominant.
Table 2. Characteristics of the considered joint distributions of |an| and δn that are described in Part (iv)

(v) Contributions of different sources to variance components
We have under assumptions (A1) and (A2)
Unfortunately, the covariance is unknown, so this equation cannot be used directly to estimate the contribution of linkage disequilibrium to the dominance variance. But it shows that if falsely Cov(h n, d n)=0 is assumed, although alleles with intermediate frequencies tend to have larger dominance effects (i.e. Cov(h n, d n)>0 due to overdominance) then Ṽ DLD would become overestimated. Similarly, we obtain under (A1)–(A3) that
Again we have to assume that Cov(h n, d n)=0 for being able to evaluate this formula. Then the contributions of dominance effects of linked loci to the additive and dominance variance depend only on the squared inbreeding depression, which can be estimated, but not directly on the unknown number of QTLs.
Since Ṽ D can be estimated from the population and Ṽ DLD can be estimated with eqn (14), the contribution of single loci to the dominance variance can be obtained from
This contribution would become underestimated if falsely Cov(h n, d n)=0 is assumed in (14) although Cov(h n, d n)>0. If additionally h n and d n are independent (A4), then the contribution of dominance effects of single loci to the additive variance can be obtained from
Under (A6a) we have
whereas under (A6b) we have
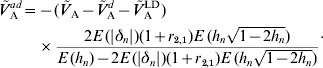
The latter formula depends, however, on E(|δn|) and r 2,1. The contribution of additive effects of single loci to the additive variance can then be obtained from
In summary, these formulae enable to estimate the contributions of different sources to the additive and dominance variance under (A1)–(A6a).
(vi) Lower bounds for the number of QTLs
In this section, we derive lower bounds for the expected number of QTLs. We obtain from eqns (5) and (6)
Thus,
Note that the proof only used (A1) and Ṽ DLD⩾0, so the bounds hold regardless of how intense the selection is and how deleterious new mutations tend to be. Under (A1)–(A4) the contribution of linkage disequilibrium Ṽ DLD can be estimated as described in the previous part if dominance variance and inbreeding depression have been estimated for the population. Note that these bounds depend neither on the distribution of the additive effects nor on the correlation between |a n| and δn. However, they can be further improved under (A1)–(A4). Since
and
we have
The factor (1+r 2) on the right-hand side is typically larger than 1 (see Table 2). Moreover, we have
and
Thus, if any of these factors is unknown, then it can be skipped in eqn (21) and the inequality still holds. In particular, we have
(vii) The role of overdominance
Using (A1)–(A5) we obtain

Thus,
That is, the second moment of the dominance coefficients depends only on the ratio Ṽ d D/Ṽ a A that can be estimated under (A1)–(A6a), but not on the unknown number of QTLs.
A lower bound for the probability of an allele to be under- or overdominant can be derived if the dominance coefficient is normally distributed and the ratio of dominance variance to additive variance is sufficient large. If Ṽ d D/Ṽ a A>d max=(1+r 2)(1−γ)/2, then eqn (24) shows that μΔ2+σΔ2⩾1. But then P(|δn|>1) is minimized if μΔ=0 and σΔ=1. It follows that
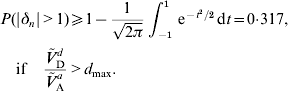
Such a large probability appears to be unrealistic in real populations for almost any trait, see for example Charlesworth et al. (Reference Daetwyler, Pong-Wong, Villanueva and Woolliams2009). Possible reasons for Ṽ d D/Ṽ a A>d max to occur are the violation of one of the assumptions (A1)–(A6) or a wrong value for r 2. If E (δn2)>1 is obtained under (A6a), then (A6b) should be used instead. That is, Ṽ ad A and Ṽ a A should be calculated again using eqn (17) with some realistic values for E (|δn|) and r 2,1.
(viii) Upper bounds for the number of large QTLs
The contribution Ṽ a A of additive effects of single loci to the additive variance is what remains if the contributions of all other factors are subtracted from the additive variance. On the other hand, we have Ṽ a A=σ2 A′QE (h n). Unfortunately, this equation cannot be used directly to estimate the number of QTLs as σ2 A′ is unknown. But for many traits the number of large QTLs which are the QTLs whose absolute additive effect |a n| exceeds a given threshold value s and whose MAF is larger than (say) k=0·01 is known from QTL mapping studies and could be used to estimate the expected number of large QTLs
where I=(0·01, 0·99). Since Ṽ a A=σ2 A′QE (h n) we obtain
where F is the distribution function of a′n/σA′, and ![]() . If a particular distribution function F (e.g. the normal distribution or the Laplace distribution) is assumed for the standardized additive effects and an estimate of ñ is given, then eqn (26) can be solved for the number Q of QTLs. Unfortunately, estimates for ñ obtained from real data are often rather poor and F is also not known with certainty. But eqn (26) can also be used to derive upper bounds for ñ. For a given distribution function F of the standardized additive effects an upper bound for the expected number of large QTLs is (see eqn (26))
. If a particular distribution function F (e.g. the normal distribution or the Laplace distribution) is assumed for the standardized additive effects and an estimate of ñ is given, then eqn (26) can be solved for the number Q of QTLs. Unfortunately, estimates for ñ obtained from real data are often rather poor and F is also not known with certainty. But eqn (26) can also be used to derive upper bounds for ñ. For a given distribution function F of the standardized additive effects an upper bound for the expected number of large QTLs is (see eqn (26))
where Q min is a lower bound for the number of QTLs. From eqn (26) it follows with the Tschebyscheff inequality that ñ⩽p k/v 2. The proof is similar to the proof of eqn (27). This bound for the expected number of large QTLs depends neither on the total number of QTLs and the distribution of the QTL effects nor on the correlation between |a n| and δn. The Vysochanskij–Petunin inequality refines the Tschebyscheff inequality for unimodal distributions. That is, if Q>8/(3v 2) and an unimodal distribution is assumed for the additive effects, then the Vysochanskij–Petunin inequality gives the better bound
The bound depends on the contribution Ṽ a A of single additive effects to the additive variance. As shown in section (v), this can be estimated under (A6a). The bound holds in principle also under (A6b). However, then Ṽ a A depends on the unknown joint distribution of the additive effects and dominance coefficients and could be even larger than the additive variance Ṽ A since Ṽ ad A is negative. In the scenarios considered so far, the bound may increase by a factor of 3 under (A6b), but then the QTLs with large effect are close to dominance or recessivity, so that they contribute little to the additive variance.
(ix) Parameter estimation
In this section, we show how the presented equations can be used, e.g. to design a simulation experiment for the assessment of genome-wide evaluations of quantitative traits in outbred populations. Estimates for Ṽ A, Ṽ D and ![]() must be available. The goal is to estimate μΔ, σΔ2, σA′2, Q and the contributions of the different sources to the additive and dominance variance by the formulae such that the simulated populations have on average the desired additive variance, dominance variance and inbreeding depression. The procedure is as follows:
must be available. The goal is to estimate μΔ, σΔ2, σA′2, Q and the contributions of the different sources to the additive and dominance variance by the formulae such that the simulated populations have on average the desired additive variance, dominance variance and inbreeding depression. The procedure is as follows:
• Estimate the parameters p k, E(h n), γ and
 that depend on the distribution of allele frequencies and the parameters D LD2,0,0 and D LD1,1,1 that describe the effect of linkage disequilibrium. This is demonstrated in section (iii). Ensure that the simulation reproduces these values on average.
that depend on the distribution of allele frequencies and the parameters D LD2,0,0 and D LD1,1,1 that describe the effect of linkage disequilibrium. This is demonstrated in section (iii). Ensure that the simulation reproduces these values on average.• Then Ṽ DLD, Ṽ ALD, Ṽ Dd and Ṽ Ad can be calculated as described in section (v).
• A joint distribution for the scaled additive effects and the scaled dominance coefficients must be postulated. For this distribution, the parameters c v, r 1, r 2, r 2,1, λ and K are to be calculated. Alternatively, the values from Table 2 can be used (see section (iv)) for the proposed joint distributions.
• The expected number of QTLs can then be calculated as
(28)
• We have
(29)and σΔ=μΔc v, where

• Under (A6a) we have Ṽ Aad=0 and under (A6b), Ṽ Aad can be obtained from eqn (17) since E (|δn|)=μΔK.
• Ṽ Aa=Ṽ A−Ṽ Ad−Ṽ Aad−Ṽ ALD and σA′2=Ṽ Aa/QE (h n).
3. Examples
In this section we use published data for the application of the derived equations. Van Tassell et al. (Reference van Tassell, Misztal and Varona2000) estimated fractions of variance accounted for by additive variance (h 2) and dominance variance (d 2) as well as inbreeding depression (![]() ) for milk yield, PL and other traits from Holstein data. The estimates are given in Table 3. They are based on milk records and PL records of more than 730 000 cows. Data were selected to maximize the number of full sibs in the analysis. Variance components were estimated by Method R. Properties of this method were examined by Duangjinda et al. (Reference Duangjinda, Misztal, Bertrand and Tsuruta2001). Unfortunately, the phenotypic variances were not reported. Therefore, literature estimates were used which are V p=12162 for preadjusted 305-day milk yield during the first lactation (Miglior et al., Reference Miglior, Burnside and Kennedy1995) and V p=13·12 for total month in milk by 84 months of age (Van Raden et al., Reference Van Raden and Klaaskate1993).
) for milk yield, PL and other traits from Holstein data. The estimates are given in Table 3. They are based on milk records and PL records of more than 730 000 cows. Data were selected to maximize the number of full sibs in the analysis. Variance components were estimated by Method R. Properties of this method were examined by Duangjinda et al. (Reference Duangjinda, Misztal, Bertrand and Tsuruta2001). Unfortunately, the phenotypic variances were not reported. Therefore, literature estimates were used which are V p=12162 for preadjusted 305-day milk yield during the first lactation (Miglior et al., Reference Miglior, Burnside and Kennedy1995) and V p=13·12 for total month in milk by 84 months of age (Van Raden et al., Reference Van Raden and Klaaskate1993).
Table 3. Estimates for milk yield and PL in Holstein cattle from literature

Clearly, the conclusions drawn in this section may hold only if these parameters have been estimated with sufficient precision and if the model assumptions hold. The precision of the estimates may be not very high for two reasons. At first, we cannot rule out the possibility of a bias due to confounding factors, and secondly, the variance components were estimated and not their expectations in the sense of this paper. But the variance components are close to their expectations if the number of QTLs is sufficiently large and therefore, the estimates should give realistic values to deal with.
We obtained the bounds shown in Table 4, where ![]() =p kQ with p k=0·71 is the expected number of QTLs with MAF>0·01. We expect at least 187 QTLs for milk and 84 QTLs for PL (obtained from eqn (23)).
=p kQ with p k=0·71 is the expected number of QTLs with MAF>0·01. We expect at least 187 QTLs for milk and 84 QTLs for PL (obtained from eqn (23)).
Table 4 Estimated parameters for Milk yield and PL

Table 5 Bounds for the parameters under different assumptions

We chose the threshold values for a QTL to be large as s=200 kg for milk yield and s=2 months for PL. More than ![]() large QTLs for milk can be excluded if a unimodal distribution of the additive effects is assumed. Furthermore, if ñ is assumed to be larger than
large QTLs for milk can be excluded if a unimodal distribution of the additive effects is assumed. Furthermore, if ñ is assumed to be larger than ![]() , then neither a normal distribution nor a Laplace distribution of the QTL effects is possible. If a normal distribution is assumed for the additive effects for PL then the expected number of large QTLs is 0·7 at most. These bounds have been derived under (A6a).
, then neither a normal distribution nor a Laplace distribution of the QTL effects is possible. If a normal distribution is assumed for the additive effects for PL then the expected number of large QTLs is 0·7 at most. These bounds have been derived under (A6a).
Figure 1 shows scatter plots of the joint distributions of additive effects and dominance coefficients that were fitted to PL under assumption (6b). The shape of the distributions were given in advance for each scenario. Only the scales were adjusted. It can be seen in the most realistic Scenarios (2)–(4) that QTLs with large additive effect are close to recessivity or dominance, so that they contribute little to the additive variance. Druet et al. (Reference Druet, Sölkner, Groen and Gengler2001) support the hypothesis that large additive QTLs for PL are absent since the fertility, which determines length of PL, has a heritability of only 1%. The QTL on the right-hand side of the vertical lines in Fig. 1 are those whose absolute additive effect exceeds s=2 months.
Table 5 shows the parameter estimates for all scenarios for milk yield and PL. For scenarios (2)–(4), the estimated number of QTLs was between 736 and 1359 and the expected number of large QTLs was about 5·3–8·8. For PL, the estimated number of QTLs was between 332 and 612 and the expected number of large QTLs was about 3·1–5·3. The table also shows for the different sources their estimated contribution to the expected genotypic variance Ṽ G=Ṽ A+Ṽ D. It can be seen that the genotypic variance is affected only little by linkage disequilibrium. Moreover, we have in all scenarios Ṽ Ad+Ṽ Aad+Ṽ ALD<0, so dominance effects diminish rather than increase the additive variance.
Equation (28) suggests that the number of QTLs depends heavily on the coefficient of variation of the dominance coefficient c v. In scenarios (1), (3) and (4), this coefficient was equal to 1·5 as it was suggested by Bennewitz & Meuwissen (Reference Bennewitz and Meuwissen2010). However, the true value may be different for some traits. In order to see how the parameter values depend on c v we calculated them also for other values. Results are shown in Figs 2 and 3 for PL (left) and milk yield (right). The dotted line shows the results obtained under assumption (6a) for independent Laplace distributed additive effects and normally distributed dominance coefficients. The dashed line shows the results obtained under assumption (6a) for dependent additive effects and dominance coefficients. Here, ![]() n~
n~![]() (0·2, (0·2 c v)2) was used and ã n was defined as in scenario (3). This choice results for large c v in a more heavy tailed distribution of a′n. The solid line shows the results obtained under assumption (6b) for the same joint distribution of additive effects and dominance coefficients.
(0·2, (0·2 c v)2) was used and ã n was defined as in scenario (3). This choice results for large c v in a more heavy tailed distribution of a′n. The solid line shows the results obtained under assumption (6b) for the same joint distribution of additive effects and dominance coefficients.
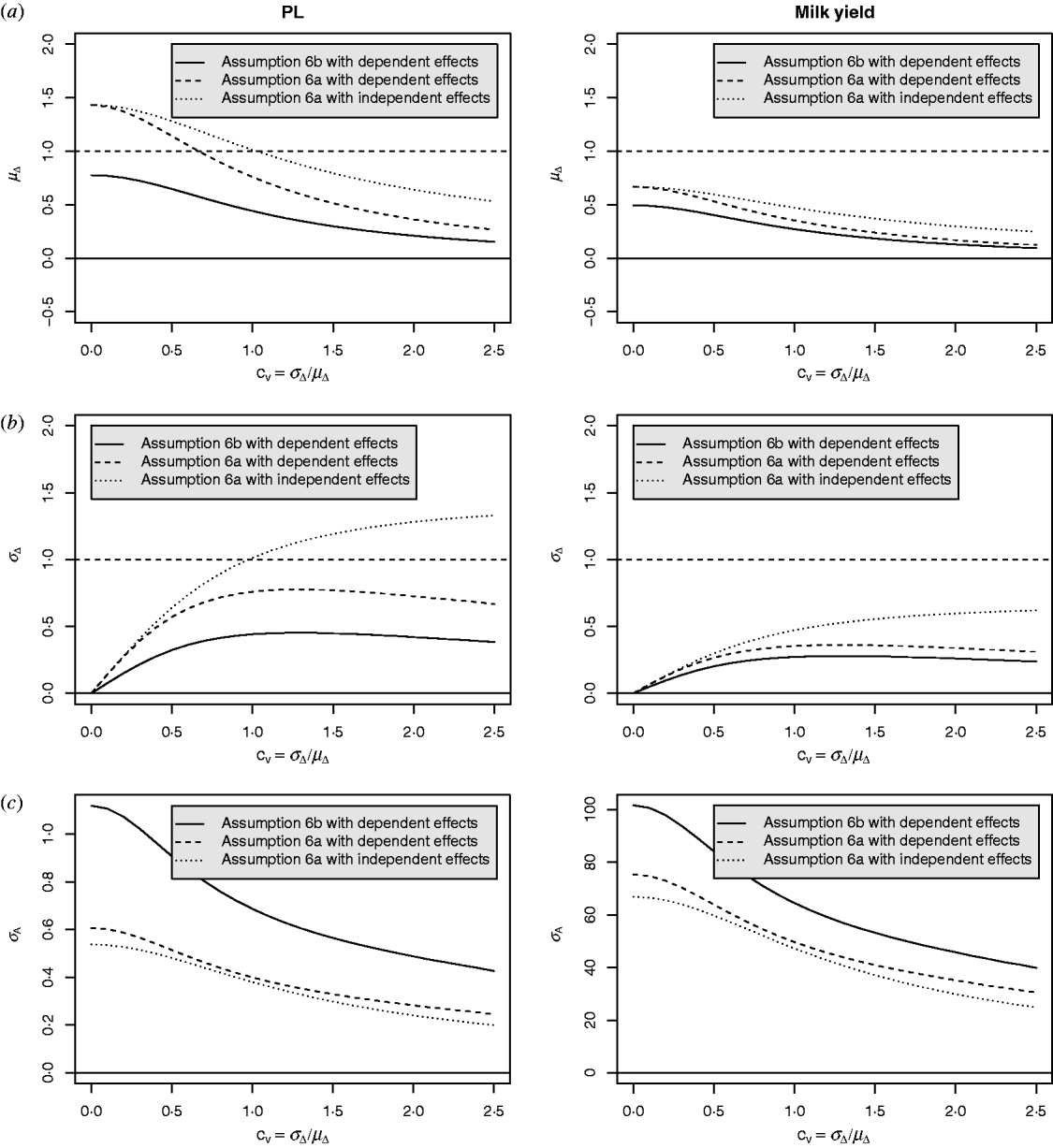
Fig. 2. Different parameters for PL and milk yield as a function of the coefficient of variation of the dominance coefficient: (a) expectation of the dominance coefficient, (b) standard deviation of the dominance coefficient and (c) standard deviation of the additive effects.
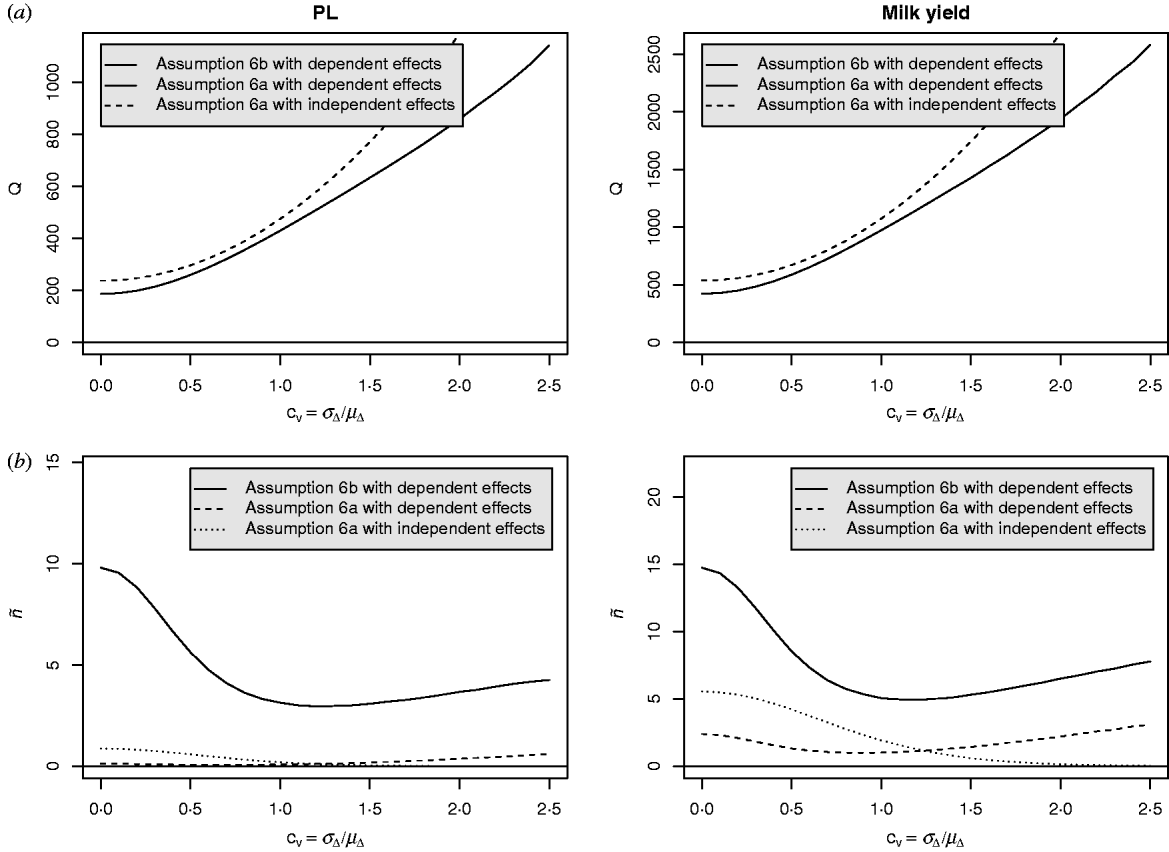
Fig. 3. Different parameters for PL and milk yield as a function of the coefficient of variation of the dominance coefficient: (a) Number of QTLs, (b) number of large QTLs.
It can be seen that under (A6b) with dependent effects (solid lines) the smallest mean and standard deviation of the dominance coefficients and therefore the smallest fraction of overdominant alleles was obtained. It also provided the highest number of large QTLs. The number of QTLs depends heavily on the coefficient of variation, i.e. if c v is small then μΔ and σA′ are small as well, so inbreeding depression must be caused by many genes. The number of large QTLs changes only little although the total number of QTLs strongly increases for increasing c v which is due to the more heavy tailed distribution of a′n for large c v.
4. Discussion
Novel methods to estimate the number of QTLs and to quantify the importance of linkage disequilibrium on the additive and dominance variance have been derived. It is demonstrated how parameters of the distribution of the QTLs effects can be estimated if estimates for the variance components and inbreeding depression are available. In the following, several aspects of the approach are critically discussed.
(i) Bounds for the number of QTLs
Lower bounds for the expected number of QTLs have been derived. The bound given by eqn (18) equals the ratio of squared inbreeding depression to dominance variance. It could be derived under weak assumptions, but may be poor if the trait shows little directional dominance. The bound could be improved if dominance effects and heterozygosity are independent (see eqn (21)). This equation gives the largest bound, but the calculation requires knowledge on the distribution of the additive effects and on the dependency between additive effects and dominance coefficients. This is not needed to calculate the bound given in eqn (23). Since this bound holds even if c v=0 although, we are likely to have c v>0, the bound is rather conservative. Larger bounds could be derived under more stringent assumptions. There could be less QTLs in a population, but the average number of QTLs (averaged over many populations with the same characteristics) would not fall below the bound.
This novel method to estimate the number of QTLs affecting a trait gives a higher number than estimates obtained from the QTL mapping experiments mentioned in the Introduction section. The reason is that inbreeding depression must be due to a sufficient number of QTLs, because otherwise it would cause more than the true dominance variance of the trait. Therefore, our estimates are larger than the estimates of other authors who neglected dominance and could not well account for QTLs with small effects. This supports the hypothesis of a large number of genes affecting a quantitative trait. An upper bound for the expected number of large QTLs is also derived.
(ii) Shape of the distribution
A critical issue is the shape of the distribution of the additive effects. It is demonstrated that the distribution of QTL effects must be heavy tailed if many QTLs with large effect are expected to segregate in a population, provided that the trait is affected by directional dominance. This means that a distribution function for standardized additive effects is admissible, only if eqn (26) can be solved for Q under side condition (21).
(iii) Quality of the estimates
Parameter estimates and bounds for the number of QTLs that are obtained as described above may be imprecise for several reasons. The estimation of dominance variance requires large amounts of data with a high proportion of full sibs. For equivalent accuracy, the estimation of dominance variance requires at least 20 times as much data than the estimation of additive variance (Misztal, Reference Misztal1997). In particular, estimates of the ratio of squared inbreeding depression to dominance variance, which determines the bound for the number of QTLs, may be poor for traits where both of them are small. Dominance variance is difficult to estimate as it could be confounded e.g. by maternal effects, environmental covariance of fullsibs and variation in relationship. We cannot rule out the possibility that the dominance variance has been overestimated, but see Duangjinda et al. (Reference Duangjinda, Misztal, Bertrand and Tsuruta2001). Moreover, our approach treats the population as a random realization. Realized additive variance, dominance variance and inbreeding depression deviate by chance from their expectations.
(iv) Assumptions that may be violated in the presence of selection
Our model could account for effects of selection on the distribution of allele frequencies and on the dependency between a n and δn, but it could not account for some other effects such as a dependency between the dominance effects and the heterozygosity. Since overdominant alleles likely have intermediate frequencies because of selection, they contribute more to dominance variance, so a smaller proportion of overdominant alleles would be sufficient to explain a large dominance variance in a long-term selected population. Independence of a n and D n,m, which was assumed to calculate Ṽ ALD, may not hold in the presence of selection because then allelic effects and allele frequencies are dependent and allele frequencies affect D n,m. This was neglected in the present study. In the examples we used estimates for LD and for parameters of the distribution of allele frequencies that were obtained for neutral alleles although the traits under examination are not neutral. Further research is needed in order to generalize the model or to find out how robust our results are when the assumptions that have been made are violated.
(v) The role of overdominance
We showed that the second moment of the dominance coefficient is determined by the ratio of dominance variance due to single dominance effects Ṽ Dd to the additive variance due to single additive effects Ṽ Aa, but does not depend on the number of QTLs. If the second moment is larger than one, then the probability of an allele to be overdominant becomes large (see eqn (25)). This may occur in computer simulations when populations are simulated without selection (according to assumption (A6a)) and the trait shows much dominance variance. But it is unlikely to occur in real populations. A large second moment does not occur if additive effects and dominance coefficients are dependent (r 2>>0) and a n and (q n−p n) d n have opposite signs (A6b). Frankham (Reference Frankham, van der Werf, Graser, Frankham and Gondro2009) argued that in long-term artificially selected populations the proportion of variation due to overdominant alleles is likely much higher than in wild populations at equilibrium. Overdominance of an allele that affects PL could arise as follows: an individual has a long PL if it is good enough for a large number of traits. Consider a pleiotropic gene with alleles a and A. The allele a improves one trait (e.g. mastitis resistance) but reduces another trait (e.g. milking speed). Suppose that one a-allele is sufficient to prevent the individual from being culled because of the first trait. But two a-alleles decrease the second trait so much that the individual would likely be culled because of the second trait. In this hypothetical example, genotype AA would be culled early because of little mastitis resistance and genotype aa would be culled early because of slow milking speed. Only genotype Aa is likely to survive several lactations. Thus, the gene would be overdominant for PL. This is called antagonistic pleiotropy. The concept of antagonistic pleiotropy was popularized by Rose (Reference Rose1982) and critically analysed by Curtsinger (Reference Curtsinger, Service and Prout1994) and Hedrick (Reference Hedrick1999). Curtsinger argued that when many loci are involved, the conditions for intermediate equilibrium frequencies are difficult to satisfy. But he did not take into account that the number of affected fitness components likely also increases when the number of loci increases that affect total fitness. He also ignored the recurrent introduction of new alleles by mutations. Our approach also could not clarify how important overdominance for PL is, since some scenarios yielded a non-negligible portion of overdominant alleles, whereas others did not. However, the most reliable scenarios yielded little overdominance.
(vi) Conclusion
In conclusion, formulae are developed that can be used to obtain estimates for the number and distribution of QTL effects. The examples demonstrated the need to estimate them for each trait separately. Our method needs estimates of dominance variance and inbreeding depression. But if reliable estimates are available, then estimates for the number and distribution of QTL effects can be obtained that are very helpful in the choice of the appropriate method for the prediction of genomic breeding values, even though the dependency between marker effects and QTL effects needs clarification. Additionally they can be used as input parameters for stochastic simulations that mimic the real situation closely.
R.W. was supported by a grant from the Deutsche Forschungsgemeinschaft (DFG). The manuscript has benefited from critical and helpful comments of the anonymous reviewers. The authors also thank Professor W. G. Hill for constructive critique and encouraging comments on an earlier version of the manuscript.