1. Introduction
The performance characteristics of swimming and flying animals have long motivated the design of autonomous swimmers with similar kinematics for propulsion and navigation. The energetics of fish propulsion and, in particular, their ability to harvest energy in schools or unsteady flow environments (Beal et al. Reference Beal, Hover, Triantafyllou, Liao and Lauder2006) have also spurred the research and development of novel energy harvesters (McKinney & DeLaurier Reference McKinney and DeLaurier1981; Jones et al. Reference Jones, Platzer, Jones and Platzer1997; Bryant, Mahtani & Garcia Reference Bryant, Mahtani and Garcia2012). Broadly, these animals rely on oscillating or undulating foils for propulsion.
Characterizing the relationship between foil performance and the downstream wake structure has been a long-standing research area. Pioneering work in this area by Triantafyllou, Triantafyllou & Grosenbaugh (Reference Triantafyllou, Triantafyllou and Grosenbaugh1993) analysed the swimming performance of several different fish and showed that fish operate within a narrow Strouhal number range, ![]() $0.2 < St < 0.35$, that leads to high propulsive efficiency. The Strouhal number is a kinematic parameter defined as
$0.2 < St < 0.35$, that leads to high propulsive efficiency. The Strouhal number is a kinematic parameter defined as ![]() $St=f A/U_{\infty }$, where
$St=f A/U_{\infty }$, where ![]() $A$ is a characteristic length describing the width of the wake,
$A$ is a characteristic length describing the width of the wake, ![]() $f$ is the frequency of oscillation and
$f$ is the frequency of oscillation and ![]() $U_{\infty }$ is the swimming speed. Laboratory experiments also showed high propulsive efficiencies from oscillating foils operating in this Strouhal number range. Complementary stability analyses showed that oscillating foils produce a jet-like wake that is convectively unstable when excited at frequencies corresponding to Strouhal numbers that yield peak propulsive efficiencies. The spatial stability analysis performed by Triantafyllou et al. (Reference Triantafyllou, Triantafyllou and Grosenbaugh1993) used the jet profile of a reverse von Kármán vortex street, where two single (S) vortex cores were shed per half-cycle of oscillation, i.e. a 2S wake pattern. Similar relationships between optimal Strouhal number ranges and instabilities of the jet wake were found by Lewin & Haj-Hariri (Reference Lewin and Haj-Hariri2003).
$U_{\infty }$ is the swimming speed. Laboratory experiments also showed high propulsive efficiencies from oscillating foils operating in this Strouhal number range. Complementary stability analyses showed that oscillating foils produce a jet-like wake that is convectively unstable when excited at frequencies corresponding to Strouhal numbers that yield peak propulsive efficiencies. The spatial stability analysis performed by Triantafyllou et al. (Reference Triantafyllou, Triantafyllou and Grosenbaugh1993) used the jet profile of a reverse von Kármán vortex street, where two single (S) vortex cores were shed per half-cycle of oscillation, i.e. a 2S wake pattern. Similar relationships between optimal Strouhal number ranges and instabilities of the jet wake were found by Lewin & Haj-Hariri (Reference Lewin and Haj-Hariri2003).
The relationship between wake instability and peak propulsive efficiency was studied further by Moored et al. (Reference Moored, Dewey, Smits and Haj-Hariri2012), who used particle image velocimetry (PIV) to visualize wake structures produced by a batoid-inspired oscillating fin. These experiments showed multiple peak efficiencies, with some corresponding to a 2P wake pattern, where two pairs (P) of vortex cores are shed per half-cycle, and others corresponding to a 2S wake. Moored et al. (Reference Moored, Dewey, Smits and Haj-Hariri2012) also pursued local stability analyses (i.e. relying on a parallel flow assumption) to show that the time-averaged velocity profile exhibits instabilities when excited at frequencies corresponding to peak propulsive efficiency. This phenomenon was termed ‘wake resonance’, suggesting that when the oscillating foil is tuned to optimally excite the wake, it produces the highest propulsive efficiencies. Moored et al. (Reference Moored, Dewey, Smits and Haj-Hariri2012) also examined the vorticity perturbations generated by the most unstable modes in an effort to better understand these instabilities. Follow-on work by Moored et al. (Reference Moored, Dewey, Boschitsch, Smits and Haj-Hariri2014) showed that the ‘resonant frequencies’ correspond to optimal momentum entrainment, both into and out of the jet region. These findings suggest that there is no single wake structure that corresponds to peak propulsive efficiency (Smits Reference Smits2019). Further examples of 2P vortex patterns have also been found in wakes produced by eels and dolphins (Tytell & Lauder Reference Tytell and Lauder2004; Smits Reference Smits2019).
Recent studies have raised questions regarding the validity of wake resonance theory (Arbie, Ehrenstein & Eloy Reference Arbie, Ehrenstein and Eloy2016), noting that although correlations exist between unstable frequencies and peak propulsive efficiency from experiments, it is more difficult to establish a causal link between the two. Arbie et al. (Reference Arbie, Ehrenstein and Eloy2016) considered the stability characteristics of momentumless wakes and noted that these wakes may be stable (even if the thrust-producing jet-like component is unstable). It has also been suggested that, while the wake structure provides insight into propulsive efficiency, it cannot provide a complete explanation (Zhang Reference Zhang2017; Taylor Reference Taylor2018). Other studies (Eloy Reference Eloy2012) suggest that the development of the wake structure is a result of, and not a cause of, high propulsive efficiency. The reverse von Kármán wake from an oscillating foil can be shed in more patterns than just the 2S and 2P wake (see, e.g. Lentink et al. Reference Lentink, Muijres, Donker-Duyvis and van Leeuwen2008; Schnipper, Andersen & Bohr Reference Schnipper, Andersen and Bohr2009; Andersen et al. Reference Andersen, Bohr, Schnipper and Walther2017), and each wake structure has an indirect relationship with propulsive efficiency. For example, Mackowski & Williamson (Reference Mackowski and Williamson2015) found from experiments that wake patterns for a pitching foil, where self-interactions of the vortices occur, do not reflect a net force. Thus, observing the wake structure alone is likely not enough to completely determine the propulsive efficiency (Floryan, Van Buren & Smits Reference Floryan, Van Buren and Smits2020).
As an alternative approach, we make use of dynamic mode decomposition (DMD) to identify coherent features (or patterns) in the wakes produced by oscillating foils and link these features to propulsive performance. Dynamic mode decomposition, as first introduced by Schmid (Reference Schmid2010), is a technique used to approximate the dynamics of a nonlinear system via the identification of a linear operator that evolves the system to the next state. Dynamic mode decomposition can also be thought of as a data-driven stability analysis because each DMD mode is associated with a specific frequency and growth or decay rate, which provides interpretable physical insight into the spatial structures and their dynamic evolution. In contrast to the stability analysis approach, DMD does not require the mean flow to be locally or globally parallel. In the fields of marine propulsion and energy harvesting, DMD and similar modal decomposition techniques have been used on propeller and turbine wakes to characterize wake instabilities, loading conditions and efficiency (Sarmast et al. Reference Sarmast, Dadfar, Mikkelsen, Schlatter, Ivanell, Sørensen and Henningson2014; Araya, Colonius & Dabiri Reference Araya, Colonius and Dabiri2017; Magionesi et al. Reference Magionesi, Dubbioso, Muscari and Di Mascio2018; Strom, Polagye & Brunton Reference Strom, Polagye and Brunton2022).
In this study we use the triple decomposition to identify coherent flow features that contribute to drag and thrust production from PIV measurements for the wake past an oscillating foil. We examine both the vorticity and the Reynolds stresses associated with optimized DMD modes across Strouhal numbers ranging from ![]() $St = 0.16$ to
$St = 0.16$ to ![]() $St = 0.35$, and compare the results to time-averaged forces and propulsive efficiencies. We find that the use of DMD enables us to link wake structure with wake stability and propulsive efficiency for oscillating foils.
$St = 0.35$, and compare the results to time-averaged forces and propulsive efficiencies. We find that the use of DMD enables us to link wake structure with wake stability and propulsive efficiency for oscillating foils.
Our study builds upon the foil configuration described by Floryan et al. (Reference Floryan, Van Buren and Smits2020). We focus on rigid foils and present results primarily in the context of swimming performance. While the use of rigid foils represents a simplification of the fluid–structure interactions pertinent to flapping foil propulsion in nature, our results may provide additional insight into coherent flow features that contribute to drag and thrust. Moreover, the observations presented herein are also relevant to the design of autonomous swimming vehicles (Van Buren, Floryan & Smits Reference Van Buren, Floryan and Smits2020) and energy harvesting systems (McKinney & DeLaurier Reference McKinney and DeLaurier1981) that use rigid oscillating foils.
2. Heave and pitch foil parameters
We consider an oscillating NACA-0012 hydrofoil with chord ![]() $c$ and span
$c$ and span ![]() $s$ as illustrated in figure 1. The distance
$s$ as illustrated in figure 1. The distance ![]() $b=0.25c$ denotes the point of rotation from the leading edge. The imposed pitching and heaving kinematics of the foil at the point of rotation are described by
$b=0.25c$ denotes the point of rotation from the leading edge. The imposed pitching and heaving kinematics of the foil at the point of rotation are described by ![]() $\theta (t) =\theta _0\sin (2{\rm \pi} f t+\phi _p)$ and
$\theta (t) =\theta _0\sin (2{\rm \pi} f t+\phi _p)$ and ![]() $h(t) =h_0\sin (2{\rm \pi} f t)$, respectively, where
$h(t) =h_0\sin (2{\rm \pi} f t)$, respectively, where ![]() $\theta _0$ and
$\theta _0$ and ![]() $h_0$ are the respective pitching and heaving amplitudes,
$h_0$ are the respective pitching and heaving amplitudes, ![]() $f$ is the frequency of oscillation and
$f$ is the frequency of oscillation and ![]() $\phi _p$ is the phase difference between heaving and pitching oscillations. For the experiments described below, the phase difference was set to
$\phi _p$ is the phase difference between heaving and pitching oscillations. For the experiments described below, the phase difference was set to ![]() ${\rm \pi} /2$ (
${\rm \pi} /2$ (![]() $90^\circ$).
$90^\circ$).

Figure 1. Geometry and parameters for a pitching and heaving hydrofoil.
The oscillation frequency can be expressed in dimensionless terms as the Strouhal number,
Note that the Strouhal number can also be interpreted as the wake width (![]() ${\sim }A_{TE}$) normalized by the wavelength (
${\sim }A_{TE}$) normalized by the wavelength (![]() ${\sim }U_{\infty }/f$). Another important parameter relative to swimming performance is the angle of attack
${\sim }U_{\infty }/f$). Another important parameter relative to swimming performance is the angle of attack ![]() $\alpha$, which is different from the pitch angle due to the influence of the heave velocity,
$\alpha$, which is different from the pitch angle due to the influence of the heave velocity, ![]() $\dot {h}(t)$, and can be expressed as
$\dot {h}(t)$, and can be expressed as
In the case where the phase angle ![]() $\phi _p$ between pitch and heave is
$\phi _p$ between pitch and heave is ![]() $90^\circ$, the maximum angle of attack
$90^\circ$, the maximum angle of attack ![]() $\alpha _0$ can be estimated as
$\alpha _0$ can be estimated as
where ![]() $\omega = 2{\rm \pi} f$ is the radian frequency. The time-averaged power and thrust coefficients are described using the following equations:
$\omega = 2{\rm \pi} f$ is the radian frequency. The time-averaged power and thrust coefficients are described using the following equations:
 \begin{equation} C_P =\frac{\bar{\wp}}{\dfrac{1}{2}\rho s c U_{\infty}^3}, \quad C_T =\frac{\bar{\tau}}{\dfrac{1}{2}\rho s c U_{\infty}^2}. \end{equation}
\begin{equation} C_P =\frac{\bar{\wp}}{\dfrac{1}{2}\rho s c U_{\infty}^3}, \quad C_T =\frac{\bar{\tau}}{\dfrac{1}{2}\rho s c U_{\infty}^2}. \end{equation}
Here ![]() $\rho$ is the density of the fluid,
$\rho$ is the density of the fluid, ![]() $\bar {\tau }$ is the time-averaged thrust and
$\bar {\tau }$ is the time-averaged thrust and ![]() $\bar {\wp }=({1}/{T})(\int _{0}^{T} \dot {h}(t) F_y(t) \,{\rm d}t + \int _{0}^{T} \dot {\theta }(t)T_z(t)\,{\rm d}t)$ is the time-averaged power input to the fluid;
$\bar {\wp }=({1}/{T})(\int _{0}^{T} \dot {h}(t) F_y(t) \,{\rm d}t + \int _{0}^{T} \dot {\theta }(t)T_z(t)\,{\rm d}t)$ is the time-averaged power input to the fluid; ![]() $F_y$ and
$F_y$ and ![]() $T_z$ are the force and torque associated with the heaving and pitching motions. Propulsive efficiency can then be calculated as
$T_z$ are the force and torque associated with the heaving and pitching motions. Propulsive efficiency can then be calculated as
The propulsive efficiency and thrust coefficient are both used to characterize swimming performance. Table 1 shows kinematic parameters and flow conditions examined in the present study. Note that we match kinematic parameters with those from Quinn, Lauder & Smits (Reference Quinn, Lauder and Smits2015), who presented a large dataset of propulsive efficiencies for a NACA-0012 foil.
Table 1. Parameters used in the present and previous oscillating-foil studies. Chord-based Reynolds number ![]() $Re_c=\rho U_\infty c/\mu$, Strouhal number,
$Re_c=\rho U_\infty c/\mu$, Strouhal number, ![]() $St$, phase between heaving and pitching
$St$, phase between heaving and pitching ![]() $\phi _p$, pitch amplitude
$\phi _p$, pitch amplitude ![]() $\theta _0$ and dimensionless heave ratio
$\theta _0$ and dimensionless heave ratio ![]() $h^*=h_0/c$.
$h^*=h_0/c$.

3. Experimental methods
Experiments were carried out in a large-scale free-surface water channel with a glass-walled test section of dimensions ![]() $7.6\ {\rm m} \times 0.6\ {\rm m} \times 0.9\ {\rm m}$. A NACA-0012 hydrofoil with a chord of
$7.6\ {\rm m} \times 0.6\ {\rm m} \times 0.9\ {\rm m}$. A NACA-0012 hydrofoil with a chord of ![]() $c=10$ cm and a span of
$c=10$ cm and a span of ![]() $s=32$ cm was used. The foil was three-dimensionally printed from polylactic acid filament, sanded and reinforced with two internal aluminum rods throughout the span. The channel was run at a free-stream speed of
$s=32$ cm was used. The foil was three-dimensionally printed from polylactic acid filament, sanded and reinforced with two internal aluminum rods throughout the span. The channel was run at a free-stream speed of ![]() $U_\infty = 0.1\ {\rm m}\ {\rm s}^{-1}$ with a turbulence intensity of 1 %. Foil motions were produced using a closed-loop control system driven by two NEMA 23 integrated stepper motors, as shown in figure 2. One of the motors was connected to a linear rail to generate the heaving motion. The other motor was mounted to the beam to create the pitching motion. Translational and angular positions of the foil were calculated from the precision micro-steps (3200 steps per revolution) of the stepper motors. Measurements of hydrodynamic forces were made concurrently with an ATI Gamma (SI-32-2.5) six-degree-of-freedom force transducer with a minimum force and torque resolution of
$U_\infty = 0.1\ {\rm m}\ {\rm s}^{-1}$ with a turbulence intensity of 1 %. Foil motions were produced using a closed-loop control system driven by two NEMA 23 integrated stepper motors, as shown in figure 2. One of the motors was connected to a linear rail to generate the heaving motion. The other motor was mounted to the beam to create the pitching motion. Translational and angular positions of the foil were calculated from the precision micro-steps (3200 steps per revolution) of the stepper motors. Measurements of hydrodynamic forces were made concurrently with an ATI Gamma (SI-32-2.5) six-degree-of-freedom force transducer with a minimum force and torque resolution of ![]() $1/80$ N and
$1/80$ N and ![]() $1/2000$ Nm, respectively. Data were acquired at a rate of 5 kHz and filtered using a zero-phase second-order Butterworth filter. Instantaneous forces were measured over oscillation frequencies
$1/2000$ Nm, respectively. Data were acquired at a rate of 5 kHz and filtered using a zero-phase second-order Butterworth filter. Instantaneous forces were measured over oscillation frequencies ![]() $f=0.4\ {\rm Hz}\unicode{x2013}1.3\ {\rm Hz}$. For the kinematic parameters used in the present study (table 1), this yielded a Strouhal number range of
$f=0.4\ {\rm Hz}\unicode{x2013}1.3\ {\rm Hz}$. For the kinematic parameters used in the present study (table 1), this yielded a Strouhal number range of ![]() $St=0.16\unicode{x2013}0.59$. Time-averaged thrust coefficients (
$St=0.16\unicode{x2013}0.59$. Time-averaged thrust coefficients (![]() $C_T$), power coefficients (
$C_T$), power coefficients (![]() $C_P$) and propulsive efficiencies (
$C_P$) and propulsive efficiencies (![]() $\eta$) were computed by combining the force measurements with the foil kinematic data. The standard Klein–McClintock procedure was used to estimate uncertainties for these parameters based on known instrument resolution and measurement uncertainty for the time-averaged thrust and power input (Taylor Reference Taylor1997). Force measurements were collected and averaged for at least 13 periods for each run. Free-stream velocity measurements were recorded using a laser Doppler velocimetry system (MSE miniLDV). Relative uncertainties in the velocity measurements were
$\eta$) were computed by combining the force measurements with the foil kinematic data. The standard Klein–McClintock procedure was used to estimate uncertainties for these parameters based on known instrument resolution and measurement uncertainty for the time-averaged thrust and power input (Taylor Reference Taylor1997). Force measurements were collected and averaged for at least 13 periods for each run. Free-stream velocity measurements were recorded using a laser Doppler velocimetry system (MSE miniLDV). Relative uncertainties in the velocity measurements were ![]() $0.11\,\%$.
$0.11\,\%$.

Figure 2. Experimental motion-control system.
Two-dimension two-component (2D-2C) PIV measurements were carried out in the near-wake region of the oscillating foil to provide further insight into the transition from drag-producing and free-swimming conditions to thrust-producing conditions. The PIV system comprised a 5 W 532 nm solid-state laser and a Phantom VEO 410-L high speed camera with ![]() $1280 \times 800$ pixel resolution. Images of the flow field were captured in a field of view of
$1280 \times 800$ pixel resolution. Images of the flow field were captured in a field of view of ![]() $27\ {\rm cm} \times 17\ {\rm cm}$ at a rate of
$27\ {\rm cm} \times 17\ {\rm cm}$ at a rate of ![]() $65$ Hz for approximately
$65$ Hz for approximately ![]() $56$ s. Standard analysis routines in DaVis (LaVision) were used to generate velocity measurements. Two
$56$ s. Standard analysis routines in DaVis (LaVision) were used to generate velocity measurements. Two ![]() $64\ {\rm pixel} \times 64\ {\rm pixel}$ and four
$64\ {\rm pixel} \times 64\ {\rm pixel}$ and four ![]() $24\ {\rm pixel} \times 24\ {\rm pixel}$ convolution windows were used with a
$24\ {\rm pixel} \times 24\ {\rm pixel}$ convolution windows were used with a ![]() $50\,\%$ overlap to determine the velocity vectors. This yielded a set of
$50\,\%$ overlap to determine the velocity vectors. This yielded a set of ![]() $77 \times 50$ velocity vectors and 3600 snapshots for each of the wakes in this study. Erroneous columns of velocity values from the far ends of the field of view were removed.
$77 \times 50$ velocity vectors and 3600 snapshots for each of the wakes in this study. Erroneous columns of velocity values from the far ends of the field of view were removed.
Particle image velocimetry flow fields were both phase averaged and time averaged. For the lowest oscillation frequency (![]() $\,f=0.4$ Hz), the available PIV data spanned more than 21 oscillation periods. Dimensions of the field of view relative to the hydrofoil are illustrated in figure 3. Time- and phase-averaged measurements of streamwise velocity and vorticity were computed for the Strouhal numbers
$\,f=0.4$ Hz), the available PIV data spanned more than 21 oscillation periods. Dimensions of the field of view relative to the hydrofoil are illustrated in figure 3. Time- and phase-averaged measurements of streamwise velocity and vorticity were computed for the Strouhal numbers ![]() $St= 0.16$,
$St= 0.16$, ![]() $0.23$,
$0.23$, ![]() $0.29$ and
$0.29$ and ![]() $0.35$. The respective maximum angles of attack were
$0.35$. The respective maximum angles of attack were ![]() $\alpha _0= 15.2^\circ$,
$\alpha _0= 15.2^\circ$, ![]() $22.3^\circ$,
$22.3^\circ$, ![]() $28.2^\circ$ and
$28.2^\circ$ and ![]() $33.1^\circ$.
$33.1^\circ$.

Figure 3. Hydrofoil and PIV experimental set-up with field-of-view dimensions.
3.1. Periodic structures via the triple decomposition
For periodic flows under natural or forced conditions, large-scale coherent motions are often present in addition to turbulence. In such situations, the Reynolds decomposition, which assumes that turbulence is the only source of fluctuations in the flow, may not be accurate and can lead to overestimation of the stochastic part of the flow. Alternatively, the full flow field ![]() $\boldsymbol {u}$ can be expressed as a triple decomposition as introduced by Hussain & Reynolds (Reference Hussain and Reynolds1970):
$\boldsymbol {u}$ can be expressed as a triple decomposition as introduced by Hussain & Reynolds (Reference Hussain and Reynolds1970):
Here ![]() $\boldsymbol {\bar {u}}$ is the mean (time-averaged) flow field,
$\boldsymbol {\bar {u}}$ is the mean (time-averaged) flow field, ![]() $\boldsymbol {\tilde{u}}$ is the periodic flow field, characterized by the phase parameter
$\boldsymbol {\tilde{u}}$ is the periodic flow field, characterized by the phase parameter ![]() $\phi (t)$, and
$\phi (t)$, and ![]() $\boldsymbol {u'}$ represents the turbulent fluctuations that are incoherent. In our case, where the flow is driven by a known forcing frequency, the periodic component can be directly obtained through phase averaging as
$\boldsymbol {u'}$ represents the turbulent fluctuations that are incoherent. In our case, where the flow is driven by a known forcing frequency, the periodic component can be directly obtained through phase averaging as
 \begin{equation} \boldsymbol{\tilde{u}}(\boldsymbol{x},\phi_0)+\boldsymbol{\bar{u}}(\boldsymbol{x})=\frac{1}{N}\sum_{n=1}^N \boldsymbol{u}(\boldsymbol{x},\phi_0), \end{equation}
\begin{equation} \boldsymbol{\tilde{u}}(\boldsymbol{x},\phi_0)+\boldsymbol{\bar{u}}(\boldsymbol{x})=\frac{1}{N}\sum_{n=1}^N \boldsymbol{u}(\boldsymbol{x},\phi_0), \end{equation}
where the specific phase position ![]() $\phi _0=\phi (t_0+n\tau )$ is defined for an initial time
$\phi _0=\phi (t_0+n\tau )$ is defined for an initial time ![]() $t_0$ and a period
$t_0$ and a period ![]() $\tau$. However, for natural flows, or those driven by a series of forcing frequencies, (3.2) may be difficult to compute. Instead, phase averaging can be attained through modal decomposition methods. In these cases, the unsteady coherent component
$\tau$. However, for natural flows, or those driven by a series of forcing frequencies, (3.2) may be difficult to compute. Instead, phase averaging can be attained through modal decomposition methods. In these cases, the unsteady coherent component ![]() $\boldsymbol {\tilde{u}}$ may be represented by a linear combination of modes obtained via techniques such as proper orthogonal decomposition (POD) or DMD, and the triple decomposition can be modified as described by Baj, Bruce & Buxton (Reference Baj, Bruce and Buxton2015):
$\boldsymbol {\tilde{u}}$ may be represented by a linear combination of modes obtained via techniques such as proper orthogonal decomposition (POD) or DMD, and the triple decomposition can be modified as described by Baj, Bruce & Buxton (Reference Baj, Bruce and Buxton2015):
 \begin{equation} \boldsymbol{u}(\boldsymbol{x},t)=\boldsymbol{\bar{u}(x)}+\sum_{n=1}^r\boldsymbol{\tilde{u}}_n(\boldsymbol{x},\phi_n(t))+\boldsymbol{u'}(\boldsymbol{x},t). \end{equation}
\begin{equation} \boldsymbol{u}(\boldsymbol{x},t)=\boldsymbol{\bar{u}(x)}+\sum_{n=1}^r\boldsymbol{\tilde{u}}_n(\boldsymbol{x},\phi_n(t))+\boldsymbol{u'}(\boldsymbol{x},t). \end{equation}
Here, ![]() $r$ is the number of modes retained from the modal decomposition. In this study we use DMD to obtain the periodic component of the flow field in (3.3) and compare this modal representation to the wake characteristics obtained via direct phase averaging, as shown in (3.2).
$r$ is the number of modes retained from the modal decomposition. In this study we use DMD to obtain the periodic component of the flow field in (3.3) and compare this modal representation to the wake characteristics obtained via direct phase averaging, as shown in (3.2).
3.2. Dynamic mode decomposition
Dynamic mode decomposition was originally presented to the fluid mechanics community by Schmid (Reference Schmid2010) as a method to decompose unsteady or turbulent flow fields into coherent structures. Dynamic mode decomposition can be interpreted as an eigendecomposition of a least squares best-fit linear operator ![]() $\boldsymbol {A}$ that advances the past snapshots of data (i.e. 2D-2C velocity fields obtained from PIV) forward in time towards future snapshots.
$\boldsymbol {A}$ that advances the past snapshots of data (i.e. 2D-2C velocity fields obtained from PIV) forward in time towards future snapshots.
For a set of ![]() $m$ snapshots (
$m$ snapshots (![]() $\boldsymbol {x}_1, \boldsymbol {x}_2, \ldots, \boldsymbol {x}_m$), the dataset is arranged into two separate matrices of the forms
$\boldsymbol {x}_1, \boldsymbol {x}_2, \ldots, \boldsymbol {x}_m$), the dataset is arranged into two separate matrices of the forms
 \begin{equation} \boldsymbol{X}=\begin{bmatrix} \vert & \vert & & \vert\\ \boldsymbol{x}_1 & \boldsymbol{x}_2 & \cdots & \boldsymbol{x}_{m-1}\\ \vert & \vert & & \vert \end{bmatrix} \end{equation}
\begin{equation} \boldsymbol{X}=\begin{bmatrix} \vert & \vert & & \vert\\ \boldsymbol{x}_1 & \boldsymbol{x}_2 & \cdots & \boldsymbol{x}_{m-1}\\ \vert & \vert & & \vert \end{bmatrix} \end{equation}and
 \begin{equation} \boldsymbol{X}'=\begin{bmatrix} \vert & \vert & & \vert\\ \boldsymbol{x}_2 & \boldsymbol{x}_2 & \cdots & \boldsymbol{x}_{m}\\ \vert & \vert & & \vert \end{bmatrix}, \end{equation}
\begin{equation} \boldsymbol{X}'=\begin{bmatrix} \vert & \vert & & \vert\\ \boldsymbol{x}_2 & \boldsymbol{x}_2 & \cdots & \boldsymbol{x}_{m}\\ \vert & \vert & & \vert \end{bmatrix}, \end{equation}with
Generally, ![]() $\boldsymbol {A}$ can be approximated by taking the Moore–Penrose pseudo inverse of
$\boldsymbol {A}$ can be approximated by taking the Moore–Penrose pseudo inverse of ![]() $\boldsymbol {X'} (\boldsymbol {A}=\boldsymbol {X' X}^{\boldsymbol {-1}})$ via the singular value decomposition (SVD):
$\boldsymbol {X'} (\boldsymbol {A}=\boldsymbol {X' X}^{\boldsymbol {-1}})$ via the singular value decomposition (SVD): ![]() $\boldsymbol {X}=\boldsymbol {U \varSigma V^*}$. However, for high-dimensional datasets such as measurements from PIV snapshots, the computation of
$\boldsymbol {X}=\boldsymbol {U \varSigma V^*}$. However, for high-dimensional datasets such as measurements from PIV snapshots, the computation of ![]() $\boldsymbol {A}$ is expensive and can be inaccurate due to noisy entries or outliers in the data. To limit computational expense and the impact of noise, we consider the projection of
$\boldsymbol {A}$ is expensive and can be inaccurate due to noisy entries or outliers in the data. To limit computational expense and the impact of noise, we consider the projection of ![]() $\boldsymbol {A}$ onto a reduced-rank representation of the data obtained via the SVD,
$\boldsymbol {A}$ onto a reduced-rank representation of the data obtained via the SVD, ![]() $\boldsymbol {X} \approx \boldsymbol {U_r \varSigma _r V_r^*}$, where the subscript denotes a truncation to rank
$\boldsymbol {X} \approx \boldsymbol {U_r \varSigma _r V_r^*}$, where the subscript denotes a truncation to rank ![]() $r$:
$r$:
Note that this is analogous to projecting ![]() $\boldsymbol {A}$ onto the leading POD modes. Subsequently, the eigenvalues of matrix
$\boldsymbol {A}$ onto the leading POD modes. Subsequently, the eigenvalues of matrix ![]() $\boldsymbol {A}$ can be estimated by taking the eigendecomposition of
$\boldsymbol {A}$ can be estimated by taking the eigendecomposition of ![]() $\boldsymbol {\tilde{A}}$,
$\boldsymbol {\tilde{A}}$,
where the matrix ![]() $\boldsymbol {W}$ contains the eigenvectors and
$\boldsymbol {W}$ contains the eigenvectors and ![]() $\boldsymbol {\varLambda }$ contains the corresponding eigenvalues (
$\boldsymbol {\varLambda }$ contains the corresponding eigenvalues (![]() $\lambda _1, \lambda _2, \ldots$). Dynamic modes for the flow field can be computed using the exact-DMD algorithm from Tu et al. (Reference Tu, Rowley, Luchtenburg, Brunton and Kutz2014) as
$\lambda _1, \lambda _2, \ldots$). Dynamic modes for the flow field can be computed using the exact-DMD algorithm from Tu et al. (Reference Tu, Rowley, Luchtenburg, Brunton and Kutz2014) as
Here the matrix ![]() $\boldsymbol {\varPhi }$ contains individual dynamic modes
$\boldsymbol {\varPhi }$ contains individual dynamic modes ![]() $(\boldsymbol {\phi }_1, \boldsymbol {\phi }_2, \ldots )$. Using this low-dimensional approximation to the dynamics represented by
$(\boldsymbol {\phi }_1, \boldsymbol {\phi }_2, \ldots )$. Using this low-dimensional approximation to the dynamics represented by ![]() $\boldsymbol {A}$, we can reconstruct the data using a linear approximation of the dynamic modes for all future times:
$\boldsymbol {A}$, we can reconstruct the data using a linear approximation of the dynamic modes for all future times:
 \begin{equation} \boldsymbol{x}(t)\approx \sum_{k=1}^r \boldsymbol{\phi}_k\exp(\boldsymbol{\omega}_k t)b_k = \varPhi \exp(\boldsymbol{\omega} t)\boldsymbol{b}. \end{equation}
\begin{equation} \boldsymbol{x}(t)\approx \sum_{k=1}^r \boldsymbol{\phi}_k\exp(\boldsymbol{\omega}_k t)b_k = \varPhi \exp(\boldsymbol{\omega} t)\boldsymbol{b}. \end{equation}
The frequency ![]() $\omega _k$ is defined based on the associated eigenvalue
$\omega _k$ is defined based on the associated eigenvalue ![]() $\lambda _k$ as
$\lambda _k$ as ![]() $\omega _k=\ln (\lambda _k)/\Delta t$, where
$\omega _k=\ln (\lambda _k)/\Delta t$, where ![]() $\Delta t$ is the time interval between individual snapshots. The vector
$\Delta t$ is the time interval between individual snapshots. The vector ![]() $\boldsymbol {b}$ contains entries of the initial amplitudes
$\boldsymbol {b}$ contains entries of the initial amplitudes ![]() $b_k$ defined as
$b_k$ defined as ![]() $\boldsymbol {b}=\boldsymbol {\varPhi }^{-1}\boldsymbol {x_1}$. Recall that the dynamic modes
$\boldsymbol {b}=\boldsymbol {\varPhi }^{-1}\boldsymbol {x_1}$. Recall that the dynamic modes ![]() $\boldsymbol {\phi }_k$ are the columns of the matrix
$\boldsymbol {\phi }_k$ are the columns of the matrix ![]() $\boldsymbol {\varPhi }$. The modes in this temporal DMD formulation represent the absolute stability of the flow field, with the eigenvalues providing insight into oscillation frequencies and growth or decay rates. Given a complex eigenvalue
$\boldsymbol {\varPhi }$. The modes in this temporal DMD formulation represent the absolute stability of the flow field, with the eigenvalues providing insight into oscillation frequencies and growth or decay rates. Given a complex eigenvalue ![]() $\lambda _k = \lambda _{k,r} + i \lambda _{k,i} = |\lambda _k| \exp (i \angle \lambda _k)$, the frequency can be estimated as
$\lambda _k = \lambda _{k,r} + i \lambda _{k,i} = |\lambda _k| \exp (i \angle \lambda _k)$, the frequency can be estimated as ![]() $\omega _k = \omega _{k,r} + {\rm i} \omega _{k,i} = {\ln |\lambda _k|}/{\Delta t} + {\rm i}({\angle \lambda _k}/{\Delta t})$. Thus, a dynamic mode
$\omega _k = \omega _{k,r} + {\rm i} \omega _{k,i} = {\ln |\lambda _k|}/{\Delta t} + {\rm i}({\angle \lambda _k}/{\Delta t})$. Thus, a dynamic mode ![]() $\boldsymbol {\phi }_k$ grows over time if the corresponding eigenvalue has amplitude
$\boldsymbol {\phi }_k$ grows over time if the corresponding eigenvalue has amplitude ![]() $|\lambda _k|>1$ and decays if
$|\lambda _k|>1$ and decays if ![]() $|\lambda _k|<1$.
$|\lambda _k|<1$.
Spatial growth rates can also be approximated by the DMD algorithm by reorganizing the series of snapshots as increasing in space. In this case, modes in spatial DMD represent convective stability, where the eigenvalues would represent spatial frequencies or wavenumbers. In practice, spatial DMD is more prone to noise due to the sparsity of spatial data from PIV measurements, since the number of time snapshots available is typically much higher than the spatial locations (Schmid Reference Schmid2010). For instance, the PIV data obtained in this study span 3600 snapshots in time but only 77 streamwise locations for each run. As a result, we focus on using the temporal DMD approach to take advantage of our time-resolved snapshot data.
3.3. Optimized DMD
For the periodic flows that are studied in this paper, it is expected that the dynamic modes should neither grow or decay in time. That is, the eigenvalues of DMD are fixed directly onto the unit circle ![]() $|\lambda _k|=1$. However, the presence of even weak noise in periodic flows is known to yield damped eigenvalues,
$|\lambda _k|=1$. However, the presence of even weak noise in periodic flows is known to yield damped eigenvalues, ![]() $|\lambda _k|<1$, that result in decay of the corresponding modes (
$|\lambda _k|<1$, that result in decay of the corresponding modes (![]() $\boldsymbol {\phi }_k$) over time (Bagheri Reference Bagheri2014). Thus, several recent methods have been proposed for debiasing the DMD algorithm in the presence of noisy data, such as measurements from PIV (Dawson et al. Reference Dawson, Hemati, Williams and Rowley2016; Hemati et al. Reference Hemati, Rowley, Deem and Cattafesta2017; Askham & Kutz Reference Askham and Kutz2018). For this purpose, we use the optimized-DMD (opt-DMD) algorithm presented by Askham & Kutz (Reference Askham and Kutz2018). This is a variant of DMD that uses a variable projection method to approximate the linear operator
$\boldsymbol {\phi }_k$) over time (Bagheri Reference Bagheri2014). Thus, several recent methods have been proposed for debiasing the DMD algorithm in the presence of noisy data, such as measurements from PIV (Dawson et al. Reference Dawson, Hemati, Williams and Rowley2016; Hemati et al. Reference Hemati, Rowley, Deem and Cattafesta2017; Askham & Kutz Reference Askham and Kutz2018). For this purpose, we use the optimized-DMD (opt-DMD) algorithm presented by Askham & Kutz (Reference Askham and Kutz2018). This is a variant of DMD that uses a variable projection method to approximate the linear operator ![]() $\boldsymbol {A}$ with reduced noise. Specifically, opt-DMD solves the nonlinear least squares problem
$\boldsymbol {A}$ with reduced noise. Specifically, opt-DMD solves the nonlinear least squares problem
where the eigenvalues in ![]() $\varLambda$ act as iterative parameters and determine the values of the eigenfunctions,
$\varLambda$ act as iterative parameters and determine the values of the eigenfunctions, ![]() $\boldsymbol {\varPhi }$, and amplitude coefficients,
$\boldsymbol {\varPhi }$, and amplitude coefficients, ![]() $\boldsymbol {b}$. The algorithm also has the advantage of projecting the modes onto the full dataset rather than a subset from an
$\boldsymbol {b}$. The algorithm also has the advantage of projecting the modes onto the full dataset rather than a subset from an ![]() $r$-rank truncation. Additional constraints can be applied to the modes, such as restricting eigenvalues to stay on the unit circle. For simplicity, we do not use any constraints for the flow fields in this study, and find that opt-DMD naturally converges towards the expected eigenvalues in a periodic flow. The DMD modes of velocity are computed using both opt-DMD and exact-DMD algorithms for comparison. We compute the vorticity directly from the opt-DMD modes of velocity to understand the differences between the modal representation and the full flow field.
$r$-rank truncation. Additional constraints can be applied to the modes, such as restricting eigenvalues to stay on the unit circle. For simplicity, we do not use any constraints for the flow fields in this study, and find that opt-DMD naturally converges towards the expected eigenvalues in a periodic flow. The DMD modes of velocity are computed using both opt-DMD and exact-DMD algorithms for comparison. We compute the vorticity directly from the opt-DMD modes of velocity to understand the differences between the modal representation and the full flow field.
4. Results
4.1. Propulsive efficiency
Measurements of the thrust coefficient and propulsive efficiency are presented in figure 4. The thrust and power coefficients increase monotonically with increasing Strouhal number. However, ![]() $C_P$ increases faster than
$C_P$ increases faster than ![]() $C_T$ at higher
$C_T$ at higher ![]() $St$ values, leading to non-monotonic behaviour in propulsive efficiency and reduced efficiency for
$St$ values, leading to non-monotonic behaviour in propulsive efficiency and reduced efficiency for ![]() $St > 0.35$. Peak propulsive efficiencies can be seen within the range of
$St > 0.35$. Peak propulsive efficiencies can be seen within the range of ![]() $0.23< St<0.35$. With the provided uncertainty estimates, it can be argued that either of the three Strouhal numbers
$0.23< St<0.35$. With the provided uncertainty estimates, it can be argued that either of the three Strouhal numbers ![]() $St=0.23$,
$St=0.23$, ![]() $0.29$ and
$0.29$ and ![]() $0.35$ result in the highest propulsive efficiency. However, simplified scaling laws suggest that, for angles of attack
$0.35$ result in the highest propulsive efficiency. However, simplified scaling laws suggest that, for angles of attack ![]() $\alpha$ where the flow remains attached to the foil, peak propulsive efficiency can be estimated as
$\alpha$ where the flow remains attached to the foil, peak propulsive efficiency can be estimated as
where ![]() $St_0$ is the Strouhal number that results in zero net thrust (Taylor Reference Taylor2018). In our case, the thrust coefficient is near zero for
$St_0$ is the Strouhal number that results in zero net thrust (Taylor Reference Taylor2018). In our case, the thrust coefficient is near zero for ![]() $St=0.16$. Using this value for
$St=0.16$. Using this value for ![]() $St_0$ gives a maximum efficiency of
$St_0$ gives a maximum efficiency of ![]() $St_{max}\approx 0.28$. This approximation is consistent with our case of
$St_{max}\approx 0.28$. This approximation is consistent with our case of ![]() $St=0.29$ for which the measured
$St=0.29$ for which the measured ![]() $\eta$ is highest. Note that the uncertainty in measured efficiency at
$\eta$ is highest. Note that the uncertainty in measured efficiency at ![]() $St=0.16$ is large, which is due to the fact that the thrust and power coefficients are close to
$St=0.16$ is large, which is due to the fact that the thrust and power coefficients are close to ![]() $0$ for this condition. Nonetheless, this case is similar to a self-propelled swimming mode, where the thrust from the foil is approximately equal to its drag. Negative efficiencies are expected for lower Strouhal numbers,
$0$ for this condition. Nonetheless, this case is similar to a self-propelled swimming mode, where the thrust from the foil is approximately equal to its drag. Negative efficiencies are expected for lower Strouhal numbers, ![]() $St<0.16$, for which the net thrust becomes negative due to the effects of viscous drag. As the foil oscillates at lower frequencies, the drag contribution on the propulsor stays approximately constant while the thrust generated decreases (Floryan et al. Reference Floryan, Van Buren, Rowley and Smits2017). The present measurements are broadly consistent with trends observed from previous studies (Triantafyllou et al. Reference Triantafyllou, Triantafyllou and Grosenbaugh1993; Quinn et al. Reference Quinn, Lauder and Smits2015).
$St<0.16$, for which the net thrust becomes negative due to the effects of viscous drag. As the foil oscillates at lower frequencies, the drag contribution on the propulsor stays approximately constant while the thrust generated decreases (Floryan et al. Reference Floryan, Van Buren, Rowley and Smits2017). The present measurements are broadly consistent with trends observed from previous studies (Triantafyllou et al. Reference Triantafyllou, Triantafyllou and Grosenbaugh1993; Quinn et al. Reference Quinn, Lauder and Smits2015).

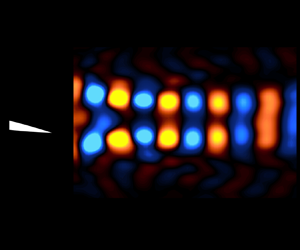
Figure 4. Comparison of time-averaged thrust coefficients and propulsive efficiencies as a function of Strouhal number.
4.2. Mean and phase-averaged flow fields
Particle image velocimetry measurements were used to study the downstream wake of the foil for a subset of the Strouhal numbers for which the force measurements were obtained. Phase-averaged vorticity (![]() $\varOmega$) and time-averaged streamwise velocity (
$\varOmega$) and time-averaged streamwise velocity (![]() $\bar {u}$) fields are shown in figure 5, where the foil is positioned to move in the positive
$\bar {u}$) fields are shown in figure 5, where the foil is positioned to move in the positive ![]() $y$ direction. An increase in magnitude of the jet wake (i.e.
$y$ direction. An increase in magnitude of the jet wake (i.e. ![]() $\bar {u}/U_\infty > 1$) can be seen with increasing
$\bar {u}/U_\infty > 1$) can be seen with increasing ![]() $St$. A near-momentumless wake is observed for
$St$. A near-momentumless wake is observed for ![]() $St=0.16$, where the wake profiles are close to zero, again indicating a resemblance to self-propelled swimming (figure 5b). Under this condition, approximately five positive and six negative vortices are shed per cycle of oscillation, signifying a small wake asymmetry. The vortices deflect laterally away from the heave and pitch centreline, resulting in an increase of the wake width from
$St=0.16$, where the wake profiles are close to zero, again indicating a resemblance to self-propelled swimming (figure 5b). Under this condition, approximately five positive and six negative vortices are shed per cycle of oscillation, signifying a small wake asymmetry. The vortices deflect laterally away from the heave and pitch centreline, resulting in an increase of the wake width from ![]() $x/c \approx 0.5\unicode{x2013}1.5$ that can be seen in figure 5(b).
$x/c \approx 0.5\unicode{x2013}1.5$ that can be seen in figure 5(b).

Figure 5. Phase-averaged vorticity and time-averaged streamwise velocity fields for (a,b) ![]() $St=0.16$, (c,d)
$St=0.16$, (c,d) ![]() $St=0.23$, (e,f)
$St=0.23$, (e,f) ![]() $St=0.29$ and (g,h)
$St=0.29$ and (g,h) ![]() $St=0.35$. See also supplementary movie 1 available at https://doi.org/10.1017/jfm.2024.446.
$St=0.35$. See also supplementary movie 1 available at https://doi.org/10.1017/jfm.2024.446.
Increasing the Strouhal number to ![]() $St=0.23$ produces a 2P wake (figure 5c), with mean profiles that are approximately trapezoidal shaped, with two small but distinct peaks. This wake characteristic matches well with the 2P structure observed by Dewey, Carriou & Smits (Reference Dewey, Carriou and Smits2012), who concluded that the presence of two vortex pairs result in two separate peaks in the mean profile. The Strouhal number
$St=0.23$ produces a 2P wake (figure 5c), with mean profiles that are approximately trapezoidal shaped, with two small but distinct peaks. This wake characteristic matches well with the 2P structure observed by Dewey, Carriou & Smits (Reference Dewey, Carriou and Smits2012), who concluded that the presence of two vortex pairs result in two separate peaks in the mean profile. The Strouhal number ![]() $St=0.29$ (figure 5e), initially produces a 2P wake with mean profiles that are trapezoidal (
$St=0.29$ (figure 5e), initially produces a 2P wake with mean profiles that are trapezoidal (![]() $0.22\leqslant x/c \leqslant 1.5$). These vortex pairs coalesce further downstream to a 2S wake, creating a mean profile resembling that produced by a single jet (
$0.22\leqslant x/c \leqslant 1.5$). These vortex pairs coalesce further downstream to a 2S wake, creating a mean profile resembling that produced by a single jet (![]() $1.5 < x/c \leqslant 2.7$). As the Strouhal number increases further to
$1.5 < x/c \leqslant 2.7$). As the Strouhal number increases further to ![]() $St = 0.35$, a classical 2S wake is observed, suggesting a transition from a 2P to 2S wake structure over the range
$St = 0.35$, a classical 2S wake is observed, suggesting a transition from a 2P to 2S wake structure over the range ![]() $0.23< St<0.35$. These observations are consistent with the results of Moored et al. (Reference Moored, Dewey, Smits and Haj-Hariri2012), who found optimal efficiencies in both wake types.
$0.23< St<0.35$. These observations are consistent with the results of Moored et al. (Reference Moored, Dewey, Smits and Haj-Hariri2012), who found optimal efficiencies in both wake types.
4.3. Modal decomposition
We now compare results between the exact-DMD and opt-DMD algorithms. Eigenvalues obtained for the first nine DMD modes for both methods are shown in figure 6. The mode corresponding to ![]() $\lambda = 0$ for each Strouhal number represents the mean flow field, while the other eigenvalues, having a non-zero imaginary part, represent the time-periodic modes. Note that the eigenvalues with non-zero imaginary components are represented in complex conjugate pairs (i.e. with
$\lambda = 0$ for each Strouhal number represents the mean flow field, while the other eigenvalues, having a non-zero imaginary part, represent the time-periodic modes. Note that the eigenvalues with non-zero imaginary components are represented in complex conjugate pairs (i.e. with ![]() $\lambda _k = \lambda _{k,r} \pm \lambda _{k,i}$), which together represent a single-frequency component of the flow field.
$\lambda _k = \lambda _{k,r} \pm \lambda _{k,i}$), which together represent a single-frequency component of the flow field.

Figure 6. Eigenvalue spectrum for (![]() $a$)
$a$) ![]() $St=0.16$, (
$St=0.16$, (![]() $b$)
$b$) ![]() $St=0.23$, (
$St=0.23$, (![]() $c$)
$c$) ![]() $St=0.29$, (
$St=0.29$, (![]() $d$)
$d$) ![]() $St=0.35$. Purple markers indicate overlap of the opt-DMD (red) and DMD (blue) eigenvalues. Here
$St=0.35$. Purple markers indicate overlap of the opt-DMD (red) and DMD (blue) eigenvalues. Here ![]() $\lambda _r$ denotes the real component of the eigenvalues while
$\lambda _r$ denotes the real component of the eigenvalues while ![]() $\lambda _i$ denotes the imaginary component.
$\lambda _i$ denotes the imaginary component.
As shown by Magionesi et al. (Reference Magionesi, Dubbioso, Muscari and Di Mascio2018), the eigenvalue problem degenerates and results in harmonic solutions when the dominant components of the flow travel at a constant speed, and with constant shape. This is noticeable in both the opt-DMD and exact-DMD modes, whereby the eigenvalues have oscillation frequencies (![]() $|\omega _{k,i}|$) that are multiples of the first harmonic. The opt-DMD eigenvalues for all Strouhal numbers lie directly on the unit circle, suggesting that the modes neither grow or decay overtime (
$|\omega _{k,i}|$) that are multiples of the first harmonic. The opt-DMD eigenvalues for all Strouhal numbers lie directly on the unit circle, suggesting that the modes neither grow or decay overtime (![]() $|\lambda _k|=1$). In contrast, the exact-DMD eigenvalues tend to fall within the circle for increasing
$|\lambda _k|=1$). In contrast, the exact-DMD eigenvalues tend to fall within the circle for increasing ![]() $St$, particularly for large values of
$St$, particularly for large values of ![]() $|\lambda _{k,i}|$, signifying that the oscillatory modes obtained via exact-DMD decay over time (
$|\lambda _{k,i}|$, signifying that the oscillatory modes obtained via exact-DMD decay over time (![]() $|\lambda _k|<1$). This is most evident for the largest Strouhal number case (
$|\lambda _k|<1$). This is most evident for the largest Strouhal number case (![]() $St=0.35$) in figure 6(d), which shows eigenvalues within the unit circle for
$St=0.35$) in figure 6(d), which shows eigenvalues within the unit circle for ![]() $|\lambda _{k,i}| > 0.2$. Similar trends were reported by Bagheri (Reference Bagheri2014), who observed that eigenvalue damping increases linearly with noise amplitude and quadratically with frequency. For the remainder of this paper, we refer to the flow field produced by the dynamic modes associated with a complex conjugate pair of eigenvalues as a single mode, and consider the first to fourth harmonics as modes 1–4.
$|\lambda _{k,i}| > 0.2$. Similar trends were reported by Bagheri (Reference Bagheri2014), who observed that eigenvalue damping increases linearly with noise amplitude and quadratically with frequency. For the remainder of this paper, we refer to the flow field produced by the dynamic modes associated with a complex conjugate pair of eigenvalues as a single mode, and consider the first to fourth harmonics as modes 1–4.
To further understand the effects of mode decay via eigenvalue damping, we computed the periodogram-based power spectral density of the original flow field and the reconstructed flow from opt-DMD and exact-DMD modes (see figure 7). Note that each of the peaks represents the flow field produced by a pair of dynamic modes (i.e. corresponding to a complex conjugate pair of eigenvalues). The normalized frequencies for these peaks, ![]() $St= f A_{TE}/U_{\infty }$, represent harmonics of the foil oscillation frequency. The power from the exact-DMD reconstruction are lower in power compared with the opt-DMD reconstruction and full flow field (figure 7c,d). This decay can be attributed to the dampened eigenvalues from the exact-DMD algorithm, observed in figure 6(c,d). As a result, the effect of reduced power worsens with increasing
$St= f A_{TE}/U_{\infty }$, represent harmonics of the foil oscillation frequency. The power from the exact-DMD reconstruction are lower in power compared with the opt-DMD reconstruction and full flow field (figure 7c,d). This decay can be attributed to the dampened eigenvalues from the exact-DMD algorithm, observed in figure 6(c,d). As a result, the effect of reduced power worsens with increasing ![]() $St$. These results suggest that the opt-DMD algorithm outperforms the exact-DMD method in retaining the energy in all modes, as also shown by Strom et al. (Reference Strom, Polagye and Brunton2022).
$St$. These results suggest that the opt-DMD algorithm outperforms the exact-DMD method in retaining the energy in all modes, as also shown by Strom et al. (Reference Strom, Polagye and Brunton2022).

Figure 7. Power spectral densities for the original flow field (black) and the reconstructed flow fields from the opt-DMD (orange) and exact-DMD (blue) method for (![]() $a$)
$a$) ![]() $St=0.16$, (
$St=0.16$, (![]() $b$)
$b$) ![]() $St=0.23$, (
$St=0.23$, (![]() $c$)
$c$) ![]() $St=0.29$ and (
$St=0.29$ and (![]() $d$)
$d$) ![]() $St=0.35$. The dotted lines represent exponential decay rates obtained from fits to the first four mode amplitudes from opt-DMD and show the following behaviour: (
$St=0.35$. The dotted lines represent exponential decay rates obtained from fits to the first four mode amplitudes from opt-DMD and show the following behaviour: (![]() $a$)
$a$) ![]() $e^{-5.1St}$, (
$e^{-5.1St}$, (![]() $b$)
$b$) ![]() $e^{-4.0St}$, (
$e^{-4.0St}$, (![]() $c$)
$c$) ![]() $e^{-1.5St}$ and (
$e^{-1.5St}$ and (![]() $d$)
$d$) ![]() $e^{-1.0St}$.
$e^{-1.0St}$.
For completeness, we also highlight the exponential decay of the amplitude peaks of the opt-DMD modes, as shown by the dotted lines in figure 7. Interestingly, the exponential fits for ![]() $St = 0.16$ and
$St = 0.16$ and ![]() $St = 0.23$ show some flattening at the higher frequencies, suggesting that the wake is not strongly locked to the actuation frequency for these cases. For example, in the case of
$St = 0.23$ show some flattening at the higher frequencies, suggesting that the wake is not strongly locked to the actuation frequency for these cases. For example, in the case of ![]() $St=0.23$ (figure 7b), the third opt-DMD and exact-DMD modes have a slightly higher energy (
$St=0.23$ (figure 7b), the third opt-DMD and exact-DMD modes have a slightly higher energy (![]() $-10.9$ dB and
$-10.9$ dB and ![]() $-12.9$ dB) compared with mode two (
$-12.9$ dB) compared with mode two (![]() $-11.1$ dB and
$-11.1$ dB and ![]() $-14.0$ dB). The other cases do not show this behaviour.
$-14.0$ dB). The other cases do not show this behaviour.
4.3.1. Opt-DMD coherent structures
In addition to characterizing oscillation frequencies and growth or decay rates, DMD also provides insight into the wake structure. Reconstructions for the first two modes are shown in figure 8. Each modal reconstruction corresponds to the phase of oscillation shown in figure 5. For all ![]() $St$ values, mode 1 exhibits top–bottom symmetry in vortex structure across the centreline (
$St$ values, mode 1 exhibits top–bottom symmetry in vortex structure across the centreline (![]() $y/c = 0$). In contrast, mode 2 has an antisymmetric structure with vortex lobes of smaller size compared with mode 1. The higher-order modes 3 and 4 are also symmetric and asymmetric, respectively, as shown in figure 9. Qualitatively, these modes better capture skews in the wake structure across the centreline, particularly for the case of
$y/c = 0$). In contrast, mode 2 has an antisymmetric structure with vortex lobes of smaller size compared with mode 1. The higher-order modes 3 and 4 are also symmetric and asymmetric, respectively, as shown in figure 9. Qualitatively, these modes better capture skews in the wake structure across the centreline, particularly for the case of ![]() $St=0.16$ (figure 9a,b).
$St=0.16$ (figure 9a,b).

Figure 8. Vorticity fields from opt-DMD modes 1 (a,c,e,g) and 2 (b,d,f,h) for (a,b) ![]() $St=0.16$, (c,d)
$St=0.16$, (c,d) ![]() $St=0.23$, (e,f)
$St=0.23$, (e,f) ![]() $St=0.29$ and (g,h)
$St=0.29$ and (g,h) ![]() $St=0.35$. See also supplementary movie 2 and movie 3 available at https://doi.org/10.1017/jfm.2024.446.
$St=0.35$. See also supplementary movie 2 and movie 3 available at https://doi.org/10.1017/jfm.2024.446.

Figure 9. Vorticity fields from opt-DMD modes 3 (a,c,e,g) and 4 (b,d,f,h) for (a,b) ![]() $St=0.16$, (c,d)
$St=0.16$, (c,d) ![]() $St=0.23$, (e,f)
$St=0.23$, (e,f) ![]() $St=0.29$ and (g,h)
$St=0.29$ and (g,h) ![]() $St=0.35$. See also supplementary movie 4 and movie 5 available at https://doi.org/10.1017/jfm.2024.446.
$St=0.35$. See also supplementary movie 4 and movie 5 available at https://doi.org/10.1017/jfm.2024.446.
It was shown by Moored et al. (Reference Moored, Dewey, Smits and Haj-Hariri2012) that the overlap in vorticity modes at certain locations in space contributes to producing the full vortex structure. Similar observations can also be made in the present study, where the modal hierarchy is trying to represent a convective process in terms of purely oscillatory DMD modes that are harmonics of the flapping frequency. This is reflected in the DMD mode structure: since mode 2 exhibits twice the oscillation frequency as mode 1, vortex lobes from mode 2 exhibit roughly twice the spatial wavenumber as mode 1 (see figure 8). A coherent vortex is formed at a particular region in space when both modes are either in-phase or in anti-phase and vortex lobes with the same sign overlay each other. This is also consistent with the fact that the foil sheds a vortex each half-cycle. Whether the vortex formed is positive or negative is determined by the sign of the spatial eigenfunctions. These features (and the modes themselves) are phase-locked in a reference frame moving with the local convective velocity.
Notable differences between the modes from the near-momentumless wake and that from the 2P and 2S wakes are observed. For instance, mode 1 for ![]() $St=0.16$ has approximately four symmetric lobes of vorticity along the lateral axis (figure 8a). These elongated vortex packets expand laterally as they advect downstream and similar trends can be seen for mode 2 (figure 8b). This is consistent with the lateral variation observed in the mean velocity profile and phase-averaged vorticity fields. In contrast, mode 1 for the cases
$St=0.16$ has approximately four symmetric lobes of vorticity along the lateral axis (figure 8a). These elongated vortex packets expand laterally as they advect downstream and similar trends can be seen for mode 2 (figure 8b). This is consistent with the lateral variation observed in the mean velocity profile and phase-averaged vorticity fields. In contrast, mode 1 for the cases ![]() $St=0.23$,
$St=0.23$, ![]() $0.29$ and
$0.29$ and ![]() $0.35$ primarily consists of two vortex lobes with decreasing streamwise extent. Thus, the size of the lobes reflects the length scale of the shed vortices, which is partially determined by the convective length scale
$0.35$ primarily consists of two vortex lobes with decreasing streamwise extent. Thus, the size of the lobes reflects the length scale of the shed vortices, which is partially determined by the convective length scale ![]() $U_\infty /f$.
$U_\infty /f$.
The differences that reflect the transition from the 2P wake to the 2S reverse von Kármán street are more subtle. In the case of ![]() $St=0.23$, which exhibits a 2P wake morphology, the vorticity lobes travel consistently downstream (see figure 8c,d). As the Strouhal number increases from
$St=0.23$, which exhibits a 2P wake morphology, the vorticity lobes travel consistently downstream (see figure 8c,d). As the Strouhal number increases from ![]() $St=0.23$ to
$St=0.23$ to ![]() $St=0.35$, the lobe pairs move inward towards the centreline over the region
$St=0.35$, the lobe pairs move inward towards the centreline over the region ![]() $0.22 \leqslant x/c \leqslant 1.0$. In the region where
$0.22 \leqslant x/c \leqslant 1.0$. In the region where ![]() $x/c>1.0$, the lobes consistently travel in the streamwise direction again. This dynamic characteristic can be observed better from modes 3 and 4 in figures 9(c)–9(h), where the lobes structures are considerably smaller. Another key distinction across the 2P to 2S wake transition is that the symmetric vorticity lobes of modes 1 and 3 start to coalesce into a single lobe towards the downstream end of the field of view,
$x/c>1.0$, the lobes consistently travel in the streamwise direction again. This dynamic characteristic can be observed better from modes 3 and 4 in figures 9(c)–9(h), where the lobes structures are considerably smaller. Another key distinction across the 2P to 2S wake transition is that the symmetric vorticity lobes of modes 1 and 3 start to coalesce into a single lobe towards the downstream end of the field of view, ![]() $x/c \geqslant 2.0$. The antisymmetric pairs for modes 2 and 4 remain apart. This is most noticeable for the case of
$x/c \geqslant 2.0$. The antisymmetric pairs for modes 2 and 4 remain apart. This is most noticeable for the case of ![]() $St=0.35$ (figures 8g and 9g).
$St=0.35$ (figures 8g and 9g).
Although the high-frequency wake structures exhibit reverse von Kármán streets – as expected for thrust-producing systems – their symmetric and antisymmetric topologies are similar to that from the classical Kármán vortex street shed from two-dimensional objects (Tu et al. Reference Tu, Rowley, Luchtenburg, Brunton and Kutz2014; Araya et al. Reference Araya, Colonius and Dabiri2017; Taira et al. Reference Taira, Hemati, Brunton, Sun, Duraisamy, Bagheri, Dawson and Yeh2020). In these drag-producing wakes, the dominant DMD or POD modes obtained for these flows can also correspond to a series of frequency harmonics. One distinction from the classical drag-producing bluff body wakes is that their symmetric mode structures may consist of a single lobe of vorticity across the ![]() $y$ axis – as shown in experiments from Tu et al. (Reference Tu, Rowley, Luchtenburg, Brunton and Kutz2014) – rather than two or more from our study.
$y$ axis – as shown in experiments from Tu et al. (Reference Tu, Rowley, Luchtenburg, Brunton and Kutz2014) – rather than two or more from our study.
4.3.2. Influence of modes on wake dynamics
To further understand how the symmetric and antisymmetric modes relate to the full flow field, we superimpose the streamwise component associated with DMD modes 1 (![]() $\tilde{u}_1$) and 2 (
$\tilde{u}_1$) and 2 (![]() $\tilde{u}_2$) separately with the time-averaged streamwise velocity (
$\tilde{u}_2$) separately with the time-averaged streamwise velocity (![]() $\bar {u}$). Figures 10 and 11 show the full opt-DMD reconstructions (i.e. comprising modes 1–4) as well as these single-mode reconstructions of the streamwise velocity component. In the original streamwise fields the vortex development is characterized by the regions where
$\bar {u}$). Figures 10 and 11 show the full opt-DMD reconstructions (i.e. comprising modes 1–4) as well as these single-mode reconstructions of the streamwise velocity component. In the original streamwise fields the vortex development is characterized by the regions where ![]() $u$ is less than that of the free-stream velocity (
$u$ is less than that of the free-stream velocity (![]() $u/U_\infty <1$), resulting in shear layer roll up. In the transition to the 2S wake, a wavy jet is observed in the original flow fields (11a,b). Mode 1 with the mean flow (
$u/U_\infty <1$), resulting in shear layer roll up. In the transition to the 2S wake, a wavy jet is observed in the original flow fields (11a,b). Mode 1 with the mean flow (![]() $u = \bar {u} + \tilde{u}_1$) reproduces most of these wake dynamics, including a reasonable portion of the shear layer roll up from which the vortices emerge.
$u = \bar {u} + \tilde{u}_1$) reproduces most of these wake dynamics, including a reasonable portion of the shear layer roll up from which the vortices emerge.

Figure 10. Reconstructed streamwise velocity fields: ![]() $u = \bar {u} + \sum _{n=1}^{4} \tilde{u}_n$ (a,b);
$u = \bar {u} + \sum _{n=1}^{4} \tilde{u}_n$ (a,b); ![]() $\bar {u} + \tilde{u}_1$ (c,d) and
$\bar {u} + \tilde{u}_1$ (c,d) and ![]() $\bar {u} + \tilde{u}_2$ (e,f). The left and right columns are of the Strouhal numbers
$\bar {u} + \tilde{u}_2$ (e,f). The left and right columns are of the Strouhal numbers ![]() $St=0.16$ and
$St=0.16$ and ![]() $St=0.23$, respectively. The mode hierarchy is in terms of frequency, with the lowest corresponding to mode 1.
$St=0.23$, respectively. The mode hierarchy is in terms of frequency, with the lowest corresponding to mode 1.

Figure 11. Reconstructed streamwise velocity fields: ![]() $u = \bar {u} + \sum _{n=1}^{4} \tilde{u}_n$ (a,b);
$u = \bar {u} + \sum _{n=1}^{4} \tilde{u}_n$ (a,b); ![]() $\bar {u} + \tilde{u}_1$ (c,d) and
$\bar {u} + \tilde{u}_1$ (c,d) and ![]() $\bar {u} + \tilde{u}_2$ (e,f). The left and right columns are of the Strouhal numbers
$\bar {u} + \tilde{u}_2$ (e,f). The left and right columns are of the Strouhal numbers ![]() $St=0.29$ and
$St=0.29$ and ![]() $St=0.35$, respectively. The mode hierarchy is the same as in figure 10.
$St=0.35$, respectively. The mode hierarchy is the same as in figure 10.
The wake dynamics associated with mode 1 and the associated symmetric vorticity perturbations closely resemble the spatial instabilities observed by Moored et al. (Reference Moored, Dewey, Smits and Haj-Hariri2012) in the 2S wake structure created by a flexible fin. The main distinction lies in the number of vorticity lobes, with the former exhibiting two lobes instead of three. This observation suggests that the opt-DMD modes yield coherent structures that are related to spatial instabilities. It is also likely that mode 1 induces a majority of the net thrust since this mode is associated with the lower velocity structures that form the vortex structures outside the central jet. In contrast, mode 2 is associated with the shedding frequency of each vortex or vortex pair for the 2S and 2P wakes (i.e. twice the oscillation frequency). Mode 2 accounts for much of the remaining shear in the centre jet region; this is particularly evident in the higher Strouhal number wakes (figure 11e,f).
4.3.3. Coherent Reynolds stress contributions from DMD modes
The subtle differences in DMD mode structure across Strouhal numbers suggest that the associated Reynolds shear stresses may provide additional insight into thrust and drag effects. Following Reynolds & Hussain (Reference Reynolds and Hussain1972) and assuming that the Reynolds stress contributions from the turbulent fluctuations ![]() $\boldsymbol {u}'$ are negligible compared with the contributions from the phase-averaged periodic components
$\boldsymbol {u}'$ are negligible compared with the contributions from the phase-averaged periodic components ![]() $\boldsymbol {\tilde{u}}$, the time-averaged momentum equation in the streamwise direction can be expressed as follows:
$\boldsymbol {\tilde{u}}$, the time-averaged momentum equation in the streamwise direction can be expressed as follows:
The equation above also assumes no external pressure gradient, a purely two-dimensional flow, and that cross-stream gradients of the viscous and Reynolds stress terms dominate over the streamwise gradients. Invoking both a strong parallel flow assumption, whereby ![]() $\bar {v} \approx 0$ and
$\bar {v} \approx 0$ and ![]() $\partial \bar {u}/\partial x \approx 0$ locally, (4.2) can be further simplified to
$\partial \bar {u}/\partial x \approx 0$ locally, (4.2) can be further simplified to
which can be used to estimate the induced mean flow. In the above equation, ![]() $\bar {u}_n$ can be thought of as the mean velocity induced by DMD mode
$\bar {u}_n$ can be thought of as the mean velocity induced by DMD mode ![]() $n$, i.e. the Reynolds shear stresses generated by the periodic velocity components
$n$, i.e. the Reynolds shear stresses generated by the periodic velocity components ![]() $\tilde{u}_n$ and
$\tilde{u}_n$ and ![]() $\tilde{v}_n$ associated with mode
$\tilde{v}_n$ associated with mode ![]() $n$. Since the DMD modes are harmonics of the foil oscillation frequency, there are no mean Reynolds shear stress contributions from interactions across modes. In other words, we expect
$n$. Since the DMD modes are harmonics of the foil oscillation frequency, there are no mean Reynolds shear stress contributions from interactions across modes. In other words, we expect ![]() $\overline {\tilde{u}_m \tilde{v}_n} = 0$ for
$\overline {\tilde{u}_m \tilde{v}_n} = 0$ for ![]() $m\neq n$. Equation (4.3) indicates that positive values of
$m\neq n$. Equation (4.3) indicates that positive values of ![]() ${{\rm d}\overline {\tilde{u}_n\tilde{v}_n}}/{{\rm d}y}$ are associated with minima in
${{\rm d}\overline {\tilde{u}_n\tilde{v}_n}}/{{\rm d}y}$ are associated with minima in ![]() $\bar {u}_n$ and vice versa. Positive
$\bar {u}_n$ and vice versa. Positive ![]() $\bar {u}_n$ contributions increase momentum in the wake and produce thrust. The opposite is true for negative
$\bar {u}_n$ contributions increase momentum in the wake and produce thrust. The opposite is true for negative ![]() $\bar {u}_n$ contributions, which result in induced drag.
$\bar {u}_n$ contributions, which result in induced drag.
Predictions made using the highly simplified momentum balance in (4.3) are complementary to the control volume analyses of momentum entrainment and expulsion presented by Moored et al. (Reference Moored, Dewey, Boschitsch, Smits and Haj-Hariri2014), which showed that the surrounding fluid is entrained into the near-wake region close the foil at wake resonance. The increase in mass flow rate of the jet wake produces thrust, and the entrainment region should therefore have a Reynolds stress distribution in which the periodic components ![]() $\overline {\tilde{u}\tilde{v}}$ induce a jet-like mean profile. We solve (4.3) numerically for
$\overline {\tilde{u}\tilde{v}}$ induce a jet-like mean profile. We solve (4.3) numerically for ![]() $\bar {u}_n$ using the Reynolds shear stress profiles for DMD modes 1 and 2 that are closest to the foil (
$\bar {u}_n$ using the Reynolds shear stress profiles for DMD modes 1 and 2 that are closest to the foil (![]() $x/c=0.22$), enforcing the boundary conditions
$x/c=0.22$), enforcing the boundary conditions ![]() $\bar {u}_n(-\infty )=\bar {u}_n(\infty )=0$.
$\bar {u}_n(-\infty )=\bar {u}_n(\infty )=0$.
Figures 12 and 13 respectively show the coherent Reynolds stress fields ![]() $\overline {\tilde{u}_n\tilde{v}_n}$ and induced mean profiles
$\overline {\tilde{u}_n\tilde{v}_n}$ and induced mean profiles ![]() $\bar {u}_n$ predicted using (4.3) for opt-DMD modes 1 and 2. The Reynolds stress fields show patterns that are antisymmetric across the centreline over the region of
$\bar {u}_n$ predicted using (4.3) for opt-DMD modes 1 and 2. The Reynolds stress fields show patterns that are antisymmetric across the centreline over the region of ![]() $0.22 < x/c < 1.0$. This antisymmetry begins to break down for the case of
$0.22 < x/c < 1.0$. This antisymmetry begins to break down for the case of ![]() $St=0.35$ (figures 12g and 13g). As expected, mode 1 (i.e. the primary harmonic) generates larger Reynolds shear stresses and induced mean flow contributions compared with mode 2. However, this discrepancy is more pronounced for the higher Strouhal number cases (
$St=0.35$ (figures 12g and 13g). As expected, mode 1 (i.e. the primary harmonic) generates larger Reynolds shear stresses and induced mean flow contributions compared with mode 2. However, this discrepancy is more pronounced for the higher Strouhal number cases (![]() $St = 0.29, 0.35$) exhibiting 2S-type wakes. The maximum magnitudes of
$St = 0.29, 0.35$) exhibiting 2S-type wakes. The maximum magnitudes of ![]() $\overline {\tilde{u}_1\tilde{v}_1}$ for mode 1 increase with Strouhal number.
$\overline {\tilde{u}_1\tilde{v}_1}$ for mode 1 increase with Strouhal number.

Figure 12. Mean Reynolds stress fields ![]() $\overline {\tilde{u}_1\tilde{v}_1}$ and induced mean flow profiles
$\overline {\tilde{u}_1\tilde{v}_1}$ and induced mean flow profiles ![]() $\bar {u}_1$ (
$\bar {u}_1$ (![]() $x/c=0.22$) for opt-DMD mode 1 at (a,b)
$x/c=0.22$) for opt-DMD mode 1 at (a,b) ![]() $St=0.16$, (c,d)
$St=0.16$, (c,d) ![]() $St=0.23$, (e,f)
$St=0.23$, (e,f) ![]() $St=0.29$ and (g,h)
$St=0.29$ and (g,h) ![]() $St=0.35$.
$St=0.35$.

Figure 13. Mean Reynolds stress fields ![]() $\overline {\tilde{u}_2\tilde{v}_2}$ and induced mean flow profiles
$\overline {\tilde{u}_2\tilde{v}_2}$ and induced mean flow profiles ![]() $\bar {u}_2$ (
$\bar {u}_2$ (![]() $x/c=0.22$) for opt-DMD mode 2 at (a,b)
$x/c=0.22$) for opt-DMD mode 2 at (a,b) ![]() $St=0.16$, (c,d)
$St=0.16$, (c,d) ![]() $St=0.23$, (e,f)
$St=0.23$, (e,f) ![]() $St=0.29$ and (g,h)
$St=0.29$ and (g,h) ![]() $St=0.35$.
$St=0.35$.
The shape of the induced mean flow profiles for mode 1 are similar for the ![]() $St=0.16$ and
$St=0.16$ and ![]() $0.23$ cases (figure 12b,d), where two distinct positive maxima can be seen (with one noticeable negative component for the case
$0.23$ cases (figure 12b,d), where two distinct positive maxima can be seen (with one noticeable negative component for the case ![]() $St=0.23$). Induced mean profiles for both 2S wakes (
$St=0.23$). Induced mean profiles for both 2S wakes (![]() $St=0.29, 0.35$) in 12(f,h) also show similar characteristics. However,
$St=0.29, 0.35$) in 12(f,h) also show similar characteristics. However, ![]() $\bar {u}_1$ for
$\bar {u}_1$ for ![]() $St = 0.29$ shows two separate maxima while the profile for
$St = 0.29$ shows two separate maxima while the profile for ![]() $St = 0.35$ shows a single maximum near the centreline. This transition from two distinct maxima in the mean profile to a single peak is consistent with the 2P-2S transition noted earlier as the Strouhal number increases from
$St = 0.35$ shows a single maximum near the centreline. This transition from two distinct maxima in the mean profile to a single peak is consistent with the 2P-2S transition noted earlier as the Strouhal number increases from ![]() $St = 0.23$ to
$St = 0.23$ to ![]() $St = 0.35$. Interestingly,
$St = 0.35$. Interestingly, ![]() $\bar {u}_1$ profiles for
$\bar {u}_1$ profiles for ![]() $St = 0.29$ and
$St = 0.29$ and ![]() $St = 0.35$ match the measured mean profile shapes shown in figure 5(c,d). Specifically, the
$St = 0.35$ match the measured mean profile shapes shown in figure 5(c,d). Specifically, the ![]() $St = 0.29$ profile is approximately trapezoidal in shape while the
$St = 0.29$ profile is approximately trapezoidal in shape while the ![]() $St = 0.35$ profile resembles a typical jet. Induced
$St = 0.35$ profile resembles a typical jet. Induced ![]() $\bar {u}_1$ profiles for these high Strouhal number cases are also much larger in magnitude compared with the lower Strouhal number cases (
$\bar {u}_1$ profiles for these high Strouhal number cases are also much larger in magnitude compared with the lower Strouhal number cases (![]() $St=0.16, 0.23$), which is indicative of higher entrainment and thrust production.
$St=0.16, 0.23$), which is indicative of higher entrainment and thrust production.
Generally, Reynolds shear stress contributions and induced velocities from mode 2 in figure 13 are lower than those from mode 1. Particularly, ![]() $\bar {u}_2 \ll \bar {u}_1$ for the 2S wakes in
$\bar {u}_2 \ll \bar {u}_1$ for the 2S wakes in ![]() $St = 0.29$ and
$St = 0.29$ and ![]() $St = 0.35$. Additionally, while the mode 1 contributions vary significantly in magnitude across Strouhal number, all of the mode 2 profiles exhibit similar maximum values of
$St = 0.35$. Additionally, while the mode 1 contributions vary significantly in magnitude across Strouhal number, all of the mode 2 profiles exhibit similar maximum values of ![]() $\overline {\tilde{u}_2\tilde{v}_2}$ and
$\overline {\tilde{u}_2\tilde{v}_2}$ and ![]() $\bar {u}_2$. Reynolds stress fields associated with mode 2 for
$\bar {u}_2$. Reynolds stress fields associated with mode 2 for ![]() $St=0.16$ and
$St=0.16$ and ![]() $St = 0.23$ (figure 13b,d) remain reasonably coherent over the field of view. The resulting mean flow profiles also show consistent negative values (
$St = 0.23$ (figure 13b,d) remain reasonably coherent over the field of view. The resulting mean flow profiles also show consistent negative values (![]() $\bar {u}_2 < 0$), which is indicative of drag generation. This aligns with Floryan et al. (Reference Floryan, Van Buren, Rowley and Smits2017), who found that scaling laws differed from experiments in efficiency due to viscous drag effects at lower Strouhal numbers. The coherent stress fields are likely characteristics of the transition to bluff body shedding. Note that these drag-inducing effects are characterized by modes with a higher frequency than that from typical bluff body shedding (cf. similar observations from Strom et al. Reference Strom, Polagye and Brunton2022).
$\bar {u}_2 < 0$), which is indicative of drag generation. This aligns with Floryan et al. (Reference Floryan, Van Buren, Rowley and Smits2017), who found that scaling laws differed from experiments in efficiency due to viscous drag effects at lower Strouhal numbers. The coherent stress fields are likely characteristics of the transition to bluff body shedding. Note that these drag-inducing effects are characterized by modes with a higher frequency than that from typical bluff body shedding (cf. similar observations from Strom et al. Reference Strom, Polagye and Brunton2022).
While the ![]() $\bar {u}_2$ profiles are primarily negative for the lower Strouhal number cases, distinct positive regions are observed as the flow transitions from a 2P wake to a 2S wake for
$\bar {u}_2$ profiles are primarily negative for the lower Strouhal number cases, distinct positive regions are observed as the flow transitions from a 2P wake to a 2S wake for ![]() $St=0.29$ and
$St=0.29$ and ![]() $0.35$ as seen in figure 13(f,h). For
$0.35$ as seen in figure 13(f,h). For ![]() $St = 0.29$, the
$St = 0.29$, the ![]() $\bar {u}_2$ profile is positive and approximately trapezoidal in shape, matching the mean flow in figure 5(f). For
$\bar {u}_2$ profile is positive and approximately trapezoidal in shape, matching the mean flow in figure 5(f). For ![]() $St = 0.35$, the induced
$St = 0.35$, the induced ![]() $\bar {u}_2$ profile has a mix of positive and negative regions, with the total area under the profile yielding a net negative value. The transition from purely negative
$\bar {u}_2$ profile has a mix of positive and negative regions, with the total area under the profile yielding a net negative value. The transition from purely negative ![]() $\bar {u}_2$ contributions for
$\bar {u}_2$ contributions for ![]() $St = 0.16$ and
$St = 0.16$ and ![]() $0.23$ to primarily positive
$0.23$ to primarily positive ![]() $\bar {u}_2$ contributions for
$\bar {u}_2$ contributions for ![]() $St=0.29$ is reminiscent of the earlier convective instability work – as noted by Triantafyllou et al. (Reference Triantafyllou, Triantafyllou and Grosenbaugh1993), in a reverse von Kármán vortex street, there is little to no competition between the drag wake and the thrust wake. This is consistent with the present observations for
$St=0.29$ is reminiscent of the earlier convective instability work – as noted by Triantafyllou et al. (Reference Triantafyllou, Triantafyllou and Grosenbaugh1993), in a reverse von Kármán vortex street, there is little to no competition between the drag wake and the thrust wake. This is consistent with the present observations for ![]() $St=0.29$.
$St=0.29$.
4.4. Deterioration of propulsive efficiency at high  $St$
$St$
The marginal deterioration in propulsive efficiency along with the negative ![]() $\bar {u}_2$ contributions for the
$\bar {u}_2$ contributions for the ![]() $St = 0.35$ case can potentially be attributed to effects from leading-edge vortices. While we do not have access to PIV data around the foil, force and torque measurements, along with the angle of attack trends support this interpretation. In particular, we expect these effects to be evident in the normal or lift forces on the foil, which also influence the power input and propulsive efficiency (see (2.4a,b) and (2.5)). Dimensionless phase-averaged lift forces
$St = 0.35$ case can potentially be attributed to effects from leading-edge vortices. While we do not have access to PIV data around the foil, force and torque measurements, along with the angle of attack trends support this interpretation. In particular, we expect these effects to be evident in the normal or lift forces on the foil, which also influence the power input and propulsive efficiency (see (2.4a,b) and (2.5)). Dimensionless phase-averaged lift forces ![]() $F_y$ and power requirements
$F_y$ and power requirements ![]() $\wp$ measured for Strouhal numbers
$\wp$ measured for Strouhal numbers ![]() $St = 0.29\unicode{x2013}0.59$ are shown in figure 14. As expected, the lift forces exhibit the same oscillation frequency as the actuation, which also matches the first mode frequencies. The relative power exhibits oscillations at twice the actuation frequency, which is also the second mode frequency.
$St = 0.29\unicode{x2013}0.59$ are shown in figure 14. As expected, the lift forces exhibit the same oscillation frequency as the actuation, which also matches the first mode frequencies. The relative power exhibits oscillations at twice the actuation frequency, which is also the second mode frequency.

Figure 14. Dimensionless heave cycle ![]() $h/c$ (dotted line) and effective angle of attack
$h/c$ (dotted line) and effective angle of attack ![]() $\alpha$ (solid lines) for one cycle (
$\alpha$ (solid lines) for one cycle (![]() $a$), together with phase-averaged lift forces
$a$), together with phase-averaged lift forces ![]() $F_y$ (
$F_y$ (![]() $b$) and power requirements
$b$) and power requirements ![]() $\wp$ (
$\wp$ (![]() $c$) normalized by maximum values (
$c$) normalized by maximum values (![]() $F_{y_0}$ and
$F_{y_0}$ and ![]() $\wp _0$) for
$\wp _0$) for ![]() $St=0.29$ (red),
$St=0.29$ (red), ![]() $St=0.35$ (blue) and
$St=0.35$ (blue) and ![]() $St=0.59$ (black).
$St=0.59$ (black).
Noticeable deviations in relative lift and power are observed between the near-optimal Strouhal numbers (![]() $St=0.29$ and
$St=0.29$ and ![]() $0.35$) and the highest Strouhal number case (
$0.35$) and the highest Strouhal number case (![]() $St=0.59$). Particularly, the small enhancements in the magnitude of the lift force observed between
$St=0.59$). Particularly, the small enhancements in the magnitude of the lift force observed between ![]() $t/T\approx 0.4\unicode{x2013}0.5$ and
$t/T\approx 0.4\unicode{x2013}0.5$ and ![]() $t/T \approx 0.9\unicode{x2013}1.0$ lead to lower relative power requirements, as shown in figure 14(b,c). For the highest propulsive efficiency case of
$t/T \approx 0.9\unicode{x2013}1.0$ lead to lower relative power requirements, as shown in figure 14(b,c). For the highest propulsive efficiency case of ![]() $St=0.29$, additional decreases in relative power at
$St=0.29$, additional decreases in relative power at ![]() $t/T \approx 0.25$ and
$t/T \approx 0.25$ and ![]() $0.75$ lower the overall power across the full oscillation cycle (figure 14c). Note that the relative lift force enhancements for this Strouhal number case appear soon after maxima and minima in the effective angle of attack (
$0.75$ lower the overall power across the full oscillation cycle (figure 14c). Note that the relative lift force enhancements for this Strouhal number case appear soon after maxima and minima in the effective angle of attack (![]() $t/T = 0.25, 0.75$).
$t/T = 0.25, 0.75$).
These relative lift force enhancements may be linked to the structure of the Reynolds shear stress contribution and positive induced velocity from DMD mode 2 for ![]() $St=0.29$ (figure 13e,f), suggesting a delay in separation of the leading-edge vortices. The separation effects may start to occur for the
$St=0.29$ (figure 13e,f), suggesting a delay in separation of the leading-edge vortices. The separation effects may start to occur for the ![]() $St = 0.35$ case, which show a negative induced velocity from mode 2 (figure 12h) and higher relative power requirements in comparison to those from
$St = 0.35$ case, which show a negative induced velocity from mode 2 (figure 12h) and higher relative power requirements in comparison to those from ![]() $St=0.29$, resulting in lower propulsive efficiency. The deterioration in performance is even more visible for the
$St=0.29$, resulting in lower propulsive efficiency. The deterioration in performance is even more visible for the ![]() $St=0.59$ case, which shows a substantial decrease in the magnitude of
$St=0.59$ case, which shows a substantial decrease in the magnitude of ![]() $F_y/F_{y0}$ and corresponding increases in
$F_y/F_{y0}$ and corresponding increases in ![]() $\wp /\wp _0$.
$\wp /\wp _0$.
The tapering of efficiency past ![]() $St=0.29$ can also be explained based on high angles of attack. The stall angle for a static NACA 0012 foil is approximately
$St=0.29$ can also be explained based on high angles of attack. The stall angle for a static NACA 0012 foil is approximately ![]() $16^\circ$. However, oscillating loads can increase the stall angle substantially (Maresca, Favier & Rebont Reference Maresca, Favier and Rebont1979). For the present experiments, the maximum angles of attack
$16^\circ$. However, oscillating loads can increase the stall angle substantially (Maresca, Favier & Rebont Reference Maresca, Favier and Rebont1979). For the present experiments, the maximum angles of attack ![]() $\alpha _0$ for the higher Strouhal number cases
$\alpha _0$ for the higher Strouhal number cases ![]() $St=0.29$,
$St=0.29$, ![]() $0.35$ and
$0.35$ and ![]() $0.59$ are
$0.59$ are ![]() $28.2^\circ$,
$28.2^\circ$, ![]() $33.1^\circ$ and
$33.1^\circ$ and ![]() $47.5^\circ$, respectively. Thus, it is likely that the induced drag effects from the secondary mode (figure 13h,f) become more relevant as the effective angle of attack increases, through which separation effects may occur – as also evident in the
$47.5^\circ$, respectively. Thus, it is likely that the induced drag effects from the secondary mode (figure 13h,f) become more relevant as the effective angle of attack increases, through which separation effects may occur – as also evident in the ![]() $F_y/F_{y0}$ traces. In turn, the efficiency tapers downward past the Strouhal number
$F_y/F_{y0}$ traces. In turn, the efficiency tapers downward past the Strouhal number ![]() $St=0.29$. However, it would be misleading to say that all cases with high angles of attack lead to reduced efficiency, as some combinations of kinematic parameters can delay these dynamic stall effects (Maresca et al. Reference Maresca, Favier and Rebont1979; Ellington et al. Reference Ellington, Van Den Berg, Willmott and Thomas1996; Anderson et al. Reference Anderson, Streitlien, Barrett and Triantafyllou1998). Instead, a high angle of attack where the flow stays attached to the foil can potentially maximize efficiency, an effect that has also been observed for flexible propulsors (Quinn et al. Reference Quinn, Lauder and Smits2015).
$St=0.29$. However, it would be misleading to say that all cases with high angles of attack lead to reduced efficiency, as some combinations of kinematic parameters can delay these dynamic stall effects (Maresca et al. Reference Maresca, Favier and Rebont1979; Ellington et al. Reference Ellington, Van Den Berg, Willmott and Thomas1996; Anderson et al. Reference Anderson, Streitlien, Barrett and Triantafyllou1998). Instead, a high angle of attack where the flow stays attached to the foil can potentially maximize efficiency, an effect that has also been observed for flexible propulsors (Quinn et al. Reference Quinn, Lauder and Smits2015).
5. Discussion and conclusions
A triple decomposition method in which the periodic component of the wake is composed of opt-DMD modes was used to provide further physical insight into the propulsive performance of oscillating foils. The experimental data in which the method was used are broadly consistent with prior literature. We observe a near-momentumless wake structure for ![]() $St = 0.16$ and peak propulsive efficiency for
$St = 0.16$ and peak propulsive efficiency for ![]() $St = 0.29$. Over this range of Strouhal numbers, PIV measurements show a transition from a momentumless wake to a 2S wake morphology associated with the classical reverse von Kármán vortex street. The opt-DMD method is employed here instead of the classical or (exact) DMD approach as it captures more energy in the periodic component of the flow field. For this particular foil, the opt-DMD modes appear as harmonics of the foil oscillating frequency, with alternating symmetric and antisymmetric morphology across the wake centreline.
$St = 0.29$. Over this range of Strouhal numbers, PIV measurements show a transition from a momentumless wake to a 2S wake morphology associated with the classical reverse von Kármán vortex street. The opt-DMD method is employed here instead of the classical or (exact) DMD approach as it captures more energy in the periodic component of the flow field. For this particular foil, the opt-DMD modes appear as harmonics of the foil oscillating frequency, with alternating symmetric and antisymmetric morphology across the wake centreline.
The most interesting finding from our study is the relationship between the coherent Reynolds stress contributions from DMD modes and their impact on propulsive performance. Although (4.3) is only an approximation to the mean flow equation for the wake, it helps delineate modal contributions to drag and thrust. In our experiments, the mean velocities induced by the primary opt-DMD mode (mode 1) generally show thrust-producing characteristics across all ![]() $St$ values, though there is a transition from a two-hump mean profile for the 2P wakes to a jet-like mean profile for the 2S wakes. However, several different trends emerge from the mean velocities induced by mode 2, representing features oscillating at twice the fundamental frequency of the foil: (i) for Strouhal numbers below the optimum (
$St$ values, though there is a transition from a two-hump mean profile for the 2P wakes to a jet-like mean profile for the 2S wakes. However, several different trends emerge from the mean velocities induced by mode 2, representing features oscillating at twice the fundamental frequency of the foil: (i) for Strouhal numbers below the optimum (![]() $St<0.29$), the induced mean velocities
$St<0.29$), the induced mean velocities ![]() $\bar {u}_2$ are negative and suggest a transition to bluff body shedding; (ii) the secondary mode for the optimum Strouhal number case (
$\bar {u}_2$ are negative and suggest a transition to bluff body shedding; (ii) the secondary mode for the optimum Strouhal number case (![]() $St=0.29$) has a prominent positive induced mean velocity, indicating that the thrust wake is dominant; (iii) past the optimum Strouhal number, mode 2 transitions back to a negative induced mean velocity, which may be indicative of flow separation as a result of high angles of attack (
$St=0.29$) has a prominent positive induced mean velocity, indicating that the thrust wake is dominant; (iii) past the optimum Strouhal number, mode 2 transitions back to a negative induced mean velocity, which may be indicative of flow separation as a result of high angles of attack (![]() $St>0.29$).
$St>0.29$).
Given the close connection between DMD and stability analyses, it may be of interest to compare the opt-DMD modes with features identified in prior stability analyses (Moored et al. Reference Moored, Dewey, Smits and Haj-Hariri2012; Arbie et al. Reference Arbie, Ehrenstein and Eloy2016). The development of the opt-DMD modes close to the foil suggest that their may be some spatial growth of these perturbations in the near field. Thus, there may be links between these opt-DMD modes and the spatially growing modes identified in the ‘wake resonance’ studies (Triantafyllou et al. Reference Triantafyllou, Triantafyllou and Grosenbaugh1993; Lewin & Haj-Hariri Reference Lewin and Haj-Hariri2003; Moored et al. Reference Moored, Dewey, Boschitsch, Smits and Haj-Hariri2014). Nonetheless, it should be emphasized that the temporal DMD method was used in this study, which extracts modes at a particular oscillation frequency. A spatial DMD approach could provide a more direct approach to understanding these instability mechanisms. In this case, a spatial resolution that is higher than the PIV data collected in this study would be necessary to allow for an appropriate spatial DMD analysis.
This study focused on a narrow parameter range: we studied a single, rigid foil exhibiting periodic single-frequency oscillations. However, modal analysis methods similar to those employed here could provide substantial insights into wakes involving more complex kinematics, dynamic fluid–structure interactions, multiple-foil interactions or massively separated flows (see, e.g. Raspa, Godoy-Diana & Thiria Reference Raspa, Godoy-Diana and Thiria2013; Andersen et al. Reference Andersen, Bohr, Schnipper and Walther2017).
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2024.446.
Funding
This material is based on work supported by the National Science Foundation under grant no. 1943105. The authors thank Professor G. Spedding and S. Brunton for insightful discussions, as well as the reviewers for their constructive feedback on this paper.
Declaration of interests
The authors report no conflict of interest.