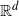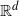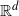1. Introduction and main results
Random graphs with underlying geometry are becoming the model of choice when it comes to modeling and understanding real-world networks [Reference Bringmann, Keusch and Lengler6, Reference Deijfen, van der Hofstad and Hooghiemstra12, Reference Gracar, Heydenreich, Mönch and Mörters18, Reference Krioukov25] (see also [Reference Van der Hofstad22, Section 9.5]). The presence of an ambient geometric space enables one to model the natural tendency for connections to form between entities that are close to each other, where closeness is measured in terms of the underlying geometry. The power of these models is the inherent diversity of the geometric component. It can encode actual physical distance, such as two servers in adjacent cities, as well as a more abstract form of similarity, e.g., users with similar interests or hobbies. Spatial networks have been employed to study social networks [Reference Wong, Pattison and Robins33]. Empirical research shows that the spatial positions of individuals often play a role in the formation of friendships among them [Reference Athanasiou and Yoshioka1, Reference Lee and Campbell28, Reference Wellman, Carrington and Hall31, Reference Wellman and Wortley32].
The prototypical random graph model in this setting is the random geometric graph, first introduced by Gilbert [Reference Gilbert16] and later popularized by Penrose [Reference Penrose29]. Here the graph is formed by placing edges between pairs of points of some Poisson point process on a Euclidean space, if and only if their metric distance is smaller than some fixed parameter. In general, one can consider models in which the connection probabilities are a decreasing function of the distance between pairs of vertices. Since nearby vertices are more likely to be connected in these spatial models, they naturally exhibit clustering, which captures the tendency for a connection to exist between two entities having a common neighbor, a feature that is often observed in real-world networks.
Other than clustering, experimental studies suggest that most real-world networks are sparse (i.e., the number of connections is often of the same order as the number of individuals) and that they are small worlds (i.e., for most pairs of nodes, it takes only a small number of connection steps to reach one from the other). Finally, many networks have highly inhomogeneous degree distributions (i.e., many vertices have only a few connections, while a small proportion of vertices have a lot of connections). The most notable spatial random graph models capable of capturing all these features are scale-free percolation [Reference Deijfen, van der Hofstad and Hooghiemstra12], geometric inhomogeneous random graphs [Reference Bringmann, Keusch and Lengler8], and hyperbolic random graphs [Reference Krioukov25].
When studying network models, one is often interested in the limits of specific network measures, e.g., degree distribution, average path length, or clustering coefficients. There is plenty of literature analyzing limits of such measures for a wide variety of models. Here, however, one first must prove convergence. Suppose that instead we have a limit object for our graph models, which implies convergence of the network measures of interest. Then we no longer have to worry about convergence and can instead focus on actually analyzing the limit measures. For sparse graphs such a framework exists under the name of local weak convergence [Reference Aldous and Steele2, Reference Benjamini and Schramm4]. At a high level, if a model has a local weak limit, then any local property converges to an associated measure on the limit graph. Therefore, if we know the local graph limit, we immediately obtain the limits of a wide variety of local network measures [Reference Van der Hofstad22, Chapter 2]. Furthermore, sometimes conclusions about sufficiently global properties of the graph can also be obtained from its local behavior (see [Reference Van der Hofstad21] and [Reference Van der Hofstad22, Chapter 2]).
In this paper, we study local convergence of a general class of spatial random graphs, which cover as particular cases many well-known models that are sparse, have inhomogeneous degree distributions, have short path lengths, and exhibit non-vanishing clustering. We establish that the typical local behavior in these ensembles matches the expected local behavior of the natural infinite version of the model. Our results immediately imply convergence of several local network measures, such as the degree distribution of a random vertex and the local clustering coefficient.
Organization of the paper. In the rest of this section, we review the basics of local convergence of graphs, introduce our model, and state our main results. Next, in Section 2, we present examples of models that are covered, as well as results on degrees and clustering in our graphs, and a small discussion on typical distances in our models. All the proofs are deferred to Section 3.
1.1. The space of rooted graphs and local convergence
The notion of local convergence of graphs was first introduced by Benjamini and Schramm [Reference Benjamini and Schramm4] and independently by Aldous and Steele [Reference Aldous and Steele2]. Intuitively, this notion studies the asymptotic local properties of a graph sequence, as observed from a typical vertex.
A (possibly infinite) graph
![]() $G=(V(G),E(G))$
is called locally finite when every vertex has finite degree. A rooted locally finite graph is a tuple (G, o), where
$G=(V(G),E(G))$
is called locally finite when every vertex has finite degree. A rooted locally finite graph is a tuple (G, o), where
![]() $G=(V(G),E(G))$
is a locally finite graph, with a designated vertex
$G=(V(G),E(G))$
is a locally finite graph, with a designated vertex
![]() $o \in V(G)$
called the root.
$o \in V(G)$
called the root.
Definition 1.
(Rooted isomorphism.) For rooted locally finite graphs
![]() $(G_1,o_1)$
and
$(G_1,o_1)$
and
![]() $(G_2,o_2)$
where
$(G_2,o_2)$
where
![]() $G_1=(V(G_1),E(G_1))$
and
$G_1=(V(G_1),E(G_1))$
and
![]() $G_2=(V(G_2),E(G_2))$
, we say that
$G_2=(V(G_2),E(G_2))$
, we say that
![]() $(G_1,o_1)$
is rooted isomorphic to
$(G_1,o_1)$
is rooted isomorphic to
![]() $(G_2,o_2)$
when there exists a graph isomorphism between
$(G_2,o_2)$
when there exists a graph isomorphism between
![]() $G_1$
and
$G_1$
and
![]() $G_2$
mapping
$G_2$
mapping
![]() $o_1$
to
$o_1$
to
![]() $o_2$
, i.e., when there exists a bijective function
$o_2$
, i.e., when there exists a bijective function
![]() $\phi\colon V(G_1) \to V(G_2)$
such that
$\phi\colon V(G_1) \to V(G_2)$
such that
and such that
![]() $\phi(o_1)=o_2$
.
$\phi(o_1)=o_2$
.
We use the notation
to denote that there is a rooted isomorphism between
![]() $(G_1,o_1)$
and
$(G_1,o_1)$
and
![]() $(G_2,o_2)$
.
$(G_2,o_2)$
.
Let
![]() $\mathcal{G}_{\star}$
be the space of all rooted isomorphic equivalence classes of locally finite rooted graphs; i.e.,
$\mathcal{G}_{\star}$
be the space of all rooted isomorphic equivalence classes of locally finite rooted graphs; i.e.,
![]() $\mathcal{G}_{\star}$
consists of the equivalence classes [(G, o)] of rooted locally finite graphs, where two rooted locally finite graphs
$\mathcal{G}_{\star}$
consists of the equivalence classes [(G, o)] of rooted locally finite graphs, where two rooted locally finite graphs
![]() $(G_1,o_1)$
and
$(G_1,o_1)$
and
![]() $(G_2,o_2)$
belong to the same class if they are rooted isomorphic to each other. We often omit the equivalence class notation, and just write (G, o) for an element of
$(G_2,o_2)$
belong to the same class if they are rooted isomorphic to each other. We often omit the equivalence class notation, and just write (G, o) for an element of
![]() $\mathcal{G}_{\star}$
.
$\mathcal{G}_{\star}$
.
Fix a graph
![]() $G=(V(G),E(G))$
. We denote the graph distance in G by
$G=(V(G),E(G))$
. We denote the graph distance in G by
![]() $d_G$
; i.e., for any two vertices
$d_G$
; i.e., for any two vertices
![]() $u,v \in V(G)$
,
$u,v \in V(G)$
,
![]() $d_G(u,v)$
equals the length of the shortest path in G from u to v, and we adopt the convention that
$d_G(u,v)$
equals the length of the shortest path in G from u to v, and we adopt the convention that
![]() $d_G(u,v)=\infty$
whenever u and v are not connected by a sequence of edges.
$d_G(u,v)=\infty$
whenever u and v are not connected by a sequence of edges.
Definition 2.
(Neighborhood of the root.) For any
![]() $R\geq 1$
and
$R\geq 1$
and
![]() $(G,o) \in \mathcal{G}_{\star}$
where
$(G,o) \in \mathcal{G}_{\star}$
where
![]() $G=(V(G),E(G))$
, we call the element
$G=(V(G),E(G))$
, we call the element
![]() $\left(B^G_o(R),o\right)$
of
$\left(B^G_o(R),o\right)$
of
![]() $\mathcal{G}_{\star}$
the R-neighborhood of o in G, where
$\mathcal{G}_{\star}$
the R-neighborhood of o in G, where
![]() $B^G_o(R)$
is the subgraph of G induced by
$B^G_o(R)$
is the subgraph of G induced by
We sometimes abbreviate
![]() $(B^G_o(R),o)$
as
$(B^G_o(R),o)$
as
![]() $B^G_o(R)$
.
$B^G_o(R)$
.
The space
![]() $\mathcal{G}_{\star}$
is usually endowed with the local topology, which is the smallest topology that makes the functions of the form
$\mathcal{G}_{\star}$
is usually endowed with the local topology, which is the smallest topology that makes the functions of the form
![]() $(G,o) \mapsto {\mathbb{1}_{\left\{B^G_o(K) \cong (G',o')\right\}}}$
for
$(G,o) \mapsto {\mathbb{1}_{\left\{B^G_o(K) \cong (G',o')\right\}}}$
for
![]() $K \geq 1$
and
$K \geq 1$
and
![]() $(G',o') \in \mathcal{G}_{\star}$
continuous. This topology is metrizable with an appropriate metric
$(G',o') \in \mathcal{G}_{\star}$
continuous. This topology is metrizable with an appropriate metric
![]() $d_{\star}$
(see [Reference Van der Hofstad22, Definition 2.4]), and
$d_{\star}$
(see [Reference Van der Hofstad22, Definition 2.4]), and
![]() $(\mathcal{G}_{\star},d_{\star})$
is a Polish space, which enables one to do probability on it. We omit further details on this.
$(\mathcal{G}_{\star},d_{\star})$
is a Polish space, which enables one to do probability on it. We omit further details on this.
For the next two definitions, we assume that
![]() $(G_n)_{n \geq 1}$
with
$(G_n)_{n \geq 1}$
with
![]() $G_n=(V(G_n),E(G_n))$
is a sequence of (possibly random) graphs that are (almost surely) finite, i.e.,
$G_n=(V(G_n),E(G_n))$
is a sequence of (possibly random) graphs that are (almost surely) finite, i.e.,
![]() $|V(G_n)| \stackrel{a.s.}{<} \infty$
for all
$|V(G_n)| \stackrel{a.s.}{<} \infty$
for all
![]() $n \geq 1$
, and, conditionally on
$n \geq 1$
, and, conditionally on
![]() $G_n$
,
$G_n$
,
![]() $U_n$
is a uniformly chosen random vertex of
$U_n$
is a uniformly chosen random vertex of
![]() $G_n$
. Note then that
$G_n$
. Note then that
![]() $(G_n,U_n)$
is a random variable taking values in
$(G_n,U_n)$
is a random variable taking values in
![]() $\mathcal{G}_{\star}$
. Local weak convergence of such random variables is defined as follows.
$\mathcal{G}_{\star}$
. Local weak convergence of such random variables is defined as follows.
Definition 3.
(Local weak convergence.) The sequence of graphs
![]() $(G_n)_{n \geq 1}$
is said to converge locally weakly to the random element
$(G_n)_{n \geq 1}$
is said to converge locally weakly to the random element
![]() $(G,o) \in \mathcal{G}_{\star}$
having law
$(G,o) \in \mathcal{G}_{\star}$
having law
![]() $\mu_{\star}$
, as
$\mu_{\star}$
, as
![]() $n \to \infty$
, when, for every
$n \to \infty$
, when, for every
![]() $r>0$
, and for every
$r>0$
, and for every
![]() $(G_{\star},o_{\star}) \in \mathcal{G}_{\star}$
,
$(G_{\star},o_{\star}) \in \mathcal{G}_{\star}$
,
as
![]() $n \to \infty$
.
$n \to \infty$
.
Definition 3 is in fact equivalent to saying that the sequence
![]() $((G_n,U_n))_{n \geq 1}$
of random variables taking values in
$((G_n,U_n))_{n \geq 1}$
of random variables taking values in
![]() $\mathcal{G}_{\star}$
converges in distribution to the random variable (G, o) taking values in
$\mathcal{G}_{\star}$
converges in distribution to the random variable (G, o) taking values in
![]() $\mathcal{G}_{\star}$
as
$\mathcal{G}_{\star}$
as
![]() $n \to \infty$
, under the topology induced by the metric
$n \to \infty$
, under the topology induced by the metric
![]() $d_{\star}$
on
$d_{\star}$
on
![]() $\mathcal{G}_{\star}$
(for a proof of this fact, see [Reference Van der Hofstad22, Definition 2.10 and Theorem 2.13]).
$\mathcal{G}_{\star}$
(for a proof of this fact, see [Reference Van der Hofstad22, Definition 2.10 and Theorem 2.13]).
This concept of local convergence can be adapted to the setting of convergence in probability. For a sequence of random variables Z,
![]() $(Z_n)_{n \geq 1}$
, we write
$(Z_n)_{n \geq 1}$
, we write
![]() $Z_n {{\stackrel{\mathbb{P}}{\,\rightarrow}}}\, Z$
to indicate that
$Z_n {{\stackrel{\mathbb{P}}{\,\rightarrow}}}\, Z$
to indicate that
![]() $Z_n$
converges in probability to Z, as
$Z_n$
converges in probability to Z, as
![]() $n \to \infty$
.
$n \to \infty$
.
Definition 4.
(Convergence locally in probability.) The sequence of graphs
![]() $(G_n)_{n \geq 1}$
is said to converge locally in probability to the (possibly random) element
$(G_n)_{n \geq 1}$
is said to converge locally in probability to the (possibly random) element
![]() $(G,o) \in \mathcal{G}_{\star}$
having (possibly random) law
$(G,o) \in \mathcal{G}_{\star}$
having (possibly random) law
![]() $\mu$
if for any
$\mu$
if for any
![]() $r>0$
and any
$r>0$
and any
![]() $(G_{\star},o_{\star}) \in \mathcal{G}_{\star}$
,
$(G_{\star},o_{\star}) \in \mathcal{G}_{\star}$
,
as
![]() $n \to \infty$
.
$n \to \infty$
.
For more on local convergence, we refer the reader to [Reference Van der Hofstad22, Chapter 2].
1.2. Model description and assumptions
Let S be either
![]() $[n]=\{1,\dots,n\}$
or
$[n]=\{1,\dots,n\}$
or
![]() $\mathbb{N}\cup \{0\}$
.
$\mathbb{N}\cup \{0\}$
.
Consider a sequence
![]() $\textbf{X}=(X_i)_{i \in S}$
of (possibly random) points in
$\textbf{X}=(X_i)_{i \in S}$
of (possibly random) points in
![]() $\mathbb{R}^d$
, a sequence of (possibly random) reals
$\mathbb{R}^d$
, a sequence of (possibly random) reals
![]() $\textbf{W}=(W_i)_{i \in S}$
, and a function
$\textbf{W}=(W_i)_{i \in S}$
, and a function
![]() $\kappa\,{:}\, \mathbb{R}_+ \times \mathbb{R} \times \mathbb{R} \to [0,1]$
which is symmetric in its second and third arguments.
$\kappa\,{:}\, \mathbb{R}_+ \times \mathbb{R} \times \mathbb{R} \to [0,1]$
which is symmetric in its second and third arguments.
Conditionally on
![]() $\textbf{X}$
and
$\textbf{X}$
and
![]() $\textbf{W}$
, form the (undirected) random graph
$\textbf{W}$
, form the (undirected) random graph
![]() $G=(V(G), E(G))$
with vertex set
$G=(V(G), E(G))$
with vertex set
![]() $V(G)=S$
, and with each possible edge
$V(G)=S$
, and with each possible edge
![]() $\{i,j\} \in E(G) \subset S \times S$
being included independently with probability
$\{i,j\} \in E(G) \subset S \times S$
being included independently with probability
Note that the requirement of symmetry is necessary since the probability of including the edge
![]() $\{i,j\}$
has to be the same as the probability of including the edge
$\{i,j\}$
has to be the same as the probability of including the edge
![]() $\{j,i\}$
. For each vertex i, we think of
$\{j,i\}$
. For each vertex i, we think of
![]() $X_i$
as the spatial location of the vertex, and
$X_i$
as the spatial location of the vertex, and
![]() $W_i$
as the weight associated to it.
$W_i$
as the weight associated to it.
We call such a graph G a spatial inhomogeneous random graph, or SIRG for short, and we use the notation
to denote the SIRG corresponding to the location sequence
![]() $\textbf{X}$
, weight sequence
$\textbf{X}$
, weight sequence
![]() $\textbf{W}$
, and connection function
$\textbf{W}$
, and connection function
![]() $\kappa$
.
$\kappa$
.
Remark 1. (Non-spatial inhomogeneous random graphs.) In the setting of (non-spatial) inhomogeneous random graph as proposed by Bollobás, Janson and Riordan in [Reference Bollobás, Janson and Riordan5], the vertex locations of the SIRGs can be thought of as types associated to each vertex. However, the type space in [Reference Bollobás, Janson and Riordan5] was taken to be an abstract space without any structure. In our model, these are locations in a Euclidean space, with connections depending upon distances between vertex locations, incorporating the underlying metric structure. In particular, in our models, the edge probabilities are large for nearby vertices, while in [Reference Bollobás, Janson and Riordan5], edge probabilities are typically of the order
![]() $1/n$
. This allows for non-trivial clustering to be present in our models, unlike in [Reference Bollobás, Janson and Riordan5], where the local limits are multitype branching processes; see [Reference Van der Hofstad22, Chapter 3].
$1/n$
. This allows for non-trivial clustering to be present in our models, unlike in [Reference Bollobás, Janson and Riordan5], where the local limits are multitype branching processes; see [Reference Van der Hofstad22, Chapter 3].
Consider a sequence
![]() $G_n=(V(G_n)=[n],E(G_n))=G(\textbf{X}^{(n)}, \textbf{W}^{(n)}, \kappa_n)$
of SIRGs of size n. Then
$G_n=(V(G_n)=[n],E(G_n))=G(\textbf{X}^{(n)}, \textbf{W}^{(n)}, \kappa_n)$
of SIRGs of size n. Then
![]() $\textbf{X}^{(n)}=(X^{(n)}_i)_{i\in[n]}$
and
$\textbf{X}^{(n)}=(X^{(n)}_i)_{i\in[n]}$
and
![]() $\textbf{W}^{(n)}=(W^{(n)}_i)_{i\in[n]}$
are the location and weight sequences, respectively, while
$\textbf{W}^{(n)}=(W^{(n)}_i)_{i\in[n]}$
are the location and weight sequences, respectively, while
![]() $\kappa_n$
is the sequence of connection functions. If
$\kappa_n$
is the sequence of connection functions. If
![]() $\textbf{X}^{(n)}$
,
$\textbf{X}^{(n)}$
,
![]() $\textbf{W}^{(n)}$
, and
$\textbf{W}^{(n)}$
, and
![]() $\kappa_n$
have limits
$\kappa_n$
have limits
![]() $\textbf{X}$
,
$\textbf{X}$
,
![]() $\textbf{W}$
, and
$\textbf{W}$
, and
![]() $\kappa$
, respectively, as
$\kappa$
, respectively, as
![]() $n \to \infty$
and in some appropriate sense, it is natural to expect the sequence of random graphs
$n \to \infty$
and in some appropriate sense, it is natural to expect the sequence of random graphs
![]() $G(\textbf{X}^{(n)},\textbf{W}^{(n)},\kappa_n)$
to have the graph
$G(\textbf{X}^{(n)},\textbf{W}^{(n)},\kappa_n)$
to have the graph
![]() $G(\textbf{X},\textbf{W},\kappa)$
as its limit. Our main contribution formalizes this intuition using local convergence, under appropriate convergence assumptions on
$G(\textbf{X},\textbf{W},\kappa)$
as its limit. Our main contribution formalizes this intuition using local convergence, under appropriate convergence assumptions on
![]() $\textbf{X}^{(n)}$
,
$\textbf{X}^{(n)}$
,
![]() $\textbf{W}^{(n)}$
, and
$\textbf{W}^{(n)}$
, and
![]() $\kappa_n$
, which we discuss next.
$\kappa_n$
, which we discuss next.
Assumption 1. (Law of vertex locations.) Define the box
For each
![]() $n \in \mathbb{N}$
, the collection
$n \in \mathbb{N}$
, the collection
![]() $(X^{(n)}_i)_{i\in[n]}$
is a collection of independent and uniformly distributed random variables on the box I.
$(X^{(n)}_i)_{i\in[n]}$
is a collection of independent and uniformly distributed random variables on the box I.
Assumption 2. (Weight distributions.) Let
![]() $\textbf{W}^{(n)}=(W^{(n)}_i)_{i\in[n]}$
be the sequence of weights associated to the vertices of
$\textbf{W}^{(n)}=(W^{(n)}_i)_{i\in[n]}$
be the sequence of weights associated to the vertices of
![]() $G_n$
, and assume that
$G_n$
, and assume that
![]() $\textbf{W}^{(n)}$
is independent of
$\textbf{W}^{(n)}$
is independent of
![]() $\textbf{X}^{(n)}$
. Furthermore, we assume that there exists a random variable W, with distribution function
$\textbf{X}^{(n)}$
. Furthermore, we assume that there exists a random variable W, with distribution function
![]() $\textrm{F}_W(x)\,{:\!=}\,\mathbb{P}\left(W \leq x\right)$
, such that for every continuity point x of
$\textrm{F}_W(x)\,{:\!=}\,\mathbb{P}\left(W \leq x\right)$
, such that for every continuity point x of
![]() $\textrm{F}_W(x)$
,
$\textrm{F}_W(x)$
,
as
![]() $n \to \infty$
. That is, we assume convergence in probability of the (possibly random) empirical distribution function to the (deterministic) distribution function
$n \to \infty$
. That is, we assume convergence in probability of the (possibly random) empirical distribution function to the (deterministic) distribution function
![]() $\textrm{F}_W$
of some limiting weight random variable W.
$\textrm{F}_W$
of some limiting weight random variable W.
The above assumption on the weights in our model is natural. Note that if we let
![]() $U_n$
be uniform on
$U_n$
be uniform on
![]() $[n]=\{1,\dots,n\}$
, then (4) is equivalent to the convergence in distribution of the typical weight
$[n]=\{1,\dots,n\}$
, then (4) is equivalent to the convergence in distribution of the typical weight
![]() $W^{(n)}_{U_n}$
, conditionally on the entire weight sequence
$W^{(n)}_{U_n}$
, conditionally on the entire weight sequence
![]() $(W^{(n)}_i)_{i \in [n]}$
, to W. Such regularity conditions are essential for understanding the behavior of the typical vertex, which is what local convergence aims to understand. Similar regularity assumptions on the weight of a typical vertex are also required for generalized random graphs (see e.g. [Reference Van der Hofstad20, Condition 6.4]) to make sure the typical degree distribution has a limit.
$(W^{(n)}_i)_{i \in [n]}$
, to W. Such regularity conditions are essential for understanding the behavior of the typical vertex, which is what local convergence aims to understand. Similar regularity assumptions on the weight of a typical vertex are also required for generalized random graphs (see e.g. [Reference Van der Hofstad20, Condition 6.4]) to make sure the typical degree distribution has a limit.
In most spatial random graph models, one starts with an infinite weight sequence and assigns the first n entries of this sequence as weights to the vertices of
![]() $G_n$
. This infinite weight sequence usually is deterministic, or is an independent and identically distributed (i.i.d.) sequence of weights from some given distribution. Note that for the latter, the above assumption is satisfied using the strong law of large numbers, and for the former case, (4) ensures that we have convergence in distribution of the typical weight.
$G_n$
. This infinite weight sequence usually is deterministic, or is an independent and identically distributed (i.i.d.) sequence of weights from some given distribution. Note that for the latter, the above assumption is satisfied using the strong law of large numbers, and for the former case, (4) ensures that we have convergence in distribution of the typical weight.
We also need some convergence assumptions for the sequence of connection functions
![]() $\kappa_n$
.
$\kappa_n$
.
Assumption 3. (Connection functions.)
-
1. There exists a function
 $\kappa\,{:}\, \mathbb{R}_+ \times \mathbb{R} \times \mathbb{R} \to [0,1]$
such that for every pair of real sequences
$\kappa\,{:}\, \mathbb{R}_+ \times \mathbb{R} \times \mathbb{R} \to [0,1]$
such that for every pair of real sequences
 $x_n\to x$
and
$x_n\to x$
and
 $y_n\to y$
, and for almost every
$y_n\to y$
, and for almost every
 $t \in \mathbb{R}_+$
,(5)as
$t \in \mathbb{R}_+$
,(5)as \begin{equation} \kappa_n(n^{1/d}t,x_n,y_n)\to \kappa(t,x,y), \end{equation}
\begin{equation} \kappa_n(n^{1/d}t,x_n,y_n)\to \kappa(t,x,y), \end{equation}
 $n \to \infty$
.
$n \to \infty$
.
-
2. Let
 $W^{(1)}$
and
$W^{(1)}$
and
 $W^{(2)}$
be two i.i.d. copies of the limiting weight random variable W. Then there exist
$W^{(2)}$
be two i.i.d. copies of the limiting weight random variable W. Then there exist
 $t_0>0$
,
$t_0>0$
,
 $\alpha>0$
, such that, for any
$\alpha>0$
, such that, for any
 $t \in \mathbb{R}_+$
with
$t \in \mathbb{R}_+$
with
 $t>t_0$
,(6)
$t>t_0$
,(6) \begin{equation} \mathbb{E}\left[\kappa(t,W^{(1)},W^{(2)})\right]\leq t^{-\alpha}. \end{equation}
\begin{equation} \mathbb{E}\left[\kappa(t,W^{(1)},W^{(2)})\right]\leq t^{-\alpha}. \end{equation}
Before stating our results, let us reflect on Assumption 3 a little. The term
![]() $n^{1/d}$
in the first argument of
$n^{1/d}$
in the first argument of
![]() $\kappa_n$
is required, because to obtain a local limit, we need to blow up the vertex locations from being uniform on I (recall (3)) to being uniform on
$\kappa_n$
is required, because to obtain a local limit, we need to blow up the vertex locations from being uniform on I (recall (3)) to being uniform on
This is done via the transformation
![]() $x \mapsto n^{1/d}x$
, and the
$x \mapsto n^{1/d}x$
, and the
![]() $n^{1/d}$
term in (5) ensures convergence of
$n^{1/d}$
term in (5) ensures convergence of
![]() $\kappa_n$
after this transformation.
$\kappa_n$
after this transformation.
Next, the ‘strong’ form of continuity in (5) is required so that the connection function sequence
![]() $\kappa_n$
is continuous with respect to convergence of weights as formulated in (4). To explain this, let
$\kappa_n$
is continuous with respect to convergence of weights as formulated in (4). To explain this, let
![]() $j \in \mathbb{N}$
, and consider a sequence
$j \in \mathbb{N}$
, and consider a sequence
![]() $(h_n)_{n \geq 1}$
of bounded continuous functions
$(h_n)_{n \geq 1}$
of bounded continuous functions
![]() $h_n\colon \mathbb{R}^j \to \mathbb{R}$
, converging to a bounded continuous function
$h_n\colon \mathbb{R}^j \to \mathbb{R}$
, converging to a bounded continuous function
![]() $h\colon \mathbb{R}^j \to \mathbb{R}$
in the following ‘strong’ sense analogous to (5): for any collection
$h\colon \mathbb{R}^j \to \mathbb{R}$
in the following ‘strong’ sense analogous to (5): for any collection
![]() $\{(x^i_n)_{n \geq 1}\colon 1\leq i \leq j\}$
of j real sequences satisfying
$\{(x^i_n)_{n \geq 1}\colon 1\leq i \leq j\}$
of j real sequences satisfying
![]() $x^i_n \to x_i$
as
$x^i_n \to x_i$
as
![]() $n \to \infty$
for
$n \to \infty$
for
![]() $1 \leq i \leq j$
,
$1 \leq i \leq j$
,
![]() $h_n(x^1_n,\ldots,x^j_n) \to h(x_1,\ldots,x_j)$
. Then, if for each
$h_n(x^1_n,\ldots,x^j_n) \to h(x_1,\ldots,x_j)$
. Then, if for each
![]() $n \in \mathbb{N}$
we let
$n \in \mathbb{N}$
we let
![]() $U_{n,1},\ldots,U_{n,j}$
be j independent uniformly distributed random variables on [n] and let
$U_{n,1},\ldots,U_{n,j}$
be j independent uniformly distributed random variables on [n] and let
![]() $W^{(1)},\ldots,W^{(j)}$
be j i.i.d. copies of the limiting weight random variable W, (4) implies that
$W^{(1)},\ldots,W^{(j)}$
be j i.i.d. copies of the limiting weight random variable W, (4) implies that
as
![]() $n \to \infty$
. In particular, as a consequence of (5) and (4), one can take
$n \to \infty$
. In particular, as a consequence of (5) and (4), one can take
![]() $h_n$
in (8) to be
$h_n$
in (8) to be
![]() $\kappa_n$
, or products of
$\kappa_n$
, or products of
![]() $\kappa_n$
, which will enable us to compute probabilities that paths exist in our finite graphs
$\kappa_n$
, which will enable us to compute probabilities that paths exist in our finite graphs
![]() $G_n$
. Note that (8) is not true in general if we just assume that the function
$G_n$
. Note that (8) is not true in general if we just assume that the function
![]() $h_n$
is continuous on
$h_n$
is continuous on
![]() $\mathbb{R}^j$
for each fixed
$\mathbb{R}^j$
for each fixed
![]() $n \in \mathbb{N}$
.
$n \in \mathbb{N}$
.
The above strong sense of continuity is in line with the assumption of graphical kernels in [Reference Bollobás, Janson and Riordan5] (see [Reference Bollobás, Janson and Riordan5, (2.10)]). In the setting of [Reference Bollobás, Janson and Riordan5], if we now consider the weights (instead of vertex locations as in Remark 1) associated to each vertex as vertex types, then we merely require the connection kernels to be continuous with respect to convergence of types, which is one of the key properties of graphical kernels in [Reference Bollobás, Janson and Riordan5].
Finally, let us discuss the technicality of having the convergence (5) hold for almost every
![]() $t \in \mathbb{R}_+$
, instead of all t. This is a purely technical condition, to avoid pathological examples. For example, consider the sequence of connection functions
$t \in \mathbb{R}_+$
, instead of all t. This is a purely technical condition, to avoid pathological examples. For example, consider the sequence of connection functions
![]() $\kappa_n(t,x,y)\,{:\!=}\,\mathbb{1}_{\left\{t<n^{1/d}xy\right\}}$
. We naturally want the limit of this sequence of connection functions to be
$\kappa_n(t,x,y)\,{:\!=}\,\mathbb{1}_{\left\{t<n^{1/d}xy\right\}}$
. We naturally want the limit of this sequence of connection functions to be
![]() $\mathbb{1}_{\left\{t < xy\right\}}$
. It is easily verified that for any pair of real sequences
$\mathbb{1}_{\left\{t < xy\right\}}$
. It is easily verified that for any pair of real sequences
![]() $x_n\to x$
and
$x_n\to x$
and
![]() $y_n \to y$
, (5) holds, except possibly for
$y_n \to y$
, (5) holds, except possibly for
![]() $t\in \{xy\}$
, a set of measure zero, with limiting connection function
$t\in \{xy\}$
, a set of measure zero, with limiting connection function
![]() $\kappa(t,x,y)=\mathbb{1}_{\left\{t < xy\right\}}$
. In particular, Assumption 3(1) holds. Typically, t will be replaced by
$\kappa(t,x,y)=\mathbb{1}_{\left\{t < xy\right\}}$
. In particular, Assumption 3(1) holds. Typically, t will be replaced by
![]() $\|X^{(n)}_i-X^{(n)}_j\|$
, with
$\|X^{(n)}_i-X^{(n)}_j\|$
, with
![]() $X^{(n)}_i,X^{(n)}_j$
being the respective locations of two vertices i and j. Since, under Assumption 1, the random variable
$X^{(n)}_i,X^{(n)}_j$
being the respective locations of two vertices i and j. Since, under Assumption 1, the random variable
![]() $\|X^{(n)}_i-X^{(n)}_j\|$
is a continuous random variable, it will avoid sets of measure zero, and Assumption 3(1) will continue to hold in our probabilistic statements.
$\|X^{(n)}_i-X^{(n)}_j\|$
is a continuous random variable, it will avoid sets of measure zero, and Assumption 3(1) will continue to hold in our probabilistic statements.
1.3. Statement of main results
Let us now formally discuss the limit of the SIRG model. As mentioned before, we shall consider the ‘blown-up’ SIRG sequence
![]() $\mathbb{G}_n=G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
, where
$\mathbb{G}_n=G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
, where
![]() $\textbf{Y}^{(n)}=(Y^{(n)}_i)_{i\in[n]}$
, with
$\textbf{Y}^{(n)}=(Y^{(n)}_i)_{i\in[n]}$
, with
![]() $Y^{(n)}_i=n^{1/d}X^{(n)}_i$
for all
$Y^{(n)}_i=n^{1/d}X^{(n)}_i$
for all
![]() $i\in[n]$
, and
$i\in[n]$
, and
![]() $\textbf{X}^{(n)}=(X^{(n)}_i)_{i\in[n]}$
satisfies Assumption 1, i.e., the locations of
$\textbf{X}^{(n)}=(X^{(n)}_i)_{i\in[n]}$
satisfies Assumption 1, i.e., the locations of
![]() $\mathbb{G}_n$
are now i.i.d. uniform variables on
$\mathbb{G}_n$
are now i.i.d. uniform variables on
![]() $I_n$
(recall (7)).
$I_n$
(recall (7)).
For convenience, we also define the point process on
![]() $\mathbb{R}^d$
, corresponding to the spatial locations of
$\mathbb{R}^d$
, corresponding to the spatial locations of
![]() $\mathbb{G}_n$
, as
$\mathbb{G}_n$
, as
where
![]() $\delta_x$
denotes the Dirac measure at
$\delta_x$
denotes the Dirac measure at
![]() $x \in \mathbb{R}^d$
.
$x \in \mathbb{R}^d$
.
If
![]() $\mathbb{G}_n$
has a local limit, then it is natural to expect that the weights associated to each vertex in this limit are i.i.d. copies of the limiting weight random variable W because of Assumption 2, and that the limiting connection function is
$\mathbb{G}_n$
has a local limit, then it is natural to expect that the weights associated to each vertex in this limit are i.i.d. copies of the limiting weight random variable W because of Assumption 2, and that the limiting connection function is
![]() $\kappa$
. For the locations, it is standard that the sequence
$\kappa$
. For the locations, it is standard that the sequence
![]() $\Gamma_n$
, viewed as random measures on
$\Gamma_n$
, viewed as random measures on
![]() $\mathbb{R}^d$
, converges to a unit-rate homogeneous Poisson point process on
$\mathbb{R}^d$
, converges to a unit-rate homogeneous Poisson point process on
![]() $\mathbb{R}^d$
(see [Reference Kallenberg23]), whose points will serve as the locations of the vertices of the limiting graph.
$\mathbb{R}^d$
(see [Reference Kallenberg23]), whose points will serve as the locations of the vertices of the limiting graph.
To this end, let us consider a unit-rate homogeneous Poisson point process
![]() $\Gamma$
, and write its atoms as
$\Gamma$
, and write its atoms as
![]() $\Gamma=\{Y_i\}_{i \in \mathbb{N}}$
(such an enumeration is possible by [Reference Last and Penrose27, Corollary 6.5]). Define the point process
$\Gamma=\{Y_i\}_{i \in \mathbb{N}}$
(such an enumeration is possible by [Reference Last and Penrose27, Corollary 6.5]). Define the point process
(where
![]() $\textbf{0}=(0,0,\dots,0) \in \mathbb{R}^d$
), which is the Palm version of
$\textbf{0}=(0,0,\dots,0) \in \mathbb{R}^d$
), which is the Palm version of
![]() $\Gamma$
, and write the sequence of its atoms as
$\Gamma$
, and write the sequence of its atoms as
![]() $\textbf{Y}=(Y_i)_{i \in \mathbb{N}\cup \{0\}}$
, where
$\textbf{Y}=(Y_i)_{i \in \mathbb{N}\cup \{0\}}$
, where
![]() $Y_0 = \textbf{0}$
. Also let
$Y_0 = \textbf{0}$
. Also let
![]() $\textbf{W}=(W_i)_{i \in \mathbb{N}\cup\{\textbf{0}\}}$
be a collection of i.i.d. copies of the limiting weight random variable W. Then we define the infinite SIRG, whose vertex set is given by
$\textbf{W}=(W_i)_{i \in \mathbb{N}\cup\{\textbf{0}\}}$
be a collection of i.i.d. copies of the limiting weight random variable W. Then we define the infinite SIRG, whose vertex set is given by
![]() $\mathbb{N\cup \{\textbf{0}\}}$
, as
$\mathbb{N\cup \{\textbf{0}\}}$
, as
![]() $\mathbb{G}_{\infty} =G(\textbf{Y}, \textbf{W}, \kappa)$
.
$\mathbb{G}_{\infty} =G(\textbf{Y}, \textbf{W}, \kappa)$
.
Our first result establishes that
![]() $\mathbb{G}_n$
converges locally weakly to
$\mathbb{G}_n$
converges locally weakly to
![]() $\mathbb{G}_\infty$
.
$\mathbb{G}_\infty$
.
Theorem 1. (Convergence of SIRGs in the local weak sense.) Consider the sequence
![]() $(\mathbb{G}_n)_{n\geq 1}=(G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n))_{n \geq 1}$
of SIRGs, where
$(\mathbb{G}_n)_{n\geq 1}=(G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n))_{n \geq 1}$
of SIRGs, where
![]() $Y^{(n)}_i=n^{1/d}X^{(n)}_i$
for each n and each
$Y^{(n)}_i=n^{1/d}X^{(n)}_i$
for each n and each
![]() $i\in [n]$
, with
$i\in [n]$
, with
![]() $\textbf{X}^{(n)}=(X^{(n)}_i)_{i\in[n]}$
,
$\textbf{X}^{(n)}=(X^{(n)}_i)_{i\in[n]}$
,
![]() $\textbf{W}^{(n)}=(W^{(n)}_i)_{i\in[n]}$
, and
$\textbf{W}^{(n)}=(W^{(n)}_i)_{i\in[n]}$
, and
![]() $\kappa_n$
satisfying Assumptions 1, 2, and 3, respectively, with the parameter
$\kappa_n$
satisfying Assumptions 1, 2, and 3, respectively, with the parameter
![]() $\alpha$
in (6) satisfying
$\alpha$
in (6) satisfying
Then
![]() $(\mathbb{G}_n)_{n \geq 1}$
converges locally weakly to the infinite rooted SIRG
$(\mathbb{G}_n)_{n \geq 1}$
converges locally weakly to the infinite rooted SIRG
![]() $(\mathbb{G}_{\infty},0)$
, rooted at vertex 0, where
$(\mathbb{G}_{\infty},0)$
, rooted at vertex 0, where
![]() $\mathbb{G}_{\infty}=G(\textbf{Y},\textbf{W},\kappa)$
.
$\mathbb{G}_{\infty}=G(\textbf{Y},\textbf{W},\kappa)$
.
Remark 2. (Regularly varying connection functions.) Note that if
![]() $\mathbb{E}\left[\kappa(t,W^{(1)},W^{(2)})\right]$
, as a function of t, either is itself, or is dominated by, a regularly varying function in t, with some exponent greater than d, then by Potter’s theorem (see e.g. [Reference Potter30]), Assumption 3(2) is satisfied, with some
$\mathbb{E}\left[\kappa(t,W^{(1)},W^{(2)})\right]$
, as a function of t, either is itself, or is dominated by, a regularly varying function in t, with some exponent greater than d, then by Potter’s theorem (see e.g. [Reference Potter30]), Assumption 3(2) is satisfied, with some
![]() $\alpha >d$
. Hence, for such connection functions, Theorem 1 goes through.
$\alpha >d$
. Hence, for such connection functions, Theorem 1 goes through.
Theorem 1 is equivalent to the statement that if
![]() $U_n$
is uniformly distributed on [n], then the random rooted graph
$U_n$
is uniformly distributed on [n], then the random rooted graph
![]() $(\mathbb{G}_n, U_n)$
converges in distribution to the random rooted graph
$(\mathbb{G}_n, U_n)$
converges in distribution to the random rooted graph
![]() $(\mathbb{G}_{\infty},0)$
, in the space
$(\mathbb{G}_{\infty},0)$
, in the space
![]() $(\mathcal{G}_{\star},d_{\star})$
.
$(\mathcal{G}_{\star},d_{\star})$
.
The condition
![]() $\alpha > d$
is required to avoid non-integrability of
$\alpha > d$
is required to avoid non-integrability of
![]() $z\mapsto$
$z\mapsto$
![]() $\mathbb{E}\left[\kappa(\|z\|,W^{(1)},W^{(2)})\right]$
as a function on
$\mathbb{E}\left[\kappa(\|z\|,W^{(1)},W^{(2)})\right]$
as a function on
![]() $\mathbb{R}^d$
. Integrability of
$\mathbb{R}^d$
. Integrability of
![]() $\mathbb{E}\left[\kappa(\|z\|,W^{(1)},W^{(2)})\right]$
implies that the degrees in
$\mathbb{E}\left[\kappa(\|z\|,W^{(1)},W^{(2)})\right]$
implies that the degrees in
![]() $\mathbb{G}_{\infty}$
have finite mean, which ensures that our random graph model is sparse. It also ensures that
$\mathbb{G}_{\infty}$
have finite mean, which ensures that our random graph model is sparse. It also ensures that
![]() $\mathbb{G}_{\infty}$
is locally finite almost surely, which we need for local weak convergence to make sense.
$\mathbb{G}_{\infty}$
is locally finite almost surely, which we need for local weak convergence to make sense.
There are two main challenges in proving Theorem 1. The first is to formulate the probability that the rooted subgraph induced by vertices whose locations fall inside a Euclidean ball with some fixed radius centered at the location
![]() $Y^{(n)}_{U_n}$
of
$Y^{(n)}_{U_n}$
of
![]() $U_n$
is isomorphic to a given graph, in terms of suitable functionals of the spatial locations of the vertices. The latter have nice limiting behavior owing to vague convergence of the spatial locations to a homogeneous Poisson process. The second is a careful path-counting analysis to conclude that the expected number of paths starting at
$U_n$
is isomorphic to a given graph, in terms of suitable functionals of the spatial locations of the vertices. The latter have nice limiting behavior owing to vague convergence of the spatial locations to a homogeneous Poisson process. The second is a careful path-counting analysis to conclude that the expected number of paths starting at
![]() $U_n$
, containing vertices with spatial locations far away from the location of
$U_n$
, containing vertices with spatial locations far away from the location of
![]() $U_n$
, can be made arbitrarily small.
$U_n$
, can be made arbitrarily small.
The result of Theorem 1 can be improved to local convergence in probability, as follows.
Theorem 2. (Convergence of SIRGs locally in probability.) Under the assumptions of Theorem 1, the sequence of SIRGs
![]() $(\mathbb{G}_n)_{n \geq 1}$
converges locally in probability to the infinite rooted SIRG
$(\mathbb{G}_n)_{n \geq 1}$
converges locally in probability to the infinite rooted SIRG
![]() $(\mathbb{G}_{\infty},0)$
, where
$(\mathbb{G}_{\infty},0)$
, where
![]() $\mathbb{G}_{\infty}=G(\textbf{Y},\textbf{W},\kappa)$
.
$\mathbb{G}_{\infty}=G(\textbf{Y},\textbf{W},\kappa)$
.
The improvement in Theorem 2 is achieved via a second moment analysis on neighborhood counts. The required independence essentially follows from the fact that the spatial locations of two uniformly chosen vertices of
![]() $\mathbb{G}_n$
are with high probability far apart from each other.
$\mathbb{G}_n$
are with high probability far apart from each other.
2. Consequences and discussion
In this section, we discuss implications of Theorems 1 and 2. We first discuss some standard examples that are covered under our setting. We then discuss how local convergence implies convergence of interesting graph functionals. We focus our attention on the degree and clustering structure of our SIRGs. Finally we provide a lower bound on typical distances in our graphs.
2.1. Examples
In this section, we discuss examples of spatial random graph models that are covered under our set-up.
2.1.1. Product SIRGs.
We begin by discussing a particular type of SIRG, in which the connection has a product form.
Definition 5. (Product SIRGs.) For a SIRG
![]() $G(\textbf{X},\textbf{W},\kappa)$
, if the connection function
$G(\textbf{X},\textbf{W},\kappa)$
, if the connection function
![]() $\kappa$
has the product form
$\kappa$
has the product form
for some non-negative functions
![]() $f\colon \mathbb{R}_+ \to \mathbb{R}_+$
and
$f\colon \mathbb{R}_+ \to \mathbb{R}_+$
and
![]() $g\colon\mathbb{R}^2 \to \mathbb{R}_+$
, where g is symmetric, then we call the SIRG a product SIRG, or PSIRG for short, and we call
$g\colon\mathbb{R}^2 \to \mathbb{R}_+$
, where g is symmetric, then we call the SIRG a product SIRG, or PSIRG for short, and we call
![]() $\kappa$
a product kernel.
$\kappa$
a product kernel.
Theorem 1 can be directly adapted to the PSIRG setting under appropriate conditions on the product kernel.
Assumption 4. (PSIRG connection functions.) Let
![]() $\kappa\colon \mathbb{R}_+\times \mathbb{R} \times \mathbb{R} \to [0,1]$
be a product kernel
$\kappa\colon \mathbb{R}_+\times \mathbb{R} \times \mathbb{R} \to [0,1]$
be a product kernel
![]() $\kappa(t,x,y) = 1\wedge f(t)g(x,y)$
such that the following hold:
$\kappa(t,x,y) = 1\wedge f(t)g(x,y)$
such that the following hold:
-
1. There exist
 $\alpha_p > 1$
and
$\alpha_p > 1$
and
 $t_1 \in \mathbb{R}_+$
such that for all
$t_1 \in \mathbb{R}_+$
such that for all
 $t>t_1$
,
$t>t_1$
, \begin{align*}f(t)\leq t^{-\alpha_p}.\end{align*}
\begin{align*}f(t)\leq t^{-\alpha_p}.\end{align*}
-
2. There exist
 $\beta_p > 0$
and
$\beta_p > 0$
and
 $t_2 \in \mathbb{R}_+$
such that for all
$t_2 \in \mathbb{R}_+$
such that for all
 $t> t_2$
,where
$t> t_2$
,where \begin{align*}\mathbb{P}\left(g(W^{(1)},W^{(2)})>t\right)\leq t^{-\beta_p},\end{align*}
\begin{align*}\mathbb{P}\left(g(W^{(1)},W^{(2)})>t\right)\leq t^{-\beta_p},\end{align*}
 $W^{(1)}, W^{(2)}$
are i.i.d. copies of the limiting weight random variable W in (4).
$W^{(1)}, W^{(2)}$
are i.i.d. copies of the limiting weight random variable W in (4).
Let
![]() $W^{(1)}$
and
$W^{(1)}$
and
![]() $W^{(2)}$
be two i.i.d. copies of W (see Assumption 2). The following lemma derives a useful bound on product kernels that satisfy Assumption 4.
$W^{(2)}$
be two i.i.d. copies of W (see Assumption 2). The following lemma derives a useful bound on product kernels that satisfy Assumption 4.
Lemma 1. (Bound on product kernel.) Under Assumption 4, for any
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $t_0=t_0(\epsilon)>0$
such that whenever
$t_0=t_0(\epsilon)>0$
such that whenever
![]() $t>t_0$
,
$t>t_0$
,
In other words, if the limiting connection function
![]() $\kappa$
in Theorem 2 satisfies Assumption 4, it also satisfies Assumption 3(3), with
$\kappa$
in Theorem 2 satisfies Assumption 4, it also satisfies Assumption 3(3), with
![]() $\alpha=\min\{\alpha_p,\alpha_p\beta_p\}-\epsilon$
for any
$\alpha=\min\{\alpha_p,\alpha_p\beta_p\}-\epsilon$
for any
![]() $\epsilon>0$
. So, if
$\epsilon>0$
. So, if
then using Lemma 1, we have that
![]() $\kappa$
satisfies Assumption 3(3) with some
$\kappa$
satisfies Assumption 3(3) with some
![]() $\alpha>d$
, by choosing
$\alpha>d$
, by choosing
![]() $\epsilon>0$
sufficiently small. Hence we obtain the following direct corollary to Theorem 2, whose proof we omit. Recall the vector
$\epsilon>0$
sufficiently small. Hence we obtain the following direct corollary to Theorem 2, whose proof we omit. Recall the vector
![]() $\textbf{W}=(W_i)_{i \in \mathbb{N} \cup \{0\}}$
of i.i.d. copies of the limiting weight variable W (see (4)), and
$\textbf{W}=(W_i)_{i \in \mathbb{N} \cup \{0\}}$
of i.i.d. copies of the limiting weight variable W (see (4)), and
![]() $\textbf{Y}=(Y_i)_{i \in \mathbb{N} \cup \{0\}}$
the atoms of
$\textbf{Y}=(Y_i)_{i \in \mathbb{N} \cup \{0\}}$
the atoms of
![]() $\Gamma_{\infty}$
(see (10)), with
$\Gamma_{\infty}$
(see (10)), with
![]() $Y_0=\textbf{0}$
.
$Y_0=\textbf{0}$
.
Corollary 1. (Convergence of PSIRGs locally in probability.) Consider the sequence
![]() $(\mathbb{G}_n)_{n\geq 1}=(G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n))_{n \geq 1}$
of SIRGs, where, for each n and each
$(\mathbb{G}_n)_{n\geq 1}=(G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n))_{n \geq 1}$
of SIRGs, where, for each n and each
![]() $i\in[n]$
,
$i\in[n]$
,
![]() $Y^{(n)}_i=n^{1/d}X^{(n)}_i$
, with
$Y^{(n)}_i=n^{1/d}X^{(n)}_i$
, with
![]() $\textbf{X}^{(n)}=(X^{(n)}_i)_{i\in[n]}$
and
$\textbf{X}^{(n)}=(X^{(n)}_i)_{i\in[n]}$
and
![]() $\textbf{W}^{(n)}=(W^{(n)}_i)_{i\in[n]}$
satisfying Assumptions 1 and 2,
$\textbf{W}^{(n)}=(W^{(n)}_i)_{i\in[n]}$
satisfying Assumptions 1 and 2,
![]() $\kappa_n$
satisfying Assumption 3(1),
$\kappa_n$
satisfying Assumption 3(1),
![]() $\kappa$
satisfying Assumption 4, and
$\kappa$
satisfying Assumption 4, and
Then
![]() $(\mathbb{G}_n)_{n \geq 1}$
converges locally in probability to the infinite rooted SIRG
$(\mathbb{G}_n)_{n \geq 1}$
converges locally in probability to the infinite rooted SIRG
![]() $(\mathbb{G}_{\infty},0)$
, rooted at vertex 0, where
$(\mathbb{G}_{\infty},0)$
, rooted at vertex 0, where
![]() $\mathbb{G}_{\infty}=G(\textbf{Y},\textbf{W},\kappa)$
.
$\mathbb{G}_{\infty}=G(\textbf{Y},\textbf{W},\kappa)$
.
Remark 3. (Regularly varying product forms.) Note that if f(t) and
![]() $\mathbb{P}\left(g(W^{(1)},W^{(2)})>t\right)$
are regularly varying functions of t outside some compact sets, with respective exponents
$\mathbb{P}\left(g(W^{(1)},W^{(2)})>t\right)$
are regularly varying functions of t outside some compact sets, with respective exponents
![]() $\alpha_p>0$
and
$\alpha_p>0$
and
![]() $\beta_p>0$
with
$\beta_p>0$
with
![]() $\min\{\alpha_p,\alpha_p\beta_p\}>d$
, then by Potter’s theorem (see [Reference Potter30]), they respectively satisfy Assumptions 4(1) and 4(2) with some exponents
$\min\{\alpha_p,\alpha_p\beta_p\}>d$
, then by Potter’s theorem (see [Reference Potter30]), they respectively satisfy Assumptions 4(1) and 4(2) with some exponents
![]() $\overline{\alpha_p}>0$
and
$\overline{\alpha_p}>0$
and
![]() $\overline{\beta_p}>0$
, with
$\overline{\beta_p}>0$
, with
![]() $\min\{\overline{\alpha_p},\overline{\alpha_p}\overline{\beta_p}\}>d$
. Hence for these kinds of connection functions, Lemma 1, and hence Corollary 1, continue to be true.
$\min\{\overline{\alpha_p},\overline{\alpha_p}\overline{\beta_p}\}>d$
. Hence for these kinds of connection functions, Lemma 1, and hence Corollary 1, continue to be true.
Remark 4. (Dominance by PSIRG connections.) Note that even if
![]() $\kappa$
is not of product form, but instead is dominated by
$\kappa$
is not of product form, but instead is dominated by
![]() $1 \wedge f(t)g(x,y)$
, with f and g respectively satisfying Assumptions 4(1) and 4(2), with
$1 \wedge f(t)g(x,y)$
, with f and g respectively satisfying Assumptions 4(1) and 4(2), with
![]() $\gamma_p>d$
, then Lemma 1, and hence Corollary 1, continue to be true.
$\gamma_p>d$
, then Lemma 1, and hence Corollary 1, continue to be true.
Next we discuss several known models which are all examples of PSIRGs, or of SIRGs with connection functions dominated by PSIRG connection functions. The results that follow are presented as corollaries of Theorem 2, and their proofs are in Section 3.7.
2.1.2. Geometric inhomogeneous random graphs.
Geometric inhomogeneous random graphs (GIRGs) [Reference Bringmann, Keusch and Lengler6–Reference Bringmann, Keusch and Lengler8] were motivated as spatial versions of the classic Chung–Lu random graphs [Reference Chung and Lu9, Reference Chung and Lu10]. Although Chung–Lu random graphs with suitable parameters are scale-free and exhibit small-world properties, they fail to capture clustering, a ubiquitous property of real-world networks.
GIRGs have four parameters: the number of vertices n,
![]() $\alpha_G \in (1,\infty]$
,
$\alpha_G \in (1,\infty]$
,
![]() $\beta_G>2$
, and the dimension
$\beta_G>2$
, and the dimension
![]() $d\geq 1$
. To each vertex
$d\geq 1$
. To each vertex
![]() $i \in \mathbb{N}$
, one associates an independent, uniformly distributed random location
$i \in \mathbb{N}$
, one associates an independent, uniformly distributed random location
![]() $X^{(n)}_i$
on I (recall (3)) and a real weight
$X^{(n)}_i$
on I (recall (3)) and a real weight
![]() $W^{(n)}_i$
(possibly random) such that (4) holds. Here the limiting weight variable W has a power-law tail with exponent
$W^{(n)}_i$
(possibly random) such that (4) holds. Here the limiting weight variable W has a power-law tail with exponent
![]() $\beta_G$
: there exists
$\beta_G$
: there exists
![]() $t_G \in \mathbb{R}_+$
such that
$t_G \in \mathbb{R}_+$
such that
whenever
![]() $z > t_G$
, for some absolute constants
$z > t_G$
, for some absolute constants
![]() $c_G, C_G>0$
. In particular, we have
$c_G, C_G>0$
. In particular, we have
![]() $\mathbb{E}\left[W\right]< \infty$
. Conditionally on
$\mathbb{E}\left[W\right]< \infty$
. Conditionally on
![]() $(X^{(n)}_i)_{i \in [n]}$
and
$(X^{(n)}_i)_{i \in [n]}$
and
![]() $(W^{(n)}_i)_{i \in [n]}$
, each edge
$(W^{(n)}_i)_{i \in [n]}$
, each edge
![]() $\{i,j\}$
is included independently with probability
$\{i,j\}$
is included independently with probability
![]() $p_{i,j}$
given by
$p_{i,j}$
given by
 \begin{equation} \begin{split} p_{i,j}= \begin{cases} 1 \wedge \left(\frac{W^{(n)}_iW^{(n)}_j}{\sum_{i\in[n]} W^{(n)}_i}\right)^{\alpha_G}\frac{1}{\|X^{(n)}_i-X^{(n)}_j\|^{d\alpha_G}} &\text{if}\; 1<\alpha_G<\infty, \\ \mathbb{1}_{\left\{\left(\frac{W^{(n)}_iW^{(n)}_j}{\sum_{i\in[n]} W^{(n)}_i}\right)^{1/d}>\|X^{(n)}_i-X^{(n)}_j\|\right\}} & \text{if}\; \alpha_G = \infty. \end{cases} \end{split} \end{equation}
\begin{equation} \begin{split} p_{i,j}= \begin{cases} 1 \wedge \left(\frac{W^{(n)}_iW^{(n)}_j}{\sum_{i\in[n]} W^{(n)}_i}\right)^{\alpha_G}\frac{1}{\|X^{(n)}_i-X^{(n)}_j\|^{d\alpha_G}} &\text{if}\; 1<\alpha_G<\infty, \\ \mathbb{1}_{\left\{\left(\frac{W^{(n)}_iW^{(n)}_j}{\sum_{i\in[n]} W^{(n)}_i}\right)^{1/d}>\|X^{(n)}_i-X^{(n)}_j\|\right\}} & \text{if}\; \alpha_G = \infty. \end{cases} \end{split} \end{equation}
We denote the resulting random graph by
Remark 5. (Relationship to GIRGs in [Reference Bringmann, Keusch and Lengler8].) Our formulation of GIRGs is closer to the formulation adopted in [Reference Komjáthy and Lodewijks24] than to that of [Reference Bringmann, Keusch and Lengler8]. In the original definition of GIRGs (see [Reference Bringmann, Keusch and Lengler8]), the connection function is only assumed to be bounded above and below by multiples of (13), and vertex locations are assumed to be uniform on the torus
![]() $\mathbb{T}_n$
which is obtained by identifying the boundaries of I. However, to define a local limit, we need the connection function to converge to a limiting function, for which we have taken the explicit form (13). Finally, using the observation that only a negligible proportion of vertex locations fall near the boundary of I, our results can easily be transferred to the torus setting.
$\mathbb{T}_n$
which is obtained by identifying the boundaries of I. However, to define a local limit, we need the connection function to converge to a limiting function, for which we have taken the explicit form (13). Finally, using the observation that only a negligible proportion of vertex locations fall near the boundary of I, our results can easily be transferred to the torus setting.
Now consider the infinite SIRG
![]() $G(\textbf{Y},\textbf{W},\kappa^{\alpha_G})$
, where
$G(\textbf{Y},\textbf{W},\kappa^{\alpha_G})$
, where
![]() $\textbf{Y}=(Y_i)_{i \in \mathbb{N}\cup \{0\}}$
is the sequence of atoms of
$\textbf{Y}=(Y_i)_{i \in \mathbb{N}\cup \{0\}}$
is the sequence of atoms of
![]() $\Gamma \cup \{\textbf{0}\}$
(with
$\Gamma \cup \{\textbf{0}\}$
(with
![]() $Y_0=\textbf{0}$
),
$Y_0=\textbf{0}$
),
![]() $\Gamma$
is a unit-rate homogeneous Poisson point process on
$\Gamma$
is a unit-rate homogeneous Poisson point process on
![]() $\mathbb{R}^d$
,
$\mathbb{R}^d$
,
![]() $\textbf{W}=(W_i)_{i \in \mathbb{N}\cup \{0\}}$
is an i.i.d. collection of limiting weight random variables W, and
$\textbf{W}=(W_i)_{i \in \mathbb{N}\cup \{0\}}$
is an i.i.d. collection of limiting weight random variables W, and
![]() $\kappa^{(\alpha_G)}$
is the connection function
$\kappa^{(\alpha_G)}$
is the connection function
 \begin{equation} \begin{split} \kappa^{(\alpha_G)}(t,x,y)= \begin{cases} 1 \wedge \left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{\alpha_G}{t^{-d\alpha_G}} &\text{if}\; 1<\alpha_G<\infty, \\ \mathbb{1}_{\left\{\left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{1/d}>t\right\}} & \text{if}\; \alpha_G = \infty. \end{cases} \end{split} \end{equation}
\begin{equation} \begin{split} \kappa^{(\alpha_G)}(t,x,y)= \begin{cases} 1 \wedge \left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{\alpha_G}{t^{-d\alpha_G}} &\text{if}\; 1<\alpha_G<\infty, \\ \mathbb{1}_{\left\{\left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{1/d}>t\right\}} & \text{if}\; \alpha_G = \infty. \end{cases} \end{split} \end{equation}
As a corollary to Theorem 2, we establish the local limit of the GIRG sequence to be
![]() $(G(\textbf{Y},\textbf{W},\kappa^{\alpha_G}),0)$
. This answers a question posed in [Reference Komjáthy and Lodewijks24] (see [Reference Komjáthy and Lodewijks24, Section 2.1]) in the affirmative. We call the above infinite SIRG the infinite GIRG, and denote it by
$(G(\textbf{Y},\textbf{W},\kappa^{\alpha_G}),0)$
. This answers a question posed in [Reference Komjáthy and Lodewijks24] (see [Reference Komjáthy and Lodewijks24, Section 2.1]) in the affirmative. We call the above infinite SIRG the infinite GIRG, and denote it by
![]() $\textrm{GIRG}_{\infty,\alpha_G,\beta_G,d}$
.
$\textrm{GIRG}_{\infty,\alpha_G,\beta_G,d}$
.
Corollary 2. (Convergence of GIRGs locally in probability.) As
![]() $n\rightarrow \infty$
, the sequence
$n\rightarrow \infty$
, the sequence
![]() $(\textrm{GIRG}_{n,\alpha_G,\beta_G,d})_{n \geq 1}$
converges locally in probability to the rooted infinite GIRG
$(\textrm{GIRG}_{n,\alpha_G,\beta_G,d})_{n \geq 1}$
converges locally in probability to the rooted infinite GIRG
![]() $(\textrm{GIRG}_{\infty,\alpha_G,\beta_G,d},0)$
, rooted at 0, where
$(\textrm{GIRG}_{\infty,\alpha_G,\beta_G,d},0)$
, rooted at 0, where
![]() $\alpha_G \in (1,\infty]$
,
$\alpha_G \in (1,\infty]$
,
![]() $\beta_G > 2$
,
$\beta_G > 2$
,
![]() $d \in \mathbb{N}$
.
$d \in \mathbb{N}$
.
2.1.3. Hyperbolic random graphs.
Hyperbolic random graphs (HRGs) were first proposed by Krioukov et al. in 2010 [Reference Krioukov25], as a model that captures the three main properties of most real-world networks: scale-free, small distances, and non-vanishing clustering coefficient.
HRGs have three parameters, namely the number of vertices n,
![]() $\alpha_H>\frac{1}{2}$
, and
$\alpha_H>\frac{1}{2}$
, and
![]() $\nu>0$
, which are fixed constants. Let
$\nu>0$
, which are fixed constants. Let
The vertex set of the graph is the set of n i.i.d. points
![]() $u^{(n)}_1,\ldots,u^{(n)}_n$
on the hyperbolic plane
$u^{(n)}_1,\ldots,u^{(n)}_n$
on the hyperbolic plane
![]() $\mathbb{H}$
, where
$\mathbb{H}$
, where
![]() $u^{(n)}_i=(r^{(n)}_i,\theta^{(n)}_i)$
is the polar representation of
$u^{(n)}_i=(r^{(n)}_i,\theta^{(n)}_i)$
is the polar representation of
![]() $u^{(n)}_i$
. The angular component vector
$u^{(n)}_i$
. The angular component vector
![]() $(\theta^{(n)}_i)_{i=1}^n$
is a vector with i.i.d. coordinates, each coordinate having the uniform distribution on
$(\theta^{(n)}_i)_{i=1}^n$
is a vector with i.i.d. coordinates, each coordinate having the uniform distribution on
![]() $[-\pi,\pi]$
. The radial component vector
$[-\pi,\pi]$
. The radial component vector
![]() $(r^{(n)}_i)_{i=1}^n$
is independent of
$(r^{(n)}_i)_{i=1}^n$
is independent of
![]() $(\theta_i)_{i=1}^n$
and has i.i.d. coordinates, with cumulative distribution function
$(\theta_i)_{i=1}^n$
and has i.i.d. coordinates, with cumulative distribution function
 \begin{equation} F^{(n)}_{\alpha_H,\nu}(r)= \begin{cases} 0 &\text{if}\;\;r<0, \\ \dfrac{\cosh{\alpha_H r-1}}{\cosh{\alpha_H R_n -1}} &\text{if}\;\;0\leq r \leq R_n, \\ 1 & \text{if}\;\; r> R_n. \end{cases} \end{equation}
\begin{equation} F^{(n)}_{\alpha_H,\nu}(r)= \begin{cases} 0 &\text{if}\;\;r<0, \\ \dfrac{\cosh{\alpha_H r-1}}{\cosh{\alpha_H R_n -1}} &\text{if}\;\;0\leq r \leq R_n, \\ 1 & \text{if}\;\; r> R_n. \end{cases} \end{equation}
Given
![]() $(u^{(n)}_i)_{i=1}^n=((r^{(n)}_i,\theta^{(n)}_i))_{i=1}^n$
, one forms the threshold HRG (THRG) by placing edges between all pairs of vertices
$(u^{(n)}_i)_{i=1}^n=((r^{(n)}_i,\theta^{(n)}_i))_{i=1}^n$
, one forms the threshold HRG (THRG) by placing edges between all pairs of vertices
![]() $u^{(n)}_i$
and
$u^{(n)}_i$
and
![]() $u^{(n)}_j$
with conditional probability
$u^{(n)}_j$
with conditional probability
where
![]() $d_{\mathbb{H}}$
denotes the distance in the hyperbolic plane
$d_{\mathbb{H}}$
denotes the distance in the hyperbolic plane
![]() $\mathbb{H}$
; i.e., the edge between
$\mathbb{H}$
; i.e., the edge between
![]() $u^{(n)}_i$
and
$u^{(n)}_i$
and
![]() $u^{(n)}_j$
is included if and only if
$u^{(n)}_j$
is included if and only if
![]() $d_{\mathbb{H}}\big(u^{(n)}_i,u^{(n)}_j\big)<R_n$
.
$d_{\mathbb{H}}\big(u^{(n)}_i,u^{(n)}_j\big)<R_n$
.
Similarly, one forms a parametrized version of the THRG (see [Reference Krioukov25, Section 6]), which we call the parametrized HRG (PHRG), by placing edges independently between
![]() $u^{(n)}_i$
and
$u^{(n)}_i$
and
![]() $u^{(n)}_j$
with conditional probability
$u^{(n)}_j$
with conditional probability
 \begin{align} {p^{(n)}_{\textrm{PHRG}}\big(u^{(n)}_i,u^{(n)}_j\big)}\,{:\!=}\,\left(1 + \exp{\left(\frac{d_{\mathbb{H}}\big(u^{(n)}_i,u^{(n)}_j\big)-R_n}{2T_H}\right)}\right)^{-1}, \end{align}
\begin{align} {p^{(n)}_{\textrm{PHRG}}\big(u^{(n)}_i,u^{(n)}_j\big)}\,{:\!=}\,\left(1 + \exp{\left(\frac{d_{\mathbb{H}}\big(u^{(n)}_i,u^{(n)}_j\big)-R_n}{2T_H}\right)}\right)^{-1}, \end{align}
where
![]() $T_H>0$
is another parameter.
$T_H>0$
is another parameter.
We denote the THRG model with parameters n,
![]() $\alpha_H$
,
$\alpha_H$
,
![]() $\nu$
by
$\nu$
by
![]() $\textrm{THRG}_{n,\alpha_H,\nu},$
and the PHRG model with parameters
$\textrm{THRG}_{n,\alpha_H,\nu},$
and the PHRG model with parameters
![]() $n,\alpha_H,T_H,\nu$
by
$n,\alpha_H,T_H,\nu$
by
![]() $\textrm{PHRG}_{n,\alpha_H,T_H,\nu}.$
$\textrm{PHRG}_{n,\alpha_H,T_H,\nu}.$
Both the THRG and PHRG models can be seen as finite SIRGs, which gives us the local limits for these models, as a corollary to Theorem 2.
Corollary 3. (Convergence of HRGs locally in probability.) Let
![]() $\alpha_H> {\tfrac{1}{2}}$
,
$\alpha_H> {\tfrac{1}{2}}$
,
![]() $0<T_H<1$
, and
$0<T_H<1$
, and
![]() $n \in \mathbb{N}$
. Let
$n \in \mathbb{N}$
. Let
![]() $\textbf{Y}$
be the sequence of atoms of (10). Then there exists a random variable W having a power-law distribution with exponent
$\textbf{Y}$
be the sequence of atoms of (10). Then there exists a random variable W having a power-law distribution with exponent
![]() $2\alpha_H+1$
, such that if
$2\alpha_H+1$
, such that if
![]() $\textbf{W}=(W_i)_{i \in \mathbb{N}\cup\{0\}}$
is a sequence of i.i.d. copies of W, the following hold:
$\textbf{W}=(W_i)_{i \in \mathbb{N}\cup\{0\}}$
is a sequence of i.i.d. copies of W, the following hold:
-
(a) The sequence
 $(\textrm{THRG}_{n,\alpha_H,\nu})_{n \geq 1}$
converges locally in probability to the infinite SIRG
$(\textrm{THRG}_{n,\alpha_H,\nu})_{n \geq 1}$
converges locally in probability to the infinite SIRG
 $G(\textbf{Y},\textbf{W},\kappa_{\textrm{THRG},\infty})$
, where
$G(\textbf{Y},\textbf{W},\kappa_{\textrm{THRG},\infty})$
, where \begin{align*} \kappa_{\textrm{THRG},\infty}(t,x,y)\,{:\!=}\, \mathbb{1}_{\left\{t \leq \frac{\nu xy}{\pi}\right\}}. \end{align*}
\begin{align*} \kappa_{\textrm{THRG},\infty}(t,x,y)\,{:\!=}\, \mathbb{1}_{\left\{t \leq \frac{\nu xy}{\pi}\right\}}. \end{align*}
-
(b) The sequence
 $(\textrm{PHRG}_{n,\alpha_H,T_H,\nu})_{n \geq 1}$
converges locally in probability to the infinite SIRG
$(\textrm{PHRG}_{n,\alpha_H,T_H,\nu})_{n \geq 1}$
converges locally in probability to the infinite SIRG
 $G(\textbf{Y},\textbf{W},\kappa_{\textrm{PHRG},\infty})$
, where
$G(\textbf{Y},\textbf{W},\kappa_{\textrm{PHRG},\infty})$
, where
 \begin{align*} \kappa_{\textrm{PHRG},\infty}(t,x,y)\,{:\!=}\, \left(1+\left(\frac{ \pi t}{\nu xy} \right)^{1/T_H} \right)^{-1}. \end{align*}
\begin{align*} \kappa_{\textrm{PHRG},\infty}(t,x,y)\,{:\!=}\, \left(1+\left(\frac{ \pi t}{\nu xy} \right)^{1/T_H} \right)^{-1}. \end{align*}
2.1.4. Continuum scale-free percolation.
The continuum scale-free percolation (CSFP) model [Reference Deprez and Wüthrich13] was introduced as a continuum analogue of the discrete scale-free percolation (SFP) model [Reference Deijfen, van der Hofstad and Hooghiemstra12], a model that captures power-law degree distributions while preserving non-zero clustering and logarithmic typical distances.
We now formally define the model following [Reference Deprez and Wüthrich13]. The vertex set is the set of points of a homogeneous Poisson point process
![]() $(Y_i)_{i \in \mathbb{N}}$
, marked with i.i.d. weights
$(Y_i)_{i \in \mathbb{N}}$
, marked with i.i.d. weights
![]() $(W_i)_{i \in \mathbb{N}}$
which have a Pareto distribution with power-law tail parameter
$(W_i)_{i \in \mathbb{N}}$
which have a Pareto distribution with power-law tail parameter
![]() $\beta>0$
and scale parameter 1:
$\beta>0$
and scale parameter 1:
whenever
![]() $w>1$
. Conditionally on
$w>1$
. Conditionally on
![]() $(Y_i)_{i \in \mathbb{N}}$
and
$(Y_i)_{i \in \mathbb{N}}$
and
![]() $(W_i)_{i \in \mathbb{N}}$
, each edge
$(W_i)_{i \in \mathbb{N}}$
, each edge
![]() $\{Y_i,Y_j\}$
is included independently with probability
$\{Y_i,Y_j\}$
is included independently with probability
where
![]() $\lambda>0$
is a parameter. Here we remark that in the original definition in [Reference Deprez and Wüthrich13], instead of a homogeneous Poisson process
$\lambda>0$
is a parameter. Here we remark that in the original definition in [Reference Deprez and Wüthrich13], instead of a homogeneous Poisson process
![]() $(Y_i)_{i \in \mathbb{N}}$
, a Poisson process with some constant intensity
$(Y_i)_{i \in \mathbb{N}}$
, a Poisson process with some constant intensity
![]() $\nu>0$
was considered. By standard scaling arguments, this does not make any difference in our results.
$\nu>0$
was considered. By standard scaling arguments, this does not make any difference in our results.
Considering the Palm version
![]() $(Y_i)_{i \in \mathbb{N}\cup \{0\}}$
of
$(Y_i)_{i \in \mathbb{N}\cup \{0\}}$
of
![]() $(Y_i)_{i \in \mathbb{N}}$
, where
$(Y_i)_{i \in \mathbb{N}}$
, where
![]() $Y_0=\textbf{0} \in \mathbb{R}^d$
, marking
$Y_0=\textbf{0} \in \mathbb{R}^d$
, marking
![]() $Y_0$
with an independent weight
$Y_0$
with an independent weight
![]() $W_0$
, and rooting the resulting graph at 0, it is immediate that the resulting rooted infinite CSFP model is the rooted SIRG
$W_0$
, and rooting the resulting graph at 0, it is immediate that the resulting rooted infinite CSFP model is the rooted SIRG
![]() $(G(\textbf{Y},\textbf{W},\kappa),0)$
, where
$(G(\textbf{Y},\textbf{W},\kappa),0)$
, where
![]() $\textbf{Y}=(Y_i)_{i \in \mathbb{N}\cup \{0\}}$
,
$\textbf{Y}=(Y_i)_{i \in \mathbb{N}\cup \{0\}}$
,
![]() $\textbf{W}=(W_i)_{i \in \mathbb{N}\cup\{0\}}$
, and
$\textbf{W}=(W_i)_{i \in \mathbb{N}\cup\{0\}}$
, and
![]() $\kappa(t,x,y)\,{:\!=}\,1-\exp{\left(-\frac{\lambda xy}{t^{\alpha}}\right)} $
.
$\kappa(t,x,y)\,{:\!=}\,1-\exp{\left(-\frac{\lambda xy}{t^{\alpha}}\right)} $
.
For each
![]() $n \geq 1$
, let
$n \geq 1$
, let
![]() $\textbf{X}^{(n)}=(X^{(n)}_i)_{i \in [n]}$
satisfy Assumption 1, and consider the ‘blown-up’ finite CSFP model
$\textbf{X}^{(n)}=(X^{(n)}_i)_{i \in [n]}$
satisfy Assumption 1, and consider the ‘blown-up’ finite CSFP model
![]() $G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
, where
$G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
, where
![]() $Y^{(n)}_i=n^{1/d}X^{(n)}_i$
for
$Y^{(n)}_i=n^{1/d}X^{(n)}_i$
for
![]() $i \in [n]$
,
$i \in [n]$
,
![]() $\textbf{W}^{(n)}=(W^{(n)}_i)_{i \in [n]}$
is a vector of i.i.d. weight variables having law (19), and
$\textbf{W}^{(n)}=(W^{(n)}_i)_{i \in [n]}$
is a vector of i.i.d. weight variables having law (19), and
![]() $\kappa_n(t,x,y)=1-\exp{\left(-\frac{\lambda xy}{n^{-\frac{\alpha}{d}}t^{\alpha}}\right)}$
. Then as corollary to Theorem 2, we have that the infinite CSFP is the local limit of finite CSFPs under suitable assumptions.
$\kappa_n(t,x,y)=1-\exp{\left(-\frac{\lambda xy}{n^{-\frac{\alpha}{d}}t^{\alpha}}\right)}$
. Then as corollary to Theorem 2, we have that the infinite CSFP is the local limit of finite CSFPs under suitable assumptions.
Corollary 4. (Convergence of CSFPs locally in probability.) Let
Then, as
![]() $n \to \infty$
, the graph sequence
$n \to \infty$
, the graph sequence
![]() $G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
converges locally in probability to the infinite rooted CSFP
$G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
converges locally in probability to the infinite rooted CSFP
![]() $(G(\textbf{Y},\textbf{W},\kappa),0)$
.
$(G(\textbf{Y},\textbf{W},\kappa),0)$
.
2.1.5. Weight-dependent random connection models.
Another very general class of spatial random graph model, called the weight-dependent random connection model (WDRCM), was first introduced in [Reference Gracar, Heydenreich, Mönch and Mörters18], motivated by the study of recurrence and transience properties of general geometric graphs, which we briefly discuss.
To construct the graph, one takes a unit-rate Poisson process on
![]() $\mathbb{R}^d \times[0,1]$
, conditionally on which edges between pairs of vertices
$\mathbb{R}^d \times[0,1]$
, conditionally on which edges between pairs of vertices
![]() $(\textbf{x},s)$
and
$(\textbf{x},s)$
and
![]() $(\textbf{y},t)$
are placed independently with probability
$(\textbf{y},t)$
are placed independently with probability
for some profile function
![]() $\rho\,{:}\,\mathbb{R}_+ \to [0,1]$
and a suitable kernel
$\rho\,{:}\,\mathbb{R}_+ \to [0,1]$
and a suitable kernel
![]() $h\,{:}\,[0,1]\times[0,1]\times \mathbb{R}_+ \to \mathbb{R}_+$
. The vertex
$h\,{:}\,[0,1]\times[0,1]\times \mathbb{R}_+ \to \mathbb{R}_+$
. The vertex
![]() $(\textbf{x},s)$
is thought of as being located at
$(\textbf{x},s)$
is thought of as being located at
![]() $\textbf{x} \in \mathbb{R}^d$
, and having a weight of
$\textbf{x} \in \mathbb{R}^d$
, and having a weight of
![]() $s^{-1}$
associated to it.
$s^{-1}$
associated to it.
Including the point
![]() $\textbf{r}=(\textbf{0},U) \in \mathbb{R}^d \times [0,1]$
, where U is uniformly distributed on [0, 1] and independent of the weights and locations of other vertices, and rooting the graph at
$\textbf{r}=(\textbf{0},U) \in \mathbb{R}^d \times [0,1]$
, where U is uniformly distributed on [0, 1] and independent of the weights and locations of other vertices, and rooting the graph at
![]() $\textbf{r}$
, we obtain the infinite rooted SIRG
$\textbf{r}$
, we obtain the infinite rooted SIRG
![]() $(G(\textbf{Y},\textbf{W},\kappa),0)$
, where
$(G(\textbf{Y},\textbf{W},\kappa),0)$
, where
![]() $\textbf{Y}=(Y_i)_{i \in \mathbb{N}\cup \{0\}}$
are the atoms of (10),
$\textbf{Y}=(Y_i)_{i \in \mathbb{N}\cup \{0\}}$
are the atoms of (10),
![]() $\textbf{W}=(W_i)_{i \in \mathbb{N}\cup\{0\}}$
is a sequence of i.i.d. random weights that are uniform on [0, 1], and
$\textbf{W}=(W_i)_{i \in \mathbb{N}\cup\{0\}}$
is a sequence of i.i.d. random weights that are uniform on [0, 1], and
![]() $\kappa = \rho \circ h$
.
$\kappa = \rho \circ h$
.
For
![]() $n \geq 1$
, let
$n \geq 1$
, let
![]() $(X^{(n)}_i)_{i \in [n]}$
satisfy Assumption 1, let
$(X^{(n)}_i)_{i \in [n]}$
satisfy Assumption 1, let
![]() $(W^{(n)}_i)_{i \in [n]}$
be a collection of n i.i.d. weights that are uniform on [0, 1], and let
$(W^{(n)}_i)_{i \in [n]}$
be a collection of n i.i.d. weights that are uniform on [0, 1], and let
![]() $\kappa_n:\mathbb{R}\times \mathbb{R} \times \mathbb{R}_+ \to [0,1]$
be defined as
$\kappa_n:\mathbb{R}\times \mathbb{R} \times \mathbb{R}_+ \to [0,1]$
be defined as
![]() $\kappa_n(t,x,y)=\rho(h(x,y,n^{-1/d}t))$
, with
$\kappa_n(t,x,y)=\rho(h(x,y,n^{-1/d}t))$
, with
![]() $\kappa(t,x,y)=\rho(g(x,y,t))$
satisfying Assumption 3(2). Then as a direct consequence of Theorem 2 we have the following corollary, whose proof we omit.
$\kappa(t,x,y)=\rho(g(x,y,t))$
satisfying Assumption 3(2). Then as a direct consequence of Theorem 2 we have the following corollary, whose proof we omit.
Corollary 5. (Convergence of WDRCMs locally in probability.) Let
![]() $\textbf{Y}^{(n)}=(Y^{(n)}_i)_{i \in [n]}=(n^{1/d}X^{(n)}_i)_{i \in [n]}$
. Then, as
$\textbf{Y}^{(n)}=(Y^{(n)}_i)_{i \in [n]}=(n^{1/d}X^{(n)}_i)_{i \in [n]}$
. Then, as
![]() $n \to \infty$
, the sequence of SIRGS
$n \to \infty$
, the sequence of SIRGS
![]() $G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
converges locally in probability to the infinite rooted WDRCM
$G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
converges locally in probability to the infinite rooted WDRCM
![]() $(G(\textbf{Y},\textbf{W},\kappa),0)$
.
$(G(\textbf{Y},\textbf{W},\kappa),0)$
.
2.2. Consequences of local convergence: degrees
Theorem 2 is equivalent to the statement that for any subset
![]() $A \subset \mathcal{G}_{\star}$
,
$A \subset \mathcal{G}_{\star}$
,
converges in probability to
![]() $\mathbb{P}\left((\mathbb{G}_{\infty},0)\in A\right)$
(see e.g. [Reference Van der Hofstad22, (2.3.5)]).
$\mathbb{P}\left((\mathbb{G}_{\infty},0)\in A\right)$
(see e.g. [Reference Van der Hofstad22, (2.3.5)]).
In particular, for fixed
![]() $k\in \mathbb{N}$
, one can take
$k\in \mathbb{N}$
, one can take
![]() $A_k$
to be the subset of those rooted graphs (G, o) for which the root o has degree k in G, to conclude that
$A_k$
to be the subset of those rooted graphs (G, o) for which the root o has degree k in G, to conclude that
where
![]() $N_k(\mathbb{G}_n)$
is the number of vertices with degree k in
$N_k(\mathbb{G}_n)$
is the number of vertices with degree k in
![]() $\mathbb{G}_n$
, and where D is the degree of 0 in
$\mathbb{G}_n$
, and where D is the degree of 0 in
![]() $\mathbb{G}_{\infty}$
.
$\mathbb{G}_{\infty}$
.
Taking expectation and applying dominated convergence, we have that for any
![]() $ {k} \in \mathbb{N}$
,
$ {k} \in \mathbb{N}$
,
![]() $\mathbb{P}\left(D_n=k\right)\to \mathbb{P}\left(D=k\right)$
as
$\mathbb{P}\left(D_n=k\right)\to \mathbb{P}\left(D=k\right)$
as
![]() $n \to \infty$
, where
$n \to \infty$
, where
![]() $D_n$
is the degree of
$D_n$
is the degree of
![]() $U_n$
in
$U_n$
in
![]() $\mathbb{G}_n$
, which implies
$\mathbb{G}_n$
, which implies
(where
![]() ${{\stackrel{d}{\rightarrow}}}$
means convergence in distribution) as
${{\stackrel{d}{\rightarrow}}}$
means convergence in distribution) as
![]() $n \to \infty$
. We next give a description of the random variable D. For this, let
$n \to \infty$
. We next give a description of the random variable D. For this, let
![]() $W_0$
be the weight of 0 in
$W_0$
be the weight of 0 in
![]() $\mathbb{G}_{\infty}$
, and let
$\mathbb{G}_{\infty}$
, and let
![]() $W^{(1)}$
be an independent copy of
$W^{(1)}$
be an independent copy of
![]() $W_0$
.
$W_0$
.
Proposition 1. (Degree distribution.) Under the assumptions of Theorem 1, the random variable D is distributed as
i.e. it has a mixed Poisson distribution with mixing parameter
Note that Proposition 1, Assumption 3(3), and Fubini’s theorem imply that
which is finite. Since the expectation of the mixing parameter is finite, the mixing parameter is finite almost surely, and hence Proposition 1 makes sense.
In particular, when the mixing parameter
![]() $\int_{\mathbb{R}^d} \mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(1)})\right | W_0\right]dz$
is regularly varying with some exponent
$\int_{\mathbb{R}^d} \mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(1)})\right | W_0\right]dz$
is regularly varying with some exponent
![]() $\zeta>0$
, the random variable D is also regularly varying with the same exponent
$\zeta>0$
, the random variable D is also regularly varying with the same exponent
![]() $\zeta>0$
. This allows for the existence of power-law degree distributions in spatial random graphs.
$\zeta>0$
. This allows for the existence of power-law degree distributions in spatial random graphs.
Recall that
![]() $D_n$
is the degree of the uniform vertex
$D_n$
is the degree of the uniform vertex
![]() $U_n$
in
$U_n$
in
![]() $\mathbb{G}_n$
.
$\mathbb{G}_n$
.
Proposition 2. (Uniform integrability of typical degree sequence.) Under the assumptions of Theorem 1, the sequence
![]() $(D_n)_{n \geq 1}$
is a uniformly integrable sequence of random variables.
$(D_n)_{n \geq 1}$
is a uniformly integrable sequence of random variables.
The proof is given in Section 3.8. This result is of independent interest. Uniform integrability of the typical degree sequence in general does not follow from local convergence, even when the limiting degree distribution has finite mean; see for example [Reference Van der Hofstad22, Exercise 2.14].
Combining Proposition 2 with (20), we note that
as
![]() $n \to \infty$
. Note that one cannot directly conclude this from Theorem 1, because the function
$n \to \infty$
. Note that one cannot directly conclude this from Theorem 1, because the function
![]() $\textrm{D}\,{:}\,\mathcal{G}_{\star}\to \mathbb{R}_+$
defined by
$\textrm{D}\,{:}\,\mathcal{G}_{\star}\to \mathbb{R}_+$
defined by
is continuous, but not necessarily bounded.
2.3. Consequences of local convergence: clustering
In this section, we discuss convergence of various clustering measures of SIRGs.
For any graph
![]() $G=(V(G),E(G))$
, we let
$G=(V(G),E(G))$
, we let
(where
![]() $d_v$
is the degree of v in G) be twice the number of wedges in the graph G, and we let
$d_v$
is the degree of v in G) be twice the number of wedges in the graph G, and we let
be six times the number of triangles in the graph G, where the sums in (21) and (22) are over distinct vertices
![]() $v_1,v_2,v_3 \in V(G)$
.
$v_1,v_2,v_3 \in V(G)$
.
Then the global clustering coefficient
![]() $\textrm{CC}_{G}$
of the graph G is defined as
$\textrm{CC}_{G}$
of the graph G is defined as
We next discuss a local notion of clustering. For
![]() $v \in V(G)$
, define
$v \in V(G)$
, define
 \begin{align*} \textrm{CC}_{G}(v)\,{:\!=}\, \begin{cases} \frac{\Delta_v(G)}{d_v(d_v-1)} &\mbox{if } d_v \ge 2, \\[3pt] 0 &\mbox{otherwise,} \end{cases} \end{align*}
\begin{align*} \textrm{CC}_{G}(v)\,{:\!=}\, \begin{cases} \frac{\Delta_v(G)}{d_v(d_v-1)} &\mbox{if } d_v \ge 2, \\[3pt] 0 &\mbox{otherwise,} \end{cases} \end{align*}
where
is twice the number of triangles in G containing the vertex v, and
![]() $d_v$
, as before, is the degree of v in G. The local clustering coefficient
$d_v$
, as before, is the degree of v in G. The local clustering coefficient
![]() $\overline{\textrm{CC}}_{G}$
of G is then defined as
$\overline{\textrm{CC}}_{G}$
of G is then defined as
Finally, we discuss a notion of clustering contribution from only vertices of a certain degree. For
![]() $k \in \mathbb{N}$
, define the clustering function to be
$k \in \mathbb{N}$
, define the clustering function to be
where
![]() $\textrm{CC}_{G,k}$
is defined as
$\textrm{CC}_{G,k}$
is defined as
 \begin{equation} \textrm{CC}_{G,k}\,{:\!=}\, \begin{cases} \frac{1}{N_k(G)}\sum_{v \in v(G),d_v=k} {\frac{\Delta_v(G)}{k(k-1)}} &\text{if}\;N_k(G)>0,\\ \\[-8pt] 0&\text{otherwise}, \end{cases} \end{equation}
\begin{equation} \textrm{CC}_{G,k}\,{:\!=}\, \begin{cases} \frac{1}{N_k(G)}\sum_{v \in v(G),d_v=k} {\frac{\Delta_v(G)}{k(k-1)}} &\text{if}\;N_k(G)>0,\\ \\[-8pt] 0&\text{otherwise}, \end{cases} \end{equation}
where
![]() $N_k(G)$
is the total number of vertices in G with degree k. Thus,
$N_k(G)$
is the total number of vertices in G with degree k. Thus,
![]() $\textrm{CC}_{G,k}$
measures the proportion of wedges that are triangles, where one of the participant vertices has degree k.
$\textrm{CC}_{G,k}$
measures the proportion of wedges that are triangles, where one of the participant vertices has degree k.
We now present the results on convergence of these various clustering measures for SIRGs.
Corollary 6. (Convergence of clustering coefficients of SIRGs.) Under the assumptions of Theorem 1, as
![]() $n \to \infty$
, the following hold:
$n \to \infty$
, the following hold:
-
1. If
 $\alpha> 2d$
, then
(26)where
$\alpha> 2d$
, then
(26)where \begin{equation} \textrm{CC}_{\mathbb{G}_n} {{\stackrel{\mathbb{P}}{\rightarrow}}} \frac{\mathbb{E}\left[\Delta_0\right]}{\mathbb{E}\left[D(D-1)\right]}, \end{equation}
\begin{equation} \textrm{CC}_{\mathbb{G}_n} {{\stackrel{\mathbb{P}}{\rightarrow}}} \frac{\mathbb{E}\left[\Delta_0\right]}{\mathbb{E}\left[D(D-1)\right]}, \end{equation}
 $\Delta_0\,{:\!=}\,\sum_{i,j \in \mathbb{N}}\mathbb{1}_{\left\{\{0,i\},\{0,j\},\{i,j\}\in E(\mathbb{G}_{\infty})\right\}}$
is twice the number of triangles containing 0 in
$\Delta_0\,{:\!=}\,\sum_{i,j \in \mathbb{N}}\mathbb{1}_{\left\{\{0,i\},\{0,j\},\{i,j\}\in E(\mathbb{G}_{\infty})\right\}}$
is twice the number of triangles containing 0 in
 $\mathbb{G}_{\infty}$
, and D is the degree of 0 in
$\mathbb{G}_{\infty}$
, and D is the degree of 0 in
 $\mathbb{G}_{\infty}$
.
$\mathbb{G}_{\infty}$
.
-
2. We have
(27) \begin{equation} \overline{\textrm{CC}}_{\mathbb{G}_n} {{\stackrel{\mathbb{P}}{\rightarrow}}} \mathbb{E}\left[\frac{\Delta_0}{D(D-1)}\right]. \end{equation}
\begin{equation} \overline{\textrm{CC}}_{\mathbb{G}_n} {{\stackrel{\mathbb{P}}{\rightarrow}}} \mathbb{E}\left[\frac{\Delta_0}{D(D-1)}\right]. \end{equation}
-
3. For any
 $k \in \mathbb{N}$
,(28)
$k \in \mathbb{N}$
,(28) \begin{equation} \textrm{CC}_{G,k} {{\stackrel{\mathbb{P}}{\rightarrow}}} \frac{1}{\binom{k}{2}}\mathbb{E}\left[\left.\Delta_0\right | D=k\right]. \end{equation}
\begin{equation} \textrm{CC}_{G,k} {{\stackrel{\mathbb{P}}{\rightarrow}}} \frac{1}{\binom{k}{2}}\mathbb{E}\left[\left.\Delta_0\right | D=k\right]. \end{equation}
Parts 2 and 3 of Corollary 6 are direct consequences of local convergence (see [Reference Van der Hofstad22, Section 2.4.2]). For Corollary 6(1), we need an additional uniform convergence property of the square of the degree of a uniform vertex, which we prove is implied by the condition
![]() $\alpha>2d$
.
$\alpha>2d$
.
Remark 6. (Condition on
![]() $\alpha$
.) The condition
$\alpha$
.) The condition
![]() $\alpha>2d$
in Corollary 6(1) is not optimal, as will be evident in the proof. Our purpose is not to find the optimal conditions under which the global clustering coefficient converges, but to demonstrate how local convergence of graphs implies convergence of the global clustering coefficient.
$\alpha>2d$
in Corollary 6(1) is not optimal, as will be evident in the proof. Our purpose is not to find the optimal conditions under which the global clustering coefficient converges, but to demonstrate how local convergence of graphs implies convergence of the global clustering coefficient.
Recently, in [Reference Fountoulakis, van der Hoorn, Müller and Schepers15], precise results have been obtained concerning convergence of clustering coefficients and scaling of the clustering function as k grows to infinity for hyperbolic random graphs. Also, it was shown in [Reference Dalmau and Salvi11] that under suitable conditions, the CSFP model has non-zero clustering in the limit.
2.4. Consequences of our local convergence proof: distance lower bound
Finally, we provide a result on typical distances in our graphs. Let
![]() $U_{n,1}$
and
$U_{n,1}$
and
![]() $U_{n,2}$
be two i.i.d. uniformly distributed vertices of
$U_{n,2}$
be two i.i.d. uniformly distributed vertices of
![]() $\mathbb{G}_n$
, so that
$\mathbb{G}_n$
, so that
![]() $d_{\mathbb{G}_n}(U_{n,1},U_{n,2})$
is the graph distance in
$d_{\mathbb{G}_n}(U_{n,1},U_{n,2})$
is the graph distance in
![]() $\mathbb{G}_n$
between
$\mathbb{G}_n$
between
![]() $U_{n,1}$
and
$U_{n,1}$
and
![]() $U_{n,2}$
. Recall that by convention we let
$U_{n,2}$
. Recall that by convention we let
![]() $d_{\mathbb{G}_n}(U_{n,1},U_{n,2})=\infty$
when
$d_{\mathbb{G}_n}(U_{n,1},U_{n,2})=\infty$
when
![]() $U_{n,1}$
and
$U_{n,1}$
and
![]() $U_{n,2}$
are not in the same connected component of
$U_{n,2}$
are not in the same connected component of
![]() $\mathbb{G}_n$
, so that
$\mathbb{G}_n$
, so that
![]() $d_{\mathbb{G}_n}(U_{n,1},U_{n,2})$
is a well-defined random variable.
$d_{\mathbb{G}_n}(U_{n,1},U_{n,2})$
is a well-defined random variable.
Theorem 3. (Lower bound on typical distances.) Under the assumptions of Theorem 1, for any
![]() $C \in \left( 0, \frac{1}{\log(\frac{\alpha}{\alpha-d})}\right)$
,
$C \in \left( 0, \frac{1}{\log(\frac{\alpha}{\alpha-d})}\right)$
,
as
![]() $n \to \infty$
.
$n \to \infty$
.
In fact, we believe that the limit in the above display holds with C replaced by
![]() $\frac{1}{\log(\frac{\alpha}{\alpha-d})}$
, but our method of proof does not allow us to establish this improvement. As we will see, the proof is a direct byproduct of the proof of the local weak limit in Theorem 1. Note that as
$\frac{1}{\log(\frac{\alpha}{\alpha-d})}$
, but our method of proof does not allow us to establish this improvement. As we will see, the proof is a direct byproduct of the proof of the local weak limit in Theorem 1. Note that as
![]() $\alpha$
approaches d, the lower bound in Theorem 3 becomes trivial.
$\alpha$
approaches d, the lower bound in Theorem 3 becomes trivial.
If, instead of a regularly varying domination as in Assumption 3(2), we have that
![]() $\mathbb{E}\left[\kappa(t,W_0,W_1)\right]$
itself is regularly varying in t with exponent
$\mathbb{E}\left[\kappa(t,W_0,W_1)\right]$
itself is regularly varying in t with exponent
![]() $\alpha$
, then it follows from Proposition 1 that the expectation of the limiting degree distribution D is infinite in the regime
$\alpha$
, then it follows from Proposition 1 that the expectation of the limiting degree distribution D is infinite in the regime
![]() $\alpha \in (0,d)$
. We conjecture that the distances are of constant order in this regime.
$\alpha \in (0,d)$
. We conjecture that the distances are of constant order in this regime.
Conjecture 1. (Constant distances for
![]() $\alpha \in (0,d)$
.) Let
$\alpha \in (0,d)$
.) Let
![]() $\mathbb{G}_n=G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
satisfy the assumptions of Theorem 1 except for Assumption 3(2), instead of which we assume that the limiting connection function
$\mathbb{G}_n=G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
satisfy the assumptions of Theorem 1 except for Assumption 3(2), instead of which we assume that the limiting connection function
![]() $\kappa$
is such that
$\kappa$
is such that
![]() $\mathbb{E}\left[\kappa(t,W_0,W_1)\right]$
is regularly varying with exponent
$\mathbb{E}\left[\kappa(t,W_0,W_1)\right]$
is regularly varying with exponent
![]() $\alpha \in (0,d)$
. Then if
$\alpha \in (0,d)$
. Then if
![]() $U_{n,1}$
and
$U_{n,1}$
and
![]() $U_{n,2}$
are two uniformly chosen vertices in the SIRG
$U_{n,2}$
are two uniformly chosen vertices in the SIRG
![]() $\mathbb{G}_n=G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
, conditionally on the event that
$\mathbb{G}_n=G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
, conditionally on the event that
![]() $U_{n,1}$
and
$U_{n,1}$
and
![]() $U_{n,2}$
are connected in
$U_{n,2}$
are connected in
![]() $\mathbb{G}_n$
,
$\mathbb{G}_n$
,
as
![]() $n \to \infty$
, where
$n \to \infty$
, where
![]() $K(\alpha,d)$
is a constant depending only on the exponent
$K(\alpha,d)$
is a constant depending only on the exponent
![]() $\alpha$
and dimension d.
$\alpha$
and dimension d.
For the case
![]() $\alpha=d$
, we do not expect universal behavior, and the question then becomes model-dependent. Results for constant distances when the limiting degree distribution has infinite mean are known for lattice models such as long-range percolation (see [Reference Benjamini, Kesten, Peres and Schramm3, Example 6.1]), for scale-free percolation (see [Reference Heydenreich, Hulshof and Jorritsma19, Theorem 2.1]), and for the configuration model [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski14], which is a model without geometry.
$\alpha=d$
, we do not expect universal behavior, and the question then becomes model-dependent. Results for constant distances when the limiting degree distribution has infinite mean are known for lattice models such as long-range percolation (see [Reference Benjamini, Kesten, Peres and Schramm3, Example 6.1]), for scale-free percolation (see [Reference Heydenreich, Hulshof and Jorritsma19, Theorem 2.1]), and for the configuration model [Reference Van den Esker, van der Hofstad, Hooghiemstra and Znamenski14], which is a model without geometry.
Theorem 3 poses the following question: when are the typical distances exactly doubly logarithmic? Interestingly, distances can be larger than doubly logarithmic, even when the limiting degree distribution has infinite second moment,
![]() $\mathbb{E}\left[D^2\right]=\infty$
, as was shown in [Reference Gracar, Grauer and Mörters17]; see for example [Reference Gracar, Grauer and Mörters17, Theorem 1.1(a)]. We conjecture that if certain lower-order moments below a (model-dependent) critical threshold are infinite, this implies ultra-small distances. This is also the behavior that the authors of [Reference Gracar, Grauer and Mörters17] observe, for a special class of models, but we believe this behavior is universal.
$\mathbb{E}\left[D^2\right]=\infty$
, as was shown in [Reference Gracar, Grauer and Mörters17]; see for example [Reference Gracar, Grauer and Mörters17, Theorem 1.1(a)]. We conjecture that if certain lower-order moments below a (model-dependent) critical threshold are infinite, this implies ultra-small distances. This is also the behavior that the authors of [Reference Gracar, Grauer and Mörters17] observe, for a special class of models, but we believe this behavior is universal.
Conjecture 2. (Ultra-small distances.) Under the assumptions of Theorem 3, there is a constant
![]() $\varepsilon_{\ast} \in (0,1)$
, depending on the model parameters, such that for any
$\varepsilon_{\ast} \in (0,1)$
, depending on the model parameters, such that for any
![]() $\varepsilon>\varepsilon_{\ast}$
,
$\varepsilon>\varepsilon_{\ast}$
,
![]() $\mathbb{E}\left[D^{2-\varepsilon}\right]=\infty$
implies that there is a constant
$\mathbb{E}\left[D^{2-\varepsilon}\right]=\infty$
implies that there is a constant
![]() $C(\alpha,d)>0$
such that
$C(\alpha,d)>0$
such that
as
![]() $n \to \infty$
.
$n \to \infty$
.
3. Proofs
In this section we give all the proofs. We start, in Section 3.1, by defining the notation that we use throughout this section, and by outlining the general proof strategy for our main results, Theorems 1 and 2. Sections 3.2 and 3.3 contain proofs of some of the key tools that we employ to prove our main results. The proofs of Theorems 1 and 2 can be found in Sections 3.4 and 3.5 respectively. The proof of Theorem 3 can be found in Section 3.6. Proofs of results on examples covered under our set-up are in Section 3.7. Proofs of degree and clustering results can be found respectively in Sections 3.8 and 3.9.
3.1. Notation and general proof strategy for Theorems 1 and 2
Recall the SIRGs
![]() $\mathbb{G}_n=G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
and
$\mathbb{G}_n=G(\textbf{Y}^{(n)},\textbf{W}^{(n)},\kappa_n)$
and
![]() $\mathbb{G}_{\infty}=G(\textbf{Y},\textbf{W},\kappa)$
from Theorem 1. We first define some notation which we will use throughout. Recall that
$\mathbb{G}_{\infty}=G(\textbf{Y},\textbf{W},\kappa)$
from Theorem 1. We first define some notation which we will use throughout. Recall that
![]() $\mathbb{G}_n$
has vertex set
$\mathbb{G}_n$
has vertex set
![]() $V(\mathbb{G}_n)=[n]$
, and
$V(\mathbb{G}_n)=[n]$
, and
![]() $\mathbb{G}_{\infty}$
has vertex set
$\mathbb{G}_{\infty}$
has vertex set
![]() $V(\mathbb{G}_{\infty})=\mathbb{N}\cup\{0\}$
.
$V(\mathbb{G}_{\infty})=\mathbb{N}\cup\{0\}$
.
For
![]() $r>0$
, define the set
$r>0$
, define the set
Thus,
![]() $A^r_n$
is a sub-box of the box
$A^r_n$
is a sub-box of the box
![]() $I_n$
, such that for any point in
$I_n$
, such that for any point in
![]() $A^r_n$
the open Euclidean ball of radius r around that point is contained in the box
$A^r_n$
the open Euclidean ball of radius r around that point is contained in the box
![]() $I_n$
. Hence, the number of points of the binomial process
$I_n$
. Hence, the number of points of the binomial process
![]() $\Gamma_n$
(recall (9)) falling in this open ball has the same distribution as the number of points of
$\Gamma_n$
(recall (9)) falling in this open ball has the same distribution as the number of points of
![]() $\Gamma_n$
falling in the open ball of radius r around the origin
$\Gamma_n$
falling in the open ball of radius r around the origin
![]() $\textbf{0} \in \mathbb{R}^d$
. We will use this property of
$\textbf{0} \in \mathbb{R}^d$
. We will use this property of
![]() $A^r_n$
in a suitable manner, which we formally explain next.
$A^r_n$
in a suitable manner, which we formally explain next.
To this end, for any
![]() $x \in \mathbb{R}^d$
, define the ball
$x \in \mathbb{R}^d$
, define the ball
Then if we let
![]() $\partial(I_n)=I_n\setminus\text{int}(I_n)$
denote the boundary of the set
$\partial(I_n)=I_n\setminus\text{int}(I_n)$
denote the boundary of the set
![]() $I_n$
, where
$I_n$
, where
![]() $\text{int}(I_n)$
is the interior of
$\text{int}(I_n)$
is the interior of
![]() $I_n$
, i.e. the union of all open subsets of
$I_n$
, i.e. the union of all open subsets of
![]() $I_n$
, we note that for any vertex
$I_n$
, we note that for any vertex
![]() $j \in V(\mathbb{G}_n)$
with location
$j \in V(\mathbb{G}_n)$
with location
![]() $Y^{(n)}_j \in A^r_n$
, the ball
$Y^{(n)}_j \in A^r_n$
, the ball
![]() $\mathscr{B}^r_{Y^{(n)}_j}$
does not intersect the boundary
$\mathscr{B}^r_{Y^{(n)}_j}$
does not intersect the boundary
![]() $\partial(I_n)$
of
$\partial(I_n)$
of
![]() $I_n$
, i.e.
$I_n$
, i.e.
![]() $\mathscr{B}^r_{Y^{(n)}_j} \subset \text{int}(I_n)$
. As a result, the distribution of the number of vertices of
$\mathscr{B}^r_{Y^{(n)}_j} \subset \text{int}(I_n)$
. As a result, the distribution of the number of vertices of
![]() $\mathbb{G}_n$
(other than j) with locations in
$\mathbb{G}_n$
(other than j) with locations in
![]() $\mathscr{B}^r_{Y^{(n)}_j}$
does not depend on
$\mathscr{B}^r_{Y^{(n)}_j}$
does not depend on
![]() $Y^{(n)}_j$
, and it follows a
$Y^{(n)}_j$
, and it follows a
![]() $\text{Bin}\left(n-1, \frac{\lambda_d(\mathscr{B}^r_{\textbf{0}})}{n}\right)$
distribution (where
$\text{Bin}\left(n-1, \frac{\lambda_d(\mathscr{B}^r_{\textbf{0}})}{n}\right)$
distribution (where
![]() $\lambda_d$
denotes the Lebesgue measure on
$\lambda_d$
denotes the Lebesgue measure on
![]() $\mathbb{R}^d$
).
$\mathbb{R}^d$
).
In particular, since
![]() $\frac{\lambda_d(I_n \setminus A^r_n)}{n}\to 0$
as
$\frac{\lambda_d(I_n \setminus A^r_n)}{n}\to 0$
as
![]() $n \to \infty$
, the location
$n \to \infty$
, the location
![]() $Y^{(n)}_{U_n}$
of the uniformly chosen vertex
$Y^{(n)}_{U_n}$
of the uniformly chosen vertex
![]() $U_n$
of
$U_n$
of
![]() $\mathbb{G}_n$
will with high probability fall in
$\mathbb{G}_n$
will with high probability fall in
![]() $A^r_n$
. We will condition on this good event, under which the number of points of
$A^r_n$
. We will condition on this good event, under which the number of points of
![]() $\Gamma_n$
in
$\Gamma_n$
in
![]() $\mathscr{B}^r_{Y^{(n)}_{U_n}}$
follows a
$\mathscr{B}^r_{Y^{(n)}_{U_n}}$
follows a
![]() $\text{Bin}\left(n-1, \frac{\lambda_d(\mathscr{B}^r_{\textbf{0}})}{n}\right)$
distribution, and this will simplify our computations.
$\text{Bin}\left(n-1, \frac{\lambda_d(\mathscr{B}^r_{\textbf{0}})}{n}\right)$
distribution, and this will simplify our computations.
Definition 6.
(Euclidean graph neighborhoods around a vertex.) For a vertex
![]() $i \in V(\mathbb{G}_n)$
, we define
$i \in V(\mathbb{G}_n)$
, we define
![]() $(F^{\mathbb{G}_n}_i(r),i)$
to be the rooted subgraph of
$(F^{\mathbb{G}_n}_i(r),i)$
to be the rooted subgraph of
![]() $\mathbb{G}_n$
rooted at i, induced by those vertices j whose locations
$\mathbb{G}_n$
rooted at i, induced by those vertices j whose locations
![]() $Y^{(n)}_j$
satisfy
$Y^{(n)}_j$
satisfy
![]() $Y^{(n)}_j \in \mathscr{B}^r_{Y^{(n)}_i}$
.
$Y^{(n)}_j \in \mathscr{B}^r_{Y^{(n)}_i}$
.
Similarly, we define
![]() $(F^{\mathbb{G}_{\infty}}_0(r),0)$
to be the rooted subgraph of
$(F^{\mathbb{G}_{\infty}}_0(r),0)$
to be the rooted subgraph of
![]() $G_{\infty}$
rooted at 0, induced by the vertices
$G_{\infty}$
rooted at 0, induced by the vertices
![]() $j \in V(\mathbb{G}_{\infty})$
whose locations
$j \in V(\mathbb{G}_{\infty})$
whose locations
![]() $Y_j$
satisfy
$Y_j$
satisfy
![]() $Y_j \in \mathscr{B}^r_{Y_0}=\mathscr{B}^r_{\textbf{0}}$
.
$Y_j \in \mathscr{B}^r_{Y_0}=\mathscr{B}^r_{\textbf{0}}$
.
For
![]() $i \in [n]$
, we will sometimes abbreviate the rooted graph
$i \in [n]$
, we will sometimes abbreviate the rooted graph
![]() $(F^{\mathbb{G}_n}_i(r),i)$
as simply
$(F^{\mathbb{G}_n}_i(r),i)$
as simply
![]() $F^{\mathbb{G}_n}_i(r)$
, and similarly for
$F^{\mathbb{G}_n}_i(r)$
, and similarly for
![]() $F^{\mathbb{G}_{\infty}}_0(r)$
.
$F^{\mathbb{G}_{\infty}}_0(r)$
.
For any graph
![]() $G=(V(G), E(G))$
, edge
$G=(V(G), E(G))$
, edge
![]() $e=\{v_1,v_2\} \in E(G)$
, and vertex
$e=\{v_1,v_2\} \in E(G)$
, and vertex
![]() $v \in V(G)$
, by the graph distance of the edge
$v \in V(G)$
, by the graph distance of the edge
![]() $e {=\{v_1,v_2\}}$
from v we mean the number
$e {=\{v_1,v_2\}}$
from v we mean the number
where
![]() $d_G$
is the graph distance on G.
$d_G$
is the graph distance on G.
Having introduced the main notation, we next discuss the main ingredients and the proof strategy for Theorems 1 and 2.
Local convergence of Euclidean graph neighborhoods. Recall the graphs
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
and
$F^{\mathbb{G}_n}_{U_n}(r)$
and
![]() $F^{\mathbb{G}_{\infty}}_{0}(r)$
from Definition 6. In Section 3.2, we will prove that the typical local graph structure in any deterministic Euclidean ball around the root location is asymptotically what it should be, i.e., for any r,
$F^{\mathbb{G}_{\infty}}_{0}(r)$
from Definition 6. In Section 3.2, we will prove that the typical local graph structure in any deterministic Euclidean ball around the root location is asymptotically what it should be, i.e., for any r,
![]() $(F^{\mathbb{G}_n}_{U_n}(r),U_n)$
is close in distribution to
$(F^{\mathbb{G}_n}_{U_n}(r),U_n)$
is close in distribution to
![]() $(F^{\mathbb{G}_{\infty}}_0(r),0)$
.
$(F^{\mathbb{G}_{\infty}}_0(r),0)$
.
Proposition 3. (Local convergence of Euclidean graph neighborhoods.) For any fixed rooted finite graph
![]() $H_*=(H ,h) \in \mathcal{G}_{\star}$
, and for any
$H_*=(H ,h) \in \mathcal{G}_{\star}$
, and for any
![]() $r>0$
,
$r>0$
,
as
![]() $n \to \infty$
, where
$n \to \infty$
, where
![]() $U_n$
is uniformly distributed on
$U_n$
is uniformly distributed on
![]() $V(\mathbb{G}_n)=[n]$
.
$V(\mathbb{G}_n)=[n]$
.
Path-counting analysis. Next, in Section 3.3, we do a path-counting analysis. We begin by proving a technical lemma that will help us in implementing this path-counting analysis. To state this lemma, we first introduce some more notation to keep things neat. Recall that
![]() $U_n$
is uniformly distributed on [n].
$U_n$
is uniformly distributed on [n].
For
![]() $n,j \in \mathbb{N}$
,
$n,j \in \mathbb{N}$
,
![]() $v_1,\ldots,v_j \in [n]$
, and
$v_1,\ldots,v_j \in [n]$
, and
![]() $\vec{x}= (x_0,\ldots,x_j) \in (\mathbb{R}^d)^{j+1}$
, we define
$\vec{x}= (x_0,\ldots,x_j) \in (\mathbb{R}^d)^{j+1}$
, we define
and for
![]() $j \in \mathbb{N}$
,
$j \in \mathbb{N}$
,
![]() $u_1,\dots,u_j \in \mathbb{N}$
,
$u_1,\dots,u_j \in \mathbb{N}$
,
![]() $x_0,\ldots,x_j \in \mathbb{R}^d$
, we define
$x_0,\ldots,x_j \in \mathbb{R}^d$
, we define
Note that the values of the expectations on the right-hand sides of (32) and (33), respectively, do not depend on the values of the
![]() $v_i$
’s and
$v_i$
’s and
![]() $u_i$
’s.
$u_i$
’s.
Then our main path-counting tool is the following lemma.
Lemma 2. (Path-counting estimate.) For any
![]() $j \geq 1$
,
$j \geq 1$
,
![]() $a>1$
, we have
$a>1$
, we have
 \begin{equation} \begin{split} \lim_{m \to \infty} \limsup_{n \to \infty} \frac{1}{n}\int_{I_n}\cdots\int_{I_n}& \frac{1}{n^j} \sum_{v_1,\ldots,v_j \in [n]}\mathbb{W}^{v_1,\ldots,v_j}_{n}(\vec{x})\\& {\times}{\left(\prod_{i=0}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\right)}\mathbb{1}_{\left\{\|x_{j}-x_{j-1}\|>a^{m^j}\right\}} dx_{0}\cdots dx_j =0 \end{split} \end{equation}
\begin{equation} \begin{split} \lim_{m \to \infty} \limsup_{n \to \infty} \frac{1}{n}\int_{I_n}\cdots\int_{I_n}& \frac{1}{n^j} \sum_{v_1,\ldots,v_j \in [n]}\mathbb{W}^{v_1,\ldots,v_j}_{n}(\vec{x})\\& {\times}{\left(\prod_{i=0}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\right)}\mathbb{1}_{\left\{\|x_{j}-x_{j-1}\|>a^{m^j}\right\}} dx_{0}\cdots dx_j =0 \end{split} \end{equation}
and
 \begin{equation} \begin{split} \lim_{m \to \infty} \int_{\mathbb{R}^d}\ldots \int_{\mathbb{R}^d} &\mathbb{W}_j(\textbf{0},x_1\ldots,x_j)\\& {\times}\mathbb{1}_{\left\{\|x_1\|<a^m\right\}}{\left( \prod_{i=1}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\right)}\mathbb{1}_{\left\{\|x_j-x_{j-1}\|>a^{m^j}\right\}} dx_1\cdots dx_j =0. \end{split} \end{equation}
\begin{equation} \begin{split} \lim_{m \to \infty} \int_{\mathbb{R}^d}\ldots \int_{\mathbb{R}^d} &\mathbb{W}_j(\textbf{0},x_1\ldots,x_j)\\& {\times}\mathbb{1}_{\left\{\|x_1\|<a^m\right\}}{\left( \prod_{i=1}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\right)}\mathbb{1}_{\left\{\|x_j-x_{j-1}\|>a^{m^j}\right\}} dx_1\cdots dx_j =0. \end{split} \end{equation}
As a corollary to Lemma 2, we will show that for any fixed
![]() $K \in \mathbb{N}$
and
$K \in \mathbb{N}$
and
![]() $a,m>1$
, if we choose
$a,m>1$
, if we choose
then as
![]() $m \to \infty$
, with high probability, the K-neighborhood of the rooted graph
$m \to \infty$
, with high probability, the K-neighborhood of the rooted graph
![]() $(F^{\mathbb{G}_n}_{U_n}(r),U_n)$
will be the K-neighborhood
$(F^{\mathbb{G}_n}_{U_n}(r),U_n)$
will be the K-neighborhood
![]() $B^{\mathbb{G}_n}_{U_n}(K)$
of
$B^{\mathbb{G}_n}_{U_n}(K)$
of
![]() $(\mathbb{G}_n,U_n)$
, and a similar result holds for
$(\mathbb{G}_n,U_n)$
, and a similar result holds for
![]() $(\mathbb{G}_{\infty},0)$
. This will help us in proving Theorems 1 and 2. To state the result, we again introduce some shorthand notation:
$(\mathbb{G}_{\infty},0)$
. This will help us in proving Theorems 1 and 2. To state the result, we again introduce some shorthand notation:
 \begin{align} B_n&\,{:\!=}\,B^{\mathbb{G}_n}_{{U_n}}(K),\quad B\,{:\!=}\,B^{\mathbb{G}_{\infty}}_{0}(K),\qquad F_{n,r}\,{:\!=}\,F^{\mathbb{G}_n}_{{U_n}}(r),\quad F_r\,{:\!=}\,F^{\mathbb{G}_{\infty}}_{0}(r), \nonumber\\[3pt] BF_{n,r}&\,{:\!=}\,B^{F_{n,r}}_{{U_n}}(K),\quad BF_{r}\,{:\!=}\,B^{F_{r}}_{0}(K). \end{align}
\begin{align} B_n&\,{:\!=}\,B^{\mathbb{G}_n}_{{U_n}}(K),\quad B\,{:\!=}\,B^{\mathbb{G}_{\infty}}_{0}(K),\qquad F_{n,r}\,{:\!=}\,F^{\mathbb{G}_n}_{{U_n}}(r),\quad F_r\,{:\!=}\,F^{\mathbb{G}_{\infty}}_{0}(r), \nonumber\\[3pt] BF_{n,r}&\,{:\!=}\,B^{F_{n,r}}_{{U_n}}(K),\quad BF_{r}\,{:\!=}\,B^{F_{r}}_{0}(K). \end{align}
Remark 7. (Spatial and graph neighborhoods.) At this point, we emphasize that we rely on two kinds of neighborhoods around the root
![]() $U_n$
(respectively 0) of
$U_n$
(respectively 0) of
![]() $\mathbb{G}_n$
(respectively
$\mathbb{G}_n$
(respectively
![]() $\mathbb{G}_{\infty}$
). These are the graph
$\mathbb{G}_{\infty}$
). These are the graph
![]() $F_{n,r}$
(respectively
$F_{n,r}$
(respectively
![]() $F_r$
), which is the subgraph induced by those vertices whose spatial locations are within Euclidean distance r of the root location
$F_r$
), which is the subgraph induced by those vertices whose spatial locations are within Euclidean distance r of the root location
![]() $Y^{(n)}_{U_n}$
(respectively
$Y^{(n)}_{U_n}$
(respectively
![]() $Y_0$
), and the graph
$Y_0$
), and the graph
![]() $B_n$
(respectively B), which is the graph neighborhood of radius K around the root
$B_n$
(respectively B), which is the graph neighborhood of radius K around the root
![]() $U_n$
(respectively 0) (see Figure 1). The difference between these two kinds of neighborhoods should be understood clearly. For example, the graph
$U_n$
(respectively 0) (see Figure 1). The difference between these two kinds of neighborhoods should be understood clearly. For example, the graph
![]() $F_{n,r}$
may possibly be disconnected, while
$F_{n,r}$
may possibly be disconnected, while
![]() $B_n$
is always a connected graph. Moreover,
$B_n$
is always a connected graph. Moreover,
![]() $BF_{n, r}$
(respectively
$BF_{n, r}$
(respectively
![]() $BF_{r}$
) is the graph neighborhood of radius K, of the rooted graph
$BF_{r}$
) is the graph neighborhood of radius K, of the rooted graph
![]() $(F_{n,r},U_n)$
(respectively
$(F_{n,r},U_n)$
(respectively
![]() $(F_r,0)$
).
$(F_r,0)$
).

Figure 1. Illustration to distinguish between the two kinds of neighborhoods. The star in the middle is the location
![]() $Y^{(n)}_{U_n}$
of the root
$Y^{(n)}_{U_n}$
of the root
![]() $U_n$
, and the big circle around it is the boundary of the Euclidean ball centered at
$U_n$
, and the big circle around it is the boundary of the Euclidean ball centered at
![]() $Y^{(n)}_{U_n}$
of radius r, in
$Y^{(n)}_{U_n}$
of radius r, in
![]() $\mathbb{R}^d$
. Diamonds are the vertices of the graph neighborhood
$\mathbb{R}^d$
. Diamonds are the vertices of the graph neighborhood
![]() $B^{\mathbb{G}_n}_{U_n}(2)$
of radius 2 around the root. Black dots are the vertices which are not in
$B^{\mathbb{G}_n}_{U_n}(2)$
of radius 2 around the root. Black dots are the vertices which are not in
![]() $B^{\mathbb{G}_n}_{U_n}(2)$
. The circled vertices are the vertices of
$B^{\mathbb{G}_n}_{U_n}(2)$
. The circled vertices are the vertices of
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
. The circled diamonds are the vertices of
$F^{\mathbb{G}_n}_{U_n}(r)$
. The circled diamonds are the vertices of
![]() $BF_{n,r}$
, the graph neighborhood of radius 2 about the root
$BF_{n,r}$
, the graph neighborhood of radius 2 about the root
![]() $U_n$
, of the graph
$U_n$
, of the graph
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
.
$F^{\mathbb{G}_n}_{U_n}(r)$
.
We have the following corollary to Lemma 2.
Corollary 7. (Coupling spatial and graph neighborhoods.) Let
![]() $BF_{n,r}$
,
$BF_{n,r}$
,
![]() $B_n$
,
$B_n$
,
![]() $BF_r$
, B be as in (37), where
$BF_r$
, B be as in (37), where
![]() $r=r(a,m,K)$
is as in (36). Then
$r=r(a,m,K)$
is as in (36). Then
and
In proving Corollary 7, we perform a careful path-counting analysis to bound the expected number of K-paths of
![]() $\mathbb{G}_n$
which are not K-paths in
$\mathbb{G}_n$
which are not K-paths in
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
by the integral expression (34), and to obtain the similar bound (35) for
$F^{\mathbb{G}_n}_{U_n}(r)$
by the integral expression (34), and to obtain the similar bound (35) for
![]() $\mathbb{G}_{\infty}$
. Corollary 7 then follows directly using the technical Lemma 2.
$\mathbb{G}_{\infty}$
. Corollary 7 then follows directly using the technical Lemma 2.
In the course of proving Corollary 7, we develop a general path estimate, where for
![]() $r=r(a,m,K)$
as in (36), we can have
$r=r(a,m,K)$
as in (36), we can have
![]() $a=a_n$
,
$a=a_n$
,
![]() $K=K_n$
be n dependent sequences, while m does not depend on n. This general estimate will be used in the proof of Theorem 3.
$K=K_n$
be n dependent sequences, while m does not depend on n. This general estimate will be used in the proof of Theorem 3.
Proof strategy for Theorem 1. In Section 3.4, we prove Theorem 1. Recall that, to conclude Theorem 1, we need to show that for any
![]() $K \in \mathbb{N}$
, the K-neighborhoods of
$K \in \mathbb{N}$
, the K-neighborhoods of
![]() $(\mathbb{G}_n,U_n)$
and
$(\mathbb{G}_n,U_n)$
and
![]() $(\mathbb{G}_{\infty},0)$
are close in distribution in
$(\mathbb{G}_{\infty},0)$
are close in distribution in
![]() $\mathcal{G}_{\star}$
. Consequently, to conclude Theorem 1, using Corollary 7, it will be enough to show that the K-neighborhoods of
$\mathcal{G}_{\star}$
. Consequently, to conclude Theorem 1, using Corollary 7, it will be enough to show that the K-neighborhoods of
![]() $(F^{\mathbb{G}_n}_{U_n}(r),U_n)$
and
$(F^{\mathbb{G}_n}_{U_n}(r),U_n)$
and
![]() $(F^{\mathbb{G}_{\infty}}_{0}(r),0)$
are close in distribution. This we will observe to be an easy consequence of Proposition 3.
$(F^{\mathbb{G}_{\infty}}_{0}(r),0)$
are close in distribution. This we will observe to be an easy consequence of Proposition 3.
Proof strategy for Theorem 2. In Section 3.5, we prove Theorem 2. The first step is to show that the empirical Euclidean graph neighborhood distribution concentrates. That is, for
![]() $H_*=(H,h) \in \mathcal{G}_{\star}$
, where
$H_*=(H,h) \in \mathcal{G}_{\star}$
, where
![]() $h \in V(H)$
, and for any
$h \in V(H)$
, and for any
![]() $r>0$
, we define the random variables
$r>0$
, we define the random variables
and show these random variables concentrate, as follows.
Lemma 3. (Concentration of empirical Euclidean graph neighborhood measure.) For any
![]() $r>0$
and a locally finite rooted graph
$r>0$
and a locally finite rooted graph
![]() $H_*= (H,h) \in \mathcal{G}_{\star}$
, the variance of the random variable
$H_*= (H,h) \in \mathcal{G}_{\star}$
, the variance of the random variable
![]() $C_{r,n} (H,h)$
converges to 0 as
$C_{r,n} (H,h)$
converges to 0 as
![]() $n \to \infty$
, i.e.
$n \to \infty$
, i.e.
as
![]() $n \to \infty$
.
$n \to \infty$
.
The key observation in proving this lemma is that the Euclidean graph neighborhoods around two uniformly chosen vertices of
![]() $\mathbb{G}_n$
are asymptotically independent, which is a consequence of the fact that the distance between the locations of two uniformly chosen vertices of
$\mathbb{G}_n$
are asymptotically independent, which is a consequence of the fact that the distance between the locations of two uniformly chosen vertices of
![]() $\mathbb{G}_n$
in
$\mathbb{G}_n$
in
![]() $\mathbb{R}^d$
diverges in probability, as
$\mathbb{R}^d$
diverges in probability, as
![]() $n \to \infty$
.
$n \to \infty$
.
Next, we combine Lemma 3 with Corollary 7 to show that the empirical neighborhood distribution of
![]() $\mathbb{G}_n$
also concentrates. That is, for any
$\mathbb{G}_n$
also concentrates. That is, for any
![]() $K \in \mathbb{N}$
and
$K \in \mathbb{N}$
and
![]() $G_*=(G,g) \in \mathcal{G}_{\star}$
, if we define random variables
$G_*=(G,g) \in \mathcal{G}_{\star}$
, if we define random variables
for
![]() $n \in \mathbb{N}$
, then these random variables also concentrate. This is achieved by first using Lemma 3 and taking a sum over all rooted graphs
$n \in \mathbb{N}$
, then these random variables also concentrate. This is achieved by first using Lemma 3 and taking a sum over all rooted graphs
![]() $H_*= (H,h)$
with
$H_*= (H,h)$
with
![]() $B^{H}_h(K) \cong (G,g)$
, to show that the random variables
$B^{H}_h(K) \cong (G,g)$
, to show that the random variables
 \begin{align*}\frac{1}{n}\sum_{i =1}^n\mathbb{1}_{\left\{ B^{F^{\mathbb{G}_n}_i(r)}_i(K)\cong (G,g)\right\}}\end{align*}
\begin{align*}\frac{1}{n}\sum_{i =1}^n\mathbb{1}_{\left\{ B^{F^{\mathbb{G}_n}_i(r)}_i(K)\cong (G,g)\right\}}\end{align*}
concentrate, and then employing Corollary 7 to obtain the same conclusion for the variables
![]() $B_n(G,g)$
. Theorem 2 is then a direct consequence of these observations, combined with Proposition 3.
$B_n(G,g)$
. Theorem 2 is then a direct consequence of these observations, combined with Proposition 3.
3.2. Proof of Proposition 3
Let us first discuss the proof strategy informally. We make use of the following two key observations:
The number of vertices in
 $F^{\mathbb{G}_n}_{U_n}(r)$
converges in distribution to the number of vertices in
$F^{\mathbb{G}_n}_{U_n}(r)$
converges in distribution to the number of vertices in
 $F^{\mathbb{G}_{\infty}}_0(r)$
.
$F^{\mathbb{G}_{\infty}}_0(r)$
.Conditionally on the number of vertices of
 $F^{\mathbb{G}_n}_{U_n}(r)$
(respectively
$F^{\mathbb{G}_n}_{U_n}(r)$
(respectively
 $F^{\mathbb{G}_{\infty}}_0(r)$
) other than the root, their locations are uniform on
$F^{\mathbb{G}_{\infty}}_0(r)$
) other than the root, their locations are uniform on
 $\mathscr{B}^r_{Y^{(n)}_{U_n}}$
(respectively
$\mathscr{B}^r_{Y^{(n)}_{U_n}}$
(respectively
 $\mathscr{B}^r_{\textbf{0}}$
). It will then follow that any ‘not so bad’ translation-invariant function, evaluated at the locations of the vertices of
$\mathscr{B}^r_{\textbf{0}}$
). It will then follow that any ‘not so bad’ translation-invariant function, evaluated at the locations of the vertices of
 $F^{\mathbb{G}_n}_{U_n}(r)$
, should have nice limiting behavior.
$F^{\mathbb{G}_n}_{U_n}(r)$
, should have nice limiting behavior.
In particular, we define functions
![]() $\mathcal{F}^{n}_{ (H,h)}$
and
$\mathcal{F}^{n}_{ (H,h)}$
and
![]() $\mathcal{F}^{\infty}_{ (H,h)}$
(see (52)), which for a given rooted graph
$\mathcal{F}^{\infty}_{ (H,h)}$
(see (52)), which for a given rooted graph
![]() $ (H,h) \in \mathcal{G}_{\star}$
count the number of rooted isomorphisms between (H, h) and
$ (H,h) \in \mathcal{G}_{\star}$
count the number of rooted isomorphisms between (H, h) and
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
, and between (H, h) and
$F^{\mathbb{G}_n}_{U_n}(r)$
, and between (H, h) and
![]() $F^{\mathbb{G}_{\infty}}_0(r)$
. We show that for any such rooted graph
$F^{\mathbb{G}_{\infty}}_0(r)$
. We show that for any such rooted graph
![]() $ (H,h) \in \mathcal{G}_{\star}$
, the probability of the event
$ (H,h) \in \mathcal{G}_{\star}$
, the probability of the event
![]() $\{\mathcal{F}^{n}_{ (H,h)}>0\}$
converges to that of the event
$\{\mathcal{F}^{n}_{ (H,h)}>0\}$
converges to that of the event
![]() $\{\mathcal{F}^{\infty}_{ (H,h)}>0\}$
. In turn, this implies that the random rooted graph
$\{\mathcal{F}^{\infty}_{ (H,h)}>0\}$
. In turn, this implies that the random rooted graph
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
converges in distribution to the random rooted graph
$F^{\mathbb{G}_n}_{U_n}(r)$
converges in distribution to the random rooted graph
![]() $F^{\mathbb{G}_{\infty}}_{0}(r)$
, on the space
$F^{\mathbb{G}_{\infty}}_{0}(r)$
, on the space
![]() $\mathcal{G}_{\star}$
. We now go into the details.
$\mathcal{G}_{\star}$
. We now go into the details.
Proof of Proposition 3. The random variable
![]() $Y^{(n)}_{U_n}$
is uniformly distributed on
$Y^{(n)}_{U_n}$
is uniformly distributed on
![]() $I_n$
. We write
$I_n$
. We write
 \begin{align*} &\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h)\right) \\ &= \mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h), Y^{(n)}_{U_n} \in A^r_n\right) +\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h), Y^{(n)}_{U_n} \notin A^r_n\right) \end{align*}
\begin{align*} &\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h)\right) \\ &= \mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h), Y^{(n)}_{U_n} \in A^r_n\right) +\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h), Y^{(n)}_{U_n} \notin A^r_n\right) \end{align*}
and observe that, as
![]() $n \to \infty$
,
$n \to \infty$
,
Therefore, it is enough to show that, as
![]() $n \to \infty$
,
$n \to \infty$
,
Note that
 \begin{align*} &\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h), Y^{(n)}_{U_n} \in A^r_n\right) \\& \qquad\quad =\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h), Y^{(n)}_{U_n} \in A^r_n, |V(F^{\mathbb{G}_n}_{U_n}(r))|=|V(H)|\right), \end{align*}
\begin{align*} &\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h), Y^{(n)}_{U_n} \in A^r_n\right) \\& \qquad\quad =\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h), Y^{(n)}_{U_n} \in A^r_n, |V(F^{\mathbb{G}_n}_{U_n}(r))|=|V(H)|\right), \end{align*}
and so we can repeatedly condition to rewrite
 \begin{equation} \begin{split} &\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h), Y^{(n)}_{U_n} \in A^r_n\right) \\& \qquad= \mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h) \bigg| |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=|V(H)|, Y^{(n)}_{U_n} \in A^r_n\right) \\& \qquad\quad \times \mathbb{P}\left(|V(F^{\mathbb{G}_n}_{{U_n}}(r))|=|V(H)| \bigg| Y^{(n)}_{U_n} \in A^r_n\right)\mathbb{P}\left(Y^{(n)}_{U_n} \in A^r_n\right). \end{split} \end{equation}
\begin{equation} \begin{split} &\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h), Y^{(n)}_{U_n} \in A^r_n\right) \\& \qquad= \mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h) \bigg| |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=|V(H)|, Y^{(n)}_{U_n} \in A^r_n\right) \\& \qquad\quad \times \mathbb{P}\left(|V(F^{\mathbb{G}_n}_{{U_n}}(r))|=|V(H)| \bigg| Y^{(n)}_{U_n} \in A^r_n\right)\mathbb{P}\left(Y^{(n)}_{U_n} \in A^r_n\right). \end{split} \end{equation}
Using (42), the last term in the right-hand side of (44) tends to 1 as
![]() $n \to \infty$
. Observe that
$n \to \infty$
. Observe that
where
![]() $\mathcal{Y}_n$
follows a
$\mathcal{Y}_n$
follows a
![]() $\text{Bin}(n-1, \lambda_d(\mathscr{B}^r_{\textbf{0}})/n)$
distribution.
$\text{Bin}(n-1, \lambda_d(\mathscr{B}^r_{\textbf{0}})/n)$
distribution.
Since
![]() $\mathcal{Y}_n$
converges in distribution to
$\mathcal{Y}_n$
converges in distribution to
![]() $\mathcal{Y}\sim \text{Poi}(\lambda_d(\mathscr{B}^r_{\textbf{0}}))$
, and since
$\mathcal{Y}\sim \text{Poi}(\lambda_d(\mathscr{B}^r_{\textbf{0}}))$
, and since
![]() $\mathcal{Y}$
is equal in distribution to
$\mathcal{Y}$
is equal in distribution to
![]() $\Gamma(\mathscr{B}^r_{\textbf{0}})$
(recall
$\Gamma(\mathscr{B}^r_{\textbf{0}})$
(recall
![]() $\Gamma$
from (10)), it follows that
$\Gamma$
from (10)), it follows that
![]() $\mathcal{Y}_n {{\stackrel{d}{\rightarrow}}} \Gamma(\mathscr{B}^r_{\textbf{0}})$
, as
$\mathcal{Y}_n {{\stackrel{d}{\rightarrow}}} \Gamma(\mathscr{B}^r_{\textbf{0}})$
, as
![]() $n \to \infty$
.
$n \to \infty$
.
Observe that
![]() $\Gamma(\mathscr{B}^r_{\textbf{0}})\stackrel{d}{=}|V(F^{\mathbb{G}_{\infty}}_{\textbf{0}}(r))|-1$
, so that
$\Gamma(\mathscr{B}^r_{\textbf{0}})\stackrel{d}{=}|V(F^{\mathbb{G}_{\infty}}_{\textbf{0}}(r))|-1$
, so that
 \begin{align*} \lim_{n \to \infty} \mathbb{P}\left(|V(F^{\mathbb{G}_n}_{{U_n}}(r))|=|V(H)| \bigg| Y^{(n)}_{U_n} \in A^r_n\right) &=\lim_{n \to \infty} \mathbb{P}\left(\mathcal{Y}_n=|V(H)|-1\right) \\&= \mathbb{P}\left(|V(F^{\mathbb{G}_{\infty}}_{0}(r))|-1=|V(H)|-1\right) \\&=\mathbb{P}\left(|V(F^{\mathbb{G}_{\infty}}_{0}(r))|=|V(H)|\right). \end{align*}
\begin{align*} \lim_{n \to \infty} \mathbb{P}\left(|V(F^{\mathbb{G}_n}_{{U_n}}(r))|=|V(H)| \bigg| Y^{(n)}_{U_n} \in A^r_n\right) &=\lim_{n \to \infty} \mathbb{P}\left(\mathcal{Y}_n=|V(H)|-1\right) \\&= \mathbb{P}\left(|V(F^{\mathbb{G}_{\infty}}_{0}(r))|-1=|V(H)|-1\right) \\&=\mathbb{P}\left(|V(F^{\mathbb{G}_{\infty}}_{0}(r))|=|V(H)|\right). \end{align*}
Hence, from (44), we note that to conclude (43), it is enough to show that
 \begin{equation} \begin{split} \lim_{n \to \infty}\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h) \bigg| |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=|V(H)|, Y^{(n)}_{U_n} \in A^r_n\right) \\&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!=\mathbb{P}\left((F^{\mathbb{G}_{\infty}}_{0}(r),0) \cong (H,h) \bigg| |V(F^{\mathbb{G}_{\infty}}_{0}(r))|=|V(H)|\right). \end{split} \end{equation}
\begin{equation} \begin{split} \lim_{n \to \infty}\mathbb{P}\left((F^{\mathbb{G}_n}_{{U_n}}(r),U_n) \cong (H,h) \bigg| |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=|V(H)|, Y^{(n)}_{U_n} \in A^r_n\right) \\&\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!=\mathbb{P}\left((F^{\mathbb{G}_{\infty}}_{0}(r),0) \cong (H,h) \bigg| |V(F^{\mathbb{G}_{\infty}}_{0}(r))|=|V(H)|\right). \end{split} \end{equation}
For the remainder of the proof, we assume
![]() $|V(H)|=l+1$
. We continue by making some observations on the locations and weights of the vertices of the graph
$|V(H)|=l+1$
. We continue by making some observations on the locations and weights of the vertices of the graph
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
(respectively
$F^{\mathbb{G}_n}_{U_n}(r)$
(respectively
![]() $F^{\mathbb{G}_\infty}_{\textbf{0}}(r)$
), conditionally on
$F^{\mathbb{G}_\infty}_{\textbf{0}}(r)$
), conditionally on
![]() $\{|V(F^{\mathbb{G}_n}_{U_n}(r))|=l+1, Y^{(n)}_{U_n} \in A^r_n\}$
(respectively {
$\{|V(F^{\mathbb{G}_n}_{U_n}(r))|=l+1, Y^{(n)}_{U_n} \in A^r_n\}$
(respectively {
![]() $|V(F^{\mathbb{G}_\infty}_{\textbf{0}}(r))|=l+1$
}).
$|V(F^{\mathbb{G}_\infty}_{\textbf{0}}(r))|=l+1$
}).
Locations of
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
. Since
$F^{\mathbb{G}_n}_{U_n}(r)$
. Since
![]() $(Y^{(n)}_i)_{i\in[n]}$
is an i.i.d. collection of uniform random variables on
$(Y^{(n)}_i)_{i\in[n]}$
is an i.i.d. collection of uniform random variables on
![]() $I_n$
, conditionally on the event
$I_n$
, conditionally on the event
![]() $\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, the locations
$\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, the locations
![]() $P_1,\ldots,P_l$
of the l vertices of
$P_1,\ldots,P_l$
of the l vertices of
![]() $\mathbb{G}_n$
(in some order) falling in
$\mathbb{G}_n$
(in some order) falling in
![]() $\mathscr{B}^r_{Y^{(n)}_{U_n}}$
, other than
$\mathscr{B}^r_{Y^{(n)}_{U_n}}$
, other than
![]() $Y^{(n)}_{U_n}$
, are at independent uniform locations in the ball
$Y^{(n)}_{U_n}$
, are at independent uniform locations in the ball
![]() $\mathscr{B}^r_{Y^{(n)}_{U_n}}$
, given
$\mathscr{B}^r_{Y^{(n)}_{U_n}}$
, given
![]() $Y^{(n)}_{U_n}$
. Hence, conditionally on
$Y^{(n)}_{U_n}$
. Hence, conditionally on
![]() $\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, the random variables
$\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, the random variables
![]() $P_1-Y^{(n)}_{U_n},\ldots,P_l-Y^{(n)}_{U_n}$
are independently, uniformly distributed on the ball
$P_1-Y^{(n)}_{U_n},\ldots,P_l-Y^{(n)}_{U_n}$
are independently, uniformly distributed on the ball
![]() $\mathscr{B}^r_{\textbf{0}}$
.
$\mathscr{B}^r_{\textbf{0}}$
.
Conditionally on
![]() $\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, let the locations of all the vertices of
$\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, let the locations of all the vertices of
![]() $\mathbb{G}_n$
falling in
$\mathbb{G}_n$
falling in
![]() $\mathscr{B}^r_{Y^{(n)}_{U_n}}$
(including
$\mathscr{B}^r_{Y^{(n)}_{U_n}}$
(including
![]() $Y^{(n)}_{U_n}$
) be
$Y^{(n)}_{U_n}$
) be
![]() $P_0, P_1, \ldots, P_l$
, where
$P_0, P_1, \ldots, P_l$
, where
![]() $Y^{(n)}_{U_n}=P_0$
. So, conditionally on
$Y^{(n)}_{U_n}=P_0$
. So, conditionally on
![]() $\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, the random matrix
$\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, the random matrix
![]() $(\|P_i-P_j\|)_{0\leq i,j \leq l; i\neq j}$
is equal in distribution to
$(\|P_i-P_j\|)_{0\leq i,j \leq l; i\neq j}$
is equal in distribution to
![]() $(\|Y_i-Y_j\|)_{0\leq i,j \leq l; i\neq j}$
, where the set
$(\|Y_i-Y_j\|)_{0\leq i,j \leq l; i\neq j}$
, where the set
![]() $\{Y_i\colon 1\leq i\leq l\}$
consists of l i.i.d. uniform points in
$\{Y_i\colon 1\leq i\leq l\}$
consists of l i.i.d. uniform points in
![]() $\mathscr{B}^r_{\textbf{0}}$
(independent of
$\mathscr{B}^r_{\textbf{0}}$
(independent of
![]() $\textbf{Y}^{(n)}$
,
$\textbf{Y}^{(n)}$
,
![]() $\textbf{W}^{(n)}$
,
$\textbf{W}^{(n)}$
,
![]() $\textbf{Y}$
,
$\textbf{Y}$
,
![]() $\textbf{W}$
) and
$\textbf{W}$
) and
![]() $Y_0=\textbf{0}$
.
$Y_0=\textbf{0}$
.
Locations of
![]() $F^{\mathbb{G}_{\infty}}_0(r)$
. Again, conditionally on the event
$F^{\mathbb{G}_{\infty}}_0(r)$
. Again, conditionally on the event
![]() $\{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}=\{|V(F^{\mathbb{G}_{\infty}}_{0}(r))|=l+1\}$
, the locations of the l vertices of
$\{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}=\{|V(F^{\mathbb{G}_{\infty}}_{0}(r))|=l+1\}$
, the locations of the l vertices of
![]() $\mathbb{G}_{\infty}$
in
$\mathbb{G}_{\infty}$
in
![]() $\mathscr{B}^r_{\textbf{0}}$
other than 0 are i.i.d. uniform on
$\mathscr{B}^r_{\textbf{0}}$
other than 0 are i.i.d. uniform on
![]() $\mathscr{B}^r_{\textbf{0}}$
(since
$\mathscr{B}^r_{\textbf{0}}$
(since
![]() $\Gamma$
is a homogeneous Poisson point process). So if
$\Gamma$
is a homogeneous Poisson point process). So if
![]() $Z_0,\ldots,Z_l$
are the locations of the
$Z_0,\ldots,Z_l$
are the locations of the
![]() $l+1$
vertices of
$l+1$
vertices of
![]() $\mathbb{G}_{\infty}$
in
$\mathbb{G}_{\infty}$
in
![]() $\mathscr{B}^r_{\textbf{0}}$
(in some order), where
$\mathscr{B}^r_{\textbf{0}}$
(in some order), where
![]() $Z_0=\textbf{0}$
, the random matrix
$Z_0=\textbf{0}$
, the random matrix
![]() $(\|Z_i-Z_j\|)_{0\leq i,j \leq l; i\neq j}$
is also equal in distribution to
$(\|Z_i-Z_j\|)_{0\leq i,j \leq l; i\neq j}$
is also equal in distribution to
![]() $(\|Y_i-Y_j\|)_{0\leq i,j \leq l; i\neq j}$
, where the set
$(\|Y_i-Y_j\|)_{0\leq i,j \leq l; i\neq j}$
, where the set
![]() $\{Y_i\colon 1\leq i\leq l\}$
consists of l i.i.d. uniform points in
$\{Y_i\colon 1\leq i\leq l\}$
consists of l i.i.d. uniform points in
![]() $\mathscr{B}^r_{\textbf{0}}$
(independent of
$\mathscr{B}^r_{\textbf{0}}$
(independent of
![]() $\textbf{Y}^{(n)}$
,
$\textbf{Y}^{(n)}$
,
![]() $\textbf{W}^{(n)}$
,
$\textbf{W}^{(n)}$
,
![]() $\textbf{Y}$
,
$\textbf{Y}$
,
![]() $\textbf{W}$
) and
$\textbf{W}$
) and
![]() $Y_0=\textbf{0}$
.
$Y_0=\textbf{0}$
.
We conclude that
 \begin{align} &(\|P_i-P_j\|)_{0\leq i,j \leq l; i\neq j}\bigg|{\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}} \nonumber\\&\qquad\quad \stackrel{d}{=}(\|Y_i-Y_j\|)_{1\leq i,j \leq l+1; i\neq j} \nonumber\\&\qquad\quad \stackrel{d}{=} (\|Z_i-Z_j\|)_{0\leq i,j \leq l; i\neq j}\bigg|{\{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}}. \end{align}
\begin{align} &(\|P_i-P_j\|)_{0\leq i,j \leq l; i\neq j}\bigg|{\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}} \nonumber\\&\qquad\quad \stackrel{d}{=}(\|Y_i-Y_j\|)_{1\leq i,j \leq l+1; i\neq j} \nonumber\\&\qquad\quad \stackrel{d}{=} (\|Z_i-Z_j\|)_{0\leq i,j \leq l; i\neq j}\bigg|{\{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}}. \end{align}
Weights of
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
. Next, conditionally on
$F^{\mathbb{G}_n}_{U_n}(r)$
. Next, conditionally on
![]() $\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, for
$\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, for
![]() $0 \leq i \leq l$
, let
$0 \leq i \leq l$
, let
![]() $W_{n,i}$
denote the weight of the vertex of
$W_{n,i}$
denote the weight of the vertex of
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
with location
$F^{\mathbb{G}_n}_{U_n}(r)$
with location
![]() $P_i$
. Then
$P_i$
. Then
![]() $(W_{n,0},\ldots,W_{n,l})$
has the distribution of
$(W_{n,0},\ldots,W_{n,l})$
has the distribution of
![]() $l+1$
uniformly chosen weights from the weight set
$l+1$
uniformly chosen weights from the weight set
![]() $\{W^{(n)}_1,\ldots,W^{(n)}_n\}$
without replacement, in some arbitrary order. This is because for any
$\{W^{(n)}_1,\ldots,W^{(n)}_n\}$
without replacement, in some arbitrary order. This is because for any
![]() $i_0,\ldots,i_l \in [n]$
,
$i_0,\ldots,i_l \in [n]$
,
 \begin{align} & \mathbb{P}\left((W_{n,0},\ldots,W_{n,l})=(W^{(n)}_{i_0},\ldots,W^{(n)}_{i_l}) \bigg| Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\right)\nonumber\\ & = \frac{\mathbb{P}\left((W_{n,0},\ldots,W_{n,l})=(W^{(n)}_{i_0},\ldots,W^{(n)}_{i_l}) \bigg| Y^{(n)}_{U_n}\in A^r_n\right)}{\mathbb{P}\left(|V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1 \bigg| Y^{(n)}_{U_n}\in A^r_n\right)}, \end{align}
\begin{align} & \mathbb{P}\left((W_{n,0},\ldots,W_{n,l})=(W^{(n)}_{i_0},\ldots,W^{(n)}_{i_l}) \bigg| Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\right)\nonumber\\ & = \frac{\mathbb{P}\left((W_{n,0},\ldots,W_{n,l})=(W^{(n)}_{i_0},\ldots,W^{(n)}_{i_l}) \bigg| Y^{(n)}_{U_n}\in A^r_n\right)}{\mathbb{P}\left(|V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1 \bigg| Y^{(n)}_{U_n}\in A^r_n\right)}, \end{align}
where in the second step we use the fact that the event that the vector of weights of the vertices of
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
is of length
$F^{\mathbb{G}_n}_{U_n}(r)$
is of length
![]() $l+1$
is contained in the event that
$l+1$
is contained in the event that
![]() $\{|V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
. The numerator in (47) is
$\{|V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
. The numerator in (47) is
where the term
![]() $ {1/n}$
is just the probability that
$ {1/n}$
is just the probability that
![]() $U_n = i_0$
, and the term
$U_n = i_0$
, and the term
![]() $\frac{1}{l!}$
accounts for the choice of the ordering
$\frac{1}{l!}$
accounts for the choice of the ordering
![]() $P_k=Y^{(n)}_{i_k}$
for
$P_k=Y^{(n)}_{i_k}$
for
![]() $1 \leq k \leq l$
among all
$1 \leq k \leq l$
among all
![]() $l!$
possible labelings. This evaluates to
$l!$
possible labelings. This evaluates to
The denominator in (47) is just the probability that a
![]() $\text{Bin}\left(n-1, \frac{\lambda_d(\mathscr{B}^r_{\textbf{0}})}{n}\right)$
random variable takes the value l, which evaluates to
$\text{Bin}\left(n-1, \frac{\lambda_d(\mathscr{B}^r_{\textbf{0}})}{n}\right)$
random variable takes the value l, which evaluates to
Combining, we get that
 \begin{align} &\mathbb{P}\left((W_{n,0},\ldots,W_{n,l})=(W^{(n)}_{i_0},\ldots,W^{(n)}_{i_l}) \bigg| Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\right)\nonumber \\&=\frac{1}{n(n-1)\cdots(n-l)}. \end{align}
\begin{align} &\mathbb{P}\left((W_{n,0},\ldots,W_{n,l})=(W^{(n)}_{i_0},\ldots,W^{(n)}_{i_l}) \bigg| Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\right)\nonumber \\&=\frac{1}{n(n-1)\cdots(n-l)}. \end{align}
We also make the observation that the random vector
![]() $(W_{n,0},\ldots,W_{n,l})$
is permutation-invariant: for any
$(W_{n,0},\ldots,W_{n,l})$
is permutation-invariant: for any
![]() $\sigma \in S(l+1)$
, where
$\sigma \in S(l+1)$
, where
![]() $S(l+1)$
denotes the set of all permutations of
$S(l+1)$
denotes the set of all permutations of
![]() $\{0,\ldots,l\}$
,
$\{0,\ldots,l\}$
,
Weights of
![]() $F^{\mathbb{G}_{\infty}}_0(r)$
. Again, conditionally on
$F^{\mathbb{G}_{\infty}}_0(r)$
. Again, conditionally on
![]() $\{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}$
, for
$\{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}$
, for
![]() $0 \leq i \leq l$
, let
$0 \leq i \leq l$
, let
![]() $W_{\infty,i}$
denote the weight of the vertex of
$W_{\infty,i}$
denote the weight of the vertex of
![]() $F^{\mathbb{G}_{\infty}}_{0}(r)$
with location
$F^{\mathbb{G}_{\infty}}_{0}(r)$
with location
![]() $Z_i$
. Since the weights in the limiting graph
$Z_i$
. Since the weights in the limiting graph
![]() $\mathbb{G}_{\infty}$
are i.i.d., it immediately follows that the random weight vector
$\mathbb{G}_{\infty}$
are i.i.d., it immediately follows that the random weight vector
![]() $(W_{\infty,0},\ldots,W_{\infty,l})$
is permutation-invariant, i.e. for any
$(W_{\infty,0},\ldots,W_{\infty,l})$
is permutation-invariant, i.e. for any
![]() $\sigma \in S(l+1)$
,
$\sigma \in S(l+1)$
,
and that given
![]() $\{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}$
, the vector
$\{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}$
, the vector
![]() $(W_{\infty,0},\ldots,W_{\infty,l})\stackrel{d}{=}(\textrm{W}_0,\ldots,\textrm{W}_l)$
, where each entry of the vector
$(W_{\infty,0},\ldots,W_{\infty,l})\stackrel{d}{=}(\textrm{W}_0,\ldots,\textrm{W}_l)$
, where each entry of the vector
![]() $(\textrm{W}_0,\ldots,\textrm{W}_l)$
is an i.i.d. copy of the limiting weight variable W (recall (4)).
$(\textrm{W}_0,\ldots,\textrm{W}_l)$
is an i.i.d. copy of the limiting weight variable W (recall (4)).
We now continue with the proof.
Convergence of weights of
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
to the weights of
$F^{\mathbb{G}_n}_{U_n}(r)$
to the weights of
![]() $F^{\mathbb{G}_{\infty}}_0(r)$
. We also note that
$F^{\mathbb{G}_{\infty}}_0(r)$
. We also note that
 \begin{align} &(W_{n,0},\ldots,W_{n,l}) \bigg| \{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\} \nonumber\\[3pt]& {{\stackrel{d}{\rightarrow}}} (W_{\infty,0},\ldots,W_{\infty,l}) \bigg| \{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}. \end{align}
\begin{align} &(W_{n,0},\ldots,W_{n,l}) \bigg| \{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\} \nonumber\\[3pt]& {{\stackrel{d}{\rightarrow}}} (W_{\infty,0},\ldots,W_{\infty,l}) \bigg| \{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}. \end{align}
This is because for any continuity set
![]() $A_0 \times\dots\times A_l$
of
$A_0 \times\dots\times A_l$
of
![]() $(\textrm{W}_0,\ldots,\textrm{W}_l)$
, by (48),
$(\textrm{W}_0,\ldots,\textrm{W}_l)$
, by (48),
 \begin{align*} & \mathbb{P}\left((W_{n,0},\ldots,W_{n,l})\in A_0 \times\dots\times A_l \bigg| Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\right) \\ & \geq \mathbb{E}\left[\sum_{j_0,\ldots,j_l}\frac{1}{n^l}\prod_{k=0}^l{\mathbb{1}_{\left\{W^{(n)}_{j_k}\in A_k\right\}}}\right]= \mathbb{E}\left[\prod_{k=0}^l \left(\frac{1}{n}\sum_{i=1}^n {\mathbb{1}_{\left\{W^{(n)}_i \in A_k\right\}}} \right)\right] \end{align*}
\begin{align*} & \mathbb{P}\left((W_{n,0},\ldots,W_{n,l})\in A_0 \times\dots\times A_l \bigg| Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\right) \\ & \geq \mathbb{E}\left[\sum_{j_0,\ldots,j_l}\frac{1}{n^l}\prod_{k=0}^l{\mathbb{1}_{\left\{W^{(n)}_{j_k}\in A_k\right\}}}\right]= \mathbb{E}\left[\prod_{k=0}^l \left(\frac{1}{n}\sum_{i=1}^n {\mathbb{1}_{\left\{W^{(n)}_i \in A_k\right\}}} \right)\right] \end{align*}
and
 \begin{align*} & \mathbb{P}\left((W_{n,0},\ldots,W_{n,l})\in A_0 \times\cdots\times A_l \bigg| Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\right) \\ & \leq \mathbb{E}\left[\sum_{j_0,\ldots,j_l}\frac{1}{(n-l)^l}\prod_{k=0}^l{\mathbb{1}_{\left\{W^{(n)}_{j_k}\in A_k\right\}}}\right] =\mathbb{E}\left[\prod_{k=0}^l \left(\frac{1}{n-l}\sum_{i=1}^n {\mathbb{1}_{\left\{W^{(n)}_i \in A_k\right\}}} \right)\right], \end{align*}
\begin{align*} & \mathbb{P}\left((W_{n,0},\ldots,W_{n,l})\in A_0 \times\cdots\times A_l \bigg| Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\right) \\ & \leq \mathbb{E}\left[\sum_{j_0,\ldots,j_l}\frac{1}{(n-l)^l}\prod_{k=0}^l{\mathbb{1}_{\left\{W^{(n)}_{j_k}\in A_k\right\}}}\right] =\mathbb{E}\left[\prod_{k=0}^l \left(\frac{1}{n-l}\sum_{i=1}^n {\mathbb{1}_{\left\{W^{(n)}_i \in A_k\right\}}} \right)\right], \end{align*}
where the sums in the last two displays are taken over all cardinality-
![]() $(l+1)$
subsets
$(l+1)$
subsets
![]() $\{j_0,\ldots,j_l\}$
of [n]. Since the right-hand sides of the last two displays are bounded from above by 1, we use dominated convergence and apply (4) to conclude that both right-hand sides converge to
$\{j_0,\ldots,j_l\}$
of [n]. Since the right-hand sides of the last two displays are bounded from above by 1, we use dominated convergence and apply (4) to conclude that both right-hand sides converge to
 \begin{align*} \prod_{k=0}^l \mathbb{P}\left(W \in A_k\right) & = \mathbb{P}\left((\textrm{W}_0,\ldots,\textrm{W}_l)\in A_0\times \cdots \times A_l\right)\\ & = \mathbb{P}\left((W_{\infty,0},\ldots,W_{\infty,l})\in A_0\times \cdots \times A_l \bigg| \Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\right). \end{align*}
\begin{align*} \prod_{k=0}^l \mathbb{P}\left(W \in A_k\right) & = \mathbb{P}\left((\textrm{W}_0,\ldots,\textrm{W}_l)\in A_0\times \cdots \times A_l\right)\\ & = \mathbb{P}\left((W_{\infty,0},\ldots,W_{\infty,l})\in A_0\times \cdots \times A_l \bigg| \Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\right). \end{align*}
Functions counting rooted isomorphisms, and their symmetry properties. Now we proceed to define the functions we use to count the number of isomorphisms between the given rooted graph (H, h) and the Euclidean graph neighborhoods
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
,
$F^{\mathbb{G}_n}_{U_n}(r)$
,
![]() $F^{\mathbb{G}_{\infty}}_0(r)$
. Let the vertices of (H, h) be
$F^{\mathbb{G}_{\infty}}_0(r)$
. Let the vertices of (H, h) be
![]() $v_0,\ldots,v_l$
, where
$v_0,\ldots,v_l$
, where
![]() $h=v_0$
. Let us denote the subset of the set of permutations
$h=v_0$
. Let us denote the subset of the set of permutations
![]() $S(l+1)$
of
$S(l+1)$
of
![]() $\{0,1,\ldots,l\}$
that fix 0 by
$\{0,1,\ldots,l\}$
that fix 0 by
![]() $S_0(l+1)$
; i.e., for all
$S_0(l+1)$
; i.e., for all
![]() $\sigma \in S_0(l+1)$
,
$\sigma \in S_0(l+1)$
,
![]() $\sigma(0)=0$
.
$\sigma(0)=0$
.
Let
![]() $M^S_{l+1}(\mathbb{R})$
denote the space of all symmetric square matrices of order
$M^S_{l+1}(\mathbb{R})$
denote the space of all symmetric square matrices of order
![]() $l+1$
with entries in
$l+1$
with entries in
![]() $\mathbb{R}$
. For each
$\mathbb{R}$
. For each
![]() $n \in \mathbb{N}$
, define the function
$n \in \mathbb{N}$
, define the function
![]() $\mathcal{F}^n_{ (H,h)}\,{:}\, \left(\mathbb{R}^d\right)^{l+1}\times \left(\mathbb{R}^d\right)^{l+1} \times M^S_{l+1}(\mathbb{R}) \to \mathbb{R}$
by
$\mathcal{F}^n_{ (H,h)}\,{:}\, \left(\mathbb{R}^d\right)^{l+1}\times \left(\mathbb{R}^d\right)^{l+1} \times M^S_{l+1}(\mathbb{R}) \to \mathbb{R}$
by
 \begin{equation} \begin{split} \mathcal{F}^n_{ (H,h)}\left(\vec{x},\vec{y},(a_{ij})_{i,j=0}^l\right)\\ \,{:\!=}\,\sum_{\pi \in S_0(l+1)} & \prod_{\{v_i,v_j\}\in E(H)} \left({\mathbb{1}_{\left\{a_{\pi(i)\pi(j)}<\kappa_n\left(\|x_{\pi(i)}-x_{\pi(j)}\|,y_{\pi(i)},y_{\pi(j)}\right)\right\}}}\right) \\& \times \prod_{\{v_i,v_j\}\notin E(H)}\left({\mathbb{1}_{\left\{a_{\pi(i)\pi(j)}>\kappa_n\left(\|x_{\pi(i)}-x_{\pi(j)}\|,y_{\pi(i)},y_{\pi(j)}\right)\right\}}} \right), \end{split} \end{equation}
\begin{equation} \begin{split} \mathcal{F}^n_{ (H,h)}\left(\vec{x},\vec{y},(a_{ij})_{i,j=0}^l\right)\\ \,{:\!=}\,\sum_{\pi \in S_0(l+1)} & \prod_{\{v_i,v_j\}\in E(H)} \left({\mathbb{1}_{\left\{a_{\pi(i)\pi(j)}<\kappa_n\left(\|x_{\pi(i)}-x_{\pi(j)}\|,y_{\pi(i)},y_{\pi(j)}\right)\right\}}}\right) \\& \times \prod_{\{v_i,v_j\}\notin E(H)}\left({\mathbb{1}_{\left\{a_{\pi(i)\pi(j)}>\kappa_n\left(\|x_{\pi(i)}-x_{\pi(j)}\|,y_{\pi(i)},y_{\pi(j)}\right)\right\}}} \right), \end{split} \end{equation}
for
![]() $\vec{x}=(x_0,\dots,x_l), \vec{y}=(y_0,\dots,y_l) \in (\mathbb{R}^d)^{l+1}$
and
$\vec{x}=(x_0,\dots,x_l), \vec{y}=(y_0,\dots,y_l) \in (\mathbb{R}^d)^{l+1}$
and
![]() $(a_{ij})_{i,j=0}^l \in M^S_{l+1}(\mathbb{R})$
. Similarly define the function
$(a_{ij})_{i,j=0}^l \in M^S_{l+1}(\mathbb{R})$
. Similarly define the function
![]() $\mathcal{F}^{\infty}_{ (H,h)}\colon \left(\mathbb{R}^d\right)^{l+1}\times \left(\mathbb{R}^d\right)^{l+1} \times M^S_{l+1}(\mathbb{R})\to \mathbb{R}$
, where
$\mathcal{F}^{\infty}_{ (H,h)}\colon \left(\mathbb{R}^d\right)^{l+1}\times \left(\mathbb{R}^d\right)^{l+1} \times M^S_{l+1}(\mathbb{R})\to \mathbb{R}$
, where
![]() $\mathcal{F}^{\infty}_{ (H,h)}$
is just
$\mathcal{F}^{\infty}_{ (H,h)}$
is just
![]() $\mathcal{F}^n_{ (H,h)}$
with
$\mathcal{F}^n_{ (H,h)}$
with
![]() $\kappa_n$
replaced by
$\kappa_n$
replaced by
![]() $\kappa$
.
$\kappa$
.
Heuristically, we want the indicators
to be the indicators of the events
![]() $\{\text{the edge}\; \{\pi(i),\pi(j)\}\; \text{is present}\}$
. Since in our graphs these events occur independently, each with probability
$\{\text{the edge}\; \{\pi(i),\pi(j)\}\; \text{is present}\}$
. Since in our graphs these events occur independently, each with probability
![]() $\kappa_n\left(\|x_{\pi(i)}-x_{\pi(j)}\|,y_{\pi(i)},y_{\pi(j)}\right)$
when the locations and weights of the vertices
$\kappa_n\left(\|x_{\pi(i)}-x_{\pi(j)}\|,y_{\pi(i)},y_{\pi(j)}\right)$
when the locations and weights of the vertices
![]() $\pi(i)$
and
$\pi(i)$
and
![]() $\pi(j)$
are respectively
$\pi(j)$
are respectively
![]() $(x_{\pi(i)},y_{\pi(i)})$
and
$(x_{\pi(i)},y_{\pi(i)})$
and
![]() $(x_{\pi(j)},y_{\pi(j)})$
, we will take the matrix
$(x_{\pi(j)},y_{\pi(j)})$
, we will take the matrix
![]() $(a_{ij})_{i,j,=0}^l$
to be a symmetric i.i.d. uniform matrix. Before that, we first discuss some symmetry properties of the functions
$(a_{ij})_{i,j,=0}^l$
to be a symmetric i.i.d. uniform matrix. Before that, we first discuss some symmetry properties of the functions
![]() $\mathcal{F}^n_{ (H,h)}$
and
$\mathcal{F}^n_{ (H,h)}$
and
![]() $\mathcal{F}^{\infty}_{ (H,h)}$
.
$\mathcal{F}^{\infty}_{ (H,h)}$
.
Observe the following symmetry: for any permutation
![]() $\pi \in S_0(l+1)$
, and for
$\pi \in S_0(l+1)$
, and for
![]() $ {\bullet}$
being either n or
$ {\bullet}$
being either n or
![]() $\infty$
,
$\infty$
,
 \begin{align*} & \mathcal{F}^{ {\bullet}}_{ (H,h)}\left((x_0,\ldots,x_l),(y_0,\ldots,y_l),(a_{ij})_{i,j=0}^l\right) \\ & = \mathcal{F}^{ {\bullet}}_{ (H,h)}\left((x_{\pi(0)},\ldots,x_{\pi(l)}),(y_{\pi(0)},\ldots,y_{\pi(l)}),(a_{\pi(i)\pi(j)})_{i,j=0}^l\right). \end{align*}
\begin{align*} & \mathcal{F}^{ {\bullet}}_{ (H,h)}\left((x_0,\ldots,x_l),(y_0,\ldots,y_l),(a_{ij})_{i,j=0}^l\right) \\ & = \mathcal{F}^{ {\bullet}}_{ (H,h)}\left((x_{\pi(0)},\ldots,x_{\pi(l)}),(y_{\pi(0)},\ldots,y_{\pi(l)}),(a_{\pi(i)\pi(j)})_{i,j=0}^l\right). \end{align*}
Recall the permutation-invariance of the weights of
![]() $F^{\mathbb{G}_n}_{U_n}(r)$
and
$F^{\mathbb{G}_n}_{U_n}(r)$
and
![]() $F^{\mathbb{G}_{\infty}}_{0}(r)$
from (49) and (50), and note that for
$F^{\mathbb{G}_{\infty}}_{0}(r)$
from (49) and (50), and note that for
![]() $(x_0,\ldots,x_l), (z_0,\ldots,z_l)\in \left(\mathbb{R}^d\right)^{l+1}$
, if there exists a permutation
$(x_0,\ldots,x_l), (z_0,\ldots,z_l)\in \left(\mathbb{R}^d\right)^{l+1}$
, if there exists a permutation
![]() $\pi \in S_0(l+1)$
such that
$\pi \in S_0(l+1)$
such that
then for any
![]() $(a_{ij})_{i,j=0}^l\in M^S_{l+1}(\mathbb{R})$
, conditionally on
$(a_{ij})_{i,j=0}^l\in M^S_{l+1}(\mathbb{R})$
, conditionally on
![]() $\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
,
$\{Y^{(n)}_{U_n}\in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
,
 \begin{align} & \mathcal{F}^n_{ (H,h)}\left((x_0,\ldots,x_l),(W_{n,0},\ldots,W_{n,l}),(a_{ij})_{i,j=0}^l\right) \nonumber \\& \stackrel{d}{=}\mathcal{F}^n_{ (H,h)}\left((z_0,\ldots,z_l),(W_{n,0},\ldots,W_{n,l}),(a_{ij})_{i,j=0}^l)\right), \end{align}
\begin{align} & \mathcal{F}^n_{ (H,h)}\left((x_0,\ldots,x_l),(W_{n,0},\ldots,W_{n,l}),(a_{ij})_{i,j=0}^l\right) \nonumber \\& \stackrel{d}{=}\mathcal{F}^n_{ (H,h)}\left((z_0,\ldots,z_l),(W_{n,0},\ldots,W_{n,l}),(a_{ij})_{i,j=0}^l)\right), \end{align}
and a similar distributional equality holds for
![]() $\mathcal{F}^{\infty}_{ (H,h)}$
, conditionally on
$\mathcal{F}^{\infty}_{ (H,h)}$
, conditionally on
![]() $\{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}$
.
$\{\Gamma_{\infty}(\mathscr{B}^r_{\textbf{0}})=l+1\}$
.
Simplifying the events
![]() $\{F^{\mathbb{G}_n}_{{U_n}}(r)\cong (H,h)\}$
and
$\{F^{\mathbb{G}_n}_{{U_n}}(r)\cong (H,h)\}$
and
![]() $\{F^{\mathbb{G}_{\infty}}_{0}(r) \cong (H,h)\}$
. Now, let
$\{F^{\mathbb{G}_{\infty}}_{0}(r) \cong (H,h)\}$
. Now, let
![]() $(U_{ij})_{i,j=0}^l$
and
$(U_{ij})_{i,j=0}^l$
and
![]() $(U^{\prime}_{ij})_{i,j=0}^l$
be two i.i.d. random elements of
$(U^{\prime}_{ij})_{i,j=0}^l$
be two i.i.d. random elements of
![]() $M^S_{l+1}(\mathbb{R})$
which are also independent from
$M^S_{l+1}(\mathbb{R})$
which are also independent from
![]() $\textbf{X}^{(n)}$
,
$\textbf{X}^{(n)}$
,
![]() $\textbf{W}^{(n)}$
,
$\textbf{W}^{(n)}$
,
![]() $\textbf{X}$
,
$\textbf{X}$
,
![]() $\textbf{W}$
, and
$\textbf{W}$
, and
![]() $\{Y_i\,{:}\,0\leq i\leq l\}$
, where for each
$\{Y_i\,{:}\,0\leq i\leq l\}$
, where for each
![]() $i<j$
,
$i<j$
,
![]() $U_{ij}\sim \text{U}([0,1])$
, all the entries above the diagonal of the random matrix
$U_{ij}\sim \text{U}([0,1])$
, all the entries above the diagonal of the random matrix
![]() $(U_{ij})_{i,j=1}^{l+1}$
are independent, and for each i,
$(U_{ij})_{i,j=1}^{l+1}$
are independent, and for each i,
![]() $U_{ii}\,{:\!=}\,0$
(the diagonal elements will not come into the picture and can be defined arbitrarily).
$U_{ii}\,{:\!=}\,0$
(the diagonal elements will not come into the picture and can be defined arbitrarily).
Let
and
Note from (45) that our target is to show that
![]() $\mathbb{E}\left[\mathcal{A}_n\right]\to \mathbb{E}\left[\mathcal{A}_{\infty}\right]$
, as
$\mathbb{E}\left[\mathcal{A}_n\right]\to \mathbb{E}\left[\mathcal{A}_{\infty}\right]$
, as
![]() $n \to \infty$
.
$n \to \infty$
.
Recall (46). Observe that
since, conditionally on the event
![]() $\{Y^{(n)}_{U_n} \in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, if for some
$\{Y^{(n)}_{U_n} \in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}$
, if for some
![]() $\pi \in S_0(l+1)$
the corresponding term in the sum in
$\pi \in S_0(l+1)$
the corresponding term in the sum in
![]() $\mathcal{F}^n_{ (H,h)}$
is positive, then
$\mathcal{F}^n_{ (H,h)}$
is positive, then
![]() $v_i \mapsto P_{\pi(i)}$
gives a rooted isomorphism (note that the fact that every permutation in
$v_i \mapsto P_{\pi(i)}$
gives a rooted isomorphism (note that the fact that every permutation in
![]() $S_0(l+1)$
fixes 0 ensures that the isomorphism is rooted), and if there is a rooted isomorphism
$S_0(l+1)$
fixes 0 ensures that the isomorphism is rooted), and if there is a rooted isomorphism
![]() $\phi\colon G\to F^{G_n}_{U_n}(r)$
, then the term in the sum corresponding to the permutation
$\phi\colon G\to F^{G_n}_{U_n}(r)$
, then the term in the sum corresponding to the permutation
![]() $\sigma \in S_0(l+1)$
is positive, where
$\sigma \in S_0(l+1)$
is positive, where
![]() $\phi(v_i)=P_{\sigma(i)}$
.
$\phi(v_i)=P_{\sigma(i)}$
.
Using the symmetry (53) with (46), we obtain
 \begin{align} \mathcal{A}_n &\stackrel{d}{=} {\mathbb{1}_{\left\{\mathcal{F}^n_{ (H,h)}\left((Y_0,\ldots,Y_l), (W_{n,0},\ldots,W_{n,l}), (U_{ij})_{i,j=0}^l\right)>0\right\}}}\bigg|{\{Y^{(n)}_{U_n} \in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}}\nonumber \\&\,{=\!:}\,\mathscr{A}_n. \end{align}
\begin{align} \mathcal{A}_n &\stackrel{d}{=} {\mathbb{1}_{\left\{\mathcal{F}^n_{ (H,h)}\left((Y_0,\ldots,Y_l), (W_{n,0},\ldots,W_{n,l}), (U_{ij})_{i,j=0}^l\right)>0\right\}}}\bigg|{\{Y^{(n)}_{U_n} \in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}}\nonumber \\&\,{=\!:}\,\mathscr{A}_n. \end{align}
Using exactly similar arguments for the random variable
![]() $\mathcal{A}_{\infty}$
and the function
$\mathcal{A}_{\infty}$
and the function
![]() $\mathcal{F}^{\infty}_{ (H,h)}$
, we obtain
$\mathcal{F}^{\infty}_{ (H,h)}$
, we obtain
Finally, using that
![]() $(U^{\prime}_{ij})_{i,j=0}^l\stackrel{d}{=}(U_{ij})_{i,j=0}^l$
, and that both the matrices
$(U^{\prime}_{ij})_{i,j=0}^l\stackrel{d}{=}(U_{ij})_{i,j=0}^l$
, and that both the matrices
![]() $U_{ij}$
and
$U_{ij}$
and
![]() $U^{\prime}_{ij}$
are independent of everything else, it is easy to see that
$U^{\prime}_{ij}$
are independent of everything else, it is easy to see that
Conclusion. Using (51), and using the convergence of connection functions (5), for any
![]() $(x_0,\ldots,x_l) \in \left( \mathbb{R}^d \right)^{l+1}$
such that the collection of positive reals
$(x_0,\ldots,x_l) \in \left( \mathbb{R}^d \right)^{l+1}$
such that the collection of positive reals
![]() $\{\|x_i-x_j\|\,{:}\,1\leq i,j, \leq l,i\neq j\}$
avoids some set of measure zero, and for any
$\{\|x_i-x_j\|\,{:}\,1\leq i,j, \leq l,i\neq j\}$
avoids some set of measure zero, and for any
![]() $(a_{ij})_{i,j=0}^l \in M^S_{l+1}([0,1])$
, as
$(a_{ij})_{i,j=0}^l \in M^S_{l+1}([0,1])$
, as
![]() $n\rightarrow \infty$
,
$n\rightarrow \infty$
,
 \begin{equation} \begin{split} & \mathcal{F}^n_{ (H,h)}\left((x_0,\ldots,x_l),(W_{n,0},\ldots,W_{n,l}),(a_{ij})_{i,j=0}^l \right)\bigg|{\{Y^{(n)}_{U_n} \in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}} \\ & {{\stackrel{d}{\rightarrow}}} \mathcal{F}^{\infty}_{ (H,h)}\left((x_0,\ldots,x_l), (W_{\infty,0},\ldots,W_{\infty,l}), (a_{ij})_{i,j=0}^l\right)\bigg|{\{|V(F^{\mathbb{G}_{\infty}}_{0}(r))|=l+1\}}, \end{split} \end{equation}
\begin{equation} \begin{split} & \mathcal{F}^n_{ (H,h)}\left((x_0,\ldots,x_l),(W_{n,0},\ldots,W_{n,l}),(a_{ij})_{i,j=0}^l \right)\bigg|{\{Y^{(n)}_{U_n} \in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}} \\ & {{\stackrel{d}{\rightarrow}}} \mathcal{F}^{\infty}_{ (H,h)}\left((x_0,\ldots,x_l), (W_{\infty,0},\ldots,W_{\infty,l}), (a_{ij})_{i,j=0}^l\right)\bigg|{\{|V(F^{\mathbb{G}_{\infty}}_{0}(r))|=l+1\}}, \end{split} \end{equation}
which implies that, as
![]() $n\rightarrow \infty$
, writing
$n\rightarrow \infty$
, writing
![]() $\vec{x}=(x_0,x_1\dots,x_n)$
,
$\vec{x}=(x_0,x_1\dots,x_n)$
,
 \begin{equation} \begin{split} & \mathbb{P}\left(\mathcal{F}^n_{ (H,h)}\left({\vec{x}},(W_{n,0},\ldots,W_{n,l}),(a_{ij})_{i,j=0}^l \right)>0 \bigg| \{Y^{(n)}_{U_n} \in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}\right) \\ & \to \mathbb{P}\left(\mathcal{F}^{\infty}_{ (H,h)}\left({\vec{x}}, (W_{\infty,0},\ldots,W_{\infty,l}), (a_{ij})_{i,j=0}^l\right)>0 \bigg| \{|V(F^{\mathbb{G}_{\infty}}_{0}(r))|=l+1\}\right). \end{split}\end{equation}
\begin{equation} \begin{split} & \mathbb{P}\left(\mathcal{F}^n_{ (H,h)}\left({\vec{x}},(W_{n,0},\ldots,W_{n,l}),(a_{ij})_{i,j=0}^l \right)>0 \bigg| \{Y^{(n)}_{U_n} \in A^r_n, |V(F^{\mathbb{G}_n}_{{U_n}}(r))|=l+1\}\right) \\ & \to \mathbb{P}\left(\mathcal{F}^{\infty}_{ (H,h)}\left({\vec{x}}, (W_{\infty,0},\ldots,W_{\infty,l}), (a_{ij})_{i,j=0}^l\right)>0 \bigg| \{|V(F^{\mathbb{G}_{\infty}}_{0}(r))|=l+1\}\right). \end{split}\end{equation}
Combining (61) with the fact that both
![]() $(Y_0,\ldots, Y_l)$
and
$(Y_0,\ldots, Y_l)$
and
![]() $(U_{ij})_{i,j=0}^l$
are independent of
$(U_{ij})_{i,j=0}^l$
are independent of
![]() $\textbf{W}^{(n)}$
and
$\textbf{W}^{(n)}$
and
![]() $\textbf{W}$
, and the fact that the random variables
$\textbf{W}$
, and the fact that the random variables
![]() $\|Y_i-Y_j\|$
for
$\|Y_i-Y_j\|$
for
![]() $1\leq i,j \leq l$
with
$1\leq i,j \leq l$
with
![]() $i \neq j$
are continuous random variables and hence almost surely avoid sets of measure 0, we have (recalling
$i \neq j$
are continuous random variables and hence almost surely avoid sets of measure 0, we have (recalling
![]() $\mathscr{A}_n$
and
$\mathscr{A}_n$
and
![]() $\mathscr{A}_{ {\infty}}$
from (57) and (59))
$\mathscr{A}_{ {\infty}}$
from (57) and (59))
which implies, using dominated convergence (note that domination by 1 works), that
as
![]() $n \to \infty$
.
$n \to \infty$
.
Hence, again using (57) and (59), we have
![]() $\mathbb{E}\left[\mathcal{A}_n\right] \to \mathbb{E}\left[\mathcal{A}_{ {\infty}}\right]$
, which is just (45), as can be seen by recalling the definition of
$\mathbb{E}\left[\mathcal{A}_n\right] \to \mathbb{E}\left[\mathcal{A}_{ {\infty}}\right]$
, which is just (45), as can be seen by recalling the definition of
![]() $\mathcal{A}_n$
from (54) and the definition of
$\mathcal{A}_n$
from (54) and the definition of
![]() $\mathcal{A}_{ {\infty}}$
from (55). This completes the proof of Proposition 3. □
$\mathcal{A}_{ {\infty}}$
from (55). This completes the proof of Proposition 3. □
3.3. Proofs of path-counting results: Lemma 2 and Corollary 7
Proof of Lemma 2
. Recall the notation
![]() $\mathscr{B}^r_x$
from (30), which denotes the open Euclidean ball of radius r in
$\mathscr{B}^r_x$
from (30), which denotes the open Euclidean ball of radius r in
![]() $\mathbb{R}^d$
centered at
$\mathbb{R}^d$
centered at
![]() $x \in \mathbb{R}^d$
. We first prove (35).
$x \in \mathbb{R}^d$
. We first prove (35).
We first bound
![]() $\mathbb{W}_j(\textbf{0},x_1,\ldots,x_j)$
from above by
$\mathbb{W}_j(\textbf{0},x_1,\ldots,x_j)$
from above by
![]() $\mathbb{E}\left[\kappa(\|x_j-x_{j-1}\|,W_0,W_1)\right]$
, where
$\mathbb{E}\left[\kappa(\|x_j-x_{j-1}\|,W_0,W_1)\right]$
, where
![]() $W_0$
and
$W_0$
and
![]() $W_1$
are i.i.d. copies of the limiting weight distribution W (recall (4)). Then we apply the change of variables
$W_1$
are i.i.d. copies of the limiting weight distribution W (recall (4)). Then we apply the change of variables
where
![]() $x_0=\textbf{0}$
, and apply Fubini’s theorem to obtain
$x_0=\textbf{0}$
, and apply Fubini’s theorem to obtain
 \begin{align} & \int_{\mathbb{R}^d}\cdots \int_{\mathbb{R}^d} \mathbb{W}_j(\textbf{0},x_1\ldots,x_j) \nonumber\\&\hspace{50 pt} \mathbb{1}_{\left\{\|x_1\|<a^m\right\}}\prod_{i=1}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\mathbb{1}_{\left\{\|x_j-x_{j-1}\|>a^{m^j}\right\}} dx_1\cdots dx_j \nonumber\\ & \leq \int_{\mathscr{B}^{a^m}_{\textbf{0}}}\cdots \int_{\mathscr{B}^{a^{m^{j-1}}}_{\textbf{0}}}\int_{\mathbb{R}^d \setminus \mathscr{B}^{a^{m^j}}_{\textbf{0}}} \mathbb{E}\left[\kappa(\|z_j\|,W_0,W_1)\right] dz_jdz_{j-1}\cdots dz_1 \nonumber\\ & \leq C_0 (a^m)^d \cdots (a^{m^{j-1}})^d \int_{\mathbb{R}^d \setminus \mathscr{B}^{a^{m^j}}_{\textbf{0}}} \mathbb{E}\left[\kappa(\|z\|,W_0,W_1)\right] dz, \end{align}
\begin{align} & \int_{\mathbb{R}^d}\cdots \int_{\mathbb{R}^d} \mathbb{W}_j(\textbf{0},x_1\ldots,x_j) \nonumber\\&\hspace{50 pt} \mathbb{1}_{\left\{\|x_1\|<a^m\right\}}\prod_{i=1}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\mathbb{1}_{\left\{\|x_j-x_{j-1}\|>a^{m^j}\right\}} dx_1\cdots dx_j \nonumber\\ & \leq \int_{\mathscr{B}^{a^m}_{\textbf{0}}}\cdots \int_{\mathscr{B}^{a^{m^{j-1}}}_{\textbf{0}}}\int_{\mathbb{R}^d \setminus \mathscr{B}^{a^{m^j}}_{\textbf{0}}} \mathbb{E}\left[\kappa(\|z_j\|,W_0,W_1)\right] dz_jdz_{j-1}\cdots dz_1 \nonumber\\ & \leq C_0 (a^m)^d \cdots (a^{m^{j-1}})^d \int_{\mathbb{R}^d \setminus \mathscr{B}^{a^{m^j}}_{\textbf{0}}} \mathbb{E}\left[\kappa(\|z\|,W_0,W_1)\right] dz, \end{align}
for some constant
![]() $C_0>0$
. Recall the polynomial domination from (6) and the assumption
$C_0>0$
. Recall the polynomial domination from (6) and the assumption
![]() $\alpha>d$
in Theorem 1.
$\alpha>d$
in Theorem 1.
We note, by first making a change of variables to bring the integral
down to an integral on
![]() $\mathbb{R}$
, and then using (6), that for any m sufficiently large so that
$\mathbb{R}$
, and then using (6), that for any m sufficiently large so that
![]() $a^{m^j}>t_0$
,
$a^{m^j}>t_0$
,
for some constant
![]() $C_1>0$
.
$C_1>0$
.
Combining (63) with (62), we note that for some constant
![]() $C_2>0$
,
$C_2>0$
,
 \begin{align} &\int_{\mathbb{R}^d}\cdots \int_{\mathbb{R}^d} \mathbb{W}_j(\textbf{0},x_1,\ldots,x_j)\nonumber\\&\hspace{50 pt} \mathbb{1}_{\left\{\|x_1\|<a^m\right\}}\prod_{i=1}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\mathbb{1}_{\left\{\|x_j-x_{j-1}\|>a^{m^j}\right\}} dx_1\cdots dx_j\nonumber \\& \leq C_2 \frac{1}{a^{dm^j\left(\frac{\alpha}{d}-1-\frac{1}{m}-\cdots-\frac{1}{m^{j-1}} \right)}} \to 0, \end{align}
\begin{align} &\int_{\mathbb{R}^d}\cdots \int_{\mathbb{R}^d} \mathbb{W}_j(\textbf{0},x_1,\ldots,x_j)\nonumber\\&\hspace{50 pt} \mathbb{1}_{\left\{\|x_1\|<a^m\right\}}\prod_{i=1}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\mathbb{1}_{\left\{\|x_j-x_{j-1}\|>a^{m^j}\right\}} dx_1\cdots dx_j\nonumber \\& \leq C_2 \frac{1}{a^{dm^j\left(\frac{\alpha}{d}-1-\frac{1}{m}-\cdots-\frac{1}{m^{j-1}} \right)}} \to 0, \end{align}
as
![]() $m \to \infty$
, since
$m \to \infty$
, since
![]() $\frac{\alpha}{d}>1$
. This finishes the proof of (35).
$\frac{\alpha}{d}>1$
. This finishes the proof of (35).
We next go into the proof of (34). Recall the definition of
![]() $\mathbb{W}^{v_1,\ldots,v_j}_{n}(x_0,x_1,\ldots,x_j)$
from (32), where
$\mathbb{W}^{v_1,\ldots,v_j}_{n}(x_0,x_1,\ldots,x_j)$
from (32), where
![]() $v_0=U_n$
is the uniformly chosen vertex of
$v_0=U_n$
is the uniformly chosen vertex of
![]() $\mathbb{G}_n$
.
$\mathbb{G}_n$
.
We use the notation
For fixed
![]() $x_0,\ldots,x_j \in \mathbb{R}^d$
, we define the function
$x_0,\ldots,x_j \in \mathbb{R}^d$
, we define the function
![]() $\mathcal{W}^{\vec{x}}_n\,{:}\,\mathbb{R}^{j+1} \to \mathbb{R}$
by
$\mathcal{W}^{\vec{x}}_n\,{:}\,\mathbb{R}^{j+1} \to \mathbb{R}$
by
for
![]() $\vec{t}=(t_0,t_1,\dots,t_j) \in \mathbb{R}^{j+1}$
.
$\vec{t}=(t_0,t_1,\dots,t_j) \in \mathbb{R}^{j+1}$
.
Note that
 \begin{align} & \frac{1}{n^j}\sum_{v_1,\ldots,v_j \in [n]} \mathbb{W}^{\vec{v}}_{n}(\vec{x}) = \mathbb{E}\left[\frac{1}{n^{j+1}} \sum_{i_0,i_1,\ldots,i_j} \mathcal{W}^{\vec{x}}_{n}(W^{(n)}_{i_0},\ldots,W^{(n)}_{i_j})\right], \end{align}
\begin{align} & \frac{1}{n^j}\sum_{v_1,\ldots,v_j \in [n]} \mathbb{W}^{\vec{v}}_{n}(\vec{x}) = \mathbb{E}\left[\frac{1}{n^{j+1}} \sum_{i_0,i_1,\ldots,i_j} \mathcal{W}^{\vec{x}}_{n}(W^{(n)}_{i_0},\ldots,W^{(n)}_{i_j})\right], \end{align}
where we have used (32) and the fact that
![]() $v_0=U_n$
is uniformly distributed over n.
$v_0=U_n$
is uniformly distributed over n.
Since clearly
 \begin{align*} \mathbb{E}\left[\frac{1}{n^{j+1}} \sum_{i_0,i_1,\ldots,i_j} \mathcal{W}^{\vec{x}}_{n}(W^{(n)}_{i_0},\ldots,W^{(n)}_{i_j})\right] = \mathbb{E}\left[\mathcal{W}^{\vec{x}}_{n}(W^{(n)}_{U_{n,0}},\ldots,W^{(n)}_{U_{n,j}})\right], \end{align*}
\begin{align*} \mathbb{E}\left[\frac{1}{n^{j+1}} \sum_{i_0,i_1,\ldots,i_j} \mathcal{W}^{\vec{x}}_{n}(W^{(n)}_{i_0},\ldots,W^{(n)}_{i_j})\right] = \mathbb{E}\left[\mathcal{W}^{\vec{x}}_{n}(W^{(n)}_{U_{n,0}},\ldots,W^{(n)}_{U_{n,j}})\right], \end{align*}
where
![]() $U_{n,0},\ldots,U_{n,j}$
is an i.i.d. collection of uniformly distributed random variables on
$U_{n,0},\ldots,U_{n,j}$
is an i.i.d. collection of uniformly distributed random variables on
![]() $[n]=\{1,\ldots,n\}$
, we can take
$[n]=\{1,\ldots,n\}$
, we can take
![]() $h_n$
in (8) to be
$h_n$
in (8) to be
![]() $\mathcal{W}^{\vec{x}}_{n}$
and conclude (recalling the definition of
$\mathcal{W}^{\vec{x}}_{n}$
and conclude (recalling the definition of
![]() $\mathbb{W}_j(\vec{x})=\mathbb{W}_j(x_0,x_1\cdots,x_j)$
from (33)) that
$\mathbb{W}_j(\vec{x})=\mathbb{W}_j(x_0,x_1\cdots,x_j)$
from (33)) that
as
![]() $n \to \infty$
. Now, (34) can be concluded using (67), a routine change of variables, Fatou’s lemma, and (35). □
$n \to \infty$
. Now, (34) can be concluded using (67), a routine change of variables, Fatou’s lemma, and (35). □
Remark 8. (Efficacy of our bounds.) In the proof of Lemma 2, we have bounded
![]() $\mathbb{W}_j(\textbf{0},x_1,\ldots,x_j)$
from above by
$\mathbb{W}_j(\textbf{0},x_1,\ldots,x_j)$
from above by
That is, we have bounded all except the last term in the product inside the expectation
![]() $\mathbb{W}_j(\textbf{0},x_1,\ldots,x_j)$
by 1. This is usually a poor bound. However, as we see in the proof, this loss is well compensated by the strong double-exponential growth of
$\mathbb{W}_j(\textbf{0},x_1,\ldots,x_j)$
by 1. This is usually a poor bound. However, as we see in the proof, this loss is well compensated by the strong double-exponential growth of
![]() $r=r(a,m,K)$
(recall (36)). In particular, for our purpose, we have been able to avoid the question of how correlated the random variables
$r=r(a,m,K)$
(recall (36)). In particular, for our purpose, we have been able to avoid the question of how correlated the random variables
![]() $\kappa(\|x_0-x_1\|,W^{(0)},W^{(1)})$
and
$\kappa(\|x_0-x_1\|,W^{(0)},W^{(1)})$
and
![]() $\kappa(\|x_1-x_2\|,W^{(1)},W^{(2)})$
are, where
$\kappa(\|x_1-x_2\|,W^{(1)},W^{(2)})$
are, where
![]() $x_0,x_1,x_2 \in \mathbb{R}^d$
, and
$x_0,x_1,x_2 \in \mathbb{R}^d$
, and
![]() $W^{(0)},W^{(1)},W^{(2)}$
are i.i.d. copies of the limiting weight distribution. We believe this question to be hard to tackle in general, under our general assumptions on
$W^{(0)},W^{(1)},W^{(2)}$
are i.i.d. copies of the limiting weight distribution. We believe this question to be hard to tackle in general, under our general assumptions on
![]() $\kappa$
as formulated in Assumption 3.
$\kappa$
as formulated in Assumption 3.
Next we go into the proof of Corollary 7.
Proof of Corollary 7 . Recall the definition of the distance of an edge from a vertex from (31). Also recall the abbreviations in (37).
We begin by analyzing the event
![]() $\{BF_{n,r}\neq B_n\}$
. Note that if
$\{BF_{n,r}\neq B_n\}$
. Note that if
![]() $\|Y^{(n)}_i-Y^{(n)}_j\|<a^{m^{L+1}}$
for every edge
$\|Y^{(n)}_i-Y^{(n)}_j\|<a^{m^{L+1}}$
for every edge
![]() $\{i,j\}$
in
$\{i,j\}$
in
![]() $B_n$
that is at graph distance L (
$B_n$
that is at graph distance L (
![]() $0\leq L \leq K-1$
) from the root
$0\leq L \leq K-1$
) from the root
![]() $U_n$
, then
$U_n$
, then
![]() $B_n$
is a subgraph of
$B_n$
is a subgraph of
![]() $F_{n,r}$
with the same root
$F_{n,r}$
with the same root
![]() ${U_n}$
, which implies that
${U_n}$
, which implies that
![]() $BF_{n,r}=B_n$
. Hence, the event
$BF_{n,r}=B_n$
. Hence, the event
![]() $\{BF_{n,r}\neq B_n\}$
implies the event
$\{BF_{n,r}\neq B_n\}$
implies the event
where a bad edge is an edge
![]() $\{i,j\}$
in
$\{i,j\}$
in
![]() $B_n$
with
$B_n$
with
![]() $\|Y^{(n)}_i-Y^{(n)}_j\|>a^{m^{L+1}}$
, where
$\|Y^{(n)}_i-Y^{(n)}_j\|>a^{m^{L+1}}$
, where
![]() $0\leq L \leq K-1$
is the graph distance of the edge
$0\leq L \leq K-1$
is the graph distance of the edge
![]() $\{i,j\}$
from the root
$\{i,j\}$
from the root
![]() $U_n$
of
$U_n$
of
![]() $B_n$
.
$B_n$
.

Figure 2. Illustration demonstrating bad edges. The star is the root. The dashed edges are bad: each of them connects a pair of vertices whose locations are at least
![]() $a^{m^{L+1}}$
apart, where L is the distance of the edge from the root. The solid edges are good.
$a^{m^{L+1}}$
apart, where L is the distance of the edge from the root. The solid edges are good.
Therefore,
By a similar argument,
where the event
![]() $\textbf{Bad}_r$
is similarly defined for the rooted graph
$\textbf{Bad}_r$
is similarly defined for the rooted graph
![]() $(\mathbb{G}_{\infty},0)$
.
$(\mathbb{G}_{\infty},0)$
.
Define the event
![]() $\mathcal{I}_{n,j}$
, for
$\mathcal{I}_{n,j}$
, for
![]() $n \in \mathbb{N},j \in [n]$
, as
$n \in \mathbb{N},j \in [n]$
, as
 \begin{align} \mathcal{I}_{n,j}\,{:\!=}\, & \{\exists\;v_1,\ldots,v_j \in V(\mathbb{G}_n)=[n]\,{:}\,\{v_0,v_1,\ldots,v_j\}\;\text{is a}\;j\text{-path in}\;(\mathbb{G}_n,U_n)\; \text{starting from} \nonumber\\[3pt] & \text{the root}\;v_0=U_n,\; \|Y^{(n)}_{v_{i-1}}-Y^{(n)}_{v_i}\|<a^{m^{i}} \forall {i \in[j-1]}, \|Y^{(n)}_{v_{j-1}}-Y^{(n)}_{v_j}\|>a^{m^{j}} \}. \end{align}
\begin{align} \mathcal{I}_{n,j}\,{:\!=}\, & \{\exists\;v_1,\ldots,v_j \in V(\mathbb{G}_n)=[n]\,{:}\,\{v_0,v_1,\ldots,v_j\}\;\text{is a}\;j\text{-path in}\;(\mathbb{G}_n,U_n)\; \text{starting from} \nonumber\\[3pt] & \text{the root}\;v_0=U_n,\; \|Y^{(n)}_{v_{i-1}}-Y^{(n)}_{v_i}\|<a^{m^{i}} \forall {i \in[j-1]}, \|Y^{(n)}_{v_{j-1}}-Y^{(n)}_{v_j}\|>a^{m^{j}} \}. \end{align}
A simple union bound gives
 \begin{equation} \mathbb{P}\left(\textbf{Bad}_{r,n}\right)\leq \sum_{j=1}^K\mathbb{P}\left( \mathcal{I}_{n,j}\right). \end{equation}
\begin{equation} \mathbb{P}\left(\textbf{Bad}_{r,n}\right)\leq \sum_{j=1}^K\mathbb{P}\left( \mathcal{I}_{n,j}\right). \end{equation}
Similarly,
 \begin{equation} \mathbb{P}\left(\textbf{Bad}_r\right) \leq \sum_{j=1}^K \mathbb{P}\left(\mathcal{I}_j\right), \end{equation}
\begin{equation} \mathbb{P}\left(\textbf{Bad}_r\right) \leq \sum_{j=1}^K \mathbb{P}\left(\mathcal{I}_j\right), \end{equation}
where the event
![]() $\mathcal{I}_j$
for
$\mathcal{I}_j$
for
![]() $j \in \mathbb{N}$
is similarly defined for the rooted graph
$j \in \mathbb{N}$
is similarly defined for the rooted graph
![]() $(\mathbb{G}_{\infty},0)$
.
$(\mathbb{G}_{\infty},0)$
.
Note that since K is fixed, it suffices to prove that
![]() $\lim_{m \to \infty} \limsup_{n \to \infty} \mathbb{P}\left(\mathcal{I}_{n,j}\right) = 0$
and
$\lim_{m \to \infty} \limsup_{n \to \infty} \mathbb{P}\left(\mathcal{I}_{n,j}\right) = 0$
and
![]() $\lim_{m \to \infty} \limsup_{n \to \infty} \mathbb{P}\left(\mathcal{I}_{j}\right) = 0$
for
$\lim_{m \to \infty} \limsup_{n \to \infty} \mathbb{P}\left(\mathcal{I}_{j}\right) = 0$
for
![]() $1 \le j \le K$
.
$1 \le j \le K$
.
We proceed by bounding the probabilities
![]() $\mathbb{P}\left(\mathcal{I}_{n,j}\right)$
and
$\mathbb{P}\left(\mathcal{I}_{n,j}\right)$
and
![]() $\mathbb{P}\left(\mathcal{I}_{j}\right)$
. Recall that we use
$\mathbb{P}\left(\mathcal{I}_{j}\right)$
. Recall that we use
![]() $v_0$
to denote the typical vertex
$v_0$
to denote the typical vertex
![]() $U_n$
of
$U_n$
of
![]() $\mathbb{G}_n$
from the definition of the event
$\mathbb{G}_n$
from the definition of the event
![]() $\mathcal{I}_{n,j}$
from (71). Note that, by Markov’s inequality, using the notation
$\mathcal{I}_{n,j}$
from (71). Note that, by Markov’s inequality, using the notation
![]() $\vec{v}=(v_0,v_1,\ldots,v_n)$
,
$\vec{v}=(v_0,v_1,\ldots,v_n)$
,
 \begin{equation}\begin{split} & \mathbb{P}\left(\mathcal{I}_{n,j}\right) \leq \\& \sum_{{v_1},\ldots,{v_j} \in [n]} \mathbb{P}\left(\vec{v}\;\text{is a}\;j\text{-path},\; \|Y^{(n)}_{v_{i-1}}-Y^{(n)}_{v_i}\|\lt a^{m^{i}}\; \forall {i \in[j-1]}, \|Y^{(n)}_{v_{j-1}}-Y^{(n)}_{v_j}\|\gt a^{m^{j}}\right). \end{split} \end{equation}
\begin{equation}\begin{split} & \mathbb{P}\left(\mathcal{I}_{n,j}\right) \leq \\& \sum_{{v_1},\ldots,{v_j} \in [n]} \mathbb{P}\left(\vec{v}\;\text{is a}\;j\text{-path},\; \|Y^{(n)}_{v_{i-1}}-Y^{(n)}_{v_i}\|\lt a^{m^{i}}\; \forall {i \in[j-1]}, \|Y^{(n)}_{v_{j-1}}-Y^{(n)}_{v_j}\|\gt a^{m^{j}}\right). \end{split} \end{equation}
For convenience, for
![]() $v_0,\ldots,v_j \in [n]$
, we define the event
$v_0,\ldots,v_j \in [n]$
, we define the event
We compute
 \begin{align} & \mathbb{P}\left(\{v_0,v_1,\ldots,v_j\}\;j\text{-path},\; \|Y^{(n)}_{v_{i-1}}-Y^{(n)}_{v_i}\|<a^{m^{i}}\; \forall {i \in[j-1]}, \|Y^{(n)}_{v_{j-1}}-Y^{(n)}_{v_j}\|>a^{m^{j}}\right) \nonumber \\& = \mathbb{E}\left[\mathbb{1}_{\mathcal{E}_{n,j}(\vec{v})}\;\mathbb{P}\left(\{v_0,v_1,\ldots,v_j\}\;j\text{-path} \bigg| Y^{(n)}_{v_0},\ldots,Y^{(n)}_{v_j},W^{(n)}_{v_0},\ldots,W^{(n)}_{v_j}\right)\right] \nonumber \\& = \mathbb{E}\left[\mathbb{1}_{\mathcal{E}_{n,j}(\vec{v})}\;\kappa_n\left(\|Y^{(n)}_{v_0}-Y^{(n)}_{v_1}\|,W^{(n)}_{v_0},W^{(n)}_{v_1}\right)\cdots\kappa_n\left(\|Y^{(n)}_{v_{j-1}}-Y^{(n)}_{v_j}\|,W^{(n)}_{v_{j-1}},W^{(n)}_{v_j}\right)\right]. \end{align}
\begin{align} & \mathbb{P}\left(\{v_0,v_1,\ldots,v_j\}\;j\text{-path},\; \|Y^{(n)}_{v_{i-1}}-Y^{(n)}_{v_i}\|<a^{m^{i}}\; \forall {i \in[j-1]}, \|Y^{(n)}_{v_{j-1}}-Y^{(n)}_{v_j}\|>a^{m^{j}}\right) \nonumber \\& = \mathbb{E}\left[\mathbb{1}_{\mathcal{E}_{n,j}(\vec{v})}\;\mathbb{P}\left(\{v_0,v_1,\ldots,v_j\}\;j\text{-path} \bigg| Y^{(n)}_{v_0},\ldots,Y^{(n)}_{v_j},W^{(n)}_{v_0},\ldots,W^{(n)}_{v_j}\right)\right] \nonumber \\& = \mathbb{E}\left[\mathbb{1}_{\mathcal{E}_{n,j}(\vec{v})}\;\kappa_n\left(\|Y^{(n)}_{v_0}-Y^{(n)}_{v_1}\|,W^{(n)}_{v_0},W^{(n)}_{v_1}\right)\cdots\kappa_n\left(\|Y^{(n)}_{v_{j-1}}-Y^{(n)}_{v_j}\|,W^{(n)}_{v_{j-1}},W^{(n)}_{v_j}\right)\right]. \end{align}
Recall the notation
![]() $\mathbb{W}^{v_1,\ldots,v_j}_{n}$
from (32). Using Fubini’s theorem and the fact that
$\mathbb{W}^{v_1,\ldots,v_j}_{n}$
from (32). Using Fubini’s theorem and the fact that
![]() $\{Y^{(n)}_{v_0},Y^{(n)}_{v_1},\ldots,Y^{(n)}_{v_j}\}$
is an i.i.d. collection of
$\{Y^{(n)}_{v_0},Y^{(n)}_{v_1},\ldots,Y^{(n)}_{v_j}\}$
is an i.i.d. collection of
![]() $j+1$
uniform random variables on
$j+1$
uniform random variables on
![]() $I_n$
, recalling (75), and using the notation
$I_n$
, recalling (75), and using the notation
![]() $\vec{x}=(x_0,x_1,\dots,x_j)$
, we find that (76) becomes
$\vec{x}=(x_0,x_1,\dots,x_j)$
, we find that (76) becomes
 \begin{equation} \begin{split} \frac{1}{n^{j+1}} \int_{I_n}\cdots\int_{I_n} \mathbb{W}^{v_1,\ldots,v_j}_{n}(\vec{x}) \prod_{i=0}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\mathbb{1}_{\left\{\|x_{j}-x_{j-1}\|>a^{m^j}\right\}} dx_{0}\cdots dx_j. \end{split} \end{equation}
\begin{equation} \begin{split} \frac{1}{n^{j+1}} \int_{I_n}\cdots\int_{I_n} \mathbb{W}^{v_1,\ldots,v_j}_{n}(\vec{x}) \prod_{i=0}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\mathbb{1}_{\left\{\|x_{j}-x_{j-1}\|>a^{m^j}\right\}} dx_{0}\cdots dx_j. \end{split} \end{equation}
 \begin{align} \mathbb{P}\left(\mathcal{I}_{n,j}\right) &\leq \frac{1}{n^{j+1}}\int_{I_n}\cdots\int_{I_n} \sum_{v_1,\ldots,v_j \in [n]}\mathbb{W}^{v_1,\ldots,v_j}_{n}(\vec{x}) \nonumber\\ &\quad \times \prod_{i=0}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\mathbb{1}_{\left\{\|x_{j}-x_{j-1}\|>a^{m^j}\right\}} dx_{0}\cdots dx_j. \end{align}
\begin{align} \mathbb{P}\left(\mathcal{I}_{n,j}\right) &\leq \frac{1}{n^{j+1}}\int_{I_n}\cdots\int_{I_n} \sum_{v_1,\ldots,v_j \in [n]}\mathbb{W}^{v_1,\ldots,v_j}_{n}(\vec{x}) \nonumber\\ &\quad \times \prod_{i=0}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\mathbb{1}_{\left\{\|x_{j}-x_{j-1}\|>a^{m^j}\right\}} dx_{0}\cdots dx_j. \end{align}
Recall the notation
![]() $\mathbb{W}_j$
from (33). Similarly, by the multivariate Mecke formula for Poisson processes [Reference Last and Penrose27, Theorem 4.4],
$\mathbb{W}_j$
from (33). Similarly, by the multivariate Mecke formula for Poisson processes [Reference Last and Penrose27, Theorem 4.4],
 \begin{align} \mathbb{P}\left(\mathcal{I}_j\right) &\leq \int_{\mathbb{R}^d}\cdots \int_{\mathbb{R}^d} \mathbb{W}_j(\textbf{0},x_1,\ldots,x_j) \mathbb{1}_{\left\{\|x_1\|<a^m\right\}}\nonumber\\ &\quad \times \prod_{i=1}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\mathbb{1}_{\left\{\|x_j-x_{j-1}\|>a^{m^j}\right\}} dx_1\dots dx_j. \end{align}
\begin{align} \mathbb{P}\left(\mathcal{I}_j\right) &\leq \int_{\mathbb{R}^d}\cdots \int_{\mathbb{R}^d} \mathbb{W}_j(\textbf{0},x_1,\ldots,x_j) \mathbb{1}_{\left\{\|x_1\|<a^m\right\}}\nonumber\\ &\quad \times \prod_{i=1}^{j-2}\mathbb{1}_{\left\{\|x_{i+1}-x_i\|<a^{m^{i+1}}\right\}}\mathbb{1}_{\left\{\|x_j-x_{j-1}\|>a^{m^j}\right\}} dx_1\dots dx_j. \end{align}
Now we apply Lemma 2 for the bounds (79) and (77), and use the bounds (69), (70), (72), and (73) to conclude Corollary 7. □
Remark 9. (A general estimate.) Recall the notation (37), and recall r(a, m, K) from (36). Note that the bound (69) is true even when one has
![]() $a=a_n$
and
$a=a_n$
and
![]() $K=K_n$
in
$K=K_n$
in
![]() $r=r(a_n,m,K_n)$
, and so is the simple union bound (72). The integral bound (78) also works in this generality. Recalling the definition of the function
$r=r(a_n,m,K_n)$
, and so is the simple union bound (72). The integral bound (78) also works in this generality. Recalling the definition of the function
![]() $\mathcal{W}^{(x_0,\ldots,x_j)}_n$
from (65), the equality (66), and the display below it, bounding
$\mathcal{W}^{(x_0,\ldots,x_j)}_n$
from (65), the equality (66), and the display below it, bounding
![]() $\mathbb{E}\left[\mathcal{W}^{(x_0,\ldots,x_j)}_{n}(W^{(n)}_{U_{n,0}},\ldots,W^{(n)}_{U_{n,j}})\right]$
from above by
$\mathbb{E}\left[\mathcal{W}^{(x_0,\ldots,x_j)}_{n}(W^{(n)}_{U_{n,0}},\ldots,W^{(n)}_{U_{n,j}})\right]$
from above by
![]() $\mathbb{E}\left[\kappa_n(\|x_j-x_{j-1}\|,W^{(n)}_{U_{n,j}},W^{(n)}_{U_{n,j-1}})\right]$
(where
$\mathbb{E}\left[\kappa_n(\|x_j-x_{j-1}\|,W^{(n)}_{U_{n,j}},W^{(n)}_{U_{n,j-1}})\right]$
(where
![]() $U_{n,0},\dots,U_{n,j}$
are i.i.d. uniformly distributed random variables on [n]), and making an easy change of variable, we obtain the general bound
$U_{n,0},\dots,U_{n,j}$
are i.i.d. uniformly distributed random variables on [n]), and making an easy change of variable, we obtain the general bound
 \begin{align} & \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_{n}}(r_n)}_{U_{n}}(K_n) \neq B^{\mathbb{G}_n}_{U_{n}}(K_n)\right) \nonumber\\ & \leq \sum_{j=1}^{K_n} \int_{\mathscr{B}^{a_n^m}_{\textbf{0}}}\cdots\int_{\mathscr{B}^{a_n^{m^{j-1}}}_{\textbf{0}}}\int_{\mathbb{R}^d \setminus \mathscr{B}^{a_n^{m^j}}_{\textbf{0}}} \mathbb{E}\left[\kappa_n(\|z_j\|,W^{(n)}_{\textrm{U}^{\prime}_{n,1}},W^{(n)}_{\textrm{U}^{\prime}_{n,2}})\right] dz_j\cdots dz_1, \end{align}
\begin{align} & \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_{n}}(r_n)}_{U_{n}}(K_n) \neq B^{\mathbb{G}_n}_{U_{n}}(K_n)\right) \nonumber\\ & \leq \sum_{j=1}^{K_n} \int_{\mathscr{B}^{a_n^m}_{\textbf{0}}}\cdots\int_{\mathscr{B}^{a_n^{m^{j-1}}}_{\textbf{0}}}\int_{\mathbb{R}^d \setminus \mathscr{B}^{a_n^{m^j}}_{\textbf{0}}} \mathbb{E}\left[\kappa_n(\|z_j\|,W^{(n)}_{\textrm{U}^{\prime}_{n,1}},W^{(n)}_{\textrm{U}^{\prime}_{n,2}})\right] dz_j\cdots dz_1, \end{align}
where
![]() $\textrm{U}^{\prime}_{n,1}$
and
$\textrm{U}^{\prime}_{n,1}$
and
![]() $\textrm{U}^{\prime}_{n,2}$
are two i.i.d. uniform elements in [n]. Below, we will use the bound (80) with suitable choices of
$\textrm{U}^{\prime}_{n,2}$
are two i.i.d. uniform elements in [n]. Below, we will use the bound (80) with suitable choices of
![]() $a=a_n$
and
$a=a_n$
and
![]() $K=K_n$
to prove Theorem 3.
$K=K_n$
to prove Theorem 3.
3.4. Proof of Theorem 1
Proposition 3 implies that the random rooted graph
![]() $(F^{\mathbb{G}_n}_{U_n}(r),U_n)$
converges in distribution to the random rooted graph
$(F^{\mathbb{G}_n}_{U_n}(r),U_n)$
converges in distribution to the random rooted graph
![]() $(F^{\mathbb{G}_{\infty}}_0(r),0)$
in the space
$(F^{\mathbb{G}_{\infty}}_0(r),0)$
in the space
![]() $\mathcal{G}_{\star}$
. The proof of this fact can be carried out in the same manner as [Reference Van der Hofstad22, Theorem 2.13] is proved assuming [Reference Van der Hofstad22, Definition 2.10], and so we leave this for the reader to check. In particular, as a consequence of Proposition 3,
$\mathcal{G}_{\star}$
. The proof of this fact can be carried out in the same manner as [Reference Van der Hofstad22, Theorem 2.13] is proved assuming [Reference Van der Hofstad22, Definition 2.10], and so we leave this for the reader to check. In particular, as a consequence of Proposition 3,
for any subset
![]() $A \subset \mathcal{G}_{\star}$
.
$A \subset \mathcal{G}_{\star}$
.
Proof of Theorem 1
. Recall the definition of local weak convergence from Definition 3. Recall the abbreviations in (37). Let
![]() $G_*=(G,g) \in \mathcal{G}_\star$
.
$G_*=(G,g) \in \mathcal{G}_\star$
.
Fix
![]() $K \in \mathbb{N}$
and
$K \in \mathbb{N}$
and
![]() $\varepsilon >0$
. To conclude Theorem 1, we need to find an
$\varepsilon >0$
. To conclude Theorem 1, we need to find an
![]() $N \in \mathbb{N}$
such that for all
$N \in \mathbb{N}$
such that for all
![]() $n>N$
,
$n>N$
,
that is
Note that
where
and
Clearly,
and
For the rest of the proof, we fix
![]() $m>0$
and
$m>0$
and
![]() $n_0 \in \mathbb{N}$
such that, for all
$n_0 \in \mathbb{N}$
such that, for all
![]() $n \geq n_0$
,
$n \geq n_0$
,
which is possible by Corollary 7.
Note that
where
![]() $A(K,(G,g))\subset \mathcal{G}_{\star}$
is defined as
$A(K,(G,g))\subset \mathcal{G}_{\star}$
is defined as
By (81), as
![]() $n \to \infty$
,
$n \to \infty$
,
Combining (90) with (88) and (83), we can choose
![]() $n_1 \in \mathbb{N}$
such that for all
$n_1 \in \mathbb{N}$
such that for all
![]() $n>N=\max\{n_1,n_0\}$
, (82) holds. This completes the proof of Theorem 1. □
$n>N=\max\{n_1,n_0\}$
, (82) holds. This completes the proof of Theorem 1. □
3.5. Proof of Theorem 2
For
![]() $ (H,h) \in \mathcal{G}_{\star}$
and
$ (H,h) \in \mathcal{G}_{\star}$
and
![]() $r>0$
, recall the empirical Euclidean graph neighborhood distribution as defined in (40). We first give the proof of Lemma 3.
$r>0$
, recall the empirical Euclidean graph neighborhood distribution as defined in (40). We first give the proof of Lemma 3.
Proof of Lemma 3
. To ease notation, let us write
![]() $C_{r,n}$
for
$C_{r,n}$
for
![]() $C_{r,n} (H,h)$
.
$C_{r,n} (H,h)$
.
Note that
 \begin{align*} C_{r,n}^2 & = \frac{1}{n^2}\sum_{i,j=1}^n\mathbb{1}_{\left\{F^{\mathbb{G}_n}_i(r)\cong (H,h)\right\}}\mathbb{1}_{\left\{F^{\mathbb{G}_n}_j(r)\cong (H,h)\right\}} \\ & = \mathbb{P}\left(F^{\mathbb{G}_n}_{U_{n,1}}(r)\cong (H,h),F^{\mathbb{G}_n}_{U_{n,2}}(r)\cong (H,h) \bigg| \mathbb{G}_n\right), \end{align*}
\begin{align*} C_{r,n}^2 & = \frac{1}{n^2}\sum_{i,j=1}^n\mathbb{1}_{\left\{F^{\mathbb{G}_n}_i(r)\cong (H,h)\right\}}\mathbb{1}_{\left\{F^{\mathbb{G}_n}_j(r)\cong (H,h)\right\}} \\ & = \mathbb{P}\left(F^{\mathbb{G}_n}_{U_{n,1}}(r)\cong (H,h),F^{\mathbb{G}_n}_{U_{n,2}}(r)\cong (H,h) \bigg| \mathbb{G}_n\right), \end{align*}
where
![]() $U_{n,1},U_{n,2}$
are i.i.d. uniformly distributed random variables on [n]. Therefore,
$U_{n,1},U_{n,2}$
are i.i.d. uniformly distributed random variables on [n]. Therefore,
We introduce the following abbreviations, which we will use throughout this proof to keep notation concise (recall the point process
![]() $\Gamma_n$
of the locations of the vertices of
$\Gamma_n$
of the locations of the vertices of
![]() $\mathbb{G}_n$
from (9), the set
$\mathbb{G}_n$
from (9), the set
![]() $A^r_n$
from (29), and the ball
$A^r_n$
from (29), and the ball
![]() $\mathscr{B}^r_x$
from (30)):
$\mathscr{B}^r_x$
from (30)):
 \begin{align} \mathscr{E}&\,{:\!=}\,\left\{F^{\mathbb{G}_n}_{U_{n,1}}(r)\cong (H,h)\right\},\quad \mathscr{F}\,{:\!=}\,\left\{F^{\mathbb{G}_n}_{U_{n,2}}(r)\cong (H,h)\right\},\nonumber\\ \mathscr{U}&\,{:\!=}\,\left\{\Gamma_n\left(\mathscr{B}^{r}_{Y^{(n)}_{U_{n,1}}}\right)=|V(H)|\right\},\quad \mathscr{V}\,{:\!=}\,\left\{\Gamma_n\left(\mathscr{B}^{r}_{Y^{(n)}_{U_{n,2}}}\right)=|V(H)|\right\}, \nonumber\\ \mathscr{J}&\,{:\!=}\,\left\{\mathscr{B}^r_{Y^{(n)}_{U_{n,1}}}\cap \mathscr{B}^r_{Y^{(n)}_{U_{n,2}}}=\varnothing\right\},\quad \mathscr{W}\,{:\!=}\,\left\{U_{n,1},U_{n,2} \in A^{r}_n\right\}. \end{align}
\begin{align} \mathscr{E}&\,{:\!=}\,\left\{F^{\mathbb{G}_n}_{U_{n,1}}(r)\cong (H,h)\right\},\quad \mathscr{F}\,{:\!=}\,\left\{F^{\mathbb{G}_n}_{U_{n,2}}(r)\cong (H,h)\right\},\nonumber\\ \mathscr{U}&\,{:\!=}\,\left\{\Gamma_n\left(\mathscr{B}^{r}_{Y^{(n)}_{U_{n,1}}}\right)=|V(H)|\right\},\quad \mathscr{V}\,{:\!=}\,\left\{\Gamma_n\left(\mathscr{B}^{r}_{Y^{(n)}_{U_{n,2}}}\right)=|V(H)|\right\}, \nonumber\\ \mathscr{J}&\,{:\!=}\,\left\{\mathscr{B}^r_{Y^{(n)}_{U_{n,1}}}\cap \mathscr{B}^r_{Y^{(n)}_{U_{n,2}}}=\varnothing\right\},\quad \mathscr{W}\,{:\!=}\,\left\{U_{n,1},U_{n,2} \in A^{r}_n\right\}. \end{align}
Recall that the target is to show
as
![]() $n \to \infty$
(note that conditionally on
$n \to \infty$
(note that conditionally on
![]() $\mathbb{G}_n$
, the random variables
$\mathbb{G}_n$
, the random variables
![]() $\mathbb{1}_{\mathscr{E}}$
and
$\mathbb{1}_{\mathscr{E}}$
and
![]() $\mathbb{1}_{\mathscr{F}}$
are identically distributed, so that they have the same conditional expectation, and hence the same expectation).
$\mathbb{1}_{\mathscr{F}}$
are identically distributed, so that they have the same conditional expectation, and hence the same expectation).
First we write
Note that the term in (95) is bounded from above by
and it is easily observed that the first term is equal to 0, while the last term tends to 0 as
![]() $n \to \infty$
by (42). Also note that
$n \to \infty$
by (42). Also note that
 \begin{align*}\mathbb{P}\left(\mathscr{J}^c\right)\leq \mathbb{P}\left(Y^{(n)}_{U_{n,1}} \in \mathscr{B}^{2r}_{Y^{(n)}_{U_{n,2}}} \cap I_n\right).\end{align*}
\begin{align*}\mathbb{P}\left(\mathscr{J}^c\right)\leq \mathbb{P}\left(Y^{(n)}_{U_{n,1}} \in \mathscr{B}^{2r}_{Y^{(n)}_{U_{n,2}}} \cap I_n\right).\end{align*}
Clearly,
 \begin{align*}\mathbb{P}\left(Y^{(n)}_{U_{n,1}} \in \mathscr{B}^{2r}_{Y^{(n)}_{U_{n,2}}} \cap I_n \bigg| Y^{(n)}_{U_{n,2}}\right)\stackrel{\text{a.s.}}{\leq} \frac{\lambda_d(\{y \in \mathbb{R}^d\,{:}\, \|y\|< 2r\})}{n},\end{align*}
\begin{align*}\mathbb{P}\left(Y^{(n)}_{U_{n,1}} \in \mathscr{B}^{2r}_{Y^{(n)}_{U_{n,2}}} \cap I_n \bigg| Y^{(n)}_{U_{n,2}}\right)\stackrel{\text{a.s.}}{\leq} \frac{\lambda_d(\{y \in \mathbb{R}^d\,{:}\, \|y\|< 2r\})}{n},\end{align*}
which tends to 0 as
![]() $n \to \infty$
. Hence, taking expectations of both sides in the last display and letting
$n \to \infty$
. Hence, taking expectations of both sides in the last display and letting
![]() $n \to \infty$
, we get
$n \to \infty$
, we get
![]() $\mathbb{P}\left(\mathscr{J}^c\right)\to0$
. Hence the term in (95) tends to 0 as
$\mathbb{P}\left(\mathscr{J}^c\right)\to0$
. Hence the term in (95) tends to 0 as
![]() $n \to \infty$
.
$n \to \infty$
.
To analyze the term in (94), we observe that, conditionally on
![]() $\mathscr{J}\cap \mathscr{U}\cap \mathscr{V}\cap \mathscr{W}$
, the random variables
$\mathscr{J}\cap \mathscr{U}\cap \mathscr{V}\cap \mathscr{W}$
, the random variables
![]() $\mathbb{1}_{\mathscr{E}}$
and
$\mathbb{1}_{\mathscr{E}}$
and
![]() $\mathbb{1}_{\mathscr{F}}$
are independent, since they are just functions of the locations of the
$\mathbb{1}_{\mathscr{F}}$
are independent, since they are just functions of the locations of the
![]() $|V(H)|$
points falling in
$|V(H)|$
points falling in
![]() $\mathscr{B}^r_{Y^{(n)}_{U_{n,1}}}$
and
$\mathscr{B}^r_{Y^{(n)}_{U_{n,1}}}$
and
![]() $\mathscr{B}^r_{Y^{(n)}_{U_{n,2}}}$
, and these locations are independent (since the locations of different vertices of
$\mathscr{B}^r_{Y^{(n)}_{U_{n,2}}}$
, and these locations are independent (since the locations of different vertices of
![]() $\mathbb{G}_n$
are independent). Hence,
$\mathbb{G}_n$
are independent). Hence,
Now note that
![]() $\mathscr{E}$
is independent of
$\mathscr{E}$
is independent of
![]() $\mathscr{V}$
, conditionally on
$\mathscr{V}$
, conditionally on
![]() $\{\mathscr{J}\cap \mathscr{U}\cap \mathscr{W}\}$
. Similarly,
$\{\mathscr{J}\cap \mathscr{U}\cap \mathscr{W}\}$
. Similarly,
![]() $\mathscr{F}$
is independent of
$\mathscr{F}$
is independent of
![]() $\mathscr{U}$
, conditionally on
$\mathscr{U}$
, conditionally on
![]() $\{\mathscr{J}\cap \mathscr{V}\cap \mathscr{W}\}$
.
$\{\mathscr{J}\cap \mathscr{V}\cap \mathscr{W}\}$
.
Hence,
As argued earlier,
![]() $\mathbb{P}\left(\mathscr{J}^c\right)\to0$
, so
$\mathbb{P}\left(\mathscr{J}^c\right)\to0$
, so
![]() $\mathbb{P}\left(\mathscr{J}\right)\to1$
, and it is easy to observe that
$\mathbb{P}\left(\mathscr{J}\right)\to1$
, and it is easy to observe that
![]() $\mathbb{P}\left(\mathscr{W}\right)\to1$
using (42). Hence we can forget about the ‘almost’ certain events
$\mathbb{P}\left(\mathscr{W}\right)\to1$
using (42). Hence we can forget about the ‘almost’ certain events
![]() $\mathscr{W}$
and
$\mathscr{W}$
and
![]() $\mathscr{J}$
for the first two terms from the last display, and condition on
$\mathscr{J}$
for the first two terms from the last display, and condition on
![]() $\mathscr{J}\cap \mathscr{W}$
for the third term, to conclude that (recall (94))
$\mathscr{J}\cap \mathscr{W}$
for the third term, to conclude that (recall (94))
 \begin{align} & \left|\mathbb{P}\left(\mathscr{E}\cap \mathscr{F} \bigg| \mathscr{J}\cap \mathscr{U}\cap \mathscr{V} \cap \mathscr{W}\right)\mathbb{P}\left(\mathscr{J}\cap \mathscr{U}\cap \mathscr{V}\cap \mathscr{W}\right) \right. \nonumber \\ &\quad \left. - \mathbb{P}\left(\mathscr{E} \bigg| \mathscr{U}\right)\mathbb{P}\left(\mathscr{F} \bigg| \mathscr{V}\right)\mathbb{P}\left(\mathscr{U}\cap \mathscr{V} \bigg| \mathscr{J}\cap \mathscr{W}\right) \right|\to 0; \end{align}
\begin{align} & \left|\mathbb{P}\left(\mathscr{E}\cap \mathscr{F} \bigg| \mathscr{J}\cap \mathscr{U}\cap \mathscr{V} \cap \mathscr{W}\right)\mathbb{P}\left(\mathscr{J}\cap \mathscr{U}\cap \mathscr{V}\cap \mathscr{W}\right) \right. \nonumber \\ &\quad \left. - \mathbb{P}\left(\mathscr{E} \bigg| \mathscr{U}\right)\mathbb{P}\left(\mathscr{F} \bigg| \mathscr{V}\right)\mathbb{P}\left(\mathscr{U}\cap \mathscr{V} \bigg| \mathscr{J}\cap \mathscr{W}\right) \right|\to 0; \end{align}
that is, the difference between (94) and
![]() $\mathbb{P}\left(\mathscr{E} \bigg| \mathscr{U}\right)\mathbb{P}\left(\mathscr{F} \bigg| \mathscr{V}\right)\mathbb{P}\left(\mathscr{U}\cap \mathscr{V} \bigg| \mathscr{J}\cap \mathscr{W}\right)$
tends to 0.
$\mathbb{P}\left(\mathscr{E} \bigg| \mathscr{U}\right)\mathbb{P}\left(\mathscr{F} \bigg| \mathscr{V}\right)\mathbb{P}\left(\mathscr{U}\cap \mathscr{V} \bigg| \mathscr{J}\cap \mathscr{W}\right)$
tends to 0.
We claim that to conclude the proof, it suffices to check that
This is because (97), combined with (96) and the observations that
![]() $\mathscr{E} \subset \mathscr{U}$
and
$\mathscr{E} \subset \mathscr{U}$
and
![]() $\mathscr{F} \subset \mathscr{V}$
, implies that the difference between the expression (94) and
$\mathscr{F} \subset \mathscr{V}$
, implies that the difference between the expression (94) and
![]() $\mathbb{P}\left(\mathscr{E}\right)\mathbb{P}\left(\mathscr{F}\right)$
goes to 0. Combining this with the fact that the expression in (95) goes to 0, we obtain (93).
$\mathbb{P}\left(\mathscr{E}\right)\mathbb{P}\left(\mathscr{F}\right)$
goes to 0. Combining this with the fact that the expression in (95) goes to 0, we obtain (93).
We now show (97). Recall that
![]() $|V(H)|$
denotes the size of the vertex set of the graph H. Observe that
$|V(H)|$
denotes the size of the vertex set of the graph H. Observe that
where
![]() $\textbf{M}=(M_1,M_2,M_3)$
is a multinomial vector with parameters
$\textbf{M}=(M_1,M_2,M_3)$
is a multinomial vector with parameters
Hence,
 \begin{align*} & \mathbb{P}\left(\mathscr{U}\cap \mathscr{V} \bigg| \mathscr{J}\cap \mathscr{W}\right)\\ & = \frac{n!}{(|V(H)|-1)!\;(|V(H)|-1)!\;(n-2|V(H)|)!}\\ & \times \left(\frac{\lambda_d(\mathscr{B}^{r}_{\textbf{0}})}{n}\right)^{|V(H)|-1}\left(\frac{\lambda_d(\mathscr{B}^{r}_{\textbf{0}})}{n}\right)^{|V(H)|-1}\left(1-2\frac{\lambda_d(\mathscr{B}^{r}_{\textbf{0}})}{n}\right)^{n-2|V(H)|}. \end{align*}
\begin{align*} & \mathbb{P}\left(\mathscr{U}\cap \mathscr{V} \bigg| \mathscr{J}\cap \mathscr{W}\right)\\ & = \frac{n!}{(|V(H)|-1)!\;(|V(H)|-1)!\;(n-2|V(H)|)!}\\ & \times \left(\frac{\lambda_d(\mathscr{B}^{r}_{\textbf{0}})}{n}\right)^{|V(H)|-1}\left(\frac{\lambda_d(\mathscr{B}^{r}_{\textbf{0}})}{n}\right)^{|V(H)|-1}\left(1-2\frac{\lambda_d(\mathscr{B}^{r}_{\textbf{0}})}{n}\right)^{n-2|V(H)|}. \end{align*}
It is an easy analysis to check that this converges to
![]() $\mathbb{P}\left(Y=|V(H)|-1\right)^2$
, where
$\mathbb{P}\left(Y=|V(H)|-1\right)^2$
, where
![]() $Y\sim \text{Poi}(\lambda_d(\mathscr{B}^{r}_{\textbf{0}}))$
.
$Y\sim \text{Poi}(\lambda_d(\mathscr{B}^{r}_{\textbf{0}}))$
.
Again,
where
![]() $Y^{\prime}_n \sim \text{Bin}(n-1, \frac{\lambda_d(\mathscr{B}^{r}_{\textbf{0}})}{n})$
.
$Y^{\prime}_n \sim \text{Bin}(n-1, \frac{\lambda_d(\mathscr{B}^{r}_{\textbf{0}})}{n})$
.
Since
![]() $\mathbb{P}\left(Y^{\prime}_n=|V(H)|-1\right)^2\to\mathbb{P}\left(Y=|V(H)|-1\right)^2$
, and both
$\mathbb{P}\left(Y^{\prime}_n=|V(H)|-1\right)^2\to\mathbb{P}\left(Y=|V(H)|-1\right)^2$
, and both
(using (42)), we have shown that
 \begin{align*} &|\mathbb{P}\left(\mathscr{U}\cap \mathscr{V} \bigg| \mathscr{J}\cap \mathscr{W}\right)-\mathbb{P}\left(\mathscr{U}\right)\mathbb{P}\left(\mathscr{V}\right)|\\ &\leq \left|\mathbb{P}\left(\mathscr{U}\cap \mathscr{V} \bigg| \mathscr{J}\cap \mathscr{W}\right)-\mathbb{P}\left(\mathscr{U} \bigg| Y^{(n)}_{U_{n,1}}\in A^{r}_n\right)\mathbb{P}\left(\mathscr{V} \bigg| Y^{(n)}_{U_{n,2}}\in A^{r}_n\right) \right|\\ &+\left|\mathbb{P}\left(\mathscr{U} \bigg| Y^{(n)}_{U_{n,1}}\in A^{r}_n\right)\mathbb{P}\left(\mathscr{V} \bigg| Y^{(n)}_{U_{n,2}}\in A^{r}_n\right)-\mathbb{P}\left(\mathscr{U}\right)\mathbb{P}\left(\mathscr{V}\right) \right|\to0. \end{align*}
\begin{align*} &|\mathbb{P}\left(\mathscr{U}\cap \mathscr{V} \bigg| \mathscr{J}\cap \mathscr{W}\right)-\mathbb{P}\left(\mathscr{U}\right)\mathbb{P}\left(\mathscr{V}\right)|\\ &\leq \left|\mathbb{P}\left(\mathscr{U}\cap \mathscr{V} \bigg| \mathscr{J}\cap \mathscr{W}\right)-\mathbb{P}\left(\mathscr{U} \bigg| Y^{(n)}_{U_{n,1}}\in A^{r}_n\right)\mathbb{P}\left(\mathscr{V} \bigg| Y^{(n)}_{U_{n,2}}\in A^{r}_n\right) \right|\\ &+\left|\mathbb{P}\left(\mathscr{U} \bigg| Y^{(n)}_{U_{n,1}}\in A^{r}_n\right)\mathbb{P}\left(\mathscr{V} \bigg| Y^{(n)}_{U_{n,2}}\in A^{r}_n\right)-\mathbb{P}\left(\mathscr{U}\right)\mathbb{P}\left(\mathscr{V}\right) \right|\to0. \end{align*}
This completes the proof of (97) and hence of Lemma 3. □
Note that using Lemma 3 with Proposition 3, a direct application of Chebyshev’s inequality gives, for any
![]() $ (H,h) \in \mathcal{G}_{\star}$
,
$ (H,h) \in \mathcal{G}_{\star}$
,
In particular, this implies that the empirical Euclidean graph neighborhood measure of
![]() $\mathbb{G}_n$
converges in probability to the measure induced by the random element
$\mathbb{G}_n$
converges in probability to the measure induced by the random element
![]() $(F^{\mathbb{G}_{\infty}}_0(r),0)$
in
$(F^{\mathbb{G}_{\infty}}_0(r),0)$
in
![]() $\mathcal{G}_{\star}$
: for any subset
$\mathcal{G}_{\star}$
: for any subset
![]() $A \subset \mathcal{G}_{\star}$
and for any
$A \subset \mathcal{G}_{\star}$
and for any
![]() $r>0$
(recall the Euclidean graph neighborhoods from Definition 6),
$r>0$
(recall the Euclidean graph neighborhoods from Definition 6),
as
![]() $n \to \infty$
. We now use (98) to prove Theorem 2.
$n \to \infty$
. We now use (98) to prove Theorem 2.
Proof of Theorem 2. For
![]() $K \in \mathbb{N}$
and
$K \in \mathbb{N}$
and
![]() $(G,g) \in \mathcal{G}_{\star}$
, recall the random variables
$(G,g) \in \mathcal{G}_{\star}$
, recall the random variables
![]() $B_n(G,g)$
as defined in (41). Furthermore, recall the definition of local convergence in probability from Definition 4.
$B_n(G,g)$
as defined in (41). Furthermore, recall the definition of local convergence in probability from Definition 4.
Fix
![]() $\varepsilon>0$
. Note that the target is to show that, for every
$\varepsilon>0$
. Note that the target is to show that, for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $N \in \mathbb{N}$
such that for all
$N \in \mathbb{N}$
such that for all
![]() $n > N$
,
$n > N$
,
We abbreviate the Euclidean graph neighborhoods
![]() $F^{n,r,i}\,{:\!=}\,F^{\mathbb{G}_n}_i(r)$
, with
$F^{n,r,i}\,{:\!=}\,F^{\mathbb{G}_n}_i(r)$
, with
![]() $r=r(a,m,K)$
as in (36), and
$r=r(a,m,K)$
as in (36), and
![]() $i \in V(\mathbb{G}_n)=[n]$
. We note that
$i \in V(\mathbb{G}_n)=[n]$
. We note that
 \begin{align} B_n(G,g) & =\frac{1}{n}\sum_{i=1}^n \mathbb{1}_{\left\{B^{\mathbb{G}_n}_i(K)\cong (G,g)\right\}} \nonumber \\ & =\frac{1}{n}\sum_{i=1}^n \mathbb{1}_{\left\{B^{\mathbb{G}_n}_i(K)\cong (G,g)\right\}}\mathbb{1}_{\left\{B^{\mathbb{G}_n}_i(K)=B^{F_{n,r,i}}_i(K)\right\}} \end{align}
\begin{align} B_n(G,g) & =\frac{1}{n}\sum_{i=1}^n \mathbb{1}_{\left\{B^{\mathbb{G}_n}_i(K)\cong (G,g)\right\}} \nonumber \\ & =\frac{1}{n}\sum_{i=1}^n \mathbb{1}_{\left\{B^{\mathbb{G}_n}_i(K)\cong (G,g)\right\}}\mathbb{1}_{\left\{B^{\mathbb{G}_n}_i(K)=B^{F_{n,r,i}}_i(K)\right\}} \end{align}
Writing the first term on the right-hand side of (101) as
we note from (101) that
where (recall the event
![]() $\textbf{Bad}_{r,n}$
from (68)) the expectation
$\textbf{Bad}_{r,n}$
from (68)) the expectation
![]() $\mathbb{E}\left[{|\varepsilon^{\prime}_{n,r}|}\right]$
of the absolute value of the error
$\mathbb{E}\left[{|\varepsilon^{\prime}_{n,r}|}\right]$
of the absolute value of the error
![]() $\varepsilon^{\prime}_{n,r}$
is bounded from above by
$\varepsilon^{\prime}_{n,r}$
is bounded from above by
![]() $2\mathbb{P}\left(\textbf{Bad}_{r,n}\right)$
.
$2\mathbb{P}\left(\textbf{Bad}_{r,n}\right)$
.
It can be shown using a similar argument that (recall the notation (37))
where
![]() $\mathbb{E}\left[{|\varepsilon^{\prime}_r|}\right]$
is bounded from above by
$\mathbb{E}\left[{|\varepsilon^{\prime}_r|}\right]$
is bounded from above by
![]() $2\mathbb{P}\left(\textbf{Bad}_r\right)$
.
$2\mathbb{P}\left(\textbf{Bad}_r\right)$
.
Using Corollary 7, it is easy to see that there exists
![]() $n_0 \in \mathbb{N}$
such that for
$n_0 \in \mathbb{N}$
such that for
![]() $m>0$
sufficiently large (recall
$m>0$
sufficiently large (recall
![]() $r=r(a,m,K)$
), for all
$r=r(a,m,K)$
), for all
![]() $n>n_0$
,
$n>n_0$
,
Recall the subset
![]() $A(K,(G,g)) \subset \mathcal{G}_{\star}$
from (89). Note that using (98),
$A(K,(G,g)) \subset \mathcal{G}_{\star}$
from (89). Note that using (98),
 \begin{align*} \frac{1}{n}\sum_{i=1}^n \mathbb{1}_{\left\{B^{F_{n,r,i}}_{i}(K)\cong (G,g)\right\}} &=\frac{1}{n}\sum_{i=1}^n \mathbb{1}_{\left\{(F_{n,r,i},i) \in A(K,(G,g))\right\}} \\ & {{\stackrel{\mathbb{P}}{\rightarrow}}} \mathbb{P}\left((F^{\mathbb{G}_{\infty}}_0(r),0)\in A(K,(G,g))\right)\\ &=\mathbb{P}\left(BF_r \cong (G,g)\right), \end{align*}
\begin{align*} \frac{1}{n}\sum_{i=1}^n \mathbb{1}_{\left\{B^{F_{n,r,i}}_{i}(K)\cong (G,g)\right\}} &=\frac{1}{n}\sum_{i=1}^n \mathbb{1}_{\left\{(F_{n,r,i},i) \in A(K,(G,g))\right\}} \\ & {{\stackrel{\mathbb{P}}{\rightarrow}}} \mathbb{P}\left((F^{\mathbb{G}_{\infty}}_0(r),0)\in A(K,(G,g))\right)\\ &=\mathbb{P}\left(BF_r \cong (G,g)\right), \end{align*}
and so there exists
![]() $n_1 \in \mathbb{N}$
such that for all
$n_1 \in \mathbb{N}$
such that for all
![]() $n>n_1$
we have
$n>n_1$
we have
 \begin{equation} {\mathbb{P}\left(\Big|\frac{1}{n}\sum_{i=1}^n {\mathbb{1}_{\left\{B^{F_{n,r,i}}_{i}(K)\cong (G,g)\right\}}}-\mathbb{P}\left(BF_r \cong (G,g)\right)\Big|>\varepsilon/2\right)< \varepsilon/2.} \end{equation}
\begin{equation} {\mathbb{P}\left(\Big|\frac{1}{n}\sum_{i=1}^n {\mathbb{1}_{\left\{B^{F_{n,r,i}}_{i}(K)\cong (G,g)\right\}}}-\mathbb{P}\left(BF_r \cong (G,g)\right)\Big|>\varepsilon/2\right)< \varepsilon/2.} \end{equation}
Hence, for all
![]() $n>N=\max\{n_0,n_1\}$
, we note that by (105) and (106), (99) holds. This completes the proof of Theorem 2. □
$n>N=\max\{n_0,n_1\}$
, we note that by (105) and (106), (99) holds. This completes the proof of Theorem 2. □
3.6. Proof of Theorem 3
The main idea in this proof is that the first result of Corollary 7 can be pushed to the case when
![]() $K=K_n$
is allowed to grow in a doubly logarithmic manner, instead of being fixed. For this, we need a finer analysis of the error terms we encounter while proving Lemma 2. We now go into the formal argument.
$K=K_n$
is allowed to grow in a doubly logarithmic manner, instead of being fixed. For this, we need a finer analysis of the error terms we encounter while proving Lemma 2. We now go into the formal argument.
Proof. Recall
![]() $C \in \left( 0, \frac{1}{\log(\frac{\alpha}{\alpha-d})}\right)$
. Fix some
$C \in \left( 0, \frac{1}{\log(\frac{\alpha}{\alpha-d})}\right)$
. Fix some
![]() $\overline{C} \in \left( C, \frac{1}{\log(\frac{\alpha}{\alpha-d})}\right)$
, and let
$\overline{C} \in \left( C, \frac{1}{\log(\frac{\alpha}{\alpha-d})}\right)$
, and let
Since
![]() $\overline{C}< \frac{1}{\log(\frac{\alpha}{\alpha-d})}$
,
$\overline{C}< \frac{1}{\log(\frac{\alpha}{\alpha-d})}$
,
Let
and
where
![]() $\delta>0$
is such that
$\delta>0$
is such that
![]() $\frac{1}{d}-\delta >0$
. Note that by the choice of
$\frac{1}{d}-\delta >0$
. Note that by the choice of
![]() $K_n$
, we have
$K_n$
, we have
We also let
![]() $r_n=r(a_n,m,K_n)$
be as in (36).
$r_n=r(a_n,m,K_n)$
be as in (36).
Note that, since
![]() $C < \frac{1}{\log m}$
by the choice of m, for all large n,
$C < \frac{1}{\log m}$
by the choice of m, for all large n,
Then for
![]() $U_{n,1}$
and
$U_{n,1}$
and
![]() $U_{n,2}$
two uniformly chosen vertices of
$U_{n,2}$
two uniformly chosen vertices of
![]() $\mathbb{G}_n$
, for all large n,
$\mathbb{G}_n$
, for all large n,
 \begin{align} & \mathbb{P}\left(d_{\mathbb{G}_n}(U_{n,1},U_{n,2})\leq C\log \log n\right)\nonumber\\ & \leq \mathbb{P}\left(d_{\mathbb{G}_n}(U_{n,1},U_{n,2})\leq K_n\right)\nonumber\\ &= \mathbb{P}\left(U_{n,2}\in B^{\mathbb{G}_n}_{U_{n,1}}(K_n)\right)\nonumber\\ & \leq \mathbb{P}\left(U_{n,2} \in B^{F^{\mathbb{G}_n}_{U_{n,1}}(r_n)}_{U_{n,1}}(K_n)\right) + \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_{n,1}}(r_n)}_{U_{n,1}}(K_n) \neq B^{\mathbb{G}_n}_{U_{n,1}}(K_n)\right) \nonumber\\ & \leq \mathbb{P}\left(U_{n,2} \in F^{\mathbb{G}_n}_{U_{n,1}}(r_n)\right)+ \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_{n,1}}(r_n)}_{U_{n,1}}(K_n) \neq B^{\mathbb{G}_n}_{U_{n,1}}(K_n)\right)\nonumber\\ & =\mathbb{P}\left(Y^{(n)}_{U_{n,2}}\in \mathscr{B}^{r_n}_{Y^{(n)}_{U_{n,1}}}\right) + \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_{n,1}}(r_n)}_{U_{n,1}}(K_n) \neq B^{\mathbb{G}_n}_{U_{n,1}}(K_n)\right), \end{align}
\begin{align} & \mathbb{P}\left(d_{\mathbb{G}_n}(U_{n,1},U_{n,2})\leq C\log \log n\right)\nonumber\\ & \leq \mathbb{P}\left(d_{\mathbb{G}_n}(U_{n,1},U_{n,2})\leq K_n\right)\nonumber\\ &= \mathbb{P}\left(U_{n,2}\in B^{\mathbb{G}_n}_{U_{n,1}}(K_n)\right)\nonumber\\ & \leq \mathbb{P}\left(U_{n,2} \in B^{F^{\mathbb{G}_n}_{U_{n,1}}(r_n)}_{U_{n,1}}(K_n)\right) + \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_{n,1}}(r_n)}_{U_{n,1}}(K_n) \neq B^{\mathbb{G}_n}_{U_{n,1}}(K_n)\right) \nonumber\\ & \leq \mathbb{P}\left(U_{n,2} \in F^{\mathbb{G}_n}_{U_{n,1}}(r_n)\right)+ \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_{n,1}}(r_n)}_{U_{n,1}}(K_n) \neq B^{\mathbb{G}_n}_{U_{n,1}}(K_n)\right)\nonumber\\ & =\mathbb{P}\left(Y^{(n)}_{U_{n,2}}\in \mathscr{B}^{r_n}_{Y^{(n)}_{U_{n,1}}}\right) + \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_{n,1}}(r_n)}_{U_{n,1}}(K_n) \neq B^{\mathbb{G}_n}_{U_{n,1}}(K_n)\right), \end{align}
where we recall the Euclidean graph neighborhoods
![]() $F^{\mathbb{G}_n}_i(r)$
from Definition 6.
$F^{\mathbb{G}_n}_i(r)$
from Definition 6.
Note that to conclude Theorem 3, it is sufficient to establish that the right-hand side of (111) tends to 0 as
![]() $n \to \infty$
.
$n \to \infty$
.
Via a simple conditioning on
![]() $Y^{(n)}_{U_{n,1}}$
, and using that
$Y^{(n)}_{U_{n,1}}$
, and using that
![]() $Y^{(n)}_{U_{n,2}}$
is uniformly distributed on
$Y^{(n)}_{U_{n,2}}$
is uniformly distributed on
![]() $I_n$
and is independent of
$I_n$
and is independent of
![]() $Y^{(n)}_{U_{n,1}}$
, we have
$Y^{(n)}_{U_{n,1}}$
, we have
 \begin{align*} & \mathbb{P}\left(Y^{(n)}_{U_{n,2}}\in \mathscr{B}^{r_n}_{Y^{(n)}_{U_{n,1}}}\right) \leq \frac{\lambda_d(\mathscr{B}^{r_n}_{\textbf{0}})}{n}. \end{align*}
\begin{align*} & \mathbb{P}\left(Y^{(n)}_{U_{n,2}}\in \mathscr{B}^{r_n}_{Y^{(n)}_{U_{n,1}}}\right) \leq \frac{\lambda_d(\mathscr{B}^{r_n}_{\textbf{0}})}{n}. \end{align*}
Furthermore (recalling r(a, m, K) from (36)), note that using the upper bound
we have
as
![]() $n \to \infty$
, by the choice of
$n \to \infty$
, by the choice of
![]() $K_n$
as in (109), where
$K_n$
as in (109), where
![]() $w>1$
is some constant upper bound on
$w>1$
is some constant upper bound on
![]() $\lambda_d(\mathscr{B}^1_{\textbf{0}})$
, and in the last inequality we have used (110). So the first term on the right-hand side of (111) tends to 0 as
$\lambda_d(\mathscr{B}^1_{\textbf{0}})$
, and in the last inequality we have used (110). So the first term on the right-hand side of (111) tends to 0 as
![]() $n \to \infty$
, and it remains for us to show that
$n \to \infty$
, and it remains for us to show that
as
![]() $n \to \infty$
, where
$n \to \infty$
, where
![]() $U_n$
is uniformly distributed on
$U_n$
is uniformly distributed on
![]() $V(\mathbb{G}_n)=[n]$
.
$V(\mathbb{G}_n)=[n]$
.
We now recall the general estimate from Remark 9:
 \begin{align} & \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_n}(r_n)}_{U_n}(K_n) \neq B^{\mathbb{G}_n}_{U_n}(K_n)\right) \nonumber \\ & \leq \sum_{j=1}^{K_n} \int_{\mathscr{B}^{a_n^m}_{\textbf{0}}}\cdots\int_{\mathscr{B}^{a_n^{m^{j-1}}}_{\textbf{0}}}\int_{\mathbb{R}^d \setminus \mathscr{B}^{a_n^{m^j}}_{\textbf{0}}} \mathbb{E}\left[\kappa_n(\|z_j\|,W^{(n)}_{{U}^{\prime}_{n,1}},W^{(n)}_{{U}^{\prime}_{n,2}})\right] dz_j\cdots dz_1, \end{align}
\begin{align} & \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_n}(r_n)}_{U_n}(K_n) \neq B^{\mathbb{G}_n}_{U_n}(K_n)\right) \nonumber \\ & \leq \sum_{j=1}^{K_n} \int_{\mathscr{B}^{a_n^m}_{\textbf{0}}}\cdots\int_{\mathscr{B}^{a_n^{m^{j-1}}}_{\textbf{0}}}\int_{\mathbb{R}^d \setminus \mathscr{B}^{a_n^{m^j}}_{\textbf{0}}} \mathbb{E}\left[\kappa_n(\|z_j\|,W^{(n)}_{{U}^{\prime}_{n,1}},W^{(n)}_{{U}^{\prime}_{n,2}})\right] dz_j\cdots dz_1, \end{align}
where
![]() $a=a_n$
is as in (108), m is as in (107),
$a=a_n$
is as in (108), m is as in (107),
![]() $K=K_n$
is as in (109),
$K=K_n$
is as in (109),
![]() $r_n=r(a_n,m,K_n)$
is as in (36), and
$r_n=r(a_n,m,K_n)$
is as in (36), and
![]() ${U}^{\prime}_{n,1}, {U}^{\prime}_{n,2}$
are two independent uniformly distributed random variables on [n].
${U}^{\prime}_{n,1}, {U}^{\prime}_{n,2}$
are two independent uniformly distributed random variables on [n].
Using (113) and Assumption 3(3), taking
![]() $h_n\colon\mathbb{R}^2 \to \mathbb{R}$
in (8) as being equal to
$h_n\colon\mathbb{R}^2 \to \mathbb{R}$
in (8) as being equal to
![]() $h_n(s,t)=\kappa_n(\|z_j\|,s,t,)$
, we note that for n sufficiently large so that
$h_n(s,t)=\kappa_n(\|z_j\|,s,t,)$
, we note that for n sufficiently large so that
![]() $a_n^m > t_0$
and
$a_n^m > t_0$
and
we have
 \begin{align} \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_n}(r_n)}_{U_n}(K_n) \neq B^{\mathbb{G}_n}_{U_n}(K_n)\right) & \leq \sum_{j=1}^{K_n} \int_{\mathscr{B}^{a_n^m}_{\textbf{0}}}\cdots\int_{\mathscr{B}^{a_n^{m^{j-1}}}_{\textbf{0}}}\int_{\mathbb{R}^d \setminus \mathscr{B}^{a_n^{m^j}}_{\textbf{0}}} \frac{1}{\|z_j\|^{\alpha}} dz_j\cdots dz_1.\nonumber\\ &= \sum_{j=1}^{K_n} \frac{w^{j}}{a_n^{dm^j\left(\frac{\alpha}{d}-1-\frac{1}{m}-\cdots-\frac{1}{m^{j-1}} \right)}}, \end{align}
\begin{align} \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_n}(r_n)}_{U_n}(K_n) \neq B^{\mathbb{G}_n}_{U_n}(K_n)\right) & \leq \sum_{j=1}^{K_n} \int_{\mathscr{B}^{a_n^m}_{\textbf{0}}}\cdots\int_{\mathscr{B}^{a_n^{m^{j-1}}}_{\textbf{0}}}\int_{\mathbb{R}^d \setminus \mathscr{B}^{a_n^{m^j}}_{\textbf{0}}} \frac{1}{\|z_j\|^{\alpha}} dz_j\cdots dz_1.\nonumber\\ &= \sum_{j=1}^{K_n} \frac{w^{j}}{a_n^{dm^j\left(\frac{\alpha}{d}-1-\frac{1}{m}-\cdots-\frac{1}{m^{j-1}} \right)}}, \end{align}
where
![]() $w>1$
is some constant upper bound on
$w>1$
is some constant upper bound on
![]() $\lambda_d(\mathscr{B}^1_{\textbf{0}})$
.
$\lambda_d(\mathscr{B}^1_{\textbf{0}})$
.
Since
![]() $\frac{\alpha}{d}> \frac{m}{m-1}$
, and if we let
$\frac{\alpha}{d}> \frac{m}{m-1}$
, and if we let
![]() $C_0=d \left(\frac{\alpha}{d}- \frac{m}{m-1}\right)>0$
, it follows from (114) that for all n large enough so that
$C_0=d \left(\frac{\alpha}{d}- \frac{m}{m-1}\right)>0$
, it follows from (114) that for all n large enough so that
![]() $\frac{w}{a_n^{C_0}}<1$
, and for some
$\frac{w}{a_n^{C_0}}<1$
, and for some
![]() $J > 1$
sufficiently large so that for all
$J > 1$
sufficiently large so that for all
![]() $j>J$
we have
$j>J$
we have
![]() $j^{1/j}<m$
(note that such a J exists since
$j^{1/j}<m$
(note that such a J exists since
![]() $m>1$
), we can write (assuming n is large so that
$m>1$
), we can write (assuming n is large so that
![]() $K_n>J+1$
)
$K_n>J+1$
)
 \begin{align} \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_n}(r_n)}_{U_n}(K_n) \neq B^{\mathbb{G}_n}_{U_n}(K_n)\right) \leq \sum_{j=1}^{K_n} \frac{w^{j}}{a_n^{C_0m^j}} {=\sum_{j=1}^{J} \frac{w^{j}}{a_n^{C_0m^j}}}{+\sum_{j=J+1}^{K_n}\frac{w^{j}}{a_n^{C_0m^j}}.} \end{align}
\begin{align} \mathbb{P}\left(B^{F^{\mathbb{G}_n}_{U_n}(r_n)}_{U_n}(K_n) \neq B^{\mathbb{G}_n}_{U_n}(K_n)\right) \leq \sum_{j=1}^{K_n} \frac{w^{j}}{a_n^{C_0m^j}} {=\sum_{j=1}^{J} \frac{w^{j}}{a_n^{C_0m^j}}}{+\sum_{j=J+1}^{K_n}\frac{w^{j}}{a_n^{C_0m^j}}.} \end{align}
Note that the first term on the right-hand side of (115) clearly converges to 0 as
![]() $n \to \infty$
since
$n \to \infty$
since
![]() $a_n \to \infty$
. For the second term on the right-hand side of (115), we note that since for all
$a_n \to \infty$
. For the second term on the right-hand side of (115), we note that since for all
![]() $j \geq J+1$
,
$j \geq J+1$
,
![]() $m^j>j$
, and since
$m^j>j$
, and since
![]() $\frac{w}{a_n^{C_0}}<1$
, we have
$\frac{w}{a_n^{C_0}}<1$
, we have
 \begin{align*} {\sum_{j=J+1}^{K_n}\frac{w^{j}}{a_n^{C_0m^j}}} {\leq \sum_{j=J+1}^{K_n}\frac{w^{m^j}}{a_n^{C_0m^j}}} {\leq \sum_{j=J+1}^{K_n}\left(\frac{w}{a_n^{C_0}}\right)^{j}} {\leq \sum_{j=1}^{\infty}\left(\frac{w}{a_n^{C_0}}\right)^{j}} {=\frac{w}{a_n^{C_0}} \frac{1}{1-\frac{w}{a_n^{C_0}}} \to 0,} \end{align*}
\begin{align*} {\sum_{j=J+1}^{K_n}\frac{w^{j}}{a_n^{C_0m^j}}} {\leq \sum_{j=J+1}^{K_n}\frac{w^{m^j}}{a_n^{C_0m^j}}} {\leq \sum_{j=J+1}^{K_n}\left(\frac{w}{a_n^{C_0}}\right)^{j}} {\leq \sum_{j=1}^{\infty}\left(\frac{w}{a_n^{C_0}}\right)^{j}} {=\frac{w}{a_n^{C_0}} \frac{1}{1-\frac{w}{a_n^{C_0}}} \to 0,} \end{align*}
as
![]() $n \to \infty$
. This implies (112), completing the proof of Theorem 3.
$n \to \infty$
. This implies (112), completing the proof of Theorem 3.
3.7. Proofs of results on examples
Proof of Lemma 1 . We write
 \begin{align} &\hspace{-30pt}\mathbb{E}\left[\kappa(t,W^{(1)},W^{(2)})\right] \nonumber\\ &= \mathbb{E}\left[1 \wedge f(t)g(W^{(1)},W^{(2)})\right] \nonumber\\ &= {\mathbb{P}\left(g(W^{(1)}, W^{(2)})> 1/f(t)\right)}+ f(t) \mathbb{E}\left[g(W^{(1)}W^{(2)})\mathbb{1}_{\left\{g(W^{(1)}W^{(2)})<1/f(t)\right\}}\right]. \end{align}
\begin{align} &\hspace{-30pt}\mathbb{E}\left[\kappa(t,W^{(1)},W^{(2)})\right] \nonumber\\ &= \mathbb{E}\left[1 \wedge f(t)g(W^{(1)},W^{(2)})\right] \nonumber\\ &= {\mathbb{P}\left(g(W^{(1)}, W^{(2)})> 1/f(t)\right)}+ f(t) \mathbb{E}\left[g(W^{(1)}W^{(2)})\mathbb{1}_{\left\{g(W^{(1)}W^{(2)})<1/f(t)\right\}}\right]. \end{align}
Let us define
Note that since Y is a non-negative random variable,
![]() $\mathbb{E}\left[Y\right]=\int_{0}^{\infty} \mathbb{P}\left(Y \geq l\right) dl$
. We note that
$\mathbb{E}\left[Y\right]=\int_{0}^{\infty} \mathbb{P}\left(Y \geq l\right) dl$
. We note that
 \begin{equation} \begin{split} \mathbb{P}\left(Y\geq l\right) \leq \begin{cases} 0 & \text{if}\;l > 1/f(t), \\ \\[-8pt] \mathbb{P}\left( {g(W^{(1)},W^{(2)})} > l\right) & \text{if}\; l \leq 1/f(t). \end{cases} \end{split} \end{equation}
\begin{equation} \begin{split} \mathbb{P}\left(Y\geq l\right) \leq \begin{cases} 0 & \text{if}\;l > 1/f(t), \\ \\[-8pt] \mathbb{P}\left( {g(W^{(1)},W^{(2)})} > l\right) & \text{if}\; l \leq 1/f(t). \end{cases} \end{split} \end{equation}
Hence,
 \begin{equation} \begin{split} \mathbb{E}\left[g(W^{(1)}W^{(2)})\mathbb{1}_{\left\{g(W^{(1)},W^{(2)})<1/f(t)\right\}}\right]&=\mathbb{E}\left[Y\right]=\int_{\mathbb{R}_+} \mathbb{P}\left(Y \geq l\right)dl\\ & \leq \int_{0}^{1/f(t)} \mathbb{P}\left(g(W^{(1)}W^{(2)}) > l\right) dl. \end{split} \end{equation}
\begin{equation} \begin{split} \mathbb{E}\left[g(W^{(1)}W^{(2)})\mathbb{1}_{\left\{g(W^{(1)},W^{(2)})<1/f(t)\right\}}\right]&=\mathbb{E}\left[Y\right]=\int_{\mathbb{R}_+} \mathbb{P}\left(Y \geq l\right)dl\\ & \leq \int_{0}^{1/f(t)} \mathbb{P}\left(g(W^{(1)}W^{(2)}) > l\right) dl. \end{split} \end{equation}
Recall
![]() $t_1$
and
$t_1$
and
![]() $t_2$
from Assumption 4. Let
$t_2$
from Assumption 4. Let
Note from Assumption 4(2) that, since
![]() $f(t)^{-1}$
increases to
$f(t)^{-1}$
increases to
![]() $\infty$
as
$\infty$
as
![]() $t \to \infty$
,
$t \to \infty$
,
![]() $\overline{t}_1$
is well defined.
$\overline{t}_1$
is well defined.
Let
Then for any
![]() $t>t_0$
, we bound
$t>t_0$
, we bound
 \begin{align*} \int_{0}^{1/f(t)} \mathbb{P}\left(g(W^{(1)}W^{(2)}) > l\right) dl &\leq t_2+\int_{t_2}^{f(t)^{-1}} l^{- \beta_p} dl\\ &=t_2+\frac{1}{1-\beta_p}\left(f(t)^{\beta_p-1}-t_2^{1-\beta_p}\right). \end{align*}
\begin{align*} \int_{0}^{1/f(t)} \mathbb{P}\left(g(W^{(1)}W^{(2)}) > l\right) dl &\leq t_2+\int_{t_2}^{f(t)^{-1}} l^{- \beta_p} dl\\ &=t_2+\frac{1}{1-\beta_p}\left(f(t)^{\beta_p-1}-t_2^{1-\beta_p}\right). \end{align*}
Hence, from (116), for
![]() $t>t_0$
we have
$t>t_0$
we have
 \begin{align} \mathbb{E}\left[\kappa(t,W^{(1)},W^{(2)})\right] &\leq f(t)^{\beta_p}+t_2f(t)+\frac{1}{1-\beta_p}\left(f(t)^{\beta_p}-t_2^{1-\beta_p}f(t)\right) \nonumber\\ &\leq t^{-\alpha_p\beta_p}+t_2t^{-\alpha_p}+\frac{1}{1-\beta_p}\left(t^{-\alpha_p\beta_p}-t_2^{1-\beta_p}t^{-\alpha_p}\right). \end{align}
\begin{align} \mathbb{E}\left[\kappa(t,W^{(1)},W^{(2)})\right] &\leq f(t)^{\beta_p}+t_2f(t)+\frac{1}{1-\beta_p}\left(f(t)^{\beta_p}-t_2^{1-\beta_p}f(t)\right) \nonumber\\ &\leq t^{-\alpha_p\beta_p}+t_2t^{-\alpha_p}+\frac{1}{1-\beta_p}\left(t^{-\alpha_p\beta_p}-t_2^{1-\beta_p}t^{-\alpha_p}\right). \end{align}
Since, for any
![]() $\epsilon>0$
, the right-hand side of (119) is dominated by
$\epsilon>0$
, the right-hand side of (119) is dominated by
![]() $t^{-\min\{\alpha_p,\alpha_p\beta_p\}+\epsilon}$
outside a compact set (depending on
$t^{-\min\{\alpha_p,\alpha_p\beta_p\}+\epsilon}$
outside a compact set (depending on
![]() $\epsilon$
), we are done. □
$\epsilon$
), we are done. □
Proof of Corollary 2 . We will rely upon Corollary 1 and Remark 4 to conclude the proof.
Note that by definition,
![]() $\textrm{GIRG}_{n,\alpha_G,\beta_G,d}$
is the SIRG
$\textrm{GIRG}_{n,\alpha_G,\beta_G,d}$
is the SIRG
![]() $G(\textbf{X}^{(n)},\textbf{W}^{(n)},\kappa_n^{\alpha_G})$
, where the locations
$G(\textbf{X}^{(n)},\textbf{W}^{(n)},\kappa_n^{\alpha_G})$
, where the locations
![]() $(\textbf{X}^{(n)})_{i \in [n]}$
satisfy Assumption 1, the weights
$(\textbf{X}^{(n)})_{i \in [n]}$
satisfy Assumption 1, the weights
![]() $(\textbf{W}^{(n)}_i)_{i \in [n]}$
satisfy Assumption 2, and
$(\textbf{W}^{(n)}_i)_{i \in [n]}$
satisfy Assumption 2, and
![]() $\kappa_n^{\alpha_G}\,{:}\,\mathbb{R}_+ \times \mathbb{R} \times \mathbb{R} \to [0,1]$
is defined as
$\kappa_n^{\alpha_G}\,{:}\,\mathbb{R}_+ \times \mathbb{R} \times \mathbb{R} \to [0,1]$
is defined as
 \begin{equation} \begin{split} \kappa_n^{\alpha_G}(t,x,y)\,{:\!=}\, \begin{cases} 1 \wedge \left(\frac{xy}{\sum_{i\in[n]} W^{(n)}_i}\right)^{\alpha_G}\frac{1}{t^{d\alpha_G}} &\text{if}\; 1<\alpha_G<\infty, \\ \\[-8pt] \mathbb{1}_{\left\{\left(\frac{xy}{\sum_{i\in[n]} W^{(n)}_i}\right)^{1/d}>t\right\}} & \text{if}\; \alpha_G = \infty. \end{cases} \end{split} \end{equation}
\begin{equation} \begin{split} \kappa_n^{\alpha_G}(t,x,y)\,{:\!=}\, \begin{cases} 1 \wedge \left(\frac{xy}{\sum_{i\in[n]} W^{(n)}_i}\right)^{\alpha_G}\frac{1}{t^{d\alpha_G}} &\text{if}\; 1<\alpha_G<\infty, \\ \\[-8pt] \mathbb{1}_{\left\{\left(\frac{xy}{\sum_{i\in[n]} W^{(n)}_i}\right)^{1/d}>t\right\}} & \text{if}\; \alpha_G = \infty. \end{cases} \end{split} \end{equation}
It is not very difficult to check that
![]() $\kappa^{\alpha_G}_n$
satisfies Assumption 3(1) with limiting connection function
$\kappa^{\alpha_G}_n$
satisfies Assumption 3(1) with limiting connection function
![]() $\kappa^{\alpha_G}$
as defined in (14); hence we only need to check Assumption 4 for
$\kappa^{\alpha_G}$
as defined in (14); hence we only need to check Assumption 4 for
![]() $\kappa^{(\alpha_G)}$
to directly apply Corollary 1.
$\kappa^{(\alpha_G)}$
to directly apply Corollary 1.
Case 1:
![]() $\alpha_G< \infty$
. Note that for the
$\alpha_G< \infty$
. Note that for the
![]() $\alpha<\infty$
case,
$\alpha<\infty$
case,
![]() $\kappa^{\alpha_G}$
is a PSIRG connection function with
$\kappa^{\alpha_G}$
is a PSIRG connection function with
![]() $g(x,y)=\left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{\alpha_G}$
, and
$g(x,y)=\left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{\alpha_G}$
, and
![]() $f(t)={{t^{-d\alpha_G}}}$
.
$f(t)={{t^{-d\alpha_G}}}$
.
Since W has a power-law tail with exponent
![]() $\beta_G-1$
, using Breiman’s lemma [Reference Kulik and Soulier26, Lemma 1.4.3], for any
$\beta_G-1$
, using Breiman’s lemma [Reference Kulik and Soulier26, Lemma 1.4.3], for any
![]() $\epsilon>0$
, the tail
$\epsilon>0$
, the tail
![]() $\mathbb{P}\left(W_1W_2>t\right)$
of the product of two i.i.d. copies
$\mathbb{P}\left(W_1W_2>t\right)$
of the product of two i.i.d. copies
![]() $W_1$
and
$W_1$
and
![]() $W_2$
of W is dominated from above by a regularly varying function with exponent
$W_2$
of W is dominated from above by a regularly varying function with exponent
![]() $\beta_G-1-\epsilon$
for all sufficiently large t. Hence if we choose
$\beta_G-1-\epsilon$
for all sufficiently large t. Hence if we choose
![]() $\epsilon>0$
sufficiently small so that
$\epsilon>0$
sufficiently small so that
![]() $\beta_G-1-\epsilon>1$
, then g(x, y) satisfies Assumption 4(3) with
$\beta_G-1-\epsilon>1$
, then g(x, y) satisfies Assumption 4(3) with
![]() $\beta_p=(\beta_G-1-\epsilon)/\alpha_G$
. Also, clearly f(t) satisfies Assumption 4(2) with
$\beta_p=(\beta_G-1-\epsilon)/\alpha_G$
. Also, clearly f(t) satisfies Assumption 4(2) with
![]() $\alpha_p=d\alpha_G$
. Hence in this case
$\alpha_p=d\alpha_G$
. Hence in this case
![]() $\gamma_p=\min\{\alpha_p,\alpha_p\beta_p\}=\min\{d\alpha_G,d(\beta_G-1-\epsilon)\}>d$
, since both
$\gamma_p=\min\{\alpha_p,\alpha_p\beta_p\}=\min\{d\alpha_G,d(\beta_G-1-\epsilon)\}>d$
, since both
![]() $\alpha_G,(\beta_G-1-\epsilon)>1$
. So we can conclude the result in this case using Corollary 1.
$\alpha_G,(\beta_G-1-\epsilon)>1$
. So we can conclude the result in this case using Corollary 1.
Case 2:
![]() $\alpha_G = \infty$
. Fix
$\alpha_G = \infty$
. Fix
![]() $\gamma>d$
. When
$\gamma>d$
. When
![]() $\alpha_G=\infty$
, we note from (14) that the function
$\alpha_G=\infty$
, we note from (14) that the function
![]() $\kappa^{(\infty)}(t,x,y)$
can be bounded from above as
$\kappa^{(\infty)}(t,x,y)$
can be bounded from above as
 \begin{align*} \kappa^{(\infty)}(t,x,y)= \mathbb{1}_{\left\{\left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{\gamma/d}>t^{\gamma}\right\}} \leq 1 \wedge \frac{\left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{\gamma/d}}{t^{\gamma}} \,{=\!:}\, h(t,x,y). \end{align*}
\begin{align*} \kappa^{(\infty)}(t,x,y)= \mathbb{1}_{\left\{\left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{\gamma/d}>t^{\gamma}\right\}} \leq 1 \wedge \frac{\left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{\gamma/d}}{t^{\gamma}} \,{=\!:}\, h(t,x,y). \end{align*}
Clearly h(t, x, y) is a PSIRG connection function with
![]() $f(t)=\frac{1}{t^{\gamma}}$
satisfying Assumption 4(2) with
$f(t)=\frac{1}{t^{\gamma}}$
satisfying Assumption 4(2) with
![]() $\alpha_p=\gamma$
, and
$\alpha_p=\gamma$
, and
![]() $g(x,y)=\left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{\gamma/d}$
satisfies Assumption 4(3) with
$g(x,y)=\left(\frac{xy}{\mathbb{E}\left[W\right]}\right)^{\gamma/d}$
satisfies Assumption 4(3) with
![]() $\beta_p= d(\beta_G-1-\epsilon)/\gamma$
, for
$\beta_p= d(\beta_G-1-\epsilon)/\gamma$
, for
![]() $\epsilon>0$
sufficiently small so that
$\epsilon>0$
sufficiently small so that
![]() $\beta_G-1-\epsilon>1$
, again by Breiman’s lemma [Reference Kulik and Soulier26, Lemma 1.4.3]. Since in this case also we have
$\beta_G-1-\epsilon>1$
, again by Breiman’s lemma [Reference Kulik and Soulier26, Lemma 1.4.3]. Since in this case also we have
![]() $\gamma_p=\min\{\alpha_p,\alpha_p\beta_p\}=\min\{\gamma,d(\beta_G-1-\epsilon)\}>d$
, we can conclude the proof using Remark 4. □
$\gamma_p=\min\{\alpha_p,\alpha_p\beta_p\}=\min\{\gamma,d(\beta_G-1-\epsilon)\}>d$
, we can conclude the proof using Remark 4. □
Proof of Corollary 3
. We first transform the hyperbolic random graph models into 1-dimensional SIRGs with appropriate parameters. To do this, we follow the proof of [Reference Komjáthy and Lodewijks24, Theorem 9.6]. Recall respectively, from Section 2.1.3, the radial component vector
![]() $(r_i^{(n)})_{i=1}^n$
and the angular component vector
$(r_i^{(n)})_{i=1}^n$
and the angular component vector
![]() $(\theta_i^{(n)})_{i=1}^n$
of the vertices
$(\theta_i^{(n)})_{i=1}^n$
of the vertices
![]() $(u_i^{(n)})_{i=1}^n$
of the THRG and PHRG models. Consider the transformations
$(u_i^{(n)})_{i=1}^n$
of the THRG and PHRG models. Consider the transformations
Clearly,
![]() $(X_i^{(n)})_{i=1}^n$
is then a vector with i.i.d. coordinates on
$(X_i^{(n)})_{i=1}^n$
is then a vector with i.i.d. coordinates on
![]() $[-1/2,1/2]$
, and using (16), it can be shown the i.i.d. components of the vector
$[-1/2,1/2]$
, and using (16), it can be shown the i.i.d. components of the vector
![]() $(W_i^{(n)})_{i=1}^n$
have a power-law distribution with parameter
$(W_i^{(n)})_{i=1}^n$
have a power-law distribution with parameter
![]() $2\alpha_H+1$
when
$2\alpha_H+1$
when
![]() $\alpha_H>1/2$
(see [Reference Komjáthy and Lodewijks24, (9.8)] and the text following it).
$\alpha_H>1/2$
(see [Reference Komjáthy and Lodewijks24, (9.8)] and the text following it).
Recall the connection functions
![]() $p^{(n)}_{\textrm{THRG}}$
and
$p^{(n)}_{\textrm{THRG}}$
and
![]() $p^{(n)}_{\textrm{PHRG}}$
from (17) and (18) respectively. The hyperbolic distance
$p^{(n)}_{\textrm{PHRG}}$
from (17) and (18) respectively. The hyperbolic distance
![]() $d_{\mathbb{H}}(u_i^{(n)},u_j^{(n)})$
between
$d_{\mathbb{H}}(u_i^{(n)},u_j^{(n)})$
between
![]() $u_i^{(n)}=(r_i^{(n)},\theta_i^{(n)})$
and
$u_i^{(n)}=(r_i^{(n)},\theta_i^{(n)})$
and
![]() $u_j^{(n)}=(r_j^{(n)},\theta_j^{(n)})$
depends on the angular coordinates
$u_j^{(n)}=(r_j^{(n)},\theta_j^{(n)})$
depends on the angular coordinates
![]() $\theta_i^{(n)}$
and
$\theta_i^{(n)}$
and
![]() $\theta_j^{(n)}$
through
$\theta_j^{(n)}$
through
![]() $\cos(\theta_i^{(n)}-\theta_j^{(n)})$
(see [Reference Komjáthy and Lodewijks24, (9.1)]). Hence, it can be seen as a function of
$\cos(\theta_i^{(n)}-\theta_j^{(n)})$
(see [Reference Komjáthy and Lodewijks24, (9.1)]). Hence, it can be seen as a function of
![]() $|\theta_i^{(n)}-\theta_j^{(n)}|$
, since
$|\theta_i^{(n)}-\theta_j^{(n)}|$
, since
![]() $\cos(\!\cdot\!)$
is symmetric. Consequently, there exist functions
$\cos(\!\cdot\!)$
is symmetric. Consequently, there exist functions
![]() $\overline{p}_{\textrm{THRG}}$
and
$\overline{p}_{\textrm{THRG}}$
and
![]() $\overline{p}_{\textrm{PHRG}}$
such that
$\overline{p}_{\textrm{PHRG}}$
such that
 \begin{align} &p^{(n)}_{\textrm{THRG}}\big(u^{(n)}_i,u^{(n)}_j\big)=\overline{p}^{(n)}_{\textrm{THRG} }(|\theta_i^{(n)}-\theta_j^{(n)}|,r_i^{(n)},r_j^{(n)}),\nonumber\\ &p^{(n)}_{\textrm{PHRG}}\big(u^{(n)}_i,u^{(n)}_j\big)=\overline{p}^{(n)}_{\textrm{PHRG} }(|\theta_i^{(n)}-\theta_j^{(n)}|,r_i^{(n)},r_j^{(n)}). \end{align}
\begin{align} &p^{(n)}_{\textrm{THRG}}\big(u^{(n)}_i,u^{(n)}_j\big)=\overline{p}^{(n)}_{\textrm{THRG} }(|\theta_i^{(n)}-\theta_j^{(n)}|,r_i^{(n)},r_j^{(n)}),\nonumber\\ &p^{(n)}_{\textrm{PHRG}}\big(u^{(n)}_i,u^{(n)}_j\big)=\overline{p}^{(n)}_{\textrm{PHRG} }(|\theta_i^{(n)}-\theta_j^{(n)}|,r_i^{(n)},r_j^{(n)}). \end{align}
Write
 \begin{align} &\kappa_{\textrm{THRG},n}\left(t,x,y\right)=\overline{p}^{(n)}_{\textrm{THRG} }(2\pi t,g_n(x),g_n(y)),\nonumber \\ &\kappa_{\textrm{PHRG},n}\left(t,x,y\right)=\overline{p}^{(n)}_{\textrm{PHRG} }(2\pi t,g_n(x),g_n(y)), \end{align}
\begin{align} &\kappa_{\textrm{THRG},n}\left(t,x,y\right)=\overline{p}^{(n)}_{\textrm{THRG} }(2\pi t,g_n(x),g_n(y)),\nonumber \\ &\kappa_{\textrm{PHRG},n}\left(t,x,y\right)=\overline{p}^{(n)}_{\textrm{PHRG} }(2\pi t,g_n(x),g_n(y)), \end{align}
where the function
![]() $g_n$
satisfies
$g_n$
satisfies
It was shown in [Reference Komjáthy and Lodewijks24, (9.17)] and [Reference Komjáthy and Lodewijks24, (9.16)] respectively that for fixed (t, x, y) as
![]() $n \to \infty$
,
$n \to \infty$
,
 \begin{align*} &\kappa_{\textrm{THRG},n}\left(t,x,y\right)=\overline{p}^{(n)}_{\textrm{THRG} }(2\pi t,g_n(x),g_n(y)) \to \kappa_{\textrm{THRG},\infty}(t,x,y),\\ &\kappa_{\textrm{PHRG},n}\left(t,x,y\right)=\overline{p}^{(n)}_{\textrm{PHRG} }(2\pi t,g_n(x),g_n(y)) \to \kappa_{\textrm{THRG},\infty}(t,x,y), \end{align*}
\begin{align*} &\kappa_{\textrm{THRG},n}\left(t,x,y\right)=\overline{p}^{(n)}_{\textrm{THRG} }(2\pi t,g_n(x),g_n(y)) \to \kappa_{\textrm{THRG},\infty}(t,x,y),\\ &\kappa_{\textrm{PHRG},n}\left(t,x,y\right)=\overline{p}^{(n)}_{\textrm{PHRG} }(2\pi t,g_n(x),g_n(y)) \to \kappa_{\textrm{THRG},\infty}(t,x,y), \end{align*}
where
 \begin{align} \kappa_{\textrm{THRG},\infty}(t,x,y)\,{:\!=}\, \mathbb{1}_{\left\{t \leq \frac{\nu xy}{\pi}\right\}}, \qquad \kappa_{\textrm{PHRG},\infty}(t,x,y)\,{:\!=}\, \left(1+\left(\frac{ \pi t}{\nu xy} \right)^{1/T_H} \right)^{-1}. \end{align}
\begin{align} \kappa_{\textrm{THRG},\infty}(t,x,y)\,{:\!=}\, \mathbb{1}_{\left\{t \leq \frac{\nu xy}{\pi}\right\}}, \qquad \kappa_{\textrm{PHRG},\infty}(t,x,y)\,{:\!=}\, \left(1+\left(\frac{ \pi t}{\nu xy} \right)^{1/T_H} \right)^{-1}. \end{align}
In particular, the THRG and PHRG models can be seen as finite 1-dimensional SIRGs, where the vertex locations
![]() $(X_i^{(n)})_{i=1}^n$
satisfy Assumption 1, the vertex weights
$(X_i^{(n)})_{i=1}^n$
satisfy Assumption 1, the vertex weights
![]() $(W_i^{(n)})_{i=1}^n$
satisfy Assumption 2 with the function
$(W_i^{(n)})_{i=1}^n$
satisfy Assumption 2 with the function
![]() $F_{W}(x)$
being a power-law distribution function with exponent
$F_{W}(x)$
being a power-law distribution function with exponent
![]() $2\alpha_H+1$
, and where the connection functions are as in (123), converging pointwise to limiting connection functions as in (124). The pointwise convergence can in fact be improved to the case where one has sequences
$2\alpha_H+1$
, and where the connection functions are as in (123), converging pointwise to limiting connection functions as in (124). The pointwise convergence can in fact be improved to the case where one has sequences
![]() $x_n\to x,y_n\to y$
as in Assumption 3(1). This is because the error terms are uniformly bounded (see [Reference Komjáthy and Lodewijks24, (9.15)]), which implies
$x_n\to x,y_n\to y$
as in Assumption 3(1). This is because the error terms are uniformly bounded (see [Reference Komjáthy and Lodewijks24, (9.15)]), which implies
![]() $\kappa_{\textrm{THRG},n}(t,x_n,y_n)\to \kappa_{\textrm{THRG},\infty}(t,x,y)$
and
$\kappa_{\textrm{THRG},n}(t,x_n,y_n)\to \kappa_{\textrm{THRG},\infty}(t,x,y)$
and
![]() $\kappa_{\textrm{PHRG},n}(t,x_n,y_n)\to \kappa_{\textrm{PHRG},\infty}(t,x,y)$
, with t avoiding a set of measure zero for the THRG case, namely the set
$\kappa_{\textrm{PHRG},n}(t,x_n,y_n)\to \kappa_{\textrm{PHRG},\infty}(t,x,y)$
, with t avoiding a set of measure zero for the THRG case, namely the set
![]() $\{\frac{\nu xy}{\pi}\}$
. Thus, the sequences of connection functions
$\{\frac{\nu xy}{\pi}\}$
. Thus, the sequences of connection functions
![]() $\kappa_{\textrm{THRG},n}$
and
$\kappa_{\textrm{THRG},n}$
and
![]() $\kappa_{\textrm{PHRG},n}$
satisfy Assumption 3(1) with limiting connection functions (124).
$\kappa_{\textrm{PHRG},n}$
satisfy Assumption 3(1) with limiting connection functions (124).
Finally, we need to check that the limiting connection functions
![]() $\kappa_{\textrm{THRG},\infty}$
and
$\kappa_{\textrm{THRG},\infty}$
and
![]() $\kappa_{\textrm{PHRG},\infty}$
satisfy Assumption 3(2) with some
$\kappa_{\textrm{PHRG},\infty}$
satisfy Assumption 3(2) with some
![]() $\alpha>d$
. For this, we use Corollary 1 and Remark 4.
$\alpha>d$
. For this, we use Corollary 1 and Remark 4.
Case 1:
THRG. Let
![]() $\gamma>1$
be any constant. Note that the function
$\gamma>1$
be any constant. Note that the function
![]() $\kappa_{\textrm{THRG},\infty}$
can be bounded from above as
$\kappa_{\textrm{THRG},\infty}$
can be bounded from above as
Note that this is a PSIRG connection function with
![]() $f(t)=\frac{1}{t^{\gamma}}$
satisfying Assumption 4(1) with
$f(t)=\frac{1}{t^{\gamma}}$
satisfying Assumption 4(1) with
![]() $\alpha_p=\gamma$
, and
$\alpha_p=\gamma$
, and
![]() $g(x,y)=\left(\frac{\nu xy}{\pi}\right)^{\gamma}$
. In addition, from (121) it follows that the limiting weights are i.i.d. and have a power-law distribution with exponent
$g(x,y)=\left(\frac{\nu xy}{\pi}\right)^{\gamma}$
. In addition, from (121) it follows that the limiting weights are i.i.d. and have a power-law distribution with exponent
![]() $2\alpha_H+1$
. Hence, by Breiman’s lemma [Reference Kulik and Soulier26, Lemma 1.4.3], if
$2\alpha_H+1$
. Hence, by Breiman’s lemma [Reference Kulik and Soulier26, Lemma 1.4.3], if
![]() $W^{(1)}$
and
$W^{(1)}$
and
![]() $W^{(2)}$
are i.i.d. copies of the limiting weight distribution, then
$W^{(2)}$
are i.i.d. copies of the limiting weight distribution, then
![]() $g(W^{(1)},W^{(2)})$
is regularly varying with exponent
$g(W^{(1)},W^{(2)})$
is regularly varying with exponent
![]() $2 \alpha_H/\gamma$
. Applying Potter’s bounds, we conclude that
$2 \alpha_H/\gamma$
. Applying Potter’s bounds, we conclude that
![]() $g(W_1,W_2)$
satisfies Assumption 4(2) with
$g(W_1,W_2)$
satisfies Assumption 4(2) with
![]() $\beta_p= (2 \alpha_H-\epsilon)/\gamma$
, for
$\beta_p= (2 \alpha_H-\epsilon)/\gamma$
, for
![]() $\epsilon>0$
sufficiently small so that
$\epsilon>0$
sufficiently small so that
![]() $2\alpha_H-\epsilon>1$
.
$2\alpha_H-\epsilon>1$
.
Since in this case we have
![]() $\gamma_p=\min\{\alpha_p,\alpha_p\beta_p\}=\min\{\gamma,(2\alpha_H-\epsilon)\}>1$
, we can conclude the proof using Corollary 1 and Remark 4.
$\gamma_p=\min\{\alpha_p,\alpha_p\beta_p\}=\min\{\gamma,(2\alpha_H-\epsilon)\}>1$
, we can conclude the proof using Corollary 1 and Remark 4.
Case 2:
PHRG. The function
![]() $\kappa_{\textrm{PHRG},\infty}$
can be bounded from above as
$\kappa_{\textrm{PHRG},\infty}$
can be bounded from above as
for some constants
![]() $C_1,a_1>0$
. To see this, combine [Reference Komjáthy and Lodewijks24, (9.14)], [Reference Komjáthy and Lodewijks24, (9.16)], and Assumption 3(1). Using the fact that
$C_1,a_1>0$
. To see this, combine [Reference Komjáthy and Lodewijks24, (9.14)], [Reference Komjáthy and Lodewijks24, (9.16)], and Assumption 3(1). Using the fact that
![]() $\kappa_{\textrm{PHRG},\infty}(t,x,y)$
is a probability, and hence
$\kappa_{\textrm{PHRG},\infty}(t,x,y)$
is a probability, and hence
![]() $\leq 1$
, we can further get an upper bound from (125) as
$\leq 1$
, we can further get an upper bound from (125) as
Note that this is a PSIRG connection function, with
![]() $f(t)=\frac{C_1a_1}{t^{1/T_H}}$
and
$f(t)=\frac{C_1a_1}{t^{1/T_H}}$
and
![]() $g(x,y)=\left(xy\right)^{1/T_H}$
. Recall from the statement of Corollary 3 that
$g(x,y)=\left(xy\right)^{1/T_H}$
. Recall from the statement of Corollary 3 that
![]() $0<T_H<1$
. Note that f(t) then satisfies Assumption 4(1) with
$0<T_H<1$
. Note that f(t) then satisfies Assumption 4(1) with
![]() $\alpha_p=1/(T_H-\epsilon_1)$
, for some
$\alpha_p=1/(T_H-\epsilon_1)$
, for some
![]() $\epsilon_1>0$
sufficiently small so that
$\epsilon_1>0$
sufficiently small so that
![]() $1/T_H-\epsilon_1>1$
. Also note that from (121), the limiting weights are i.i.d. and have a power-law distribution with exponent
$1/T_H-\epsilon_1>1$
. Also note that from (121), the limiting weights are i.i.d. and have a power-law distribution with exponent
![]() $2\alpha_H+1$
. So if we let
$2\alpha_H+1$
. So if we let
![]() $W^{(1)}$
and
$W^{(1)}$
and
![]() $W^{(2)}$
be i.i.d. copies of the limiting weight distribution, then by Breiman’s lemma [Reference Kulik and Soulier26, Lemma 1.4.3],
$W^{(2)}$
be i.i.d. copies of the limiting weight distribution, then by Breiman’s lemma [Reference Kulik and Soulier26, Lemma 1.4.3],
![]() $g(W^{(1)},W^{(2)})$
is regularly varying with exponent
$g(W^{(1)},W^{(2)})$
is regularly varying with exponent
![]() $2\alpha_HT_H$
. Hence, applying Potter’s bounds, we note that
$2\alpha_HT_H$
. Hence, applying Potter’s bounds, we note that
![]() $g(W^{(1)},W^{(2)})$
satisfies Assumption 4(2) with
$g(W^{(1)},W^{(2)})$
satisfies Assumption 4(2) with
![]() $\beta_p= (2\alpha_H-\epsilon_2)T_H$
, for some
$\beta_p= (2\alpha_H-\epsilon_2)T_H$
, for some
![]() $\epsilon_2>0$
sufficiently small so that
$\epsilon_2>0$
sufficiently small so that
![]() $2\alpha_H-\epsilon_2>1$
. Since in this case also we have
$2\alpha_H-\epsilon_2>1$
. Since in this case also we have
![]() $\gamma_p=\min\{\alpha_p,\alpha_p\beta_p\}=\min\{1/(T_H-\epsilon_1),(2\alpha_H-\epsilon_2)T_H/(T_H-\epsilon_1)\}>1$
, we can conclude the proof using Corollary 1 and Remark 4. □
$\gamma_p=\min\{\alpha_p,\alpha_p\beta_p\}=\min\{1/(T_H-\epsilon_1),(2\alpha_H-\epsilon_2)T_H/(T_H-\epsilon_1)\}>1$
, we can conclude the proof using Corollary 1 and Remark 4. □
Proof of Corollary 4
. We apply Corollary 1, using Remark 4. Note that Assumptions 1 and 2 are immediate. Since Assumption 3(1) is immediate for
![]() $\kappa_n$
with limit
$\kappa_n$
with limit
![]() $\kappa$
, we only need to check that
$\kappa$
, we only need to check that
![]() $\kappa$
is dominated by a PSIRG connection function which satisfies Assumption 4.
$\kappa$
is dominated by a PSIRG connection function which satisfies Assumption 4.
We use the easy bound
to observe that the limiting connection function
![]() $\kappa$
is dominated by the PSIRG connection function
$\kappa$
is dominated by the PSIRG connection function
![]() $1 \wedge f(t)g(x,y)$
, where
$1 \wedge f(t)g(x,y)$
, where
![]() $f(t)=1/t^{\alpha}$
and
$f(t)=1/t^{\alpha}$
and
![]() $g(x,y)=\lambda xy$
.
$g(x,y)=\lambda xy$
.
Note that for i.i.d. copies
![]() $W_1$
and
$W_1$
and
![]() $W_2$
of the weight distribution W as in (19), for any
$W_2$
of the weight distribution W as in (19), for any
![]() $\epsilon>0$
, the tail
$\epsilon>0$
, the tail
![]() $\mathbb{P}\left(g(W_1,W_2)>t\right)$
of the random variable
$\mathbb{P}\left(g(W_1,W_2)>t\right)$
of the random variable
![]() $g(W_1,W_2)$
is dominated by a regularly varying function with exponent
$g(W_1,W_2)$
is dominated by a regularly varying function with exponent
![]() $\beta-\epsilon>0$
by Breiman’s lemma [Reference Kulik and Soulier26, Lemma 1.4.3], which implies that g satisfies Assumption 4(2) with
$\beta-\epsilon>0$
by Breiman’s lemma [Reference Kulik and Soulier26, Lemma 1.4.3], which implies that g satisfies Assumption 4(2) with
![]() $\beta_p=\beta-\epsilon$
. Also, clearly f satisfies Assumption 4(1) with
$\beta_p=\beta-\epsilon$
. Also, clearly f satisfies Assumption 4(1) with
![]() $\alpha_p = \alpha$
. For
$\alpha_p = \alpha$
. For
![]() $\epsilon>0$
sufficiently small so that
$\epsilon>0$
sufficiently small so that
![]() $\beta-\epsilon>1$
, since we have
$\beta-\epsilon>1$
, since we have
![]() $\gamma_p=\min\{\alpha_p\beta_p,\alpha_p\}=\min\{\alpha(\beta-\epsilon),\alpha\}>d$
, the proof of Corollary 4 is complete using Remark 4 and Corollary 1. □
$\gamma_p=\min\{\alpha_p\beta_p,\alpha_p\}=\min\{\alpha(\beta-\epsilon),\alpha\}>d$
, the proof of Corollary 4 is complete using Remark 4 and Corollary 1. □
3.8. Proofs of degree results
Proof of Proposition 1. We argue by showing that the moment generating function converges to the moment generating function of the claimed limit. Also, we write interchangeably the vertex set
![]() $V(\mathbb{G}_{\infty})$
and
$V(\mathbb{G}_{\infty})$
and
![]() $\mathbb{N} \cup \{0\}$
. In particular, the set of all vertices of
$\mathbb{N} \cup \{0\}$
. In particular, the set of all vertices of
![]() $\mathbb{G}_{\infty}$
other than 0 is
$\mathbb{G}_{\infty}$
other than 0 is
![]() $\mathbb{N}$
.
$\mathbb{N}$
.
Note that we have to show that for all
![]() $t \in \mathbb{R}$
,
$t \in \mathbb{R}$
,
Recall that
![]() $E(\mathbb{G}_{\infty})$
is the edge set of
$E(\mathbb{G}_{\infty})$
is the edge set of
![]() $\mathbb{G}_{\infty}$
. For any
$\mathbb{G}_{\infty}$
. For any
![]() $r>0$
, we define
$r>0$
, we define
![]() $D_{\leq r}$
as
$D_{\leq r}$
as
Clearly,
![]() $D_{\leq r}$
increases to D as
$D_{\leq r}$
increases to D as
![]() $r \to \infty$
. So, applying conditional monotone convergence when
$r \to \infty$
. So, applying conditional monotone convergence when
![]() $t \geq 0$
and conditional dominated convergence when
$t \geq 0$
and conditional dominated convergence when
![]() $t<0$
, for any
$t<0$
, for any
![]() $t \in \mathbb{R}$
we have
$t \in \mathbb{R}$
we have
Let
![]() $\mathscr{B}^r_{\textbf{0}}=\{y \in \mathbb{R}^d\,{:}\,\|y\|<r\}$
denote the open Euclidean ball of radius r in
$\mathscr{B}^r_{\textbf{0}}=\{y \in \mathbb{R}^d\,{:}\,\|y\|<r\}$
denote the open Euclidean ball of radius r in
![]() $\mathbb{R}^d$
, centered at
$\mathbb{R}^d$
, centered at
![]() $\textbf{0}$
.
$\textbf{0}$
.
Let
![]() $Q_r$
be a
$Q_r$
be a
![]() $\text{Poi}\left(\lambda_d(\mathscr{B}^r_{\textbf{0}})\right)$
random variable, and conditionally on
$\text{Poi}\left(\lambda_d(\mathscr{B}^r_{\textbf{0}})\right)$
random variable, and conditionally on
![]() $Q_r$
, make the following definitions:
$Q_r$
, make the following definitions:
-
a. Let
 $\{\mathcal{R}_i\}_{i=1}^{Q_r}$
be a collection of
$\{\mathcal{R}_i\}_{i=1}^{Q_r}$
be a collection of
 $Q_r$
i.i.d. uniform random variables on
$Q_r$
i.i.d. uniform random variables on
 $\mathscr{B}^r_{\textbf{0}}$
.
$\mathscr{B}^r_{\textbf{0}}$
. -
b. Let
 $\{\mathcal{U}_i\}_{i=1}^{Q_r}$
be a collection of
$\{\mathcal{U}_i\}_{i=1}^{Q_r}$
be a collection of
 $Q_r$
i.i.d. uniform random variables on [0, 1].
$Q_r$
i.i.d. uniform random variables on [0, 1]. -
c. Let
 $\{W^{(i)}\}_{i=1}^{Q_r}$
be
$\{W^{(i)}\}_{i=1}^{Q_r}$
be
 $Q_r$
i.i.d. copies of
$Q_r$
i.i.d. copies of
 $W_0$
, independent of
$W_0$
, independent of
 $\{\mathcal{R}_i\}_{i=1}^{Q_r}$
,
$\{\mathcal{R}_i\}_{i=1}^{Q_r}$
,
 $\{\mathcal{U}_i\}_{i=1}^{Q_r}$
, and
$\{\mathcal{U}_i\}_{i=1}^{Q_r}$
, and
 $W_0$
.
$W_0$
.
Note then that
 \begin{equation} e^{t D_{\leq r}}\Big|W_0 \stackrel{d}{=} \prod_{i=1}^{Q_r} \exp{\left(t\mathbb{1}_{\left\{\mathcal{U}_i\leq \kappa(\|\mathcal{R}_i\|,W_0,W^{(i)})\right\}}\right)}\Big|W_0, \end{equation}
\begin{equation} e^{t D_{\leq r}}\Big|W_0 \stackrel{d}{=} \prod_{i=1}^{Q_r} \exp{\left(t\mathbb{1}_{\left\{\mathcal{U}_i\leq \kappa(\|\mathcal{R}_i\|,W_0,W^{(i)})\right\}}\right)}\Big|W_0, \end{equation}
and observe that the product on the right-hand side of (129) is, conditionally on
![]() $W_0$
, a product of (conditionally) independent random variables.
$W_0$
, a product of (conditionally) independent random variables.
We compute that
 \begin{align} &\mathbb{E}\left[\left.\exp{\left(t\mathbb{1}_{\left\{\mathcal{U}_i\leq \kappa(\|\mathcal{R}_i\|,W_0,W^{(i)})\right\}}\right)}\right | W_0,W^{(i)},\mathcal{R}_i\right]\nonumber\\ &\qquad \stackrel{\text{a.s.}}{=} 1-\kappa(\|\mathcal{R}_i\|,W_0,W^{(i)})+e^t \kappa(\|\mathcal{R}_i\|,W_0,W^{(i)}), \end{align}
\begin{align} &\mathbb{E}\left[\left.\exp{\left(t\mathbb{1}_{\left\{\mathcal{U}_i\leq \kappa(\|\mathcal{R}_i\|,W_0,W^{(i)})\right\}}\right)}\right | W_0,W^{(i)},\mathcal{R}_i\right]\nonumber\\ &\qquad \stackrel{\text{a.s.}}{=} 1-\kappa(\|\mathcal{R}_i\|,W_0,W^{(i)})+e^t \kappa(\|\mathcal{R}_i\|,W_0,W^{(i)}), \end{align}
so that
 \begin{align} &\mathbb{E}\left[\left.\exp{\left(t\mathbb{1}_{\left\{\mathcal{U}_i\leq \kappa(\|\mathcal{R}_i\|,W_0,W^{(i)})\right\}}\right)}\right | W_0\right] \nonumber\\ & \stackrel{\text{a.s.}}{=} 1-\frac{1}{\lambda_d(\mathscr{B}^r_{\textbf{0}})}\int_{\mathscr{B}^r_{\textbf{0}}}\mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(i)})\right | W_0\right]dz \nonumber\\& \hspace{10 pt}+e^t \frac{1}{\lambda_d(\mathscr{B}^r_{\textbf{0}})}\int_{\mathscr{B}^r_{\textbf{0}}}\mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(i)})\right | W_0\right]dz \nonumber\\ & \stackrel{\text{a.s.}}{=} (e^t-1)\frac{1}{\lambda_d(\mathscr{B}^r_{\textbf{0}})}\int_{\mathscr{B}^r_{\textbf{0}}}\mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(1)})\right | W_0\right]dz+1. \end{align}
\begin{align} &\mathbb{E}\left[\left.\exp{\left(t\mathbb{1}_{\left\{\mathcal{U}_i\leq \kappa(\|\mathcal{R}_i\|,W_0,W^{(i)})\right\}}\right)}\right | W_0\right] \nonumber\\ & \stackrel{\text{a.s.}}{=} 1-\frac{1}{\lambda_d(\mathscr{B}^r_{\textbf{0}})}\int_{\mathscr{B}^r_{\textbf{0}}}\mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(i)})\right | W_0\right]dz \nonumber\\& \hspace{10 pt}+e^t \frac{1}{\lambda_d(\mathscr{B}^r_{\textbf{0}})}\int_{\mathscr{B}^r_{\textbf{0}}}\mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(i)})\right | W_0\right]dz \nonumber\\ & \stackrel{\text{a.s.}}{=} (e^t-1)\frac{1}{\lambda_d(\mathscr{B}^r_{\textbf{0}})}\int_{\mathscr{B}^r_{\textbf{0}}}\mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(1)})\right | W_0\right]dz+1. \end{align}
Hence, by (129),
 \begin{align} &\mathbb{E}\left[\left.e^{tD_{\leq r}}\right | W_0\right] \nonumber \\ & \stackrel{\text{a.s.}}{=} \mathbb{E}\left[\left.\left((e^t-1)\frac{1}{\lambda_d(\mathscr{B}^r_{\textbf{0}})}\int_{\mathscr{B}^r_{\textbf{0}}}\mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(1)})\right | W_0\right]dz+1\right)^{Q_r}\right | W_0\right] \nonumber\\ & \stackrel{\text{a.s.}}{=} \exp{\left((e^t-1)\int_{\mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(1)})\right | W_0\right]dz\right)}, \end{align}
\begin{align} &\mathbb{E}\left[\left.e^{tD_{\leq r}}\right | W_0\right] \nonumber \\ & \stackrel{\text{a.s.}}{=} \mathbb{E}\left[\left.\left((e^t-1)\frac{1}{\lambda_d(\mathscr{B}^r_{\textbf{0}})}\int_{\mathscr{B}^r_{\textbf{0}}}\mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(1)})\right | W_0\right]dz+1\right)^{Q_r}\right | W_0\right] \nonumber\\ & \stackrel{\text{a.s.}}{=} \exp{\left((e^t-1)\int_{\mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(1)})\right | W_0\right]dz\right)}, \end{align}
since
![]() $Q_r$
has a Poisson distribution with parameter
$Q_r$
has a Poisson distribution with parameter
![]() $\lambda_d(\mathscr{B}^r_{\textbf{0}})$
. Now, we let
$\lambda_d(\mathscr{B}^r_{\textbf{0}})$
. Now, we let
![]() $r \to \infty$
on both sides of (132) and use (128) to establish (126), which concludes the proof of Proposition 1. □
$r \to \infty$
on both sides of (132) and use (128) to establish (126), which concludes the proof of Proposition 1. □
Proof of Proposition 2. Recall that
![]() $D_n$
is the degree of the uniformly chosen vertex
$D_n$
is the degree of the uniformly chosen vertex
![]() $U_n$
of
$U_n$
of
![]() $\mathbb{G}_n$
. Fix
$\mathbb{G}_n$
. Fix
![]() $\varepsilon>0$
, and note that the target is to show that there exist
$\varepsilon>0$
, and note that the target is to show that there exist
![]() $M_0,N \in \mathbb{N}$
such that for all
$M_0,N \in \mathbb{N}$
such that for all
![]() $M>M_0$
and
$M>M_0$
and
![]() $n> N=N(M_0)$
,
$n> N=N(M_0)$
,
For any
![]() $r>0$
, we can write
$r>0$
, we can write
where (recall that
![]() $E(\mathbb{G}_n)$
is the edge set of
$E(\mathbb{G}_n)$
is the edge set of
![]() $\mathbb{G}_n$
)
$\mathbb{G}_n$
)
By applying the case
![]() $j=1$
of (34), it is not hard to see that we can choose and fix
$j=1$
of (34), it is not hard to see that we can choose and fix
![]() $r_0=r_0(\varepsilon)>0$
and
$r_0=r_0(\varepsilon)>0$
and
![]() $n_0 \in \mathbb{N}$
such that, whenever
$n_0 \in \mathbb{N}$
such that, whenever
![]() $r\geq r_0$
and
$r\geq r_0$
and
![]() $n>n_0$
,
$n>n_0$
,
Splitting depending on whether
![]() $D_{n,<r_0}$
or
$D_{n,<r_0}$
or
![]() $D_{n,\geq r_0}$
is larger, we obtain
$D_{n,\geq r_0}$
is larger, we obtain
 \begin{align} \mathbb{E}\left[D_n \mathbb{1}_{\left\{D_n>M\right\}}\right]&\leq \mathbb{E}\left[D_n \mathbb{1}_{\left\{D_n>M\right\}}\big(\mathbb{1}_{\left\{D_{n,<r_0}\leq D_{n,\geq r_0}\right\}} +\mathbb{1}_{\left\{D_{n,<r_0}>D_{n,\geq r_0}\right\}}\big)\right] \nonumber\\ &\leq 2\mathbb{E}\left[D_{n,\geq r_0} \mathbb{1}_{\left\{D_{n,\geq r_0}>M/2\right\}}\right]+ 2\mathbb{E}\left[D_{n,<r_0} \mathbb{1}_{\left\{D_{n,<r_0}>M/2\right\}}\right] \nonumber\\ & \leq \varepsilon/2+2\mathbb{E}\left[D_{n,<r_0} \mathbb{1}_{\left\{D_{n,<r_0}>M/2\right\}}\right], \end{align}
\begin{align} \mathbb{E}\left[D_n \mathbb{1}_{\left\{D_n>M\right\}}\right]&\leq \mathbb{E}\left[D_n \mathbb{1}_{\left\{D_n>M\right\}}\big(\mathbb{1}_{\left\{D_{n,<r_0}\leq D_{n,\geq r_0}\right\}} +\mathbb{1}_{\left\{D_{n,<r_0}>D_{n,\geq r_0}\right\}}\big)\right] \nonumber\\ &\leq 2\mathbb{E}\left[D_{n,\geq r_0} \mathbb{1}_{\left\{D_{n,\geq r_0}>M/2\right\}}\right]+ 2\mathbb{E}\left[D_{n,<r_0} \mathbb{1}_{\left\{D_{n,<r_0}>M/2\right\}}\right] \nonumber\\ & \leq \varepsilon/2+2\mathbb{E}\left[D_{n,<r_0} \mathbb{1}_{\left\{D_{n,<r_0}>M/2\right\}}\right], \end{align}
where in the last step we have used (137).
Now observe that
![]() $D_{n,<r_0}$
is stochastically dominated by
$D_{n,<r_0}$
is stochastically dominated by
![]() $Y_n$
, where
$Y_n$
, where
![]() $Y_n$
is a
$Y_n$
is a
![]() $\text{Bin}\left(n-1,\frac{\lambda_d(\mathscr{B}^{r_0}_{\textbf{0}})}{n}\right)$
random variable, so that
$\text{Bin}\left(n-1,\frac{\lambda_d(\mathscr{B}^{r_0}_{\textbf{0}})}{n}\right)$
random variable, so that
![]() $(Y_n)_{n \geq 1}$
is uniformly integrable. Hence, there exist
$(Y_n)_{n \geq 1}$
is uniformly integrable. Hence, there exist
![]() $M_0 \in \mathbb{N}$
and
$M_0 \in \mathbb{N}$
and
![]() $n_1=n_1(M_0) \in \mathbb{N}$
such that, whenever
$n_1=n_1(M_0) \in \mathbb{N}$
such that, whenever
![]() $M>M_0$
and
$M>M_0$
and
![]() $n>n_1$
, we have
$n>n_1$
, we have
Hence, using (139) and (138), we note that (133) holds for
![]() $M>M_0$
and
$M>M_0$
and
![]() $n>N=\max\{n_1(M_0),n_0\}$
. □
$n>N=\max\{n_1(M_0),n_0\}$
. □
3.9. Proofs of clustering results
Proof of Corollary 6. Parts 2 and 3 follow directly from using Theorem 2 with [Reference Van der Hofstad22, Theorem 2.22] and [Reference Van der Hofstad22, Exercise 2.31], respectively.
For Part 1, using [Reference Van der Hofstad22, Theorem 2.21], we only have to verify the uniform integrability of
![]() $(D_n^2)_{n \geq 1}$
and the fact that
$(D_n^2)_{n \geq 1}$
and the fact that
![]() $\mathbb{P}\left(D>1\right)>0$
, where, as before,
$\mathbb{P}\left(D>1\right)>0$
, where, as before,
![]() $D_n$
is the degree of the uniformly chosen vertex
$D_n$
is the degree of the uniformly chosen vertex
![]() $U_n$
of
$U_n$
of
![]() $\mathbb{G}_n$
, and D is the degree of 0 in
$\mathbb{G}_n$
, and D is the degree of 0 in
![]() $\mathbb{G}_{\infty}$
. By Proposition 1,
$\mathbb{G}_{\infty}$
. By Proposition 1,
![]() $\mathbb{P}\left(D>1\right)>0$
is trivial (we do not focus on the pathological case where
$\mathbb{P}\left(D>1\right)>0$
is trivial (we do not focus on the pathological case where
![]() $\int_{\mathbb{R}^d} \mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(1)})\right | W_0\right]dz=0$
, in which case it is not hard to see that
$\int_{\mathbb{R}^d} \mathbb{E}\left[\left.\kappa(\|z\|,W_0,W^{(1)})\right | W_0\right]dz=0$
, in which case it is not hard to see that
![]() $\mathbb{G}_n$
is an empty graph). So we need only verify that
$\mathbb{G}_n$
is an empty graph). So we need only verify that
![]() $\alpha>2d$
(where
$\alpha>2d$
(where
![]() $\alpha$
is as in Assumption 3(3)) implies the uniform integrability of the sequence
$\alpha$
is as in Assumption 3(3)) implies the uniform integrability of the sequence
![]() $(D_n^2)_{n \geq 1}$
.
$(D_n^2)_{n \geq 1}$
.
Fix
![]() $\varepsilon>0$
. We want to show there exist
$\varepsilon>0$
. We want to show there exist
![]() $M_0 \in \mathbb{N}$
and
$M_0 \in \mathbb{N}$
and
![]() $N=N(M_0) \in \mathbb{N}$
such that whenever
$N=N(M_0) \in \mathbb{N}$
such that whenever
![]() $M>M_0$
and
$M>M_0$
and
![]() $n>N$
,
$n>N$
,
Recall the decomposition (134). Note that
 \begin{align} D_{n,\geq r}^2 &= 2\sum_{i,j \in [n], \; i<j} \mathbb{1}_{\left\{\{U_n,i\} \in E(\mathbb{G}_{\infty}),\|Y^{(n)}_{U_n}-Y^{(n)}_i\|\geq r\right\}}\mathbb{1}_{\left\{\{U_n,j\} \in E(\mathbb{G}_{\infty}),\|Y^{(n)}_{U_n}-Y^{(n)}_j\|\geq r\right\}} \nonumber \\&\quad +\sum_{i=1}^n\mathbb{1}_{\left\{\{U_n,i\} \in E(\mathbb{G}_{\infty}),\|Y^{(n)}_{U_n}-Y^{(n)}_i\|\geq r\right\}}. \end{align}
\begin{align} D_{n,\geq r}^2 &= 2\sum_{i,j \in [n], \; i<j} \mathbb{1}_{\left\{\{U_n,i\} \in E(\mathbb{G}_{\infty}),\|Y^{(n)}_{U_n}-Y^{(n)}_i\|\geq r\right\}}\mathbb{1}_{\left\{\{U_n,j\} \in E(\mathbb{G}_{\infty}),\|Y^{(n)}_{U_n}-Y^{(n)}_j\|\geq r\right\}} \nonumber \\&\quad +\sum_{i=1}^n\mathbb{1}_{\left\{\{U_n,i\} \in E(\mathbb{G}_{\infty}),\|Y^{(n)}_{U_n}-Y^{(n)}_i\|\geq r\right\}}. \end{align}
Taking expectations on both sides of (141), and after applying a routine change of variables, we get the bound
 \begin{align*} &\mathbb{E}\left[D_{n,\geq r}^2\right] \\& \leq \int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}}\int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\kappa_n\left(\|x\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,2}}\right)\kappa_n\left(\|y\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,3}}\right)\right]dx dy \\& \hspace{10 pt} + \int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\kappa_n\left(\|z\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,2}}\right)\right]dz, \end{align*}
\begin{align*} &\mathbb{E}\left[D_{n,\geq r}^2\right] \\& \leq \int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}}\int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\kappa_n\left(\|x\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,2}}\right)\kappa_n\left(\|y\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,3}}\right)\right]dx dy \\& \hspace{10 pt} + \int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\kappa_n\left(\|z\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,2}}\right)\right]dz, \end{align*}
where
![]() $U_{n,1},U_{n,2},U_{n,3}$
are i.i.d. uniformly distributed random variables on [n]; recall that
$U_{n,1},U_{n,2},U_{n,3}$
are i.i.d. uniformly distributed random variables on [n]; recall that
![]() $(W^{(n)}_i)_{i\in [n]}$
is the weight sequence corresponding to the random graph
$(W^{(n)}_i)_{i\in [n]}$
is the weight sequence corresponding to the random graph
![]() $\mathbb{G}_n$
.
$\mathbb{G}_n$
.
Applying the Cauchy–Schwarz inequality on the integrand of the first term, and noting that
![]() $\kappa_n \leq 1$
, we have the bound
$\kappa_n \leq 1$
, we have the bound
 \begin{align} &\mathbb{E}\left[D_{n,\geq r}^2\right] \nonumber\\& \leq \left(\int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\kappa_n\left(\|x\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,2}}\right)\right]^{1/2}dx\right) \nonumber\\ &\qquad \times \left( \int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\kappa_n\left(\|y\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,3}}\right)\right]^{1/2} dy \right) \nonumber \\ &\quad + \int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\kappa_n\left(\|z\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,2}}\right)\right]dz. \end{align}
\begin{align} &\mathbb{E}\left[D_{n,\geq r}^2\right] \nonumber\\& \leq \left(\int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\kappa_n\left(\|x\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,2}}\right)\right]^{1/2}dx\right) \nonumber\\ &\qquad \times \left( \int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\kappa_n\left(\|y\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,3}}\right)\right]^{1/2} dy \right) \nonumber \\ &\quad + \int_{\mathbb{R}^d \setminus \mathscr{B}^r_{\textbf{0}}} \mathbb{E}\left[\kappa_n\left(\|z\|,W^{(n)}_{U_{n,1}},W^{(n)}_{U_{n,2}}\right)\right]dz. \end{align}
Since
![]() $\alpha>2d$
, we can choose and fix
$\alpha>2d$
, we can choose and fix
![]() $r_0=r_0(\varepsilon)>0$
such that there exists
$r_0=r_0(\varepsilon)>0$
such that there exists
![]() $n_0=n_0(r_0) \in \mathbb{N}$
such that, whenever
$n_0=n_0(r_0) \in \mathbb{N}$
such that, whenever
![]() $n>n_0$
, by (142),
$n>n_0$
, by (142),
Hence, by splitting according to which of
![]() $D_{n,<r_0}$
and
$D_{n,<r_0}$
and
![]() $D_{n,\geq r_0}$
is larger, we have
$D_{n,\geq r_0}$
is larger, we have
 \begin{align} & \mathbb{E}\left[D_n^2 \mathbb{1}_{\left\{D_n^2>M\right\}}\right] \nonumber\\ & = \mathbb{E}\left[D_n^2 \mathbb{1}_{\left\{D_n^2>M\right\}}\left(\mathbb{1}_{\left\{D_{n,<r_0}>D_{n,\geq r_0}\right\}}+\mathbb{1}_{\left\{D_{n,<r_0}\leq D_{n,\geq r_0}\right\}}\right)\right] \nonumber\\ & \leq \mathbb{E}\left[4D_{n,<r_0}^2 \mathbb{1}_{\left\{4 D_{n,<r_0}^2 >M\right\}}\right]+ {4}\mathbb{E}\left[D_{n, {\geq} r_0}^2\right] \nonumber\\ & \leq \mathbb{E}\left[4D_{n,<r_0}^2 \mathbb{1}_{\left\{4 D_{n,<r_0}^2 >M\right\}}\right]+\varepsilon/2. \end{align}
\begin{align} & \mathbb{E}\left[D_n^2 \mathbb{1}_{\left\{D_n^2>M\right\}}\right] \nonumber\\ & = \mathbb{E}\left[D_n^2 \mathbb{1}_{\left\{D_n^2>M\right\}}\left(\mathbb{1}_{\left\{D_{n,<r_0}>D_{n,\geq r_0}\right\}}+\mathbb{1}_{\left\{D_{n,<r_0}\leq D_{n,\geq r_0}\right\}}\right)\right] \nonumber\\ & \leq \mathbb{E}\left[4D_{n,<r_0}^2 \mathbb{1}_{\left\{4 D_{n,<r_0}^2 >M\right\}}\right]+ {4}\mathbb{E}\left[D_{n, {\geq} r_0}^2\right] \nonumber\\ & \leq \mathbb{E}\left[4D_{n,<r_0}^2 \mathbb{1}_{\left\{4 D_{n,<r_0}^2 >M\right\}}\right]+\varepsilon/2. \end{align}
As argued previously in the proof of Proposition 2,
![]() $D_{n,<r_0}$
is stochastically dominated by a
$D_{n,<r_0}$
is stochastically dominated by a
![]() $\text{Bin}\left(n-1, \frac{\lambda_d(\mathscr{B}^{r_0}_{\textbf{0}})}{n}\right)$
-distributed random variable. Hence, by standard arguments, the sequence
$\text{Bin}\left(n-1, \frac{\lambda_d(\mathscr{B}^{r_0}_{\textbf{0}})}{n}\right)$
-distributed random variable. Hence, by standard arguments, the sequence
![]() $\left(4D_{n,<r_0}^2\right)_{n \geq 1}$
is uniformly integrable. Hence there exist
$\left(4D_{n,<r_0}^2\right)_{n \geq 1}$
is uniformly integrable. Hence there exist
![]() $M_0 \in \mathbb{N}$
and
$M_0 \in \mathbb{N}$
and
![]() $n_1=n_1(M_0) \in \mathbb{N}$
such that, whenever
$n_1=n_1(M_0) \in \mathbb{N}$
such that, whenever
![]() $M>M_0$
and
$M>M_0$
and
![]() $n>n_1$
, the first term on the right-hand side of (144) is smaller than
$n>n_1$
, the first term on the right-hand side of (144) is smaller than
![]() $\varepsilon/2$
. We conclude that (140) holds whenever
$\varepsilon/2$
. We conclude that (140) holds whenever
![]() $M>M_0$
and
$M>M_0$
and
![]() $n>N(M_0)=\max\{n_0,n_1\}$
. This finishes the proof of Part 1. □
$n>N(M_0)=\max\{n_0,n_1\}$
. This finishes the proof of Part 1. □
Acknowledgements
N. M. thanks Joost Jorritsma and Suman Chakraborty for helpful discussions and pointers to the literature, and Martijn Gösgens for help with the pictures. The authors thank the anonymous reviewers for their helpful comments, which greatly improved the presentation of the paper, and especially for pointing out the confusions regarding the statement of Corollary 3 and the error in Conjecture 2 in the first version of the paper. We also thank Peter Mörters for his input on the reformulation of Conjecture 2.
Funding information
The work of R. v. d. H. was supported in part by the Dutch Research Council (NWO) through the Gravitation grant NETWORKS-024.002.003.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.