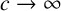1 Introduction
Otto Rössler introduced his set of equations:
 $$ \begin{align} \begin{aligned} \dot{x}&=-y-z,\\ \dot{y}&=x+ay,\\ \dot{z}&=b+(x-c)z, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \dot{x}&=-y-z,\\ \dot{y}&=x+ay,\\ \dot{z}&=b+(x-c)z, \end{aligned} \end{align} $$
where a, b and c are positive constants, as a simple prototype system which has chaotic solutions despite the presence of only a single nonlinearity [Reference Rössler15]. The system has a strange attractor which, as shown in Figure 1, has a pleasingly simple form and, in particular, is almost sheet-like. Our purpose in this note is to provide an explanation of this fact and thereby provide an analytic solution of the equations. In the course of this analysis, we will show that the solutions take on the characteristics of “bursting” action potentials, which are familiar from models of signal propagation in neurons (for example, see [Reference Mpitsos, Burton, Creech and Soinila12, Reference Williams and Stuart19]).

Figure 1 The Rössler attractor obtained by solving equation (1.1) at parameter values
![]() $a=0.2$
,
$a=0.2$
,
![]() $b=0.2$
,
$b=0.2$
,
![]() $c=10$
.
$c=10$
.
The Rössler system has generated huge interest which continues apace; much of this work is numerically based (for example, [Reference Barrio, Blesa, Denac and Serrano1, Reference Malykin, Bakhanova, Kazakov, Pusulun and Shilnikov10, Reference Sprott and Li18]), but there have been several attempts to provide approximate methods for solving the equations. The first of these is the paper by Nauenberg [Reference Nauenberg14]; in his study, he considers an asymptotic limit for equation (1.1) in which
![]() $c=O(1)$
, but
$c=O(1)$
, but
![]() $a,b\ll 1$
. After rescaling z with b, the equations for x and y take the form of a weakly perturbed oscillator, and so long as (the rescaled)
$a,b\ll 1$
. After rescaling z with b, the equations for x and y take the form of a weakly perturbed oscillator, and so long as (the rescaled)
![]() $z=O(1)$
, the model can be solved by averaging, which produces a one-dimensional unimodal map of the type found numerically. Nauenberg emphasises that his method only works for the relatively flat parts of Figure 1 and not for what we will call the pulses, where z becomes large. Maris and Goussis [Reference Maris and Goussis11] also discuss asymptotic methods based on the discrepancy between slow and fast time scales, but without basing their discussion on specific asymptotic limits. Cheng and Chen [Reference Cheng and Chen2] provide approximate solutions for the pulses (and some of their results mirror our own), but again without reference to specific asymptotic limits: the approximations are made intuitively.
$z=O(1)$
, the model can be solved by averaging, which produces a one-dimensional unimodal map of the type found numerically. Nauenberg emphasises that his method only works for the relatively flat parts of Figure 1 and not for what we will call the pulses, where z becomes large. Maris and Goussis [Reference Maris and Goussis11] also discuss asymptotic methods based on the discrepancy between slow and fast time scales, but without basing their discussion on specific asymptotic limits. Cheng and Chen [Reference Cheng and Chen2] provide approximate solutions for the pulses (and some of their results mirror our own), but again without reference to specific asymptotic limits: the approximations are made intuitively.
In anticipation of our analysis below, we begin by rescaling the variables
![]() $x,y,z\sim c$
, so that equation (1.1) takes the form
$x,y,z\sim c$
, so that equation (1.1) takes the form
 $$ \begin{align} \begin{aligned} \dot{x}&=-y-z,\\[-2pt] \dot{y}&=x+ay,\\[-2pt] \varepsilon\dot{z}&=\varepsilon^2b+(x-1)z, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \dot{x}&=-y-z,\\[-2pt] \dot{y}&=x+ay,\\[-2pt] \varepsilon\dot{z}&=\varepsilon^2b+(x-1)z, \end{aligned} \end{align} $$
where
![]() $\varepsilon =1/c$
. The system in equation (1.2) has two fixed points
$\varepsilon =1/c$
. The system in equation (1.2) has two fixed points
![]() $P_\pm $
, where
$P_\pm $
, where
so that when c is large,
The values of the parameters chosen by Rössler [Reference Rössler15] were
![]() $a=0.2$
,
$a=0.2$
,
![]() $b=0.2$
,
$b=0.2$
,
![]() $c=5.7$
and, for these parameters, equation (1.4) provides a useful approximation to the fixed points. Linearising the system about each fixed point, we find that the eigenvalues of the solutions
$c=5.7$
and, for these parameters, equation (1.4) provides a useful approximation to the fixed points. Linearising the system about each fixed point, we find that the eigenvalues of the solutions
![]() $e^{\lambda t}$
are approximately (with
$e^{\lambda t}$
are approximately (with
![]() $\varepsilon \ll 1$
)
$\varepsilon \ll 1$
)
for the fixed point
![]() $P_+$
corresponding to
$P_+$
corresponding to
![]() $z_+$
and
$z_+$
and
for
![]() $P_-$
, corresponding to
$P_-$
, corresponding to
![]() $z_-$
. The large fixed point
$z_-$
. The large fixed point
![]() $P_+$
is an unstable saddle and will be of no further concern, while
$P_+$
is an unstable saddle and will be of no further concern, while
![]() $P_-$
near the origin is an unstable saddle-focus.
$P_-$
near the origin is an unstable saddle-focus.
As shown by Barrio et al. [Reference Barrio, Blesa, Denac and Serrano1], the saddle-focus near the origin has a homoclinic orbit near the values
![]() $a=0.2$
,
$a=0.2$
,
![]() $b=0.2$
,
$b=0.2$
,
![]() $c=10$
, which is the origin of the attracting chaotic set shown in Figure 1. As can be seen, the attractor consists of a spiral sheet of trajectories which winds out in the
$c=10$
, which is the origin of the attracting chaotic set shown in Figure 1. As can be seen, the attractor consists of a spiral sheet of trajectories which winds out in the
![]() $(x,y)$
plane before folding up and then back on to the spiral as a Möbius band. One of the noticeable things about this figure is the fact that the attractor has the form of a sheet and is thus nearly two-dimensional. This apparent reduction in dimension is the hallmark of an asymptotic limit; an entirely similar process occurs in the Lorenz equations [Reference Lorenz9], where Lorenz famously discovered an approximately one-dimensional Poincaré map. In that case, the collapse of the attractor to an approximate sheet is associated with the asymptotic limit
$(x,y)$
plane before folding up and then back on to the spiral as a Möbius band. One of the noticeable things about this figure is the fact that the attractor has the form of a sheet and is thus nearly two-dimensional. This apparent reduction in dimension is the hallmark of an asymptotic limit; an entirely similar process occurs in the Lorenz equations [Reference Lorenz9], where Lorenz famously discovered an approximately one-dimensional Poincaré map. In that case, the collapse of the attractor to an approximate sheet is associated with the asymptotic limit
![]() $r\sim \sigma \gg 1$
, and this was used to derive the map by Fowler and McGuinness [Reference Fowler and McGuinness4, Reference Fowler and McGuinness5]. As a consequence of the sheet-like attractor, an appropriate Poincaré map for the Rössler equations is also approximately one-dimensional. Figure 2 shows an example of such a map, defined on the Poincaré section
$r\sim \sigma \gg 1$
, and this was used to derive the map by Fowler and McGuinness [Reference Fowler and McGuinness4, Reference Fowler and McGuinness5]. As a consequence of the sheet-like attractor, an appropriate Poincaré map for the Rössler equations is also approximately one-dimensional. Figure 2 shows an example of such a map, defined on the Poincaré section
![]() $y=0$
,
$y=0$
,
![]() $x<0$
. The map relates successive values of
$x<0$
. The map relates successive values of
![]() $C=-x$
on the section.
$C=-x$
on the section.

Figure 2 Form of the Poincaré map for the system in equation (1.1) on the Poincaré section
![]() $y=0$
,
$y=0$
,
![]() $x<0$
. The successive values
$x<0$
. The successive values
![]() $C_n=-x_n$
on this section are plotted. The parameter values used are
$C_n=-x_n$
on this section are plotted. The parameter values used are
![]() $a=0.2$
,
$a=0.2$
,
![]() $b=0.2$
,
$b=0.2$
,
![]() $c=10$
.
$c=10$
.
2 The limit
 $\boldsymbol {c\gg 1}$
$\boldsymbol {c\gg 1}$
Our analysis begins with the equations in the scaled form of equation (1.2); we eliminate y to form the set
 $$ \begin{align} \begin{aligned} &\ddot{x}-a\dot{x}+x=az-\dot{z},\\ &\varepsilon\dot{z}=\varepsilon^2b+(x-1)z, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\ddot{x}-a\dot{x}+x=az-\dot{z},\\ &\varepsilon\dot{z}=\varepsilon^2b+(x-1)z, \end{aligned} \end{align} $$
and consider the limiting form of the solution when
![]() $\varepsilon \ll 1$
. We will take
$\varepsilon \ll 1$
. We will take
![]() $a,b\sim O(1)$
, although the small values
$a,b\sim O(1)$
, although the small values
![]() $a=b=0.2$
which we use certainly help the approximation.
$a=b=0.2$
which we use certainly help the approximation.
2.1 Slow phase,
 $\boldsymbol {z\ll 1}$
$\boldsymbol {z\ll 1}$
It is evident from Figure 1 that the solution naturally separates into two distinct phases; in the first of these, which we call the slow phase, the trajectories sit on an unstable spiral close to the plane
![]() $z=0$
. In the other phase, which we call a pulse, the spiral sheet lifts up off the z plane before being folded back down on to the spiral. The pulses occur at irregular intervals, as is clearly seen in Figure 3, and they are of relatively short duration; Figure 4 shows a close-up of one of the pulses.
$z=0$
. In the other phase, which we call a pulse, the spiral sheet lifts up off the z plane before being folded back down on to the spiral. The pulses occur at irregular intervals, as is clearly seen in Figure 3, and they are of relatively short duration; Figure 4 shows a close-up of one of the pulses.

Figure 3
z versus t in the solution of equation (1.2) (the rescaled version). The parameter values used are
![]() $a=0.2$
,
$a=0.2$
,
![]() $b=0.2$
,
$b=0.2$
,
![]() $c=10$
, and thus
$c=10$
, and thus
![]() $\varepsilon =0.1$
.
$\varepsilon =0.1$
.
The slow phase is described by the regular solution of equation (2.1), where
![]() $t\sim 1$
and
$t\sim 1$
and
![]() $x<1$
. Here, z rapidly relaxes to a quasi-equilibrium in which
$x<1$
. Here, z rapidly relaxes to a quasi-equilibrium in which
 $$ \begin{align}z\sim -\frac{\varepsilon^2b}{x-1},\end{align} $$
$$ \begin{align}z\sim -\frac{\varepsilon^2b}{x-1},\end{align} $$
and consequently
with solution
where we define
This solution remains valid so long as
![]() $x<1$
and provides the increasing part of the Poincaré map seen in Figure 2. Specifically (since
$x<1$
and provides the increasing part of the Poincaré map seen in Figure 2. Specifically (since
![]() $y\approx -\dot {x}$
when
$y\approx -\dot {x}$
when
![]() $z\ll 1$
), this part of the map is just
$z\ll 1$
), this part of the map is just
2.2 Transition,
 $\boldsymbol {x\approx 1}$
$\boldsymbol {x\approx 1}$
The slow phase approximation breaks down when
![]() $x\approx 1$
and there is then a transition phase. We denote the value of t when x in equation (2.4) reaches one as
$x\approx 1$
and there is then a transition phase. We denote the value of t when x in equation (2.4) reaches one as
![]() $t_c$
, and the value of
$t_c$
, and the value of
![]() $\dot {x}$
there as
$\dot {x}$
there as
![]() $\beta $
. We thus have
$\beta $
. We thus have
 $$ \begin{align} x\sim 1+\beta(t-t_c)-\gamma(t-t_c)^2,\quad z\sim -\frac{\varepsilon^2b}{\beta(t-t_c)-\gamma(t-t_c)^2}\quad \text{as } t\to t_c{-}. \end{align} $$
$$ \begin{align} x\sim 1+\beta(t-t_c)-\gamma(t-t_c)^2,\quad z\sim -\frac{\varepsilon^2b}{\beta(t-t_c)-\gamma(t-t_c)^2}\quad \text{as } t\to t_c{-}. \end{align} $$
The expression for x is just a local Taylor expansion. Because of equation (2.3),
A suitable balance of terms follows by defining
whence the equations take the form
 $$ \begin{align}\begin{aligned}\frac{1}{\sqrt{\varepsilon}}\ddot{X}-a\dot{X}+1+\sqrt{\varepsilon}X={\varepsilon}^{3/2}b\bigg[aZ-\frac{1}{\sqrt{\varepsilon}}\dot{Z}\bigg],\dfrac{}{}\\\dot{Z}=1+XZ, \qquad\qquad\quad\qquad\end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned}\frac{1}{\sqrt{\varepsilon}}\ddot{X}-a\dot{X}+1+\sqrt{\varepsilon}X={\varepsilon}^{3/2}b\bigg[aZ-\frac{1}{\sqrt{\varepsilon}}\dot{Z}\bigg],\dfrac{}{}\\\dot{Z}=1+XZ, \qquad\qquad\quad\qquad\end{aligned}\end{align} $$
and the matching conditions are
 $$ \begin{align} X\sim \beta T-\sqrt{\varepsilon}\gamma T^2,\quad Z\sim -\frac{1}{\beta T-\sqrt{\varepsilon}\gamma T^2}\quad \text{as } T\to -\infty. \end{align} $$
$$ \begin{align} X\sim \beta T-\sqrt{\varepsilon}\gamma T^2,\quad Z\sim -\frac{1}{\beta T-\sqrt{\varepsilon}\gamma T^2}\quad \text{as } T\to -\infty. \end{align} $$
We frequently refer to matching conditions in this paper: for example, here and at equations (2.13) and (2.35). The formal principle of matching uses the concept of an intermediate matching region [Reference Kevorkian and Cole8], but the essence of the matter is that two approximations in adjoining regions should be the same in an overlap region. In practice, this can be effected as follows. We have an outer approximation given by equation (2.6) and an inner region which satisfies equation (2.9). We take the outer approximation and rewrite it in terms of the inner variables described by equation (2.8), and this yields equation (2.10). More subtle effects commonly occur in higher order approximations, including the possibility of transition layers when terms appear which cannot be matched, and the use of (small) translations in the time variable. At leading order, such effects can be ignored; for a classic treatment of such a problem, see Kevorkian and Cole’s treatment of the relaxation van der Pol oscillator.
In the present situation, it is clear from equation (2.9) that the solution has the form of an expansion
![]() $X\sim X_0+\sqrt {\varepsilon }X_1+\cdots $
. At leading order,
$X\sim X_0+\sqrt {\varepsilon }X_1+\cdots $
. At leading order,
![]() $X=\beta T$
and thus Z satisfies
$X=\beta T$
and thus Z satisfies
with solution
 $$ \begin{align*} Z=\int_0^\infty\exp\big[\beta Ts-\tfrac{1}{2} s^2\big]\,ds, \end{align*} $$
$$ \begin{align*} Z=\int_0^\infty\exp\big[\beta Ts-\tfrac{1}{2} s^2\big]\,ds, \end{align*} $$
which satisfies the matching condition. In turn, this solution breaks down, because
 $$ \begin{align*} Z\sim\sqrt{\frac{2\pi}{\beta}}e^{\beta T^2/2}\quad \text{as } T\to\infty, \end{align*} $$
$$ \begin{align*} Z\sim\sqrt{\frac{2\pi}{\beta}}e^{\beta T^2/2}\quad \text{as } T\to\infty, \end{align*} $$
and the solution enters the pulse phase.
2.3 Pulse,
 $\boldsymbol {z=O(1)}$
$\boldsymbol {z=O(1)}$
The pulse phase is rather awkward to deal with, as we shall see, because it involves logarithmic terms in the asymptotic expansions. It is convenient to keep the same time scale T. We seek a balance in which
![]() $z\sim O(1)$
, and equation (2.9) becomes
$z\sim O(1)$
, and equation (2.9) becomes
 $$ \begin{align} \frac{1}{\sqrt{\varepsilon}}\ddot{X}-a\dot{X}+1+\sqrt{\varepsilon}X=az-\frac{1}{\sqrt{\varepsilon}}\dot{z},\nonumber\\ \dot{z}=\varepsilon^{3/2}b+Xz. \end{align} $$
$$ \begin{align} \frac{1}{\sqrt{\varepsilon}}\ddot{X}-a\dot{X}+1+\sqrt{\varepsilon}X=az-\frac{1}{\sqrt{\varepsilon}}\dot{z},\nonumber\\ \dot{z}=\varepsilon^{3/2}b+Xz. \end{align} $$
It is convenient to define
so that correct to
![]() $O(\varepsilon ^{3/2})$
, the second equation in equation (2.11) implies
$O(\varepsilon ^{3/2})$
, the second equation in equation (2.11) implies
and the matching conditions as
![]() $T\to 0$
areFootnote
1
$T\to 0$
areFootnote
1
where
 $$ \begin{align}\theta_m=\ln\bigg\{\frac{1}{\varepsilon^{3/2}b}\sqrt{\frac{\beta}{2\pi}}\bigg\},\end{align} $$
$$ \begin{align}\theta_m=\ln\bigg\{\frac{1}{\varepsilon^{3/2}b}\sqrt{\frac{\beta}{2\pi}}\bigg\},\end{align} $$
and is thus formally large. Equivalently,
![]() $\theta $
satisfies the initial conditions
$\theta $
satisfies the initial conditions
At leading order,
![]() $\ddot {X}=-\dot {z}$
, whence
$\ddot {X}=-\dot {z}$
, whence
to satisfy the matching condition, and thus
![]() $\theta $
satisfies
$\theta $
satisfies
subject to the initial conditions (2.15). This equation is that of a conservative nonlinear oscillator and has a first integral
where the value of E is obtained from the matching condition. Since E is large, asymptotic solutions of this equation can be found and these were given by Fowler [Reference Fowler3]. The analysis below closely follows this and is therefore only summarised here.
2.3.1 The rise
If we consider the graph of
![]() $V(\theta )$
when E is large, it is fairly clear that for
$V(\theta )$
when E is large, it is fairly clear that for
![]() $\theta $
near
$\theta $
near
![]() $-\theta _m$
,
$-\theta _m$
,
![]() $V\approx -\beta \theta $
and the exponential is negligible, whereas at the maximum
$V\approx -\beta \theta $
and the exponential is negligible, whereas at the maximum
![]() $\theta _M$
of
$\theta _M$
of
![]() $\theta $
, the opposite is true and, in particular,
$\theta $
, the opposite is true and, in particular,
For sufficiently small T, we can suppose the exponential is negligible and thus
and this approximation becomes invalid when
![]() $\theta $
becomes of
$\theta $
becomes of
![]() $O(1)$
and thus at
$O(1)$
and thus at
![]() $T\sim \sqrt {2\theta _m/\beta }$
, near where
$T\sim \sqrt {2\theta _m/\beta }$
, near where
![]() $\theta $
has a sharp peak.
$\theta $
has a sharp peak.
2.3.2 The peak
In the vicinity of the maximum,
which yields
The solution must match to equation (2.18) as
![]() $\eta \to -\infty $
, and if we choose to define
$\eta \to -\infty $
, and if we choose to define
![]() $T_M$
and
$T_M$
and
![]() $\theta _M$
precisely via
$\theta _M$
precisely via
 $$ \begin{align*} T_M &=\bigg[\frac{2}{\beta}(\theta_M+\theta_m+2\ln 2)\bigg]^{1/2}\approx \sqrt{\dfrac{2\theta_m}{\beta}},\\ \theta_M&=2\ln\bigg(\frac{\beta T_M}{\sqrt{2}}\bigg), \end{align*} $$
$$ \begin{align*} T_M &=\bigg[\frac{2}{\beta}(\theta_M+\theta_m+2\ln 2)\bigg]^{1/2}\approx \sqrt{\dfrac{2\theta_m}{\beta}},\\ \theta_M&=2\ln\bigg(\frac{\beta T_M}{\sqrt{2}}\bigg), \end{align*} $$
then this is (using also equation (2.17))
The solution of equation (2.20) with the matching condition (2.21) is
and on the other side of the (sharp) peak,
![]() $\phi \sim 2\ln 2-\sqrt {2}\eta $
as
$\phi \sim 2\ln 2-\sqrt {2}\eta $
as
![]() $\eta \to \infty $
.
$\eta \to \infty $
.
2.3.3 The fall
To the right of the peak, the exponential is again negligible and if the next minimum is at
![]() $T=T_m$
, then
$T=T_m$
, then
and adopting equation (2.19), this matches to the peak if
![]() $T_m=2T_M$
, as we might expect. The period of the oscillation is thus
$T_m=2T_M$
, as we might expect. The period of the oscillation is thus
![]() $2T_M\approx 2\sqrt {2\theta _m/\beta }$
.
$2T_M\approx 2\sqrt {2\theta _m/\beta }$
.
We have compared the various analytic approximations we have constructed here to the actual numerical solution and they appear, even at this leading order level of accuracy, to give a relatively good account of the analytic structure of the solution.
2.4 Multiple pulses
A difficulty with the approximation now becomes apparent. Although the pulse shown in Figure 4 decays smoothly back to zero, which we would anticipate as occurring through another transition region, efforts to compute this fail (for the moment), as the solution apparently continues to oscillate.

Figure 4 A close-up of the pulse at
![]() $t=287$
in Figure 3.
$t=287$
in Figure 3.
The clue to the resolution of this conundrum lies in Figure 5, which shows part of a solution at the much smaller value
![]() $\varepsilon =0.001$
. The figure plots
$\varepsilon =0.001$
. The figure plots
![]() $\theta $
and a scaled value of
$\theta $
and a scaled value of
![]() $x-1$
(or X). It can be seen that at
$x-1$
(or X). It can be seen that at
![]() $t=30$
,
$t=30$
,
![]() $\theta \approx -15$
so that
$\theta \approx -15$
so that
![]() $z\approx 0.3\times 10^{-6}\sim \varepsilon ^2b$
and the solution is in the slow phase. As
$z\approx 0.3\times 10^{-6}\sim \varepsilon ^2b$
and the solution is in the slow phase. As
![]() $x\to 1$
(
$x\to 1$
(
![]() $5(x-1)\to 0$
in the figure),
$5(x-1)\to 0$
in the figure),
![]() $\theta $
increases and there is a transition to a pulse at approximately
$\theta $
increases and there is a transition to a pulse at approximately
![]() $t=30.7$
. And not just one pulse, but a sequence of four, with a late aborted one, before the trajectory recovers back to the slow phase. These pulses manifest themselves as “bursts” in the time series for z.
$t=30.7$
. And not just one pulse, but a sequence of four, with a late aborted one, before the trajectory recovers back to the slow phase. These pulses manifest themselves as “bursts” in the time series for z.

Figure 5 A series of bursts. Shown are
![]() $\theta =\ln z$
and
$\theta =\ln z$
and
![]() $5(x-1)$
. The parameter values used are
$5(x-1)$
. The parameter values used are
![]() $a=0.2$
,
$a=0.2$
,
![]() $b=0.2$
,
$b=0.2$
,
![]() $c=1,\!000$
.
$c=1,\!000$
.
The clue consists of the observation that the slope of X clearly decays between pulses, and this causes a gradual waning of the amplitude of the oscillations until, when
![]() $X<0$
, no further oscillations take place. Inspection of the graph of
$X<0$
, no further oscillations take place. Inspection of the graph of
![]() $\dot {x}$
suggests that this change in slope is just part of the secular change due to the evolution of X. In more detail, equation (2.11) can be written in the form
$\dot {x}$
suggests that this change in slope is just part of the secular change due to the evolution of X. In more detail, equation (2.11) can be written in the form
At leading order,
![]() $\dot {X}+z$
is constant, and in view of the matching conditions in equation (2.13) which imply
$\dot {X}+z$
is constant, and in view of the matching conditions in equation (2.13) which imply
![]() $\dot {X}\to \beta $
and (using equation (2.14))
$\dot {X}\to \beta $
and (using equation (2.14))
![]() $z\sim \varepsilon ^{3/2}$
as
$z\sim \varepsilon ^{3/2}$
as
![]() $T\to 0$
, this constant is
$T\to 0$
, this constant is
![]() $\beta $
. Substituting this into the right-hand side of equation (2.23) allows an improved approximation in the form
$\beta $
. Substituting this into the right-hand side of equation (2.23) allows an improved approximation in the form
bearing in mind the definition of
![]() $\gamma $
in equation (2.7), and therefore a correction to equation (2.16) is
$\gamma $
in equation (2.7), and therefore a correction to equation (2.16) is
again subject to the initial conditions in equation (2.15).
For sufficiently small
![]() $\varepsilon $
, equation (2.24) suggests that there will be a series of pulsesFootnote
1
, which terminate approximately when
$\varepsilon $
, equation (2.24) suggests that there will be a series of pulsesFootnote
1
, which terminate approximately when
![]() $\bar {\beta }$
in equation (2.25) becomes negative. The reason then that Figure 4 exhibits a single pulse is because the value of
$\bar {\beta }$
in equation (2.25) becomes negative. The reason then that Figure 4 exhibits a single pulse is because the value of
![]() $\beta $
is also formally small, or the value of
$\beta $
is also formally small, or the value of
![]() $\sqrt {\varepsilon }$
is not so small. We will explore this in the following section.
$\sqrt {\varepsilon }$
is not so small. We will explore this in the following section.
2.5 The last pulse
Formally, for sufficiently small
![]() $\varepsilon $
, we would treat the series of pulses as a slowly varying nonlinear oscillator, and use the method of Kuzmak and Luke (see [Reference Kevorkian and Cole8]). The final pulse then occurs when
$\varepsilon $
, we would treat the series of pulses as a slowly varying nonlinear oscillator, and use the method of Kuzmak and Luke (see [Reference Kevorkian and Cole8]). The final pulse then occurs when
![]() $\bar {\beta }$
approaches zero. However, for the more commonly viewed lower values of c wherein a single pulse occurs, it is of interest to address that case directly. Much of our discussion below is closely related to the work of Cheng and Chen [Reference Cheng and Chen2], except that the approximations we make are based on explicit asymptotic limits.
$\bar {\beta }$
approaches zero. However, for the more commonly viewed lower values of c wherein a single pulse occurs, it is of interest to address that case directly. Much of our discussion below is closely related to the work of Cheng and Chen [Reference Cheng and Chen2], except that the approximations we make are based on explicit asymptotic limits.
A single pulse may occur if
![]() $\beta $
is small. This occurs if a is small. Specifically, if we expand equation (2.4) for small a (and hence suppose
$\beta $
is small. This occurs if a is small. Specifically, if we expand equation (2.4) for small a (and hence suppose
![]() ), we find that, starting with
), we find that, starting with
![]() $\dot {x}=0$
at
$\dot {x}=0$
at
![]() $t=0$
, then
$t=0$
, then
![]() $x=1$
at
$x=1$
at
![]() $t\approx \pi -\{\pi a-2(1-C)\}^{1/2}$
, and consequently
$t\approx \pi -\{\pi a-2(1-C)\}^{1/2}$
, and consequently
A puritan approach would then start again with the additional assumption that
![]() $a\ll 1$
, but in the interests of brevity, we will go off-piste and anticipate that equation (2.25) applies, but we will suppose that
$a\ll 1$
, but in the interests of brevity, we will go off-piste and anticipate that equation (2.25) applies, but we will suppose that
![]() $\beta $
as well as
$\beta $
as well as
![]() $\varepsilon $
is small. With both a and
$\varepsilon $
is small. With both a and
![]() $\beta $
being small, we can take
$\beta $
being small, we can take
![]() $\gamma =1/2$
, and we presume the initial conditions in equation (2.15) still apply. (Note that properly speaking, the solution would require a multiple scales expansion.)
$\gamma =1/2$
, and we presume the initial conditions in equation (2.15) still apply. (Note that properly speaking, the solution would require a multiple scales expansion.)
An appropriate distinguished limit is to assume that
![]() $\beta \sim \varepsilon ^{1/3}$
and, to this end, we define the quantity B by the relation
$\beta \sim \varepsilon ^{1/3}$
and, to this end, we define the quantity B by the relation
and we will assume that
![]() $B=O(1)$
. We then define
$B=O(1)$
. We then define
so that equation (2.25) becomes
where the dashes denote differentiation with respect to
![]() $\tau $
and the initial conditions are
$\tau $
and the initial conditions are
where
 $$ \begin{align} \Theta_m=\ln\bigg[\frac{1}{\varepsilon b}\sqrt{\frac{B}{2\pi}}\bigg]. \end{align} $$
$$ \begin{align} \Theta_m=\ln\bigg[\frac{1}{\varepsilon b}\sqrt{\frac{B}{2\pi}}\bigg]. \end{align} $$
To solve this, we use the same asymptotic procedure as before, since
![]() $\Theta _m$
is large. Initially, we can neglect the exponential, so that
$\Theta _m$
is large. Initially, we can neglect the exponential, so that
This has a maximum at
![]() $\tau =2B$
, where
$\tau =2B$
, where
Formally, if
![]() $B=O(1)$
, this solution is uniformly valid and provides the aborted pulse seen in Figure 5. If B is slightly larger,
$B=O(1)$
, this solution is uniformly valid and provides the aborted pulse seen in Figure 5. If B is slightly larger,
there will be another sharp peak.
Let us consider this in more detail. With the definitions in equations (2.6), (2.8), (2.12) and (2.28), we can define
where we write
In addition, bearing in mind equations (2.26) and (2.27), it is appropriate to define
and to suppose that
![]() $\alpha =O(1)$
. (Actually, for the example we have used with
$\alpha =O(1)$
. (Actually, for the example we have used with
![]() $c=10$
and
$c=10$
and
![]() $a=0.2$
, one has
$a=0.2$
, one has
![]() $\alpha \approx 0.93$
.) The equations then take the exact form
$\alpha \approx 0.93$
.) The equations then take the exact form
 $$ \begin{align}{\xi}"+1+\nu^2\xi+e^\Theta{\Theta}'&=\nu^3\alpha({\xi}'+e^\Theta),\dfrac{}{}\nonumber\\ {\Theta}'&=\nu^3be^{-\Theta}+\xi,\end{align} $$
$$ \begin{align}{\xi}"+1+\nu^2\xi+e^\Theta{\Theta}'&=\nu^3\alpha({\xi}'+e^\Theta),\dfrac{}{}\nonumber\\ {\Theta}'&=\nu^3be^{-\Theta}+\xi,\end{align} $$
with matching conditions as
![]() $\tau \to 0$
,
$\tau \to 0$
,
At leading order, this gives
![]() $\xi ={\Theta }'$
and therefore also
$\xi ={\Theta }'$
and therefore also
with the first integral
which regains equation (2.29).
As for the earlier pulse analysis and supposing that
![]() , there is a rise phase in which equation (2.31) applies:
, there is a rise phase in which equation (2.31) applies:
followed by a peak in which, as in equation (2.19),
so that the solution is again given by equation (2.22), provided we choose
 $$ \begin{align} &\Theta_M=-\Theta_m+\tfrac{1}{2} B\tau_M^2-\tfrac{1}{6}\tau_M^3-2\ln 2,\nonumber\\ &\big(B\tau_M-\tfrac{1}{2}\tau_M^2\big)e^{-\Theta_M/2}=\sqrt{2}, \end{align} $$
$$ \begin{align} &\Theta_M=-\Theta_m+\tfrac{1}{2} B\tau_M^2-\tfrac{1}{6}\tau_M^3-2\ln 2,\nonumber\\ &\big(B\tau_M-\tfrac{1}{2}\tau_M^2\big)e^{-\Theta_M/2}=\sqrt{2}, \end{align} $$
with order of magnitude solutions
 $$ \begin{align}\tau_M\sim\sqrt{\frac{2\Theta_m}{B}},\quad \Theta_M\sim 2\ln\bigg(\frac{B\tau_M}{\sqrt{2}}\bigg),\end{align} $$
$$ \begin{align}\tau_M\sim\sqrt{\frac{2\Theta_m}{B}},\quad \Theta_M\sim 2\ln\bigg(\frac{B\tau_M}{\sqrt{2}}\bigg),\end{align} $$
consistent with equation (2.32). Following the sharp peak, there is a decline in which
and matching to the peak solution given by equation (2.38) and also equation (2.22) implies
In seeking to determine the downward sloping part of the map in Figure 2, the key observation is in Figure 6, which shows a close-up of the passage of x and
![]() $\ln z$
(and thus
$\ln z$
(and thus
![]() $\Theta $
) through a pulse when
$\Theta $
) through a pulse when
![]() $c=10$
. Clearly, the sharp peak in
$c=10$
. Clearly, the sharp peak in
![]() $\Theta $
causes a rapid decrease in
$\Theta $
causes a rapid decrease in
![]() ${\Theta }'=\xi $
and thus also x. This can also be seen in Figure 5. However, whereas the drop in Figure 5 is relatively small, it can be seen in Figure 6 that it is actually of numerical
${\Theta }'=\xi $
and thus also x. This can also be seen in Figure 5. However, whereas the drop in Figure 5 is relatively small, it can be seen in Figure 6 that it is actually of numerical
![]() $O(1)$
.
$O(1)$
.
From equation (2.39), using the fact that the jump in slope of
![]() $\phi (\eta )$
across the pulse is
$\phi (\eta )$
across the pulse is
![]() $-2\sqrt {2}$
, it follows that the jump in x across the pulse is
$-2\sqrt {2}$
, it follows that the jump in x across the pulse is
where we have used the crude estimates in equation (2.40). Using the definition of
![]() $\Theta _m$
in equation (2.30),
$\Theta _m$
in equation (2.30),
 $$ \begin{align*} \lambda\sim 2\varepsilon^{2/3}\bigg\{2B\ln\bigg(\frac{1}{\varepsilon b}\sqrt{\frac{B}{2\pi}}\bigg)\bigg\}^{1/2}. \end{align*} $$
$$ \begin{align*} \lambda\sim 2\varepsilon^{2/3}\bigg\{2B\ln\bigg(\frac{1}{\varepsilon b}\sqrt{\frac{B}{2\pi}}\bigg)\bigg\}^{1/2}. \end{align*} $$
If we use values
![]() $B=1$
,
$B=1$
,
![]() $b=0.2$
, then for
$b=0.2$
, then for
![]() $c=10$
, we find
$c=10$
, we find
![]() $\lambda \approx 1.05$
, whereas for
$\lambda \approx 1.05$
, whereas for
![]() $c=1,\!000$
, it is
$c=1,\!000$
, it is
![]() $0.078$
. If we want to be fastidious, we could then consider a distinguished limit in which
$0.078$
. If we want to be fastidious, we could then consider a distinguished limit in which
 $$ \begin{align*} b=\frac{b^*}{\varepsilon\sqrt{2\pi}}\exp\bigg[-\frac{1}{8\varepsilon^{4/3}}\bigg],\quad b^*=O(1), \end{align*} $$
$$ \begin{align*} b=\frac{b^*}{\varepsilon\sqrt{2\pi}}\exp\bigg[-\frac{1}{8\varepsilon^{4/3}}\bigg],\quad b^*=O(1), \end{align*} $$
but in the present note, we will avoid such delicacy. The quotation from Montaigne’s essay “Of usefulness and honesty” (De l’utile et de l’honnête) at the head of Murray’s [Reference Murray13] book is wonderfully apt and provides our watchword here.
Figure 7 illustrates what happens when
![]() $c=10$
. Relatively low values of C and thus B cause low pulses, which return to the plane approximately on the y axis. Higher values of C and thus B and hence also
$c=10$
. Relatively low values of C and thus B cause low pulses, which return to the plane approximately on the y axis. Higher values of C and thus B and hence also
![]() $\lambda $
give higher peaks of z (as can be seen in Figure 1) and also x, but the subsequent drop is larger, and brings the trajectory almost back to the origin, and thus lower values of C. This will explain the descending part of the map in Figure 2.
$\lambda $
give higher peaks of z (as can be seen in Figure 1) and also x, but the subsequent drop is larger, and brings the trajectory almost back to the origin, and thus lower values of C. This will explain the descending part of the map in Figure 2.

Figure 7 A view looking directly down on the attractor of equation (1.1) for the values
![]() $a=0.18$
,
$a=0.18$
,
![]() $b=0.2$
,
$b=0.2$
,
![]() $c=10$
. Note that the coordinates are unscaled.
$c=10$
. Note that the coordinates are unscaled.
2.6 A Poincaré map
We can use these approximations to construct an approximate Poincaré map for the solution. We use the plane
![]() $y=0$
,
$y=0$
,
![]() $x<0$
as the Poincaré surface. From equation (1.2), this is
$x<0$
as the Poincaré surface. From equation (1.2), this is
![]() $\dot {x}+z=0$
, and in the slow phase where
$\dot {x}+z=0$
, and in the slow phase where
![]() $z=O(\varepsilon ^2)$
(equation (2.2)), this is approximately
$z=O(\varepsilon ^2)$
(equation (2.2)), this is approximately
![]() $\dot {x}=0$
,
$\dot {x}=0$
,
![]() $x<0$
, which we used to derive equation (2.5), which gives the rising limb of the map in Figure 2.
$x<0$
, which we used to derive equation (2.5), which gives the rising limb of the map in Figure 2.
We restrict attention to the single-pulse case described in the previous section. Working our way through the various scalings, we find from equation (2.33) (bearing in mind that
![]() $\xi \approx {\Theta }'$
) that
$\xi \approx {\Theta }'$
) that
Since
![]() ${\Theta }"+e^\Theta =B-\tau $
in the pulse, we see that
${\Theta }"+e^\Theta =B-\tau $
in the pulse, we see that
![]() $y=0$
when
$y=0$
when
![]() $\tau =B$
, but this is when
$\tau =B$
, but this is when
![]() $x>0$
, as is also clear in Figure 7. The next crossing of
$x>0$
, as is also clear in Figure 7. The next crossing of
![]() $y=0$
when
$y=0$
when
![]() $x<0$
is back on the slow phase, and for x, this begins immediately after the sharp peak, where equation (2.41) implies
$x<0$
is back on the slow phase, and for x, this begins immediately after the sharp peak, where equation (2.41) implies
where we define
as earlier, and also
In the slow phase, the exponential in equation (2.37) is negligible and x satisfies equation (2.3) again, and thus also equation (2.4), which we write in the form
where, if the next intersection with
![]() $\dot {x}=0$
,
$\dot {x}=0$
,
![]() $x<0$
, is at
$x<0$
, is at
![]() $t=t_2>t_M$
, we define
$t=t_2>t_M$
, we define
![]() $t'=t-t_2$
, so that equation (2.42) implies
$t'=t-t_2$
, so that equation (2.42) implies
The value of
![]() $C'$
is the next iterate of the approximate Poincaré map. We retain the
$C'$
is the next iterate of the approximate Poincaré map. We retain the
![]() $\lambda =\nu ^2L$
term in view of its significance at lower values of c, but note that equation (2.42) then appears to be inconsistent with the fact that
$\lambda =\nu ^2L$
term in view of its significance at lower values of c, but note that equation (2.42) then appears to be inconsistent with the fact that
![]() $\ddot {x}+x\approx 0$
; the resolution is that the quadratic term coefficient also has a correction to
$\ddot {x}+x\approx 0$
; the resolution is that the quadratic term coefficient also has a correction to
![]() $(1-\nu ^2L)/2$
, as can easily be checked by including the
$(1-\nu ^2L)/2$
, as can easily be checked by including the
![]() $O(\nu ^2)$
correction in equation (2.34); but choosing to satisfy equation (2.43) automatically caters for this.
$O(\nu ^2)$
correction in equation (2.34); but choosing to satisfy equation (2.43) automatically caters for this.
The value of
![]() $C'$
is then determined by eliminating s from the pair of equations
$C'$
is then determined by eliminating s from the pair of equations
Putting all of this together and defining
![]() $\omega s=\pi +\sigma $
, the Poincaré map can be approximated as a one-dimensional map
$\omega s=\pi +\sigma $
, the Poincaré map can be approximated as a one-dimensional map
![]() $C\to C'$
, where
$C\to C'$
, where
where, from equations (2.30) and (2.39),
S is given in terms of B by the zero contour of
 $$ \begin{align}F(S,B)=B^3\bigg(\frac{1}{2} S^2-\frac{1}{6} S^3\bigg)-2\ln\bigg[B^2\bigg(S-\frac{1}{2} S^2\bigg)\bigg]-\ln\bigg[\frac{2}{\varepsilon b}\sqrt{\frac{B}{2\pi}}\bigg],\end{align} $$
$$ \begin{align}F(S,B)=B^3\bigg(\frac{1}{2} S^2-\frac{1}{6} S^3\bigg)-2\ln\bigg[B^2\bigg(S-\frac{1}{2} S^2\bigg)\bigg]-\ln\bigg[\frac{2}{\varepsilon b}\sqrt{\frac{B}{2\pi}}\bigg],\end{align} $$
and finally B is given in terms of C by equation (2.26):
 $$ \begin{align}B=\frac{\{\pi a+2(C-1)\}^{1/2}}{\varepsilon^{1/3}}.\end{align} $$
$$ \begin{align}B=\frac{\{\pi a+2(C-1)\}^{1/2}}{\varepsilon^{1/3}}.\end{align} $$
We assume that the drop in x across the pulse,
![]() $\lambda $
, is less than
$\lambda $
, is less than
![]() $1- a\beta _M/2$
, otherwise equation (2.44) implies that
$1- a\beta _M/2$
, otherwise equation (2.44) implies that
![]() $C'<0$
. In fact, what happens in this latter case is that the bottom-most (lowest y) strand of the collapsing pulse in Figure 7 lands back on the slow phase plane in
$C'<0$
. In fact, what happens in this latter case is that the bottom-most (lowest y) strand of the collapsing pulse in Figure 7 lands back on the slow phase plane in
![]() $y<0$
, so that its next traverse through
$y<0$
, so that its next traverse through
![]() $y=0$
is in
$y=0$
is in
![]() $x>0$
and a further half-turn is necessary to reach the Poincaré surface; this occurs for
$x>0$
and a further half-turn is necessary to reach the Poincaré surface; this occurs for
![]() $a=0.2$
, which is why there is an upturn at the right in Figure 2 and also why Figure 7 uses the value
$a=0.2$
, which is why there is an upturn at the right in Figure 2 and also why Figure 7 uses the value
![]() $a=0.18$
, for which this does not occur (and the corresponding map is simply unimodal).
$a=0.18$
, for which this does not occur (and the corresponding map is simply unimodal).
Given C, equation (2.47) determines B and then equation (2.46) determines the function
![]() $S(B)$
implicitly. After that, the other definitions in equations (2.44) and (2.45) provide an explicit recipe for
$S(B)$
implicitly. After that, the other definitions in equations (2.44) and (2.45) provide an explicit recipe for
![]() $C'$
. Just as the end is in sight, a final complication occurs: the function
$C'$
. Just as the end is in sight, a final complication occurs: the function
![]() $S(B)$
is multi-valued, as shown in Figure 8. It is easy to explain this, as there are two distinct asymptotic limits of
$S(B)$
is multi-valued, as shown in Figure 8. It is easy to explain this, as there are two distinct asymptotic limits of
![]() $F=0$
as
$F=0$
as
![]() $B\to \infty $
or
$B\to \infty $
or
![]() $S\to 0$
, these being
$S\to 0$
, these being

Figure 8 The zero contour of
![]() $F(S,B)$
as defined in equation (2.46).
$F(S,B)$
as defined in equation (2.46).
Which should we choose? The answer to this lies in the dynamics of the pulse and can be seen in Figure 6, for example. It is clear that x reaches its maximum before
![]() $\Theta $
does. The latter is at
$\Theta $
does. The latter is at
![]() $\tau =\tau _M$
, while the former is at
$\tau =\tau _M$
, while the former is at
![]() $\tau \approx B$
(where
$\tau \approx B$
(where
![]() $e^\Theta $
can be ignored). Therefore,
$e^\Theta $
can be ignored). Therefore,
![]() $\tau _M>B$
, or equivalently (see equation (2.45)),
$\tau _M>B$
, or equivalently (see equation (2.45)),
![]() $S>1$
. It is perhaps significant that the graph in Figure 8 has its sole (that is, the left-hand limit of the curve, or the sole of the foot of the sleeping giant) at
$S>1$
. It is perhaps significant that the graph in Figure 8 has its sole (that is, the left-hand limit of the curve, or the sole of the foot of the sleeping giant) at
![]() $S\approx 1$
. Therefore, we choose the upper branch of the figure to provide a suitable uniquely defined function
$S\approx 1$
. Therefore, we choose the upper branch of the figure to provide a suitable uniquely defined function
![]() $S(B)$
. It should be noted, nevertheless, that
$S(B)$
. It should be noted, nevertheless, that
![]() $S<1$
on the upper branch for
$S<1$
on the upper branch for
![]() , so the reliability of this argument may require further attention. However,
, so the reliability of this argument may require further attention. However,
![]() corresponds to
corresponds to
![]() , which is where the approximate map starts to break down anyway. It is tempting to suppose that the lower branch corresponds to the minimum in x after the pulse maximum.
, which is where the approximate map starts to break down anyway. It is tempting to suppose that the lower branch corresponds to the minimum in x after the pulse maximum.
Figure 9 shows the map we obtain from the combination of the approximations in equation (2.5) for
![]() $C<1-\pi a/2\approx 0.686$
and equation (2.44) for C values larger than this. In fact, we have simply plotted the minimum of the two expressions, where the join occurs at approximately 0.715. The approximation in equation (2.44) assumes a sharp peak of
$C<1-\pi a/2\approx 0.686$
and equation (2.44) for C values larger than this. In fact, we have simply plotted the minimum of the two expressions, where the join occurs at approximately 0.715. The approximation in equation (2.44) assumes a sharp peak of
![]() $\Theta $
and it is reasonable to suppose that the region near the join is in fact smooth, accommodating the weak pulses in that part of the graph. The approximate map also breaks down near
$\Theta $
and it is reasonable to suppose that the region near the join is in fact smooth, accommodating the weak pulses in that part of the graph. The approximate map also breaks down near
![]() $C=1.6$
, since the increasing value of
$C=1.6$
, since the increasing value of
![]() $\lambda $
causes
$\lambda $
causes
![]() $\sigma $
to rapidly increase towards
$\sigma $
to rapidly increase towards
![]() $\pi /2$
, causing the upturn in
$\pi /2$
, causing the upturn in
![]() $C'$
. In fact, Figure 7 illustrates the issue. At these large values of
$C'$
. In fact, Figure 7 illustrates the issue. At these large values of
![]() $\lambda $
, the end-pulse trajectory lands very close to the origin and thus also the fixed point of the equations. Our approximate map is actually mimicking the upturn in Figure 2, but it is unable to deal with the homoclinic approach to the fixed point, which in these kinds of approximation requires separate approximation [Reference Glendinning and Sparrow7]).
$\lambda $
, the end-pulse trajectory lands very close to the origin and thus also the fixed point of the equations. Our approximate map is actually mimicking the upturn in Figure 2, but it is unable to deal with the homoclinic approach to the fixed point, which in these kinds of approximation requires separate approximation [Reference Glendinning and Sparrow7]).

Figure 9 One-dimensional approximate map for the rescaled Rössler equations, at
![]() $a=0.2$
,
$a=0.2$
,
![]() $b=0.2$
,
$b=0.2$
,
![]() $c=10$
. The upper branch of the curve in Figure 8 has been approximated by a function which fits well until the sole in Figure 8 is approached. Note in comparing this with Figure 2 that the present figure is in scaled units, whereas Figure 2 is in the original variables, a factor of ten larger.
$c=10$
. The upper branch of the curve in Figure 8 has been approximated by a function which fits well until the sole in Figure 8 is approached. Note in comparing this with Figure 2 that the present figure is in scaled units, whereas Figure 2 is in the original variables, a factor of ten larger.
3 Conclusions
We have sketched a way in which the Rössler equations can be asymptotically solved in the limit
![]() $c\gg 1$
. When dealing with chaotic systems, it is natural to question how approximation methods can give useful information when the solutions display sensitive dependence on initial conditions. Although we will not attempt to elaborate the argument here, the resolution of this conundrum is similar to that involved in the use of Shilnikov’s method to construct strange attractors (see, for example, [Reference Fowler and McGuinness6, Ch. 4]), which is, in fact, a procedure based on matched asymptotic expansions as we use here. The key point is that one constructs an approximate Poincaré map over a finite time interval: precisely the context in which asymptotic expansions “converge”. The two key ingredients of chaos – the existence of an infinite number of periodic orbits and the existence of a Smale horseshoe – are guaranteed by the smoothness of the approximation and the implicit function theorem. The fact that an individual trajectory will deviate from its approximation over long times does not alter this essential fact.
$c\gg 1$
. When dealing with chaotic systems, it is natural to question how approximation methods can give useful information when the solutions display sensitive dependence on initial conditions. Although we will not attempt to elaborate the argument here, the resolution of this conundrum is similar to that involved in the use of Shilnikov’s method to construct strange attractors (see, for example, [Reference Fowler and McGuinness6, Ch. 4]), which is, in fact, a procedure based on matched asymptotic expansions as we use here. The key point is that one constructs an approximate Poincaré map over a finite time interval: precisely the context in which asymptotic expansions “converge”. The two key ingredients of chaos – the existence of an infinite number of periodic orbits and the existence of a Smale horseshoe – are guaranteed by the smoothness of the approximation and the implicit function theorem. The fact that an individual trajectory will deviate from its approximation over long times does not alter this essential fact.
The basic approximation is relatively straightforward and leads to the prediction of the observed structure at values
![]() $c\sim 10^3$
in which more or less periodic sequences of bursts occur. The asymptotic limit is manifested by the almost two-dimensional structure of the attractor and this feature is maintained at lower values of
$c\sim 10^3$
in which more or less periodic sequences of bursts occur. The asymptotic limit is manifested by the almost two-dimensional structure of the attractor and this feature is maintained at lower values of
![]() $c\sim 10$
. We have taken the risky step of endeavouring to explain the chaotic solutions which occur at such values. The investigation is clouded with a number of difficulties, not the least of which is the blurring of the distinction between the sizes of
$c\sim 10$
. We have taken the risky step of endeavouring to explain the chaotic solutions which occur at such values. The investigation is clouded with a number of difficulties, not the least of which is the blurring of the distinction between the sizes of
![]() $\varepsilon ^{1/3}$
and
$\varepsilon ^{1/3}$
and
![]() $\ln (1/\varepsilon )$
compared to one. Nevertheless, we are able to produce a credible approximation to the unimodal map which can occur.
$\ln (1/\varepsilon )$
compared to one. Nevertheless, we are able to produce a credible approximation to the unimodal map which can occur.
That said, the study is one that only dips an asymptotic toe into the analysis of these equations and their further investigation warrants a much more thorough treatment. In the same way that Sparrow sorted out the Lorenz equations in his thesis [Reference Sparrow16] and published the results as a book [Reference Sparrow17], we hope that our exploration of the Rössler equations will inspire a future examination of these equations in much greater depth than we have attempted here.
Acknowledgement
A. C. Fowler acknowledges the support of the Mathematics Applications Consortium for Science and Industry ( www.macsi.ul.ie ) funded by the Science Foundation Ireland mathematics grant 12/IA/1683.