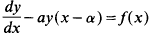A (local) Lie loop is a real analytic manifold M with a base point e and three analytic functions (x, y) → x° y, x\y, x/y: M × M → M (respectively, U × U → M for an open neighbourhood U of e in M) such that the following conditions are satisfied: (i) x ° e = e ° x = e, (ii) x ° (x\y) = y, and (iii) (x/y)° y = x for all x, y ε M (respectively, U). If the multiplication ° is associative, then M is a (local) Lie group. The tangent vector space L(M) in e is equipped with an anticommutative bilinear operation (X, Y) →[X, Y] and a trilinear operation (X, Y, Z) →〈X, Y, Z〉. These are defined as follows: Let B be a convex symmetric open neighbourhood of 0 in L(M) such that the exponential function maps B diffeomorphically onto an open neighbourhood V of e in M and transport the operation ° into L(M) by defining X ° Y = (exp|B)−1((exp X)° (exp Y)) for X and Y in a neighbourhood C of 0 in B such that (exp C) ° (exp C) ⊂ V. Similarly, we transport / and \.