1. Introduction and motivation
Wall-bounded turbulent flows are common in a wide range of engineering applications, such as flows over ships and submarines, and in pipes. In such cases, the bounding walls generally have a ‘rough’ surface topography, which adds a drag penalty in the form of pressure drag. This drag is generated from the local flow separation and subsequent wake formation behind the protruding roughness elements, similar to that noted for bluff bodies (Choi, Jeon & Kim Reference Choi, Jeon and Kim2008). An increase in the size of surface roughness increases the relative contributions of the pressure drag to the total drag, but reduces the relative viscous drag contributions (Jiménez Reference Jiménez2004; Chung et al. Reference Chung, Hutchins, Schultz and Flack2021). The latter is associated with obliteration of the drag-producing near-wall cycle, by roughness, thereby making pressure drag the dominant contributor to the total drag in the ‘fully rough’ regime. These fundamental differences in smooth and rough wall drag-generating mechanisms pose a significant challenge for shipping as well as piping industries, wherein the exposed surfaces degrade from a hydraulically smooth to fully rough regime in their operation cycle. In such cases, a drag reduction strategy that can attenuate both smooth and fully rough wall drag-generating mechanisms is required, and this forms the focus of the present study. Here, we will refer to a fully rough scenario as when the total drag comes almost entirely from the pressure drag. In this respect, it is important to take note of some recent findings (Marusic et al. Reference Marusic, Chandran, Rouhi, Fu, Wine, Holloway, Chung and Smits2021) based on high friction Reynolds number (![]() $Re_{\tau }$) experiments, which reveal that inertia-dominated scales also make statistically significant contributions to the total skin-friction drag at
$Re_{\tau }$) experiments, which reveal that inertia-dominated scales also make statistically significant contributions to the total skin-friction drag at ![]() $Re_{\tau } \gtrsim 10^3$. Contributions from these inertial scales, however, are kept negligible in this study by limiting all our simulations to low
$Re_{\tau } \gtrsim 10^3$. Contributions from these inertial scales, however, are kept negligible in this study by limiting all our simulations to low ![]() $Re_{\tau }$ (
$Re_{\tau }$ (![]() $\lesssim$300).
$\lesssim$300).
1.1. Literature on rough wall drag reduction
Numerous active and passive drag reduction strategies have been proposed in the past for turbulent wall-bounded flows (Corke & Thomas Reference Corke and Thomas2018). However, the majority of these strategies focused on reducing the viscous drag by targeting the near-wall self-sustaining cycle (Kim Reference Kim2011; Jiménez Reference Jiménez2018), rendering them ineffective for attenuating the fully rough wall drag. Some studies have found large-eddy break-up devices to be effective in reducing both smooth (Corke, Nagib & Guezennec Reference Corke, Nagib and Guezennec1982) and rough wall skin-friction drag (Bandyopadhyay Reference Bandyopadhyay1986). However, using such devices also adds significant parasitic drag, effectively making the total drag reduction negligible. Interestingly, recent studies by Banchetti, Luchini & Quadrio (Reference Banchetti, Luchini and Quadrio2020), Nguyen, Ricco & Pironti (Reference Nguyen, Ricco and Pironti2021) and Garcia, Ahmad & Hussain (Reference Garcia, Ahmad and Hussain2021) found that the well-known strategy of imposing spanwise oscillations on a turbulent rough wall flow can significantly reduce the pressure drag emerging from the roughness. This is promising since the same drag reduction strategy is also known to substantially reduce the smooth wall (i.e. viscous) drag (Akhavan, Jung & Mangiavacchi Reference Akhavan, Jung and Mangiavacchi1993; Gatti & Quadrio Reference Gatti and Quadrio2013, Reference Gatti and Quadrio2016; Ricco, Skote & Leschziner Reference Ricco, Skote and Leschziner2021), suggesting continued drag reduction, if implemented on a surface with varying roughness properties over time. Notably, the same strategy has also been found to yield significant drag reduction in the scenario of a transonic flow over a wing (Quadrio et al. Reference Quadrio, Chiarini, Banchetti, Gatti, Memmolo and Pirozzoli2022), indicating success of this strategy across a broad range of flows.
The drag of a rough wall, as well as its overlying boundary layer properties, is a function of the geometric parameters describing the surface topography (Chung et al. Reference Chung, Hutchins, Schultz and Flack2021). This has often led to consideration of simplified roughness geometries for a systematic investigation of the influence of these parameters. For instance, past studies have considered square (Leonardi et al. Reference Leonardi, Orlandi, Smalley, Djenidi and Antonia2003; Lee & Sung Reference Lee and Sung2007) or cylindrical (Furuya, Miyata & Fujita Reference Furuya, Miyata and Fujita1976; Leonardi et al. Reference Leonardi, Orlandi, Djenidi and Antonia2015) rods spanning the entire width of the testing domain – known as two-dimensional (2-D) roughness – or three-dimensional (3-D) sinusoidal (Chan et al. Reference Chan, MacDonald, Chung, Hutchins and Ooi2015), hemispherical (Wu, Christensen & Pantano Reference Wu, Christensen and Pantano2020) or cubic (Coceal et al. Reference Coceal, Dobre, Thomas and Belcher2007; Lee, Sung & Krogstad Reference Lee, Sung and Krogstad2011) roughness distributed over the wall. The same philosophy has also been adopted by past studies in understanding the efficacy of drag reduction strategies on the rough wall drag (Bandyopadhyay Reference Bandyopadhyay1986; Banchetti et al. Reference Banchetti, Luchini and Quadrio2020; Garcia et al. Reference Garcia, Ahmad and Hussain2021; Nguyen et al. Reference Nguyen, Ricco and Pironti2021). For example, Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020) simulated a turbulent channel flow with an isolated 2-D bump on one wall, to generate a pressure drag contribution to the total drag. The drag reduction strategy considered by Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020) involved imposition of streamwise travelling waves of spanwise velocity on the bump wall (Quadrio, Ricco & Viotti Reference Quadrio, Ricco and Viotti2009), which was found to enlarge the separation bubble in the bump's wake, while also strongly stabilizing its temporal activity. A pressure drag reduction of ![]() $\sim$10 % was noted by Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020), alongside some viscous drag reduction, for actuation parameters that previously yielded maximum drag reduction for a smooth wall channel flow. Similarly, Nguyen et al. (Reference Nguyen, Ricco and Pironti2021) simulated a turbulent channel flow with transverse (i.e. 2-D) square bars placed on both walls, positioned at a streamwise offset of 39 times the bar height (imposed by periodicity of the computational domain). Their study involved imposing a time-oscillating pressure gradient in the spanwise direction across the entire channel cross-section, which yielded a maximum pressure drag reduction of 22 % at an optimum oscillating frequency (alongside some viscous drag reduction). Their observations were consistent with Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020), who also observed pressure drag reduction due to a decrease in the pressure upstream of the rough element, along with an increase in the base pressure (i.e. downstream of the bar). Based on a control volume analysis of the change in momentum between consecutive roughness elements, Nguyen et al. (Reference Nguyen, Ricco and Pironti2021) hypothesized the reduction of the Reynolds shear stresses, in the wake of the roughness elements, to be a manifestation of the reduction of pressure as well as viscous drag. A similar weakening of the Reynolds stresses in the roughness wake was noted by Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020), suggesting applicability of the same pressure drag reduction mechanism despite differences in the roughness geometry (2-D bump or square roughness).
$\sim$10 % was noted by Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020), alongside some viscous drag reduction, for actuation parameters that previously yielded maximum drag reduction for a smooth wall channel flow. Similarly, Nguyen et al. (Reference Nguyen, Ricco and Pironti2021) simulated a turbulent channel flow with transverse (i.e. 2-D) square bars placed on both walls, positioned at a streamwise offset of 39 times the bar height (imposed by periodicity of the computational domain). Their study involved imposing a time-oscillating pressure gradient in the spanwise direction across the entire channel cross-section, which yielded a maximum pressure drag reduction of 22 % at an optimum oscillating frequency (alongside some viscous drag reduction). Their observations were consistent with Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020), who also observed pressure drag reduction due to a decrease in the pressure upstream of the rough element, along with an increase in the base pressure (i.e. downstream of the bar). Based on a control volume analysis of the change in momentum between consecutive roughness elements, Nguyen et al. (Reference Nguyen, Ricco and Pironti2021) hypothesized the reduction of the Reynolds shear stresses, in the wake of the roughness elements, to be a manifestation of the reduction of pressure as well as viscous drag. A similar weakening of the Reynolds stresses in the roughness wake was noted by Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020), suggesting applicability of the same pressure drag reduction mechanism despite differences in the roughness geometry (2-D bump or square roughness).
While both of these past studies (Banchetti et al. Reference Banchetti, Luchini and Quadrio2020; Nguyen et al. Reference Nguyen, Ricco and Pironti2021) have improved our understanding significantly, they were confined to a quasi-isolated arrangement of roughness elements, thereby limiting their applicability to transitional rough wall scenarios. Although no detailed discussion on the pressure drag reduction mechanism was presented in either of these studies, it was speculated to be a direct consequence of the viscous drag reduction. For instance, Nguyen et al. (Reference Nguyen, Ricco and Pironti2021) hypothesized that the pressure drag reduction ‘could be due to the reduced dynamic pressure of the flow encountering the bar’. Similarly, Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020) mentioned ‘the pressure distribution is modified by changes in friction’, suggesting that pressure drag reduction is dependent on the viscous drag reduction mechanism. The present study tests this hypothesis by imposing spanwise wall oscillations on a fully rough scenario (i.e. having negligible viscous drag contributions), obtained by maintaining small streamwise offsets between subsequent roughness elements (Leonardi et al. Reference Leonardi, Orlandi, Smalley, Djenidi and Antonia2003).
1.2. Drawing inspiration from separation control strategies
Besides being an artefact of the viscous drag-reduced flow upstream of the roughness element, it is plausible that the pressure drag reduction could be a direct consequence of the spanwise oscillations influencing the separating shear layer or roughness wake (Choi et al. Reference Choi, Jeon and Kim2008; Yakeno et al. Reference Yakeno, Kawai, Nonomura and Fujii2015). This motivates some discussion on the findings of previous studies that have investigated the flow physics and control of separated shear layers. For both streamlined bodies (e.g. wings at a non-zero angle of attack) and bluff bodies subjected to separation/pressure drag, one can find several past studies discussing active (Seifert & Pack Reference Seifert and Pack2002; Post & Corke Reference Post and Corke2006; Yakeno et al. Reference Yakeno, Kawai, Nonomura and Fujii2015; Brackston, Wynn & Morrison Reference Brackston, Wynn and Morrison2016; Cho, Choi & Choi Reference Cho, Choi and Choi2016) and passive (Lin, Howard & Selby Reference Lin, Howard and Selby1990; Son et al. Reference Son, Choi, Jeon and Choi2011) methods for reducing pressure drag via delay in flow separation. The control mechanism used in all these studies aims to energize the separated shear layer (or separating boundary layer) to promote flow reattachment, thereby reducing the separation bubble (i.e. wake) size, which subsequently reduces the pressure drag. Based on the observations of Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020) and Nguyen et al. (Reference Nguyen, Ricco and Pironti2021), however, this is not the case when spanwise oscillations are imposed on the flow over 2-D roughness elements (they found separation bubbles to enlarge). Energizing the boundary layer via momentum injection also enhances the shear layer activity (and consequently the turbulent stresses) in the separated flow, which is also opposite to what is observed in case of rough wall drag reduction via spanwise oscillations (Banchetti et al. Reference Banchetti, Luchini and Quadrio2020; Nguyen et al. Reference Nguyen, Ricco and Pironti2021).
Another way to reduce pressure drag, besides reducing the separation bubble size, is by weakening/attenuating the vortex shedding activity in the bluff body wake (Choi et al. Reference Choi, Jeon and Kim2008), which increases its base pressure and consequently reduces pressure drag. Interestingly, this control mechanism also reduces the Reynolds stresses in the bluff body wake (Desai, Mittal & Mittal Reference Desai, Mittal and Mittal2020; Chopra & Mittal Reference Chopra and Mittal2022), which matches with observations made by Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020) and Nguyen et al. (Reference Nguyen, Ricco and Pironti2021) in the roughness wake, for drag-reduced cases. Several past studies have demonstrated weakening of the shedding activity by enforcing a mismatch in the phase of the separating 2-D shear layer from the bluff body, along its spanwise direction. For example, Bearman & Owen (Reference Bearman and Owen1998) demonstrated suppression of vortex shedding activity by introduction of spanwise waviness on the front stagnation face of a 2-D rectangular bar. The same concept was later extended successfully to a circular cylinder by Owen, Bearman & Szewczyk (Reference Owen, Bearman and Szewczyk2001), by changing the straight axis of the cylinder to a sinusoidal one. Darekar & Sherwin (Reference Darekar and Sherwin2001) explained that such a 3-D forcing, distorts the quasi-2-D separated shear layers, making them less susceptible to roll up into a Kármán vortex street, thereby suppressing the vortex shedding activity. Their explanation was reinforced later by Hwang, Kim & Choi (Reference Hwang, Kim and Choi2013), who performed linear stability analysis on 2-D wakes, thereby revealing that the phenomenon is not dependent on the ‘geometry’ of the bluff body. The same suppression has also been achieved in a cylinder wake via active control techniques, such as distributed forcing (Kim & Choi Reference Kim and Choi2005), which imposes blowing and suction on the top and bottom surfaces of the cylinder, with sinusoidally varying intensity along the span. Considering this background, one would expect imposition of time-varying spanwise oscillations on the 2-D roughness elements immersed in a wall-bounded flow (which act essentially as bluff bodies) to also disrupt the two-dimensionality of the separating shear layer in the roughness wake (for any roughness geometry).
1.3. Present contributions
The present study draws inspiration from the previous works of Leonardi et al. (Reference Leonardi, Orlandi, Smalley, Djenidi and Antonia2003, Reference Leonardi, Orlandi, Djenidi and Antonia2015) and Nguyen et al. (Reference Nguyen, Ricco and Pironti2021), and reports direct numerical simulations of a turbulent flow in an open channel configuration, with 2-D semi-cylindrical rods fixed on the bottom wall in a streamwise periodic manner. Individual simulations are conducted for different streamwise offsets between rods, thereby enabling investigation of the drag reduction mechanisms for scenarios of high-pressure drag domination (small offsets), as well as those with near equal pressure and viscous drag contributions (large offsets). For convenience, we will henceforth refer to the arrangement of semi-cylindrical elements as a ‘rough’ wall, but we note that generalizing the present observations to practical roughness geometries (e.g. 3-D or sandpaper) would require further studies. Here, we impose time-periodic wall oscillations in the spanwise direction to achieve drag reduction (Akhavan et al. Reference Akhavan, Jung and Mangiavacchi1993), which is tested here for the first time on fully rough cases. Discussion in § 1.2 suggests that weakening of vortex shedding activity could be the plausible mechanism behind pressure drag reduction noted previously for transitional rough wall cases (Banchetti et al. Reference Banchetti, Luchini and Quadrio2020; Nguyen et al. Reference Nguyen, Ricco and Pironti2021). This hypothesis will be tested rigorously in the present study.
2. Flow configuration and simulation strategy
As shown in figure 1(a), we consider an open-channel flow of an incompressible fluid of density ![]() $\rho$ and kinematic viscosity
$\rho$ and kinematic viscosity ![]() $\nu$ past a rough bottom wall. The latter is composed of a series of plane, smooth wall regions parallel to the
$\nu$ past a rough bottom wall. The latter is composed of a series of plane, smooth wall regions parallel to the ![]() $x$–
$x$–![]() $y$ plane, in between semi-cylindrical rough elements of radius
$y$ plane, in between semi-cylindrical rough elements of radius ![]() $k$ that extend across the span and are spaced at a centre-to-centre distance
$k$ that extend across the span and are spaced at a centre-to-centre distance ![]() $\varLambda$ in the streamwise direction. The flow depth
$\varLambda$ in the streamwise direction. The flow depth ![]() $H$ is defined as the wall-normal distance between the bottom plane wall and the upper free-shear boundary, with roughness height fixed at
$H$ is defined as the wall-normal distance between the bottom plane wall and the upper free-shear boundary, with roughness height fixed at ![]() $k = 0.1H$ for all but one rough wall scenario (
$k = 0.1H$ for all but one rough wall scenario (![]() $k = 0.2H$ is considered for one case; see table 1). Throughout this paper, we use
$k = 0.2H$ is considered for one case; see table 1). Throughout this paper, we use ![]() $x$,
$x$, ![]() $y$ and
$y$ and ![]() $z$ as the streamwise, spanwise and wall-normal directions, respectively, with
$z$ as the streamwise, spanwise and wall-normal directions, respectively, with ![]() $\tilde {U},\tilde {V},\tilde {W}$ representing instantaneous velocities in these directions. Here, we chose the semi-cylindrical roughness geometry over the commonly researched square bar geometry (Bandyopadhyay Reference Bandyopadhyay1986; Leonardi et al. Reference Leonardi, Orlandi, Smalley, Djenidi and Antonia2003; Lee & Sung Reference Lee and Sung2007; Nguyen et al. Reference Nguyen, Ricco and Pironti2021), to avoid a geometrically imposed flow separation location on the individual roughness elements. While the presence of sharp corners, on the upstream and downstream faces of the square bars inherently ‘locks’ the flow separation location, the same is not observed when a rounded bar geometry is considered (Deshpande et al. Reference Deshpande, Desai, Kanti and Mittal2017; Alam Reference Alam2022). In this way, the choice of a semi-cylindrical roughness element permits an unambiguous investigation of the effect of spanwise wall oscillations on the roughness wake (i.e. pressure drag).
$\tilde {U},\tilde {V},\tilde {W}$ representing instantaneous velocities in these directions. Here, we chose the semi-cylindrical roughness geometry over the commonly researched square bar geometry (Bandyopadhyay Reference Bandyopadhyay1986; Leonardi et al. Reference Leonardi, Orlandi, Smalley, Djenidi and Antonia2003; Lee & Sung Reference Lee and Sung2007; Nguyen et al. Reference Nguyen, Ricco and Pironti2021), to avoid a geometrically imposed flow separation location on the individual roughness elements. While the presence of sharp corners, on the upstream and downstream faces of the square bars inherently ‘locks’ the flow separation location, the same is not observed when a rounded bar geometry is considered (Deshpande et al. Reference Deshpande, Desai, Kanti and Mittal2017; Alam Reference Alam2022). In this way, the choice of a semi-cylindrical roughness element permits an unambiguous investigation of the effect of spanwise wall oscillations on the roughness wake (i.e. pressure drag).

Figure 1. (a) Schematic of an open-channel flow of an incompressible fluid over a rough wall, made up of spanwise-aligned semi-cylindrical rough elements. Terminology is defined in § 2. The shaded light blue region shows the extent of the domain over what is referred to as the streamwise periodic unit (![]() $0 \le x/\varLambda \le 1$). Dashed green lines are used to indicate the crest of the roughness elements, referred to in § 3. (b) Depiction of the 2-D quadrilateral spectral elements used to discretize the computational domain (shown only over a streamwise periodic unit).
$0 \le x/\varLambda \le 1$). Dashed green lines are used to indicate the crest of the roughness elements, referred to in § 3. (b) Depiction of the 2-D quadrilateral spectral elements used to discretize the computational domain (shown only over a streamwise periodic unit).
Table 1. A summary of direct numerical simulations for static and actuated cases, with ![]() $A^+ = A/{\bar {U}_{{\tau }_{s}}} = 12$ and oscillation period
$A^+ = A/{\bar {U}_{{\tau }_{s}}} = 12$ and oscillation period ![]() ${T^+_{osc}} = {T_{osc}}{\bar {U}^2_{{\tau }_{s}}}/{\nu }$. Values marked with
${T^+_{osc}} = {T_{osc}}{\bar {U}^2_{{\tau }_{s}}}/{\nu }$. Values marked with ![]() $^{*}$ correspond to the sole
$^{*}$ correspond to the sole ![]() $k = 0.2H$ case, while
$k = 0.2H$ case, while ![]() $k = 0.1H$ for all other cases.
$k = 0.1H$ for all other cases.

Two sets of direct numerical simulations of the above configuration were performed, and are referred to as the static and actuated cases. In the static cases, the bottom rough wall is kept stationary, while in the actuated cases, the entire bottom wall (including the rough elements) oscillates in the spanwise direction at a prescribed oscillation amplitude ![]() $A$ and frequency
$A$ and frequency ![]() $1/T_{osc}$, expressed as
$1/T_{osc}$, expressed as ![]() $\tilde {V}_w(t) = -A \sin (2{{\rm \pi} }t/{T_{osc}} )$, where
$\tilde {V}_w(t) = -A \sin (2{{\rm \pi} }t/{T_{osc}} )$, where ![]() $t$ is time. The no-slip boundary condition is imposed at the bottom wall, whereas the standard free-slip boundary condition mimics the free surface at the top boundary. All the simulations are performed in a computational domain that is periodic in the streamwise and spanwise directions, and has size
$t$ is time. The no-slip boundary condition is imposed at the bottom wall, whereas the standard free-slip boundary condition mimics the free surface at the top boundary. All the simulations are performed in a computational domain that is periodic in the streamwise and spanwise directions, and has size ![]() $L_x \times L_y \times L_z = 6H\times 3H \times H$, consistent with the domain size considered by previous studies investigating flow over 2-D roughness (Miyake, Tsujimoto & Nakaji Reference Miyake, Tsujimoto and Nakaji2001; Nagano, Hattori & Houra Reference Nagano, Hattori and Houra2004; Leonardi et al. Reference Leonardi, Orlandi, Djenidi and Antonia2015). Notably, Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) found this box size to be adequate for computing accurate one-point statistics, even in case of a smooth wall channel flow. The present simulations are carried out using the open-source spectral element solver Nektar++ (Cantwell et al. Reference Cantwell2015). To exploit the spanwise homogeneity of the configuration, the domain is discretized by
$L_x \times L_y \times L_z = 6H\times 3H \times H$, consistent with the domain size considered by previous studies investigating flow over 2-D roughness (Miyake, Tsujimoto & Nakaji Reference Miyake, Tsujimoto and Nakaji2001; Nagano, Hattori & Houra Reference Nagano, Hattori and Houra2004; Leonardi et al. Reference Leonardi, Orlandi, Djenidi and Antonia2015). Notably, Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) found this box size to be adequate for computing accurate one-point statistics, even in case of a smooth wall channel flow. The present simulations are carried out using the open-source spectral element solver Nektar++ (Cantwell et al. Reference Cantwell2015). To exploit the spanwise homogeneity of the configuration, the domain is discretized by ![]() $N_{elem}$ 2-D spectral elements in the
$N_{elem}$ 2-D spectral elements in the ![]() $x$–
$x$–![]() $z$ plane, combined with Fourier series expansion in the homogeneous
$z$ plane, combined with Fourier series expansion in the homogeneous ![]() $y$-direction along 192 grid points. Within each spectral element, velocity and pressure fields are represented by Lagrange polynomials of degree 7 through the Gauss–Lobatto–Legendre points, giving viscous-scaled nominal grid resolutions
$y$-direction along 192 grid points. Within each spectral element, velocity and pressure fields are represented by Lagrange polynomials of degree 7 through the Gauss–Lobatto–Legendre points, giving viscous-scaled nominal grid resolutions ![]() ${\rm \Delta} x^+ \approx 1.4$–
${\rm \Delta} x^+ \approx 1.4$–![]() $5.0$ and
$5.0$ and ![]() ${\rm \Delta} z^+ \approx 0.6$–
${\rm \Delta} z^+ \approx 0.6$–![]() $7.3$. The spanwise grid resolution is
$7.3$. The spanwise grid resolution is ![]() ${\rm \Delta} {y^+} \approx 4.7$. More details of the adopted numerical parameters, and evaluation of the adequacy of the grid resolution and domain size, are provided in the Appendix.
${\rm \Delta} {y^+} \approx 4.7$. More details of the adopted numerical parameters, and evaluation of the adequacy of the grid resolution and domain size, are provided in the Appendix.
The simulation campaign was as follows: initially, eight static cases at varying ![]() $6 \lesssim \varLambda /k \lesssim 60$ were performed at a target friction Reynolds number
$6 \lesssim \varLambda /k \lesssim 60$ were performed at a target friction Reynolds number ![]() ${{Re}_{\tau _s}} = {{\bar {U}_{\tau _s}}}H/{\nu }\approx 300$. Seven of these eight cases had roughness height
${{Re}_{\tau _s}} = {{\bar {U}_{\tau _s}}}H/{\nu }\approx 300$. Seven of these eight cases had roughness height ![]() $k = 0.1H$, while another had
$k = 0.1H$, while another had ![]() $k = 0.2H$ (for which
$k = 0.2H$ (for which ![]() $\varLambda = 10k$). Here,
$\varLambda = 10k$). Here, ![]() ${\bar {U}_{\tau _s}}$ is the friction velocity calculated based on the momentum balance of the static cases, with
${\bar {U}_{\tau _s}}$ is the friction velocity calculated based on the momentum balance of the static cases, with ![]() ${\bar {U}_{\tau _s}}^2 = {\bar {C}_{{D}_{s}}}{{\bar {U}_b}^2}/{2}$ (where
${\bar {U}_{\tau _s}}^2 = {\bar {C}_{{D}_{s}}}{{\bar {U}_b}^2}/{2}$ (where ![]() ${\bar {C}_{{D}_{s}}}$ is the mean total drag coefficient for the static case). Detailed information on calculating
${\bar {C}_{{D}_{s}}}$ is the mean total drag coefficient for the static case). Detailed information on calculating ![]() ${\bar {C}_{{D}_{s}}}$ is given later in this section. As a consequence of varying
${\bar {C}_{{D}_{s}}}$ is given later in this section. As a consequence of varying ![]() $\varLambda$, and in order to ensure a matched
$\varLambda$, and in order to ensure a matched ![]() ${{Re}_{\tau _s}}$, the value of the bulk Reynolds number
${{Re}_{\tau _s}}$, the value of the bulk Reynolds number ![]() ${{Re}_b}=\bar{U}_{b} H /\nu$ varies amongst the different static cases (here,
${{Re}_b}=\bar{U}_{b} H /\nu$ varies amongst the different static cases (here, ![]() ${\bar {U}_b} \equiv q_f/H$ is the bulk velocity, and
${\bar {U}_b} \equiv q_f/H$ is the bulk velocity, and ![]() $q_f$ is the flow rate). However, this was required to fix the roughness Reynolds number
$q_f$ is the flow rate). However, this was required to fix the roughness Reynolds number ![]() $k^+ = {k}{{\bar {U}_{\tau _s}}}/{\nu } = 30$ for all static rough wall cases corresponding to
$k^+ = {k}{{\bar {U}_{\tau _s}}}/{\nu } = 30$ for all static rough wall cases corresponding to ![]() $k = 0.1H$, since it can dictate the characteristics of the separating shear layer/wake of the roughness element. It is worth noting here that the present roughness height is a significant fraction of the characteristic outer scale (
$k = 0.1H$, since it can dictate the characteristics of the separating shear layer/wake of the roughness element. It is worth noting here that the present roughness height is a significant fraction of the characteristic outer scale (![]() $H$), owing to which outer-layer similarity of the velocity statistics cannot be expected (Jiménez Reference Jiménez2004). However, our
$H$), owing to which outer-layer similarity of the velocity statistics cannot be expected (Jiménez Reference Jiménez2004). However, our ![]() $k$ value is smaller than or equal to the roughness height in past studies considering 2-D roughness elements (Leonardi et al. Reference Leonardi, Orlandi, Smalley, Djenidi and Antonia2003, Reference Leonardi, Orlandi, Djenidi and Antonia2015; Lee & Sung Reference Lee and Sung2007; Nguyen et al. Reference Nguyen, Ricco and Pironti2021), and has negligible blockage effect on the bulk flow characteristics.
$k$ value is smaller than or equal to the roughness height in past studies considering 2-D roughness elements (Leonardi et al. Reference Leonardi, Orlandi, Smalley, Djenidi and Antonia2003, Reference Leonardi, Orlandi, Djenidi and Antonia2015; Lee & Sung Reference Lee and Sung2007; Nguyen et al. Reference Nguyen, Ricco and Pironti2021), and has negligible blockage effect on the bulk flow characteristics.
Next, starting from an established flow field of the static cases, their actuated counterparts were simulated such that the same flow rate ![]() $q_f$ (and
$q_f$ (and ![]() ${Re}_{b}$) was maintained for the static and actuated cases at matched
${Re}_{b}$) was maintained for the static and actuated cases at matched ![]() $\varLambda /k$. Here, for all (except one) actuated cases, we consider the optimum wall actuation parameters noted by Gatti & Quadrio (Reference Gatti and Quadrio2016) for a smooth wall channel flow, i.e.
$\varLambda /k$. Here, for all (except one) actuated cases, we consider the optimum wall actuation parameters noted by Gatti & Quadrio (Reference Gatti and Quadrio2016) for a smooth wall channel flow, i.e. ![]() $A^+ = A/{\bar {U}_{{\tau }_{s}}} = 12$ and
$A^+ = A/{\bar {U}_{{\tau }_{s}}} = 12$ and ![]() $T^+_{osc} = {T_{osc}}{\bar {U}^2_{{\tau }_{s}}}/{\nu } = 100$. By imposing oscillations at fixed
$T^+_{osc} = {T_{osc}}{\bar {U}^2_{{\tau }_{s}}}/{\nu } = 100$. By imposing oscillations at fixed ![]() $T^+_{osc}$ and
$T^+_{osc}$ and ![]() $A^+$ on rough wall cases having constant roughness Reynolds number (
$A^+$ on rough wall cases having constant roughness Reynolds number (![]() $k^+ = 30$), we can investigate unambiguously the effect of spanwise wall oscillations on the roughness wake and pressure drag at various
$k^+ = 30$), we can investigate unambiguously the effect of spanwise wall oscillations on the roughness wake and pressure drag at various ![]() ${\varLambda }/k$ (i.e. from transitional to fully rough scenarios). The majority of the analysis in this paper will be based on
${\varLambda }/k$ (i.e. from transitional to fully rough scenarios). The majority of the analysis in this paper will be based on ![]() $k = 0.1H$ (i.e.
$k = 0.1H$ (i.e. ![]() $k^+ = 30$) cases, with one case considered for
$k^+ = 30$) cases, with one case considered for ![]() $k = 0.2H$ to demonstrate the generalizability of present conclusions. Apart from these rough wall simulations, reference static and actuated cases with a smooth bottom wall were also run at matched
$k = 0.2H$ to demonstrate the generalizability of present conclusions. Apart from these rough wall simulations, reference static and actuated cases with a smooth bottom wall were also run at matched ![]() ${{Re}_{\tau _s}}$, domain size and oscillation parameter values. All these simulations have been summarized in table 1.
${{Re}_{\tau _s}}$, domain size and oscillation parameter values. All these simulations have been summarized in table 1.
Considering the imposed streamwise periodicity from roughness elements arranged on the bottom wall, as well as the very low ![]() ${{Re}_{\tau _s}}$ (which leads to negligible large-scale/inertial contributions), the streamwise extent of the present computational domain (
${{Re}_{\tau _s}}$ (which leads to negligible large-scale/inertial contributions), the streamwise extent of the present computational domain (![]() $L_x = 6H$) does not act as a limitation for the majority of the rough wall cases (
$L_x = 6H$) does not act as a limitation for the majority of the rough wall cases (![]() ${\varLambda }\le 20k$). In the case
${\varLambda }\le 20k$). In the case ![]() $\varLambda /k = 60$, however, our numerical domain had only a single roughness element, owing to which flow statistics may not be completely de-correlated from the effects of the computational domain. Further, based on the previous investigations of Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) and Gatti & Quadrio (Reference Gatti and Quadrio2016), the present computational domain size may not be sufficient to estimate accurately two-point or higher-order statistics for the smooth wall case. However, we consider results from these two cases (smooth wall and
$\varLambda /k = 60$, however, our numerical domain had only a single roughness element, owing to which flow statistics may not be completely de-correlated from the effects of the computational domain. Further, based on the previous investigations of Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) and Gatti & Quadrio (Reference Gatti and Quadrio2016), the present computational domain size may not be sufficient to estimate accurately two-point or higher-order statistics for the smooth wall case. However, we consider results from these two cases (smooth wall and ![]() $\varLambda = 60k$) solely for completeness, so their uncertainties do not influence the conclusions of our study.
$\varLambda = 60k$) solely for completeness, so their uncertainties do not influence the conclusions of our study.
2.1. Definition of flow statistics
For the purpose of analysing flow properties in this paper, we define a spanwise and time-averaging operator ![]() $\langle \varphi \rangle$ of any instantaneous flow quantity
$\langle \varphi \rangle$ of any instantaneous flow quantity ![]() $\tilde {\varphi }$ that exploits the inherent periodicity of length
$\tilde {\varphi }$ that exploits the inherent periodicity of length ![]() $\varLambda$ along
$\varLambda$ along ![]() $x$ (figure 1a) following
$x$ (figure 1a) following
 \begin{equation} \langle \varphi \rangle (x,z) =\frac{1}{N_{cyl}}\,\frac{1}{T_{obs}}\,\frac{1}{L_y} \sum_{i=1}^{N_{cyl}}\int^{T_{obs}}_{0} \int^{L_{y}}_{0} \tilde{\varphi} \,{\rm d}y\,{\rm d}t, \end{equation}
\begin{equation} \langle \varphi \rangle (x,z) =\frac{1}{N_{cyl}}\,\frac{1}{T_{obs}}\,\frac{1}{L_y} \sum_{i=1}^{N_{cyl}}\int^{T_{obs}}_{0} \int^{L_{y}}_{0} \tilde{\varphi} \,{\rm d}y\,{\rm d}t, \end{equation}
where ![]() $T_{obs}$ is the simulation steady-state interval, and
$T_{obs}$ is the simulation steady-state interval, and ![]() $N_{cyl} =L_x/\varLambda$ is the number of rough elements or streamwise periodic units. In (2.1),
$N_{cyl} =L_x/\varLambda$ is the number of rough elements or streamwise periodic units. In (2.1), ![]() $x$ spans from the centre of one rough element (
$x$ spans from the centre of one rough element (![]() $x=0$) to that of the next downstream (
$x=0$) to that of the next downstream (![]() $x=\varLambda$), which we refer to here as the streamwise periodic unit of the computational domain (
$x=\varLambda$), which we refer to here as the streamwise periodic unit of the computational domain (![]() $0 \le x/\varLambda \le 1$). Figure 1(a) highlights this periodic unit in light blue shading.
$0 \le x/\varLambda \le 1$). Figure 1(a) highlights this periodic unit in light blue shading.
In the presence of the rough elements, the ![]() $x$-component of the instantaneous hydrodynamic force acting upon the bottom wall (i.e. the total drag
$x$-component of the instantaneous hydrodynamic force acting upon the bottom wall (i.e. the total drag ![]() $\tilde {D}$) comprises both viscous (
$\tilde {D}$) comprises both viscous (![]() $\tilde {V}$) and pressure (
$\tilde {V}$) and pressure (![]() $\tilde {P}$) force contributions. The streamwise variation of the time- and span-averaged total drag force (per unit streamwise width) is given as
$\tilde {P}$) force contributions. The streamwise variation of the time- and span-averaged total drag force (per unit streamwise width) is given as
 \begin{equation} {\langle{D}\rangle}(x) =\langle \sigma_{1j}n_j\rangle{L_y} = \underbrace{\langle \tau_{1j}n_j \rangle{L_y}}_{{\langle{V}\rangle}(x)} \underbrace{- \langle {p\delta_{1j}n_j} \rangle{L_y}}_{{\langle{P}\rangle}(x)}, \end{equation}
\begin{equation} {\langle{D}\rangle}(x) =\langle \sigma_{1j}n_j\rangle{L_y} = \underbrace{\langle \tau_{1j}n_j \rangle{L_y}}_{{\langle{V}\rangle}(x)} \underbrace{- \langle {p\delta_{1j}n_j} \rangle{L_y}}_{{\langle{P}\rangle}(x)}, \end{equation}
where ![]() $\boldsymbol {n}$ is the unit normal, and
$\boldsymbol {n}$ is the unit normal, and ![]() $p$ is the hydrostatic pressure (i.e. different from pressure force
$p$ is the hydrostatic pressure (i.e. different from pressure force ![]() $P$). We can further integrate (2.2) in the streamwise direction to obtain the total hydrodynamic force (i.e. the total drag
$P$). We can further integrate (2.2) in the streamwise direction to obtain the total hydrodynamic force (i.e. the total drag ![]() $\bar {D}$) acting on the rough wall as
$\bar {D}$) acting on the rough wall as
 \begin{equation} \bar{D} =\int^{\varLambda}_{0} {\langle{\boldsymbol{D}}\rangle}(x)\,{\rm d}S = \underbrace{\int^{\varLambda}_{0} {{\langle{V}\rangle}(x)}\,{\rm d}S}_{\bar{V}} + \underbrace{\int^{\varLambda}_{0} {{\langle{P}\rangle}(x)}\,{\rm d}S}_{\bar{P}}, \end{equation}
\begin{equation} \bar{D} =\int^{\varLambda}_{0} {\langle{\boldsymbol{D}}\rangle}(x)\,{\rm d}S = \underbrace{\int^{\varLambda}_{0} {{\langle{V}\rangle}(x)}\,{\rm d}S}_{\bar{V}} + \underbrace{\int^{\varLambda}_{0} {{\langle{P}\rangle}(x)}\,{\rm d}S}_{\bar{P}}, \end{equation}
where ![]() ${\rm d}S$ is the differential surface length along the bottom boundary. Note that the pressure drag force is
${\rm d}S$ is the differential surface length along the bottom boundary. Note that the pressure drag force is ![]() ${\langle }{P}{\rangle }(x) = 0$ over the plane sections in between the semi-cylindrical rough elements (figure 1a), while
${\langle }{P}{\rangle }(x) = 0$ over the plane sections in between the semi-cylindrical rough elements (figure 1a), while ![]() $\bar {V}$ is the sum of viscous force contributions from both the plane and semi-cylindrical sections. Following (2.3), the total drag coefficient is
$\bar {V}$ is the sum of viscous force contributions from both the plane and semi-cylindrical sections. Following (2.3), the total drag coefficient is ![]() $\bar {C}_{D} = 2\bar {D}/(\rho {{\bar {U}_b}^2}\varLambda L_y) = \bar {C}_{p} + \bar {C}_{v}$, where
$\bar {C}_{D} = 2\bar {D}/(\rho {{\bar {U}_b}^2}\varLambda L_y) = \bar {C}_{p} + \bar {C}_{v}$, where ![]() $\bar {C}_{p} = 2\bar {P}/(\rho {{\bar {U}_b}^2}{\varLambda L_y})$ and
$\bar {C}_{p} = 2\bar {P}/(\rho {{\bar {U}_b}^2}{\varLambda L_y})$ and ![]() $\bar {C}_{v} =2\bar {V}/(\rho {{\bar {U}_b}^2}{\varLambda L_y})$ are respectively the coefficients of pressure and viscous force contributions to
$\bar {C}_{v} =2\bar {V}/(\rho {{\bar {U}_b}^2}{\varLambda L_y})$ are respectively the coefficients of pressure and viscous force contributions to ![]() $\bar {C}_{D}$. Similarly, the streamwise-resolved viscous force coefficient is
$\bar {C}_{D}$. Similarly, the streamwise-resolved viscous force coefficient is ![]() $\langle C_{v} \rangle (x) = 2\langle V \rangle /(\rho {{\bar {U}_b}^2} L_y)$. To differentiate the force coefficients associated with the static and actuated cases, subscripts ‘
$\langle C_{v} \rangle (x) = 2\langle V \rangle /(\rho {{\bar {U}_b}^2} L_y)$. To differentiate the force coefficients associated with the static and actuated cases, subscripts ‘![]() $s$’ and ‘
$s$’ and ‘![]() $a$’ are used, respectively, which are tabulated in table 1 for all the simulation cases. Here, with
$a$’ are used, respectively, which are tabulated in table 1 for all the simulation cases. Here, with ![]() $Re_{b}$ kept constant, the friction velocities are different for the static (
$Re_{b}$ kept constant, the friction velocities are different for the static (![]() ${\bar {U}_{\tau _s}}$) and actuated (
${\bar {U}_{\tau _s}}$) and actuated (![]() ${\bar {U}_{\tau _a}}$) cases, which are determined directly from the mean streamwise momentum balance by following
${\bar {U}_{\tau _a}}$) cases, which are determined directly from the mean streamwise momentum balance by following ![]() ${\bar {U}_{\tau _s}}^2 = {\bar {C}_{{D}_{s}}}{{\bar {U}_b}^2}/{2}$ and
${\bar {U}_{\tau _s}}^2 = {\bar {C}_{{D}_{s}}}{{\bar {U}_b}^2}/{2}$ and ![]() ${\bar {U}_{\tau _a}}^2 = {\bar {C}_{{D}_{a}}}{{\bar {U}_b}^2}/{2}$. This yields the definition of the total drag reduction, which is
${\bar {U}_{\tau _a}}^2 = {\bar {C}_{{D}_{a}}}{{\bar {U}_b}^2}/{2}$. This yields the definition of the total drag reduction, which is ![]() ${\rm DR}\% = 100\times ({{\bar {C}_{{D}_{s}}} - {\bar {C}_{{D}_{a}}}})/{\bar {C}_{{D}_{s}}} =100\times ({ {{\bar {U}_{\tau _s}}^2} - {{\bar {U}_{\tau _a}}^2} })/{{{\bar {U}_{\tau _s}}^2}}$, reported in table 1. For example, DR% for the present smooth wall case is 33.9 %, which, despite the marginal computational box size (Gatti & Quadrio Reference Gatti and Quadrio2016), lies within the predictions made by Gatti & Quadrio (Reference Gatti and Quadrio2013, Reference Gatti and Quadrio2016) at this
${\rm DR}\% = 100\times ({{\bar {C}_{{D}_{s}}} - {\bar {C}_{{D}_{a}}}})/{\bar {C}_{{D}_{s}}} =100\times ({ {{\bar {U}_{\tau _s}}^2} - {{\bar {U}_{\tau _a}}^2} })/{{{\bar {U}_{\tau _s}}^2}}$, reported in table 1. For example, DR% for the present smooth wall case is 33.9 %, which, despite the marginal computational box size (Gatti & Quadrio Reference Gatti and Quadrio2016), lies within the predictions made by Gatti & Quadrio (Reference Gatti and Quadrio2013, Reference Gatti and Quadrio2016) at this ![]() ${{Re}_{\tau _s}}$.
${{Re}_{\tau _s}}$.
3. Results and discussions
We begin by comparing the present static rough wall statistics with data published previously (Leonardi et al. Reference Leonardi, Orlandi, Djenidi and Antonia2015). For this purpose, results presented in figures 2(a), 3(a,c) and 4(a,b) will be discussed first, before proceeding towards investigating the change in statistics owing to drag reduction. Figure 2(a) shows fractions of the total drag coefficient (![]() $\bar {C}_{{D}_{s}}$) coming from the pressure drag (
$\bar {C}_{{D}_{s}}$) coming from the pressure drag (![]() $\bar {C}_{{p}_{s}}$) and viscous drag (
$\bar {C}_{{p}_{s}}$) and viscous drag (![]() $\bar {C}_{{v}_{s}}$) contributions, for cases corresponding to both
$\bar {C}_{{v}_{s}}$) contributions, for cases corresponding to both ![]() $k = 0.1H$ and
$k = 0.1H$ and ![]() $k = 0.2H$. For cases with
$k = 0.2H$. For cases with ![]() $\varLambda /k\lesssim 10$,
$\varLambda /k\lesssim 10$, ![]() $\bar {C}_{{p}_{s}}$ is essentially the sole contributor to
$\bar {C}_{{p}_{s}}$ is essentially the sole contributor to ![]() $\bar {C}_{{D}_{s}}$, with relative contributions from
$\bar {C}_{{D}_{s}}$, with relative contributions from ![]() $\bar {C}_{{v}_{s}}$ increasing gradually (and those from
$\bar {C}_{{v}_{s}}$ increasing gradually (and those from ![]() $\bar {C}_{{p}_{s}}$ decreasing) with increasing
$\bar {C}_{{p}_{s}}$ decreasing) with increasing ![]() $\varLambda /k\gtrsim 10$. At
$\varLambda /k\gtrsim 10$. At ![]() $\varLambda /k = 60$, notably, both contribute nearly equally to
$\varLambda /k = 60$, notably, both contribute nearly equally to ![]() $\bar {C}_{{D}_{s}}$. Further, for
$\bar {C}_{{D}_{s}}$. Further, for ![]() $\varLambda /k= 10$, the pressure and viscous contributions to the total drag are found to be similar irrespective of
$\varLambda /k= 10$, the pressure and viscous contributions to the total drag are found to be similar irrespective of ![]() $k = 0.1H$ or 0.2
$k = 0.1H$ or 0.2![]() $H$. This nature of variation of
$H$. This nature of variation of ![]() $\bar {C}_{{p}_{s}}$ and
$\bar {C}_{{p}_{s}}$ and ![]() $\bar {C}_{{v}_{s}}$ with
$\bar {C}_{{v}_{s}}$ with ![]() $\varLambda /k$ is consistent with Leonardi et al. (Reference Leonardi, Orlandi, Djenidi and Antonia2015), suggesting that the mean flow physics observed by the latter can be extended to the present study. This is despite Leonardi et al. (Reference Leonardi, Orlandi, Djenidi and Antonia2015) employing a circular rod geometry for the rough elements, and conducting simulations for different
$\varLambda /k$ is consistent with Leonardi et al. (Reference Leonardi, Orlandi, Djenidi and Antonia2015), suggesting that the mean flow physics observed by the latter can be extended to the present study. This is despite Leonardi et al. (Reference Leonardi, Orlandi, Djenidi and Antonia2015) employing a circular rod geometry for the rough elements, and conducting simulations for different ![]() ${\varLambda }/k$ at a constant bulk flow Reynolds number, both of which are different from the approach adopted in the present study. Leonardi et al. (Reference Leonardi, Orlandi, Djenidi and Antonia2015) also noted that the variation of pressure and viscous drag with
${\varLambda }/k$ at a constant bulk flow Reynolds number, both of which are different from the approach adopted in the present study. Leonardi et al. (Reference Leonardi, Orlandi, Djenidi and Antonia2015) also noted that the variation of pressure and viscous drag with ![]() ${\varLambda }/k$ did not change significantly on increasing the flow Reynolds number (at least in the low Reynolds number regime). This establishes that a similar variation in pressure drag domination can be expected on changing the streamwise offsets between 2-D rough elements (for
${\varLambda }/k$ did not change significantly on increasing the flow Reynolds number (at least in the low Reynolds number regime). This establishes that a similar variation in pressure drag domination can be expected on changing the streamwise offsets between 2-D rough elements (for ![]() $0.1H\le k\le 0.2H$), irrespective of differences in roughness geometry, flow Reynolds number and simulation approach (i.e. constant friction versus bulk Reynolds numbers). Hence figure 2(a) demonstrates that the present rough wall cases are valid for testing the efficacy of spanwise wall oscillations on varying degrees of pressure drag domination. Based on our definition given in § 1, we henceforth refer to the
$0.1H\le k\le 0.2H$), irrespective of differences in roughness geometry, flow Reynolds number and simulation approach (i.e. constant friction versus bulk Reynolds numbers). Hence figure 2(a) demonstrates that the present rough wall cases are valid for testing the efficacy of spanwise wall oscillations on varying degrees of pressure drag domination. Based on our definition given in § 1, we henceforth refer to the ![]() $\varLambda /k\lesssim 10$ cases as fully rough, while those corresponding to
$\varLambda /k\lesssim 10$ cases as fully rough, while those corresponding to ![]() $10<\varLambda /k \le 60$ are referred to as transitionally rough.
$10<\varLambda /k \le 60$ are referred to as transitionally rough.

Figure 2. (a) Fractional contribution to the total drag experienced by a static rough wall (![]() ${\bar {C}_{D_{s}}}$) from viscous forces
${\bar {C}_{D_{s}}}$) from viscous forces ![]() ${\bar {C}_{v_{s}}}$ (blue shading) and pressure forces
${\bar {C}_{v_{s}}}$ (blue shading) and pressure forces ![]() ${\bar {C}_{p_{s}}}$ (red shading), for cases of varying streamwise offsets between rough elements (
${\bar {C}_{p_{s}}}$ (red shading), for cases of varying streamwise offsets between rough elements (![]() $\varLambda /k$). (b) Total percentage drag reduction (black diamonds), and percentage drag reduction due to decrease in pressure drag (red squares) and due to decrease in viscous drag (blue circles), on imposition of wall oscillations at
$\varLambda /k$). (b) Total percentage drag reduction (black diamonds), and percentage drag reduction due to decrease in pressure drag (red squares) and due to decrease in viscous drag (blue circles), on imposition of wall oscillations at ![]() $T^+_{osc} = 100$. In both plots, fully and partially filled symbols correspond to present simulations with
$T^+_{osc} = 100$. In both plots, fully and partially filled symbols correspond to present simulations with ![]() $k = 0.1H$ and 0.2
$k = 0.1H$ and 0.2![]() $H$, respectively, while empty symbols in (a) correspond to data of Leonardi et al. (Reference Leonardi, Orlandi, Djenidi and Antonia2015). Dash-dotted magenta lines highlight cases
$H$, respectively, while empty symbols in (a) correspond to data of Leonardi et al. (Reference Leonardi, Orlandi, Djenidi and Antonia2015). Dash-dotted magenta lines highlight cases ![]() $\varLambda = 10k$ and 20
$\varLambda = 10k$ and 20![]() $k$ analysed in figures 3–5.
$k$ analysed in figures 3–5.

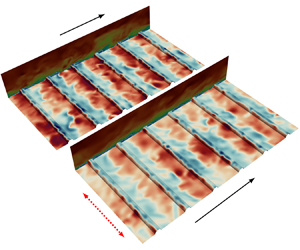
Figure 3. Non-dimensional Reynolds shear stresses ![]() $-{\langle }{{u'}{w'}}{\rangle }/\bar {U}^2_b$ (in coloured contours) and mean flow streamlines (represented by solid grey lines) estimated for the streamwise periodic unit of the rough wall simulations (
$-{\langle }{{u'}{w'}}{\rangle }/\bar {U}^2_b$ (in coloured contours) and mean flow streamlines (represented by solid grey lines) estimated for the streamwise periodic unit of the rough wall simulations (![]() $0\le x/\varLambda \le 1$), in the wall-normal plane, for: (a)
$0\le x/\varLambda \le 1$), in the wall-normal plane, for: (a) ![]() $\varLambda = 10k$, static; (b)
$\varLambda = 10k$, static; (b) ![]() $\varLambda = 10k$, actuated at
$\varLambda = 10k$, actuated at ![]() $T^+_{osc} = 100$; (c)
$T^+_{osc} = 100$; (c) ![]() $\varLambda = 20k$, static; (d)
$\varLambda = 20k$, static; (d) ![]() $\varLambda = 20k$, actuated at
$\varLambda = 20k$, actuated at ![]() $T^+_{osc} = 100$. All plots correspond to the simulations with roughness height
$T^+_{osc} = 100$. All plots correspond to the simulations with roughness height ![]() $k = 0.1H$.
$k = 0.1H$.

Figure 4. (a,b) Spanwise- and time-averaged viscous force coefficients ![]() ${\langle }{C_v}{\rangle }$ (black) and normalized surface-pressure
${\langle }{C_v}{\rangle }$ (black) and normalized surface-pressure ![]() $2\langle p \rangle /\rho {\bar {U}_b}^2$ (magenta) plotted as functions of
$2\langle p \rangle /\rho {\bar {U}_b}^2$ (magenta) plotted as functions of ![]() $x/k$ in the streamwise periodic unit (
$x/k$ in the streamwise periodic unit (![]() $0 \le x/\varLambda \le 1$), for the
$0 \le x/\varLambda \le 1$), for the ![]() $k = 0.1H$ rough wall cases: (a)
$k = 0.1H$ rough wall cases: (a) ![]() $\varLambda = 10k$ and (b)
$\varLambda = 10k$ and (b) ![]() $\varLambda = 20k$. (c) Root mean square of the surface pressure fluctuations (
$\varLambda = 20k$. (c) Root mean square of the surface pressure fluctuations (![]() ${2\sqrt {\langle {p'}^2 \rangle }/\rho {\bar {U}_b}^2 }$) along the curvature (
${2\sqrt {\langle {p'}^2 \rangle }/\rho {\bar {U}_b}^2 }$) along the curvature (![]() $0 \le \theta \le {\rm \pi}$) of the semi-cylindrical rough elements for the same two cases with
$0 \le \theta \le {\rm \pi}$) of the semi-cylindrical rough elements for the same two cases with ![]() $k= 0.1H$ as in (a,b), and one with
$k= 0.1H$ as in (a,b), and one with ![]() $k = 0.2H$. In all plots, blue and orange shading represent upstream (
$k = 0.2H$. In all plots, blue and orange shading represent upstream (![]() $0\le \theta \le {\rm \pi}/2$) and downstream (
$0\le \theta \le {\rm \pi}/2$) and downstream (![]() ${\rm \pi} /2\le \theta \le {\rm \pi}$) sections of the semi-cylindrical rough element, respectively.
${\rm \pi} /2\le \theta \le {\rm \pi}$) sections of the semi-cylindrical rough element, respectively.
The flow physics associated with the variation of ![]() $\bar {C}_{{v}_{s}}$ and
$\bar {C}_{{v}_{s}}$ and ![]() $\bar {C}_{{p}_{s}}$ can be understood based on figures 3(a,c) and 4(a,b). The former depict the normalized Reynolds shear stresses (
$\bar {C}_{{p}_{s}}$ can be understood based on figures 3(a,c) and 4(a,b). The former depict the normalized Reynolds shear stresses (![]() $\langle {u'}{w'}\rangle /{\bar {U}_b}^2$) and mean flow streamlines, while the latter show the time- and spanwise-averaged viscous force coefficients (
$\langle {u'}{w'}\rangle /{\bar {U}_b}^2$) and mean flow streamlines, while the latter show the time- and spanwise-averaged viscous force coefficients (![]() ${\langle }{C_v}{\rangle }$) and normalized surface pressure (
${\langle }{C_v}{\rangle }$) and normalized surface pressure (![]() $2\langle p \rangle /\rho {\bar {U}_b}^2$), plotted across the streamwise periodic unit (
$2\langle p \rangle /\rho {\bar {U}_b}^2$), plotted across the streamwise periodic unit (![]() $0 \le x/{\varLambda }\le 1$) for
$0 \le x/{\varLambda }\le 1$) for ![]() $\varLambda = 10k$ and 20
$\varLambda = 10k$ and 20![]() $k$, with
$k$, with ![]() $k = 0.1H$. These two cases were selected as representatives of the fully and transitionally rough scenarios, respectively. Here,
$k = 0.1H$. These two cases were selected as representatives of the fully and transitionally rough scenarios, respectively. Here, ![]() $u'$ and
$u'$ and ![]() $w'$ are respectively the streamwise and wall-normal velocity fluctuations obtained via
$w'$ are respectively the streamwise and wall-normal velocity fluctuations obtained via ![]() $u'=\tilde {U}-\langle U \rangle$. It is evident from figure 4(a) that
$u'=\tilde {U}-\langle U \rangle$. It is evident from figure 4(a) that ![]() ${\langle }{C_v}{\rangle }\lesssim 0$ across the plane region between the rough elements (
${\langle }{C_v}{\rangle }\lesssim 0$ across the plane region between the rough elements (![]() $1\le x/k\le 9$), for
$1\le x/k\le 9$), for ![]() $\varLambda = 10k$. On the other hand, for
$\varLambda = 10k$. On the other hand, for ![]() $\varLambda = 20k$,
$\varLambda = 20k$, ![]() ${\langle }{C_v}{\rangle }<0$ holds only immediately downstream of the rough element (
${\langle }{C_v}{\rangle }<0$ holds only immediately downstream of the rough element (![]() $1\le x/k\le 9$), after which
$1\le x/k\le 9$), after which ![]() ${\langle }{C_v}{\rangle }>0$ for
${\langle }{C_v}{\rangle }>0$ for ![]() $7\le x/k\le 19$ (figure 4b). These trends are consistent with observations from the mean flow field in figure 3(a), wherein the wake/recirculation region can be noted across the majority of the plane region between subsequent rough elements, in the case of small streamwise offsets (
$7\le x/k\le 19$ (figure 4b). These trends are consistent with observations from the mean flow field in figure 3(a), wherein the wake/recirculation region can be noted across the majority of the plane region between subsequent rough elements, in the case of small streamwise offsets (![]() $\varLambda \lesssim 10k$). Qualitatively similar mean flow fields and surface statistics
$\varLambda \lesssim 10k$). Qualitatively similar mean flow fields and surface statistics ![]() ${\langle }{C_v}{\rangle }$ and
${\langle }{C_v}{\rangle }$ and ![]() ${\langle }p{\rangle }$ were noted in the cases
${\langle }p{\rangle }$ were noted in the cases ![]() $k = 0.1H$ and 0.2
$k = 0.1H$ and 0.2![]() $H$ for
$H$ for ![]() $\varLambda = 10k$ (not shown here for brevity). For larger
$\varLambda = 10k$ (not shown here for brevity). For larger ![]() $\varLambda /k$ (figure 3c), however, the separated shear layer from upstream roughness reattaches in the plane region between these elements (
$\varLambda /k$ (figure 3c), however, the separated shear layer from upstream roughness reattaches in the plane region between these elements (![]() $x\sim 7k$), leading to an extended region of wall-attached flow impinging onto the downstream roughness element (resulting in
$x\sim 7k$), leading to an extended region of wall-attached flow impinging onto the downstream roughness element (resulting in ![]() ${\langle }{C_v}{\rangle }>0$). While the variation of
${\langle }{C_v}{\rangle }>0$). While the variation of ![]() ${\langle }{C_v}{\rangle }(x)$ in the plane region is opposite for the transitional and fully rough cases (figure 4), the nature of variation of the surface pressure is very similar, with
${\langle }{C_v}{\rangle }(x)$ in the plane region is opposite for the transitional and fully rough cases (figure 4), the nature of variation of the surface pressure is very similar, with ![]() $\langle p \rangle (x)$ much higher on the upstream (relative to the downstream) section of the rough element, which generates the pressure drag. Notably, both of the present results plotted in figures 3(a,c) and 4(a,b) are consistent with the observations made previously by Leonardi et al. (Reference Leonardi, Orlandi, Djenidi and Antonia2015), explaining the similar trends in pressure and viscous drag noted in figure 2(a).
$\langle p \rangle (x)$ much higher on the upstream (relative to the downstream) section of the rough element, which generates the pressure drag. Notably, both of the present results plotted in figures 3(a,c) and 4(a,b) are consistent with the observations made previously by Leonardi et al. (Reference Leonardi, Orlandi, Djenidi and Antonia2015), explaining the similar trends in pressure and viscous drag noted in figure 2(a).
With the static cases demonstrated to be consistent with the literature, we next investigate the drag reduction achieved on imposing spanwise wall oscillations for the same rough wall cases. Figure 2(b) plots DR%, on imposition of wall oscillations at ![]() $A^+ = 12$ and
$A^+ = 12$ and ![]() $T^+_{osc}= 100$, for various
$T^+_{osc}= 100$, for various ![]() ${\varLambda }/k$. The plot suggests that substantial DR% is achieved for all wall oscillation cases at
${\varLambda }/k$. The plot suggests that substantial DR% is achieved for all wall oscillation cases at ![]() $T^+_{osc}= 100$, corresponding to
$T^+_{osc}= 100$, corresponding to ![]() $k = 0.1H$. The DR% associated with
$k = 0.1H$. The DR% associated with ![]() $k = 0.2H$, however, is not as high as noted for
$k = 0.2H$, however, is not as high as noted for ![]() $k = 0.1H$ at
$k = 0.1H$ at ![]() $\varLambda = 10k$, and this difference is likely owing to the same spanwise forcing magnitude (
$\varLambda = 10k$, and this difference is likely owing to the same spanwise forcing magnitude (![]() $A^+ = 12$) imposed on flows with significantly different pressure drag magnitudes (nearly double for
$A^+ = 12$) imposed on flows with significantly different pressure drag magnitudes (nearly double for ![]() $k = 0.2H$ than 0.1
$k = 0.2H$ than 0.1![]() $H$; see table 1). The most interesting observation is the maximum DR% (
$H$; see table 1). The most interesting observation is the maximum DR% (![]() $\approx$34 %) noted at
$\approx$34 %) noted at ![]() ${\varLambda }/k = 7.5$, which is on a par with that noted via pure viscous drag reduction for a smooth wall (for the same
${\varLambda }/k = 7.5$, which is on a par with that noted via pure viscous drag reduction for a smooth wall (for the same ![]() $A^+$ and
$A^+$ and ![]() $T^+_{osc}$). This is a novel result and is particularly notable considering our findings in figure 2(a), which indicate negligible viscous drag contributions at
$T^+_{osc}$). This is a novel result and is particularly notable considering our findings in figure 2(a), which indicate negligible viscous drag contributions at ![]() ${\varLambda }/k = 7.5$. It suggests this DR% is solely from pressure drag reduction, which has to be driven by an independent mechanism.
${\varLambda }/k = 7.5$. It suggests this DR% is solely from pressure drag reduction, which has to be driven by an independent mechanism.
To quantify what fraction of the total DR% is achieved by decreasing the pressure and viscous drag, figure 2(b) also shows ![]() $100\times (\bar {C}_{{p}_{s}} - \bar {C}_{{p}_{a}})/\bar {C}_{{D}_{s}}$ and
$100\times (\bar {C}_{{p}_{s}} - \bar {C}_{{p}_{a}})/\bar {C}_{{D}_{s}}$ and ![]() $100\times (\bar {C}_{{v}_{s}} - \bar {C}_{{v}_{a}})/\bar {C}_{{D}_{s}}$ for varying
$100\times (\bar {C}_{{v}_{s}} - \bar {C}_{{v}_{a}})/\bar {C}_{{D}_{s}}$ for varying ![]() $\varLambda /k$. For significantly large streamwise offsets (
$\varLambda /k$. For significantly large streamwise offsets (![]() $10k<\varLambda \le 60k$), which is the scenario investigated by Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020) and Nguyen et al. (Reference Nguyen, Ricco and Pironti2021), both viscous drag reduction and pressure drag reduction contribute to the total DR% significantly. This can be understood by comparing the mean flow field (figures 3c,d), as well as
$10k<\varLambda \le 60k$), which is the scenario investigated by Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020) and Nguyen et al. (Reference Nguyen, Ricco and Pironti2021), both viscous drag reduction and pressure drag reduction contribute to the total DR% significantly. This can be understood by comparing the mean flow field (figures 3c,d), as well as ![]() ${\langle }{C_v}{\rangle }(x)$ and
${\langle }{C_v}{\rangle }(x)$ and ![]() $\langle p \rangle (x)$ between static and actuated cases (figure 4b), for
$\langle p \rangle (x)$ between static and actuated cases (figure 4b), for ![]() $\varLambda = 20k$. Consistent with Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020), the pressure drag reduction can be associated with extension of the wake size downstream of the roughness elements (refer to streamlines in figures 3c,d), while viscous drag reduction can be associated with the weakening of the near-wall turbulence in the wall-attached flow between the elements (refer to Reynolds shear stresses at
$\varLambda = 20k$. Consistent with Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020), the pressure drag reduction can be associated with extension of the wake size downstream of the roughness elements (refer to streamlines in figures 3c,d), while viscous drag reduction can be associated with the weakening of the near-wall turbulence in the wall-attached flow between the elements (refer to Reynolds shear stresses at ![]() $z< 0.1H$). This is supported quantitatively by figure 4(b), where
$z< 0.1H$). This is supported quantitatively by figure 4(b), where ![]() ${\langle }{C_v}{\rangle }$ immediately upstream of the rough element (
${\langle }{C_v}{\rangle }$ immediately upstream of the rough element (![]() $7\lesssim x/k\lesssim 19$) reduces, compared to the static case. This is accompanied by a reduction in
$7\lesssim x/k\lesssim 19$) reduces, compared to the static case. This is accompanied by a reduction in ![]() ${\langle }{C_v}{\rangle }$ in the upstream section of the semi-cylindrical surface, combination of which leads to a considerable viscous drag reduction noted in figure 2(b). Similarly,
${\langle }{C_v}{\rangle }$ in the upstream section of the semi-cylindrical surface, combination of which leads to a considerable viscous drag reduction noted in figure 2(b). Similarly, ![]() $2\langle p \rangle /\rho {\bar {U}_b}^2$ can be noted to decrease in the upstream section of the rough element (
$2\langle p \rangle /\rho {\bar {U}_b}^2$ can be noted to decrease in the upstream section of the rough element (![]() $7\lesssim x/k\lesssim 19.5$; figure 4b), while it increases downstream of the roughness (
$7\lesssim x/k\lesssim 19.5$; figure 4b), while it increases downstream of the roughness (![]() $0\lesssim x/k \lesssim 4$). This explains the drop in pressure drag in figure 2(b), which Nguyen et al. (Reference Nguyen, Ricco and Pironti2021) had associated with the decrease in the dynamic pressure in
$0\lesssim x/k \lesssim 4$). This explains the drop in pressure drag in figure 2(b), which Nguyen et al. (Reference Nguyen, Ricco and Pironti2021) had associated with the decrease in the dynamic pressure in ![]() $7 \lesssim x/k \lesssim 19$. Consistent with the literature (Banchetti et al. Reference Banchetti, Luchini and Quadrio2020; Nguyen et al. Reference Nguyen, Ricco and Pironti2021), the drag reduced flow for
$7 \lesssim x/k \lesssim 19$. Consistent with the literature (Banchetti et al. Reference Banchetti, Luchini and Quadrio2020; Nguyen et al. Reference Nguyen, Ricco and Pironti2021), the drag reduced flow for ![]() $\varLambda = 20k$ also corresponds to weakening of the Reynolds shear stresses in the roughness wake (
$\varLambda = 20k$ also corresponds to weakening of the Reynolds shear stresses in the roughness wake (![]() $z\approx 0.1H$; figures 3c,d). This reaffirms the weakening of the Reynolds shear stresses on pressure drag reduction, irrespective of differences in the roughness geometries (semi-cylindrical, cylindrical or square).
$z\approx 0.1H$; figures 3c,d). This reaffirms the weakening of the Reynolds shear stresses on pressure drag reduction, irrespective of differences in the roughness geometries (semi-cylindrical, cylindrical or square).
As ![]() ${\varLambda }/k$ decreases along
${\varLambda }/k$ decreases along ![]() $60\ge {\varLambda }/k\ge 10$, the streamwise extent of the wall-attached flow between rough elements reduces (figures 3a,c), which reduces the contribution of viscous drag reduction to the total DR% (figure 2b). For
$60\ge {\varLambda }/k\ge 10$, the streamwise extent of the wall-attached flow between rough elements reduces (figures 3a,c), which reduces the contribution of viscous drag reduction to the total DR% (figure 2b). For ![]() $5\lesssim \varLambda /k\lesssim 10$, owing to the absence of flow reattachment/wall-attached flow between rough elements (i.e.
$5\lesssim \varLambda /k\lesssim 10$, owing to the absence of flow reattachment/wall-attached flow between rough elements (i.e. ![]() ${\langle }{C_v}{\rangle }(x) \lesssim 0$; Leonardi et al. Reference Leonardi, Orlandi, Djenidi and Antonia2015), almost all the drag reduction is associated with a decrease in the pressure drag. This is observed irrespective of the variation in roughness height, i.e. for both
${\langle }{C_v}{\rangle }(x) \lesssim 0$; Leonardi et al. Reference Leonardi, Orlandi, Djenidi and Antonia2015), almost all the drag reduction is associated with a decrease in the pressure drag. This is observed irrespective of the variation in roughness height, i.e. for both ![]() $k = 0.1H$ and
$k = 0.1H$ and ![]() $k = 0.2H$. The dominant pressure drag reduction can be confirmed by comparing
$k = 0.2H$. The dominant pressure drag reduction can be confirmed by comparing ![]() ${\langle }{C_v}{\rangle }$ and
${\langle }{C_v}{\rangle }$ and ![]() ${\langle }{p}{\rangle }$ plotted for the static and actuated cases (
${\langle }{p}{\rangle }$ plotted for the static and actuated cases (![]() $T^+_{osc} = 100$) at
$T^+_{osc} = 100$) at ![]() $\varLambda = 10k$ and
$\varLambda = 10k$ and ![]() $k = 0.1H$ (figure 4a), where one can note the drop in
$k = 0.1H$ (figure 4a), where one can note the drop in ![]() ${\langle }{p}{\rangle }$ upstream of the roughness (
${\langle }{p}{\rangle }$ upstream of the roughness (![]() $5\lesssim x/k \lesssim 9.5$), and increase in
$5\lesssim x/k \lesssim 9.5$), and increase in ![]() ${\langle }{p}{\rangle }$ downstream of the roughness (
${\langle }{p}{\rangle }$ downstream of the roughness (![]() $0\lesssim x/k \lesssim 4$), while there is negligible variation in
$0\lesssim x/k \lesssim 4$), while there is negligible variation in ![]() ${\langle }{C_v}{\rangle }$ across the plane region (
${\langle }{C_v}{\rangle }$ across the plane region (![]() $1 \lesssim x/k\lesssim 9$). The same can be understood qualitatively by comparing the mean flow fields of the static and actuated cases depicted for
$1 \lesssim x/k\lesssim 9$). The same can be understood qualitatively by comparing the mean flow fields of the static and actuated cases depicted for ![]() $\varLambda = 10k$, in figures 3(a,b). In the static scenario, a very small region of wall-attached mean flow can be noted between the two roughness elements, which, however, vanishes completely on imposition of wall oscillations. The fact that significant pressure drag reduction is noted without any changes in the viscous drag (for
$\varLambda = 10k$, in figures 3(a,b). In the static scenario, a very small region of wall-attached mean flow can be noted between the two roughness elements, which, however, vanishes completely on imposition of wall oscillations. The fact that significant pressure drag reduction is noted without any changes in the viscous drag (for ![]() $6\lesssim \varLambda \lesssim 10k$) suggests existence of a unique pressure drag reduction mechanism. This observation is valid for both
$6\lesssim \varLambda \lesssim 10k$) suggests existence of a unique pressure drag reduction mechanism. This observation is valid for both ![]() $k = 0.1H$ and
$k = 0.1H$ and ![]() $k = 0.2H$ (figure 2b), and confirms that the same pressure drag reduction mechanism would be applicable for varying roughness heights. These results are novel, and confirm that pressure drag reduction in a 2-D rough wall is not dependent on the viscous drag reduction. Another new observation from figures 3(a,b) is that the Reynolds shear stresses are attenuated in the wake of the roughness elements, even when viscous drag reduction is negligible. It suggests that this attenuation of the turbulent stresses, which are noted across
$k = 0.2H$ (figure 2b), and confirms that the same pressure drag reduction mechanism would be applicable for varying roughness heights. These results are novel, and confirm that pressure drag reduction in a 2-D rough wall is not dependent on the viscous drag reduction. Another new observation from figures 3(a,b) is that the Reynolds shear stresses are attenuated in the wake of the roughness elements, even when viscous drag reduction is negligible. It suggests that this attenuation of the turbulent stresses, which are noted across ![]() $6\le \varLambda /k\le 60$ (not shown), is likely associated with the pressure drag reduction mechanism. Despite differences in their roughness geometries compared to the present study, both Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020) and Nguyen et al. (Reference Nguyen, Ricco and Pironti2021) noted a similar reduction in the Reynolds stresses and an increase in base pressure in their roughness wake (on imposition of oscillations). These consistent results suggest that the same pressure drag reduction mechanism is applicable for different roughness geometries, which, however, can be confirmed only after conducting dedicated simulations (which is beyond the present scope).
$6\le \varLambda /k\le 60$ (not shown), is likely associated with the pressure drag reduction mechanism. Despite differences in their roughness geometries compared to the present study, both Banchetti et al. (Reference Banchetti, Luchini and Quadrio2020) and Nguyen et al. (Reference Nguyen, Ricco and Pironti2021) noted a similar reduction in the Reynolds stresses and an increase in base pressure in their roughness wake (on imposition of oscillations). These consistent results suggest that the same pressure drag reduction mechanism is applicable for different roughness geometries, which, however, can be confirmed only after conducting dedicated simulations (which is beyond the present scope).
3.1. Mechanism behind pressure drag reduction
Referring to our previous discussion in § 1.2, regarding bluff body drag reduction based on increases in base pressure (i.e. ![]() ${\langle }{p}{\rangle }$ at
${\langle }{p}{\rangle }$ at ![]() $x/k\sim 1$) accompanied by weakening of Reynolds stresses, our observations from figures 3 and 4(a,b) point towards weakening of the vortex shedding in the roughness wake as the plausible pressure drag reduction mechanism (Choi et al. Reference Choi, Jeon and Kim2008). This can be investigated by analysing the surface pressure fluctuations (
$x/k\sim 1$) accompanied by weakening of Reynolds stresses, our observations from figures 3 and 4(a,b) point towards weakening of the vortex shedding in the roughness wake as the plausible pressure drag reduction mechanism (Choi et al. Reference Choi, Jeon and Kim2008). This can be investigated by analysing the surface pressure fluctuations (![]() ${p'}$) on the rough element; past studies on the flow past a circular cylinder (Deshpande et al. Reference Deshpande, Desai, Kanti and Mittal2017; Desai et al. Reference Desai, Mittal and Mittal2020; Chopra & Mittal Reference Chopra and Mittal2022) have shown that weakening of its shedding activity is reflected by a drop in the lift force fluctuations, as well as surface pressure fluctuations at the crest of the cylinder (i.e. at
${p'}$) on the rough element; past studies on the flow past a circular cylinder (Deshpande et al. Reference Deshpande, Desai, Kanti and Mittal2017; Desai et al. Reference Desai, Mittal and Mittal2020; Chopra & Mittal Reference Chopra and Mittal2022) have shown that weakening of its shedding activity is reflected by a drop in the lift force fluctuations, as well as surface pressure fluctuations at the crest of the cylinder (i.e. at ![]() $\theta = {\rm \pi}/2$, where
$\theta = {\rm \pi}/2$, where ![]() $\theta$ is the azimuthal angle from the front stagnation point). This sensitivity is owing to its proximity to the azimuthal location, from where the shear layer separates and sheds into the wake (
$\theta$ is the azimuthal angle from the front stagnation point). This sensitivity is owing to its proximity to the azimuthal location, from where the shear layer separates and sheds into the wake (![]() $0.4{\rm \pi} \le \theta \le 0.65{\rm \pi}$; Desai et al. Reference Desai, Mittal and Mittal2020; Chopra & Mittal Reference Chopra and Mittal2022). With this background, we consider
$0.4{\rm \pi} \le \theta \le 0.65{\rm \pi}$; Desai et al. Reference Desai, Mittal and Mittal2020; Chopra & Mittal Reference Chopra and Mittal2022). With this background, we consider ![]() ${p'} (x,y,z,t) = {\tilde {p}} (x,y,z,t) - \langle {p} \rangle (x)$ over the surface of the cylinder, where tilde (
${p'} (x,y,z,t) = {\tilde {p}} (x,y,z,t) - \langle {p} \rangle (x)$ over the surface of the cylinder, where tilde (![]() ${\sim}$) and prime (
${\sim}$) and prime (![]() $'$) respectively denote instantaneous and fluctuating properties. Figure 4(c) plots the normalized root mean square of the surface pressure fluctuations (
$'$) respectively denote instantaneous and fluctuating properties. Figure 4(c) plots the normalized root mean square of the surface pressure fluctuations (![]() ${ 2\sqrt {\langle {p'}^2 \rangle }/\rho {\bar {U}_b}^2 }$) across the surface of the semi-cylindrical rough element, with
${ 2\sqrt {\langle {p'}^2 \rangle }/\rho {\bar {U}_b}^2 }$) across the surface of the semi-cylindrical rough element, with ![]() $0\le \theta \le {\rm \pi}/2$ in blue shading, and
$0\le \theta \le {\rm \pi}/2$ in blue shading, and ![]() ${\rm \pi} /2\le \theta \le {\rm \pi}$ in orange shading. It is evident that pressure fluctuations drop at
${\rm \pi} /2\le \theta \le {\rm \pi}$ in orange shading. It is evident that pressure fluctuations drop at ![]() $\theta = {\rm \pi}/2$, on imposition of wall oscillations at
$\theta = {\rm \pi}/2$, on imposition of wall oscillations at ![]() $T^+_{osc} = 100$, for both
$T^+_{osc} = 100$, for both ![]() $\varLambda = 10k$ and
$\varLambda = 10k$ and ![]() $\varLambda = 20k$, and different roughness heights (
$\varLambda = 20k$, and different roughness heights (![]() $k = 0.1H$ and 0.2
$k = 0.1H$ and 0.2![]() $H$). Notably, the drop in pressure fluctuations for
$H$). Notably, the drop in pressure fluctuations for ![]() $k = 0.2H$ is relatively smaller than that for
$k = 0.2H$ is relatively smaller than that for ![]() $k = 0.1H$ at
$k = 0.1H$ at ![]() $\theta ={\rm \pi} /2$, and this is consistent with the relatively lower DR% noted in case of the former (figure 2b).
$\theta ={\rm \pi} /2$, and this is consistent with the relatively lower DR% noted in case of the former (figure 2b).
The fact that wall actuations weaken the vortex shedding suggests that the actuation frequency (![]() $1/T^+_{osc}$) must have a connection with the shedding frequency. Hence we test the sensitivity of pressure drag reduction to
$1/T^+_{osc}$) must have a connection with the shedding frequency. Hence we test the sensitivity of pressure drag reduction to ![]() $T^+_{osc}$, by imposing actuations differing by an order of magnitude. Interestingly,
$T^+_{osc}$, by imposing actuations differing by an order of magnitude. Interestingly, ![]() $T^+_{osc} = 10$ yields negligible pressure and total drag reduction for
$T^+_{osc} = 10$ yields negligible pressure and total drag reduction for ![]() $\varLambda =10k$ (table 1). Indeed, when
$\varLambda =10k$ (table 1). Indeed, when ![]() ${\langle }{p}{\rangle }$,
${\langle }{p}{\rangle }$, ![]() ${\langle }{C_v}{\rangle }$ and
${\langle }{C_v}{\rangle }$ and ![]() ${\sqrt {\langle {p'}^2\rangle }}$ profiles are plotted for the
${\sqrt {\langle {p'}^2\rangle }}$ profiles are plotted for the ![]() ${T^+_{osc} = 10}$ actuation case in figures 4(a,c), the corresponding profiles overlap with those of the static case, suggesting negligible changes in the mean flow physics. We can thus conclude that pressure drag reduction, on imposition of spanwise wall oscillations, is associated with weakening of the vortex shedding activity, and this explains the sensitivity of DR% to
${T^+_{osc} = 10}$ actuation case in figures 4(a,c), the corresponding profiles overlap with those of the static case, suggesting negligible changes in the mean flow physics. We can thus conclude that pressure drag reduction, on imposition of spanwise wall oscillations, is associated with weakening of the vortex shedding activity, and this explains the sensitivity of DR% to ![]() $T^+_{osc}$ (also see Nguyen et al. Reference Nguyen, Ricco and Pironti2021). Interested readers may note that this weakening of the vortex shedding activity has also been confirmed by comparing the mean spanwise vorticity in the roughness wake, between static and actuated cases, but is not shown here for brevity.
$T^+_{osc}$ (also see Nguyen et al. Reference Nguyen, Ricco and Pironti2021). Interested readers may note that this weakening of the vortex shedding activity has also been confirmed by comparing the mean spanwise vorticity in the roughness wake, between static and actuated cases, but is not shown here for brevity.
In order to confirm the causal relationship that weakening of shedding activity leads to pressure drag reduction, we investigate the spectral distribution of ![]() $p'$ at
$p'$ at ![]() ${\theta = {\rm \pi}/2}$, and of the fluctuating pressure force coefficient (
${\theta = {\rm \pi}/2}$, and of the fluctuating pressure force coefficient (![]() $C'_p$). Here,
$C'_p$). Here, ![]() $C'_p$ is obtained via
$C'_p$ is obtained via ![]() $C'_p(y,t) = \int ^{L_x}_{0}{\widetilde {C_p}}(x,y,t)\,{\rm d}S-\bar {C}_p$, where
$C'_p(y,t) = \int ^{L_x}_{0}{\widetilde {C_p}}(x,y,t)\,{\rm d}S-\bar {C}_p$, where ![]() ${\rm d} S$ is the differential streamwise distance across the entire bottom wall. We analyse their energy spectra in the time/frequency domain to relate the spectral distribution to the imposed wall oscillation frequency (
${\rm d} S$ is the differential streamwise distance across the entire bottom wall. We analyse their energy spectra in the time/frequency domain to relate the spectral distribution to the imposed wall oscillation frequency (![]() $1/{T^+_{osc}}$). Figures 5(a,b) respectively plot the two spectra in the premultiplied form (i.e.
$1/{T^+_{osc}}$). Figures 5(a,b) respectively plot the two spectra in the premultiplied form (i.e. ![]() ${f}{{\phi }_{{p'}{p'}}}$ and
${f}{{\phi }_{{p'}{p'}}}$ and ![]() ${f}{{\phi }_{{C'_p}{C'_p}}}$), for all the static rough wall cases (
${f}{{\phi }_{{C'_p}{C'_p}}}$), for all the static rough wall cases (![]() $6\le {\varLambda }/k\le 60$) corresponding to
$6\le {\varLambda }/k\le 60$) corresponding to ![]() $k = 0.1H$. They are plotted against the frequency scale (
$k = 0.1H$. They are plotted against the frequency scale (![]() $f$), which is normalized in viscous units (
$f$), which is normalized in viscous units (![]() $f{\nu }/{\bar {U}^{2}_{{\tau }_{s}}}$). Here, considering that the semi-cylindrical rough element is exposed to an incoming turbulent shear flow, we would expect the spectra to be much more broadband than that noted for a cylinder exposed to a free stream (Darekar & Sherwin Reference Darekar and Sherwin2001). Indeed, on looking at the spectra for all the static cases, we found that both
$f{\nu }/{\bar {U}^{2}_{{\tau }_{s}}}$). Here, considering that the semi-cylindrical rough element is exposed to an incoming turbulent shear flow, we would expect the spectra to be much more broadband than that noted for a cylinder exposed to a free stream (Darekar & Sherwin Reference Darekar and Sherwin2001). Indeed, on looking at the spectra for all the static cases, we found that both ![]() ${\phi }_{{p'}{p'}}$ and
${\phi }_{{p'}{p'}}$ and ![]() ${\phi }_{{C'_p}{C'_p}}$ are most energetic across a common broadband frequency range
${\phi }_{{C'_p}{C'_p}}$ are most energetic across a common broadband frequency range ![]() ${O}(10^{-3})\lesssim f{\nu }/{\bar {U}^{2}_{{\tau }_{s}}}\lesssim {O}(10^{-2})$ (shaded in magenta), which is also exhibited by their cross-correlation spectra
${O}(10^{-3})\lesssim f{\nu }/{\bar {U}^{2}_{{\tau }_{s}}}\lesssim {O}(10^{-2})$ (shaded in magenta), which is also exhibited by their cross-correlation spectra ![]() ${\phi }_{{C'_p}{p'}}$ (not shown here to avoid clutter). This close correspondence in spectral energy distribution suggests that the pressure drag (which is represented by
${\phi }_{{C'_p}{p'}}$ (not shown here to avoid clutter). This close correspondence in spectral energy distribution suggests that the pressure drag (which is represented by ![]() ${\phi }_{{C'_p}{C'_p}}$) is associated directly with the vortex shedding activity (represented by
${\phi }_{{C'_p}{C'_p}}$) is associated directly with the vortex shedding activity (represented by ![]() ${\phi }_{{p'}{p'}}$ for
${\phi }_{{p'}{p'}}$ for ![]() $\theta = {\rm \pi}/2$). It should be noted here that the correlation between
$\theta = {\rm \pi}/2$). It should be noted here that the correlation between ![]() ${\phi }_{{p'}{p'}}$ (at
${\phi }_{{p'}{p'}}$ (at ![]() $\theta = {\rm \pi}/2$) and
$\theta = {\rm \pi}/2$) and ![]() ${\phi }_{{C'_p}{C'_p}}$ is not obvious, given that the surface pressure at the crest does not contribute to the pressure drag along
${\phi }_{{C'_p}{C'_p}}$ is not obvious, given that the surface pressure at the crest does not contribute to the pressure drag along ![]() $x$. Such a correlation is possible only if the pressure drag is dependant on the vortex shedding phenomenon, which is established by comparing the two spectra. Another noteworthy observation from figures 5(a,b) is that the energetic frequency range for both
$x$. Such a correlation is possible only if the pressure drag is dependant on the vortex shedding phenomenon, which is established by comparing the two spectra. Another noteworthy observation from figures 5(a,b) is that the energetic frequency range for both ![]() ${\phi }_{{p'}{p'}}$ and
${\phi }_{{p'}{p'}}$ and ![]() ${\phi }_{{C'_p}{C'_p}}$ remains consistent despite variation in the pressure drag domination across
${\phi }_{{C'_p}{C'_p}}$ remains consistent despite variation in the pressure drag domination across ![]() $6\le {\varLambda }/k\le 60$. This suggests that despite the variation from fully to transitionally rough scenarios on increasing
$6\le {\varLambda }/k\le 60$. This suggests that despite the variation from fully to transitionally rough scenarios on increasing ![]() ${\varLambda }/k$, the pressure drag mechanism always corresponds to the same frequency range (for the present case,
${\varLambda }/k$, the pressure drag mechanism always corresponds to the same frequency range (for the present case, ![]() $k = 0.1H$).
$k = 0.1H$).

Figure 5. Premultiplied frequency spectra of the fluctuating surface pressure ![]() ${f}{{\phi }_{{p'}{p'}}}$ (black) at the crest of the rough element (
${f}{{\phi }_{{p'}{p'}}}$ (black) at the crest of the rough element (![]() $\theta = {\rm \pi}/2$), and of the fluctuating pressure force coefficient
$\theta = {\rm \pi}/2$), and of the fluctuating pressure force coefficient ![]() ${f}{{\phi }_{{C'_p}{C'_p}}}$ (red), as a function of the viscous-scaled frequency
${f}{{\phi }_{{C'_p}{C'_p}}}$ (red), as a function of the viscous-scaled frequency ![]() $f{\nu }/{\bar {U}^{2}_{{\tau }_{s}}}$ for various rough wall scenarios. (a,b) Plots of
$f{\nu }/{\bar {U}^{2}_{{\tau }_{s}}}$ for various rough wall scenarios. (a,b) Plots of ![]() ${f}{{\phi }_{{p'}{p'}}}$ and
${f}{{\phi }_{{p'}{p'}}}$ and ![]() ${f}{{\phi }_{{C'_p}{C'_p}}}$, respectively, for the static rough wall cases at
${f}{{\phi }_{{C'_p}{C'_p}}}$, respectively, for the static rough wall cases at ![]() $6 \le {\varLambda }/k\le 60$. (c–e) Comparisons of the spectra for both the static and actuated cases, at (c)
$6 \le {\varLambda }/k\le 60$. (c–e) Comparisons of the spectra for both the static and actuated cases, at (c) ![]() $\varLambda = 10k$,
$\varLambda = 10k$, ![]() $k = 0.1H$, (d)
$k = 0.1H$, (d) ![]() $\varLambda = 20k$,
$\varLambda = 20k$, ![]() $k = 0.1H$, and (e)
$k = 0.1H$, and (e) ![]() $\varLambda = 10k$,
$\varLambda = 10k$, ![]() $k = 0.2H$. Green arrows are used to indicate (
$k = 0.2H$. Green arrows are used to indicate (![]() ${T_{osc}}{\bar {U}^{2}_{{\tau }_{s}}}/{\nu }$) on the
${T_{osc}}{\bar {U}^{2}_{{\tau }_{s}}}/{\nu }$) on the ![]() $x$-axis, and the magenta shaded background nominally represents the most energetic frequency range for both the spectra (
$x$-axis, and the magenta shaded background nominally represents the most energetic frequency range for both the spectra (![]() $10^{-3}\lesssim f{\nu }/{\bar {U}^{2}_{{\tau }_{s}}}\lesssim 10^{-2}$). Here,
$10^{-3}\lesssim f{\nu }/{\bar {U}^{2}_{{\tau }_{s}}}\lesssim 10^{-2}$). Here, ![]() ${f}{{\phi }_{{p'}{p'}}}$ is normalized by
${f}{{\phi }_{{p'}{p'}}}$ is normalized by ![]() $({\rho }{\bar {U}^2_{b}}/2)^2$.
$({\rho }{\bar {U}^2_{b}}/2)^2$.
Next, on considering wall-oscillations imposed at ![]() $T^+_{osc}= 100$ (figures 5c–e), the corresponding oscillation frequency lies within the most energetic frequency ranges of
$T^+_{osc}= 100$ (figures 5c–e), the corresponding oscillation frequency lies within the most energetic frequency ranges of ![]() ${\phi }_{{p'}{p'}}$ and
${\phi }_{{p'}{p'}}$ and ![]() ${\phi }_{{C'_p}{C'_p}}$, for both
${\phi }_{{C'_p}{C'_p}}$, for both ![]() $\varLambda = 10k$ and
$\varLambda = 10k$ and ![]() $\varLambda = 20k$, corresponding to
$\varLambda = 20k$, corresponding to ![]() $k = 0.1H$ and 0.2
$k = 0.1H$ and 0.2![]() $H$ (see green arrows in figures 5c–e). One would thus expect the imposed wall oscillations to weaken the vortex shedding phenomenon, likely by disturbing the two-dimensionality of the separated shear layer, and consequently reducing the pressure drag (Darekar & Sherwin Reference Darekar and Sherwin2001; Choi et al. Reference Choi, Jeon and Kim2008). This explains the significant attenuation of
$H$ (see green arrows in figures 5c–e). One would thus expect the imposed wall oscillations to weaken the vortex shedding phenomenon, likely by disturbing the two-dimensionality of the separated shear layer, and consequently reducing the pressure drag (Darekar & Sherwin Reference Darekar and Sherwin2001; Choi et al. Reference Choi, Jeon and Kim2008). This explains the significant attenuation of ![]() ${\phi }_{{p'}{p'}}$ and
${\phi }_{{p'}{p'}}$ and ![]() ${\phi }_{{C'_p}{C'_p}}$ for the actuated cases (
${\phi }_{{C'_p}{C'_p}}$ for the actuated cases (![]() $T^+_{osc} = 100$) as compared to the static cases. The same was also noted in case of their cross-correlation spectra
$T^+_{osc} = 100$) as compared to the static cases. The same was also noted in case of their cross-correlation spectra ![]() ${\phi }_{{C'_p}{p'}}$ (not shown here). Hence the choice of
${\phi }_{{C'_p}{p'}}$ (not shown here). Hence the choice of ![]() $T^+_{osc} = 100$ lying within the energetic frequency range, for all rough wall cases (figures 5a,b), explains the significant pressure drag reduction noted for these cases. This can be confirmed further by considering wall oscillations at a frequency much higher than the energetic range, for example
$T^+_{osc} = 100$ lying within the energetic frequency range, for all rough wall cases (figures 5a,b), explains the significant pressure drag reduction noted for these cases. This can be confirmed further by considering wall oscillations at a frequency much higher than the energetic range, for example ![]() $T^+_{osc} = 10$ (figure 5c). Indeed, both
$T^+_{osc} = 10$ (figure 5c). Indeed, both ![]() ${\phi }_{{p'}{p'}}$ and
${\phi }_{{p'}{p'}}$ and ![]() ${\phi }_{{C'_p}{C'_p}}$ spectra for
${\phi }_{{C'_p}{C'_p}}$ spectra for ![]() $T^+_{osc} = 10$ overlap with the corresponding spectra for the static case at
$T^+_{osc} = 10$ overlap with the corresponding spectra for the static case at ![]() $\varLambda = 10k$, since such a high oscillation frequency is incapable of disturbing the vortex shedding activity. This explains the negligible DR% corresponding to
$\varLambda = 10k$, since such a high oscillation frequency is incapable of disturbing the vortex shedding activity. This explains the negligible DR% corresponding to ![]() $T^+_{osc} = 10$. Along the same lines, in the case
$T^+_{osc} = 10$. Along the same lines, in the case ![]() $k = 0.2H$ (figure 5e), we can note that the attenuation of both the spectra (for the actuated case relative to the static case) is not as significant as noted for
$k = 0.2H$ (figure 5e), we can note that the attenuation of both the spectra (for the actuated case relative to the static case) is not as significant as noted for ![]() $k = 0.1H$ (figure 5c), which again is consistent with the different magnitudes of DR% for the two cases (figure 2b). The results for
$k = 0.1H$ (figure 5c), which again is consistent with the different magnitudes of DR% for the two cases (figure 2b). The results for ![]() $k = 0.2H$ thus support the notion that the magnitude of pressure drag reduction is correlated with the intensity with which shedding activity in the roughness wake is weakened (depicted by
$k = 0.2H$ thus support the notion that the magnitude of pressure drag reduction is correlated with the intensity with which shedding activity in the roughness wake is weakened (depicted by ![]() ${\phi }_{{p'}{p'}}$), and this is applicable despite the variation in roughness heights. The results also confirm that imposition of wall oscillation frequency, of the order of the vortex shedding frequencies, leads to pressure drag reduction.
${\phi }_{{p'}{p'}}$), and this is applicable despite the variation in roughness heights. The results also confirm that imposition of wall oscillation frequency, of the order of the vortex shedding frequencies, leads to pressure drag reduction.
4. Concluding remarks
The present study investigates drag reduction in a simplified (i.e. 2-D) rough wall scenario, with the intention to answer the following two open questions. (i) Can the well-known viscous drag reduction strategy of imposing spanwise wall oscillations yield pressure drag reduction in a fully-rough case (i.e. with negligible viscous drag contributions)? (ii) What is the mechanism driving this pressure drag reduction? These are answered here via a set of systematically conducted direct numerical simulations of a turbulent flow over 2-D semi-cylindrical rods, maintained at matched roughness Reynolds numbers (![]() $k^+$). The study also considers a case for higher roughness Reynolds number, to investigate the applicability of the pressure drag reduction mechanism across different roughness heights. It is found that spanwise wall oscillations are capable of attenuating the pressure drag when the wall oscillation frequency is of the order of the frequency of vortex shedding from the rough elements. In all the rough wall cases simulated for the present study, the spectral distribution of the vortex shedding phenomenon corresponded to a nominally similar range of viscous-scaled frequencies. This explained the pressure drag reduction on imposition of spanwise wall oscillations for all rough wall cases, given that they were imposed at constant viscous-scaled actuation parameters.
$k^+$). The study also considers a case for higher roughness Reynolds number, to investigate the applicability of the pressure drag reduction mechanism across different roughness heights. It is found that spanwise wall oscillations are capable of attenuating the pressure drag when the wall oscillation frequency is of the order of the frequency of vortex shedding from the rough elements. In all the rough wall cases simulated for the present study, the spectral distribution of the vortex shedding phenomenon corresponded to a nominally similar range of viscous-scaled frequencies. This explained the pressure drag reduction on imposition of spanwise wall oscillations for all rough wall cases, given that they were imposed at constant viscous-scaled actuation parameters.
Although the present study is limited to semi-cylindrical roughness geometry, the flow physics observed in association with the pressure drag reduction (namely, weakening of Reynolds stresses and increasing base pressure in the roughness wake) was found to be consistent with past observations noted in case of 2-D bumps (Banchetti et al. Reference Banchetti, Luchini and Quadrio2020) and square bar roughness (Nguyen et al. Reference Nguyen, Ricco and Pironti2021). This supports applicability of the pressure drag reduction mechanism (i.e. weakening of vortex shedding) for varying roughness geometries, roughness heights and transitional/fully rough scenarios. A thorough quantification of this argument, however, would require an extensive simulation campaign, which is beyond the scope of the present study.
A natural follow-up of this work would involve testing the drag reduction strategy on practical surface conditions, such as sandpaper or 3-D roughness geometries, and at high ![]() $Re_{\tau }$. In this case, the pressure drag is likely to be contributed from highly 3-D vortical structures shedding at very small viscous-scaled frequencies, thereby requiring significant input power to directly affect the vortex shedding (and associated pressure drag). In this respect, the ability to affect this high-frequency phenomenon, via low-frequency wall oscillations (Marusic et al. Reference Marusic, Chandran, Rouhi, Fu, Wine, Holloway, Chung and Smits2021), by leveraging the inherent triadic interactions between the large and small time scales (Deshpande et al. Reference Deshpande, Chandran, Smits and Marusic2023), could offer an energy-efficient pathway for rough wall drag reduction.
$Re_{\tau }$. In this case, the pressure drag is likely to be contributed from highly 3-D vortical structures shedding at very small viscous-scaled frequencies, thereby requiring significant input power to directly affect the vortex shedding (and associated pressure drag). In this respect, the ability to affect this high-frequency phenomenon, via low-frequency wall oscillations (Marusic et al. Reference Marusic, Chandran, Rouhi, Fu, Wine, Holloway, Chung and Smits2021), by leveraging the inherent triadic interactions between the large and small time scales (Deshpande et al. Reference Deshpande, Chandran, Smits and Marusic2023), could offer an energy-efficient pathway for rough wall drag reduction.
Funding
Financial support from the Australian Research Council (grant no. DP210102172) and the Office of Naval Research (grant no. N62909-23-1-2068) is gratefully acknowledged. R.D. also acknowledges partial financial support by the University of Melbourne through the Melbourne Postdoctoral Fellowship. This research was undertaken with the assistance of resources from the National Computational Infrastructure (NCI Australia), an NCRIS enabled capability supported by the Australian Government.
Declaration of interests
The authors report no conflict of interest.
Appendix. Numerical parameters of the simulations
As discussed in § 2, the present simulations are carried out using the open-source spectral element solver Nektar++ (Cantwell et al. Reference Cantwell2015). In all the production simulations performed, the grid resolution per the cylindrical roughness element was kept identical. Each element was represented with Lagrange polynomials of degree ![]() $N_p = 7$ on Gauss–Lobatto–Legendre points. The computational parameters of the simulation cases are listed in table 2. The size of the quadrilateral elements used to discretize the domain varies in space, with the smallest element located at the wall next to the cylinder edge, while the largest element is located at the top boundary (shown by the arrows in figure 6a). Denoting the streamwise and wall-normal sizes of the elements as
$N_p = 7$ on Gauss–Lobatto–Legendre points. The computational parameters of the simulation cases are listed in table 2. The size of the quadrilateral elements used to discretize the domain varies in space, with the smallest element located at the wall next to the cylinder edge, while the largest element is located at the top boundary (shown by the arrows in figure 6a). Denoting the streamwise and wall-normal sizes of the elements as ![]() $l^{elem}_x$ and
$l^{elem}_x$ and ![]() $l^{elem}_z$, respectively, the streamwise and wall-normal grid resolutions within the smallest element can be estimated as
$l^{elem}_z$, respectively, the streamwise and wall-normal grid resolutions within the smallest element can be estimated as ![]() ${\rm \Delta} x_{min}^+ = l^{elem+}_x/(N_p-1) \approx 1.38$ and
${\rm \Delta} x_{min}^+ = l^{elem+}_x/(N_p-1) \approx 1.38$ and ![]() ${\rm \Delta} z_{min}^+ = l^{elem+}_z/(N_p-1) \approx 0.624$. The corresponding grid resolutions within the largest element are
${\rm \Delta} z_{min}^+ = l^{elem+}_z/(N_p-1) \approx 0.624$. The corresponding grid resolutions within the largest element are ![]() ${\rm \Delta} x^+_{max} \approx 4.98$ and
${\rm \Delta} x^+_{max} \approx 4.98$ and ![]() ${\rm \Delta} z^+_{max} \approx 7.29$. (As shown in table 2, the values are slightly different for case
${\rm \Delta} z^+_{max} \approx 7.29$. (As shown in table 2, the values are slightly different for case ![]() $\varLambda = 10k^*$, in which
$\varLambda = 10k^*$, in which ![]() $k=0.2H$.) The grid resolution in the homogeneous spanwise direction is kept constant at
$k=0.2H$.) The grid resolution in the homogeneous spanwise direction is kept constant at ![]() ${\rm \Delta} {y^+}\approx 4.7$. These grid resolutions are more than sufficient to resolve the near-wall turbulent scales of a smooth wall channel flow (Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014). To ascertain the adequacy of the grid resolution to resolve the turbulence associated with the vortex shedding downstream of the roughness elements, we have run two additional simulations (case
${\rm \Delta} {y^+}\approx 4.7$. These grid resolutions are more than sufficient to resolve the near-wall turbulent scales of a smooth wall channel flow (Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014). To ascertain the adequacy of the grid resolution to resolve the turbulence associated with the vortex shedding downstream of the roughness elements, we have run two additional simulations (case ![]() $\varLambda = 10k_{fine}$ in table 2) that are identical to the static and actuated cases of
$\varLambda = 10k_{fine}$ in table 2) that are identical to the static and actuated cases of ![]() $k = 0.1H$ and
$k = 0.1H$ and ![]() $\varLambda = 10k$ but at a higher grid resolution (see figure 6b). In figure 6(c), we compare the variation of the instantaneous total drag coefficient (
$\varLambda = 10k$ but at a higher grid resolution (see figure 6b). In figure 6(c), we compare the variation of the instantaneous total drag coefficient (![]() $C_D$) as a function of time for both the static and actuated cases at the two grid resolutions. The match between the temporal evolution of the
$C_D$) as a function of time for both the static and actuated cases at the two grid resolutions. The match between the temporal evolution of the ![]() $C_D$ values from both grid resolutions indicates the adequacy of the adopted grid resolution to capture the dominant pressure drag reduction mechanisms at the actuation frequencies of the present study. Indeed, the mean drag coefficient values
$C_D$ values from both grid resolutions indicates the adequacy of the adopted grid resolution to capture the dominant pressure drag reduction mechanisms at the actuation frequencies of the present study. Indeed, the mean drag coefficient values ![]() $\bar {C}_{D_{s}} = 36.1\times 10^{-3}$ and
$\bar {C}_{D_{s}} = 36.1\times 10^{-3}$ and ![]() $\bar {C}_{D_{a}} = 25.0\times 10^{-3}$ for the static and actuated cases of
$\bar {C}_{D_{a}} = 25.0\times 10^{-3}$ for the static and actuated cases of ![]() $\varLambda = 10k_{fine}$ are very close to the corresponding values of
$\varLambda = 10k_{fine}$ are very close to the corresponding values of ![]() $\varLambda = 10k$ for
$\varLambda = 10k$ for ![]() $k = 0.1H$ (cf. table 1). A more quantitative assessment of the grid resolution is provided in figures 6(d,e), which show the wall-normal profiles of the global velocity fluctuation covariances (averaged over the corresponding steady-state interval). Note that the fluctuations include the turbulent, form-induced and wall-oscillation contributions. The very good match observed between the profiles is a further demonstration of the sufficiency of the considered resolution.
$k = 0.1H$ (cf. table 1). A more quantitative assessment of the grid resolution is provided in figures 6(d,e), which show the wall-normal profiles of the global velocity fluctuation covariances (averaged over the corresponding steady-state interval). Note that the fluctuations include the turbulent, form-induced and wall-oscillation contributions. The very good match observed between the profiles is a further demonstration of the sufficiency of the considered resolution.
Table 2. Numerical parameters of the simulations. The computational box size ![]() $L_x \times L_y \times L_z = 6H\times 3H \times H$ is the same in all the simulations;
$L_x \times L_y \times L_z = 6H\times 3H \times H$ is the same in all the simulations; ![]() $N_{cyl} = L_x/\varLambda$ represents the number of roughness units or streamwise periodic units in the computational box;
$N_{cyl} = L_x/\varLambda$ represents the number of roughness units or streamwise periodic units in the computational box; ![]() $N_{elem}$ is the number of 2-D spectral elements in the
$N_{elem}$ is the number of 2-D spectral elements in the ![]() $x$–
$x$–![]() $z$ plane, while
$z$ plane, while ![]() $N_y$ is the number of Fourier modes in the homogeneous spanwise direction;
$N_y$ is the number of Fourier modes in the homogeneous spanwise direction; ![]() ${\rm \Delta} x^+$,
${\rm \Delta} x^+$, ![]() ${\rm \Delta} y^+$ and
${\rm \Delta} y^+$ and ![]() ${\rm \Delta} z^+$ are representative grid resolutions (normalized with the static viscous length scale
${\rm \Delta} z^+$ are representative grid resolutions (normalized with the static viscous length scale ![]() $\nu /{\bar {U}_{{\tau }_s}}$); and
$\nu /{\bar {U}_{{\tau }_s}}$); and ![]() $T_{obs}$ is the steady-state simulation interval over which statistics are accumulated after discarding an initial transient. Values marked with
$T_{obs}$ is the steady-state simulation interval over which statistics are accumulated after discarding an initial transient. Values marked with ![]() $^{*}$ correspond to the sole
$^{*}$ correspond to the sole ![]() $k = 0.2H$ case, while
$k = 0.2H$ case, while ![]() $k = 0.1H$ for all other cases.
$k = 0.1H$ for all other cases.


Figure 6. Depiction of the spectral element resolution in the vicinity of the cylindrical roughness elements for (a) ![]() $\varLambda =10k$ and (b)
$\varLambda =10k$ and (b) ![]() $\varLambda =10k_{fine}$. The arrows point to the smallest and largest elements.(c) Time evolution of the instantaneous total drag force coefficient for case
$\varLambda =10k_{fine}$. The arrows point to the smallest and largest elements.(c) Time evolution of the instantaneous total drag force coefficient for case ![]() $\varLambda =10k$ (blue) and
$\varLambda =10k$ (blue) and ![]() $\varLambda =10k_{fine}$ (red). Solid lines show
$\varLambda =10k_{fine}$ (red). Solid lines show ![]() $C_D$ values for the actuated case, while the dashed lines show those for the corresponding static case. (d,e) Wall-normal profiles of the velocity fluctuation covariances (with respect to the global space and time averaged mean velocity
$C_D$ values for the actuated case, while the dashed lines show those for the corresponding static case. (d,e) Wall-normal profiles of the velocity fluctuation covariances (with respect to the global space and time averaged mean velocity ![]() $\bar {U}_i$) for the (d) static and (e) actuated cases corresponding to
$\bar {U}_i$) for the (d) static and (e) actuated cases corresponding to ![]() $\varLambda =10k$ (blue) and
$\varLambda =10k$ (blue) and ![]() $\varLambda =10k_{fine}$ (red). All results are for cases of roughness height,
$\varLambda =10k_{fine}$ (red). All results are for cases of roughness height, ![]() $k = 0.1H$.
$k = 0.1H$.
In order to test the adequacy of adopted box size to accommodate the dominant turbulent structures, we have computed the streamwise and spanwise pre-multiplied energy spectra of the streamwise velocity fluctuation on an ![]() $x$–
$x$–![]() $y$ plane located above the crest of the cylinders where the mean turbulent kinetic energy attains a maximum value (within the shear layer region). Figure 7 shows the spectra for both the static and actuated cases,
$y$ plane located above the crest of the cylinders where the mean turbulent kinetic energy attains a maximum value (within the shear layer region). Figure 7 shows the spectra for both the static and actuated cases, ![]() $\varLambda =10k$ and
$\varLambda =10k$ and ![]() $\varLambda =60k$ for
$\varLambda =60k$ for ![]() $k = 0.1H$. Although very large box size is required to achieve complete de-correlation in the streamwise direction, it can be seen that the peaks of the energy spectra, in both the streamwise and spanwise directions, are captured in the box size
$k = 0.1H$. Although very large box size is required to achieve complete de-correlation in the streamwise direction, it can be seen that the peaks of the energy spectra, in both the streamwise and spanwise directions, are captured in the box size ![]() $L_x \times L_y \times L_z = 6H\times 3H \times H$.
$L_x \times L_y \times L_z = 6H\times 3H \times H$.

Figure 7. (a) Streamwise and (b) spanwise pre-multiplied spectra of the streamwise velocity fluctuations on an ![]() $x$–
$x$–![]() $y$ plane located at
$y$ plane located at ![]() $z^+\approx 35$, for
$z^+\approx 35$, for ![]() $\varLambda =10k$ (black) and
$\varLambda =10k$ (black) and ![]() $\varLambda =60k$ (red) for
$\varLambda =60k$ (red) for ![]() $k = 0.1H$.
$k = 0.1H$.