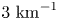1. Introduction
Electron-cyclotron resonance heating (ECRH) is one the most common mechanisms of plasma heating. It is applied in both tokamak and stellarator experiments. At high plasma temperature, linear theory describes the heating. However, during plasma initiation, nonlinear effects are very important because both the time of flight of an electron through the beam and the collision time are larger than the wave–particle interaction time (Taylor, Cairns & O'Brien Reference Taylor, Cairns and O'Brien1988; Farina & Pozzoli Reference Farina and Pozzoli1991).
The importance of nonlinear wave–particle interaction during plasma initiation was previously demonstrated for a plane-wave approximation (Jaeger, Lichtenberg & Lieberman Reference Jaeger, Lichtenberg and Lieberman1972; Carter et al. Reference Carter, Callen, Batchelor and Goldfinger1986), and in a homogeneous magnetic field for a Gaussian beam structure (Farina & Pozzoli Reference Farina and Pozzoli1991; Seol, Hegna & Callen Reference Seol, Hegna and Callen2009; Farina Reference Farina2018). Therefore, it is instrumental to understand the nonlinear interaction when designing and optimising reactor startup scenarios, such as ECRH-assisted startup in the International Thermonuclear Experimental Reactor (ITER), and higher-harmonic startup in Wendelstein 7-X (W7-X) (Marushchenko et al. Reference Marushchenko, Aleynikov, Beidler, Dinklage, Geiger, Helander, Laqua, Maassberg and Turkin2019). In particular, Farina (Reference Farina2018) highlights the difficulty of using the third harmonic (X3) for startup, demonstrating that, in a homogeneous background field, the interaction is too weak to support a startup using modern gyrotrons.
At the earliest stages before breakdown, the characteristic energy of the particles is assumed to be in the range of meV. Nonlinear wave–particle interaction in such conditions has been studied by Seol et al. (Reference Seol, Hegna and Callen2009) and Farina (Reference Farina2018). The ionisation avalanche, however, is facilitated by the secondary electrons. These electrons have a typical energy of a few eVs. Successful ionisation avalanche requires that the secondary electron energy gain exceed the ionisation potential and losses. Energy gain of such electrons is the main focus of our work.
Both the ambient magnetic field inhomogeneity and relativistic effects can have a significant effect on resonance detuning, i.e. the imperfection in the resonance condition
where $\omega$![]() and ${k}_{\parallel }$
and ${k}_{\parallel }$![]() are the wave frequency and parallel component (to the unperturbed magnetic field $\boldsymbol {B}$
are the wave frequency and parallel component (to the unperturbed magnetic field $\boldsymbol {B}$![]() ) of the wave vector, $v_{\parallel }$
) of the wave vector, $v_{\parallel }$![]() is the particle parallel velocity, $\gamma \equiv 1/\sqrt {1 - v^2/\mathrm{c}^2}$
is the particle parallel velocity, $\gamma \equiv 1/\sqrt {1 - v^2/\mathrm{c}^2}$![]() is the relativistic gamma factor for the electron with speed v, $n$
is the relativistic gamma factor for the electron with speed v, $n$![]() is the resonance number and $\omega _c \equiv \mathrm {e}|{\boldsymbol {B}}|/m$
is the resonance number and $\omega _c \equiv \mathrm {e}|{\boldsymbol {B}}|/m$![]() is the non-relativistic electron-cyclotron frequency. Here e is the elementary charge, m is the electron rest mass and c is the speed of light. For instance, a 10 eV electron with parallel energy of 1 eV executes around $5 \times 10^{3}$
is the non-relativistic electron-cyclotron frequency. Here e is the elementary charge, m is the electron rest mass and c is the speed of light. For instance, a 10 eV electron with parallel energy of 1 eV executes around $5 \times 10^{3}$![]() gyrations as it passes through a 4 cm beam in a 1.7 T magnetic field. The resulting accumulated relativistic phase shift is of order unity, since the relativistic detuning per gyration is of order $2 {\rm \pi}(\gamma - 1) \approx 10^{-4}$
gyrations as it passes through a 4 cm beam in a 1.7 T magnetic field. The resulting accumulated relativistic phase shift is of order unity, since the relativistic detuning per gyration is of order $2 {\rm \pi}(\gamma - 1) \approx 10^{-4}$![]() for a 10 eV electron. A similar variation of the ambient magnetic field would also yield a phase shift of order unity.
for a 10 eV electron. A similar variation of the ambient magnetic field would also yield a phase shift of order unity.
In this paper, we outline the derivation of the equations of motion relevant for an inhomogeneous beam shape and ambient magnetic field using the relativistic guiding-centre motion. Apart from parameters changing on long length scales compared with the gyro-radius, there is no assumption on the beam structure (wave-vector or field-strength variations). These equations are used to numerically solve the single wave-interaction energy gain for experimentally relevant magnetic field inhomogeneity length scales. We demonstrate that, at third harmonic in W7-X-relevant conditions, it is possible for electrons to gain energies up to 100 eV starting from a few eV – a condition necessary for the ionisation avalanche. However, the phase-space region where this is the case is very narrow. The region can be extended by using multiple beams with neighbouring resonances. Combining the resonance regions of multiple beams results in a much larger energy gain.
The results are analysed using the Hamiltonian phase-space structure. We analyse the impact of power, beam field inhomogeneity and plasma temperature on the averaged energy gain.
2. Electron cyclotron resonance extension to guiding-centre theory
In W7-X, several gyrotrons, each with a power output of 1 MW, are responsible for the breakdown process. The electromagnetic wave created by a single gyrotron is approximately of Gaussian profile. At the focus, the wave is spread out over a disc with a radius of the order of 2 cm (Hailer et al. Reference Hailer, Dammertz, Erckmann, Gantenbein, Hollmann, Kasparek, Leonhardt, Schmid, Schüller and Thumm2003). The maximum wave magnetic field strength is of order $10^{-3}$![]() to $10^{-2}$
to $10^{-2}$![]() T. In SI units, the maximum wave electric field is ${1.1}\ {\rm MV}\ {\rm m}^{-1}$
T. In SI units, the maximum wave electric field is ${1.1}\ {\rm MV}\ {\rm m}^{-1}$![]() for a 1 MW beam focused to a 2 cm beam waist. In this case, the wave introduces a small perturbation to the otherwise large background magnetic field. This permits usage of the guiding-centre approach.
for a 1 MW beam focused to a 2 cm beam waist. In this case, the wave introduces a small perturbation to the otherwise large background magnetic field. This permits usage of the guiding-centre approach.
A number of ECRH extensions of the guiding-centre theory have been considered previously (Grebogi, Kaufman & Littlejohn Reference Grebogi, Kaufman and Littlejohn1979; Rognlien Reference Rognlien1983; Taylor et al. Reference Taylor, Cairns and O'Brien1988; Ye & Kaufman Reference Ye and Kaufman1992). Here, we outline the derivation of the equations of motion and wave–particle Hamiltonian using the Lagrangian formalism, paying particular attention to the role of the ambient field inhomogeneity.
2.1. Wave correction to guiding-centre Lagrangian
Particle motion in electromagnetic fields can be described using a Lagrangian formalism, with the relativistic phase-space Lagrangian given by
where $\boldsymbol {r}$![]() represents the particle position, $\boldsymbol {p}$
represents the particle position, $\boldsymbol {p}$![]() the momentum and $\phi$
the momentum and $\phi$![]() and $\boldsymbol {A}$
and $\boldsymbol {A}$![]() are the scalar and vector potentials. By splitting the field term, $\boldsymbol {A}$
are the scalar and vector potentials. By splitting the field term, $\boldsymbol {A}$![]() , into a sum of a slowly varying background field, $\boldsymbol {A} _B$
, into a sum of a slowly varying background field, $\boldsymbol {A} _B$![]() , and a wave field, $\boldsymbol {A} _w$
, and a wave field, $\boldsymbol {A} _w$![]() , and similarly for the scalar potential $\phi = \phi _B + \tilde {\phi }_w$
, and similarly for the scalar potential $\phi = \phi _B + \tilde {\phi }_w$![]() , the Lagrangian in (2.1) may be represented as a sum of a part corresponding to the waveless relativistic guiding-centre motion dependent on $\boldsymbol {A}_B, \phi_B$
, the Lagrangian in (2.1) may be represented as a sum of a part corresponding to the waveless relativistic guiding-centre motion dependent on $\boldsymbol {A}_B, \phi_B$![]() , $L_{{\rm GC}}$
, $L_{{\rm GC}}$![]() and the wave part $L_{w}=q{\dot {\boldsymbol {r}}} \boldsymbol {\cdot } \boldsymbol {A}_w - q \tilde {\phi }_w$
and the wave part $L_{w}=q{\dot {\boldsymbol {r}}} \boldsymbol {\cdot } \boldsymbol {A}_w - q \tilde {\phi }_w$![]()
We consider the wave field in the form
where $\omega$![]() is the wave frequency. We assume that the wave amplitude, $\boldsymbol {E}(\boldsymbol {r})$
is the wave frequency. We assume that the wave amplitude, $\boldsymbol {E}(\boldsymbol {r})$![]() , potential amplitude $\phi _w$
, potential amplitude $\phi _w$![]() and the wave vector
and the wave vector
vary slowly. We suppose that the wave field created by ${\boldsymbol {A}} _w, \tilde {\phi }_w$![]() is small, in the sense that it introduces only a small correction to the fast time-scale gyro-motion. The details of the ordering scheme can be found in Appendix A.
is small, in the sense that it introduces only a small correction to the fast time-scale gyro-motion. The details of the ordering scheme can be found in Appendix A.
We ultimately want to describe wave–particle resonance on a time scale of many gyrations. An appropriate transformation of (2.1) into slowly varying variables has to be found. Without the wave it is appropriate to use the guiding-centre coordinates, corresponding to a transformation to the frame moving with the velocity $-(\boldsymbol {\nabla }\phi + \partial \boldsymbol {A}_B/\partial t) \boldsymbol {\times } \boldsymbol {B} / B^2$![]() in which the fast time-scale equations of motion reduce to
in which the fast time-scale equations of motion reduce to
However, the guiding-centre coordinates are perturbed by high frequency fields. In Appendix C, we find that, in the presence of a wave, the correction to the guiding-centre velocity yielding the fast time scale equation of motion (2.6) is given by (C9) (which yields (C10)). This correction scales linearly with $|{{\boldsymbol {E}}}|$![]() for both resonant and non-resonant particles. In this work, we consider resonant particles for which the long term deviation from the unperturbed trajectories is expected to scale as $\sqrt {|{{\boldsymbol {E}}}|}$
for both resonant and non-resonant particles. In this work, we consider resonant particles for which the long term deviation from the unperturbed trajectories is expected to scale as $\sqrt {|{{\boldsymbol {E}}}|}$![]() . This implies that, for small enough fields, the deviation significantly exceeds the coordinate correction. We therefore ignore this correction and rely on the unperturbed guiding-centre coordinates in the guiding-centre formulation. Furthermore, we verify the validity of this approximation against full orbit calculations.
. This implies that, for small enough fields, the deviation significantly exceeds the coordinate correction. We therefore ignore this correction and rely on the unperturbed guiding-centre coordinates in the guiding-centre formulation. Furthermore, we verify the validity of this approximation against full orbit calculations.
The waveless guiding-centre part takes the form of Wimmel (Reference Wimmel1983), Littlejohn (Reference Littlejohn1983) and Cary & Brizard (Reference Cary and Brizard2009) as

where the dynamical variables are the position of the guiding centre $\boldsymbol {R}$![]() , the momentum parallel to the magnetic field $p_\parallel$
, the momentum parallel to the magnetic field $p_\parallel$![]() , the gyro-phase $\zeta$
, the gyro-phase $\zeta$![]() and the magnetic moment $\mu$
and the magnetic moment $\mu$![]() , which is related to the perpendicular momentum, $p_\perp$
, which is related to the perpendicular momentum, $p_\perp$![]() , through $\mu \equiv {p_{\perp }^2}/{2\,m B}$
, through $\mu \equiv {p_{\perp }^2}/{2\,m B}$![]() . The vector $\hat b$
. The vector $\hat b$![]() denotes the field direction, $\hat {b} \equiv \boldsymbol {B}/B$
denotes the field direction, $\hat {b} \equiv \boldsymbol {B}/B$![]() . The particle position $\boldsymbol {r}$
. The particle position $\boldsymbol {r}$![]() differs from the $\zeta$
differs from the $\zeta$![]() -independent guiding centre $\boldsymbol {R}$
-independent guiding centre $\boldsymbol {R}$![]() by the gyro-radius $\boldsymbol {\rho }$
by the gyro-radius $\boldsymbol {\rho }$![]() , i.e. $\boldsymbol {r} = \boldsymbol {R} + \boldsymbol {\rho }$
, i.e. $\boldsymbol {r} = \boldsymbol {R} + \boldsymbol {\rho }$![]() .
.
We introduce a local coordinate system with $\hat {x} \equiv \boldsymbol {k}_\perp (\boldsymbol {R})/|\boldsymbol {k}_\perp |$![]() and $\hat {y} \equiv \hat {b} \times \hat {x}$
and $\hat {y} \equiv \hat {b} \times \hat {x}$![]() . The perpendicular wave vector is given by $\boldsymbol {k}_\perp \equiv \boldsymbol {k} - \boldsymbol {k}_\parallel$
. The perpendicular wave vector is given by $\boldsymbol {k}_\perp \equiv \boldsymbol {k} - \boldsymbol {k}_\parallel$![]() , where the parallel wave vector is $\boldsymbol {k} _\parallel \equiv \boldsymbol {k} \boldsymbol {\cdot } \hat {b}\hat {b}$
, where the parallel wave vector is $\boldsymbol {k} _\parallel \equiv \boldsymbol {k} \boldsymbol {\cdot } \hat {b}\hat {b}$![]() . Then, the wave part of the Lagrangian is
. Then, the wave part of the Lagrangian is
The wave-vector potential part of $L_w$![]() can be rewritten approximately as
can be rewritten approximately as
and similarly for the wave scalar potential
Field strengths and the wave vector are approximated by the value at the guiding-centre position $\boldsymbol {R}$![]() . The gyro-radius is given by
. The gyro-radius is given by
and to lowest order in $\rho$![]() , the particle velocity perpendicular to $\boldsymbol {B}$
, the particle velocity perpendicular to $\boldsymbol {B}$![]()
The ordering in Appendix A allows us to use the gyro-radius and velocity at the guiding centre, where $B(\boldsymbol {r}) \approx B(\boldsymbol {R})$![]() , even for the wave phase.
, even for the wave phase.
Equation (2.9) describes different types of interaction: longitudinal $X$![]() -mode interaction with $E_x$
-mode interaction with $E_x$![]() , and transverse $X$
, and transverse $X$![]() -mode interaction with $E_y$
-mode interaction with $E_y$![]() , interaction due to the gyro-motion
, interaction due to the gyro-motion
and the interaction due to the guiding-centre motion, which mainly comes from $O$![]() -mode interaction
-mode interaction
The interpretation of $E_x$![]() being longitudinal is true if ${k}_{\parallel }=0$
being longitudinal is true if ${k}_{\parallel }=0$![]() , otherwise the $E_x$
, otherwise the $E_x$![]() term could consist of some combination of longitudinal/transverse components. The variable
term could consist of some combination of longitudinal/transverse components. The variable
is the product of the perpendicular wave vector and gyro-radius, possibly with a sign from $q$![]() . With these definitions, $L_w$
. With these definitions, $L_w$![]() can be written as
can be written as
Equation (2.16) is expanded in terms of Bessel functions (see for e.g. Shafranov Reference Shafranov1967, p. 145). Focusing on resonant waves, we introduce a new slow variable
which represents the phase shift between the phase of the wave and the phase of the particle gyro-motion. Here, $n$![]() is the integer corresponding to the resonance of interest. The frequency $\omega$
is the integer corresponding to the resonance of interest. The frequency $\omega$![]() is assumed to be positive, and we work with negatively charged particles. Equations for positively charged particles can be obtained by letting $\omega < 0$
is assumed to be positive, and we work with negatively charged particles. Equations for positively charged particles can be obtained by letting $\omega < 0$![]() . A time average of (2.16) removes all non-resonant terms from the expansion series, resulting in
. A time average of (2.16) removes all non-resonant terms from the expansion series, resulting in

Here, we can replace $\dot {\zeta }\approx \omega /n$![]() since $\dot {\psi }/ \omega$
since $\dot {\psi }/ \omega$![]() is small and $\omega |{\boldsymbol {A}_w}| / c B \sim \mathcal {O}(1)$
is small and $\omega |{\boldsymbol {A}_w}| / c B \sim \mathcal {O}(1)$![]() .
.
The time average of $\dot {\boldsymbol {R}} \boldsymbol {\cdot } {\boldsymbol {A}}_{w,i}$![]() is computed analogously, but can be further simplified because ${\dot {\boldsymbol {R}}}_\perp$
is computed analogously, but can be further simplified because ${\dot {\boldsymbol {R}}}_\perp$![]() is negligible. Only the $E_z$
is negligible. Only the $E_z$![]() term is of importance and $\sum \dot {\boldsymbol {R}} \boldsymbol {\cdot } {\boldsymbol {A}}_{w,i} \approx \dot {\boldsymbol {R}} \boldsymbol {\cdot } {\boldsymbol {A}}_{w,z}$
term is of importance and $\sum \dot {\boldsymbol {R}} \boldsymbol {\cdot } {\boldsymbol {A}}_{w,i} \approx \dot {\boldsymbol {R}} \boldsymbol {\cdot } {\boldsymbol {A}}_{w,z}$![]() , resulting in
, resulting in

The time average of $\tilde {\phi }_w$![]() is analogous to the time average of $\dot {\boldsymbol {R}} \boldsymbol {\cdot } {\boldsymbol {A}}_{w,z}$
is analogous to the time average of $\dot {\boldsymbol {R}} \boldsymbol {\cdot } {\boldsymbol {A}}_{w,z}$![]() and yields
and yields
A formal approach to removal of the non-resonant terms is presented in Appendix B.
Combining these results, the full Lagrangian in (2.8) in guiding-centre coordinates becomes
where the guiding-centre Hamiltonian is given by

This Hamiltonian reduces to the one obtained in Suvorov & Tokman (Reference Suvorov and Tokman1988), Taylor et al. (Reference Taylor, Cairns and O'Brien1988), Farina & Pozzoli (Reference Farina and Pozzoli1991) and Litvak et al. (Reference Litvak, Sergeev, Suvorov, Tokman and Khazanov1993) for the cases studied therein. The resonance number $n$![]() is governed by the resonance condition $-n q B / (m \gamma ) + {k}_{\parallel } v_{\parallel } - \omega = 0$
is governed by the resonance condition $-n q B / (m \gamma ) + {k}_{\parallel } v_{\parallel } - \omega = 0$![]() . Note that, far away from the resonance, the ‘resonant’ terms given by (2.18) and (2.19) decrease and become comparable to the other neglected terms of the corresponding series. The term $({\omega }/{n})({m \mu }/{-q} + W)$
. Note that, far away from the resonance, the ‘resonant’ terms given by (2.18) and (2.19) decrease and become comparable to the other neglected terms of the corresponding series. The term $({\omega }/{n})({m \mu }/{-q} + W)$![]() originates from changing to a rotating frame of reference when introducing $\psi$
originates from changing to a rotating frame of reference when introducing $\psi$![]() in (2.17).
in (2.17).
In the case of multiple waves with different $\boldsymbol {k}$![]() or $\boldsymbol {E}$
or $\boldsymbol {E}$![]() , their contributions can be accounted for in an additive manner, i.e. $L = L_{{\rm GC}} + \sum _i L_{w}^{(i)}$
, their contributions can be accounted for in an additive manner, i.e. $L = L_{{\rm GC}} + \sum _i L_{w}^{(i)}$![]() . No new independent variables need to be introduced in this case. If they have different $\omega$
. No new independent variables need to be introduced in this case. If they have different $\omega$![]() (by factor of $\mathbb {R}\setminus \mathbb {Q}$
(by factor of $\mathbb {R}\setminus \mathbb {Q}$![]() ) no common rotating frame of reference exists and the Hamiltonian becomes time dependent.
) no common rotating frame of reference exists and the Hamiltonian becomes time dependent.
2.2. Equations of motion
By varying the Lagrangian in (2.16) with respect to ${p_{\parallel }}, \boldsymbol {R}, \mu$![]() , and $\psi$
, and $\psi$![]() , the following equations of motion are obtained:
, the following equations of motion are obtained:
where the effective magnetic field is
These equations of motion reduce to, for example, the ones in Litvak et al. (Reference Litvak, Sergeev, Suvorov, Tokman and Khazanov1993) for the case studied there.
Substituting $\dot {\psi }$![]() and $\dot {\mu }$
and $\dot {\mu }$![]() in (2.23b) it is simplified and takes the form
in (2.23b) it is simplified and takes the form
where the effective force is

We used
since ${\partial {\bar {\boldsymbol {A}}}_{w}}/{\partial \mu }$![]() and ${\partial {\bar {\boldsymbol {A}}}_{w}}/{\partial \psi }$
and ${\partial {\bar {\boldsymbol {A}}}_{w}}/{\partial \psi }$![]() are parallel.
are parallel.
3. The X3 startup in the W7-X stellarator
Startup at the third harmonic is prohibitively difficult in homogeneous magnetic fields, due to a very week interaction. Farina (Reference Farina2018) demonstrated that, for slow particles, the nonlinear energy gain is well below 1 eV, which is not enough to support startup. In this section, we discuss numerical solutions of the equations of motion for electrons. These simulations account for both the wave field and the background magnetic field inhomogeneity. They show that the energy gain can be much larger than in a homogeneous background magnetic field.
For these numerical solutions, we use a background field structure relevant to a reduced B-field W7-X configuration. This field can be represented approximately by
and the electron trajectories lie approximately on $x=y=0$![]() (since the cross-field drifts are small during the time of one beam interaction). A typical mirror ratio in W7-X is of order $|B_{\max } - B_{\min }|/|B_{\min }| \approx 0.1$
(since the cross-field drifts are small during the time of one beam interaction). A typical mirror ratio in W7-X is of order $|B_{\max } - B_{\min }|/|B_{\min }| \approx 0.1$![]() . We therefore let $B_1 = 0.069004\ {\rm T}$
. We therefore let $B_1 = 0.069004\ {\rm T}$![]() and $B_0$
and $B_0$![]() is varied slightly around $B(z=0) = {1.6671}\ {\rm T}$
is varied slightly around $B(z=0) = {1.6671}\ {\rm T}$![]() depending on the exact desired location of the resonance within the structure given by (3.1).
depending on the exact desired location of the resonance within the structure given by (3.1).
The wave field in W7-X is created by 140 GHz gyrotrons. Such a gyrotron is assumed to create a beam with a Gaussian profile with elliptic polarisation and plane-wave phase. That is, the wave field is

where $r$![]() here is the radial distance from the centre axis of the beam, i.e. $r^2 = y^2 + (-x {k}_{\parallel }/k + z {k}_{\perp }/k)^2$
here is the radial distance from the centre axis of the beam, i.e. $r^2 = y^2 + (-x {k}_{\parallel }/k + z {k}_{\perp }/k)^2$![]() and $w = 2$
and $w = 2$![]() cm (Hailer et al. Reference Hailer, Dammertz, Erckmann, Gantenbein, Hollmann, Kasparek, Leonhardt, Schmid, Schüller and Thumm2003). In a vacuum, the total field must be such that $\boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {E} = 0$
cm (Hailer et al. Reference Hailer, Dammertz, Erckmann, Gantenbein, Hollmann, Kasparek, Leonhardt, Schmid, Schüller and Thumm2003). In a vacuum, the total field must be such that $\boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {E} = 0$![]() . The Gaussian profile (3.2) has a small non-zero divergence
. The Gaussian profile (3.2) has a small non-zero divergence
and must be compensated with the scalar potential. This potential enters the equations of motion at one higher order in ${k}_{\perp } \rho$![]() than the field created by $\boldsymbol {A}_w$
than the field created by $\boldsymbol {A}_w$![]() and is therefore ignored (compare (2.20) and (2.18) where $b = {k}_{\perp } \rho$
and is therefore ignored (compare (2.20) and (2.18) where $b = {k}_{\perp } \rho$![]() ).
).
Expanding the Bessel functions in (2.23a) to (2.23d) in ${k}_{\perp } \rho \ll 1$![]() , the wave term becomes
, the wave term becomes

where the interaction parameter $\epsilon$![]() is
is

where
The other terms are of higher order. Then, the equations of motion to relevant order take the form



where the cross-field drifts are ignored together with terms containing $({{\rm d}B}/{{\rm d}z}) \epsilon (z)$![]() .
.
This system is solved numerically using Runge–Kutta–Fehlberg 4,5 explicit scheme from the GNU science library (Reference Galassi2009) with a fixed time step of $10 m/ \mathrm{e} B(z=0)$![]() . This numerical scheme ensures conservation of the Hamiltonian to 12 decimal places (i.e. approximately ${0.5}\ {\mathrm {\mu }}{\rm eV}$
. This numerical scheme ensures conservation of the Hamiltonian to 12 decimal places (i.e. approximately ${0.5}\ {\mathrm {\mu }}{\rm eV}$![]() ). The evaluation is stopped when either $t \mathrm {e} B(z=0)/m = 4\times 10^{6}$
). The evaluation is stopped when either $t \mathrm {e} B(z=0)/m = 4\times 10^{6}$![]() or when the particle leaves the beam, i.e. $|{z / w}| > 2$
or when the particle leaves the beam, i.e. $|{z / w}| > 2$![]() for an X3 single beam, $|{z / w}| > 4$
for an X3 single beam, $|{z / w}| > 4$![]() for two X3 beams and $|{z/ w}| > 3$
for two X3 beams and $|{z/ w}| > 3$![]() for X2. This yields a single interaction energy gain.
for X2. This yields a single interaction energy gain.
Figure 1 (solid curves) shows an example trajectory of an electron interacting with the beam once. The perpendicular energy evolution is shown in the top graph together with the $z$![]() motion in the bottom graph. In this case, the cold resonance is located at $z={-1.32}\ {\rm cm}$
motion in the bottom graph. In this case, the cold resonance is located at $z={-1.32}\ {\rm cm}$![]() with $\alpha = 0.013538$
with $\alpha = 0.013538$![]() and the magnetic field is $B_0 = 1.598133$
and the magnetic field is $B_0 = 1.598133$![]() T. The corresponding field inhomogeneity length scale is $B/\hat {b}\boldsymbol {\cdot } \boldsymbol {\nabla } B = 2045$
T. The corresponding field inhomogeneity length scale is $B/\hat {b}\boldsymbol {\cdot } \boldsymbol {\nabla } B = 2045$![]() m. The beam centre is always at $z=0$
m. The beam centre is always at $z=0$![]() (see (3.2)). The initial perpendicular particle energy is 1.03 eV, whilst the initial parallel energy is very small at 0.25 meV. The initial phase of the particle is chosen to maximise the energy gain. The corresponding unperturbed trajectory is plotted as a dashed curve. The energy gain of the particle with the same initial conditions but in homogeneous magnetic field is also shown with the dashed–dotted curve. In this case, $B_0 = 1.667107$
(see (3.2)). The initial perpendicular particle energy is 1.03 eV, whilst the initial parallel energy is very small at 0.25 meV. The initial phase of the particle is chosen to maximise the energy gain. The corresponding unperturbed trajectory is plotted as a dashed curve. The energy gain of the particle with the same initial conditions but in homogeneous magnetic field is also shown with the dashed–dotted curve. In this case, $B_0 = 1.667107$![]() T and $B_1 = 0$
T and $B_1 = 0$![]() . We observe that the interaction is extended considerably in the inhomogeneous case, which results in much higher excursions during nonlinear trapping in the wave field and approximately a doubling in the single interaction energy gain. Note that this particle turns around near $z=0$
. We observe that the interaction is extended considerably in the inhomogeneous case, which results in much higher excursions during nonlinear trapping in the wave field and approximately a doubling in the single interaction energy gain. Note that this particle turns around near $z=0$![]() due to the mirror force. This particle has a very slow initial parallel velocity of $0.1 v_{th, 300\ {\rm K}}$
due to the mirror force. This particle has a very slow initial parallel velocity of $0.1 v_{th, 300\ {\rm K}}$![]() .
.

Figure 1. Example electron trajectory in X3 wave (solid curves). The dash–dotted curve shows the same trajectory in a homogeneous case. The dashed curve represents the particle trajectory in the absence of the wave, highlighting that the bounce is caused by the increase in magnetic moment. These trajectories are for very slow parallel velocities of $0.1 v_{th, 300\ {\rm K}}$![]() . A trajectory of a particle from inside the 80 eV contour of figure 2 is shown with the red dotted curve.
. A trajectory of a particle from inside the 80 eV contour of figure 2 is shown with the red dotted curve.
We also show a typical orbit for high energy gain at higher parallel velocity in dotted red. Because the beam travel time is shorter, the interaction strength must be stronger for a significant interaction. Because the interaction strength scales with $v_{\perp }^3$![]() , see (3.7d), increasing initial $v_{\perp }$
, see (3.7d), increasing initial $v_{\perp }$![]() achieves just that. The interaction is no longer several energy excursions but an interaction with an approximately stationary phase. The interaction is significantly extended compared with the homogeneous case because $\gamma$
achieves just that. The interaction is no longer several energy excursions but an interaction with an approximately stationary phase. The interaction is significantly extended compared with the homogeneous case because $\gamma$![]() and $B$
and $B$![]() change in conjunction.
change in conjunction.
Figure 2 shows contours (in eV) of the single interaction energy gain for electrons with various initial energies and pitch angles. The energy gain is maximised over the initial phase. The inhomogeneous background field is the same as in figure 1 ($B_0 = 1.6671$![]() ). Positive parallel energy corresponds to electrons moving toward increasing $B$
). Positive parallel energy corresponds to electrons moving toward increasing $B$![]() . The maximised energy gain in an analogous homogeneous situation is shown in figure 3. These calculations show that a small inhomogeneity not only increases the maximum gain to around 80 eV, but also significantly extends the phase-space region over which efficient interaction takes place. A factor of $4$
. The maximised energy gain in an analogous homogeneous situation is shown in figure 3. These calculations show that a small inhomogeneity not only increases the maximum gain to around 80 eV, but also significantly extends the phase-space region over which efficient interaction takes place. A factor of $4$![]() increase in energy gain can alternatively be achieved by a 10–100 times increase of the ECRH beam power if the ambient magnetic field is homogeneous. This is because the X3 interaction scales between $\sqrt {E_-}\sim P^{1/4}$
increase in energy gain can alternatively be achieved by a 10–100 times increase of the ECRH beam power if the ambient magnetic field is homogeneous. This is because the X3 interaction scales between $\sqrt {E_-}\sim P^{1/4}$![]() and $E_-\sim P^{1/2}$
and $E_-\sim P^{1/2}$![]() (see (4.9)). However, for electrons, where the stationary phase is the major interaction, energy gain scales as $E_-\sim P^{1/2}$
(see (4.9)). However, for electrons, where the stationary phase is the major interaction, energy gain scales as $E_-\sim P^{1/2}$![]() and 16 times power would be required to achieve an energy increase of a factor 4.
and 16 times power would be required to achieve an energy increase of a factor 4.

Figure 2. Contours of the energy gain (eV), maximised over initial phase for a range parallel and perpendicular initial energy of the particles in an X3 wave. Inhomogeneous magnetic field as per (3.1) with $B_0 = 1.599343$![]() T, $B_1 = 0.069004$
T, $B_1 = 0.069004$![]() T and $\alpha = 0.190400$
T and $\alpha = 0.190400$![]() . The 1 MW beam is assumed to have a Gaussian profile with 2 cm width.
. The 1 MW beam is assumed to have a Gaussian profile with 2 cm width.

Figure 3. Same as figure 2, but homogeneous field $B_0 = 1.667078$![]() T so resonance is fulfilled at 24 eV.
T so resonance is fulfilled at 24 eV.
Note, however, that these results are quantitatively sensitive to the location of the resonance. They merely highlight a significant effect of the inhomogeneity on the energy gain. More general results are presented in the next sections.
The energy gain averaged over the initial phase is lower. It is shown in figure 4. The red contour corresponds to a gain of 13.6 eV, which is necessary for maintaining the ionisation avalanche process. However, this phase-space region is very narrow, in particular in $v_{\parallel }$![]() . Because secondary electrons are distributed uniformly over the pitch angles during ionisation avalanche it is unlikely that such a beam can maintain ionisation.
. Because secondary electrons are distributed uniformly over the pitch angles during ionisation avalanche it is unlikely that such a beam can maintain ionisation.

Figure 4. Contours of the mean energy gain (eV), averaged over initial phase for the parameters of figure 2.
Another feature of the 13.6 eV contour in figure 4 is that its minimal initial electron energy is above 13.6 eV, i.e. an electron needs to already have more than 13.6 eV in order to gain significant energy. This feature (the location of the 13.6 eV phase-space contour), however, depends on the inhomogeneity length scale. This is discussed for in the next section (see figure 14).
3.1. Configuration with multiple beams
The energy gain required for the breakdown process during startup is approximately 13.6 eV. Robust breakdown requires that a significant fraction of particles are accelerated from below 13.6 eV to tens of eV during the interaction. As shown in the previous section, this is difficult to achieve with a single beam set-up. In the presence of multiple beams, an overlap of multiple resonances can lead to significantly larger overall gains. We consider such a scenario in this section.
The second beam is set up analogously to the first one with an extra shift along the field line, $z_0$![]() ,
,
The relative phase shift is generally important. Due to the chaotic nature of the slow phase drifts of the gyrotrons, we expect that all phase shifts are present during a startup scenario. The relative phase shift is indirectly controlled through $z_0$![]() and difference in ${k}_{\parallel }$
and difference in ${k}_{\parallel }$![]() . Therefore, we ignore the explicit relative phase shift to reduce the number of optimisation variables.
. Therefore, we ignore the explicit relative phase shift to reduce the number of optimisation variables.
Figures 5 and 6 demonstrate the results of an optimisation procedure. In figure 5 the maximum single interaction energy gain is optimised, whereas in figure 6 optimisation is of energy gain maximised over initial $\psi$![]() and then averaged over initial $v_{\parallel }$
and then averaged over initial $v_{\parallel }$![]() and $v_{\perp }$
and $v_{\perp }$![]() . Both results are in the presence of two beams. The conditions are similar to those of figure 2, with the optimisation parameters being $B_0$
. Both results are in the presence of two beams. The conditions are similar to those of figure 2, with the optimisation parameters being $B_0$![]() , $\alpha$
, $\alpha$![]() (i.e. $\hat {b}\boldsymbol {\cdot } \boldsymbol {\nabla } B / B$
(i.e. $\hat {b}\boldsymbol {\cdot } \boldsymbol {\nabla } B / B$![]() ), ${k}_{\parallel }{}_1$
), ${k}_{\parallel }{}_1$![]() , ${k}_{\parallel }{}_2$
, ${k}_{\parallel }{}_2$![]() and the second beam position $z_0$
and the second beam position $z_0$![]() . The Nealder–Mead method with 50 random starting points and 250 000 trajectories per step is used.
. The Nealder–Mead method with 50 random starting points and 250 000 trajectories per step is used.

Figure 5. Contours of maximum energy gain in a case of 2 X3 beams with injection geometry optimised for maximum energy gain.

Figure 6. Same as figure 5 but optimisation for the average maximum energy gain in $E_\perp \times E_\parallel \in [0, {13.6}\ {\rm eV}]\times [0, {4}\ {\rm eV}]$![]() .
.
The first optimisation maximises the energy gain in $\mu B_0 \in [0, {13.6}\ {\rm eV}]$![]() , and ${m v_{\parallel }^2}/{2} \in [0, {4}\ {\rm eV}]$
, and ${m v_{\parallel }^2}/{2} \in [0, {4}\ {\rm eV}]$![]() . The best result is ${{k}_{\parallel } \mathrm{c}}/{\omega } = 0.243/3$
. The best result is ${{k}_{\parallel } \mathrm{c}}/{\omega } = 0.243/3$![]() , ${k_{\parallel,2} \mathrm{c}}/{\omega } = 0.214/3$
, ${k_{\parallel,2} \mathrm{c}}/{\omega } = 0.214/3$![]() , $1 - {m \omega }/{3 e B} = -5.28 / 511\,000$
, $1 - {m \omega }/{3 e B} = -5.28 / 511\,000$![]() , $z_0 = -0.826 w$
, $z_0 = -0.826 w$![]() , $\alpha = 2.90$
, $\alpha = 2.90$![]() . The results are shown in figure 5. The maximum energy gain is ${\sim }{200}\ {\rm eV}$
. The results are shown in figure 5. The maximum energy gain is ${\sim }{200}\ {\rm eV}$![]() , which is approximately twice as high as that in the case of one beam. Moreover, the initial energy required for reaching 13.6 eV is now lower than 13.6 eV and the initial $v_{\parallel }$
, which is approximately twice as high as that in the case of one beam. Moreover, the initial energy required for reaching 13.6 eV is now lower than 13.6 eV and the initial $v_{\parallel }$![]() range is increased significantly.
range is increased significantly.
The second optimisation optimises energy gain maximised over initial $\psi$![]() and then averaged over initial $v_{\parallel }$
and then averaged over initial $v_{\parallel }$![]() and $v_{\perp }$
and $v_{\perp }$![]() in the phase-space area $\mu B_0\in [0,{13.6}\ {\rm eV}]$
in the phase-space area $\mu B_0\in [0,{13.6}\ {\rm eV}]$![]() , and ${m v_{\parallel }^2}/{2} \in [0,{4}\ {\rm eV}]$
, and ${m v_{\parallel }^2}/{2} \in [0,{4}\ {\rm eV}]$![]() . The best result is ${{k}_{\parallel } \mathrm{c}}/{\omega } = 0.0259/3$
. The best result is ${{k}_{\parallel } \mathrm{c}}/{\omega } = 0.0259/3$![]() , ${k_{\parallel,2} \mathrm{c}}/{\omega } = 0.0193/3$
, ${k_{\parallel,2} \mathrm{c}}/{\omega } = 0.0193/3$![]() , $1 - {m \omega }/{3 e B} = -0.8125 / 511\,000$
, $1 - {m \omega }/{3 e B} = -0.8125 / 511\,000$![]() , $z_0 = 0.741$
, $z_0 = 0.741$![]() , $\alpha = 0.0775$
, $\alpha = 0.0775$![]() . The maximum energy gain is shown in figure 6. Although it was not possible to achieve mean energy gains comparable to those from the second harmonic interaction, which is several hundreds of eVs (see figure 8), the optimisation procedure has extended the range of $v_{\parallel }$
. The maximum energy gain is shown in figure 6. Although it was not possible to achieve mean energy gains comparable to those from the second harmonic interaction, which is several hundreds of eVs (see figure 8), the optimisation procedure has extended the range of $v_{\parallel }$![]() for which high gain is expected by at least an order of magnitude. Kinetic modelling of the ionisation avalanche is required in order to answer the question as to whether such double beam X3 particle energisation is efficient to sustain startup.
for which high gain is expected by at least an order of magnitude. Kinetic modelling of the ionisation avalanche is required in order to answer the question as to whether such double beam X3 particle energisation is efficient to sustain startup.
3.2. Effect of magnetic field inhomogeneity on X2 interaction
The X2 ECRH startup is routinely performed at W7-X. In this section, we look into effects of inhomogeneity on X2 interaction. In the second-harmonic case, the cold resonance is at 2.5 T for a 140 GHz W7-X gyrotron.
Once again, the equations (3.7) are solved numerically, with $n=2$![]() this time. Figures 7 and 8 show the mean (over initial gyro-phase) single interaction energy gain for the homogeneous and inhomogeneous cases, respectively. For the homogeneous case we set $\omega = 2 {\rm \pi}\times {140}\ {\rm GHz}$
this time. Figures 7 and 8 show the mean (over initial gyro-phase) single interaction energy gain for the homogeneous and inhomogeneous cases, respectively. For the homogeneous case we set $\omega = 2 {\rm \pi}\times {140}\ {\rm GHz}$![]() , and the magnetic field strength such that the resonance energy is $\mu B = {186.5}\ {\rm eV}$
, and the magnetic field strength such that the resonance energy is $\mu B = {186.5}\ {\rm eV}$![]() . For the inhomogeneous case, we set $B_1 = {0.1}\ {\rm T}$
. For the inhomogeneous case, we set $B_1 = {0.1}\ {\rm T}$![]() and $B_0 \approx {2.5}\ {\rm T}$
and $B_0 \approx {2.5}\ {\rm T}$![]() , so that the $\mu B = {186.5}\ {\rm eV}$
, so that the $\mu B = {186.5}\ {\rm eV}$![]() resonance is at $z = 0$
resonance is at $z = 0$![]() . The inhomogeneity at $z=0$
. The inhomogeneity at $z=0$![]() is $B/\hat {b} \boldsymbol {\cdot } \boldsymbol {\nabla } B = 174$
is $B/\hat {b} \boldsymbol {\cdot } \boldsymbol {\nabla } B = 174$![]() m. We let ${k}_{\parallel } = 0$
m. We let ${k}_{\parallel } = 0$![]() .
.

Figure 7. Contours of the energy gain (eV), averaged over initial phase, X2 homogeneous background field ($B_1 = 0$![]() ).
).

Figure 8. Same as figure 7, but with inhomogeneous magnetic field ($\alpha = {{\rm \pi} }/{2}, B_1 = {0.1}\ {\rm T}$![]() ).
).
As expected, the gain in both cases is much greater than for X3. In addition, the $v_{||}$![]() range is much broader as well: note the difference in $x$
range is much broader as well: note the difference in $x$![]() -axis scale between figures 4 and 8. A relatively strong effect of inhomogeneity on X2 mean energy gain is observed for low $v_{\parallel }$
-axis scale between figures 4 and 8. A relatively strong effect of inhomogeneity on X2 mean energy gain is observed for low $v_{\parallel }$![]() , where the nonlinear interaction is also extended considerably. The affected phase-space region is quite narrow for typical plasmas after startup, but quite large when considering low temperature plasma or breakdown. We therefore expect at least a small improvement of X2 interaction by the inhomogeneity.
, where the nonlinear interaction is also extended considerably. The affected phase-space region is quite narrow for typical plasmas after startup, but quite large when considering low temperature plasma or breakdown. We therefore expect at least a small improvement of X2 interaction by the inhomogeneity.
These results are analysed in the next sections from the point of view of the Hamiltonian phase-space structure.
4. Phase-space structure
In the previous section we demonstrated that the ambient $B$![]() -field inhomogeneity has a significant effect on the resonant electron dynamics and the energy gain of electrons. We will use the known weakly relativistic Hamiltonian expression to analyse these results.
-field inhomogeneity has a significant effect on the resonant electron dynamics and the energy gain of electrons. We will use the known weakly relativistic Hamiltonian expression to analyse these results.
The Hamiltonian (2.22) can be transformed and expanded into a weakly relativistic form to
for the $X$![]() mode (Farina & Pozzoli Reference Farina and Pozzoli1991; Litvak et al. Reference Litvak, Sergeev, Suvorov, Tokman and Khazanov1993; Farina Reference Farina2018), where the normalised perpendicular energy $\varPhi = n P_\chi (-q B)/ m^2c^2$
mode (Farina & Pozzoli Reference Farina and Pozzoli1991; Litvak et al. Reference Litvak, Sergeev, Suvorov, Tokman and Khazanov1993; Farina Reference Farina2018), where the normalised perpendicular energy $\varPhi = n P_\chi (-q B)/ m^2c^2$![]() is introduced together with the normalised canonical $Z$
is introduced together with the normalised canonical $Z$![]() momentum $P = P_Z / m c$
momentum $P = P_Z / m c$![]() . The canonical momentum $P_\chi$
. The canonical momentum $P_\chi$![]() is associated with the gyro-motion through
is associated with the gyro-motion through
and the canonical momentum $P_Z$![]() is associated with the parallel motion
is associated with the parallel motion
The wave-phase coordinate is $\chi = n \psi + \varphi (\boldsymbol {R}) - n ({{\rm \pi} }/{2})$![]() . These canonical coordinates were introduced by the use of the generating function
. These canonical coordinates were introduced by the use of the generating function
Resonant particles typically experience quick quasi-periodic motion in the ($\chi, P_\chi$![]() ) plane. The structure of the corresponding Hamiltonian contours provides important insights into the particle dynamics (see e.g. Neishtadt & Timofeev Reference Neishtadt and Timofeev1987; Farina & Pozzoli Reference Farina and Pozzoli1991; Kotel'Nikov & Stupakov Reference Kotel'Nikov and Stupakov1991; Litvak et al. Reference Litvak, Sergeev, Suvorov, Tokman and Khazanov1993). The shape of a given Hamiltonian contour in the ($\chi, P_\chi$
) plane. The structure of the corresponding Hamiltonian contours provides important insights into the particle dynamics (see e.g. Neishtadt & Timofeev Reference Neishtadt and Timofeev1987; Farina & Pozzoli Reference Farina and Pozzoli1991; Kotel'Nikov & Stupakov Reference Kotel'Nikov and Stupakov1991; Litvak et al. Reference Litvak, Sergeev, Suvorov, Tokman and Khazanov1993). The shape of a given Hamiltonian contour in the ($\chi, P_\chi$![]() ) plane is set by the three remaining ‘slower changing’ parameters of (4.1). The first parameter is the relativistic frequency shift
) plane is set by the three remaining ‘slower changing’ parameters of (4.1). The first parameter is the relativistic frequency shift
where $\varOmega _0 = {\mathrm {e} B}/{m}$![]() is the non-relativistic gyro-frequency. The second parameter characterises the Doppler shift $\xi _n = {k}_{\parallel } \mathrm{c} / n \varOmega _0$
is the non-relativistic gyro-frequency. The second parameter characterises the Doppler shift $\xi _n = {k}_{\parallel } \mathrm{c} / n \varOmega _0$![]() . The third parameter is the interaction strength as a function of the field strengths, $\epsilon _* = \epsilon (E_x, E_y)$
. The third parameter is the interaction strength as a function of the field strengths, $\epsilon _* = \epsilon (E_x, E_y)$![]() , which is given by (3.5). It is assumed that $\epsilon >0$
, which is given by (3.5). It is assumed that $\epsilon >0$![]() . If $\epsilon <0$
. If $\epsilon <0$![]() , a redefinition of $\epsilon \mapsto - \epsilon$
, a redefinition of $\epsilon \mapsto - \epsilon$![]() and $\chi \mapsto \chi + {\rm \pi}$
and $\chi \mapsto \chi + {\rm \pi}$![]() restores the Hamiltonian to its form with $\epsilon >0$
restores the Hamiltonian to its form with $\epsilon >0$![]() .
.
The contours of the Hamiltonian in (2.22) for typical W7-X parameters at the peak wave field are shown in figure 9 with the solid curves. Numerical solutions to the full orbit equations of motion from (2.1) are shown in dotted green. These solutions include fast time-scale wave effects, however, as discussed earlier, these effects have little effect on the general character of the resonant dynamics. The parameters of the X2 case are given by a plane wave with $E_y = {1.46\times 10^{-3}} B \mathrm{c}$![]() , $E_x = E_z = 0$
, $E_x = E_z = 0$![]() , ${k}_{\parallel } \mathrm{c} / \omega = 0$
, ${k}_{\parallel } \mathrm{c} / \omega = 0$![]() , $k \mathrm{c} / \omega = 1$
, $k \mathrm{c} / \omega = 1$![]() , in a homogeneous magnetic field with the frequency relation $\omega = 2 \mathrm {e} B / m$
, in a homogeneous magnetic field with the frequency relation $\omega = 2 \mathrm {e} B / m$![]() . This corresponds to the maximum field created by a 1 MW gyrotron with a radius of 2 cm aimed at 2.5 T. The parameters of the X3 case are given by $E_y = {2\times 10^{-3}}B \mathrm{c}$
. This corresponds to the maximum field created by a 1 MW gyrotron with a radius of 2 cm aimed at 2.5 T. The parameters of the X3 case are given by $E_y = {2\times 10^{-3}}B \mathrm{c}$![]() , $E_x = E_z = 0$
, $E_x = E_z = 0$![]() , ${k}_{\parallel } \mathrm{c} / \omega = 0.25$
, ${k}_{\parallel } \mathrm{c} / \omega = 0.25$![]() , ${k}_{\perp } \mathrm{c} / \omega = 0.968$
, ${k}_{\perp } \mathrm{c} / \omega = 0.968$![]() , $\omega = 2.9999 \mathrm {e} B / m$
, $\omega = 2.9999 \mathrm {e} B / m$![]() . This corresponds to the maximum field created by a 1 MW gyrotron with a radius of 2 cm aimed at 1.8 T (or slightly lower than maximum electric field at 1.7 T).
. This corresponds to the maximum field created by a 1 MW gyrotron with a radius of 2 cm aimed at 1.8 T (or slightly lower than maximum electric field at 1.7 T).

Figure 9. Hamiltonian contours in X2 and X3. Centre of resonance in dash dotted, trapped region in dashed. Full solution to (2.1) in green; (a) X2 and (b) X3.
The trapped region can be determined analytically through singular points, see for e.g. Lichtenberg & Lieberman (Reference Lichtenberg and Lieberman2013), Farina & Pozzoli (Reference Farina and Pozzoli1991), Litvak et al. (Reference Litvak, Sergeev, Suvorov, Tokman and Khazanov1993) and references therein. The second harmonic has a trapped region inside
where the energy excursions are given by

and centre by
These analytical trapped regions are shown with dashed lines in figure 9.
The third-harmonic Hamiltonian is not a polynomial in $P_\chi$![]() , so to work out the trapped region we work with $\beta ^2 \equiv 2 \varPhi$
, so to work out the trapped region we work with $\beta ^2 \equiv 2 \varPhi$![]() instead. Centre of resonance is found normally. To find the maximum excursions we expand the Hamiltonian in perpendicular velocity around the centre to avoid solving a fourth degree polynomial. This yields the trapped region as
instead. Centre of resonance is found normally. To find the maximum excursions we expand the Hamiltonian in perpendicular velocity around the centre to avoid solving a fourth degree polynomial. This yields the trapped region as
with

and centre of resonance
where
and $H_{{\rm sep}}$![]() is the value of the Hamiltonian on the separatrix. These regions are shown in dashed lines of figure 9.
is the value of the Hamiltonian on the separatrix. These regions are shown in dashed lines of figure 9.
Figure 10 shows the width of the resonance as a function of $\varDelta _n$![]() , which can be interpreted approximately as the “perpendicular relativistic Lorentz factor” $\gamma _\perp \equiv \sqrt {1+2 \varPhi }$
, which can be interpreted approximately as the “perpendicular relativistic Lorentz factor” $\gamma _\perp \equiv \sqrt {1+2 \varPhi }$![]() yielding perfect resonance. We use an electric field strength corresponding to the maximum field from a 1 MW beam spread over a disc with radius 2 cm. For X2 this is $E_-/\mathrm{c} B = {1.46\times 10^{-3}}$
yielding perfect resonance. We use an electric field strength corresponding to the maximum field from a 1 MW beam spread over a disc with radius 2 cm. For X2 this is $E_-/\mathrm{c} B = {1.46\times 10^{-3}}$![]() (with $B = {2.5}\ {\rm T}$
(with $B = {2.5}\ {\rm T}$![]() ) whereas for X3 it corresponds to $E_-/\mathrm{c} B \approx {2.15\times 10^{-3}}$
) whereas for X3 it corresponds to $E_-/\mathrm{c} B \approx {2.15\times 10^{-3}}$![]() (with $B = {1.7}\ {\rm T}$
(with $B = {1.7}\ {\rm T}$![]() ). A small parallel component of the wave vector is introduced, ${k}_{\parallel } \mathrm{c} / \omega = \sin (10^\circ )$
). A small parallel component of the wave vector is introduced, ${k}_{\parallel } \mathrm{c} / \omega = \sin (10^\circ )$![]() for both X2 and X3 cases, although ${k}_{\parallel }$
for both X2 and X3 cases, although ${k}_{\parallel }$![]() only plays a minor role until it approaches $\omega / \mathrm{c}$
only plays a minor role until it approaches $\omega / \mathrm{c}$![]() (almost full parallel propagation). The $\Delta v_{\parallel }$
(almost full parallel propagation). The $\Delta v_{\parallel }$![]() axis is calculated assuming $\varDelta _n=\xi _n P$
axis is calculated assuming $\varDelta _n=\xi _n P$![]() and is only valid for small $P$
and is only valid for small $P$![]() as $\varDelta _n$
as $\varDelta _n$![]() is also dependent on $P^2$
is also dependent on $P^2$![]() . Figure 10 demonstrates a large resonance width for X2 (this is typical for a broad range of startup-relevant parameters). The resonance region reaches all the way to low initial particle energies and therefore no special conditions are necessary for X2 startup.
. Figure 10 demonstrates a large resonance width for X2 (this is typical for a broad range of startup-relevant parameters). The resonance region reaches all the way to low initial particle energies and therefore no special conditions are necessary for X2 startup.

Figure 10. Resonance regions for resonance condition fulfilled at different perpendicular energies; X2 (a) and X3 (b).
For X3, the resonance width is much more narrow, and to sustain ionisation a careful selection of inhomogeneous ambient magnetic field and beam properties is required.
This is further evident from consideration of the resonance width as a function of power. Figure 11 shows the dependence of the resonance regions ((4.6) and (4.9)) on the beam power assuming W7-X magnetic field strengths and $\varDelta _n = {2\times 10^{-5}}$![]() . The relation to power and electric field strength is taken as
. The relation to power and electric field strength is taken as
Note that, in the case of X2, the trapped region scales differently with power depending on the sign of $({\varDelta _2 - \epsilon _{X2}})/({1 - \xi _2^2})$![]() (4.6). For small powers, the width scales as $P^{1/4}$
(4.6). For small powers, the width scales as $P^{1/4}$![]() , and for higher powers (in relation to $\varDelta _2$
, and for higher powers (in relation to $\varDelta _2$![]() ) it scales as $P^{1/2}$
) it scales as $P^{1/2}$![]() . Due to our choice of low $\varDelta _2$
. Due to our choice of low $\varDelta _2$![]() , only the $P^{1/2}$
, only the $P^{1/2}$![]() is visible in figure 11.
is visible in figure 11.

Figure 11. Resonance regions for different power; X2 (a) and X3 (b).
With the analysis of the general differences between X2 and X3 introduced (based essentially on the homogeneous picture), we proceed to the analysis of our numerical results for the inhomogeneous cases presented in the previous section. We first consider X2 calculations presented in figures 7 and 8. These figures show that a significantly large phase space exhibits very efficient energy gain in the inhomogeneous case, specifically in low $v_{\parallel }$![]() region.
region.
The value of the Hamiltonian is always conserved on particle trajectories, but the shape of the Hamiltonian contours in ($\chi, P_\chi$![]() ) plane evolves with the passage of the particle through higher field strengths. The character of the particle trajectory changes accordingly: a resonant particle becomes nonlinearly trapped in the wave field and will follow the closed contours instead. This occurs when the trapping region reaches the electron phase-space position. As the particle continues toward the weaker wave field the closed contours disappear, leaving the particle with new values of $P_\chi, P_Z$
) plane evolves with the passage of the particle through higher field strengths. The character of the particle trajectory changes accordingly: a resonant particle becomes nonlinearly trapped in the wave field and will follow the closed contours instead. This occurs when the trapping region reaches the electron phase-space position. As the particle continues toward the weaker wave field the closed contours disappear, leaving the particle with new values of $P_\chi, P_Z$![]() . This is demonstrated with a solid line in figure 1, where a sequence of spikes on the energy curve corresponds to quasi-periodic motion of the particle around the resonance.
. This is demonstrated with a solid line in figure 1, where a sequence of spikes on the energy curve corresponds to quasi-periodic motion of the particle around the resonance.
Equation (4.1) has only two solutions for $\varPhi$![]() outside the beam for fixed $H, P, \varDelta _n, \xi _n$
outside the beam for fixed $H, P, \varDelta _n, \xi _n$![]() . If these quantities are conserved before and after the interaction, as they are for the case of constant field and adiabatic interaction (see for e.g. Farina Reference Farina2018), then the jump in orthogonal energy $\varPhi$
. If these quantities are conserved before and after the interaction, as they are for the case of constant field and adiabatic interaction (see for e.g. Farina Reference Farina2018), then the jump in orthogonal energy $\varPhi$![]() is two times the distance to the line $\varPhi = \varDelta _n/(1-\xi _n^2)$
is two times the distance to the line $\varPhi = \varDelta _n/(1-\xi _n^2)$![]() . The $B$
. The $B$![]() field inhomogeneity changes $\varDelta _n$
field inhomogeneity changes $\varDelta _n$![]() and $P$
and $P$![]() during the interaction so that the interaction is a complicated four-dimensional motion.
during the interaction so that the interaction is a complicated four-dimensional motion.
If $B$![]() increases as the electron transverses the magnetic field line, the resonance centre $\varDelta _n$
increases as the electron transverses the magnetic field line, the resonance centre $\varDelta _n$![]() will move upwards and ultimately allow large energy gain. This is easiest observed in a plane-wave interaction. In this case, adiabacity forces a new constant of the motion $\oint P_\chi \,{\rm d}\chi$
will move upwards and ultimately allow large energy gain. This is easiest observed in a plane-wave interaction. In this case, adiabacity forces a new constant of the motion $\oint P_\chi \,{\rm d}\chi$![]() . We show constant Hamiltonian intersected with this constant in $z, P_\chi, \chi$
. We show constant Hamiltonian intersected with this constant in $z, P_\chi, \chi$![]() space in figure 12. Here, we clearly see the resonance centre moving upwards in energy, and the particle trajectory follows. Movement of the resonance centre plays a favourable role, regardless of adiabatic interaction or not.
space in figure 12. Here, we clearly see the resonance centre moving upwards in energy, and the particle trajectory follows. Movement of the resonance centre plays a favourable role, regardless of adiabatic interaction or not.

Figure 12. An X2 toy example of the adiabatic case, inhomogeneous magnetic field, plane wave. Hamiltonian surface (red) and particle trajectory (blue).
If $B$![]() decreases instead, the resonance centre $\varDelta _n$
decreases instead, the resonance centre $\varDelta _n$![]() will come from above, and allow for large excursions and energy gains. These are larger than the homogeneous case because there typically exists a more optimal $\varDelta _n$
will come from above, and allow for large excursions and energy gains. These are larger than the homogeneous case because there typically exists a more optimal $\varDelta _n$![]() along the path than in the homogeneous case.
along the path than in the homogeneous case.
The adiabatic interaction is only valid for very low parallel velocities. Seol et al. (Reference Seol, Hegna and Callen2009) calculate the frequency of revolving the nonlinear trapped region. Dividing this frequency with the beam travel time (the second fastest time scale) we find

where $k_B T_\parallel$![]() is the parallel kinetic energy and $P$
is the parallel kinetic energy and $P$![]() the beam power. The ratio is independent of beam width, and large only for very very low parallel velocities.
the beam power. The ratio is independent of beam width, and large only for very very low parallel velocities.
It is the beam structure that breaks the adiabatic condition. The beam shaping creates a finite ${k}_{\parallel }$![]() component of the wave vector, which breaks the conservation of $P_Z$
component of the wave vector, which breaks the conservation of $P_Z$![]() even in the case of ${k}_{\parallel } = 0$
even in the case of ${k}_{\parallel } = 0$![]() in the wave phase. Generally, a small kick in $P_Z$
in the wave phase. Generally, a small kick in $P_Z$![]() is allowed due to shaping of $\epsilon _{X2}$
is allowed due to shaping of $\epsilon _{X2}$![]() in $z$
in $z$![]() . This allows for a larger energy gain compared with the adiabatic case, even for a very small kick $\delta P$
. This allows for a larger energy gain compared with the adiabatic case, even for a very small kick $\delta P$![]() in $P=P_Z/mc$
in $P=P_Z/mc$![]() . This can be understood by perturbing the Hamiltonian with a small kick $\delta P$
. This can be understood by perturbing the Hamiltonian with a small kick $\delta P$![]() and equating it with a kick $\delta P_\chi$
and equating it with a kick $\delta P_\chi$![]() . We find the energy change by solving
. We find the energy change by solving
which results in (for relativistic $P_Z$![]() only inside $\varDelta _n$
only inside $\varDelta _n$![]() )
)

due to $P_Z$![]() no longer being conserved. This change in $P_Z, P_\chi$
no longer being conserved. This change in $P_Z, P_\chi$![]() is the difference between figure 7 and an adiabatic interaction.
is the difference between figure 7 and an adiabatic interaction.
The X3 interaction is much weaker than the X2, so that several excursions for single beam pass is only possible for electrons with very low transverse energy (meV). As the consequence, if the resonance centre moves from above, the particles do not typically complete a single revolution around the resonance centre before the electron is outside the trapped region. Therefore, we see the larger asymmetry with respect to $v_{\parallel }$![]() in figures 2 and 4 to 6 than in figure 7 and 8.
in figures 2 and 4 to 6 than in figure 7 and 8.
In this type of interaction, the particle motion in the phase space coincides with the trapped region evolution such that the phase $\chi$![]() is approximately constant. This kind of interaction is very efficient. This ‘stationary phase’ regime of the interaction is demonstrated with the dotted red curve in figure 1. It should not be confused with the stationary phase approximation of the liner wave–particle interaction, since several nonlinear effects cancel to allow for a long interaction time in our case.
is approximately constant. This kind of interaction is very efficient. This ‘stationary phase’ regime of the interaction is demonstrated with the dotted red curve in figure 1. It should not be confused with the stationary phase approximation of the liner wave–particle interaction, since several nonlinear effects cancel to allow for a long interaction time in our case.
The main reason for the enhanced energy gain in X3 is extended period of the stationary phase, where $B$![]() and $\gamma$
and $\gamma$![]() changes in conjunction to extend the resonance interaction. The particle is then allowed to travel ‘up’ in figure 10, because $\varDelta _3$
changes in conjunction to extend the resonance interaction. The particle is then allowed to travel ‘up’ in figure 10, because $\varDelta _3$![]() changes accordingly. Long stationary phase is characterised by $\dot {\psi } = 0$
changes accordingly. Long stationary phase is characterised by $\dot {\psi } = 0$![]() and $\ddot {\psi } = 0$
and $\ddot {\psi } = 0$![]() which, for ${k}_{\parallel } = 0$
which, for ${k}_{\parallel } = 0$![]() , is equivalent to
, is equivalent to
Approximating $\dot {\gamma }\approx \dot {\varPhi } \sim \epsilon _{X3} \varPhi ^{3/2} \sim \epsilon _{X3}({v_{\perp }^3}/{\mathrm{c}^3})$![]() we find
we find
so that, for the longer magnetic field length scales, lower energies satisfy the stationary phase condition. This scaling approximately yields the shape of the contours of figures 2 and 4. For example, the 13.6 eV line in figure 2 that starts at 0 energy and goes to 90 eV perpendicular energy at 0.04 eV parallel energy follows the scaling (4.18).
Numerical solution to (3.7) shows that the nonlinear energy gain scales approximately as a square with the maximum of $\epsilon _{X3}$![]() . This quadratic scaling is shown in figure 13. Here, the average energy gain is shown as function of maximum $\epsilon _{X3}$
. This quadratic scaling is shown in figure 13. Here, the average energy gain is shown as function of maximum $\epsilon _{X3}$![]() . The rest of the parameters match those of figure 2, except $\alpha ={\rm \pi} /10$
. The rest of the parameters match those of figure 2, except $\alpha ={\rm \pi} /10$![]() . This scaling sets the scaling of the average energy gain to be linear in beam power for fixed beam width and is expected from linear wave absorption theory.
. This scaling sets the scaling of the average energy gain to be linear in beam power for fixed beam width and is expected from linear wave absorption theory.

Figure 13. Average energy gain as function of interaction parameter $\epsilon _{X3}$![]() (3.5).
(3.5).
5. Optimal $B$ field inhomogeneity
field inhomogeneity
The discussion in the previous section hints at the existence of an optimal $B$![]() field inhomogeneity length scale for every characteristic parallel velocity and therefore every plasma temperature. The inhomogeneity length scale dependence of the minimal initial energy required for a significant gain is investigated in figure 14. Orange, blue and green curves correspond to gains of 5, 13.6 and 25 eV, respectively. These calculations demonstrate that, when the inhomogeneity length scale varies, electrons with as low energy as 2–3 eV can be accelerated to above 13.6 eV by a 1 MW beam in W7-X-like conditions. We also observe that a smaller magnetic field slope is favourable for lower initial energies, in agreement with the predictions of (4.18).
field inhomogeneity length scale for every characteristic parallel velocity and therefore every plasma temperature. The inhomogeneity length scale dependence of the minimal initial energy required for a significant gain is investigated in figure 14. Orange, blue and green curves correspond to gains of 5, 13.6 and 25 eV, respectively. These calculations demonstrate that, when the inhomogeneity length scale varies, electrons with as low energy as 2–3 eV can be accelerated to above 13.6 eV by a 1 MW beam in W7-X-like conditions. We also observe that a smaller magnetic field slope is favourable for lower initial energies, in agreement with the predictions of (4.18).

Figure 14. Minimal initial energy of an electron gaining 5 eV (dashed curve), 13.6 eV (solid curve) and 25 eV (dash–dotted curve) as a function of $B$![]() gradient.
gradient.
In figure 14 we have set $B_0$![]() , so that resonance at $z=0$
, so that resonance at $z=0$![]() is at 2.58 eV. This then creates a maximum energy gain of around 5 eV at constant field. Moving the centre of resonance at $z=0$
is at 2.58 eV. This then creates a maximum energy gain of around 5 eV at constant field. Moving the centre of resonance at $z=0$![]() to arbitrary energy then yields an absolute maximum energy gain of approximately the width of resonance, given approximately by the separatrix width, see figure 10. Thus, we could gain 13.6 eV at no magnetic field gradient. The cost is that the first particle that gains a substantial amount of energy must have an initial energy of approximately 10 eV, see figure 3. Therefore, resonance at around 2 eV is chosen as this is a typical low energy during the ionisation avalanche.
to arbitrary energy then yields an absolute maximum energy gain of approximately the width of resonance, given approximately by the separatrix width, see figure 10. Thus, we could gain 13.6 eV at no magnetic field gradient. The cost is that the first particle that gains a substantial amount of energy must have an initial energy of approximately 10 eV, see figure 3. Therefore, resonance at around 2 eV is chosen as this is a typical low energy during the ionisation avalanche.
Figure 15 shows the effect of the inhomogeneity on the average energy gain from a single beam pass for a Maxwellian population of incoming particles. The varied parameters are the $B$![]() field gradient length scale and the plasma temperature. Because the beam typically propagates across field lines with different magnetic field strengths, for each magnetic field gradient we maximise over different magnetic field strengths at $z=0$
field gradient length scale and the plasma temperature. Because the beam typically propagates across field lines with different magnetic field strengths, for each magnetic field gradient we maximise over different magnetic field strengths at $z=0$![]() .
.

Figure 15. Average energy gained in meV by electrons passing the beam once at different magnetic field inhomogeneities. The average energy gain was maximised over magnetic field strengths near cold resonance, motivated by that the beam cuts different field lines with slightly different field strengths at beam centre.
The contours show average energy gain in meV. Note that the maximum energy gain (reaching 100 eV) is much larger than the average, since only the narrow region of the phase space experiences the nonlinear enhancement from the inhomogeneity.
The gradients chosen are those approximately available to W7-X with a 10 % mirror ratio. Note that the maximum energy gained is not fully correlated with the average energy gain. Increasing the inhomogeneity length scale also forces particles to bounce, particularly with low $v_{\parallel }$![]() , which had the strongest normal interaction at no field gradient. Although the inhomogeneity length scaled increased the maximum energy gained by a factor of 4 or more, the average energy gained increase is lower, partly because the phase-space area that gains energy is lower. We observe an optimum at magnetic field-scale gradients of the order of ${1}\ {\rm km}^{-1}$
, which had the strongest normal interaction at no field gradient. Although the inhomogeneity length scaled increased the maximum energy gained by a factor of 4 or more, the average energy gained increase is lower, partly because the phase-space area that gains energy is lower. We observe an optimum at magnetic field-scale gradients of the order of ${1}\ {\rm km}^{-1}$![]() to $3\ {\rm km}^{-1}$
to $3\ {\rm km}^{-1}$![]() for both average energy gain and lowest minimal energy required for 13.6 eV energy gain.
for both average energy gain and lowest minimal energy required for 13.6 eV energy gain.
6. Conclusion
In this paper, we have considered electron orbits in W7-X-like background fields with microwave heating in the X2 and X3 startup scenarios. The main effect of the background magnetic field inhomogeneity is to extend the interaction, resulting in a significant increase of the maximum energy gain during the interaction. A large energy gain is made possible for lower initial energies.
In the adiabatic interaction regime, the particles would be trapped in the resonance, which follows the strength of the inhomogeneous $B$![]() -field. Unfortunately, adiabatic interaction does not apply to the majority of orbits in X3, which complicates the analysis. Yet, the magnetic field inhomogeneity can be chosen favourably to increase both the overall energy gain and to extend the phase space of the efficient interaction. We find a 4-fold increase of the maximum energy gain of a few eV electrons with the introduction of a small inhomogeneity. To achieve similar increase in energy gain in homogeneous fields a 10 times higher beam power is required. Moreover, we find that the magnetic field gradient allows electrons with 2 eV to gain above 13.6 eV in W7-X-like conditions.
-field. Unfortunately, adiabatic interaction does not apply to the majority of orbits in X3, which complicates the analysis. Yet, the magnetic field inhomogeneity can be chosen favourably to increase both the overall energy gain and to extend the phase space of the efficient interaction. We find a 4-fold increase of the maximum energy gain of a few eV electrons with the introduction of a small inhomogeneity. To achieve similar increase in energy gain in homogeneous fields a 10 times higher beam power is required. Moreover, we find that the magnetic field gradient allows electrons with 2 eV to gain above 13.6 eV in W7-X-like conditions.
A scan in magnetic field gradient shows that the average energy gain can be increased by around a factor of 1.5–3 for electron temperatures in the eV range, when inhomogeneity is taken into account. The optimal beam inhomogeneity is found to be $1$![]() to $3\ {\rm km}^{-1}$
to $3\ {\rm km}^{-1}$![]() . However, the single third-harmonic $X$
. However, the single third-harmonic $X$![]() mode with a 1 MW wave is not sufficient to achieve breakdown in W7-X-like conditions – the mean energy gain remains much smaller than in the analogous X2 case.
mode with a 1 MW wave is not sufficient to achieve breakdown in W7-X-like conditions – the mean energy gain remains much smaller than in the analogous X2 case.
When two 1 MW beams are present, their resonance regions can be combined. The beams’ focal points are placed next to each other. In this case, the maximum energy gain approaches the energy gain observed in a single beam X2 case (up to 200 eV compared with ${\sim }1$![]() keV), which is known to produce a startup in W7-X. However, the phase-space area for efficient interaction is still found to be much smaller than in an analogous X2 case. This area is limited by the parallel energy, and has a width of around 0.1 eV, whereas the corresponding width in X2 is of the order of 300 eV. The energy increase for low energy electrons is still stronger than using a single beam with twice the power.
keV), which is known to produce a startup in W7-X. However, the phase-space area for efficient interaction is still found to be much smaller than in an analogous X2 case. This area is limited by the parallel energy, and has a width of around 0.1 eV, whereas the corresponding width in X2 is of the order of 300 eV. The energy increase for low energy electrons is still stronger than using a single beam with twice the power.
We conclude that, while a B field inhomogeneity plays an important role in wave–particle interaction in startup conditions, yielding a noticeable increase of the electron energy gain, inhomogeneity alone is unlikely to achieve X3 startup in W7-X-like conditions. A careful design of a multi-wave set-up is shown to improve the situation considerably. A further work study is required to find an optimal scheme. Furthermore, a kinetic modelling of the ionisation process is needed for a predictive study of X3 and X2 startups.
Acknowledgements
The authors would like to acknowledge helpful discussions with B.N. Breizman and P. Helander.
Editor Peter Catto thanks the referees for their advice in evaluating this article.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200 – EUROfusion). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Ordering
The ordering of ambient fields is performed using the same scheme as in Cary & Brizard (Reference Cary and Brizard2009). Denoting by a subscript $w$![]() the wave fields, we add the wave fields into the ordering scheme in table 1. The ordering is in the Lorentz–transformed frame moving at the $\boldsymbol {E} \boldsymbol {\times } \boldsymbol {B}$
the wave fields, we add the wave fields into the ordering scheme in table 1. The ordering is in the Lorentz–transformed frame moving at the $\boldsymbol {E} \boldsymbol {\times } \boldsymbol {B}$![]() drift velocity $\boldsymbol {v}_{E}$
drift velocity $\boldsymbol {v}_{E}$![]() . Therefore, there is no perpendicular electric field in our frame.
. Therefore, there is no perpendicular electric field in our frame.
Table 1. Ordering scheme for the Guiding-centre Lagrangian with wave field. The parameters $L$![]() and $\tau$
and $\tau$![]() give the length scale and time scale at which fields change. Only exception is that the time scale of the phase of the wave is $\omega$
give the length scale and time scale at which fields change. Only exception is that the time scale of the phase of the wave is $\omega$![]() , and the length scale of its wavelength is $1/k$
, and the length scale of its wavelength is $1/k$![]() . The changes of the wavelength in length and time are of order $L$
. The changes of the wavelength in length and time are of order $L$![]() and $\tau$
and $\tau$![]() , respectively.
, respectively.

Appendix B. Formal removal of non-resonant terms for further simplification
Consider a Lagrangian which yields equations of motion such that its solution has a quasi-periodic motion in $\boldsymbol {r}$![]() with frequency $\omega / 2 {\rm \pi}$
with frequency $\omega / 2 {\rm \pi}$![]() . If we can transform to coordinates $q$
. If we can transform to coordinates $q$![]() such that they have the property
such that they have the property
then a Fourier expansion of the Lagrangian yields
where $\tau$![]() is to be seen as the slow time variation of $L_n$
is to be seen as the slow time variation of $L_n$![]() compared with $\omega$
compared with $\omega$![]() , and must be slow for the time averaging procedure to be valid. In our case, this is done by the ordering scheme and a transformation to the slowly varying guiding-centre coordinates. For $n\neq 0$
, and must be slow for the time averaging procedure to be valid. In our case, this is done by the ordering scheme and a transformation to the slowly varying guiding-centre coordinates. For $n\neq 0$![]() we have
we have

The full time derivative can always be removed without changing the equations of motion. The sum is of order $\epsilon$![]() so, to order $1$
so, to order $1$![]() , the Lagrangian is only $L_0$
, the Lagrangian is only $L_0$![]() . This argument can be used on the non-resonant terms instead of an time average. Because a time average also results in $L_0$
. This argument can be used on the non-resonant terms instead of an time average. Because a time average also results in $L_0$![]() , there is no formal difference between the two. In a stricter setting, where $q=q(\epsilon t)$
, there is no formal difference between the two. In a stricter setting, where $q=q(\epsilon t)$![]() and $|{\delta ^m L_n}| < M$
and $|{\delta ^m L_n}| < M$![]() , the time average becomes exact through repetitively expressing terms as exact time derivatives. With $\delta ^m L_n$
, the time average becomes exact through repetitively expressing terms as exact time derivatives. With $\delta ^m L_n$![]() , we mean any combination of partial derivatives to a total of $m$
, we mean any combination of partial derivatives to a total of $m$![]() th order (with respect to $q, \dot {q}, \tau$
th order (with respect to $q, \dot {q}, \tau$![]() ), and $M$
), and $M$![]() is an arbitrary fixed constant.
is an arbitrary fixed constant.
Consideration of arbitrary field strengths is only possible if we solve the motion perturbed by the wave (on fast time scales) to order unity in $E_w / (c B)$![]() . We solve this system in Appendix C, and show that it is sufficient in our case to use the gyro-motion as approximation of our fast time-scale motion.
. We solve this system in Appendix C, and show that it is sufficient in our case to use the gyro-motion as approximation of our fast time-scale motion.
Convergence to the time-averaged equations of motion is found as

because $q, \dot {q}, \tau$![]() are slowly varying. Analogously, we obtain
are slowly varying. Analogously, we obtain

because $q, \dot {q}, \tau$![]() are slowly varying.
are slowly varying.
Appendix C. Particle motion perturbed by the wave
The guiding-centre theory builds on knowing the solution to the fast time-scale equation of motion and performing the time average in Appendix B. We could manipulate the Lagrangian in the same manner, but using the fast time-scale solution to the wave–particle interaction in a constant magnetic field instead. This would yield the interaction between the wave and the perturbed orbit that the wave creates.
We numerically solved the system of equation in homogeneous magnetic field for a plane wave to find when the electric field yields observable deviations of the particle orbits from the Hamiltonian contours. These numerical checks show that the interaction between the wave and the perturbed orbit from the wave is important for the X2 mode when the fields are around $E_\perp / (c B) \approx 0.05$![]() and above. We will solve the relativistic equations of motion for electrons, that is $\boldsymbol {k} \boldsymbol {\cdot } \boldsymbol {v} \ll \omega$
and above. We will solve the relativistic equations of motion for electrons, that is $\boldsymbol {k} \boldsymbol {\cdot } \boldsymbol {v} \ll \omega$![]() , to verify this numerical estimate and obtain an estimate for X3. We assume that ${{\rm d}\gamma }/{{\rm d}t} /(\gamma \omega ) \approx 0$
, to verify this numerical estimate and obtain an estimate for X3. We assume that ${{\rm d}\gamma }/{{\rm d}t} /(\gamma \omega ) \approx 0$![]() for the relativistic Lorentz factor $\gamma$
for the relativistic Lorentz factor $\gamma$![]() .
.
Introduce the notation
In this notation
The Newtonian equation of motion in a constant magnetic field with a plane wave and $\dot {\gamma }\approx 0$![]() reads
reads
We neglect the wave magnetic term because $v k \ll \omega$![]() , and not because the magnetic field of the wave is small. The wave electric field is $\boldsymbol {E} |{k\omega }\rangle _{\phi }$
, and not because the magnetic field of the wave is small. The wave electric field is $\boldsymbol {E} |{k\omega }\rangle _{\phi }$![]() and the wave magnetic field is $({\boldsymbol {k} \boldsymbol {\times } \boldsymbol {E}}/{\omega }) |{k\omega }\rangle _{\phi }$
and the wave magnetic field is $({\boldsymbol {k} \boldsymbol {\times } \boldsymbol {E}}/{\omega }) |{k\omega }\rangle _{\phi }$![]() . Shifting the velocity to
. Shifting the velocity to
removes the parallel electric field, that is
where $\boldsymbol {E}_\parallel = \boldsymbol {E} \boldsymbol {\cdot } \hat {z}\hat {z}$![]() and $\boldsymbol {E}_\perp = \boldsymbol {E} - \boldsymbol {E}_\parallel$
and $\boldsymbol {E}_\perp = \boldsymbol {E} - \boldsymbol {E}_\parallel$![]() .
.
The solution to this new equation in $\boldsymbol {w}$![]() is to introduce drift velocity $\boldsymbol {u}_{D0}$
is to introduce drift velocity $\boldsymbol {u}_{D0}$![]() so that ${{\rm d}\boldsymbol {u}_{Dn}}/{{\rm d}t}$
so that ${{\rm d}\boldsymbol {u}_{Dn}}/{{\rm d}t}$![]() cancels with the electric field term. Taking
cancels with the electric field term. Taking
accomplishes just this. Inserting into the equation of motion yields
where we assumed $|{\boldsymbol {k} \boldsymbol {\cdot } \boldsymbol {v}}| \ll \omega$![]() . Here, $\varOmega = -q B_0 / m \gamma$
. Here, $\varOmega = -q B_0 / m \gamma$![]() . This is now the same equation as before but with the new field $({\varOmega }/{\omega })\boldsymbol {E} \boldsymbol {\times } \hat {z} |{k \omega }\rangle _{\phi -{\rm \pi} /2}$
. This is now the same equation as before but with the new field $({\varOmega }/{\omega })\boldsymbol {E} \boldsymbol {\times } \hat {z} |{k \omega }\rangle _{\phi -{\rm \pi} /2}$![]() . The idea is to shift the drift velocity compared with the wave with phase $-{\rm \pi} /2$
. The idea is to shift the drift velocity compared with the wave with phase $-{\rm \pi} /2$![]() and that the new field will be multiplied with $\varOmega /\omega$
and that the new field will be multiplied with $\varOmega /\omega$![]() and crossed with $\hat {z}$
and crossed with $\hat {z}$![]() . Therefore, we introduce the $n$
. Therefore, we introduce the $n$![]() th drift velocities, together with $\boldsymbol {u} _n$
th drift velocities, together with $\boldsymbol {u} _n$![]() as
as
so that

The cross-product $\boldsymbol {E}_\perp (\boldsymbol {\times } \hat {z})^{n}$![]() is to be evaluated as $(\ldots (\boldsymbol {E}_\perp \boldsymbol {\times } \hat {z})\ldots )\boldsymbol {\times } \hat {z}$
is to be evaluated as $(\ldots (\boldsymbol {E}_\perp \boldsymbol {\times } \hat {z})\ldots )\boldsymbol {\times } \hat {z}$![]() . If $|{\varOmega }| < |{\omega }|$
. If $|{\varOmega }| < |{\omega }|$![]() , the sum is convergent and the last equation reads
, the sum is convergent and the last equation reads
This is just the gyro-motion, and thus gives the definition of the magnetic moment. If $|{\varOmega }| > |{\omega }|$![]() , it is instead possible to introduce the drift velocities
, it is instead possible to introduce the drift velocities
so that the magnetic Lorentz force cancels with the electric field. One still reaches the conclusion in (C8b), (C9) and (C10), but now for $|{\varOmega }| > |{\omega }|$![]() .
.
The sum in (C9) can be evaluated as a geometric sum by using $|{k\omega }\rangle _{\phi \pm {\rm \pi}} = - |{k\omega }\rangle _{\phi }$![]() and $\boldsymbol {E}_\perp (\boldsymbol {\times } \hat {z})^{2} = -\boldsymbol {E}_\perp$
and $\boldsymbol {E}_\perp (\boldsymbol {\times } \hat {z})^{2} = -\boldsymbol {E}_\perp$![]() . This yields
. This yields

This solution is to be added to the guiding-centre motion to be able to perform the time average for arbitrary field strengths. Note that we then also need to solve the position equation. This is easily done if $kv \ll \omega$![]() , the position change is then the velocity divided by $-\omega$
, the position change is then the velocity divided by $-\omega$![]() and phase of $|{k \omega }\rangle$
and phase of $|{k \omega }\rangle$![]() shifted by $-{\rm \pi} /2$
shifted by $-{\rm \pi} /2$![]() . This is realised by looking at (C2).
. This is realised by looking at (C2).
Now, interaction between the perturbed orbit and the wave field is important when

We approximate this condition with

Equation (C10) is solved in terms of the magnetic moment, which yields

The perturbed orbit is thus unimportant when

that is, the perpendicular energy stored in gyro-motion is much greater than perpendicular kinetic energy stored in instantaneous $\boldsymbol {E} \boldsymbol {\times } \boldsymbol {B}$![]() drifting. For W7-X parameters the right-hand side is $10^{-6} m c^2 \sim {0.5}\ {\rm eV}$
drifting. For W7-X parameters the right-hand side is $10^{-6} m c^2 \sim {0.5}\ {\rm eV}$![]() , but the resonance area is much larger than the contours of 0.5 eV difference. Thus the wave perturbation to the orbit can be ignored.
, but the resonance area is much larger than the contours of 0.5 eV difference. Thus the wave perturbation to the orbit can be ignored.
Moreover, the first term in (C12) is ${\rm \pi} /2$![]() out of phase with the electric field and the second term orthogonal to it. This means that the time average of the power transferred $q \sum \boldsymbol {u}_{Dn} \boldsymbol {\cdot } \boldsymbol {E} \cos (\varphi (\boldsymbol {r}) - \omega t)$
out of phase with the electric field and the second term orthogonal to it. This means that the time average of the power transferred $q \sum \boldsymbol {u}_{Dn} \boldsymbol {\cdot } \boldsymbol {E} \cos (\varphi (\boldsymbol {r}) - \omega t)$![]() yields 0 if the wave phase experienced by the particle has an equal distribution of positive and negative interferences. The same assumption yields a zero net drift in $\boldsymbol {r}$
yields 0 if the wave phase experienced by the particle has an equal distribution of positive and negative interferences. The same assumption yields a zero net drift in $\boldsymbol {r}$![]() .
.
Note that no conclusion is to be drawn for $\omega \sim \varOmega$![]() because the geometric series is not converging for $|{\omega }| = |{\varOmega }|$
because the geometric series is not converging for $|{\omega }| = |{\varOmega }|$![]() . From a physics perspective, the perpendicular energy storing argument should be sufficient for motivation of ignoring this term in the fast solution. However, we cannot supply the correct coordinate transformation such that we achieve (C10).
. From a physics perspective, the perpendicular energy storing argument should be sufficient for motivation of ignoring this term in the fast solution. However, we cannot supply the correct coordinate transformation such that we achieve (C10).