No CrossRef data available.
Article contents
A Note on a Separation of Equations of Variation of the Elliptic Restricted Three-Body Problem Into Hill's Equations
Published online by Cambridge University Press: 14 August 2015
Abstract
The equations of variation of the three-dimensional elliptic restricted three-body problem corresponding to the equilibrium solutions (the libration points) have been separated into three Hill's equations. As regards the equation ‘corresponding’ to the motion of the infinitesemal body in the z-axis (perpendicular to the plane of motion of the primaries), the matter is trivial one since the initial equation - as known - reads d2z/dv2 + (Ai + e cosv)/(l + e cosv) = 0 (e, 0<e< 1, and v are the eccentricity and the true anomaly of the relative motion of the primaries) with Ai > 1 for the straight-line libration points Li (i= 1, 2, 3) and Ai=l for the triangular libration points Li, i=4, 5. As concerns the remaining two components, x and y, of the motion of the infinitesimal body (x, y and z are the Nechvíle's variables), in the case of the straight-line libration points, L1, L2 and L3, the corresponding equations of variation have been transformed and separated into two further - mutually independent - Hill's equations without any limitation. In the case of the equilateral triangle libration points, L4 and L5, the separation has been found only when the eccentricity e and the dimensionless mass μ, 0<μ≦1/2 of the ‘minor’ primary satisfy the additional conditions:
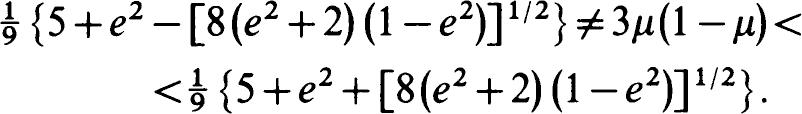 Let us write the latter two Hill's equations obtained in the form
Let us write the latter two Hill's equations obtained in the form
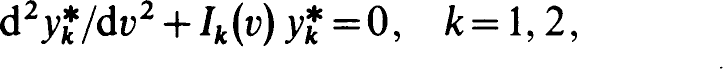 where Ik, k= 1, 2, are 2π-periodic even functions of the true anomaly v. The functions Ik, k = 1, 2, are real functions in the case of the straight-line libration points, L1, L2 and L3, without a limitation but in the case of the triangular libration points, L4 and L5, they are real only if
where Ik, k= 1, 2, are 2π-periodic even functions of the true anomaly v. The functions Ik, k = 1, 2, are real functions in the case of the straight-line libration points, L1, L2 and L3, without a limitation but in the case of the triangular libration points, L4 and L5, they are real only if
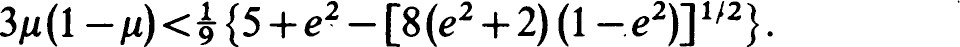 Provided
Provided
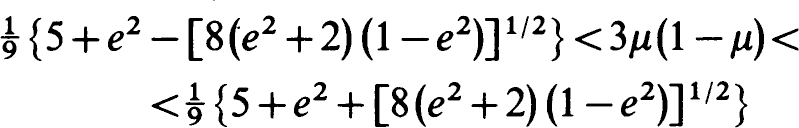 the functions Ik, k= 1, 2, are complex-valued functions of the real variable v.
the functions Ik, k= 1, 2, are complex-valued functions of the real variable v.
- Type
- Research Article
- Information
- Copyright
- Copyright © Reidel 1974




