1. Introduction
The appearance of massive black holes is one of the most remarkable events in the first billion years. While standard stellar evolution models predict the formation of black holes with masses comparable to the Sun up to hundreds of solar masses, there is currently no general consensus about supermassive black holes. Observational programmes have led to detection of supermassive black holes with billions of solar masses up to z ≃ 7.5 (Fan et al. Reference Fan, Narayanan, Lupton, Strauss and Knapp2001, Reference Fan, Strauss, Richards and Hennawi2006; Mortlock et al. Reference Mortlock2011; Wu et al. Reference Wu2015; Bañados et al. Reference Bañados2017). Theoretical analyses based on gas accretion on primordial stars have failed in reproducing such large masses in such a short lapse of time: even large metal-free stars of 10–1 000 solar masses are not able to leave remnant black-hole seeds having more than 400 solar masses (Hirano et al. Reference Hirano, Hosokawa, Yoshida, Umeda, Omukai, Chiaki and Yorke2014). Massive black-hole seeds of masses around 104–106 M⊙ have been conjectured (Rees Reference Rees1984; Loeb & Rasio Reference Loeb and Rasio1994) as possible seeds of supermassive black holes. Despite never being observed nor yet fully understood (de Vita et al. Reference de Vita, Trenti, Bianchini, Askar, Giersz and van de Ven2017), they could be good candidates to grow up to the desired masses in less than a billion years.
An attracting scenario for the formation of massive black holes is the so-called ‘direct-collapse’, a rapid collapse of the gas residing in primordial haloes (Bromm & Loeb Reference Bromm and Loeb2003; Begelman, Volonteri, & Rees Reference Begelman, Volonteri and Rees2006; Mayer et al. Reference Mayer, Kazantzidis, Escala and Callegari2010; Latif et al. Reference Latif, Schleicher, Schmidt and Niemeyer2013 etc.). Albeit direct-collapse black holes (DCBHs) could explain the quasar population at z > 6, the conditions to form them are very peculiar. Indeed, they are expected to assemble in atomic cooling haloes hosting inflowing pristine material (i.e. with no heavy elements nor dust), in the presence of a strong H2 dissociating UV field in the Lyman–Werner (LW) band, [11.2, 13.6] eV (e.g. Omukai, Schneider, & Haiman Reference Omukai, Schneider and Haiman2008). Under these hypotheses, cooling below 104 K, normally driven by H2 molecules or metals Maio et al. Reference Maio, Dolag, Ciardi and Tornatore2007, Reference Maio, Dotti, Petkova, Perego and Volonteri2013b, is not possible, hence fragmentation is completely inhibited and the halo gas content could collapse into a DCBH by gravitational instability. The currently established critical level of dissociating LW radiation to be effective ranges between intensities (in units of 10−21 erg/s/cm2/Hz/sr, hereafter J 21) J LW ~ J 21 and ~ 1 000J 21 (Shang, Bryan, & Haiman Reference Shang, Bryan and Haiman2010; Wolcott-Green, Haiman, & Bryan Reference Wolcott-Green, Haiman and Bryan2011; Sugimura, Omukai, & Inoue Reference Sugimura, Omukai and Inoue2014; Johnson & Dijkstra Reference Johnson and Dijkstra2017).
Lately, Habouzit et al. (Reference Habouzit, Volonteri, Latif, Dubois and Peirani2016b) have shown that fiducial values around 30–300J 21 are required to obtain a number of DCBHs compatible with observations of supermassive black holes. The amount of photons emitted in the LW band depends strongly on the adopted spectral properties of primordial sources (Sugimura et al. Reference Sugimura, Omukai and Inoue2014), as well as on H2 photo-dissociation and H− photo-detachment rates (Agarwal & Khochfar Reference Agarwal and Khochfar2015; Wolcott-Green, Haiman, & Bryan Reference Wolcott-Green, Haiman and Bryan2017).
While values of the order of J 21 should be sufficient to prevent primordial metal-free runaway cooling (Yoshida et al. Reference Yoshida, Abel, Hernquist and Sugiyama2003; Valiante et al. Reference Valiante, Agarwal, Habouzit and Pezzulli2017), critical intensities for DCBH formation are still controversial. In practice, the establishment of an LW background has the net effect of delaying gas collapse and the epoch of DCBH formation (Machacek, Bryan, & Abel Reference Machacek, Bryan and Abel2001; O’Shea & Norman Reference O’shea and Norman2008). However, the role of additional local radiation has not been fully assessed, yet, despite an intense burst of LW photons seems required to completely suppress primordial star formation in nearby galaxies.
The implications of molecular self-shielding are still under debate (see Gnedin Draine 2014, 2016; Hartwig et al. Reference Hartwig, Glover, Klessen, Latif and Volonteri2015, for recent updates), because it is not clear if gas self-shielding can significantly preserve molecules formed in pristine environments and limit DCBH formation.
The presence of an early population of cosmic rays could provide enough free electrons to promote the formation of molecular hydrogen (Jasche, Ciardi, & Enßlin Reference Jasche, Ciardi and Enßlin2007; Leite et al. Reference Leite, Evoli, D’Angelo, Ciardi, Sigl and Ferrara2017) and hence inhibit the birth of DCBHs.
Similarly, the emission of UV and X-ray photons should enhance H2 formation and increase the amount of LW radiation required to form DCBHs (Inayoshi & Tanaka Reference Inayoshi and Tanaka2015; Inayoshi et al. Reference Inayoshi, Kashiyama, Visbal and Haiman2016; Latif et al. Reference Latif, Bovino, Grassi, Schleicher and Spaans2015).
The statistical occurrence of DCBHs is still obscure: different studies have proposed number of densities varying from 1 DCBH per 10 Mpc3 comoving volume to 1 DCBH per Gpc3 volume (Habouzit et al. Reference Habouzit, Volonteri, Latif, Dubois and Peirani2016b). Since DCBHs are accreting objects, it is likely that they will have a hot corona (Pacucci et al. Reference Pacucci, Pallottini, Ferrara and Gallerani2017; Valiante et al. Reference Valiante, Schneider, Zappacosta, Graziani, Pezzulli and Volonteri2018).
Observationally, no DCBHs have been identified so far and initial speculations based on HST, VLT, and Keck data (Sobral et al. Reference Sobral, Matthee, Darvish, Schaerer, Mobasher, Röttgering, Santos and Hemmati2015) are now ruled out by [CII] detections consistent with normal star-forming galaxies (Matthee et al. Reference Matthee2017).
Our understanding of DCBHs is still very limited. As an example, little is known about: the exact mass distribution and growth mechanism; the physical properties of the hosting haloes; the final fate of a DCBH, such as its possible ejection from the hosting structure or its inclusion into larger massive black holes; the inhibiting role of local gas fragmentation as consequence of star formation and metal pollution from heavy elements, acquired either in situ or via minor mergers; and the effects of merger-induced vigorous turbulence halting collapse of pristine material. Furthermore, the effects of radiation from primordial population III (popIII) stars and the following population II-I (popII-I) regime might vary strongly depending on the assumptions about spectral energy distribution (SED) and initial mass function (IMF).
Given the lack of definitive answers to these open questions, throughout this work we will investigate some of the above topics by employing cosmological N-body hydrodynamical simulations including non-equilibrium chemistry calculations and full radiative transfer from PopIII and PopII-I stellar sources. We will explore chemical and thermal implications of the different populations on DCBH host halo candidates.
The paper is organised as follows. Details on the numerical implementation and the data analysis are given in Section 2; results are presented in Section 3 and discussed in Section 4; conclusions are summarised in Section 5.
2. Method
In the following subsections, we briefly describe the most important features of the cosmological calculations we have performed (Section 2.1), as well as the selection criteria for our analyses (Section 2.2).
2.1. Simulations
The numerical calculations performed in this work are based on radiative hydrodynamical calculations carried out via the parallel numerical code P-Gadget3, an updated version of P-Gadget2 (Springel Reference Springel2005). The code implementation combines several physical processes and, in particular, besides gravity and smoothed-particle hydrodynamics (SPH), contains a self-consistent treatment of non-equilibrium chemistry, metal cooling, low-temperature cooling by molecules and fine-structure lines (Maio et al. Reference Maio, Dolag, Ciardi and Tornatore2007, Reference Maio, Ciardi, Dolag, Tornatore and Khochfar2010) as well as a multi-frequency implementation of photon propagation based on the Eddington tensor scheme (Petkova Springel 2009, 2011; Petkova Maio 2012; Maio et al. Reference Maio, Petkova, De Lucia and Borgani2016) which takes into account radiative transfer from 150 frequency bins in the energy range [0.7, 100] eV—including H, He, D, H2, HD, HeH+ transitions as well as LW band ([11.2, 13.6] eV), near-IR (at energies ≲1.7 eV) and UV (~[3, 100]eV) radiation.Footnote a
Stellar evolution is followed for a range of stellar masses and initial metallicities. Stars with masses above 8M⊙ explode as SNe II and inject a kinetic energy of 1051 erg in the surrounding medium. Lower-mass stars evolve through AGB or SNe Ia phase (Tornatore et al. Reference Tornatore, Borgani, Dolag and Matteucci2007) with consequent mass loss. Explosion energies of massive (>100M⊙) PopIII stars range between 1051 and 1053 erg, depending on the mass. Metal yields for stars with different masses and initial metallicities are traced for a number of species (He, C, N, O, Ne, Mg, Si, S, Ca, Fe, etc.) according to the input tables listed, for example, in the final paragraph of Section 2.1 of Maio et al. (Reference Maio, Petkova, De Lucia and Borgani2016).
Star formation takes place stochastically in particles with densities above a threshold of 1 cm−3 and gas and heavy elements are ejected by star-forming regions via winds (at 500 km/s) (Springel & Hernquist Reference Springel and Hernquist2003; Maio et al. Reference Maio, Ciardi, Yoshida, Dolag and Tornatore2009).
Metal diffusion in the surrounding medium is mimicked by smoothing individual metallicities over the neighbouring particles in the SPH kernel.
We use the full radiative-transfer simulations performed by Maio et al. (Reference Maio, Petkova, De Lucia and Borgani2016) in boxes of 0.5 Mpc/h (comoving) a side. They sample gas and dark-matter fields with 1283 particles for each species, which results in gas and dark-matter resolutions of 6.6×102 M⊙/h and 4.3×103 M⊙/h, respectively, and comoving softening length of 0.2 kpc/h (i.e. 20 pc/h at z = 9). We note that for a precise picture radiative hydrodynamical simulations should resolve the small structures collapsing at early times below kpc-scales. In terms of space resolution, the softening length used in this work is enough to provide a realistic description of collapsing material at high z.
Sources of radiative transfer are distinguished into popIII and popII-I stars, according to the underlying gas metallicity, Z. Stars forming in pristine environments or in regions with Z < Z crit=10−4 Z ⊙ are assumed to be popIII; otherwise they are assumed to be popII-I. The IMF adopted for these latter is always a Salpeter IMF over the range [0.1, 100] M⊙, while their input SED is a black body with effective temperature T eff = 104 K, well suited to describe low-mass stars.
Due to our ignorance on the properties of primordial stars, we consider three cases, as also summarised in Table 1: (i) very massive stars with top-heavy popIII IMF (with slope −2.35 and range [100, 500] M⊙) that emit as a black body with T eff = 105 K (TH.1e5); (ii) massive hot starsFootnote b with Salpeter popIII IMF (with slope −2.35 and range [0.1, 100]M⊙) that emit as a black body with T eff = 4×104 K (SL.4e4); and (iii) regular stars with Salpeter popIII IMF (with slope −2.35 and range [0.1, 100]M⊙) that emit as a black body with T eff = 104 K (SL.1e4). Estimating the exact amounts of ionising photons produced by a star is not a trivial issue, since it requires detailed stellar modelling to quantify total luminosity and spectral properties as a function of the stellar lifetime. Thus, in the radiative transfer calculations, we assume an ionising luminosity for top-heavy popIII stars of 1051 photons per second, while for popII or lower-mass popIII sources we assume 1049 photons per second. Since each star particle represents a simple stellar population, the emissivity for each star particle is normalised by weighting over the corresponding IMF. Density-dependent gas self-shielding, which alters rates of the non-equilibrium chemical network, is evaluated following the seminal work by Draine & Bertoldi (Reference Draine and Bertoldi1996), as mentioned in Maio et al. (Reference Maio, Petkova, De Lucia and Borgani2016).
Table 1. Model assumptions for the three radiative scenarios.

Self-shielding is effective in a small range of physical conditions (at large gas densities and gas temperatures around or below a few thousands Kelvin). Hence, additional dependences on metallicity can be neglected Sugimura et al. Reference Sugimura, Omukai and Inoue2014). The radiative rates implied by the different SEDs in the different cases are computed consistently with the assumptions and employed, jointly with the relevant collisional rates, to get the correct non-equilibrium abundances from the differential equations describing the evolution of the species number densities and of the photon number density in each frequency bin. For sake of convergence, the integration of the chemical equations is performed on a timescale which is 1/10th the actual timestep (Anninos et al. Reference Anninos, Zhang, Abel and Norman1997).
At each snapshot, cosmic structures are identified by means of a friends-of-friends algorithm with a linking length of 20% the mean inter-particle separation. Substructures are identified by the Subfind algorithm (see Dolag et al. Reference Dolag, Borgani, Murante and Springel2009, and references therein) and are post-processed to trace: masses, positions, radii, velocities, star formation rates, mass-weighted temperatures, abundances of e−, H, H+, H−, He, He+, He++, H2, ![]() $${\rm{H}}_2^ + $$, D, D+, HD, HeH+, C, N, O, Ne, Mg, Si, S, Ca, Fe, etc., angular momentum, substructures, and all the relevant physical properties of each object.
$${\rm{H}}_2^ + $$, D, D+, HD, HeH+, C, N, O, Ne, Mg, Si, S, Ca, Fe, etc., angular momentum, substructures, and all the relevant physical properties of each object.
We adopt a ΛCDM background cosmological model with present-day expansion parameter normalised to 100 km/s/Mpc of h = 0.7. Baryon, matter, and cosmological-constant parameters are assumed to be Ω0,b = 0.04, Ω0,m = 0.3, Ω0,Λ = 0.7, respectively. Adopted spectral parameters are σ 8 = 0.8 for the z = 0 mass variance within 8 Mpc/h radius and n = 1 for the slope of the primordial power spectrum. We note that our choices for initial conditions, box size, and resolution are determined by the necessary trade-off between the required accuracy of the physical descriptions implemented in the code and the numerical feasibility of the runs. The set-up adopted here satisfies such constraints. We refer the interested reader to Petkova & Maio (Reference Petkova and Maio2012) and Maio et al. (Reference Maio, Petkova, De Lucia and Borgani2016) for more details.
The simulation data considered in this work have redshifts z = 14.5, 11.5, 9.5, 9.0, 8.5, corresponding to cosmic times of about 0.28, 0.38, 0.5, 0.54, 0.58 Gyr.
2.2. Selection criteria for DCBH host candidates
The formation of a DCBH is a difficult event. Popular analytical models require a number of hypotheses to allow the gas to collapse without fragmenting (see e.g. Bromm & Loeb Reference Bromm and Loeb2003; Begelman et al. Reference Begelman, Volonteri and Rees2006; Mayer et al. Reference Mayer, Kazantzidis, Escala and Callegari2010; Visbal et al. Reference Visbal, Haiman, Terrazas, Bryan and Barkana2014; Choi et al. Reference Choi, Shlosman and Begelman2015; Valiante et al. Reference Valiante, Schneider, Volonteri and Omukai2016, Reference Valiante, Agarwal, Habouzit and Pezzulli2017; Regan et al. Reference Regan, Visbal, Wise, Haiman, Johansson and Bryan2017; Barrow, Aykutalp, & Wise Reference Barrow, Aykutalp and Wise2018; Chon, Hosokawa, & Yoshida Reference Chon, Hosokawa and Yoshida2018, for details and reviews).
Host haloes should have null star formation rate to assure that there is no ongoing gas fragmentation nor local metal enrichment. Then, they should have pristine chemical composition to rule out cooling by heavy elements.
The host structure should also be lighted up by a strong radiation field in the LW band to prevent molecule (mainly H2) formation and consequent cooling. In pristine media without molecular content, H and He collisions would be able to bring gas temperatures down to only ~ 8000K (Oh & Haiman Reference Oh and Haiman2002; Smith, Bromm, & Loeb Reference Smith, Bromm and Loeb2017). This implies a temperature floor below which the gas cannot cool due to the lack of metallic and molecular coolants.
As it will be clear by the basic properties of early haloes (see also next section), common solar-like stars are able to dissociate H2 molecules down to mean fractional values of the order of 10−13.
At the same time, though, the hosting dark-matter mass should be at least ~ 2 × 106 M⊙, since gas in lower-mass haloes does not collapse and can be susceptible to photo-evaporation or nearby stellar feedback (e.g. Whalen, Abel, & Norman Reference Whalen, Abel and Norman2004; Maio et al. Reference Maio, Khochfar, Johnson and Ciardi2011b; Jeon et al. Reference Jeon, Pawlik, Greif, Glover, Bromm, Milosavljević and Klessen2012; Wise et al. Reference Wise, Abel, Turk, Norman and Smith2012a,b, Reference Wise, Demchenko, Halicek, Norman, Turk, Abel and Smith2014; Kannan et al. Reference Kannan2014; de Souza et al. Reference de Souza, Maio, Biffi and Ciardi2014, Reference de Souza2015; Maio et al. Reference Maio, Petkova, De Lucia and Borgani2016; Dayal & Ferrara Reference Dayal and Ferrara2018, etc.). Furthermore, smaller haloes are not suitable to form massive black hole seeds because of the deficiency of available gas.
Due to such basic constraints, we adopt the following commonly used criteria for the identification of DCBH host candidates in our simulations, choosing haloes with:
null star formation rate (SFR = 0);
pristine gas (Z = 0);
mass-weighted gas temperatures higher than 8 ×103 K;
mean H2 content x mol < 10–13, as proxy for H2 destruction by external radiation;
minimum dark-matter mass of 2 × 106 M⊙.
The first two conditions are easily fulfilled in early epochs, because at those times only relatively few haloes experience star formation and metal enrichment, while, besides very unusual cases, dust production is probably in its earliest phases (Mancini et al. Reference Mancini, Schneider, Graziani, Valiante, Dayal, Maio, Ciardi and Hunt2015). On the contrary, the third and fourth conditions are strongly related to the presence of a background or local radiation field that heats the gas and dissociates H2 molecules.
Studies in the literature have clearly shown that the main effect of a uniform dissociating LW background is a shift in the masses and timescales before collapse (Wise & Abel Reference Wise and Abel2005; Ahn et al. Reference Ahn, Shapiro, Iliev, Mellema and Pen2009; Visbal et al. Reference Visbal, Haiman, Terrazas, Bryan and Barkana2014). The effects on DCBH formation are small or modest for intensity values around a few up to hundreds times J 21. They are dramatic for much bigger values, preventing DCBH formation by the end of the first Gyr when the radiation field exceeds ~1 000J 21 (Shang et al. Reference Shang, Bryan and Haiman2010; Regan et al. Reference Regan, Visbal, Wise, Haiman, Johansson and Bryan2017).
More complicated is the role of local radiation, for which there is no simple foreseeable trend, that, in fact, strongly depends on the properties and environment of the local radiative sources (SED, emitting power, lifetime, isolated location, or clustered regions).
In this paper we account self-consistently for the LW radiation originating by the radiative emission of formed stars and for the consequent build-up of an LW background. Given the small boxes, though, we do not account for the effect of sources located further away. In fact, their contribution is expected to be lower than the local contribution (Ciardi et al. Reference Ciardi, Ferrara, Governato and Jenkins2000). Here, we focus on the intriguing implications of local LW radiation from different types of radiative sources.
We stress that the conventional limits outlined above come from popular analytical arguments for DCBH formation and they should be simply considered as necessary conditions.
It is not clear whether they are also sufficient conditions, since additional nonlinear processes, such as mergers, substructure formation, rotational motions, and/or turbulence, might halt direct collapse or even enhance star formation. These additional phenomena will be addressed throughout this paper.
3. Results
In this section we present the main results from our analysis and illustrate the evolutionary pathways of cosmic gaseous systems which could directly collapse into a massive black hole.
3.1. Basic halo properties
To understand the basic properties of the halos that could be able to host DCBH events, we start our investigation by looking at their typical dark-matter masses, chemical content, thermal conditions, and star formation rate.
The halo samples at different redshifts contain objects with dark-matter masses between ~ 105 M⊙ and 108 M⊙. Their baryonic properties are affected by the assumed features of the primordial stellar populations, as well as of the emitting radiation spectrum.
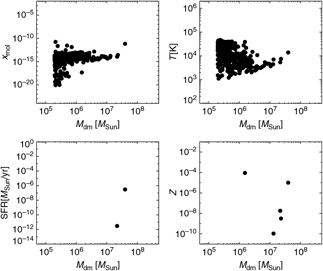
In Figure 1, halo properties at z = 9 are shown for the run with top-heavy popIII IMF and black-body spectrum with T eff = 105 K (TH.1e5 model). At this epoch there are two star-forming sites with masses of about 2 × 107 M⊙ and 4 × 107 M⊙, respectively. The same stellar populations that provide UV photons are also responsible for enriching nearby regions up to metallicities of ~10−2Z⊙ once they explode as supernovae. As a result, metal spreading involves both the halo hosting star formation and four additional halos in which star formation is not taking place. The powerful radiation emitted is responsible for destroying most of the molecular content in the simulated volume. The residual H2 fraction (x mol) usually lies below 10−10 and reaches values as low as 10−20 in the smaller unshielded haloes. The gas mass-weighted temperatures vary correspondingly between 103 K and a few times 104 K due to radiative heating from primordial stars. The haloes mostly affected are the ones with small masses—below a few 106 M⊙—that are not dense enough to cool against photo-heating, are not able to efficiently self-shield, and suffer strong evaporation effects (Maio et al. Reference Maio, Petkova, De Lucia and Borgani2016). Most of the objects have been heated to temperatures around 104 K, corresponding to average molecular fractions of x mol ~ 10−13–10−15. Haloes with temperatures as low as ~103 K still retain certain amounts of H2, resulting in x mol ~ 10−10–10−12. The biggest halo undergoes star formation, has a mass of ~ 4 × 107 M⊙, an average fraction x mol ≃ 10−11, and a mass-weighted gas temperature T≃104 K.

Figure 1. Mean H2 content, x mol, temperature, T, star formation rate, SFR, and metallicity, Z, as a function of the dark-matter mass, M dm, of haloes at z = 9 for the run with a T eff = 105 K black body as popIII SED.
Different assumptions for the popIII IMF and SED have clear implications on the basic halo properties. In Figure 2 results corresponding to the run with Salpeter-like popIII IMF and T eff = 4 × 104 K black body (SL.4e4 model) are displayed. In this case, there are four star-forming haloes, that is, twice as much as the TH.1e5 case, although only the most massive halo with mass of ~4 × 107M⊙ is found to be enriched at Z≃10−2Z⊙. The other three haloes (with masses between ~7 × 106 M⊙ and ~2 × 107 M⊙) do not feature signatures of metal enrichment, yet. This is not surprising, because, once compared to the previous TH.1e5 model, the SEDs of the SL.4e4 model are less powerful (up to 2 dex), hence radiative feedback is not able to rapidly shut off star formation in distant haloes and metal spreading is less efficient in enriching nearby haloes. The trend for the average molecular content in each halo, x mol, shows that radiative feedback in the SL.4e4 scenario reduces the molecular fraction down to 10−8–10−15, but x mol never reaches values of the order of 10−20, as in the TH.1e5 case. This means that the gas is not heated up to very high values and stays confined below 104 K, as shown by the trend for T as function of mass.Footnote c In particular, photon propagation seems to play a little role for the thermal behaviour of the haloes. There is a well-defined trend of increasing temperature for increasing mass, whose corresponding molecular content shows typical fractions x mol ~ 10−8–10−12. The few haloes that are affected by radiation deviate from the displayed increasing trend (low masses and gas temperatures of 2 × 103–103K) and suffer molecule destruction with x mol values going down to ~10−13–10−15.

Figure 2. As Figure 1 for the run with a T eff = 4 × 104 K black body as popIII SED.
The most conservative scenario with a Salpeter-like popIII IMF and a T eff = 104 K black body as popIII SED (SL.1e4) is shown in Figure 3. The SL.1e4 model is the least powerful in terms of radiation emitted. As a consequence, it predicts more star-forming haloes (7) than in the TH.1e5 and SL.4e4 models, as well as localised metal enrichment in one single halo with Z ≃ 10−2 Z⊙, consistently with the previous considerations. In this scenario, radiative effects are negligible, as clearly visible from the trend of both x mol and T. Molecules are not significantly dissociated and thus average molecular fractions never decline below 10−12 at z = 9 and barely reach 10−13 at later times. The trend for mass-weighted gas temperatures is little affected by emitted photons, too. In this case, the chemical and thermal evolutions are mainly led by cosmological growth and mechanical feedback, rather than radiative feedback.

Figure 3. As Figure 1 for the run with a T eff = 104 K black body as popIII SED.
We mention that basic host properties at higher redshift do not show evident differences among the models considered, due to the limited structure evolution at early times. In all the cases, there is no or little star formation and metal enrichment; there is no relevant effect from radiative feedback; average molecular fractions are close to initial-condition values, i.e. x mol ~ 10−4 –10−6; and the haloes are smaller, with mass-weighted gas temperatures between a few hundreds and a few thousands Kelvin.
We summarise mean halo properties for star-forming haloes in the different models in Table 2. Statistics are shown for three samples corresponding to the three different scenarios considered here, TH.1e5, SL.4e4, and SL.1e4. Each sample consists of all the haloes found at redshift z ≥ 9. The different columns refer to the mean values of stellar mass (M ⋆) in solar units, fraction of haloes hosting metal-enriched star formation (f host), star formation efficiency (M ⋆/M gas), gas fraction (f gas), absolute UV magnitude in the AB system at 1 500Å (MUV), bolometric luminosity (L bol) in solar units, and number of ionising photons per second (Ṅ ph,ion). AB magnitudes and luminosities are computed by employing the spectral templates for the emission at 1 500Å, as a function of stellar lifetimes and metallicities, from the stellar population synthesis code GALAXEV (Bruzual & Charlot Reference Bruzual and Charlot2003). We use the star particle properties as inputs, adopt the instantaneous burst model, assume a Salpeter IMF, and do not consider any nebular emission. Since GALAXEV is calibrated for enriched stellar populations with conventional low-mass IMFs (either Salpeter or Chabrier), the resulting magnitudes and luminosities lack the contribution of harder radiation from powerful popIII sources, that for a 105 K black body accounts for roughly one dex increased emission at 1 500 Å, and that we consider for massive popIII stars. In the TH.1e5 scenario, where star formation is more inhibited by early powerful popIII stars, the resulting mean stellar mass is slightly smaller, although, due to the higher emitting power, the mean magnitude and bolometric-luminosity estimates are brighter than in SL.4e4 or SL.1e4. In these latter cases, star formation suppression due to radiative feedback is milder, hence mean stellar masses are ~0.3 dex larger, mean absolute AB magnitudes more than one unit fainter, and mean bolometric luminosities about one dex dimmer. The effects of radiative feedback in the different cases can be better revealed from star formation efficiencies and gas fractions. The TH.1e5 scenario has a lower mean star formation efficiency, M ⋆/M gas, due to stronger gas heating and cooling suppression linked to powerful popIII sources. In the SL.4e4 and SL.1e4 scenarios, mean star formation efficiencies, M ⋆/M gas, are a factor ~1.6 larger, because of the more limited impact of early solar-like stars on the surrounding gas. This is also reflected by their ~6% larger mean gas fractions that, in average, are less subject to photo-heating and/or photo-evaporation than in the TH.1e5 case. The fraction of haloes hosting metal-enriched star formation shows an opposite trend, highlighting the effects of metal spreading: the more powerful the source the higher its ability to enrich and contaminate the medium out to larger distances. For this reason, the mean f host varies from unity in the TH.1e5 case down to 0.18 and 0.12 in the SL.4e4 and SL.1e4 cases, respectively. The average rate of ionising photons is estimated by Ṅ ph,ion = f escQ iM ⋆, with f esc escape fraction, Qi ionisation parameter giving the number of ionising photons per second per unit mass of simple stellar population, and M ⋆ stellar mass. An escape fraction of f esc = 0.5 is adopted,Footnote d consistently with expectations for star-forming haloes in the mass range around 107 M⊙. Qi parameters are taken from the tabulated values of the evolutionary synthesis model by Schaerer (Reference Schaerer2003) for starbursts with given IMF and metallicity. For our SL.1e4, SL.4e4, and TH.1e5 models, we use Schaerer (Reference Schaerer2003)’s case A, case B, and case C, respectively. While the two scenarios for regular and massive stars SL.1e4 and SL.4e4 adopt a Salpeter IMF similar to Schaerer (Reference Schaerer2003)’s case A and case B, our extreme case TH.1e5 has no close equivalent in Schaerer (Reference Schaerer2003) and we have to rely on case C therein. TH.1e5 model results to be more powerful than SL.1e4 and SL.4e4 models by ~1 dex. We have to stress, though, that f esc is a poorly known parameter in the literature and its value might span over a wide range. While Wise et al. (Reference Wise, Demchenko, Halicek, Norman, Turk, Abel and Smith2014) suggest average values of the order of 50%, other authors, such as Yoshida et al. (Reference Yoshida, Oh, Kitayama and Hernquist2007), suggest values closer to unity, that is, a factor of 2 larger, and dependent both on the particular stellar mass range considered and on the features of the environment. Because of these uncertainties, expected Ṅ ph,ion values could vary sensibly.
Table 2. Mean halo properties at z ≥ 9 for the three different models adopted.

From left to right, different columns indicate: name of the model considered, mean stellar mass in solar units (1), mean fraction of haloes hosting metal-enriched star formation (2), mean star formation efficiency (3), mean gas fraction (4), mean absolute UV magnitude in the AB system at 1500Å (5), mean bolometric luminosity in solar units (6), mean number of ionising photons per second (7).
3.2. DCBH host candidates
To understand the properties of the haloes hosting DCBH events in the three models considered in this work, we select the simulated candidates by referring to the conditions listed and discussed in Section 2.2. The resulting trends and requirements for DCBH formation are shown in Figures 4 and 5 for z = 11.5 and z = 9, respectively. They refer to the baryon properties that need to be checked to investigate the possibility of a direct collapse of the gas. In each figure, the host gas mass is plotted against the molecular fraction for the TH.1e5 model (top), the SL.4e4 model (middle), and the SL.1e4 model (bottom). Since only gas (and not dark matter) would collapse directly into a black hole, the gas masses quoted in the figures are comparable to the expected mass of the DCBH which would be born from such process. Metal-enriched haloes are denoted by red triangles, star-forming haloes by blue diamonds, and haloes more massive than 2 × 106 M⊙ by green asterisks. Magenta squares refer to pristine non-star-forming haloes, while the resulting DCBH host candidates are highlighted by bullet points. The halo population at very early times (first hundreds of million years after the Big Bang) is dominated by pristine non-star-forming small haloes that retain their molecular content irrespectively from the radiative model considered for primordial stars. Larger amounts of molecules start to form only in halos with dark-matter mass higher than 2 × 106 M⊙ and gas content of about 3 × 105 M⊙. Because of the local metal pollution, ongoing star formation, and large molecular fraction, these primordial halos are not suitable candidates for hosting a DCBH, since local gas is going to cool below 8 000 K and fragment further (McCourt et al. Reference McCourt, Oh, O’Leary and Madigan2016). Most of the haloes are still H2 rich and too small to induce a direct gas collapse and no DCBH candidates are found at these epochs.
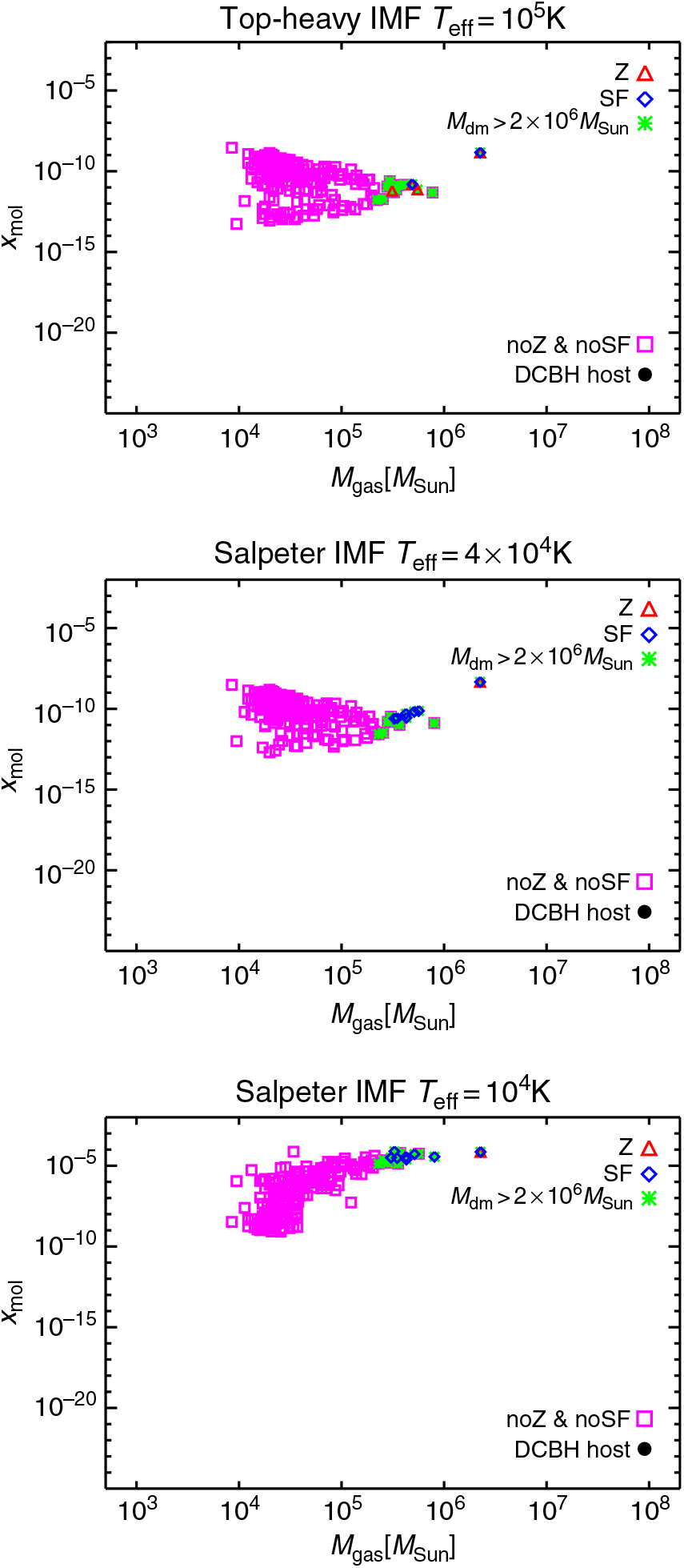
Figure 4. Gas mass versus molecular fraction of the simulated haloes at z = 11.5 for runs with different popIII SEDs: TH.1e5 (top panel), SL.4e4 (middle panel), and SL.1e4 (bottom panel). Different symbols refer to different types of haloes: metal-enriched haloes (red triangles), star-forming haloes (blue diamonds), haloes with dark-matter mass larger than 2 × 106 M⊙ (green asterisks), pristine non-star-forming haloes (magenta squares), and DCBH host candidates (black bullets) that have no metals, no star formation, dark-matter mass larger than 2 × 106 M⊙, gas temperature larger than 8 × 103 K, and molecular fraction lower than 10−13. No DCBH host candidates are present at this epoch in any of the radiative models.
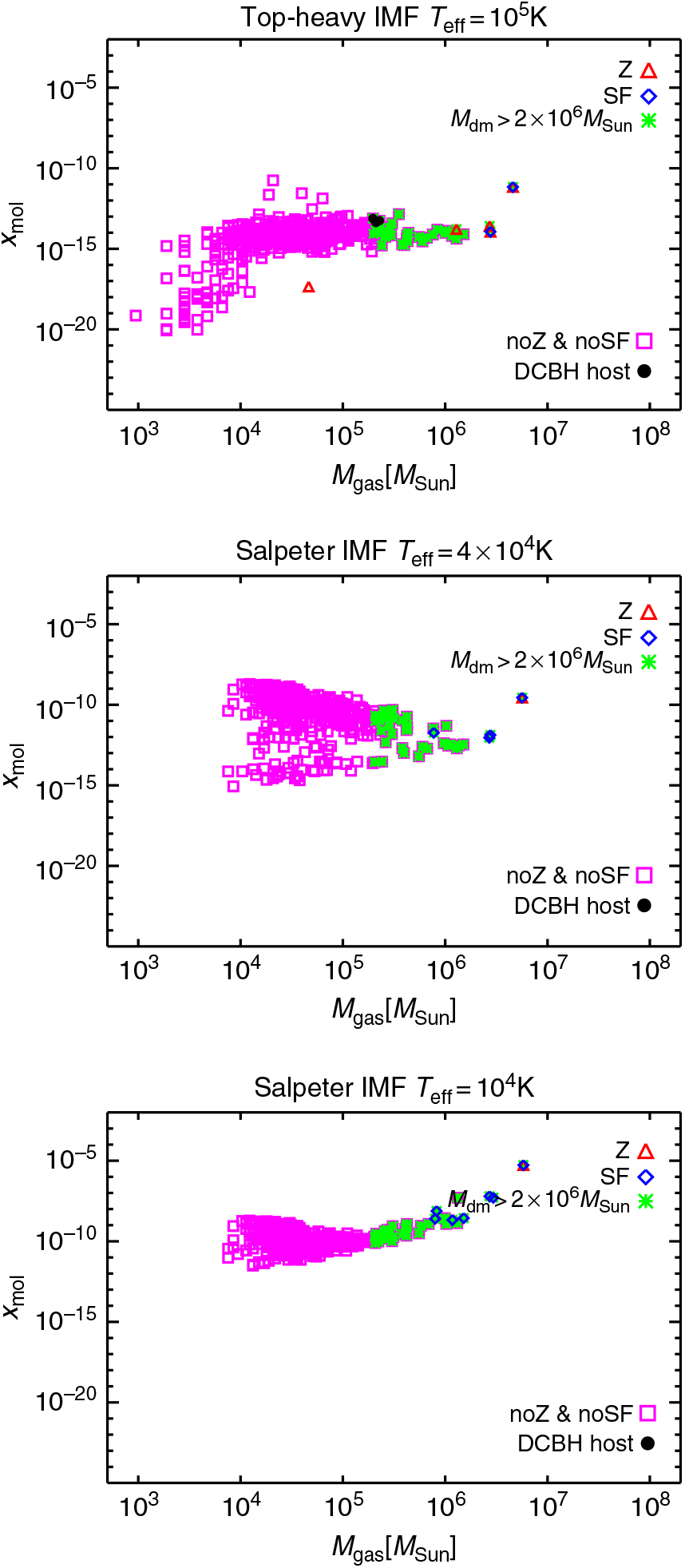
Figure 5. At z = 9 there are three possible DCBH host candidates in the top panel. Gas mass versus molecular fraction of the simulated haloes at z = 9 for runs with different popIII SEDs: TH.1e5 (top panel), SL.4e4 (middle panel), and SL.1e4 (bottom panel). Different symbols refer to different types of haloes: metal-enriched haloes (red triangles), star-forming haloes (blue diamonds), haloes with dark-matter mass larger than 2 × 106M⊙ (green asterisks), pristine non-star-forming haloes (magenta squares), and DCBH host candidates (black bullets) that have no metals, no star formation, dark-matter mass larger than 2 × 106M⊙, gas temperature larger than 8 × 103 K, and molecular fraction lower than 10−13.
Results at z = 11.5 are shown in Figure 4, about 380 million yrs after the Big Bang. The first stars have formed at z ≃ 14.5 and have evolved for about ~100 million yrs, while new stars are born in the meantime.
In the top panel (TH.1e5), we see that photon propagation dissociates molecules up to levels as low as x mol ~ 10−8–10−14 and that, due to the powerful stellar feedback, there are only two star-forming haloes and four enriched haloes, two of which are quiescent non-star-forming objects polluted by nearby spreading events.
The SL.4e4 model (centre) produces similarly strong variations (with x mol ~ 10−8–10−13), although mechanical and radiative feedback is not so extreme to push metals into other haloes (they rather remain confined in their birth place) and to shut off star formation in the larger ones. Consequently, there are several massive objects (green asterisks) with typical dark masses above 2 × 106 M⊙ and typical gas masses between a few times 105 and 106 M⊙, but none of them is a good DCBH host candidate. In fact, these massive-enough haloes feature values of x mol that are always higher than 10−13 and range around x mol ≃ 10−12–10−10. Considering that lower-mass objects reach smaller x mol values, it is clear that shielding effects in the denser regions of the bigger haloes play a crucial role to prevent DCBH formation (see also Sections 2.1 and 3.1).
The trends in the bottom panel follow from the weaker sources assumed for this case (SL.1e4). Thus, most of the haloes with dark-matter mass > 2 × 106 M⊙ undergo star formation and/or get enriched with metals, still keeping average molecular fractions of the order of x mol ~10−6 – 10−4. Smaller haloes suffer minimal radiative effects and x mol always stays above 10−10. The bulk of the haloes in this scenario is either ‘large’ and star forming or small and quiescent; therefore, they are unlikely to host DCBHs.
Environmental effects (such as mergers, feedback, and ongoing cosmological growth) contribute to spreading the trends in the plots.
We show the results at z = 9 in Figure 5. This redshift corresponds to a cosmic time of half Gyr, that is, slightly more than 100 million yrs after z = 11.5. At such epoch, the differences among the three models are striking.
In the TH.1e5 case (top panel), powerful radiative emissions from primordial stars have heavily dissociated H2, so that most of the haloes have x mol ~ 10−15 and the smaller ones get down to 10−20. The two largest haloes (blue diamonds) with gas masses of about 2–4 × 106 M⊙ are forming stars and are metal enriched, as well as two other smaller nearby objects (red triangles). The quiescent pristine haloes with dark-matter mass larger than 2 × 106 M⊙, despite their low molecular fraction, are mostly cold, with gas temperatures below 8 × 103 K (see Section 3.1). Thus, they cannot host DCBH formation. Only three objects with dark mass of roughly 2 × 106 M⊙ and gas mass of about 2–3 × 105 M⊙ are hotter and poor of molecules; hence they are good DCBH host candidates. We note that the minimum temperature threshold of 8 × 103 K is mainly led by H collisional cooling ((e.g. Oh & Haiman Reference Oh and Haiman2002; Smith et al. Reference Smith, Bromm and Loeb2017)), active during cosmic structure formation, when diffuse cosmic gas falls into the growing potential wells of dark-matter haloes and gets shock-heated to typical temperatures of the order of 104−105 K. In absence of additional coolants, it is not possible to bring temperatures below ~8 × 103 K. In the quiescent haloes mentioned above, gas is still at a diffuse stage, as demonstrated by their small masses. Thus, the hosted gas simply follows the thermal cosmic expansion; hence it is by no means able to collapse nor to survive nearby feedback events. Only haloes with dark-matter masses larger than ~ 2 × 106 M⊙ × are going to host collapsing events and survive nearby star formation or photo-evaporation feedback (Whalen et al. Reference Whalen, Abel and Norman2004; Jeon et al. Reference Jeon, Pawlik, Greif, Glover, Bromm, Milosavljević and Klessen2012; Wise et al. Reference Wise, Abel, Turk, Norman and Smith2012a,b, Reference Wise, Demchenko, Halicek, Norman, Turk, Abel and Smith2014; Maio et al. Reference Maio, Petkova, De Lucia and Borgani2016).
In the SL.4e4 case (middle panel), the behaviour of the gas is bimodal, with many pristine quiescent haloes having still an average molecular fraction x mol > 10−13 and a few others lying at x mol < 10−13. These latter are the ones that surround star-forming haloes (blue diamonds) and result affected by the nearby radiative feedback, although not by chemical feedback. These objects are too small to host DCBHs, though. Some of the largest haloes are undergoing star formation and/or metal enrichment; however, the remaining ones (green asterisks) are still cold or feature x mol > 10−13. Thus, no eligible DCBH hosts are found for this model.
In the SL.1e4 case (bottom panel), the scenario is much less dramatic for the environment of star-forming halos. Indeed, radiation from weaker solar-like sources affects very marginally the thermal and chemical properties of the local gas and has little implications for external haloes. For this reason, star formation is not severely inhibited by radiation and all the objects with gas masses higher than ~ 106 M⊙ form stars and are locally enriched by metals. The entire population of primordial haloes has an average molecular content that is always above the threshold of 10−13, and therefore, it cannot host DCBH formation. In this case, gas molecular evolution is mainly led by mergers and feedback effects, while photon propagation acts as a minor character.
In general, cosmological evolution in the first-half Gyr is responsible for spreading the values displayed in the plots, mostly in the low-mass end that is very susceptible to environmental processes.
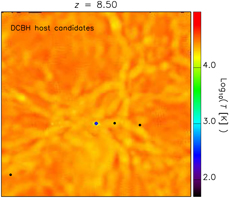
3.3. DCBH host candidate location
In Figure 6, we display the position where DCBH host candidates are found (bullet points) with respect to the dissociating radiative sources (blue diamond) at redshift z = 9 in the TH.1e5 model (top). These hosts have similar total masses slightly larger than 2 × 106 M⊙. The three candidates are found at comoving (physical) distances of about 72 (7.2) kpc/ h, 290 (29) kpc/ h, and 80 (8) kpc/ h from the central radiative source. For sake of clarity, they have been marked by letters A, B, and C, and we will refer to them in the following as candidates A, B, and C, respectively. Since temperature is the main driver of DCBH formation, the temperature map allows us to get hints about the thermal properties of cosmic gas in different environments.Footnote e Interestingly, DCBH candidates are all located near cosmic filaments that preserve mass-weighted temperatures of ~104 K. Isolated haloes are found not to be suitable DCBH host candidates. This is not surprising, because early isolated objects are usually smaller (hence they do not satisfy the mass requirement for DCBH formation) and thinner (hence they can severely suffer radiative heating and photo-evaporation effects, instead of gas collapse). In clustered environments, such as filaments or filament intersections, there is a wider variety of halo masses, thermal conditions, and molecular content, so there are higher chances that DCBH formation requirements are fulfilled.
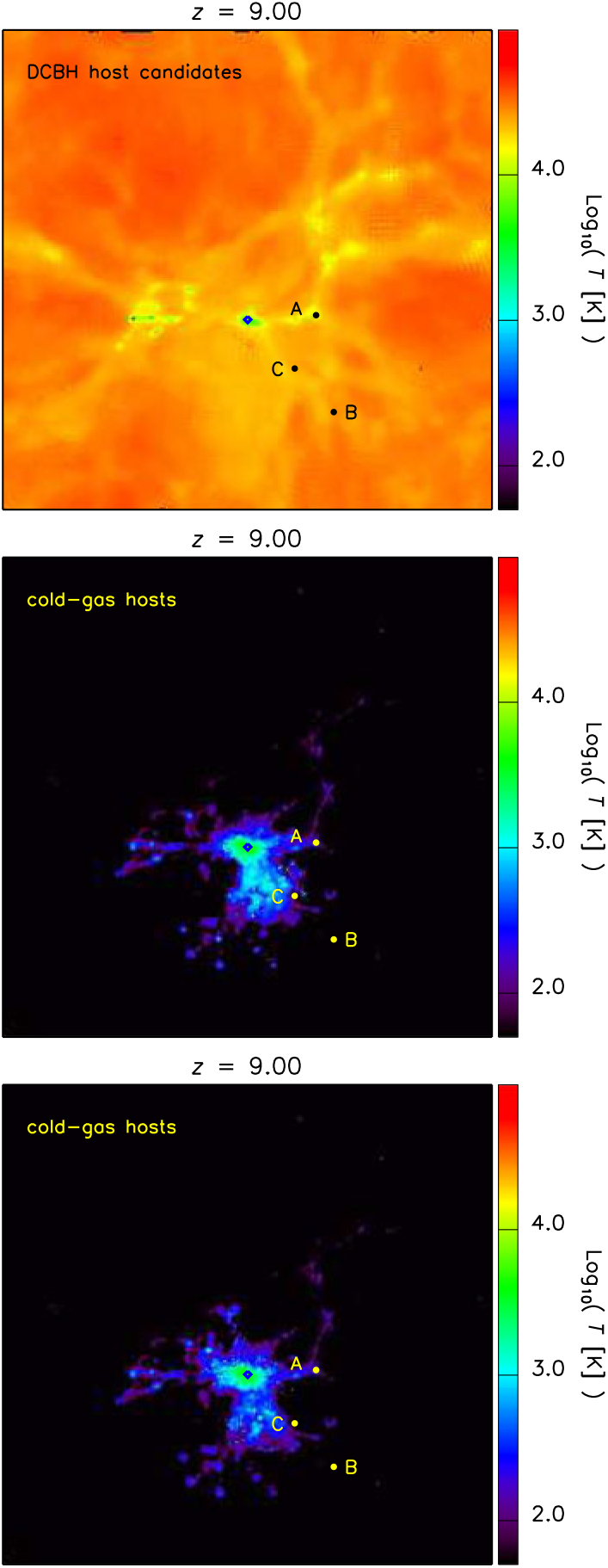
Figure 6. Top. Mass-weighted temperature map where we have marked the position of the DCBH host candidates at z = 9 for the run with top-heavy popIII SED (TH.1e5). The map is a projection of the simulated structures on the xy plane centred on the middle of the z-axis and within a slice of width equal to 1/20th the box length. The DCBH host candidates are denoted by black bullets and the letters A, B, and C. Centre. Same as top panel, but for the run with OB-like popIII SED (SL.4e4). The positions of the haloes marked by the yellow bullets and the letters A, B, and C are the same as in the top; but in this case, they are not DCBH host candidates. Bottom. Same as top panel, but for the run with standard solar-like popIII SED (SL.1e4). Also in this case, the haloes marked by the yellow bullets and the letters A, B, and C are not DCBH host candidates.
As a comparison, in the figure we also check the thermal conditions of the corresponding haloes in the SL.4e4 (centre) and SL.1e4 (bottom) models. In both cases, the medium is typically colder because of more efficient molecular cooling and weaker radiative fluxes. In fact, haloes denoted by A, B, and C (yellow bullets) host colder gas with mass-weighted temperatures below 104 K and ranging between roughly 102 and 103 K. In the SL.4e4 scenario, haloes A and C have mass-weighted temperatures of ~103 K, while halo B features values ≲102 K. In the weaker SL.1e4 scenario, instead, only halo A has a mass-weighted temperature of ~103 K, while haloes B and C are both at ≲102 K. Given these typical thermal conditions, the gas in these haloes results too cold to experience direct collapse, irrespectively from the hosting dark-matter mass, chemical composition, and local star formation. The main reason why the temperatures of these haloes are lower than in the previous case lies in the adopted features of stellar sources. In these two cases, central sources are not powerful enough to reach haloes at large distances and to dissociate their molecular content. Therefore, the hosts A, B, and C evolve almost unaffected by them, can retain cold gas, and will probably fragment in the next epochs. With such thermal conditions they are unlikely to turn into DCBHs. These structures could be, instead, small diffuse cold objects that are just assembling and represent the theoretical counterparts of currently debated early damped Lyman-alpha systems or dwarf galaxies forming at the end of reionisation (for further discussions on these topics we refer the interested reader to available works in the literature, such as the ones by Simcoe et al. (Reference Simcoe, Sullivan, Cooksey, Kao, Matejek and Burgasser2012), Maio, Ciardi, & Müller (Reference Maio, Ciardi and Müller2013a), Keating et al. (Reference Keating, Haehnelt, Becker and Bolton2014), Bosman & Becker (Reference Bosman and Becker2015), Bosman et al. (Reference Bosman, Becker, Haehnelt, Hewett, McMahon, Mortlock, Simpson and Venemans2017), García et al. (Reference García, Tescari, Ryan-Weber and Wyithe2017).
3.4. DCBH host candidate radiative properties
The DCBH host candidates are exposed to external local radiation; therefore, it is interesting to estimate the average spectral intensity, Jv, they experience at different times and frequencies, v. As we are interested in the LW band, if not otherwise specified we will refer to this frequency range for the next calculations of Jv. To this aim, we focus on the locations of the three hosts identified at z = 9 at physical distances from the radiative sources of 7.2 kpc/ h (A), 29 kpc/ h (B), and 8 kpc/ h (C), respectively. Due to the cosine law for isotropic radiation, they observe a spectral intensity Jv = Fv / π, where Fv is the average monochromatic flux and π is the value of the solid angle under which each of the three host candidates ‘sees’ the radiation.Footnote f The average monochromatic flux emitted by radiative sources is given by luminosity divided by surface area and frequency bin. Under spherical approximation this leads to:
with Ṅ ph number of ionising photons per second, hp Planck constant, v central frequency of the considered frequency range, r distance, and Δv frequency bin. To have an estimate of the expected order of magnitude for v LW central frequency (corresponding to 12.4 eV) and Δv LW band (corresponding to [11.2, 13.6] eV), it is convenient to rewrite the previous expression as
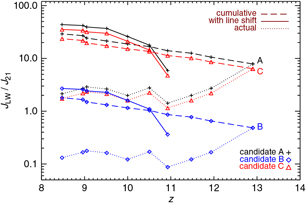
The redshift evolution of the spectral intensity, in units of J 21 = 10−21 erg/s/cm2/Hz/sr, to which the three halos, A, B, and C are exposed to, is displayed in Figure 7. We note that such commonly adopted reference unit, that is, J 21, represents a quite large spectral intensity, being equal to 100 Jansky per steradiant.
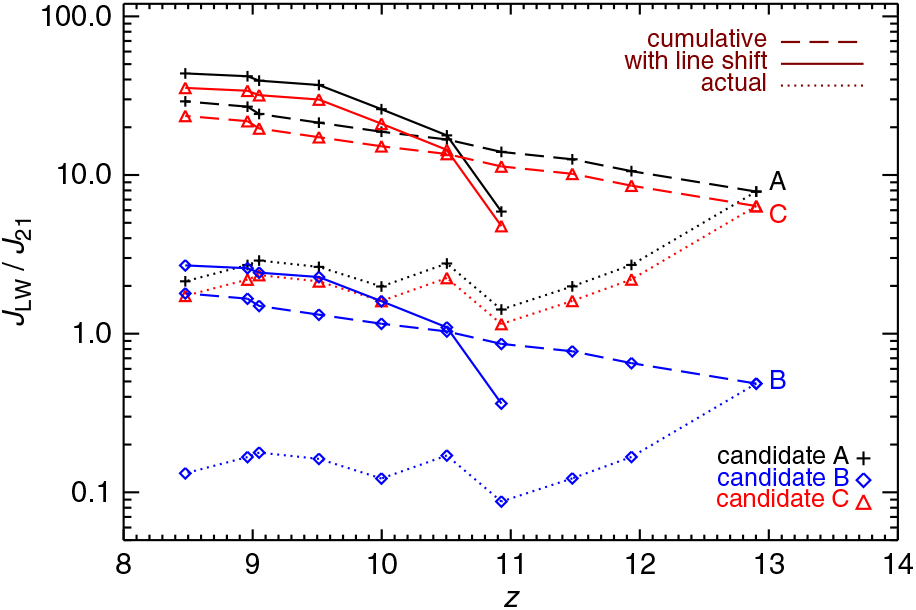
Figure 7. Spectral intensity in the LW band, J LW, in units of J 21 at the locations of the three DCBH host candidates (A, B, and C) identified at z = 9 as function of redshift, z. For each candidate, as indicated by the legends, the figure shows the actual amount of LW radiation produced at each snapshot (dotted lines), the cumulative LW radiation resulting from the sum of all the LW radiation produced until any given redshift z (dashed lines), and the radiation entering the LW band estimated by including redshifted photons from earlier times (solid lines).
The actual production of LW photons (due to radiation emitted by sources at that specific redshift), considering the processes of stellar mass growth and loss, is described by the dotted lines, while their cumulative distribution is given by the dashed lines. In order to quantify the exact amounts of LW radiation influencing the DCBH candidates at z = 9, the solid lines include the integrated effect of line shift into the LW band of LW photons produced at earlier times. For the sake of simplicity, we treat the LW central line at 12.4 eV as representative of the whole LW band. This is not a crude approximation, because the range of Δv around the central frequency is rather small. Thus, we impose a redshift constrain for z ref = 9 of |Δz / (1 + z ref)|< Δv / v ≃ 0.2, or z ≲ 11. This means that, roughly speaking, LW photons produced until z ~11 result redshifted in the LW band itself at z = 9, hence increasing the total amount of radiative intensity experienced by the three involved structures. We additionally take into account harder UV energies that can be shifted into the LW band. We limit our calculations only to a few representative linesFootnote g at about 15, 15.4, 24.6, 44.5, 54.4 eV. They increase the resulting LW intensity according to their relative contribution to the adopted black-body shape, ∝ v 3[1 − exp(h pv/kT)]−1, rescaled by redshift as [(1+z)/ (1+z ref)]−4. These lines are produced at earlier times, when they have higher frequency than the LW central frequency. During cosmological evolution they get redshifted into the LW range and become dimmer.
The values experienced by the three DCBH host candidates are quite heterogeneous. Candidates A and C feature actual values (dotted lines) that are always above J 21, with an initial burst of J LW ~ 10J 21 and z = 9 values of 2–3J 21. Candidate B instead is located further away and is exposed to radiation of spectral intensity around only ~ 0.1−1J 21. In all the three cases the cumulative amount of LW photons emitted (dashed lines) is always higher than 2J 21 at z = 9 and sums up to 20–30J 21 for candidates A and C. When including line shift (solid lines), these latter ones result exposed to values of J LW ≃ 50J 21 and J LW ≃ 40J 21, respectively. In this case, the radiation entering the LW band from previous epochs is accounted for. In general, line shift into the LW band from earlier sources appears to have a certain relevance (a factor of ~ 2). Despite the large uncertainties on the exact critical level of LW radiation, we definitely find the three candidates in conditions where resolved molecular cooling is severely inhibited (i.e. when molecular gas is exposed to J LW > J 21) and that favour DCBH formation. We highlight that the presence of metal spreading inhibits DCBH formation where J LW is larger, that is, closer to stellar sources, around or below kpc distance (see Equation 2). Differently from more idealised setups, these findings strengthen the role of metal pollution for assessing DCBH formation within numerical three-dimensional studies (see, however, Valiante et al. Reference Valiante, Schneider, Volonteri and Omukai2016). When checking similar radiative properties for the other two runs, we find J LW values that are always smaller than J 21 due to the 100-times lower adopted Ṅ ph. This explains why the two runs with solar-like and OB-type sources fail in producing viable DCBH host candidates and is consistent with the thermodynamical trends presented in the previous section.
Finally, as a warning, we point out that literature works are very uncertain about J LW critical values and different authors give different LW thresholds varying in the large range between 1 and 105J 21. Thus, there is no general consensus about the exact critical flux. For example, Shang et al. (Reference Shang, Bryan and Haiman2010) run three-dimensional simulations of pristine gas and manage to identify different candidates in the presence of LW fluxes of 1–1 000J 21, for standard stars, and of 1–105 J 21, for primordial stars. For the production of the observed population of z ~ 6 black holes, large values of the order of ~104 –105J 21 are considerably too high and it is by no means clear whether such fluxes are in fact required for the formation of massive objects. In addition, the stabilising impact of viscous heating alleviates the need for a strong UV background to keep the gas atomic and objects more massive than 104 M⊙ can form even with moderate values of J LW ~ 100J 21 (Latif & Schleicher Reference Latif and Schleicher2015). Analyses of simulations by, for example, Latif et al. (Reference Latif, Bovino, Van Borm, Grassi, Schleicher and Spaans2014b) conclude that the typical mean flux may vary from halo to halo, although values larger than ~ 1 500J 21 are rare, while massive objects still form for radiative fluxes of 10–500J 21 (Latif et al. Reference Latif, Schleicher, Bovino, Grassi and Spaans2014c). Habouzit et al. (Reference Habouzit, Volonteri, Latif, Dubois and Peirani2016b,a) find that, depending on the feedback scheme and the metal spreading implementation, the critical flux must be at least one or two orders of magnitude lower than predicted by pristine-chemistry models. These works practically set an upper limit of J LW << 1000J 21 (in clear contrast with e.g. Sugimura et al. Reference Sugimura, Omukai and Inoue2014) and favour smaller values around 30–300J 21. Yoshida et al. (Reference Yoshida, Abel, Hernquist and Sugiyama2003) even suggest values of the order of J 21 to prevent primordial gas runaway cooling (for a deeper discussion we refer the interested reader to the review by Valiante et al. Reference Valiante, Agarwal, Habouzit and Pezzulli2017) Furthermore, pristine-chemistry studies finding very large J LW thresholds in the close vicinity of star-forming regions typically neglect stellar evolution and metal pollution from stellar sources. This can seriously affect the results about critical J LW values. Given the large uncertainties, we have no reason to favour the results of some authors with respect to other authors and, in practice, the only general agreement among the various literature studies is that required critical J LW values should be between J 21 and 103J 21.
3.5. DCBH host candidate structure
To discuss the possibility that a halo candidate selected with the basic necessary requirements mentioned above turns in fact into a DCBH host, it is important to understand whether the local halo structural properties could have an impact on the actual gas direct collapse. Indeed, mergers and/or substructure formation alter the gas thermal state and lead to fragmentation, inhibiting a ‘pure’ direct collapse. For this reason we check the presence of substructures in the three halo candidates.
The biggest halo at z = 9 (candidate A) has no sub-haloes, while the other two candidates (candidate B and C) are composed by one major halo and one smaller sub-halo.Footnote h The shape of the three candidates can be retrieved from the left panels of Figure 8, where gas over-density maps, δ, of the DCBH host candidates at z = 9 are displayed. For each candidate, we show the projection on the xy plane containing the vertical coordinate of the centre of mass. From the δ distributions, three equally spaced contour levels are derived and overplotted in black solid lines. Candidate A is a quiescent halo featuring a fairly spherical structure, mostly on the xy plane. On the contrary, candidates B and C show more irregular shapes because of the presence of a main halo and a smaller sub-halo. The presence of a smaller halo (on the right) constituting candidate B is well visible from the central stream bridging it with the main halo (on the left). Candidate C, instead, is clearly constituted by two distinct bound objects. The projection highlights that active interactions between the two components (merging event) are taking place and are responsible for the asymmetric compression of the material surrounding them.
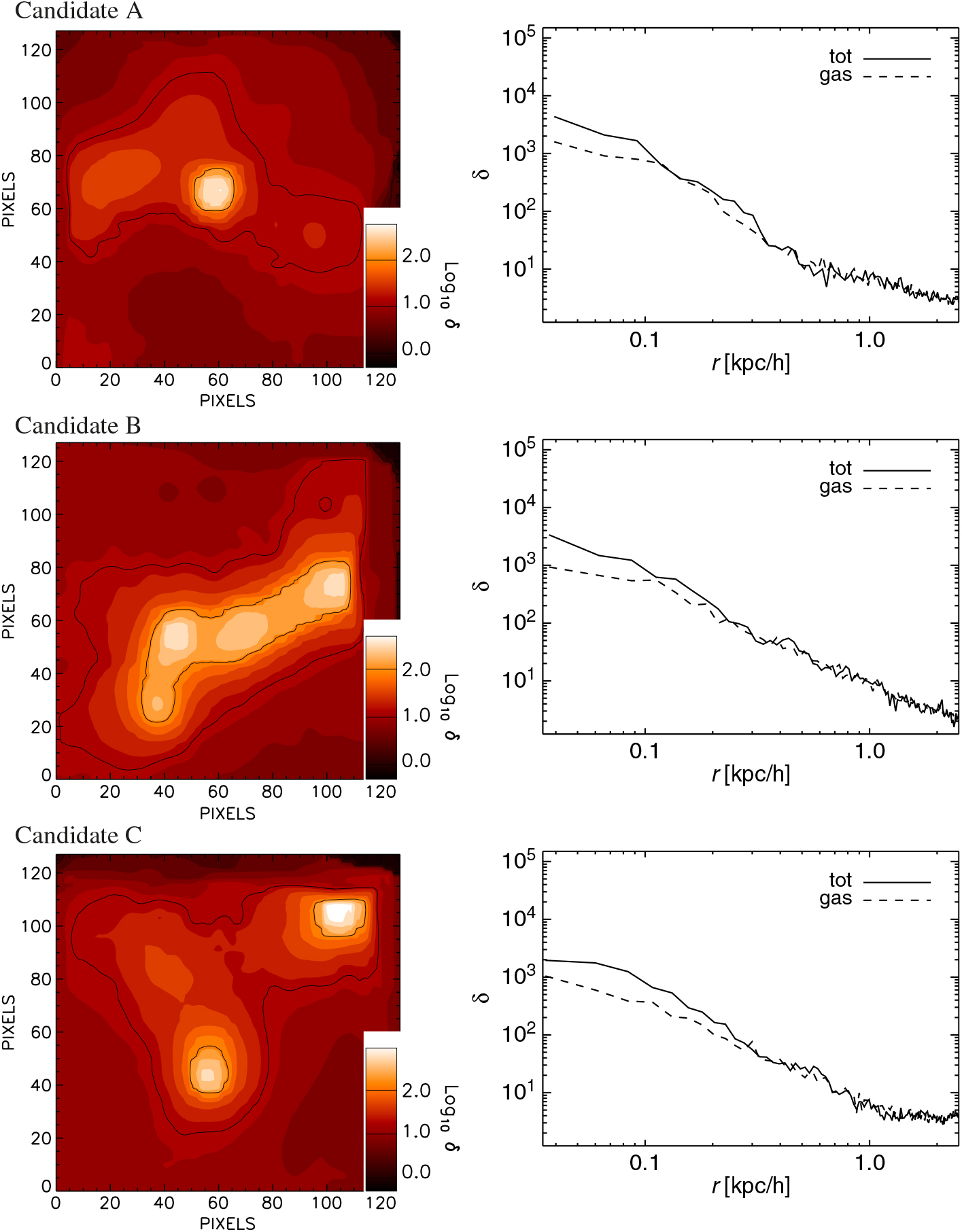
Figure 8. Left: Maps of the gas over-density with respect to the mean, δ, of three DCBH host candidates at z = 9 for the run with a T eff = 105 K black body as popIII SED. The maps are obtained via projection of each candidate on its xy plane containing the vertical coordinate of the centre of mass and smoothed over a grid of 128 pixels a side. Three equally spaced isocontour levels are overplotted in solid black lines. The colour scale is the Log10 δ. Right: Over-density profiles, δ, of gas (dashed lines) and total-matter (solid lines) as function of the physical radial distance, r, for candidate A (top), B (centre), and C (bottom).
Despite their local molecular content being rather low and the typical gas temperature being around 104 K, the multiple structure of candidates B and C suggests that the occurrence of a pure direct collapse is unlikely for them and that they are not favoured DCBH hosts. On the contrary, candidate A is composed by one single quiescent gaseous structure with mean temperature of about 104 K and is not subject to evident fragmentation (x mol << 1) nor merger activity.
The presence of satellites in two out of three cases implies that the formation of a pure DCBH is a rare event, even in those haloes where the basic criteria mentioned in Section 2.2 are met.
The right panels of Figure 8 show corresponding over-density profiles of the candidates A (top), B (centre), and C (bottom) as function of the radius normalised to the virial one. Gas profiles and total-matter profiles are displayed in the three panels by dashed and solid lines, respectively. The three profiles are computed over radial shells around the centre of mass of each halo; therefore, the differences in the shapes of the objects are smeared out. Over-densities reach values ≳103 (consistently with the maps on the left panels) and in all cases the declining trend for both gas and total content is well visible. In particular, gas behaviour is very regular due to the lack of ongoing star formation and feedback effects. These results are consistent with quiescent haloes, since active star-forming structures are expected to have larger central over-densities, δ. For example, molecular cooling ignites catastrophic runaway and collapses at typical number densities of ~1 cm−3, that is, at values roughly 105 times the critical density (with a modest z dependence).Footnote i
The profiles of the total-matter content are led by dark-matter, while the gas profiles show some divergence towards the centre of about a factor of 2 for candidates A and C, and of a factor of 3 for candidate B. Smaller deviations from the total trend can be observed even at larger distances, where δ ~ 10–102. Since the candidates B and C contain substructures, it is unlikely that they will collapse directly and form a DCBH, because, in order to do so, their substructures should merge during collapse. However, mergers are commonly accompanied by gas compression and shocks that cause H2 (re)formation capable of stimulating violent thin-shell instabilities even in the presence of intense LW flux and for a significant range of shock velocities, as well as a boost of HD abundances determined by the increased H2 fractions (Shapiro Kang 1987; Ahn & Shapiro Reference Ahn and Shapiro2007; Whalen & Norman Reference Whalen and Norman2008; Petkova & Maio Reference Petkova and Maio2012). More quantitatively, the cooling timescale, t cool, for H-dominated monoatomic gas around 104 K can be written as
where k B is the Boltzmann constant, T the gas temperature, Λ the cooling function, and n H the gas H number density (see e.g. Figure 4 in Maio et al. Reference Maio, Dolag, Ciardi and Tornatore2007).
During merger events, gas compression, molecule reformation, and tidal effects are likely to make the gas fragment into several clumps, instead of leading the formation of a massive black-hole seed (mediated by the collapse of a single supermassive star; Hosokawa, Omukai, & Yorke Reference Hosokawa, Omukai and Yorke2012; Hosokawa et al. Reference Hosokawa, Yorke, Inayoshi, Omukai and Yoshida2013, Reference Hosokawa, Hirano, Kuiper, Yorke, Omukai and Yoshida2016).
3.6. DCBH host candidate thermal and chemical characteristics
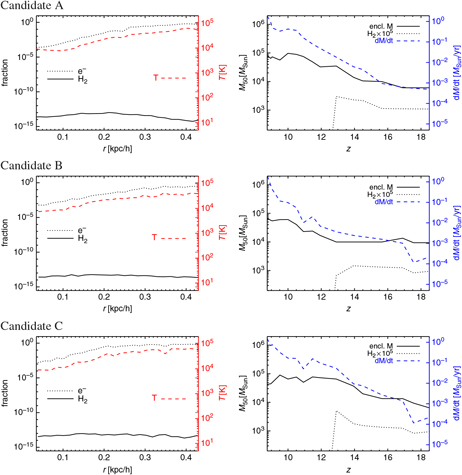
In Figure 9 we show the main chemical and thermal characteristics of the three candidates.
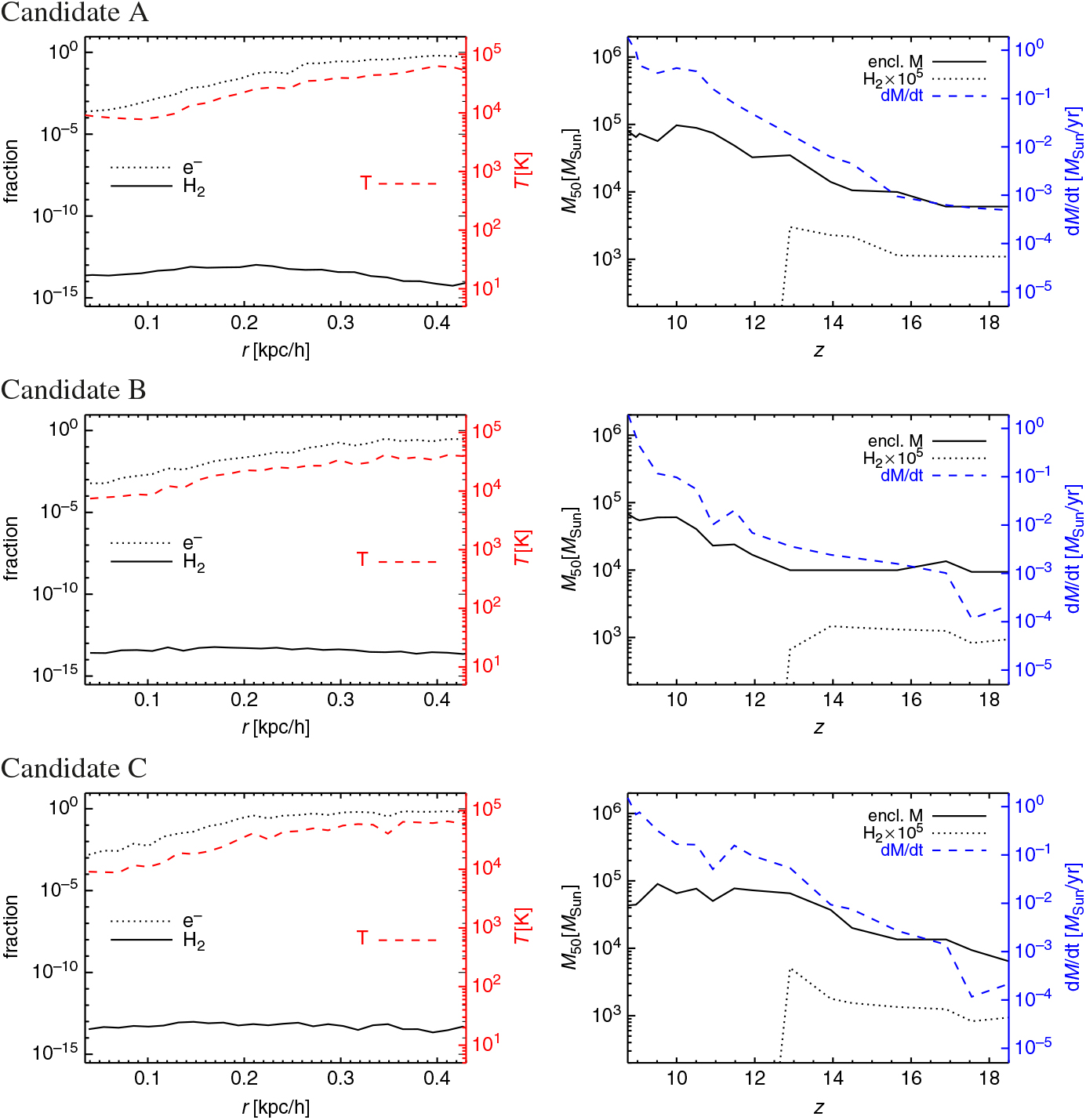
Figure 9. Left: Radial profile of electron fraction (dotted lines), H2 molecular fraction (solid lines), and mass-weighted temperature (dashed lines) for candidate A (top), B (middle), and C (bottom). The right scale (in red) refers to temperature values in Kelvin. Right: Evolution as a function of redshift, z, of the enclosed mass within the innermost 50 pc/ h (solid lines), of the H2 molecular mass times 105 (dotted lines) and of the expected inflow rate (dashed lines). The right scale (in blue) refers to the values of the inflow rate in solar masses per year.
On the left column we show radial profiles of electron fraction, H2 molecular fraction and mass-weighted temperature for the candidate A (top raw), B (middle raw), and C (bottom raw). On the right column, the redshift evolution of the mass within the innermost 50 physical pc/h, M 50, is displayed for the enclosed material, as well as for the corresponding H2 molecular mass and inflow rates.
The radial profiles are computed under spherical approximation and by assuming that the centre of the halo corresponds to the position of its most bound particle.Footnote j The resulting shapes are very similar for all three candidates. Due to dissociating radiation, residual H2 fractions are always tiny, with values about 10−14 (left column in Figure 9), while electron abundances vary between ~ 10−4 (in the neutral central regions with T ≲ 104 K) and fractions of unity (around or beyond the virial radii, ≳ 0.3 kpc/h, where T ≳ 104 K and H atoms start getting ionised). These trends are consistent with the profiles of gas temperature (dashed line, right scale in the panels) that give typical values of about or slightly lower than 104 K in the innermost denser regions and slightly larger in the diffuse outskirts. This is in line with the corresponding gas density profiles of these haloes (dashed lines in previous Figure 8) and consistent with previous studies by, for example, Kitayama et al. (Reference Kitayama, Yoshida, Susa and Umemura2004), Whalen et al. (Reference Whalen, Abel and Norman2004) and Abel, Wise, & Bryan (Reference Abel, Wise and Bryan2007), who showed that ionising shocks from massive popIII sources can leave behind a warm ~3 × 104 K diffuse medium. Ionisation and recombination processes around 104 K are very fast and give origin to the patterns observed in the three profiles of the electron fraction. Given the negligible amount of available H2 molecules, the gas of these pristine haloes cannot ignite metal-free cooling nor fragmentation below ~8 × 103 K.
On the right column of Figure 9, the redshift evolution of the three candidates, A, B, and C, is computed by tracing in time their progenitors and by evaluating the mass in a sphere of 50 pc/h radius around the most bound particle, M 50, at each snapshot, for both the enclosed halo mass and the H2 content. We also compute the corresponding mass inflow rate, ![]() $$\dot M_{{\rm{in}}} \sim c_s^3 /G$$, with cs sound speed and G gravitation constant (O’Shea & Norman Reference O’shea and Norman2007, Reference O’shea and Norman2008). Mass evolution appears to be quite smooth. The progenitors of the considered haloes feature M 50 values increasing by one order of magnitude, from roughly 104 M⊙ at z ≃ 20 up to almost 105 M⊙ at z ≃ 9. In particular, candidate A reaches M 50 ≃ 8 × 104 M⊙, candidate B M 50 ≃ 7 × 104 M⊙, and candidate C M 50 ≃ 4 × 104 M⊙. The evolution of candidate B is the most regular one, instead candidates A and C that are closer to the star-forming regions suffer more photo-heating at lower redshifts, as visible from the small decline of M 50 at z ~ 10 and its subsequent stabilisation. Since the total mass of these candidate haloes is around 106 M⊙, the amount of material enclosed in the innermost 50 pc/h constitutes a kernel of almost 1/10th the halo mass. The most striking event is definitely the dramatic decrease of H2 molecules, that, during the star formation episodes at z ≳ 10, are destroyed down to fractions < 10−13 by the dissociating radiation coming from the newly established star-forming regions. As a comparison, mass profiles do not show such sudden variations. The expected inflow rates (right scale in the plots) evolve accordingly to the mass growth and are sensitive to the thermal state of the gas. The final value achieved by candidates A and B is almost 2M⊙/yr, while candidates C features Ṁin ≃ 1M⊙/yr. These values are reached only in the final part of their evolution (z ≃ 9 – 10), when the kernel mass M 50 stabilises and Ṁin steepens. Before z ~ 10 typical inflow rates are small, Ṁin << 10−1 M⊙/yr. We warn the reader that exact estimates for the inflow rates bear dependences on assumptions and environment. Standard commonly used rates of
$$\dot M_{{\rm{in}}} \sim c_s^3 /G$$, with cs sound speed and G gravitation constant (O’Shea & Norman Reference O’shea and Norman2007, Reference O’shea and Norman2008). Mass evolution appears to be quite smooth. The progenitors of the considered haloes feature M 50 values increasing by one order of magnitude, from roughly 104 M⊙ at z ≃ 20 up to almost 105 M⊙ at z ≃ 9. In particular, candidate A reaches M 50 ≃ 8 × 104 M⊙, candidate B M 50 ≃ 7 × 104 M⊙, and candidate C M 50 ≃ 4 × 104 M⊙. The evolution of candidate B is the most regular one, instead candidates A and C that are closer to the star-forming regions suffer more photo-heating at lower redshifts, as visible from the small decline of M 50 at z ~ 10 and its subsequent stabilisation. Since the total mass of these candidate haloes is around 106 M⊙, the amount of material enclosed in the innermost 50 pc/h constitutes a kernel of almost 1/10th the halo mass. The most striking event is definitely the dramatic decrease of H2 molecules, that, during the star formation episodes at z ≳ 10, are destroyed down to fractions < 10−13 by the dissociating radiation coming from the newly established star-forming regions. As a comparison, mass profiles do not show such sudden variations. The expected inflow rates (right scale in the plots) evolve accordingly to the mass growth and are sensitive to the thermal state of the gas. The final value achieved by candidates A and B is almost 2M⊙/yr, while candidates C features Ṁin ≃ 1M⊙/yr. These values are reached only in the final part of their evolution (z ≃ 9 – 10), when the kernel mass M 50 stabilises and Ṁin steepens. Before z ~ 10 typical inflow rates are small, Ṁin << 10−1 M⊙/yr. We warn the reader that exact estimates for the inflow rates bear dependences on assumptions and environment. Standard commonly used rates of ![]() $$0.975 c_s^3 /G$$ refer to spherical hydrostatic isothermal clouds accreting at constant rate (Shu Reference Shu1977; Hunter Reference Hunter1977). Violent inflow rates of
$$0.975 c_s^3 /G$$ refer to spherical hydrostatic isothermal clouds accreting at constant rate (Shu Reference Shu1977; Hunter Reference Hunter1977). Violent inflow rates of ![]() $$46.84 c_s^3 /G$$ removed are expected for Larson (Reference Larson1969)–Penston (Reference Penston1969) self-similar solutions after a discontinuous jump from an initial value of
$$46.84 c_s^3 /G$$ removed are expected for Larson (Reference Larson1969)–Penston (Reference Penston1969) self-similar solutions after a discontinuous jump from an initial value of ![]() $$29 c_s^3 /G$$ removed (Whitworth & Summers Reference Whitworth and Summers1985) Time-dependent accretion rates with initial central values of
$$29 c_s^3 /G$$ removed (Whitworth & Summers Reference Whitworth and Summers1985) Time-dependent accretion rates with initial central values of ![]() $$47 c_s^3 /G$$ removed were suggested by Foster & Chevalier (Reference Foster and Chevalier1993) who also found a rapid decline at later times to
$$47 c_s^3 /G$$ removed were suggested by Foster & Chevalier (Reference Foster and Chevalier1993) who also found a rapid decline at later times to ![]() $$ \mathbin{\lower.3ex\hbox{$\buildrel<\over {\smash{\scriptstyle\sim}\vphantom{_x}}$}} 10 c_s^3 /G$$. Modest inflow rates in more realistic axisymmetric MHD contracting cloud undergoing runaway collapse may vary up to maximum rates of
$$ \mathbin{\lower.3ex\hbox{$\buildrel<\over {\smash{\scriptstyle\sim}\vphantom{_x}}$}} 10 c_s^3 /G$$. Modest inflow rates in more realistic axisymmetric MHD contracting cloud undergoing runaway collapse may vary up to maximum rates of ![]() $$40 c_s^3 /G$$, with late-phase lower limit
$$40 c_s^3 /G$$, with late-phase lower limit ![]() $$ \sim 2.5 c_s^3 /G$$ and time-averaged value of
$$ \sim 2.5 c_s^3 /G$$ and time-averaged value of ![]() $$ \sim 4 c_s^3 /G$$ (Galli & Shu Reference Galli and Shu1993a,b; Tomisaka Reference Tomisaka1996; Safier, McKee, Stahler 1997). These values are not dramatically different from more recent studies of magnetic and non-magnetic clouds (Mellon & Li Reference Mellon and Li2008; Machida & Doi Reference Machida and Doi2013; Susa, Doi, & Omukai Reference Susa, Doi and Omukai2015. With respect to these considerations, the values showed in the right plots of Figure 9 might represent a lower limit and actual rates can episodically reach values of a few to tens times higher.
$$ \sim 4 c_s^3 /G$$ (Galli & Shu Reference Galli and Shu1993a,b; Tomisaka Reference Tomisaka1996; Safier, McKee, Stahler 1997). These values are not dramatically different from more recent studies of magnetic and non-magnetic clouds (Mellon & Li Reference Mellon and Li2008; Machida & Doi Reference Machida and Doi2013; Susa, Doi, & Omukai Reference Susa, Doi and Omukai2015. With respect to these considerations, the values showed in the right plots of Figure 9 might represent a lower limit and actual rates can episodically reach values of a few to tens times higher.
These trends clearly suggest that the three candidates A, B, and C can remain metal free during their entire lifetimes, because they are sufficiently far from star-forming haloes and metal-free star formation is prevented by the fact that destroyed H2 molecules in the halo progenitors are not able to form again by z ~ 9.
3.7. DCBH host candidate rotational patterns
Independently of the structure of the haloes, rotational patterns play an important role for the occurrence of gas collapse. In fact, gas rotational motions will halt direct collapse and prevent DCBH formation. For this reason, we investigate the angular momentum per unit mass of the material hosted by the DCBH host candidates, j = r × v, with r and v particle position and velocity vectors (Binney & Tremaine Reference Binney and Tremaine2008). For each particle, we compute the circularity ε = j z/j circ distributions, being j z the component of the angular momentum perpendicular to the plane of rotation and j circ the expected angular momentum of a circular orbit in the gravitational potential determined by the enclosed mass, M, at the same radial distance, r, that is, j circ = r v circ, with v circ = [GM(r)/r]1/2. Obviously, ε is sensitive to the rotational patterns of the constituting halo particles and can give us hints about the dynamics of the material inside the hosting halo. Values of ε≃0 represent test particles that have negligible angular momentum and that can eventually collapse. The closer is ε to unity, the closer is the motion of a test particle to a stable (i.e. non-collapsing) circular orbit. Larger ε values refer to unbound particles that move along escaping orbits.
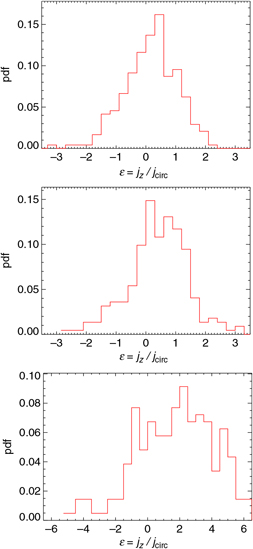
In Figure 10 the distributions of the ε values for the gas of the three DCBH candidates are plotted. The trends reflect the structure of the haloes, and the spread of the distributions is consistent with the variety of statistical properties of rotational patterns expected at these early times (Biffi & Maio Reference Biffi and Maio2013; de Souza et al. Reference de Souza, Ciardi, Maio and Ferrara2013; Prieto et al. Reference Prieto, Jimenez, Haiman and González2015). In particular, candidate A is an isolated object with a quite regular distribution, while candidate B shows a double peak that is linked to its internal substructure. The candidate C shows a very irregular behaviour as a consequence of its disturbed state due to the ongoing internal interactions. Values of |ε| > 1 refer to particles which are not dynamically bound to the structure. Their amounts vary significantly in the three host candidates. For candidate A, a fraction ≲20% of gas parcels is going to escape, while the other two candidates feature larger amounts of escaping material, ranging from more than 25% for candidate B up to about 75% for candidate C. The unbound material has little implications for candidates A and B, which are going to preserve most of their gas mass. However, for candidate C the situation is more critical, as it is going to be left with a gas mass that is almost one order of magnitude smaller. This complicates the formation of any intermediate-mass black hole from this halo.
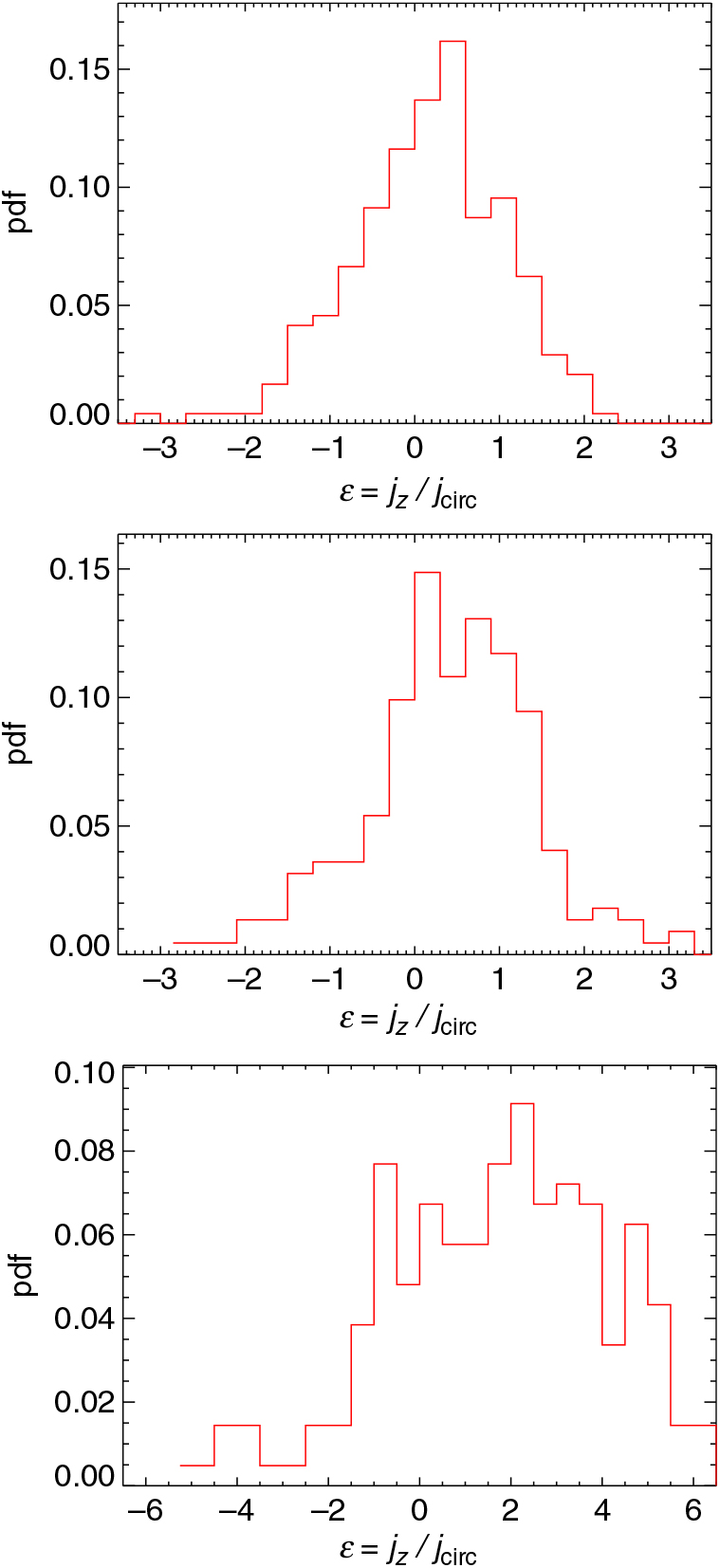
Figure 10. Distributions of the gas circularity, ε, for the three DCBH host candidates A (top), B (centre), and C (bottom) at z = 9 for the run with a T eff = 105 K black body as popIII SED.
A similar conclusion is reached in Figure 11, where the ratio between jz and the absolute value of the mean halo angular momentum, |j mean|, for both gas and dark-matter is considered. This ratio is linked to disk formation in the inner structure of the halo and provides a measure of the alignment of the angular momentum of every single particle with the mean angular momentum.
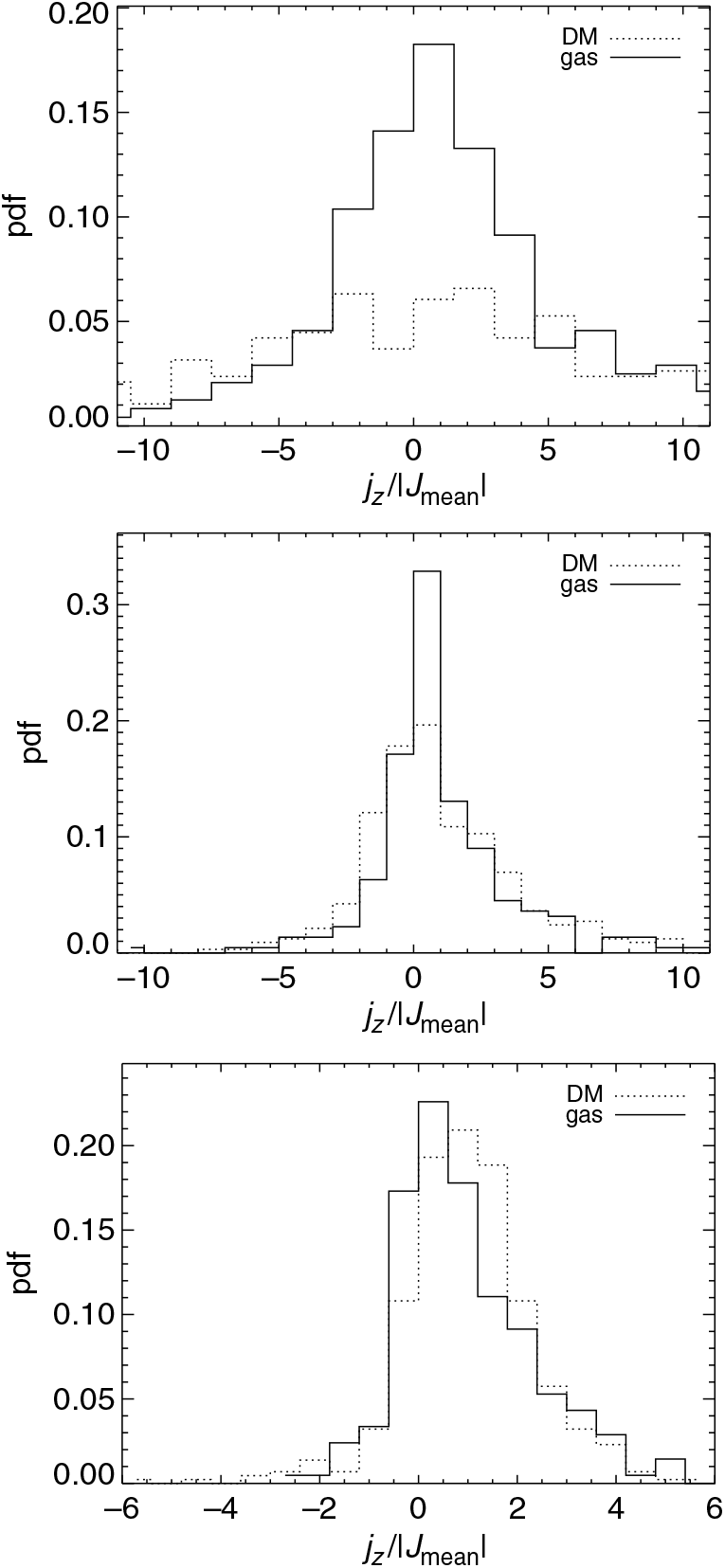
Figure 11. Distributions of the ratios between gas and dark-matter j z values and the mean halo angular momentum for the three DCBH host candidates A (top), B (centre), and C (bottom) at z = 9 for the run with a T eff = 105 K black body as popIII SED.
Candidate A shows a gas ratio distribution that is peaked around zero and declines symmetrically as a consequence of its roughly spherical shape. Candidates B and C, instead, have distributions that decline in a non-symmetric way, with a more prominent high-j z tail. This arises from the particles of the sub-halo that are located at distances larger than those of the main halo.
The trends of gas and dark-matter are quite similar, although for j z/ |j mean| ≃ 0 there is a higher gas peak in the gas distribution. This originates mostly from the central regions of the halo, where gas settles in a spherical shape, and also explains why the difference is more marked in candidate A, rather than in the more irregular candidates B and C.
The tails of the distributions for gas and dark-matter angular momenta have similar behaviours for values different from zero, meaning that the dynamical state of those gas particles is significantly influenced by the underlying dark-matter distribution.
3.8. DCBH candidate host turbulent motions
Turbulence is another important limiting factor for gas direct collapse, since it enhances gas fragmentation and hinders DCBH formation. Strictly speaking, turbulence arises from the nonlinear advection term, (u · ▽) u, and the dissipative term, v ▽2u, in the equations of motion for a fluid whose velocity field is u and kinematic viscosity is v. The (dimensionless) Reynolds number quantifies the effects of inertial forces with respect to viscosity forces and is defined as Re ≡||(u · ▽) u|| / ||(v ▽2)u|| ~ ul/v, where l is the typical scale of the turbulent motion. When Re tends to zero the system is viscosity dominated and turbulence decays. The scale at which Re = 1 is denominated dissipation scale. When Re >> 1 the advection term dominates and the influence of viscous forces is negligible. In most practical situations this usually happens for fluids with Re values above 4 000 that are commonly considered turbulent. As an example, in the cool ISM, it is well established since long time that the Reynolds number assumes values between 105 and 107 (Cordes, Weisberg, & Boriakoff Reference Cordes, Weisberg and Boriakoff1985; Armstrong, Rickett, & Spangler Reference Armstrong, Rickett and Spangler1995).
Quantitatively, the kinematic viscosity of the gas, v, can be estimated as v ~ c / nσ, with c sound speed, n mean number density, and σ ~ 10−15cm2 typical interaction cross section (Elmegreen & Scalo Reference Elmegreen and Scalo2004). Consequently, Re depends on the Mach number of the gas and its thermal state. Despite these idealisations, in reality turbulence is not uniformly distributed but shows clear spatial and temporal intermittency effects: regions particularly active coexist with regions completely inactive. In general, it is possible to take into account these effects, but they will not be considered here, because the expected deviations are small in comparison to the order-of-magnitude estimates presented below.
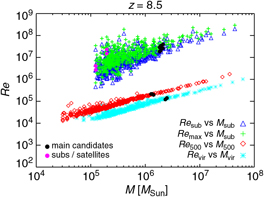
Figure 12 shows results for Re as expected at z = 9. To have an idea of the global behaviour of the gas in each halo, we estimate Re by employing the (physical) quantities describing each object, as computed at post-processing time, both via friend-of-friend algorithm (velocities, radii, and masses at over-densities of 200 and 500 with respect to the background) and substructure finder (namely, velocity dispersion, maximum radial velocities and corresponding radii, as well as substructure masses). Given the different nature of all these quantities, Re results are not expected to coincide exactly, but should give us a broad overview of the orders of magnitudes reached case by case.
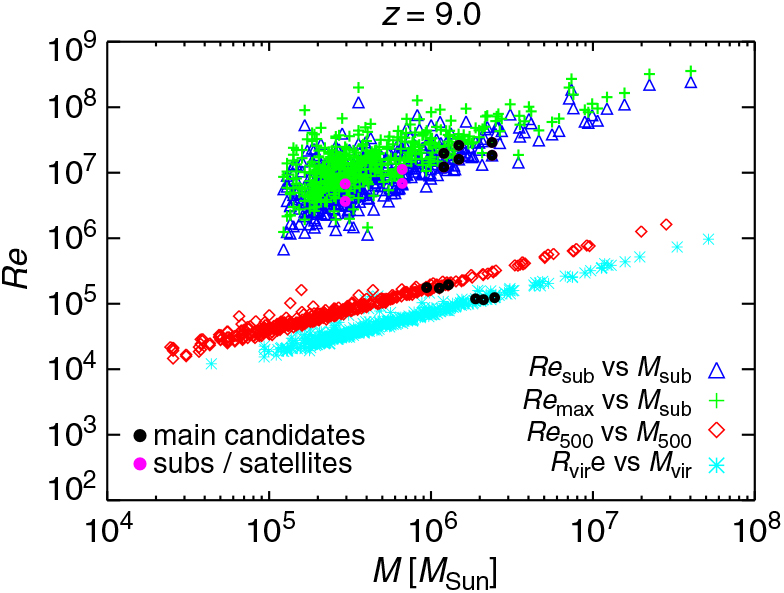
Figure 12. Reynolds number estimated with different approaches (Re sub, Re max, Re 500, and Re vir) as a function of substructure mass, M sub, mass within an over-density of 500, M 500, and virial mass, M vir, at z = 9 for the run with a T eff = 105 K black body as popIII SED (see details in the text). Black bullet points highlight the values for DCBH host candidates (three friend-of-friend objects overplotted on the red diamonds and cyan asterisks). Main haloes and substructures/satellite haloes are overplotted, respectively, by black and magenta bullets on the sequences of blue triangles and green crosses.
We show them as function of the substructure mass, M sub, the mass within an over-density of 500, M 500, and the virial mass M vir to get the corresponding Re sub, Re max, Re 500, and Re vir values. In particular, Re sub is obtained by substructure velocity dispersion and maximum radial velocities (blue triangles); Re max is obtained by maximum radial velocities and the radii at which such velocities are reached (green crosses); Re 500 is obtained by velocity dispersions and radii within an over density of 500 (red diamonds); Re vir is obtained by velocity dispersion and virial radii (cyan asterisks).
We warn that the smallest haloes, despite their virial values can be obtained, do not always have well-defined quantities for Re sub and Re max calculations, due to the limited number of their constituting particles.
Bullet points highlight the values for the DCBH host candidates identified in the previous sections. Consistently with what mentioned before, there are three friend-of-friend objects candidate to host a DCBH and they are over-plotted both on the sequences of red diamonds and on the sequences of cyan asterisks. Among these three halo candidates, two are composed by a main halo and a satellite, for resulting five substructures that are over-plotted by bullets on the green crosses and the blue triangles (black bullets refer to main haloes and magenta bullets to satellites).
Independently from the details about Re in the figure, the turbulent nature of the primordial haloes is striking. The values obtained for bigger objects vary between roughly 105 and 108, depending on the assumptions; however, they are in broad agreement with previous studies of early star-forming haloes (Maio et al. Reference Maio, Khochfar, Johnson and Ciardi2011b) as well as with the values expected in turbulent ISM environments. Moreover, in most cases Mach numbers are close to unity, which makes early turbulent motions nearly supersonic.
Figure 12 shows the effects of different ways of estimating Re; however, it does not give us information on the role of metallicity for DCBH candidates. For this reason, in Figure 13 the results for metal-free haloes (grey symbols) are directly compared to the results for haloes that are not metal-free (color symbols).
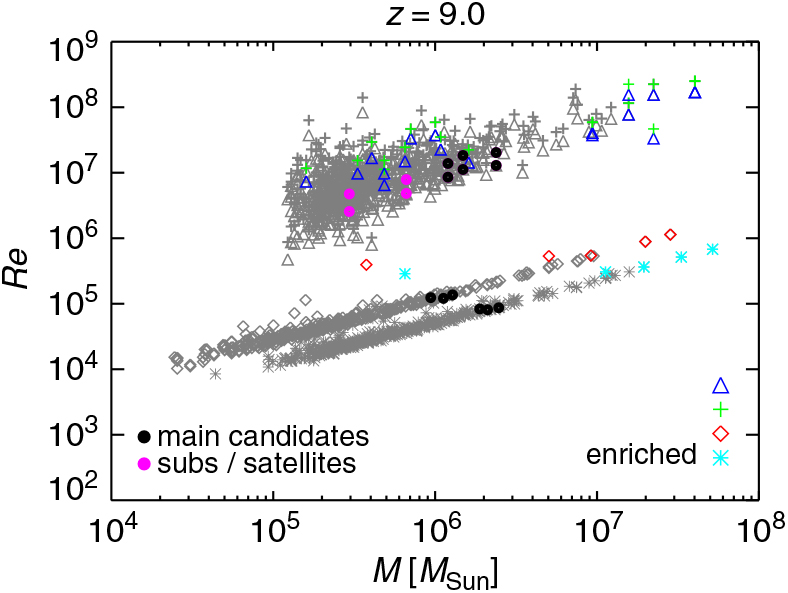
Figure 13. Reynolds numbers, estimated with the same approaches as Figure 12, are shown in grey for pristine haloes and with coloured symbols for metal-enriched haloes.
In this case, cyan asterisks refer to metal-enriched haloes whose Re numbers have been computed through virial quantities (i.e. Re vir vs M vir). They lie along the trend of the whole halo population, although their Re > 105 values are higher than DCBH candidates (bullets) both at larger (~107 M⊙) and smaller (≲ 106 M⊙) masses. Similarly, also red diamonds (Re 500 vs M 500 for metal-enriched haloes) are above the bullet points, roughly following the general trend. In the high-mass end, the larger Re values are mainly due to the larger masses of haloes above ~ 107 M⊙. In the low-mass end (see red diamond and cyan asterisk at masses ≲ 106 M⊙), Re values are affected by the metal enrichment process.
The values denoted by green crosses (Re max vs M sub) and blue triangles (Re sub vs M sub) are computed by using substructure information and refer to both enriched haloes and satellites. Their distribution is quite sparse; however, most of the points lie above the trend inferred from the bullets by up to 1 dex. In this respect, DCBH candidates host lower chaotic motions than metal-enriched haloes, although they are in line with the expectations for the most quiescent pristine haloes (grey symbols).
The physical reason for such behaviour relies on the additional entropy injected during metal pollution from nearby star-forming regions. Enriched material spreading into the surrounding objects affects the velocity and thermodynamical structure of hosting haloes, possibly causing an increase in the resulting Re with respect to DCBH host candidates and pristine haloes. This is particularly clear from the deviations from the general trend of the smaller enriched structures (asterisks and diamonds). Re values of larger polluted objects, instead, seem to be less sensitive to metal spreading, due to the higher degree of stochasticity implied by their bigger masses.
The wide scatter in the relations denoted by crosses and triangles indicates a strong influence of cosmic environment and substructure formation, too, that will influence velocity and thermodynamical features depending on whether haloes are in clustered or isolated regions (in fact, the spread is wider at the low-mass end, that is dominated by small structures and satellites). The position of DCBH host candidates on the bottom edge of these two samples in the figure reveals their formation preferentially in weakly clustered regimes or in isolation, where shocks from structure formation Wise & Abel Reference Wise and Abel2007; Wise et al. Reference Wise, Abel, Turk, Norman and Smith2012b) are less common.
From these considerations it emerges that DCBH host candidates are on average less turbulent structures than metal-enriched haloes (diamonds and asterisks) and are among the lowest-turbulence structures with pristine composition in the corresponding mass range (crosses and triangles).

Figure 14. Distributions of the Reynolds number estimated at the hydro smoothing length scale for the three DCBH candidates A (solid line), B (dotted line), and C (dashed line). The distributions are normalised to their peak value.
To judge better the level of turbulence within the DCBH hosting structures we compute the Re values for their constituting gas particles, by employing the gas SPH smoothing length (hsml) and the gas velocity. This allows us to assess turbulent motion locally rather than globally. In Figure 14 we show the distribution of Re numbers at the SPH smoothing scales (hsml). We find a broad trend within Re ≳ 103 and ~ 105 for all the three candidates, with peak values at Re ~104 –104.7 for candidate A, Re ~ 104 for candidate B, and Re ~ 103.6 – 104.2 for candidate C. The distributions are very disperse, but all of them lie at Re ≳ 103.6 ~ 4 000, meaning that even at particle level, turbulent motions are relevant. The orders of magnitude of these local estimates are consistent with the orders of magnitude of the global estimates shown above, once taken into account the different typical scales (radius vs hsml) involved in the two cases. In practice, they show that turbulence plays an important role at all resolved scales.
We have checked that by adopting the mean square velocity, instead of the particle velocity, as typical velocity of the fluid, the results about Re remain unchanged.
3.9. DCBH host candidate fate
The presence of turbulence might affect direct collapse, providing additional non-thermal pressure support to the gas. Since the turbulent dissipation timescale can be written as l/σ ≈ 4 Myr (l/40 pc)(σ/10 km/s)−1, with l turbulent scale and σ velocity dispersion (Semenov, Kravtsov, Gnedin 2016), the timescales during which direct-collapse events are possible lie between ~ 4 and 40 Myr. The former estimate is led by turbulence decay, while the latter by molecular-chemistry arguments. In practice, the conditions for DCBH formation hold less than 40 Myr and hence the direct collapse should be as rapid as that. As an example, the innermost isothermal core of the candidate A at z = 9 has a typical dimension of ~ 100 pc. Reasonably, this value is comparable or larger than the turbulent decay scale and, considering the typical σ ~ 10 km/s, the resulting dissipation timescale is ≲10 Myr.
Hydro- and magneto-hydrodynamical simulations generally show turbulence dissipation on times that are much shorter than crossing times, both in subsonic and supersonic regimes (Stone, Ostriker, & Gammie Reference Stone, Ostriker and Gammie1998; Mac Low et al. Reference Mac Low, Klessen, Burkert and Smith1998; Burkert Reference Burkert2006; Kim & Basu Reference Kim and Basu2013; Semenov et al. Reference Semenov, Kravtsov and Gnedin2016), albeit still of the order of a few Myr.
So, the occurrence of turbulent motions should delay DCBH formation until turbulence dissipates.
At the same time, two-third of the candidates show substructures, which means that a pure direct collapse is rather unlikely and the process must be eventually accompanied by a merger (Latif et al. Reference Latif, Bovino, Grassi, Schleicher and Spaans2015; Becerra et al. Reference Becerra, Greif, Springel and Hernquist2015).
Merger events and substructure evolution (as e.g. in candidates B and C) are likely to inhibit gas direct collapse, enhancing gas fragmentation and halting accretion via tidal forces (in agreement with Chon et al. Reference Chon, Hosokawa and Yoshida2018).
Local rotational patterns and photo-evaporation effects (see previous sections) have maybe less severe implications, as they could cause the loss of only a fraction of the gas hosted in the halo potential wells.
Thus, it turns out that the basic requirements necessary for DCBH formation, whenever met, do not guarantee the actual gas direct collapse. In practice, the required necessary conditions are not sufficient for pure DCBH formation in two-third of the cases, while DCBH is probably expected for the remaining candidate A.

Figure 15. DCBH host candidates at z = 8.5 for the run with a T eff = 105 K black body as popIII SED.
What happens next will strongly depend on the surroundings of the host halos. If gas photo-evaporation is stronger than the host potential wells (no matter whether they are generated by the whole halo or the newly formed DCBH) accretion will be inhibited. Otherwise, accretion is expected to be episodic. When averaged over several duty cycles, it should typically proceed at sub-Eddington rates (Johnson & Bromm Reference Johnson and Bromm2007; Milosavljević et al. Reference Milosavljević, Bromm, Couch and Oh2009; Maio et al. Reference Maio, Dotti, Petkova, Perego and Volonteri2013b; Ricci et al. Reference Ricci2017). In cases when the surrounding environment is very dense, it is possible to reach super-Eddington rates (Wyithe & Loeb Reference Wyithe and Loeb2012; Alexander & Natarajan Reference Alexander and Natarajan2014; Madau, Haardt, & Dotti Reference Madau, Haardt and Dotti2014; Inayoshi et al. Reference Inayoshi, Kashiyama, Visbal and Haiman2016; Pezzulli, Valiante, & Schneider Reference Pezzulli, Valiante and Schneider2016; Pezzulli et al. Reference Pezzulli, Volonteri, Schneider and Valiante2017). The existence of massive black holes at z ~ 7 is challenging to explain, because it requires a growth process taking place in less than a billion years. More likely, the growth mechanisms could be active for only a few 100 s Myr, since massive black-hole seeds are usually expected at redshifts of z ~ 6–20, after the first structures form. Currently, no observational detections of DCBHs are available. Studies of possible identifications of DCBH candidates in the CANDELS/GOODS-S survey have claimed only two candidates with predicted mass greater than 105 M⊙, with robust X-ray detection and with photometric redshift z > 6 (Pacucci et al. Reference Pacucci, Ferrara, Grazian, Fiore, Giallongo and Puccetti2016). In theory, ad hoc seeding with 105M⊙ black holes at z ≳ 10 of all the haloes with mass larger than 109 M⊙ (as commonly done in large numerical simulations) could lead to Eddington accretion rates at z = 9–6 and to black hole masses higher than 109 M⊙ at z ≲ 7. Nevertheless, early attainment of a minimum mass of at least 106 M⊙ remains crucial for a fast growth. These considerations suggest that DCBHs could be interesting massive seeds, since the 105 M⊙ black-hole seeds commonly adopted in large numerical simulations are easily justified with this channel, although it is quite unlikely that all the early haloes blindly seeded in simulations are actual hosts of DCBHs.
To conclude, we briefly investigate thermal and chemical properties of the halo populations identified at a time later than z = 9, specifically at z = 8.5 (when the Universe is about 0.58 Gyr old). In Figure 15, DCBH host candidates (bullet points) for the run with top-heavy IMF and a T eff = 105 K black body as popIII SED (TH.1e5) are shown for redshift z = 8.5. Once compared to the corresponding results of Figures 4 and 5 at z = 11.5 and z = 9, the changes in the molecular content are evident. They are a consequence of the strong dissociating photon field established by primordial massive stars. As mentioned before, at z = 9.5 no DCBH host candidate is found, while a few Myrs later, at z = 9, we have identified three haloes satisfying the basic requirements (previous Figure 5). Later on, at z = 8.5 we find three additional systems. Of the three z = 8.5 DCBH candidates (mapped in Figure A1 in Appendix), two are composed by two substructures. The third candidate is, instead, an isolated object (see host properties in Figure A2 in Appendix). Notwithstanding the similarities, the three DCBH host candidates identified at z = 8.5 do not coincide with the ones in Figure 5 at z = 9. Their comoving (physical) distances from the central star-forming region are about 348 (37) kpc/h 179 (19) kpc/h and 48 (5) kpc/h, respectively. In comparison to the situation at z = 9, these candidates are slightly farther from the radiation sources, but they are still found in proximity of denser filamentary regions. Given the presence of substructures, rotational patterns (Figure A2), photo-heating, and turbulent Re numbers (Figures A3, A4), the formation of DCBHs in the z = 8.5 candidates is as difficult as for the z = 9 candidates.
4. Discussion
We have employed cosmological N-body hydrodynamical chemistry calculations to trace the origin of primordial DCBHs. Our simulations follow photon propagation, gas atomic and molecular chemistry, and heavy-element production from stars with different masses and metallicities during the first Gyr of the Universe. Our detailed implementation (Petkova & Maio Reference Petkova and Maio2012; Maio et al. Reference Maio, Petkova, De Lucia and Borgani2016) takes into account multi-frequency radiative transfer from 150 frequency bins in the energy range [0.7, 100] eV–H, He, D, H2, HD, HeH+ transitions as well as LW band ([11.2, 13.6] eV), near-IR (at energies ≲ 1.7 eV) and UV (~[3, 100] eV) radiation. This is coupled to non-equilibrium chemistry integration of e−, H, H+, H−, He, He+, He++, D, D+, H2, ![]() $${\rm{H}}_2^ +$$, HD, HeH+ abundances, stellar evolution, and metal enrichment from different species (He, C, N, O, Ne, Mg, Si, S, Ca, Fe, etc.) and stellar populations (Woosley & Weaver Reference Woosley and Weaver1995; van den Hoek & Groenewegen Reference van den Hoek and Groenewegen1997; Woosley, Heger, & Weaver Reference Woosley, Heger and Weaver2002; Thielemann et al. Reference Thielemann2003), as well as include PISN/SNII, AGB, and SNIa stellar phases according to suited stellar lifetimes (Padovani & Matteucci Reference Padovani and Matteucci1993).
$${\rm{H}}_2^ +$$, HD, HeH+ abundances, stellar evolution, and metal enrichment from different species (He, C, N, O, Ne, Mg, Si, S, Ca, Fe, etc.) and stellar populations (Woosley & Weaver Reference Woosley and Weaver1995; van den Hoek & Groenewegen Reference van den Hoek and Groenewegen1997; Woosley, Heger, & Weaver Reference Woosley, Heger and Weaver2002; Thielemann et al. Reference Thielemann2003), as well as include PISN/SNII, AGB, and SNIa stellar phases according to suited stellar lifetimes (Padovani & Matteucci Reference Padovani and Matteucci1993).
Such implementation allows us to investigate the physical properties of early hosts of DCBHs and to compare the predictions of our calculations for different assumptions about the adopted IMF and SED of popIII stars.
We find that DCBHs are very rare events that could be favoured by the existence of powerful primordial sources. Standard stellar sources are unlikely to establish a radiative cosmological background in the first Gyr, while massive sources are able to emit larger amounts of photons and to form a background field that can both dissociate molecules and photo-evaporate primordial haloes.
Albeit exposed to significative LW radiation, ranging from a few up to ~ 50J 21 at z = 9, the basic environmental requirements necessary for their formation, whenever met, do not guarantee the actual gas direct collapse. In fact, a number of highly nonlinear processes (merger events, substructure evolution, local rotational patterns, gas turbulence, photo-evaporation) play a significant role to halt or delay the birth of a DCBH. In practice, the required necessary conditions turn out not to be sufficient for pure DCBH formation in two-third of the cases.
Our findings are obviously subject to some caveats. It is noteworthy that alternative modelling accounting for increased physical viscosity would lower Re (Section 3.8), favouring DCBH formation, while, on the contrary, implementations reducing artificial viscosity would lead to opposite results (Morris & Monaghan Reference Morris and Monaghan1997; Dolag et al. Reference Dolag, Vazza, Brunetti and Tormen2005; Cullen & Dehnen Reference Cullen and Dehnen2010; Price Reference Price2012; Latif et al. Reference Latif, Bovino, Grassi, Schleicher and Spaans2015; Biffi & Valdarnini Reference Biffi and Valdarnini2015; Beck et al. Reference Beck2016). Overall, viscous heating provides an important pathway to obtain an atomic gas phase within the centre of the halo and helps the formation of very massive objects.
The exact numerical parameters adopted for the IMFs, wind prescriptions, initial-condition gas velocities, and related issues are likely to induce some small changes (Campisi et al. Reference Campisi, Maio, Salvaterra and Ciardi2011; Maio, Koopmans, & Ciardi Reference Maio, Koopmans and Ciardi2011a; Tescari et al. Reference Tescari, Katsianis, Wyithe, Dolag, Tornatore, Barai, Viel and Borgani2014).
Uncertainties might derive from the lack of a definitive treatment of metal diffusion mechanisms, which, despite several attempts, still remain an unsolved problem in astrophysics and further studies are still required for an accurate assessment.
Theoretical stellar yields are affected by a plethora of physical processes in stars (such as explosion mechanisms, differential rotation, initial composition, magnetic fields, nuclear reaction rates, etc.) all of which can influence the final ratios. Detailed values of popIII or popII-I metal yields for individual elements (see e.g. François et al. Reference François, Matteucci, Cayrel, Spite, Spite and Chiappini2004; Maio & Tescari Reference Maio and Tescari2015; Ma et al. Reference Ma, Maio, Ciardi and Salvaterra2015, Reference Ma, Maio, Ciardi and Salvaterra2017a) are not expected to change gas hydrodynamics significantly, because metal content and cooling in the regimes investigated here are usually dominated by oxygen, which is fairly well explored.
Besides that, molecular self-shielding is still under debate, due to its dependence on gas density and numerical resolution (Hartwig et al. Reference Hartwig, Glover, Klessen, Latif and Volonteri2015). High-resolution studies are needed to clarify its effects in promoting molecule formation and inhibiting DCBHs.
Lately, studies by Wolcott-Green et al. (Reference Wolcott-Green, Haiman and Bryan2017) have suggested that the effective temperature of popII stars might be larger than 104 K, hence using a 104 K black-body spectrum can lead to underestimating the level of LW radiation required to photo-dissociate H2. That work shows little or no difference in the H2 photo-dissociation rate for black-body effective temperatures of 2 × 104-105 K, while some variations appear between 104 K and 2 × 104 K. However, in the one-zone model developed by Wolcott-Green et al. (Reference Wolcott-Green, Haiman and Bryan2017) overestimates in the photo-dissociation rate are relatively small, just by a factor of ~ 2. Once embedded in three-dimensional calculations, the resulting effects are not expected to have a strong impact and, in fact, we did not find significant differences between the SL.1e4 and SL.4e4 cases analysed here. Similarly, recently improved calculations including additional resonance contributions to the H− photo-detachment rate give only very small corrections (less than 20%) up to black-body temperatures of 105 K (Miyake et al. Reference Miyake, Stancil, Sadeghpour, Dalgarno, McLaughlin and Forrey2010;Wolcott-Green et al. Reference Wolcott-Green, Haiman and Bryan2017).
Different stellar feedback modelling might have some implications on the DCBH scenario. In practice, different velocities acquired by gas parcels through feedback mechanisms could have an effect on the optimal distance from the central source where DCBHs can be located, although we do not expect huge variations with respect to the results found here, as long as velocity values are realistically of the order of ~ 102 km / s.
Despite the small-number statistics, it is instructive to make some comparisons to similar available works. There is a vast literature of three-dimensional radiative simulations studying pristine-gas collapse and the role of UV radiation (Machacek et al. Reference Machacek, Bryan and Abel2001; Yoshida et al. Reference Yoshida, Abel, Hernquist and Sugiyama2003; O’Shea et al. Reference O’shea, Bryan, Bordner, Norman, Abel, Harkness and Kritsuk2004; O’Shea & Norman Reference O’shea and Norman2008), as well as the birth of stars, galaxies, and their feedback effects in a cosmological context (Maio et al. Reference Maio, Ciardi, Dolag, Tornatore and Khochfar2010, Reference Maio, Khochfar, Johnson and Ciardi2011b; Wise et al. Reference Wise, Abel, Turk, Norman and Smith2012a,b, Reference Wise, Demchenko, Halicek, Norman, Turk, Abel and Smith2014; Lopez et al. Reference Lopez, Krumholz, Bolatto, Prochaska, Ramirez-Ruiz and Castro2014; Mancini et al. Reference Mancini, Schneider, Graziani, Valiante, Dayal, Maio, Ciardi and Hunt2015, Reference Mancini, Schneider, Graziani, Valiante, Dayal, Maio and Ciardi2016; Ma et al. Reference Ma, Maio, Ciardi and Salvaterra2015, Reference Ma, Maio, Ciardi and Salvaterra2017a,b). These studies have been performed with different codes (such as SPH Gadget code and AMR Enzo code) and by adopting different resolutions. Their findings highlighted that feedback prescriptions are among the main causes of differences in the final results and have a crucial role for photon production and massive black-hole seeding.
Recent pristine-gas simulations (Regan et al. Reference Regan, Visbal, Wise, Haiman, Johansson and Bryan2017, and references therein) have confirmed that LW radiation inevitably moves the gas in the host protogalaxy onto the isothermal atomic cooling track (as shown earlier by e.g. Machacek et al. Reference Machacek, Bryan and Abel2001), without the deleterious effects of either photo-evaporating the gas or polluting it with heavy elements. Star formation and feedback modelling in these studies were absent, though.
We do find that LW radiation is responsible for dissociating H2 and HD and for keeping the gas in the host protogalaxy almost isothermal (Maio et al. Reference Maio, Petkova, De Lucia and Borgani2016); however we do not rule out photo-evaporation, since this issue is tightly linked to the type of the original radiative sources considered. A similar conclusion on gas photo-evaporation in early halos was reached by Wise et al. (Reference Wise, Demchenko, Halicek, Norman, Turk, Abel and Smith2014), who stressed its role in addition to heating and ionising the surrounding medium out to a (physical) radiusFootnote k of 10–15 kpc at z = 9. These respectively reduce the in situ and external cold gas supply that could feed future star formation.
Photo-ionisation feedback is definitely responsible for evacuating gas from mini-haloes and for generating large HII regions around the central emitting source, but the implications for DCBH formation must be evaluated carefully. Regan, Johansson, & Wise (Reference Regan, Johansson and Wise2016) have noted that, due to photo-ionisation, there could exist an optimal metal-free zone for DCBH formation between 1 and 4 kpc from the emitting source. Nevertheless, this is in tension with metal spreading, not included in that study. Previous calculations by Wise et al. (Reference Wise, Abel, Turk, Norman and Smith2012a) found that one primordial SN is sufficient to enrich the entire star-forming halo and surrounding ~ 5 kpc to a metallicity of 10−3 Z⊙. Metal enrichment would, then, inhibit DCBH formation at distances shorter than 5 kpc. These arguments suggest a distance ≳5 kpc required for DCBH formation. Consistently with Wise et al. (Reference Wise, Abel, Turk, Norman and Smith2012a), we find that DCBH conditions can be fulfilled only at radii above ~5 kpc, since closer regions are polluted by metal enrichment and subject to suppression of gas collapse through photo-ionisation feedback (Kannan et al. Reference Kannan2014). Metal pollution is not included in the work by Regan et al. (Reference Regan, Johansson and Wise2016). This is also why we do not find eligible DCBH candidates in the SL.1e4 and SL.4e4 models: near the emitting source, DCBH formation is inhibited by metal spreading, while far away the radiation flux from standard solar-like or OB-type stars drops dramatically and the molecular gas fraction remains too high. Furthermore, photo-heating is also responsible for increasing the thermal energy of the gas and causing its escape from mostly low-mass haloes. The impact can be dramatic for the case of powerful sources, while, for solar-like and OB-type scenarios they are much more modest.
Other studies have investigated the possibility to have DCBH formation in pristine regions within halos where star formation has recently occurred (Dunn et al. Reference Dunn, Bellovary, Holley-Bockelmann, Christensen and Quinn2018). They have relied on Gasoline and implemented a common stochastic model with star formation probability scaling with H2 fractions, that are, in turn, tightly dependent on gas density. They study the effects on massive black-hole seeds for different assumptions on the critical flux, although do not use any radiative transfer code to propagate photons nor implement stellar evolution calculations to spread heavy elements. They confirm the strong dependence of DCBH formation on the adopted critical flux, finding results that are in line with previous ones (Habouzit et al. Reference Habouzit, Volonteri, Latif, Dubois and Peirani2016b).
Lately, Barrow et al. (Reference Barrow, Aykutalp and Wise2018) have suggested observational features of DCBH, claiming that the upcoming JWST telescope might be able to detect and distinguish a young galaxy that hosts a DCBH at z ~ 15.
The low number of DCBH candidates in comparison to the whole halo population at the redshifts of interest and the occurrence of DCBH candidates only in the TH.1e5 scenario suggest that DCBH formation is a rare event. This is confirmed by recent calculations by Chon et al. (Reference Chon, Hirano, Hosokawa and Yoshida2016, Reference Chon, Hosokawa and Yoshida2018), who explore the formation and collapse of pristine gas clouds in DCBH hosts. They follow a sink-particle scheme in high-density gas and focus on the first 0.1 Myr evolution of the accretion phase of supermassive stars finding that only few gas clouds are able to collapse, while, in most cases, tidal forces of nearby galaxies hinder gas collapse.
A full statistical analysis of the DCBH number density would require much larger high-resolution boxes that are currently beyond computational capabilities. We caution the reader that extrapolations from smaller to larger volumes are dangerous and lead to overestimates of the precise DCBH statistics, because small boxes, like the ones used here, are likely to collapse into one single object at z ≲ 6.
In realistic large-scale cosmological environments, DCBH candidates could be present only around powerful popIII sources that contribute ~10−5 to the total star formation at redshift z ~ 6 (Tornatore et al. Reference Tornatore, Borgani, Dolag and Matteucci2007), or lower (Wise et al. Reference Wise, Abel, Turk, Norman and Smith2012a). Thus, if one DCBH formed in our box and grew up to masses of 109 M⊙ by z ~ 6, we should infer an upper limit to the DCBH abundance of < 2.7 × 10−5 Mpc−3. The lower limit for the observed number density of supermassive black holes powered by masses of ~1–2 × 109 M⊙ at z ~ 6 is ≳1.1 × 10−9 Mpc−3 (Venemans et al. Reference Venemans2013). This means that possible values for DCBH number densities should be bracketed within the range ~10−9 -10−5 Mpc−3. The present-day number density of active galactic nuclei is about 10−4 Mpc−3 (Shankar Reference Shankar2009; Johnson et al. Reference Johnson, Whalen, Li and Holz2013) which is higher than our estimate and makes unlikely that all present-day supermassive black holes are originated from DCBHs, consistently with Sugimura et al. (Reference Sugimura, Omukai and Inoue2014) and Habouzit et al. (Reference Habouzit, Volonteri, Latif, Dubois and Peirani2016b). They could explain at least part of the population, though. Previous semi-analytic works in the literature (e.g. Dijkstra, Ferrara, & Mesinger Reference Dijkstra, Ferrara and Mesinger2014) had highlighted the rarity of DCBH events based on the necessary assumptions mentioned at the beginning of this paper. In light of our results, their estimates must be interpreted as upper limits for the actual occurrence of DCBHs, since we find that only one-third of the haloes where the necessary conditions are met could lead to pure DCBHs. This is in line with numerical results by Latif et al. (Reference Latif, Bovino, Grassi, Schleicher and Spaans2015), who found that DCBH host candidates could host merger events.
Furthermore, Latif & Volonteri (Reference Latif and Volonteri2015) have found in numerical simulations of isolated structures that rotational motions should not halt the formation of DCBHs, although we caution that dynamical effects might be responsible for lowering the resulting collapsed mass of about 20% or more, as a consequence of unbound gas escaping from the potential wells. Independently from that, turbulence will always be present, possibly slowing down gas collapse. From these considerations it emerges that most of the gas mass in the halo candidates should collapse under a very turbulent regime, with mean square velocities close to the local sound speed.
At variance with the conventional gas direct-collapse proposal, Mayer et al. (Reference Mayer, Kazantzidis, Escala and Callegari2010) suggested that the formation of supermassive black holes of 108 – 109 M⊙ could occur simply via major mergers of gas-rich galaxies at z > 6 and no need to suppress cooling and star formation. Crucial ingredients of such conjecture are a temperature floor of 2 × 104 K, to mimic turbulence pressure support, and a rapidly accreting nuclear disks due to efficient angular momentum loss during mergers. In their actual calculations, performed with the Gasoline code, radiative cooling is shut off at 2 × 104 K to avoid strong gravitational instabilities and widespread fragmentation of gas-rich disks (Kazantzidis et al. Reference Kazantzidis2005). Despite this forcing, it has not been possible to show how two supermassive black holes bind during a galaxy merger with gas because of the difficulty of modelling a wide range of spatial scales (Mayer & Bonoli Reference Mayer and Bonoli2019).
Valiante et al. (Reference Valiante, Schneider, Volonteri and Omukai2016) also investigated semi-analytically the relative role of light and heavy seeds as progenitors of the first supermassive black holes at z > 6. Although light seeds are unlikely to produce large black-hole masses, the authors found a strong dependence on the interplay between chemical, radiative, and mechanical feedback effects, which could easily enhance metal and/or dust cooling. Furthermore, in agreement with our results, they noted the importance of the adopted stellar mass range (IMF) for primordial stars that dramatically affect the history of cold gas.
We expect that primordial baryonic streaming velocities originated at decoupling (Tseliakhovich & Hirata Reference Tseliakhovich and Hirata2010; Maio et al. Reference Maio, Koopmans and Ciardi2011a; Greif et al. Reference Greif, White, Klessen and Springel2011) might delay initial gas evolution, but they have quite modest effects on DCBHs and their hosts (Latif, Niemeyer, & Schleicher Reference Latif, Niemeyer and Schleicher2014a; Hirano et al. Reference Hirano, Hosokawa, Yoshida and Kuiper2017).
The additional presence of early X-ray photons (Inayoshi & Tanaka Reference Inayoshi and Tanaka2015; Latif et al. Reference Latif, Bovino, Grassi, Schleicher and Spaans2015) or cosmic rays (Jasche et al. Reference Jasche, Ciardi and Enßlin2007) might enhance free electrons and H2 formation around 104 K, limiting the role of DCBHs in primordial epochs and lowering the (still vague) expectations for their occurrence (Habouzit et al. Reference Habouzit, Volonteri, Latif, Dubois and Peirani2016b; Smith et al. Reference Smith, Bromm and Loeb2017). This would make the formation of supermassive black hole seeds much more problematic and would complicate the explanation of the observed population of supermassive black holes at z ≃ 7 (Fan et al. Reference Fan, Strauss, Richards and Hennawi2006).
Throughout this work we have assumed a Λ CDM scenario. We warn the reader, though, that in some particular cases (such as for warm dark matter, Maio & Viel Reference Maio and Viel2015), the background cosmological model can influence the baryonic-structure evolution, mostly at higher redshift. This can play a role during the very beginning of the onset of star formation, but in the epochs of interest here baryon evolution tends to dominate and alleviate the discrepancies due either to alternative cosmologies (Maio et al. Reference Maio, Dolag, Meneghetti, Moscardini, Yoshida, Baccigalupi, Bartelmann and Perrotta2006) or to possible non-Gaussianities (see Maio & Iannuzzi Reference Maio and Iannuzzi2011; Maio Reference Maio2011; Maio et al. Reference Maio, Salvaterra, Moscardini and Ciardi2012; Maio & Khochfar Reference Maio and Khochfar2012).
5. Conclusions
In this study, we have tried to quantify DCBH appearance and their host features under three scenarios for primordial radiative emissions. We have considered a scenario of powerful very massive primordial stars (TH.1e5), a scenario with OB-type primordial stars (SL.4e4) and a conservative scenario with solar-like primordial stars (SL.1e4). While in the latter two scenarios newly formed stars are not able to provide sufficient amounts of LW radiation to dissociate molecules in close pristine haloes and to cause DCBH events, in the former one star formation provides enough photons to dissociate H2 in many low-mass haloes. As a result, three DCBH host candidates are identified according to the basic requirements for DCBH formation and studied in detail. They are found in the filamentary structures of the cosmic web with dark-matter masses around a few times 106 M⊙. This means that they are smaller than typical star-forming haloes (which have masses of 107–108 M⊙), but large enough not to be disrupted by nearby feedback effects (as it happens to ≲106 M⊙ haloes). Their evolution is rather complex, because DCBH host candidates present neat evidences of substructure formation, local gas motions, and turbulent patterns. In particular, two-third of the candidates are composed by a main halo and a smaller (bound) satellite. Thus, pure DCBH formation should not be possible, since the satellite should merge with the main halo before or during the direct collapse, inducing gas compression, cooling, and star formation. In all the DCBH host candidates, gas angular momentum, albeit small in average, displays non-null z-component at |ε|~1 or higher. This means that rotational motions are present and some material might escape from the halo and affect the final mass for more than 20%. An important point is related to local turbulence in the primordial halo population, with DCBH host candidates featuring large Reynolds numbers. This is in contrast with a rapid direct collapse of gas into a black hole and implies time delays of the order of ~4–40 Myr. These findings are relevant for the seeding and growth of accreting supermassive black holes at high z and demonstrate that DCBHs could be born in the early Universe only under very particular conditions.
Our results rule out the possibility that primordial solar-like or OB-type stars might have contributed significantly to the establishment of an LW background and to any direct-collapse event. Despite early DCBH host candidates could have existed, it seems difficult to sustain the necessary conditions for their formation for a very long time. Indeed, in most cases such necessary conditions are not sufficient for pure DCBH formation.
Joint efforts of upcoming international facilities devoted to study the seeds of supermassive black holes in the infant and high-energy Universe, such as SKA (Koopmans et al. Reference Koopmans, Pritchard and Mellema2015), ATHENA (Nandra et al. Reference Nandra2013), JWST (Gardner & JWST Science Working Group 2009), E-ELT (Puech et al. Reference Puech, Rosati, Toft, Cimatti, Neichel and Fusco2010; Maiolino et al. Reference Maiolino, Haehnelt, Murphy, Queloz and Origlia2013), WFIRST (Whalen et al. Reference Whalen, Fryer, Holz, Heger, Woosley, Stiavelli, Even and Frey2013), and SPICA (Roelfsema et al. Reference Roelfsema2018), will help shed light on the still many unanswered questions.
Acknowledgements
We warmly acknowledge the anonymous referee for useful and constructive comments that significantly improved the quality of the manuscript. We also acknowledge constructive interactions with S. Chon, M. Habouzit, L. Hernquist, C. Pfrommer, R. Schneider, and M. Volonteri. U. M. acknowledges kind hospitality at the Harvard Smithsonian Center for Astrophysics and, particularly, the Institute for Theory and Computation of the Harvard University, Cambridge, MA (USA). He has completed this work through a research grant awarded by the German Research Foundation (DFG) project no. 390015701 and through the HPC-Europa3 Transnational Access Programme project no. HPC17ERW30. S. B. acknowledges financial support from PRIN-MIUR 2015W7KAWC and the INFN INDARK grant. The numerical simulations and analysis have been performed under the PRACE-2IP programme, grant agreement no. RI-283493, with resources allocated at the NOTUR computing centre, Norway, project no. NN9903K, and supported by the facilities of the Italian Computing Center (CINECA), the Leibniz Institute for Astrophysics and the Max Planck Institute for Astrophysics, Germany. We acknowledge the NASA Astrophysics Data System and the JSTOR archive for their bibliographic tools.
Appendix A
For sake of completeness, here we briefly report results for z = 8.5 DCBH host candidates, as already done and extensively discussed in the main body of the text for z = 9. The mass-weighted temperature map with highlighted DCBH host candidates at z = 8.5 for the run with top-heavy popIII SED is depicted in Figure A1, while, in Figure A2, corresponding density profiles, circularity and angular momentum ratio distributions of the three DCBH host candidates are displayed. As mentioned, these are host haloes different from the ones identified at z = 9.
In Figure A3, expected Reynolds numbers, Re, for both the entire halo population and the DCBH host candidates at z = 8.5 are displayed. Re values have been estimated by following the different approaches discussed in Section 3.8 about Figure 12. The distributions of the Reynolds number estimated at the hsml scale for the three DCBH candidates are shown in Figure A4. The moderately high Re number values point towards a mildly turbulent medium (see discussion in Section 3.8).
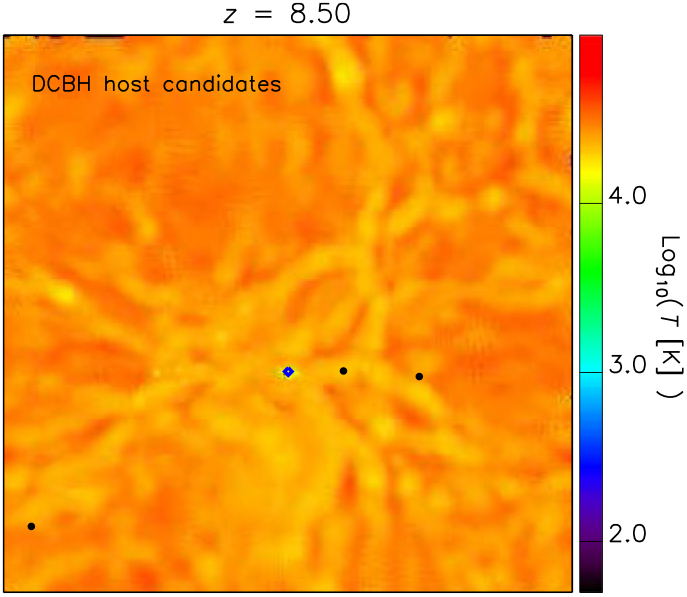
Figure A1. Mass-weighted temperature map and DCBH host candidates (bullet points) identified at z = 8.5 for the run with top-heavy popIII SED.
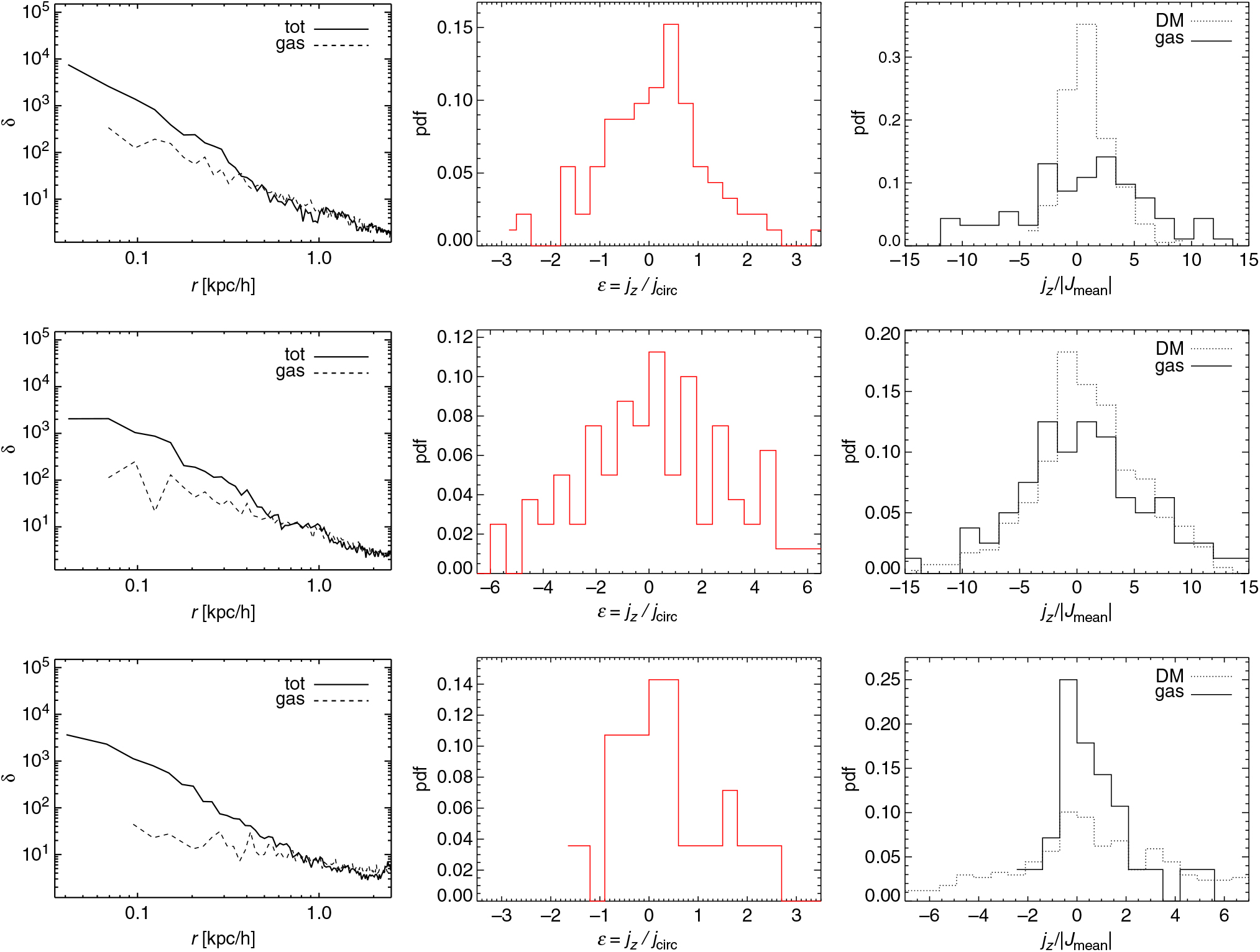
Figure A2. From top to bottom, the distributions of gas and total-matter profiles (left), circularity (centre), and angular momentum ratios (right) of the three DCBH host candidates at z = 8.5 in the run with top-heavy popIII sources (TH.1e5) are shown.
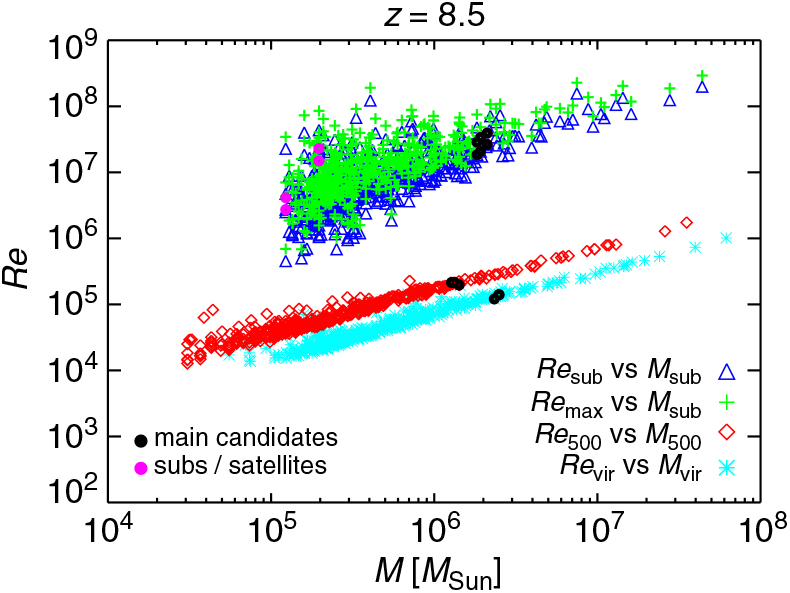
Figure A3. Halo population (symbols) and DCBH host candidates (bullets) Reynolds numbers at redshift z = 8.5 estimated with different approaches (see legends and text in Section 3.8).

Figure A4. Distributions of the Reynolds number estimated at the hsml scale for the three DCBH candidates, namely A (solid line), B (dotted line), and C (dashed line). The distributions are normalised to their peak value. Although identified with the same name, the three DCBH host candidates at z = 8.5 do not correspond to the ones at z = 9 (see discussion in Section 3.8).