Hostname: page-component-848d4c4894-tn8tq Total loading time: 0 Render date: 2024-06-30T04:03:31.307Z Has data issue: false hasContentIssue false
  • English
  • Français

IX.—Harmonic Riemannian Spaces

Published online by Cambridge University Press:  15 September 2014

E. T. Copson  and
H. S. Ruse
Get access

Extract

In this paper we consider a new class of Riemannian spaces which arise in the theory of the solution of the tensor generalisation of Laplace's equation ∇2V = o. To obtain this generalisation Beltrami's second differential parameter is defined in terms of the metric

of the associated n-dimensional Riemannian space by the usual formulæ

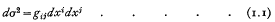
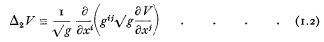
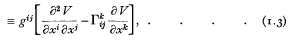
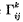where denotes the Christoffel symbol 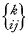. The generalised Laplace's equation is then Δ2V = o. For simplicity the quadratic differential form (1.1) is taken to be positive definite, which involves no essential loss of generality.

Type
Proceedings
Information
Proceedings of the Royal Society of Edinburgh , Volume 60 , Issue 1 , 1940 , pp. 117 - 133
Copyright
Copyright © Royal Society of Edinburgh 1940

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References to Literature.

Blaschke, W., 1924. Vorlesungen über Differentialgeometrie, vol. i, Berlin.Google Scholar
Duschek, A., and Mayer, W., 1930. Lehrbuch der Differentialgeometrie, vol. i (Kurven und Flächen); vol. ii (Riemannsche Geometrie), Leipzig.Google Scholar
Eisenhart, L. P., 1909. Differential Geometry, Boston, Mass.Google Scholar
Eisenhart, L. P., 1926. Riemannian Geometry, Princeton.Google Scholar
Hadamard, J., 1923. Lectures on Cauchy's Problem, New Haven.Google Scholar
McConnell, A. J., 1931. Applications of the Absolute Differential Calculus, London and Glasgow.Google Scholar
Van Mieghem, J., 1932. “Over de partieele differentiaalvergelijking van D'Alembert,” Wis.- en Natuurkundig Tijdschrift, vol. vi, pp. 78–90.Google Scholar
Ruse, H. S., 1930. “On the Elementary Solution of Laplace's Equation,” Proc. Edinburgh Math. Soc. (2), vol. ii, pp. 135–139.Google Scholar
Ruse, H. S., 1939. “Solutions of Laplace's Equation in an n-dimensional Space of Constant Curvature,” Proc. Edinburgh Math. Soc. (2), vol. vi, pp. 24–45.Google Scholar
Schur, F., 1886. “Ueber Räume constanten Krümmungsmaasses, II,” Math. Annalen, vol. xxvii, pp. 537–567.CrossRefGoogle Scholar
Synge, J. L., 1930. “A Characteristic Function in Riemannian Space and its Application to the Solution of Geodesic Triangles,” Proc. London Math. Soc. (2), vol. xxxii, pp. 241–258.Google Scholar
Thomas, T. Y., and Titt, E. W., 1939. “On the Elementary Solution of the General Linear Differential Equation of the Second Order with Analytic Coefficients,” Journ. de Math. pures appl., vol. xviii, pp. 217–248.Google Scholar
Tolman, R. C., 1934. Relativity Thermodynamics and Cosmology, Oxford.Google Scholar
Veblen, O., 1933. Invariants of Quadratic Differential Forms (Cambridge Tract No. 24).Google Scholar
Weatherburn, C. E., 1938. Riemannian Geometry and the Tensor Calculus, Cambridge.Google Scholar