Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-25T05:47:46.140Z Has data issue: false hasContentIssue false
  • English
  • Français

Units of indefinite quaternion algebras

Published online by Cambridge University Press:  14 November 2011

J. H. H. Chalk
J. H. H. Chalk
Affiliation:
University of Toronto, Canada
Get access Rights & Permissions [Opens in a new window]

Synopsis

If ℍ is a rational indefinite quaternion algebra and T is an order of ℍ, let G+(T) denote the subgroup of units u ∊ T with norm n(u) = + 1. For a certain class of orders, Eichler has determined the measure μ(G+(T)) of G+(T), viewed as a Fuchsian group. This is extended to arbitrary orders by methods depending only upon classical number-theory and group theory. As an application, an estimate of the magnitude of a small non-trivial solution of the diophantine Pellian equation

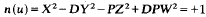
is supplied and the restrictions on the integers D and P associated with previous work on this question are eliminated.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 87 , Issue 1-2 , 1980 , pp. 111 - 126
Copyright
Copyright © Royal Society of Edinburgh 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bachmann, P.. Die Arithmetic der Quadratischen Formen, Erste Abteilung (Leipzig, 1925).Google Scholar
2Chalk, J. H. H.. An estimate for the fundamental solutions of a generalized Pell equation. Math. Ann. 132 (1956), 263–276.CrossRefGoogle Scholar
3Chalk, J. H. H.. Quelques équations de Pell generalisées. CR. Acad. Sci. Paris Sér. A-B 244 (1957), 985–988.Google Scholar
4Chalk, J. H. H.. The number of solutions of congruences in incomplete residue systems. Canad. J. Math. 15 (1963), 291–298.Google Scholar
5Davenport, H.. Cubic forms in 32 variables. Philos. Trans. Roy. Soc. London Ser. A 251 (1959), 193–232.Google Scholar
6Eichler, M.. Lectures on Modular Correspondences. (Bombay: Tata Institute, 1955–56), re-issued 1965.Google Scholar
7Eichler, M.. Allgemeine Kongruenzklasseneinteilungen der Ideale einfacher Algebren über algebraischen Zahlkörpern und ihre L-Reihen. J. Reine Angew. Math. 179 (1938), 227–251.Google Scholar
8Estermann, T.. A new application of the Hardy-Littlewood-Kloosterman method. Proc. London Math. Soc. 12 (1962), 425–444.Google Scholar
9Hey, Frl.K.. Analytische Zahlentheorie in Systemen hyperkomplexer Zahlen (Dissertation, Hamburg, 1929).Google Scholar
10Mordell, L. J.. On the number of solutions in incomplete residue sets of quadratic congruences. Arch. Math. 8 (1957), 153–157.Google Scholar
11Siegel, C. L.. Topics in Complex Function Theory, II (New York: Wiley-Interscience, 1971).Google Scholar
12Siegel, C. L.. Some remarks on discontinuous groups. Ann. of Math. 46 (1945), 708–718 (Theorem 5).CrossRefGoogle Scholar
13Vigneras, M.-F.. Quaternions. Lecture Notes in Mathematics 800 (Berlin: Springer, 1980).Google Scholar
14Tsuji, M.. Theory of Fuchsian groups. Japan J. Math. 21 (1951), 1–27, (cf. Theorem 1 and footnote).CrossRefGoogle Scholar
15Watson, G. L.. Representation of Integers by Indefinite Quadratic Forms. Mathematika 2 (1955), 32–38.Google Scholar
16Watson, G. L.. Quadratic diophantine equations. Philos. Trans. Roy. Soc. London Ser. A 253 (1960), 227–254.Google Scholar