Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-25T17:10:47.731Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillation and variation for the Riesz transform associated with Bessel operators

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  18 September 2018

Huoxiong Wu ,
Dongyong Yang  and
Jing Zhang
Huoxiong Wu
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen 361005, People's Republic of China (huoxwu@xmu.edu.cn; dyyang@xmu.edu.cn)
Dongyong Yang*
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen 361005, People's Republic of China (huoxwu@xmu.edu.cn; dyyang@xmu.edu.cn)
Jing Zhang
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen 361005, People's Republic of China and School of Mathematics and Statistics, Yili Normal College, Yining Xinjiang 835000, People's Republic of China (zjmath66@126.com)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let λ > 0 and let

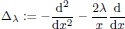
be the Bessel operator on ℝ+ := (0,∞). We show that the oscillation operator 𝒪(RΔλ,∗) and variation operator 𝒱ρ(RΔλ,∗) of the Riesz transform RΔλ associated with Δλ are both bounded on Lp(ℝ+, dmλ) for p ∈ (1,∞), from L1(ℝ+, dmλ) to L1,∞(ℝ+, dmλ), and from L∞(ℝ+, dmλ) to BMO(ℝ+, dmλ), where ρ ∈ (2,∞) and dmλ(x) := x2λ dx. As an application, we give the corresponding Lp-estimates for β-jump operators and the number of up-crossings.

Keywords

oscillationvariationBessel operatorRiesz transform

MSC classification

Primary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Secondary: 42B35: Function spaces arising in harmonic analysis
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 149 , Issue 1 , February 2019 , pp. 169 - 190
Copyright
Copyright © Royal Society of Edinburgh 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)