Hostname: page-component-77c89778f8-sh8wx Total loading time: 0 Render date: 2024-07-20T22:19:01.851Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Titchmarsh–Weyl m -function

Published online by Cambridge University Press:  14 November 2011

B. J. Harris
B. J. Harris
Affiliation:
Department of Mathematical Sciences, Northern Illinois University, Dekalb, Illinois 60115, U.S.A
Get access Rights & Permissions [Opens in a new window]

Synopsis

The Weyl theory assets that there exist circles, possibly degenerate, in the complex plane which are associated with Sturm–Liouville equations. Closely related to these circles is the Titchmarch–Weyl m-function which plays a major role in the theory of Sturm-Liouville equations. In this paper, we investigate the asymptotic behaviour of the m-function and derive results of the form

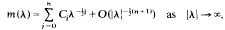
for λ in a certain subset of the compledx plane.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 95 , Issue 3-4 , 1983 , pp. 223 - 237
Copyright
Copyright © Royal Society of Edinburgh 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Akhiezer, N. I.. The classical moment problem (Edinburgh: Oliver and Boyd, 1965).Google Scholar
2Atkinson, F. V.. On the location of the Weyl circles. Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 345–356.CrossRefGoogle Scholar
3Bennewitz, C. and Everitt, W. N.. Some remarks on the Titchmarch-Weyl m-coefficient. In A Tribute to Åke Pleijel, pp. 49–108 (Uppsala: Uppsala Universeitet, 1980).Google Scholar
4Everitt, W. N.. On a property on the m-coefficient of a second order linear differential equation. J. London Math. Soc. 4 (1972), 443–457.CrossRefGoogle Scholar
5Everitt, W. N. and Halvorsen, S. G.. On the asymptotic form of the Titchmarsh–Weyl m-coefficient. Applicable Anal. 8 (1978), 153–169.CrossRefGoogle Scholar
6Harris, B. J.. Bounds for the point spectra of Sturm–Liouville equations. J. London Math. Soc. 25 (1982), 145–161.CrossRefGoogle Scholar
7Harris, B. J.. On the zeros of solutions of differential equations. J. London Math. Soc. to appear.Google Scholar
8Titchmarsh, E. C.. Eigenfunction expansions associated with second order differential equations, Vol. I (Oxford University Press, 1962).Google Scholar
9Weyl, H.. Ueber gewöhnliche differential gleichungen mit singularitaten und die zugehörigen entwicklungen willkurlicher funktion. Math. Ann. 68 (1910), 220–269.CrossRefGoogle Scholar