Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-06-29T21:32:32.185Z Has data issue: false hasContentIssue false
  • English
  • Français

On some infinite integrals involving logarithmic exponential and powers

Published online by Cambridge University Press:  14 November 2011

M. Aslam Chaudhry  and
Munir Ahmad
M. Aslam Chaudhry
Affiliation:
Department of Mathematical Sciences, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia
Munir Ahmad
Affiliation:
Department of Mathematical Sciences, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper we define an integral function Iμ(α; a, b) for non-negative integral values of μ by

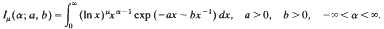
It is proved that the function Iμ(α; a, b) satisfies a functional recurrence-relation which is then exploited to evaluate the infinite integral

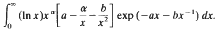
Some special cases of the result are also discussed.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 122 , Issue 1-2 , 1992 , pp. 11 - 15
Copyright
Copyright © Royal Society of Edinburgh 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Aslam, M. Chaudhry and Munir Ahmad. On a new probability function with applications (to appear).Google Scholar
2, Erdélyi et al. Higher Transcendental Functions, vol. 1 (New York: McGraw-Hill, 1953).Google Scholar
3, Erdélyi et al. Tables of Integral Transforms, vol. 1 (New York: McGraw-Hill, 1954).Google Scholar
4Budak, B. M. and Fomin, S. V.. Multiple Integrals, Field Theory and Series (Moscow: Mir Publishers, 1978).Google Scholar
5Gradshteyn, I. S. and Ryzhik, I. M.. Tables of Integrals, Series and Products (New York: Academic Press, 1980).Google Scholar
6Ilyin, V. A. and Poznyak, E. G.. Fundamentals of Mathematical Analysis (Moscow: Nauka, 1967).Google Scholar
7Rahman, M.. On a generalization of the Poisson kernel for Jacobi polynomials. SIAM J. Math. Anal. 8(1977), 1014–1031.CrossRefGoogle Scholar
8Watson, G. N.. A. Treatise on Theory of Bessel Functions (Cambridge: Cambridge University Press, 1966).Google Scholar