Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-25T15:35:13.731Z Has data issue: false hasContentIssue false
  • English
  • Français

On a fourth-order singular integral inequality*

Published online by Cambridge University Press:  14 November 2011

A. Russell
A. Russell
Affiliation:
Department of Mathematics, University of Dundee
Get access Rights & Permissions [Opens in a new window]

Synopsis

The inequality considered in this paper is

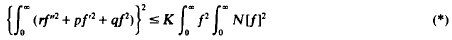
where N is the real-valued symmetric differential expression defined by

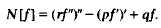
General properties of this inequality are considered which result in giving an alternative account of a previously considered inequality

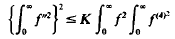
to which (*) reduces in the case p = q = 0, r = 1.

Inequality (*) is also an extension of the inequality

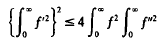
as given by Hardy and Littlewood in 1932. This last inequality has been extended by Everitt to second-order differential expressions and the methods in this paper extend it to fourth-order differential expressions. As with many studies of symmetric differential expressions the jump from the second-order to the fourth-order introduces difficulties beyond the extension of technicalities: problems of a new order appear for which complete solutions are not available.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 80 , Issue 3-4 , 1978 , pp. 249 - 260
Copyright
Copyright © Royal Society of Edinburgh 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Atkinson, F. V.Limit-n criteria of integral type. Proc. Roy. Soc. Edinburgh Sect. A 73 (1975), 167–198.CrossRefGoogle Scholar
2Braaksma, B. L. J., personal communication.Google Scholar
3Brown, B. M. and Evans, W. D.On the limit-point and strong limit-point classification on the 2nth-order differential expressions with wildly oscillating coefficients. Math. Z. 134 (1973), 351–368.CrossRefGoogle Scholar
4Bradley, J. S. and Everitt, W. N.On the inequality ‖f″‖2 ≦ K‖f‖ ‖f (4)‖ Quart. J. Math. Oxford Ser. 25 (1974), 241–52.CrossRefGoogle Scholar
5Eastham, M. S. P.On the L 2 classifications of fourth-order differential equations. J. London Math. Soc. 3 (1971), 297–300.CrossRefGoogle Scholar
6Everitt, W. N.Integrable-square solutions of ordinary differential equations, III. Quart. J. Math. Oxford Ser. 14 (1963), 170–180.Google Scholar
7Everitt, W. N.Some positive definite differential operators. J. London Math. Soc. 43 (1968), 465–473.Google Scholar
8Everitt, W. N.On an extension to an integro-differential inequality of Hardy, Littlewood and Polya. Proc. Roy. Soc. Edinburgh Sect. A 69 (1971), 295–333.Google Scholar
9Everitt, W. N., Giertz, M. and Weidmann, J.Some remarks on a separation and limit-point criterion of second-order ordinary differential expressions. Math. Ann. 200 (1973), 335–346.CrossRefGoogle Scholar
10Everitt, W. N., Hinton, D. B. and Wong, J. S. W.On the strong-limit-n classification of linear ordinary differential expressions of order 2n. Proc. London Math. Soc. 29 (1974), 351–367.Google Scholar
11Hardy, G. H., Littlewood, J. E. and Polya, G.Inequalities (Cambridge: Univ. Press, 1934).Google Scholar
12Kuptsov, N. P.Kilmogorovskie otsenki dlya troizvodnykh v L 2[0,∞). Trudy Mat. Inst. Steklov 138 (1975), 94–117.Google Scholar
13Kumar, V. K.The strong limit-2 case of fourth-order differential equations. Proc. Roy. Soc. Edinburgh Sect. A 71 (1972), 297–304.Google Scholar
14Ljubič, Ju.I.On inequalities between the powers of a linear operator. Amer. Math. Soc. Transl. 40 (1964), 39–84.Google Scholar
15Naimark, M. A.Linear differential operators, II. (New York: Ungar, 1968).Google Scholar
16Russell, A. Integral inequalities and spectral theory of certain ordinary differential operators (Dundee Univ. Ph.D. Thesis, 1975).Google Scholar