Article contents
Multiplicity of positive and nodal solutions for nonlinear elliptic problems in RN
Published online by Cambridge University Press: 14 November 2011
Abstract
We consider the following problem:
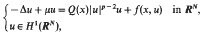
where
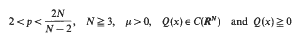
for x ∈ RN, f(x, t), ft (x, t) ∈ C(RN × R), and f (x, t) ≧ 0 for all x ∈ RN and t ∈ R+, f(x, t) is an odd function of t. We show that if the maximum of Q(x) is achieved at k different points of RN, then for μ large enough the above problem has at least k positive solutions and k nodal solutions.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 128 , Issue 5 , 1998 , pp. 1069 - 1097
- Copyright
- Copyright © Royal Society of Edinburgh 1998
References
- 2
- Cited by




